Revisit to the Impacts of Rattlers on Thermal Conductivity of Clathrates

Energy conversion from waste heat to electric power is a promising approach for energy harvest, and the clathrates crystals have received lots of attentions in this field from the concept of “phonon-glass and electron-crystal”. However, the thermal transport mechanisms and roles of rattlers have yet been clearly revealed in clathrates. By using iterative solution of Peierls-Boltzmann transport equation and first principle calculations, we have systematically revisited the thermal transport properties of a simple binary representative of clathrates, Ba₈Si₄₆. Our results confirm that the suppressed phonon lifetime is responsible for the huge reduction of lattice thermal conductivity (κ_l) in clathrates, in addition to the decrease of phonon group velocity. Furthermore, we clarify that phonon scatterings in a wide frequency range and the resonant characteristic scatterings coexist in clathrates, due to the emergence of hybridized modes introduced by the rattlers. We also elucidate that the hybridized modes dramatically suppress the acoustic phonon contribution to κ_l, leading to the non-negligible relative contribution from optical phonon to thermal transport in clathrates. Moreover, the impacts of the hybridized modes on different scattering channels in the phase space are also discussed. Our study provides fundamental physical insights into the impacts of rattlers on thermal conductivity of clathrates, which is valuable toward the design of efficient thermoelectric materials based on the concept of “phonon-glass and electron-crystal.”

Introduction

Thermoelectric devices can convert waste heat into electricity, as a promising approach to address two urgent problems worldwide, energy crisis and greenhouse effect, and thus have received lots of research interests (Zhao et al., 2014; Zhang and Zhao, 2015). There are extensive studies searching for efficient thermoelectric materials, which are required to have low thermal conductivity, high thermopower and electric conductivity simultaneously (Boukai et al., 2008; Zhang et al., 2016). A novel guideline concept, phonon-glass and electron-crystal, is proposed to optimize thermoelectric performance (Slack and Rowe, 1995; Beekman et al., 2015). The previous studies have demonstrated that host-guest systems are ideal platform for this concept, such as clathrates (Takabatake et al., 2014), perovskites (Lee et al., 2017), and skutterudites (Ren et al., 2017), in which the lattice thermal conductivity (κ_l) can be dramatically reduced to a glass-like value while maintaining excellent electric properties. Because of their desirable thermoelectric behaviors, host-guest systems are identified as one of the most promising materials in practical thermoelectric applications.

Clathrates as a class of host-guest system materials exhibit a glass-like extremely low κ_l and promising thermoelectric properties (Pailhès et al., 2014; Tadano et al., 2015; Xi et al., 2017). The rattling of guest atoms induce hybridized modes to the acoustic branch in the phonon dispersion for the host cage, which is identified as the origin for the suppressed κ_l in the clathrates. As a main mechanism, the role of guest atoms has been investigated by numerous experimental and theoretical studies. However, the underlying mechanisms for the rattling effects are still contentious. For instance, the experimental study on Ba₈Ga₁₆Ge₃₀ revealed that the reduction of phonon group velocity around the avoided crossing of the hybridized modes is responsible for the huge reduction of thermal conductivity in clathrates (Christensen et al., 2008). From the harmonic aspects, Pailhès et al. found in Ba₈Si₄₆ clathrate that the suppression mechanism is the localization of propagative phonons (Pailhès et al., 2014). On the other hand, the suppression of phonon lifetime in a wide frequency range and the throughout phase space coupling of rattling modes are also reported (Koza et al., 2008; Tadano et al., 2015). However, a recent experimental work has shown in clathrate Ba_7.81Ge_40.67Au_5.33 that the low-energy acoustic phonons still possess unexpected long lifetimes and dominate the thermal transport in clathrates (Lory et al., 2017). Therefore, further investigations on the clathrates systems are needed to better understand the rattling mechanisms and to further enhance the thermoelectric figure of merit in host-guest systems.

In this work, we revisit the thermal transport properties of clathrates by using the iterative solution of Peierls-Boltzmann transport equation and first principles calculations, which can well grasp the phonon scatterings mechanisms in crystalline solids. Firstly, our results confirm that the suppressed phonon lifetime is responsible for the huge reduction of κ_l in clathrates, in addition to the decrease of phonon group velocity. More interestingly, the combinations of the wide frequency range scatterings and the resonant scatterings scenario together result in the suppression of phonon lifetime. This phenomenon is explained by the variation of scattering channels in the clathrates. Our calculations provide novel physical insights into the reduction of κ_l in clathrates and clarify the underlying scattering mechanisms.

Computational Method and Model

From the solution of Peierls-Boltzmann transport equation (PBTE), the lattice thermal conductivity (κ_l) can be obtained as Li et al. (2014):

$\begin{array}{ll}{\kappa }_l^{\alpha \beta }=\frac{1}{k_B{T}^2\Omega N}{\displaystyle \sum _{\lambda }{n}_0(n_0+1){\left(\hslash {\omega }_{\lambda }\right)}^2{\upsilon }_{\lambda }^{\alpha }{F}_{\lambda }^{\beta },}& (1)\end{array}$

where k_B, T, Ω and N are Boltzmann constant, temperature, the volume of the unit cell, and the number of q points in the first Brillouin zone, respectively. The sum goes over phonon mode λ that consists of both wave vector and phonon branch. n₀ is the equilibrium Bose-Einstein distribution function, ℏ is the reduced Planck constant, ω_λ is the phonon frequency, and ${\upsilon }_{\lambda }^{\alpha }$ is the phonon group velocity in the α direction. The last term $F_{\lambda }^{\beta }$ is expressed as Omini and Sparavigna (1995), Lindsay and Broido (2008), and Li et al. (2014):

$\begin{array}{ll}{F}_{\lambda }^{\beta }={\tau }_{\lambda }^0\left({\upsilon }_{\lambda }^{\beta }+{\Delta }_{\lambda }\right),& (2)\end{array}$

where ${\tau }_{\lambda }^0$ is phonon lifetime of mode λ under the relaxation time approximation (RTA) as obtained from the perturbation theory, and Δ_λ is a correction term that incorporates the inelastic three-phonon scattering processes. As implemented in ShengBTE package (Li et al., 2014), Equation (2) is iteratively solved starting from a zeroth-order approximation under RTA solution, $F_{\lambda }^{\beta }={\tau }_{\lambda }^0{\upsilon }_{\lambda }^{\beta }$. The stopping criterion is that the relative change in the calculated conductivity tensor is less than a configurable parameter. When Δ_λ is equal to zero, the RTA result for thermal conductivity is obtained.

The anharmonic three-phonon scattering process is the dominating phonon scattering mechanism in pristine crystals, which is computed as the inversion of the intrinsic scattering rate (Li et al., 2012):

$\begin{array}{ll}{\tau }_{\lambda }^{ph}=N{({\displaystyle \sum _{{\lambda }^{\prime }{\lambda }^{″}}{\Gamma }_{\lambda {\lambda }^{\prime }{\lambda }^{″}}^{+}+\frac{1}{2}{\displaystyle \sum _{{\lambda }^{\prime }{\lambda }^{″}}{\Gamma }_{\lambda {\lambda }^{\prime }{\lambda }^{″}}^{-}}})}^{-1},& (3)\end{array}$

where λ′ and λ″ denote the second and third phonon mode scattering with the first phonon mode λ, ${\Gamma }_{\lambda {\lambda }^{\prime }{\lambda }^{″}}^{+}$ and ${\Gamma }_{\lambda {\lambda }^{\prime }{\lambda }^{″}}^{-}$ refer to the intrinsic three-phonon scattering rate for absorption process (λ + λ′ → λ″) and emission process (λ → λ′ + λ″), respectively. The linewidth ${\Gamma }_{\lambda {\lambda }^{\prime }{\lambda }^{″}}^{\pm }$ can be calculated from Fermi's Golden Rule (Luo and Chen, 2013) and the third-order force-constant matrix by using ShengBTE software (Li et al., 2014). In addition to the anharmonic phonon-phonon scatterings, the phonon-isotopic scattering is also considered in this work, and the scattering rate is given by Tamura (1983) and Kundu et al. (2011):

$\begin{array}{ll}{\Gamma }_{\lambda {\lambda }^{\prime }}=\frac{\pi {\omega }^2}{2}{\displaystyle \sum _{i\in u.c.}g\left(i\right){\left|e_{\lambda }^{\ast }\left(i\right)·e_{{\lambda }^{\prime }}\left(i\right)\right|}^2}\delta \left({\omega }_{\lambda }-{\omega }_{{\lambda }^{\prime }}\right),& (4)\end{array}$

where $g(i)=\sum _s{f}_s(i){\left[1-M_s(i)/\overline{M}(i)\right]}^2$ is the Pearson deviation coefficient for the mass M_s(i) of isotopes s for atom i (with concentration 0 < f_s(i) ≤ 1) and $\overline{M}(i)=\sum _s{f}_s(i)M_s(i)$ is the average mass. We consider the natural isotopic concentration of Si and Ba atoms, which is taken from the report by Berglund et al. (Berglund and Wieser, 2011), as implemented in ShengBTE package. Finally, all scatterings rate are combined by the Matthiessen rule (Ziman, 1960).

Based on phonon dispersions and Fermi's Golden Rule, the phase space of all possible three-phonon scattering events that conserve both energy and quasi-lattice momentum is determined. The allowed three-phonon scattering processes must satisfy:

$\begin{array}{ll}{\omega }_{\lambda }\left(\overrightarrow{q}\right)\pm {\omega }_{{\lambda }^{\prime }}\left({\overrightarrow{q}}^{\prime }\right)={\omega }_{{\lambda }^{″}}\left({\overrightarrow{q}}^{″}\right);\overrightarrow{q}\pm {\overrightarrow{q}}^{\prime }={\overrightarrow{q}}^{″}+\overrightarrow{G},& (5)\end{array}$

where $\vec{G}$ is the reciprocal lattice vector. It is the normal (N) processes when $\vec{G}=0$, and $\vec{G}\ne 0$ denotes the umklapp (U) processes. In the RTA solution of PBTE, N-processes are incorrectly treated as the same scattering events as the U-processes that contribute to thermal resistance. In contrast, the N-process and U-process can be separately handled in the iterative process, similar to the full solution approach. Moreover, the parameter $W_{\lambda }^{\pm }$ can be used to denote the phase space corresponding to absorption and emission of a given phonon λ, which are defined as the sum of frequency-dependent factors in the expression of three-phonon transition probabilities as following (Li and Mingo, 2015):

$\begin{array}{ll}{W}_{\lambda }^{\pm }=\frac{1}{2N}{\displaystyle \sum _{{\lambda }^{\prime }{\lambda }^{″}}\left\{\begin{array}{l}\begin{array}{l}2(n_{{\lambda }^{\prime }}^0-n_{{\lambda }^{″}}^0)\\ n_{{\lambda }^{\prime }}^0+n_{{\lambda }^{″}}^0+1\end{array}\hfill \end{array}\right\}\frac{\delta \left({\omega }_{\lambda }\pm {\omega }_{{\lambda }^{\prime }}-{\omega }_{{\lambda }^{″}}\right)}{{\omega }_{\lambda }{\omega }_{{\lambda }^{\prime }}{\omega }_{{\lambda }^{″}}}}.& (6)\end{array}$

Our calculations are performed on the simplest representative of clathrates, the type-I clathrate Ba₈Si₄₆, as shown in Figure 1. All phonon calculations were performed by the Vienna ab initio simulation package (VASP) based on density functional theory (Kresse and Furthmüller, 1996). The cut energy of 300 eV was employed on the Ba₈Si₄₆ and Si₄₆ clathrate with 4 × 4 × 4 k-point mesh. For the exchange-correlation functional, the Perdew-Burke-Ernzerhof (PBE) functional was employed. In order to emphasize the accuracy of our calculations and the impact of N-process on thermal transport, we also calculate the κ_l of single-layer graphene with the cut energy of 450 eV and the 16 × 16 × 1 k-point mesh. The harmonic and cubic force constants were obtained by the finite-displacement approach as applied in PHONOPY software (Togo et al., 2008). The cutoff distance in the force constants calculations is up to 5.2 Å, which is large enough to include all essential interactions. Then, the lattice thermal conductivities of Ba₈Si₄₆ and Si₄₆ are calculated, by using ShengBTE software, based on an 8 × 8 × 8 q grid. After sufficient structure optimization, the lattice parameters for Ba₈Si₄₆ and Si₄₆ are 10.25 and 10.22 Å, respectively. Therefore, the Ba filling induces negligible change in the lattice structure, which indicates that there exists only weak interaction between the Ba atom and Si cage. Moreover, a 7 × 7 × 1 supercell is used for graphene to obtain the correct harmonic and anharmonic interatomic force constants, with 48 × 48 × 48 q grid to calculate κ_l. The convergences of q grid and force cut-off are well tested and verified.

FIGURE 1

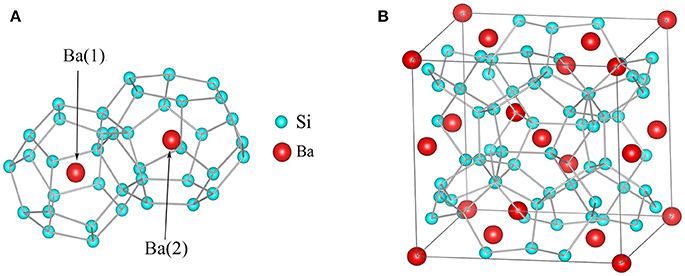
Figure 1. Atomic structure of the type-I clathrate Ba₈Si₄₆. (A) Building units with face sharing large cage BaSi₂₄ and small cage BaSi₂₀. Ba(1) and Ba(2) denote Ba atom in the small and large cage, respectively. (B) The unit cell of crystal structure of Ba₈Si₄₆.

The unit cell of the type-I clathrate compounds is consisted of networked cages formed by nanoscale dodecahedrons with 12 flat faces in the small cage and tetrakaidecahedrons with 14 flat faces in the large cage. Group-I or group-II elements in the periodic table are used as the so-called rattling guest atoms to fill in the cages (Takabatake et al., 2014). The simplest binary type-I clathrate is Ba₈Si₄₆ (Figure 1), in which the guest atom Ba is at the center of the cage (on-center). There are also some other type-I clathrates in which the guest atoms are distributed in the off-center positions away from the cage center, such as Sr and Eu. In this study, we focus on the Ba rattlers in Ba₈Si₄₆ to study the underlying mechanism for the thermal transport in host-guest systems.

Results and Discussion

Phonon Dispersion and Group Velocity

Figure 2A shows the calculation results of the phonon dispersion for Ba₈Si₄₆ (solid line), and for the host-only system Si₄₆ (dashed line). For Ba₈Si₄₆, our calculation result agrees with the experimental data (circles) from literature (Pailhès et al., 2014), which highlights the accuracy of our DFT calculations. In the Ba₈Si₄₆ clathrate, each host Si cage is covalently bonded with nearest neighbor cages while the guest Ba atoms, as rattlers, have non-bonded weak interaction with the host cage. This structure character results in a remarkable feature in phonon dispersion, as show in Figure 2A, that is the existence of the hybridized modes with frequency ω_h as a result of the so-called avoided crossing between the acoustic phonon mode in the host system and the flat guest modes (Nakayama and Kaneshita, 2011). Previous studies (Tse et al., 2001; Pailhès et al., 2014) claimed that the hybridized modes are caused by the rattling of Ba(2) atom in the large cage, which is also confirmed by our calculation of phonon density of states (DOS) in Figure 2B. Moreover, we find that DOS for Ba(2) atom is mainly distributed in the low-frequency region (below 2.5 THz), and is almost separated with the DOS peaks for the host Si atom. This feature suggests Ba(2) atom acts as an independent rattler in the host Si cage, due to the non-bonded weak interaction between Ba(2) guest and the large Si cage. In contrast, DOS for Ba(1) atom exhibits similar peaks to the DOS peaks for Si atom below 4 THz, suggesting a strong vibration coupling between Ba(1) atom and the small Si cage. This observation is further confirmed by examining the interatomic force in our calculations. We find that the coupling force constant between Ba(1) and small Si host cage is more than 12 times stronger than that in the large cage. Furthermore, the complex orientations of tetrakaidecahedrons cages in type-I clathrates result in the broadened frequency distribution of hybridized modes in phonon dispersion (Figure 2A), which is different from the single-frequency hybridized mode in host-guest system of YbFe₄Sb₁₂ (Li and Mingo, 2014). The broadened distribution of hybridized modes can provide more scattering channels for the low frequency acoustic phonons, ${\omega }_h+{\omega }_{low}\to {\omega }_h^{\prime }$.

FIGURE 2

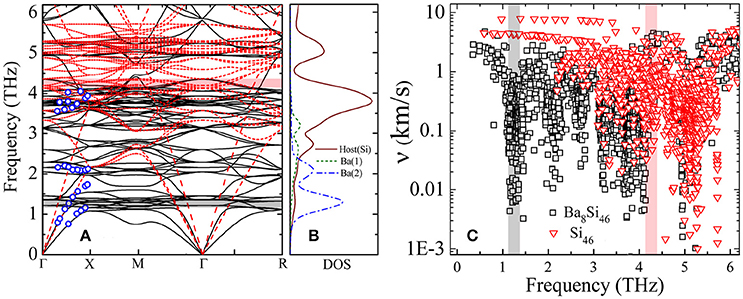
Figure 2. Phonon dispersion and group velocity for Ba₈Si₄₆ and Si₄₆, respectively. (A) Calculation results of phonon dispersion for Ba₈Si₄₆ (solid line) and Si₄₆ (dashed line). The experimental phonon dispersion data for Ba₈Si₄₆ (circle) from literature (Pailhès et al., 2014) is also displayed for comparison. (B) Density of states (DOS) of host Si, Ba(1), and Ba(2) atoms in Ba₈Si₄₆, respectively. (C) Group velocity of Ba₈Si₄₆ and Si₄₆, respectively. The shadowed regions in (A,C) highlight the upper bound of acoustic branches for Ba₈Si₄₆ (black) and Si₄₆ (red), respectively.

The direct impact of the hybridized modes induced by the rattlers in clathrates is the suppression of phonon group velocity, as shown in Figure 2C. Similar to the reports in other clathrates (Tadano et al., 2015), we find that the phonon group velocity of Ba₈Si₄₆ becomes suppressed compared to that of the host-only system Si₄₆, especially for frequency close to the hybridized modes, because of the remarkable phonon softening phenomenon caused by guest atoms. For phonon frequency away from the hybridized modes, the group velocity of other phonon modes is only reduced by several times (see for instance frequency ~0.5 THz), or is even comparable for some frequencies (~5 THz), which is consistent to the retained dispersive (non-flat) modes in phonon dispersion after inserting the guest atom into the host cage (Figure 2A).

Thermal Conductivity

In this work, two kinds of solutions of PBTE, iterative and RTA solutions, are separately performed to compute the κ_l of each structure. The RTA solution improperly treats the N-process and U-process events as the same contribution to thermal resistance. Therefore, it always underestimates κ_l when N-process is stronger than U-process for the indirect participation of N-process in resistive scatterings (Cepellotti and Marzari, 2016; Zhang et al., 2017b). For example, the calculated κ_l of graphene from iterative solution is higher than the RTA prediction, as shown in Figure 3, which is in good agreement with a previous work (Lindsay et al., 2010). More interestingly, the strong N-process in graphene results in hydrodynamic like phonon transport phenomenon (Cepellotti et al., 2015; Lee et al., 2015). However, the impacts of hybridized modes on the selection rules (Eq. 2) for N-process and U-process, respectively, and further on thermal transport are still unknown. Our calculation results in Figure 3 show that there is no difference in the calculated thermal conductivities between two solutions for Ba₈Si₄₆ and Si₄₆ clathrates. Therefore, although the emergence of hybridized modes in clathrates provide more scattering channels for low frequency phonons, and low frequency phonons always dominate the N-process (Lee et al., 2015), it is still less important in clathrates because of the small phonon population in the low-frequency region, as observed from DOS in Figure 2B.

FIGURE 3

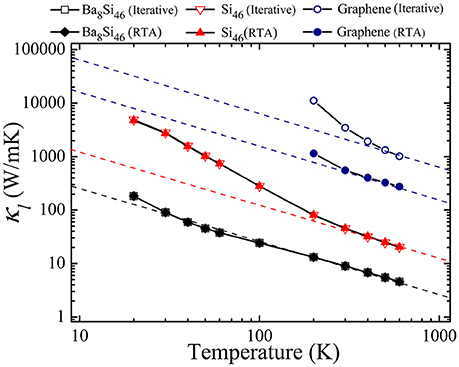
Figure 3. The calculated κ_l for Ba₈Si₄₆ clathrate, host-only system Si₄₆ and graphene vs. temperature, respectively, from iterative solution (empty symbols) and RTA solution (filled symbols). The dashed lines show the corresponding 1/T temperature dependence.

Next, the specific thermal transport properties in clathrates are discussed. Our calculated room temperature κ_l of graphene based on iterative solution is 3475.8 Wm⁻¹K⁻¹, which is in good agreement with previous works (Zhang et al., 2017a) and highlights the accuracy of our PBTE calculations. We can also find in Figure 3 that, compared to the host-only system Si₄₆, the inclusion of guest atoms inside the cages greatly suppresses the κ_l of Ba₈Si₄₆ in the whole temperature range. For instance, the room temperature κ_l of Ba₈Si₄₆ is 8.9 Wm⁻¹K⁻¹, which is much smaller than the value of 45.4 Wm⁻¹K⁻¹ in Si₄₆. In more details, the ratio of κ_l between Si₄₆ and Ba₈Si₄₆ varies from 30 to 4 times for the temperature ranging from 10 to 600 K, and thus the reduction of κ_l is steeply declined with temperature. Moreover, at high temperature, the thermal conductivity of each structure approaches to 1/T dependence (Figure 3), indicating the crystalline nature of on-center clathrates and the dominance of anharmonic phonon-phonon scatterings in clathrates at high temperature.

In order to further explore the suppression effect from the rattling of guest atoms on κ_l, the normalized accumulative thermal conductivities at room temperature vs. phonon frequency are calculated, as shown in Figure 4. The accumulative thermal conductivities in Si₄₆ and Ba₈Si₄₆ both increase sharply in the low-frequency region, corresponding to the significant contributions from acoustic modes. With continuously increasing frequency, the accumulative κ_l in Si₄₆ gradually converges after ~4.2 THz, which corresponds to the upper bound of acoustic branches (red shadowed region in Figure 2)

FIGURE 4

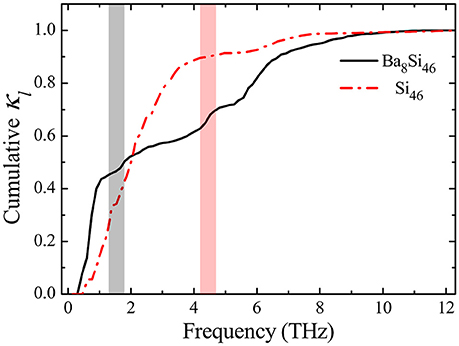
Figure 4. Normalized accumulative thermal conductivities for Ba₈Si₄₆ (solid line) and Si₄₆ (dash-dot line) at room temperature. The shadowed regions highlight the upper bound of acoustic branches for Ba₈Si₄₆ (black) and Si₄₆ (red), respectively.

In the Si₄₆, the total κ_l is dominantly (about 90%) contributed by the acoustic phonons, which is quite common in various crystalline solids due to the large group velocity of acoustic phonons. Surprisingly, our calculations reveal that more than 50% of κ_l in Ba₈Si₄₆ is contributed by optical phonons, as shown in Figure 4. This result highlights the importance of optical phonons to thermal transport in clathrates, which has also been found in silicon nanowires (Tian et al., 2011). This unusual phenomenon is caused by the flattening of acoustic branches by the hybridized modes and the non-negligible group velocity of optical modes in Ba₈Si₄₆ (Figure 2). On the other hand, our additional calculations show that the absolute value of optical phonon contributions to thermal conductivity in Ba₈Si₄₆ and Si₄₆ are 4.9 and 4.8 Wm⁻¹K⁻¹, respectively. Therefore, we can conclude that the dramatic reduction of κ_l in clathrates is originated from the substantial suppression of acoustic phonons via the hybridized modes, which in turn leads to the non-negligible relative contribution to thermal conductivity from optical phonons.

The reduction in κ_l can be directly understood from the reduction in phonon group velocity shown in Figure 2C. Since the reduction in phonon group velocity is highly non-uniform for different frequencies, we compute the averaged phonon group velocity over all phonon modes in Figure 2C. We find that the average phonon group velocity in Si₆₄ is only 1.4 times greater than that in Ba₈Si₄₆, which is much smaller than the thermal conductivity ratio between Si₄₆ and Ba₈Si₄₆ shown in Figure 3 (more than one order of magnitude at low temperature). This suggests that the remarkable reduction in κ_l in clathrates could be mainly caused by other physical mechanisms, in addition to the decrease of phonon group velocity.

Phonon Lifetime

To further search for alternative physical quantity responsible for the significant reduction in κ_l by the rattler, we compare the lifetime of Ba₈Si₄₆ and host-only Si₄₆ based on Equation 3, as shown in Figure 5. It can be found that, compared to less affected optical phonons, the phonon lifetime of acoustic phonon in Si₄₆ is greatly suppressed by guest atoms below ~4.2 THz. In other words, the phonon lifetimes in a wide frequency range are affected by the rattling of guest atoms. Similar behavior is also found in the reduction of phonon group velocity, as discussed above in Figure 2C. This phenomenon coincides well with the experimental and theoretical observation of strong rattling effect in a wide frequency region (Koza et al., 2008; Tadano et al., 2015). However, the extremely low frequency acoustic phonons still exhibit quite large lifetime in the long wavelength limit, which is consistent with the recent report on Ba_7.81Ge_40.67Au_5.33 (Lory et al., 2017).

FIGURE 5

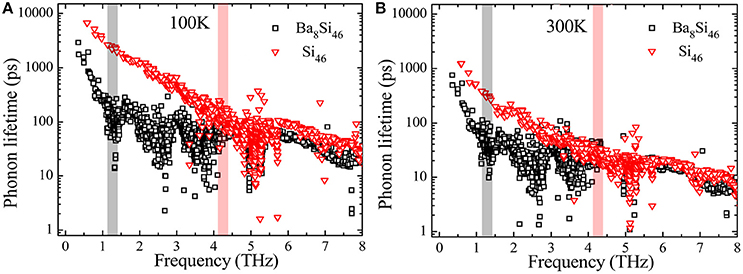
Figure 5. Phonon lifetime for Ba₈Si₄₆ and Si₄₆ at 100 K (A) and 300 K (B), respectively. The shadowed regions highlight the upper bound of acoustic branches for Ba₈Si₄₆ (black) and Si₄₆ (red), respectively.

On the other hand, there exist obvious dips in the phonon lifetime for Ba₈Si₄₆, and the frequencies for the dips correspond to the frequencies of hybridized modes in phonon dispersion (Figure 2A). That is to say, the hybridized modes in clathrates also exhibit the character of resonant scattering scenario, causing substantial drop (by 2 orders of magnitude at 100 K) in phonon lifetime around the frequencies for the hybridized modes. Thus, the combinations of these two scattering mechanisms, a wide frequency suppression of acoustic phonons together with the resonant scattering around hybridized mode frequency, are responsible for the significant suppression of phonon lifetime and thus κ_l in clathrates.

Furthermore, our calculation results show that the phonon lifetimes of Si₄₆ and Ba₈Si₄₆ vary distinctly with temperature, as shown in Figures 5A,B. With temperature increasing from 100 to 300 K, the enhanced anharmonic phonon-phonon scattering leads to suppression of phonon lifetime in Si₄₆ for the full frequency range. However, in the case of Ba₈Si₄₆, the notable suppression of phonon lifetime is only observed for phonon frequencies away from the hybridized mode frequency ω_h, while it is less affected around ω_h, suggesting that resonant scattering with the hybridized mode is the dominant scattering mechanism for phonons around ω_h. As a result, the differences in phonon lifetime between Si₄₆ and Ba₈Si₄₆ are decreased at higher temperature. This also explains the decreasing ratio of κ_l between Si₄₆ and Ba₈Si₄₆ with the increase of temperature (Figure 3).

Phase Space

The suppression of phonon lifetime should be originated from the variation of phonon-phonon scattering channels, which can be evaluated by the phase space in Equation (6), as shown in Figure 6. The W parameter in Figure 6 essentially quantifies the scattering channels for various phonons, with a large value indicating a strong phonon scattering thus a reduced phonon lifetime (Li and Mingo, 2014). One distinct character of hybridized modes is they are nearly non-dispersive, i.e., almost the same frequency for all wavevectors. Due to the emergence of hybridized modes, the scattering channels for both absorption and emission process in Ba₈Si₄₆ increase dramatically compared to that in the host-only system Si₄₆, especially for frequency below ~4.2 THz, which agrees well with the strong suppression frequency region for phonon lifetime (Figure 5) and group velocity (Figure 2C). For the absorption process, the hybridized modes can easily assist the wide range of low frequency phonons to create high frequency phonons, ω_h + ω_low → ω_high. Correspondingly, the phase space for the absorption process is dramatically promoted in a wide frequency range, and no sudden change in W near the hybridized mode frequency is observed for the absorption process in Ba₈Si₄₆. Thus, the phonon lifetime is decreased in a wide frequency range in Ba₈Si₄₆.

FIGURE 6

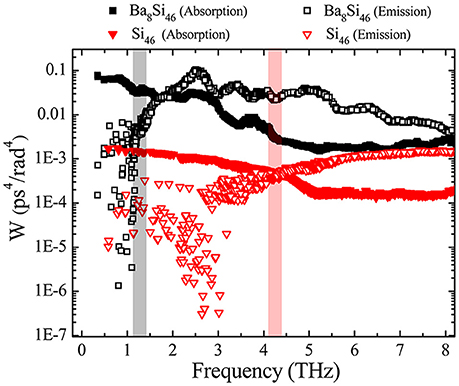
Figure 6. Phase space in Ba₈Si₄₆ and Si₄₆ for the absorption (filled symbols) and emission (empty symbols) process at 100 K. The shadowed regions highlight the upper bound of acoustic branches for Ba₈Si₄₆ (black) and Si₄₆ (red), respectively.

Generally speaking, it is difficult for the low-frequency acoustic phonons to participate in the emission process, because it demands the emission of two even lower frequency phonons that satisfy the quasi-lattice momentum conservation. Therefore, W for the emission process in Si₄₆ is quite low at low frequency, and mainly the optical phonons in Si₄₆ (above the red shadowed region in Figure 6) take part in the emission process (empty triangles in Figure 6). However, in the clathrate Ba₈Si₄₆, the emergence of low-frequency hybridized modes induces two effects on the scattering channels for the emission process. Firstly, it shifts the upper bound of the acoustic branches to a much lower frequency around 1.2 THz (black shadowed region in Figure 6) in Ba₈Si₄₆, causing more than 2 orders of magnitude enhancement for the emission process in Ba₈Si₄₆ for frequency between 1.2 and 4.2 THz compared to that in Si₄₆. Secondly, it also provides additional channels to split a high-frequency acoustic phonon into two lower frequency acoustic phonons, ${\omega }_h+{\omega }_{low}\to {\omega }_{low}^{\prime }$, which can significantly enhance the phonon-phonon scattering around hybridized modes, as shown in Figure 6, corresponding to the dips in phonon lifetime around hybridized modes. In other words, the notable emission process channels raised by hybridized modes lead to great suppression of phonon lifetime around this frequency under the resonant scatterings scenario.

Conclusion

In summary, by iteratively solving Peierls-Boltzmann transport equation with interatomic force constants obtained from first principles calculations, we revisit thermal transport properties for the type-I clathrate Ba₈Si₄₆ and compare with the host-only system Si₄₆. Our results show that the hybridized modes from the rattling of guest atoms dramatically suppress the acoustic phonon contribution to thermal conductivity, leading to the non-negligible contribution from optical phonons to the thermal transport in clathrates. Our further analysis confirms that the suppressed phonon lifetime is responsible for the reduction of thermal conductivity, in addition to the decrease in phonon group velocity. Furthermore, the emergence of hybridized modes not only provides scattering channels for a wide frequency range of acoustic phonons, but also effectively participates in the emission process. Therefore, we clarify that two types of suppression in phonon lifetime, in a wide frequency range and around the hybridized modes frequency under resonant scatterings scenario, both take place in Ba₈Si₄₆. Our calculations provide physical insight into the reduction of thermal conductivity in clathrates and clarify the underlying scattering mechanisms. Based on our results, we also expect that the thermal conductivity of clathrates can be further suppressed by effectively engineering the optical phonons.

Author Contributions

CC: Performed all the simulations and data analysis; ZZ and JC: Conceived and supervised the study. All of the authors wrote the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This project is supported in part by the grants from the National Key Research and Development Program of China (Grant No. 2017YFB0406000), the National Natural Science Foundation of China (Grant Nos. 51506153 and 11334007), and Science and Technology Commission of Shanghai Municipality (Grant No. 17ZR1448000). JC acknowledges support from the National Youth 1,000 Talents Program in China, and the startup grant at Tongji University. The authors thank the National Supercomputing Center in Guangzhou (NSCC-GZ) for the computing resources.

References

Beekman, M., Morelli, D. T., and Nolas, G. S. (2015). Better thermoelectrics through glass-like crystals. Nat. Mater. 14, 1182–1185. doi: 10.1038/nmat4461

PubMed Abstract | CrossRef Full Text | Google Scholar

Berglund, M., and Wieser, M. E. (2011). Isotopic compositions of the elements 2009 (IUPAC technical report). Pure Appl. Chem. 83, 397–410. doi: 10.1351/PAC-REP-10-06-02

CrossRef Full Text | Google Scholar

Boukai, A. I., Bunimovich, Y., Tahir-Kheli, J., Yu, J. K., Goddard, W. A. III, and Heath, J. R. (2008). Silicon nanowires as efficient thermoelectric materials. Nature 451, 168–171. doi: 10.1038/nature06458

PubMed Abstract | CrossRef Full Text | Google Scholar

Cepellotti, A., Fugallo, G., Paulatto, L., Lazzeri, M., Mauri, F., and Marzari, N. (2015). Phonon hydrodynamics in two-dimensional materials. Nat. Commun. 6:6400. doi: 10.1038/ncomms7400

PubMed Abstract | CrossRef Full Text | Google Scholar

Cepellotti, A., and Marzari, N. (2016). Thermal transport in crystals as a kinetic theory of relaxons. Phys. Rev. X 6:041013. doi: 10.1103/PhysRevX.6.041013

CrossRef Full Text | Google Scholar

Christensen, M., Abrahamsen, A. B., Christensen, N. B., Juranyi, F., Andersen, N. H., Lefmann, K., et al. (2008). Avoided crossing of rattler modes in thermoelectric materials. Nat. Mater. 7, 811–815. doi: 10.1038/nmat2273

PubMed Abstract | CrossRef Full Text | Google Scholar

Koza, M. M., Johnson, M. R., Viennois, R., Mutka, H., Girard, L., and Ravot, D. (2008). Breakdown of phonon glass paradigm in La- and Ce-filled Fe4Sb12 skutterudites. Nat. Mater. 7, 805–810. doi: 10.1038/nmat2260

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186. doi: 10.1103/PhysRevB.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

Kundu, A., Mingo, N., Broido, D. A., and Stewart, D. A. (2011). Role of light and heavy embedded nanoparticles on the thermal conductivity of SiGe alloys. Phys. Rev. B 84:125426. doi: 10.1103/PhysRevB.84.125426

CrossRef Full Text | Google Scholar

Lee, S., Broido, D., Esfarjani, K., and Chen, G. (2015). Hydrodynamic phonon transport in suspended graphene. Nat. Commun. 6:6290. doi: 10.1038/ncomms7290

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, W., Li, H., Wong, A. B., Zhang, D., Lai, M., Yu, Y., et al. (2017). Ultralow thermal conductivity in all-inorganic halide perovskites. Proc. Natl. Acad. Sci. U.S.A. 114, 8693–8697. doi: 10.1073/pnas.1711744114

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, W., Carrete, J. A., Katcho, N., and Mingo, N. (2014). ShengBTE: a solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 185, 1747–1758. doi: 10.1016/j.cpc.2014.02.015

CrossRef Full Text | Google Scholar

Li, W., Lindsay, L., Broido, D. A., Stewart, D. A., and Mingo, N. (2012). Thermal conductivity of bulk and nanowire Mg₂Si_xSn₁-xalloys from first principles. Phys. Rev. B 86:174307. doi: 10.1103/PhysRevB.86.174307

CrossRef Full Text | Google Scholar

Li, W., and Mingo, N. (2014). Thermal conductivity of fully filled skutterudites: role of the filler. Phys. Rev. B 89:184304. doi: 10.1103/PhysRevB.89.184304

CrossRef Full Text | Google Scholar

Li, W., and Mingo, N. (2015). Ultralow lattice thermal conductivity of the fully filled skutteruditeYbFe4Sb12due to the flat avoided-crossing filler modes. Phys. Rev. B 91:144304. doi: 10.1103/PhysRevB.91.144304

CrossRef Full Text | Google Scholar

Lindsay, L., and Broido, D. A. (2008). Three-phonon phase space and lattice thermal conductivity in semiconductors. J. Phys. Condens. Matter 20:165209. doi: 10.1088/0953-8984/20/16/165209

CrossRef Full Text | Google Scholar

Lindsay, L., Broido, D. A., and Mingo, N. (2010). Flexural phonons and thermal transport in graphene. Phys. Rev. B 82:115427. doi: 10.1103/PhysRevB.82.115427

CrossRef Full Text | Google Scholar

Lory, P. F., Pailhès, S., Giordano, V. M., Euchner, H., Nguyen, H. D., Ramlau, R., et al. (2017). Direct measurement of individual phonon lifetimes in the clathrate compound Ba7.81Ge40.67Au5.33. Nat. Commun. 8:491. doi: 10.1038/s41467-017-00584-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, T., and Chen, G. (2013). Nanoscale heat transfer–from computation to experiment. Phys. Chem. Chem. Phys. 15, 3389–3412. doi: 10.1039/c2cp43771f

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakayama, T., and Kaneshita, E. (2011). Significance of off-center rattling for emerging low-lying THz modes in Type-I clathrates. J. Phys. Soc. Jpn. 80:104604. doi: 10.1143/JPSJ.80.104604

CrossRef Full Text | Google Scholar

Omini, M., and Sparavigna, A. (1995). An iterative approach to the phonon Boltzmann equation in the theory of thermal conductivity. Phys. B Condens. Matter 212, 101–112. doi: 10.1016/0921-4526(95)00016-3

CrossRef Full Text | Google Scholar

Pailhès, S., Euchner, H., Giordano, V. M., Debord, R., Assy, A., Gomès, S., et al. (2014). Localization of propagative phonons in a perfectly crystalline solid. Phys. Rev. Lett. 113:025506. doi: 10.1103/PhysRevLett.113.025506

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, W., Geng, H., Zhang, Z., and Zhang, L. (2017). Filling-fraction fluctuation leading to glasslike ultralow thermal conductivity in caged skutterudites. Phys. Rev. Lett. 118:245901. doi: 10.1103/PhysRevLett.118.245901

PubMed Abstract | CrossRef Full Text | Google Scholar

Slack, G. A., and Rowe, D. (1995). CRC Handbook of Thermoelectrics. Boca Raton, FL: CRC.

Tadano, T., Gohda, Y., and Tsuneyuki, S. (2015). Impact of rattlers on thermal conductivity of a thermoelectric clathrate: a first-principles study. Phys. Rev. Lett. 114:095501. doi: 10.1103/PhysRevLett.114.095501

PubMed Abstract | CrossRef Full Text | Google Scholar

Takabatake, T., Suekuni, K., Nakayama, T., and Kaneshita, E. (2014). Phonon-glass electron-crystal thermoelectric clathrates: experiments and theory. Rev. Mod. Phys. 86, 669–716. doi: 10.1103/RevModPhys.86.669

CrossRef Full Text | Google Scholar

Tamura, S.-I. (1983). Isotope scattering of dispersive phonons in Ge. Phys. Rev. B 27, 858–866. doi: 10.1103/PhysRevB.27.858

CrossRef Full Text | Google Scholar

Tian, Z., Esfarjani, K., Shiomi, J., Henry, A. S., and Chen, G. (2011). On the importance of optical phonons to thermal conductivity in nanostructures. Appl. Phys. Lett. 99:053122. doi: 10.1063/1.3615709

CrossRef Full Text | Google Scholar

Togo, A., Oba, F., and Tanaka, I. (2008). First-principles calculations of the ferroelastic transition between rutile-type andCaCl₂-typeSiO₂at high pressures. Phys. Rev. B 78:134106. doi: 10.1103/PhysRevB.78.134106

CrossRef Full Text | Google Scholar

Tse, J. S., Li, Z., and Uehara, K. (2001). Phonon band structures and resonant scattering in Na₈Si₄₆ and Cs₈Sn₄₄ clathrates. Europhys. Lett. 56:261. doi: 10.1209/epl/i2001-00515-8

CrossRef Full Text | Google Scholar

Xi, Q., Zhang, Z., Chen, J., Zhou, J., Nakayama, T., and Li, B. (2017). Hopping processes explain linear rise in temperature of thermal conductivity in thermoelectric clathrates with off-center guest atoms. Phys. Rev. B 96:064306. doi: 10.1103/PhysRevB.96.064306

CrossRef Full Text | Google Scholar

Zhang, X., and Zhao, L.-D. (2015). Thermoelectric materials: energy conversion between heat and electricity. J. Mater. 1, 92–105. doi: 10.1016/j.jmat.2015.01.001

CrossRef Full Text | Google Scholar

Zhang, Z., Chen, J., and Li, B. (2017a). Negative Gaussian curvature induces significant suppression of thermal conduction in carbon crystals. Nanoscale 9, 14208–14214. doi: 10.1039/C7NR04944G

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., Xie, Y., Ouyang, Y., and Chen, Y. (2017b). A systematic investigation of thermal conductivities of transition metal dichalcogenides. Int. J. Heat Mass Transf. 108, 417–422. doi: 10.1016/j.ijheatmasstransfer.2016.12.041

CrossRef Full Text | Google Scholar

Zhang, Z., Xie, Y., Peng, Q., and Chen, Y. (2016). A theoretical prediction of super high-performance thermoelectric materials based on MoS₂/WS₂ hybrid nanoribbons. Sci. Rep. 6:21639. doi: 10.1038/srep21639

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, L. D., Lo, S. H., Zhang, Y., Sun, H., Tan, G., Uher, C., et al. (2014). Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 508, 373–377. doi: 10.1038/nature13184

PubMed Abstract | CrossRef Full Text | Google Scholar

Ziman, J. M. (1960). Electrons and Phonons: the Theory of Transport Phenomena in Solids. Oxford: Oxford University Press.

Google Scholar