Experimental Study on the Condensation of Steam With Air Out of the Vertical Tube Bundles

In this paper, experimental study was carried out in an open natural circulation loop, to figure out the condensation heat transfer characteristic on the outside of the vertical pipe tube bundle and single- tube. Condensation heat transfer coefficients have been obtained under the wall subcooling ranging from 5 to 22°C, total pressure ranging from 0.3 to 0.6 MPa and air mass fraction ranging from 0.05 to 0.65. The influence of mixed gas pressure, condensate depression of walls, and content of non-condensable gas on the condensation heat transfer performance is analyzed. Under the condition of the same air mass fraction, the condensation heat transfer coefficient increases with the increase of pressure. Also, as the air mass fraction is more than 30%, the effect of pressure will be weakened. The heat transfer features of pipe bundle and single tube is compared and studied, and an empirical correlation of the pipe bundle for the heattransfer coefficient is developed, covered all data points within 10%. According to the research results, heat transfer coefficient for pipe bundle decreases with the increase in non-condensable gas quality and wall subcooling, but increases with the increase in pressure.

Introduction

In recent years, with the public's increasing concerns over the safety of the nuclear power plant,full deterministic evidence of evidence of nuclear power plants (NPP) safety is required (Wang et al., 2014), more natural circulation systems were applied in the designs of the advanced nuclear plants, because of the inherent passive safety. For example, Hualong Pressurized water reactor, Chinese Generation III nuclear reactor, uses an open natural circulation as the passive containment cooling system (PCCS) (Lakshmanan and Pandey, 2009). PCCS, which is one of the most important part in protecting the integrity of the containment under serve accidental conditions, can remove the heat in the containment by the condensation of steam over the specific heat transfer surface (Yu et al., 2008; Ye et al., 2012). The operating pressure of the open natural circulation is atmosphere pressure. It can make the vaporizing process easily occur and has a faster startup time.

However, the flow rate of the cooling water is constantly changing in the natural circulation process which is different from the forced circulation cooling water loop. Therefore, in order to understand the steam condensation phenomenon with non-condensing gas under the condition of natural circulation, and to provide the reliable empirical data and analysis models for the practical engineering applications, a more detailed research of the effect of the steam condensation is necessary.

Dehbi et al. (Dehbi, 1991) investigated the condensation phenomenon of steam with no-condensing gas in a vertical tube, and the calculation models of forced convection, natural convection and mixed convection were then established, which can be used to evaluate the effect of the molecular weight, the non-condensing gas content, the mixed gas pressure, the inlet flow rate of mixed gas et al. on the steam condensation process; Liu et al. (2000) conducted significant experimental research on the steam condensation process including the effect of non-condensing gas for the PCCS system of nuclear power plant, and evaluated the thermal elimination ability of the passive containment cooling system; Dehbi used the experimental model to calculate the total heat transfer for uncondensed gas vapor condensing outside the vertical tube and establishing forced convection, natural convection and mixed convection conditions. By using this model, the influence of non-condensable gas molecular weight, non-condensable gas content, mixed gas pressure and mixed gas inlet flow rate on the steam condensing can be judged. A large number of experimental studies have been conducted on the vapor condensation of gases by Liu, and the heat elimination capabilities of passive containment cooling systems have been evaluated (Wang, 2014; Su, 2016); Although the experiments of Liu and Dehbi took into account many factors, they had opposite results on the effect of undercooling on the heat transfer coefficient of the condensation.

Othmer (1929) carried out research by placing a single brass tube in stationary vapor atmosphere, and the empirical equations for the heat transfer coefficient correlated with the air volume and the supercooling degree of the tube surface had been further obtained. Ivashchenco (1989) carried out an experimental study on the condensation heat transfer process outside the vertical single tube with vapor containing nitrogen under the pressure of 0.5 MPa, the results showed that the heat transfer coefficient decreased rapidly with the increase of non- condensing gas content. Also, the empirical equations obtained by Uchida (Uchida et al., 1964; Tagami, 1965) associated the decrement of the condensation heat transfer coefficient with the percentage of air weight together. Zhuang et al. (2000) investigated the condensation heat transfer characteristics of the horizontal tube bundles and further analyzed the effect of cooling water flow rate as well as the impact of the mass fraction of non-condensing gas on condensation heat transfer of the tube bundles.

Despite of many contributions have been made, the previous research shows that the studies of the condensation heat transfer process mainly focus on the single tube and horizontal tube bundles. However, it is quite shortage for the experimental studies of condensation outside vertical tube bundles, especially with an open natural circulation.

In order to investigate the impact of various parameters on the external condensation heat transfer of tube bundles and obtain the empirical equations with the corresponding parameter ranges, experimental studies for the natural convection condensation process of vertical tube bundles and a single tube are carried out in this paper.

The Experiment System

The experiment system mainly consists of steam supply equipment, experimental vessel as well as its inner heat transfer tubes, water tank, experimental pipes and measuring instruments, as shown in Figure 1.

FIGURE 1

Figure 1. Diagram of the experimental system.

The internal diameter and the height of the experimental vessel are 416 and 3,550 mm, respectively. In the tube bundle experiment, the heating section consists of three parallel uniform stainless steel tubes with the inside and outside diameters of 34 and 38 mm separately, whose tube spacing and length are 45.76 and 2,234 mm, respectively. The inside and outside diameters of the heat transfer tube in the single tube experiment are identical with that of the heat transfer tubes in the tube bundle experiment.

The internal pressure of the experimental vessel is measured by a pressure sensor with a precision of 0.075%. Cooling water flux is measured by an electromagnetic flowmeter with a precision of 0.5%, and measuring range is−30~30 m3/h. Steam flow measurement is achieved by the use of two vortex flowmeters with a precision of 0.75%, and measuring range are 0~120 m3/h and 0~40 m3/h, respectively. At the inlet and outlet of the experimental section, the temperatures of cooling water are measured by installing one nickel chromium-nickel silicon thermocouple.

The distribution of thermocouples in the experimental vessel is shown in Figure 2. Figure 2A shows thermocouples distribution in the single tube experimental vessel, and the thermocouples are vertically welded on the 9 cross sections of the experiment tube section (A~I). Two thermocouples are symmetrically installed on the wall of each section. Meanwhile, one of the thermocouples is installed on each section to measure the temperature of the main mixture stream. In the experimental section of tube bundle, the thermocouples are vertically welded on the 5 cross sections (A~E), as shown in Figure 2B. Two thermocouples are installed on each section of the bracket which is arranged on the left and right pipes. For measuring the main temperature, two thermocouples are welded on both side of each tube in each section to measure wall temperature. A thermocouple is welded in the middle of the inlet and outlet header to measure the temperature of inlet and outlet header.

FIGURE 2

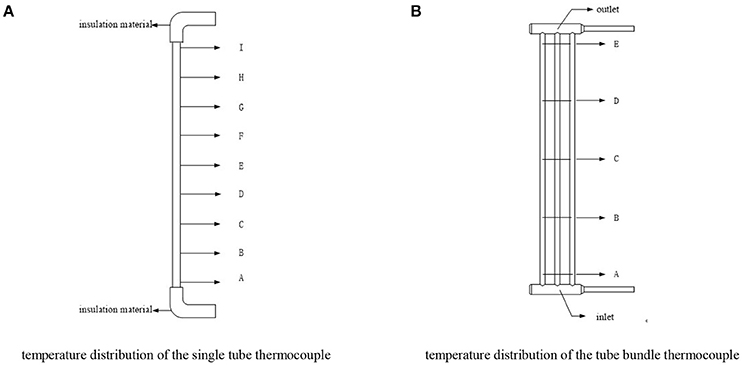
Figure 2. Distribution of the thermocouple (A) temperature distribution of the single tube thermocouple. (B) temperature distribution of the tube bundle thermocouple.

Experimental Data Processing

The steam heat transfer rate through the tube is equal to the cooling water heat transfer rate, which is determined by the cooling water temperature change and the mass flow rate in the tube. The bulk temperature and the wall temperature as well as cooling water temperature are measured by themocouples. The bulk temperature and the wall temperature as well as cooling water temperature are measured by thermocouples. The enthalpy of cooling water is obtained from steam properties table. The flowrate of the cooling water is also measured by turbine flowmeter. Hence, the average heat transfer coefficient can be expressed as:

$\begin{array}{ll}h=\frac{M\left(h_{gi}-h_l\right)}{A\left(T_b-T_W\right)}& (1)\end{array}$

where M is the mass flow rate of the steam, kg/s; h_gi and h_l are the saturated steam enthalpy value and the condensate enthalpy value, kj/kg; A is the surface area of the heat transfer tube, m²; T_b and T_w are standing for the mainstream temperature of the mixed gas and the outer surface temperature of the experimental tube, °C.

According to the measurement error of each instrument in the experiment, the total measurement error of the average heat transfer coefficient is < 15%.

The non-condensable air quality can be calculated as:

Firstly, calculate the gas composition according to the Dalton partial pressure law:

$\begin{array}{ll}\frac{N_a}{N_s}=\frac{P_a}{P_s}& (2)\end{array}$

Then, the non-condensable air quality:

$\begin{array}{l}{\omega }_a=\frac{m_a}{m_a+m_s}=\frac{29n_a}{29n_a+18n_s}=\frac{29p_a}{29P_a+18P_s}\\ =\frac{29(P-P_a)}{29(P-P_a)+18P_s}=\frac{29P-29P_s}{29P-11P_s}& (3)\end{array}$

m is the mass, kg; n is the number of molecules, mol; M is the molecular weight; a is air; s is steam. The total pressure P is accurately collected by a pressure transmitter that condenses the experimental section.

When the saturated steam enters the condensation experimental section, the saturated steam becomes superheated steam due to the decrease of the partial pressure of the steam, and the cooling water will cool the superheated steam during the flow along the path so that the superheat loss is lost. Therefore, there is a certain degree of overheating in the process. However, since the condensation heat transfer coefficient is less affected by the superheat of the steam, it can be assumed that the steam is saturated. The partial pressure of steam can be obtained by checking the table of saturated steam properties, the formula is:

$\begin{array}{ll}{P}_s=f(T_s)& (4)\end{array}$

Therefore, the non-condensable air quality is expressed as

$\begin{array}{ll}{\omega }_a=\frac{29P-29f(T_s)}{29P-11f(T_s)}& (5)\end{array}$

Analysis of Experimental Results

The Effect of Supercooling Degree of the Tube Surface

In the condensation process, the pressure and the air mass fraction will have a great influence on the supercooling degree of the tube surface. The single impact of supercooling degree on the condensation heat transfer coefficient cannot be investigated precisely as the above two parameters vary. Therefore, we choose two start-up conditions for studying the effect of supercooling degree of the tube surface. One set of parameters are that the tube surface pressure P is 0.6 MPa and the air mass fraction W_a is 75%. The other set of parameters are that the tube surface pressure P is 0.5 MPa and the air mass fraction W_a is 75%.

As is shown in Figure 3, it can be known that the condensation heat transfer coefficient of the tube bundle decreases with the increase of the supercooling degree of the tube surface, and increases with the increase of pressure, which is similar to the trend of Dehbi correlation. The thickness of the condensation film will increase gradually with the increment of supercooling degree of the tube surface, which increases the heat and mass transfer resistance and leads to a decrease of the condensation heat transfer coefficient.

FIGURE 3

Figure 3. Effect of wall subcooling on the condensation heat transfer coefficient.

The Effect of Mixed Gas Pressure and the Mass Fraction of Air

The experimental study for the steam condensation heat transfer process is carried out under the conditions of different pressure and air mass fraction. As is shown in Figure 4, under the condition of constant pressure, the condensation heat transfer coefficient decreases with the increase of air mass fraction, and the rate of descent decreases gradually. However, under the condition of the same air mass fraction, the condensation heat transfer coefficient increases with the increase of pressure, which is consistent with the results in Figure 3. Also, as the air mass fraction is more than 30%, the effect of pressure will be weakened. This trend is due to the competition between gas pressure impact and air content impact. The partial pressure of the steam rises and saturation temperature increases accordingly along with the increment of mixture gas pressure, which strengthens the heat transfer. But the non-condensing gas layer will thickened due to the higher air content, which further leads the deterioration of heat transfer.

FIGURE 4

Figure 4. Change curve of air mass fraction with condensation heat transfer coefficient.

A Comparison of Heat Transfer Characteristics of the Tube Bundle and the Single Tube

Figure 5 shows the curve of the condensation heat transfer coefficient of the tube bundle and the single tube. The result indicate that the heat transfer coefficient of the tube bundle is higher than that of the single tube while the air content is low, but the heat transfer coefficient of the tube bundle will decrease rapidly with the air mass fraction grows, whereas the descending rate of the heat transfer coefficient of the single tube will decrease more slowly. After the air mass fraction reaches 40%, the heat transfer coefficient of the tube bundle will be almost consistent with that of the single. There are two main factors that affect the difference of heat transfer characteristics of the single tube and tube bundle: The steam flow rate of tube bundle is higher than that of the single tube in the experiment; The surface of the tube bundle in the process of condensation is covered by a convergence of non-condensing gas layer in the gap, which will lead to a heat transfer deterioration. Figure 5 shows that the heat transfer coefficient of tube bundle is better than that of single tube, especially when the air content is low. This could be due to the steam flow rate of the tube bundle is greater than that of the single tube in the experiment, the higher steam flow rate near the tube surface may destroy the non-condensing gas layer and reduce the thermal resistance, thus the heat transfer coefficient is then strengthened. However, with the increase of non-condensing gas content, the convergence phenomenon of the non-condensing gas layer in the tube bundle gap will be more obvious, which is equivalent to add a layer of condensation heat transfer thermal resistance on the surface of the vertical tube, so the condensation heat transfer coefficient then decreases, the heat exchange amount is reduced, and the steam flow rate of the decreases accordingly, which leads to a further deterioration of the heat transfer.

FIGURE 5

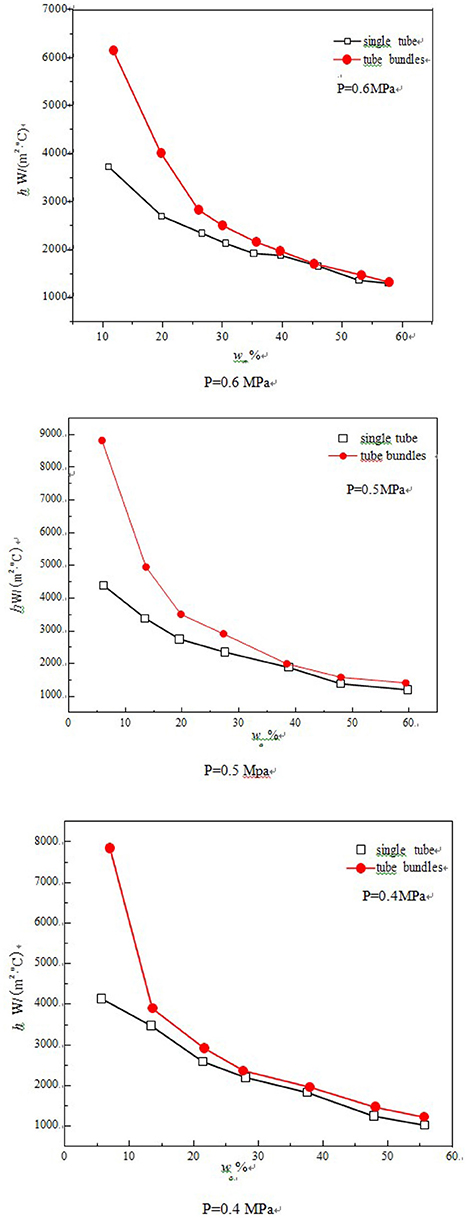
Figure 5. Comparison of condensation heat transfer coefficient between single tube and tube bundles.

The Derivation for Calculation Relations

As can be seen in Figure 6, we have compared the experimental values of condensation heat transfer coefficient with Liu' and Dehbi's correlations under the pressure of 0.4 Mpa and the air mass fraction of 40%. It can be seen that the experimental data fluctuates greatly and are very different from the calculation values of Liu and Dehbi, which is mainly due to the instability of the flow in the natural circulation system and the effect of the tube bundle. Figure 6 shows that when the heat transfer coefficient experimental curve represents as a wave crest, the prediction curve of Liu will be a wave trough by coincidence, and the prediction curve of Dehbi will be a wave crest, which is basically the same for the Dehbi's with a defference of one-half cycle. This is due to both the proposed experimental correation and the Liu's correlation are established by the linear fitting course with the mean value of data sets, whereas Liu's data is relatively fewer, and the effect of the index of supercooling degree expressed by equations, is not taken into account. Hence, there is a deviation in the trend of the transient curve obtained.

FIGURE 6

Figure 6. Comparison of correlation against experimental data.

In this paper, by combining with the influence factors of the condensation heat transfer coefficient of the tube bundle, i.e., the effect of the index of supercooling degree has been taken into account, and using the multiple linear fitting method and the experimental data, the experimental correlation among the condensation heat transfer coefficient of the tube bundle, the mixed gas pressure, supercooling degree of the tube surface, and the non-condensing gas content can be given as follows:

$\begin{array}{ll}h=1047\times \frac{p^{0.24}}{{(T_b-T_w)}^{2.18}{w_a}^{0.87}}& (6)\end{array}$

The applicable ranges of the given equations are 0.05 ≤ w_a ≤ 0.65,0.3 ≤ P ≤ 0.6 MPa and 5 ≤ T_b−T_w ≤ 22°C. Comparison results between the predicted values of the experimental correlation and the experimental data are shown in Figure 7. The result indicates that the experimental correlation obtained by the linear fitting course are able to well predict the experimental condensation heat transfer coefficient, and experimental data almost all fall within the error band of ±10%.

FIGURE 7

Figure 7. Comparison of the predictions by correlation with experimental date.

As can be seen in Figure 7, we have compared the experimental values of condensation heat transfer coefficient with Liu' and Dehbi's correlations under the pressure of 0.5 MPa. The experimental values close to the Liu's correlation due to the proposed experimental correlation and the Liu's correlation are both established by the linear fitting course with the mean value of data sets.

Conclusions

1) Within the experimental conditions in this paper, the condensation heat transfer coefficient of the surface of the tube bundle decreases with the increment of the supercooling degree. Under the condition of the same air mass fraction, the condensation heat transfer coefficient increases with the increment of mixed air pressure, and the effect of pressure will be weakened while the air content has a relatively large proportion.

2) Under the condition of high pressure with low content of non-condensing gas, the heat transfer effect of the tube bundle is much better than that of the single tube.

3) Considering the effects of supercooling degree of the tube surface, air mass fraction and the pressure of condensation heat transfer coefficient, the experimental data fitting course has been implemented consequently. As a result, the calculation relational expressions of the condensation heat transfer coefficient of the tube bundle then has been obtained, and error of experimental correlation and experimental data is < ±10%.

Author Contributions

LW: First author and the writer of the manuscript. ZM and YZ: Provided guidance for the manuscript. WL and PC: Provided help with writing this manuscript and the data analysis. CT and YM: Provided help with building the experimental bench and performing the experiment.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Dehbi, A. (1991). The Effects of Noncondensable Gases on Steam Condensation Under Turbulent Natural Convection Conditions. Department of Nuclear Engineering, Minneapolis, MN.

Ivashchenco, A. I. (1989). Heat transfer with steam condensation from a steam-gas mixture. Heat Trans. Soviet Res. 21, 42–47.

Lakshmanan, S. P., and Pandey, M. (2009). Analysis of startup oscillations in natural circulation boiling systems. Nucl. Eng. Des. 239, 2391–2398. doi: 10.1016/j.nucengdes.2009.06.017

CrossRef Full Text | Google Scholar

Liu, H., Todreas, N. E., and Driscoll, M. J. (2000). An experimental investigation of a passive cooling unit for nuclear plant containment. Nucl. Eng. Des. 199, 243–255. doi: 10.1016/S0029-5493(00)00229-6

CrossRef Full Text | Google Scholar

Othmer, D. F. (1929). The condensation of steam. Ind. Eng. Chem. 21, 576–583. doi: 10.1021/ie50234a018

CrossRef Full Text | Google Scholar

Su, J. (2016). Review of steam condensation heat transfer in containment cooling system. Atomic Energ. Sci. Technol. 11, 1956–1966. doi: 10.7538/yzk.2016.50.11.1956

CrossRef Full Text | Google Scholar

Tagami, T. (1965). Interim Report on Safety Assessments and Facilities Establishment[R], Project for June 1965, No 1. Japanese Atomic Energy Research Agency, Unpublished Work.

Uchida, H., Oyama, A., and Togo, Y. (1964). “Evaluation of post-incident cooling systems of light water reactors,” in Proceedings of the Second. United Nations International Conference on the Peaceful Uses of Atomic Energy, 3rd Conference.

Google Scholar

Wang, H. (2014). Numerical simulation of heat transfer characteristics of air vapor condensate. J. Chem. Ind. 76, 3425–3433. doi: 10.3969/j.issn.0438-1157.2014.09.016

CrossRef Full Text | Google Scholar

Wang, J., Tian, W., Zhang, Y., Chen, L., Li, L., Zhang, L., et al. (2014). The development of Module In-vessel degraded severe accident Analysis Code MIDAC and the relevant research for CPR1000 during the station blackout scenario. Prog. Nucl. Energ. 76, 44–54. doi: 10.1016/j.pnucene.2014.05.015

CrossRef Full Text | Google Scholar

Ye, C., Zheng, M., and Han, X. (2012). Comparative advantages of AP1000 passive safety system. Atomic Energ. Sci. Technol. 46, 1221–1225.

Google Scholar

Yu, L., Xie, H., and Cai, Z. (2008). Mathematic model research and operating characteristic analysis of passive residual heat removal system. Chinese J. Nucl. Sci. Eng. 28, 233–243. doi: 10.3321/j.issn:0258-0918.2008.03.008

CrossRef Full Text | Google Scholar

Zhuang, Z., Tang, G., and Zhu, C. (2000). Condensation heat transfer characteristics of a horizontal tube bundle with non-condensable gas. J. Xi'an JiaoTong Univ. 34, 35–38. doi: 10.3321/j.issn:0253-987X.2000.11.008

CrossRef Full Text | Google Scholar