
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 21 April 2016
Sec. Electrochemical Energy Storage
Volume 4 - 2016 | https://doi.org/10.3389/fenrg.2016.00016
This article is part of the Research Topic Fast ionic conductors and solid-solid interfaces designed for next generation solid-state batteries View all 15 articles
 Balachandran Radhakrishnan
Balachandran Radhakrishnan Shyue Ping Ong*
Shyue Ping Ong*
Ceramic alkali superionic conductor solid electrolytes (SICEs) play a prominent role in the development of rechargeable alkali-ion batteries, ranging from replacement of organic electrolytes to being used as separators in aqueous batteries. The aqueous stability of SICEs is an important property in determining their applicability in various roles. In this work, we analyze the aqueous stability of twelve well-known Li-ion and Na-ion SICEs using Pourbaix diagrams constructed from first-principles calculations. We also introduce a quantitative free-energy measure to compare the aqueous stability of SICEs under different environments. Our results show that though oxides are, in general, more stable in aqueous environments than sulfides and halide-containing chemistries, the cations present play a crucial role in determining whether solid phases are formed within the voltage and pH ranges of interest.
Ceramic alkali superionic conductor solid electrolytes (SICEs) are key enablers to new rechargeable alkali-ion battery architectures that can significantly outperform today’s Li-ion batteries (Goodenough et al., 1976; Aono et al., 1990; Kanno et al., 2000; Mizuno et al., 2005; Murugan et al., 2007; Kamaya et al., 2011; Rao and Adams, 2011; Rangasamy et al., 2012). SICEs are non-flammable and may potentially support wider electrochemical windows, leading to enhanced safety and higher energy densities compared to traditional liquid organic solvent electrolytes (Xu, 2014). A good SICE must satisfy many properties, namely, excellent alkali ionic conductivity, a wide electrochemical window and interfacial stability, mechanical compatibility with the electrodes, and phase and aqueous stability. Though properties other than ionic conductivity have not received as much attention in the past, there have been several recent efforts aimed at addressing other properties such as elastic properties (Deng et al., 2016) and electrochemical stability (Zhu et al., 2015; Richards et al., 2016) that have arguably become a more critical bottleneck in SICE design than ionic conductivity.
The aqueous stability of SICEs is also important in all-solid state batteries. In the event of mechanical abuse (Doughty and Pesaran, 2012), the SICE is exposed to environmental elements. On such exposures, the SICEs can react with moisture in the air to either form passivating layers that could alter their ionic conductivity or form hazardous materials. SICEs can also be used as separators between electrodes and electrolytes in aqueous batteries (Luo et al., 2010; Ma et al., 2015). In particular, separators are necessary when Li metal is used as an anode, for example, in Li-air systems (Visco and Chu, 2000; Liu et al., 2015), as Li reduces most electrolytes on contact. Separators in such applications must be stable against Li metal as well as aqueous electrolytes of varying pH values. In particular, the NAtrium SuperIonic CONductor (NASICON), such as Li1.4Al0.4Ti1.4Ge0.2(PO4)3 and garnet-type SICEs, have shown great promise in such roles (Zhang et al., 2008; Imanishi et al., 2014).
Determination of the aqueous stability of solid electrolytes has thus far been predominantly based on experimental observations. Such experiments take anywhere between a week to a month (Fuentes et al., 2001), where the electrolyte is immersed in an aqueous solution, sometimes with LiOH, LiCl, etc. (Hasegawa et al., 2009; Imanishi et al., 2014), and tested for changes in surface morphology, chemistry, and ionic conductivity. These experiments are time-consuming as well as limited in the set of environmental elements that can be tested. Also, typical experiments are performed at 0 V vs. the standard hydrogen electrode (SHE) and do not reflect the environment that the electrolyte is exposed during battery operation.
In this work, we apply and extend the Pourbaix diagram formalism developed by Persson et al. (2012) to develop a quantitative measure of the aqueous stability of solid electrolytes based on the free-energy change and the phase of the products formed. We then apply this methodology to twelve well-known SICEs that are of current interest. Unsurprisingly, we find that oxide SICEs are significantly more stable than sulfide and halide-containing SICEs. However, we also find wide variations in aqueous stability even within the same anion chemistry. We will discuss these findings in context of the various potential applications of SICEs in energy storage.
To keep the discussion self-contained, we provide a brief description of the equations used in plotting the aqueous stability plots here, and interested readers are referred to the previous work of Persson et al. (2012) for more details. For a given material, operating under an externally applied potential, Vext, the chemical reaction with an aqueous medium can be represented by the following equation:
From the Nernst equation, we can then derive the free-energy change as follows:
where, is the free-energy change in the reaction under ideal environments (1 molar concentrations and Vext = 0 V), R is the Universal gas constant, T is the temperature(=298 K), pH (=−log[H+]) is the measure of acidity of the aqueous medium, and [Mat] and [Prod] represent the concentration of the chemical species involved in the reaction. The activity of H2O is assumed to be 1. In our analysis, we use −ΔGrxn as a quantitative measure of aqueous stability of the material. The larger the value of this free-energy change, the greater is the thermodynamic driving force for the reaction to occur.
All first principles calculated energies are obtained with the Vienna Ab initio Simulation Package (VASP) (Kresse and Furthmüller, 1996) implementation of density functional theory (DFT), using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (Perdew et al., 1996) description of the exchange-correlation energy. The calculation parameters are similar to those used in the Materials Project (Jain et al., 2013), and all analyses were performed using the Python Materials Genomics package (Ong et al., 2013).
As per the formalism proposed by Persson et al. (2012), the reference energies for O2 gas and H2O are fitted to experimental values (Kubaschewski et al., 1993), and the H2 energy is fixed to reproduce the H2O formation energy. The free energies of aqueous ions were calculated from the dissolution energy of solids as given in Johnson et al. (1992) and Pourbaix (1966). The Pourbaix diagrams of SICEs are constructed by fixing the relative ratios of all chemical species except H and O. For example, to generate the Pourbaix diagram of the Na3Zr2Si2PO12 NASICON, the Na:Zr:Si:P ratio is fixed at 3:2:2:1, and the Pourbaix diagram at that composition is plotted as a function of pH and the applied voltage.
Twelve well-known Li-ion and Na-ion SICEs in a wide range of cation and anion chemistries are studied in this work. For each chemistry, we selected the most stable polymorph for analysis. While many metastable polymorphs are of greater interest due to their higher ionic conductivities, we argue that our analysis provides an upper limit to the free energy of decomposition in aqueous media, i.e., the metastable polymorph will be less stable (in a thermodynamic sense) than the specific phases investigated in this work. Furthermore, the relative energy differences between different polymorphs are on the order of ~10 meV, about 2–3 orders magnitude smaller than the free-energy change of solvation. Our analysis is also limited to the undoped structures as we do not expect small dopant concentrations to alter the aqueous stability significantly. The SICEs studied in this work are as follows:
1. Oxides: The NAtrium SuperIonic CONductor (NASICON) and garnet families are two of the most widely explored oxide SICEs. In this work, we have studied the Na3Zr2Si2PO12 (Goodenough et al., 1976), NaZr2(PO4)3, and LiTi2(PO4)3 (Subramanian et al., 1986) members of the NASICON family, which allows us to study the effect of alkali ion and cation chemistry on aqueous stability. We have also selected the tetragonal Li7La3Zr2O12 (LLZO) (Murugan et al., 2007) garnet, which is the stable polymorph of the cubic garnet phase that is of interest because of its good ionic conductivity of 0.4 mS/cm and excellent stability against Li metal anodes.
2. Sulfides: Sulfide SICEs have received wide attention recently due to their significantly higher ionic conductivities compared to oxides. Among these sulfides, two of the most promising candidates are Li10GeP2S12 (LGPS), which was reported by Kamaya et al. (2011) to have an ionic conductivity of 12 mS/cm, and Li7P3S11 (Minami et al., 2007), which has the highest reported conductivity of 17 mS/cm thus far. We also included γ-Li3PS4 (Liu et al., 2013), which is one of the parent structures of the widely used LiPON solid electrolyte, and tetragonal Na3PS4 (t-Na3PS4), which is the stable polymorph of the cubic Na3PS4 SICE (Hayashi et al., 2012).
3. Halide-containing chemistries: Several halide-containing compounds have recently emerged as potential SICEs. The lithium-rich anti-perovskites (LRAP) (Zhao and Daemen, 2012) are a recently discovered class of SICEs, and we have included the Li3OCl and Li3OBr compounds in our analysis. We have also included both the oxide Li6PO5Cl and sulfide Li6PS5Cl members of the argyrodite family (Kong et al., 2010).
Using the above methodology, we have analyzed the aqueous stability of twelve well-known SICEs in a pH range of 4.0–10.0, i.e., from acidic to basic environments. The externally applied voltage is varied between −3.5 V and 2.5 V (versus SHE), which encompasses an equivalent voltage range of −0.46 to 5.54 V versus Li/Li+ (−3.04 V vs SHE) and −0.79 to 5.21 V versus Na/Na+ (−2.71 V vs SHE) (Vanysek, 2011). In all Pourbaix diagrams, the corresponding alkali anode half-cell voltage is indicated for reference, and all aqueous ions other than H+ are fixed at a molality of 10–6 mol/L.
The Pourbaix diagram of the Na3Zr2Si2PO12 NASICON is shown in Figure 1. On exposure to neutral environments, the non-silicon version of NASICON:NaZr2(PO4)3 is formed along with ZrSiO4 at 0 V, materials known to be less ionically conductive compared to NASICON. This is qualitatively in good agreement with the experiments explaining the change in the surface morphology as well as the conductivity (Ahmad et al., 1987; Mauvy et al., 1999; Fuentes et al., 2001). Fuentes et al. (2001) attributes the change in surface morphology to the formation of hydronium NASICON, but positive identification has been found lacking. In the voltage range −3.5 to −1 V (SHE), exposure to aqueous environments leads to formation of phosphine, which in gaseous form is known to be toxic and highly flammable. Otherwise, the Pourbaix diagram predicts that the NASICON forms solid insulating phases at high voltages. At low voltages, however, ZrH2, a metallic alloy (Bickel and Berlincourt, 1970), is predicted to be the only solid product formed, which may not protect the SICE against further reaction.
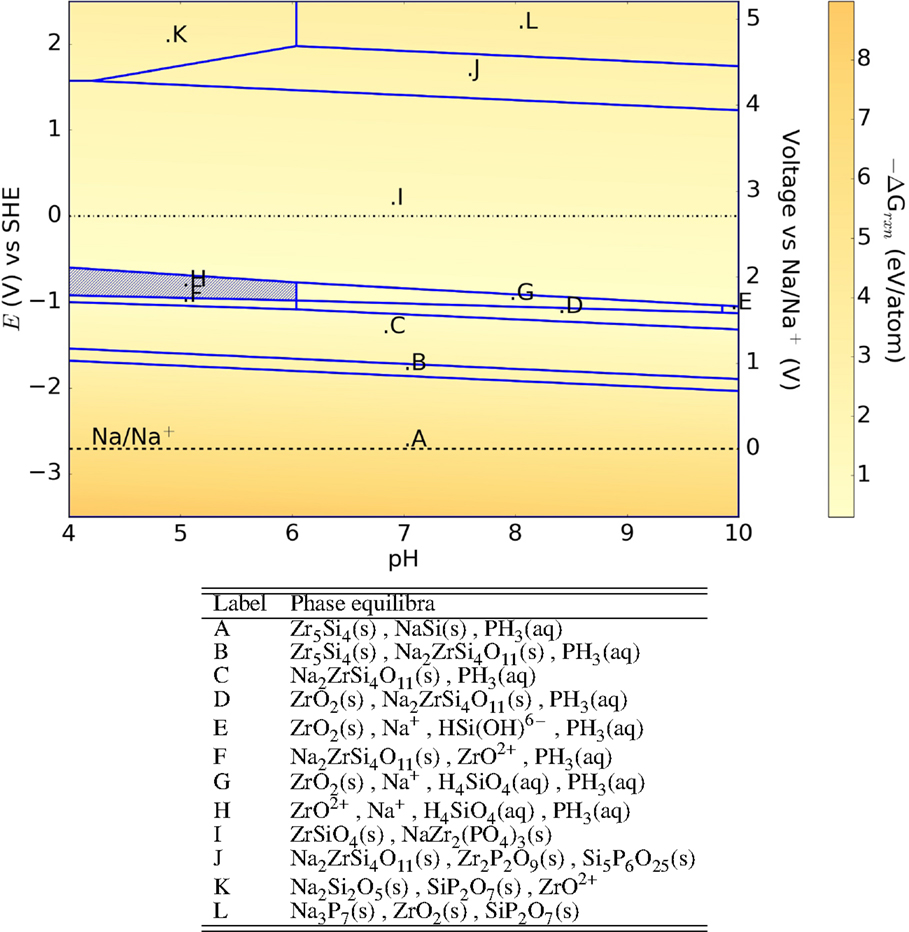
Figure 1. Pourbaix diagram of Na3Zr2Si2PO12. Shaded region indicates absence of any solid phase products.
The free-energy change shows that NASICON is more stable at reducing environments than oxidizing environments, especially at neutral environments with −ΔGrxn ≤ 1 eV/atom. In comparison, we observe that NaZr2(PO4)3 (Figure 2) is more stable at neutral environments than Na3Zr2Si2PO12 (lower free-energy change), but corrodes in acidic environments.
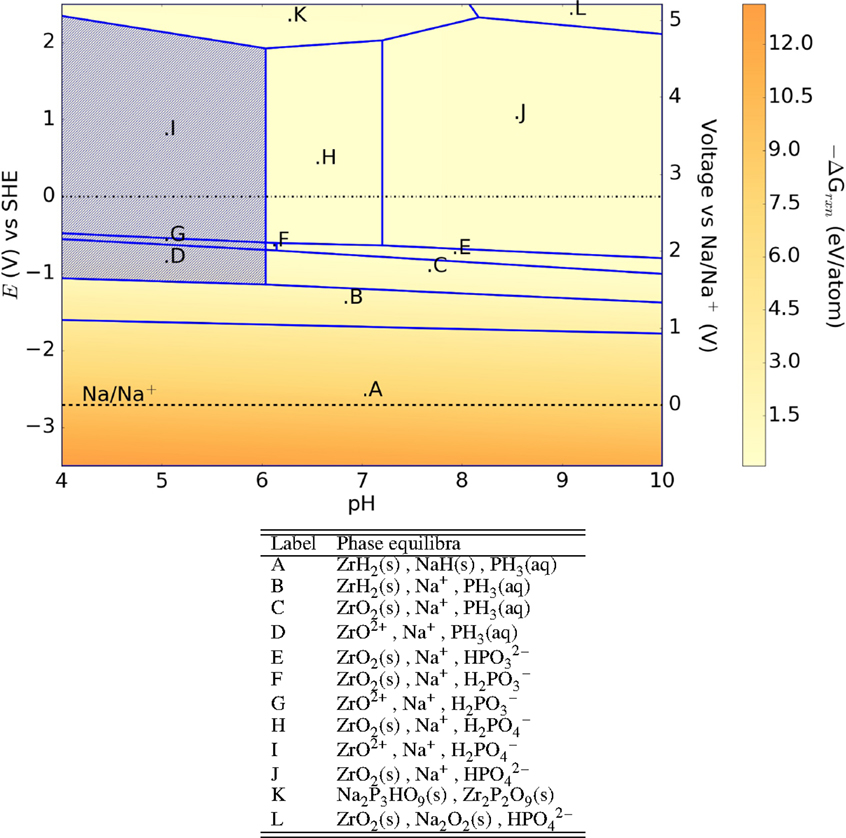
Figure 2. Pourbaix diagram of NaZr2(PO4)3. Shaded region indicates absence of any solid phase products.
LiTi2(PO4)3 (LTP), which also crystallizes in the NASICON structure, is one of the most stable electrolytes at 0 V across the pH range with a −ΔGrxn ≤ 0.2 eV/atom, as shown in Figure 3. When exposed to aqueous environments at anodic voltages, it forms LiH, TiH2, and phosphine gas. At voltages >0 V (SHE), the solid products formed, such as TiO2 and Li2O2, can potentially provide a stable passivating layer. Acidity of the aqueous medium does not alter the composition of the passivating layers. The passivity predicted in the Pourbaix diagram explains the experimental observations that LTP is generally quite stable in aqueous environments (Zhang et al., 2008; Hasegawa et al., 2009). The same experiments also reported that exposure to LiCl and LiOH, which are used in aqueous batteries, alters only the surface chemistry while the electrolyte material itself was stable. At anodic voltages, the tendency for Ti4+ to be reduced to Ti2+-forming TiH2 may account for the larger driving force toward decomposition. It should be noted that TiH2 (Ito et al., 2006) is metallic.
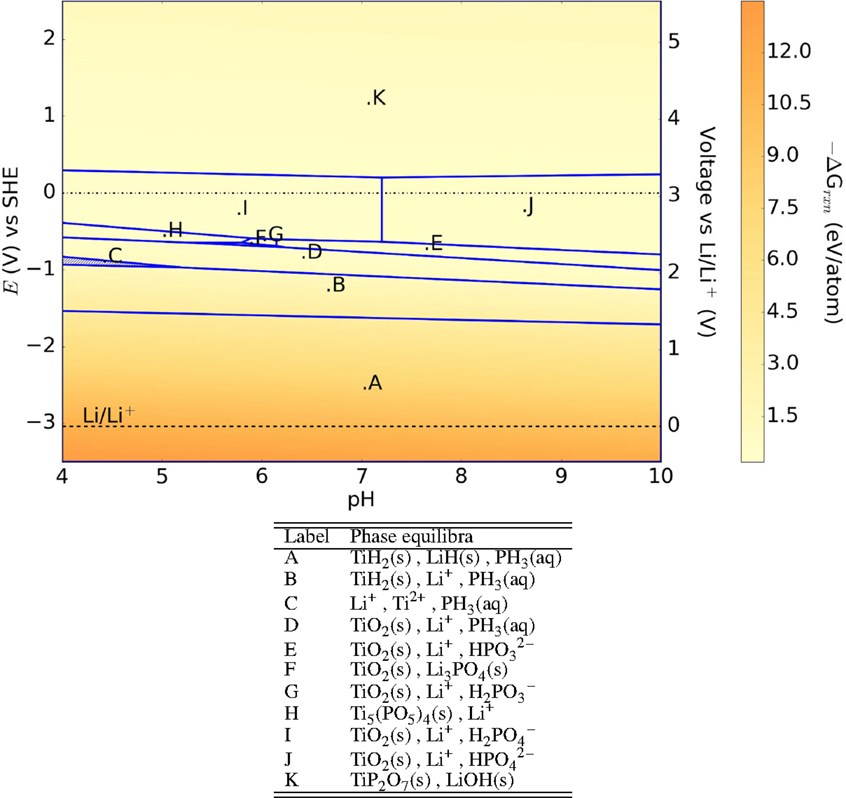
Figure 3. Pourbaix diagram of LiTi2(PO4)3. Shaded region indicates absence of any solid phase products.
The Pourbaix diagram of garnet Li7La3Zr2O12 (Figure 4) shows that it is relatively stable in aqueous environments, with solid phases formed throughout the voltage range of interest. Li2ZrO3, formed at 0 V and oxidizing environments, is known to be a stable solid with low ionic conductivity. At anodic voltages <−1 V (SHE), hydrides of Li, Zr, and La are formed.
Like LTAP, garnet SICEs have been explored for the role of a separator in aqueous electrolytes with Li metal anodes (Imanishi et al., 2014). Similar to the NASICONs, we find that the acidity of the aqueous medium does not significantly alter the products formed. Also, the low free-energy change (≤1 eV/atom at 0 V) throughout the pH range shows that the garnet is relatively stable in aqueous environments, consistent with previous experimental observations (Murugan et al., 2007; Shimonishi et al., 2011).
From Figure 5, we may observe that the Li10GeP2S12 (LGPS) (Kamaya et al., 2011) superionic conductor is predicted to form solid phases throughout the entire voltage range. At 0 V (SHE) and oxidizing environments, Li2Ge7O15 is one of the products formed, which can potentially form a good passivation layer even though it has much lower ionic conductivity compared to LGPS. However, either LiGe or Ge are formed at voltages ≤−1 V (SHE), which being poor electronic insulators, may not passivate the SICE against further reaction. Between voltages ±0.5 V (SHE), Li2GeS3 is formed which has a reasonable ionic conductivity of 0.1 mS/cm (Seo and Martin, 2011). As with other phosphorous containing compounds, phosphine gas is one of the predicted products at voltages ≤0 V (SHE).
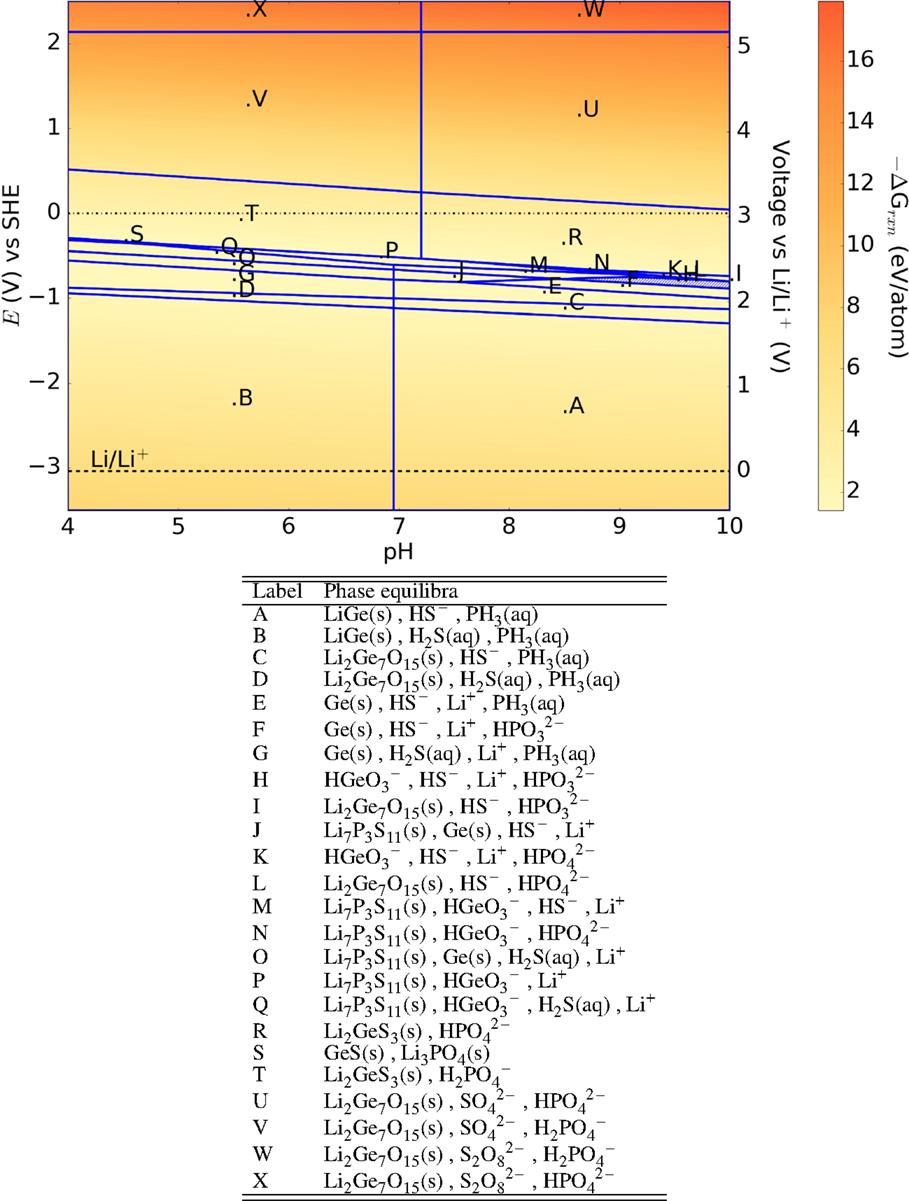
Figure 5. Pourbaix diagram of Li10GeP2S12. Shaded region indicates absence of any solid phase products.
Though solid phases are generally formed for LGPS throughout the pH and voltage range of interest, we find that the driving force for the formation of these products is generally higher than for the oxide phases. Unlike the NASICON and garnet, LGPS shows greater driving force toward oxidation rather than reduction.
In contrast to Li10GeP2S12, the Li7P3S11 (Minami et al., 2007) glass–ceramic is predicted to be significantly less stable in aqueous environments. There are large E–pH regions where no solid phases are stable (shaded regions in Figure 6). The potentially passivating LiPO3 phase is formed at cathodic voltages of 5 V (vs SHE), while hydrides and phosphine are formed at anodic voltages ≤−1.5 V (SHE), similar to other SICEs.
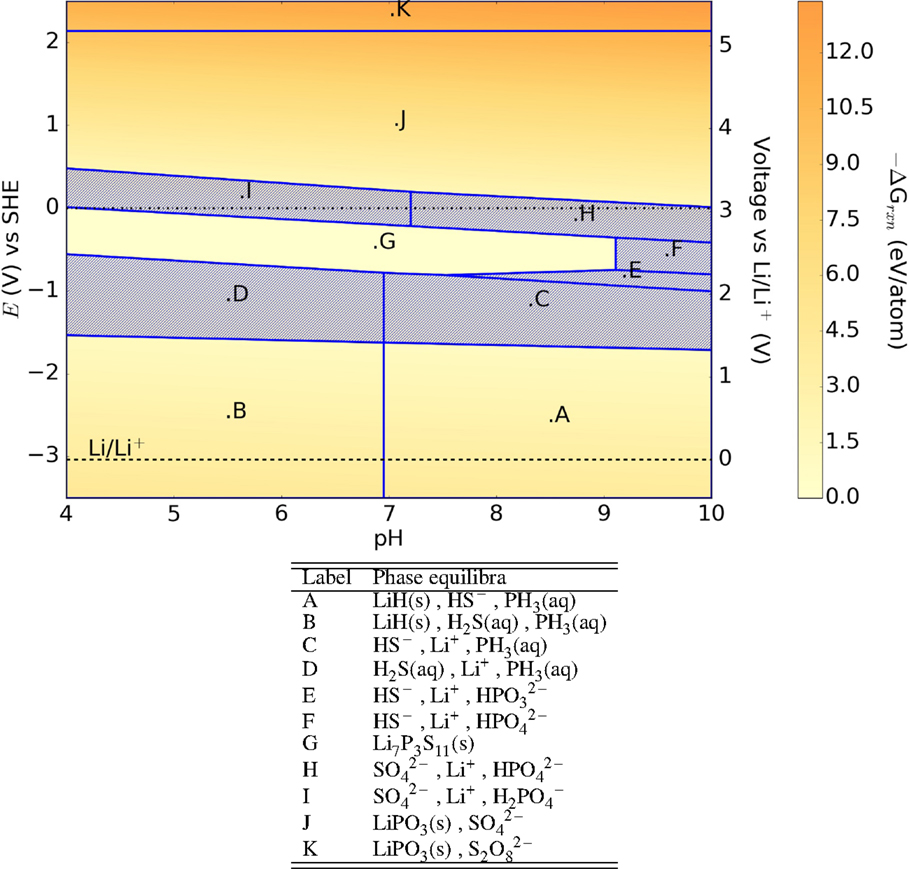
Figure 6. Pourbaix diagram of Li7P3S11. Shaded region indicates absence of any solid phase products.
M3PS4 (M = Na and Li) also belongs to the M2S–P2S5 glass–ceramic system. The qualitative features of their Pourbaix diagrams (Figures 7 and 8) are very similar to that of Li7P3S11, with large E–pH regions where no solid phases are stable. Phosphates and hydrated phosphates are generally formed at cathodic voltages, while hydrides are formed at anodic voltages.
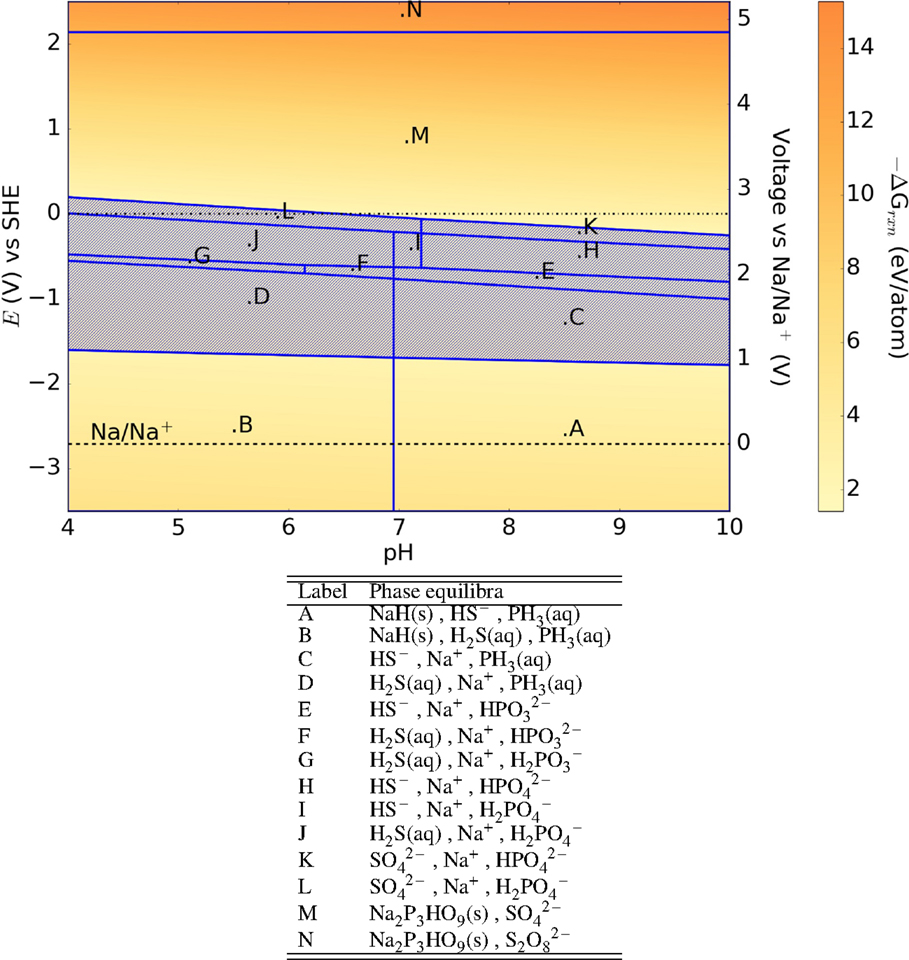
Figure 7. Pourbaix diagram of t-Na3PS4. Shaded region indicates absence of any solid phase products.
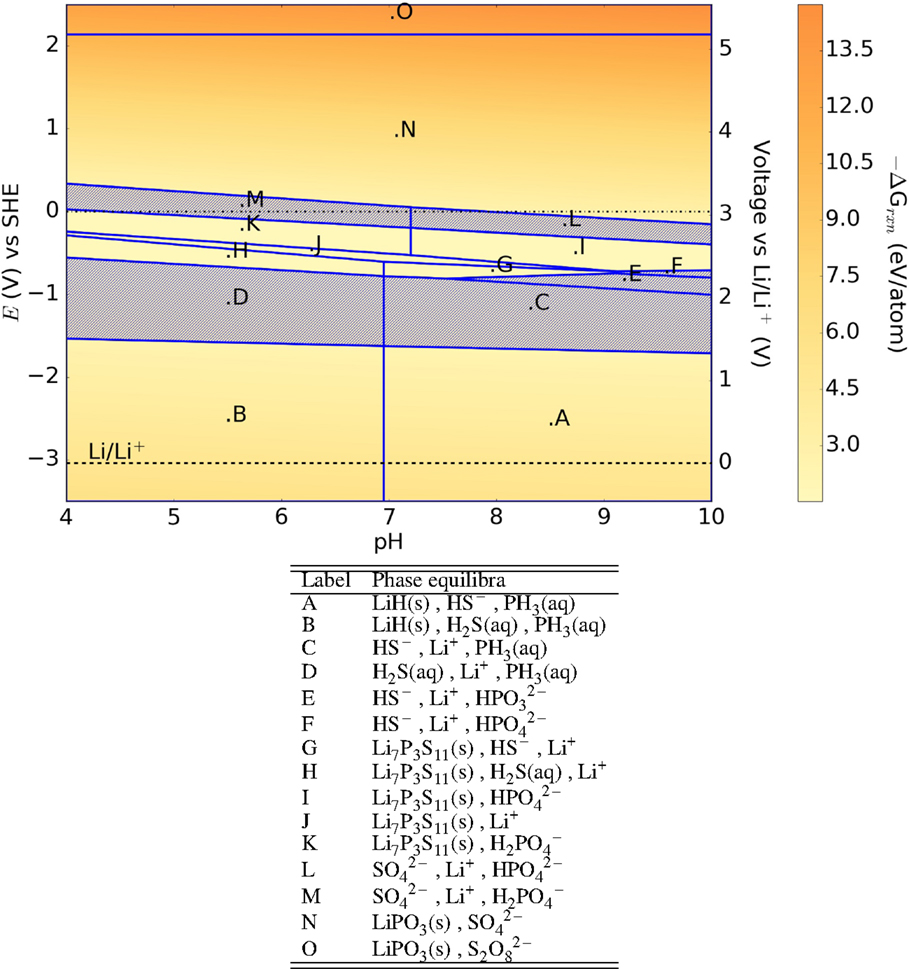
Figure 8. Pourbaix diagram of γ-Li3PS4. Shaded region indicates absence of any solid phase products.
Figures 9 and 10 show the Pourbaix diagrams of the Li3OCl and Li3OBr anti-perovskites, respectively. In general, the anti-perovskites are predicted to be unstable in aqueous environments with large regions where no solid phases are formed. Lithium peroxide Li2O2 is predicted to form at voltages ≥1 V (SHE), while LiH is predicted to form at voltages ≤−1.5 V (SHE). Between the two anion chemistries, the key difference is in the free-energy change of reaction. The chloride is predicted to have a higher free-energy change, i.e., larger driving force for decomposition, compared to the bromide. Nevertheless, these free-energy changes are much smaller in magnitude compared to the sulfides, which suggest that the LRAPs are less reactive compared to the sulfides in aqueous media.
The Pourbaix diagram of the oxide-argyrodite Li6PO5Cl (Figure 11) has generally similar features as that of the LRAPs, with large E–pH regions containing no stable solid phases. Somewhat surprisingly, we find that the sulfur-argyrodite Li6PS5Cl may form a passivating layer of Li7P3S11 at 0 V (SHE) as shown in Figure 12. A computational study on the sulfur-argyrodites (Li6PS5X) by Chen et al. (2015) hypothesized the formation of LiX, LiOH, H2S, and Li3PO4 on hydrolysis with predicted decomposition energies of the order of 0.3 eV/atom. Our results predict decomposition energies ranging 1.5–12 eV/atom with a range of both solid and aqueous products formed across the E–pH range.
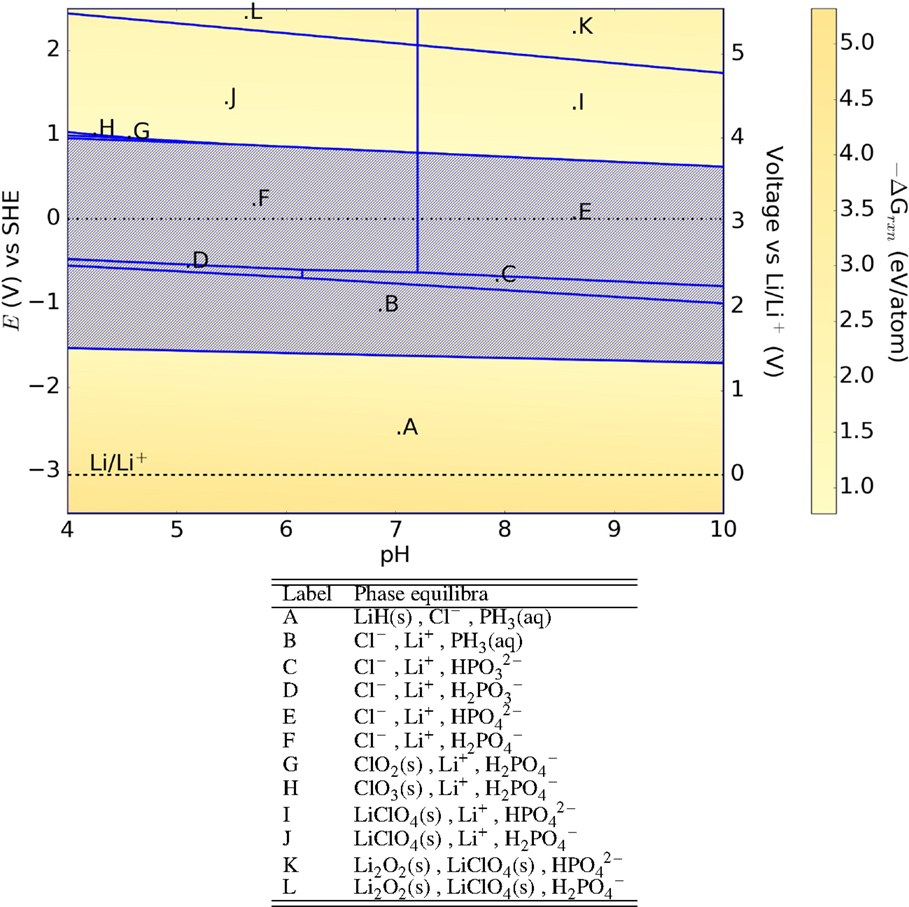
Figure 11. Pourbaix diagram of Li6PO5Cl. Shaded region indicates absence of any solid phase products.
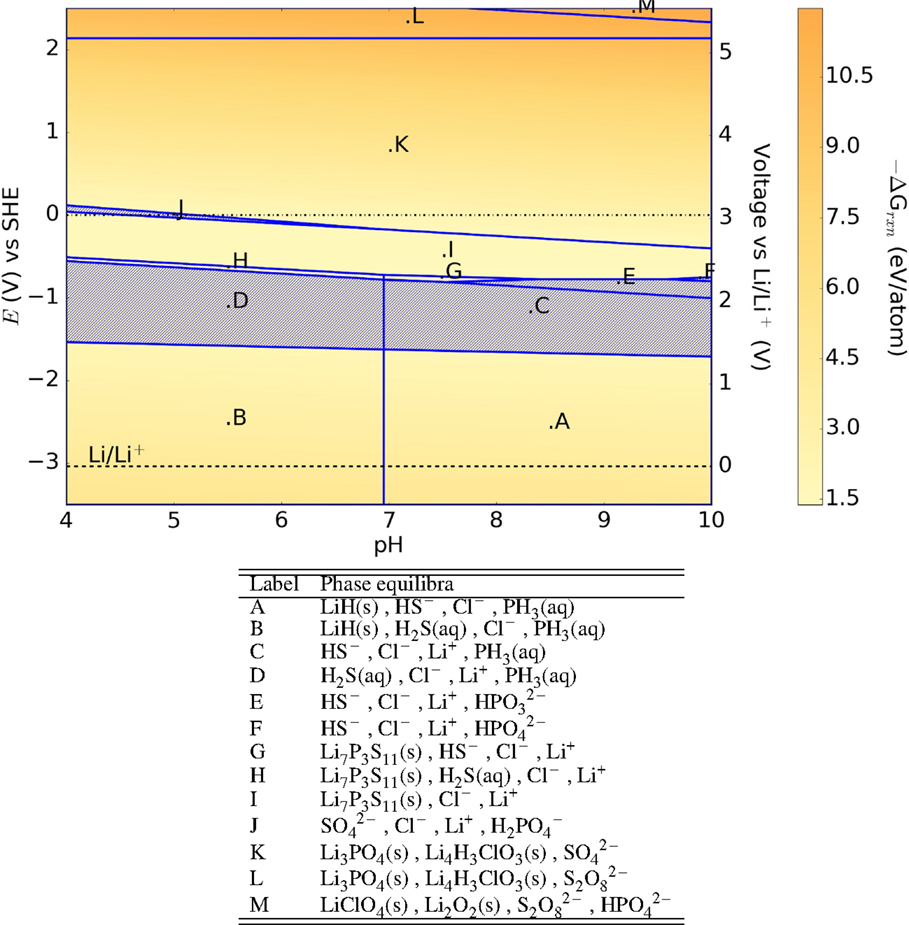
Figure 12. Pourbaix diagram of Li6PS5Cl. Shaded region indicates absence of any solid phase products.
In this work, we investigated the aqueous stability of twelve well-known SICE chemistries using a Pourbaix diagram formalism. None of the SICEs investigated are found to be completely non-reactive on exposure to moisture. However, the decomposition of an electrolyte itself is not necessarily fatal to the electrochemical performance. After all, the organic solvents, such as ethylene carbonate and dimethylcarbonate, are unstable with respect to reduction by Li metal. The key is whether a good passivation layer can be formed that will protect the SICE against further reaction and still provide a reasonable pathway for alkali-ion transport.
Our broad findings are in general agreement with previous experimental studies and expected behavior of chemistries, i.e., that sulfide and halide-containing SICEs are less stable under aqueous media than oxide SICEs, with larger driving forces to oxidize at cathodic (high) voltages vs SHE. However, we find that there are significant variations in stability even within the same anion chemistry. For instance, comparing the Na3Zr2Si2PO12 and NaZr2(PO4)3 NASICONs, we find that the former is more stable, particularly under acidic environments at high voltages, due to the presence of Si which promotes formation of solid silicate phases. Indeed, this observation suggests that the choice of cation (other than the alkali ion) may be a possible means to tune the phases formed at various E–pH. Another example can be seen by comparing the Pourbaix diagrams of LGPS, Li7P3S11, and γ-Li3PS4. Although all the three materials are thiophosphates, the presence of Ge in LGPS results in the formation of stable solid phases across most of the investigated E–pH range.
In rechargeable alkali batteries, an ultimate goal is the use of a metal anode, which would yield significant increases in energy density over traditional carbon-based (graphitic for Li and hard carbons for Na) anodes. However, the inherent reactivity of the alkali metal, as well as the potential for dendrite formation during plating (for Li), has thus far pose a great challenge in the real-world applications. One potential strategy of addressing both issues is to use a separator to protect the alkali metal, as well as act as a barrier against dendrite formation. Indeed, the two common SICEs explored for this purpose, LiTi2(PO4)3 and garnet LLZO (Zhang et al., 2008; Imanishi et al., 2014), are predicted to have relatively good stability in aqueous media. The garnet LLZO, in particular, is remarkable for its relative lack of reactivity across wide voltage and pH ranges, and low driving forces for decomposition.
It should be noted that the analysis presented is a purely thermodynamic one, and no kinetic factors are taken into account. Furthermore, while the lack of any stable solid phase would certainly preclude the possibility of passivation in a particular E–pH region, the existence of stable solid phases does not necessarily mean that a stable passivation layer will be formed. Ultimately, whether a solid phase can form a useful passivation layer depends on its morphology upon formation, its electronic conductivity, and its ionic conductivity. Nevertheless, we believe this work provides useful predictions of the phase equilibria at various E–pH and a quantification of the thermodynamic driving forces for reaction. These predictions can, and hopefully would be, validated against comprehensive experimental studies of SICEs in aqueous media.
To conclude, we have analyzed and compared the aqueous stability of twelve SICEs using a Pourbaix diagram formalism. In general, the predicted relative stabilities of the SICEs are in line with previous experimental results, where available, and expected behavior of chemistries. We find that the anion chemistry is a primary determinant of aqueous stability, though careful tuning of the cation chemistry can alter the solid phases formed and is a potential means of tuning SICEs for specific applications. Beyond SICEs, the first-principles approach presented here can be similarly applied to other technological applications, where aqueous stability of a material is a design concern.
BR designed and implemented the study on aqueous stability of alkali superionic conductors. SO is the principal investigator of this project and supervised the conceptualization and implementation. Both authors made equal contribution toward analysis of results and drafting the manuscript.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work was supported by the National Science Foundation’s Designing Materials to Revolutionize and Engineer our Future (DMREF) program under Grant No. 1436976. Some of the computations in this work were performed using the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1053575.
Ahmad, A., Wheat, T., Kuriakose, A., Canaday, J., and McDonald, A. (1987). Dependence of the properties of NASICONS on their composition and processing. Solid State Ionics 24, 89–97. doi: 10.1016/0167-2738(87)90070-1
Aono, H., Sugimoto, E., Sadaoka, Y., Manaka, N., and Adachi, G. (1990). Ionic conductivity of solid electrolytes based on lithium titanium phosphate. J. Electrochem. Soc. 137, 1023–1027. doi:10.1149/1.2086597
Bickel, P. W., and Berlincourt, T. G. (1970). Electrical properties of hydrides and deuterides of zirconium. Phys. Rev. B 2, 4807–4813. doi:10.1103/PhysRevB.2.4807
Chen, H. M., Maohua, C., and Adams, S. (2015). Stability and ionic mobility in argyrodite-related lithium-ion solid electrolytes. Phys. Chem. Chem. Phys. 17, 16494–16506. doi:10.1039/c5cp01841b
Deng, Z., Wang, Z., Chu, I.-H., Luo, J., and Ong, S. P. (2016). Elastic properties of alkali superionic conductor electrolytes from first principles calculations. J. Electrochem. Soc. 163, A67–A74. doi:10.1149/2.0061602jes
Doughty, D. H., and Pesaran, A. A. (2012). Vehicle Battery Safety Roadmap Guidance. Golden: National Renewable Energy Laboratory.
Fuentes, R. O., Figueiredo, F., Marques, F. M. B., and Franco, J. I. (2001). Reaction of NASICON with water. Solid State Ionics. 139, 309–314. doi:10.1016/S0167-2738(01)00683-X
Goodenough, J. B., Hong, H. Y.-P., and Kafalas, J. A. (1976). Fast Na/+/-ion transport in skeleton structures. Mater. Res. Bull. 11, 203–220. doi:10.1016/0025-5408(76)90077-5
Hasegawa, S., Imanishi, N., Zhang, T., Xie, J., Hirano, A., Takeda, Y., et al. (2009). Study on lithium/air secondary batteries-stability of NASICON-type lithium ion conducting glass-ceramics with water. J. Power Sources 189, 371–377. doi:10.1016/j.jpowsour.2008.08.009
Hayashi, A., Noi, K., Sakuda, A., and Tatsumisago, M. (2012). Superionic glass-ceramic electrolytes for room-temperature rechargeable sodium batteries. Nat. Commun. 3, 856. doi:10.1038/ncomms1843
Imanishi, N., Matsui, M., Takeda, Y., and Yamamoto, O. (2014). Lithium ion conducting solid electrolytes for aqueous lithium-air batteries. Electrochemistry 82, 938–945. doi:10.5796/electrochemistry.82.938
Ito, M., Setoyama, D., Matsunaga, J., Muta, H., Kurosaki, K., Uno, M., et al. (2006). Electrical and thermal properties of titanium hydrides. J. Alloys Comp. 420, 25–28. doi:10.1016/j.jallcom.2005.10.032
Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., et al. (2013). Commentary: the materials project: a materials genome approach to accelerating materials innovation. APL Mater. 1, 011002. doi:10.1063/1.4812323
Johnson, W. J., Oelkers, H. E., and Helgeson, C. H. (1992). SUPCRT92: a software package for calculating the standard molal thermodynamic properties of minerals, gases, aqueous species, and reactions from 1 to 5000 bar and 0 to 1000C. Comput. Geosci. 18, 899–947. doi:10.1016/0098-3004(92)90029-Q
Kamaya, N., Homma, K., Yamakawa, Y., Hirayama, M., Kanno, R., Yonemura, M., et al. (2011). A lithium superionic conductor. Nat. Mater. 10, 682–686. doi:10.1038/nmat3066
Kanno, R., Hata, T., Kawamoto, Y., and Irie, M. (2000). Synthesis of a new lithium ionic conductor, thio-LISICON – lithium germanium sulfide system. Solid State Ionics. 130, 97–104. doi:10.1016/S0167-2738(00)00277-0
Kong, S. T., Deiseroth, H. J., Maier, J., Nickel, V., Weichert, K., and Reiner, C. (2010). Li6PO5Br and Li6PO5Cl: the first lithium-oxide-argyrodites. Z. Anorg. Allg. Chem. 636, 1920–1924. doi:10.1002/zaac.201000121
Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter 54, 11169–11186. doi:10.1103/PhysRevB.54.11169
Kubaschewski, O., Alcock, C. B., and Spencer, P. J. (1993). Materials Thermochemistry. New York: Pergamon Press.
Liu, T., Leskes, M., Yu, W., Moore, A. J., Zhou, L., Bayley, P. M., et al. (2015). Cycling Li-O2 batteries via LiOH formation and decomposition. Science 350, 530–533. doi:10.1126/science.aac7730
Liu, Z., Fu, W., Payzant, E. A., Yu, X., Wu, Z., Dudney, N. J., et al. (2013). Anomalous high ionic conductivity of nanoporous beta-Li3PS4. J. Am. Chem. Soc. 135, 975–978. doi:10.1021/ja3110895
Luo, J.-Y., Cui, W.-J., He, P., and Xia, Y.-Y. (2010). Raising the cycling stability of aqueous lithium-ion batteries by eliminating oxygen in the electrolyte. Nat. Chem. 2, 760–765. doi:10.1038/nchem.763
Ma, C., Rangasamy, E., Liang, C., Sakamoto, J., More, K. L., and Chi, M. (2015). Excellent stability of a lithium-ion-conducting solid electrolyte upon reversible Li+/H+ exchange in aqueous solutions. Angew. Chem. Int. Ed. Engl. 127, 131–135. doi:10.1002/ange.201500056
Mauvy, F., Siebert, E., and Fabry, P. (1999). Reactivity of NASICON with water and interpretation of the detection limit of a NASICON based Na+ ion selective electrode. Talanta 48, 293–303. doi:10.1016/S0039-9140(98)00234-3
Minami, K., Mizuno, F., Hayashi, A., and Tatsumisago, M. (2007). Lithium ion conductivity of the Li2SP2S5 glass-based electrolytes prepared by the melt quenching method. Solid State Ionics 178, 837–841. doi:10.1016/j.ssi.2007.03.001
Mizuno, F., Hayashi, A., Tadanaga, K., and Tatsumisago, M. (2005). New, highly ion-conductive crystals precipitated from Li2S-P2S5 glasses. Adv. Mater. Weinheim 17, 918–921. doi:10.1002/adma.200401286
Murugan, R., Thangadurai, V., and Weppner, W. (2007). Fast lithium ion conduction in garnet-type Li(7)La(3)Zr(2)O(12). Angew. Chem. Int. Ed. Engl. 46, 7778–7781. doi:10.1002/anie.200701144
Ong, S. P., Richards, W. D., Jain, A., Hautier, G., Kocher, M., Cholia, S., et al. (2013). Python Materials Genomics (pymatgen): a robust, open-source python library for materials analysis. Comput. Mater. Sci. 68, 314–319. doi:10.1016/j.commatsci.2012.10.028
Perdew, J., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865
Persson, K. A., Waldwick, B., Lazic, P., and Ceder, G. (2012). Prediction of solid-aqueous equilibria: scheme to combine first-principles calculations of solids with experimental aqueous states. Phys. Rev. B 85, 235438. doi:10.1103/PhysRevB.85.235438
Pourbaix, M. (1966). Atlas of Electrochemical Equilibria in Aqueous Solutions. Oxford: Pergamon Press.
Rangasamy, E., Wolfenstine, J., and Sakamoto, J. (2012). The role of Al and Li concentration on the formation of cubic garnet solid electrolyte of nominal composition Li7La3Zr2O12. Solid State Ionics 206, 28–32. doi:10.1016/j.ssi.2011.10.022
Rao, R. P., and Adams, S. (2011). Studies of lithium argyrodite solid electrolytes for all-solid-state batteries. Phys Status Solidi A Appl. Mater. 208, 1804–1807. doi:10.1002/pssa.201001117
Richards, W. D., Miara, L. J., Wang, Y., Kim, J. C., and Ceder, G. (2016). Interface stability in solid-state batteries. Chem. Mater. 28, 266–273. doi:10.1021/acs.chemmater.5b04082
Seo, I., and Martin, S. W. (2011). Preparation and characterization of fast ion conducting lithium thio-germanate thin films grown by RF magnetron sputtering. J. Electrochem. Soc. 158, A465. doi:10.1149/1.3552927
Shimonishi, Y., Toda, A., Zhang, T., Hirano, A., Imanishi, N., Yamamoto, O., et al. (2011). Synthesis of garnet-type Li7-xLa3Zr2O12-1/2x and its stability in aqueous solutions. Solid State Ionics 183, 48–53. doi:10.1016/j.ssi.2010.12.010
Subramanian, M., Subramanian, R., and Clearfield, A. (1986). Lithium ion conductors in the system AB(IV)2(PO4)3 (B = Ti, Zr and Hf). Solid State Ionics 18-19, 562–569. doi:10.1016/0167-2738(86)90179-7
Vanysek, P. (2011). “Electrochemical series,” in Handbook of Chemistry and Physics, ed. W. M. Haynes, 92nd Edn (London: CRC Press), 5-80–5-89.
Visco, S. J., and Chu, M.-Y. (2000). Protective Coatings for Negative Electrodes. Patent No: US 6025094 A
Xu, K. (2014). Electrolytes and interphases in Li-ion batteries and beyond. Chem. Rev. 114, 11503–11618. doi:10.1021/cr500003w
Zhang, T., Imanishi, N., Hasegawa, S., Hirano, A., Xie, J., Takeda, Y., et al. (2008). Li polymer electrolyte water stable lithium-conducting glass ceramics composite for lithium-air secondary batteries with an aqueous electrolyte. J. Electrochem. Soc. 155, A965. doi:10.1149/1.2990717
Zhao, Y., and Daemen, L. L. (2012). Superionic conductivity in lithium-rich anti-perovskites. J. Am. Chem. Soc. 134, 15042–15047. doi:10.1021/ja305709z
Keywords: superionic conductors, Pourbaix diagrams, aqueous stability, passivation, corrosion
Citation: Radhakrishnan B and Ong SP (2016) Aqueous Stability of Alkali Superionic Conductors from First-Principles Calculations. Front. Energy Res. 4:16. doi: 10.3389/fenrg.2016.00016
Received: 01 February 2016; Accepted: 04 April 2016;
Published: 21 April 2016
Edited by:
Guoxiu Wang, University of Technology Sydney, AustraliaReviewed by:
Li Wang, Tsinghua University, ChinaCopyright: © 2016 Radhakrishnan and Ong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shyue Ping Ong, b25nc3BAZW5nLnVjc2QuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.