Mathematical modeling and simulation of thyroid homeostasis: Implications for the Allan-Herndon-Dudley syndrome

Introduction: A mathematical model of the pituitary-thyroid feedback loop is extended to deepen the understanding of the Allan-Herndon-Dudley syndrome (AHDS). The AHDS is characterized by unusual thyroid hormone concentrations and a mutation in the SLC16A2 gene encoding for the monocarboxylate transporter 8 (MCT8). This mutation leads to a loss of thyroid hormone transport activity. One hypothesis to explain the unusual hormone concentrations of AHDS patients is that due to the loss of thyroid hormone transport activity, thyroxine (T₄) is partially retained in thyroid cells.

Methods: This hypothesis is investigated by extending a mathematical model of the pituitary-thyroid feedback loop to include a model of the net effects of membrane transporters such that the thyroid hormone transport activity can be considered. A nonlinear modeling approach based on the Michaelis-Menten kinetics and its linear approximation are employed to consider the membrane transporters. The unknown parameters are estimated through a constrained parameter optimization.

Results: In dynamic simulations, damaged membrane transporters result in a retention of T₄ in thyroid cells and ultimately in the unusual hormone concentrations of AHDS patients. The Michaelis-Menten modeling approach and its linear approximation lead to similar results.

Discussion: The results support the hypothesis that a partial retention of T₄ in thyroid cells represents one mechanism responsible for the unusual hormone concentrations of AHDS patients. Moreover, our results suggest that the retention of T₄ in thyroid cells could be the main reason for the unusual hormone concentrations of AHDS patients.

Introduction

The AHDS is a rare and severe disease which was first described in 1944 by Allan, Herndon and Dudley (1). Patients suffer from different symptoms like, e.g., hypotonia, primitive reflexes, scoliosis, muscular hypoplasia and dystonia (2).

A first key observation regarding AHDS patients are low free T₄ (FT₄), slightly elevated thyroid stimulating hormone (TSH) and high free triiodothyronine (FT₃) concentrations compared to healthy individuals (2, 3). A second key observation of AHDS patients are mutations in the SLC16A2 gene encoding for the monocarboxylate transporter 8 (MCT8) (4, 5), which is a specific thyroid hormone transporter (6). A mutation in the related gene often goes along with a complete loss of thyroid hormone transport activity (7).

To elucidate the exact mechanisms that lead to the altered hormone concentrations of this disease, several studies have been made with Mct8 knockout (KO) mice (8–10). These mice miss the MCT8 and are therefore suitable for investigations related to this disease (10). Furthermore, the hormone concentrations of Mct8 KO mice are strongly similar to those of AHDS patients (11).

The thyroids of Mct8 KO mice contain approximately a 3-fold elevation of T₄ compared to wild-type littermates (8). Based on this finding, the hypothesis was made that one mechanism responsible for the unusual hormone concentrations of AHDS patients is a partial retention of T₄ in thyroid cells (12). In this case, more T₄ would be converted into T₃ by thyroidal 5’-deiodinase type I (D1) (12). The result would be that the serum FT₄ concentrations of AHDS patients are lower compared to healthy individuals. Assuming that the T₃ release of the thyroid is not harmed in MCT8-deficiency (which could be explained by further membrane transporters) (8), the serum FT₃ concentrations of AHDS patients would be higher compared to healthy individuals. The feedback signal of T₄ at the pituitary would induce a higher serum concentration of TSH.

If there were no additional mechanisms in the genesis of the unusual hormone concentrations than the one described by (12), one would expect that athyroid Mct8 KO mice receiving exogenous thyroid hormone supply do not show the unusual hormone concentrations. In athyroid mice no retention of T₄ in the thyroid can take place and thus the effects of this mechanism should not exist. Investigations with athyroid Mct8 KO mice reveal that it is possible to establish normal T₃ concentrations by exogenous T₄ supply (8). In turn, the T₄ concentrations remain very low (8). This observation indicates that the retention of T₄ in the thyroid gland does contribute to the high T₃ concentrations but not to the low T₄ concentration (12). Therefore, the authors in (12) draw the conclusion that additional mechanisms must contribute to the unusual hormone concentrations. Particularly, they suggest a renal contribution, since T₄ accumulates in the kidney and the activity of D1 inside the kidney is increased for Mct8 KO mice (9).

In this work, we investigate the mechanisms leading to the unusual hormone concentrations of AHDS patients by means of a mathematical model of the pituitary–thyroid feedback loop and dynamic simulations. In detail, we further extend the model originally developed by (13–15) to include membrane transporters exemplarily between the thyroid gland and the periphery. Our results indicate that damaged membrane transporters, i.e., a loss of thyroid hormone transport activity leads to an increased T₄ content in thyroid cells and ultimately to the unusual hormone concentrations that are measured at AHDS patients. These results lead to a partially different conclusion compared to the suggestions given in (12), since they suggest that the entirety of the unusual hormone concentrations of AHDS patients be explained by a retention of T₄ in thyroid cells, without additional renal contribution.

Methods

First, we introduce the mathematical model of the pituitary-thyroid feedback loop and its extension to membrane transporters. Second, we estimate the unknown parameters using a constrained parameter optimization.

Extended model

In general, a mathematical model describes a system by taking into account the available knowledge about the underlying cause-effect relationships. To understand the fundamental principles of the model used throughout this work, a simplified block diagram of it is illustrated in Figure 1, whereas a more detailed description is given in Figure 2. The basic principle is that TSH stimulates the production of T₃ and T₄ at the thyroid gland. By means of D1 and 5’-deiodinase type II (D2), T₄ is converted into T₃ in peripheral organs like the liver and the kidney as well as muscle tissue. The production of TSH at the pituitary is inhibited by T₄, whereas the production of TSH is stimulated by thyrotropin-releasing hormone (TRH). The detailed mathematical model used in this work describes the cause-effect relationships by six nonlinear differential equations visible in Figure 2. A detailed state of the art description of the mathematical model as developed by (13–15) is given in Section S1 of the Supplementary Material, so that this paper is as self-contained as possible. In the main part, we will emphasize on the extension of the model, conducted within this work.

FIGURE 1

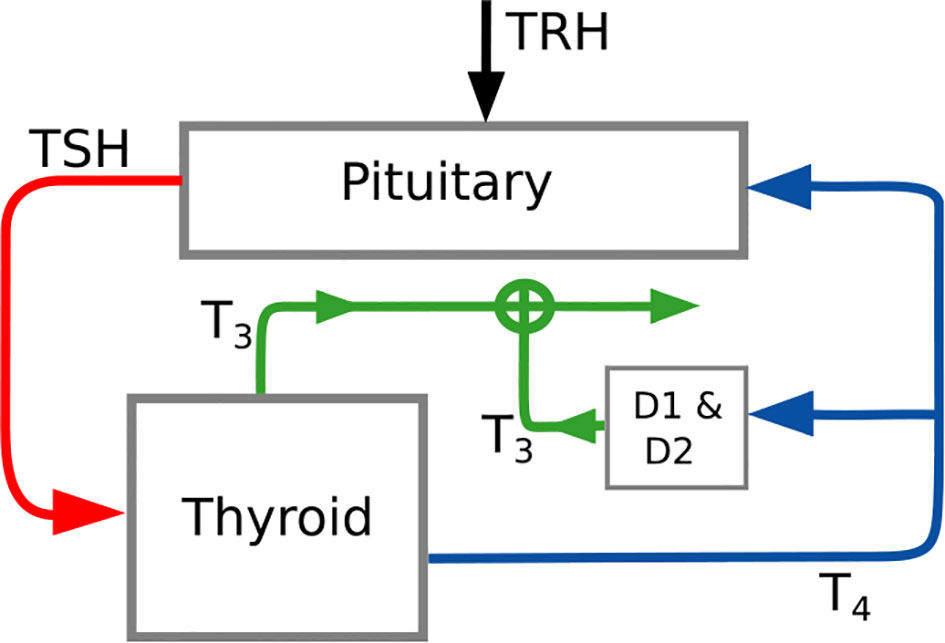
Figure 1 Simplified block diagram of the pituitary thyroid feedback loop. This diagram illustrates the main structure of the applied mathematical model. The detailed model is illustrated in Figure 2. The parameter D2 and the variable TRH denote the 5’-deiodinase type II and the thyrotropin-releasing hormone, respectively.

FIGURE 2

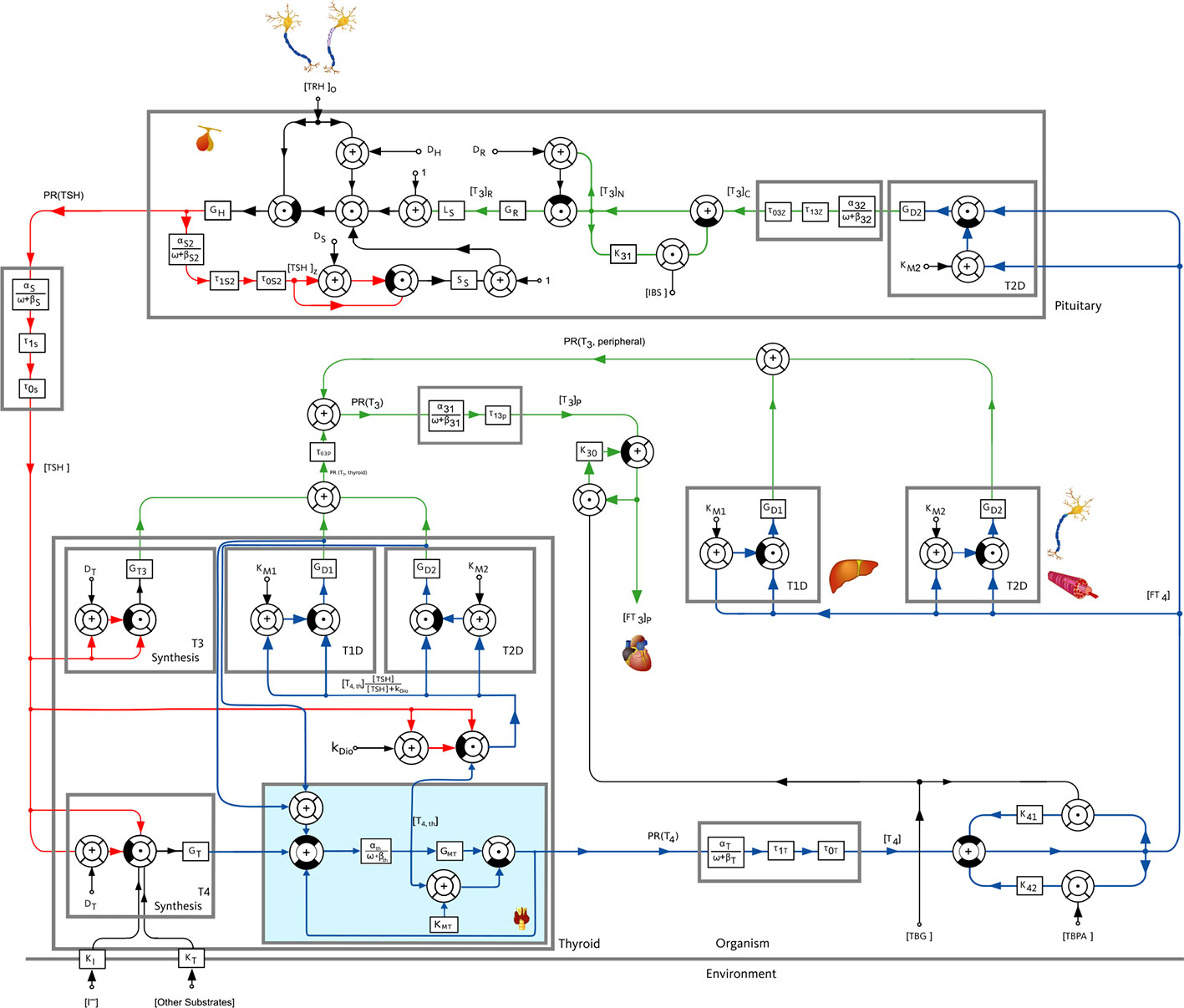
Figure 2 Block diagram of the pituitary-thyroid feedback loop including membrane transporters, extended from (13–15). The extension presented in this paper is shown with a slight blue background color in the block “Thyroid”. The numerical parameter values are mostly taken from (13, 15). The values of G_D1, G_T3 and G_MT are estimated through a constrained parameter optimization using real hormone measurements from (16).

The investigations of the effects of damaged membrane transporters on the hormone concentrations necessitate a representation of the net effects of the membrane transporters in the mathematical model of the pituitary-thyroid feedback loop from (13–15). For simplicity, we will call the modeled net effects of the membrane transporters “Michaelis-Menten modeling” (or “linear modeling”) of the membrane transporters, even though we do not refer to a specific concentration or state variable but to the net effects.

We incorporate membrane transporters exemplarily between the thyroid gland and the periphery for T₄ (illustrated in Figure 2 by the slight blue background color) in order to analyze the mentioned hypothesis. Obviously, one could incorporate membrane transporters at a number of different locations in the model, but this would further complicate the model and result in difficulties in the estimation of the additional parameters of the membrane transporters. Moreover, further incorporations of the effects of MCT8 deficiency (or of damaged membrane transporters) are not crucial to pursue the objective of analyzing the hypothesis mentioned in (12) that a retention of T₄ in thyroid cells represents one mechanism responsible for the unusual hormone concentrations of AHDS patients. Furthermore, one could also distinguish between MCT8-mediated and MCT8-independent transport mechanisms. However, the estimation becomes more challenging, if not impossible. Therefore, the here considered membrane transporters can be interpreted as the net effects of all transporters (to which the MCT8 contributes mainly).

The incorporation of the membrane transporters into the already existing model (15) is done by an introduction of a new state, named T_4,th. The differential equation of T_4,th is defined by

$\begin{array}{ll}\begin{array}{c}\frac{d{T}_{4,th}}{dt}(t)={\alpha }_{th}(G_T\frac{TSH(t)}{TSH(t)+D_T}-G_{MT}\frac{T_{4,th}(t)}{K_{MT}+T_{4,th}(t)}\\ -G_{D1}\frac{T_{4,th}(t)\frac{TSH(t)}{TSH(t)+k_{Dio}}}{T_{4,th}(t)\frac{TSH(t)}{TSH(t)+k_{Dio}}+K_{M1}}\\ - G_{D2}\frac{T_{4,th}(t)\frac{TSH(t)}{TSH(t)+k_{Dio}}}{T_{4,th}(t)\frac{TSH(t)}{TSH(t)+k_{Dio}}+K_{M2}})-{\beta }_{th}{T}_{4,th}(t).\end{array}& (1)\end{array}$

Following the common modeling approach of enzyme/substrate reactions based on the well known Michaelis-Menten kinetics (17), the functionality of the membrane transporters is considered by

$\begin{array}{ll}{G}_{MT}\frac{T_{4,th}\left(t\right)}{K_{MT}+T_{4,th}\left(t\right)},& (2)\end{array}$

where T_4,th represents the T₄ concentration in thyroid cells. The parameter G_MT stands for the maximal activity of the net effects of all membrane transporters that are involved in the transport of T₄ (for which the MCT8 plays a crucial role). The parameter K_MT is the Michaelis-Menten constant of the membrane transporters. Our model reflects the organ level. Hence, the modeled membrane transporters can be interpreted as the cumulated effect of single membrane transporters on cell level. The complete term thus stands for the part of T₄, which is transported out of the thyroid cells. The first term of (1) describes the production rate of T_4,th, with G_T being the secretory capacity of the thyroid gland and D_T representing the damping constant at the thyroid gland (compare Section S1 of the Supplementary Material for a more detailed explanation of the model and the meaning of the parameters). The remaining terms represent the thyroidal conversion of T_4,th into T₃ by D1 and D2, where the maximal activity of D1/D2 is denoted by G_D1/G_D2 and the dissociation constant of D1/D2 by K_M1/K_M2, respectively¹. The constant k_Dio is the same in the terms related to D1 and D2 since we assume that the stimulation of the thyroidal D1 and D2 by TSH is the same for D1 and D2, compare (15) for a detailed discussion of the TSH-T₃ shunt. This conversion rate is considered positively in the differential equation of T_3p, equation (S3) of the Supplementary Material. Thus, this conversion rate must be considered negatively in the differential equation of T_4,th. In (15), these two terms were only present in the differential equation of T_3p, because T_4,th was not considered as additional state. The constants α_th and β_th are the dilution factor and the clearance exponent for T_4,th, respectively. Furthermore, the differential equation of T₄ in plasma changes to

$\begin{array}{ll}\frac{d{T}_4}{dt}\left(t\right)={\alpha }_T{G}_{MT}\frac{T_{4,th}\left(t-{\tau }_{0T}\right)}{K_{MT}+T_{4,th}\left(t-{\tau }_{0T}\right)}-{\beta }_T{T}_4\left(t\right).& (3)\end{array}$

The parameters α_T and β_T are again the dilution factor and the clearance rate constant, respectively, for T₄. The dead time τ_0T is introduced in order to account for diffusion processes. Compared to (15), the production rate of the peripheral T₄ does no longer correspond to G_T TSH/(D_T+TSH), but to the part of T_4,th which is transported out of the thyroid cells.

The numerical values of the majority of the model’s parameters can be taken from (13–15). They have been determined experimentally or derived from known quantities like the half-life of the hormone concentrations. However, the parameters G_T, G_D1 and G_T3² must be re-estimated by fitting them to real measurements of hormone concentrations, because the previous versions of the model did not consider membrane transporters (13–15). In addition, the introduced maximal activity of the membrane transporter G_MT must also be fitted to real hormone measurements. In turn, the Michaelis-Menten constant of the MCT8 for the transport of T₄ was determined experimentally in (6) and its value is applied here for K_MT (although this is a simplification since different mutations will most likely lead to different sensitivities to T₄ and since the net effects of all membrane transporters will also result in a different sensitivity of T₄ compared to the sensitivity of MCT8 alone). This is a meaningful approach, since the Michaelis-Menten constant remains the same for a specific transporter/substrate process (19). To find the numerical parameter values, we neglect the age dependence of the T₃ concentrations of AHDS patients, as documented in (2) and the age dependence of the T₄ content in thyroid cells documented in (20). Even though such a consideration would certainly be advantageous, it is probably not indispensable and would further add complexity to the model.

The factor α_th is defined as the inverse of the volume of distribution of T₄ in the thyroid gland. We choose ${\alpha }_{th}=250\frac{1}{\text{l}}$, which corresponds to a volume of distribution of 4 ml. This volume of distribution is based on the assumption that the intracellular parts of the thyroid gland make up one third of the whole volume of the thyroid gland. Furthermore, we choose the clearance exponent for T₄ in the thyroid gland as β_th = 4.4·10^-6 s^-1 corresponding to a half-life of T₄ in the thyroid gland of 44 h, a value determined in [20] for rat thyroids. We want to emphasize that the exact numerical values of α_th and β_th do not considerably influence our results. Even if the true values differ to some extent from the ones that we suggest here, our main results (see next section) remain the same, i.e., that the hormone levels of AHDS patients can be explained by damaged membrane transporters. A summary of the entire numerical parameter values can be found in Section S9 in the Supplementary Material.

Note that the MCT8 also transports T₃ (21). Membrane transporters for T₃ could be considered in the model by means of an additional state representing the T₃ content in thyroid cells. The mathematical formulation and the results of this consideration are given in Section S6 in the Supplementary Material. Problematically, the consideration of membrane transporters for T₃ lead to parameters that are structurally not identifiable using the measurable hormone quantities only. Consequently, our model did not allow to consider membrane transporters for T₃ in a reliable and physiologically meaningful way. Moreover, since the T₃ transport may not be harmed in MCT8 deficiency, compare (8), we do not consider membrane transporters for T₃ in the following. Nevertheless, neglecting membrane transporters for T₃ is a simplification, since it has been explicitly shown that the MCT8 transports T₃ in humans (21).

Parameter estimation

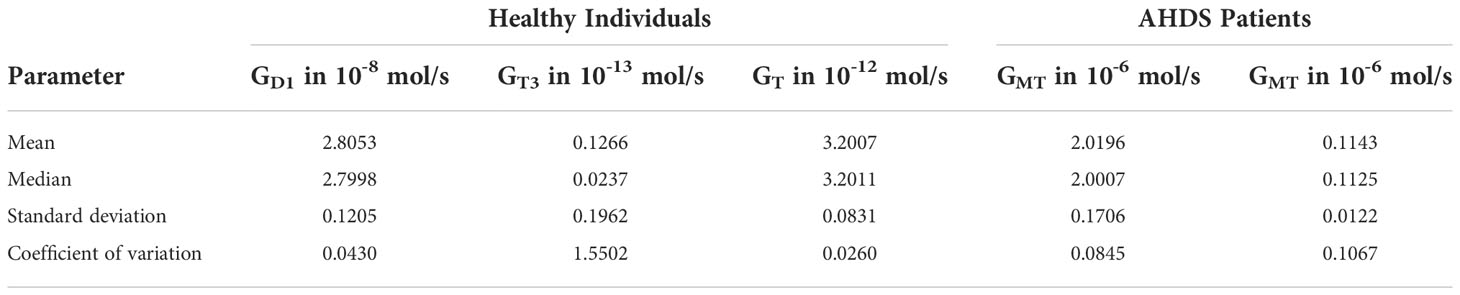
The parameter estimation of G_T, G_D1 G_T3 and G_MT is done through a constrained parameter optimization. The idea is to find the optimal configuration of parameters with respect to a cost function by adhering to the system dynamics. We choose the cost function as the normalized quadratic error between real measured hormone concentrations and hormone concentrations computed by the model. Regarding healthy individuals, we use the mean dynamic hormone concentrations documented in (16). In order to quantify the uncertainty related to the parameter estimation, we perform parametric bootstrapping. In other words, we first determine the optimal parameters of the mathematical model using the mean hormone concentrations. The mathematical formulation of this estimation can be found in Section S3 in the Supplementary Material. Then, we simulate the mathematical model (using the optimal parameters) 100 times and artificially corrupt the simulated hormone concentrations by noise that follows a normal distribution with μ =0 and σ =0.1. For each of the 100 datasets, we determine the optimal parameters. Finally, based on this set of optimal parameters, we compute the mean, median, standard deviation and coefficient of variation of all parameters.

For AHDS patients, the estimated (mean) G_T, G_D1 and G_T3 parameters are held constant and only G_MT is re-estimated for AHDS patients³. To this end, we use steady-state hormone concentrations measured in (22–26). Note that, in contrast to the parameter estimation related to healthy individuals, we use steady-state hormone measurements to estimate the G_MT parameter for AHDS patients. To the best of the authors’ knowledge, there are no dynamic hormone measurements of AHDS patients available in the literature that could be applied here. Once again, we perform parametric bootstrapping in order to quantify the uncertainty in the parameters. Here, we use the steady-state hormone concentrations to determine the optimal G_MT parameter for AHDS patients. The exact mathematical formulation of the estimation regarding AHDS patients is given in Section S4 in the Supplementary Material. Based on this optimal parameter, we simulate the hormone concentrations of AHDS patients dynamically 100 times and corrupt the simulated FT₃, FT₄ and TSH concentrations by some normally distributed noise with μ =0 and σ =0.1. From here on, we proceed in the same way as for healthy individuals. Note that the estimation of the parameters in both cases requires a normalization of the state variables, which is described in Section S2 in the Supplementary Material.

Moreover, for healthy individuals and AHDS patients, we compute the parameters individually. Regarding healthy individuals, we use 27 dynamic hormone measurements documented in (16) and regarding AHDS patients, we use 13 measurements from (22–26). This allows to quantify the variability in the estimated parameters differently, namely by computing the mean, median, standard deviation and the coefficient of variation regarding the individually estimated parameters. Subsequently, we compute a two-sample t-test to analyze whether the mean of the G_MT parameter (describing the maximal activity of the transporters) differs significantly between healthy individuals and AHDS patients for a significance level of 5%. Furthermore, we determine the individual steady-state hormone concentrations of healthy individuals and AHDS patients and analyze whether the mean hormone concentrations differ significantly between healthy individuals and AHDS patients. These results are shown in the Supplementary Material in Section S5. Note that one could also perform a parametric bootstrapping for each healthy individual (or AHDS patient) if one is interested in quantifying the individual parameter uncertainty. However, this is beyond the scope of this work.

Finally, we perform dynamic simulations to illustrate the course of the hormone concentrations related to healthy individuals and to AHDS patients. We chose arbitrarily a simulation length of 30 days. For the dynamic simulations, we apply the mean parameters (using bootstrapping) determined in both cases. Therefore, the simulation results can be interpreted as hormone concentrations from a generic euthyroid subject and a generic AHDS patient.

When taking a closer look on the expression of (2), one recognizes that a linear approximation of the term is possible if K_MT>> T_4,th. By defining the constant k_l = G_MT/K_MT, expression (2) becomes

$\begin{array}{ll}{G}_{MT}\frac{T_{4,th}}{K_{MT}+T_{4,th}}\approx G_{MT}\frac{T_{4,th}}{K_{MT}}& (4)\end{array}$

$\begin{array}{ll}=k_l{T}_{4,th}.& (5)\end{array}$

This means that we can model the functionality of the membrane transporters linearly if the mentioned condition is fulfilled. In this case, equations (1) and (3) must be changed accordingly. The procedure of the parameter estimation remains the same. The only difference is that we have to estimate k_l instead of G_MT. Once again, we perform bootstrapping to quantify the uncertainty of the estimated parameters regarding healthy individuals and AHDS patients. Furthermore, we estimate the parameters individually and quantify the uncertainty based on the individually estimated parameters and show the results in Section S5 of the Supplementary Material.

As an additional contribution, we perform a local stability analysis. So far, this was not done for any other version of the here applied mathematical model of the pituitary-thyroid feedback loop (13–15). A stability analysis is interesting for the highly perturbed pituitary-thyroid feedback loop system of AHDS patients. It helps to answer the question whether the feedback loop is stable for damaged membrane transporters. The presentation of the employed method and of the corresponding results are given in the Supplementary Material Section S7. This analysis reveals local exponential stability of the equilibrium hormone concentrations.

Results

First, the results of the parameter estimation and of the dynamic simulations for the Michaelis-Menten modeling of the membrane transporters are presented. Second, the analogous results for the linear modeling of the membrane transporters are shown.

Michaelis-Menten modeling

The results of the parameter estimation are shown in Table 1. This table illustrates the mean, median, standard deviation, and coefficient of variation of all the estimated parameters for healthy individuals and for AHDS patients using bootstrapping. Regarding healthy individuals, one can see that the parameters G_D1, G_T, and G_MT show a relatively small coefficient of variation, i.e., a low uncertainty. However, the G_T3 parameter shows a high coefficient of variation, i.e., a high uncertainty. Most importantly, there is great difference in the numerical values between the G_MT parameter for healthy individuals and the one for AHDS patients in addition to the low uncertainty of this parameter. The G_MT parameter related to healthy individuals is approximately 18 times higher compared to the G_MT parameter related to AHDS patients.

TABLE 1

Table 1 Statistics of the Parameter estimation.

Once the unknown parameter values are determined, dynamic simulations can be performed using the mean parameter estimates as documented in Table 1. The course of the hormone concentrations of TSH, FT₄, FT₃ and T_4,th are given in Figure 3, where a sinusoidal TRH input was used (as an approximation of the real pulsatile TRH course). Regarding the hormone concentrations, one can see that the FT₃ and the TSH concentrations are approximately 1.4 times higher for AHDS patients compared to healthy individuals. In turn, the FT₄ concentration is 2.1 times higher for healthy individuals compared to AHDS patients. Interestingly, the T_4,th concentration is approximately 18 times higher for AHDS patients compared to healthy individuals. Note the advantage of applying a mathematical model: we are able to make conclusions about the T₄ content in thyroid cells which cannot be measured in AHDS patients.

FIGURE 3

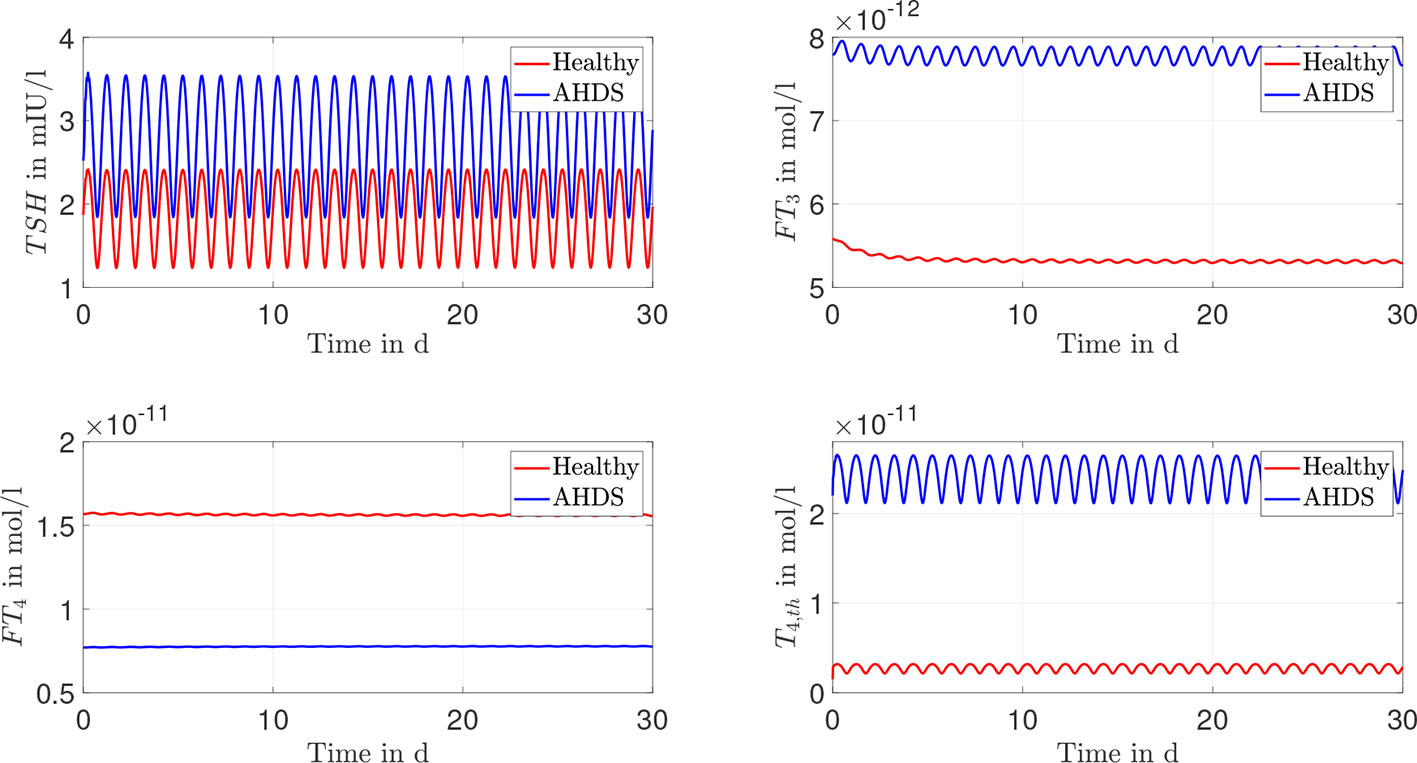
Figure 3 Results of the dynamic simulations for the Michaelis-Menten modeling of the membrane transporters. Most of the numerical parameter values are based on the suggestions of (13, 15). The remaining unknown parameters of the model are estimated through a constrained parameter optimization and shown in Table 1.

Linear modeling

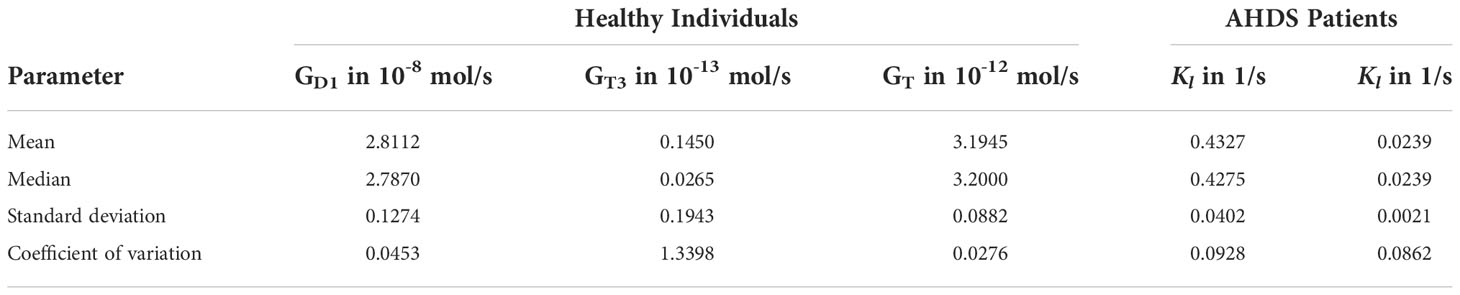
We now focus on the results of the linear approximation of the membrane transporters. As can be seen from Figure 3 and Section S9 of the Supplementary Material, the assumption K_MT = 4.7·10^-6 >> T_4,th ≈ 2.5·10^-12 is fulfilled. Therefore, the same analysis as in the previous subsection is performed with the linear approximation of the membrane transporters. The results of the parameter estimation are shown in Table 2.

TABLE 2

Table 2 Statistics of the Parameter estimation.

The mean values of the G_D1 G_T3, and G_T parameters of the linear modeling of the membrane transporters are similar to the ones of the Michaelis-Menten modeling. The mean value k_l = 0.4327 for healthy individuals (k_l = 0.0239 for AHDS patients) corresponds approximately to G_MT/K_MT = 0.4297 (G_MT/K_MT = 0.0243 for AHDS patients), compare Table 1 and Section S9 of the Supplementary Material. Once again, the value of k_l is approximately 18 times higher for healthy individuals compared to AHDS patients. The uncertainty related to the parameters is similar compared to the Michaelis-Menten modeling of the membrane transporters.

Again, one can perform dynamic simulations with the model considering the linearly approximated membrane transporters and the mean value of the estimated parameters as indicated in Table 2. The courses of the hormone concentrations are given in Figure 4. One can see that there is virtually no difference in the dynamic course of the hormone concentrations between the Michaelis-Menten modeling of the membrane transporters and its linear approximation.

Discussion

In this section, we discuss the obtained results and place them in a larger context. First, we focus on our main contribution, the investigations around the mechanisms of the AHDS. Second, we compare the Michaelis-Menten modeling approach to its linear approximation. Finally, we discuss the parameter estimation.

Mechanisms of the AHDS

The documented results of the dynamic simulations (compare Figures 3, 4) clearly demonstrate that the unusual hormone concentrations of AHDS patients are observed in the simulations of the mathematical model when damaged membrane transporters are considered. This result holds true for the Michaelis-Menten and the linear modeling of the membrane transporters. The simulated hormone concentrations of AHDS patients are additionally in line with the mean measured hormone concentrations presented by (2), which is a large study dealing with MCT8 deficiency (TSH = 2.97 mIU/l, FT₄ = 9.48·10^-12 mol/l).

FIGURE 4

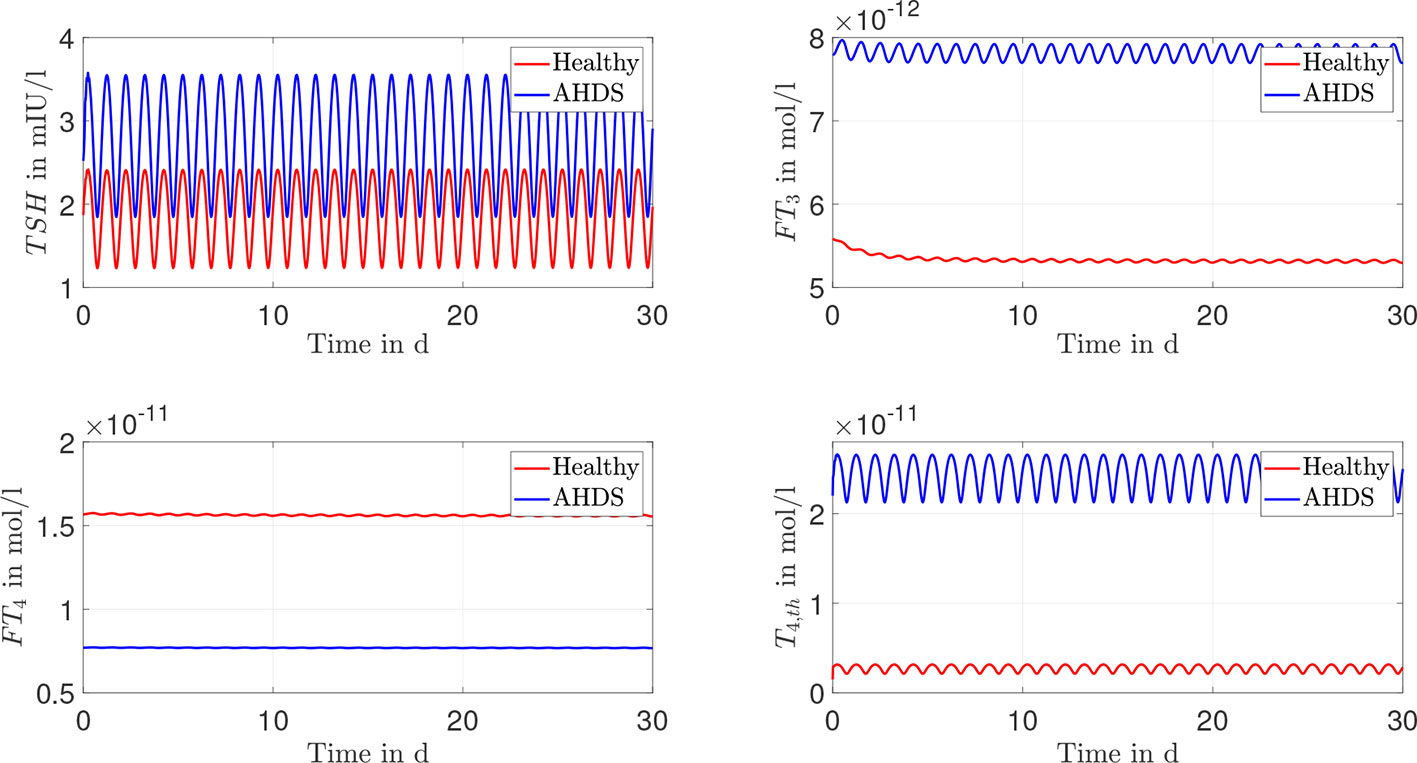
Figure 4 Results of the dynamic simulations of the linear modeling of the membrane transporter. Again, most of the numerical parameter values are based on (13, 15). The remaining parameters are estimated through a constrained parameter optimization approach and shown in Table 2.

One must also keep in mind that the hormone concentrations of healthy individuals should not change substantially, when incorporating membrane transporters. They should remain in the reference range of healthy individuals (TSH: 0.5 - 4.5 mIU/l, FT₄: 1.2 – 2.7·10^-11 mol/l and FT₃: 3.5 – 6.3·10^-12 mol/l (27)). The dynamic simulations of the mathematical model reveal (see Figures 3, 4) that the hormone concentrations of healthy individuals remain within the reference range of healthy individuals. Thus, the introduction of the membrane transporters does not impact the usability of the mathematical model for healthy individuals. The incorporation of the membrane transporters extends the possible applications of the mathematical model.

Since the concentration of T_4,th does not correspond to a hormone concentration which can be measured with today’s assay technology, it is difficult to evaluate its accordance with human data. Alternatively, the concentration can be compared to studies that are made with mice, e.g., the study (8). In this study, an investigation is done regarding the thyroidal T₄ content of Mct8 KO mice. It is reported that the thyroids of these mice contain approximately a 3-fold elevation of T₄ compared to wild-type littermates (8). In the presented mathematical model one can interpret the state T_4,th on a high level as T₄ content in thyroid cells. Regarding the Michaelis-Menten modeling approach of the membrane transporters and its linear approximation, the T₄ content in thyroid cells (described by the state T_4,th) is approximately 18 times higher for AHDS patients compared to healthy individuals.

Therefore, the mathematical model is in line with the documented observation that the T₄ content in thyroid cells is increased in MCT8 deficiency (8). This is an indication that the T₄ content in thyroid cells is not only increased for Mct8 KO mice, but also for AHDS patients. Compared to the results of (8), one must keep in mind that the difference between the T₄ content in thyroid cells of AHDS patients to healthy individuals is higher in the mathematical model (18-fold increase), than the documented difference of Mct8 KO mice to wild-type littermates (3-fold increase).

At that point we can additionally evaluate the hypothesis that the T₄ retention in thyroid cells represents one important mechanism to the unusual hormone concentrations of AHDS patients (12). In the simulations of this work, damaged membrane transporters go along with an increased T₄ content in thyroid cells and ultimately the unusual hormone concentrations of AHDS patients. Thus, additional evidence is given to the hypothesis stated in (12) by means of the mathematical model.

If we take a more precise look on the considerations mentioned in (12), one remarks a small but important difference between their considerations and our results. The authors in (12) assign the high concentration of FT₃ to the retention of T₄ inside the thyroid. In turn, the assumption is made that the low concentrations of FT₄ are due to a renal contribution, as the renal T₄ content is increased in MCT8 deficiency (9, 12).

The difference to our results is that the simulations lead to the entirety of the unusual hormone concentrations of AHDS patients, including a lower concentration of FT₄. This is an indication that the T₄ retention in thyroid cells does not only represent one mechanism leading to the unusual hormone concentrations of AHDS patients, but could even be fully responsible for these unusual concentrations. In other words, the simulations of the mathematical model suggest that an additional renal contribution might not be necessary to replicate the entirety of the unusual hormone concentrations of AHDS patients.

To evaluate the role of the kidney in the genesis of the unusual hormone concentrations of AHDS patients by means of the mathematical model, an explicit representation of it is necessary. This is currently not the case, because the model merges the effects of the different peripheral organs like the kidney and the liver as well as the effects of muscle tissue under one general component, the periphery. Once an explicit representation of the kidney is incorporated into the model, membrane transporters could be considered at the edge of the kidney to the bloodstream, which would allow a more precise investigation of the assumptions from (12). However, the further refinement of the model usually goes along with more parameters that must be estimated, which becomes more difficult. Nevertheless, the explicit consideration of the kidney in the mathematical model is an interesting issue for further research.

Finally, we discuss our results with respect to the single case report documented in (11) in which one AHDS patient was examined before and after thyroidectomy. Before thyroidectomy the patient received 75 (or 10 µ/g per day) of levothyroxine (L-T₄) to normalize the TSH concentration. The exact hormone concentrations were FT₄ ≈ 1.06·10^-11 mol/l, T₃ ≈ 7.92·10^-9 mol/l and TSH =0.1 mIU/l [compare Figure 2 in (11)]. After thyroidectomy and 125 µg (or 6 µg/kg per day) of L-T₄, the patient’s hormone concentrations were FT₄ ≈ 1.05·10^-11 mol/l, T₃ ≈ 4.21·10^-9 mol/l and TSH =0.48 mIU/l [again, compare Figure 2 in (11)].

Note that the normalization of the TSH concentration goes along with a substantially higher concentration of T₃ before thyroidectomy compared to the concentration of T₃ after thyroidectomy. This indicates that a retention of T₄ in thyroid cells could be responsible for the high T₃ concentrations, which is a conclusion in line with the simulation results. The FT₄ concentrations remain approximately constant in both cases. As already mentioned, this points to extrathyroidal mechanisms explaining the low FT₄ concentrations of AHDS patients. In contrast, the simulation results suggest that such extrathyroidal events do not have to be present in order to replicate the hormone concentrations, which seems to be a contradiction at first sight. However, since we do not consider the kidney explicitly in the mathematical model, we also do not exclude extrathyroidal mechanisms from possibly contributing to the unusual hormone concentrations. This aspect can currently not be answered by means of the model, since the kidney is not considered explicitly.

Furthermore, future work could focus on other phenomena related to MCT8 deficiency that were not treated in the context of this work. For example, in Mct8/D1 double KO mice, a partial normalization of thyroid hormone concentrations takes place [compare (28)]. An analysis whether the same observation can be made exploiting the mathematical model of the pituitary-thyroid feedback loop would potentially further deepen the knowledge regarding the AHDS.

Comparison of the Michaelis-Menten modeling approach to its linear approximation

Two possibilities to model the membrane transporters are presented in this paper. The Michaelis-Menten modeling of the membrane transporters follows a common approach to model transporter/substrate reactions (29). A saturation of the transported T₄ can take place, when no membrane transporters are available, i.e., T_4,th >>K_MT in equation (2). The linear modeling of the membrane transporters has an appealing simplicity. The intuitive idea that a certain percentage (k_l) of T₄ is transported out of thyroid cells is easy to understand. However, this approximation is only applicable for a specific range of T_4,th, namely as long as T_4,th<<K_MT. If this is not the case, the linear approximation is not valid anymore.

In our case, the necessary requirement in order to model the functionality of the membrane transporters linearly is fulfilled (K_MT = 4.7·10^-6 >> 2.50·10^-12 = T_4,th). The results of the parameter estimation demonstrate that this approximation is meaningful. This can be seen in the following way. For healthy individuals the term G_MT/K_MT ≈ 0.43 of the Michaelis-Menten modeling is approximately equal to k_l ≈ 0.43 of the linear modeling of the membrane transporters (compare Tables 1, 2). The same holds true for the estimated parameters of AHDS patients: G_MT/K_MT ≈ 0.02, k_l ≈ 0.02. Given these results, there might be no substantial advantage applying the Michaelis-Menten modeling of the membrane transporters over the linear modeling of the membrane transporters. In conclusion, the application of the linear modeling of the membrane transporters reduces the complexity of the model and leads to similar results.

The applied mathematical model exploits parameters that were determined for humans as well as parameters that were determined for rodents, even though some aspects of the thyroid homeostasis are different. The model does not aim for an exact representation of humans which would be impossible due to an inter-variability of the parameters even for humans only. However, note that it is possible to obtain an understanding of the cause-effect relationships even for these “generic” parameter values (that do not correspond to one individual human subject). Namely, the qualitative behavior that is obtained from simulating the model is the same for different parameter values. Mathematically, this can be shown by a sensitivity analysis for the parameters, compare (15). So even if the parameters do not all correspond to the true parameters of a (one individual) human subject, the observed phenomena are still representative for the cause-effect relationships in the human HPT axis.

So far, the loss of thyroid hormone transport activity is only considered at the thyroid gland for T₄. Investigating how MCT8 deficiency affects the complete pituitary-thyroid feedback loop (i.e., considering a loss of thyroid hormone transport activity at further locations) is an interesting topic for future research.

Parameter estimation

In the context of the parameter estimation, we considered the estimated values of G_D1, G_T, and G_T3 for healthy individuals as fixed for AHDS patients. This approach can be interpreted in a physiological sense that the biological maximal activity of D1 (corresponding to G_D1 in the model) is the same for healthy individuals and AHDS patients. It is difficult to evaluate whether this approach is reasonable, since most studies only evaluate the activity of D1 and not the maximal activity. Additionally, the total D1 activity is an extensive parameter, i.e., it depends on the number of expressing cells, approximately on body mass. Therefore, results from cell culture experiments and expression data from biopsies cannot be readily translated to the organismal level.

For example, the activity of D1 inside the thyroid does not change for Mct8 KO mice compared to wild-type littermates (8). In turn, no results regarding the maximal activity exist. These observations motivated us to assume a constant maximal activity of D1 and constant values of G_T3 and G_T in our parameter estimation, although there are no studies in the literature available examining this fact.

Furthermore, we consider dynamic hormone measurements of healthy individuals in order to calibrate our mathematical model. This improves the model in the sense that it approximates the dynamics of the real pituitary-thyroid feedback loop much better. Notice also that dynamic hormone measurements have so far not been used to estimate model parameters in any of the previous works related to the here applied model (13–15, 18).

Conclusion

In this paper, we included membrane transporters in the mathematical model of the pituitary-thyroid feedback loop, originally developed by (13–15). The extended model fully replicates the unusual hormone concentrations of AHDS patients and suggests that the retention of T₄ in thyroid cells could fully explain the unusual hormone concentrations of AHDS patients. Future work could focus on an explicit consideration of the kidney in the model in order to evaluate whether/how an accumulation of T₄ in the kidney (in MCT8 deficiency) leads to the unusual hormone concentrations of AHDS patients.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author. The Matlab/Simulink files that were used to perform the simulations are available online https://doi.org/10.25835/0049176.

Author contributions

TW drafted the manuscript and performed the calculations/simulations with Matlab/Simulink, under the supervision of MM and with input from JD. CV derived the Michaelis-Menten modeling approach of the membrane transporters and its linear approximation and worked on the incorporation of the membrane transporters into the mathematical model, also under the supervision of MM and with input of JD. All authors contributed to the article and approved the submitted version.

Funding

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 948679).

Acknowledgments

We wish to thank Professor Richard Ross, Department of Oncology and Metabolism, University of Sheffield, United Kingdom for generously supplying data.

Conflict of interest

JD received funding and personal fees by Sanofi-Henning, Hexal AG, Bristol-Myers Squibb, and Pfizer, and is co-owner of the intellectual property rights for the patent “System and Method for Deriving Parameters for Homeostatic Feedback Control of an Individual” Singapore Institute for Clinical Sciences, Biomedical Sciences Institutes, Application Number 201208940-5, WIPO number WO/2014/088516.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fendo.2022.882788/full#supplementary-material

Footnotes

1. ^ Note that one could also sum up the net effects of D1 and D2 in a single term. Here, we do not follow this approach since it is less suitable to analyze, e.g., the effects of genetic variants [compare (18)] affecting the activity of D1 or D2 in the context of AHDS, which is an interesting subject for future research.
2. ^ The maximal activity regarding the direct T₃ synthesis path is denoted by G_T3, compare Figure 2.
3. ^ Note that by using this approach, we assume that the complete physiology (except for the introduced membrane transporters) is equal for AHDS patients and healthy individuals.

References

1. Allan W, Herndon CN, Dudley FC. Some examples of the inheritance of mental deficiency: Apparently sex-linked idiocy and microcephaly. Am J Ment Defic (1944) 48:325–34.

Google Scholar

2. Groeneweg S, van Geest FS, Abacı A, Alcantud A, Ambegaonkar GP, Armour CM, et al. Disease characteristics of MCT8 deficiency: An international, retrospective, multicentre cohort study. Lancet Diabetes Endocrinol (2020) 8:594–605. doi: 10.1016/S2213-8587(20)30153-4

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Schwartz CE, May MM, Carpenter NJ, Rogers RC, Martin J, Bialer MG, et al. Allan-Herndon-Dudley syndrome and the monocarboxylate transporter 8 (MCT8) gene. Am J Hum Genet (2005) 77:41–53. doi: 10.1086/431313

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Dumitrescu AM, Liao XH, Best TB, Brockmann K, Refetoff S. A novel syndrome combining thyroid and neurological abnormalities is associated with mutations in a monocarboxylate transporter gene. Am J Hum Genet (2004) 74:168–75. doi: 10.1086/380999

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Friesema ECH, Grueters A, Biebermann H, Krude H, von Moers A, Reeser M, et al. Association between mutations in a thyroid hormone transporter and severe x-linked psychomotor retardation. Lancet (London England) (2004) 364:1435–7. doi: 10.1016/S0140-6736(04)17226-7

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Friesema ECH, Ganguly S, Abdalla A, Manning Fox JE, Halestrap AP, Visser TJ. Identification of monocarboxylate transporter 8 as a specific thyroid hormone transporter. J Biol Chem (2003) 278:40128–35. doi: 10.1074/jbc.M300909200

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Friesema ECH, Visser WE, Visser TJ. Genetics and phenomics of thyroid hormone transport by MCT8. Mol Cell Endocrinol (2010) 322:107–13. doi: 10.1016/j.mce.2010.01.016

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Trajkovic-Arsic M, Mueller J, Darras VM, Groba C, Lee S, Weih D, et al. Impact of monocarboxylate transporter-8 deficiency on the hypothalamus-pituitary-thyroid axis in mice. Endocrinology (2010) 151:5053–62. doi: 10.1210/en.2010-0593

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Trajkovic-Arsic M, Visser TJ, Darras VM, Friesema ECH, Schlott B, Mittag J, et al. Consequences of monocarboxylate transporter 8 deficiency for renal transport and metabolism of thyroid hormones in mice. Endocrinology (2010) 151:802–9. doi: 10.1210/en.2009-1053

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Dumitrescu AM, Liao XH, Weiss RE, Millen K, Refetoff S. Tissue-specific thyroid hormone deprivation and excess in monocarboxylate transporter (MCT) 8-deficient mice. Endocrinology (2006) 147:4036–43. doi: 10.1210/en.2006-0390

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wirth EK, Sheu S, Chiu-Ugalde J, Sapin R, Klein MO, Mossbrugger I, et al. Monocarboxylate transporter 8 deficiency: Altered thyroid morphology and persistent high triiodothyronine/thyroxine ratio after thyroidectomy. European Journal of Endocrinology (2011) 165(4), 555–561.

PubMed Abstract | Google Scholar

12. Müller J, Heuer H. Understanding the hypothalamus-pituitary-thyroid axis in Mct8 deficiency. Eur Thyroid J (2012) 1:72–9. doi: 10.1159/000339474

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Dietrich JW. Der Hypophysen-Schilddrüsen-Regelkreis: Entwicklung und klinische Anwendung eines nichtlinearen Modells. (Berlin, Germany: Logos Verlag) (2001). doi: 10.13140/RG.2.1.4845.9368.

CrossRef Full Text | Google Scholar

14. Dietrich JW, Tesche A, Pickardt CR, Mitzdorf U. Thyrotropic feedback control: Evidence for an additional ultrashort feedback loop from fractal analysis. Cybernet Syst (2004) 35:315–31. doi: 10.1080/01969720490443354

CrossRef Full Text | Google Scholar

15. Berberich J, Dietrich JW, Hoermann R, Müller MA. Mathematical modeling of the pituitary-thyroid feedback loop: Role of a TSH-T3-shunt and sensitivity analysis. Front Endocrinol (2018) 9:91. doi: 10.3389/fendo.2018.00091

CrossRef Full Text | Google Scholar

16. Russell W, Harrison RF, Smith N, Darzy K, Shalet S, Weetman AP, et al. Free triiodothyronine has a distinct circadian rhythm that is delayed but parallels thyrotropin levels. J Clin Endocrinol Metab (2008) 93:2300–6. doi: 10.1210/jc.2007-2674

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Murray JD. Mathematical biology: I. an introduction vol. 17. Springer Science & Business Media (Berlin/Heidelberg, Germany) (2007).

Google Scholar

18. Wolff TM, Dietrich JW, Müller MA. Optimal hormone replacement therapy in hypothyroidism - a model predictive control approach. Front Endocrinol (2022) 13:884018. doi: 10.3389/fendo.2022.884018

CrossRef Full Text | Google Scholar

19. Berg JM, Tymoczko JL, Stryer L. Biochemistry. New York: w. h. New York: Freeman and Company (2002).

Google Scholar

20. Di Cosmo C, Liao XH, Dumitrescu AM, Philp NJ, Weiss RE, Refetoff S. Mice deficient in MCT8 reveal a mechanism regulating thyroid hormone secretion. J Clin Invest (2010) 120:3377–88. doi: 10.1172/JCI42113

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kinne A, Kleinau G, Hoefig CS, Grüters A, Köhrle J, Krause G, et al. Essential molecular determinants for thyroid hormone transport and first structural implications for monocarboxylate transporter 8. J Biol Chem (2010) 285:28054–63. doi: 10.1074/jbc.M110.129577

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Maranduba C, Friesema EC, Kok F, Kester MH, Jansen J, Sertie AL, et al. Decreased cellular uptake and metabolism in Allan-Herndon-Dudley syndrome (ahds) due to a novel mutation in the MCT8 thyroid hormone transporter. J Med Genet (2006) 43:457–60. doi: 10.1136/jmg.2005.035840

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Chen X, Liu L, Zeng C. A novel variant in SLC16A2 associated with typical Allan-Herndon-Dudley syndrome: A case report. BMC Pediatr (2022) 22:1–5. doi: 10.1186/s12887-022-03259-5

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Anik A, Kersseboom S, Demir K, Çatlı G, Yiş U, Böber E, et al. Psychomotor retardation caused by a defective thyroid hormone transporter: Report of two families with different MCT8 mutations. Hormone Res Paediat (2014) 82:261–71. doi: 10.1159/000365191

CrossRef Full Text | Google Scholar

25. Rego T, Lado CG, Rodríguez PC, Santos FS, Angueira FB, Castro-Feijóo L, et al. Severe neurological abnormalities in a young boy with impaired thyroid hormone sensitivity due to a novel mutation in the mct8 gene. Hormones (2017) 16:194–9. Available at: https://doi.org/10.14310/horm.2002.1733.

PubMed Abstract | Google Scholar

26. Azzolini S, Nosadini M, Balzarin M, Sartori S, Suppiej A, Mardari R, et al. Delayed myelination is not a constant feature of Allan-Herndon-Dudley syndrome: Report of a new case and review of the literature. Brain Dev (2014) 36:716–20. doi: 10.1016/j.braindev.2013.10.009

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Visser WE, van Mullem AAA, Visser TJ, Peeters RP. Different causes of reduced sensitivity to thyroid hormone: Diagnosis and clinical management. Clin Endocrinol (2013) 79:595–605. doi: 10.1111/cen.12281

CrossRef Full Text | Google Scholar

28. Liao XH, Di Cosmo C, Dumitrescu AM, Hernandez A, Van Sande J, St Germain DL, et al. Distinct roles of deiodinases on the phenotype of MCT8 defect: A comparison of eight different mouse genotypes. Endocrinology (2011) 152:1180–91. doi: 10.1210/en.2010-0900

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Alberts B. Molecular biology of the cell. 6 edn. New York, NY: Garland Science (2015).

Google Scholar