
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Electron. Mater, 15 February 2024
Sec. Superconducting Materials
Volume 4 - 2024 | https://doi.org/10.3389/femat.2024.1346235
This article is part of the Research TopicProgress on Superconducting Materials for SRF ApplicationsView all 8 articles
Muon spins precess in transverse magnetic fields and emit a positron preferentially in the spin direction at the instant of decay, enabling muon spin rotation (μSR) as a precise probe of local magnetic fields in matter. μSR has been used to characterize superconducting radio-frequency (SRF) materials since 2010. At TRIUMF, a beam of 4.2 MeV μ+ is implanted at a material-dependent depth of approximately 150 μm. A dedicated spectrometer was developed to measure the field of first vortex penetration and pinning strength in SRF materials in parallel magnetic fields of up to 300 mT. A low-energy beam available at PSI implants μ+ at variable depth in the London layer allowing for direct measurements of the London penetration depth from which other material parameters relevant for SRF applications, such as the lower critical field and the superheating field, can be calculated. Beta-detected nuclear magnetic resonance (β-NMR) is a technique similar to low-energy μSR using beams of low-energy β radioactive ions. With a recent upgrade, it is capable of detecting the penetration of parallel magnetic vortices, depth resolved with nanometer resolution at applied fields of up to 200 mT. In this paper, we review the impact and capabilities of these techniques for SRF research.
Superconducting radio-frequency (SRF) cavities made of niobium are the backbone of modern high-power particle accelerators for subatomic physics research. Advanced surface and heat treatments have pushed the performance of the state-of-the-art elliptical cavities optimized to accelerate electrons close to fundamental material limitations in terms of maximum accelerating gradient and power dissipation. Cavities are made of metal sheets with a typical thickness of a few mm, while RF shielding currents only flow within a thin layer as superconducting currents decay exponentially over the length scale of the London penetration depth, which is approximately 30 nm for clean niobium. Optimized performance is achieved by baking cavities in vacuum or in a low-pressure gas atmosphere. These treatments alter the concentrations of oxygen and other impurities of the outermost layer through diffusion. Depending on the desired performance characteristics, different tailored treatments are chosen. For example, different treatments yield the highest accelerating gradients or lowest losses. Often, cavity treatments have been found accidentally, and optimization was performed by empirical studies varying treatment parameters rather than based on dedicated material science studies. Muon spin rotation (μSR) and beta-detected nuclear magnetic resonance (β-NMR) are material science techniques that can measure relevant material parameters such as critical fields, pinning strength, Meissner screening, and magnetic impurities of superconducting niobium prepared for SRF applications. Low-energy muon spin rotation (LE-μSR) and β-NMR further allow for depth-resolved measurements with nanometer resolution of these properties.
The current material of choice for SRF cavities is niobium. It has the highest critical temperature among all elemental superconductors and the highest lower critical field Hc1 of all known superconductors. Power dissipation can be minimized using superconductors with a higher critical temperature with technical Nb3Sn, already outperforming Nb at 4.2K (Posen and Hall, 2017) at a moderate accelerating gradient. The highest accelerating gradients are currently still achieved with bulk niobium technology, and it is unlikely that the accelerating gradient of niobium can be pushed much beyond the current state of the art as the best cavities reach surface magnetic fields close to the superheating field. A potential approach to reaching accelerating gradients beyond the fundamental limitations of niobium technology is to coat superconducting layers thinner than the London penetration depth on niobium cavities. Several mechanisms have been proposed by which such structures can enable larger accelerating gradients; some require dielectric interlayers as initially proposed by Gurevich (2006). So far, only a few cavity measurements have been reported, and generally, coated cavities show lower quality factors and accelerating gradients compared to bulk niobium. The origin of current limitations remains unclear, signifying the need for microscopic studies to further develop heterostructures for SRF application. LE-μSR and β-NMR studies can provide depth-resolved information on the nanometer scale and are, therefore, well suited for studying SRF materials beyond niobium.
In this paper, we first introduce μSR, LE-μSR, and β-NMR in Section 2 and give some examples of work on superconductors that has motivated investigations into SRF materials. In SRF cavities, the magnetic field is on the order of 200 mT and is applied parallel to the surface. In order to achieve these conditions in μSR and β-NMR experiments, dedicated spectrometers have been developed. These are reviewed in Section 3. Since 2010, μSR has been used to study SRF materials, including niobium, Nb3Sn; and multilayers, while β-NMR investigations into SRF materials have only started in 2019. The results on the field of first vortex penetration, pinning strength, magnetic screening, and magnetic impurities are reviewed in Section 4. Finally, Section 5 summarizes the paper with a focus on measurement capabilities relevant to SRF application.
In this section, we briefly review the general aspects of μSR and β-NMR with a focus on how these methods have been applied to superconductors. The results on SRF materials are reviewed in Section 4.
μSR (Schenck, 1985; Lee et al., 1999; Yaouanc and Reotier, 2011; Blundell et al., 2022) is a powerful condensed matter technique for understanding superconductors in terms of their magnetic phase diagram and penetration depth, as well as for characterizing magnetic impurities. In the early 1970s, new high-intensity intermediate-energy accelerators were built at PSI, TRIUMF, and the LAMPF. These new ‘meson factories’ produced pions (and, therefore, muons) several orders of magnitude more than those from previous sources and, in doing so, ushered in a new era in the techniques and applications of μSR.
In these facilities, a high-energy proton beam (E ≥ 500 MeV) is targeted onto a low-Z material (typically beryllium or carbon). Via nuclear reaction, pions are produced. The pions π± have a mean lifetime of 26 ns and decay into muons and neutrinos.
Since the pion decay is a two-body decay with a defined helicity of the neutrino, the muons μ± are fully spin-polarized. Positively charged pions (π+) decaying at rest close to the surface of the target will produce muons (μ+) with a momentum of approximately 29.8 MeV/c and kinetic energy of 4.1 MeV. These positively charged muons are most commonly used in solid-state physics applications and are called “surface muons.” Implanted into solids, “surface muons” stop at a depth of 0.1–1 mm, depending on the composition and density (Eckstein, 1991).
The muon is a radioactive spin 1/2 particle with an average lifetime of τμ ≃ 2.2 μs. Its decay (given here for μ+)
is anisotropic (Scheck, 1978). The gyromagnetic ratio of the muon is γμ = 2π × 135.5 MHz/T, and therefore, the muon will undergo Larmor precession in a magnetic field B with an angular frequency of
By monitoring the decay positrons, the time evolution of the muon ensemble will lead to the following form:
where Ni(t) is the histogram of the time differences recorded in the positron detector i.
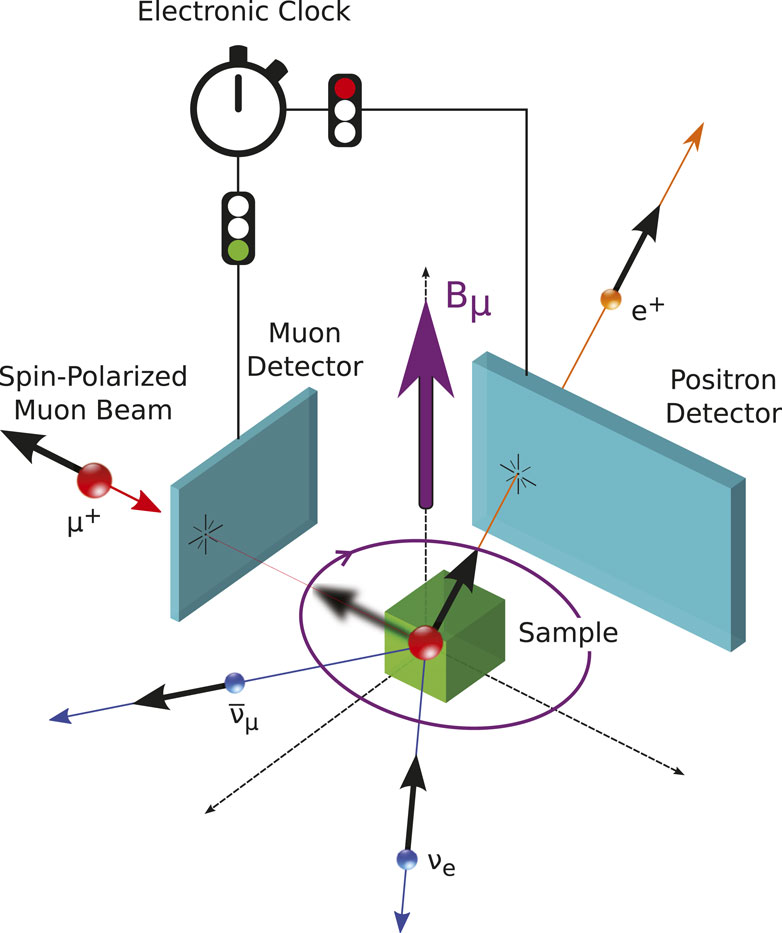
FIGURE 1. Schematic representation of a typical μSR setup. The muon detector will start a clock. An outgoing detected positron will stop the electronic clock. The time difference will be recorded in a positron decay histogram, which, after many decay events, will lead to the form of Eq. 1.
There are three principle setup geometries used in μSR: i) There is no external magnetic field applied, i.e., Bext = 0. These measurements are called zero-field μSR measurements (ZF-μSR). ZF-μSR measurements can be used to determine internal magnetic field distributions in solids. For example, it is possible to measure the sub-lattice magnetization of an antiferromagnet. ii) An external magnetic field is applied perpendicular to the muon spin, S, and therefore, these measurements are called transverse field measurements (TF-μSR). Here, the muon spin will precess around the total magnetic field B = Bext + Bint at the muon stopping site. This is widely used to study the vortex state of superconductors. iii) A magnetic field is applied collinearly to the muon spin. These measurements are called longitudinal field measurements (LF-μSR). In LF measurements, there is no muon spin precession present. The collinear field will lead to a Zeeman splitting of the muon spin energy levels. Since this splitting is energetically extremely small, there is essentially no spontaneous emission of radio quanta possible, even if the muon spin is in the excited state. The only way to flip the muon spin, which, in turn, leads to a depolarization of the muon spin ensemble, is to couple to magnetic fluctuations which have a spectral density at the muon Zeeman splitting. Therefore, this type of measurement can be used to study dynamics, i.e., internal magnetic field fluctuations.
The μ+ spin in a solid is dominated by dipolar interaction with its surroundings (Schenck, 1985; Lee et al., 1999; Yaouanc and Reotier, 2011; Blundell et al., 2022). This is different to NMR in solids, where most often, the nuclear spin interaction is predominantly of the Fermi-contact type (Abragam, 1961; Slichter, 1990). In para- and diamagnetic materials, the nuclear–muon dipolar interaction will be the only relevant one, whereas the details of the muon–nuclear interaction might be relevant, for example., as in the so-called F-μ-F states (Brewer et al., 1986; Wilkinson and Blundell, 2020), often the nuclear ensemble dipolar field distribution can be treated as a Gaussian continuum; i.e., the distribution for each magnetic field component is given as follows:
Here, ⟨ΔB2⟩ is the second moment of the magnetic field distribution of the nuclear dipolar fields, and Bα is one of the three field components. Since ⟨Bα⟩ = 0, the second moment simplifies to
assuming that the initial muon spin
where
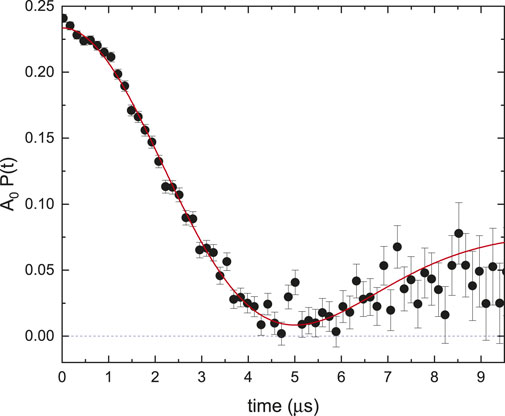
FIGURE 2. ZF time spectrum of Cu at T =5 K. The red curve is a fit to Eq. 4 with Δ =0.346 (4) μs−1. This corresponds to
Using the μSR technique, important characteristic length scales of superconductors can be determined, namely, the magnetic penetration depth λ and the coherence length ξ (Sonier et al., 2000). If a type-II superconductor is cooled below Tc in an applied magnetic field, H, for which Hc1 < H < Hc2, a flux-line lattice (FLL) is formed, which is in general incommensurate to the crystal lattice, and the vortex cores will be separated by a much larger distance than the unit cell. The muons stop at some specific crystallographic sites; they will quasi-randomly sample the magnetic field distribution of the FLL. In TF-μSR measurements, the muon spin will precess around the local field, and therefore, the muon spin ensemble measurement will lead to the following polarization function:
where σ0 is a broadening term due to nuclear dipoles, imperfections in the crystal structure, and the FLL. γμ = 2π × 135.5 MHz T−1 is the gyromagnetic ratio of the muon. ϕ is an initial phase of the muon spin in respect to the positron detector. p(B) is the magnetic field distribution probability.
For a perfect FLL, the magnetic field distribution can be expressed by a Fourier series (Brandt, 1988; Yaouanc et al., 1997; Brandt, 2003)
where r is the two-dimensional spatial vector in the plane perpendicular to the applied magnetic field. G is the reciprocal lattice vector of the FLL, and bG (λ, ξ) is the Fourier coefficient. ⟨B⟩ is the mean of the magnetic field distribution. Often, Eq. 5 can be well approximated by the following:
In this Gaussian approximation, σ is the depolarization rate, with
where Φ0 is the magnetic flux quantum. This approximation is valid in a wide range 0.13/κ2 ≪ (H/Hc2) ≪ 1, for a Ginzburg–Landau parameter κ = λ/ξ ≳ 70. This is true for the cuprates (Sonier et al., 2000), iron-based superconductors (Bhattacharyya et al., 2018), and other strongly correlated superconductors. Therefore, by measuring the depolarization rate σ(T), the temperature dependence of λ(T) can be determined.
While this simple mapping from the measured muon depolarization rate σ to the magnetic penetration depth λ (see Eq. 8) works very well for large-κ superconductors, it fails for low-κ materials such as niobium in the vortex state. Here, the field distribution of the FLL needs to be analyzed not only by Ginzburg–Landau theory but also with the Delrieu solution of the BCS-Gor’kov equation close to Hc2 (Herlach et al., 1990; Yaouanc et al., 2014).
The μSR technique has also been used to study elemental type-I superconductors in the intermediate state (Egorov et al., 2001). The field distribution of the normal domains and domain walls can be studied, and it has been shown for white tin that close to Hc, there is a phase transition from laminar to thread-like structure.
The so far presented description of μSR polarization functions ignores any potential magnetic fluctuations. In case of any static magnetic field distribution, the muon spin ensemble is dephasing, which leads to a reduction of the muon spin polarization function, as was sketched in the ZF case, leading to Eq. 4. This process is coherent and could, in principle, be reversed, as it is carried out in spin-echo techniques in NMR. If there are any magnetic fluctuations present at the muon site, with spectral density at the Larmor frequency, muon spin transitions can take place. These processes are incoherent and also lead to a loss of the muon spin polarization. In μSR, the dynamics is handled most often in the strong-collision scenario, i.e., assuming the Gaussian–Markovian process (Hayano et al., 1979; de Reotier and Yaouanc, 1992). Within this framework, the muon spin polarization function can be described by the following equation:
where
It should be noted that most often, the magnetic fluctuations originate from the host material studied. However, in some materials, the muon itself might diffuse. In this case, the fluctuation rate ν must be understood as a hopping rate of the muon. Here, the dynamics of the muon is leading to time-dependent magnetic fields. This, for example, is true for niobium and has been used to study defects (Niinikoski et al., 1979).
Surface muons have a typical stopping range of 0.1–1 mm in solids, depending on their density. In case of niobium, the implantation depth is approximately 150 μm, which is large compared to the London penetration depth, which is typically in the nanometer range. Therefore, by μSR, the London penetration can only be extracted by FLL measurements, as outlined above. In order to probe magnetic properties of a solid on a desired nanometer scale, positive muons, μ+, in the keV range are needed. This can be achieved using a moderation technique which has been pioneered first by the slow positron community (Gullikson and Mills, 1986) and afterward first demonstrated for μ+ by Harshman et al. (1986) and Harshman et al. (1987) at TRIUMF. In this moderation technique, the surface muon beam passes through a thin layer of a wide-band-gap insulator, typically a frozen van der Waals solid, such as argon. Muons will scatter in this layer, and some will fall into the energy gap (15–20 eV, depending on the moderator material). Since there are essentially no electronic and phononic excitations possible, the material becomes transparent, which results in a rather large diffusion length of these low-energy μ+. Therefore, the resulting low-energy μ+ beam has an initial energy of 15–20 eV. Unfortunately, the described process has a very low production yield of only 10–5 − 10–4 and, henceforth, requires extremely high initial surface muon flux. For further details on the generation of ultra-low-energy positive muons, which also describes a second approach, see the work of Bakule and Morenzoni (2004). Currently, the only suitable beamlines for the generation of a sufficiently high surface muon flux to generate enough low-energy μ+ to run a user program are present at the PSI. Here, the redesigned muE4 beamline (Prokscha et al., 2008) is part of the LE-μSR facility. In the LE-μSR beamline, the μ+ are re-accelerated to typically 15 keV, separated from the scattered surface muons, and transported to the sample region. The implantation energy of the muon is achieved by biasing the sample, and therefore, implantation energies E = 1–30 keV are achieved, with an energy uncertainty of ΔE < 0.4 keV. This results in implantation ranges from 5 to 300 nm, depending on the material and density. In order to calculate the muon stopping profiles, the Monte Carlo code TRIMSP (Eckstein, 1991) is used. The validity of this Monte Carlo code has been experimentally cross-checked (Morenzoni et al., 2002).
The first measurements applying LE-μSR to determine the Meissner screening profile were performed on the high-temperature superconductor YBa2Cu3O7 (Jackson et al., 2000) and were cross-checked against FLL measurements on the same sample (Pleines et al., 2000). After zero-field cooling the sample, a field of B = 10 mT is applied. This generates Meissner screening currents and, hence, the typical Meissner screening profile B(z). For high-temperature superconductors, which are large-κ materials, the Meissner screening profile is expressed as follows:
This magnetic field profile can “directly” be measured by LE-μSR, by sampling the precession frequency ω = γμB at various depths. This is carried out using a series of measurements for a range of different implantation energies. Essentially, this is a 1D magnetic tomography. Figure 3 shows the principle of the measurements performed by Jackson et al. (2000).
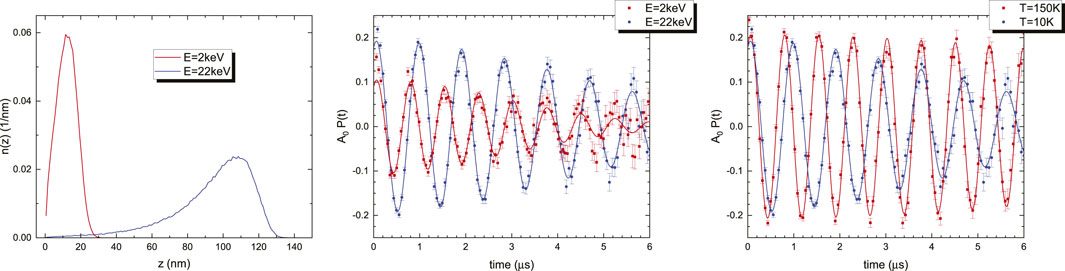
FIGURE 3. LE-μSR experiment of the type-II superconductor YBa2Cu3O7 (critical temperature Tc = 89 K). The left panel shows two μ+ stopping profiles calculated with TRIMSP. The middle panel shows the μ+ precession signal in the Meissner state at T = 10 K, for two implantation energies: E =2 keV (z ≃15 nm) and E = 22 keV (z ≃110 nm). The right panel shows the E = 22 keV asymmetry for T = 10 K (Meissner state) and 150 K (normal state).
Already, a very simple fitting function such as
is catching the B-value surprisingly precise such that BG vs. ⟨z⟩≃ B(z). A more elaborate fitting approach is to take into account the exact form of the μ+ stopping profile, resulting in the following equation:
where σ is a damping term caused by nuclear damping, which also collects imperfections such as surface roughness (Lindstrom et al., 2016). n(z) is the muon stopping profile, and B(z) is the parametrizable model of the magnetic field profile. If there is no clear model for B(z) available, or if a model for B(z) should be verified, Eq. 11 is a way of a model-independent B-vs-z mapping. It has been demonstrated that subtle effects can, indeed, be measured by measuring the effects of photopersistent conductivity on Meissner screening in YBa2Cu3O6+x (Stilp et al., 2014a), as well as the effects of gold nano-particle doping in YBa2Cu3O7−δ, leading to increased Meissner screening (Stilp et al., 2014b). Kiefl et al. (2010) measured the anisotropy of the London penetration depth in YBa2Cu3O7−δ single crystals, which allows separating the contribution of the superconducting chains present in this compound. In a study by Ofer et al. (2012), the in-plane penetration depth in the Meissner state on a single crystal of
With his seminal work, Pippard (1953) not only found a second length scale relevant in superconductors, the coherence length, but also delivered the theory for the magnetic screening response, which has, afterward, been verified by the BCS theory (Bardeen et al., 1957). For low-κ materials (κ ≲ 1) in the clean limit, rather than a local screening response
A typical B(z) for a non-local response is presented in Figure 4. There are three apparent features of the non-local screening: i) The initial slope is less pronounced and would lead to an apparently larger λL when fitted. ii) On a log-scale, there is a clear curvature present. iii) There is even a field reversal at large distances, though on a very small scale. Pippard (1953) stated “It is unlikely that any direct experimental demonstration of existence can be devised.” The sensitivity of LE-μSR is good enough to resolve at least the first two points of the list given. Some of us have demonstrated non-local Meissner screening in lead (Suter et al., 2004), niobium, lead, and tantalum (Suter et al., 2005; Suter et al., 2006), and tin (Kozhevnikov et al., 2013).
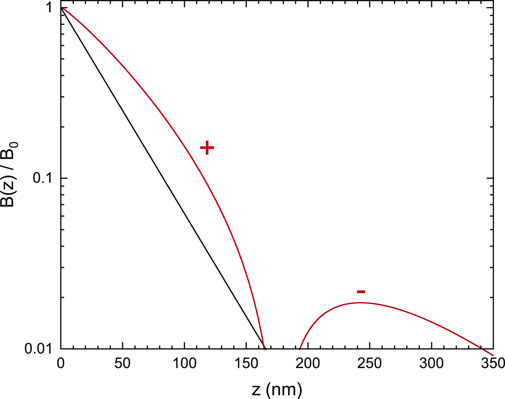
FIGURE 4. Normalized magnetic field profile B(z)/B0 for λL =36 nm and ξ =310 nm, as found in tin (Kozhevnikov et al., 2013). Black: exponential B(z) for the given λL. Red: B(z)/B0 as defined in Eq. 13. The ‘+’ sign means B(z)>0, and the ‘−’ sign means B(z)<0.
For type-I superconductors, in the field range 1 − η < Happl/Hc < 1, where η is the demagnetization factor, one finds the intermediate state (Tinkham, 1975). In the intermediate state, one finds filaments of normal and superconducting domains. Surprisingly, very little is known about the field distribution in the normal domain and how the field distribution changes close to the surface. This has been studied experimentally in some detail by Kozhevnikov et al. (2017), coming to the conclusion that the field distribution is different to the current theoretical understanding. In this study, the field distribution was studied not only in the superconductor indium but also on the “vacuum side” by growing a layer of solid N2 in situ, thus allowing measuring the field distribution just outside the superconductor.
Since LE-μSR allows magnetic depth profiling, the interplay between different materials and orders can be studied. In particular, the interplay between magnetic systems and superconductors is of interest since typically, a magnetic state close to or in a superconductor can act as a pair-break mechanism. In the highly correlated superconductor families of the cuprates and iron-based superconductors, magnetism and superconductivity seem to be closely related states, and hence, heterostructure studies can help understand these systems better. Wojek et al. (2012) studied the interplay between the magnetic and superconducting properties of YBa2Cu3O7−δ/PrBa2Cu3O7−δ trilayer and bilayer heterostructures and found that a finite superfluid density can be induced in otherwise semiconducting antiferromagnetic PrBa2Cu3O7−δ layers. Understanding the interplay between different orders in a solid is a key challenge in highly correlated electronic systems. In real systems, this is even more difficult since disorder can have a strong influence on the subtle balance between these orders and, thus, can obscure the interpretation of the observed physical properties. In the so-called δ-doped La2CuO4, the interplay between the antiferromagnetic order with an ultra-clean quasi-2D superconducting state has been studied (Suter et al., 2018). In this system, the superconducting state strengthens the antiferromagnetic ordered state. The interplay between niobium and thin magnetic layers of ferromagnets has been extensively studied over the last decade (Flokstra et al., 2014; Di Bernardo et al., 2015; Flokstra et al., 2016; Flokstra et al., 2018; Flokstra et al., 2019; Stewart et al., 2019; Flokstra et al., 2021; Flokstra et al., 2023). Various effects were addressed in these studies: spin–orbit coupling, spin-valve physics, and proximity and anti-proximity effects, to name just a few. The most surprising result was the discovery of the electromagnetic proximity effect (Flokstra et al., 2018; Mironov et al., 2018; Flokstra et al., 2019; Stewart et al., 2019). An enhanced Meissner screening is observed in the presence of a thin ferromagnetic layer. Although there is some pair-breaking present close to the ferromagnetic layer, the overall Meissner screening is more pronounced as compared to pure niobium. The cause of this effect is the vector potential of the ferromagnetic layer as outlined by Mironov et al. (2018). This is similar to the well-known Aharonov–Bohm effect.
The basis for beta-detected NMR is the same as for muon spin rotation, namely, the nuclear spin state is observed via the parity-violating β decay process that correlates the direction of the emitted β particle with the direction of the nuclear spin at the instant of the decay. Practically, however, there are important differences. At the fundamental level, the decaying entity and the decay product are composite nuclei (rather than leptons), so the weak interaction transition matrix element is more complicated. However, the result is simply a β-decay asymmetry parameter [related to A in Eq. (1)], which for the most common probe
In the context of superconductors, NMR is primarily used as a local magnetic probe to measure the static (time-average) and low-frequency dynamic response of the superconducting state (MacLaughlin, 1976). For this purpose, the quadrupolar interaction is an added complication. While being similar in principle to conventional NMR, β-NMR has important distinctions: 1) Like the muon, it can be used to study any superconductor since the extrinsic probe can be implanted in any material, but 2) the site of the implanted ion (or muon) is not known a priori and must be determined for any interpretation that depends on the precise crystallographic site. 3) Like LE-μSR (see Section 2.4), the low beam energy makes it possible to study thin-film superconductors that are inaccessible by conventional NMR because they contain too few nuclei to obtain a signal. Importantly for SRF materials, one can also study the Meissner phase of a superconductor by implanting the probes within the London penetration depth λL of the surface to reveal the details of the supercurrent screening at the local level.
While β-NMR has been used to study a number of compound superconductors, such as NbSe2, MgB2, YBCO, Sr2RuO4, and LiTi2O4(MacFarlane, 2015; MacFarlane, 2022), we will focus on the simple metals of relevance to current SRF technologies. Present SRF uses elemental niobium. Parolin et al. (2009) reported the β-NMR of
For SRF applications, the Meissner phase at much lower magnetic fields is of central interest. Moreover, the relevant field direction is parallel to the surface of the superconductor. At TRIUMF, the latter condition is met by electrostatically bending the ion beam direction by 90° from the polarization direction (defined by the polarizing laser), as shown in Figure 5. This alters the beam direction without changing the polarization, and one obtains a transversely polarized beam that is transported into the “βNQR spectrometer,” named for the zero-applied-field technique of nuclear quadrupole resonance (Bloom et al., 1955). The former condition is straightforward to satisfy using a conventional Helmholtz pair electromagnet. However, the applied field is transverse to the beam direction in this geometry, and the Lorentz force deflects it, so one needs to compensate electrostatically. Recently, a new spectrometer for fields up to 200 mT in this geometry has been commissioned (Thoeng et al., 2023a) (see Section 4.2). One of its primary applications will be SRF research.
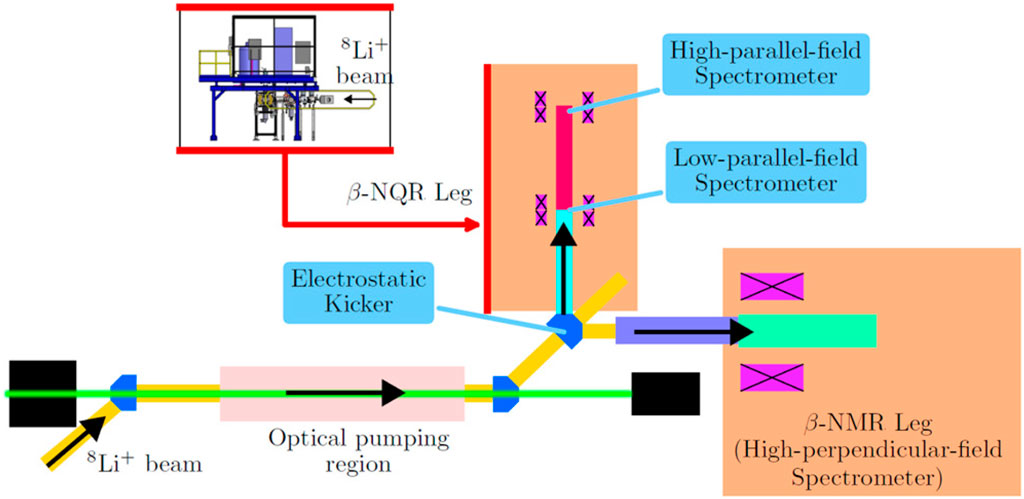
FIGURE 5. Beamline layout of the β-NMR facility at TRIUMF. Typical beam energy extracted from the source for
While some of the original NMR studies of the superconducting state (Hebel and Slichter, 1959) were accomplished at low applied field (in this case, by field cycling), it is much more common that NMR is carried out in high field since the field is used to polarize the nuclei. With the optical polarizer, the applied field is unimportant for this purpose, but, on the other hand, at low field, the probe spin is increasingly sensitive to cross-relaxation (Stöckmann et al., 1989; Chow et al., 2012) with other stable nuclear spins of the host, for example, the 100% abundant
on the time-averaged internal field ⟨B⟩ sampled at energy E, and this can be calibrated so that the rate can be used as a local magnetometer. If one implants the probe nuclei to depths comparable to λL in the Meissner phase, one can observe the decay of the field due to the surface supercurrent screening and measure λL. Hossain et al. (2009) nicely demonstrated this in the highly two-dimensional superconductor NbSe2.
Further studies of the Meissner state were carried out by Morenzoni et al. (2012) in a Pb film and a proximity effect bilayer structure composed of a Ag overlayer on a Nb film, where below the TC of Nb, superconductivity is induced in the Ag layer by the proximity effect. This work not only confirmed the phenomenology developed in NbSe2 but also discovered an unanticipated critical peak in the relaxation rate at TC. The peak occurs in a very narrow temperature range, and it is quite strongly suppressed by the applied field. It was concluded that it is due to fluctuating diamagnetism on kHz timescales in the vicinity of the transition, but a detailed theoretical account has not yet appeared.
Recently, the same niobium film studied previously by Parolin et al. (2009) was tested in the Meissner state under parallel magnetic fields (McFadden et al., 2023a). These are challenging measurements because the low-field cross-relaxation rate in Nb is quite fast compared to the
In SRF cavities, the goal is to maintain the flux-free Meissner state in a magnetic field applied parallel to the surface. Prior to SRF investigations, μSR and β-NMR spectrometers were either designed for high longitudinal fields up to several Teslas or small parallel fields of approximately 30 mT or less. When designing a spectrometer with the field applied perpendicular to the momentum of the implanted probe, one has to take into account that not only the magnetic field will cause spin rotation but the stray fields will also bend the beam trajectory, which has to be counteracted. As the bending radius is proportional to the particle momentum, this effect is most pronounced for low-energy beams of light particles. For example, the bending radius of 4.2 MeV surface muons is roughly equal to the bending radius of 50 keV
A spectrometer dedicated to the requirements of SRF named high parallel field (HPF) apparatus has been added to the TRIUMF μSR facility (Gheidi et al., 2015; Junginger et al., 2018). An upstream steering magnet is used to pre-steer off-axis, and the applied field at the sample bends the particles back to the sample, as shown in Figure 6.
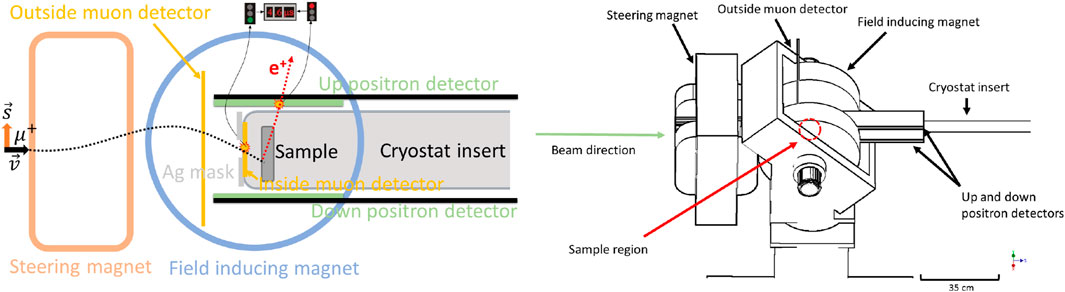
FIGURE 6. Left: schematic displaying the components of the HPF spectrometer and the beam trajectory. Right: 3D render of the spectrometer [reproduced from the work of Junginger et al. (2018)].
The high parallel field surface muon beamline in the previous section gives useful information on flux entry into the bulk for a parallel geometry. The muon energy is such that the probe is implanted at 100 μm into the material orders of magnitude deeper than required to give detailed information on the surface where field screening occurs over the first 100 nm. On the other hand, LE-μSR has been used for screening profile measurements as detailed in Section 2.4. Considerations of momentum limit LE-μSR beams to
The TRIUMF β-NMR facility including β-SRF is shown in Figure 5. There are two legs: the β-NMR leg for high transverse fields and the β-NQR leg for parallel fields. The new β-SRF facility has been added to the β-NQR leg. Fields parallel to the surface of the sample are provided by normal conducting Helmholtz coils. To achieve depth profiling, the sample ladder and cryostat are raised to the bias of the HV platform, which can be varied in order to decelerate the ion beam as it approaches the sample. The bias capability spans from 0 kV to 30 kV, and typical beam energies are 20–30 keV. At the β-SRF spectrometer, a large Helmholtz magnet generates up to 200 mT at the sample 2 location, as shown in Figure 7. Electrostatic quadrupoles are used to control the beam shape during transport and to focus the ions onto the sample. Steering plates compensate for the vertical deflection due to the fringe field of the Helmholtz coil transverse to the beam direction. The blue envelope in the figure indicates the beam trajectory. Technical details on the facility can be found in Thoeng et al. (2023a).
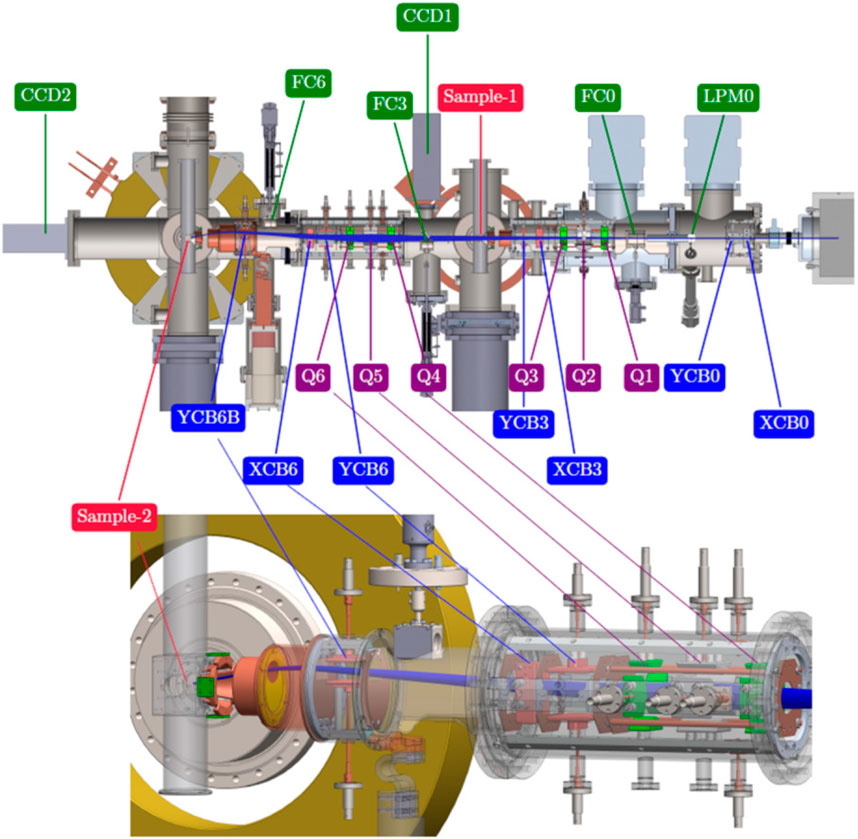
FIGURE 7. β-NQR leg at the ISAC β-NMR facility. The ion beam is going from right to left. The (longstanding) sample 1 position is used for parallel fields up to 24 mT, and the new β-SRF beam line extension includes the 1 m section downstream of sample 1 leading to the sample 2 position where fields up to 200 mT are possible. Superimposed on the beamline is the beam trajectory due to the interaction of the beam with the fringe field of the Helmholtz coil [reproduced with permission from the work of Thoeng et al. (2023a)].
Since 2010, the SRF group at TRIUMF has been using the μSR technique to characterize materials and processing techniques typical for the SRF community using the TRIUMF surface muon beam. For the first studies (Grassellino et al., 2013), samples that were cut out from large- and small-grain 1.5 GHz radio-frequency (RF) single-cell niobium cavities were characterized. The results showed that standard cavity surface treatments such as mild baking and buffered chemical polishing performed on the studied samples affect their surface pinning strength. In these studies, the magnetic field was applied perpendicular to the surface of flat cylindrical samples. This geometry is most sensitive to pinning of the sample material as later studies (Junginger et al., 2018) with different field configurations and sample geometries showed (Figure 8). It was also concluded that accurate measurements of the field of first vortex penetration require ellipsoidal samples annealed at 1,400 °C with the magnetic field applied along the major axis and the muons implanted at the equator where the local field is at maximum. This geometry requires the use of the HPF spectrometer described in Section 3.
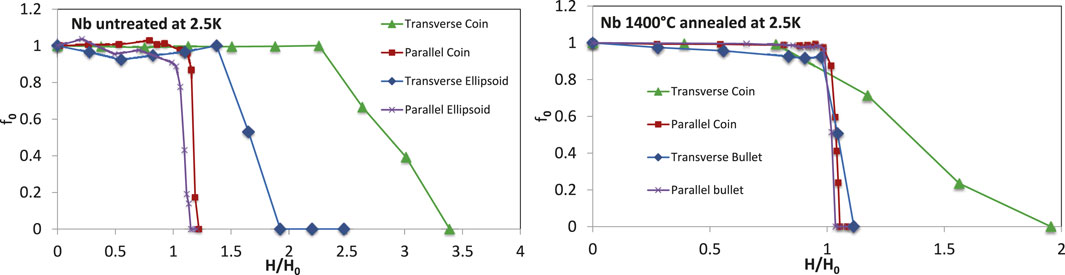
FIGURE 8. Fit parameter f0 signifying the volume fraction probed by the muons which is in the field-free Meissner state as a function of the applied field in four geometries. Left: chemically etched samples with no heat treatment: The apparent differences in H/H0 are correlated to the different sensitivity to the pinning of the four geometries. Right: annealing at 1,400 °C virtually eliminates all pinning. H0 is the expected field of first vortex penetration in the absence of a Bean–Livingston barrier (Hc1) taking into account its temperature dependence and the field enhancement caused by each sample at the muon implantation site [reproduced from the work of Junginger et al. (2018)].
Junginger et al. (2017a) showed that the field of first flux penetration Hentry in Nb is enhanced by approximately 30% if coated with an overlayer of Nb3Sn or MgB2, as shown in Figure 9. This is consistent with an increase from the lower critical magnetic field Hc1 up to the superheating field Hsh of the Nb substrate. In these experiments, coatings of Nb3Sn and MgB2 with a thickness between 50 and 2000 nm were used. It was found that Hentry does not depend on the material or the thickness of the overlayer. This suggests that the energy barrier at the boundary between the two materials prevents flux entry up to Hsh of the substrate. A mechanism consistent with these findings is that the proximity effect recovers the stability of the energy barrier for flux penetration, which is suppressed by defects for uncoated samples. Additionally, a low-temperature-baked Nb sample had been tested and a 6% increase in Hentry was found, also pushing Hentry beyond Hc1. Although pinning is weakest in the parallel ellipsoid geometry, as shown in Figure 8, it could not be completely ruled out that the apparent Hentry increase for LTB-baked niobium was caused by surface pinning introduced by low-temperature baking. Later magnetometry studies on identically prepared samples suggested that LTB does not affect the field of first vortex penetration but significantly increases the pinning strength (Turner et al., 2022). Motivated by these seemingly contradictory results, an experiment was devised in which the muon implantation depth was varied using silver moderating foils (Asaduzzaman et al., 2023). In case of an interface barrier, one would expect Hentry to be independent of implantation depth, while for surface pinning, Hvp should increase with implantation depth. It was confirmed that the apparent increase in Hentry for LTB niobium was due to surface pinning and confirmed the presence of an interface barrier for bilayers of two different materials (Asaduzzaman et al., 2023). This finding is important for further SRF material development as it shows that the reason why some niobium SRF cavities reach peak surface magnetic fields above Hc1 is not an energy interface barrier. Low-temperature-baked niobium cannot be considered an effective bilayer, whereas actual bilayers composed of two different superconductors can potentially be used to reach surface magnetic fields up to the superheating field of the substrate.
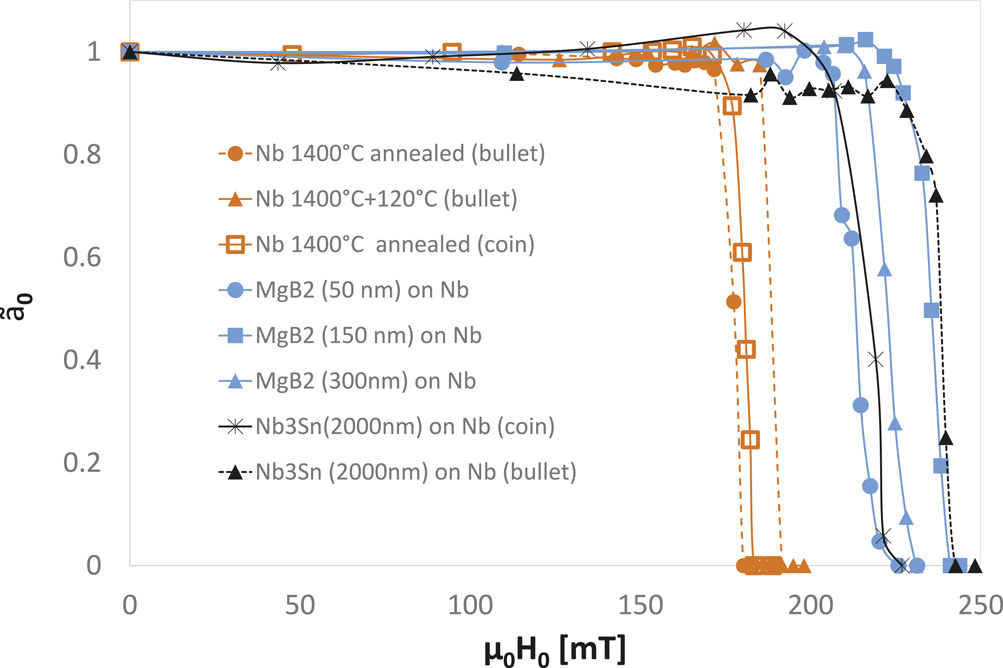
FIGURE 9. Normalized fit parameter
The London penetration depth of SRF materials can, in principle, be derived from RF surface impedance measurements. These can be performed either directly on cavities or on samples using sample test cavities such as a quadrupole resonator (Goudket et al., 2017). However, RF surface resistance is sensitive to a wide variety of parameters which are often fixed (Maniscalco et al., 2017; Miyazaki and Delsolaro, 2019), or additional mechanisms are neglected (Gurevich, 2014; Kubo and Gurevich, 2019). Measurement of the imaginary part of the surface impedance through frequency shift as a function of temperature is a more direct way to obtain λL but only suitable if the penetration depth does not change with depth over a distance of several λL. Unlike RF measurements, low-energy muon spin rotation can directly measure the London penetration depth without implicitly assuming an exponential decay with constant λL.
Romanenko et al. (2014) used LE-μSR to measure the Meissner screening profile in cutouts from Nb SRF cavities, systematically comparing how different surface treatments affect the screening properties of the elemental type-II superconductor. They reported a “strong” modification of the character of the screening profile after a mild baking at 120°C for 48 h which was interpreted as a depth-dependent carrier mean-free-path resulting from a “gradient in vacancy concentration” near the surface. Later LE-μSR studies on 120°C-baked niobium, two-step baking, and nitrogen infusion, all processes that modify the oxygen or nitrogen concentration in the near-field region in a similar manner, could not find any evidence for a depth-dependent carrier mean-free-path (McFadden RM. et al., 2023). All data could be well described using the London model; non-local effects did not need to be taken into account to obtain excellent fits. To accurately determine the magnetic screening, the implantation depth of muons in niobium as a function of energy has to be well known. Previous LE-μSR experiments on niobium have generally found shorter values of the London penetration depth (Suter et al., 2005; Romanenko et al., 2014; Junginger et al., 2017b) compared to other methods such as RF frequency shift. Therefore, the parameterization of Nb’s electronic stopping cross section for proton-like projectiles was revised using an up-to-date compilation of experimental values. This resulted in λ values in better agreement with the literature than reported in previous studies, as shown in Figure 10. This figure also includes a reanalysis of data from the work of Junginger et al. (2017b) and Suter et al. (2005).
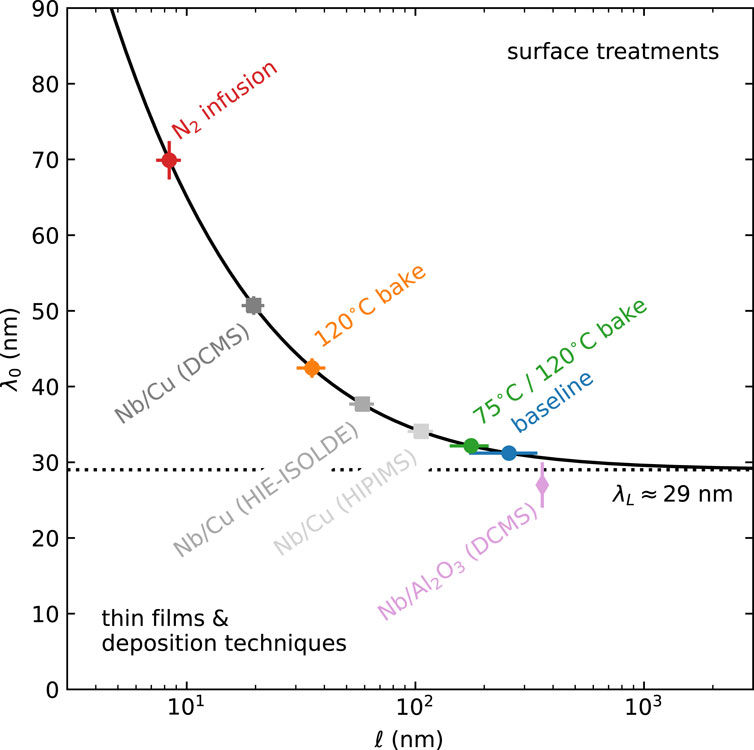
FIGURE 10. Dependence of Nb’s magnetic penetration depth at 0 K, λ0, on the carrier mean-free path, l, for common surface treatments used to fabricate SRF cavities. The values are calculated using representative values for the London penetration depth λL = 29.01 nm and the Bardeen–Cooper–Schrieffer coherence length ξ0 = 40.3 nm [reproduced with permission from the work of McFadden RM. et al. (2023)].
The analysis approach from the work of McFadden RM. et al. (2023) was then applied to the data from the work of Romanenko et al. (2014). The field screening could again be well described using an exponential London model (McFadden et al., 2023c). Interestingly, the reanalysis also uncovered an unusually large “dead layer,” which may suggest the presence of spatial inhomogeneities in the screening properties close to the surface (e.g., from a depth-dependent penetration depth). The data suggest that their effect on B(z) is likely subtle, necessitating high-resolution measurements, probing the near-surface region (z ≲40 nm) to be conclusive.
In heterostructures comprising different materials, three effects relevant for SRF application occur. 1) If superconducting layers thinner than their London penetration depth are decoupled by dielectric layers, penetration of parallel vortices is suppressed (Gurevich, 2006). 2) There is an interface barrier for flux penetration similar to the Bean–Livingston barrier, as discussed in Sec. 4.2. 3) If the London penetration depth of an outer layer is larger than the substrate’s, the current will be suppressed as required to fulfill boundary and continuity conditions at the interfaces (Kubo, 2017). 2) and 3) are valid for heterostructures with and without dielectric interlayers. Therefore, one can potentially use bilayers of two materials for SRF application or at least study this easier system to get general insight into loss mechanisms of heterostructures in general.
In the work of Asaduzzaman et al. (2024), the depth-dependent field screening profile in the superconductor–superconductor (SS) bilayers was measured using LE-μSR. A collective fit of the magnetic screening profile, taking into account boundary and continuity conditions at the interface, gave an excellent fit to samples of different NbTiN thicknesses, as shown in Figure 11. It should be noted that the screening is very different for each sample, but the collective fit used single-valued λ for NbTiN 187.7 (34) nm and Nb 47.4 (23) nm. The change in screening can be attributed to the current suppression. From these results, one can estimate the ideal layer thickness for optimal Hentry. A thin NbTiN layer strongly suppresses the surface current but provides little shielding to the substrate. The strong current suppression found for the NbTiN/Nb system suggests an optimal layer thickness that exceeds the λ of NbTiN. Such a thick layer is not expected to remain in the Meissner state above Hc1. Therefore, it is suggested that multilayers comprised of several NbTiN layers intersected by dielectric interlayers are best suited to achieve the largest accelerating gradients.
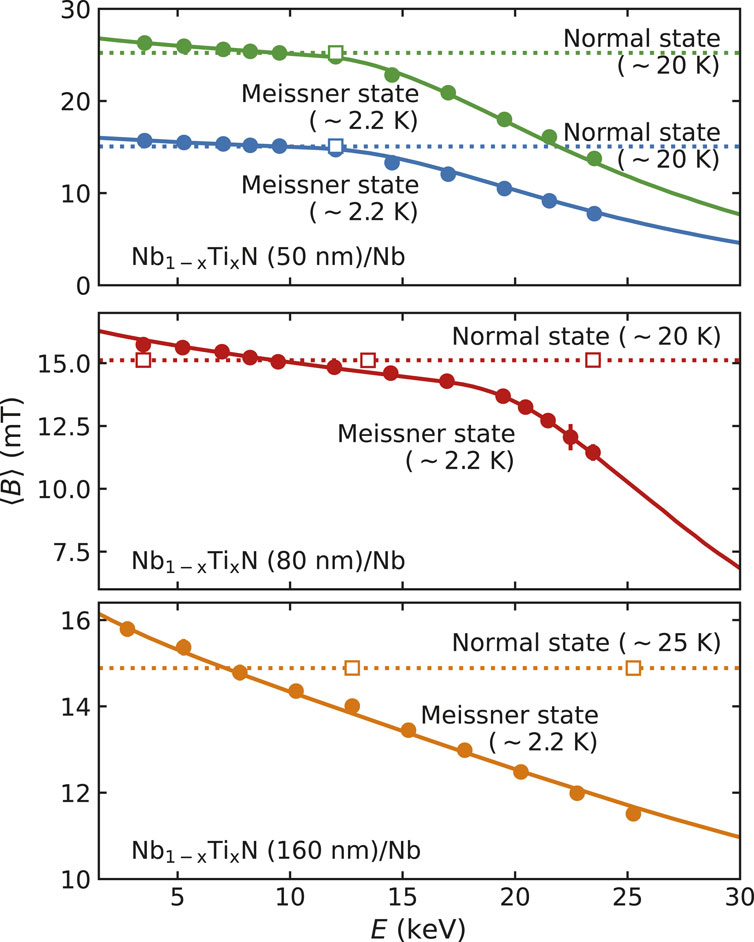
FIGURE 11. Global fit to NbTiN/Nb field profiles: Plot of the mean magnetic field, ⟨B⟩, sensed by positive muons (μ+) at different implantation energies, E, in samples of different NbTiN thicknesses (i.e., 50 nm, 80 nm, and, 160 nm) at applied fields of 15.0≲ B0≲25.0 mT), parallel to the sample surface in the Meissner state (T ∼2.7 K) and normal state (20.0≤ T ≤25.0 K). The colored closed circles are data points, and the solid lines represent a (global) fit to the data in the Meissner state. The colored opened squares are the normal state data points, and colored dashed lines are fit to the data. In the normal state, there is no energy or depth dependence to ⟨B⟩, which represents the strength of the applied magnetic field, B0. However, in the Meissner state, ⟨B⟩ decays with an increase in E [reproduced from the work of Asaduzzaman et al. (2024)].
Nb3Sn is currently the most promising bulk material other than niobium for future superconducting radio-frequency cavities. Critical fields above 120 mT in pulsed operation and approximately 80 mT in CW have been achieved in cavity tests (Posen et al., 2015). In the work of Keckert et al. (2019), several methods were combined to gain insights into the critical fields of the material as prepared by thermal diffusion for SRF application. The London penetration depth was measured using the LE-μSR-technique from which the lower critical field Hc1 and the superheating field Hsh were derived. The field of first vortex penetration was directly measured using surface μSR and found to be consistent with Hc1 as derived from LE-μSR. The RF critical field measured using a quadrupole resonator (QPR) was found to be significantly greater than Hc1, as shown in Figure 12. The combined results confirm that Nb3Sn cavities are indeed operated in a metastable state above Hc1 but are currently limited to a critical field well below the superheating field potentially by local suppression of the superheating field at coating flaws.
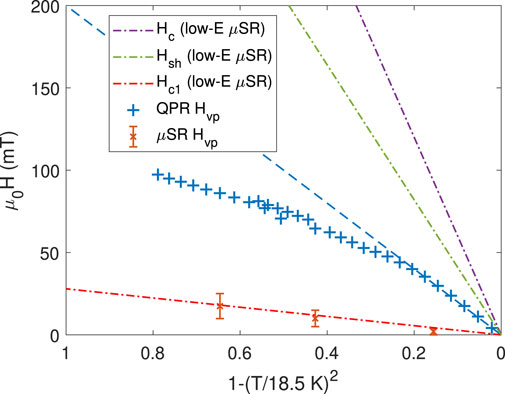
FIGURE 12. Combined plot showing data for Hc, Hsh, and Hc1 from low-energy μSR measurement and field of first vortex penetration as obtained from QPR (RF) and surface-μSR (DC) measurements [reproduced from the work of Keckert et al. (2019)].
In an initial experiment with the beta-SRF facility, a set of spin-lattice relaxation (SLR) measurements were performed on two rectangular niobium samples of approximately 10 × 10 × 2 mm treated with two different processes common in the SRF community (Thoeng et al., 2023b). Sample A (baseline sample) is an RRR niobium slab annealed at 1,400°C for 3 h with a final flash buffered chemical polish (BCP). Sample B (oxygen-doped sample) is a baseline sample further treated at 400°C for 3 hours. Each sample is tested at a range of applied parallel fields from 100 mT to 200 mT, and for each applied field, the depth profiles of the magnetic screening in the sample are measured by taking data at five different 8Li + energies from 4 keV to 20 keV. The values of the fit parameters in Eq. (14) are determined by measuring 1/T1 values for known field levels. Given that the depolarization rate 1/T1 is dependent on the local field, the variation of magnetic fields in the superconducting Nb due to Meissner screening can, therefore, be measured from the asymmetry spectra at different implantation energies. Experimental results for three different implantation energies and at an applied field of 100 mT are shown in Figure 13 for the baseline sample. The increase in 1/T1 as the ion is implanted deeper in the material is evidence of Meissner screening. Clear differences in screening were found for the two samples. These early results, therefore, highlight the ability of the β-SRF facility to explore the magnetic screening of treated Nb and layered SRF materials at the limits of the Meissner state.
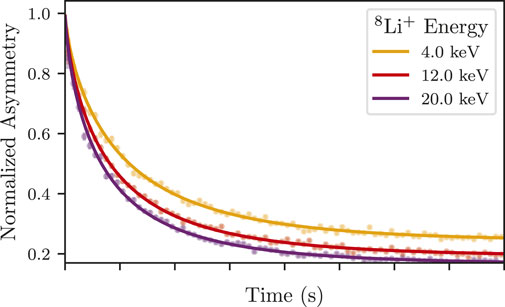
FIGURE 13. Raw asymmetry spectra and fits to the data of the Nb contributions (i.e., with background contributions subtracted) at various implantation energies for the baseline sample at an applied field of 100 mT and at T = ∼4.5 K.
Zero- and longitudinal-field LE-μSR measurements are sensitive to randomly fluctuating microscopic magnetic fields, see Section 2.4. A muon could experience fluctuating fields due to diffusion if it is not static during its lifetime or if a static muon experiences a fluctuating field caused by magnetic impurities. Although Nb generally showed evidence of fluctuating fields, it is impossible to directly distinguish between these two scenarios from LE-μSR measurements. To overcome this limitation, a 180 (20) nm N2 layer was grown on top of a niobium sample, and the muons have been stopped in this N2 layer, close to the niobium. Figure 14 (left) displays the muon stopping profile obtained from the Monte Carlo code TRIM.SP. From previous studies, it is known that muons are static, which means they do not diffuse in nitrogen as grown under the given conditions. Nevertheless, an additional measurement has been performed to verify this important assumption. A 1.83 μm-thick nitrogen layer has been grown on a Ni-coated sample plate. The asymmetry function has been measured at 10 K in zero field, as shown in Figure 14. The data can be well described by Eq. (9) with a very low hop rate ν or even a static Gaussian Kubo–Toyabe depolarization function [Eq. (4)]. This clearly demonstrates that the muons are indeed static, that is, they are not diffusing, in the N2 layer on Ni. For the muons stopped in N2 on top of Nb, the static Gaussian Kubo–Toyabe function cannot give a reasonable fit since the asymmetry function does not relax to 1/3 of its initial value as expected for static muons. In fact, the signal clearly shows a dynamic response, which further supports the presence of magnetic impurities in these films since muon diffusion is fully suppressed here, and hence, the origin of the fluctuation rate can only be caused by magnetic fluctuations present in the niobium. Using Eq. (9) instead gives an excellent fit to the data, see Figure 14 (right) (Junginger et al., 2017b).
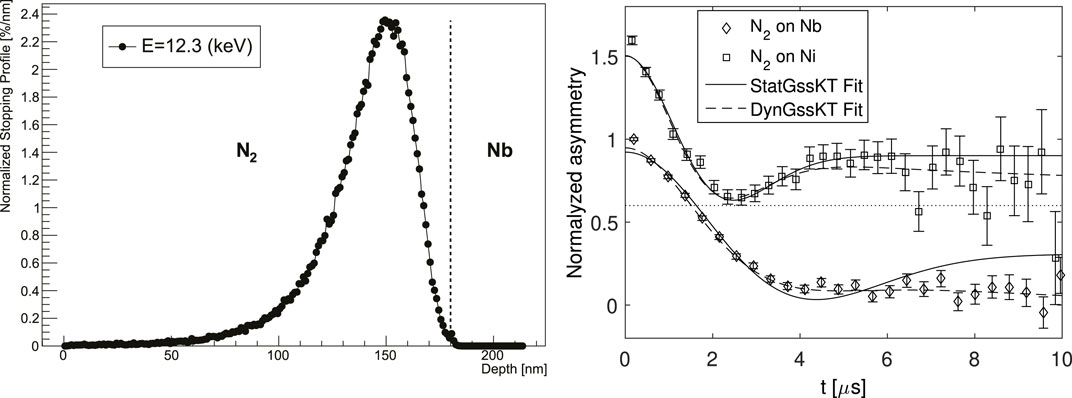
FIGURE 14. Left: muon stopping profile for the applied bias voltage of 2.3 keV. Right: normalized asymmetry function of muons stopped in a N2-overlayer on top of a Nb sample and a Ni plate at 10 K. The latter dataset has been shifted along the y-axis by 0.6 [reproduced with permission from the work of Junginger et al. (2017b)].
μSR and β-NMR can provide insight into important material properties for SRF application. LE-μSR and β-NMR provide implantation with nanometer depth resolution, enabling unique possibilities to study inhomogeneous materials such as doped niobium and heterostructures. Future studies should focus on the properties of heterostructures to reveal if current limitations are intrinsic or could be overcome by further material development. With the β-SRF facility, we are now able to test SRF materials at parallel fields beyond the highest values achieved in SRF cavities. This offers unique possibilities. Future experiments will examine changes in the Meissner screening close to HC1 for different surface treatments on niobium and heterostructures comprised of different superconductors and insulating layers. While theory predicts that thin decoupled layers should provide screening above their lower critical field, it is technologically challenging to achieve this in practice. With β-SRF, we are able to measure flux penetration as a function of depth, allowing us to probe flux penetration in each layer in a multilayered heterostructure. It is also suggested to directly compare μSR and β-NMR results on identical samples to surface analytic measurements such as secondary ion mass spectroscopy or transmission electron microscopy to best guide further material development. The studies presented in this review have focused on the influence of the superconducting material on SRF performance. Rather little attention was paid to the influence of the oxide layer which becomes relevant for reaching ultimate quality factors in SRF cavities and to achieve the longest coherence times in quantum hardware. The ability of LE-μSR and β-NMR to implement low-energy beams with nanometer depth allows studying the oxide layer in depth and relating these findings to SRF performance (Krasnikova et al., 2023). Table 1 gives an overview of the three experimental techniques described in this contribution in terms of their capabilities for SRF material studies.
TJ: writing–original draft and writing–review and editing. RL: writing–original draft. WM: writing–original draft. AS: writing–original draft.
The authors declare that financial support was received for the research, authorship, and/or publication of this article. TJ, RL, and WM received support from the Natural Sciences and Engineering Research Council of Canada (NSERC) to support their research. Open access funding was obtained from the Paul Scherrer Institute (PSI).
The original research was conducted by many students and postdocs and would not have been possible without the support of the local scientists and technologists at TRIUMF and or the TRIUMF and the PSI.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Asaduzzaman, M., McFadden, R. M. L., Thoeng, E., Laxdal, R. E., and Junginger, T. (2023). Muon spin rotation studies of bilayer superconductors and low temperature baked niobium. JACoW SRF2023, 62–66. doi:10.18429/JACoW-SRF2023-MOPMB005
Asaduzzaman, M., McFadden, R. M. L., Valente-Feliciano, A. M., Beverstock, D. R., Suter, A., Salman, Z., et al. (2024). Evidence for current suppression in superconductor–superconductor bilayers. Supercond. Sci. Technol. 37, 025002. doi:10.1088/1361-6668/ad1462
Bakule, P., and Morenzoni, E. (2004). Generation and applications of slow polarized muons. Contemp. Phys. 45, 203–225. doi:10.1080/00107510410001676803
Bardeen, J., Cooper, L. N., and Schrieffer, J. R. (1957). Theory of superconductivity. Phys. Rev. 108, 1175–1204. doi:10.1103/PhysRev.108.1175
Bhattacharyya, A., Adroja, D. T., Smidman, M., and Anand, V. K. (2018). A brief review on μsr studies of unconventional fe- and cr-based superconductors. Sci. China Phys. Mech. Astronomy 61, 127402. doi:10.1007/s11433-018-9292-0
Bloom, M., Hahn, E. L., and Herzog, B. (1955). Free magnetic induction in nuclear quadrupole resonance. Phys. Rev. 97, 1699–1709. doi:10.1103/PhysRev.97.1699
S. J. Blundell, R. D. Renzi, T. Lancaster, and F. L. Pratt (2022). Muon spectroscpy – an introduction (Oxford University Press).
Brandt, E. H. (1988). Flux distribution and penetration depth measured by muon spin rotation in high-Tc superconductors. Phys. Rev. B 37, 2349–2352. doi:10.1103/PhysRevB.37.2349
Brandt, E. H. (2003). Properties of the ideal ginzburg-landau vortex lattice. Phys. Rev. B 68, 054506. doi:10.1103/PhysRevB.68.054506
Brewer, J. H., Kreitzman, S. R., Noakes, D. R., Ansaldo, E. J., Harshman, D. R., and Keitel, R. (1986). Observation of muon-fluorine “hydrogen bonding” in ionic crystals. Phys. Rev. B 33, 7813–7816. doi:10.1103/PhysRevB.33.7813
Chow, K. H., Mansour, A. I., Fan, I., Kiefl, R. F., Morris, G. D., Salman, Z., et al. (2012). Detection and decoherence of level-crossing resonances of 8Li in Cu. Phys. Rev. B 85, 092103. doi:10.1103/PhysRevB.85.092103
de Reotier, P. D., and Yaouanc, A. (1992). Quantum calculation of the muon depolarization function: effect of spin dynamics in nuclear dipole systems. J. Phys. Condens. Matter 4, 4533–4556. doi:10.1088/0953-8984/4/18/020
Di Bernardo, A., Salman, Z., Wang, X. L., Amado, M., Egilmez, M., Flokstra, M. G., et al. (2015). Intrinsic paramagnetic meissner effect due to s-wave odd-frequency superconductivity. Phys. Rev. X 5, 041021. doi:10.1103/PhysRevX.5.041021
Eckstein, W. (1991). “Computer simulation of ion-solid interactions,” in Springer series in materials scienceR. Hull, C. Jagadish, Y. Kawazoe, J. Kruzic, R. Osgood, J. Parisiet al. (Springer Berlin Heidelberg). doi:10.1007/978-3-642-73513-4
Egorov, V. S., Solt, G., Baines, C., Herlach, D., and Zimmermann, U. (2001). Superconducting intermediate state of white tin studied by muon-spin-rotation spectroscopy. Phys. Rev. B 64, 024524. doi:10.1103/PhysRevB.64.024524
Flokstra, M., Stewart, R., Yim, C. M., Trainer, C., Wahl, P., Miller, D., et al. (2023). Spin-orbit driven superconducting proximity effects in pt/nb thin films. Nat. Commun. 14, 5081. doi:10.1038/s41467-023-40757-1
Flokstra, M. G., Ray, S. J., Lister, S. J., Aarts, J., Luetkens, H., Prokscha, T., et al. (2014). Measurement of the spatial extent of inverse proximity in a py/nb/py superconducting trilayer using low-energy muon-spin rotation. Phys. Rev. B 89, 054510. doi:10.1103/PhysRevB.89.054510
Flokstra, M. G., Satchell, N., Kim, J., Burnell, G., Curran, P. J., Bending, S. J., et al. (2016). Remotely induced magnetism in a normal metal using a superconducting spin-valve. Nat. Phys. 12, 57–61. doi:10.1038/nphys3486
Flokstra, M. G., Stewart, R., Satchell, N., Burnell, G., Luetkens, H., Prokscha, T., et al. (2018). Observation of anomalous meissner screening in Cu/Nb and Cu/Nb/Co thin films. Phys. Rev. Lett. 120, 247001. doi:10.1103/PhysRevLett.120.247001
Flokstra, M. G., Stewart, R., Satchell, N., Burnell, G., Luetkens, H., Prokscha, T., et al. (2019). Manifestation of the electromagnetic proximity effect in superconductor-ferromagnet thin film structures. Appl. Phys. Lett. 115, 072602. doi:10.1063/1.5114689
Flokstra, M. G., Stewart, R., Satchell, N., Burnell, G., Luetkens, H., Prokscha, T., et al. (2021). Meissner screening as a probe for inverse superconductor-ferromagnet proximity effects. Phys. Rev. B 104, L060506. doi:10.1103/PhysRevB.104.L060506
Gheidi, S., Buck, T., Dehn, T., Junginger, T., Kiefl, R. R., Laxdal, R., et al. (2015). “Muon spin rotation on treated nb samples in parallel field geometry,” in Proceedings of SRF2015, Whistler, Canada, September 13-18, 2015, 210–213.
Goudket, P., Junginger, T., and Xiao, B. (2017). Devices for srf material characterization. Supercond. Sci. Technol. 30, 013001. doi:10.1088/0953-2048/30/1/013001
Grassellino, A., Beard, C., Kolb, P., Laxdal, R., Lockyer, N. S., Longuevergne, D., et al. (2013). Muon spin rotation studies of niobium for superconducting rf applications. Phys. Rev. St. Accel. Beams 16, 062002. doi:10.1103/physrevstab.16.062002
Gullikson, E. M., and Mills, A. P. (1986). Positron dynamics in rare-gas solids. Phys. Rev. Lett. 57, 376–379. doi:10.1103/PhysRevLett.57.376
Gurevich, A. (2006). Enhancement of rf breakdown field of superconductors by multilayer coating. Appl. Phys. Lett. 88, 012511. doi:10.1063/1.2162264
Gurevich, A. (2014). Reduction of dissipative nonlinear conductivity of superconductors by static and microwave magnetic fields. Phys. Rev. Lett. 113, 087001. doi:10.1103/PhysRevLett.113.087001
Harshman, D. R., Mills, A. P., Beveridge, J. L., Kendall, K. R., Morris, G. D., Senba, M., et al. (1987). Generation of slow positive muons from solid rare-gas moderators. Phys. Rev. B 36, 8850–8853. doi:10.1103/PhysRevB.36.8850
Harshman, D. R., Warren, J. B., Beveridge, J. L., Kendall, K. R., Kiefl, R. F., Oram, C. J., et al. (1986). Observation of low-energy μ+ emission from solid surfaces. Phys. Rev. Lett. 56, 2850–2853. doi:10.1103/PhysRevLett.56.2850
Hayano, R. S., Uemura, Y. J., Imazato, J., Nishida, N., Yamazaki, T., and Kubo, R. (1979). Zero-and low-field spin relaxation studied by positive muons. Phys. Rev. B 20, 850–859. doi:10.1103/PhysRevB.20.850
Hebel, L. C., and Slichter, C. P. (1959). Nuclear spin relaxation in normal and superconducting aluminum. Phys. Rev. 113, 1504–1519. doi:10.1103/PhysRev.113.1504
Herlach, D., Majer, G., Major, J., Rosenkranz, J., Schmolz, M., Schwarz, W., et al. (1990). Magnetic flux distribution in the bulk of the pure type-ii superconductor niobium measured with positive muons. Hyperfine Interact. 63, 41–48. doi:10.1007/BF02395983
Hossain, M. D., Salman, Z., Wang, D., Chow, K. H., Kreitzman, S., Keeler, T. A., et al. (2009). Low-field cross spin relaxation of 8Li in superconducting nbse2. Phys. Rev. B 79, 144518. doi:10.1103/PhysRevB.79.144518
Jackson, T. J., Riseman, T. M., Forgan, E. M., Glückler, H., Prokscha, T., Morenzoni, E., et al. (2000). Depth-resolved profile of the magnetic field beneath the surface of a superconductor with a few nm resolution. Phys. Rev. Lett. 84, 4958–4961. doi:10.1103/PhysRevLett.84.4958
Junginger, T., Abidi, S., Maffett, R., Buck, T., Dehn, M., Gheidi, S., et al. (2018). Field of first magnetic flux entry and pinning strength of superconductors for rf application measured with muon spin rotation. Phys. Rev. Accel. Beams 21, 032002. doi:10.1103/PhysRevAccelBeams.21.032002
Junginger, T., Calatroni, S., Sublet, A., Terenziani, G., Prokscha, T., Salman, Z., et al. (2017b). A low energy muon spin rotation and point contact tunneling study of niobium films prepared for superconducting cavities. Supercond. Sci. Technol. 30, 125013. doi:10.1088/1361-6668/aa8926
Junginger, T., Wasserman, W., and Laxdal, R. E. (2017a). Superheating in coated niobium. Supercond. Sci. Technol. 30, 125012. doi:10.1088/1361-6668/aa8e3a
Keckert, S., Junginger, T., Buck, T., Hall, D., Kolb, P., Kugeler, O., et al. (2019). Critical fields of nb3sn prepared for superconducting cavities. Supercond. Sci. Technol. 32, 075004. doi:10.1088/1361-6668/ab119e
Keren, A. (1994). Generalization of the abragam relaxation function to a longitudinal field. Phys. Rev. B 50, 10039–10042. doi:10.1103/PhysRevB.50.10039
Kiefl, R. F., Hossain, M. D., Wojek, B. M., Dunsiger, S. R., Morris, G. D., Prokscha, T., et al. (2010). Direct measurement of the london penetration depth in yba2cu3o6.92 using low-energy μSR. Phys. Rev. B 81, 180502. doi:10.1103/PhysRevB.81.180502
Kozhevnikov, V., Suter, A., Fritzsche, H., Gladilin, V., Volodin, A., Moorkens, T., et al. (2013). Nonlocal effect and dimensions of cooper pairs measured by low-energy muons and polarized neutrons in type-i superconductors. Phys. Rev. B 87, 104508. doi:10.1103/PhysRevB.87.104508
Kozhevnikov, V., Valente-Feliciano, A. M., Curran, P. J., Suter, A., Liu, A. H., Richter, G., et al. (2017). Equilibrium properties of superconducting niobium at high magnetic fields: a possible existence of a filamentary state in type-ii superconductors. Phys. Rev. B 95, 174509. doi:10.1103/PhysRevB.95.174509
Krasnikova, Y., Murthy, A. A., Crisa, F., Bal, M., Sung, Z., Lee, J., et al. (2023). Magnetic fluctuations in niobium pentoxide. arxiv 2312.10697.
Kubo, R., and Toyabe, T. (1967). “Magnetic resonance and relaxation,” in Proceedings of the XIVth colloque ampère (North-Holland), 810–823.
Kubo, T. (2017). Multilayer coating for higher accelerating fields in superconducting radio-frequency cavities: a review of theoretical aspects. Supercond. Sci. Technol. 30, 023001. doi:10.1088/1361-6668/30/2/023001
Kubo, T., and Gurevich, A. (2019). Field-dependent nonlinear surface resistance and its optimization by surface nanostructuring in superconductors. Phys. Rev. B 100, 064522. doi:10.1103/PhysRevB.100.064522
S. Lee, S. Kilcoyne, and R. Cywinski (1999). Muon science – muons in physics, chemistry, and materials (Boca Raton, Florida, United States: CRC Press).
Lindstrom, M., Y Fang, A. C., and Kiefl, R. F. (2016). Effect of surface roughness on the magnetic field profile in the meissner state of a superconductor. J. Supercond. Nov. Magnetism 29, 1499–1507. doi:10.1007/s10948-016-3449-7
MacFarlane, W. (2015). Implanted-ion βNMR: a new probe for nanoscience. Solid State Nucl. Magn. Reson. 68-69, 1–12. doi:10.1016/j.ssnmr.2015.02.004
MacFarlane, W., Shenton, J., Salman, Z., Chatzichristos, A., Cortie, D., Dehn, M., et al. (2023). The site and high field βNMR properties of 8Li+ implanted in α-Al2O3. J. Phys. Conf. Ser. 2462, 012009. doi:10.1088/1742-6596/2462/1/012009
MacFarlane, W. A. (2022). Status and progress of ion-implanted βNMR at TRIUMF. Z. für Phys. Chem. 236, 757–798. doi:10.1515/zpch-2021-3154
MacFarlane, W. A., Chow, K. H., Hossain, M. D., Karner, V. L., Kiefl, R. F., McFadden, R. M. L., et al. (2018). “The spin Relaxation of8Li+ in gold at low magnetic field,” in Proceedings of the 14th International Conference on Muon Spin Rotation, Relaxation and Resonance (μSR2017), Sapporo, Japan, June 25-30, 2017. doi:10.7566/JPSCP.21.011020
MacLaughlin, D. E. (1976). Magnetic resonance in the superconducting state. Solid State Phys. 31, 1–69. doi:10.1016/S0081-1947(08)60541-X
Maniscalco, J. T., Gonnella, D., and Liepe, M. (2017). The importance of the electron mean free path for superconducting radio-frequency cavities. J. Appl. Phys. 121. doi:10.1063/1.4974909
McFadden, R. M., Asaduzzaman, M., Prokscha, T., Salman, Z., Suter, A., and Junginger, T. (2023b). Depth-resolved measurements of the meissner screening profile in surface-treated nb. Phys. Rev. Appl. 19, 044018. doi:10.1103/PhysRevApplied.19.044018
McFadden, R. M. L., Asaduzzaman, M., Buck, T. J., Cortie, D. L., Dehn, M. H., Dunsiger, S. R., et al. (2023a). Depth-resolved measurement of the Meissner screening profile in a niobium thin film from spin-lattice relaxation of the implanted β-emitter 8Li. J. Appl. Phys. 134. doi:10.1063/5.0175532
McFadden, R. M. L., Asaduzzaman, M., and Junginger, T. (2023c). Comment on “strong meissner screening change in superconducting radio frequency cavities due to mild baking. Appl. Phys. Lett. 104. Available at: https://arxiv.org/abs/2305.02129
McFadden, R. M. L., Chatzichristos, A., Dehn, M. H., Fujimoto, D., Funakubo, H., Gottberg, A., et al. (2018). “On the use of 31 mg for β-detected nmr studies of solids,” in Proceedings of the 14th International Conference on Muon Spin Rotation, Relaxation and Resonance (μSR2017), Sapporo, Japan, June 25-30, 2017. doi:10.7566/jpscp.21.011047
Mironov, S., Mel’nikov, A. S., and Buzdin, A. (2018). Electromagnetic proximity effect in planar superconductor-ferromagnet structures. Appl. Phys. Lett. 113, 022601. doi:10.1063/1.5037074
Miyazaki, A., and Delsolaro, W. V. (2019). Determination of the bardeen-cooper-schrieffer material parameters of the hie-isolde superconducting resonator. Supercond. Sci. Technol. 32, 025002. doi:10.1088/1361-6668/aaf049
Morenzoni, E., Glückler, H., Prokscha, T., Khasanov, R., Luetkens, H., Birke, M., et al. (2002). Implantation studies of kev positive muons in thin metallic layers. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 192, 254–266. doi:10.1016/s0168-583x(01)01166-1
Morenzoni, E., Saadaoui, H., Wang, D., Horisberger, M., Kirk, E. C., MacFarlane, W. A., et al. (2012). Slow order-parameter fluctuations in superconducting pb and ag/nb films observed using β-detected nuclear magnetic resonance. Phys. Rev. B 85, 220501. doi:10.1103/PhysRevB.85.220501
Niinikoski, T. O., Hartmann, O., Karlsson, E., Norlin, L. O., Pernestål, K., Kehr, K. W., et al. (1979). Muon diffusion in niobium in the presence of traps. Hyperfine Interact. 6, 229–232. doi:10.1007/BF01028797
Ofer, O., Baglo, J. C., Hossain, M. D., Kiefl, R. F., Hardy, W. N., Thaler, A., et al. (2012). Absolute value and temperature dependence of the magnetic penetration depth in ba({\text{co}}_{0.074}{\text{fe}}_{0.926})_{2}\text{as}_{2}. Phys. Rev. B 85, 060506. doi:10.1103/PhysRevB.85.060506
Parolin, T. J., Shi, J., Salman, Z., Chow, K. H., Dosanjh, P., Saadaoui, H., et al. (2009). Nuclear magnetic resonance study of Li implanted in a thin film of niobium. Phys. Rev. B 80, 174109. doi:10.1103/PhysRevB.80.174109
Pippard, A. B. (1953). An experimental and theoretical study of the relation between magnetic field and current in a superconductor. Proc. Roy. Soc. Lond. 547. doi:10.1098/rspa.1953.0040
Pleines, M., Forgan, E., Glückler, H., Hofer, A., Morenzoni, E., Niedermayer, C., et al. (2000). Temperature dependence of the magnetic penetration depth in an yba2cu3o7-δ film. Phys. B Condens. Matter 289-290, 369–372. doi:10.1016/S0921-4526(00)00413-0
Posen, S., and Hall, D. L. (2017). Nb3Sn superconducting radiofrequency cavities: fabrication, results, properties, and prospects. Supercond. Sci. Technol. 30, 033004. doi:10.1088/1361-6668/30/3/033004
Posen, S., Valles, N., and Liepe, M. (2015). Radio frequency magnetic field limits of nb and nb3sn. Phys. Rev. Lett. 115, 047001. doi:10.1103/physrevlett.115.047001
Prokscha, T., Morenzoni, E., Deiters, K., Foroughi, F., George, D., Kobler, R., et al. (2008). The new μe4 beam at psi: a hybrid-type large acceptance channel for the generation of a high intensity surface-muon beam. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 595, 317–331. doi:10.1016/j.nima.2008.07.081
Romanenko, A., Grassellino, A., Barkov, F., Suter, A., Salman, Z., and Prokscha, T. (2014). Strong meissner screening change in superconducting radio frequency cavities due to mild baking. Appl. Phys. Lett. 104. doi:10.1063/1.4866013
Schenck, A. (1985). Muon spin rotation spectroscopy: principles and applications in solid state physics. Boca Raton, Florida, United States: Taylor and Francis Inc.
Sonier, J. E., Brewer, J. H., and Kiefl, R. F. (2000). μsr studies of the vortex state in type-ii superconductors. Rev. Mod. Phys. 72, 769–811. doi:10.1103/RevModPhys.72.769
Stewart, R., Flokstra, M. G., Rogers, M., Satchell, N., Burnell, G., Miller, D., et al. (2019). Controlling the electromagnetic proximity effect by tuning the mixing between superconducting and ferromagnetic order. Phys. Rev. B 100, 020505. doi:10.1103/PhysRevB.100.020505
Stilp, E., Suter, A., Prokscha, T., Salman, Z., Morenzoni, E., Keller, H., et al. (2014a). Controlling the near-surface superfluid density in underdoped yba2cu3o6+x by photo-illumination. Sci. Rep. 4, 6250. doi:10.1038/srep06250
Stilp, E., Suter, A., Prokscha, T., Salman, Z., Morenzoni, E., Keller, H., et al. (2014b). Modifications of the meissner screening profile in yba2cu3o7−δ thin films by gold nanoparticles. Phys. Rev. B 89, 020510. doi:10.1103/PhysRevB.89.020510
Stöckmann, H. J., Jäger, E., Sulzer, G., Ittermann, B., Ackermann, H., Diehl, E., et al. (1989). Cross relaxation studied by βNMR. Hyperfine Interact. 49, 235–252. doi:10.1007/BF02405144
Suter, A., Logvenov, G., Boris, A. V., Baiutti, F., Wrobel, F., Howald, L., et al. (2018). Superconductivity drives magnetism in δ-doped la2cuo4. Phys. Rev. B 97, 134522. doi:10.1103/PhysRevB.97.134522
Suter, A., Morenzoni, E., Garifianov, N., Khasanov, R., Kirk, E., Luetkens, H., et al. (2005). Observation of nonexponential magnetic penetration profiles in the meissner state: a manifestation of nonlocal effects in superconductors. Phys. Rev. B 72, 024506. doi:10.1103/physrevb.72.024506
Suter, A., Morenzoni, E., Garifianov, N., Khasanov, R., Kirk, E., Luetkens, H., et al. (2006). Nonlocal meissner screening. Phys. B Condens. Matter 374-375, 243–246. doi:10.1016/j.physb.2005.11.065
Suter, A., Morenzoni, E., Khasanov, R., Luetkens, H., Prokscha, T., and Garifianov, N. (2004). Direct observation of nonlocal effects in a superconductor. Phys. Rev. Lett. 92, 087001. doi:10.1103/PhysRevLett.92.087001
Thoeng, E., Asaduzzaman, M., McFadden, R. M. L., Junginger, T., and Laxdal, R. E. (2023b). First results from beta-srf - testing srf samples at high parallel field.
Thoeng, E., McFadden, R. M. L., Saminathan, S., Morris, G. D., Kolb, P., Matheson, B., et al. (2023a). A new high parallel-field spectrometer at TRIUMF’s β-NMR facility. Rev. Sci. Instrum. 94, 023305. doi:10.1063/5.0137368
Turner, D., Burt, G., and Junginger, T. (2022). No interface energy barrier and increased surface pinning in low temperature baked niobium. Sci. Rep. 12, 5522. doi:10.1038/s41598-022-09023-0
van der Klink, J., and Brom, H. (2000). Nmr in metals, metal particles and metal cluster compounds. Prog. Nucl. Magnetic Reson. Spectrosc. 36, 89–201. doi:10.1016/S0079-6565(99)00020-5
Wilkinson, J. M., and Blundell, S. J. (2020). Information and decoherence in a muon-fluorine coupled system. Phys. Rev. Lett. 125, 087201. doi:10.1103/PhysRevLett.125.087201
Wojek, B. M., Morenzoni, E., Eshchenko, D. G., Suter, A., Prokscha, T., Keller, H., et al. (2012). Magnetism, superconductivity, and coupling in cuprate heterostructures probed by low-energy muon-spin rotation. Phys. Rev. B 85, 024505. doi:10.1103/PhysRevB.85.024505
Yaouanc, A., Dalmas de Réotier, P., and Brandt, E. H. (1997). Effect of the vortex core on the magnetic field in hard superconductors. Phys. Rev. B 55, 11107–11110. doi:10.1103/PhysRevB.55.11107
Yaouanc, A., Maisuradze, A., Nakai, N., Machida, K., Khasanov, R., Amato, A., et al. (2014). Magnetic field distribution and characteristic fields of the vortex lattice for a clean superconducting niobium sample in an external field applied along a three-fold axis. Phys. Rev. B 89, 184503. doi:10.1103/PhysRevB.89.184503
Keywords: muon spin rotation, beta-detected nuclear magnetic resonance, superconductivity, superconducting radio-frequency, superconducting cavities
Citation: Junginger T, Laxdal R, MacFarlane WA and Suter A (2024) SRF material research using muon spin rotation and beta-detected nuclear magnetic resonance. Front. Electron. Mater. 4:1346235. doi: 10.3389/femat.2024.1346235
Received: 29 November 2023; Accepted: 25 January 2024;
Published: 15 February 2024.
Edited by:
Pashupati Dhakal, Jefferson Lab (DOE), United StatesReviewed by:
Yasmine Sassa, Royal Institute of Technology, SwedenCopyright © 2024 Junginger, Laxdal, MacFarlane and Suter. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tobias Junginger, SnVuZ2luZ2VyQHV2aWMuY2E=; Robert Laxdal, bGF4QHRyaXVtZi5jYQ==; W. A. MacFarlane, d2FtQGNoZW0udWJjLmNh; Andreas Suter, YW5kcmVhcy5zdXRlckBwc2kuY2g=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.