Superheating field in superconductors with nanostructured surfaces

We report calculations of a DC superheating field H_sh in superconductors with nanostructured surfaces. Numerical simulations of the Ginzburg–Landau (GL) equations were performed for a superconductor with an inhomogeneous impurity concentration, a thin superconducting layer on top of another superconductor, and superconductor–insulator–superconductor (S-I-S) multilayers. The superheating field was calculated taking into account the instability of the Meissner state with a non-zero wavelength along the surface, which is essential for the realistic values of the GL parameter κ. Simulations were performed for the material parameters of Nb and Nb₃Sn at different values of κ and the mean free paths. We show that the impurity concentration profile at the surface and thicknesses of S-I-S multilayers can be optimized to enhance H_sh above the bulk superheating fields of both Nb and Nb₃Sn. For example, an S-I-S structure with a 90-nm-thick Nb₃Sn layer on Nb can boost the superheating field up to ≈500 mT, while protecting the superconducting radio-frequency (SRF) cavity from dendritic thermomagnetic avalanches caused by local penetration of vortices.

1 Introduction

The superconducting radio-frequency (SRF) resonant cavities in particle accelerators enable high accelerating gradients with low power consumption. The best Nb cavities can have high quality factors Q ∼ 10¹⁰–10¹¹ and sustain accelerating fields up to 50 MV/m at T = 1.5–2 K and 0.6–2 GHz (Padamsee et al., 2018; Gurevich, 2023). The peak RF fields B₀ ≃ 200 mT at the equatorial surface of Nb cavities can approach the thermodynamic critical field B_c ≈ 200 mT at which the screening current density flowing at the inner cavity surface is close to the depairing current density J_c ≃ B_c/μ₀λ—the maximum DC current density a superconductor can carry in the Meissner state (Tinkham, 2004), where λ is the penetration depth of the magnetic field. Thus, the breakdown fields of the best Nb cavities have nearly reached the DC superheating field B_sh ≃ B_c (Galaiko, 1966; Matricon and Saint-James, 1967; Christiansen, 1969; Chapman, 1995; Catelani and Sethna, 2008; Transtrum et al., 2011; Lin and Gurevich, 2012). The Q factors can be increased by material treatments such as high-temperature annealing followed by low-temperature baking which not only increase Q (B₀) and the breakdown field but also reduce the deterioration of Q at high fields (Ciovati et al., 2010; Posen et al., 2020). High-temperature treatments combined with the infusion of nitrogen, titanium, or oxygen can produce an anomalous increase of Q (B₀) with RF field amplitude B₀ = μ₀H₀ (Ciovati et al., 2016; Grassellino et al., 2017; Dhakal, 2020; Lechner et al., 2021). These advances raise the question about the fundamental limit of the breakdown fields of SRF cavities and the extent to which it can be pushed by surface nanostructuring and impurity management (Gurevich and Kubo, 2017; Gurevich, 2023).

Several ways of increasing the SRF breakdown fields by surface nanostructuring have been proposed. They include depositing high-T_c superconducting multilayers with thin dielectric interlayers (Gurevich, 2006; Gurevich, 2015; Kubo et al., 2014; Liarte et al., 2017; Kubo, 2021) or a dirty overlayer with a higher impurity concentration at the surface (Ngampruetikorn and Sauls, 2019). The DC superheating field of such structures has been evaluated using the London, Ginzburg–Landau (GL), and quasiclassical Usadel and Eilenberger equations in the limit of an infinite GL parameter κ = λ/ξ → ∞ in which the breakdown of the Meissner state at H₀ = H_sh occurs once the current density at the surface reaches the depairing limit (Gurevich, 2006; Gurevich, 2015; Kubo et al., 2014; Liarte et al., 2017; Kubo, 2021; Ngampruetikorn and Sauls, 2019). Yet, it has been well-established that in a more realistic case of a finite κ, the breakdown of the Meissner state at H = H_sh occurs due to the exponential growth of periodic perturbations of the order parameter and the magnetic field with a wavelength ${\lambda }_c\sim {({\xi }^3\lambda )}^{1/4}$ along the surface, where ξ is the coherence length (Christiansen, 1969; Chapman, 1995; Transtrum et al., 2011). The effect of such periodic Turing instability (Cross and Hohenberg, 1993) on H_sh can be particularly important for Nb cavities with κ ∼ 1. Addressing the effect of finite κ (which in turn depends on the mean free path) on H_sh in superconductors with nanostructured surfaces is the goal of this work.

We present the results of numerical calculations of a DC superheating field for different superconducting geometries in materials with finite κ and determine optimal surface nanostructures that can withstand the maximum magnetic field in the vortex-free Meissner state. In particular, we consider a bulk superconductor with a thin impurity diffusion layer, a clean superconducting overlayer separated by an insulating layer from the bulk (e.g., Nb₃Sn-I-Nb₃Sn), a thin dirty superconducting layer on the top of the same superconductor (e.g., dirty Nb₃Sn-I-clean Nb₃Sn), and a thin high-T_c superconducting layer on the top of a low-T_c superconductor (e.g., Nb₃Sn-I-Nb). We calculate H_sh and determine an optimal layer thickness for each geometry by numerically solving the GL equations, taking into account both the non-linear screening of the applied magnetic field and the periodic instability of the Meissner state in a nanostructured superconductor.

The paper is organized as follows. The GL equations and methods of numerical detection of H_sh and the wavelength λ_c of a critical perturbation causing the instability of the Meissner state are presented in Section 2. The results of numerical calculations of H_sh for impurity diffusion layers and various S-I-S structures are given in Section 3 and Section 4, respectively. Section 5 contains discussion of the results, and Section 6 provides the conclusion with a summary. Computational details are given in Section Method and other technical details are given in Supplementary Appendices A, B.

2 GL equations and numerical detection of H_sh and k_c

We first consider a semi-infinite uniform superconductor in a magnetic field H₀ applied along the z-axis, parallel to the planar surface. In this case, the induced supercurrents flow in the xy plane and GL equations for the complex order parameter ψ = Δe^iφ, and two components of the vector potential A_x and A_y can be reduced to two coupled partial differential equations for the amplitude Δ(x, y, t) and the z-component of the magnetic field H (x, y, t). As shown in Supplementary Appendix A, these equations can be written in the following dimensionless form:

$\dot{f}-f+f^3-{\nabla }^{2}f+\frac{{\kappa }^2}{f^3}\left[{\left({\partial }_{x}h\right)}^2+{\left({\partial }_{y}h\right)}^2\right]=0,(1)$

$\nabla \cdot \left(\frac{\nabla h}{f^2}\right)=\frac{h}{{\kappa }^2}.(2)$

Here, f (x, y) = Δ(x, y)/Δ₀, Δ₀(T) is the equilibrium order parameter in the bulk, $h(x,y)=H(x,y)/\sqrt{2}{H}_c$, and all lengths are in units of the coherence length ξ and κ = λ/ξ. Despite the presence of the time derivative $\dot{f}$ in Eqs (1, 2), they are essentially the quasi-static GL equations, but not the true time-dependent Ginzburg–Landau (TDGL) equations (Watts-Tobin et al., 1981; Sheikhzada and Gurevich, 2020) which describe a non-equilibrium superconductor at T ≈ T_c. Here, $\dot{f}$ is added just to detect the instability of the Meissner state in numerical simulations upon slow ramping the applied magnetic field. This procedure allows us to find the field H₀ = H_sh above which the GL equations no longer have stationary solutions. Another way of numerical calculation of H_sh is based on finding the applied field at which the linearized Eqs (1, 2) have zero eigenmode with $\dot{f}=0$ (Christiansen, 1969; Chapman, 1995; Transtrum et al., 2011; Liarte et al., 2017), as summarized in Supplementary Appendix B. It turns out that the direct solving Eqs (1, 2) with the ad hoc term $\dot{f}$ is much faster than solving the eigenmode problem. For slow magnetic ramp rates ${\dot{H}}_0$ used in our simulations, the resulting H_sh calculated by these two methods only differ by ≃ 1%, as it is shown in the next Sections. Equations (1, 2) were solved with the following boundary conditions:

$\begin{array}{cc}\hfill & h\left(0,y\right)=h_0\left(t\right),\hfill \\ \hfill & h\left(x,0\right)=h\left(x,L_y\right),f\left(x,0\right)=f\left(x,L_y\right),\hfill \\ \hfill & f\left(L_x,y\right)=1,h\left(L_x,y\right)=0,\hfill \end{array}(3)$

where $h_0=H_0/\sqrt{2}{H}_c$ and the lengths L_x and L_y of the simulation box L_x × L_y were chosen to be ≃ (50–150)ξ depending on κ. The details of the numerical calculations are given in the Supplementary Method.

Shown in Figures 1A,B are f (x, y) calculated at κ = 10 and the applied fields H₀ slightly below and above H_sh. At H₀ < H_sh, the order parameter f(x) is reduced at the surface by the flowing screening currents. At H₀ > H_sh, the stationary f(x) becomes unstable with respect to spontaneously growing periodic perturbations δf (x, y, t) along the surface, as shown in Figure 1B. This Turing instability (Cross and Hohenberg, 1993) occurs with respect to a small disturbance δf (x, y, t) ∝ δf(x)e^iky+Γt, where the increment Γ(H₀, k) depends on the wave vector k of spatial oscillations of f (x, y) along the surface as shown in Figure 2A. Below the superheating field, Γ(k) is negative so perturbations with all k decay exponentially and the Meissner state is stable. At the superheating field, Γ(k) first vanishes at a critical wave number k = k_c at which Γ(k) is maximum. At H₀ = H_sh + 0, the increment Γ(k) becomes positive at k = k_c, making the Meissner state unstable with respect to a growing critical perturbation $\delta f(x,y,t)\propto \delta f(x)e^{i{k}_{c}y+\mathrm{\Gamma }(k_c)t}$ with the wavelength λ_c = 2π/k_c, while all other perturbations with k ≠ k_c decay exponentially. We calculated H_sh by slowly ramping the applied field and detecting the onset of the exponential growth of f (x, y, t) with time as described in Method. The critical wavelength λ_c was evaluated from the maximum peak in the spatial Fourier transform of δf (0, y), as shown in Figure 2B. This instability is a precursor of the penetration of the vortex structure with the initial period ${\lambda }_c\sim {({\xi }^3\lambda )}^{1/4}$ smaller than the stationary vortex spacing $\sim \sqrt{\lambda \xi }$ at H₀ ≃ H_sh and κ > 1. The aforementioned direct method for the calculation of H_sh is based on the numerical detection of the field threshold above which the stationary Meissner state does not exist. Here, the time scales of the transition to the vortex state at H₀ > H_sh are irrelevant, provided that H_sh is calculated at low enough magnetic ramp rates at which H_sh is independent of ${\dot{h}}_0$. We calculated H_sh at ${\dot{h}}_0\simeq 10^{-5}$ and verified that H_sh is indeed practically independent of ${\dot{h}}_0$, which is also consistent with the calculations of H_sh using both the TDGL and full non-equilibrium equations for dirty superconductors (Sheikhzada and Gurevich, 2020).

FIGURE 1

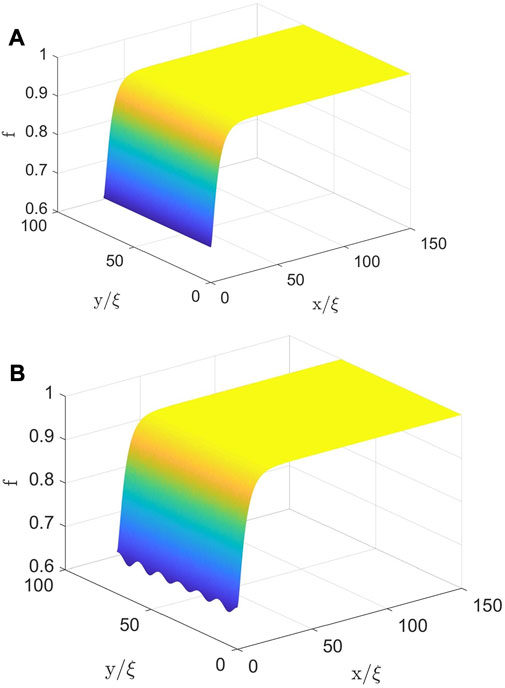
FIGURE 1. Spatial distribution of the order parameter calculated at κ =10, H₀= H_sh −0 (A), and H₀= H_sh +0 (B).

FIGURE 2

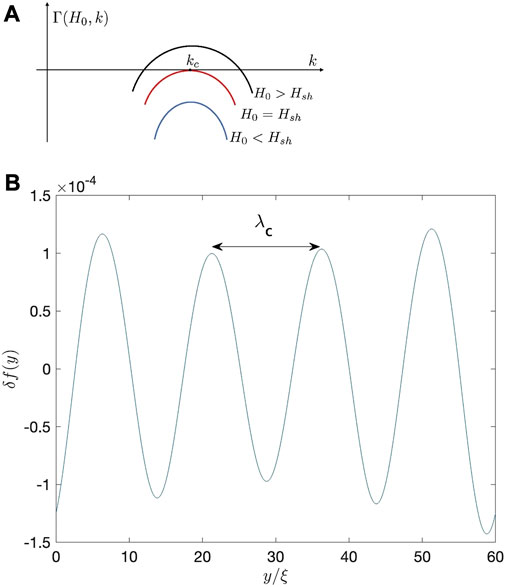
FIGURE 2. (A) Qualitative dependence of the instability increment Γ(H₀, k) on the wave vector of perturbation k at different applied fields H₀. (B) Snapshot of δf(y) at x =0, and H₀= H_sh +0 calculated at κ =10.

We then compare some of our numerical results with the known analytical approximations for H_sh and k_c at κ ≫ 1, given as follows (Christiansen, 1969; Chapman, 1995; Transtrum et al., 2011; Liarte et al., 2017).

$\frac{H_{sh}}{H_c}\approx \frac{\sqrt{5}}{3}+\frac{0.545}{\sqrt{\kappa }},(4)$

$\lambda k_c\approx 0.956{\kappa }^{3/4}.(5)$

At κ = 10–20, Eqs (4, 5) give the instability wavelength ${\lambda }_c=6.57{({\xi }^3\lambda )}^{1/4}\simeq (1.17-0.21)\lambda$ and H_sh approximately (23–16)% higher than H_sh = 0.745H_c in the limit of κ → ∞ in which λ_c → 0 and the breakdown of the Meissner state at H = H_sh occurs once the current density at the surface reaches the depairing limit (Christiansen, 1969). Thus, even at κ = 10–20, characteristic of a dirty Nb or a clean stoichiometric Nb₃Sn (Orlando et al., 1979; Posen and Hall, 2017), the periodic instability along the surface occurs on the scale of the order of the field penetration depth, so the self-consistent GL calculation of H_sh is required.

3 Superconductor with an impurity diffusion layer

We consider a dirty layer at the surface with a higher impurity concentration, as shown in Figure 3A. In our simulations, such a layer was modeled by a spatially varying coherence length and penetration depths ${\xi }^2(x)/{\xi }_{\infty }^2={\lambda }_{\infty }^2/{\lambda }^2(x)=1-\alpha \exp (-x/l_d)$, as shown in Figure 3B. Here, ξ_∞ and λ_∞ are the corresponding bulk values far away from the surface, l_d is the thickness of the diffusion layer, and the parameter α < 1 quantifies the reduction of ξ(0) = (1 − α)^1/2ξ_∞ and the enhancement of λ(0) = (1 − α)^−1/2λ_∞ at the surface. The ratio ${\xi }^2(x)/{\xi }_{\infty }^2={\lambda }_{\infty }^2/{\lambda }^2(x)$ is controlled by the impurity function χ(ℏv_F/2πT_cl(x)) (Werthamer, 1969) with an inhomogeneous mean free path l(x), which is defined in Supplementary Appendix A. The resulting GL equations take the following form:

$\dot{f}=f-f^3+\nabla \cdot \left(S_{\gamma }\nabla f\right)-\frac{{\kappa }^2}{S_{\gamma }{f}^3}\left[{\left({\partial }_{x}h\right)}^2+{\left({\partial }_{y}h\right)}^2\right],(6)$

$\nabla \cdot \left(\frac{\nabla h}{S_{\gamma }{f}^2}\right)-\frac{h}{{\kappa }^2}=0,(7)$

where κ = λ_∞/ξ_∞, $S_{\gamma }={\xi }^2(x)/{\xi }_{\infty }^2=1-\alpha \exp (-x/l_d)$, and the lengths are in units of ξ_∞. The boundary conditions are the same as in Eq. (3). Different impurity profiles were investigated by changing α and l_d at κ = 2 and κ = 10, respectively, representing a cleaner and dirtier Nb.

FIGURE 3

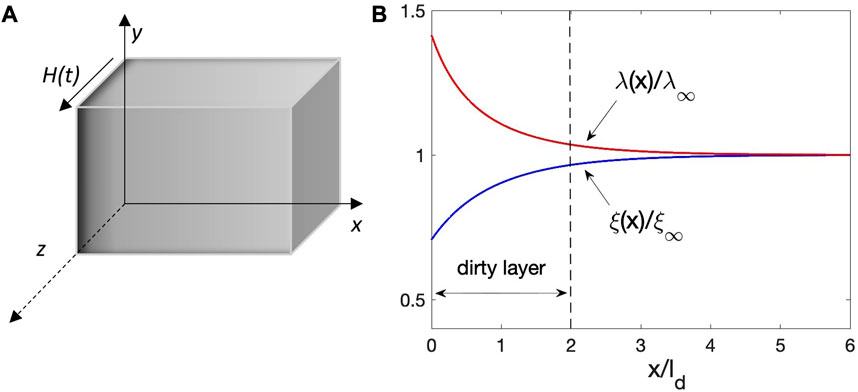
FIGURE 3. (A) Impurity diffusion layer at the surface shown by the dark gray contrast. (B) Variations of normalized coherence length and penetration depth across a dirty layer with α =0.5.

The calculated dependencies of H_sh(l_d) on the diffusion layer thickness at different α for κ = 2 and κ = 10 are shown in Figures 4A, B, respectively. One can see that H_sh(l_d) first increases with l_d, reaches a maximum, and then decreases with l_d approaching a lower value of H_sh at l_d ≫ ξ_∞. At κ = 2, H_sh(l_d) is maximum at l_d/ξ_∞ = 0.8, 0.9, 1.5 for α = 0.2, 0.5, 0.8. Similarly, at κ = 10, H_sh(l_d) is maximum at l_d/ξ_∞ = 4, 5, 10. Here, the diffusion layer can increase H_sh by $\approx 9\%$ at κ = 2 and by $\approx 14\%$ at κ = 10 as compared to a superconductor with an ideal surface. A qualitatively similar non-monotonic dependence of H_sh on l_d was also obtained by solving the quasiclassical Eilenberger equations in the entire temperature range 0 < T < T_c (Ngampruetikorn and Sauls, 2019). The maximum in H_sh(d) results from a current counterflow induced in the dirty surface layer by a cleaner substrate with a smaller λ_∞ < λ(0) (Kubo et al., 2014; Gurevich, 2015), the magnitude of the peak increases as the diffusion layer gets dirtier. The curves H_sh(l_d) cross over at larger l_d for which H_sh(∞) is determined by the surface GL parameter κ(0) = κ_∞/(1 − α). As a result, H_sh(∞) decreases as the material gets dirtier, in agreement with Eq. (4).

FIGURE 4

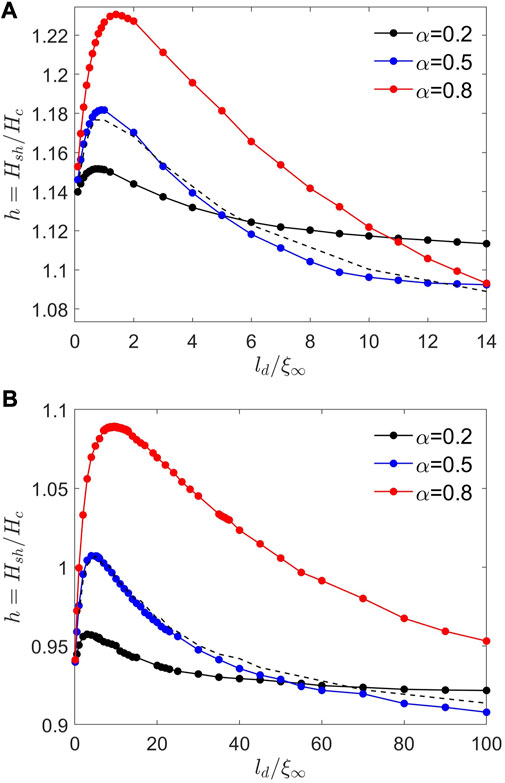
FIGURE 4. Superheating field H_sh(l_d) as a function of the dirty layer thickness calculated at (A) κ =2 (B) κ =10 for different α. The dashed line shows H_sh(l_d) calculated from the condition δ²F =0 and ∂_kδ²F =0 at (A) κ =2 and (B) κ =10 at α =0.5.

The direct numerical calculation of H_sh involves detecting the instability of the Meissner state with respect to an infinitesimal perturbation $\delta f(x,y)=\delta f(x)e^{i{k}_{c}y+\mathrm{\Gamma }t}$ with a finite wave number k_c and an increment Γ(H₀) changing the sign from negative at H₀ < H_sh to positive at H₀ > H_sh. Figure 5 shows the fast Fourier transform of a snapshot of δf (0, y, t) along y calculated at H₀ = H_sh + 0 at α = 0.5, κ = 10, and different ratios l_d/ξ_∞. One can see that δf (0, y) has several harmonics even at the slow field ramp rate ${\dot{h}}_0=5\cdot 10^{-5}$ used in our simulations. Such multi-mode temporal oscillations of δf (0, y) can result from a nonlinear mode coupling above the Turing instability threshold (Cross and Hohenberg, 1993), as well as a finite size of the computational box. In this case, the critical wave number k_c would correspond to the highest peak in the Fourier spectrum of δf_k (0, t). Yet, Figure 5 reveals two uneven peaks whose heights change differently as the ratio l_d/ξ_∞ is varied. For instance, at l_d/ξ_∞ = 5, the critical wave number k_c is determined by the higher left peak observed in Figure 5, but as l_d/ξ_∞ is increased to 6, the right peak becomes higher than the left one, so k_c changes jumpwise at l_d/ξ_∞ ≈ 5.5. The peak shifts toward higher λ_∞k values, providing a constant k_c in this range of l_d/ξ_∞. The switching of k_c between two values as l_d/ξ_∞ is increased can be seen in “Fourier Transform. mp4” in Supplementary Video S1. To see the extent to which this ambiguity in k_c may affect H_sh, we have also calculated k_c and H_sh from the sign change of the second variation of the free energy δ²F caused by small perturbations of δf (x, y) and δh (x, y). In this method (Christiansen, 1969; Chapman, 1995; Transtrum et al., 2011), H_sh is determined by the conditions δ²F (k_c, H_sh) = 0 and ∂δ²F/∂k_c = 0. Figures 6A, B show λ_∞k_c as a function of l_d/ξ_∞ at κ = 2 and κ = 10 and different α computed from the second variation δ²F, as described in Supplementary Appendix B. One can see that the peaks in k_c shown in Figure 5 are in the range of λk_c ≈ 5–7 qualitatively matching λk_c (l_d) ≈ 5 at α = 0.5, as shown in Figure 6. Yet, the H_sh(l_d/ξ_∞) curves calculated by these two methods at α = 0.5 turned out to be very similar (the difference is approximately 1%), as shown by the dashed lines in Figure 4.

FIGURE 5

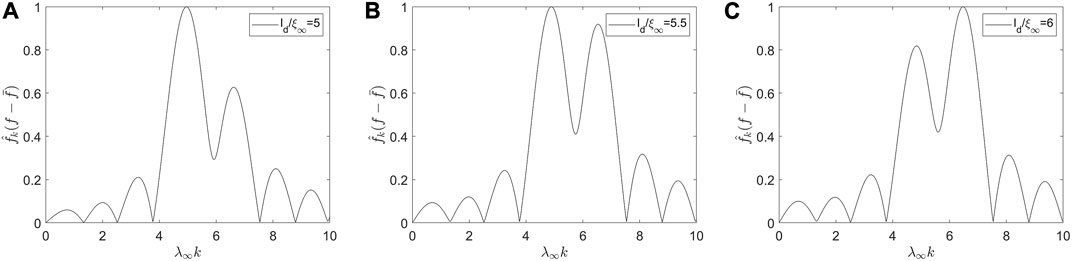
FIGURE 5. Discrete fast Fourier transform of δf (0, y) at H₀= H_sh +0, α =0.5, and κ =10; (A) l_d/ξ_∞=5, (B) l_d/ξ_∞=5.5, and (C) l_d/ξ_∞=6. Evolution of these peaks with l_d/ξ_∞ is shown in “Fourier Transform.gif” in Supplementary Video S1.

FIGURE 6

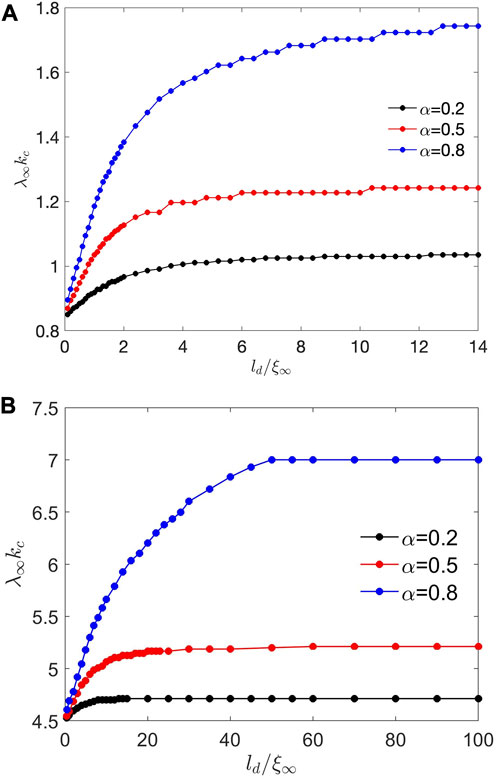
FIGURE 6. Dependencies of λk_c on l_d calculated from the conditions δ²F =0 and ∂_kδ²F =0 at (A) κ =2 and (B) κ =10 for different α.

4 S-I-S structures

Using the direct simulation method outlined in Section 2, we have calculated H_sh(d) and the critical wave number k_c(d) for various S-I-S structures: the S layer of thickness d is separated by an insulator from the S substrate of the same material, a dirty S layer on the top of a cleaner superconductor (e.g., dirty Nb-I-clean Nb), and a thin high T_c overlayer on the top of a low T_c superconductor (e.g., Nb₃Sn-I-Nb). Here, the I layer is assumed to be thick enough to fully suppress the Josephson coupling between the S overlayer and the bulk, but thinner than the S overlayer. The screening of the applied field in an S-I-S multilayer is shown in Figure 7.

FIGURE 7

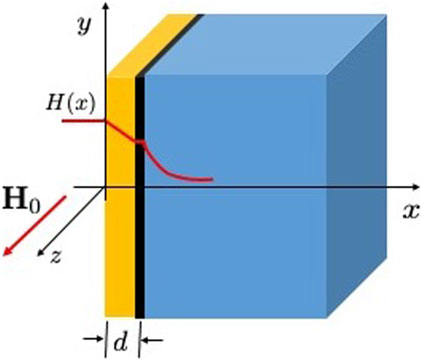
FIGURE 7. Superconductor–insulator–superconductor structure. The vertical black line represents the insulating layer, and the red line shows the screened magnetic field profile H(x).

4.1 S overlayer on the top of the S-substrate

The GL Eqs (1, 2) for the S overlayer separated by the I layer from the substrate made of the same superconductor were solved in both S-domains with the boundary conditions given by Eq. (3) supplemented by the conditions of continuity of h (d + 0, y) = h (d − 0, y), parallel electric field E_y (d + 0, y) = E_y (d − 0, y), and zero current ∂_yh (d + 0) = ∂_yh (d − 0) = 0 through the I layer. Figure 8 shows that H_sh is a function of the thickness of the S overlayer d calculated at κ = 17 representing Nb₃Sn. Here, a very thin S overlayer reduces H_sh(d), which then gradually increases with d, reaching a higher bulk value of H_sh at d > 9ξ₂, where ξ₂ is the coherence length in the S-substrate. The reduction of H_sh(d) at small d results from the I layer blocking the perpendicular currents produced by the critical perturbation and reducing its decay length in the bulk from $\sim \sqrt{\lambda \xi }$ to d. In turn, the critical wave number k_c(d) along the surface shown in Figure 9 increases jumpwise from k_c ≈ 1.8/λ₂ at d < 9ξ₂ in a thin overlayer to k_c ≈ 7.2/λ₂ at d > 9ξ₂, corresponding to the instability of the Meissner state in a semi-infinite superconductor. The calculated k_c at d > 9ξ₂ is approximately 10% smaller than k_c ≈ 8/λ₂ given by the asymptotic Eq. (5) at κ₂ = 17.

FIGURE 8

FIGURE 8. Superheating field H_sh(d) calculated for the Nb₃Sn-I-Nb₃Sn structure.

FIGURE 9

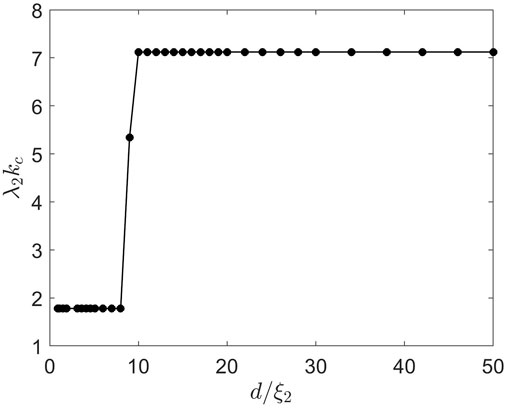
FIGURE 9. Critical wave number k_c(d) calculated for the Nb₃Sn-I-Nb₃Sn structure by solving the quasistatic GL equations directly as described in Section 2.

4.2 Dirty S overlayer on a cleaner S-substrate

A dirty S overlayer with a higher concentration of non-magnetic impurities on a cleaner S substrate of the same material is considered, assuming that both have the same T_c unaffected by non-magnetic impurity scattering (Tinkham, 2004). Superconductivity in the bulk is described by the following GL equations

${\dot{f}}_2={\nabla }^2{f}_2+f_2-f_2^3-\frac{{\kappa }_2^2}{f_2^3}\left[{\left({\partial }_x{h}_2\right)}^2+{\left({\partial }_y{h}_2\right)}^2\right],(8)$

$\nabla \cdot \left(\frac{\nabla h_2}{f_2^2}\right)=\frac{h_2}{{\kappa }_2^2},(9)$

where index 2 corresponds to the substrate parameters in which the lengths and f₂ are in units of their respective bulk values of ξ₂ and Δ₂. In turn, the GL equations in the overlayer are as follows:

${\dot{f}}_1=f_1-f_1^3+\frac{{\xi }_1^2}{{\xi }_2^2}{\nabla }^2{f}_1-\frac{{\xi }_1^2}{{\xi }_2^2}\frac{{\kappa }_1^2}{f_1^3}\left[{\left({\partial }_x{h}_1\right)}^2+{\left({\partial }_y{h}_1\right)}^2\right],(10)$

$\nabla \cdot \left(\frac{\nabla h_1}{f_1^2}\right)=\frac{h_1{\xi }_2^2}{{\xi }_1^2{\kappa }_1^2}.(11)$

Equations (8–11) were solved for a dirty Nb₃Sn overlayer on a cleaner Nb₃Sn with a mean free path l = 2 nm, ${\lambda }_1\approx {\lambda }_2{({\xi }_2/l)}^{1/2}\approx 135$ nm, ${\xi }_1\approx {(l{\xi }_2)}^{1/2}\approx 3$ nm, κ₁ = 45 in the overlayer, and κ₂ = 17 in the bulk. Figure 10 shows the calculated dependence of H_sh on the overlayer thickness which has a maximum at the optimum thickness d_m ≈ 9ξ₂. Such an optimal dirty overlayer can increase H_sh by approximately 10% as compared to the bulk H_sh. The behavior of H_sh(d) at a finite κ turns out to be similar to that calculated using the London and GL theories in the limit of κ → ∞ in which the enhancement of H_sh at d ≃ d_m results from the current counterflow induced by the substrate with a shorter λ₂ in the overlayer with a larger λ₁ (Kubo et al., 2014; Gurevich, 2015). Here, the cusp-like dependence of H_sh(d) is controlled by the instability of the Meissner state in the substrate at d < d_m and by the instability of the Meissner state in the overlayer at d > d_m, the overlayer partly screening the substrate and allowing it to withstand external fields higher than the bulk H_sh. The corresponding critical wave number k_c(d) is shown in Figure 11. The jumpwise change of k_c(d) reflects the switch from the instability of the Meissner state at the inner surface of the substrate at d < d_m to the instability at the outer surface in the overlayer at d > d_m. Such a jump in k_c also follows Eq. (5) which gives $k_c{\lambda }_2=0.956{\kappa }_2^{3/2}\approx 8$ at d < d_m and $k_c{\lambda }_2=0.956{\kappa }_1^{1/4}{\kappa }_2^{1/2}\approx 10.2$.

FIGURE 10

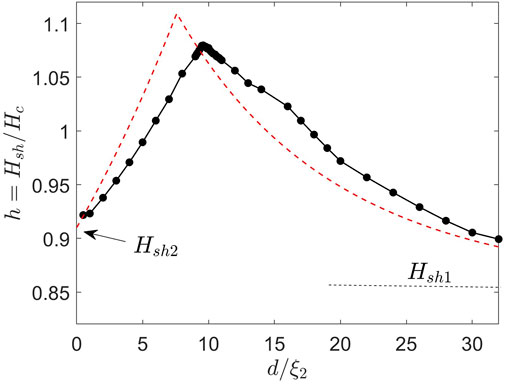
FIGURE 10. Superheating field H_sh(d) calculated for the Nb₃Sn(dirty)-I-Nb₃Sn structure. The red dashed line shows H_sh(d) calculated from the London Eqs (15–17) with H_sh1=0.855H_c and H_sh2=0.91H_c taken from the asymptotic limits of H_sh(d) at d ≫ λ₁ and d =0, respectively.

FIGURE 11

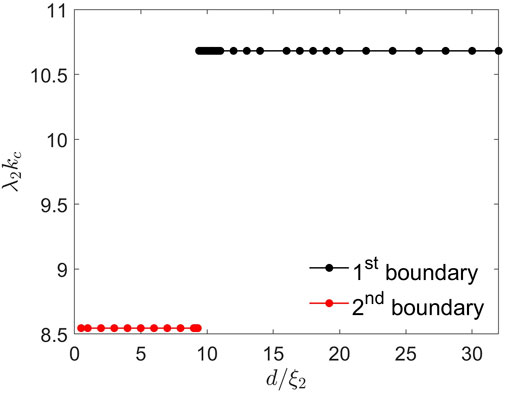
FIGURE 11. The critical wave number k_c(d) calculated for the Nb₃Sn(dirty)-I-Nb₃Sn structure by solving the quasi-static GL equations directly as described in Section 2.

4.3 High-T_c superconducting overlayer

Finally, we consider an S-I-S structure comprising a high-T_c layer on the top of a lower-T_c substrate. The order parameter f₂ and the field h₂ in the substrate are described in Eqs (8, 9), and the GL equations for f₁ and h₁ in the overlayer are given by

${\dot{f}}_1=\zeta f_1-f_1^3+s{\nabla }^2{f}_1-\frac{{\tilde{\kappa }}^2}{f_1^3}\left[{\left({\partial }_x{h}_1\right)}^2+{\left({\partial }_y{h}_1\right)}^2\right],(12)$

$\nabla \cdot \left(\frac{\nabla h_1}{f_1^2}\right)=\frac{{\lambda }_2^2{h}_1}{{\lambda }_1^2\zeta {\kappa }_2^2},(13)$

$\zeta =\frac{1-T/T_{c1}}{1-T/T_{c2}},s=\frac{{\xi }_1^2}{{\xi }_2^2}\zeta ,{\tilde{\kappa }}^2=\frac{{\xi }_1^2{\lambda }_1^4}{{\xi }_2^2{\lambda }_2^4}{\kappa }_2^2{\zeta }^3,(14)$

where T_c1 and T_c2 are the critical temperatures of the overlayer and the substrate, respectively, and the order parameter and lengths are normalized to the respective parameters of the substrate. Equations (12–14) are supplemented by the boundary conditions given by Eq. (3) and the conditions of field continuity and zero current through the I layer.

We solved the GL equations for a clean Nb₃Sn overlayer on a bulk Nb using κ₂ = 50/22 and κ₁ = 17 (Orlando et al., 1979; Posen and Hall, 2017). The calculated superheating field H_sh(d) shown in Figure 12 has a maximum at d_m ≈ 4ξ₂. This behavior of H_sh(d) is similar to that of H_sh(d) considered in the previous section: H_sh(d) at d < d_m is limited by the instability of the Meissner state in the Nb substrate partly screened by the Nb₃Sn overlayer, while H_sh at d > d_m is determined by the superheating field of Nb₃Sn enhanced at d ≈ d_m by the current counterflow caused by the Nb substrate. The corresponding dependence of k_c(d) on the overlayer thickness is shown in Figure 13. The jumpwise change of k_c(d) reflects the switch from the instability of the Meissner state at the inner surface of the low-T_c substrate at d < d_m to the instability at the outer surface in the high-T_c overlayer at d > d_m, which is similar to that shown in Figure 11. For the parameters used in the simulations, such Nb₃Sn-I-Nb structures with d ≈ d_m can boost the superheating field up to $\sim 2.2$ times higher than the bulk H_sh2 of Nb (Gurevich, 2006; Gurevich, 2015) and approximately 5.3% higher than the bulk H_sh1 of Nb₃Sn.

FIGURE 12

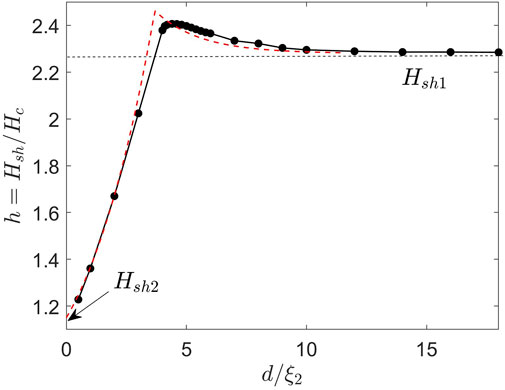
FIGURE 12. Superheating field H_sh(d) calculated for the Nb₃Sn-I-Nb structure. The red dashed line shows H_sh(d) calculated from the London Eqs (15–17) with H_sh1=2.28H_c and H_sh2=1.08H_c taken from the asymptotic limits of H_sh(d) at d ≫ λ₁ and d =0, respectively.

FIGURE 13

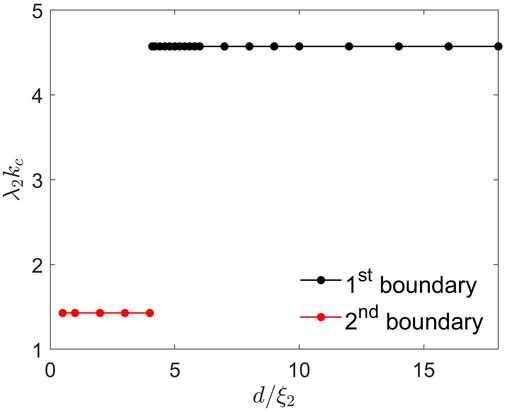
FIGURE 13. The critical wave number k_c(d) calculated for the Nb₃Sn-I-Nb structure by solving the quasistatic GL equations directly as described in Section 2.

5 Discussion

The GL calculations of the DC superheating field at T ≈ T_c self-consistently take into account the essential non-linear field screening and the periodic instability of the Meissner state in the entire range of the GL parameters which can be tuned by the impurities. This approach shows that the thicknesses of the impurity diffusion layer or S-I-S layers can be optimized to increase H_sh above the superheating fields of individual components. For instance, optimizing the diffusion length can enhance H_sh by ≃ 5–20% at κ = 10 and by ≃ 2–9% at κ = 2. An optimized dirty Nb₃Sn overlayer deposited onto the Nb₃Sn field by ≃ 10% as compared to H_sh of a clean Nb₃Sn. This effect manifests itself in a non-monotonic dependence of H_sh on the dirty layer thickness due to the current counterflow induced at the surface by a superconducting substrate with a shorter field penetration depth. Such behavior of H_sh(d) is consistent with the previous calculations of H_sh based on the London (Gurevich, 2006; Gurevich, 2015; Kubo et al., 2014) or Usadel (Kubo, 2021) and Eilenberger (Ngampruetikorn and Sauls, 2019) theories at κ → ∞. To see the extent to which the London model is consistent with the GL results, we consider H_sh(d) calculated for an S-I-S multilayer in the London limit (Gurevich, 2015).

$H_{sh}\left(d\right)=\left[\cosh \left(d/{\lambda }_1\right)+\left({\lambda }_2/{\lambda }_1\right)\sinh \left(d/{\lambda }_1\right)\right]H_{\mathit{sh}2},d<d_m(15)$

$H_{sh}\left(d\right)=\left[\frac{{\lambda }_1+{\lambda }_2\tanh \left(d/{\lambda }_1\right)}{{\lambda }_1\tanh \left(d/{\lambda }_1\right)+{\lambda }_2}\right]H_{\mathit{sh}1},d>d_m(16)$

$d_m={\lambda }_1\ln \left\{\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}\left[\frac{H_{\mathit{sh}1}}{H_{\mathit{sh}2}}+\sqrt{\frac{H_{\mathit{sh}1}^2}{H_{\mathit{sh}2}^2}+1-\frac{{\lambda }_2^2}{{\lambda }_1^2}}\right]\right\},(17)$

where H_sh1 and H_sh2 are the bulk superheating fields of the overlayer and the substrate, respectively. Equation (15) describes H_sh(d) of S-I-S structures with thin overlayers (d < d_m), where the Meissner state first breaks down at the surface of the substrate. Here, the high-H_c overlayer partly screens the substrate, allowing it to stay in the Meissner state at a higher applied field H₀ = H_sh(d) than the bare substrate. If d > d_m, the Meissner state first breaks down at the outer surface of the overlayer so that H_sh(d) → H_sh1 at d ≫ λ₁. The maximum H_sh(d_m) is given by:

$H_{sh}\left(d_m\right)={\left[H_{\mathit{sh}1}^2+\left(1-\frac{{\lambda }_2^2}{{\lambda }_1^2}\right)H_{\mathit{sh}2}^2\right]}^{1/2}.(18)$

The maximum $H_{sh}(d_m)={(H_{\mathit{sh}1}^2+H_{\mathit{sh}2}^2)}^{1/2}$ in an S-I-S multilayer occurs if ${({\lambda }_2/{\lambda }_1)}^2\ll 1$.

Equations (15–17) do not take into account the reduction of the superfluid density by current, non-linear field screening and the periodic instability of the Meissner state at a finite κ. The London model does not account for the size effect of reducing H_sh(d) if the overlayer thickness is smaller than the decay length $\sim \sqrt{{\lambda }_1{\xi }_1}$ of the critical perturbation, as was discussed in Section 4.1. Indeed, for identical materials of the substrate and overlayer (λ₁ = λ₂, H_sh1 = H_sh2), Eqs (15–17) give d_m = 0 and H_sh(d) = H_sh1 independent of d, which is inconsistent with the reduction of H_sh(d) at d ≲ 10ξ₂, as shown in Figure 8. Yet, the London model captures the non-monotonic thickness dependence H_sh(d) calculated from the GL theory if the overlayer has different properties than those of the substrate, and the input parameters H_sh1 and H_sh2 in Eqs (15–17) are exact bulk superheating fields for given values of κ and H_c, respectively (Gurevich, 2015). For instance, Figure 10 compares the GL and the London H_sh(d) calculated for an Nb₃Sn(dirty)-I-Nb₃Sn structure with a dirty overlayer for which the London model works reasonably well. For the Nb₃Sn-I-Nb multilayers considered in Section 4.3, we observed a rather good agreement between H_sh(d) calculated from the GL theory and Eqs (15–17), as shown in Figure 12. Such surprising accuracy of Eqs (15–17) was also observed by Kubo (2021) in the Usadel simulations of dirty S-I-S multilayers in the entire temperature range of 0 < T < T_c at κ → ∞.

In the GL region T ≈ T_c2, Eqs (15–17) predict a significant change in the temperature dependence of H_sh(T) of the S-I-S multilayer with a higher-T_c overlayer as compared to H_sh2(T) of the bare substrate. If T → T_c2, the penetration depth ${\lambda }_2(T)\propto {(T_{c2}-T)}^{-1/2}$ diverges and H_sh2(T) ∝ T_c2 − T vanishes, while λ₁ and H_sh1 remain nearly independent of T. This case is characteristic of Nb₃Sn-I-Nb for which T_c1 ≃ 2T_c2, the crossover thickness d_m(T) increases with T and diverges logarithmically at T → T_c2. In turn, H_sh(d, T) obtained by Eq. (15) is limited by the small superheating field of the substrate partially screened by the high-T_c overlayer:

$H_{sh}\left(T\right)\simeq \left({\lambda }_2/{\lambda }_1\right)\sinh \left(d/{\lambda }_1\right)H_{\mathit{sh}2}\left(T\right)\propto \sqrt{T_{c2}-T},(19)$

Hence, H_sh(T) can be significantly higher than H_sh2(T) ∝ T_c2 − T at T ≈ T_c2, particularly if d > λ₁. As an illustration, Figure 14 shows H_sh(T) calculated from Eqs (15–17) for different ratios d/λ₁ and the parameters of Nb₃Sn-I-Nb specified in Section 4.3. One can see both the square root temperature dependence given by Eq. (19) at T ≈ T_c2 and a sharp change in H_sh(T) upon decreasing T as d_m(T) becomes shorter than d and H_sh(T) crosses over to a nearly constant H_sh1(T) of the overlayer. For d/λ₁ < 2, such a transition in H_sh(T) happens at lower T outside the GL temperature range shown in the figure.

FIGURE 14

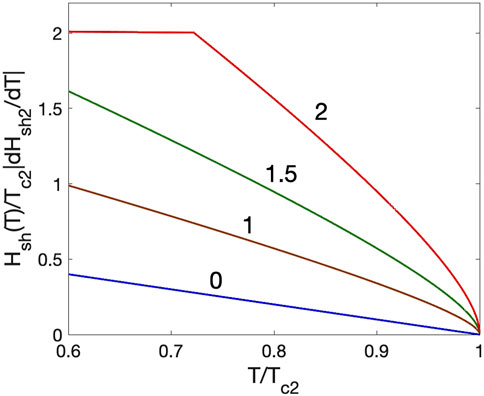
FIGURE 14. Temperature dependencies of H_sh(T) calculated from Eqs (15–17) for different ratios d/λ₁ and the superconducting parameters of Nb₃Sn-I-Nb specified in the text. The sharp change in the behavior of H_sh(T) upon decreasing T at d/λ₁=2 occurs as d_m(T) becomes shorter than d and H_sh(T) crosses over to a nearly constant H_sh1(T) of the overlayer. For smaller d/λ₁, such a transition in H_sh(T) takes place at lower T outside the GL temperature range shown in the figure. Here, the blue line with d/λ₁=0 represents H_sh2(T) of the bare substrate.

The relation between the static H_sh calculated here and the dynamic superheating field H_sd (T, ω) representing the fundamental field limit of superconductivity breakdown in SRF cavities depends on the rf frequency ω, temperature, and the material purity (Gurevich, 2023). The calculation of H_sd for S-I-S structures generally requires solving complex equations of non-equilibrium superconductivity, which in some cases can be reduced to TDGL equations at T ≈ T_c (Watts-Tobin et al., 1981). The dynamic superheating field of an alloyed superconductor with an ideal surface at T ≈ T_c was calculated from the microscopic theory (Sheikhzada and Gurevich, 2020), where it was shown that H_sd(T) approaches the static H_sh(T) at low frequencies ω ≪ ω_c but can be by a factor $\sqrt{2}$ larger than H_sh at ω ≫ ω_c. Here, the crossover frequency ${\omega }_c\sim \text{min}({\tau }_{ϵ}^{-1},{\tau }_{\mathrm{\Delta }}^{-1})$ is set by the inelastic electron–phonon scattering time τ_ϵ(T) ∝ T⁻³ and the TDGL relaxation time of the order parameter τ_Δ = πℏ/8k_B(T_c − T) (Gurevich, 2023). For Nb and Nb₃Sn at $T\approx T_c^{Nb}=9.2$ K, both τ_ϵ(9K) ∼ 10^–11 s and τ_Δ ∼ 10^–11 s at T_c − T = 0.2 K are much shorter than the rf period at 1 GHz. In this case, the superconducting and quasiparticle screening currents follow practically instantaneously the driving rf field, and the quasistatic H_sh(T) considered here is applicable. The dynamic superheating field at lower temperatures T ≃ 2 K at GHz frequencies has not yet been calculated from a microscopic theory.

In this work, H_sh was calculated for S-I-S structures with ideal surfaces and interfaces without topographical and material defects or weakly coupled grain boundaries in the overlayer and the substrate. Topographical and other surface defects can locally reduce the field onset of the dissipative penetration of vortices and reduce the global H_sh, as was shown by TDGL simulations (Vodolazov, 2000; Pack et al., 2020; Wang et al., 2022). Likewise, H_sh(T) can be reduced by weakly coupled grain boundaries causing premature proliferation of mixed Abrikosov–Josephson vortices or phase slips (Sheikhzada and Gurevich, 2017). The I interlayer in S-I-S coating can mitigate these detrimental effects by the following: 1. increasing the cavity breakdown field by thin high-H_c overlayers and 2. confining vortices penetrating at surface defects in a thin overlayer and blocking flux penetration in the cavity wall, where it can trigger thermo-magnetic avalanches, causing global superconductivity breakdown (Gurevich, 2015; Gurevich, 2023). The S-I-S coating can provide these two goals if the overlayer thickness does not exceed λ₁ (Gurevich, 2006). In this work, we calculated the upper limit of H_sh and showed how the S-I-S geometry can be optimized to increase H_sh at d ≲ λ₁.

6 Conclusion

Our numerical GL calculations of the DC superheating field in superconductors with nanostructured surfaces cover the entire range of 1 < κ < ∞ and account for both the non-linear Meissner screening and the instability with a finite wave number k_c at H₀ = H_sh. We showed that there are optimum thicknesses of the impurity diffusion layer and the superconducting overlayer which maximize H_sh. These results suggest the possible ways of increasing the breakdown fields by surface nanostructuring and can help understand the ways of optimizing SRF cavities to achieve higher accelerating gradients.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

WP performed all numerical simulations, analyzed the results, and wrote the first draft of the manuscript. AG initiated and supervised the project and wrote the revised manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by DOE under grant DE-SC 100387–020 (ODU) and by the Virginia Military Institute (VMI).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/femat.2023.1246016/full#supplementary-material

References

Catelani, G., and Sethna, J. P. (2008). Temperature dependence of the superheating field for superconductors in the high-κ London limit. Phys. Rev. B 78, 224509. doi:10.1103/PhysRevB.78.224509

CrossRef Full Text | Google Scholar

Chapman, S. J. (1995). Superheating field of type II superconductors. SIAM J. Appl. Math. 55 (5), 1233–1258. doi:10.1137/S0036139993254760

CrossRef Full Text | Google Scholar

Christiansen, P. V. (1969). Magnetic superheating field in high-κ superconductors. Solid State Commun. 7 (10), 727–729. doi:10.1016/0038-1098(69)90652-8

CrossRef Full Text | Google Scholar

Ciovati, G., Myneni, G., Stevie, F., Maheshwari, P., and Griffis, D. (2010). High field Q slope and the baking effect: review of recent experimental results and new data on Nb heat treatments. Phys. Rev. St. Accel. Beams 13, 022002. doi:10.1103/PhysRevSTAB.13.022002

CrossRef Full Text | Google Scholar

Ciovati, G., Dhakal, P., and Myneni, G. (2016). Superconducting radio-frequency cavities made from medium and low-purity niobium ingots. Supercond. Sci. Technol. 29, 064002. doi:10.1088/0953-2048/29/6/064002

CrossRef Full Text | Google Scholar

COMSOL COMSOL Multiphysics modeling software. Available at: https://www.comsol.com (Accessed March 15, 2017).

Google Scholar

Cross, M. C., and Hohenberg, P. C. (1993). Pattern formation outside of equilibrium. Rev. Mod. Phys. 65, 851–1112. doi:10.1103/RevModPhys.65.851

CrossRef Full Text | Google Scholar

Dhakal, P. (2020). Nitrogen doping and infusion in SRF cavities: A review. Open Phys. J. 5, 100034. doi:10.1016/j.physo.2020.100034

CrossRef Full Text | Google Scholar

Galaiko, V. P. (1966). Stability limits of the superconducting state in a magnetic field for superconductors of the second kind. Zh. Exp. Teor. Fiz. 50, 717–723.

Google Scholar

Grassellino, A., Romanenko, A., Trenikhina, Y., Checchin, M., Martinello, M., Melnychuk, P., et al. (2017). Unprecedented quality factors at accelerating gradients up to 45 MVm^-1 in niobium superconducting resonators via low temperature nitrogen infusion. Supercond. Sci. Technol. 30, 094004. doi:10.1088/1361-6668/aa7afe

CrossRef Full Text | Google Scholar

Gurevich, A. (2006). Enhancement of rf breakdown field of superconductors by multilayer coating. Appl. Phys. Lett. 88 (1), 012511. doi:10.1063/1.2162264

CrossRef Full Text | Google Scholar

Gurevich, A., and Kubo, T. (2017). Surface impedance and optimum surface resistance of a superconductor with an imperfect surface. Phys. Rev. B 96, 184515. doi:10.1103/PhysRevB.96.184515

CrossRef Full Text | Google Scholar

Gurevich, A. (2015). Maximum screening fields of superconducting multilayer structures. AIP Adv. 5 (1), 017112. doi:10.1063/1.4905711

CrossRef Full Text | Google Scholar

Gurevich, A. (2023). Tuning microwave losses in superconducting resonators. Supercond. Sci. Technol. 36, 063002. doi:10.1088/1361-6668/acc214

CrossRef Full Text | Google Scholar

Kubo, T., Iwashita, Y., and Saeki, T. (2014). Radio-frequency electromagnetic field and vortex penetration in multilayered superconductors. Appl. Phys. Lett. 104, 032603. doi:10.1063/1.4862892

CrossRef Full Text | Google Scholar

Kubo, T. (2021). Superheating fields of semi-infinite superconductors and layered superconductors in the diffusive limit: structural optimization based on the microscopic theory. Supercond. Sci. Technol. 34, 045006. doi:10.1088/1361-6668/abdedd

CrossRef Full Text | Google Scholar

Lechner, E. M., Angle, J. W., Stevie, F. A., Kelley, M. J., Reece, C. E., and Palczewski, A. D. (2021). RF surface resistance tuning of superconducting niobium via thermal diffusion of native oxide. Appl. Phys. Lett. 119, 082601. doi:10.1063/5.0059464

CrossRef Full Text | Google Scholar

Liarte, D. B., Posen, S., Transtrum, M. K., Catelani, G., Liepe, M., and Sethna, J. P. (2017). Theoretical estimates of maximum fields in superconducting resonant radio frequency cavities: stability theory, disorder, and laminates. Supercond. Sci. Technol. 30, 033002. doi:10.1088/1361-6668/30/3/033002

CrossRef Full Text | Google Scholar

Lin, F. P. J., and Gurevich, A. (2012). Effect of impurities on the superheating field of type-II superconductors. Phys. Rev. B 85 (5), 054513. doi:10.1103/PhysRevB.85.054513

CrossRef Full Text | Google Scholar

Matricon, J., and Saint-James, D. (1967). Superheating fields in superconductors. Phys. Lett. A 24 (5), 241–242. doi:10.1016/0375-9601(67)90412-4

CrossRef Full Text | Google Scholar

MATLAB Matlab. Available at: https://www.mathworks.com/products/matlab.html (Accessed March 15, 2017).

Google Scholar

Ngampruetikorn, V., and Sauls, J. A. (2019). Effect of inhomogeneous surface disorder on the superheating field of superconducting RF cavities. Phys. Rev. Res. 1, 012015. doi:10.1103/PhysRevResearch.1.012015

CrossRef Full Text | Google Scholar

Orlando, T. P., McNiff, E. J., Foner, S., and Beasley, M. R. (1979). Critical fields, Pauli paramagnetic limiting, and material parameters of Nb₃Sn and V₃Si. Phys. Rev. B 19, 4545–4561. doi:10.1103/physrevb.19.4545

CrossRef Full Text | Google Scholar

Pack, A. R., Carlson, J., Wadsworth, S., and Transtrum, M. K. (2020). Vortex nucleation in superconductors within time-dependent Ginzburg-Landau theory in two and three dimensions: role of surface defects and material inhomogeneities. Phys. Rev. B 101, 144504. doi:10.1103/PhysRevB.101.144504

CrossRef Full Text | Google Scholar

Padamsee, H., Knobloch, J., and Hays, T. (2018). RF superconductivity for accelerators. 2nd ed. Germany: Wiley-VCH Verlag GmbH and Co. KGaA.

Google Scholar

Posen, S., and Hall, D. L. (2017). Nb₃Sn superconducting radiofrequency cavities: fabrication, results, properties, and prospects. Supercond. Sci. Technol. 30, 033004. doi:10.1088/1361-6668/30/3/033004

CrossRef Full Text | Google Scholar

Posen, S., Romanenko, A., Grassellino, A., Melnychuk, O. S., and Sergatskov, D. A. (2020). Ultralow surface resistance via vacuum heat treatment of superconducting radio-frequency cavities. Phys. Rev. Appl. 13, 014024. doi:10.1103/PhysRevApplied.13.014024

CrossRef Full Text | Google Scholar

Sheikhzada, A., and Gurevich, A. (2020). Dynamic pair-breaking current, critical superfluid velocity, and nonlinear electromagnetic response of nonequilibrium superconductors. Phys. Rev. B 102, 104507. doi:10.1103/PhysRevB.102.104507

CrossRef Full Text | Google Scholar

Sheikhzada, A., and Gurevich, A. (2017). Dynamic transition of vortices into phase slips and generation of vortex-antivortex pairs in thin film Josephson junctions under dc and ac currents. Phys. Rev. B 95, 214507. doi:10.1103/PhysRevB.95.214507

CrossRef Full Text | Google Scholar

Tinkham, M. (2004). Introduction to superconductivity. New York: Dover Publication.

Google Scholar

Transtrum, M. K., Catelani, G., and Sethna, J. P. (2011). Superheating field of superconductors within Ginzburg-Landau theory. Phys. Rev. B 83 (9), 094505. doi:10.1103/PhysRevB.83.094505

CrossRef Full Text | Google Scholar

Vodolazov, D. Yu. (2000). Effect of surface defects on the first field for vortex entry in type-II superconductors. Phys. Rev. B 62, 8691–8694. doi:10.1103/PhysRevB.62.8691

CrossRef Full Text | Google Scholar

Wang, Q-Y., Xue, C., Dong, C. C., and Zhou, Y-H. (2022). Effects of defects and surface roughness on the vortex penetration and vortex dynamics in superconductor–insulator–superconductor multilayer structures exposed to RF magnetic fields: numerical simulations within TDGL theory. Supercond. Sci. Technol. 35, 045004. doi:10.1088/1361-6668/ac4ad1

CrossRef Full Text | Google Scholar

Watts-Tobin, R. J., Krähenbühl, Y., and Kramer, L. (1981). Nonequilibrium theory of dirty, current-carrying superconductors: phase-slip oscillators in narrow filaments near T_c. J. Low. Temp. Phys. 42, 459–501. doi:10.1007/BF00117427

CrossRef Full Text | Google Scholar

Werthamer, N. R. (1969). in Superconductivity. Editor R. D. Parks (New York: Marcel Dekker Inc.), 321–370.

Google Scholar