
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Electron. Mater, 21 October 2022
Sec. Superconducting Materials
Volume 2 - 2022 | https://doi.org/10.3389/femat.2022.944873
This article is part of the Research TopicNew Heavy Fermion SuperconductorsView all 8 articles
Symmetry breaking beyond a global U(1) phase is the key signature of unconventional superconductors. As prototypical strongly correlated materials, heavy-fermion metals provide ideal platforms for realizing unconventional superconductivity. In this article, we review heavy-fermion superconductivity, with a focus on those materials with multiple superconducting phases. In this context, we highlight the role of orbital-selective (matrix) pairing functions, which are defined as matrices in the space of effective orbital degrees of freedom such as electronic orbitals and sublattices as well as equivalent descriptions in terms of intra- and inter-band pairing components in the band basis. The role of quantum criticality and the associated strange-metal physics in the development of unconventional superconductivity is emphasized throughout. We discuss in some detail the recent experimental observations and theoretical perspectives in the illustrative cases of UTe2, CeRh2As2, and CeCu2Si2, where applied magnetic fields or pressure induce a variety of superconducting phases. We close by providing a brief overview of overarching issues and implications for possible future directions.
Unconventional superconductivity broadly refers to Cooper paired states which deviate from the Bardeen-Cooper-Schrieffer (BCS) paradigm, either in their pairing interactions or in the related issue of pairing symmetry (Bardeen et al., 1957). It is a field with a history spanning more than four decades and several families of correlated materials. Heavy-fermion (HF) compounds enjoy a certain distinction: The first signatures of unconventional superconductivity were observed in CeCu2Si2 (Steglich et al., 1979), which together with fifty or so other subsequently discovered unconventional superconductors (SCs), belongs to this class (Stewart, 2017). A common feature of these materials is that the electron-electron interactions play a leading role in stabilizing a variety of low-temperature phases (Steglich and Wirth, 2016; Kirchner et al., 2020; Paschen and Si, 2021). Most of these HF compounds are either in the vicinity of or can be tuned near to quantum critical points (QCPs) where pronounced non-Fermi liquid behavior emerges. This can be traced to the fact that correlation effects, like Kondo screening, antiferro-/ferro-magnetic (AFM/FM), and valance fluctuations share similar small energy scales (Coleman and Schofield, 2005; Gegenwart et al., 2008; White et al., 2015; Weng et al., 2016; Paschen and Si, 2021). The interplay between these interaction-induced effects underlies the rich low-temperature physics.
This article is primarily concerned with the nature of the superconducting phases and, thus, we will be very brief in discussing the mechanism for HF superconductivity. Many HF superconductors develop at the border of magnetic order in their phase diagrams. Quantum criticality, and the associated strange-metal physics, is thus believed to cause superconductivity. Almost by definition, HF behavior involves Kondo screening, which is most naturally associated with Kondo-exchange interactions between quasi-localized f and more dispersive conduction electrons. HFs exhibit characteristic scales associated with the initial onset of Kondo-singlet correlations, in the form of Kondo temperatures or coherence scales Tcoh (Steglich and Wirth, 2016; Kirchner et al., 2020). As already alluded to, the presence of several small scales in HF materials facilitates tuning in experiment, and is ultimately behind the emergence of rich phase diagrams. A hierarchy of multiple scales also leads to important general conclusions in the context of superconductivity. Indeed, based on the ratio of the critical superconducting and effective Fermi temperatures Tc/TF, many HFs would qualify as high-temperature SCs (Steglich, 2014; Stewart, 2017). In addition, Ruderman-Kittel-Kasuya-Yoshida (RKKY) interactions between local moments, originating from quasi-localized f electron states, are closely associated with Kondo interactions. RKKY and Kondo interactions typically compete, as proposed in the seminal work by Doniach (Doniach, 1977). It has been recognized in recent years that the RKKY-Kondo competition, together with the quantum fluctuations of the local moments, gives rise to a global phase diagram (Si, 2006; Si, 2010; Paschen and Si, 2021). Extensive efforts, both experimental and theoretical, have been directed toward the elucidation of HF quantum criticality (Coleman and Schofield, 2005; Löhneysen et al., 2007; Si and Steglich, 2010; Steglich and Wirth, 2016; Kirchner et al., 2020; Paschen and Si, 2021).
Broadly, two classes of QCPs have been advanced. One class is within the Landau framework where the quantum critical degrees of freedom (DOFs) correspond to the magnetic fluctuations (Hertz, 1976; Miyake et al., 1986; Millis 1993; Mathur et al., 1998; Monthoux and Lonzarich, 2001). In the other, the Kondo effect itself is critical along with the fluctuations of the magnetic order parameter leading to Kondo-destruction (KD) QCPs (Coleman et al., 2001; Si et al., 2001; Senthil et al., 2004; Si et al., 2014; Steglich and Wirth, 2016; Kirchner et al., 2020; Paschen and Si, 2021). For the AFM case, it has been recognized that, even in the order-parameter fluctuation description i.e. nominally the first class, the quantum criticality is actually distinct from the original Hertz-Millis picture and is accordingly labeled SDWr quantum criticality instead (Hu et al., 2021a). Here, the subscript “r” marks the fact that the underlying quasiparticles are highly renormalized by the Kondo effect, which makes the Landau description valid only below a very small energy scale kBTcr*. For scales above kBTcr* but below the bare Kondo scale kBTK, the quantum criticality also involves KD effects. Characteristic features of the KD quantum criticality include dynamical Planckian (
Experimental evidence for the KD quantum criticality has been extensively reported, especially in compounds such as YbRh2Si2 (Paschen et al., 2004; Friedemann et al., 2010; Prochaska et al., 2020), CeCu6-xAux (Löhneysen et al., 1994; Schröder et al., 2000), CeRhIn5 (Shishido et al., 2005; Park et al., 2006; Knebel et al., 2008), and Ce3Pd20Si6 (Custers et al., 2012; Martelli et al., 2019). In other cases, such as CeCu2Si2, there is evidence for quantum criticality in the form of magnetic order-parameter fluctuations (Arndt et al., 2011; Stockert et al., 2011; Steglich and Wirth, 2016; Smidman et al., 2018) and that, based on the temperature dependence of the spin damping rate and specific heat, Tcr* is about 1–2 K and is indeed small compared to the bare Kondo scale TK of about 20 K (Gegenwart et al., 2008; Arndt et al., 2011; Smidman et al., 2018; Smidman et al., 2022). Related effects on superconductivity, similarly due to quantum criticality are also expected in a number of cases, for example: CeIn3 (Walker et al., 1997), CeRh2Si2 (Movshovich et al., 1996), CePd2Si2 (Grosche et al., 2001), and CeIrSi3 (Sugitani et al., 2006). In this respect, HFs resemble other strongly-correlated materials like the cuprates, where superconductivity appears when AFM order, or the associated Mott insulator, is suppressed by chemical doping. Along the same lines, many Fe-based superconductors in the “1111” and “122” families also reach their highest Tc’s when the AFM order is suppressed. Moreover, non-magnetic quantum criticality in HF compounds, for instance associated with charge instabilities or multi-polar ordering as illustrated by examples covered previously, also appear to drive superconductivity.
We close this subsection with a remark on the energetics. For the heavy-fermion superconductors we will discuss, their normal states are typically at or close to being in the quantum critical regime. This means that their RKKY interaction is on the same order as their kinetic energy. As such, pairing between bands that are separated within the energy width of the RKKY-interaction-induced magnetic fluctuations will be energetically competitive.
We now turn to reviewing HF superconducting regimes. Focusing in particular on HF systems with multiple superconducting phases, we show the ways in which the internal DOFs play an important role. A natural starting point is the case of superfluid 3He (Leggett, 1975; Vollhardt and Wölfle, 1990). From a historic perspective, 3He set the stage for Cooper pairing with nontrivial symmetry and (matrix) structure, both of which are associated with multiple superfluid phases. To illustrate, we consider the simplest pairing theories and the emergent conceptual framework. In a Ginzburg–Landau (GL) framework, the order parameter in 3He is believed to preserve separate rotations in real space and spin space, as well as changes in the global phase. The relevant Cooper pairs have total angular momentum and spin 1, corresponding to odd-parity, spin-triplet pairing. The associated degeneracy is lifted in the Balian-Werthamer (BW) pairing state of the superfluid B phase, which is accessible at most pressures in zero magnetic field. In addition to selecting a global phase, the BW order parameter breaks a relative spin-orbit symmetry, by “locking together” the angular momentum and spin DOFs. It has a well-known
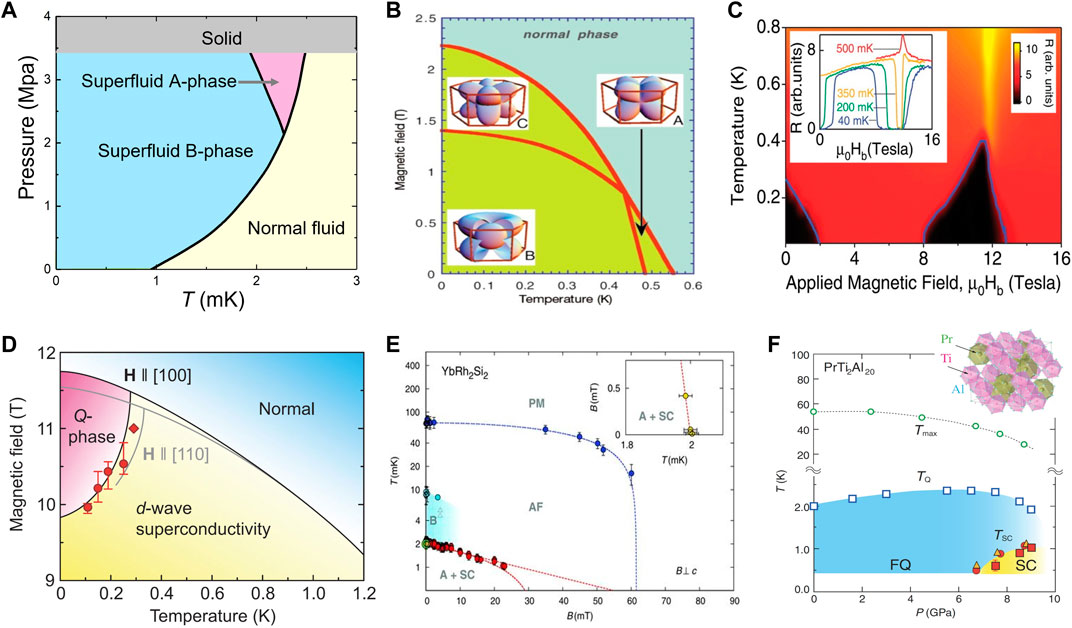
FIGURE 1. Low temperature phase diagrams of 3He (A), and of several heavy-fermion (HF) superconductors (SCs): (B) UPt3 (Huxley et al., 2000), Reproduced with permission from Springer Nature. (C) URhGe (Lévy et al., 2005), Adapted with permission from The American Association for the Advancement of Science. (D) CeCoIn5 (Kim et al., 2016), (E) YbRh2Si2 (Adapted from Schuberth et al., 2016; see also Nguyen et al., 2021), Reproduced with permission from The American Association for the Advancement of Science. (F) PrTi2Al20 (Matsubayashi et al., 2012). Reproduced with permission from The American Physical Society.
UBe13 was the first instance of a solid-state system exhibiting multiple superconducting phases (Bucher et al., 1975). Upon Th substitution at U sites, U1−xThxBe13 showed multiple superconducting phases driven by Th concentration or even temperature (Ott et al., 1985). This discovery further supported the notion that superconductivity could be driven by unconventional pairing mechanisms. A more direct connection between superfluid 3He and unconventional superconductivity was provided by the HF compound UPt3 (Stewart et al., 1984; Adenwalla et al., 1990). Indeed, at ambient pressure and in zero magnetic field, UPt3 has two superconducting phases with decreasing temperature, see Figure 1B (Huxley et al., 2000). In the presence of a field, this compound exhibits no less than five superconducting phases, among which are three flux phases, together with a tetracritical point (Joynt and Taillefer, 2002). While the phase diagram of UPt3 suggests similarities with 3He, most notably spin-triplet pairing, the two systems also differ in ways which are shared by most HF SCs. In the presence of spin-orbit coupling (SOC), the Cooper pairs can be classified according to a symmetry group
Before moving on to multiple superconducting phases in a number of prominent HF compounds, we further illustrate the extent of superconductivity in the broader HF family. Following the discovery of unconventional superconductivity in CeCu2Si2 (Steglich et al., 1979), several uranium-based superconductors have been subsequently identified, including the already-mentioned UBe13 (Bucher et al., 1975), UPt3 (Stewart et al., 1984), but also URu2Si2 (Palstra et al., 1985), prior to the appearance of the cuprates. Around the year 2000, instances of FM SCs, i.e., URhGe (Aoki et al., 2001), UGe2 (Huxley et al., 2001), and UCoGe (Huy et al., 2007) have been reported. Unlike in Ce, where localized 4f-electrons underlie the Kondo effect, the 5f-electrons in U have more extended orbitals with higher itinerancy. In addition, 5f electrons also have lower symmetry. In U-based compounds, 5f-electrons could also induce AFM, FM, and/or superconductivity. For example, Figure 1C shows the phase diagram of URhGe (Lévy et al., 2005), where coexisting superconductivity and ferromagnetism have been observed. Since the magnetic moment is due to the itinerant 5f electrons, the induced FM order has strong Ising anisotropy. The FM fluctuations favor an equal-spin pairing scenario, which in turn gives rise to strong anisotropic superconducting gap. More strikingly, a field-induced superconducting phase is observed in URhGe, which also implies a field-induced QCP in the vicinity of a metamagnetic transition.
Other HF compounds, such as CeCoIn5 (Kim et al., 2016), YbRh2Si2 (Schuberth et al., 2016; Nguyen et al., 2021) and PrTi2Al20 (Matsubayashi et al., 2012) demonstrate rather unique superconducting regimes (Figures 1D–F). A field-induced “Q-phase” is observed in CeCoIn5, as shown in Figure 1D. This phase was also proposed as a candidate to a Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) state (Bianchi et al., 2003), in which the Cooper pairs have residual total momentum. Recent research indicated that this phase could be a pair density wave phase with a spatial modulation of the order parameter (Gerber et al., 2014). Similar superconducting phases have also been proposed in a few other compounds. Substituting Co. with Rh or Ir generates the family of the “115” materials. Here, the interplay between superconductivity and antiferromagnetism has been thoroughly examined due to the availability of high-quality single crystals. Notably, a combined pressure and chemical doping study on Ce(Rh,Ir)In5 reveals how a single superconducting dome splits into two. While the first dome is in the vicinity of an AFM QCP, the other emerges from the heavy-Fermi liquid state without any trace of critical magnetic fluctuations, suggesting that charge/valence instabilities play leading roles instead (Kawasaki et al., 2006). Nevertheless, this picture needs further clarifications as evidence for AFM fluctuations have been observed for pure CeIrIn5 at ambient pressure by Shang et al. (Shang et al., 2014).
The compound YbRh2Si2 is a prototypical HF exhibiting an AFM QCP (Trovarelli et al., 2000; Gegenwart et al., 2002; Custers et al., 2003; Ernst et al., 2011). It has become a canonical case of KD QCP (Si et al., 2001; Paschen et al., 2004; Prochaska et al., 2020) and been discussed extensively as such (Steglich and Wirth, 2016; Kirchner et al., 2020; Paschen and Si, 2021). However, superconductivity in this compound was not detected until recently. Upon being cooled down to the mK range, superconductivity was observed in YbRh2Si2 using magnetic susceptibility (Schuberth et al., 2016) and electrical resistivity measurements (Nguyen et al., 2021). In Ref. (Schuberth et al., 2016), the development of a hybrid nuclear-electronic magnetic order is also observed. It was proposed that the nuclear-spin ordering reduces the primary electronic order, thereby pushing the system closer to the KD quantum criticality, which promotes unconventional superconductivity (Schuberth et al., 2016). Upon replacing the naturally abundant Yb by 174Yb, which has no nuclear magnetic moment, superconductivity is weakened (Nguyen et al., 2021), a result that is consistent with the role played by the nuclear spins. Nguyen et al. furthermore provided evidence for two different superconducting phases in YbRh2Si2 that, in the 174Yb case, splits into two adjacent domes, thus making YbRh2Si2 a new example of a multiple-phase SC (Nguyen et al., 2021). This is an exciting result, suggesting that the pair-breaking effect of the external magnetic field is not as severe as previously thought, and that the innate quantum criticality at the quantum critical field can still nucleate superconductivity (Nguyen et al., 2021). Taken together, these experiments (Schuberth et al., 2016; Nguyen et al., 2021) provide compelling evidence that superconductivity is driven by the KD quantum criticality. Moreover, the high-field superconducting phase was tentatively identified as a potential case of spin-triplet pairing (Nguyen et al., 2021), a result that is supported by the calculations of pairing correlations near the KD QCP of a cluster Bose-Fermi Kondo model in the Ising-anisotropic case (Pixley et al., 2015; Hu et al., 2021b), especially when the Zeeman effect of the external magnetic field is considered (Hu et al., 2021b).
Another example of complex superconducting order in HF is provided by PrTi2Al20 (Matsubayashi et al., 2012; Sakai et al., 2012). Just like a local magnetic moment can be screened by itinerant electrons in a conventional HF compound, the electric quadrupole moment of Pr3+ can in principle be screened by conduction electrons. The f-electrons in PrTi2Al20 belong to low energy, non-magnetic (non-Kramers) Γ3 doublets which further transition into a long-range ferro-quadrupole (FQ) ordered state at low temperatures. Superconductivity appears upon suppressing the FQ order via high pressure. Around 9 GPa, the superconducting transition temperature and the effective masses of the heavy quasiparticles are dramatically enhanced, indicating the presence of a QCP associated with quadrupolar order.
In spite of the multitude of superconducting phases alluded to previously, virtually all HF compounds are expected to share a number of common features, which can also guide our understanding of the pairing mechanisms. We have already mentioned the Kondo-RKKY competition and the resulting quantum criticality in the normal state. As also alluded to earlier, the presence of several small scales in HF materials facilitates tuning in experiment, and is ultimately behind the emergence of rich phase diagrams. We refer to Section 1.1 for further discussions in this regard.
According to the BCS theory, the formation of Cooper pairs spontaneously breaks the U(1) gauge symmetry. Unconventional SCs can further break crystal symmetry (rotation or inversion) and/or TRS. The latter often involves the effective release of additional DOFs, such as spin, orbital, quadrupole, valley et al. Given the success of GL theory within the canonical BCS paradigm, and in the case of superfluid 3He (Leggett, 1975; Vollhardt and Wölfle, 1990), it is not altogether surprising that most studies of unconventional superconductivity in complex, multiband HF compounds have focused on a broad, symmetry-based classification of the pairing states according to the PG. For spin-singlet pairing, the central question typically being asked is whether the pairing state is an (effectively) single band s- or d-wave, with an implicit understanding that the two cases are mutually exclusive. Similar symmetry-based classifications approaches have been adopted for spin-triplet superconductors (Sigrist and Ueda, 1991; Joynt and Taillefer, 2002).
One focus of our discussion concerns the nature of the pairing states when multiple internal DOFs are involved, such as orbitals and sublattices. Such an extension of the set of candidate pairing states, which goes beyond the effectively single-band picture and which has immediate implications for HF superconductivity, has been driven by recent surprising experimental results. A notable case in this respect is that of the alkaline Fe-selenide compounds (Si et al., 2016; Lee 2017). Here, multiple ARPES experiments detected fully-gapped superconductivity (Wang et al., 2011; Xu et al., 2012), normally associated with a fully-gapped s-wave pairing candidate. By contrast, inelastic neutron scattering (INS) experiments detected the presence of a resonance in the spin spectrum (Park et al., 2011; Friemel et al., 2012), which requires a sign-change in the order parameter between different FS sheets. Due to the presence of a small hole pocket near the center of the Brillouin Zone (BZ) (Wang et al., 2011; Xu et al., 2012), the INS experiments would suggest a d-wave pairing candidate instead. As discussed in greater detail below, a remarkably similar experimental picture subsequently emerged in the HF CeCu2Si2.
To address the discrepancy between the experiments, which suggest in turn incompatible s- and d-wave single-band pairing candidates, Ref. (Nica et al., 2017). proposed an s
In the alkaline Fe-selenides, the s
The matrix structure of d + d pairing in the band basis bears a resemblance to the matrix structure of superfluid 3He-B, defined in a spin basis (Nica and Si, 2021), which hints at a natural generalization of matrix pairing. While the d + d pairing state mixes two distinct d-wave components via a nontrivial matrix structure in band space, the canonical pairing state for 3He-B mixes three distinct p-wave components in a matrix structure which combines equal- and opposite-spin fermions, with the consequence that the FS is gapped in both cases. Moreover, states with a trivial matrix structure in band space, i.e., proportional to an identity matrix, such as a d + id pairing candidates, are conceptually similar to the most basic equal-spin pairing in 3He-A. Thus, 3He in general provides important precedents for nontrivial matrix pairing states. It can guide our understanding of matrix pairing states generalized to orbital/spin-orbital DOFs in crystalline SCs, in spite of the differences in parity, dimensionality, symmetry, and symmetry-breaking.
An important feature of the Fe-chalcogenide (as well as Fe-arsenide) superconductors is that the band width of the magnetic fluctuations is large, typically on the order of 200 meV (Dai, 2015). Such a large bandwith is associated with the large magnitude of the short-range spin-exchange interactions. As a result, the involved interband pairing is expected to be energetically competitive. Indeed, for microscopic models of the alkaline Fe-selenides, the s
In the following, we review the recent progress in understanding multiple superconducting phases in HFs, as exemplified by UTe2, CeRh2As2, and CeCu2Si2. We illustrate the remarkable tunability of superconductivity in these compounds and discuss evidence in favor of pairing states with nontrivial symmetry and structure.
UTe2 is a recently discovered spin-triplet candidate SC (Ran et al., 2019a). While the superconducting state of UTe2 closely resembles that of FM SCs, e.g., URhGe (Aoki et al., 2001) and UCoGe (Huy et al., 2007), the normal state of UTe2 is paramagnetic (Aoki et al., 2019; Ran et al., 2019a). Nonetheless, the pronounced magnetic susceptibility (along one crystalline direction) and the H/T1.5 scaling of the magnetization provided initial indication for the importance of FM quantum fluctuations (Ran et al., 2019a). Spin-triplet pairing is strongly indicated by the extremely large, anisotropic upper critical field Hc2, possible nodes on the superconducting gap, and the temperature-independent NMR Knight shift in the superconducting state (Aoki et al., 2019; Metz et al., 2019; Nakamine et al., 2019; Ran et al., 2019a; Bae et al., 2021; Nakamine et al., 2021). A nontrivial topology is also suggested by the observation of chiral in-gap bound states from scanning tunneling spectroscopy (Jiao et al., 2020). As expected for unconventional superconductors, UTe2 likely has a nontrivial order parameter. It hosts multiple superconducting phases when magnetic field or external pressure is applied, some of which hold surprisingly high temperature and magnetic field stability. In the scope of this brief review, we focus on the order parameter and on the multiple superconducting phases of UTe2.
The initial specific heat measurements showed a single transition at Tc. However, when the specific heat was measured by means of the small-pulse method, a shoulder-like feature appears at a temperature of about 75–100 mK above the peak in Cp/T (Hayes et al., 2021). This feature is quite sharp and divides the jump in the specific heat into two local maxima in the derivative, d(Cp/T)/dT, representing two thermodynamic anomalies. In principle, the two transitions could be the result of inhomogeneity in the crystals. On the other hand, if there is indeed a multicomponent order parameter, TRS could be broken, which cannot be explained by inhomogeneity. To test for possible TRS breaking in the superconducting state of UTe2, high-resolution polar Kerr effects measurements were performed using a zero-area Sagnac interferometer (Hayes et al., 2021). Initial measurements indicated that without an applied magnetic field, the Kerr signal can be either finite or zero. This observation led to the speculation that TRS breaking domains form spontaneously upon cooling the sample, which can orient in opposite directions and give average signal of zero.
To orient all of the domains in one direction, a small field of +25 G was applied upon cooling the sample, and removed once the base temperature (∼300 mK) was reached. The Kerr angle was subsequently measured as the sample was warmed slowly, and it was found that a positive finite Kerr value develops around Tc in this zero-field measurement. The sign of the Kerr value was reversed with a negative training field (−25 G), indicating that the broken TRS order parameter is analogous to a magnetic moment (Hayes et al., 2021), as shown in Figure 2. As a finite Kerr signal cannot be explained by the inhomogeneity, the combination of the specific heat and Kerr effect measurements point to a multi-component order parameter.
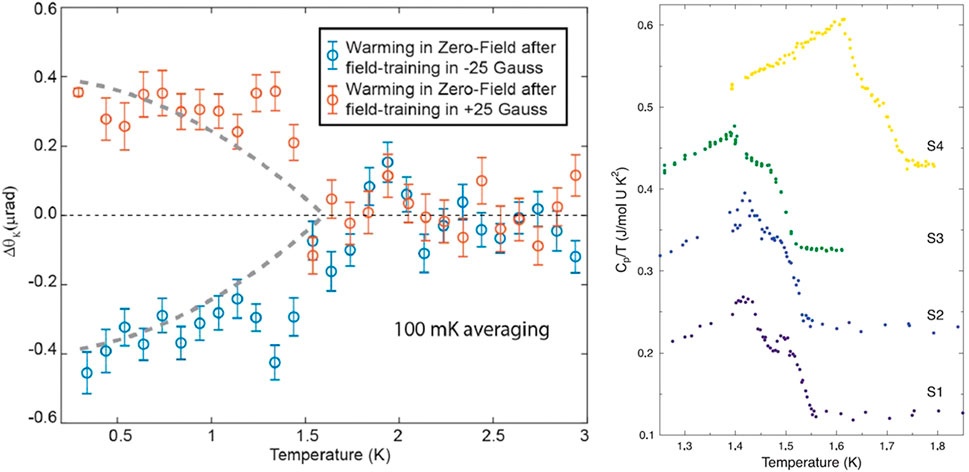
FIGURE 2. (A). Finite Kerr signal below the superconducting transition temperature of UTe2 indicating time reversal symmetry breaking. (B). Specific heat of UTe2 showing shoulder-like feature at critical temperature. After (Hayes et al., 2021).
In applied magnetic fields, two independent, high-field superconducting phases were discovered in UTe2 (Ran et al., 2019b; Knebel et al., 2019; Knafo et al., 2021), for a total of three superconducting phases, as shown in Figure 3. This is an example of two field-induced superconducting phases emerging in a single compound, one of which has the highest lower and upper limiting fields of any field-induced superconducting phase: more than 40 T and 65 T, respectively.
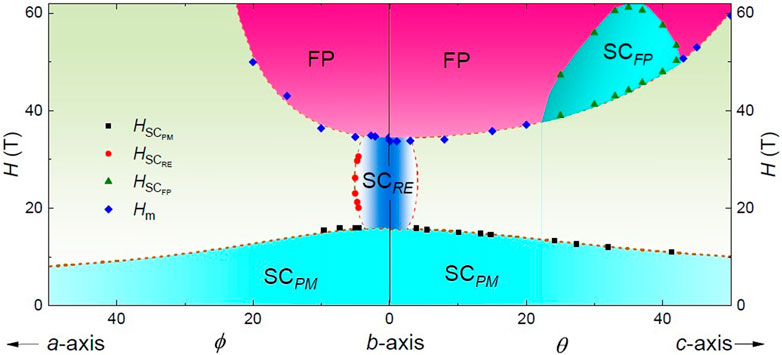
FIGURE 3. Magnetic field–angle phase diagram of UTe2 showing the three superconducting phases SCPM, SCRE and SCFP. After (Ran et al., 2019b).
When the magnetic field is perfectly aligned along the b-axis, zero resistance persists up to 34.5 T at 0.35 K, with a transition from SCPM to SCRE at around 21 T. While evidence from thermodynamic measurements is absent, the transition between two separate superconducting phases is clear when the magnetic field is slightly rotated away from b axis, towards either a- or c-axis, as shown in Figure 3. For example, a small misalignment of less than 5° from the b-axis towards the a-axis decreases the Hc2 value of SCPM to 15.8 T. When the magnetic field is further increased, a field-induced superconducting phase SCRE appears between 21 T and 30 T. Resistance measurements show that this re-entrant phase, SCRE, is present in a small angle range, within 7° when the field is rotated from b-axis towards the a-axis, and within 4° towards the c-axis (Ran et al., 2019b).
The upper-field limit of SCRE of 35 T coincides with a dramatic magnetic transition into a field-polarized phase, evidenced by a magnetic moment change from 0.35 to 0.65 μB. The critical field Hm of this magnetic transition has little temperature dependence up to 10 K, but Hm increases as the magnetic field rotates away from the b-axis to either the a- or c-axis (Ran et al., 2019b; Knafo et al., 2021; Miyake et al., 2019). As Hm limits the SCRE phase, it gives rise to the second field-induced superconducting phase, SCFP, existing in the angular range of θ = 20–40° from the b-axis towards the c-axis. The onset field of the SCFP phase precisely follows the angle dependence of Hm, while the upper critical field goes through a dome, with the maximum value exceeding 65 T, the largest field strength of these measurements. With Tc of 1.5 K, this new superconducting phase largely exceeds the magnetic field range of all known field-induced superconducting phases. Its special angle range is roughly the normal direction of the (011) plane, the easy cleave plane of UTe2, indicating a quasi-2D nature for this superconducting phase. These results are summarized in Figure 3.
The critical temperature Tc of UTe2 shows a two-fold enhancement under pressure (Braithwaite et al., 2019; Ran et al., 2020; Thomas et al., 2020). Below 1.31 GPa, Tc forms a clear dome feature under pressure peaked at 1 GPa, where Tc is doubled compared to the ambient-pressure value, reaching 3.2 K. The bulk nature of the SC is confirmed by magnetization data. Specific heat measurements indicate a phase transition from an ambient-pressure superconducting phase to a SC2 phase under higher pressure (Aoki et al., 2020), as shown in Figure 4. A new phase, magnetic in nature, appears above 1.5 GPa, which has been assigned to both FM and AFM order (Ran et al., 2020; Thomas et al., 2020). On one hand, hysteresis has been observed, indicating a possible FM nature. On the other hand, the critical temperature of the magnetic phase is suppressed with applied field in all directions, suggesting an AFM order instead. The shapes of the resistivity curves at the phase transition are also more consistent with antiferromagnetism. The exact nature of this phase needs to be confirmed by additional experiments.
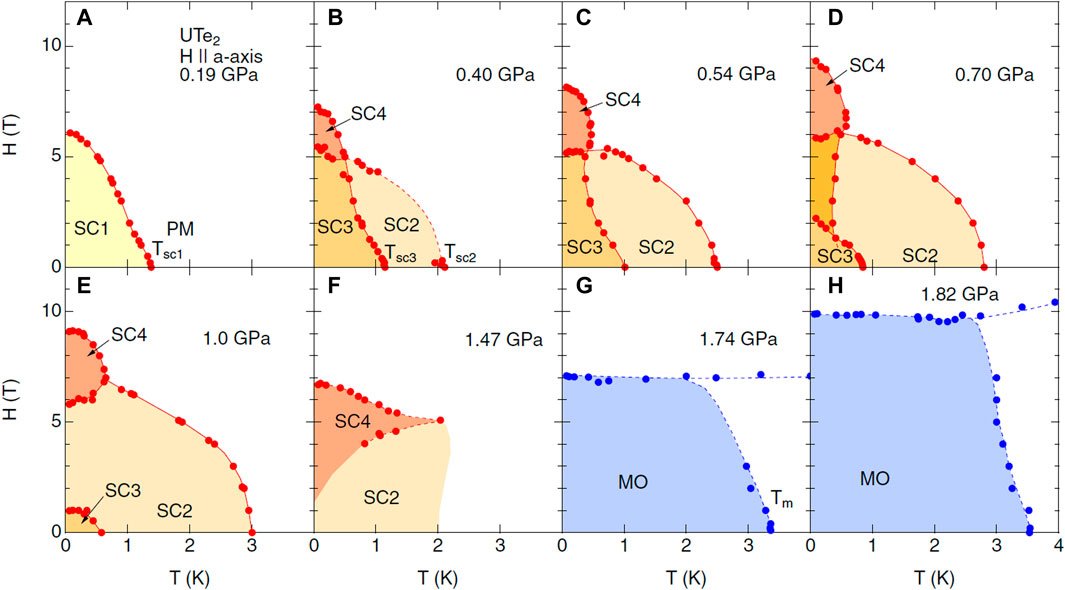
FIGURE 4. H-T phase diagrams of UTe2 for H//a-axis at several pressures. After (Aoki et al., 2020). Please see main text for a discussion.
A remarkably rich phase diagram emerges when the magnetic field is further applied under pressure. With (externally-applied) pressure, the magnetic field cannot be rotated relative to the sample in-situ. Therefore, only a few magnetic field directions have been explored: along the a-axis, b-axis, and for those special angles where high field induced SCFP appears.
Specific heat and resistance measurements have been carried out under pressure for magnetic fields applied along the a-axis (Figure 4). Within the zero-resistance region, different features in the specific heat curves have been used to delineate phase boundaries between different superconducting regimes. In the low-pressure region, a single superconducting phase was observed under magnetic field. As pressure was increased, SC1 disappeared, in agreement with the zero magnetic field results, and up to three new superconducting phases were observed. One phase only exists in the applied magnetic field along a-axis. Another emerged only at higher temperatures. The phase diagram in the intermediate pressure region, ∼0.5 GPa, resembles that of the UPt3 at ambient pressure (Joynt and Taillefer, 2002). Given the important role of specific heat measurements in determining superconducting phase boundaries, it is conceivable that similar measurements might reveal additional paired phases when the magnetic field is applied in other directions. However, such measurements have not yet been performed. Discussions for other field directions are based mainly on transport measurements.
As already mentioned, when the field was applied along the b-axis, two superconducting phases, SCPM and SCRE were observed, as shown in Figure 5A. SCRE persisted up to the metamagnetic phase transition at Hm. Under applied pressure, Hm remained close to the upper limit of SCRE and was continuously suppressed, even though the critical temperature of SCRE was enhanced (Lin et al., 2020; Ran et al., 2021). Based on tunneling diode oscillator and resistance measurements, the phase boundaries between SCPM and SCRE were determined, which were also suppressed under pressure. To study the evolution of the high-field superconducting phase, SCFP, the magnetic field was applied 25°–30° away from the b axis toward c (Figure 5B). At ambient pressure, two superconducting phases, SCPM and SCFP, were established. Upon an initial increase in pressure, the stability of both superconducting phases was enhanced: the upper critical field of SCPM, Hc2, increased, and the critical onset field of SCFP, which coincided with the metamagnetic transition field, decreased. In an intermediate crossover pressure range, the phase boundary between SCPM and SCFP was no longer visible in the electrical resistance; resistance remained zero up to 45 T at base temperature, which was the largest DC magnetic field available to the experiment (Ran et al., 2021).
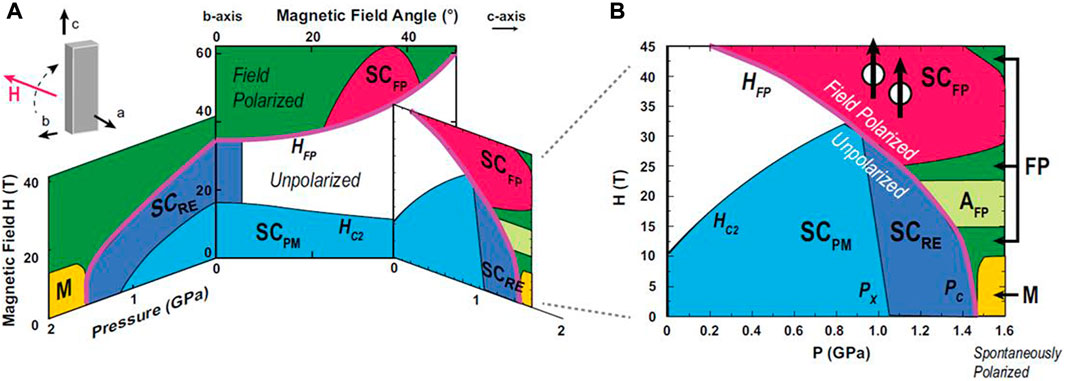
FIGURE 5. (A). H-P phase diagram of UTe2 for magnetic fields applied along b-axis. (B) H-P phase diagram of UTe2 for magnetic fields applied 25°–30° away from the b-axis toward c-axis. After (Ran et al., 2021).
Under pressure, the metamagnetic phase transition remains pinned to the upper limit of SCPM phase. As the pressure further increases, the metamagnetic transition is suppressed, as is the upper critical field of SCPM. But the critical onset field of SCFP starts to increase, and the two superconducting phases are no longer connected above 1.2 GPa. When the metamagnetic transition vanishes under a pressure of 1.4 GPa, SCPM is also suppressed completely. SCFP persists under the highest pressure in these studies. The low- and high-field superconducting phases always exist on opposite sides of the metamagnetic transition HFP, for which a FS reconstruction scenario has been suggested based on thermoelectric power and Hall effect measurements. These imply that the SCPM and SCFP phases which are separated by the metamagnetic transition might exhibit different pairings states that are unique to PM and FP phases, respectively.
The novelty of superconductivity in UTe2 and the complexity of the phase diagram, as a function temperature, pressure, and magnetic fields, preclude a firm consensus on the pairing candidates at this point (Aoki et al., 2022). We will not attempt a comprehensive review of existing theories but will instead briefly cover a few representative studies in an attempt to identify those points which appear to distinguish UTe2 from other unconventional superconductors. Given the strong evidence for spin-triplet pairing, many proposals focus on this case. Even so, two major issues tentatively set UTe2 apart. First, the orthorhombic lattice and the associated D2h PG symmetry restrict the order parameter to one-dimensional irreducible representations. The degeneracy of the order parameters in other spin-triplet candidates, like 3He and UPt3, which can naturally account for the presence of multiple broken-symmetry states, does not seem to hold for UTe2. It should be mentioned that proposals based on accidental degeneracy between one-dimensional irreducible representations, which appear to naturally account for the observation of two superconducting transitions in UTe2 in zero field and ambient pressure, have also been advanced for UPt3 (Joynt and Taillefer, 2002). Secondly, the absence of FM fluctuations and ordering, as determined by inelastic neutron scattering (INS) measurements (Duan et al., 2021), which are expected to stabilize spin-triplet pairing, provides a challenge for theory. Indeed, INS experiments rather point to dominant AFM fluctuations instead. In this regard, UTe2 can also be contrasted to UPt3, where a weak AFM order plays an important role in lifting the degeneracy inherent to multi-dimensional E1g and E2u irreducible representations (Vollhardt and Wölfle, 1990; Sigrist and Ueda, 1991; Sauls, 1994). It is tempting to note that AFM fluctuations in UTe2, as evidenced by INS experiments, and in UPt3, where an incipient AFM order was established, appear to play important roles for both candidates to spin-triplet pairing. Although not conclusive at this stage, this commonality suggests that AFM fluctuations, in the presence of anisotropy inherent to materials with significant SOC, might also provide a pairing mechanism for spin-triplet SCs.
We note that pairing candidates typically take into account the band structure and FS, the low-energy gapped or gapless Bogoliubov-de Gennes (BdG) spectrum, the pairing mechanism, the existence of multiple superconducting phases, and nontrivial topology. In the first category, we note that a number of ab initio studies predict a similar shape of the FS (Ishizuka et al., 2019; Xu et al., 2019; Duan et al., 2020; Miao et al., 2020; Nevidomskyy, 2020), consisting of quasi-2D cylinder-like electron and hole FS sheets, although other shapes were also advanced (Miao et al., 2020; Shishidou et al., 2021). In a related manner, a number of authors proposed non-unitary, mixed-representation, TRS-breaking spin-triplet states (Ran et al., 2019a; Aoki et al., 2019; Hayes et al., 2021) such as B1u + iB3u (Nevidomskyy, 2020) or B3u + iB2u (Shishidou et al., 2021) which can in principle account for the presence of point nodes and topologically nontrivial chiral edge states consistent with experiments. Possible nontrivial topology is further discussed in Refs. (Ishizuka et al., 2019; Shishidou et al., 2021). As noted previously, the quasi-degeneracy of the two components included in these mixed representation states is not guaranteed by symmetry. Nonetheless, such candidates can in principle also provide a resolution to the presence of multiple superconducting phases with applied fields, especially since non-unitary pairing states exhibit nontrivial effective magnetic moments which can couple to magnetism, like in UPt3, at least at the conceptual level. Note that TRS-preserving unitary states have also been advanced (Xu et al., 2019; Ishizuka et al., 2019; Ishizuka and Yanase, 2021). Finally, the interplay between AFM and FM fluctuations leading to triplet pairing has been addressed by a number of recent works (Hu and Si, 2020; Chen et al., 2021; Kreisel et al., 2022).
FM, intra-unit cell exchange interactions within a pair of uranium-“dimer”, have been especially invoked as promoting triplet pairing (Hu and Si, 2020; Chen et al., 2021; Shishidou et al., 2021). This has led to a matrix pairing state via additional effective orbital DOFs due to inequivalent U sites. Starting from the DMFT-derived band structure of the normal state, Ref. (Chen et al., 2021). considered an effective, strong intra-unit cell FM exchange interaction and additional weaker, inter-unit cell AFM exchange couplings as supported by DFT calculations. The resulting spin spectrum in the normal state was found to be in agreement with the AFM fluctuations extracted from INS experiments (Duan et al., 2020; Duan et al., 2021). Following a strong-coupling approach along the lines of an effective, generalized t-J model, it was shown that the intra-unit cell FM dimers promote a spin-triplet pairing state with nontrivial orbital (layer) DOFs. This state also reproduces a resonance in the spin-spectrum, as observed in INS experiments (Duan et al., 2021). In addition, STM measurements also observed anticorrelated modulation between superconducting gap size and Kondo resonance, even within one unit cell (Jiao et al., 2020). Ishizuka and Yanase proposed that applied pressure enhances AFM vs FM fluctuations. The resulting pressure-temperature phase diagram includes an odd-parity spin-triplet state at low pressures, an even-parity spin-singlet phase at intermediate pressures, together with possible mixed odd- and even-parity states in between (Ishizuka and Yanase, 2021).
The majority of SCs, including HFs, preserve inversion symmetry, which, together with the Pauli exclusion principle, ensures that the Cooper pairs with a singlet (triplet) spin matrix structure must have a corresponding even (odd)-parity wavefunction. Consequently, the pairing states in centrosymmetric SCs can be classified as either even-parity, spin-singlet or odd-parity, spin-triplet. For example, CeCu2Si2 crystallizes in a tetragonal ThCr2Si2-type (I4/mmm) structure with inversion symmetry, see Figure 6 (Kibune et al., 2021), and the Cooper pairing instability is believed to occur in the even-parity spin-singlet channel. However, if the crystal structure lacks a global inversion center, an electronic antisymmetric spin-orbit coupling (SOC) is allowed, which in turn lifts the spin degeneracy, inducing Rashba SOC interaction (Gor’kov and Rashba, 2001). Since parity is no longer preserved, a strong antisymmetric SOC can mix spin-singlet and spin-triplet states. Indeed, such parity-mixed superconducting states have been proposed in many non-centrosymmetric compounds such as CePt3Si (Bauer et al., 2004), CeRhSi3 (Kimura et al., 2007), CeCoGe3 (Kawai et al., 2008). These materials can simultaneously exhibit features associated with both s-wave and p-wave pairing states (Frigeri et al., 2004; Smidman et al., 2017).
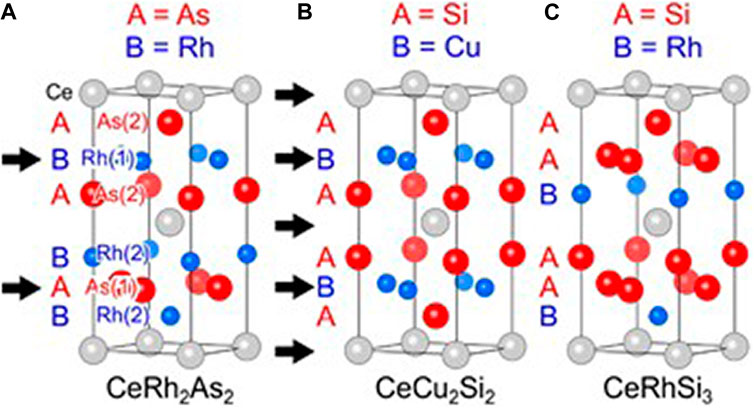
FIGURE 6. Crystal structure of CeRh2As2 (A), CeCu2Si2 (B), and CeRhSi3 (C). To clarify the stacking order, each element is assigned A and B labels. The arrows indicate the cross-section planes of the inversion center. After (Kibune et al., 2021). Adapted with permission from The American Physical Society.
Moreover, for some crystal structures, the paired electrons originate from sites which lack a local inversion symmetry, although a global inversion symmetry is preserved. The recently-discovered HF SC CeRh2As2 (with a CaBe2Ge2-type crystal structure) is one example (Khim et al., 2021). A superconducting transition is observed around Tc = 0.26 K (Khim et al., 2021; Hafner et al., 2022). While the crystal structure of CeRh2As2 is similar to that of CeCu2Si2, the stacking order differs in the two cases, as shown in Figure 6. Due to this, in CeRh2As2, the Ce sites lack inversion symmetry. Furthermore, the space-group of the lattice is non-symmorphic. As in a (globally) non-centrosymmetric SC, the absence of local inversion symmetry generates a local electric field (Kimura et al., 2021). If the spin-orbit interaction is sufficiently strong, the spin degeneracy can be lifted by forming a Rashba spin-texture (Bihlmayer et al., 2015). It has been proposed that the combination of Rashba-type SOC and applied magnetic fields could lead to a change in the parity of the superconducting order parameters in quasi-2D materials, i.e., from even to odd (Yoshida et al., 2012). The observed superconducting states in CeRh2As2 are seemingly consistent with this simple picture. The large value of specific heat jump at Tc confirms that the superconductivity involves heavy quasiparticles.
In the normal state, CeRh2As2 shows characteristic Kondo lattice behavior with TK ≈ 30 K. Low temperature resistivity and specific heat show typical non-Fermi liquid behaviour, indicating that the system is located around a QCP (Khim et al., 2021; Hafner et al., 2022). In addition, the temperature dependence of the NMR relaxation rate demonstrates a singular form for the low-frequency spin dynamics (Kitagawa et al., 2022); the experimental result is compatible with the temperature dependence expected from a KD QCP (Si et al., 2001). All of these observations imply an important role for the AFM fluctuations and Kondo effect in CeRh2As2, which in this respect is therefore similar to many other HF SC.
For H//c, this compound exhibits very high upper critical fields of ∼14 T, more than 20 times larger than the Pauli-limiting field μ0HP ∼ 1.84 Tc ∼ 0.6 T. For H || ab, the upper critical field is around 1.9 T. The large anisotropic behaviour of Hc2, which stands in clear contrast to the case of CeCu2Si2, is however similar to that observed in non-centrosymmetric HF SCs like CeRhSi3. This implies that CeRh2As2 is a quasi-2D SC with pronounced Rashba SOC. Intriguingly, magnetic and thermodynamic probes unveil an apparent first-order transition around 4 T for H || c, as shown in Figure 7. This anomaly also suggests a change in the symmetry of the superconducting order-parameter with increasing magnetic field. In addition to highlighting the absence of local inversion symmetry, recent experiments also uncovered several other intriguing aspects. 2D AFM fluctuations were observed below a Kondo coherence temperature ∼40 K (Kitagawa et al., 2022), with AFM order below Tc. The fact that AFM orders occurs within the superconducting phase is quite unusual, with only few examples among thousands of superconductors, such as pressure-induced coexistence of superconducting and AFM order in CeRhIn5 (Park et al., 2006). In CeRh2As2, this behaviour might be related to the absence of local inversion symmetry at the Ce site, which could induce an effective Zeeman field (Kibune et al., 2021). Slightly above Tc, an additional phase transition to a putative non-magnetic, quadrupole density wave was reported (Hafner et al., 2022). Here, Kondo screening and the crystalline-electric-field both play important roles when it comes to determining the low-energy manifold of the Ce 4f-states. The interplay between superconductivity and quadrupole density waves is still not well understood at this point.
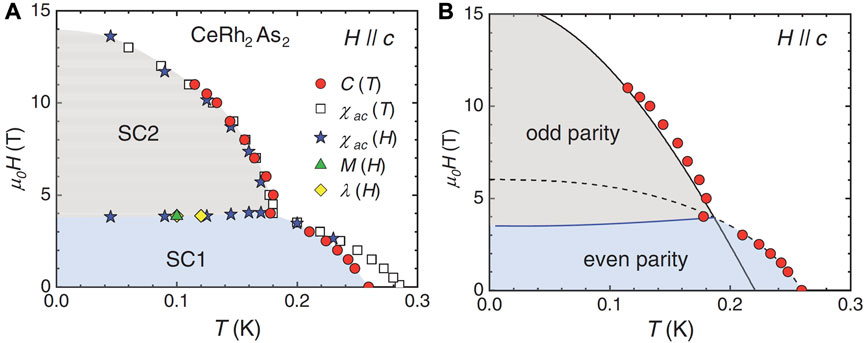
FIGURE 7. Superconducting phase diagrams of CeRh2As2. (A) H || c. (B) Fits to the upper critical fields based on an even-to odd-parity transition proposal. After (Khim et al., 2021). Reproduced with permission from The American Association for the Advancement of Science.
Much like for UTe2, the multiple-phase superconductivity in CeRh2As2 (Khim et al., 2021) does not yet allow for a robust consensus on the nature of the Cooper pairing. Nevertheless, we mention those aspects which are unique to CeRh2As2 and discuss existing work in this context. The absence of local inversion symmetry provides a natural connection to previous studies of non-centrosymmetric SCs, where symmetry-allowed Rashba SOC terms can lead to a mixing between even-parity spin-singlet and odd-parity spin-triplet states (Bauer and Sigrist, 2012), as already mentioned.
The two inequivalent effective Ce layers in CeRh2As2 (Figure 6) can be considered as two non-centrosymmetric superconducting subsystems. Consequently, these layers provide effective orbital DOFs which allow for the construction of matrix pairing states, by analogy to the
While the studies mentioned up to this point assumed dominant intra-plane SOC, Ref. (Möckli and Ramires, 2022). considered the effects of stronger inter-layer coupling. In addition to the even-odd parity transition for weak interlayer coupling, the authors also find a distinct transition between two odd-parity spin-triplet states in the opposite limit (Möckli, 2022). Finally, we note that CeRh2As2 has also been considered in the context of crystalline topological superconductivity protected by non-symmorphic symmetry in Ref. (Nogaki et al., 2021). Among others, the authors advance the notion that odd-parity pairing states, as required by topological superconductivity, can be realized even in the spin-singlet case, due to the alternating sign of pairing with layer, as proposed for the high-field phase of CeRh2As2.
We have emphasized that superconductivity often develops at the border of charge/spin instabilities. In the vicinity of an AFM order, spin-singlet states are generally favored, ensuring that the angular momentum of the Cooper pairs is even. Therefore, a d-wave pairing state is normally expected in this case, as also proposed for cuprate and organic SCs (Stewart 2017). In CeCu2Si2, the d-wave scenario is supported by the absence of a coherence peak in the spin lattice relaxation rate 1/T1 from NQR measurements (Ishida et al., 1999). INS suggests
As discussed in a broader context (Section 1.3), including that of the Fe-based SCs, the orbital DOFs can play a leading role for Cooper paring. This is also likely the case for HFs in general, which typically exhibit multiple bands of varying orbital content in the vicinity of the Fermi level. The difficulties in resolving the experimental results in CeCu2Si2 via single-band pairing states naturally suggest that the pool of available candidates must be enlarged. One way of achieving this is to consider the nontrivial effects of additional bands, or equivalently, that of additional local orbital/spin-orbital DOF in the context of pairing states. To illustrate this approach, we review a recently proposed, two-band d + d pairing state, consisting of distinct intra- and inter-band d-wave components in 2D (Nica and Si, 2021). This candidate has provided a resolution to the puzzle raised by the aforementioned experiments in CeCu2Si2 (Pang et al., 2018; Smidman et al., 2018; Smidman et al., 2022). In contrast to single-band d-wave pairing, d + d pairing exhibits a nontrivial matrix structure:
Thus, while the intra- and inter-band components have nodes along the diagonals and axes of the BZ, much like two, distinct simple d-waves, their superposition is significantly different. Most notably, due to the matrix structure, the pairing gap is determined by the addition in quadrature of the two components. Since these are distinct d-waves, for instance
While pairing with nontrivial matrix structure provides a new and general way of bypassing the mutually-exclusive nature of single-band s- and d-wave states, its associated pairing mechanisms and regimes of stability are more conveniently considered in an equivalent representation, involving electrons in local orbital/spin-orbital multiplets. These DOFs provide a natural basis for constructing pairing states from correlated electrons subject to strong Coulomb repulsion. As discussed in Section 1.3, the idea is that pairing states with a nontrivial matrix structure in an orbital/spin-orbital basis, which transform nontrivially under the PG, lead to pairing states with nontrivial structure in the band basis, like for the d + d state. This is due to the interplay between the local multiplet structure and the normal-state dispersion. The latter is determined by effective intra- and inter-orbital hybridization terms which generally do not commute with nontrivial matrix pairing states. This ensures the presence of both intra- and inter-band components in the band basis, although the pairing state preserves those features associated with PG symmetry. This was explicitly shown in the context of two-orbital models for the alkaline Fe-selenides (Section 1.3). The equivalence of d + d pairing to a matrix pairing state consisting of an s-wave form factor multiplied by a
Charge instabilities can also enhance effective pairing interactions (Monthoux et al., 2007). CeCu2Si2 and its isostructural compound CeCu2Ge2 both exhibit a superconducting dome around the border of an AFM QCP, see Figure 8. However, by tuning the samples away from the QCP using pressure, superconductivity is first (completely) suppressed, but subsequently re-emerges to form a secondary dome in the pressure-temperature phase diagram. Several models have been proposed to explain the second dome superconductivity in CeCu2Si2 and CeCu2Ge2 (Weng et al., 2016). The point of these proposals is that pressure induces a change of a Ce valence transition, which is more likely associated with an effective charge instability, instead of spin. A number of experimental results corroborate this picture. These include a reduction in the electronic scattering and a maximum Sommerfeld coefficient around the center of the second superconducting dome, as detected from transport measurements (Yuan et al., 2003; Holmes et al., 2004), and a continuous change in the Ce valence for CeCu2Si2 under increasing pressure, as observed by x-ray absorption spectroscopy (Rueff et al., 2011). Recent research finds additional examples which appear to deviate from the central theme of spin fluctuation-mediated Cooper pairing. For instance, superconductivity and antiferromagnetism can coexist over a wide pressure range in CeAu2Si2 (Ren et al., 2014), with both superconducting and magnetic transition temperatures showing a parallel increase with pressure. The pressure-temperature phase diagram also resembles those of CeCu2Si2 and CeCu2Ge2.
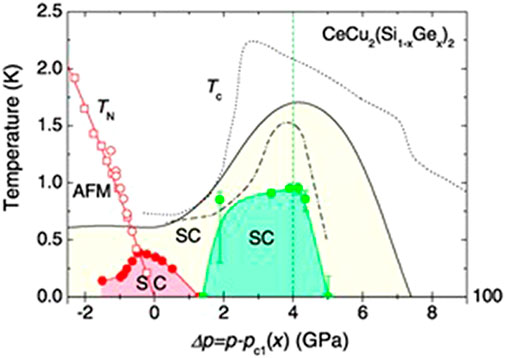
FIGURE 8. Temperature-pressure phase diagram of CeCu2(Si1−xGex)2, showing two superconducting phases under pressure (Yuan et al., 2003). Reproduced with permission from The American Association for the Advancement of Science.
While single-phase, spin-singlet superconductivity emerging near an AFM QCP still probably provides the most robust understanding of unconventional superconductivity, it is by no means unique, as illustrated in previous sections. For instance, in UTe2, one could argue that the traditional competition between antiferromagnetism and Kondo screening must also include the effects of FM fluctuations. This complicated interplay likely underlies the complex superconducting phase diagram, which includes up to five distinct regimes, as accessed by applying magnetic field and pressure. Furthermore, additional multi-orbital or equivalent microscopic DOFs, which emerge from the interplay of lattice structure and symmetry of the f-electron sites, can significantly enrich the emerging superconducting phase diagrams. In CeRh2As2, magnetic fields can in principle induce a change in the parity of the superconducting order parameter from odd to even, in a scenario made plausible by the lack of local inversion symmetry due to stacking order. The two-domed phase diagram of CeCu2Si2 suggests that spin and charge instabilities can in turn play leading roles in driving multiple superconducting phases in the same compound, as accessed via distinct tuning parameters. In general, we have emphasized how quantum criticality and the associated strange-metal physics promote unconventional superconductivity in heavy-fermion metals. Nevertheless, many aspects of the paring symmetries for these HF superconductors remain to be clarified and further studies are highly desired.
The common multi-orbital/band nature of HFs can play an important role in determining the paring symmetry. Consider such multi-band pairing states such as
Symmetry-protected topological pairing states have also received a great deal of attention in recent years. As noted previously, spin-triplet pairing in 3He has provided important precedents in this context as well, particularly in the case of the gapped and topologically nontrivial B phase with Majorana edge modes, see for instance Refs. (Murakawa et al., 2011; Bunkov and Gazizulin, 2020) and work cited therein, but also as an early realization of Weyl fermions in the A phase (Volovik 2003). There are some similarities between the phase diagrams of 3He and the HF superconductor UPt3 (Vollhardt and Wölfle, 1990; Joynt and Taillefer, 2002). UTe2 has also emerged as a promising HF candidate to spin-triplet superconductivity. Signatures of TRS breaking (Hayes et al., 2021) as well as reports of edge modes (Jiao et al., 2020) have also singled out this compound as a potential realization of topologically nontrivial (chiral) superconductivity (Aoki et al., 2022). CeRh2As2 has also been advanced as a candidate for crystalline topological superconductivity protected by the non-symmorphic space group (Nogaki et al., 2021). The required odd-parity pairing is due to a matrix pairing structure (in an effective orbital DOF) instead of the more traditional spin-triplet candidates. In the context of the much-sought topological superconductivity, the larger space of pairing candidates which goes hand-in-hand with multiple superconducting phases in a number of HFs is very promising, for predicting and ultimately realizing these exotic states. As illustrated by these recent developments, pairing with matrix structure is inherently richer than the effectively single-band candidates (Nica et al., 2017; Nica and Si, 2021).
Although HFs have been the focus of this work, it is important to note that multiple superconducting phases have also been observed in YBa2Cu3Oy (Grissonnanche et al., 2014), LaFeAsO1-x (H/F)x (Iimura et al., 2012), BaTi2(Sb1-xBix)2O (Zhai et al., 2013), and very recently, in the kagome superconductors CsV3Sb5 (Zhang, 2021; Nguyen and Li, 2022) and RbV3Sb5 (Guguchia et al., 2022). As illustrated here, recent advances in experimental techniques have provided a much-improved characterization of sample properties in transport, thermodynamic, and various spectroscopies. In such cases as UTe2 and CeRh2As2, these advances have significantly accelerated the discovery of multiple superconducting phases. This progress has also led to dramatic reversals in so-called “standard” cases. Indeed, owing to the development of precise measurements below 100 mK, a completely new understanding of CeCu2Si2, the very first unconventional superconductor is now emerging, with possible implications for other classes of well-studied superconductors. The great diversity of unconventional superconductors provides unprecedented opportunities for realizing novel pairing states.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
EN was supported by the NSF Grant No. DMR-1904716 and an ASU startup grant. The work at Washington University was supported by McDonnell International Scholars Academy. LJ acknowledges financial support from National High Magnetic Field Laboratory, which is funded by the National Science Foundation (DMR-1644779) and the State of Florida. The work at Rice University has primarily been supported by the DOE BES Award #DE-SC0018197; additional support has been provided by the Robert A. Welch Foundation Grant No. C-1411.
We thank Lei Chen, Pengcheng Dai, Chunruo Duan, Onur Erten, Elena Hassinger, Haoyu Hu, Silke Paschen, Frank Steglich, Rong Yu, Vidya Madhavan, and Steffen Wirth for useful discussions.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Adenwalla, S., Lin, S. W., Ran, Q. Z., Zhao, Z., Ketterson, J. B., Sauls, J. A., et al. (1990). Phase diagram of UPt3 from ultrasonic velocity measurements. Phys. Rev. Lett. 65, 2298–2301. doi:10.1103/physrevlett.65.2298
Aoki, D., Huxley, A., Ressouche, E., Braithwaite, D., Flouquet, J., Brison, J. -P., et al. (2001). Coexistence of superconductivity and ferromagnetism in URhGe. Nature 413, 613–616. doi:10.1038/35098048
Aoki, D., Nakamura, A., Honda, F., Li, D. X., Homma, Y., Shimizu, Y., et al. (2019). Unconventional superconductivity in heavy fermion UTe2. J. Phys. Soc. Jpn. 88, 043702. doi:10.7566/JPSJ.88.043702
Aoki, D., Honda, F., Knebel, G., Braithwaite, D., Nakamura, A., Li, D. X., et al. (2020). Multiple superconducting phases and unusual enhancement of the upper critical field in UTe2. J. Phys. Soc. Jpn. 89, 053705. doi:10.7566/jpsj.89.053705
Aoki, D., Brison, J. -P., Flouquet, J., Ishida, K., Knebel, G., Tokunaga, Y., et al. (2022). Unconventional superconductivity in UTe2. J. Phys. Condens. Matter 34, 243002. doi:10.1088/1361-648X/ac5863
Arndt, J., Stockert, O., Schmalzl, K., Faulhaber, E., Jeevan, H. S., Geibel, C., et al. (2011). Spin fluctuations in normal state CeCu2Si2 on approaching the quantum critical point. Phys. Rev. Lett. 106, 246401. doi:10.1103/physrevlett.106.246401
Bae, S., Kim, H. S., Eo, Y. S., Ran, S., Liu, I., Fuhrman, W. T., et al. (2021). Anomalous normal uid response in a chiral superconductor UTe2. Nat. Commun. 12, 2644. doi:10.1038/s41467-021-22906-6
Bardeen, J., Cooper, L. N., and Schrieffer, J. R. (1957). Microscopic theory of superconductivity. Phys. Rev. 106, 162–164. doi:10.1103/physrev.106.162
Bauer, E., and Sigrist, M. (2012). “Non-centrosymmetric superconductors: Introduction and overview,” in Lecture notes in physics (Springer-Verlag Berlin Heidelberg).
Bauer, E., Hilscher, G., Michor, H., Paul, C., Scheidt, E. W., Gribanov, A., et al. (2004). Heavy fermion superconductivity and magnetic order in NoncentrosymmetricCePt3Si. Phys. Rev. Lett. 92, 027003. doi:10.1103/physrevlett.92.027003
Bianchi, A., Movshovich, R., Vekhter, I., Pagliuso, P. G., and Sarrao, J. L. (2003). Avoided antiferromagnetic order and quantum critical point in CeCoIn5. Phys. Rev. Lett. 91, 257001. doi:10.1103/physrevlett.91.257001
Bihlmayer, G., Rader, O., and Winkler, R. (2015). Focus on the Rashba effect. New J. Phys. 17, 050202. doi:10.1088/1367-2630/17/5/050202
Braithwaite, D., Vališka, M., Knebel, G., Lapertot, G., Brison, J. -P., Pourret, A., et al. (2019). Multiple superconducting phases in a nearly ferromagnetic system. Commun. Phys. 2, 147. doi:10.1038/s42005-019-0248-z
Bucher, E., Maita, J. P., Hull, G. W., Fulton, R. C., and Cooper, A. S. (1975). Electronic properties of beryllides of the rare Earth and some actinides. Phys. Rev. B 11, 440–449. doi:10.1103/PhysRevB.11.440
Bunkov, Y. M., and Gazizulin, R. R. (2020). Direct observation of the specific heat of Majorana quasiparticles in superfluid 3He B phase. Sci. Rep. 10, 20120. doi:10.1038/s41598-020-77128-5
Cavanagh, D. C., Shishidou, T., Weinert, M., Brydon, P. M. R., and Agterberg, D. F. (2022). Nonsymmorphic symmetry and field-driven odd-parity pairing in CeRh2As2. Phys. Rev. B 105, L020505. doi:10.1103/physrevb.105.l020505
Chen, L., Hu, H., Lane, C., Nica, E. M., Zhu, J. X., and Si, Q. (2021). Multiorbital spin-triplet pairing and spin resonance in the heavy-fermion superconductor UTe2. arXiv:2112.14750.
Coleman, P., and Schofield, A. J. (2005). Quantum criticality. Nature 433, 226–229. doi:10.1038/nature03279
Coleman, P., Pépin, C., Si, Q., and Ramazashvili, R. (2001). How do Fermi liquids get heavy and die? J. Phys. Condens. Matter 13, R723–R738. doi:10.1088/0953-8984/13/35/202
Custers, J., Gegenwart, P., Wilhelm, H., Neumaier, K., Tokiwa, Y., Trovarelli, O., et al. (2003). The break-up of heavy electrons at a quantum critical point. Nature 424, 524–527. doi:10.1038/nature01774
Custers, J., Lorenzer, K., Müller, M., Prokofiev, A., Sidorenko, A., Winkler, H., et al. (2012). Destruction of the Kondo effect in the cubic heavy-fermion compound Ce3Pd20Si6. Nat. Mater. 11, 189–194. doi:10.1038/nmat3214
Dai, P. C. (2015). Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev. Mod. Phys. 87, 855–896. doi:10.1103/revmodphys.87.855
Doniach, S. (1977). The Kondo lattice and weak antiferromagnetism. Phys. B+C 91, 231–234. doi:10.1016/0378-4363(77)90190-5
Duan, C., Sasmal, K., Maple, M. B., Podlesnyak, A., Zhu, J.-X., Si, Q., et al. (2020). Incommensurate spin fluctuations in the spin-triplet superconductor candidate UTe2. Phys. Rev. Lett. 125, 237003. doi:10.1103/physrevlett.125.237003
Duan, C. R., Baumbach, R. E., Podlesnyak, A., Deng, Y. H., Moir, C., Breindel, A. J., et al. (2021). Resonance from antiferromagnetic spin fluctuations for superconductivity in UTe2. Nature 600, 636–640. doi:10.1038/s41586-021-04151-5
Eremin, I., Zwicknagl, G., Thalmeier, P., and Fulde, P. (2008). Feedback spin resonance in superconducting CeCu2Si2 and CeCoIn5. Phys. Rev. Lett. 101, 187001. doi:10.1103/physrevlett.101.187001
Ernst, S., Kirchner, S., Krellner, C., Geibel, C., Zwicknagl, G., Steglich, F., et al. (2011). Emerging local Kondo screening and spatial coherence in the heavy-fermion metal YbRh2Si2. Nature 474, 362–366. doi:10.1038/nature10148
Friedemann, S., Oeschler, N., Wirth, S., Krellner, C., Geibel, C., Steglich, F., et al. (2010). Fermi-surface collapse and dynamical scaling near a quantum-critical point. Proc. Natl. Acad. Sci. U. S. A. 107, 14547–14551. doi:10.1073/pnas.1009202107
Friemel, G., Park, J. T., Maier, T. A., Tsurkan, V., Li, Y., Deisenhofer, J., et al. (2012). Reciprocal-space structure and dispersion of the magnetic resonant mode in the superconducting phase of RbxFe2-ySe2 single crystals. Phys. Rev. B 85, 140511. doi:10.1103/physrevb.85.140511
Frigeri, P. A., Agterberg, D. F., and Sigrist, M. (2004). Spin susceptibility in superconductors without inversion symmetry. New J. Phys. 6, 115. doi:10.1088/1367-2630/6/1/115
Gegenwart, P., Custers, J., Geibel, C., Neumaier, K., Tayama, T., Tenya, K., et al. (2002). Magnetic-field induced quantum critical point in YbRh2Si2. Phys. Rev. Lett. 89, 056402. doi:10.1103/physrevlett.89.056402
Gegenwart, P., Si, Q., and Steglich, F. (2008). Quantum criticality in heavy-fermion metals. Nat. Phys. 4, 186–197. doi:10.1038/nphys892
Gerber, S., Bartkowiak, M., Gavilano, J. L., Ressouche, E., Egetenmeyer, N., Niedermayer, C., et al. (2014). Switching of magnetic domains reveals spatially inhomogeneous superconductivity. Nat. Phys. 10, 126–129. doi:10.1038/nphys2833
Gor’kov, L. P., and Rashba, E. I. (2001). Superconducting 2D system with lifted spin degeneracy: Mixed singlet-triplet state. Phys. Rev. Lett. 87, 037004. doi:10.1103/physrevlett.87.037004
Grissonnanche, G., Cyr-Choinière, O., Laliberté, F., René de Cotret, S., Juneau-Fecteau, A., Dufour-Beauséjour, S., et al. (2014). Direct measurement of the upper critical field in cuprate superconductors. Nat. Commun. 5, 3280. doi:10.1038/ncomms4280
Grosche, F. M., Walker, I. R., Julian, S. R., Mathur, N. D., Freye, D. M., Steiner, M. J., et al. (2001). Superconductivity on the threshold of magnetism in CePd2Si2 and CeIn3. J. Phys. Condens. Matter 13, 2845–2860. doi:10.1088/0953-8984/13/12/309
Guguchia, Z., Mielke, C., Das, D., Gupta, R., Yin, J.-X., Liu, H., et al. (2022). Tunable nodal kagome superconductivity in charge ordered RbV3Sb5. arXiv:2202.07713
Hafner, D., Khanenko, P., Eljaouhari, E.-O., Kuchler, R., Banda, J., Mishra, S., et al. (2022). Possible quadrupole density wave in the superconducting kondo lattice CeRh2As2. Phys. Rev. X 12, 011023. doi:10.1103/physrevx.12.011023
Hayes, I. M., Wei, D. S., Metz, T., Zhang, J., Eo, Y. S., Ran, S., et al. (2021). Multicomponent superconducting order parameter in UTe2. Science 373, 797–801. doi:10.1126/science.abb0272
Hertz, J. A. (1976). Quantum critical phenomena. Phys. Rev. B 14, 1165–1184. doi:10.1103/physrevb.14.1165
Holmes, A. T., Jaccard, D., and Miyake, K. (2004). Signatures of valence fluctuations in CeCu2Si2 under high pressure. Phys. Rev. B 69, 024508. doi:10.1103/physrevb.69.024508
Hu, H., and Si, Q. (2020). Talk given at the January 2020 fundamentals of quantum materials workshop on superconductivity of UTe2. College Park, MD: University of Maryland.
Hu, H., Cai, A., Chen, L., Deng, L., Pixley, J. H., Ingersent, K., et al. (2021a). Unconventional superconductivity from fermi surface fluctuations in strongly correlated metals. arXiv:2109.13224.
Hu, H., Cai, A., Chen, L., and Si, Q. (2021b). Spin-singlet and spin-triplet pairing correlations in antiferromagnetically coupled kondo systems. arXiv:2109.12794.
Huxley, A., Rodière, P., Paul, D. M., Dijk, N. v., Cubitt, R., and Flouquet, J. (2000). Realignment of the flux-line lattice by a change in the symmetry of superconductivity in UPt3. Nature 406, 160–164. doi:10.1038/35018020
Huxley, A., Sheikin, I., Ressouche, E., Kernavanois, N., Braithwaite, D., Calemczuk, R., et al. (2001). UGe2: A ferromagnetic spin-triplet superconductor. Phys. Rev. B 63, 144519. doi:10.1103/physrevb.63.144519
Huy, N. T., Gasparini, A., de Nijs, D. E., Huang, Y., Klaasse, J. C. P., Gortenmulder, T., et al. (2007). Superconductivity on the border of weak itinerant ferromagnetism in UCoGe. Phys. Rev. Lett. 99, 067006. doi:10.1103/physrevlett.99.067006
Iimura, S., Matsuishi, S., Sato, H., Hanna, T., Muraba, Y., Kim, S. W., et al. (2012). Two-dome structure in electron-doped iron arsenide superconductors. Nat. Commun. 3, 943. doi:10.1038/ncomms1913
Ishida, K., Kawasaki, Y., Tabuchi, K., Kashima, K., Kitaoka, Y., Asayama, K., et al. (1999). Evolution from magnetism to unconventional superconductivity in a series of CexCu2Si2 compounds probed by Cu NQR. Phys. Rev. Lett. 82, 5353–5356. doi:10.1103/physrevlett.82.5353
Ishizuka, J., Sumita, S., Daido, A., and Yanase, Y. (2019). Insulator-metal transition and topological superconductivity in UTe2 from a first-principles calculation. Phys. Rev. Lett. 123, 217001. doi:10.1103/physrevlett.123.217001
Ishizuka, J., and Yanase, Y. (2021). Periodic Anderson model for magnetism and superconductivity in UTe2. Phys. Rev. B 103, 094504. doi:10.1103/PhysRevB.103.094504
Jiao, L., Howard, S., Ran, S., Wang, Z. Y., Rodriguez, J. O., Sigrist, M., et al. (2020). Chiral superconductivity in heavy-fermion metal UTe2. Nature 579, 523–527. doi:10.1038/s41586-020-2122-2
Joynt, R., and Taillefer, L. (2002). The superconducting phases of UPt3. Rev. Mod. Phys. 74, 235–294. doi:10.1103/revmodphys.74.235
Kawai, T., Muranaka, H., Measson, M., Shimoda, T., Doi, Y., Matsuda, T. D., et al. (2008). Magnetic and superconducting properties of CeTX3 (T: Transition metal and X: Si and Ge) with non-centrosymmetric crystal structure. J. Phys. Soc. Jpn. 77, 064716. doi:10.1143/JPSJ.77.064716
Kawasaki, S., Yashima, M., Mugino, Y., Mukuda, H., Kitaoka, Y., Shishido, H., et al. (2006). Enhancing the superconducting transition temperature of CeRh1−xIrxIn5 due to the strong-coupling effects of antiferromagnetic spin fluctuations: An 115In nuclear quadrupole resonance study. Phys. Rev. Lett. 96, 147001. doi:10.1103/physrevlett.96.147001
Khim, S., Landaeta, J. F., Banda, J., Bannor, N., Brando, M., Brydon, P. M. R., et al. (2021). Field-induced transition within the superconducting state of CeRh2As2. Science 373, 1012–1016. doi:10.1126/science.abe7518
Kibune, M., Kitagawa, S., Kinjo, K., Ogata, S., Manago, M., Taniguchi, T., et al. (2021). Observation of antiferromagnetic order as odd-parity multipoles inside the superconducting phase in CeRh2As2. Phys. Rev. X 128, 057002. doi:10.1103/PhysRevLett.128.057002
Kim, D. Y., Lin, S. Y., Weickert, F., Kenzelmann, M., Bauer, E. D., Ronning, F., et al. (2016). Intertwined orders in heavy-fermion superconductor CeCoIn5. Phys. Rev. X 6, 041059. doi:10.1103/physrevx.6.041059
Kimura, N., Ito, K., Aoki, H., Uji, S., and Terashima, T. (2007). Extremely high upper critical magnetic field of the noncentrosymmetric heavy fermion superconductor CeRhSi3. Phys. Rev. Lett. 98, 197001. doi:10.1103/physrevlett.98.197001
Kimura, S., Sichelschmidt, J., and Khim, S. Y. (2021). Optical study on electronic structure of the locally non-centrosymmetric CeRh2As2. Phys. Rev. B 104, 245116. doi:10.1103/PhysRevB.104.245116
Kirchner, S., Paschen, S., Chen, Q., Wirth, S., Feng, D., Thompson, J. D., et al. (2020). Colloquium: Heavy-electron quantum criticality and single-particle spectroscopy. Rev. Mod. Phys. 92, 011002. doi:10.1103/revmodphys.92.011002
Kitagawa, S., Kibune, M., Kinjo, K., Manago, M., Taniguchi, T., Ishida, K., et al. (2022). Two-dimensional XY-type magnetic properties of locally noncentrosymmetric superconductor CeRh2As2. J. Phys. Soc. Jpn. 91, 043702. doi:10.7566/jpsj.91.043702
Kittaka, S., Aoki, Y., Shimura, Y., Sakakibara, T., Seiro, S., Geibel, C., et al. (2014). Multiband superconductivity with unexcepted deficiency of nodal quasiparticles in Cecu2Si2. Phys. Rev. Lett. 112, 067002. doi:10.1103/physrevlett.112.067002
Knafo, W., Nardone, M., Vališka, M., Zitouni, A., Lapertot, G., Aoki, D., et al. (2021). Comparison of two superconducting phases induced by a magnetic field in UTe2. Commun. Phys. 4, 40. doi:10.1038/s42005-021-00545-z
Knebel, G., Aoki, D., Brison, N. J. -P., and Flouquet, J. (2008). The quantum critical point in cerhin5: A resistivity study. J. Phys. Soc. Jpn. 77, 114704. doi:10.1143/JPSJ.77.114704
Knebel, G., Knafo, W., Pourret, A., Niu, Q., Vališka, M., Braithwaite, D., et al. (2019). Field-reentrant superconductivity close to a metamagnetic transition in the heavy-fermion superconductor UTe2. J. Phys. Soc. Jpn. 88, 063707. doi:10.7566/JPSJ.88.063707
Kreisel, A., Quan, Y. D., and Hirschfeld, P. J. (2022). Spin triplet superconductivity driven by finite-momentum spin fluctuations. Phys. Rev. B 105, 104507. doi:10.1103/physrevb.105.104507
Lee, D.-H. (2017). Hunting down unconventional superconductors. Science 357, 32–33. doi:10.1126/science.aan2657
Leggett, A. J. (1975). A theoretical description of the new phases of liquid 3He. Rev. Mod. Phys. 47, 331–414. doi:10.1103/revmodphys.47.331
Lévy, F., Sheikin, I., Grenier, B., and Huxley, A. D. (2005). Magnetic field-induced Superconductivity in the ferromagnet URhGe. Science 309, 1343–1346. doi:10.1126/science.1115498
Lin, W.-C., Campbell, D. J., Ran, S., Liu, I., Kim, H. S., Nevidomskkyy, A. H., et al. (2020). Tuning magnetic confinement of spin-triplet superconductivity. npj Quantum Mater. 5, 68. doi:10.1038/s41535-020-00270-w
Lindquist, A. W., Clepkens, J., and Kee, H.-Y. (2022). Evolution of interorbital superconductor to intraorbital spin-density wave in layered ruthenates. Phys. Rev. Res. 4, 023109. doi:10.1103/physrevresearch.4.023109
Löhneysen, H. v., Pietrus, T., Portisch, G., Schlager, H. G., Schröder, A., Sieck, M., et al. (1994). Non-fermi-liquid behavior in a heavy-fermion alloy at a magnetic instability. Phys. Rev. Lett. 72, 3262–3265. doi:10.1103/physrevlett.72.3262
Löhneysen, H. v., Rosch, A., Vojta, M., and Wölfle, P. (2007). Fermi-liquid instabilities at magnetic quantum phase transitions. Rev. Mod. Phys. 79, 1015–1075. doi:10.1103/revmodphys.79.1015
Martelli, V., Cai, A., Nica, E. M., Taupin, M., Prokofiev, A., Liu, C.-C., et al. (2019). Sequential localization of a complex electron fluid. Proc. Natl. Acad. Sci. U. S. A. 116, 17701–17706. doi:10.1073/pnas.1908101116
Mathur, N. D., Grosche, F. M., Julian, S. R., Walker, I. R., Freye, D. M., Haselwimmer, R. K. W., et al. (1998). Magnetically mediated superconductivity in heavy fermion compounds. Nature 394, 39–43. doi:10.1038/27838
Matsubayashi, K., Tanaka, T., Sakai, A., Nakatsuji, S., Kubo, Y., and Uwatoko, Y. (2012). Pressure-induced heavy fermion superconductivity in the nonmagnetic quadrupolar system PrTi2Al20. Phys. Rev. Lett. 109, 187004. doi:10.1103/physrevlett.109.187004
Metz, T., Bae, S. J., Ran, S., Liu, I., Eo, Y. S., Fuhrman, W. T., et al. (2019). Point-node gap structure of the spin-triplet superconductor UTe2. Phys. Rev. B 100, 220504. doi:10.1103/PhysRevB.100.220504
Miao, L., Liu, S. Z., Xu, Y. S., Kotta, E. C., Kang, C. -J., Ran, S., et al. (2020). Low energy band structure and symmetries of UTe2 from angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 124, 076401. doi:10.1103/physrevlett.124.076401
Millis, A. J. (1993). Effect of a nonzero temperature on quantum critical points in itinerant fermion systems. Phys. Rev. B 48, 7183–7196. doi:10.1103/physrevb.48.7183
Miyake, K., Schmitt-Rink, S., and Varma, C. M. (1986). Spin-fluctuation-mediated even-parity pairing in heavy-fermion superconductors. Phys. Rev. B 34, 6554–6556. doi:10.1103/physrevb.34.6554
Miyake, A., Shimizu, Y., Sato, Y. J., Li, D. X., Nakamura, A., Homma, Y., et al. (2019). Metamagnetic transition in heavy fermion superconductor UTe2. J. Phys. Soc. Jpn. 88, 063706. doi:10.7566/JPSJ.88.063706
Möckli, D., and Ramires, A. (2021). Two scenarios for superconductivity in CeRh2As2. Phys. Rev. Res. 3, 023204. doi:10.1103/physrevresearch.3.023204
Möckli, D. (2022). Unconventional singlet-triplet superconductivity. J. Phys. Conf. Ser. 2164, 012009. doi:10.1088/1742-6596/2164/1/012009
Monthoux, P., and Lonzarich, G. G. (2001). Magnetically mediated superconductivity in quasi-two and three dimensions. Phys. Rev. B 63, 054529. doi:10.1103/physrevb.63.054529
Monthoux, P., Pines, D., and Lonzarich, G. G. (2007). Superconductivity without phonons. Nature 450, 1177–1183. doi:10.1038/nature06480
Movshovich, R., Graf, T., Mandrus, D., Thompson, J. D., Smith, J. L., and Fisk, Z. (1996). Superconductivity in heavy-fermion CeRh2Si2. Phys. Rev. B 53, 8241–8244. doi:10.1103/physrevb.53.8241
Murakawa, S., Wada, Y., Tamura, Y., Wasai, M., Saitoh, M., Aoki, Y., et al. (2011). Surface Majorana cone of the superfluid 3He B phase. J. Phys. Soc. Jpn. 80, 013602. doi:10.1143/JPSJ.80.013602
Nagamatsu, J., Nakagawa, N., Muranaka, T., Zenitani, Y., and Akimitsu, J. (2001). Superconductivity at 39 K in magnesium diboride. Nature 410, 63–64. doi:10.1038/35065039
Nagato, K., Yamamoto, M., and Nagai, K. (1998). Rough surface effects on the p-wave Fermi superfluids. J. Low. Temp. Phys. 110, 1135–1171. doi:10.1023/a:1022368301143
Nakamine, G., Kitagawa, S., Ishida, K., Tokunaga, Y., Sakai, H., Kambe, S., et al. (2019). Superconducting properties of heavy fermion UTe2 revealed by 125Te-nuclear magnetic resonance. J. Phys. Soc. Jpn. 88, 113703. doi:10.7566/JPSJ.88.113703
Nakamine, G., Kinjo, K., Kitagawa, S., Ishida, K., Tokunaga, Y., Sakai, H., et al. (2021). Anisotropic response of spin susceptibility in the superconducting state of UTe2 probed with 125Te-NMR measurement. Phys. Rev. B 103, L100503. doi:10.1103/PhysRevB.103.L100503
Nevidomskyy, A. H. (2020). Stability of a nonunitary triplet pairing on the border of magnetism in UTe2. arXiv:2001.02699.
Nguyen, T., and Li, M. D. (2022). Electronic properties of correlated kagomé metals AV3Sb5 (A = K, Rb, and Cs): A perspective. J. Appl. Phys. 131, 060901. doi:10.1063/5.0079593
Nguyen, D. H., Sidorenko, A., Taupin, M., Knebel, G., Lapertot, G., Schuberth, E., et al. (2021). Superconductivity in an extreme strange metal. Nat. Commun. 12, 4341. doi:10.1038/s41467-021-24670-z
Nica, E. M., and Si, Q. (2021). Multiorbital singlet pairing and d+d superconductivity. npj Quantum Mater. 6, 3. doi:10.1038/s41535-020-00304-3
Nica, E. M., Yu, R., and Si, Q. (2017). Orbital-selective pairing and superconductivity in iron selenides. NPJ Quantum Mater. 2, 24. doi:10.1038/s41535-017-0027-6
Nogaki, K., Daido, A., Ishizuka, J., and Yanase, Y. (2021). Topological crystalline superconductivity in locally noncentrosymmetric CeRh2As2. Phys. Rev. Res. 3, L032071. doi:10.1103/physrevresearch.3.l032071
Ott, H. R., Rudigier, H., Fisk, Z., and Smith, J. L. (1985). Phase transition in the superconducting state of U1−xThxBe13 (x = 0–0.06). Phys. Rev. B Condens. Matter 31, 1651–1653. doi:10.1103/physrevb.31.1651
Palstra, T. T. M., Menovsky, A. A., Berg, J. v., Dirkmaat, A. J., Kes, P. H., Nieuwenhuys, G. J., et al. (1985). Superconducting and magnetic transitions in the heavy-fermion system URu2Si2. Phys. Rev. Lett. 55, 2727–2730. doi:10.1103/physrevlett.55.2727
Pang, G. M., Smidman, M., Zhang, J. L., Jiao, L., Weng, Z. F., Nica, E. M., et al. (2018). Fully gapped d-wave superconductivity in CeCu2Si2. Proc. Natl. Acad. Sci. U. S. A. 115, 5343–5347. doi:10.1073/pnas.1720291115
Park, T., Ronning, F., Yuan, H. Q., Salamon, M. B., Movshovich, R., Sarrao, J. L., et al. (2006). Hidden magnetism and quantum criticality in the heavy fermion superconductor CeRhIn5. Nature 440, 65–68. doi:10.1038/nature04571
Park, J. T., Friemel, G., Li, Y., Kim, J. -H., Tsurkan, V., Deisenhofer, J., et al. (2011). Magnetic resonant mode in the low-energy spin-excitation spectrum of superconducting Rb2Fe4Se5 single crystals. Phys. Rev. Lett. 107, 177005. doi:10.1103/physrevlett.107.177005
Paschen, S., and Si, Q. (2021). Quantum phases driven by strong correlations. Nat. Rev. Phys. 3, 9–26. doi:10.1038/s42254-020-00262-6
Paschen, S., Lühmann, T., Wirth, S., Gegenwart, P., Trovarelli, O., Geibel, C., et al. (2004). Hall-effect evolution across a heavy-fermion quantum critical point. Nature 432, 881–885. doi:10.1038/nature03129
Pixley, J. H., Deng, L. L., Ingersent, K., and Si, Q. (2015). Pairing correlations near a kondo-destruction quantum critical point. Phys. Rev. B 91, 201109. doi:10.1103/physrevb.91.201109
Prochaska, L., Li, X., MacFarland, D. C., Andrews, A. M., Bonta, M., Bianco, E. F., et al. (2020). Singular charge fluctuations at a magnetic quantum critical point. Science 367, 285–288. doi:10.1126/science.aag1595
Puetter, C. M., and Kee, H.-Y. (2012). Identifying spin-triplet pairing in spin-orbit coupled multi-band superconductors. Europhys. Lett. 98, 27010. doi:10.1209/0295-5075/98/27010
Ramires, A. (2021). Nodal gaps from local interactions in Sr2RuO4. J. Phys. Conf. Ser. 2164, 012002. doi:10.1088/1742-6596/2164/1/012002
Ran, S., Eckberg, C., Ding, Q. -P., Furukawa, Y., Metz, T., Saha, S. R., et al. (2019a). Nearly ferromagnetic spin-triplet superconductivity. Science 365, 684–687. doi:10.1126/science.aav8645
Ran, S., Liu, I., Eo, Y. S., Campbell, D. J., Neves, P. M., Fuhrman, W. T., et al. (2019b). Extreme magnetic field-boosted superconductivity. Nat. Phys. 15, 1250–1254. doi:10.1038/s41567-019-0670-x
Ran, S., Kim, H. S., Liu, I., Saha, S. R., Hayes, I., Metz, T., et al. (2020). Enhancement and reentrance of spin triplet superconductivity in UTe2 under pressure. Phys. Rev. B 101, 140503. doi:10.1103/PhysRevB.101.140503
Ran, S., Saha, S. R., Liu, I., Graf, D., Paglione, J., and Butch, N. P. (2021). Expansion of the high field-boosted superconductivity in UTe2 under pressure. npj Quantum Mater. 6, 75. doi:10.1038/s41535-021-00376-9
Ren, Z., Pourovskii, L. V., Giriat, G., Lapertot, G., Georges, A., and Jaccard, D. (2014). Giant overlap between the magnetic and superconducting phases of CeAu2Si2 under pressure. Phys. Rev. X 4, 031055. doi:10.1103/physrevx.4.031055
Rueff, J. -P., Raymond, S., Taguchi, M., Sikora, M., Itié, J. -P., Baudelet, F., et al. (2011). Pressure-induced valence crossover in superconducting CeCu2Si2. Phys. Rev. Lett. 106, 186405. doi:10.1103/physrevlett.106.186405
Sakai, A., Kuga, K., and Nakatsuji, S. (2012). Superconductivity in the ferroquadrupolar state in the quadrupolar Kondo lattice PrTi2Al20. J. Phys. Soc. Jpn. 81, 083702. doi:10.1143/jpsj.81.083702
Sauls, J. A. (1994). The order parameter for the superconducting phases of UPt3. Adv. Phys. 43, 113–141. doi:10.1080/00018739400101475
Schertenleib, E. G., Fischer, M. H., and Sigrist, M. (2021). Unusual H-T phase diagram of CeRh2As2: The role of staggered noncentrosymmetricity. Phys. Rev. Res. 3, 023179. doi:10.1103/physrevresearch.3.023179
Schröder, A., Aeppli, G., Coldea, R., Adams, M., Stockert, O., Löhneysen, H. v., et al. (2000). Onset of antiferromagnetism in heavy-fermion metals. Nature 407, 351–355. doi:10.1038/35030039
Schuberth, E., Tippmann, M., Steinke, L., Lausberg, S., Steppke, A., Brando, M., et al. (2016). Emergence of superconductivity in the canonical heavy-electron metal YbRh2Si2. Science 351, 485–488. doi:10.1126/science.aaa9733
Senthil, T., Vojta, M., and Sachdev, S. (2004). Weak magnetism and non-Fermi liquids near heavy-fermion critical points. Phys. Rev. B 69, 035111. doi:10.1103/physrevb.69.035111
Shang, T., Baumbach, R. E., Gofryk, K., Ronning, F., Weng, Z. F., Zhang, J. L., et al. (2014). CeIrIn5: Superconductivity on a magnetic instability. Phys. Rev. B 89, 041101. doi:10.1103/physrevb.89.041101
Shishido, H., Settai, R., Harima, H., and Ōnuki, Y. (2005). A drastic change of the fermi surface at a critical pressure in CeRhIn5: dHvA study under pressure. J. Phys. Soc. Jpn. 74, 1103–1106. doi:10.1143/JPSJ.74.1103
Shishidou, T., Suh, H. G., Brydon, P. M. R., Weinert, M., and Agterberg, D. F. (2021). Topological band and superconductivity in UTe2. Phys. Rev. B 103, 104504. doi:10.1103/physrevb.103.104504
Si, Q., and Steglich, F. (2010). Heavy fermions and quantum phase transitions. Science 329, 1161–1166. doi:10.1126/science.1191195
Si, Q., Rabello, S., Ingersent, K., and Smith, J. L. (2001). Locally critical quantum phase transitions in strongly correlated metals. Nature 413, 804–808. doi:10.1038/35101507
Si, Q. (2006). Global magnetic phase diagram and local quantum criticality in heavy fermion metals. Physica B 378-380, 23–27.
Si, Q. (2010). Quantum criticality and global phase diagram of magnetic heavy fermions. Phys. Status Solidi B 247, 476–484.
Si, Q., Pixley, J. H., Nica, E., Yamamoto, S. J., Goswami, P., Yu, R., et al. (2014). Kondo destruction and quantum criticality in kondo lattice systems. J. Phys. Soc. Jpn. 83, 061005. doi:10.7566/jpsj.83.061005
Si, Q., Yu, R., and Abrahams, E. (2016). High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 1, 16017. doi:10.1038/natrevmats.2016.17
Sigrist, M., and Ueda, K. (1991). Phenomenological theory of unconventional superconductivity. Rev. Mod. Phys. 63, 239–311. doi:10.1103/revmodphys.63.239
Smidman, M., Salamon, M. B., Yuan, H. Q., and Agterberg, D. F. (2017). Superconductivity and spin–orbit coupling in non-centrosymmetric materials: a review. Rep. Prog. Phys. 80, 036501. doi:10.1088/1361-6633/80/3/036501
Smidman, M., Stockert, O., Arndt, J., Pang, G. M., Jiao, L., Yuan, H. Q., et al. (2018). Interplay between unconventional superconductivity and heavy-fermion quantum criticality: CeCu2Si2 versus YbRh2Si2. Philos. Mag. 98, 2930–2963. doi:10.1080/14786435.2018.1511070
Smidman, M., Stockert, O., Nica, E. M., Liu, Y., Yuan, H. Q., Si, Q., et al. (2022). Unconventional and fully-gapped heavy-fermion superconductivity in CeCu2Si2. Preprint.
Steglich, F., and Wirth, S. (2016). Foundations of heavy-fermion superconductivity: lattice kondo effect and Mott physics. Rep. Prog. Phys. 79, 084502. doi:10.1088/0034-4885/79/8/084502
Steglich, F., Aarts, J., Bredl, C. D., Lieke, W., Meschede, D., Franz, W., et al. (1979). Superconductivity in the presence of strong Pauli paramagnetism: CeCu2Si2. Phys. Rev. Lett. 43, 1892–1896. doi:10.1103/physrevlett.43.1892
Steglich, F. (2014). Heavy fermions: superconductivity and its relationship to quantum criticality. Philos. Mag. 94, 3259–3280. doi:10.1080/14786435.2014.956835
Stewart, G. R., Fisk, Z., Willis, J. O., and Smith, J. L. (1984). Possibility of coexistence of bulk superconductivity and spin fluctuations in UPt3. Phys. Rev. Lett. 52, 679–682. doi:10.1103/physrevlett.52.679
Stewart, G. R. (2017). Unconventional superconductivity. Adv. Phys. 66, 75–196. doi:10.1080/00018732.2017.1331615
Stockert, O., Arndt, J., Faulhaber, E., Geibel, C., Jeevan, H., Kirchner, S., et al. (2011). Magnetically driven superconductivity in CeCu2Si2. Nat. Phys. 7, 119–124. doi:10.1038/nphys1852
Sugitani, I., Okuda, Y., Shishido, H., Yamada, T., Thamizhavel, A., Yamamoto, E., et al. (2006). Pressure-induced heavy-fermion superconductivity in antiferromagnet CeIrSi3 without inversion symmetry. J. Phys. Soc. Jpn. 75, 043703. doi:10.1143/jpsj.75.043703
Thomas, S. M., Santos, F. B., Christensen, M. H., Asaba, T., Ronning, F., Thompson, J. D., et al. (2020). Evidence for a pressure-induced antiferromagnetic quantum critical point in intermediate-valence UTe2. Sci. Adv. 6, eabc8709. URL: http://advances.sciencemag.org/content/6/42/eabc8709.abstract. doi:10.1126/sciadv.abc8709
Trovarelli, O., Geibel, C., Mederle, S., Langhammer, C., Grosche, F. M., Gegenwart, P., et al. (2000). YbRh2Si2: Pronounced non-fermi-liquid effects above a low-lying magnetic phase transition. Phys. Rev. Lett. 85, 626–629. doi:10.1103/physrevlett.85.626
Vieyra, H. A., Oeschler, N., Seiro, S., Jeevan, H. S., Geibel, C., Parker, D., et al. (2011). Determination of gap symmetry from angle-dependent Hc2 measurements on CeCu2Si2. Phys. Rev. Lett. 106, 207001. doi:10.1103/physrevlett.106.207001
Walker, I. R., Grosche, F. M., Freye, D. M., and Lonzarich, G. G. (1997). The normal and superconducting states of CeIn3 near the border of antiferromagnetic order. Phys. C 282-7, 3003–3306.
Wang, X.-P., Qian, T., Richard, P., Zhang, P., Dong, J., Wang, H.-D., et al. (2011). Strong nodeless pairing on separate electron Fermi surface sheets in (Tl, K)Fe1.78Se2 probed by ARPES. Eur. Lett. 93, 57001. doi:10.1209/0295-5075/93/57001
Weng, Z. F., Smidman, M., Jiao, L., Lu, X., and Yuan, H. Q. (2016). Multiple quantum phase transitions and superconductivity in Ce-based heavy fermions. Rep. Prog. Phys. 79, 094503. doi:10.1088/0034-4885/79/9/094503
White, B. D., Thompson, J. D., and Maple, M. B. (2015). Unconventional superconductivity in heavy-fermion compounds. Phys. C Supercond. its Appl. 514, 246–278. doi:10.1016/j.physc.2015.02.044
Xu, M., Ge, Q. Q., Peng, R., Ye, Z. R., Jiang, J., Chen, F., et al. (2012). Evidence for an s-wave superconducting gap in KxFe2-ySe2 from angle-resolved photoemission. Phys. Rev. B 85, 220504. doi:10.1103/physrevb.85.220504
Xu, Y. J., Sheng, Y. T., and Yang, Y. F. (2019). Quasi-two dimensional fermi surfaces and unitary spin-triplet pairing in the heavy fermion superconductor UTe2. Phys. Rev. Lett. 123, 217002. doi:10.1103/physrevlett.123.217002
Yamashita, T., Takenaka, T., Tokiwa, Y., Wilcox, J. A., Mizukami, Y., Terazawa, D., et al. (2017). Fully gapped superconductivity with no sign change in the prototypical heavyfermion CeCu2Si2. Sci. Adv. 3, e1601667. doi:10.1126/sciadv.1601667
Yoshida, T., Sigrist, M., and Yanase, Y. (2012). Pair-density wave states through spin-orbit coupling in multilayer superconductors. Phys. Rev. B 86, 134514. doi:10.1103/physrevb.86.134514
Yuan, H. Q., Grosche, F. M., Deppe, M., Geibel, C., Sparn, G., and Steglich, F. (2003). Observation of two distinct superconducting phases in CeCu2Si2. Science 302, 2104–2107. doi:10.1126/science.1091648
Zhai, H.-F., Jiao, W. H., Sun, Y. L., Bao, J. K., Jiang, H., Yang, X. J., et al. (2013). Superconductivity, charge- or spin-density wave, and metal–nonmetal transition in BaTi2(Sb1−xBix)2O. Phys. Rev. B 87, 100502. doi:10.1103/physrevb.87.100502
Keywords: heavy fermion, unconventional superconductor, quantum criticality, pairing symmetry, multiple superconducting phases
Citation: Nica EM, Ran S, Jiao L and Si Q (2022) Multiple superconducting phases in heavy-fermion metals. Front. Electron. Mater. 2:944873. doi: 10.3389/femat.2022.944873
Received: 16 May 2022; Accepted: 27 September 2022;
Published: 21 October 2022.
Edited by:
Xingjiang Zhou, Institute of Physics (CAS), ChinaCopyright © 2022 Nica, Ran, Jiao and Si. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Emilian M. Nica, ZW5pY2FAYXN1LmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.