- 1Department of Physics and Astronomy, Northwestern University, Evanston, IL, United States
- 2Center for Applied Physics and Superconducting Technologies, Northwestern University, Evanston, IL, United States
- 3Department of Physics and Astronomy, University of Kentucky, Lexington, KY, United States
- 4Department of Physics, University of Notre Dame, Notre Dame, IN, United States
- 5Large Scale Structures Section, Neutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN, United States
We have used small-angle neutron scattering to determine the vortex lattice phase diagram in the topological superconductor UPt3 for the applied magnetic field along the crystalline c-axis. A triangular vortex lattice is observed throughout the superconducting state, but with an orientation relative to the hexagonal basal plane that changes with field and temperature. At low temperature, in the chiral B phase, the vortex lattice undergoes a non-monotonic rotation with increasing magnetic field. The rotation amplitude decreases with increasing temperature and vanishes before reaching the A phase. Within the A phase an abrupt ±15° vortex lattice rotation was previously reported by Huxley et al., Nature 406, 160-164 (2000). The complex phase diagram may be understood from competing effects of the superconducting order parameter, the symmetry breaking field, and the Fermi surface anisotropy. The low-temperature rotated phase, centered around 0.8 T, reported by Avers et al., Nature Physics 16, 531-535 (2020), can be attributed directly to the symmetry breaking field.
1 Introduction
With three distinct superconducting phases UPt3 has attracted significant attention (Joynt and Taillefer, 2002), but despite decades of experimental and theoretical studies the unconventional superconductivity in this material is still not fully understood. Figure 2B shows the UPt3 phase diagram, indicting the extent of the superconducting A, B and C phases. The presence of two distinct zero-field superconducting transitions suggests that the order parameter belongs to one of the two-dimensional representations of the D6h point group (Hess et al., 1989). Here, f-wave pairing states with the E2u irreducible representation are the most likely (Sauls, 1994). In such a scenario the B phase breaks time reversal and mirror symmetries while the A and C phases are time-reversal symmetric. Experimental support comes from the H-T phase diagram (Shivaram et al., 1986; Adenwalla et al., 1990; Choi and Sauls, 1991; Sauls, 1994), and thermodynamic and transport studies (Taillefer et al., 1997; Graf et al., 2000). Broken time-reversal symmetry in the B phase is supported by phase-sensitive Josephson tunneling (Strand et al., 2009), the observation of polar Kerr rotation (Schemm et al., 2014), and a field history-dependent vortex lattice (VL) configuration (Avers et al., 2020). Finally, the linear temperature dependence of the London penetration depth is consistent with a quadratic dispersion of the energy gap at the polar nodes structure, which is a characteristic of the E2u model (Signore et al., 1995; Schöttl et al., 1999; Gannon et al., 2015).
A key component in the understanding of superconductivity in UPt3 is the presence of a symmetry breaking field (SBF) that couples to the E2u superconducting order parameter (Hayden et al., 1992). The SBF lifts the degeneracy of the multi-dimensional representation, splitting the zero-field transition and leading to the multiple superconducting phases (Sauls, 1994). However, the origin of the SBF is an outstanding issue, with possible candidates that include a quasi-static antiferromagnetic state that develops at 5 K above the superconducting transition (Aeppli et al., 1988a; Aeppli et al., 1988b; Hayden et al., 1992), a distortion of the hexagonal crystal structure (Walko et al., 2001), or prismatic plane stacking faults (Hong, 1999; Gannon et al., 2012).
Vortices provide a highly sensitive probe of the host superconductor. This includes anisotropies in the screening current plane perpendicular to the applied magnetic field which affect the VL symmetry and orientation. Such anisotropies may arise from the Fermi surface (Kogan, 1981; Kogan et al., 1997), and nodes in or distortions of the superconducting gap (Huxley et al., 2000; Avers et al., 2020). As an example one can consider the “simple” superconductor niobium that displays a rich VL phase diagram when the applied field is along the (100) crystalline direction and the Fermi surface anisotropy is incommensurate with an equilateral triangular VL (Laver et al., 2006; Laver et al., 2009; Mühlbauer et al., 2009). Even in materials with a hexagonal crystal structure VL rotations may occur due to competing anisotropies, as observed in MgB2 when the applied field is perpendicular to the basal plane (Cubitt et al., 2003; Das et al., 2012).
We have used small-angle neutron scattering (SANS) to determine the VL phase diagram in UPt3. This extends our previous studies at low temperature, where the VL was found to undergo a field-driven, non-monotonic rotation transition (Avers et al., 2020). We discuss how the VL phase diagram and the existence of the VL rotation transition can be directly attributed to the SBF.
2 Experimental Details
Small-angle neutron scattering studies of the VL are possible due to the periodic field modulation from the vortices (Mühlbauer et al., 2019). The scattered intensity depends strongly on the superconducting penetration depth, and for UPt3 with a large in-plane λab ∼ 680 nm (Gannon et al., 2015) necessitates a large sample volume. For this work we used a high-quality single crystal (ZR11), combined with previously published results obtained on a separate sample (ZR8) (Avers et al., 2020). Properties of both single crystals are listed in Table 1, determined from resistive measurements performed on smaller samples cut from the main crystals. Here, RRR is the residual resistivity ratio, Tc is the superconducting transition temperature and ΔTc is the width of the transition. For the SANS measurements each long, rod-like crystal was cut into two pieces, co-aligned and fixed with silver epoxy (EPOTEK E4110) to a copper cold finger. The sample assembly was mounted onto the mixing chamber of a dilution refrigerator and placed inside a superconducting magnet, oriented with the crystalline a axis vertical and the c axis horizontally along the magnetic field and the neutron beam. The neutron beam was masked off to illuminate a 7 × 11 mm2 area.
The SANS experiment was performed at the GP-SANS beam line at the High Flux Isotope Reactor at Oak Ridge National Laboratory (Heller et al., 2018). All measurements were carried out in a “rocked on” configuration, satisfying the Bragg condition for VL peaks at the top of the two-dimensional position sensitive detector, as seen in Figure 1. Background measurements, obtained either in zero field or above Hc2, were subtracted from both the field reduction and field reversal data.
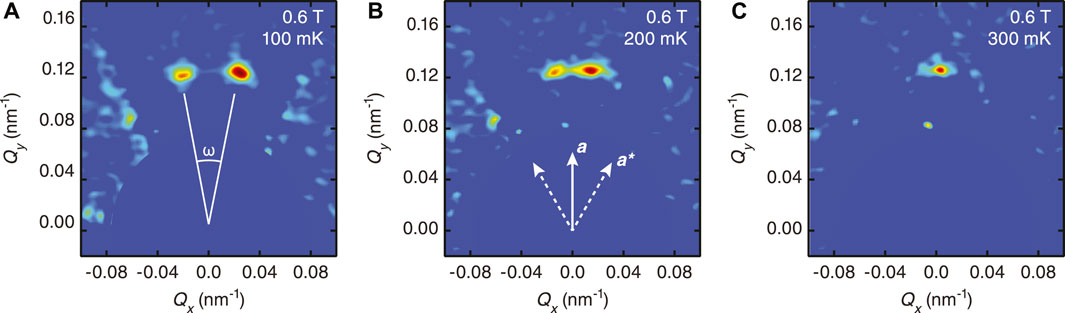
FIGURE 1. SANS VL diffraction patterns obtained at H = 0.6 T and T = 100 mK (A), 200 mK (B) and 300 mK (C). The Bragg peak splitting (ω) is indicated in (A) and crystallographic directions within the scattering plane in (B). Only peaks at the top of the detector were imaged. Zero field background scattering is subtracted, and the detector center near Q = 0 is masked off.
Measurements were performed at temperatures between 100 and 300 mK and fields between 0.4 and 1.2 T. Prior to the SANS measurements the field was reduced from above the B-C phase transition at base temperature. The sample was then heated to the measurement temperature and a damped field oscillation with an initial amplitude of 20 mT was applied to obtain a well ordered VL with a homogeneous vortex density (Avers et al., 2020). Furthermore, a 5 mT field oscillation was applied approximately every 60 s during the SANS measurements, in order to counteract VL disordering due to neutron induced fission of 235U (Avers et al., 2021).
3 Results
Figure 1 shows VL diffraction patterns obtained in an applied field of 0.6 T and temperature between 100 and 300 mK. As previously reported, the VL in UPt3 has a triangular symmetry but is in general not oriented along a high symmetry direction of the hexagonal crystalline basal lattice (a or a*) (Avers et al., 2020). This causes the VL to break up into clockwise and counterclockwise rotated domains, and gives rise to the Bragg peak splitting in Figures 1A,B. With increasing temperature the splitting decreases, and the two peaks eventually merge as seen in Figure 1C.
To quantify the VL rotation we define the peak splitting angle (ω) shown in Figure 1A, determined from two-Gaussian fits to the diffraction pattern intensity. Specific details of the fitting will be discussed in more detail later. The temperature dependence of ω is summarized in Figure 2A for all the magnetic fields measured, together with results from our previous SANS studies obtained at base temperature (Avers et al., 2020).
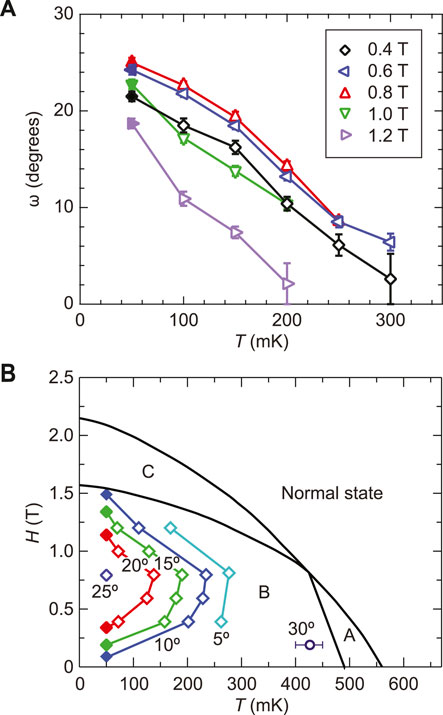
FIGURE 2. Vortex lattice rotation. (A) VL peak splitting vs. temperature for different magnetic fields. The data at 50 mK (solid symbols) was previously obtained on the ZR8 crystal (Avers et al., 2020). Error bars represent one standard deviation. (B) Constant ω contours superimposed on the UPt3 phase diagram. Values are obtained from the data in (A) by interpolation (open diamonds) and from the 50 mK field dependence in Ref. 11 (solid diamonds). The 30° data point (open circle) is from previous work by (Huxley et al., 2000).
At all fields the temperature dependence of ω appears to be linear within the measurement error, and extrapolate to zero well below the A-B phase transition. The larger error bars at higher temperature is due to an increasing penetration depth and the resulting decrease in the scattered intensity (Gannon et al., 2015). Figure 2B shows ω equicontours superimposed on the UPt3 H-T phase diagram. The nonmonotonic behavior, previously reported at base temperature (Avers et al., 2020), is clearly observed at higher temperatures, although with a decreasing amplitude. Furthermore, the splitting extrapolates to zero in the zero field limit, and also decreases upon approaching the B-C phase transition. However, once in the C phase the splitting remains at a fixed value of
Ensuring a reliable determination of ω requires a careful approach to the fitting. At all fields and temperatures the radial position (QR) as well as the radial (ΔQR) and azimuthal (Δθ) widths were constrained to be the same for both of the split peaks. Furthermore, the azimuthal width at each field was determined from fits at low temperature where the peaks are clearly separated, and then kept fixed at the higher temperature where they begin to overlap. To justify this approach, we note that when the peaks are clearly separated, Δθ does not exhibit any systematic temperature dependence. The azimuthal width does show a field dependence, however, with Δθ decreasing from
The VL density is reflected in QR and ΔQR, shown in Figure 3. The magnitude of the scattering vector in Figure 3A agrees to within a few percent with
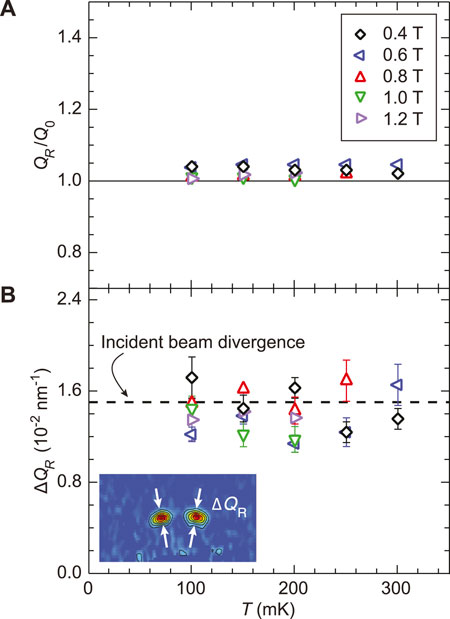
FIGURE 3. Vortex lattice density. (A) Scattering vector magnitude normalized to the value expected for a triangular VL. (B) Radial width of the VL Bragg peaks (FWHM) compared to the incident beam divergence (dashed line). The inset indicates ΔQR within the detector plane.
4 Discussion
The complex VL phase diagram in Figure 2B reflects the presence of multiple competing effects. In the following we discuss how, at the qualitative level, this phase diagram arises from the interplay between the SBF and the nodal configuration of the superconducting energy gap for the A and C phases. A more detailed treatment of the VL structure and orientation within the A phase was provided by Champel and Mineev (Champel and Mineev, 2001). First, however, we note that ω → 0 in the limit T = H = 0. For large vortex separations the order parameter has a vanishing effect on the VL, and the orientation with Bragg peaks along the a axis must be due to the Fermi surface anisotropy (Huxley et al., 2000; Champel and Mineev, 2001).
In momentum space the two-component E2u order parameter proposed for UPt3 is given by (Sauls, 1994)
Here, η1 and η2 are real amplitudes which depend on temperature and magnetic field and ϵ is due to the SBF. The A and C phases correspond to a vanishing of η2 and η1 respectively. The magnitude of the SBF determines the zero-field split in the superconducting transition (ΔTAB) and thus the width of the A phase. Experimentally, ΔTAB ≈ 55 mK which yields
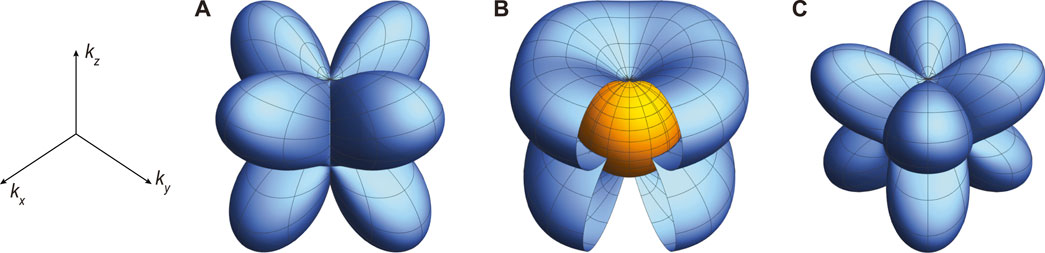
FIGURE 4. Order parameter in the (A) A phase (η1 ≠ 0, η2 = 0), (B) B phase distorted by the SBF (η1 = η2 = 1, ϵ = 0.1), and (C) C phase (η1 = 0, η2 ≠ 0).
Within the A phase SANS studies by Huxley et al. found a VL with domains rotated by ± 15° relative to the a axis (ω = 30°) (Huxley et al., 2000). The VL rotation was attributed to a competition between the sixfold Fermi surface anisotropy and the fourfold anisotropy of the nodal structure in the A phase (Huxley et al., 2000; Champel and Mineev, 2001). Notably, the rotation persists into the B phase as indicated in Figure 2B. This is not surprising since the η1/η2 → ∞ upon approaching the A phase from low temperature, where the B phase order parameter therefore exhibit a substantial fourfold anisotropy. However, as η2 increases with decreasing temperature this ratio quickly decreases, causing an abrupt transition to ω = 0 around 425 mK (Huxley et al., 2000).
Due to the SBF the order parameter in the B phase preserves a degree of fourfold anisotropy, as shown in Figure 4. This anisotropy is oriented in a manner similar to the A phase, with an effect on the vortex-vortex interactions which will increase with increasing field (vortex density). The influence of the SBF anisotropy will increase further at low temperature as the superfluid density increases (Gannon et al., 2015), even if ϵ remains fixed. This explains the initial increase of ω with field at low temperatures, with an amplitude (0.8 T) that extrapolates to a value close to 30° for T → 0.
As the field is increased further and approaches the BC phase transition, η1 decreases and finally vanish. The C phase order parameter is rotated by 45° about kz with respect to the B phase, as shown in Figure 4. This will favor a VL oriented along the a axis, i.e., the same as the Fermi surface anisotropy, and explains the non-monotonic VL rotation as a function of field. Once η1 has fully vanished no further VL rotation is expected, in agreement with the observed field-independence of ω ≈ 8° in the C phase (Avers et al., 2020).
5 Conclusion
In summary, the rotated VL phase at low temperatures and intermediate fields in Figure 2B can be directly attributed to the SBF. To our knowledge this is the first observation of such an effect at the microscopic level, and may provide further constraints on the nature of both the SBF and the order parameter in UPt3. A quantitative understanding of ω(T, H) will require a detailed theoretical analysis, taking into account the field and temperature dependence of the superfluid density as well as the complex Fermi surface of UPt3. Here, the finite value of ω in the C phase is somewhat surprising and not obviously consistent with the order parameter in Eq. 1.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
KA, WH, and ME conceived of the experiment. WG and KA grew and annealed the crystals. KA, AL, and ME performed the SANS experiments with assistance from LD-S. KA, WH, and ME wrote the paper with input from all authors.
Funding
This work was supported by the Northwestern-Fermilab Center for Applied Physics and Superconducting Technologies (KA) and by the U.S. Department of Energy, Office of Basic Energy Sciences, under Awards No. DE-SC0005051 (ME: University of Notre Dame; neutron scattering) and DE-FG02-05ER46248 (WH: Northwestern University; crystal growth and neutron scattering). A portion of this research used resources at the High Flux Isotope Reactor, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We are grateful to J. A. Sauls for numerous discussions and to V. P. Mineev for valuable feed-back.
References
Adenwalla, S., Lin, S. W., Ran, Q. Z., Zhao, Z., Ketterson, J. B., Sauls, J. A., et al. (1990). Phase Diagram ofUPt3from Ultrasonic Velocity Measurements. Phys. Rev. Lett. 65, 2298–2301. doi:10.1103/physrevlett.65.2298
Aeppli, G., Bucher, E., Broholm, C., Kjems, J. K., Baumann, J., and Hufnagl, J. (1988). Magnetic Order and Fluctuations in superconductingUPt3. Phys. Rev. Lett. 60, 615–618. doi:10.1103/physrevlett.60.615
Aeppli, G., Bucher, E., Goldman, A. I., Shirane, G., Broholm, C., and Kjems, J. K. (1988). Magnetic Correlations in UPt3 and U1−xThxPt3. J. Magnetism Magn. Mater. 76-77, 385–390. doi:10.1016/0304-8853(88)90430-1
Avers, K. E., Gannon, W. J., Kuhn, S. J., Halperin, W. P., Sauls, J. A., DeBeer-Schmitt, L., et al. (2020). Broken Time-Reversal Symmetry in the Topological Superconductor UPt3. Nat. Phys. 16, 531–535. doi:10.1038/s41567-020-0822-z
Avers, K. E., Kuhn, S. J., Leishman, A. W. D., Gannon, W. J., DeBeer-Schmitt, L., Dewhurst, C. D., et al. (2021). Reversible Ordering and Disordering of the Vortex Lattice in UPt3. arXiv:2103.09843.
Champel, T., and Mineev, V. P. (2001). Theory of Equilibrium Flux Lattice inUPt3under Magnetic Field Parallel to Hexagonal Crystal Axis. Phys. Rev. Lett. 86, 4903–4906. doi:10.1103/physrevlett.86.4903
Choi, C., and Sauls, J. (1991). Identification of Odd-Parity Superconductivity in UPt_{3} from Paramagnetic Effects on the Upper Critical Field. Phys. Rev. Lett. 66, 484–487. doi:10.1103/physrevlett.66.484
Cubitt, R., Eskildsen, M. R., Dewhurst, C. D., Jun, J., Kazakov, S. M., and Karpinski, J. (2003). Effects of Two-Band Superconductivity on the Flux-Line Lattice in Magnesium Diboride. Phys. Rev. Lett. 91, 047002. doi:10.1103/physrevlett.91.047002
Das, P., Rastovski, C., O’Brien, T. R., Schlesinger, K. J., Dewhurst, C. D., DeBeer-Schmitt, L., et al. (2012). Observation of Well-Ordered Metastable Vortex Lattice Phases in SuperconductingMgB2Using Small-Angle Neutron Scattering. Phys. Rev. Lett. 108, 167001. doi:10.1103/physrevlett.108.167001
Gannon, W. J., Halperin, W. P., Rastovski, C., Eskildsen, M. R., Dai, P., and Stunault, A. (2012). Magnetization in the Superconducting State of UPt3from Polarized Neutron Diffraction. Phys. Rev. B 86, 104510. doi:10.1103/physrevb.86.104510
Gannon, W. J., Halperin, W. P., Rastovski, C., Schlesinger, K. J., Hlevyack, J., Eskildsen, M. R., et al. (2015). Nodal gap Structure and Order Parameter Symmetry of the Unconventional Superconductor UPt3. New J. Phys. 17, 023041. doi:10.1088/1367-2630/17/2/023041
Graf, M. J., Yip, S.-K., and Sauls, J. A. (2000). Identification of the Orbital Pairing Symmetry inUPt3. Phys. Rev. B 62, 14393–14402. doi:10.1103/physrevb.62.14393
Hayden, S. M., Taillefer, L., Vettier, C., and Flouquet, J. (1992). Antiferromagnetic Order inUPt3under Pressure: Evidence for a Direct Coupling to Superconductivity. Phys. Rev. B 46, 8675–8678. doi:10.1103/physrevb.46.8675
Heller, W. T., Cuneo, M., Debeer-Schmitt, L., Do, C., He, L., Heroux, L., et al. (2018). The Suite of Small-Angle Neutron Scattering Instruments at Oak Ridge National Laboratory. J. Appl. Cryst. 51, 242–248. doi:10.1107/s1600576718001231
Hess, D. W., Tokuyasu, T. A., and Sauls, J. A. (1989). Broken Symmetry in an Unconventional Superconductor: a Model for the Double Transition in UPt3. J. Phys. Condens. Matter 1, 8135–8145. doi:10.1088/0953-8984/1/43/014
Hong, J.-I. (1999). Strucure-Property Relationships for a Heavy Fermion Superconductor UPt3. Evanston, IL: Northwestern University. PhD.
Huxley, A., Rodière, P., Paul, D. M., van Dijk, N., Cubitt, R., and Flouquet, J. (2000). Realignment of the Flux-Line Lattice by a Change in the Symmetry of Superconductivity in UPt3. Nature 406, 160–164. doi:10.1038/35018020
Joynt, R., and Taillefer, L. (2002). The Superconducting Phases ofUPt3. Rev. Mod. Phys. 74, 235–294. doi:10.1103/revmodphys.74.235
Kogan, V. G., Bullock, M., Harmon, B., Miranovic-acute, P., Dobrosavljevic-acute-Grujic-acute, L., Gammel, P. L., et al. (1997). Vortex Lattice Transitions in Borocarbides. Phys. Rev. B 55, R8693–R8696. doi:10.1103/physrevb.55.r8693
Kogan, V. G. (1981). London Approach to Anisotropic Type-II Superconductors. Phys. Rev. B 24, 1572–1575. doi:10.1103/physrevb.24.1572
Laver, M., Bowell, C. J., Forgan, E. M., Abrahamsen, A. B., Fort, D., Dewhurst, C. D., et al. (2009). Structure and Degeneracy of Vortex Lattice Domains in Pure Superconducting Niobium: A Small-Angle Neutron Scattering Study. Phys. Rev. B 79, 014518. doi:10.1103/physrevb.79.014518
Laver, M., Forgan, E. M., Brown, S. P., Charalambous, D., Fort, D., Bowell, C., et al. (2006). Spontaneous Symmetry-Breaking Vortex Lattice Transitions in Pure Niobium. Phys. Rev. Lett. 96, 167002. doi:10.1103/physrevlett.96.167002
Mühlbauer, S., Honecker, D., Périgo, E. A., Bergner, F., Disch, S., Heinemann, A., et al. (2019). Magnetic Small-Angle Neutron Scattering. Rev. Mod. Phys. 91, 015004. doi:10.1103/revmodphys.91.015004
Mühlbauer, S., Pfleiderer, C., Böni, P., Laver, M., Forgan, E. M., Fort, D., et al. (2009). Morphology of the Superconducting Vortex Lattice in Ultrapure Niobium. Phys. Rev. Lett. 102, 136408. doi:10.1103/physrevlett.102.136408
Sauls, J. A. (1994). The Order Parameter for the Superconducting Phases of UPt3. Adv. Phys. 43, 113–141. doi:10.1080/00018739400101475
Schemm, E. R., Gannon, W. J., Wishne, C. M., Halperin, W. P., and Kapitulnik, A. (2014). Observation of Broken Time-Reversal Symmetry in the Heavy-Fermion Superconductor UPt 3. Science 345, 190–193. doi:10.1126/science.1248552
Schöttl, S., Schuberth, E. A., Flachbart, K., Kycia, J. B., Hong, J. I., Seidman, D. N., et al. (1999). Anisotropic Dc Magnetization of SuperconductingUPt3and Antiferromagnetic Ordering below 20 mK. Phys. Rev. Lett. 82, 2378–2381. doi:10.1103/physrevlett.82.2378
Shivaram, B. S., Rosenbaum, T. F., and Hinks, D. G. (1986). Unusual Angular and Temperature Dependence of the Upper Critical Field in UPt3. Phys. Rev. Lett. 57, 1259–1262. doi:10.1103/physrevlett.57.1259
Signore, P. J. C., Andraka, B., Meisel, M. W., Brown, S. E., Fisk, Z., Giorgi, A. L., et al. (1995). Inductive Measurements ofUPt3in the Superconducting State. Phys. Rev. B 52, 4446–4461. doi:10.1103/physrevb.52.4446
Strand, J. D., Van Harlingen, D. J., Kycia, J. B., and Halperin, W. P. (2009). Evidence for Complex Superconducting Order Parameter Symmetry in the Low-Temperature Phase ofUPt3from Josephson Interferometry. Phys. Rev. Lett. 103, 197002. doi:10.1103/physrevlett.103.197002
Taillefer, L., Ellman, B., Lussier, B., and Poirier, M. (1997). On the gap Structure of UPt3: Phases A and B. Physica B: Condensed Matter 230-232, 327–331. doi:10.1016/s0921-4526(96)00706-5
Keywords: vortex lattice (superconductors), heavy fermion supercoductor, topological superconductor, UPt3, small-angle neutron scattering
Citation: Avers KE, Gannon WJ, Leishman AWD, DeBeer-Schmitt L, Halperin WP and Eskildsen MR (2022) Effects of the Order Parameter Anisotropy on the Vortex Lattice in UPt3. Front. Electron. Mater. 2:878308. doi: 10.3389/femat.2022.878308
Received: 17 February 2022; Accepted: 08 March 2022;
Published: 07 April 2022.
Edited by:
Jeffrey W. Lynn, National Institute of Standards and Technology (NIST), United StatesReviewed by:
Robert James Joynt, University of Wisconsin-Madison, United StatesDong Qian, Shanghai Jiao Tong University, China
Copyright © 2022 Avers, Gannon, Leishman, DeBeer-Schmitt, Halperin and Eskildsen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: M. R. Eskildsen, ZXNraWxkc2VuQG5kLmVkdQ==
†Present address: K. E. Avers, Department of Physics, University of Maryland, College Park, MD, United States
 K. E. Avers
K. E. Avers W. J. Gannon
W. J. Gannon A. W. D. Leishman4
A. W. D. Leishman4 L. DeBeer-Schmitt
L. DeBeer-Schmitt W. P. Halperin
W. P. Halperin M. R. Eskildsen
M. R. Eskildsen