
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Electron. , 15 January 2024
Sec. Integrated Circuits and VLSI
Volume 4 - 2023 | https://doi.org/10.3389/felec.2023.1331280
 Fabia Farlin Athena1
Fabia Farlin Athena1 Omobayode Fagbohungbe1
Omobayode Fagbohungbe1 Nanbo Gong1
Nanbo Gong1 Malte J. Rasch1
Malte J. Rasch1 Jimmy Penaloza1
Jimmy Penaloza1 SoonCheon Seo2
SoonCheon Seo2 Arthur Gasasira2
Arthur Gasasira2 Paul Solomon1
Paul Solomon1 Valeria Bragaglia3
Valeria Bragaglia3 Steven Consiglio4
Steven Consiglio4 Hisashi Higuchi4
Hisashi Higuchi4 Chanro Park2
Chanro Park2 Kevin Brew2
Kevin Brew2 Paul Jamison2
Paul Jamison2 Christopher Catano4
Christopher Catano4 Iqbal Saraf2
Iqbal Saraf2 Claire Silvestre2
Claire Silvestre2 Xuefeng Liu2
Xuefeng Liu2 Babar Khan1
Babar Khan1 Nikhil Jain2
Nikhil Jain2 Steven McDermott2
Steven McDermott2 Rick Johnson2
Rick Johnson2 I. Estrada-Raygoza2
I. Estrada-Raygoza2 Juntao Li2
Juntao Li2 Tayfun Gokmen1
Tayfun Gokmen1 Ning Li1
Ning Li1 Ruturaj Pujari2
Ruturaj Pujari2 Fabio Carta1
Fabio Carta1 Hiroyuki Miyazoe1
Hiroyuki Miyazoe1 Martin M. Frank1
Martin M. Frank1 Antonio La Porta3
Antonio La Porta3 Devi Koty4
Devi Koty4 Qingyun Yang4
Qingyun Yang4 Robert D. Clark4
Robert D. Clark4 Kandabara Tapily4
Kandabara Tapily4 Cory Wajda4
Cory Wajda4 Aelan Mosden4
Aelan Mosden4 Jeff Shearer4
Jeff Shearer4 Andrew Metz4
Andrew Metz4 Sean Teehan2
Sean Teehan2 Nicole Saulnier2
Nicole Saulnier2 Bert Offrein3
Bert Offrein3 Takaaki Tsunomura5
Takaaki Tsunomura5 Gert Leusink4
Gert Leusink4 Vijay Narayanan1
Vijay Narayanan1 Takashi Ando1*
Takashi Ando1*Analog memory presents a promising solution in the face of the growing demand for energy-efficient artificial intelligence (AI) at the edge. In this study, we demonstrate efficient deep neural network transfer learning utilizing hardware and algorithm co-optimization in an analog resistive random-access memory (ReRAM) array. For the first time, we illustrate that in open-loop deep neural network (DNN) transfer learning for image classification tasks, convergence rates can be accelerated by approximately 3.5 times through the utilization of co-optimized analog ReRAM hardware and the hardware-aware Tiki-Taka v2 (TTv2) algorithm. A simulation based on statistical 14 nm CMOS ReRAM array data provides insights into the performance of transfer learning on larger network workloads, exhibiting notable improvement over conventional training with random initialization. This study shows that analog DNN transfer learning using an optimized ReRAM array can achieve faster convergence with a smaller dataset compared to training from scratch, thus augmenting AI capability at the edge.
In recent years, Artificial Intelligence (AI) has surged to the forefront of the digital era. Its transformative potential has enabled it to permeate into an extensive array of applications, spanning various sectors and industries. AI’s breadth of influence encompasses everything from executing complex predictive analyses in critical sectors such as finance (Gogas and Papadimitriou, 2021; Goodell et al., 2021) and healthcare (Yu et al., 2018; Chen et al., 2019; Zhang et al., 2022) to autonomous driving systems (Arnold et al., 2019; Caesar et al., 2020). Among its myriad applications, one of AI’s most reliable usages resides in the sphere of pattern recognition. Here, it has exhibited an ability to decipher and illuminate the hidden structures that lie encrypted within vast and often convoluted landscapes of data.
Nevertheless, this rapid acceleration in the advancement and adoption of AI, particularly that of Deep Neural Networks (DNNs), has revealed a critical limitation of current computing architecture known as the von Neumann bottleneck. The von Neumann architecture that underpins most contemporary computing systems is hindered by a considerable limitation arising from its foundational structure—the physical segregation of its computational and memory units. This division necessitates continuous data transfers between the units, culminating in significantly increased power consumption and extended processing times, particularly as the data requirements for DNNs keep rising. This escalating energy demand presents a formidable challenge within the confines of our current technological capabilities and becomes ever more pressing as we consider the near future. With AI’s insatiable appetite for larger, more sophisticated DNNs (Liang et al., 2022) in a world that is becoming increasingly mindful of the importance of energy conservation and environmental sustainability, the need to devise an effective solution has never been more urgent (Schwartz et al., 2020; Wu et al., 2022).
Recently, there has been growing interest in the emerging field of analog AI, which poses a potential solution to this challenge. Analog AI, a novel concept in computing, is characterized by the integration of computation and memory units (Amirsoleimani et al., 2020; Ielmini and Pedretti, 2020; Frenkel et al., 2023). This integration aims to circumvent the von Neumann bottleneck and optimize the efficiency of computational processes. By merging these two fundamental units, analog AI presents an opportunity to revolutionize the existing computing paradigm, promising to significantly reduce the power requirements of data processing in contemporary AI applications (Burr et al., 2021; Jain et al., 2022; Seo et al., 2022). In this study, we explore transfer learning–a subset of deep learning–and its application in analog AI. We demonstrate how transfer learning can be effectively applied on analog AI hardware to accelerate computing efficiently at the edge. Our simulations further indicate that this approach can be scaled to accommodate larger networks and datasets.
Building on the discussion of analog AI, we explore the potential of transfer learning. Transfer learning aims to improve AI system efficiency by applying insights from one task to a related one, as described by Pan and Yang (2010). The core idea is to leverage already gained insights to accelerate the learning process for a new, yet related, task without starting from scratch. Historically, traditional transfer learning processes have been dominated by digital implementations, often referred to as digital transfer learning (Pan and Yang, 2010; Mormont et al., 2018). While this approach has its benefits, its inherent energy intensity calls for exploring more energy-efficient alternatives. The standard digital transfer learning procedure, depicted in Figure 1A, begins with digital pre-training. This initial stage is followed by weight transfer to adapt the model for a new task, which culminates in digital fine-tuning for optimal adjustment to this task. Another option is a hybrid system, illustrated in Figure 1B. This model retains the digital platform for the pre-training stage but shifts to a combined digital-analog environment for the crucial fine-tuning phase. It is noteworthy that the integration of analog phase-change non-volatile memory (NVM) for weight updates, coupled with digital 3T1C for gradient accumulation, can deliver accuracy equivalent to software.
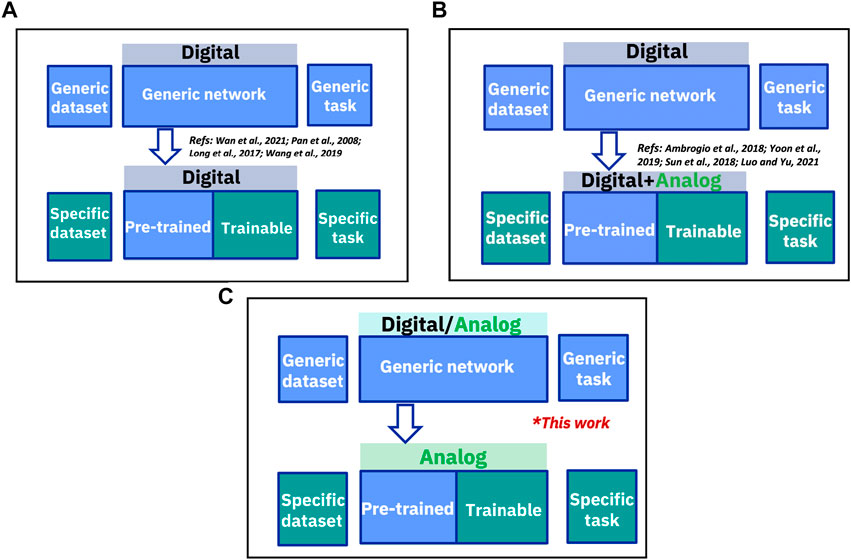
FIGURE 1. (A) A fully digital system involves stages of digital pre-training, weight transfer for a new task, and digital fine-tuning on that task (Pan et al., 2008; Long et al., 2017; Wang et al., 2019; Wan et al., 2021). (B) A hybrid system includes digital pre-training, followed by fine-tuning in a combined digital-analog environment (Ambrogio et al., 2018; Sun et al., 2018; Yoon et al., 2019; Luo and Yu, 2021). (C) Analog transfer learning can utilize either digital or analog pre-training, but the weights are ultimately transferred to analog hardware for training. Key functions such as gradient accumulation and MAC operation are performed on analog NVM.
Implementations for image classification tasks (Ambrogio et al., 2018). Nonetheless, edge computing applications pose unique challenges for digital computation due to the strict power constraints locally and the accompanying security and privacy risks related to cloud data transfer (Rafique et al., 2020). Given these constraints, an analog system, specifically implemented using NVMs, offers an attractive solution for edge computing.
In this work, we introduce a novel approach that integrates analog devices with in-memory fine-tuning methods and an optimized in-memory training algorithm to augment the efficiency of transfer learning processes in analog AI hardware platforms. Our approach harnesses the capabilities of analog resistive random-access memory (ReRAM) hardware and aligns them with an appropriate algorithm for efficient deep learning focusing on analog transfer learning, shown in Figure 1C. As highlighted in the figure, analog transfer learning can be initiated with either digital or analog pre-training. For digital pre-training, we utilize hardware-aware pre-training in software to enhance noise robustness prior to the transfer and fine-tuning stage. For analog pre-training, pre-training is performed in the analog hardware thus, weights would already reside in the analog devices. Consequently, the fine-tuning process would occur on the same devices, eliminating the need for the additional programming/transfer step required for digital pre-training. Both gradient accumulation and the Multiply-Accumulate (MAC) operation–each an integral component of the learning process–are executed on the analog hardware during the fine-tuning stage for both digital and analog pre-training, ensuring the energy efficiency benefits associated with analog AI. To substantiate our proposed model and demonstrate that it scales to more complex tasks, we carried out a series of simulations on the statistical ReRAM array data (2k devices) built on a 14 nm CMOS. We executed these simulations using an adapted version of the AIHWKIT simulator (Rasch et al., 2021), aimed at emulating a larger network capable of handling MNIST (LeCun et al., 2010) and CIFAR-100 (Krizhevsky and Hinton, 2009) image recognition tasks. These simulation-based experiments establish a solid foundation for realizing the potential of our proposed analog transfer learning system in practical resource-limited edge computing scenarios.
The foundation of our approach is built on an optimized HfOx-based ReRAM stack. This technology is integrated with 14 nm Complementary Metal-Oxide-Semiconductor (CMOS) technology, providing a robust hardware platform conducive to our analog transfer learning methodology. ReRAM was chosen and paired with CMOS technology because of its many attractive characteristics such as non-volatility, energy efficiency, high density, and ability to scale. These attributes make it a perfect fit for analog AI applications. A more detailed insight into the device structure and its fabrication process can be found in our prior work (Gong et al., 2022).
The goal of the hardware demonstration is to carry out a reduced MNIST digit classification task on analog AI hardware using transferred weights (Gong et al., 2022; Athena et al., 2023). To fit the experimental setup, only images of 0 and 1 from the MNIST dataset were utilized. These images were converted from 784 input dimensions down to 16 using random projection (Dasgupta, 2000; Bingham and Mannila, 2001), and the first 8 dimensions from the 16 were selected. The resulting dataset was used for pre-training. The TTv2 training algorithm (Gokmen and Haensch, 2020; Gokmen, 2021b; Lee et al., 2021; Kim et al., 2022) used for fine-tuning, uses two matrices: A for gradient accumulation and C for weight storage. Matrix A calculates the gradient by working around a symmetry point, while Matrix C updates based on the accumulated gradients from Matrix A (Gokmen and Haensch, 2020; Gokmen, 2021b). During training, Matrix A is updated using identical pulses, which are determined by the errors found using Matrix C and each training image. Matrix C only gets updated after Matrix A has been updated using 10 images since C’s last update. Details of this implementation are available in Gong et al. (2022); Athena et al. (2023).
Pre-training, the first step in transfer learning, can be performed digitally using either hardware-aware (HWA) algorithms or non-HWA algorithms. For HWA pre-training, there are approaches like the SoftBounds model soft-bounds model (Fusi and Abbott, 2007; Frascaroli et al., 2018; Rasch et al., 2023) or noise injection to the weights. In our study, we used the SoftBounds soft-bounds device model to simulate ReRAM devices during pre-training. On the other hand, non-HWA uses regular floating point weights. After digital pre-training, these digital weights are transferred to an analog hardware array and this transfer can cause programming errors. To reduce the effects of these errors and make the subsequent learning process more efficient, we utilized the TTv2 algorithm (Gokmen, 2021a; Kim et al., 2022) during the fine-tuning phase, as shown in Figure 2. An 8 × 4 array is used to store the two matrices A and C used by the hardware-aware algorithm TikiTaka V2. Matrix C holds the weight of the neural network. Each of these matrices is 8 × 2.
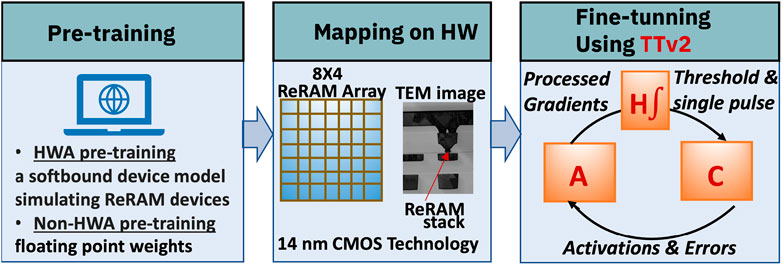
FIGURE 2. Digital pre-training is done in either HWA or non-HWA approach. Pre-trained weights are then mapped on ReRAM hardware. After mapping the pre-trained weights on the hardware, TTv2 (Gokmen, 2021a; Kim et al., 2022) algorithm is used to perform the fine-tuning. Matrix A is used for gradient accumulation, Matrix C stores the weights, and H is an integrator used to aggregate the effects of Matrix A before passing it onto Matrix C in the form of a single pulse.
We found that transferring weights originating from non-HWA training, also known as floating-point training, is not advantageous, as shown in Figure 3. The training set contained 10,000 images and the test set consisted of 1,000 images. In our experimental setup, we calculated the accuracy of the test set after training on 500 images. Each training epoch corresponds to the entire training set of 10,000 images. In this scenario, the convergence rate of floating-point transfer learning is similar to training a model initialized with random weights. However, utilizing HWA pre-trained weights improves the model’s learning significantly. The convergence speed increases about threefold compared to training from scratch with randomly initialized weights, as shown in Figure 4. This highlights the importance of appropriate weight initializations for faster learning, thus reinforcing the effectiveness of our transfer learning approach.
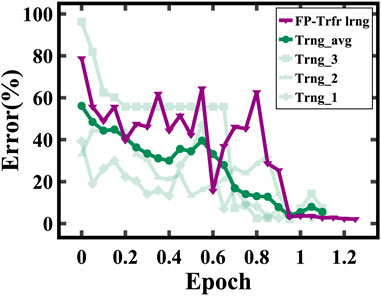
FIGURE 3. Digital pre-training using the non-HWA algorithm followed by fine-tuning on analog hardware (FP-Trfr lrng) does not show any benefit compared to training from scratch (Trng).
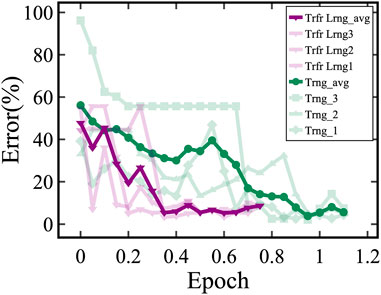
FIGURE 4. Digital pre-training using the HWA algorithm followed by fine-tuning on analog hardware shows∼ 3× faster convergence over the training from scratch (Trng). Here, light-green and light-purple traces correspond to several experiments on training and transfer learning, respectively.
In our pursuit of implementing fully analog transfer learning, we shifted to in-memory pre-training (Figure 5). The first phase of this method involved pre-training on the same analog hardware that was later used for fine-tuning. This pre-training phase was dedicated to a specific task, referred to as Task 1. Once this pre-training was completed, we transitioned into the fine-tuning stage that was aimed at a distinct, second task–Task 2. This methodology mirrors typical digital transfer learning, where insights from one task benefit another.
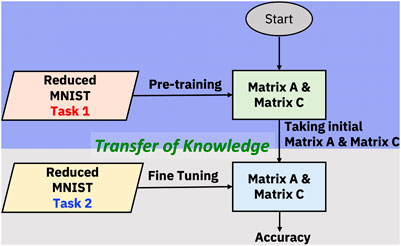
FIGURE 5. Flow diagram for transfer learning with in-memory pre-training where Task 1 is different from Task 2.
As mentioned earlier, we used images from the reduced MNIST dataset, compressed to 16 elements. Half of these elements, precisely 8, were used in the pre-training phase, allowing the model to focus on specific features and characteristics during Task 1. After the pre-training stage, we proceeded to the fine-tuning phase, but instead of using the same elements, we employed a different part of the image for Task 2.
The variability introduced by selecting a different segment is represented by N, indicating the degree of randomness—specifically, the number of image elements in Task 2 that differ from Task 1. Our aim in altering elements during the fine-tuning phase was to emulate the shifts in datasets and tasks typically observed in transfer learning. Figure 6 provides a visual distinction between the image portions used during the pre-training and fine-tuning phases. As the degree of randomness (N) increases, there is a discernible reduction in knowledge transfer. This leads to an initial decrease in test accuracy before fine-tuning. The inverse relationship between test accuracy and the degree of randomness highlights our model’s sensitivity to alterations in input, especially when compared to the initial training data, as shown in Figure 7.
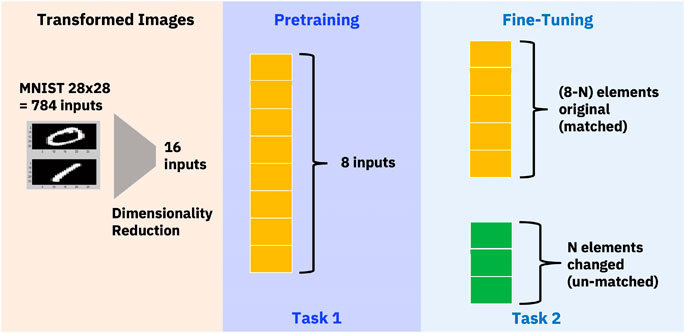
FIGURE 6. Dimensionality Reduction to reduce images to 16 dimensions. Pre-training on analog hardware on Task 1 using 8 elements. Fine tuning on task 2 with N different elements from Task 1.
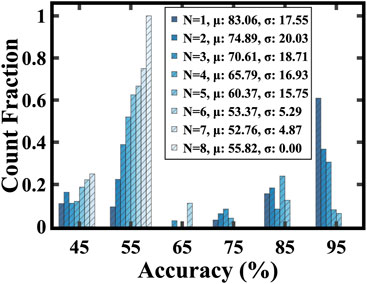
FIGURE 7. Initial test accuracy decreases with the increase of the degree of randomness (N value). µ represents the mean and σ represents the standard deviation.
To delve deeper into the effects of transfer learning, we conducted a hardware demonstration with the degree of randomness, N, fixed at 3. In the pre-training phase for Task 1, the model achieved an accuracy of approximately 94%, as depicted in Figure 8A. However, when transitioning to Task 2, which incorporated a change of 3 elements, the model’s accuracy dropped to approximately 70% before fine-tuning, as shown in Figure 8B.
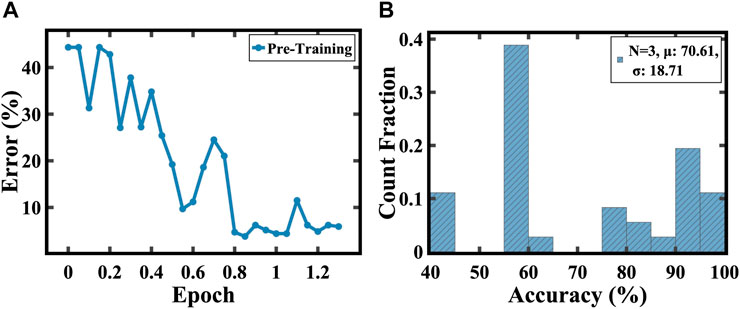
FIGURE 8. (A) Analog pre-training showing ∼ 94% test accuracy on task 1. (B) Statistical distribution of accuracy across all permutations for N = 3. Average accuracy in the initial test drops by ∼ 24% for N = 3. µ represents the mean and σ represents the standard deviation.
Next, we proceeded to train the network on Task 2, following its pre-training on Task 1. This resulted in a significant improvement in the speed of convergence. Specifically, the model achieved a 94% accuracy. Furthermore, it converged ∼ 3.5 times faster compared to training the model from scratch with random weight initialization. Moreover, with further training, the accuracy score reached a peak of 98%, as depicted in Figure 9. Our hardware-based experiment illustrates the efficacy of HWA pre-training, coupled with fine-tuning via the TTv2 algorithm. Together, these processes contribute to a significant improvement in.
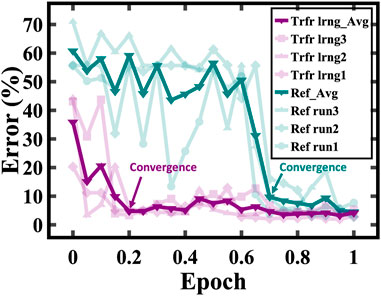
FIGURE 9. Transfer learning (Trfr lrng, purple traces) with analog pre-training reaching an accuracy of 98% shows 3.5 × faster convergence compared to training from scratch (Ref, green traces).
The convergence speed as well as the final accuracy. Despite the inherent challenges posed by variations imposed by a hardware implementation, the fully analog transfer learning framework emerges as a potent tool. Thus, it presents a promising pathway toward more efficient training of neural networks.
Building on the effective hardware demonstration of transfer learning, it is vital to determine if the method can be scaled to accommodate larger neural networks and datasets. We conducted a simulation study using a three-layer fully connected neural network on the full MNIST dataset. To mimic the hardware-based transfer learning framework, we modified the dataset by interchanging pixels in specified rows, so that it retains its overarching characteristics. The details of our simulation framework are provided in Table 1.
The pre-trained weights used to initialize the transfer learning model are the weights obtained by training the equivalent digital model using the original MNIST dataset. In all the Figures, training starts at epoch 3 and ends at epoch 42, hence no training is performed for epoch numbers 0, 1, and 2. Epoch number 0 represents the value of the test error of the digital model initialized with the pre-trained weights when tested using the test set of the modified MNIST dataset. Epoch 1 is the test error when the digital model has been converted to the analog model using the same dataset. This explains why all the graphs in each figure have the same value at epochs 0 and 1 as the pre-trained weights are the same at both epochs, particularly for the transfer learning models. Epoch 2 is the performance of the analog model on the same dataset after the effect of the programming noise on the analog model weights has been accounted for.
The starting point of the transfer learning simulation was based on the weights derived from training the digital model on the unmodified MNIST dataset. For the subsequent fine-tuning stage, we utilized only 1st of the dataset. The difficulty of the overall transfer learning simulation was varied by changing the number of swapped rows. The simulation results, illustrated in Figure 10A with one swapped row and Figure 10B with two, exhibit a consistently higher test error for the reference model in contrast to the transfer learning model, regardless of the complexity of the task. Moreover, the transfer learning model converges much faster after fine-tuning using only 781 images, thus highlighting the benefits of transfer learning in resource- or data-constrained scenarios.
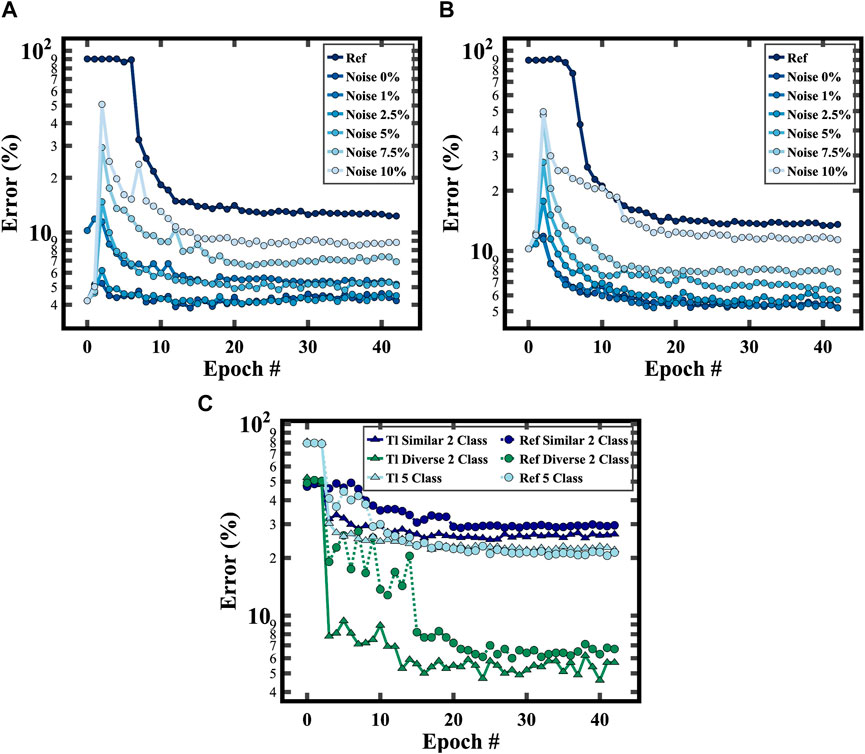
FIGURE 10. Performance of fully connected DNN models trained on a modified MNIST by swapping (A) 1 row, (B) 2 rows. Swapping 1 row with 2.5% noise generates a test error of 12.3% and 4.5% for training from scratch and transfer learning, respectively. Epoch 0 is the test error of the digital model. Epoch 1 is the test error when the digital model is converted to the analog model. Epoch 2 is the test error of the analog model with the programming noise. (C) A CNN model trained on various subsets of CIFAR100 (5-class: beaver, cockroach, leopard, orange, woman; similar 2-class: beaver and otter; diverse 2-class: beaver and dolphin) for training from scratch and transfer learning.
Moreover, in Figures 10A, B, it is observed that the test error for the model trained from scratch is even higher than the test error of the transfer learning model with noise injection. As an example, for the experiments in Figure 10A, the test error is 13.57% for the model trained from scratch and 10.61% for the transfer learning model with 10% programming noise. Similarly, in Figure 10B, the test error of the model trained from scratch is 12.32% and 8.82% for the transfer learning model with 10% programming noise. It is also observed that the size of programming noise affects the performance of the transfer learning model. This is because the test error increases as the programming noise is increased from 0% to 10% and this is true irrespective of the complexity of the task (degree of swapping).
Subsequently, we extended the transfer learning framework to a Convolutional Neural Network (CNN) with two frozen layers, trained on the CIFAR100 dataset (Figure 10C) (Krizhevsky and Hinton, 2009), to demonstrate robustness across different neural network architectures, larger datasets and different number of output classes. The network was pre-trained on the CIFAR10 dataset and fine-tuning was performed on new classes derived from the CIFAR100 dataset. These results reaffirmed the effectiveness of transfer learning, showing superior performance on the 2-class and 5-class classification tasks than reference training using randomly initialized weights. This suggests that the transfer learning of CNN can accelerate learning and demonstrate generalization between tasks, even as the number of target classes increases. Thus, our simulations underscore the advantages of using transfer learning in analog AI hardware for both fully connected and convolutional neural network architectures.
In this study, we explored the potential of DNN transfer learning using ReRAM. We experimentally demonstrated that the integration of 14 nm technology ReRAM and co-optimization of hardware and algorithms lead to a 3.5× faster convergence compared to conventional training methods. Simulation results, drawing from statistical data of 2,000 ReRAMs, further support the scalability and adaptability of this transfer learning approach, indicating its suitability for handling larger computational tasks. Our findings suggest that DNN transfer learning in ReRAM arrays can achieve improved convergence rates even with limited datasets. This is particularly significant for edge computing applications such as wearables for real-time patient monitoring and autonomous systems like self-driving cars, where energy efficiency and accelerated learning are vital.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
FFA: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. OF: Investigation, Data curation, Writing–review and editing, Conceptualization, Formal Analysis, Methodology, Software, Validation, Visualization, Writing–original draft. NG: Writing–review and editing, Conceptualization, Formal Analysis, Investigation, Methodology, Supervision, Validation. MJR: Writing–review and editing, Conceptualization, Formal Analysis, Investigation, Methodology, Supervision, Validation, Writing–original draft. JP: Writing–review and editing, Data curation, Validation. SCS: Writing–review and editing, Validation. AG: Writing–review and editing, Validation. PS: Writing–review and editing, Validation. VB: Writing–review and editing, Validation. SC: Writing–review and editing, Validation. HH: Writing–review and editing, Validation. CP: Writing–review and editing, Validation. KB: Writing–review and editing, Validation. PJ: Writing–review and editing, Validation. CC: Writing–review and editing, Validation. IS: Writing–review and editing, Validation. CS: Writing–review and editing, Validation. XL: Writing–review and editing, Validation. BK: Writing–review and editing, Validation. NJ: Writing–review and editing, Validation. SM: Writing–review and editing, Validation. RJ: Writing–review and editing, Validation. IE-R: Writing–review and editing, Validation. JL: Writing–review and editing, Validation. TG: Writing–review and editing, Validation. NL: Writing–review and editing, Validation. RP: Writing–review and editing, Validation. FC: Writing–review and editing, Validation. HM: Writing–review and editing, Validation. MMF: Writing–review and editing, Validation. ALP: Writing–review and editing, Validation. DK: Writing–review and editing, Validation. QY: Writing–review and editing, Validation. RDC: Writing–review and editing, Validation. KT: Writing–review and editing, Validation. CW: Writing–review and editing, Validation. AMo: Writing–review and editing, Validation. JS: Writing–review and editing, Validation. AMe: Writing–review and editing, Validation. ST: Writing–review and editing, Validation. NS: Writing–review and editing, Validation. BO: Writing–review and editing, Validation. TT: Writing–review and editing, Validation. GL: Writing–review and editing, Validation. VN: Funding acquisition, Project administration, Resources, Supervision, Writing–review and editing, Conceptualization, Investigation, Validation. TA: Conceptualization, Funding acquisition, Project administration, Resources, Supervision, Validation, Writing–review and editing, Formal Analysis, Investigation, Methodology, Visualization, Writing–original draft.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Authors FFA, OF, NG, MJR, JP, PS, BK, TG, NL, FC, HM, MMF, VN, TA were employed by IBM Thomas J. Watson Research Center, Yorktown Heights, NY, United States. Authors SCS, AG, CP, KB, PJ, IS, CS, XL, NJ, SM, RJ, IE-R, JL, RP, ST, NS were employed by IBM Research, Albany, NY, United States. Authors VB, ALP, BO were employed by IBM Research–Zurich, Rüschlikon, Switzerland. Authors SC, HH, CC, DK, QY, RDC, KT, CW, AMo, JS, AMe, GL were employed by TEL Technology Center, America, LLC, Albany, NY, United States. Author TT was employed by Tokyo Electron Limited, Tokyo, Japan.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Ambrogio, S., Narayanan, P., Tsai, H., Shelby, R. M., Boybat, I., Di Nolfo, C., et al. (2018). Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 558, 60–67. doi:10.1038/s41586-018-0180-5
Amirsoleimani, A., Alibart, F., Yon, V., Xu, J., Pazhouhandeh, M. R., Ecoffey, S., et al. (2020). In-memory vector-matrix multiplication in monolithic complementary metal–oxide–semiconductor-memristor integrated circuits: design choices, challenges, and perspectives. Adv. Intell. Syst. 2, 2000115. doi:10.1002/aisy.202000115
Arnold, E., Al-Jarrah, O. Y., Dianati, M., Fallah, S., Oxtoby, D., and Mouzakitis, A. (2019). A survey on 3d object detection methods for autonomous driving applications. IEEE Trans. Intelligent Transp. Syst. 20, 3782–3795. doi:10.1109/tits.2019.2892405
Athena, F. F., Gong, N., Muralidhar, R., Solomon, P., Vogel, E. M., Narayanan, V., et al. (2023). Resta: recovery of accuracy during training of deep learning models in a 14-nm technology-based reram array. IEEE Trans. Electron Devices 70, 5972–5976. doi:10.1109/ted.2023.3308527
Bingham, E., and Mannila, H. (2001). “Random projection in dimensionality reduction: applications to image and text data,” in Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining, 245–250.
Burr, G. W., Sebastian, A., Ando, T., and Haensch, W. (2021). Ohm’s law+ Kirchhoff’s current law= better ai: neural-network processing done in memory with analog circuits will save energy. IEEE Spectr. 58, 221 44–49. doi:10.1109/mspec.2021.9641759
Caesar, H., Bankiti, V., Lang, A. H., Vora, S., Liong, V. E., Xu, Q., et al. (2020). “nuscenes: a multimodal dataset for autonomous driving,” in In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 11621–11631.
Chen, P. H. C., Liu, Y., and Peng, L. (2019). How to develop machine learning models for healthcare. Nat. Mater. 18, 410–414. doi:10.1038/s41563-019-0345-0
Dasgupta, S. (2000). “Experiments with random projection,” in Proceedings of the Sixteenth conference on Uncertainty in artificial intelligence, 143–151.
Frascaroli, J., Brivio, S., Covi, E., and Spiga, S. (2018). Evidence of soft bound behaviour in analogue memristive devices for neuromorphic computing. Sci. Rep. 8, 7178. doi:10.1038/s41598-018-25376-x
Frenkel, C., Bol, D., and Indiveri, G. (2023). Bottom-up and top-down approaches for the design of neuromorphic processing systems: tradeoffs and synergies between natural and artificial intelligence. Proc. IEEE 111, 623–652. doi:10.1109/jproc.2023.3273520
Fusi, S., and Abbott, L. (2007). Limits on the memory storage capacity of bounded synapses. Nat. Neurosci. 10, 485–493. doi:10.1038/nn1859
Gogas, P., and Papadimitriou, T. (2021). Machine learning in economics and finance. Comput. Econ. 57, 1–4. doi:10.1007/s10614-021-10094-w
Gokmen, T. (2021a). Enabling training of neural networks on noisy hardware. Front. Artif. Intell. 4, 699148. doi:10.3389/frai.2021.699148
Gokmen, T. (2021b). Enabling training of neural networks on noisy hardware. Front. Artif. Intell. 4, 699148. doi:10.3389/frai.2021.699148
Gokmen, T., and Haensch, W. (2020). Algorithm for training neural networks on resistive device arrays. Front. Neurosci. 14, 103. doi:10.3389/fnins.2020.00103
Gong, N., Rasch, M. J., Seo, S. C., Gasasira, A., Solomon, P., Bragaglia, V., et al. (2022). “Deep learning acceleration in 14nm CMOS compatible ReRAM array: device, material and algorithm co-optimization,” in 2022 International Electron Devices Meeting (IEDM), San Francisco, CA, United States, 2022, 33.7.1–33.7.4. doi:10.1109/IEDM45625.2022.10019569
Goodell, J. W., Kumar, S., Lim, W. M., and Pattnaik, D. (2021). Artificial intelligence and machine learning in finance: identifying foundations, themes, and research clusters from bibliometric analysis. J. Behav. Exp. Finance 32, 100577. doi:10.1016/j.jbef.2021.100577
Ielmini, D., and Pedretti, G. (2020). Device and circuit architectures for in-memory computing. Adv. Intell. Syst. 2, 2000040. doi:10.1002/aisy.202000040
Jain, S., Tsai, H., Chen, C.-T., Muralidhar, R., Boybat, I., Frank, M. M., et al. (2022). A heterogeneous and programmable compute-in-memory accelerator architecture for analog-ai using dense 2-d mesh. IEEE Trans. Very Large Scale Integration (VLSI) Syst. 31, 114–127. doi:10.1109/tvlsi.2022.3221390
Kim, Y., Gokmen, T., Miyazoe, H., Solomon, P., Kim, S., Ray, A., et al. (2022). Neural network learning using non-ideal resistive memory devices. Front. Nanotechnol. 4, 1008266. doi:10.3389/fnano.2022.1008266
LeCun, Y., Cortes, C., and Burges, C. (2010). Mnist handwritten digit database. ATT Labs. [Online]. Available: http://yann.lecun.com/exdb/mnist.
Lee, C., Noh, K., Ji, W., Gokmen, T., and Kim, S. (2021). Impact of asymmetric weight update on neural network training with tiki-taka algorithm. Front. Neurosci. 15, 767953. doi:10.3389/fnins.2021.767953
Liang, W., Tadesse, G. A., Ho, D., Fei-Fei, L., Zaharia, M., Zhang, C., et al. (2022). Advances, challenges and opportunities in creating data for trustworthy ai. Nat. Mach. Intell. 4, 669–677. doi:10.1038/s42256-022-00516-1
Long, M., Zhu, H., Wang, J., and Jordan, M. I. (2017). “Deep transfer learning with joint adaptation networks,” in International conference on machine learning (PMLR), 2208–2217.
Luo, Y., and Yu, S. (2021). Ailc: accelerate on-chip incremental learning with compute-in-memory technology. IEEE Trans. Comput. 70, 1225–1238. doi:10.1109/tc.2021.3053199
Mormont, R., Geurts, P., and Mare´e, R. (2018). “Comparison of deep transfer learning strategies for digital pathology,” in Proceedings of the IEEE conference on computer vision and pattern recognition workshops, 2262–2271.
Pan, S. J., Kwok, J. T., and Yang, Q. (2008). Transfer learning via dimensionality reduction. AAAI 8, 677–682.
Pan, S. J., and Yang, Q. (2010). A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 22, 1345–1359. doi:10.1109/TKDE.2009.191
Rafique, W., Qi, L., Yaqoob, I., Imran, M., Rasool, R. U., and Dou, W. (2020). Complementing iot services through software defined networking and edge computing: a comprehensive survey. IEEE Commun. Surv. Tutorials 22, 1761–1804. doi:10.1109/comst.2020.2997475
Rasch, M. J., Carta, F., Fagbohungbe, O., and Gokmen, T. (2023). Fast offset corrected in-memory training. arXiv preprint arXiv:2303.04721.
Rasch, M. J., Moreda, D., Gokmen, T., Le Gallo, M., Carta, F., Goldberg, C., et al. (2021). “A flexible and fast pytorch toolkit for simulating training and inference on analog crossbar arrays,” in 2021 IEEE 3rd international conference on artificial intelligence circuits and systems (AICAS) (IEEE), 1–4.
Schwartz, R., Dodge, J., Smith, N. A., and Etzioni, O. (2020). Green ai. Commun. ACM 63, 54–63. doi:10.1145/3381831
Seo, J.-s., Saikia, J., Meng, J., He, W., Suh, H.-s., Liao, Y., et al. (2022). Digital versus analog artificial intelligence accelerators: advances, trends, and emerging designs. IEEE Solid-State Circuits Mag. 14, 65–79. doi:10.1109/mssc.2022.3182935
Sun, X., Wang, P., Ni, K., Datta, S., and Yu, S. (2018). “Exploiting hybrid precision for training and inference: a 2t-1fefet based analog synaptic weight cell,” in 2018 IEEE international electron devices meeting (IEDM) (IEEE), 3–1.
Wan, Z., Yang, R., Huang, M., Zeng, N., and Liu, X. (2021). A review on transfer learning in eeg signal analysis. Neurocomputing 421, 1–14. doi:10.1016/j.neucom.2020.09.017
Wang, K., Gao, X., Zhao, Y., Li, X., Dou, D., and Xu, C.-Z. (2019). “Pay attention to features, transfer learn faster cnns,” in International conference on learning representations. 21.
Wu, C.-J., Raghavendra, R., Gupta, U., Acun, B., Ardalani, N., Maeng, K., et al. (2022). Sustainable ai: environmental implications, challenges and opportunities. Proc. Mach. Learn. Syst. 4, 795–813.
Yoon, I., Anwar, A., Rakshit, T., and Raychowdhury, A. (2019). “Transfer and online reinforcement learning in stt-mram based embedded systems for autonomous drones,” in 2019 Design, Automation and Test in Europe Conference and Exhibition (DATE) (IEEE), 1489–1494.
Yu, K.-H., Beam, A. L., and Kohane, I. S. (2018). Artificial intelligence in healthcare. Nat. Biomed. Eng. 2, 719–731. doi:10.1038/s41551-018-0305-z
Keywords: resistive random access memory, HfOx, deep learning, analog hardware, transfer learning, open loop training
Citation: Athena FF, Fagbohungbe O, Gong N, Rasch MJ, Penaloza J, Seo S, Gasasira A, Solomon P, Bragaglia V, Consiglio S, Higuchi H, Park C, Brew K, Jamison P, Catano C, Saraf I, Silvestre C, Liu X, Khan B, Jain N, McDermott S, Johnson R, Estrada-Raygoza I, Li J, Gokmen T, Li N, Pujari R, Carta F, Miyazoe H, Frank MM, La Porta A, Koty D, Yang Q, Clark RD, Tapily K, Wajda C, Mosden A, Shearer J, Metz A, Teehan S, Saulnier N, Offrein B, Tsunomura T, Leusink G, Narayanan V and Ando T (2024) Demonstration of transfer learning using 14 nm technology analog ReRAM array. Front. Electron. 4:1331280. doi: 10.3389/felec.2023.1331280
Received: 31 October 2023; Accepted: 18 December 2023;
Published: 15 January 2024.
Edited by:
Rivu Midya, Massachusetts Institute of Technology, United StatesReviewed by:
Min-Kyu Song, Massachusetts Institute of Technology, United StatesCopyright © 2024 Athena, Fagbohungbe, Gong, Rasch, Penaloza, Seo, Gasasira, Solomon, Bragaglia, Consiglio, Higuchi, Park, Brew, Jamison, Catano, Saraf, Silvestre, Liu, Khan, Jain, McDermott, Johnson, Estrada-Raygoza, Li, Gokmen, Li, Pujari, Carta, Miyazoe, Frank, La Porta, Koty, Yang, Clark, Tapily, Wajda, Mosden, Shearer, Metz, Teehan, Saulnier, Offrein, Tsunomura, Leusink, Narayanan and Ando. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Takashi Ando, YW5kb3RAdXMuaWJtLmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.