CoFHE: Software and hardware Co-design for FHE-based machine learning as a service

Introduction: Privacy concerns arise whenever sensitive data is outsourced to untrusted Machine Learning as a Service (MLaaS) platforms. Fully Homomorphic Encryption (FHE) emerges one of the most promising solutions to implementing privacy-preserving MLaaS. But prior FHE-based MLaaS faces challenges from both software and hardware perspectives. First, FHE can be implemented by various schemes including BGV, BFV, and CKKS, which are good at different FHE operations, e.g., additions, multiplications, and rotations. Different neural network architectures require different numbers of FHE operations, thereby preferring different FHE schemes. However, state-of-the-art MLaaS just naïvely chooses one FHE scheme to build FHE-based neural networks without considering other FHE schemes. Second, state-of-the-art MLaaS uses power-hungry hardware accelerators to process FHE-based inferences. Typically, prior high-performance FHE accelerators consume $>160$ Watt, due to their huge capacity (e.g., 512 MB) on-chip SRAM scratchpad memories.

Methods: In this paper, we propose a software and hardware co-designed FHE-based MLaaS framework, CoFHE. From the software perspective, we propose an FHE compiler to select the best FHE scheme for a network architecture. We also build a low-power and high-density NAND-SPIN and SRAM hybrid scratchpad memory system for FHE hardware accelerators.

Results: On average, under the same security and accuracy constraints, on average, CoFHE accelerates various FHE-based inferences by 18%, and reduces the energy consumption of various FHE-based inferences by 26%.

Discussion: CoFHE greatly improves the latency and energy efficiency of FHE-based MLaaS.

1 Introduction

Machine Learning as a Service (MLaaS) Ribeiro et al. (2015) is one of the most important solutions to solving a wide variety of problems ranging from computer vision to recommender system. Average users feel reluctant to upload their sensitive data, e.g., health or financial records, to untrusted servers in the cloud. New legislation like the European Union General Data Protection Regulation Hoofnagle et al. (2019) and the California Consumer Privacy Act Camhi and Lyon (2018) requires MLaaS providers to be more attentive about collecting, storing, utilizing, and transferring average users’ data. To protect users’ privacy, Fully Homomorphic Encryption (FHE)-based privacy-preserving neural networks Gilad-Bachrach et al. (2016); Brutzkus et al. (2019); Dathathri et al. (2019, Dathathri et al. (2020); Lou and Jiang (2021) are proposed to perform neural inferences directly on encrypted data. The majority of state-of-the-art FHE schemes including BFV Fan and Vercauteren (2012), BGV Halevi and Shoup (2015) and CKKS Jung et al. (2020) supports only FHE multiplications and additions. Although FHE-based neural networks approximate their activation layers by degree-2 polynomials, they still can obtain competitive inference accuracy Gilad-Bachrach et al. (2016); Brutzkus et al. (2019); Dathathri et al. (2019), Dathathri et al. (2020); Lou and Jiang (2021). However, an FHE-based neural network inference is time-consuming. An inference of a typical FHE-based neural network Dathathri et al. (2019), Dathathri et al. (2020) costs $>2$ seconds on an encrypted MNIST image and $>70$ seconds on an encrypted CIFAR-10 image. There is a ∼×100 latency gap between an FHE-based inference and a unencrypted inference, due to the software and hardware drawbacks.

Although FHE can be implemented by multiple schemes, i.e., BFV Fan and Vercauteren (2012), BGV Halevi and Shoup (2015) and CKKS Jung et al. (2020), prior FHE-based neural networks Gilad-Bachrach et al. (2016); Brutzkus et al. (2019); Dathathri et al. (2019), Dathathri et al. (2020); Lou and Jiang (2021) just naïvely select one FHE scheme without considering other alternatives. Different FHE schemes have different advantages Jiang and Ju (2022). BFV and BGV support FHE integer multiplications and additions, while CKKS is good at approximate complex fixed-point arithmetics. Moreover, at the same security level, different FHE schemes have distinctive SIMD batch sizes, and different latencies when performing additions, multiplications, and rotations Jiang and Ju (2022). Different neural networks having different architectures, i.e., layer numbers, kernel sizes, and input/output channel numbers, may favor distinctive FHE schemes, because their FHE inferences have various bottlenecks, e.g., small batch size, slow multiplications, or slow rotations. Unfortunately, there is a total lack of a software tool that can select a suitable FHE scheme for a network architecture.

For FHE hardware, although multiple FHE hardware accelerators Samardzic et al. (2022); Kim et al. (2022); Samardzic et al. (2021) propose highly-optimized Number Theoretic Transform (NTT) units to process polynomial multiplications in FHE operations, all of them use many power-hungry SRAM arrays connected by a large Network-on-Chip (NoC) to form a 256 MB $\sim 512$MB SRAM Samardzic et al. (2022); Kim et al. (2022) scratchpad memory, store evaluation keys used by various FHE operations, and keep hundreds of NTT units busy. Unfortunately, 512 MB SRAM arrays and their NoC consume huge amount of power seriously limiting the further scaling of state-of-the-art FHE hardware accelerators. For instance, in the latest FHE accelerator Kim et al. (2022), the 512 MB SRAM scratchpad memory and its NoC consume 38% of the total power and occupy 63% of the chip area.

In this paper, we propose a software and hardware co-designed FHE-based MLaaS framework, CoFHE, to tackle the software and hardware shortcomings of prior FHE-based neural networks. Our contributions can be summarized as follows.

• At the software level, we propose an FHE compiler for CoFHE to select the best FHE scheme for a network architecture. The idea behind our compiler is simple, i.e., for a network architecture under a security level, our compiler generates BFV-, BGV-, and CKKS-based solutions, and then compares their client setup latencies, server inference latencies, and inference accuracies. At last, our compiler selects the best FHE scheme according to the design requirement.

• At the hardware level, we build a low-power and high-density NAND-Spintronic (SPIN) and SRAM hybrid scratchpad memory for FHE accelerators. A NAND-SPIN array is highly dense but its write latency is long. The scratchpad memory uses NAND-SPIN arrays to store various evaluation keys, since they are read-only data. The scratchpad memory adopts NAND-SPIN and SRAM hybrid arrays to keep ciphertexts, which may receive heavy write traffic. Our hybrid scratchpad memory greatly reduces the energy consumption of the FHE accelerator without greatly degrading the FHE-based network performance.

• We implemented, evaluated, and compared CoFHE against the state-of-the-art hardware-accelerated MLaaS. On average, under the same security and accuracy constraints, CoFHE improves the inference latency of various FHE-based neural networks by 18%, and reduces the energy consumption of various FHE-based inferences by 26%.

2 Background

2.1 Fully Homomorphic Encryption

Basics. Fully Homomorphic Encryption (FHE) Fan and Vercauteren (2012) allows operations on encrypted data (ciphertexts) without the secret key. We use pub to denote a public key, sec to indicate a secrete key, ϵ to represent an encryption function, and σ to symbolize a decryption function. A homomorphic operation ⋄ can be defined if there is another operation ⋆ such that σ(ϵ(x₁, pub)⋄ϵ(x₂, pub), sec) = σ(ϵ(x₁ ⋆ x₂, pub), sec), where x₁ and x₂ are two plaintexts. The state-of-the-art FHE schemes initially introduce an error to the ciphertext to guarantee security. Moreover, each homomorphic operation introduces a certain amount of noise into the ciphertext. When the accumulated noise in the ciphertext exceeds the noise budget, an error happens during the decryption. An FHE scheme with a fixed set of parameters has a limited noise budget, and thus supports only a limited number of homomorphic operations. This is called leveled FHE. The FHE scheme may periodically use a bootstrapping operation Brakerski et al. (2014) to reduce the noise in the ciphertext, so that it can support an unlimited number of homomorphic operations. This is called fully FHE.

Notations. In this paper, integer and real numbers are written in normal case, e.g., q. Polynomials and vectors are written in bold, e.g., a. Vectors of polynomials and matrices are written in upper-case bold, e.g., A. We use a subscript to denote the index, e.g., a_i is the ith polynomial or row of A. We assume that n is a power-of-two integer and define a polynomial ring $R=\mathbb{Z}[X]/(X^n+1)$ whose elements have degrees at most n−1 since Xⁿ = −1 ∈ R. We write R_q = R/qR for the residue ring of R modulo an integer q. u ⋅v denotes the multiplication of two polynomials where the product is reduced modulo Xⁿ+1 in R and reduced modulo q in R_q.

FHE Operations. We use the FHE scheme BFV as one example to explain the most important FHE operations as follows.

• Setup(λ). For a security parameter λ, we set a ring size n, a ciphertext modulus q, a special modulus p coprime to q, a key distribution χ, and an error distribution Ω over R.

• Encryption. A BFV ciphertext is encrypted as a vector of two polynomials $({\mathbf{c}}_{\mathbf{0}},{\mathbf{c}}_{\mathbf{1}})\in {\mathcal{R}}_q^2$. Specifically, we have c₀ = −a and ${\mathbf{c}}_{\mathbf{1}}=\mathbf{a}\cdot \mathbf{s}+\frac{q}{p}\mathbf{m}+{\mathbf{e}}_{\mathbf{0}}$, where a is a uniformly sampled polynomial. s and e₀ are polynomials whose coefficients drawn from ${\mathcal{X}}_{\sigma }$ (σ is the standard deviation).

• Decryption. The decryption computes $\frac{p}{q}({\mathbf{c}}_{\mathbf{0}}\cdot \mathbf{s}+{\mathbf{c}}_{\mathbf{1}})=\mathbf{m}+\frac{p}{q}{\mathbf{e}}_{\mathbf{0}}$. When $\frac{q}{p}\gg {\mathbf{e}}_{\mathbf{0}}$, e₀ can be removed. Each FHE operation enlarges e₀. To successfully decrypt the ciphertext, a bootstrapping is required to keep e₀ in check. Or we have to choose a larger q to accommodate a larger depth of FHE operations, since a larger q can omit a larger e₀.

• Addition. For two ciphertexts c₀ = (c_0,0, c_1,0) and c₁ = (c_0,1, c_1,1), an FHE addition simply adds the polynomials of the two ciphertexts and outputs the result ciphertext c = (c_0,0+c_0,1, c_1,0+c_1,1).

• Multiplication. During an FHE multiplication, two ciphertexts c₀ = (c_0,0, c_1,0) and c₁ = (c_0,1, c_1,1) are first multiplied and assembled to compute c_x = (m₀, m₁, m₂) = (c_0,0c_0,1, c_0,0c_1,1+c_1,0c_0,1, c_1,0c_1,1). And then, a key-switching (relinearization) operation happening m₀ to produce two polynomials (u₀, u₁) = keyswitch (m₀) via a relinearization key. The final output is c = (m₁+u₀, m₂+u₁).

• Rotation. FHE schemes support SIMD-style batching Fan and Vercauteren (2012), which can pack m plaintexts [p₀, …, p_m−1] into a ciphertext. A homomorphic multiplication or addition happening between two ciphertexts (c_0,0, c_1,0) and (c_0,1, c_1,1) is equivalent to m multiplications or additions between [p_0,0, …, p_m−1,0] and [p_0,1, …, p_m−1,1]. For instance, an FHE addition can achieve p_0,0+p_0,1, …, p_m−1,0+p_m−1,1. An FHE rotation operation rotates a ciphertext by several plaintext slots. For instance, [p_0,0, …, p_m−1,0] can be rotated to [p_n,0, …, p_m−1,0, p_0,0, …, p_n−1,0] by n plaintext slots. The FHE rotation is also achieved via a rotation key.

Both relinearization and rotation keys can be called evaluation keys. The size of evaluation keys greatly increases with an enlarging ciphertext modulus q.

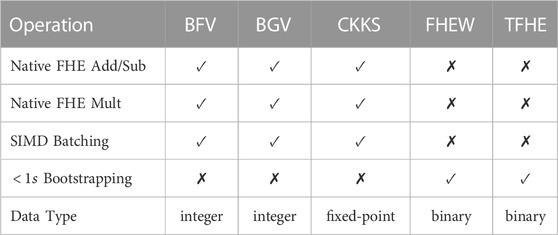
FHE Schemes. FHE can be implemented by various schemes including BFV Fan and Vercauteren (2012), BGV Halevi and Shoup (2015), CKKS Jung et al. (2020), FHEW Ducas and Micciancio (2015), and TFHE Chillotti et al. (2018). A brief comparison between these FHE schemes is shown in Table 1. The word-wise FHE schemes, i.e., BGV, BFV, CKKS, are built upon the Ring Learning With Error (RLWE) paradigm Brakerski et al. (2014). They are good at computing vectorial multiplications and additions. They support the SIMD batching, which allows a vector of plaintexts to be encrypted as a single ciphertext. BGV and BFV support only integer arithmetic operations, while CKKS is more efficient when processing complex fixed-point numbers. Compared to BGV, BFV uses a different version of relinearization in an FHE multiplication. CKKS supports only approximate computing, where each CKKS operation slightly modifies the value of the fraction part of the ciphertext. The bootstrapping operations of BGV, BFV and CKKS are super time-consuming. For instance, the latency of a BGV bootstrapping operation costs several hundred seconds Halevi and Shoup (2015). On the contrary, FHEW and TFHE are developed upon the Learning With Error (LWE) paradigm Chillotti et al. (2018). They are good at FHE binary logic operations, e.g., NAND, AND, XOR, and OR. Their bootstrapping operations are fast. For example, a TFHE bootstrapping requires only 13ms on a CPU. Although prior work Bourse et al. (2018); Lou and Jiang (2019) uses TFHE to implement an FHE neural network using low bit-width quantized weights, these highly-quantized neural networks greatly degrade the inference accuracy. Recent work Lou et al. (2020) performs linear layers by BGV and activation layers by TFHE, but the switching operations between BGV and TFHE are extremely slow, e.g., tens of seconds. In this paper, we focus on only BGV, BFV, CKKS, and neural networks implemented by these FHE schemes.

TABLE 1

TABLE 1. The comparison of FHE schemes.

2.2 FHE-based neural networks

Data Flow. The data flow of FHE-based MLaaS is shown in Figure 1. The client typically uses a CPU processor. She generates various keys, encrypts her data, and sends only the ciphertext to the cloud. The untrusted server in the cloud conducts an FHE-based neural inference Brutzkus et al. (2019) on encrypted data by FHE hardware accelerators and sends the encrypted result back to the client. In order to support SIMD-style FHE operations, an encoding step is required by the client to pack many numbers into a single ciphertext. Encoding, decoding, encryption and decryption are all performed by the client, while the server performs only FHE computations on the encrypted data without decryption.

FIGURE 1

FIGURE 1. The data flow of end-to-end encrypted FHE-based MLaaS.

FHE Neural Networks. FHE-based neural networks Gilad-Bachrach et al. (2016); Brutzkus et al. (2019); Dathathri et al. (2019, 2020); Lou and Jiang (2021) are created to support inferences directly on encrypted data. Prior FHE-based networks approximate their non-linear activation layers by degree-2 polynomials, and compute their linear (i.e., convolutional and fully-connected) layers by FHE multiplications and additions. The major operations in linear layers are homomorphic dot-product, as shown in Figure 2. For a fully-connected layer, the encrypted input vector x consisting of n (e.g., n = 4) elements, while the encrypted output vector y has m (e.g., m = 1) elements. Prior FHE-based networks keep weights on only the server side, so the weights are not encrypted. The plaintext weight matrix W has a dimension of n × m. The homomorphic dot-product can be computed as

$\left[\mathbf{y}\right]=\mathbf{W}\cdot \left[\mathbf{x}\right],\left[\mathbf{y}\right]=\sum _{i=1}^{{\log }_{2}n}rot\left(\left[\mathbf{y}\right],\frac{n}{2^i}\right)(1)$

where [x] means encrypted x; [y] is encrypted y; ⋅ indicates a FHE SIMD multiplication between a batched plaintext and a batched ciphertext; and rot means an FHE rotation. So log₂n FHE rotations are required to accumulate an element of y.

FIGURE 2

FIGURE 2. An FHE dot-product.

2.3 FHE hardware accelerators

FHE operations are time-consuming and power-inefficient when running on conventional CPUs and GPUs Riazi et al. (2020). Multiple ASIC-based FHE accelerators Samardzic et al. (2022); Kim et al. (2022); Samardzic et al. (2021) are proposed to improve the energy efficiency and latency of FHE operations. These FHE ASIC accelerators highly optimize the NTT units to accelerate the most computationally intensive kernel, i.e., polynomial multiplications, in FHE operations. However, to keep large evaluation (relinearization and rotation) keys and large ciphertexts on-chip, these accelerators adopt fast yet power-hungry SRAM arrays connected by a large NoC to form a 512 MB scratchpad memory Kim et al. (2022). To support an FHE neural network consisting of 10 ∼ 20 layers, the size of evaluation keys and ciphertexts greatly increases (e.g., 128 MB $\sim 256$MB). A 512 MB scratchpad memory can prevent most NTT units from waiting their data by keeping a ciphertext and a relinearization or rotation key on-chip. However, the huge-capacity SRAM scratchpad memory consumes huge amount of power and seriously limits the energy efficiency of prior FHE ASIC accelerators.

2.4 NAND-like spintronic memory

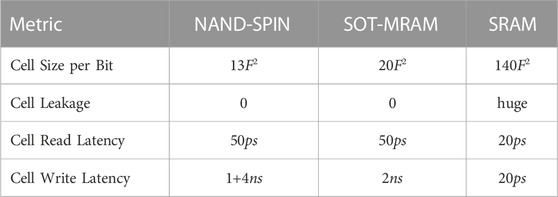
NAND-Like Spintronic (NAND-SPIN) Memory Wang et al. (2018) is a low-power and high-density memory technology, which has good CMOS compatibility and thus can be directly integrated with CMOS logic. Furthermore, the write endurance of a NAND-SPIN cell is $>10^{12}$. As Table 2 shows, NAND-SPIN has a small cell size of 13F², which is even smaller than SOT-MRAM. The read latency of NAND-SPIN is comparable to SRAM, while the write latency of NAND-SPIN is much longer than SRAM. The basic structure of a 4-bit NAND-SPIN cell is shown in Figure 3. The cell consisting of multiple magnetic tunnel junctions (MTJs) sits on a heavy metal strip. The free layers of the MTJs in the cell are all contacted with the heavy metal strip. Each MTJ has an access transistor connected to the pinned layer, and the other side of these transistors are connected to bit-lines (BLs). At one end of the heavy metal, one transistor is connected to V_dd and controlled by P source-line (PSL). On the other end of the heavy metal, another transistor is connected to GND and controlled by NSL. The cell can be selected by PSL and NSL. The write operation of this cell requires two steps. First, all MTJs are erase and reset to ‘0’. In this step, PSL is 0, while NSL is 1. All WL transistors are turned off, and a write current is generated in the heavy metal strip to reset MTJs to ‘0’. Second, the MTJs which attempt to be written to ‘1’ is programmed. All corresponding WL transistors are closed and PSL is set to 0, resulting in currents flowing through the MTJs from the free layer to the pinned layer. And then, these MTJs are written to ‘1’. For a read operation, the corresponding WL transistor is closed and NSL is set to 1. And then, a read current is produced.

TABLE 2

TABLE 2. The comparison of various memory technologies.

FIGURE 3

FIGURE 3. A NAND-like spintronic memory cell.

2.5 Motivation

Prior hardware-accelerated FHE-based MLaaS is limited by both its software and hardware designs. At software level, prior FHE-based neural networks Gilad-Bachrach et al. (2016); Brutzkus et al. (2019); Dathathri et al. (2019), Dathathri et al. (2020); Lou and Jiang (2021) just naïvely adopt one FHE scheme without considering other alternatives. For the same security level, different FHE schemes operate on different data types, support different SIMD batch sizes, and use different latencies when performing additions, multiplications, and rotations Jiang and Ju (2022), resulting in different setup latencies on the client side, inference latencies on the server side, and inference accuracies for one network architecture. The setup on the client side includes encryption, decryption, and public/private/evaluation key generation. As Figure 4 shows, we use BGV, BGV, and CKKS to implement a 4-feature logistic regression algorithm Kim et al. (2018) and a SqueezeNet Dathathri et al. (2020) working on CIFAR10. The detailed experimental methodology is shown in Section 4. Low-power IoT devices are sensitive to the computational overhead of client setup. BFV has the smallest client setup latency, while BGV is the slowest during the setup on the client side. For FHE-based inferences, BGV achieves the shortest latency on logistic, while BFV obtains the shortest latency on SqueezeNet. In contrast, CKKS has the highest accuracy for both. Therefore, average users need a software tool to select the best FHE scheme to meet their goals (i.e., client/server latency and accuracy) when building an FHE-based neural network. At hardware level, state-of-the-art FHE hardware accelerators use a huge (e.g., 512 MB) power-hungry SRAM scratchpad memory to store evaluation keys used by FHE multiplications and rotations. All SRAM arrays in the scratchpad memory are connected by a NoC that uses large SRAM buffers to temporarily store the transferring data. The SRAM scratchpad memory and its NoC dissipate huge amount of power, and degrade the energy efficiency of prior FHE accelerators. For example, on the latest 7 nm FHE accelerator Kim et al. (2022), the 512 MB SRAM scratchpad memory and the SRAM buffers (Scratch + SRAM NoC) in its NoC consume 61 W, i.e., 38% of the total power, and occupy 235mm², i.e., 63% of the chip area, as shown in Figure 5.

FIGURE 4

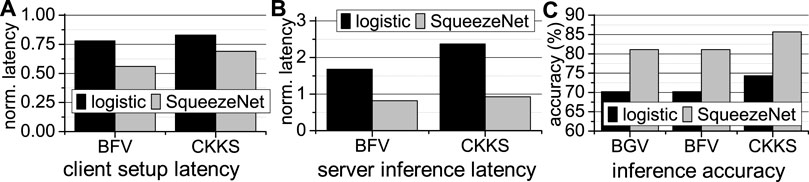
FIGURE 4. The latency and accuracy comparison Q14 of various FHE-based networks (A): client setup latency; (B): server inference latency; (C): inference accuracy; all latency results are normalized to BGV.

FIGURE 5

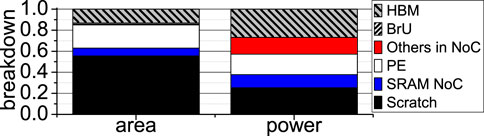
FIGURE 5. The SRAM scratchpad and NoC SRAM buffers of a prior FHE accelerator Kim et al. (2022).

3 CoFHE

W propose a software and hardware co-designed FHE-based MLaaS framework, CoFHE, to tackle the software and hardware shortcomings of prior FHE-based neural networks. At software level, we present a compiler to select the best FHE scheme for a network architecture to meet a design goal, i.e., the shortest latency on the server or client side, or the highest accuracy. At hardware level, we build a low-power NAND-SPIN and SRAM hybrid scratchpad memory system for FHE hardware accelerators.

3.1 A multi-FHE-scheme compiler for FHE-based neural networks

We first profile and benchmark major operations of three FHE schemes, and use the profiling data to build a latency/energy library for our CoFHE compiler. And then, we elaborate the design details of our CoFHE compiler.

FHE Scheme Profiling. To identify the most efficient FHE scheme for each type of FHE operation, we run OpenFHE Badawi et al. (2022) on our CPU and ASIC baselines Kim et al. (2022). We assume the client uses our CPU baseline, while the server uses our FHE ASIC baseline. We divide FHE operations into two groups: client and server. As we introduced in Section 2.2, the client needs to generate private, public, relinearization, and rotation keys to use a FHE-based neural network. Moreover, the client also has to encrypt and decrypt the sensitive data. In contrast, the server performs only FHE arithmetic operations for the FHE-based neural inference. For FHE operations, we consider only additions between two ciphertexts (AddCC), multiplications between two ciphertexts (MultCC), and rotations (Rotate). AddCC and Rotate are used in FHE dot-product operations, while MultCC is invoked during FHE activations. Because state-of-the-art FHE-based neural networks Gilad-Bachrach et al. (2016); Brutzkus et al. (2019); Dathathri et al. (2019, 2020); Lou and Jiang (2021) use only these leveled FHE operations without bootstrapping, we do not consider bootstrapping. We use the following profiling data to build a latency/energy library.

• Client. The latency comparison of the setup for FHE-based neural networks on the client side is shown in Figure 6, where “depth N” means the FHE parameters supporting N consecutive FHE multiplications. A larger FHE depth allows an FHE-based network consisting of more layers, and thus exponentially increases the setup latency on the client side. Except the decryption, BGV requires the longest latency when the depth is large, while CKKS has the longest decryption latency. When the FHE depth is small, i.e., $\le 2$, BFV requires longer latencies of key generation and decryption than BGV. Therefore, when an FHE-based network operates on integers, if the network is small, the client favors BGV; otherwise the client may use BFV. By the Intel VTune profiling tool, we have the energy values of these FHE operations, which share the same trend as their latencies.

• Server. The latency and throughput comparison of FHE multiplications and additions on the server side is shown in Figure 7. A larger FHE depth exponentially increases the latency of FHE operations on the accelerator of the server. To accommodate a large depth, BGV, BFV and CKKS have to use a larger ciphertext modulus q, which greatly prolongs the latency of FHE multiplications and additions. For the depth of $>5$, BFV uses the shortest latencies for FHE multiplications and additions. For the depth of $\le 5$, BGV has the shortest latencies of FHE multiplications and additions. Because BGV, BFV and CKKS support SIMD batching, we also show the throughput of FHE arithmetic operations (FHE operations per second). BFV achieves the largest throughput for most FHE operations. If an FHE-based network requires fixed-point arithmetics for higher accuracy, the server prefers CKKS. For an FHE-based network working on integers, when the depth is $>5$, the server favors BFV; otherwise it uses BGV. The energy values of these FHE operations also share the same trend as their latencies on our accelerator baseline.

FIGURE 6

FIGURE 6. The latency comparison of client setup operations on a CPU for FHE.

FIGURE 7

FIGURE 7. The latency and throughput comparison of server operations on an FHE hardware accelerator between various FHE schemes.

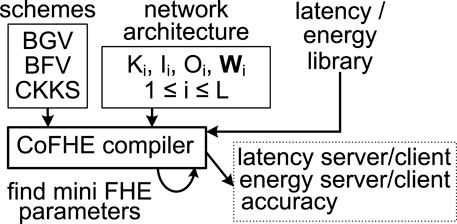
CoFHE Compiler. We present an FHE compiler for CoFHE to select the best FHE scheme for a neural network architecture in Figure 8. The compiler can be executed on the server side. For a L-layer network configuration including kernel size (K_i), input/output channel number (I_i/O_i), and weight values W_i, where 1 ≤ i ≤ L, the compiler tries three FHE schemes, i.e., BGV, BFV, and CKKS. The compiler uses the latest plaintext data encoding layout Brutzkus et al. (2019) to batch input examples and weights of the server, and then adopts different FHE parameters Boemer et al. (2019) to encrypt the batched plaintexts to find the minimal FHE parameters that can support the network. The set of minimal FHE parameters can be directly converted to an FHE depth which is used to lookup our latency/energy library to compute the latency/energy of the neural network for the server/client. Our CoFHE compiler also supports a combinatorial evaluation metric defined as α₀ ⋅ clat+α₁ ⋅ slat+α₂ ⋅ ceng+α₃ ⋅ seng+α₄ ⋅ acc, where α₀ ∼ α₄ are hyper-parameters; clat means the client side latency; slat is the server side latency; ceng means the client side energy; seng indicates the server side energy; and acc denotes the accuracy. Finally, the compiler quantizes all weights into their integer or fixed-point representations based on the data type of an FHE scheme and the plaintext modulus, and then fine-tunes the network for few epochs to produce the inference accuracy for an FHE scheme. The server can select the best FHE scheme for a FHE-based network to achieve the shortest latency on server/client, the smallest energy on server/client, the highest accuracy, or the combinatorial evaluation metric.

FIGURE 8

FIGURE 8. The CoFHE compiler.

3.2 A low-power scratchpad memory system for FHE hardware accelerators

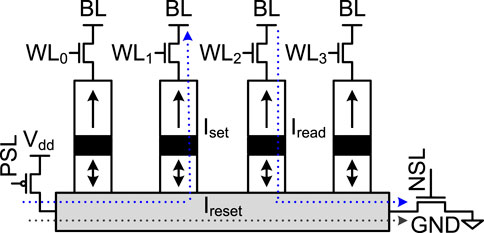
Scratchpad Memory Architecture. To reduce the energy consumption of prior FHE hardware accelerators, we build a NAND-SPIN and SRAM hybrid scratchpad memory system connected by a NAND-SPIN and SRAM hybrid NoC in Figure 9. For the NAND-SPIN and SRAM hybrid scratchpad memory system, all evaluation keys, i.e., relinearization and rotation keys, are stored in only NAND-SPIN scratchpad array, since FHE operations need to only read them while the NAND-SPIN read latency is close to SRAM. On the contrary, all ciphertexts are stored in the NAND-SPIN and SRAM hybrid arrays shown in Figure 9A, where there is a large NAND-SPIN array and a small SRAM array. As Figure 9B shows, the NAND-SPIN array consists of multiple NAND-SPIN sub-arrays connected by a H-Tree structure. Each NAND-SPIN sub-array is an array of NAND-SPIN cells connected by vertical word-lines and horizontal bit-lines, as shown in Figure 9C. Each MTJ on a NAND-SPIN cell is controlled by a word-line and selected by a row decoder. The NAND-SPIN cells in a horizontal line share a bit-line selected by a column multiplexer and can be sensed/written by a sense amplifier/write driver. All NAND-SPIN and SRAM hybrid arrays and NAND-SPIN arrays are connected by a NAND-SPIN and SRAM hybrid NoC shown in Figure 9D. The hybrid NoC consists of multiple virtual channels. One virtual channel uses a multiplexer to select NAND-SPIN banks or SRAM banks. The NAND-SPIN banks are used to store non-critical large-block transferring data, while the SRAM banks store urgent small-block transferring data.

FIGURE 9

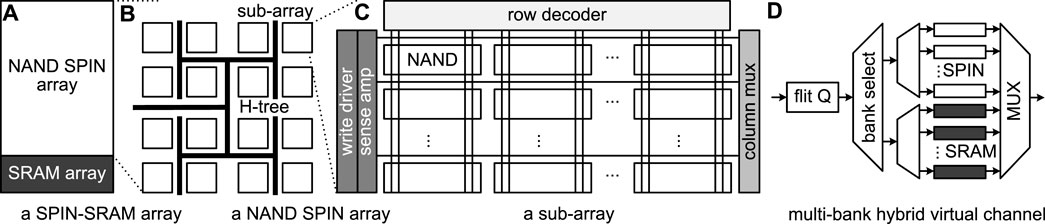
FIGURE 9. The SPIN-SRAM hybrid scratchpad memory and its hybrid NoC (A): a SPIN-SRAM array; (B): a NAND SPIN array; (C): a sub-array; (D): a multi-bank hybrid virtual channel.

Scratchpad Memory Management. The algorithm of our scratchpad memory management is simple. All read-only evaluation keys of various FHE operations are stored in large NAND-SPIN arrays, while most ciphertexts and other intermediate results are kept in small SRAM arrays. If the SRAM capacity is not large enough, data swapping operations occur to move data between NAND-SPIN and SRAM arrays.

4 Experimental methodology

In this section, we introduce the details of our experimental methodology.

FHE Scheme. We evaluated various word-wise FHE schemes including BFV Fan and Vercauteren (2012), BGV Halevi and Shoup (2015), and CKKS Jung et al. (2020). BFV and BGV support FHE exact integer arithmetic operations, while CKKS performs approximate complex and fixed-point arithmetic operations. Although three FHE schemes support bootstrapping, their bootstrapping operations are slow, e.g., $\sim 15$ minutes. In this paper, we do not consider bootstrapping, and use only leveled FHE. All FHE schemes use the FHE parameters to guarantee $>128$-bit security.

FHE Library. We studied the latest FHE library OpenFHE (.9.5) Badawi et al. (2022). The library is compiled with the Intel icc compiler using the -O3 optimization flag.

Hardware Baselines. Our CPU baseline is an Intel Xeon Gold 6138P with a 128 GB DDR4 main memory. It has 20 2 GHz x86 cores sharing a 27.5 MB L3 cache. Each core support the AVX-512 instructions. The thermal design power of our CPU baseline is 195 W. We selected the latest 7 nm FHE hardware accelerator, BTS Kim et al. (2022), as our ASIC baseline. BTS consists of 2K processing elements (PEs), each of which has a NTT unit, a base conversion unit, a modular multiplier, a modular adder, and a 256 KB SRAM scratchpad array. All scratchpad arrays are connected by a large NoC. BTS operates at 1.2 GHz and has two HBM2e DRAM memory controllers. BTS supports all three FHE schemes, i.e., BFV, BGV, and CKKS. The complete configuration of BTS can be viewed in (Kim et al., 2022). We assume the client uses our CPU baseline, while the server adopts our ASIC baseline.

Compiler Implementation. We built our CoFHE compiler upon NGraph-HE2 Boemer et al. (2019). We used OpenFHE as the FHE backend of our CoFHE compiler to compile an FHE-based neural network into a sequence of FHE operations which can be executed by our CPU baseline. Our hardware baseline can use its operation scheduler and mapper to run the sequence of FHE operations.

NAND-SPIN Scratchpad Modeling. We adopted NVSIM Dong et al. (2012) to estimate the power, latency, and area overhead of our NAND-SPIN and SRAM hybrid scratchpad memory system. We set the ratio between SRAM and NAND-SPIN in our hybrid memory to 1 : 8.

Profiling and Simulation. We used the Intel VTune tool to profile all FHE operations on our CPU baseline. We modeled BTS with our CoFHE NAND-SPIN and SRAM hybrid scratchpad memory system by a cycle-accurate FHE accelerator simulator, Sapphire-Sim Banerjee et al. (2019), which is validated against several crypto-processor chips. The input of Sapphire-Sim is the FHE operation schedule generated by our CoFHE compiler based on a neural network architecture. Based on the configuration of an accelerator, Sapphire-Sim simulates the cycle-level execution and data movement for each FHE operation, and then produces the total latency and energy consumption of an FHE-based neural network.

Network Architecture. We evaluated various FHE-based neural network architectures. For small-scale networks, we considered a 4-feature logistic regression algorithm Kim et al. (2018) (Log) on a breast lesion dataset McLaren et al. (2009). For medium-scale networks, we selected a 4-layer CNN (Lola) Brutzkus et al. (2019) inferring on the MNIST dataset. For large-scale networks, we chose CNNs including SqueezeNet (Squ) Dathathri et al. (2020) and AlexNet (Alex) Dathathri et al. (2020) working on the CIFAR10 dataset.

Schemes. We implemented and compared the following schemes.

• BTS. The ASIC hardware accelerator Kim et al. (2022) with a 512 MB SRAM scratchpad memory system runs all FHE-based neural inferences.

• CKKSBTS. The scheme implements all neural networks by CKKS using the state-of-the-art compiler Dathathri et al. (2020) and runs them on BTS with a 512 MB SRAM scratchpad memory.

• CoFHE. The scheme implements neural networks using our CoFHE compiler and runs them on BTS with a NAND-SPIN and SRAM hybrid scratchpad memory system that has the same area overhead of a 512 MB SRAM scratchpad memory.

5 Evaluation and results

5.1 CoFHE com piler

The latency, energy, and accuracy comparison of FHE-based neural networks generated by our CoFHE compiler with different FHE schemes including BGV, BFV, and CKKS is shown in Figure 10. All latency and energy results are normalized to BGV.

FIGURE 10

FIGURE 10. The latency, energy, and accuracy comparison of various FHE-based networks generated by our CoFHE compiler (A): client setup latency; (B): client setup energy; (C): server inference latency; (D): server inference energy; (E): inference accuracy; all latency and energy results are normalized to BGV.

First, all FHE setup operations including encryption, decryption, and various key generation are performed on our CPU baseline. As Figure 10A shows, the setup latency of the BGV-based neural networks is the longest, due to its slow relinearization and rotation key generation. And the BFV-based neural networks have shorter setup latency than CKKS-based neural networks, since the decryption operations of CKKS are the slowest among three FHE schemes. The energy consumption of the client setup of three FHE schemes shares the same trend as the latency result, as shown in Figure 10B, where BGV uses the largest energy while BFV consumes the smallest energy.

Second, all FHE neural network inferences are executed on our hardware accelerator baseline BTS. As Figure 10C shows, for the small-scale network Log, BGV achieves the shortest inference latency, while CKKS is the slowest, i.e., 2.3× inference latency. For the medium- and large-scale networks Lola, Squ, and Alex, BFV is the fastest while CKKS is still the slowest. Since the power consumption of BTS running these FHE-based neural inferences is similar to each other, the energy of an FHE-based neural network is decided by its latency. Therefore, as Figure 10D exhibits, the energy consumption of various FHE-based neural inferences shares the same trend as the latency result.

Third, although CKKS is typically the slowest during FHE-based neural inferences, the CKKS-based neural networks achieve the highest inference accuracy, as shown in Figure 10E. This is because CKKS supports fixed-point representations. Moreover, after each FHE multiplication, CKKS performs a rescaling operation to discard the least significant digits and focus on only the most significant digits that contribute more to the inference accuracy.

5.2 CoFHE NAND-SPIN and SRAM hybrid scratchpad memory

Latency and energy. The inference latency and energy of our NAND-SPIN and SRAM hybrid scratchpad memory system is shown in Figure 11. All results are normalized to BTS with a 512 MB SRAM scratchpad memory system. We assume our hybrid scratchpad memory has the same area overhead as the 512 MB SRAM scratchpad memory. For the same area, the CoFHE hybrid scratchpad memory system can achieve a 800 MB capacity. As Figure 11A highlights, a larger capacity hybrid scratchpad memory reduces the latency of medium- and large-scale FHE-based neural networks by 12.7% ∼ 20%. The small-scale network does not gain benefit from the larger scratchpad, since the 500 MB SRAM scratchpad is large enough to hold its working set. The 800 MB hybrid scratchpad memory still consumes much smaller power than the 512 MB SRAM scratchpad memory. As Figure 11B shows, the 800 MB hybrid scratchpad memory system reduces the energy consumption of BTS by 32% ∼ 44% for different FHE-based neural networks.

FIGURE 11

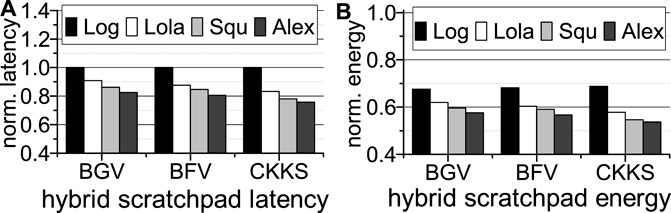
FIGURE 11. The inference latency and energy of BTS with a NAND-SPIN and SRAM hybrid scratchpad memory (A): hybrid scratchpad latency; (B): hybrid scratch energy; all are normalized to BTS with a 512 MB SRAM scratchpad memory.

Design space exploration. We adjust the capacity ratio between SRAM and NAND-SPIN arrays in our hybrid scratchpad memory system to 1/16 ∼ 1/2. The latency and energy results of Lola and Squ are shown Figure 12. Compared to the ratio of 1/8, although fewer SRAM arrays (ratio = 1/16) slightly reduce the power of the hybrid scratchpad memory system, the latency of both networks implemented by three FHE schemes is greatly prolonged by 8% ∼ 33%. Therefore, compared to the ratio of 1/8, the energy overhead of the ratio of 1/16 actually increases. On the other hand, more SRAM arrays (ratio = 1/4) only moderately reduce the latency of two networks but greatly increase the hybrid scratchpad memory power consumption by $>10\%$. Further increasing the SRAM capacity cannot improves the latency of two networks. So the ratio of 1/8 achieves the smallest energy overhead for two networks.

FIGURE 12

FIGURE 12. The design space exploration of the SRAM capacity in our NAND-SPIN and SRAM hybrid scratchpad memory (All are normalized to the BGV-based Lola having a ratio of 1/8).

5.3 Putting both together

We use both our CoFHE compiler and the hybrid scratchpad memory, and present the latency and energy results in Figure 13. To achieve the shortest client setup latency (clat), our CoFHE compiler always uses BFV. Compared to CKKSBTS, CoFHE improves the inference latency by 28% and the inference energy by 34%. To obtain the short server inference latency (slat), our CoFHE compiler adopts BGV for Log, and BFV for the other neural networks. CoFHE reduces the inference latency by 37% and the inference energy by 41% over CKKSBTS. To have the highest accuracy (acc), our CoFHE compiler always selects CKKS for all networks. The hybrid scratchpad memory of CoFHE decreases the inference latency by 18% and the inference energy 26% on average.

FIGURE 13

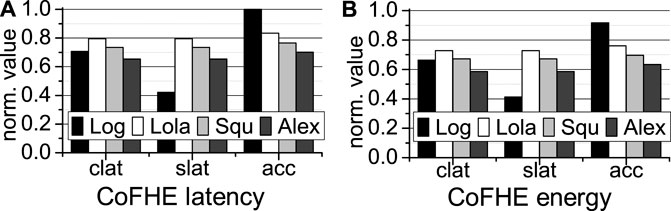
FIGURE 13. The inference latency and energy of CoFHE (A): CoFHE latency; (B): CoFHE energy; all are normalized to CKKSBTS; clat: client latency; slat: server latency; and acc: accuracy.

6 Conclusion

In this paper, we propose a software and hardware co-designed FHE-based MLaaS framework, CoFHE. On average, under the same security and accuracy constraints, CoFHE accelerates various FHE-based inferences by 18%, and reduces the energy consumption of various FHE-based inferences by 26%.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

MZ did all experiments. LJu answered some questions. LJi contributed the idea.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

[Dataset] Badawi, A. A., Bates, J., Bergamaschi, F., Cousins, D. B., Erabelli, S., Genise, N., et al. (2022). Openfhe: Open-source fully homomorphic encryption library. Cryptology ePrint Archive, Paper 2022/915. Available at: https://eprint.iacr.org/2022/915.

Google Scholar

Banerjee, U., Ukyab, T. S., and Chandrakasan, A. P. (2019). Sapphire: A configurable crypto-processor for post-quantum lattice-based protocols. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2019, 17–61. doi:10.46586/tches.v2019.i4.17-61

CrossRef Full Text | Google Scholar

Boemer, F., Costache, A., Cammarota, R., and Wierzynski, C. (2019). “Ngraph-he2: A high-throughput framework for neural network inference on encrypted data,” in ACM Workshop on Encrypted Computing & Applied Homomorphic Cryptography, 45–56.

Google Scholar

Bourse, F., Minelli, M., Minihold, M., and Paillier, P. (2018). “Fast homomorphic evaluation of deep discretized neural networks,” in Advances in cryptology, 483–512.

CrossRef Full Text | Google Scholar

Brakerski, Z., Gentry, C., and Vaikuntanathan, V. (2014). (leveled) fully homomorphic encryption without bootstrapping. ACM Trans. Comput. Theory 6, 1–36. doi:10.1145/2633600

CrossRef Full Text | Google Scholar

Brutzkus, A., Gilad-Bachrach, R., and Elisha, O. (2019). “Low latency privacy preserving inference,” in International Conference on Machine Learning, 812–821.

Google Scholar

Camhi, R., and Lyon, S. (2018). What is the California consumer privacy act? Risk Manag. 65, 12–13.

Google Scholar

Chillotti, I., Gama, N., Georgieva, M., and Izabachène, M. (2018). Tfhe: Fast fully homomorphic encryption over the torus. J. Cryptol. 33, 34–91. doi:10.1007/s00145-019-09319-x

CrossRef Full Text | Google Scholar

Dathathri, R., Kostova, B., Saarikivi, O., Dai, W., Laine, K., and Musuvathi, M. (2020). “Eva: An encrypted vector arithmetic language and compiler for efficient homomorphic computation,” in ACM SIGPLAN Conference on Programming Language Design and Implementation, 546–561.

CrossRef Full Text | Google Scholar

Dathathri, R., Saarikivi, O., Chen, H., Laine, K., Lauter, K., Maleki, S., et al. (2019). “Chet: An optimizing compiler for fully-homomorphic neural-network inferencing,” in ACM SIGPLAN Conference on Programming Language Design and Implementation, 142–156.

CrossRef Full Text | Google Scholar

Dong, X., Xu, C., Xie, Y., and Jouppi, N. P. (2012). Nvsim: A circuit-level performance, energy, and area model for emerging nonvolatile memory. IEEE Trans. Computer-Aided Des. Integr. Circuits Syst. 31, 994–1007. doi:10.1109/tcad.2012.2185930

CrossRef Full Text | Google Scholar

Ducas, L., and Micciancio, D. (2015). “Fhew: Bootstrapping homomorphic encryption in less than a second,” in Advances in cryptology -- EUROCRYPT 2015. EUROCRYPT 2015. Lecture notes in computer science(). Editors E. Oswald, and M. Fischlin (Berlin, Heidelberg: Springer), Vol. 9056, 617–640. doi:10.1007/978-3-662-46800-5_24

CrossRef Full Text | Google Scholar

[Dataset] Fan, J., and Vercauteren, F. (2012). Somewhat practical fully homomorphic encryption. Cryptology ePrint Archive, Report 2012/144.

Google Scholar

Gilad-Bachrach, R., Dowlin, N., Laine, K., Lauter, K., Naehrig, M., and Wernsing, J. (2016). “Cryptonets: Applying neural networks to encrypted data with high throughput and accuracy,” in International Conference on Machine Learning, 201–210.

Google Scholar

Halevi, S., and Shoup, V. (2015). “Bootstrapping for helib.” in International conference on the theory and applications of cryptographic techniques. Berlin, Germany: Springer, 641–670.

CrossRef Full Text | Google Scholar

Hoofnagle, C. J., van der Sloot, B., and Borgesius, F. Z. (2019). The European Union general data protection regulation: What it is and what it means. Inf. Commun. Technol. Law 28, 65–98. doi:10.1080/13600834.2019.1573501

CrossRef Full Text | Google Scholar

[Dataset] Jiang, L., and Ju, L. (2022). Fhebench: Benchmarking fully homomorphic encryption schemes. arXiv:2203.00728.

Google Scholar

[Dataset] Jung, W., Lee, E., Kim, S., Lee, K., Kim, N., Min, C., et al. (2020). Heaan demystified: Accelerating fully homomorphic encryption through architecture-centric analysis and optimization. arXiv:2003.04510.

Google Scholar

Kim, M., Song, Y., Wang, S., Xia, Y., and Jiang, X. (2018). Secure logistic regression based on homomorphic encryption: Design and evaluation. JMIR Med. Inf. 6, e19. doi:10.2196/medinform.8805

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, S., Kim, J., Kim, M. J., Jung, W., Kim, J., Rhu, M., et al. (2022). “Bts: An accelerator for bootstrappable fully homomorphic encryption,” in IEEE/ACM International Symposium on Computer Architecture, 711–725.

Google Scholar

Lou, Q., Feng, B., Fox, G. C., and Jiang, L. (2020). “Glyph: Fast and accurately training deep neural networks on encrypted data,” in Annual Conference on Neural Information Processing Systems, 9193–9202.

Google Scholar

Lou, Q., and Jiang, L. (2021). “Hemet: A homomorphic-encryption-friendly privacy-preserving mobile neural network architecture,” in International Conference on Machine Learning. vol. 139, 7102–7110.

Google Scholar

Lou, Q., and Jiang, L. (2019). “She: A fast and accurate deep neural network for encrypted data,” in Advances in neural information processing systems (Red Hook, NY, USA: Curran Associates, Inc.), Vol. 32, 10035–10043.

Google Scholar

McLaren, C. E., Chen, W.-P., Nie, K., and Su, M.-Y. (2009). Prediction of malignant breast lesions from mri features: A comparison of artificial neural network and logistic regression techniques. Acad. Radiol. 16, 842–851. doi:10.1016/j.acra.2009.01.029

PubMed Abstract | CrossRef Full Text | Google Scholar

Riazi, M. S., Laine, K., Pelton, B., and Dai, W. (2020). “Heax: An architecture for computing on encrypted data,” in ACM International Conference on Architectural Support for Programming Languages and Operating Systems, 1295–1309.

Google Scholar

Ribeiro, M., Grolinger, K., and Capretz, M. A. M. (2015). “MLaaS: Machine learning as a Service,” in IEEE International Conference on Machine Learning and Applications (Miami, FL, USA: IEEE), 896–902. doi:10.1109/ICMLA.2015.152

CrossRef Full Text | Google Scholar

Samardzic, N., Feldmann, A., Krastev, A., Devadas, S., Dreslinski, R., Peikert, C., et al. (2021). “F1: A fast and programmable accelerator for fully homomorphic encryption,” in IEEE/ACM International Symposium on Microarchitecture, 17 October 2021, 238–252. doi:10.1145/3466752.3480070

CrossRef Full Text | Google Scholar

Samardzic, N., Feldmann, A., Krastev, A., Manohar, N., Genise, N., Devadas, S., et al. (2022). “Craterlake: A hardware accelerator for efficient unbounded computation on encrypted data,” in IEEE/ACM International Symposium on Computer Architecture, 11 June 2022, 173–187. doi:10.1145/3470496.3527393

CrossRef Full Text | Google Scholar

Wang, Z., Zhang, L., Wang, M., Wang, Z., Zhu, D., Zhang, Y., et al. (2018). High-density nand-like spin transfer torque memory with spin orbit torque erase operation. IEEE Electron Device Lett. 39, 343–346. doi:10.1109/led.2018.2795039

CrossRef Full Text | Google Scholar