XMA2: A crossbar-aware multi-task adaption framework via 2-tier masks

Recently, ReRAM crossbar-based deep neural network (DNN) accelerator has been widely investigated. However, most prior works focus on single-task inference due to the high energy consumption of weight reprogramming and ReRAM cells’ low endurance issue. Adapting the ReRAM crossbar-based DNN accelerator for multiple tasks has not been fully explored. In this study, we propose XMA², a novel crossbar-aware learning method with a 2-tier masking technique to efficiently adapt a DNN backbone model deployed in the ReRAM crossbar for new task learning. During the XMA²-based multi-task adaption (MTA), the tier-1 ReRAM crossbar-based processing-element- (PE-) wise mask is first learned to identify the most critical PEs to be reprogrammed for essential new features of the new task. Subsequently, the tier-2 crossbar column-wise mask is applied within the rest of the weight-frozen PEs to learn a hardware-friendly and column-wise scaling factor for new task learning without modifying the weight values. With such crossbar-aware design innovations, we could implement the required masking operation in an existing crossbar-based convolution engine with minimal hardware/memory overhead to adapt to a new task. The extensive experimental results show that compared with other state-of-the-art multiple-task adaption methods, XMA² achieves the highest accuracy on all popular multi-task learning datasets.

1 Introduction

Deep neural networks (DNNs) have recently shown outstanding performance in many applications. However, the single task’s high degree of specialization restrains its potential development. Motivated by this, researchers began devising algorithms that could sequentially adapt a DNN model to multiple tasks while still performing well on past tasks. This process of gradually adapting the DNN model to learn from various tasks is known as multi-task adaption (MTA) (Mallya et al., 2018; Yang et al., 2021). Fine-tuning (Kornblith et al., 2019) is an intuitive way to adopt the knowledge from the current model (i.e., backbone model) to a new task. Although it offers good accuracy on the new task, updating the weights of the backbone model means forgetting old knowledge upon earlier tasks, thus resulting in significant performance degradation on previous tasks. Such a phenomenon is known as catastrophic forgetting (Parisi et al., 2019; Yang et al., 2021; Kirkpatrick et al., 2017; Mallya et al., 2018), which widely exists in MTA.

From the hardware side, DNNs require a considerable amount of multiply and accumulate (MAC) operations and data movement. In conventional hardware (e.g., CPU and GPU), the massive data communication energy could be almost two orders larger than data processing, known as “memory wall” (Mittal, 2019). In-memory computing (IMC) has attracted tremendous attention as an alternative approach due to its capability to compute MAC directly within the memory array. Such ability significantly alleviates the “memory wall” issue (Eckert et al., 2018; Fan and Angizi, 2017; Chi et al., 2016; Song et al., 2017; Cheng et al., 2019; Xue et al., 2019; Chen W.-H. et al., 2018; Li et al., 2016; Shafiee et al., 2016; Cai et al., 2019; Ankit et al., 2019; Chen and Li, 2018). Compared to other volatile or non-volatile IMC designs, the ReRAM crossbar-based design is a promising candidate for ultra-efficient DNN accelerator for inference due to its simple structure, high on/off ratio, high density, multi-bit per cell storage, and fabrication compatibility with CMOS (Mittal, 2019; Hu et al., 2016; Xu et al., 2015; Chen, 2020; Akinaga and Shima, 2010; Cai et al., 2019). Based on such benefits, many ReRAM crossbar-based designs have been proposed to support DNN inference for a single specialized task (Mittal, 2019; Song et al., 2017; Yin et al., 2020; Eckert et al., 2018; Shafiee et al., 2016; Ankit et al., 2019; Chi et al., 2016; Song et al., 2017).

A general practice to adapt a specialized DNN model deployed in the ReRAM crossbar for a new task is to fine-tune the weight parameters (i.e., cell conductance) of the backbone model using the data of the new task (Kornblith et al., 2019). However, this procedure has to update the conductance (i.e., reprogramming) of nearly all ReRAM cells to represent the new fine-tuned weight parameters. Due to the well-known non-volatile ReRAM device limitations, such as high reprogramming energy and limited endurance, and catastrophic forgetting for large-scale multi-task learning, the fine-tuning (Kornblith et al., 2019) approach is inefficient and impracticable for multi-task learning in practice.

Recently, mask-based learning algorithms (Mallya et al., 2018; Yang et al., 2021; Zhang et al., 2022a,c,b) have been proposed to perform MTA in a more efficient way. For example, piggyback (Mallya et al., 2018), as a representative work, learns a task-specific binary mask ∈ {0, 1} with respect to all weights in an element-wise manner for each new task while freezing the backbone model. Kernel-wise Soft Mask (Yang et al., 2021) extends the task-specific mask from binary to a hybrid binary and real value to improve the adaption capacity. Furthermore, our prior works—XBM (Zhang et al., 2022a) and XMA (Zhang et al., 2022b)—propose the mask-based learning method in a crossbar column-wise pattern with the consideration of deploying on the ReRAM crossbar hardware. Specifically, each learned mask value controls the operations (i.e., on/off and shift) of the entire crossbar column for the new task inference without reprogramming ReRAM cells. Thus, these methods lead to memory and energy reduction compared to the element-wise piggyback. However, the adaption capability of these works is limited, which has a clear accuracy gap compared to fine-tuning-based methods. The main reason is that these methods completely freeze the weights of the backbone model and only apply the binary (Mallya et al., 2018; Zhang et al., 2022a) or shift-value (Zhang et al., 2022b) masks, causing limited optimization space for learning new tasks. Furthermore, the performance of task adaption is highly dependent on the relevance between the source task and the new task. For example, if the data distribution of the new task (Saleh and Elgammal, 2015) is very different from the source task [e.g., Image Net (Russakovsky et al., 2015)], the accuracy of these methods is much worse than that of the fine-tuning-based methods.

In contrast, as we discussed earlier, the fine-tuning method is impractical and inefficient to be deployed on crossbar hardware for MTA due to the high reprogramming energy of ReRAM cells. Therefore, a new approach that could balance both benefits is much needed.

To tackle these issues, in this work, we propose XMA², a novel ReRAM crossbar-aware learning framework via 2-tier masks for MTA, which utilizes the hardware hierarchy of ReRAM crossbar-based DNN accelerator architecture. In XMA², each ReRAM crossbar-based accelerator is associated with a tier-1 PE-wise mask and tier-2 column-wise mask.

• In order to learn a new task, the tier-1 PE-wise mask is used to identify the most critical PEs in a small portion only, which are reprogrammed for learning essential new features. To achieve this, we compute the gradient of each PE-wise mask with respect to the new task data, where the larger gradient magnitude indicates a higher importance level of associated PE with respect to the new task. Then, those top-ranked PEs (e.g., 10%) will be disabled for the current new task to preserve old knowledge but will be replaced with newly learned PEs with task-specific weights. By doing so, each task-specific model could perform inference without forgetting prior knowledge through a combination of task-specific masks to filter prior weights and a small portion of new task-specific weights.

• In order to further improve the learning capability, with the constraint that we cannot program the majority of weight-frozen PEs (a.k.a. the PEs with lower ranking gradients), we adopt a tier-2 crossbar column-wise mask from our prior work (Zhang et al., 2022b,a), which applies a learnable and shift-based scaling factor to the output of each crossbar column. It could also provide extra learning capability to weight-frozen PEs.

The rest of this study is organized as follows: Section 2 covers the background and related works. Section 3 details the methodology of the proposed 2-tier mask learning method. Section 4 demonstrates the hardware implementation. Section 5 gives the algorithm performance on different tasks and hardware evaluation. In the end, Section 6 presents a conclusion.

2 Background

2.1 Multi-task adaption

MTA (Rebuffi et al., 2017; Rosenfeld and Tsotsos, 2018) aims to train a versatile model to adapt multiple visual tasks and domains using as few incremental parameters as possible. Rosenfeld and Tsotsos (2018) recombined the filter channels of the backbone model via controller modules. Liu et al. (2019) proposed domain-specific attention modules for the backbone model. Piggyback (Mallya et al., 2018) tackled the MTA problem by learning the task-specific learnable binary masks while freezing the backbone model except for the classifier head (known as multi-head). The real-value learnable weight masks m^r were first binarized by function Φ with threshold τ:

$\text{Forward}:{\mathit{m}}^{\mathrm{b}}=\mathrm{\Phi }\left({\mathit{m}}^{\mathrm{r}}\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{i}\mathrm{f}{\mathit{m}}^{\mathrm{r}}\ge \tau \hfill \\ 0\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\hfill \end{array}\right.(1)$

$\text{Backward}:\nabla {\mathit{m}}^{\mathrm{b}}=\nabla {\mathit{m}}^{\mathrm{r}}(2)$

As the binarization function is non-differentiable during backpropagation, the straight-through estimator (STE) (Hubara et al., 2016) is employed to estimate the mask gradient ∇m^b. Following the binary mask method, Mallya et al. (2018), Mancini et al. (2018), and Yang et al. (2021) introduced an additional floating-point scaling factor to improve the adaption capacity. However, it suffered increased computation and memory cost during training. In this work, we also leverage the popular task-specific mask-based learning methodology to overcome the forgetting of prior knowledge.

2.2 ReRAM-based NN accelerator

With the high parallelism and dense storage, ReRAM-based IMC has emerged as an attractive solution for DNN inference (Mittal, 2019; Song et al., 2017; Yin et al., 2020; Eckert et al., 2018; Zhang et al., 2022a,b; Shafiee et al., 2016; Ankit et al., 2019; Chi et al., 2016; Song et al., 2017). Figure 1 depicts the basic architecture of the 1T1R crossbar array. The parallelly performed analog computation along the column provides high efficiency to the vector–matrix multiplication (VMM). Given the pre-trained DNN model, the weights are programmed as the conductance G inside ReRAM cells. The input vector is represented as the analog voltage pulses V_in (Hu et al., 2016; Zhang and Hu, 2020; Chen, 2020), fed through the horizontal source-line. The VMM output is the product current between the incoming voltage V_in and programmed conductance G along the bit line (BL).

FIGURE 1

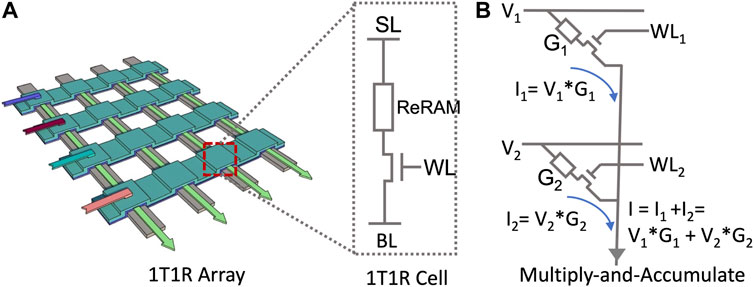
FIGURE 1. ReRAM 1T1R crossbar array (Zhang et al., 2022b).

Attracted by the high energy efficiency, various ReRAM-based neural network accelerators have been proposed (Mittal, 2019; Song et al., 2017; Yin et al., 2020; Eckert et al., 2018). However, most of the existing ReRAM-based IMC accelerators focus on DNN inference with a one-time deployed pre-trained model, which lacks the flexibility to the changing tasks. Adapting the new tasks often requires additional training and second-time deployment. Recently, several ReRAM-crossbar-based accelerator designs have been proposed to support continual learning. Efficient Multi-Task Architecture for Transfer Learning (Chen and Li, 2018; Li et al., 2022) analyzed the data flow and made the hardware modification to support backpropagation. It enabled on-device weight update and continual learning but demanded high endurance of the ReRAM device. Moreover, frequent weight update consumes a lot of energy and causes a loss of energy benefit. To avoid the expensive weight update/reprogramming, XBM (Zhang et al., 2022a) first performed the on-device mask-based multi-task adaptation in a column-wise fashion. It learns the unforeseen tasks corresponding to unraveling the column-wise masks while keeping the backbone model fixed. Compared to the prior works, enabling the columns for the new tasks eliminates the programming/fine-tuning cost, leading to the high energy efficiency of MTA. Motivated by XBM, XMA (Zhang et al., 2022b) introduced the shifted mask to enrich the learning space of multi-task adaptation, elevating the accuracy with negligible hardware overhead. Under the context of MTA, naïve fine-tuning provides the best accuracy with the highest hardware cost. Embracing fine-tuning in a hardware-friendly manner remains unexplored. Different from the prior works (Zhang et al., 2022a,b), where the MTA completely relies on the on-device adjustment while leaving the weight untouched, this work balances the ReRAM crossbar deployment cost and the accuracy-driven model fine-tuning.

2.3 Neural network quantization and pruning

Quantization has been widely studied as an effective way to compress the DNN model and elevate the energy efficiency of computation while maintaining accuracy by compressing the data precision (e.g., weight and activation) (Zhou et al., 2016; Choi et al., 2019; Park and Yoo, 2020). The stringent resource constraint of the hardware accelerator necessitates efficient quantization algorithms. Early research works (Zhou et al., 2016) demonstrated the feasibility of discretizing the full precision weights between the fixed boundaries [−1, 1]. However, the deterministic quantization range failed to fit the layer-wise distributions adaptively. It leads to sub-optimal model performance. Various studies have introduced layer-wise learnable clipping parameters to minimize quantization error during training. Under this context, PACT (Choi et al., 2018) dynamically clipped the activation based on the trainable quantization boundary. However, PACT (Choi et al., 2019) only utilized the gradient inside the truncation range, leading to insufficient learning. To avoid this issue, we adopt the quantization algorithm from PROFIT (Park and Yoo, 2020) to train the DNN model.

Orthogonal to quantization, the model size reduction obtained from the sparse neural network also leads to practical hardware benefits (e.g., energy and latency reduction). The pioneering research works (Han et al., 2015) have shown that DNNs can still retain performance with high element-wise weight sparsity. However, the high fine-grained sparsity introduces a large amount of index memory storage and irregular memory access for hardware computation. This promotes the structured pruning scheme as a hardware-friendly solution (Meng et al., 2021). For structured and unstructured pruning, selecting an appropriate importance metric is essential to localize the unimportant weights. The score-based pruning justifies the weight redundancy based on magnitude (Han et al., 2015) or normalized impact score (Lee et al., 2020) and then applies the binary mask to the forward pass. However, the score-based sparsification ignores the model’s vulnerability with respect to pruning. Motivated by this, SNIP (Lee et al., 2018) determined the connection sensitivity based on gradient rather than weight magnitude. Removing the Top-K connections with the least sensitivity mitigates the impact of pruning and further optimizes the overall sparse model architecture.

3 Methodology

3.1 Overview

In this section, we introduce our 2-tier mask-based learning method for crossbar-aware MTA. The processing element (PE) typically consists of one or more ReRAM crossbar arrays that share the peripheral circuits and buffers. For simplicity, we use one crossbar per PE as an example, where each PE is associated with one tier-1 PE-wise mask. As shown in Figure 2, during the offline training for one new task, the gradient of such tier-1 PE-wise mask will be first computed based on the new task data, where the larger magnitude of such PE-wise mask gradient indicates the higher importance level of associated PE with respect to the new task (Lee et al., 2018). Based on such theory, we pick the top-P-ranked (“P” is a parameter with a small value, e.g., 10%) PEs as our candidate weights to be reprogrammed for learning the new task, defined as adaptable weights. In comparison, we define the frozen weights in the remaining PEs as non-adaptable weights. However, to preserve the prior knowledge without forgetting, we choose to disable and retain the top-P-ranked PEs for old tasks. Meanwhile, we replace those PEs with the same number of new PEs with newly learned adaptable weights for the new task. Thus, each task-specific model could perform inference without forgetting prior knowledge through a combination of task-specific masks to filter prior weights and new task-specific adaptable weights. To further improve the learning capability, in this work, with a constraint that we cannot program the frozen weights (a.k.a non-adaptable weight in the PEs with lower gradient ranking), we adopt a tier-2 crossbar column-wise mask inherited from Zhang et al. (2022a,b). It is a learnable mask that could apply a learnable and shift-based scaling factor to the output of each corresponding crossbar column. It could also provide extra learning capability to the non-adaptable weight kernels in the weight-frozen PEs. The following subsections will present the detailed 2-tier mask for the multi-task learning procedure.

FIGURE 2

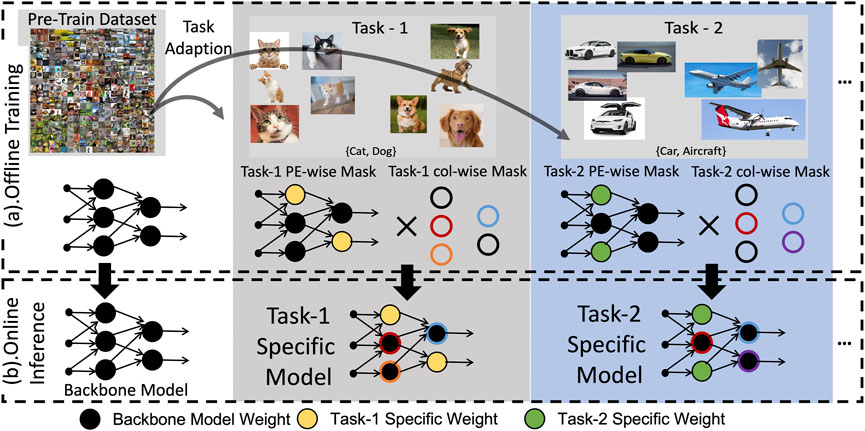
FIGURE 2. Overview of the crossbar-aware multi-task adaption framework, including PE-wise masking for retraining and col-wise masking for activation adjustment.

3.2 Tier-1 PE-wise mask learning

In the ReRAM crossbar-based DNN accelerator design, the whole structure consists of multiple PEs, the basic computing units to perform VMM to support convolution operations. Based on this, we define the PE-wise binary mask m^PE ∈ {0, 1} to identify and re-learn the adaptable weight in the corresponding small portion of PEs for the new task while freezing the weights in the remaining PEs. The “1” and “0” values of the PE-wise mask indicate the adaptable weights and the rest of the non-adaptive weights, respectively, which are learned by the gradient ranking method.

3.2.1 Gradient ranking to identify PE-wise adaptable weights

Inspired by the pruning work (Lee et al., 2018), which removed the unimportant weights before the single-task training, we propose to identify the task-adaptable weights based on their importance in the changing loss of the new task. Mathematically, given a new task $\mathcal{D}$, the optimization objective of the PE-wise mask learning can be formulated as follows:

$\underset{m^{PE}}{\min }\mathcal{L}\left(w^{PE}\odot m^{PE},\mathcal{D}\right)s.t.\frac{\Vert m^{PE}{\Vert }_0}{N}\le P(3)$

where $\mathcal{L}(\cdot )$ is the loss function, w^PE are weights distributed into PEs, N is the total number of PEs, and P is the pre-defined ratio of the adaptable weights. From the perspective of the changing loss, the impact of removing partial weights ${w_i}^{PE}$ can be formulated as follows:

$\mathrm{\Delta }\mathcal{L}\left({w_i}^{PE},\mathcal{D}\right)=\mathcal{L}\left({m_i}^{PE}=1,\mathcal{D}\right)-\mathcal{L}\left({m_i}^{PE}=0,\mathcal{D}\right)(4)$

According to Lee et al. (2018), the changed loss can be approximated as follows:

$\mathrm{\Delta }\mathcal{L}\left({w_i}^{PE},\mathcal{D}\right)\approx \frac{\partial \mathcal{L}}{\partial \left({w_i}^{PE}\odot {m_i}^{PE},\mathcal{D}\right)}\left({w_i}^{PE}\odot {m_i}^{PE}\right)=\frac{\partial \mathcal{L}}{\partial {m_i}^{PE}}(5)$

Equation 5 shows that the gradient of the PE-wise mask can approximate the loss change for the new task optimization. Therefore, we use the gradient magnitude of the PE-wise mask to indicate the adaptable weights. The large value of the unsigned gradient magnitude represents the corresponding PE-wise weights sensitive to the changing loss, which has to be re-learned. Based on this, we perform the gradient ranking to generate the sensitivity score computed by normalizing the gradient magnitude of the PE-wise masks, as shown in Algorithm 1. Subsequently, the top-P largest values are selected as “1” in PE-wise masks, and the rest of the PEs are flagged as “0” values. Here, “P” is a hyperparameter that could be tuned based on the specific dataset and hardware availability. Aligning with prior works, using only one mini-batch data to calculate the gradient is precise enough. It is worth noting that the computation cost is negligible compared to the whole training procedure.

Algorithm 1. PE-wise mask learning.

3.3 Tier-2 column-wise mask for weight-frozen PEs

3.3.1 The offline shift-based mask learning

As explained in the previous section, the main purpose of the tier-1 PE-wise mask is to select the new task-specific PEs and reprogram the corresponding weights to learn new features of the new task. To reduce the ReRAM cell programming energy, the portion of the new task-specific PEs needs to be small (e.g., 10%). Thus, it leaves the majority of PEs non-adaptable or frozen. To further incorporate learning capability into those frozen PEs, in this work, we adopt the column-wise shift mask for each crossbar column in the frozen PEs motivated by our prior work (Zhang et al., 2022b).

As in the piggyback method (Mallya et al., 2018), the adopted binary mask is generated by binarizing the trainable real-valued masks m^r, as presented in Eq. 1. Such real-valued masks’ magnitudes represent the importance of the corresponding weight of the backbone model. Inspired by this, the real-valued masks could help improve the adaption capability. However, from the hardware perspective, multiplying a mask (i.e., 32-bit floating-point number) for every weight/partial sum is a tremendous overhead in both latency and energy. The learnable shift-based mask m^s is a hardware-friendly trade-off that keeps the “1” in the binary mask but introduces additional shift factors a^s, a replacement of the zero elements in the binary mask counterpart to improve the adaption capacity with the hardware-friendly operation and negligible overhead. The shift-based mask can be expressed as follows:

$m^s=\left[m_{m^b=1}^b,a_{m^b=0}^s\right](6)$

where $m_{m^b=1}^b$ means the shift-based mask with all “1”s and $a_{m^b=0}^s$ denotes that the “0” in the binary mask replaced by the shift factor. It can be understood as we fix the important kernels (“1” in the binary mask) and scale the unimportant kernels (“0” in the binary mask) as different shift levels for the new task.

3.3.1.1 Learn the shift factor a^s

In practice, we first normalize the real-valued mask under the range [0,1], serving as a scaling factor to represent the weight importance for MTA. Then, the normalized real-valued mask is quantized to the nearest power-of-two values (i.e., 1/2, 1/4, and 1/8) or zero. Accordingly, the shift-based mask m^s could maximally include three different shift levels (i.e., 1/8, 1/4, and 1/2) and two non-shift levels (i.e., 0 and 1). By doing so, the computing/memory-hungry multiplication operation between the real-valued mask and fixed weight can be replaced by the shift operation, resulting in computation and energy reduction. Moreover, such shift operation can be implemented by reusing the existing shift adder (SA) in most ReRAM-based IMC platforms without increasing hardware overhead. In addition, selecting the number of shift levels “N” in shift-based mask is flexible that could be adjusted to achieve different trade-offs between accuracy and mask overhead. For example, if N = 3, it supports maximally three different shift levels and two non-shift levels (i.e., 0, 1/8, 1/4, 1/2, and 1), achieving the best accuracy. Notably, mask value “1” means no shift, and mask value “0” means turning off the current column. If N = 0, the shift-based mask is equivalent to the binary mask with the smallest mask memory overhead.

3.3.1.2 Learn the binary mask m^b

To learn the binary mask, we leverage the Gumbel-Sigmoid trick, inspired by Gumbel-Softmax (Jang et al., 2016), which performs a differential sampling to approximate a categorical random variable. As the Sigmoid function σ(˙̇) can be viewed as a special two-class case of softmax, it can be defined as follows:

$p\left({\mathit{m}}^r\right)=\frac{1}{1+\exp \left(-\left(\log {\pi }_0+g_0-g_1\right)/T\right)},(7)$

where π₀ represents σ(m^r). g₀ and g₁ are samples from the Gumbel distribution. The temperature T is a hyperparameter to adjust the range of input values. Benefiting from the differential property of Eq. 7, the real-value mask m^r can be embedded with existing gradient-based backpropagation training. To represent p (m^r) as binary format m^b, we use a hard threshold (i.e., 0.5) during the forward propagation of training. Because most values in the distribution of p (m^r) will move toward 0 or 1 during training, generating the binary mask by p (m^r) (instead of the real-value mask m^r directly) could have a more accurate decision, resulting in better accuracy.

3.3.2 Column-wise mask

From the system hierarchy perspective, applying an element-wise mask to a 1T1R array is challenging because it needs to manipulate every ReRAM cell independently and store the same sized mask as the 1T1R array. Inspired by the 1T1R crossbar array parallelism, the entire row or column share the same input, and the transistors’ gates are connected horizontally or vertically. Such row-/column-wise parallelism allows the row-/column-wise control for the existing crossbar design. In order to leverage the row/column-wise parallelism, the mask size is defined as G × kh × kw to make it consistent with the size of a crossbar column, namely a column-wise mask, where the group G ∈ {1, C_in}. C_in is the input channel dimension. This way, a single mask value can control the entire column of a crossbar array, which improves the computation efficiency significantly compared to the element-wise mask. In our design, the size of the crossbar column is set as 72 × 1. Equivalently, we define the group size of the kernel-wise mask as 8 × 3 × 3 with the group G = 8 in the algorithm.

4 Hardware implementation

Figure 3 shows the overview of ReRAM crossbar architecture to support the proposed 2-tier mask method. It consists of an I/O interface for data exchange, multiple processing elements (PEs) grouped as banks for computing, and the interface controller to decode the instruction. Inside the bank, PEs have been divided into two groups. Most of the PEs are used to map the backbone model. Besides, some PEs are left as spare to reserve for new task adaption as adaptable weights. Note, for XMA and XBM, the spare PEs are not used for adaptable weights because they do not have the tire-1 PE-wise mask. Each PE includes ReRAM crossbar sub-arrays for the convolution operation; global ReLU and adder tree are used to post-process the partial sum from the sub-arrays. Inside the ReRAM sub-array, convolution kernels are mapped on ReRAM cells as conductance. According to the ReRAM device and the kernel size, it may need multiple ReRAM cells to represent one convolution kernel. For example, suppose each ReRAM cell can represent four different statuses equal to 2-bit information. Moreover, the convolution kernel is quantized to 4 bits. Then, each convolution weight requires two adjacent cells to map its higher and lower bits. In convolutional neural networks (CNNs), a convolution kernel usually exists as a 4D tensor with dimensions H × W × In_c × Out_c. Traditionally, the convolution kernel is unrolled along the Out_c dimension to minimize the data movement because the inputs are identical for each Out_c dimension, although the H × W × In_c weights are unique. Analogous to the ReRAM crossbar, input is fed through the horizontal SL and shared with the entire row. Therefore, different H × W × In_c weights are unrolled to different 1D vectors and mapped to ReRAM columns to share the same inputs. Due to the precision mismatch between the quantized weight and the ReRAM cell, the weight may be divided into multiple columns. Each column only carries a partial accumulation which ADC reads as partial activation. The SA manipulates the partial activation to reconstruct the actual activation. On top of each column, we add a mask buffer that stores the column-wise mask and controls how to shift the activation. The processed activation is then sent to the global adder tree and ReLU, which subsequently is conveyed to the next layer as the input.

FIGURE 3

FIGURE 3. Hardware structure and implementation.

After the offline new task adaption learning, the tier-1 PE-wise mask indicates which PE needs to be disabled and replaced with newly learned PE (implemented through programming the spare PEs in the system). In contrast, the rest of PE will still need to be used in the new task-specific model. For the rest of the weight-frozen PEs, the tier-2 column-wise mask values are stored in the mask buffers. With the input voltage, V applied on each row-wise SL, the current through each ReRAM cell with conductance G is calculated by the multiplication operation I = V × G. The current is then accumulated on the column-wise BL as ∑I and converted to bit series by ADC as the MAC result. As explained earlier, each column’s ADC output is just a partial result and needs the SA to construct the final result. During this step, the SA also reads the column-wise shift mask from the mask buffer. Thus, the SA shifts the partial sum result based on its significance and the corresponding col-wise shift mask values. Afterward, the ReLU unit and local storage buffer process the data the same as the backbone model.

5 Experiment result

5.1 Algorithm performance

In this section, we evaluate the proposed 2-tier masking performance. For a fair comparison and following the setup of prior works, we choose the popular ResNet-50 (He et al., 2015) as our backbone model, which is pre-trained on the ImageNet dataset (Russakovsky et al., 2015). Five fine-grained object classification datasets are utilized as the new tasks to perform the MTA, including CUBS (Wah et al., 2011), Stanford Cars (Krause et al., 2013), Flowers (Nilsback and Zisserman, 2008), WikiArt (Saleh and Elgammal, 2015), and Sketch (Eitz et al., 2012). These datasets are summarized in Table 1.

TABLE 1

TABLE 1. Datasets examined in experiments.

5.1.1 Performance of col-wise mask

Table 2 shows the inference accuracy of the column-wise mask on different datasets. In this setup, there is no PE-wise mask. We assume no weight reprogramming/updating for all tasks, and the column-wise mask applies to all PEs. We quantize the backbone model to 4-bit precision (4-bit weight and 4-bit activation) to simulate the crossbar inference behavior. The quantization method is adopted from PROFIT (Park and Yoo, 2020). We choose the group size G = 8 in the experiment. The group concept also helps cut down the training parameters, which boosts the training convergence speed. Moreover, sharing the mask value among the entire column significantly saves the memory overhead for mask storage.

TABLE 2

TABLE 2. The impact of different shift levels.

Different shift levels determine the mask storage overhead and affect the accuracy. Table 2 also shows the accuracy and mask overhead for different shift levels. More shift levels show better accuracy in the cost of more mask overhead, where the mask overhead is defined as the complete storage required by the mask over the storage required by all the weights in the backbone model. As the shift level goes down, one extreme example is when no shift level is available in the range of [0,1], which means the mask only has binary values. In that case, our shift-based mask method (XMA) is equivalent to the column-wise binary mask (XBM). Due to the group mask sharing, binary group mask size is only $\frac{1}{72}$ of piggyback. For the ResNet-50 backbone model, piggyback’s element-wise binary mask requires 23M/8 = 2.88 MB, whereas the binary mask only consumes around 40 KB. Although the binary mask claims the least mask overhead, it achieves the worst accuracy than other shift-based methods. For the best accuracy, three shift levels only require less than 100 KB storage for the mask, which is only 3.4% of that in piggyback (i.e., 29.4× reduction). Despite this reduction, on average, the accuracy is 3.2% higher than that of piggyback.

5.1.2 Performance of 2-tier XMA²

Table 3 shows the performance of the 2-tier mask-based XMA² method on the aforementioned datasets with different methods and configurations. It shows fine-tuned results based on the floating-point number representation to demonstrate the theoretical performance baseline. With the help of the floating-point number’s high precision, the fine-tuned-based method has the highest flexibility to change any weight to any level. Therefore, fine-tuning the backbone model with a floating-point number achieves the best accuracy in all datasets.

TABLE 3

TABLE 3. Multi-task adaption accuracy (%).

For the other methods, we adopt quantization-aware training (QAT) to simulate the performance on the actual hardware environment. PROFIT (Park and Yoo, 2020) is used to quantize both weight and activation to 4 bits. The piggyback scheme adopts the binary element-wise mask, where the binary precision of the mask limits the flexibility of the backbone model. Thus, piggyback shows slightly worse accuracy than fine-tuning. The shift-mask-only (XMA) method adopts the column-wise shift mask with five different mask levels (three shift levels: 1/8, 1/4, 1/2; and two non-shift levels: 0, 1). We assume the ReRAM crossbar array size is 72 × 72, which means each array can map a 3 × 3 × 8 × 72 convolution kernel. Thus, the group size sharing the same mask value in each column is 3 × 3 × 8. As ImageNet is much larger and more complex than other datasets, the shift-mask-only performance is already near fine-tuning for most datasets. However, there is still a considerable gap between fine-tuning and shift-mask-only methods. Especially on the WikiArt dataset, the shift-mask-only method shows almost a 5% accuracy drop compared to fine-tuning. Our proposed 2-tier mask is marked as shift-mask + fine-tuning because the two different masks are associated with weight fine-tuning and activation shift, respectively. We conduct a series of experiments with 5% PE-wise weight fine-tuning to 40% PE-wise weight fine-tuning to explore how much weight fine-tuning is necessary to achieve a considerable accuracy improvement. The result shows that the accuracy improved significantly even with the help of 10% weight fine-tuning. It achieves higher accuracy than those of the piggyback and shift-mask-only methods for all datasets. This is especially true for the WikiArt dataset, where the piggyback and shift-mask-only methods show the most degraded accuracy. Note that the accuracy does not increase monotonically with increasing tunable parameters. This is because fine-tuning is not element-wise. We fine-tune the weights in a PE-wise fashion. We first rank the PEs based on the sensitivity score. Therefore, when we fine-tune more weights (more PEs), the extra weights (PEs) are less sensitive to the target dataset (minor sensitivity score). Thus, fine-tuning those weights (PEs) will have less benefit. On the contrary, the less sensitive PEs extract more general features. As the new task is usually way smaller than the ImageNet dataset (some dataset even has more test images than training images), fine-tuning those less sensitive PEs will lose more general features. More tunable parameters make the NN harder to train.

5.2 Hardware evaluation

We implement the proposed 2-tier mask algorithm on hardware, as shown in Figure 3. The hardware performance of different algorithms is evaluated based on NeuroSim (Peng et al., 2019). The 4-bit quantized DNN weights are programmed to the RRAM array with an HfO₂-based 2-bit per cell device, characterized by Wu et al. (2018) with a 32 nm CMOS node. The ReRAM array characteristics and the total area usage are summarized in Table 4 and Figure 4. Each ReRAM column is connected to a 5-bit successive approximation register (SAR) analog-to-digital converter (ADC). The global buffer is designated to hold the largest activation feature map of the model. Figure 5 shows the overhead of different sub-tasks with different algorithms. The total inference energy of each sub-task is the summation of inference energy and the reprogramming energy. For each updated weight element, the reprogramming energy can be computed based on the write voltage, write pulses, and conductance level changes (Wu et al., 2018; Chen P.-Y. et al., 2018). Task-specific fine-tuning generates the highest accuracy but requires universal reprogramming or even second-time deployment. The high energy consumption of reprogramming hinders the pragmatic benefits of continual learning. Piggyback (Mallya et al., 2018) partially programs the weights to zero for different tasks. Compared to the inference energy, reprogramming the element-wise sparsity elevates the total energy up to 8.16×. Furthermore, the element-wise sparsity requires additional fine-grained sparse indexes, leading to intricate hardware design and storage overhead.

TABLE 4

TABLE 4. Specification of ReRAM hardware and peripheral circuits.

FIGURE 4

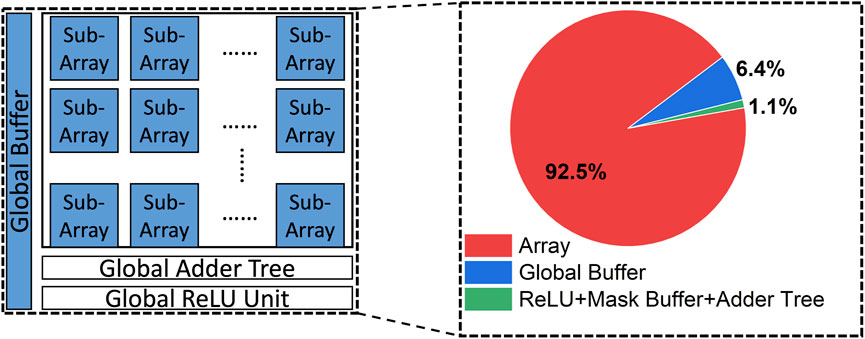
FIGURE 4. Area breakdown of 4-bit ResNet-50 backbone model hardware deployment. The peripheral circuits, including the ReLU module, adder tree, and mask buffer.

FIGURE 5

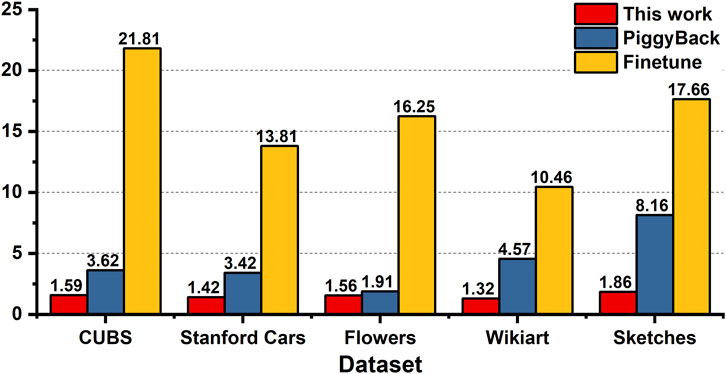
FIGURE 5. Total energy (reprogramming + inference)/inference energy for different learning tasks and methods.

Different from the naïve fine-tuning or piggyback (Mallya et al., 2018) learning, the proposed algorithm updates the model in a structured manner. The marginal 10% reprogramming ReRAM columns for different sub-tasks updates the model without fine-grained indexes. Compared to the fine-tuning and piggyback (Mallya et al., 2018) methods, this work reduces the total energy consumption to 13.72× and 4.38×, respectively, as shown in Figure 4. Such significant energy reduction of the proposed XMA² algorithm unleashes the practical advantage of continual learning.

6 Conclusion

In summary, we proposed XMA², a 2-tier mask-based learning framework, to efficiently and accurately deploy the MTA to a crossbar-based DNN accelerator. The main contribution of XMA² is that it consists of two different levels of masks that work on new knowledge learning and old knowledge recombination. It can keep the neural network structure and the data flow for new task learning. Furthermore, it is flexible to make the trade-off between weight reprogramming overhead and the new task performance. Moreover, the XMA² reuses the existing SA to apply the shift-based mask onto a fixed weight and minimize the hardware overhead. XMA² significantly saves inference energy compared to other mask-based methods while achieving higher accuracy.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, Further inquiries can be directed to the corresponding author.

Author contributions

FZ: the first author conducts most of the experiments and paper writing. LY: the second author helps conduct the experiments, paper writing, and idea discussion. JM: the third author helps conduct the hardware evaluation and related section writing. JS and YC helped discuss the idea and experiments. Also, help to proofread/polish the manuscript, DF, the corresponding author, helps conduct the cooperation, form the idea, and proofread/polish the manuscript.

Funding

This work is supported in part by the National Science Foundation under Grant No.2003749, and No. 2144751.

Acknowledgments

Some of the material published within this article first appeared as part of the Proceedings of the 59th ACM/IEEE Design Automation Conference. The corresponding conference paper can be accessed here: https://dl.acm.org/doi/10.1145/3489517.3530458. The authors confirm that they hold the copyright to the material published within this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akinaga, H., and Shima, H. (2010). Resistive random access memory (reram) based on metal oxides. Proc. IEEE 98, 2237–2251. doi:10.1109/JPROC.2010.2070830

CrossRef Full Text | Google Scholar

Ankit, A., Hajj, I. E., Chalamalasetti, S. R., Ndu, G., Foltin, M., Williams, R. S., et al. (2019). “Puma: A programmable ultra-efficient memristor-based accelerator for machine learning inference,” in Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems (New York, NY, USA: Association for Computing Machinery), 715–731. doi:10.1145/3297858.3304049

CrossRef Full Text | Google Scholar

Cai, F., Correll, J. M., Lee, S. H., Lim, Y., Bothra, V., Zhang, Z., et al. (2019). A fully integrated reprogrammable memristor–cmos system for efficient multiply–accumulate operations. Nat. Electron. 2, 290–299. doi:10.1038/s41928-019-0270-x

CrossRef Full Text | Google Scholar

Chen, F., and Li, H. (2018). “Emat: An efficient multi-task architecture for transfer learning using reram,” in 2018 IEEE/ACM International Conference on Computer-Aided Design (ICCAD). doi:10.1145/3240765.3240805

CrossRef Full Text | Google Scholar

Chen, P.-Y., Peng, X., and Yu, S. (2018a). Neurosim: A circuit-level macro model for benchmarking neuro-inspired architectures in online learning. IEEE Trans. Comput. -Aided. Des. Integr. Circuits Syst. 37, 3067–3080. doi:10.1109/tcad.2018.2789723

CrossRef Full Text | Google Scholar

Chen, W.-H., Li, K.-X., Lin, W.-Y., Hsu, K.-H., Li, P.-Y., Yang, C.-H., et al. (2018b). “A 65nm 1mb nonvolatile computing-in-memory reram macro with sub-16ns multiply-and-accumulate for binary dnn ai edge processors,” in 2018 IEEE International Solid - State Circuits Conference - (ISSCC), 494–496. doi:10.1109/ISSCC.2018.8310400

CrossRef Full Text | Google Scholar

Chen, Y. (2020). Reram: History, status, and future. IEEE Trans. Electron Devices 67, 1420–1433. doi:10.1109/TED.2019.2961505

CrossRef Full Text | Google Scholar

Cheng, M., Xia, L., Zhu, Z., Cai, Y., Xie, Y., Wang, Y., et al. (2019). Time: A training-in-memory architecture for rram-based deep neural networks. IEEE Trans. Comput. -Aided. Des. Integr. Circuits Syst. 38, 834–847. doi:10.1109/TCAD.2018.2824304

CrossRef Full Text | Google Scholar

Chi, P., Li, S., Xu, C., Zhang, T., Zhao, J., Liu, Y., et al. (2016). Prime: A novel processing-in-memory architecture for neural network computation in reram-based main memory. SIGARCH Comput. Archit. News 44, 27–39. doi:10.1145/3007787.3001140

CrossRef Full Text | Google Scholar

Choi, J., Venkataramani, S., Srinivasan, V., Gopalakrishnan, K., Wang, Z., and Chuang, P. (2019). “Accurate and efficient 2-bit quantized neural networks,” in MLSys.

Google Scholar

Choi, J., Wang, Z., Venkataramani, S., Chuang, P. I.-J., Srinivasan, V., and Gopalakrishnan, K. (2018). Pact: Parameterized clipping activation for quantized neural networks.

Google Scholar

Eckert, C., Wang, X., Wang, J., Subramaniyan, A., Iyer, R., Sylvester, D., et al. (2018). “Neural cache: Bit-serial in-cache acceleration of deep neural networks,” in Proceedings of the 45th Annual International Symposium on Computer Architecture, 383–396. doi:10.1109/ISCA.2018.00040

CrossRef Full Text | Google Scholar

Eitz, M., Hays, J., and Alexa, M. (2012). How do humans sketch objects? ACM Trans. Graph. (Proc. SIGGRAPH) 31, 1–10. doi:10.1145/2185520.2185540

CrossRef Full Text | Google Scholar

Fan, D., and Angizi, S. (2017). “Energy efficient in-memory binary deep neural network accelerator with dual-mode sot-mram,” in 2017 IEEE International Conference on Computer Design (ICCD). 609–612. doi:10.1109/ICCD.2017.107

CrossRef Full Text | Google Scholar

Han, S., Mao, H., and Dally, W. J. (2015). Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. doi:10.48550/ARXIV.1510.00149

CrossRef Full Text | Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2015). Deep residual learning for image recognition.

Google Scholar

Hu, M., Strachan, J. P., Li, Z., Grafals, E. M., Davila, N., Graves, C., et al. (2016). “Dot-product engine for neuromorphic computing: Programming 1t1m crossbar to accelerate matrix-vector multiplication,” in 2016 53nd ACM/EDAC/IEEE Design Automation Conference (DAC). doi:10.1145/2897937.2898010

CrossRef Full Text | Google Scholar

Hubara, I., Courbariaux, M., Soudry, D., El-Yaniv, R., and Bengio, Y. (2016). “Binarized neural networks,” in Advances in neural information processing systems, 4107–4115.

Google Scholar

Jang, E., Gu, S., and Poole, B. (2016). Categorical reparameterization with gumbel-softmax.

Google Scholar

Kirkpatrick, J., Pascanu, R., Rabinowitz, N., Veness, J., Desjardins, G., Rusu, A. A., et al. (2017). Overcoming catastrophic forgetting in neural networks. Proc. Natl. Acad. Sci. U. S. A. 114, 3521–3526. doi:10.1073/pnas.1611835114

PubMed Abstract | CrossRef Full Text | Google Scholar

Kornblith, S., Shlens, J., and Le, Q. V. (2019). “Do better imagenet models transfer better?,” in IEEE/CVF Conference on Computer Vision and Pattern Recognition.

Google Scholar

Krause, J., Stark, M., Deng, J., and Fei-Fei, L. (2013). “3d object representations for fine-grained categorization,” in 2013 IEEE International Conference on Computer Vision Workshops, 554–561. doi:10.1109/ICCVW.2013.77

CrossRef Full Text | Google Scholar

Lee, J., Park, S., Mo, S., Ahn, S., and Shin, J. (2020). “Layer-adaptive sparsity for the magnitude-based pruning,” in International Conference on Learning Representations.

Google Scholar

Lee, N., Ajanthan, T., and Torr, P. (2018). “Snip: Single-shot network pruning based on connection sensitivity,” in International Conference on Learning Representations.

Google Scholar

Li, S., Xu, C., Zou, Q., Zhao, J., Lu, Y., and Xie, Y. (2016). “Pinatubo: A processing-in-memory architecture for bulk bitwise operations in emerging non-volatile memories,” in Proceedings of the 53rd Annual Design Automation Conference (New York, NY, USA: Association for Computing Machinery). doi:10.1145/2897937.2898064

CrossRef Full Text | Google Scholar

Li, Y., Zhang, W., Xu, X., He, Y., Dong, D., Jiang, N., et al. (2022). Mixed-precision continual learning based on computational resistance random access memory. Adv. Intell. Syst. 4, 2200026. doi:10.1002/aisy.202200026

CrossRef Full Text | Google Scholar

Liu, S., Johns, E., and Davison, A. J. (2019). “End-to-end multi-task learning with attention,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 1871–1880.

CrossRef Full Text | Google Scholar

Mallya, A., Davis, D., and Lazebnik, S. (2018). “Piggyback: Adapting a single network to multiple tasks by learning to mask weights,” in European Conference on Computer Vision (ECCV).

CrossRef Full Text | Google Scholar

Mancini, M., Ricci, E., Caputo, B., and Bulò, S. R. (2018). “Adding new tasks to a single network with weight transformations using binary masks,” in Proceedings of the European Conference on Computer Vision (ECCV) Workshops.

Google Scholar

Meng, J., Yang, L., Peng, X., Yu, S., Fan, D., and Seo, J.-S. (2021). Structured pruning of RRAM crossbars for efficient in-memory computing acceleration of deep neural networks. IEEE Trans. Circuits Syst. Ii. 68, 1576–1580. doi:10.1109/TCSII.2021.3069011

CrossRef Full Text | Google Scholar

Mittal, S. (2019). A survey of reram-based architectures for processing-in-memory and neural networks. Mach. Learn. Knowl. Extr. (2019). 1, 75–114. doi:10.3390/make1010005

CrossRef Full Text | Google Scholar

Nilsback, M.-E., and Zisserman, A. (2008). “Automated flower classification over a large number of classes,” in 2008 Sixth Indian Conference on Computer Vision, Graphics Image Processing, 722–729. doi:10.1109/ICVGIP.2008.47

CrossRef Full Text | Google Scholar

Parisi, G. I., Kemker, R., Part, J. L., Kanan, C., and Wermter, S. (2019). Continual lifelong learning with neural networks: A review. Neural Netw. 113, 54–71. doi:10.1016/j.neunet.2019.01.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, E., and Yoo, S. (2020). “Profit: A novel training method for sub-4-bit mobilenet models,” in European Conference on Computer Vision, 430–446.

CrossRef Full Text | Google Scholar

Peng, X., Huang, S., Jiang, H., Lu, A., and Yu, S. (2019). “DNN+NeuroSim: An end-to-end benchmarking framework for compute-in-memory accelerators with versatile device technologies,” in IEEE International Electron Devices Meeting.

Google Scholar

Rebuffi, S.-A., Bilen, H., and Vedaldi, A. (2017). Learning multiple visual domains with residual adapters. Adv. Neural Inf. Process. Syst., 506–516.

Google Scholar

Rosenfeld, A., and Tsotsos, J. K. (2018). Incremental learning through deep adaptation. IEEE Trans. Pattern Anal. Mach. Intell. 42, 651–663. doi:10.1109/tpami.2018.2884462

PubMed Abstract | CrossRef Full Text | Google Scholar

Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S., Ma, S., et al. (2015). Imagenet large scale visual recognition challenge.

Google Scholar

Saleh, B., and Elgammal, A. (2015). Large-scale classification of fine-art paintings: Learning the right metric on the right feature. Corr. abs, 00855.

Google Scholar

Shafiee, A., Nag, A., Muralimanohar, N., Balasubramonian, R., Strachan, J. P., Hu, M., et al. (2016). “Isaac: A convolutional neural network accelerator with in-situ analog arithmetic in crossbars,” in Proceedings of the 43rd International Symposium on Computer Architecture, 14–26. doi:10.1109/ISCA.2016.12

CrossRef Full Text | Google Scholar

Song, L., Qian, X., Li, H., and Chen, Y. (2017). “Pipelayer: A pipelined reram-based accelerator for deep learning,” in 2017 IEEE International Symposium on High Performance Computer Architecture, 541–552. doi:10.1109/HPCA.2017.55

CrossRef Full Text | Google Scholar

Wah, C., Branson, S., Welinder, P., Perona, P., and Belongie, S. (2011). The caltech-UCSD birds-200-2011 dataset. Tech. Rep. CNS-TR-2011-001. California Institute of Technology.

Google Scholar

Wu, W., Wu, H., Gao, B., Yao, P., Zhang, X., Peng, X., et al. (2018). “A methodology to improve linearity of analog RRAM for neuromorphic computing,” in IEEE Symposium on VLSI Technology, 103–104.

CrossRef Full Text | Google Scholar

Xu, C., Niu, D., Muralimanohar, N., Balasubramonian, R., Zhang, T., Yu, S., et al. (2015). “Overcoming the challenges of crossbar resistive memory architectures,” in 2015 IEEE 21st International Symposium on High Performance Computer Architecture, 476–488. doi:10.1109/HPCA.2015.7056056

CrossRef Full Text | Google Scholar

Xue, C.-X., Chen, W.-H., Liu, J.-S., Li, J.-F., Lin, W.-Y., Lin, W.-E., et al. (2019). “24.1 a 1mb multibit reram computing-in-memory macro with 14.6ns parallel mac computing time for cnn based ai edge processors,” in 2019 IEEE International Solid- State Circuits Conference - (ISSCC), 388–390. doi:10.1109/ISSCC.2019.8662395

CrossRef Full Text | Google Scholar

Yang, L., He, Z., Zhang, J., and Fan, D. (2021). “Ksm: Fast multiple task adaption via kernel-wise soft mask learning,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 13845–13853.

CrossRef Full Text | Google Scholar

Yin, S., Sun, X., Yu, S., and Seo, J.-S. (2020). High-throughput in-memory computing for binary deep neural networks with monolithically integrated RRAM and 90-nm CMOS. IEEE Trans. Electron Devices 67, 4185–4192. doi:10.1109/TED.2020.3015178

CrossRef Full Text | Google Scholar

Zhang, F., and Hu, M. (2020). “Cccs: Customized spice-level crossbar-array circuit simulator for in-memory computing,” in Proceedings of the 39th International Conference on Computer-Aided Design. ICCAD ’20. doi:10.1145/3400302.3415627

CrossRef Full Text | Google Scholar

Zhang, F., Yang, L., Meng, J., Cao, Y. K., Seo, J.-s., and Fan, D. (2022a). “Xbm: A crossbar column-wise binary mask learning method for efficient multiple task adaption,” in 2022 27th Asia and South Pacific Design Automation Conference (ASP-DAC), 610–615. doi:10.1109/ASP-DAC52403.2022.9712508

CrossRef Full Text | Google Scholar

Zhang, F., Yang, L., Meng, J., Seo, J.-S., Cao, Y., and Fan, D. (2022b). “Xma: A crossbar-aware multi-task adaption framework via shift-based mask learning method,” in 2022 59th ACM/IEEE Design Automation Conference (DAC).

Google Scholar

Zhang, F., Yang, L., Meng, J., Seo, J.-S., Cao, Y., and Fan, D. (2022c). “Xst: A crossbar column-wise sparse training for efficient continual learning,” in 2022 Design, Automation Test in Europe Conference Exhibition (DATE). doi:10.23919/DATE54114.2022.9774660

CrossRef Full Text | Google Scholar

Zhou, S., Wu, Y., Ni, Z., Zhou, X., Wen, H., and Zou, Y. (2016). Dorefa-net: Training low bitwidth convolutional neural networks with low bitwidth gradients.

Google Scholar