Real-Time Dispatching Performance Improvement of Multiple Multi-Energy Supply Microgrids Using Neural Network Based Approximate Dynamic Programming

In the multi-energy supply microgrid, different types of energy can be scheduled from a “global” view, which can improve the energy utilization efficiency. In addition, hydrogen storage system performs as the long-term storage is considered, which can promote more renewable energy installed in the local consumer side. However, when there are large numbers of grid-connected multi-energy microgrids, the scheduling of these multiple microgrids in real-time is a problem. Because different types of devices, three types of energy, and three types of utility grid networks are considered, which make the dispatching problem difficult. In this paper, a two-stage coordinated algorithm is adopted to operate the microgrids: day-ahead scheduling and real-time dispatching. In order to reduce the time taken to solve the scheduling problem, and improve the scheduling performance, approximate dynamic programming (ADP) is used in real-time operation. Different types of value function approximations (VFA), i.e., linear function, nonlinear function, and neural network are compared to study about the influence of the VFA on the decision results. Offline and online processes are developed to study the impact of the historical data on the regression of VFA. The results show that the neural network based ADP one-step decision algorithm has almost the same performance as the Global optimization algorithm, and the highest performance among all others Local optimization algorithms. The total operation cost relative error is less than 3%, while the running time is only 31% of the Global algorithm. In the neural network based ADP, the key technology is continuously updating the training dataset online, and adopting an appropriate neural network structure, which can at last improve the scheduling performance.

1 Introduction

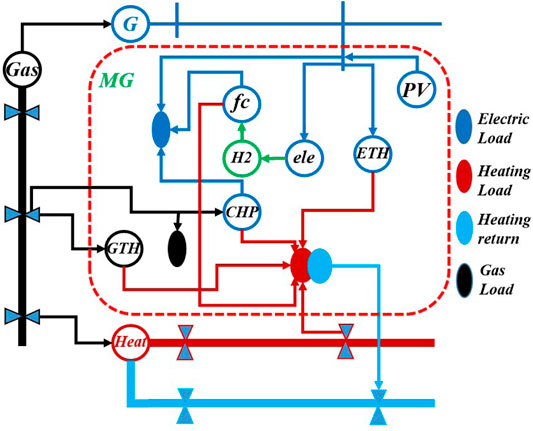
Hydrogen storage based multi-energy supply microgrids are expected to play an important role in future smart cities (Mancarella, 2014; Li et al., 2017b). In a multi-energy supply microgrid, several load demands are covered, such as electricity/heat/gas. At the same time, a hydrogen storage system can be used to alleviate the intermittence of renewable energy. For the hydrogen storage system, when the renewable energy is redundant, surplus energy is converted to hydrogen ($H_2$) through an electrolyzer; and when the energy is insufficient, a fuel cell is used to generate power based on hydrogen ($H_2$). The structure of the multi-energy supply microgrid used in this work is shown in Figure 1. Based on this hybrid microgrid, different types of energy can be utilized from a “global” view, which can improve the energy utilization efficiency (Li et al., 2018b).

FIGURE 1

FIGURE 1. Multi-energy supply microgrid.

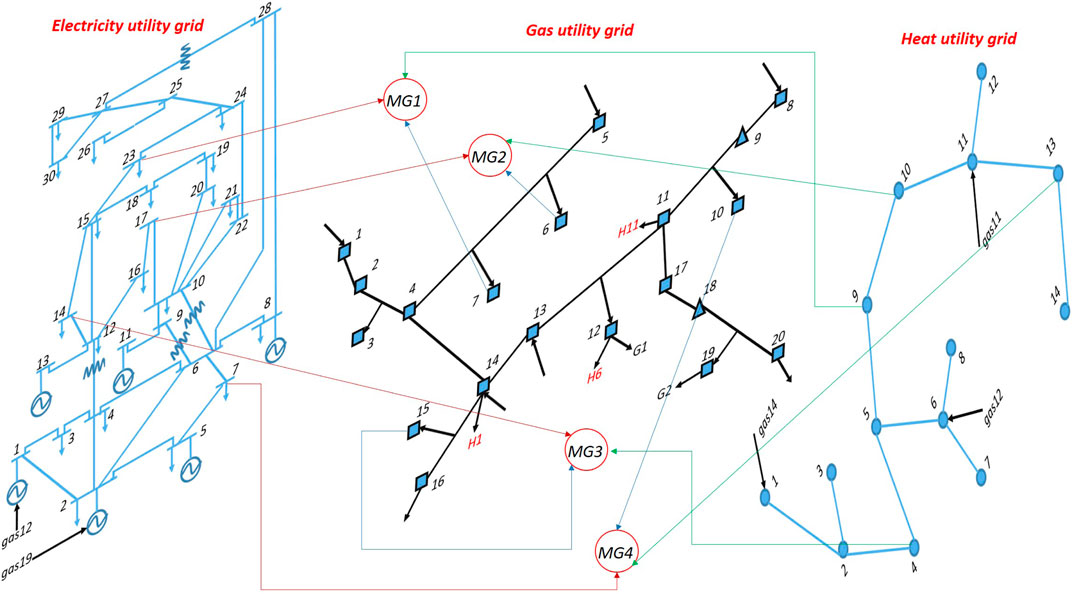
On the other hand, multi-energy supply microgrids can also interconnect with different utility grids (electricity/heat/gas) (Li et al., 2018b). The structure of utility grids is shown in Figure 2. The left network represents the electricity supply system, the middle network is the gas supply system, and the right network is the heat supply system. With this integrated utility grid networks, local loads can better resist to the natural disasters (Wang et al., 2016). For example, if the electric utility grid is destroyed under natural disasters, the gas utility grid system can supply gas to a fuel cell to produce electricity. Then the local loads can still operate.

FIGURE 2

FIGURE 2. The structure of the multiple energy supply network.

However, operating these multi-energy supply grid-connected microgrids in real-time is still a problem. Because different types of devices, three types of energy, and three types of utility grid networks are considered, which make the dispatching problem difficult.

In fact, the microgrid operation problem is often formulated as a model predictive control (MPC) problem, because MPC is widely accepted in varieties of industrial scenarios, and its effective ability to deal with optimization problems subject to large numbers of constraints (Shang and You, 2019). In fact, several methods can be adopted to solve the MPC problem.

The first category is heuristic algorithms, such as GA (Li et al., 2017a), PSO (Mohammadi-Ivatloo et al., 2013), etc. which are largely employed to solve the microgrid operation problem. This is due to their flexibility and the possibility to face complex constraints. However, heuristic algorithms do not guarantee obtaining an optimal results, because the solution is updated based on stochastic searching.

The second category is mixed integer programming (MIP). This is due to the availability of efficient commercial software, such as CPLEX and Gurobi (Gurobi, 2018). For example, in (Li and Xu, 2019), authors study the operation of a multi-energy microgrid under diverse uncertainties. The problem is represented as a two-stage operation problem. And at last is converted to a mixed-integer linear programming (MILP) problem. In (Li et al., 2021), authors study the optimal deployment of energy storage in a residential multi-energy microgrid. Based on the linearisation method, the model is converted to a MILP problem. However, in the MIP problem, the number of optimization windows is an important parameter. When the number of optimization windows is large, the solving time is long, because the variables needed to decide are large. When the number of optimization windows is small, the variables needed to decide are small, the solving time is then short, but the results are far away from the global optimal points, because more future impacts are not considered. So, the trade-off between window numbers and solving time should be considered.

The third category is dynamic programming (Xie et al., 2017), which transfers the long time horizon MPC problem into a series of smaller problems that can be easily solved. But dynamic programming suffers from the “curse-of-dimensionality” (Shi et al., 2017), which makes it difficult to use in real-time operation of large systems.

Then, a method is required which can efficiently and quickly solve the optimization problem in real-time, where the results are not far away from the global optimal points.

Approximate dynamic programming (ADP) method can resolve this problem. ADP method is a one-step decision model, and the future influence is considered as a value function approximation (VFA) in the current decision. This means that if we can find a good VFA, we can then quantify the future influence well, which leads to a reasonable decision at the current time. Since ADP is just one-step, the problem-solving time is faster than the multiple windows MPC method.

Therefore, in this paper, we adopt the ADP method to control the optimal operation of grid-connected microgrids. We focus on the performance of the ADP method and compare different factors, such as regression methods, offline/online process, and so on.

1.1 Scheduling Problem Based on Approximate Dynamic Programming

For the ADP method, the main thing is the value function approximation. In general, there are three methods to describe the value function approximation (Salas and Powell, 2013; Li and Jayaweera, 2015): lookup table, parametric approximation and nonparametric approximation. For example, in (Das and Ni, 2018), authors research about the battery storage systems operation in islanded microgrid considering battery lifetime characteristics, and the approximate value function is formulated based on lookup table idea. In (Li and Jayaweera, 2015), the authors use Q-learning method to define the approximate value function. In (Keerthisinghe et al., 2018), the piecewise linear function is used to build the approximate value function. In (Zeng et al., 2018), deep recurrent neural network learning is adopted to describe the approximate value function. The reference papers showed that ADP has better performance and lower computational burden.

Using the ADP method to optimal control the operation of microgrids has also attracted lots of attention.

1.1.1 Lookup Table and Parametric Approximate Value Function

In (Keerthisinghe et al., 2018), the authors present an ADP-based smart home energy management system. Lookup tables and piecewise linear functions are used to define approximate value function, the results show that the ADP-based algorithm reduces the daily electricity cost without an increase in the computational burden. In Salas and Powell (2013), authors present an ADP method to control the operation of the energy storage systems to achieve an economical goal. Piecewise linear function is adopted to define approximate value function. In (Jiang et al., 2014), the authors compare different ADP methods for energy storage control problem, including approximate policy iteration and approximate value iteration. In (Anderson et al., 2011), the authors apply ADP to the smart grid dispatching problem. The long-time horizon scheduling problem is transferred into a series of smaller problems, which is easier to be solved.

Authors in (Strelec and Berka, 2013), present the ADP method to solve multi-energy supply microgrid economic dispatching problems, lookup table and regression methods are used to approximate the cost function. In (Shuai et al., 2018b), the authors propose the lookup table based ADP algorithm for the real-time energy management of the microgrid under uncertainties. The dispatching problem is formulated as a long-time horizon mixed integer nonlinear programming model and is then decomposed into several single period nonlinear programming sub-problems based on ADP method. Similarly, in (Shuai et al., 2018a), a piecewise linear function based ADP algorithm is adopted to solve the stochastic microgrid economic dispatching problem. Authors in (Darivianakis et al., 2017), transfer the MPC optimal problem into VFA based multi-stage optimization problem, a piecewise linear function is adopted to approximate the value function. Authors in (Bhattacharya et al., 2018) present a two-stage dual dynamic programming method to manage energy storage in a microgrid, a piecewise linear function is also adopted to approximate cost-to-go functions.

1.1.2 Nonparametric Approximate Value Function

In (Ji et al., 2018), authors research about real-time economical operation of a grid-connected microgrid using the ADP method. Multilayer perceptron feedforward neural network is adopted to approximate value function. In (Zeng et al., 2018), the authors study the economical operation of a microgrid in real-time. ADP and deep recurrent neural network (RNN) learning are adopted to solve the problem. Deep RNN architecture is used to estimate the value function. Furthermore, authors in (Liu et al., 2015) present an approximate dynamic programming algorithms for solving undiscounted optimal control problems. Two multilayer feedforward neural networks are used to approximate both the control policy and the value function. In order to enhance the resource utilization rate and reduce the computation cost, authors in (Wang et al., 2019) present an event-based iterative adaptive critic algorithm, in which three neural networks are constructed but possessing different roles. That is: the model network employed for prediction, the critic network built for evaluation, and the action network used for control. In order to tackle dynamic uncertainties, authors in (Wang, 2019) study robust policy learning control for nonlinear plants. Neural network based actor-critic structure is designed to implement the robust control.

Authors in (Zhu et al., 2019) research the optimal management of multiple batteries over a long time horizon in order to prolong battery lifetime. Approximate dynamic programming is adopted to solve the problem, and fuzzy systems are used to approximate value functions. Compared to neural networks, the fuzzy approximation only requires to compute target values.

Based on the above papers, the ADP method is effective to solve the dispatching problem, and the ADP method can be divided into the following steps as: 1) build the dispatching optimization model; 2) transfer the multi-step decision problem into a series of one-step decision problems; 3) find the relationship between the states and future costs, using lookup table/regression/neural network methods to describe the relationship, namely, build the approximate value function; 4) integrate the approximate value function into the one-step decision model; 5) solve the approximate value function based one-step decision problem.

1.2 Electricity/Heat/Gas Utility Grids Operation

The above section reviews the related work about scheduling algorithms for microgrid. In addition, when microgrid interconnects with the electricity/heat/gas utility grids, the operation of the electricity/heat/gas utility grids should also be considered.

For the coupled multi-energy networks operation, centralized optimization algorithm is often used to solve the optimal power flow. For example, authors in (Qin et al., 2020) study the operation of integrated energy systems consisting of electricity and natural gas utility networks, a multi-objective optimization method is used to solve the coordinated operation of the coupling network. In (Sun et al., 2020), authors study the day-ahead scheduling of gas-electric integrated energy system considering the bi-directional energy flow. The goal is to minimize the operation cost, and a second-order cone programming method is utilized to solve the problem. In (Fang et al., 2018), authors study the operation of the integrated gas and electrical power system considering the different response times of the gas and power systems. The problem is transformed into a single-stage linear programming. In (Chen et al., 2017), authors study the optimal operation of electricity-gas integrated energy system. The goal is to minimize the operation costs for both electrical and natural gas systems while satisfying steady-state operational constraints.

To model the electricity/heat/gas utility grid networks. The steady-state operational equations are often built as the constraints, and added to the previous optimization problem. For example, in (Liu et al., 2020), authors present a sequential reliability assessment method considering multi-energy flow and thermal inertia. Hydraulic circulation and heat exchange equations are used to model the thermal network. Conventional power flow equations are adopted to describe distribution network model. In (Martínez Ceseña et al., 2020), the electricity network model is represented as conventional power flow equations, as well as thermal and voltage limits. The gas network is represented as steady-state equations. The conventional steady-state equations and a thermal module are utilized to model the heat network. In (Yang et al., 2020), authors present a planning strategy for a district energy sector considering the coupling of power, gas, and heat systems. An optimal multi-energy flow model is developed, and the objective is to minimize operational costs. Distflow equations are used to describe the power distribution system, steady gas flow equations are adopted to model the gas distribution system, steady-state model is deployed to describe the distribution heat system. In (Martínez Ceseña and Mancarella, 2019), authors present a robust optimization framework for smart districts with multi-energy devices and electricity/heat/gas energy networks. The electricity network is modelled with typical power flow equations. The heat network is described based on nodal balance and cumulative head losses equations. The gas network is represented based on nodal balance, pressure drops, and head losses equations.

Based on the above reviews, optimization method is often used to calculate the power flow of the electricity/heat/gas energy networks. The electricity network is modelled based on typical power flow equations. The heat network is modelled based on nodal balance and heat losses equations. The gas network is represented based on nodal balance, pressure drops equations.

1.3 Contributions

The above review shows that the operation problem of multi-energy supply microgrid and the operation problem of coupled electricity/heat/gas energy networks have drawn a lot of attention. However, using the ADP algorithm to solve the dispatching problem of the hydrogen-based multi-energy supply microgrids considering electricity/heat/gas energy networks has not drawn a lot of attention. The complexity of the whole model increases the difficulty of the control, especially the large numbers of constraints. Motivated by the aforementioned references, we present an ADP-based computationally efficient algorithm for the real-time operation of multi-energy supply grid-connected microgrids. A similar study is our previous work (Li et al., 2018a), in which only MPC algorithm is used, no other algorithms are compared.

Compared to previous works, the contribution of this paper can be concluded as follows:

• First, we build an ADP-based one-step decision model for the optimal operation of multi-energy supply grid-connected microgrids. In the one-step decision model, we consider large numbers of logical and physical constraints, and formulate the problem as a mixed-integer programming model;

• Second, in the ADP model, we research about different factors. Linear, nonlinear, and neural network regression are compared to research about the influence of the approximate value function on the decision results. Offline and online processes are developed to research about the impact of the historical data on the regression approximate value function;

• Last, we compare the performance of the sliding window MPC, the one-step decision ADP and the global optimization algorithms from different perspectives, including the running time, the real-time operation cost, total operation cost, and the exchanged energy with the utility grid networks. The results show that the neural network based ADP method has the best performance, with the less than 3% total operation cost relative error, and has a running time of only 31% of Global algorithm.

The remainder of this paper is organized as follows. Section 2 describes the microgrid scheduling problem. Section 3 describes the electricity/heat/gas utility grids model. Section 6 presents the simulation results. Finally, Section 7 concludes the paper.

In fact, to operate the electricity/heat/gas integrated microgrids system, three aspects should be considered: 1) scheduling of the grid-connected microgrid; 2) utility grids operation; 3) the operation of the whole system.

2 Microgrid Scheduling Problem Formulation

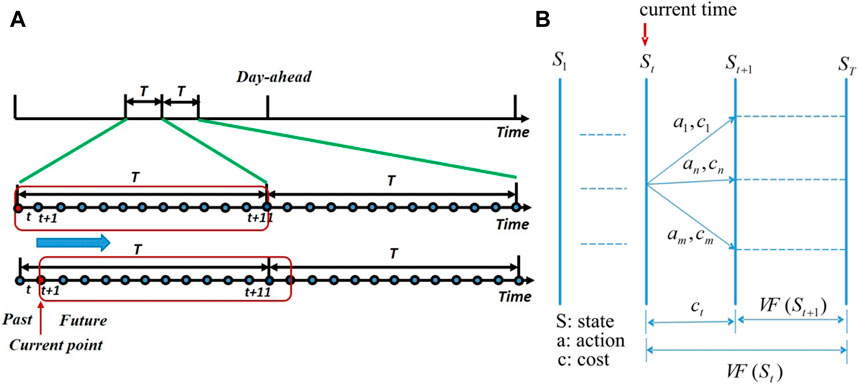
To schedule the grid-connected microgrids, the coordinated strategy is often adopted, namely, day-ahead scheduling and real-time dispatching. In day-ahead scheduling, the expected exchange energy with utility grids are calculated, based on the exchanged energy, we can decide the role of the microgrids, namely, microgrids operate as a generator or as a load. In real-time dispatching, the ADP-based one-step decision problem is solved. It takes the future operation cost into consideration and makes the current dispatching more reasonable, and at the same time reduces the solving time.

We introduce the problem from three aspects: 1) day-ahead scheduling; 2) real-time dispatching based on MPC; 3) real-time dispatching based on ADP.

2.1 Microgrid Day-Ahead Scheduling

In order to make the problem more readable, we use the simple model to describe the problem, and the detailed model is attached in Supplementary Material. The scheduling problem can be described as follows:

$\begin{array}{l}\underset{x_t,x_{t+1},\dots ,x_{t+T}}{min}\stackrel{t+T}{{\displaystyle \sum }_{\tau =t}}f\left(x_{\tau }\right)\hfill \\ s.t.A{\mathbf{x}}_{\mathbf{i}}\le b;B{\mathbf{x}}_{\mathbf{i}}=\mathbf{c}\left(\text{continuous variables}\right)\hfill \\ l_b\le {\mathbf{x}}_{\mathbf{i}}\le u_b\hfill \\ C{\mathbf{x}}_{\mathbf{j}}\le d;D{\mathbf{x}}_{\mathbf{j}}=e\left(\text{integer}/\text{logical variables}\right)\hfill \\ x_i\in \mathbf{Z};x_j\in \left\{\mathrm{0,1},\text{integer}\right\}\hfill \end{array}(1)$

where ${\mathrm{x}}_{\mathrm{i}}$ are the continuous variables, ${\mathrm{x}}_{\mathrm{j}}$ are the integer/logical variables; $A,B,C,D,b,c,d,e$ are the constraints matrix; $f(.)$ is the operation cost function; T is the time horizon.

By solving the above mixed integer programming problem, we can obtain the scheduling results. However, due to the uncertainty of the load demand and the output of renewable energy, some parameters in constraints are not deterministic parameters. The above problem is then transferred to the following problem:

$\begin{array}{l}\underset{x_t,x_{t+1},\dots ,x_{t+T}}{min}\stackrel{t+T}{{\displaystyle \sum }_{\tau =t}}f\left(x_{\tau }\right)\hfill \\ s.t.A{\mathbf{x}}_{\mathbf{i}}\le b;B{\mathbf{x}}_{\mathbf{i}}=\tilde{c}\left(\text{continuous variables}\right)\hfill \\ l_b\le {\mathbf{x}}_{\mathbf{i}}\le u_b\hfill \\ C{\mathbf{x}}_{\mathbf{j}}\le d;D{\mathbf{x}}_{\mathbf{j}}=e\left(\text{integer}/\text{logical variables}\right)\hfill \\ x_i\in \mathbf{Z};x_j\in \left\{\mathrm{0,1},\text{integer}\right\}\hfill \end{array}(2)$

where $\tilde{c}$ are the uncertainty parameters. For example, in power balance constraints, generated power must equal to load demand, but the predicted load demand is uncertain.

The common method to solve the above uncertainty problem is stochastic optimization. The above problem can be transferred as follows:

$\begin{array}{l}\underset{\begin{array}{c}{x}_t^1,x_{t+1}^1,\dots ,x_{t+T}^1\\ x_t^2,x_{t+1}^2,\dots ,x_{t+T}^2\\ \dots \\ x_t^{N_s},x_{t+1}^{N_s},\dots ,x_{t+T}^{N_s}\end{array}}{min}\stackrel{N_s}{{\displaystyle \sum }_{s=1}}{p}_s\cdot \stackrel{t+T}{{\displaystyle \sum }_{\tau =t}}f\left(x_{\tau }^s\right)\\ s.t.A{\mathbf{x}}_{\mathbf{i}}^{\mathbf{s}}\le b;B{\mathbf{x}}_{\mathbf{i}}^{\mathbf{s}}=\widetilde{{\mathbf{c}}_{\mathbf{s}}}\left(\text{continuous variables}\right)\\ l_b\le {\mathbf{x}}_{\mathbf{i}}^{\mathbf{s}}\le u_b\\ C{\mathbf{x}}_{\mathbf{j}}^{\mathbf{s}}\le d;D{\mathbf{x}}_{\mathbf{j}}^{\mathbf{s}}=e\left(\text{integer}/\text{logical variables}\right)\\ x_i^s\in \mathbf{Z};x_j^s\in \left\{\mathrm{0,1},\text{integer}\right\}\\ s=\mathrm{1,2},\dots ,N_s\end{array}(3)$

In the above stochastic problem, we use a scenario-based method to transfer the uncertainty parameters $\tilde{c}$ to typical scenarios $N_s$, and the probability of each scenario is $p_s$. Lastly, to solve the above problem, we can obtain the scheduling results in each scenario.

Assume that the variables that exchanged energy with utility grids are ${\mathrm{x}}_{\mathrm{ex}}\in {\mathrm{x}}_{\mathrm{i}}$. Then the expected exchanged energy is:

${\mathbf{x}}_{\mathbf{e}\mathbf{x}}^{\ast }=\stackrel{N_s}{{\displaystyle \sum }_{s=1}}{p}_s\cdot x_{ex}^s,s=\mathrm{1,2},\dots ,N_s(4)$

2.2 Microgrid Real-Time Dispatching Based on MPC

Based on the day-ahead scheduling results, we can then implement real-time dispatching. Due to the real-time short-term prediction uncertainty, the real-time exchanged energy with the utility grid may not equal to the day-ahead scheduling results. In order to reduce this error, it is necessary for the real-time exchanged energy to follow the day-ahead scheduling results as close as possible. The sliding window model predictive control method is then adopted to deploy the real-time dispatching, the detailed model is attached in Supplementary Material. The real-time dispatching problem can be described as follows:

$\begin{array}{l}\underset{x_t,x_{t+1},\dots ,x_{t+t_n}}{min}\stackrel{t+t_n}{{\displaystyle \sum }_{\tau =t}}g\left(x_{\tau },{\mathbf{x}}_{\mathbf{e}\mathbf{x}}^{\ast }\right)\hfill \\ s.t.A{\mathbf{x}}_{\mathbf{i}}\le b;B{\mathbf{x}}_{\mathbf{i}}=\mathbf{c}\left(\text{continuous variables}\right)\hfill \\ l_b\le {\mathbf{x}}_{\mathbf{i}}\le u_b\hfill \\ C{\mathbf{x}}_{\mathbf{j}}\le d;D{\mathbf{x}}_{\mathbf{j}}=e\left(\text{integer}/\text{logical variables}\right)\hfill \\ x_i\in \mathbf{Z};x_j\in \left\{\mathrm{0,1},\text{integer}\right\}\hfill \end{array}(5)$

where $g(.)$ is the real-time operation cost function; ${\mathbf{x}}_{\mathbf{e}\mathbf{x}}^{\ast }$ are the day-ahead scheduling results; $t_n$ is the time horizon.

In the real-time sliding window dispatching, in the first time step t, the MPC problem is solved, then only the current time decisions (current time is t) are deployed, and the future decisions (future times are $t+1,\dots ,t+t_n$) are abandoned. After that, the time slides to the next step $t+1$, and the MPC problem is solved again, then only the new current time decisions (new current time is $t+1$) are deployed, and the future decisions (future times are $t+2,\dots ,t+t_n+1$) are abandoned. This process is repeated until the last time is reached, the process can be seen in Figure 3A.

FIGURE 3

FIGURE 3. (A) Sliding window model predictive control. (B) The state transition process.

2.3 Microgrid Real-Time Dispatching Based on ADP Method

In the above section, the sliding window MPC method is adopted to deploy real-time dispatching. However, the solving time of the MPC method is long, because we need to solve the multiple windows optimization problem. In this section, the one-step decision model is developed to solve the real-time dispatching problem. With the one-step decision model, the solving time can be reduced. On the other hand, the ADP idea is also adopted, namely, integrating the future impacts into the current decision model, to make the current decision results more reasonable and effective.

In fact, the above MPC problem can be transferred into a series of smaller problems based on dynamic programming idea, which can be represented as follows:

$\begin{array}{l}\underset{x_t}{min}[g\left(x_t,{\mathbf{x}}_{\mathbf{e}\mathbf{x}}^{\mathbf{t}}\right)+\underset{x_{t+1}}{min}[g\left(x_{t+1},{\mathbf{x}}_{\mathbf{e}\mathbf{x}}^{\mathbf{t}+1}\right)+\underset{x_{t+2}}{min}[g\left(x_{t+2},{\mathbf{x}}_{\mathbf{e}\mathbf{x}}^{\mathbf{t}+2}\right)\hfill \\ +\cdots \stackrel{t+t_n}{{\displaystyle \sum }_{\tau =t+t_n-m}}g\left(x_{\tau },{\mathbf{x}}_{\mathbf{e}\mathbf{x}}^{\ast }\right)\left]\right]]\hfill \\ s.t.A{\mathbf{x}}_{\mathbf{i}}\le b;B{\mathbf{x}}_{\mathbf{i}}=\mathbf{c}\left(\text{continuous variables}\right)\hfill \\ l_b\le {\mathbf{x}}_{\mathbf{i}}\le u_b\hfill \\ C{\mathbf{x}}_{\mathbf{j}}\le d;D{\mathbf{x}}_{\mathbf{j}}=e\left(\text{integer}/\text{logical variables}\right)\hfill \\ x_i\in \mathbf{Z};x_j\in \left\{\mathrm{0,1},\text{integer}\right\}\hfill \end{array}(6)$

We use $\mathbf{V}{\mathbf{F}}_{\mathbf{t}+1}$ to describe the total future cost from $t+1$ to $t+t_n$, namely,

$\mathbf{V}{\mathbf{F}}_{\mathbf{t}+1}=\underset{x_{t+1},\dots ,x_{t+t_n}}{min}\stackrel{t+t_n}{{\displaystyle \sum }_{\tau =t+1}}g\left(x_{\tau },{\mathbf{x}}_{\mathbf{e}\mathbf{x}}^{\ast }\right)(7)$

Then the above problem can be represented as:

$\begin{array}{l}\underset{x_t}{min}[g\left(x_t,{\mathbf{x}}_{\mathbf{e}\mathbf{x}}^{\mathbf{t}}\right)+\mathbf{V}{\mathbf{F}}_{\mathbf{t}+1}]\hfill \\ s.t.A{\mathbf{x}}_{\mathbf{i}}\le b;B{\mathbf{x}}_{\mathbf{i}}=\mathbf{c}\left(\text{continuous variables}\right)\hfill \\ l_b\le {\mathbf{x}}_{\mathbf{i}}\le u_b\hfill \\ C{\mathbf{x}}_{\mathbf{j}}\le d;D{\mathbf{x}}_{\mathbf{j}}=e\left(\text{integer}/\text{logical variables}\right)\hfill \\ x_i\in \mathbf{Z};x_j\in \left\{\mathrm{0,1},\text{integer}\right\}\hfill \end{array}(8)$

Because the future cost $\mathbf{V}{\mathbf{F}}_{\mathbf{t}+1}$ is dependent on the current decisions $x_t$ and post-decision states $S_{t+1}$, then the general one-step ADP decision model can be described as follows, and the detailed model is attached in Supplementary Material:

$\begin{array}{l}\underset{x_t}{min}g\left(x_t,{\mathbf{x}}_{\mathbf{e}\mathbf{x}}^{\mathbf{t}},\mathbf{V}\mathbf{F}\left(S_{t+1}\right)\right)\hfill \\ s.t.A{\mathbf{x}}_{\mathbf{i}}\le b;B{\mathbf{x}}_{\mathbf{i}}=\mathbf{c}\left(\text{continuous variables}\right)\hfill \\ l_b\le {\mathbf{x}}_{\mathbf{i}}\le u_b\hfill \\ C{\mathbf{x}}_{\mathbf{j}}\le d;D{\mathbf{x}}_{\mathbf{j}}=e\left(\text{integer}/\text{logical variables}\right)\hfill \\ x_i\in \mathbf{Z};x_j\in \left\{\mathrm{0,1},\text{integer}\right\}\hfill \\ x_i,x_j\in x_t;\hfill \\ S_{t+1}=SF\left(S_t,x_t\right);\hfill \end{array}(9)$

where $\mathbf{V}\mathbf{F}$ is the approximate value function, $\mathbf{V}\mathbf{F}\left(S_{t+1}\right)$ is the approximate future operation cost based on the state $S_{t+1}$; $SF$ is the state transition function, which is used to describe how the current state $S_t$ is changed to the next time state $S_{t+1}$.

By solving the above one-step decision model (namely, the decision variables are only at the current time), one can obtain the optimal dispatching results. However, it can be seen that the main thing in the above one-step decision model is the approximate value function $\mathbf{V}\mathbf{F}$. If we can find a good approximate value function $\mathbf{V}\mathbf{F}$ to describe the relationship between the state $S_{t+1}$ and the future operation cost $C_{future}$, then we can obtain good and effective decision results.

2.3.1 Approximate Value Function $\mathbf{V}\mathbf{F}$

The approximate value function $\mathbf{V}\mathbf{F}$ is used to describe the relationship between the state $S_t$ and the future operation cost $C_{future}$, which can be represented as follows:

$C_{future}=\mathbf{V}\mathbf{F}\left(S_t,L_{pre}\right)(10)$

where $L_{pre}$ is the future predicted load demand and renewable energy output.

With the approximate value function $\mathbf{V}\mathbf{F}$, one can calculate the future operation cost based on the state $S_t$ and the predicted data $L_{pre}$. Then, to find a good approximate value function $\mathbf{V}\mathbf{F}$ is the key problem. In this section, we introduce how to find the approximate value function $\mathbf{V}\mathbf{F}$.

Firstly, we need to obtain the historical dataset of $\left\{C_{future},[S_t,L_{pre}]\right\}$. The dataset can be obtained based on offline simulation. Give different values of $[S_t,L_{pre}]$, solve the problem Eq. 9, we can then calculate the future operation cost $C_{future}$. In addition, in the actual operation, we can also obtain the new dataset. So, the dataset is updated continuously as the operation running forward.

Secondly, we need to analyze the dataset to find the relationship between $C_{future}$ and $[S_t,L_{pre}]$, namely, calculate the approximate value function $\mathbf{V}\mathbf{F}$. Here, we adopted three methods, i.e., the linear, nonlinear regression and neural network regression algorithms.

In the linear regression method, we use function $C_{future}=a_0+a_1\cdot S_t+a_2\cdot L_{pre}$ to describe the relationship, and the approximate value function $\mathbf{V}\mathbf{F}$ is the value of the parameters $a_0$, $a_1$, $a_2$, namely, $\mathbf{V}\mathbf{F}\equiv \left\{a_0,a_1,a_2\right\}$. In nonlinear regression method, the function is $C_{future}=b_0+b_1\cdot S_t+b_2\cdot L_{pre}+b_3\cdot S_t\cdot L_{pre}+b_4\cdot S_t^2+b_5\cdot L_{pre}^2$, the approximate value function $\mathbf{V}\mathbf{F}\equiv \left\{b_0,b_1,b_2,b_3,b_4,b_5\right\}$. In neural network regression method, the function is $C_{future}=NN\left(S_t,L_{pre}^{PV},L_{pre}^{el},L_{pre}^{heat},L_{pre}^{gas}\right)$, $NN$ is the neural network function, the approximate value function $\mathbf{V}\mathbf{F}\equiv \left\{NN\right\}$.

At last, we developed offline and online processes to deploy the ADP method. In the offline process, at each time t, there are four steps: 1) update the dataset $\left\{C_{future},[S_t,L_{pre}]\right\}$; 2) based on the dataset, calculate the approximate value function $\mathbf{V}\mathbf{F}$; 3) solve the problem Eq. 9, and obtain the dispatching results; 4) save the operation results in step 3), and return to step 1). The offline process can be summarized as:

Algorithm 1 Offline simulation process.

1: initialize dataset $\left\{C_{future},[S_t,L_{pre}]\right\}$;

2: for$t=1:T$do

3: update the dataset $\left\{C_{future},[S_t,L_{pre}]\right\}$;

4: calculate the approximate value function $\mathbf{V}\mathbf{F}$;

5: linear method: $\mathbf{V}\mathbf{F}\equiv \left\{a_0,a_1,a_2\right\}$

6: nonlinear method:$\mathbf{V}\mathbf{F}\equiv \left\{b_0,b_1,b_2,b_3,b_4,b_5\right\}$

7: neural network method: $\mathbf{V}\mathbf{F}\equiv \left\{NN\right\}$

8: solve the problem Eq. 9;

9: $\underset{x_t}{min}g\left(x_t,{\mathbf{x}}_{\mathbf{e}\mathbf{x}}^{\mathbf{t}},\mathbf{V}\mathbf{F}\left(S_{t+1}\right)\right)$

10: save the operation results;

11: t = t+1;

12: end for

In the online process, there is not enough initial dataset, so the dataset is obtained and updated based on the online operation. At each time t, the process is run $N_{it}$ times. In each running $i,i=\mathrm{1,2},\dots ,N_{it}$, firstly, the dataset $\left\{C_{future},[S_t,L_{pre}]\right\}$ is updated; and then, the approximate value function $\mathbf{V}\mathbf{F}$ is calculated; after that, problem Eq. 9 is solved; and save the operation results; at last, return to the next running $i+1$. After $N_{it}$ running times are finished, then go to the next time $t+1$. The online process can be summarized as:

Algorithm 2 Online simulation process

1: initialize $N_{it}$;

2: for$t=1:T$do.

3: initialize the dataset $\left\{C_{future},[S_t,L_{pre}]\right\}$;

4: for $i=1:N_{it}$do.

5: update the dataset $\left\{C_{future},[S_t,L_{pre}]\right\}$;

6: calculate the approximate value function $\mathbf{V}\mathbf{F}$;

7: linear method: $\mathbf{V}\mathbf{F}\equiv \left\{a_0,a_1,a_2\right\}$

8: solve the problem Eq. 9;

9: $\underset{x_t}{min}g\left(x_t,{\mathbf{x}}_{\mathbf{e}\mathbf{x}}^{\mathbf{t}},\mathbf{V}\mathbf{F}\left(S_{t+1}\right)\right)$

10: save the operation results;

11: i = i + 1;

12: end for.

13: t = t + 1;

14: end for

2.3.2 ADP State Transition Process

The state transition process can be seen in Figure 3B. It can be seen that future approximate operation cost $VF\left(S_{t+1}\right)=VF\left(S_t\right)-c_t$, where $c_t$ is the instant operation cost from time t to time $t+1$. At time t, state $S_t$ includes hydrogen tanks state $S_{gs}^t$, electricity/heat/gas load demands $L_{el}^t$, $L_{heat}^t$, $L_{gas}^t$, PV output $L_{PV}^t$. Action $a_t$ includes the dispatching strategies.

3 Utility Grids Operation Problem

For the integrated utility grids model, an IEEE30 + gas20 + heat14 hybrid network is adopted. The structure of each utility grid network is presented in Supplementary Material.

3.1 Electricity Utility Grid Operation

For the electricity utility grid operation, it is a classical optimal power flow (OPF) problem. The OPF problem can be seen as follows:

$\begin{array}{c}\underset{P_g,Q_g,V}{min}{\displaystyle \sum }_{i=1}^{n_g}\left\{f_P^i\left(P_g^i\right)+f_Q^i\left(Q_g^i\right)\right\}\\ s.t.\left(12\right),\left(13\right)\end{array}(11)$

where the $P_g^i,Q_g^i$ are the real and reactive power of the $i^{th}$ generator. $f_P^i,f_Q^i$ are the individual polynomial cost function of the $i^{th}$ generator.

Power balance constraints can be shown as the following:

$\begin{array}{c}{P}_i^g=P_i^{load}+{\displaystyle \sum }_{j=1}^{n_{bus}}{V}_i{V}_j\left(G_{ij}^{line}cos{\theta }_{ij}+B_{ij}^{line}sin{\theta }_{ij}\right)\\ Q_i^g=Q_i^{load}+{\displaystyle \sum }_{j=1}^{n_{bus}}{V}_i{V}_j\left(G_{ij}^{line}sin{\theta }_{ij}-B_{ij}^{line}cos{\theta }_{ij}\right)\end{array}(12)$

where $P_i^{load},Q_i^{load}$ are the real and reactive load demand at bus i. $G_{ij}^{line},B_{ij}^{line}$ are the parameters of the power lines from bus i to bus j.

$\begin{array}{c}{V}_m^{i,min}\le V_m^i\le V_m^{i,max};i=\mathrm{1,2},\dots ,n_{bus}\\ P_g^{i,min}\le P_g^i\le P_g^{i,max};i=\mathrm{1,2},\dots ,n_g\\ Q_g^{i,min}\le Q_g^i\le Q_g^{i,max};i=\mathrm{1,2},\dots ,n_g\end{array}(13)$

where $V_m^i,V_m^{i,min},V_m^{i,max}$ are the voltage magnitude, minimum voltage magnitude and maximum voltage magnitude at bus i. $P_g^{i,min},P_g^{i,max},Q_g^{i,min},Q_g^{i,max}$ are the minimum and maximum real and reactive power of i generator.

3.2 Heating Utility Grid Operation

For the heating utility grid, it is a heating power flow problem. During the heating transportation, heat transportation loss should be considered. The heating transportation loss can be described as follows (Pirouti, 2013; Shabanpour-Haghighi and Seifi, 2015).

$Q_{heat}^{loss}=c_p\cdot \dot{m}\left(T_{s1}-T_{s2}\right)(14)$

where $c_p$ is the specific heat capacity (KJ/kgK), $\dot{m}$ is the mass flow rate (kg/s), and $T_{s1},T_{s2}$ are the temperature at node $s1$ and node $s2$.

The temperature drop through the heating flow system can be described as:

$T_{s2}=\left(T_{s1}-T_g\right)\cdot e^{-\frac{lU}{c_p\cdot \dot{m}}}+T_g(15)$

where l is the pipe length, U is the heat transition coefficient (W/mK), and $T_g$ is the ground temperature.

Based on (Eqs. 14Eqs. 15), it can be seen that the heating loss during the transportation is a nonlinear equation. In order to reduce the complexity, in this paper, we choose a linear model to describe the heating transportation loss. We assume that the heating loss is a linear function of the transportation distance, which can be shown as the following:

$Q_{heat}^{loss}=k_{heat}^{loss}\cdot l(16)$

where $k_{heat}^{loss}$ is the coefficient of the heating loss.

Then, the heating power flow of the heating utility grid can be presented. For each heating pipeline, two state variables (binary variables, 0 or 1): $ULin{e}_{heat}^{out},ULin{e}_{heat}^{in}$ are defined. Then the heating power flow in each pipeline can be described as the following constraints:

$\begin{array}{l}0\le Lin{e}_{heat}^{out}(i,t)\le ULin{e}_{heat}^{out}(i,t)\cdot Lin{e}_{heat}^{max}\left(i\right)\\ 0\le Lin{e}_{heat}^{in}(i,t)\le ULin{e}_{heat}^{in}(i,t)\cdot Lin{e}_{heat}^{max}\left(i\right)\\ ULin{e}_{heat}^{out}(i,t)+ULin{e}_{heat}^{in}(i,t)\le 1\end{array}(17)$

An example is presented here to explain the logical illustrated in Eq. 18. In Eq. 18, there are three nodes $h1$, $h2$, and $h3$, the connections are $h1\leftrightarrow h2$, and $h2\leftrightarrow h3$. The heating power flow at node $h2$ can be described as in Eq. 19.

$h{1}_{Lin{e}_{heat}^{in}(1,t)}^{Lin{e}_{heat}^{out}(1,t)}\overrightarrow{\underleftarrow{---}}h{2}_{Lin{e}_{heat}^{in}(2,t)}^{Lin{e}_{heat}^{out}(2,t)}\overrightarrow{\underleftarrow{---}}h{3}_{Lin{e}_{heat}^{in}(3,t)}^{Lin{e}_{heat}^{out}(3,t)}\overrightarrow{\underleftarrow{---}}(18)$

$Lin{e}_{heat}^{out}\left(1,t\right)\cdot \left(1-Q_{heat}^{loss,1}\right)-Lin{e}_{heat}^{in}\left(1,t\right)/\left(1-Q_{heat}^{loss,1}\right)=Lin{e}_{heat}^{out}\left(2,t\right)-Lin{e}_{heat}^{in}\left(2,t\right)(19)$

3.3 Gas Utility Grid Operation

For the gas utility grid, it is a gas power flow problem. The gas flow can be described as follows (De Wolf and Smeers, 2000):

$sign\left(f_{ij}\right)\cdot f_{ij}^2=C_{ij}^2\left(p_i^2-p_j^2\right)(20)$

where $f_{ij}$ is the gas flow between nodes i and j, $p_i$ and $p_j$ are the pressure at nodes i and j, and $C_{ij}$ is a constant which depends on the length, the diameter and the absolute rugosity of the pipe and on the gas composition.

During the gas transportation, the pressure will drop, which is modeled as in Eq. 21.

$p1\stackrel{f_{dep}}{\to }\stackrel{f_{loss}}{----}\stackrel{f_{in}}{\to }p2(21)$

Based on Eqs. 20Eqs. 21, we can obtain $f_{dep}^2=C_{12}^2\left(p_1^2-p_2^2\right)$.

Then, the gas pressure drop can be described as:

$\begin{array}{c}{f}_{in}^2=C_{12}^2\left(p_1^2-p_2^2-H_{loss}^2\right)\\ =C_{12}^2\left(p_1^2-p_2^2\right)-C_{12}^2{H}_{loss}^2\\ =f_{dep}^2-C_{12}^2\cdot H_{loss}^2\end{array}(22)$

Assume that the loss $C_{12}^2\cdot H_{loss}^2$ can be represented as $C_{12}^2\cdot H_{loss}^2\approx f_{dep}^2\cdot f_{loss}$, where $f_{loss}$ is a coefficient parameter to describe the pressure drop. Next, we can obtain $f_{in}^2\approx f_{dep}^2-f_{dep}^2\cdot f_{loss}$, namely, $f_{in}\approx f_{dep}\sqrt{\left(1-f_{loss}\right)}$.

In (Martinez-Mares and Fuerte-Esquivel, 2012), it shows that the pressure drop $H_{loss}$ is a complex function related to the nonlinear effect of the pipeline distance $L_{gas}^{pipe}$ and the weather conditions. Coefficient parameter $f_{loss}$ is also a nonlinear function. In order to reduce the complexity, here a linear model is adopted to describe the pressure drop. Assume that coefficient parameter $f_{loss}$ is a linear function of the gas pipeline distance, which can be shown as

$f_{loss}=k_{gas}^{loss}\cdot L_{gas}^{pipe}(23)$

where $k_{gas}^{loss}$ is the coefficient of the gas loss.

Then the gas power flow in the gas utility grid can be presented. For each pipeline, two state variables (binary variables, 0 or 1) $ULin{e}_{gas}^{out},ULin{e}_{gas}^{in}$ are defined. Then the gas flow constraints are:

$\begin{array}{l}0\le Lin{e}_{gas}^{out}(i,t)\le ULin{e}_{gas}^{out}(i,t)\cdot Lin{e}_{gas}^{max}\left(i\right)\\ 0\le Lin{e}_{gas}^{in}(i,t)\le ULin{e}_{gas}^{in}(i,t)\cdot Lin{e}_{gas}^{max}\left(i\right)\\ ULin{e}_{gas}^{out}(i,t)+ULin{e}_{gas}^{in}(i,t)\le 1\end{array}(24)$

Here we also use an example to explain the gas flow, which is shown in Eq. 25. There are three nodes $g1$, $g2$, and $g3$. The connections are $g1\leftrightarrow g2$, and $g2\leftrightarrow g3$. The gas flow at node $g2$ can be described as:

$g{1}_{Lin{e}_{gas}^{in}\left(1,t\right)}^{Lin{e}_{gas}^{out}\left(1,t\right)}\overrightarrow{\underleftarrow{---}}g{2}_{Lin{e}_{gas}^{in}\left(2,t\right)}^{Lin{e}_{gas}^{out}\left(2,t\right)}\overrightarrow{\underleftarrow{---}}g{3}_{Lin{e}_{gas}^{in}\left(3,t\right)}^{Lin{e}_{gas}^{out}\left(3,t\right)}\overrightarrow{\underleftarrow{---}}(25)$

$Lin{e}_{gas}^{out}\left(1,t\right)\cdot \sqrt{\left(1-f_{gas}^{loss,1}\right)}-Lin{e}_{gas}^{in}\left(1,t\right)/\sqrt{\left(1-f_{gas}^{loss,1}\right)}=Lin{e}_{gas}^{out}\left(2,t\right)-Lin{e}_{gas}^{in}\left(2,t\right)(26)$

The gas flow in a gas pipeline is restricted by the pressure of the beginning and end nodes. This constraint can be described as:

$-\sqrt{C_{ij}^2\left(p_{j,max}^2-p_{i,min}^2\right)}\le f_{ij}\le \sqrt{C_{ij}^2\left(p_{i,max}^2-p_{j,min}^2\right)}(27)$

where $p_{i,min},p_{i,max},p_{j,min},p_{j,max}$ are the minimum and maximum pressure at node i and j.

4 The Sequential Operation of the Whole System

Four microgrids are interconnected with the hybrid IEEE30 + gas20 + heat14 network. It is actually difficult to schedule this complex system. In this paper, we present a sequential strategy as follows: 1) first, four microgrids run their scheduling algorithms based on MPC or ADP method [section (2)], and obtain the exchanged energy with electricity/heat/gas utility grids; 2) second, the utility grids receive the exchanged energy, and run their power flow problem [Section (3)].

5 System Setup

In this paper, an IEEE-30 + gas-20 + heat-14 hybrid system is adopted as the utility grids. Four multi-energy microgrids are connected with the utility grids. The structure is presented in Figure 2. Microgrid MG1 is connected at electrical node e23, gas node g7, heat node h9. Microgrid MG2 is connected at electrical node e17, gas node g6, heat node h10. Microgrid MG3 is connected at electrical node e14, gas node g15, heat node h4. Microgrid MG4 is connected at electrical node e7, gas node g10, heat node h13. The configutation of this hybrid system is summarized in Eq. 28. The model is implemented in MATLAB and solved with YALMIP (Löfberg, 2012) and Gurobi.

$\left|\begin{array}{cccc}Units& Electricalbus& Gasnode& Heatnode\\ MG1& e23& g7& h9\\ MG2& e17& g6& h10\\ MG3& e14& g15& h4\\ MG4& e7& g10& h13\end{array}\right|(28)$

A typical day is chosen. Based on the forecasted load demands and PV output, microgrids firstly run their day-ahead scheduling algorithm, and the exchanged energy results with the utility grids are obtained and then transferred to the real-time dispatching algorithm. Secondly, the real-time rolling horizon dispatching algorithm is solved based on the new forecasting data and the day-ahead exchange results.

The load demands (peak load) of each microgrid and microgrid operation parameters are presented in Supplementary Material.

6 Simulation Results

Based on the above strategy, the simulation running is deployed. The simulation results are presented from four aspects: 1) scheduling results; 2) operation cost analysis; 3) exchanged energy analysis; 4) utility grids power flow.

6.1 Scheduling Results

Different cases are presented to research about the performance of each algorithm. Cases $AD{P}_{linear}b$ and $AD{P}_{linear}c$ are used to study the linear regression AVF. Cases $AD{P}_{nonlinear}A$ and $AD{P}_{nonlinear}B$ are used to study the nonlinear regression AVF. Cases $AD{P}_{online}30$, $AD{P}_{online}neg1$, and $AD{P}_{online}neg3$ are compared to study the online process. In order to study the influence of optimization window numbers, cases $MP{C}_{12}$, $MP{C}_6$, and $MP{C}_1$ are set. Cases $AD{P}_{NN}neg1$, $AD{P}_{NN}neg5$, and $AD{P}_{NN}neg10$ are presented to study the neural network regression AVF. All cases are compared and concluded as follows:

1. $AD{P}_{linear}b$: the AVF is constructed based on linear regression, and the coefficient is $C_b={10}^{-2}$;

2. $AD{P}_{linear}c$: the AVF is constructed based on linear regression, and the coefficient is $C_c={10}^2$;

3. $AD{P}_{nonlinear}A$: the AVF is constructed based on nonlinear regression, and the coefficient is $C_A=1.2\text{*}{10}^{-8}$;

4. $AD{P}_{nonlinear}B$: the AVF is constructed based on nonlinear regression, and the coefficient is $C_B={10}^{-8}$;

5. $AD{P}_{online}30$: the AVF is constructed based on linear regression, the simulation is processed based on online Algorithm 2, and the iteration time is 30;

6. $AD{P}_{online}neg1$: the AVF is constructed based on linear regression, the simulation is processed based on online Algorithm 2, and the coefficient is $C_{online}^A={10}^{-1}$;

7. $AD{P}_{online}neg3$: the AVF is constructed based on linear regression, the simulation is processed based on online Algorithm 2, and the coefficient is $C_{online}^B={10}^{-3}$;

8. $Global$: the algorithm is the MPC method, and the optimization window is 288 (12*24 h = 288);

9. $MP{C}_{12}$: the algorithm is the MPC method, and the optimization window is 12;

10. $MP{C}_6$: the algorithm is the MPC method, and the optimization window is 6;

11. $MP{C}_1$: the algorithm is the MPC method, and the optimization window is 1, namely one-step decision method, but the future costs are not considered;

12. $AD{P}_{NN}neg1$: the AVF is constructed based on neural network regression, the simulation is processed based on offline algorithm, and the coefficient is $C_{NN}^A={10}^{-1}$;

13. $AD{P}_{NN}neg5$: the AVF is constructed based on neural network regression, the simulation is processed based on offline algorithm, and the coefficient is $C_{NN}^B={10}^{-5}$;

14. $AD{P}_{NN}neg10$: the AVF is constructed based on neural network regression, the simulation is processed based on offline algorithm, and the coefficient is $C_{NN}^C={10}^{-10}$;

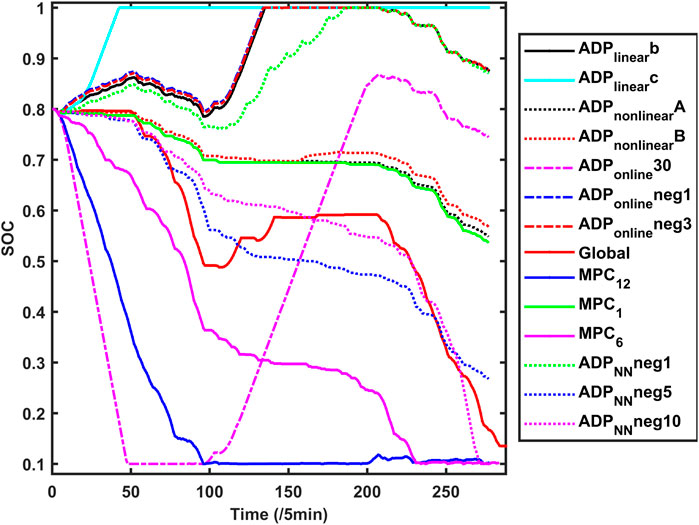
The simulation results of the real-time SOC of MG4 can be seen in Figure 4. Here SOC means the percentage of hydrogen in tanks. It can be seen that with different algorithms, the real-time dispatching results are significantly different. This is because in different algorithms, the future operation value functions are different, leading to different scheduling results.

FIGURE 4

FIGURE 4. Real-time SOC of MG4 with different optimization algorithms.

We compare these different algorithms in the following:

$\begin{array}{c}•AD{P}_{Ind}:\underset{x_t}{min}{u}_{cost}^{el}\cdot |E_{grid}^{el,T}-Z_{grid}^{el,t}|+u_{cost}^{heat}\cdot |E_{grid}^{heat,T}-Z_{grid}^{heat,t}|\\ +\mathbf{V}{\mathbf{F}}_{\mathbf{I}\mathbf{n}\mathbf{d}}\left(\mathbf{S}\left(\mathbf{t}+1\right),{\mathbf{L}}_{\mathbf{p}\mathbf{r}\mathbf{e}}\right)\cdot {\mathbf{C}}_{\mathbf{I}\mathbf{n}\mathbf{d}}\\ +\alpha \cdot \widetilde{L{S}_{gas}^t}+\beta \cdot \widetilde{L{S}_{el}^t}+\gamma \cdot \widetilde{L{S}_{heat}^t};\end{array}(29)$

where $Ind=\left\{linear,nonlinear,NN,online\right\}$ represents different types of ADP algorithms. $E_{grid}^{el,T}$ is the day-ahead exchanged electricity power at time T, $Z_{grid}^{el,t}$ is the real-time exchanged electricity power at time t, $E_{grid}^{heat,T}$ is the day-ahead exchanged heat power at time T, $Z_{grid}^{heat,t}$ is the real-time exchanged heat power at time t. $|E_{grid}^{el,T}-Z_{grid}^{el,t}|$ is used to describe the real-time electricity power deviation from the day-ahead results, and the unit is MW. $u_{cost}^{el}$, $u_{cost}^{heat}$ are the unit cost of electricity and heat power deviation from the day-ahead results, and the unit is €/MW. $\widetilde{L{S}_k^t}$, $k=\left(gas,el,heat\right)$ are the load shedding of the gas, electric, and heat load demands, the unit is $MW$. α, β, γ are penalty values of demands load shedding, the unit is €/MW.

$•\mathbf{V}{\mathbf{F}}_{\mathbf{l}\mathbf{i}\mathbf{n}\mathbf{e}\mathbf{a}\mathbf{r}}(\mathbf{S}(\mathbf{t}+1),{\mathbf{L}}_{\mathbf{p}\mathbf{r}\mathbf{e}})=a_0+a_1\cdot S_{t+1}+a_2\cdot L_{pre};(30)$

where ${\mathbf{C}}_{\mathbf{l}\mathbf{i}\mathbf{n}\mathbf{e}\mathbf{a}\mathbf{r}}\in \left\{{\mathbf{C}}_{\mathbf{b}},{\mathbf{C}}_{\mathbf{c}}\right\}$ are coefficients, which is used to adjust the proportion of linear based AVF.

$\begin{array}{c}•\mathbf{V}{\mathbf{F}}_{\mathbf{n}\mathbf{o}\mathbf{n}\mathbf{l}\mathbf{i}\mathbf{n}\mathbf{e}\mathbf{a}\mathbf{r}}(\mathbf{S}(\mathbf{t}+1),{\mathbf{L}}_{\mathbf{p}\mathbf{r}\mathbf{e}})=b_0+b_1\cdot S_{t+1}+b_2\cdot L_{pre}\\ +b_3\cdot S_{t+1}\cdot L_{pre}+b_4\cdot S_{t+1}^2+b_5\cdot L_{pre}^2;\end{array}(31)$

where ${\mathbf{C}}_{\mathbf{n}\mathbf{o}\mathbf{n}\mathbf{l}\mathbf{i}\mathbf{n}\mathbf{e}\mathbf{a}\mathbf{r}}\in \left\{{\mathbf{C}}_{\mathbf{A}},{\mathbf{C}}_{\mathbf{B}}\right\}$ are coefficients, which is used to adjust the proportion of nonlinear based AVF.

$•\mathbf{V}{\mathbf{F}}_{\mathbf{N}\mathbf{N}}(\mathbf{S}(\mathbf{t}+1),{\mathbf{L}}_{\mathbf{p}\mathbf{r}\mathbf{e}})=NN(S_{t+1},L_{pre}^{PV},L_{pre}^{el},L_{pre}^{heat},L_{pre}^{gas});(32)$

where ${\mathbf{C}}_{\mathbf{N}\mathbf{N}}\in \left\{{\mathbf{C}}_{\mathbf{N}\mathbf{N}}^{\mathbf{A}},{\mathbf{C}}_{\mathbf{N}\mathbf{N}}^{\mathbf{B}},{\mathbf{C}}_{\mathbf{N}\mathbf{N}}^{\mathbf{C}}\right\}$ are coefficients, which is used to adjust the proportion of neural network based AVF.

$•\mathbf{V}{\mathbf{F}}_{\mathbf{o}\mathbf{n}\mathbf{l}\mathbf{i}\mathbf{n}\mathbf{e}}(\mathbf{S}(\mathbf{t}+1),{\mathbf{L}}_{\mathbf{p}\mathbf{r}\mathbf{e}})=\widehat{a_0}+\widehat{a_1}\cdot S_{t+1}+\widehat{a_2}\cdot L_{pre};(33)$

where $\widehat{a_0},\widehat{a_1},\widehat{a_2}$ are changed in each iteration. ${\mathbf{C}}_{\mathbf{o}\mathbf{n}\mathbf{l}\mathbf{i}\mathbf{n}\mathbf{e}}\in \left\{{\mathbf{C}}_{\mathbf{o}\mathbf{n}\mathbf{l}\mathbf{i}\mathbf{n}\mathbf{e}}^{\mathbf{A}},{\mathbf{C}}_{\mathbf{o}\mathbf{n}\mathbf{l}\mathbf{i}\mathbf{n}\mathbf{e}}^{\mathbf{B}}\right\}$ are coefficients, which is used to adjust the proportion of AVF.

$\begin{array}{c}•MPC:\underset{x_t,\dots ,x_{t+sw}}{min}\stackrel{sw}{{\displaystyle \sum }_{j=0}}{u}_{cost}^{el}\cdot |E_{grid}^{el,T}-Z_{grid}^{el,t+j}|\\ +\stackrel{sw}{{\displaystyle \sum }_{j=0}}{u}_{cost}^{heat}\cdot |E_{grid}^{heat,T}-Z_{grid}^{heat,t+j}|\\ +\alpha \cdot \stackrel{sw}{{\displaystyle \sum }_{j=0}}\widetilde{L{S}_{gas}^{t+j}}+\beta \cdot \stackrel{sw}{{\displaystyle \sum }_{j=0}}\widetilde{L{S}_{el}^{t+j}}+\gamma \cdot \stackrel{sw}{{\displaystyle \sum }_{j=0}}\widetilde{L{S}_{heat}^{t+j}}\\ •Global:sw=288;MP{C}_{12}:sw=12;\\ MP{C}_6:sw=6;MP{C}_1:sw=1;\end{array}(34)$

where $sw$ is the optimization window number in MPC algorithm.

In Figure 4, we set the case $Global$ as the basic case, because in case $Global$, the scheduling results are “global optimization”; however, in the other cases, the results are “local optimization”. Compare cases $AD{P}_{linear}$ and case $Global$, the SOC curves are very different, especially, in cases $AD{P}_{linear}$, the SOC value reaches at the maximum point. And it can also be seen that in cases $AD{P}_{linear}$, different coefficient values ${\mathbf{C}}_{\mathbf{b}},{\mathbf{C}}_{\mathbf{c}}$ lead to different dispatching results. Compare cases $AD{P}_{nonlinear}$ and case $Global$, the SOC curves have a similar tendency, but the values are different. Compare cases $MPC$ and case $Global$, it can be seen that with different optimization window numbers, the SOC curves are very different. For example, in case $MP{C}_1$, it has a similar tendency SOC; however, in case $MP{C}_{12}$, the SOC reaches at the minimum point.

We compare different $AD{P}_{linear}$ cases in Figure 5A, namely, we choose different coefficients

$ADP1:C_a={10}^0;AD{P}_{neg}2:C_b={10}^{-2};AD{P}_{pos}2:C_c={10}^2;AD{P}_{neg}4:C_d={10}^{-4};AD{P}_{pos}4:C_e={10}^4(35)$

The linear regression of value function is shown in Figure 5B.

FIGURE 5

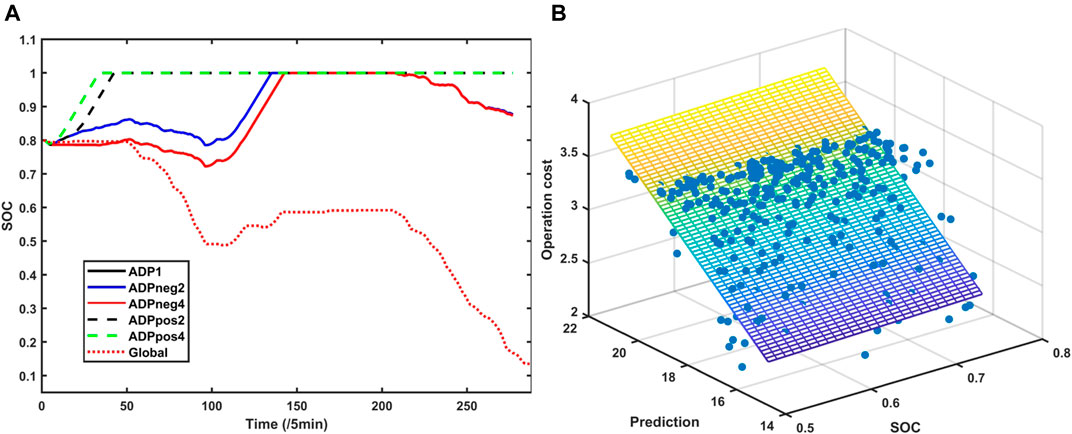
FIGURE 5. (A) Real-time SOC of MG4 with different linear value functions. (B) Linear regression of value function.

In fact, case $ADP1$ and case $AD{P}_{neg}2$ have very similar SOC curve, and they overlap together. It can be seen that the scheduling results based on linear approximate value function $AD{P}_{linear}$ deviate from the “global optimization” curve. This means that the linear approximate value function can not describe the future operation cost well. One important reason is that the dataset which is used to regress the linear value function is not completely, the other reason is that the linear function can not regress the value function well, and at last, leading to inaccuracy approximate value function.

Then, we adopt the nonlinear function to regress the dataset. And we compare different $AD{P}_{nonlinear}$ cases in Figure 6A, namely, we choose different coefficients

$AD{P}_{nonlinear}A:C_A=1.2*{10}^{-8};AD{P}_{nonlinear}B:C_B={10}^{-8};AD{P}_{nonlinear}C:C_C={10}^{-9};AD{P}_{nonlinear}D:C_D={10}^{-10};AD{P}_{nonlinear}E:C_e={10}^{-13}.$

The nonlinear regression of value function is shown in Figure 6B.

FIGURE 6

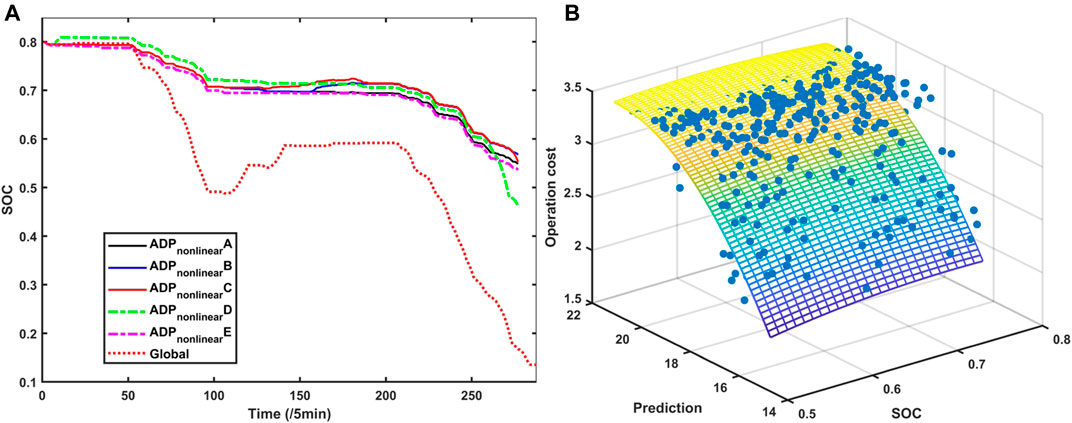
FIGURE 6. (A) Real-time SOC of MG4 with different nonlinear value functions. (B) Nonlinear regression of value function.

It can be seen that based on the nonlinear approximate value function, the scheduling results have similar tendency to the global results. And with different coefficients $C_A,C_B,C_C,C_D,C_E$, the scheduling results are similar to each other. However, the SOC curve values are still far away from the Global optimization results.

After that we adopt the neural network to regress the dataset. And we compare different $AD{P}_{NN}$ cases in Figure 7A, namely, we choose different coefficients $AD{P}_{NN}A:C_{NN}^A={10}^{-1};AD{P}_{NN}B:C_{NN}^B={10}^{-5};AD{P}_{NN}C:C_{NN}^C={10}^{-10}$.

FIGURE 7

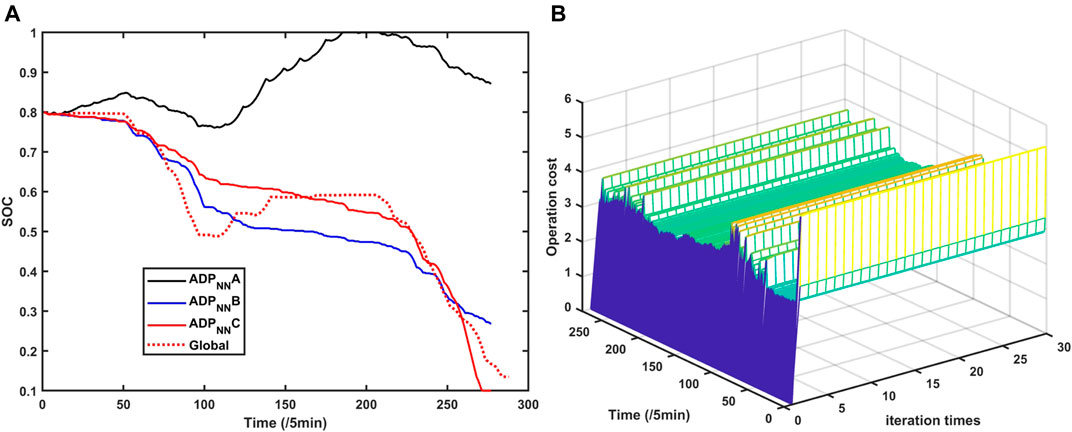
FIGURE 7. (A) Neural network regression of the value function. (B) Operation cost of MG4 based on the online ADP method.

It can be seen that based on the neural network approximate value function, if we choose the approximate coefficients, the scheduling results are very close to the global optimization results, which means that the neural network can regress the value function well.

After that we develop an online simulation process, namely, at each time, the one-step decision model is iteratively simulated 30 times. The simulated operation cost of MG4 is shown in Figure 7B.

At each time, the one-step optimization model is solved for 30 times, and in each iteration, the parameters of the approximate value function is updated. Based on Figure 7B, it can be seen that at each time step, after 30 times iteration, the operation costs keep constantly, which means that the iteration process is convergence.

6.2 Operation Cost Analysis

In this section, we analyze the operation cost of MGs based on different algorithms. Operation costs are the results of the problem Eq. 29 and problem Eq. 34. We use a 2-norm error to describe the difference between real-time operation cost of different algorithms and global optimization. The 2-norm error can be represented as:

$erro{r}_{rc}=\sqrt{{\displaystyle \sum }_{t=1}^T|R{C}_{method}^t-R{C}_{global}^t{|}^2}(37)$

where $erro{r}_{rc}$ is the 2-norm error of real-time operation cost, $R{C}_{method}^t$ is the real-time operation cost under method $method=\left\{AD{P}_{linear},AD{P}_{nonlinear},AD{P}_{NN},AD{P}_{online},MPC\right\}$ at time t, $R{C}_{global}^t$ is the real-time operation cost under global optimization at time t.

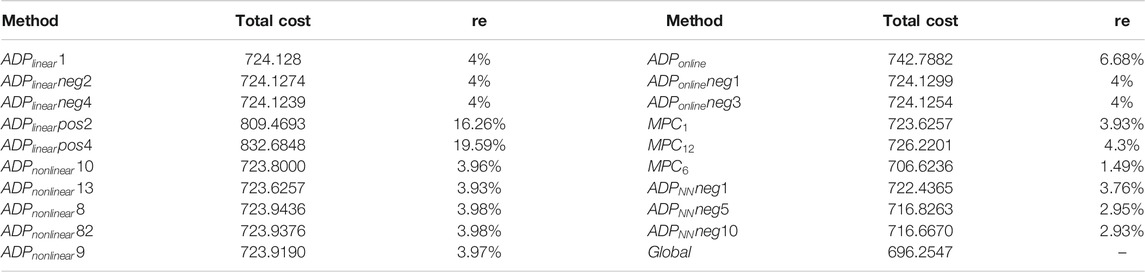
Table 1 shows the 2-norm error of real-time operation cost of MG4 with different algorithms. It can be seen that $AD{P}_{NN}neg5$ has the smallest 2-norm error, and $AD{P}_{linear}pos4$ has the largest 2-norm error. This means that at each time step, the real-time operation cost of $AD{P}_{NN}neg5$ is the closest to the Global optimization real-time operation cost, namely, algorithm $AD{P}_{NN}neg5$ has the best real-time performance.

TABLE 1

TABLE 1. Real-time operation cost 2-norm error of MG4 with different algorithms.

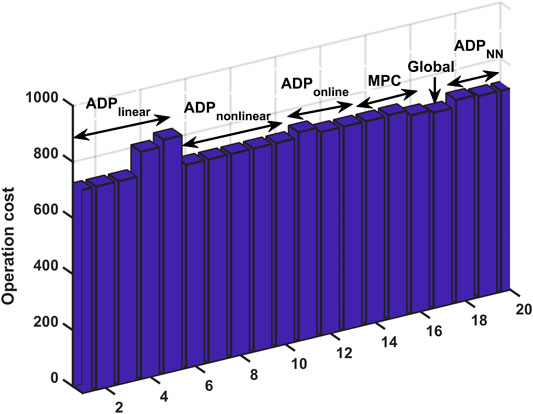
We then compare the total operation cost (total time horizon) in Table 2 and Figure 8. It can be seen that case $Global$ has the minimum total operation cost, because it is the global optimization. ADP method and the MPC method have the similar total costs. Different coefficients in ADP and MPC lead to different total costs, which means that choose appropriate coefficient is important.

TABLE 2

TABLE 2. Total operation costs.

FIGURE 8

FIGURE 8. Total operation cost based on different algorithms.

Then, we need to choose an index to evaluate different algorithms. Here, we use relative error $re$ to describe different algorithms, namely,

$re=\frac{|T{C}_{method}-T{C}_{global}|}{T{C}_{global}}(36)$

where $T{C}_m$, $m=\{AD{P}_{linear}$, $AD{P}_{nonlinear}$, $AD{P}_{NN}$, $AD{P}_{online}$, $MPC\}$ and $T{C}_{global}$ are the total cost under different algorithms and global optimization.

We can then calculate the relative error with different algorithms, which is shown in Table 2. It can be seen that in case $AD{P}_{linear}$, with different coefficients the relative errors are different, especially when the coefficients are large (for example, case $AD{P}_{linear}pos2$, $AD{P}_{linear}pos4$), the relative errors are large, which means that the scheduling results deviate far from the global optimization results. In five nonlinear cases $AD{P}_{nonlinear}$, it can be seen that the differences are small, and the relative error is less than 4%.

In the online case $AD{P}_{online}$, the relative error is less than 7%, but after adjust the coefficient, the relative error decreases to 4% in cases $AD{P}_{online}neg1$ and $AD{P}_{online}neg3$. For the online process, the inner value function and the iteration time are two important factors to influence the operation cost and the scheduling results.

For the MPC cases, the optimization window number is important, it can be seen that when the optimization window number is 6, the relative error is less than 1.5%; and the sliding window is 12, the relative error is about 4.3%. For the $AD{P}_{NN}$ cases, it can be seen that the relative error is less than 3% in cases $AD{P}_{NN}neg5$ and $AD{P}_{NN}neg10$.

At last, from the post-event analysis view (total operation cost), it can be seen that algorithm $MP{C}_6$ has the best performance (in terms of total operation cost), and the second is the algorithm $AD{P}_{NN}neg5$ and $AD{P}_{NN}neg10$.

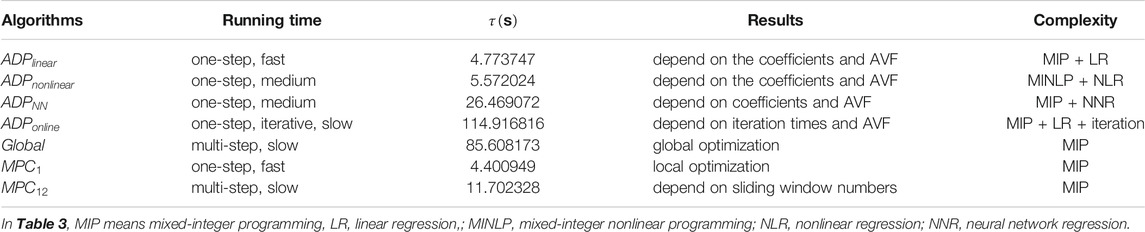
In conclusion, different algorithms have advantages and disadvantages, we choose four indexes to compare these algorithms: running time, one-step simulation time τ, results, and complexity, which can be seen in Table 3.

TABLE 3

TABLE 3. Comparison of different algorithms.

6.3 Exchanged Energy With Utility Grids

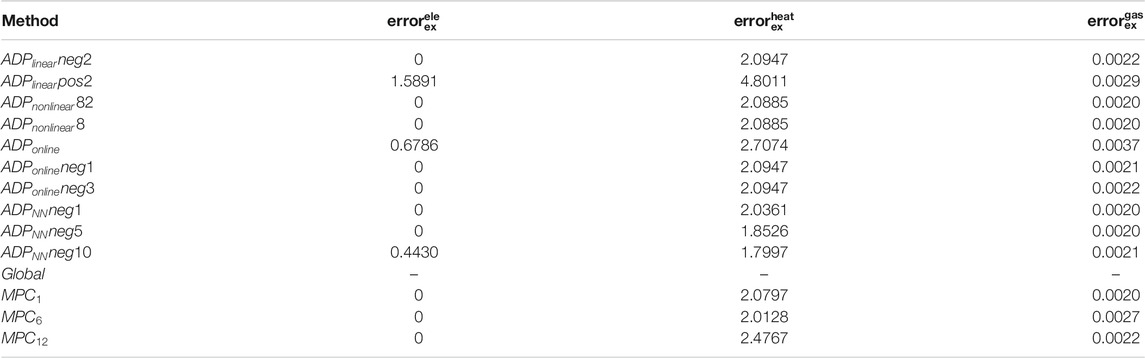
The exchanged electricity/heat/gas with utility grids are shown in Figures 9, 10, 11A. In order to make these figures readable, we calculate the 2-norm error of the exchanged energy under different algorithms (case “Global” is set as the basic case), which is shown in Table 4.

FIGURE 9

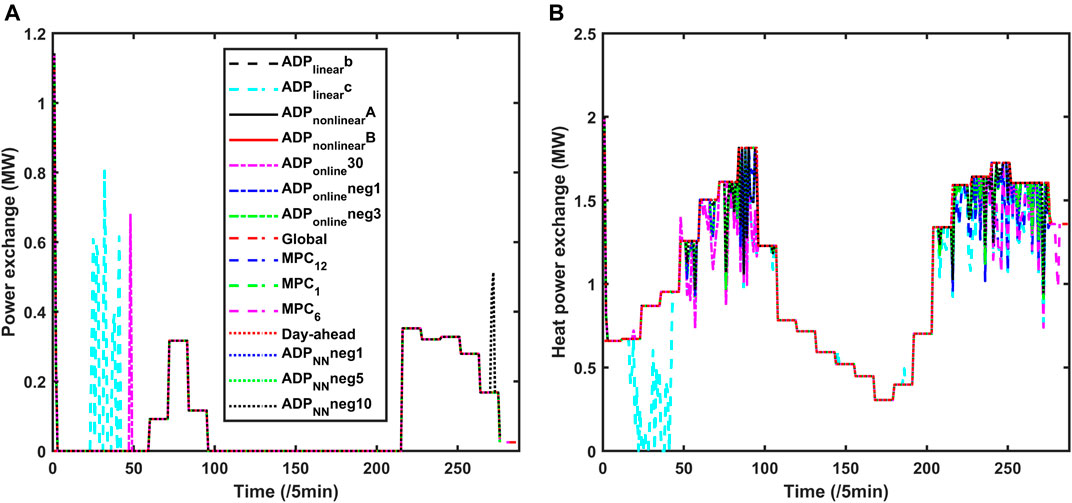
FIGURE 9. (A) Electricity power exchange with utility grid under different algorithms. (B) Heat power exchange with utility grid under different algorithms.

FIGURE 10

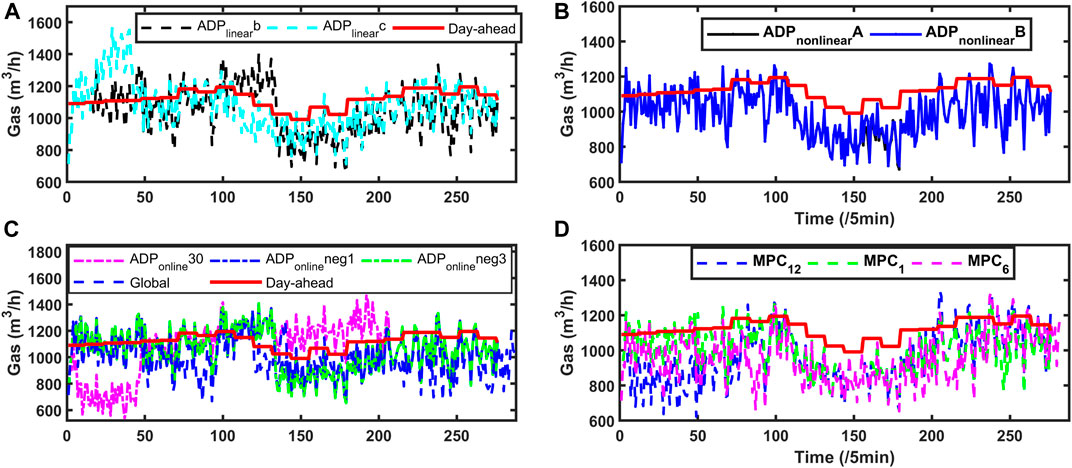
FIGURE 10. (A) Gas exchange with utility grid with $AD{P}_{linear}$ algorithms. (B) Gas exchange with utility grid with $AD{P}_{nonlinear}$ algorithms. (C) Gas exchange with utility grid with $AD{P}_{online}$ algorithms. (D) Gas exchange with utility grid with $MPC$ algorithms.

FIGURE 11

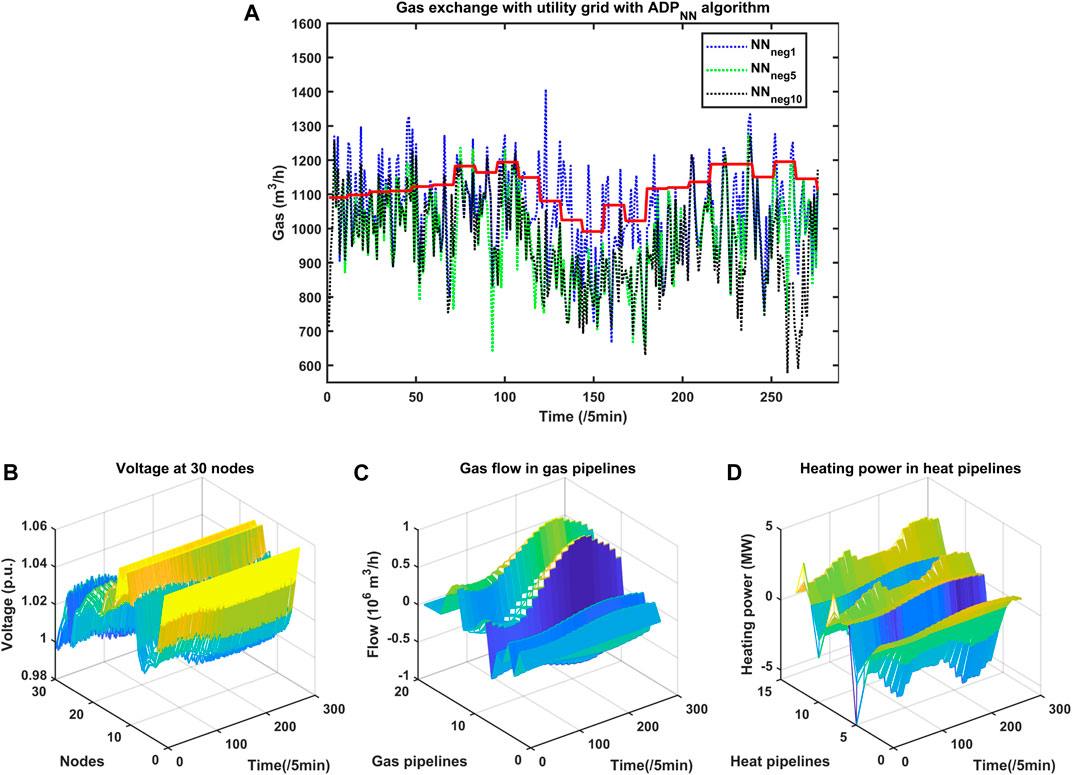
FIGURE 11. (A) Gas exchange with utility grid with $AD{P}_{NN}$ algorithms. (B) The voltage of the IEEE-30 node electricity network with $AD{P}_{NN}neg5$. (C) Gas flow in gas-20 node network with $AD{P}_{NN}neg5$. (D) Heating power flow in heat-14 node network with $AD{P}_{NN}neg5$.

TABLE 4

TABLE 4. 2-norm error of the exchanged energy with different algorithms.

For the exchanged electricity, cases $AD{P}_{linear}pos2$ and $AD{P}_{online}$ have large 2-norm errors, which means that they can not effectively follow the day-ahead exchanged electricity scheduling. However, for cases $AD{P}_{nonlinear}$ and $MPC$, the 2-norm errors are zero, which means that they can follow the day-ahead exchanged electricity well.

For the exchanged heat, it can be seen that cases $AD{P}_{linear}pos2$, $AD{P}_{online}$ and $MP{C}_{12}$ have large 2-norm errors, and for the other cases, the error is less than 2.1. Especially, for cases $AD{P}_{NN}neg5$ and $AD{P}_{NN}neg10$, the error is less than 1.9. In Figure 9, it can be seen that only case $AD{P}_{linear}pos2$ deviates largely from the day-ahead results, and other cases all can follow the day-ahead results well.

For the exchange gas, cases $AD{P}_{online}$, $AD{P}_{linear}pos2$, and $MP{C}_6$ have large 2-norm errors, and for the other cases, the error is less than 0.0022.

At last, overall consideration of $erro{r}_{ex}^{ele}$, $erro{r}_{ex}^{heat}$, and $erro{r}_{ex}^{gas}$. It can be seen that algorithm $AD{P}_{NN}neg5$ has the best performance (in terms of exchanged energy).

6.4 Utility Grids Power Flow

Based on the above exchanged energy, the electricity/heat/gas utility grids then run their power flow algorithm. The voltage of the IEEE-30 node electricity network with $AD{P}_{NN}neg5$ is presented in Figure 11B. Gas flow in gas-20 node network with $AD{P}_{NN}neg5$ is presented in Figure 11C. Heating power flow in heat-14 node network with $AD{P}_{NN}neg5$ is presented in Figure 11D. The other power flow results are presented in Supplementary Material. It can be seen that the power flow in each utility network is within the security area and satisfy the operation constraints.

7 Conclusion

In this paper, the real-time operation of grid-connected microgrid based on ADP algorithm was studied, a hybrid multi-energy supply microgrid model was adopted. We focused on studying the performance of different scheduling algorithms. Day-ahead stochastic scheduling and real-time dispatching coordinated strategy was adopted.

For the day-ahead scheduling, the scenario-based stochastic optimization was used. For the real-time dispatching, ADP and MPC algorithms were adopted, different parameters and coefficients were compared to study the performance of each algorithm.

Based on the simulation results, some conclusions were presented:

1) ADP and MPC algorithm had the ability to implement the real-time operation. Linear function based AVF ADP algorithm, one optimization window number MPC algorithm had a fast running time. Nonlinear function based AVF ADP algorithm had an average running time. Online process ADP method, global optimization and multiple window numbers MPC algorithm had a slow running time.

2) In the ADP method, AVF was the important parameter to influence the dispatching results. In fact, neural network based AVF ADP algorithm had the smallest real-time operation cost 2-norm error, less than 3% total operation cost relative error, and the smallest exchanged energy 2-norm error, which means that neural network based AVF ADP had the best performance. In addition, the running time of neural network based AVF ADP was only 31% of the Global algorithm.

3) In the online process, because there was not enough initial dataset, the regression AVF could not better describe the future operation cost, which leaded to an average performance. In addition, at each time step, the real-time optimization problem was iteratively solved for several times, which also increased the running time. However, the online process provided a method to make the decision when there was not enough initial dataset.

In conclusion, we presented a neural network based ADP real-time dispatching algorithm, which had almost the same performance with Global optimization, while only 31% running time of the Global algorithm. It can be directly utilized in industry scenarios and improve the dispatching performance compared to MPC algorithm.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

BL: Conceptualization, Methodology, Software, Writing- Original draft preparation, Reviewing and Editing. RR: Visualization, Investigation, Validation, Reviewing and Editing.

Funding

This work has been supported by the “Guangdong Basic and Applied Basic Research Foundation” (2019A1515110641), the “Fundamental Research Funds for the Shenzhen university” (000002110235), the EIPHI Graduate School (contract ANR-17-EURE-0002), and the Region Bourgogne-Franche-Comté.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/felec.2021.637736/full#supplementary-material.

References

Anderson, R. N., Boulanger, A., Powell, W. B., and Scott, W. (2011). Adaptive stochastic control for the smart grid. Proc. IEEE 99, 1098–1115. doi:10.1109/JPROC.2011.2109671

CrossRef Full Text | Google Scholar

Bhattacharya, A., Kharoufeh, J. P., and Zeng, B. (2018). Managing energy storage in microgrids: a multistage stochastic programming approach. IEEE Trans. Smart Grid 9, 483–496. doi:10.1109/TSG.2016.2618621

CrossRef Full Text | Google Scholar

Chen, S., Wei, Z., Sun, G., Cheung, K. W., and Wang, D. (2017). Identifying optimal energy flow solvability in electricity-gas integrated energy systems. IEEE Trans. Sustain. Energy 8, 846–854. doi:10.1109/TSTE.2016.2623631

CrossRef Full Text | Google Scholar

Darivianakis, G., Eichler, A., Smith, R. S., and Lygeros, J. (2017). A data-driven stochastic optimization approach to the seasonal storage energy management. IEEE Control Syst. Lett. 1, 394–399. doi:10.1109/LCSYS.2017.2714426

CrossRef Full Text | Google Scholar

Das, A., and Ni, Z. (2018). A computationally efficient optimization approach for battery systems in islanded microgrid. IEEE Trans. Smart Grid 9, 6489–6499. doi:10.1109/TSG.2017.2713947

CrossRef Full Text | Google Scholar

De Wolf, D., and Smeers, Y. (2000). The gas transmission problem solved by an extension of the simplex algorithm. Manag. Sci. 46, 1454–1465. doi:10.1287/mnsc.46.11.1454.12087

CrossRef Full Text | Google Scholar

Fang, J., Zeng, Q., Ai, X., Chen, Z., and Wen, J. (2018). Dynamic optimal energy flow in the integrated natural gas and electrical power systems. IEEE Trans. Sustain. Energy 9, 188–198. doi:10.1109/TSTE.2017.2717600

CrossRef Full Text | Google Scholar

Gurobi (2018). gurobi [Dataset]. Available at: www.gurobi.com.

Google Scholar

Ji, Y., Wang, J., Fang, X., and Zhang, H. (2018). “Online optimal operation of microgrid using approximate dynamic programming under uncertain environment,” in 2018 37th Chinese control conference (CCC), Wuhan, China, July 25–27, 2018 (New York, NY: IEEE), 2235–2241. doi:10.23919/ChiCC.2018.8483355

CrossRef Full Text | Google Scholar

Jiang, D. R., Pham, T. V., Powell, W. B., Salas, D. F., and Scott, W. R. (2014). “A comparison of approximate dynamic programming techniques on benchmark energy storage problems: does anything work?” in 2014 IEEE Symposium on adaptive dynamic programming and reinforcement learning (ADPRL), Orlando, FL, December 9–12, 2014 (New York, NY: IEEE), 1–8. doi:10.1109/ADPRL.2014.7010626

CrossRef Full Text | Google Scholar

Keerthisinghe, C., Verbic, G., and Chapman, A. C. (2018). A fast technique for smart home management: adp with temporal difference learning. IEEE Trans. Smart Grid 9, 3291–3303. doi:10.1109/TSG.2016.2629470

CrossRef Full Text | Google Scholar

Löfberg, J. (2012). Automatic robust convex programming. Optim. Methods Softw. 27, 115–129. doi:10.1080/10556788.2010.517532

CrossRef Full Text | Google Scholar

Li, B., Roche, R., and Miraoui, A. (2017a). Microgrid sizing with combined evolutionary algorithm and milp unit commitment. Appl. Energy 188, 547–562. doi:10.1016/j.apenergy.2016.12.038

CrossRef Full Text | Google Scholar

Li, B., Roche, R., Paire, D., and Miraoui, A. (2017b). Sizing of a stand-alone microgrid considering electric power, cooling/heating, hydrogen loads and hydrogen storage degradation, Appl. Energy 205, 1244–1259. doi:10.1016/j.apenergy.2017.08.142

CrossRef Full Text | Google Scholar

Li, B., Roche, R., Paire, D., and Miraoui, A. (2018a). Coordinated scheduling of a gas/electricity/heat supply network considering temporal-spatial electric vehicle demands. Electr. Power Syst. Res. 163, 382–395. doi:10.1016/j.epsr.2018.07.014

CrossRef Full Text | Google Scholar

Li, B., Roche, R., Paire, D., and Miraoui, A. (2018b). Optimal sizing of distributed generation in gas/electricity/heat supply networks. Energy 151, 675–688. doi:10.1016/j.energy.2018.03.080

CrossRef Full Text | Google Scholar

Li, D., and Jayaweera, S. K. (2015). Machine-learning aided optimal customer decisions for an interactive smart grid. IEEE Syst. J. 9, 1529–1540. doi:10.1109/JSYST.2014.2334637

CrossRef Full Text | Google Scholar

Li, Z., and Xu, Y. (2019). Temporally-coordinated optimal operation of a multi-energy microgrid under diverse uncertainties. Appl. Energy 240, 719–729. doi:10.1016/j.apenergy.2019.02.085

CrossRef Full Text | Google Scholar

Li, Z., Xu, Y., Feng, X., and Wu, Q. (2021). Optimal stochastic deployment of heterogeneous energy storage in a residential multienergy microgrid with demand-side management. IEEE Trans. Industr. Inform. 17, 991–1004. doi:10.1109/TII.2020.2971227

CrossRef Full Text | Google Scholar

Liu, D., Li, H., and Wang, D. (2015). Error bounds of adaptive dynamic programming algorithms for solving undiscounted optimal control problems. IEEE Trans. Neural Netw. Learn. Syst. 26, 1323–1334. doi:10.1109/TNNLS.2015.2402203

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W., Ma, T., and Yang, Y. (2020). Reliability assessment of integrated energy system based on coupling energy flow and thermal inertia. CSEE J. Power Energy Syst. 1–11. doi:10.17775/CSEEJPES.2019.03030

CrossRef Full Text | Google Scholar

Mancarella, P. (2014). Mes (multi-energy systems): an overview of concepts and evaluation models. Energy 65, 1–17. doi:10.1016/j.energy.2013.10.041

CrossRef Full Text | Google Scholar

Martínez Ceseña, E. A., Loukarakis, E., Good, N., and Mancarella, P. (2020). Integrated electricity-heat-gas systems: techno-economic modeling, optimization, and application to multienergy districts. Proc. IEEE 108, 1392–1410. doi:10.1109/JPROC.2020.2989382

CrossRef Full Text | Google Scholar

Martínez Ceseña, E. A., and Mancarella, P. (2019). Energy systems integration in smart districts: robust optimisation of multi-energy flows in integrated electricity, heat and gas networks. IEEE Trans. Smart Grid 10, 1122–1131. doi:10.1109/TSG.2018.2828146

CrossRef Full Text | Google Scholar

Martinez-Mares, A., and Fuerte-Esquivel, C. R. (2012). A unified gas and power flow analysis in natural gas and electricity coupled networks. IEEE Trans. Power Syst. 27, 2156–2166. doi:10.1109/tpwrs.2012.2191984

CrossRef Full Text | Google Scholar

Mohammadi-Ivatloo, B., Moradi-Dalvand, M., and Rabiee, A. (2013). Combined heat and power economic dispatch problem solution using particle swarm optimization with time varying acceleration coefficients. Electr. Power Syst. Res. 95, 9–18. doi:10.1016/j.epsr.2012.08.005

CrossRef Full Text | Google Scholar

Pirouti, M. (2013). Modelling and analysis of a district heating network. PhD thesis. Cardiff (United Kingdom): Cardiff University.

Google Scholar

Qin, Y., Wu, L., Zheng, J., Li, M., Jing, Z., Wu, Q. H., et al. (2020). Optimal operation of integrated energy systems subject to coupled demand constraints of electricity and natural gas. CSEE J. Power Energy Syst. 6, 444–457. doi:10.17775/CSEEJPES.2018.00640

CrossRef Full Text | Google Scholar

Salas, D. F., and Powell, W. B. (2013). Benchmarking a scalable approximate dynamic programming algorithm for stochastic control of multidimensional energy storage problems. Informs J. Comput. 30, 106–123. doi:10.1287/ijoc.2017.0768

CrossRef Full Text | Google Scholar

Shabanpour-Haghighi, A., and Seifi, A. R. (2015). Simultaneous integrated optimal energy flow of electricity, gas, and heat. Energy Convers. Manag. 101, 579–591. doi:10.1016/j.enconman.2015.06.002

CrossRef Full Text | Google Scholar

Shang, C., and You, F. (2019). A data-driven robust optimization approach to scenario-based stochastic model predictive control. J. Process Contr. 75, 24–39. doi:10.1016/j.jprocont.2018.12.013

CrossRef Full Text | Google Scholar

Shi, W., Li, N., Chu, C.-C., and Gadh, R. (2017). Real-time energy management in microgrids. IEEE Trans. Smart Grid 8, 228–238. doi:10.1109/tsg.2015.2462294

CrossRef Full Text | Google Scholar

Shuai, H., Fang, J., Ai, X., Tang, Y., Wen, J., and He, H. (2018a). Stochastic optimization of economic dispatch for microgrid based on approximate dynamic programming. IEEE Trans. Smart Grid 10, 2440–2452. doi:10.1109/TSG.2018.2798039

CrossRef Full Text | Google Scholar

Shuai, H., Fang, J., Ai, X., Wen, J., and He, H. (2018b). Optimal real-time operation strategy for microgrid: an ADP based stochastic nonlinear optimization approach. IEEE Trans. Sustain. Energy 10, 931–942. doi:10.1109/TSTE.2018.2855039

CrossRef Full Text | Google Scholar

Strelec, M., and Berka, J. (2013). “Microgrid energy management based on approximate dynamic programming,” in IEEE PES ISGT Europe 2013, Lyngby, Denmark, October 6–13, 2013 (New York, NY: IEEE), 1–5. doi:10.1109/ISGTEurope.2013.6695439

CrossRef Full Text | Google Scholar

Sun, Y., Zhang, B., Ge, L., Sidorov, D., Wang, J., and Xu, Z. (2020). Day-ahead optimization schedule for gas-electric integrated energy system based on second-order cone programming. CSEE J. Power Energy Syst. 6, 142–151. doi:10.17775/CSEEJPES.2019.00860

CrossRef Full Text | Google Scholar

Wang, D. (2019). Robust policy learning control of nonlinear plants with case studies for a power system application. IEEE Trans. Industr. Inform. 16, 1733. doi:10.1109/TII.2019.2925632

CrossRef Full Text | Google Scholar

Wang, D., Ha, M., and Qiao, J. (2019). Self-learning optimal regulation for discrete-time nonlinear systems under event-driven formulation. IEEE Trans. Automat. Contr. 65, 1272. doi:10.1109/TAC.2019.2926167

CrossRef Full Text | Google Scholar

Wang, Y., Chen, C., Wang, J., and Baldick, R. (2016). Research on resilience of power systems under natural disasters – a review. IEEE Trans. Power Syst. 31, 1604–1613. doi:10.1109/TPWRS.2015.2429656

CrossRef Full Text | Google Scholar

Xie, S., He, H., and Peng, J. (2017). An energy management strategy based on stochastic model predictive control for plug-in hybrid electric buses. Appl. Energy 196, 279–288. doi:10.1016/j.apenergy.2016.12.112

CrossRef Full Text | Google Scholar

Yang, W., Liu, W., Chung, C. Y., and Wen, F. (2020). Coordinated planning strategy for integrated energy systems in a district energy sector. IEEE Trans. Sustain. Energy 11, 1807–1819. doi:10.1109/TSTE.2019.2941418

CrossRef Full Text | Google Scholar

Zeng, P., Li, H., He, H., and Li, S. (2018). Dynamic energy management of a microgrid using approximate dynamic programming and deep recurrent neural network learning. IEEE Trans. Smart Grid 10, 4435. doi:10.1109/TSG.2018.2859821

CrossRef Full Text | Google Scholar

Zhu, Y., Dongbin, Z., Xiangjun, L., and Ding, W. (2019). Control-limited adaptive dynamic programming for multi-battery energy storage systems. IEEE Trans. Smart Grid 10, 4235–4244. doi:10.1109/TSG.2018.2854300

CrossRef Full Text | Google Scholar