- 1CNOOC Research Institute Co., Ltd., Beijing, China
- 2National Key Laboratory of Offshore Oil and Gas Exploitation, Beijing, China
- 3School of Petroleum Engineering, Yangtze University, Wuhan, China
During the development of loose sandstone reservoirs, the issue of production decline and bottomhole pressure reduction caused by particle migration is widespread, directly impacting well productivity. Understanding the mechanism of particle migration in sandstone and determining the main factors affecting this process are crucial for improving oilfield development. This study focuses on an offshore oilfield and utilizes real digital core models constructed through CT scanning technology. Numerical simulations of fluid-solid coupling were conducted using Fluent and EDEM software to establish a coupled particle-oil-water flow model. This model was employed to investigate particle blockage modes and the effects of particle size, concentration, and injection rate on particle migration in the reservoir. The results indicate that particle migration primarily occurs in two blockage modes: pinhole blockage and bridging blockage. In sandstone, particle retention rates are primarily controlled by particle size, with larger pore-to-particle size ratios leading to higher retention rates. Particle concentration and injection rate have relatively minor effects on the final retention rate. As for migration distance, particle size significantly influences migration, with larger pore-to-particle size ratios resulting in shorter migration distances. Under low concentration conditions, concentration has a minimal effect on migration distance. However, as the injection rate increases, migration distance also increases. In summary, this study clarifies the particle migration mechanisms and the key factors controlling migration in sandstone formations, providing valuable theoretical support for oilfield development.
1 Introduction
Amid the continuous growth of global energy demand, oil remains one of the primary energy sources (Rahman and Miah, 2017; Mwakipunda et al., 2023). However, as conventional oilfield development enters the mid-to-late stages, the issue of reservoir damage has become increasingly prominent, leading to a decline in oilfield production, which subsequently affects development efficiency and economic viability (Yang et al., 2021; Shokrollahi et al., 2015; Song et al., 2021). Therefore, how to effectively control reservoir damage and enhance recovery rates has become a key technical challenge in oilfield development (Zhang et al., 2020). Particle migration refers to the detachment of solid particles from the rock matrix under the driving force of fluid, followed by their migration through pore channels, eventually accumulating in narrow areas and forming blockages (Okere et al., 2023; Halim et al., 2022; Ikemoto et al., 2023). This phenomenon is particularly evident in loose sandstone reservoirs, where clay minerals (such as kaolinite, illite, and illite-montmorillonite mixed layers) are prone to detachment under fluid erosion, entering the pore fluid (Chen et al., 2017; Chen et al., 2023). As one of the main forms of reservoir damage, particle migration is widely considered a core factor leading to reduced reservoir permeability and decreased well productivity. Especially in loose sandstone reservoirs, the frequent occurrence of particle detachment and migration, due to the loosely structured reservoir, results in severe reservoir blockages, directly impacting oilfield development efficiency (Zeinijahromi et al., 2012; Xing et al., 2023; Miri et al., 2022; Xu et al., 2024).
The Bohai Sea region is one of China’s key offshore oil and gas production areas (Radwan, 2021; Radwan et al., 2022; Fernandes et al., 2023). Exploration results indicate that the reservoirs in this block exhibit favorable properties, with an average porosity of 27.1% and an average permeability of 1,178.1 mD, showing typical characteristics of high porosity and high permeability (Zhang et al., 2017; Liu et al., 2015; Chao et al., 2017; Guo et al., 2019). However, the reservoir structure is loosely consolidated and primarily filled with clay minerals, making the issue of particle migration particularly prominent. Production data show that more than half of the wells in the field experience early production decline and bottomhole pressure reduction, closely linked to particle migration and pore blockages (Xue et al., 2021; Zhu, 2009). To address this issue, extensive experimental and simulation studies have been conducted to reveal the mechanisms by which particle migration affects well productivity. Traditional experimental methods simulate particle migration through laboratory core flow experiments, assessing the dynamic impact of particles on reservoir permeability. However, laboratory studies are limited by the complexity of obtaining core samples and experimental conditions, making it difficult to accurately replicate the microstructure of the reservoir and particle migration behavior. With the advancement of computer technology, digital core models based on CT scanning technology provide a new solution for simulating particle migration (Lei, 2020). Digital core technology captures the internal pore structure of rocks through high-precision CT scanning, generating three-dimensional geometric models that more accurately reflect the pore morphology of the reservoir, providing a realistic geometric foundation for numerical simulations (Lin et al., 2017; Hertel et al., 2018; Wu et al., 2024). Combining Fluent and EDEM software for fluid-solid coupling numerical simulations enables the dynamic simulation of particle migration paths, retention behaviors, and their impact on reservoir permeability (Farokhian et al., 2019; Sun et al., 2023; Reilly et al., 2017; Liu et al., 2009).
In this study, real digital core models of a typical block from an oilfield were constructed based on CT scanning technology. A numerical model of particle-oil-water three-phase flow was established using Fluent and EDEM software. Through this model, we systematically studied the effects of key parameters such as particle size, concentration, and injection rate on particle migration behavior, and analyzed the time-varying effects of particles on reservoir permeability under different blockage modes. Additionally, by fitting the simulation results with field production data, the accuracy of the model was further validated, providing reliable support for particle control strategies in oilfield development, as well as offering theoretical support for the efficient development of loose sandstone reservoirs.
2 Methods and materials
2.1 Construction of real digital core using CT scanning
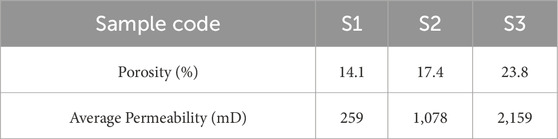
This study selected three typical sandstone samples with varying permeability characteristics. Figure 1 and Table 1 present the detailed features of these rock samples from different formations, respectively. Using 3D CT scanning technology, the internal structure of the rocks, including the skeleton and pore features, was captured in detail. After cleaning and calibrating the collected data, binarization and threshold segmentation techniques were applied to generate high-quality geometric and STL models. Based on this, a meshing tool was used to divide the digital core model into multiple computational units, thereby accurately establishing the computational domain and corresponding boundary conditions.
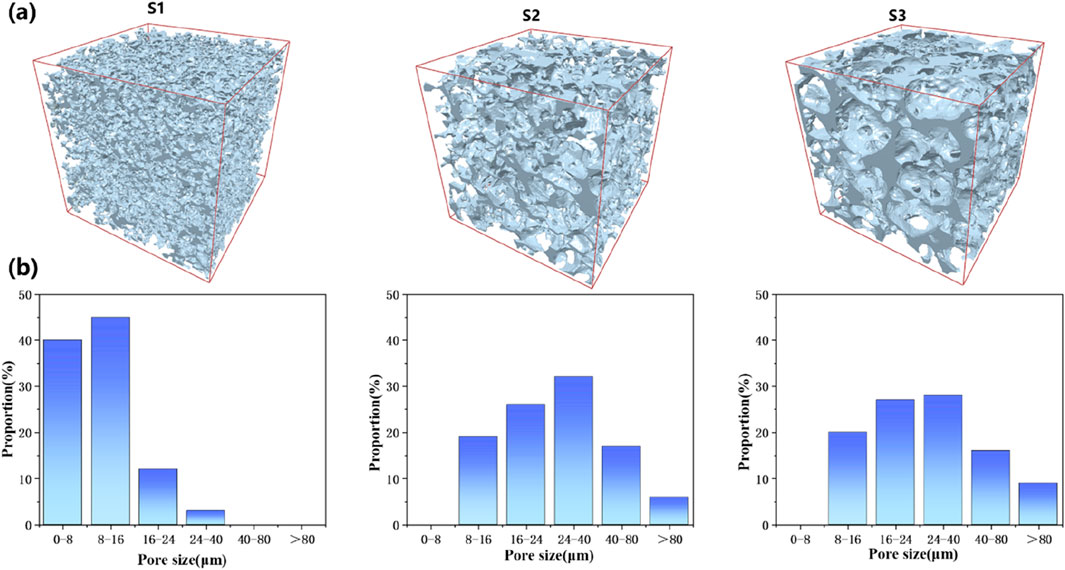
Figure 1. (A): Digital core modeling of cores with different reservoir properties. (B): Pore throat distribution characteristics of cores with different reservoir properties.
The next simulation experiments will be evaluated in detail on the three sets of previously constructed digital core models. The dynamic behavior of particles during oil-water displacement, including their trajectory, retention time in the pore space, and specific distance migrated, is systematically analyzed through the precise adjustment of key parameters such as particle size and injection concentration. Based on the simulation results, the primary modes of particle migration, controlling factors, and their temporal variation patterns were further quantified, clarifying the migration behavior of particles in the reservoir and the pore blockage modes they induce.
2.2 EDEM-fluent coupling principle
The EDEM-Fluent coupling method ingeniously combines the advantages of the Discrete Element Method (DEM) and Computational Fluid Dynamics (CFD) to provide an advanced technical approach for accurately simulating particle movement in complex flow fields. EDEM primarily handles the microscopic movement of particles and their interactions, while Fluent is used to compute the flow characteristics of fluids. This coupling method enables a comprehensive and accurate description of particle dynamics in fluids and the interactions between particles and the fluid. In the specific coupling simulation process, Fluent first simulates the flow of water and oil to obtain flow field distribution information. Fluent, using the volume of fraction method (VOF), tackles the solution of the Navier-Stokes equations and the patio-temporal discretization within the framework of computational fluid dynamics (CFD). The continuity equation is Equation 1.
where
where
This flow field data is then transmitted to EDEM as boundary conditions to control particle movement. Upon receiving the flow field data, EDEM calculates the forces acting on the particles within the flow field, such as drag force, lift force, gravity, and capillary force, and updates the position and velocity of the particles.
For the coupling between fluid flow and particle motion, the resolved CFD-DEM method is used in this model to calculate the momentum exchange between fluid and particles. In the DEM approach, based on Newton’s second law, the governing equation for the motion of particle with mass
where
where
where
where
The updated particle information is fed back to Fluent for the next time step of flow field calculations. This iterative cycle continues until the simulation conditions are met. Through this process of data exchange and iterative updates, EDEM and Fluent work in coordination to simulate particle movement in complex flow fields. This method allows for in-depth investigation of the effects of factors such as flow velocity, pore structure, and particle size on particle movement. Additionally, it provides important references and guidance for particle control, reservoir management, and optimization in field applications.
3 3. results and discussion
3.1 Two modes of particle blockage
Figure 2 reveals two primary mechanisms of particle blockage: pore throat blockage and bridging blockage. These two modes are induced by particles of different sizes, each exerting varying degrees of influence on fluid flow within the reservoir. Pore throat blockage is typically caused by larger particles that cannot pass through pore entrances or become lodged in narrow sections of the throats, forming blockages. Pinhole blockage is typically caused by larger particles that cannot pass through pore entrances and become lodged in narrow sections of the flow path, forming blockages. This type of blockage directly reduces the effective cross-sectional area of the flow channel, increasing local flow resistance and leading to a decrease in flow rate. The impact of pinhole blockage is confined to pore entrances, but its restricting effect on flow channels is pronounced, especially in reservoirs with higher permeability. Bridging blockage, on the other hand, is caused by smaller particles. These smaller particles can enter the pore spaces and gradually accumulate within the pore channels, forming unstable bridge-like structures. These structures not only trap subsequent migrating particles but may also strengthen over time, eventually leading to partial or complete pore blockage. Bridging blockage significantly affects the overall flow capacity of the reservoir’s pore network, potentially causing a severe reduction or even cessation of fluid flow. In summary, pore throat blockage pinhole blockage and bridging blockage have distinct effects on reservoir fluid flow. The former primarily impacts the cross-sectional area at flow channel entrances, while the latter may lead to deeper, more extensive blockages within the reservoir.
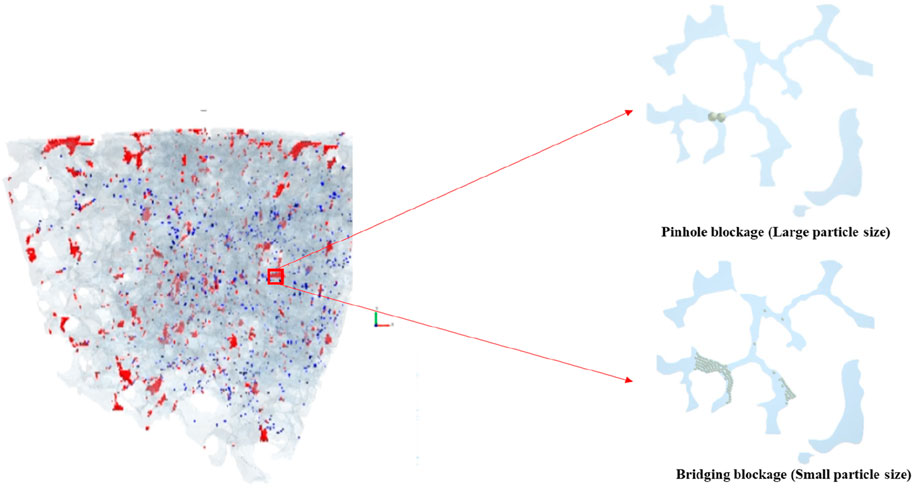
Figure 2. Schematic diagram of particle migration blockage modes. (Red: blockage particles; Blue: flowing particles).
3.2 The impact of particle retention rate
Particle retention rate refers to the proportion of particles retained in porous media due to physical and chemical interactions, serving as a key indicator for assessing the impact of particle migration on reservoir damage. Based on previous literature reviews and a detailed analysis of the rock properties in the target block, this study focuses on particle retention rate as the core evaluation parameter, systematically evaluated the retention rates of cores with different permeabilities under different conditions. The results in Figure 3 indicate that the low-permeability sandstone sample S1, due to its smaller pore throat radius, experiences more pronounced physical and chemical interactions between the particles and the rock surface, as well as among the particles themselves during flow. This strong interaction leads to significant accumulation and retention of particles at the core inlet, with a retention rate of 100%, demonstrating a severe blockage effect. As the pore throat radius increases, the interactions between particles and the rock surface, as well as between particles, gradually weaken, and the particle retention rate shows a significant downward trend, reflecting the importance of pore structure in the particle migration and retention process. This study shows that pore throat size and particle retention rate exhibit an inverse relationship, providing a strong theoretical basis for reducing particle blockage during reservoir management and water injection development.
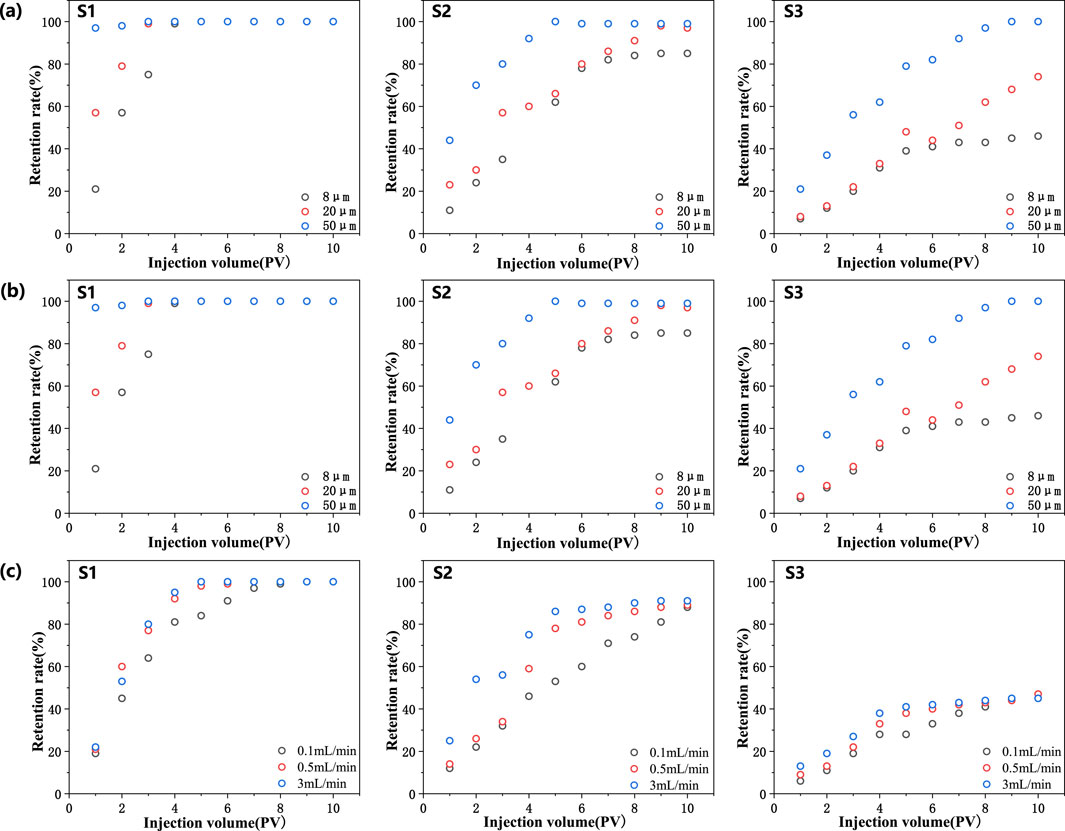
Figure 3. The impact of different factors on particle retention rate in different cores. (A) Impact of particle size. (B) Impact of particle concentration. (C) Impact of particle injection rate. S1: 259 mD; S2: 1078mD; S3: 2159mD.
3.2.1 The impact of particle size on retention rate
Particle retention rate is influenced by the interplay of physical and chemical interactions, and it serves as a key indicator for assessing the impact of particle migration on reservoir damage. Based on the previous core CT scanning results, particle sizes are set to 8 μm, 20 μm, and 50 μm, representing small, medium, and large particles in the reservoir, respectively. The simulation of the impact of different particle sizes on retention rate shows that as particle size increases, the retention rate gradually rises. The analysis of Figure 3A clearly indicates the presence of a critical particle size threshold during the particle migration process. When particle size exceeds this threshold, the particles can no longer pass through the core’s pore structure and are entirely retained within the core. This critical size threshold is closely related to the pore throat size of the rock—smaller pore throats correspond to smaller critical size thresholds. In other words, the pore structure of the rock significantly controls particle retention behavior, with larger particles having a higher retention probability in small pore throat reservoirs, making reservoir blockage more likely. The study also shown that particle retention is not only correlated with particle size, but is also influenced by the injection volume. As the injection volume increases, the retention rate increases until it reaches a constant. In summary, the particle retention rate is a multifaceted parameter that is influenced by the complex interactions between particles and the rock matrix, as well as the injection volume.
3.2.2 The impact of particle concentration on retention rate
Particle concentration not only affects the distribution and migration patterns of particles in pores but also has a significant impact on the retention rate. The simulated results experimental data presented in Figure 3B reveal that, under low-permeability sandstone conditions, particle concentration does not significantly affect the final retention rate. This is due to the dense pore structure of low-permeability sandstone, where even at lower particle concentrations, particles quickly accumulate during flow, blocking the pore network and causing nearly all particles to be retained in the reservoir. However, as particle concentration increases, the rate of particle retention accelerates. This may be because higher particle concentrations facilitate the faster formation of bridging structures, further accelerating the pore blockage process. Bridging is particularly significant in particle retention, as they can trap subsequent particles and strengthen over time, potentially leading to partial or complete clogging of pores. In medium to high-permeability sandstone, an increase in particle concentration has a certain effect on the final retention rate, but the increase is not substantial. This is likely because medium to high-permeability sandstone has better pore connectivity, allowing particles to continue migrating through unblocked channels during flow. Despite the increase in particle concentration, the openness and connectivity of the pores provide more flow paths for particles, preventing a significant rise in retention rate. Overall, particle concentration accelerates the blockage process in low-permeability sandstone, while its effect in medium to high-permeability sandstone is relatively limited.
3.2.3 The impact of injection rate on particle retention rate
The impact of injection rate on particle retention rate can reveal the dynamic behavior of particles under fluid-solid coupling mechanisms, aiding in a deeper understanding of particle flow characteristics within the reservoir. Under simulation conditions where particle concentration remains constant, the effect of injection rate on particle retention rate is analyzed. The results in Figure 3C show that the injection rate does not significantly affect the final particle retention rate. This may be because, at a fixed particle concentration, increasing the injection rate does not significantly alter the number of particles entering the reservoir per unit of time, thus having a limited effect on the final retention rate. However, an increase in injection rate significantly shortens the time required for particles to reach a stable retention rate. This indicates that at higher injection rates, particles can enter the reservoir more quickly and reach dynamic equilibrium, or a stable retention rate, in a shorter period. Therefore, while the final retention rate is not notably changed by variations in injection rate, higher injection rates accelerate the particle migration process. In practical production, although injection rate does not directly affect the final amount of particle retention, it can speed up the interaction between particles and the reservoir, allowing the system to reach a stable state in a shorter time. This acceleration allows the system to reach a stable state in a shorter time. In conclusion, the injection rate is a significant parameter that affects the dynamic behavior of particles within reservoirs. Although it does not directly alter particle retention rate, it can significantly influence the time required for particles to reach a stable retention rate.
3.2.4 Analysis of the main-controlling factors affecting retention rate
To investigate the main control factors affecting retention, the injection volumes required to achieve a specific retention rate (100%, 60%, 40%) for each of the three different models (S1, S2, S3) were analyzed and performed a principal component analysis (PCA). PCA is a feature extraction technique that generates new features, known as principal components, by combining and transforming the original features of a dataset. These principal components capture the most important features of the data and are commonly used for downscaling and feature extraction. The most critical formula in PCA is eigenvalue decomposition. For the dataset
Based on the centered data, the covariance matrix
Perform eigenvalue decomposition on the covariance matrix to obtain the eigenvalues and their corresponding eigenvectors. Select the first
Figure 4 of the analysis results identifies the controlling factors affecting the particle retention rate as particle size, particle concentration, and injection rate, listed in order of their importance. Additionally, it was observed that particle size and particle concentration have a significant effect on the retention rate, while the injection rate has a relatively much smaller effect. It is worth noting that the simulations do not account for particle detachment. In a real development process, larger injection velocities can lead to a significant increase in the number of detached particles.
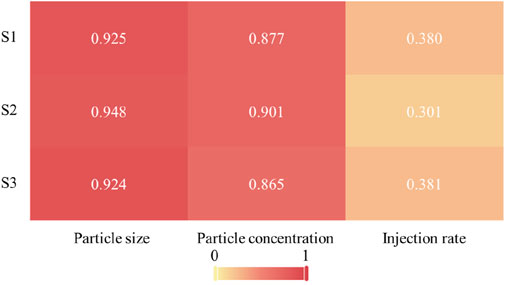
Figure 4. Factor loading matrix heat map. (The color shades and values on the heat map provide a visual indication of the extent to which each variable contributes to each principal component.)
3.3 Particle migration trajectory
To understand how particle migration is influenced by the reservoir’s pore structure and permeability, we analysis the behavior of particles within reservoirs of varying permeability levels. The simulation results presented in Figure 5 demonstrate that, in low-permeability sandstone, particles are prone to block pore channels, leading to a significant reduction in the average migration distance of the particles. Once blockage occurs, the migration distance of the particles rapidly decreases, as most particles are captured and retained near the front end of the reservoir, making it difficult for them to continue migrating deeper into the reservoir. The dense pore structure of such reservoirs hinders particle movement, and the blocking effect is more pronounced. In contrast, in medium to high-permeability sandstone, the migration distance of particles is relatively longer. Even after partial blockage occurs in the early stages, particles can still migrate through channels that are not completely blocked. Therefore, despite some initial pore blockages, particles can continue to migrate within the reservoir. Over time, the migration distance gradually stabilizes and reaches a relatively balanced value. The results show that in higher-permeability reservoirs, the connectivity of the pore structure provides more migration paths for particles, allowing the migration process to continue even when localized blockages occur. Over time, the migration distance stabilizes and reaches a relatively constant, indicating a dynamic equilibrium between particle migration and blockage. Permeability has a significant impact on particle migration behavior: migration is more restricted in low-permeability reservoirs. Medium to high-permeability reservoirs exhibit stronger connectivity of pores and migration capacity of particles, allowing particles to continue migrating even in the presence of localized blockages.
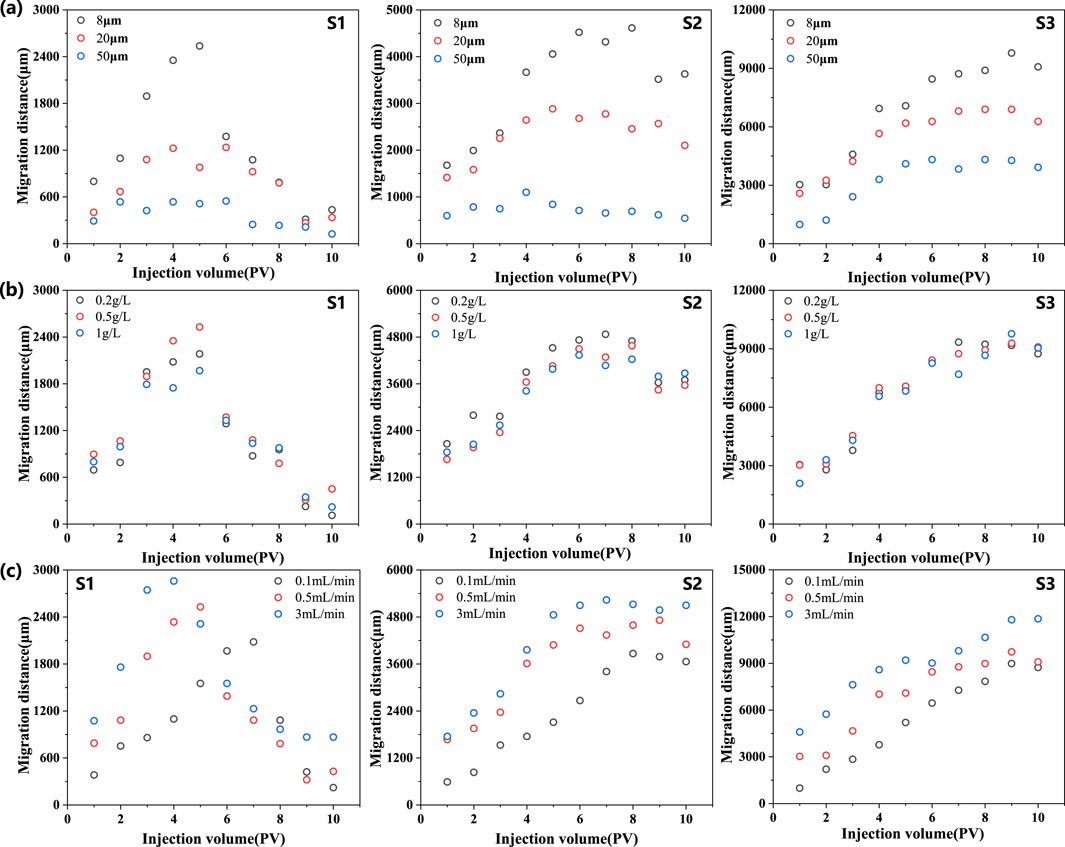
Figure 5. The impact of different factors on particle migration trajectory in different cores. (A) Impact of particle size. (B) Impact of particle concentration. (C) Impact of particle injection rate. S1: 259mD; S2: 1078mD; S3: 2159mD.
3.3.1 The impact of particle size on migration trajectory
Particle size is a key factor affecting particle migration behavior. By studying the migration trajectories of particles with different sizes, the movement characteristics of various-sized particles within the pore structure of the reservoir can be clarified, and the interaction patterns between particles and pore walls can be analyzed. The results in Figure 5A indicate that, as particle size increases, the migration distance within the core exhibits a progressively decreasing trend. This phenomenon can be attributed to the higher collision frequency of larger particles with the rock surface and other particles during movement, as well as the more significant interaction forces they experience. Due to these frequent collisions and stronger interaction forces, the migration resistance of the particles increases, limiting their ability to move through the pores and ultimately reducing their migration distance. Larger particles are more likely to be affected by flow resistance and geometric constraints in narrower pore throats, making them more prone to being captured or retained within the core. This trend indicates that the larger the particle size, the poorer its flow capacity in complex pore structures, and the shorter its average migration distance. By reasonably controlling the particle size distribution, the risk of blockage can be effectively reduced, thereby improving the reservoir’s flow capacity.
3.3.2 The impact of particle concentration on migration trajectory
Particle concentration directly affects the migration distance of particles within the reservoir. The simulation results shown in Figure 5B reveal that, under high-permeability sandstone reservoir conditions, variations in particle concentration have a relatively weak impact on migration distance. This can be because the particle concentrations studied in the experiment were low, resulting in weaker interactions between particles, allowing them to be more easily carried by fluid flow. The pore structure in high-permeability sandstone is more conducive to particle migration, as it offers a more interconnected network of pores. The fluid flow is more efficient, which can help to transport particles through the pore network. This structure allows particles to navigate the reservoir more easily, even at higher concentrations. Consequently, blockage effects such as bridging are less likely to occur, enabling particles to maintain a certain migration distance within the core. This phenomenon suggests that at lower particle concentrations, particle migration behavior is primarily influenced by pore structure and fluid dynamics rather than interactions between particles. These findings indicate that, under certain conditions, the impact of particle concentration on migration distance can be less pronounced. In high-permeability sandstone reservoirs, the pore structure and fluid dynamics play a more dominant role in determining particle migration, particularly at lower particle concentrations. However, it is important to note that the relationship between particle concentration and migration distance can be more complex in low-permeability reservoirs or at higher particle concentrations. The interactions between particles will become more significant, leading to a more pronounced impact on migration distance.
3.3.3 The impact of injection rate on particle migration trajectory
In fluid-solid coupling simulations, injection rate is a key variable influencing particle migration. The fluid velocity directly determines the path, speed, and direction of particle movement within the reservoir. Under simulation conditions where particle concentration remains constant, the effect of injection rate on particle migration trajectory was analyzed. The analysis of the simulation results, as depicted in Figure 5C, indicates that the migration distance of particles in porous media increases significantly with an increase in the injection rate. This effect is particularly evident in medium to high-permeability sandstone, where the impact of injection rate on particle migration distance is more pronounced. This is because the more open pore structure of medium to high-permeability sandstone allows faster fluid flow, which can more effectively transport particles, enabling them to migrate over greater distances. In contrast, in low-permeability sandstone, where the pores are smaller and the structure is more compact, fluid flow is slower, and particles face more resistance during migration. In this case, even with an increased injection rate, the improvement in particle migration distance is less significant compared to medium to high-permeability reservoirs. The results indicate that at higher injection rates, the fluid velocity increases, potentially resulting in accelerated particle migration. This higher velocity allows particles to travel further within the reservoir before they are retained or blocked. The increased velocity can also help to prevent the accumulation of particles over short distances, thus reducing the likelihood of pore blockages that could impede fluid flow. At lower injection rates, the fluid velocity is reduced, which can cause particles to settle and be retained more quickly. This can lead to a shorter migration distance and a higher probability of pore blockages, as particles interact more frequently with the pore walls and other particles.
3.3.4 Analysis of the main-controlling factors affecting migration trajectory
When clogging occurs, subsequent injections of particles cannot pass through the clogged location, so the transport distance tends to decrease. The maximum migration distance represents the farthest distance that the particles can migrate to the core. Therefore, the maximum migration distance (Y2) results under different particle size (X1), particle concentration (X2), injection rate (X3) and core permeability (X4) are summarized and regression analysis is performed.
3.4 The impact of particle transport on core permeability
Permeability directly reflects the seepage capacity of the core. To understand how particle transport affects permeability changes, we analyzed the permeability damage rates of different permeability cores under different conditions, the results are shown in Figure 6.
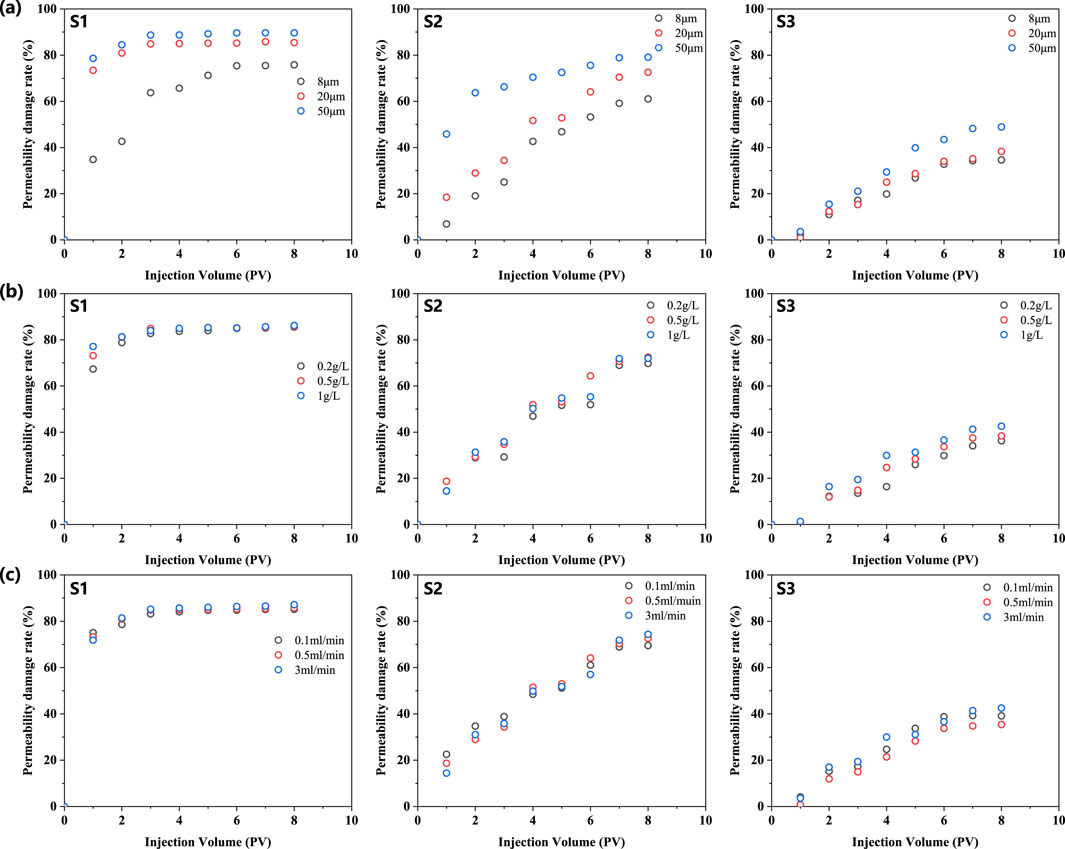
Figure 6. The impact of different factors on particle migration trajectory in different cores. (A) Impact of particle size. (B) Impact of particle concentration. (C) Impact of particle injection rate. S1: 259mD; S2: 1078mD; S3: 2159mD.
3.4.1 The impact of particle size on core permeability
Figure 6A showed the effect of particle size on the permeability damage rate of different cores at different displacement stages. With the increase of injection volume, the permeability damage rate of different cores showed a trend of increasing first and then flattening, and the smaller the core permeability, the larger the particle size, the higher the permeability damage rate. However, due to the different pore throat sizes of different cores, the permeability damage rate caused by different particle sizes is also different. For the S1 core (259mD), more than 80% of the pore throat size is less than 16μm, so when the particle size is 20 μm and 50μm, the particles will directly block the pore throat. The permeability damage rate is more than 70% when the injection volume is only 1 PV. When the injection volume is 3 PV, the permeability damage rate tends to be stable. When the particle size is 8μm, the particle size is smaller than most of the pore throat size, and the permeability damage rate tends to be stable after the injection volume is 6 PV. For S2 core (1078mD), it also shows roughly the same law. The more 50% of the pore throat size of S2 core is less than 24μm, so when the particle size is 50μm, the permeability damage rate increases greatly in the early stage, and the upward trend slows down after 2 PV injection. The permeability damage rate increases slowly under the condition of particle size of 8μm and 20 μm. For S3 core (2159mD), due to the further increase of the proportion of large pore throat, the permeability damage rate under different particle size conditions showed a gradual upward trend, and tended to be gentle after 6 PV injection volume.
3.4.2 The impact of particle concentration on core permeability
The particle concentration was changed by fixing the particle size of 8 μm and the injection rate of 0.5 mL/min, and its effect on the permeability damage rate was investigated. Figure 6B showed that for different permeability cores, the permeability damage rate increases first and then tends to be stable, but the particle concentration has little effect on the final permeability damage rate of the core. The pore throat of S1 core (259mD) is small, and it is easy to form stable blockage when the injection volume is small. Increasing the particle concentration can only advance the time it reaches stability, and will not significantly increase its final damage rate. For S2 (1078mD) and S3 (2155mD) cores, the particle size under the corresponding conditions is small, and it has certain resistance to particle blockage. Increasing the particle concentration has little effect on the permeability damage rate.
3.4.3 The impact of injection rate on core permeability
The particle size was fixed at 8 μm and the particle concentration was 0.5g/L. The injection rate was changed to investigate its effect on the permeability damage rate. The results are shown in Figure 6C. The results show that when the initial permeability is the same, the injection rate has little effect on the permeability damage rate. At the same injection volume and particle concentration, the number of particles entering the core is equal, so the flow rate has little effect on the core permeability damage. However, increasing the flow rate will accelerate the core blockage and make it reach a steady state faster.
3.4.4 Analysis of the main-controlling factors affecting permeability damage rate
The results of permeability damage rate (Y6) under different particle size (X1), particle concentration (X2), injection rate (X3) and core permeability (X4) were further summarized and analyzed by regression analysis.
3.5 History matching of typical well groups considering particle migration
Through microscopic experiments and numerical simulations, the changes in parameters such as permeability and relative permeability under the influence of particle migration can be obtained. However, the scale of microscopic and numerical models is relatively small, necessitating the upscaling of microscopic results. In terms of spatial scale, we employed a method that models multiple sets of digital cores in series. With this approach, we observed that the effect of particle transport stabilizes after a certain number of cores is reached, with no further changes occurring with an increase in the number of cores. This finding suggests that the system can be considered as the smallest representative volume element (REV) at the macroscopic scale once the effect of particle transport reaches saturation (Figure 7). Regarding time scales, we addressed the issue by employing a dimensionless number transformation. Specifically, we established a dynamic relationship between permeability and over-volume multiplicity based on the volume multiplicity relationship between detached and residual particles. This relationship elucidates the pattern of permeability changes over time, thereby providing us with a temporal dimension for modeling particle transport on a macroscopic scale. It is noteworthy that in this process, we assume the same over-volume multiplicity and the same degree of influence of particulate transport in both digital cores and macroscopic grids. With the meticulous treatment of spatial and temporal scales as described above, we have successfully extrapolated the model obtained at the pore scale to macroscopic numerical simulations. Then, a shared mortar space is established between adjacent micro and macro regions, and a segmented finite element basis function σ (x, y) is assigned to it. Then, the basic equation of pressure is constructed and projected to the interface according to the basis function and initial coefficient in the mortar space. Finally, by iterating the permeability model of the macro grid until the pressure and flow in the two regions are continuous, the coupling of the micro model and the macro grid is realized. At this time, the permeability model of the macro grid is the upgraded model of the micro model scale.
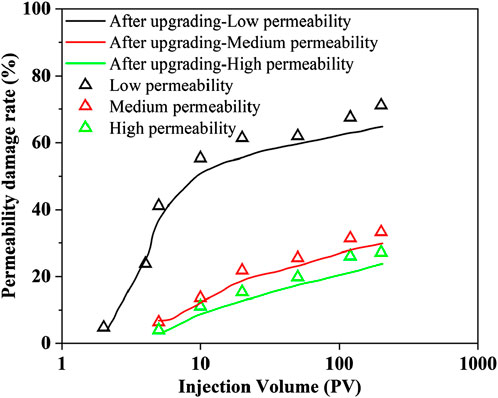
The time-varying law of permeability obtained by microscopic numerical simulation is upgraded by scale upgrading method, as shown in Figure 8. The results show that the time-varying trend of permeability after upgrading is in good agreement with that before upgrading, but the time-varying variation range of permeability after upgrading is smaller than that before upgrading, which reflects that the influence of microscopic pore structure on macro scale shows a certain decreasing trend.
Further, a micro-model and a macro-grid hybrid model are established around the wellbore. The inner ring is a micro-model area and the outer ring is a macro-grid. The mortar method is used to solve the fluid velocity and pressure of the hybrid model, as shown in Figures 9, 10. The results show that the mixed pressure field and velocity field are continuous after iteration. At the same time, the solution results of the converged permeability model are similar to the velocity field and pressure field of the mixed model, which further proves the accuracy of the upgraded model. Finally, the upscaled results are imported into the macroscopic reservoir model through Petrel’s Intersect User Edits interface, and Python code is written to incorporate the relationship between permeability, relative permeability, and grid volume multipliers into the model. This ultimately enables reservoir numerical simulations that consider the impact of particle migration.
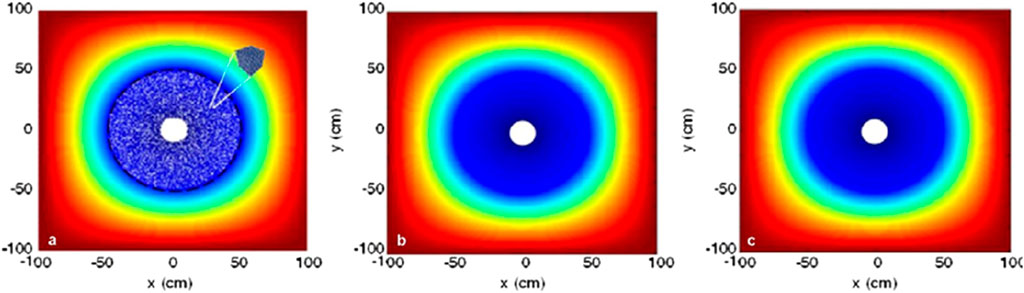
Figure 9. Pressure field comparison of different models in the process of scale upgrading. (A) mixed model. (B) upgraded model. (C) Macro model.
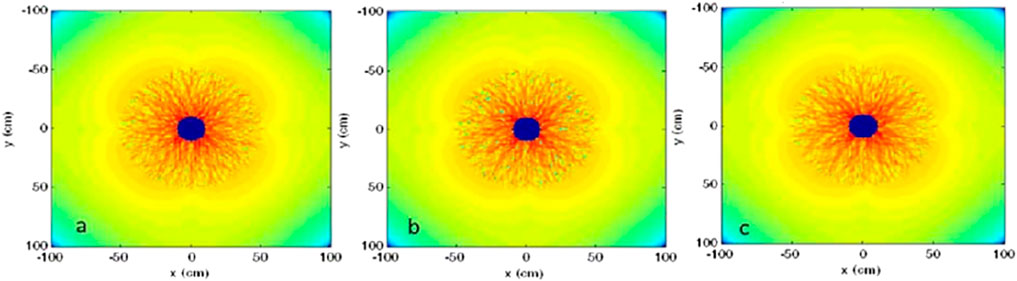
Figure 10. Velocity field comparison of different models in the process of scale upgrading. (A) mixed model. (B) upgraded model. (C) Macro model.
After considering the impact of particle migration, a history matching analysis was conducted on the target reservoir of the typical well group. The digital core data volume used in the pore-scale simulation is derived from the CT scan of the reservoir core in the oilfield corresponding to the macroscopic model, and HS-1 and SH-2 wells are typical wells in the block. Figure 11 presents the analysis results for typical wells HS-1 and HS-2, clearly indicating that the decline in production volume for both wells is primarily attributed to particle migration effects. Based on this, the study introduced a new particle migration model to rematch these production data, aiming to more accurately reflect the effect of particle migration on the liquid production capacity of the well group. The results indicate that after introducing the particle migration model, the history matching accuracy of the typical wells' liquid production significantly improved, demonstrating that the model can more effectively capture the dynamic impact of particle migration on reservoir permeability and liquid production capacity. This more accurate fitting result not only deepens the understanding of the specific mechanisms by which particle migration affects oil well production but also provides a more reliable basis for optimizing and adjusting future production strategies.
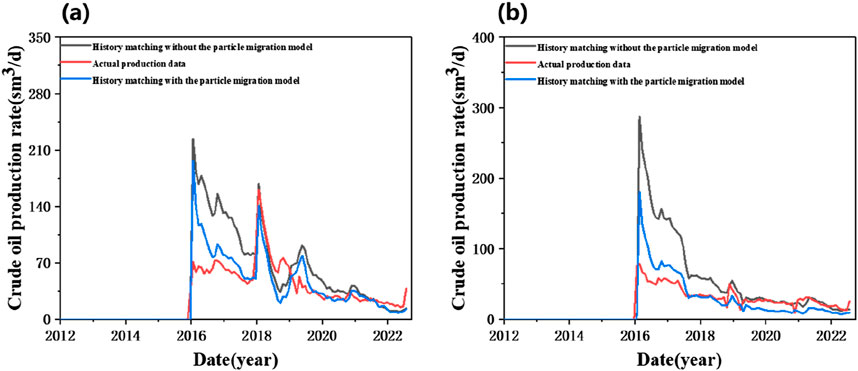
Figure 11. History matching of liquid production for typical wells before and after considering particle migration. (A) HS-1. (B) HS-2.
4 Conclusion
(1) In the process of particle migration in sandstone, two blockage modes are observed: pinhole blockage and bridging blockage. When the particle diameter is larger than the average throat radius, pinhole blockage dominates; bridging occurs when the particle diameter is small and the concentration is high.
(2) The particle retention rate in sandstone is primarily controlled by particle size. The larger the pore-to-particle size ratio, the higher the retention rate; particle concentration and injection rate have minimal impact on the final retention rate.
(3) The migration distance of particles in sandstone is significantly influenced by particle size. The larger the pore-to-particle size ratio, the shorter the migration distance; under low concentration conditions, particle concentration has little effect on migration distance; the higher the injection rate, the further the particles migrate.
(4) After considering the impact of particle migration in numerical simulations, the accuracy of liquid production matching for the typical well group improved. The numerical simulation model established in this study is constrained by the reservoir properties, particle characteristics, and field production conditions of this oilfield, and may only be applicable to this field. However, the research methodology has broad applicability.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
WZ: Conceptualization, Project administration, Writing–original draft. CT: Formal Analysis, Methodology, Writing–original draft. SC: Investigation, Writing–original draft. YH: Validation, Writing–review and editing. JJ: Writing–review and editing. KL: Writing–review and editing. ZZ: Project administration, Writing–original draft, Writing–review and editing. LC: Funding acquisition, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was supported by the National Natural Science Foundation of China (Grant No. 52074038; Grantee: Lifeng Chen).
Conflict of interest
Authors WZ, CT, SC, YH, JJ, and KL were employed by CNOOC Research Institute Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Chao, J. L., Liu, C. Y., Li, Y., Lin, X., and Yan, Y. (2017). Characteristics of the sea ice reflectance spectrum polluted by oil spills based on field experiments in the Bohai Sea. ACTA Oceanol. SIN. 36 (1), 73–79. doi:10.1007/s13131-017-0995-1
Chen, X., Li, Y. Q., Liu, Z. Y., Zhang, J., and Trivedi, J. (2023). Experimental and theoretical investigation of the migration and plugging of the particle in porous media based on elastic properties. Fuel 332, 126224. doi:10.1016/j.fuel.2022.126224
Chen, Z. H., Li, Y. C., Xie, Y. T., and Wang, X. (2017). In-situ Particle Migration and plugging mechanism in unconsolidated sandstone and sanding management. Chem. Tech. Fuels Oil+ 53 (5), 759–767. doi:10.1007/s10553-017-0858-7
Farokhian, D., Azin, R., and Ranjbar, A. (2019). Application of medical and dental CT-Scan technologies for determining porosity distribution of the Persian gulf coastal zone and zagros basin core samples. J. Afr. Earth Sci. 150, 96–106. doi:10.1016/j.jafrearsci.2018.10.009
Fernandes, F. B., Braga, A. M. B., de Souza, A. L. S., and Soares, A. C. (2023). Mechanical formation damage control in permeability Biot's effective stress-sensitive oil reservoirs with source/sink term. Geoenergy Sci. Eng. 220, 111180. doi:10.1016/j.petrol.2022.111180
Guo, W. J., Zhang, S., and Wu, G. X. (2019). Quantitative oil spill risk from offshore fields in the Bohai Sea, China. Sci. Total Environ. 688, 494–504. doi:10.1016/j.scitotenv.2019.06.226
Halim, M. C., Hamidi, H., and Akisanya, A. R. (2022). Minimizing formation damage in drilling operations: a critical point for optimizing productivity in sandstone reservoirs intercalated with clay. ENERGIES 15 (1), 162. doi:10.3390/en15010162
Hertel, S. A., Rydzy, M., Anger, B., Berg, S., Appel, M., and de Jong, H. (2018). Upscaling of digital rock porosities by correlation with whole-core CT-scan histograms. PETROPHYSICS 59 (5), 694–702. doi:10.30632/PJV59N5-2018a8
Ikemoto, A., Kazama, S., Yoshida, T., and Yanagihara, H. (2023). Evaluation of an adaptation strategy for flood damage mitigation under climate change through the use of irrigation reservoirs in Japan. Water Resour. MANAG. 37 (10), 4159–4175. doi:10.1007/s11269-023-03544-7
Lei, Y. (2020). Reconstruction and analysis of tight sandstone digital rock combined with X-ray CT scanning and multiple-point geostatistics algorithm. Math. Probl. Eng. 2020, 1–10. doi:10.1155/2020/9476060
Lin, W., Yang, Z. M., Li, X. Z., Wang, J., He, Y., Wu, G., et al. (2017). A method to select representative rock samples for digital core modeling. Fractals 25 (4), 1740013. doi:10.1142/s0218348x17400138
Liu, X., Guo, J., Guo, M. X., Hu, X., Tang, C., Wang, C., et al. (2015). Modelling of oil spill trajectory for 2011 Penglai 19-3 coastal drilling field, China. Appl. Math. Model 39 (18), 5331–5340. doi:10.1016/j.apm.2014.10.063
Liu, X. F., Sun, J. M., and Wang, H. T. (2009). Reconstruction of 3-D digital cores using a hybrid method. Appl. Geophys 6 (2), 105–112. doi:10.1007/s11770-009-0017-y
Miri, R., Haftani, M., Salimi, M., and Nouri, A. (2022). Novel laboratory methodology for fines migration testing for SAGD wells. J. Petrol Sci. Eng. 217, 110859. doi:10.1016/j.petrol.2022.110859
Mwakipunda, G. C., Jia, R., Mgimba, M. M., Ngata, M. R., Mmbuji, A. O., Said, A. A., et al. (2023). A critical review on low salinity waterflooding for enhanced oil recovery: experimental studies, simulations, and field applications. Geoenergy Sci. Eng. 227, 211936. doi:10.1016/j.geoen.2023.211936
Okere, C. J., Sheng, J. J., Fan, L. K., Huang, X. W., Zheng, L. H., and Wei, P. F. (2023). Experimental study on the degree and damage-control mechanisms of fuzzy-ball-induced damage in single and multi-layer commingled tight reservoirs. Petrol Sci. 20 (6), 3598–3609. doi:10.1016/j.petsci.2023.05.017
Radwan, A. E. (2021). Integrated reservoir, geology, and production data for reservoir damage analysis: a case study of the Miocene sandstone reservoir, Gulf of Suez, Egypt. Nterpretation-J Sub 9 (4), SH27–SH37. doi:10.1190/int-2021-0039.1
Radwan, A. E., Wood, D. A., Abudeif, A. M., Attia, M. M., Mahmoud, M., Kassem, A. A., et al. (2022). Reservoir Formation damage; reasons and mitigation: a case study of the cambrian-ordovician nubian 'C' sandstone gas and oil reservoir from the gulf of suez rift basin. Arab. J. Sci. Eng. 47 (9), 11279–11296. doi:10.1007/s13369-021-06005-8
Rahman, S. M., and Miah, M. D. (2017). The impact of sources of energy production on globalization: evidence from panel data analysis. Renew. Sust. Energ Rev. 74, 110–115. doi:10.1016/j.rser.2017.02.037
Reilly, B. T., Stoner, J. S., and Wiest, J. (2017). SedCT: MATLAB tools for standardized and quantitative processing of sediment core computed tomography (CT) data collected using a medical CT scanner. GEOCHEM GEOPHY GEOSY 18 (8), 3231–3240. doi:10.1002/2017gc006884
Shokrollahi, A., Safari, H., Esmaeili-Jaghdan, Z., Ghazanfari, M. H., and Mohammadi, A. H. (2015). Rigorous modeling of permeability impairment due to inorganic scale deposition in porous media. J. Petrol Sci. Eng. 130, 26–36. doi:10.1016/j.petrol.2015.03.013
Song, X. M., Qu, D. B., and Zou, C. Y. (2021). Low cost development strategy for oilfields in China under low oil prices. Petrol Explor Dev+ 48 (4), 1007–1018. doi:10.1016/s1876-3804(21)60085-x
Sun, P. X., Ge, L. Z., Liu, Y. X., Li, B., and Nie, X. (2023). Modeling of multi-mineral-component digital core based on Res-Unet. J. Geophys Eng. 20 (3), 483–493. doi:10.1093/jge/gxad024
Wu, Y. M., Qi, H. W., Wang, D. L., Liao, M., Zhang, Y., Zhang, J., et al. (2024). Evaluation of custom posts and cores fabricated by two digital technologies in core and post space dimensions. J. Prosthodont 33 (6), 593–605. doi:10.1111/jopr.13742
Xing, L., Guan, S. A., Gao, Y., and Jiang, M. (2023). Measurement of a three-dimensional rotating flow field and analysis of the internal oil droplet migration. Energies 16 (13), 5094. doi:10.3390/en16135094
Xu, Z. Z., Zhao, M. W., Liu, J. W., Zhang, Y., Gao, M., Song, X., et al. (2024). Study on formation process and reservoir damage mechanism of blockages caused by polyacrylamide fracturing fluid in production wells. Fuel 358, 130154. doi:10.1016/j.fuel.2023.130154
Xue, Y. G., Lyu, D. Y., Hu, Z. W., Huang, J., and Ren, J. (2021). Tectonic development of subtle faults and exploration in mature areas in Bohai Sea, East China. Petrol Explor Dev+ 48 (2), 269–285. doi:10.1016/s1876-3804(21)60022-8
Yang, R. F., Jiang, R. Z., Guo, S., Chen, H., Tang, S., and Duan, R. (2021). Analytical study on the critical water cut for water plugging: water cut increasing control and production enhancement. Energy 214, 119012. doi:10.1016/j.energy.2020.119012
Zeinijahromi, A., Vaz, A., Bedrikovetsky, P., and Borazjani, S. (2012). Effects of fines migration on well productivity during steady state production. J. Porous Media 15 (7), 665–679. doi:10.1615/JPORMEDIA.V15.I7.50
Zhang, D. Y., Yu, S. S., Wang, Y. L., and Yue, Q. j. (2017). Sea ice management for oil and gas platforms in the Bohai sea. Pol. Marit. Res. 24, 195–204. doi:10.1515/pomr-2017-0083
Zhang, X. W., You, L. J., Kang, Y. L., Zhang, C., Zhang, G., and Tan, Q. (2020). Formation damage control of saline-lacustrine fractured tight oil reservoir during well drilling. Arab. J. Geosci. 13 (20), 1087. doi:10.1007/s12517-020-06099-8
Keywords: loose sandstone, particle migration, digital core, reservoir damage, CT scanning
Citation: Zheng W, Tang C, Cai S, He Y, Jiang J, Li K, Zhang Z and Chen L (2024) Pore-scale modelling of particle migration in loose sandstone. Front. Earth Sci. 12:1509825. doi: 10.3389/feart.2024.1509825
Received: 11 October 2024; Accepted: 19 November 2024;
Published: 04 December 2024.
Edited by:
Cunqi Jia, The University of Texas at Austin, United StatesReviewed by:
Jingwei Huang, China University of Geosciences, ChinaHailong Chen, Southwest Petroleum University, China
Copyright © 2024 Zheng, Tang, Cai, He, Jiang, Li, Zhang and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhaonian Zhang, MTU4Mjc0MDI0NjJAMTYzLmNvbQ==
 Wei Zheng1,2
Wei Zheng1,2 Zhaonian Zhang
Zhaonian Zhang