- PetroChina Research Institute of Petroleum Exploration and Development, Beijing, China
Prestack amplitude versus offset (AVO) inversion is an essential tool to estimate elastic properties. Approximations of P-wave reflection coefficients based on the Zoeppritz equation are limited by the assumption of weak contrast and are inaccurate for far offset, and the existing nonlinear inversion method, like ant colony optimization (ACO), cannot converge to the global optimal solution within a limited time. Consequently, we propose a nonlinear AVO inversion method based on the exact Zoeppritz equation using hybrid quantum ant colony optimization (HQACO). The Zoeppritz equation is a forward modeling approach with high accuracy at far offset and is valid at the strong-contrast interface. HQACO, as a global optimization algorithm, not only has the potential of ACO to search global solutions but also exploits the power of quantum computing to speed up optimization procedures. The self-adaptive rotating strategy is proposed to improve the flexibility and efficiency of the conventional quantum rotating gate largely. Moreover, the quantum gate is introduced to enhance the global search ability. Numerical results show that the average evaluation number required for the global solution decreases largely and the solution converges to the global optimal solution closely using the proposed method. Synthetic applications verify that HQACO shows the most reliable exploring competence to find the global solution. The new inversion method is not only suitable for the strong-contrast interface with noise but also shows promising accuracy using the wide offset range.
1 Introduction
Prestack amplitude variation with offset (AVO) inversion is one of the commonly used techniques for estimating reservoir elastic parameters (Ostrander, 1984). In AVO inversion, an objective function is usually designed to fit the prior constraint and observation data by finding the minimum value of the objective function to obtain the true solution of the problem. Moreover, seismic data are band limited and always perturbed by noise, which inevitably leads to non-uniqueness of the solution, that is, ill-posed problem. In this sense, the inversion problem is a trade-off optimization problem with non-unique solutions and high-dimensional nonlinear characteristics. In order to improve the computational efficiency and stabilize inversion, many approximations have been developed to eliminate the nonlinear relationship between the seismic response and the elastic parameters by linearization under the assumptions of weak contrast and near offset limitations (Aki and Richards, 2002; Shuey, 1985; Smith and Gidlow, 1987; Zong et al., 2013; Zhang and Li, 2013; Lu et al., 2015; Zhang et al., 2019; Cheng et al., 2022a). The global optimization algorithm, however, can never reach the true model parameters under such assumption without considering the computational efficiency (Lu et al., 2015). Consequently, an exact inversion equation, like the Zoeppritz equation, is a necessary condition for AVO inversion, and an accurate inversion method with acceptable computation efficiency facilitates the inverse problem.
Many inversion methods are proposed to solve the nonlinear inverse problem (Stoffa and Sen, 1991; Li and Mallick, 2015; Sen and Stoffa, 2013; Mallick and Adhikari, 2015; Aleardi and Mazzotti, 2017; Zhou et al., 2017; Aleardi et al., 2019; Liu et al., 2022). The linear inversion method, that is, deterministic algorithm, solves the nonlinear function between model parameters and observational data as a linear problem and iteratively modifies the initial model until the convergence conditions are met. This inversion method has high calculation efficiency, requires less memory, and is concise and commonly used in practice (Buland and Omre, 2003; Russell et al., 2011; Zhang et al., 2019). However, the inversion result depends heavily on the initial model, and it may converge to a local solution rather than a global solution, which may cause large deviation between the solution and the actual model (Liu et al., 2022; Liu et al., 2023). Considering that the exact equations are high dimensional and nonlinear, extra assumptions like linearization make global optimization methods miss the global optimal solution, which means the desired global optimization methods still cannot acquire the real solutions without an exact forward modeling algorithm. Therefore, the inversion method based on the exact Zoeppritz equation can meet the requirements of the global optimization methods. Although the most ideal inversion method in such a problem is the exhaustive search method, it is also the most unrealistic method because the optimization method requires infinite calculation time whatever computer is used. Monte Carlo method is a typical representative of the nonlinear global optimization method, but its weaknesses is low efficiency, which may require the order of thousands or even millions to obtain acceptable precision (Cheng et al., 2022b). With the rapid development of the current computer performance, the implementation of parallel computations enables some classic meta-heuristic algorithms, based on Monte Carlo ideas, such as simulated annealing, which is based on statistical mechanics, and the ant colony algorithm, which is based on biology (Stoffa and Sen, 1991; Mallick, 1995), in order for the inversion of actual seismic data. Ant colony optimization (ACO) is an iterative algorithm based on the natural system; it is inherently highly parallel because it simulates a range of solutions and has no strict restrictions on the initial model, but the efficiency of ACO is influenced by the population size heavily, that is, convergence can be premature if a small number of models are employed, and ACO does not always guarantee it will converge to the global optimal solution within a limited time.
Quantum computing methods have been hailed as the future of computing sciences (Moradi et al., 2018). This can be attributed to their theoretically proven supercomputing speed, better stability, and effectiveness. Although many studies have been conducted to examine the applicability of quantum computing in general (e.g., Moradi et al., 2018; Liu et al., 2018), its potential in geophysics has received limited attention. Quantum computing principles such as superposition, entanglement, and quantum tunneling can bring a paradigm shift in computing by achieving substantial speed-up over its classical counterpart (Hoos and Stϋtzle, 2018; Kallel et al., 2013). Quantum computing offers reversible computational logic, which helps in the minimization of power consumption while preserving computational information, making it a good alternative for reducing overall computational complexity and resource overhead. Additionally, quantum superposition using the Hadamard gate will allow parallel exploitation of the search space and thus may offer the desired solution faster than classical ACO synthesis through quantum interference (Grover, 1996). This improvement in QACO results in improved convergence efficiency and accuracy of results in optimization problems (Lahoz-Beltra, 2016). Despite these improvements, QACO shows two major deficiencies when solving relatively more complex problems: first, the slow rate of convergence. The angle of rotation, which is usually fixed, and the direction of the quantum rotating gate are obtained from a look-up table (Han et al., 2001), making the algorithm less flexible and resulting in a slower convergence rate in the early stages. Second, there is high tendency of being trapped in a local minimum. QACO uses the quantum rotating gate to update genes with the best fit. This increases the population of the best-fit genes but ultimately results in the loss of diversity, which increases the tendency of being trapped in a local minimum.
To address these shortcomings in the QACO method, in this study, we propose an improved version called the hybrid quantum ant colony optimization (HQACO). It combines a self-adaptive search strategy and the operations of the quantum gate, enjoying the advantages of quantum computing and ACO. This positions the HQACO as a great tool for global optimization using a small population size. It also enjoys the advantages of the results being independent of the initial model and high likelihood of obtaining the global solution. We verified its reliability and stability by conducting synthetic tests using models based on synthetic and actual logging data. The results show that HQACO is a strong candidate for global optimization with fast convergence speed and robust stability.
2 Methodology
2.1 Forward modeling
Based on the three-dimensional wave equation and the boundary conditions of continuous displacement and stress at the interface of the medium, Zoeppritz (1919) deduced the expression of the reflection and transmission coefficient when the wave propagates to the interface, which is described as the Zoeppritz equation. Assuming a solid–solid interface between two homogeneous isotropic elastic half-spaces, P-wave velocity, S-wave velocity, and density of the upper half-space are denoted by
where
and
As shown above, although the Zoeppritz equation is a highly nonlinear function with respect to these properties, the formulations are explicitly valid in the isotropic media, and it uses few numbers of approximations, which allows the prediction of the reflection coefficients to be accurate from near to far incident angles. Then, global optimization schemes are suggested to be involved to treat AVO inversion. Combining the exact Zoeppritz equation with the global optimization methods can help inversion converge to global solutions.
2.2 Conventional objective optimization
Nonlinear inversions are usually done by minimizing an objective function. The L2 norm and cross-correlation coefficient are commonly objective functions to define an error, misfit, or similarity in the optimization problem. Then, we can obtain the objective function of the form as follows:
where r is the data vector, denoted as
2.3 Hybrid quantum ant colony optimization
Simple ACO functions in two operating modes: forward (from the nest toward the food) and backward (from food back to the nest). Forward ants build a solution by probabilistically choosing the next node to move to among those in the adjacent positions with respect to the current node. This probabilistic choice is biased by pheromone trails previously deposited on the paths by other ants. Forward ants do not deposit any pheromone, which, when associated with deterministic backward moves, helps eliminate loop formation.
First, an ant k locating on node i moves to j as the next node using the following constraint for the transition function:
where
where
where
In a quantum computer, a two-level quantum system called qubit acts as the physical media to store the information units. A qubit is the basic unit of information in quantum computation and is described by a superposition of the basis states
The quantum rotating gate is the core operator in the evolution operation, and it directly affects the performance of the algorithm. As model parameters are in superposition states, the genetic qubits in the population should be updated by the quantum rotating gates to adjust the probability amplitude and constitute new individuals. Quantum rotating gates can be designed according to the practical problems and can be usually defined as
where
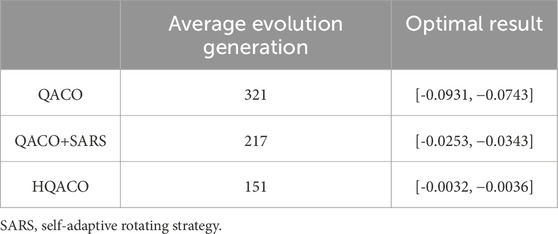
Table 1. Average numbers of model evaluations required to converge to the global minimum and the optimal result after improvements.
Quantum gate, in practical applications, is an assistant operation with the purpose to avoid losing important information of the population and enhance the local searching ability, as the diversity maintained by the superposition state is not enough to reflect the superiority of the quantum algorithm and premature convergence may occur due to the effect of noise. Therefore, quantum gates will be added to improve the performance of the algorithm.
The quantum NOT gate (Pauli-X gate) is commonly adopted to implement quantum gates. Through exchanging the probability amplitude of each gene
From the formula, we can find that the angle of the qubit is rotated by
3 Inversion test
We present two numerical examples to examine the effectiveness of our proposed algorithm. The misfit between the predicted and observed data is used as the objective function to be minimized. An objective function with multiple local minima reflects high ill-conditioning of the inversion problem. Several performance criteria are used to evaluate the performance of the algorithms, such as the number of iterations and robustness. In all synthetic examples, the incidence angles for the AVA gathers are 1°–40°, and the wavelets used for the forward modeling are Ricker wavelets. First, we design a 1-dimensional 13-layer horizontal theoretical stratigraphic model to test the accuracy and efficiency of the 3 optimization algorithms: ACO, QACO, and HQACO under different search windows. Next, the actual logging data are used to generate synthetic seismic records, and the convergence efficiency and robustness of the inversion algorithm are tested by adding random noise.
3.1 Numerical test
3.1.1 Example I
First, we build a 13-layer horizontal layered model to test the stability and accuracy of HQACO, QACO, and ACO in different search windows. Given the termination criterion, maximum generation 500 and error tolerance 10–5, two kinds of search windows with three different search ranges, are used to detail the influence and choice of search windows required for inversions without any noise. Figure 1A shows the information of model I. Figure 1B shows the amplitude versus angle gathers generated by exact Zoeppritz forward modeling from 1° to 40°. Figure 2 shows the inversion result under the fixed search window with the deviation of 15%, 10%, and 5%, respectively. Figure 3 shows the result of the optimized search window with the deviation of 15%, 10%, and 5%. The optimized search window represents the upper and lower constraint bounds, which can be obtained from the initial models in practice. It is also noted that the dynamic search window in the nonlinear inverse problem is not applied to offer the low frequency component because the low frequency trend can be obtained in the static window. Instead, the dynamic window is used for a high computational efficiency and resolution. With the same length of chromosome, the narrow-bound constraint results in high resolution. Comparing the results shown in Figures 1, 2, it can be observed that the inversion result by HQACO has the highest accuracy among the three algorithms, and the accuracy of QACO is higher than that of ACO. In addition, the results obtained by the dynamic search window show better performance than those obtained by the static search window, and the inversion results increasingly deviate from the true models as the size of the search window expands. The relative errors (REs) of the results are calculated and shown in Tables 2–4, and all of them can conclude the consistent results with the figures. It is clear that HQACO is suitable for the inversion in such a theoretical situation, and the dynamic search window with narrow bounds can significantly decrease the inversion uncertainty. Then, we test the efficiency of convergence for different algorithms. We run each algorithm with the parameter range of 5%, and the maximum number of model evaluations is set to 1,000. Figure 4 shows that the results of all of the methods are close enough to the global minimum with limited iteration numbers, whereas ACO shows the lowest convergence rate because it has the highest computational complexity, which means minimizing computational cost may cause undesirable solutions.
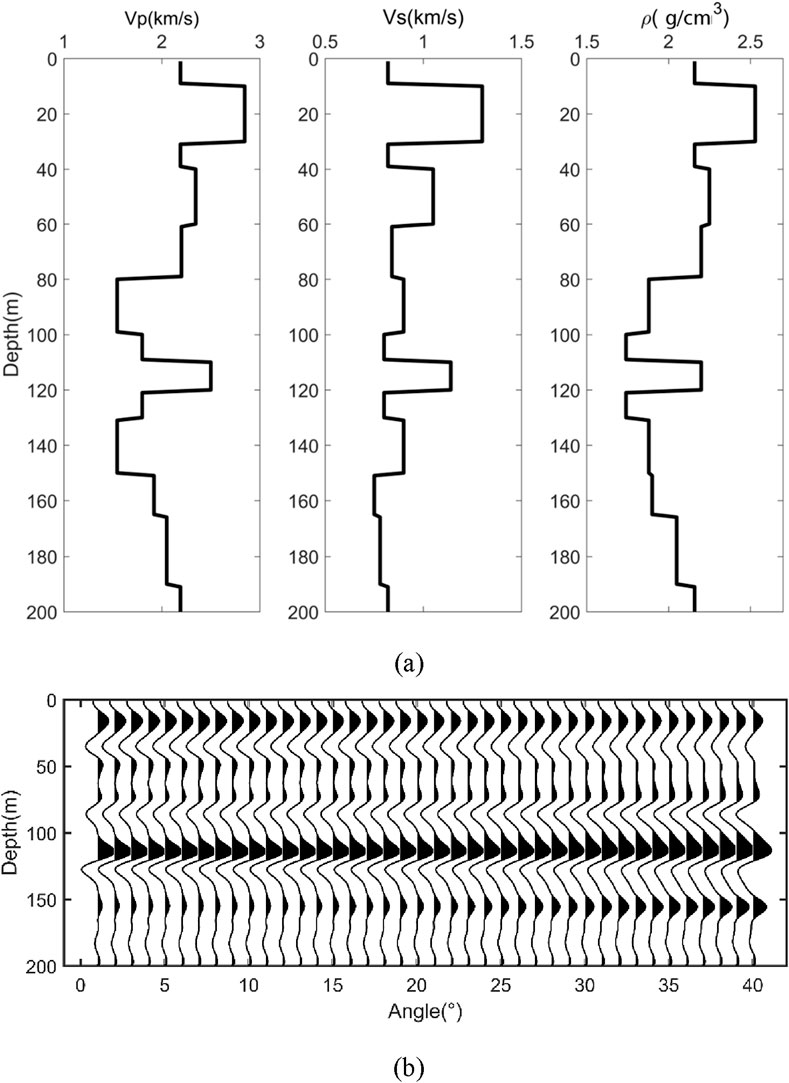
Figure 1. (A) P-wave velocity, S-wave velocity, and density of model I are shown from left to right. (B) Synthetic seismic angle gathers of model I.
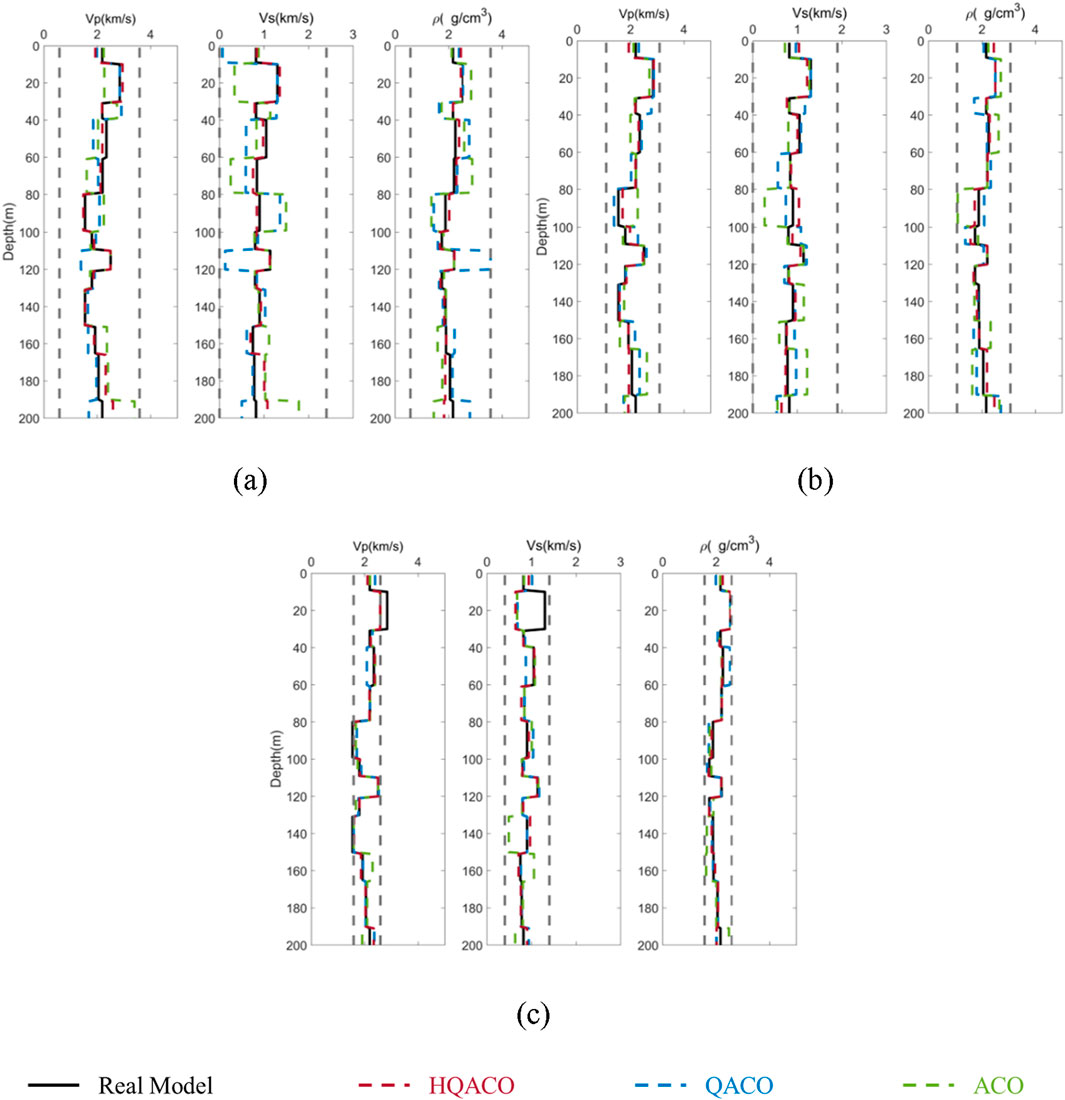
Figure 2. Using static search windows to constrain the AVO inversion with different bounds: (A) 15% deviation, (B) 10% deviation, and (C) 5% deviation. P-wave velocity, S-wave velocity, and density are shown from left to right. The solid black lines denote the true models. The red dashed curves denote the inverted models by HQACO, where the upper and lower bounds of search windows are denoted by gray dashed curves. The dashed blue lines and green lines indicate the inverted results by QACO and ACO, respectively.
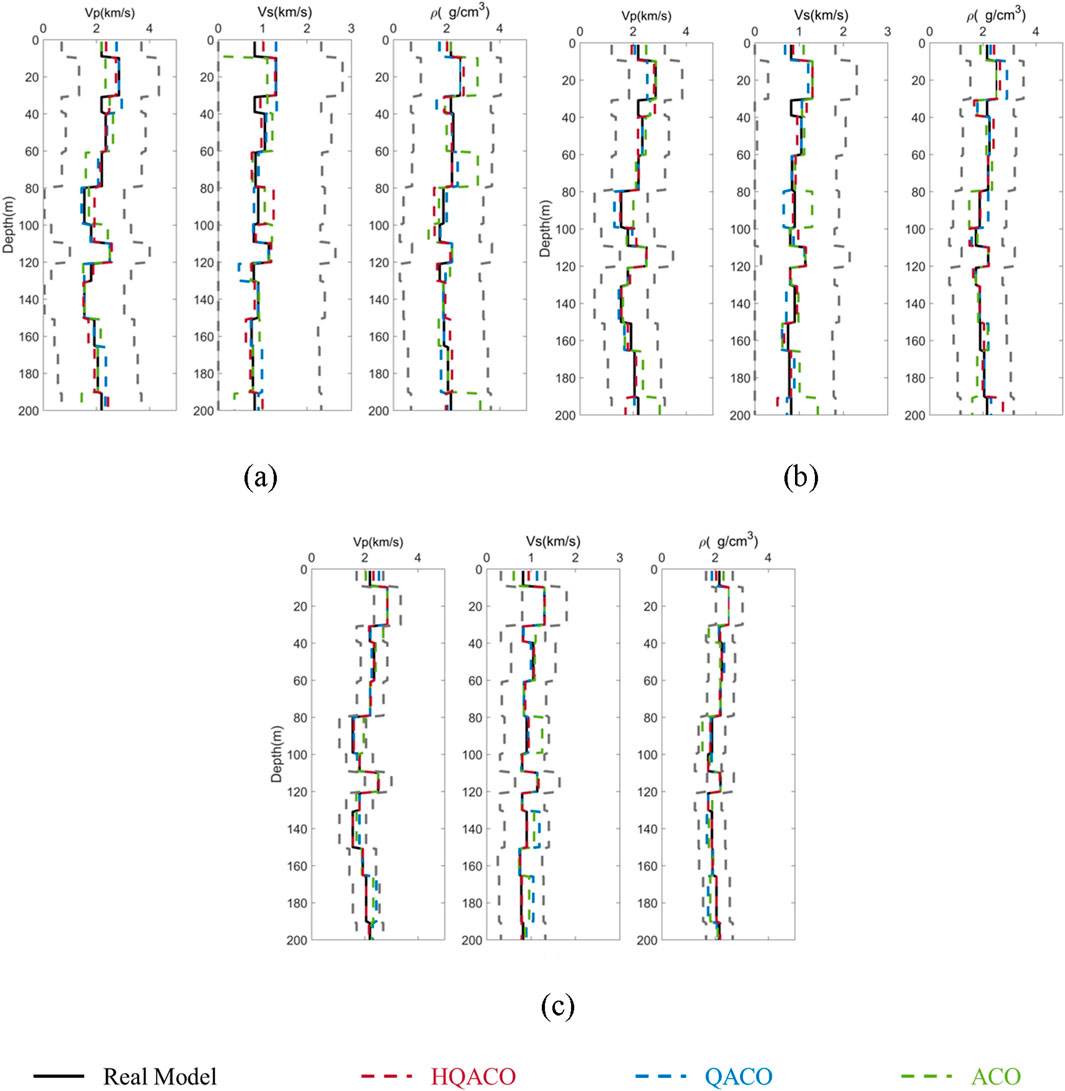
Figure 3. Using dynamic search windows to constrain the AVO inversion with different bounds: (A) 15% deviation, (B) 10% deviation, and (C) 5% deviation. P-wave velocity, S-wave velocity, and density are shown from left to right. The solid black lines denote the true models. The red dashed curves denote the inverted models by HQACO, where the upper and lower bounds of search windows are denoted by gray dashed curves. The dashed blue lines and green lines indicate the inverted results by QACO and ACO, respectively.

Table 2. Relative errors between the inversion results and true models by using ACO with different search windows.

Table 3. REs between the inversion results and true models using QACO with different search windows.

Table 4. REs between the inversion results and true models using HQACO with different search windows.

Figure 4. Evolution process with ACO (green), QACO (blue), and HQACO (red) using the 5% deviation dynamic search window.
3.1.2 Example II
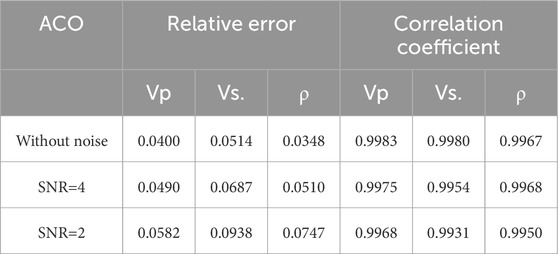
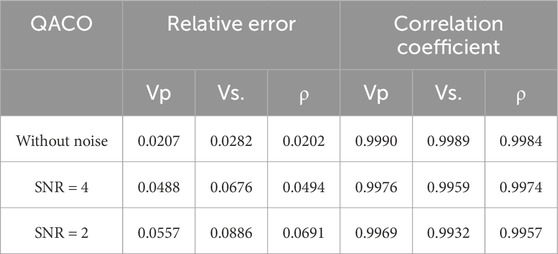
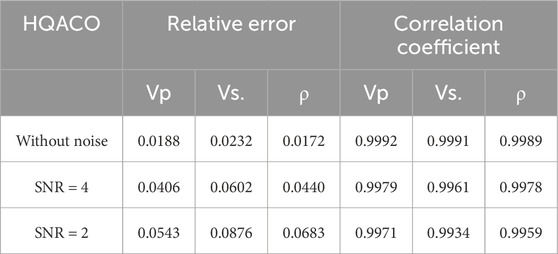
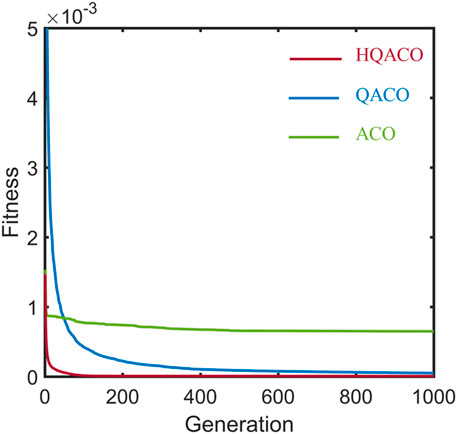
Based on the well-log information, we calculate the PP reflection coefficients using the exact Zoeppritz equation in the time domain and then generate the PP AVA gathers by convolving the reflectivity with the real wavelets in different angles. The objective function is the L2 norm between the predicted and real angle gathers. The maximum number of fitness evaluations that we allow for algorithms to minimize the error is 500*N, where N is the dimension of the problem. In addition, different noise energies are added to the synthetic data to test the robustness of the proposed algorithm. Algorithm efficiency, like the number of function evaluations and the number of iterations, are likely to be correlated with the CPU time. Figure 5 shows the P-wave velocity, S-wave velocity, and density of well log. Figure 6A represents the AVA gathers computed using the Zoeppritz equation, and random noise with a signal-to-noise ratio (SNR) of 4 and 2 is added to the synthetic gathers, as shown in Figures 6B, C. Then, the results inverted by ACO and QACO with different SNR are shown in the Figure 7. It can be seen that the inversion results by QACO show higher accuracy than those using ACO; however, the error of density badly increases with the enhancement of noise energy. The results inverted using QACO and HQACO with different SNR are shown in Figure 8, and inversion results using HQACO without noise are closely consistent with real-model parameters. Moreover, results using HQACO show higher accuracy than those using QACO in different SNR. The relative errors (REs) and correlation coefficients (CCs) of the results are calculated and shown in Tables 5–7, and the lower SNR makes relative errors become larger, whereas the lower SNR makes correlation coefficients become smaller. Figures 9–11 show the residual between the predicted seismic data and the observed data (Figure 6) with different signal-to-noise ratios. It is shown that the difference between the observed model and predicted model is closely related to the magnitude of noise, where the error of HQACO is the smallest and the results using ACO show larger errors, especially at large offsets. Moreover, the convergence graph is a useful tool to show the average error performance of the total runs, and the average iteration curves shown in Figure 12 express that HQACO can spend less time converging to global minimum and reach the highest accuracy among the three algorithms, followed by QACO, and ACO is the worst. Above all, the proposed algorithm has higher accuracy, higher efficiency, and stronger robustness than the other two algorithms, and Bayesian inference is recommended to ensure the stability of inverted density.
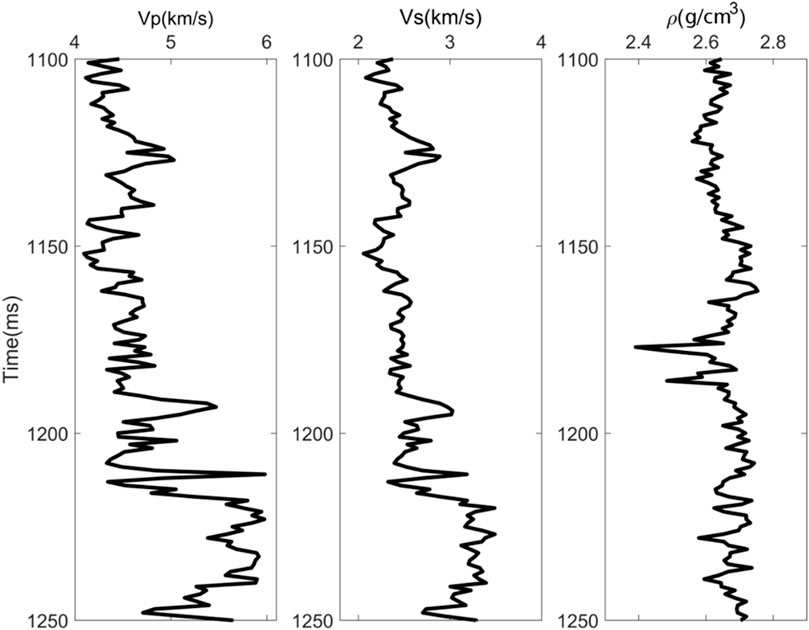
Figure 5. Model II: well data of real data are used to generate the synthetic data for inversion. P-wave velocity, S-wave velocity, and density are shown from left to right.
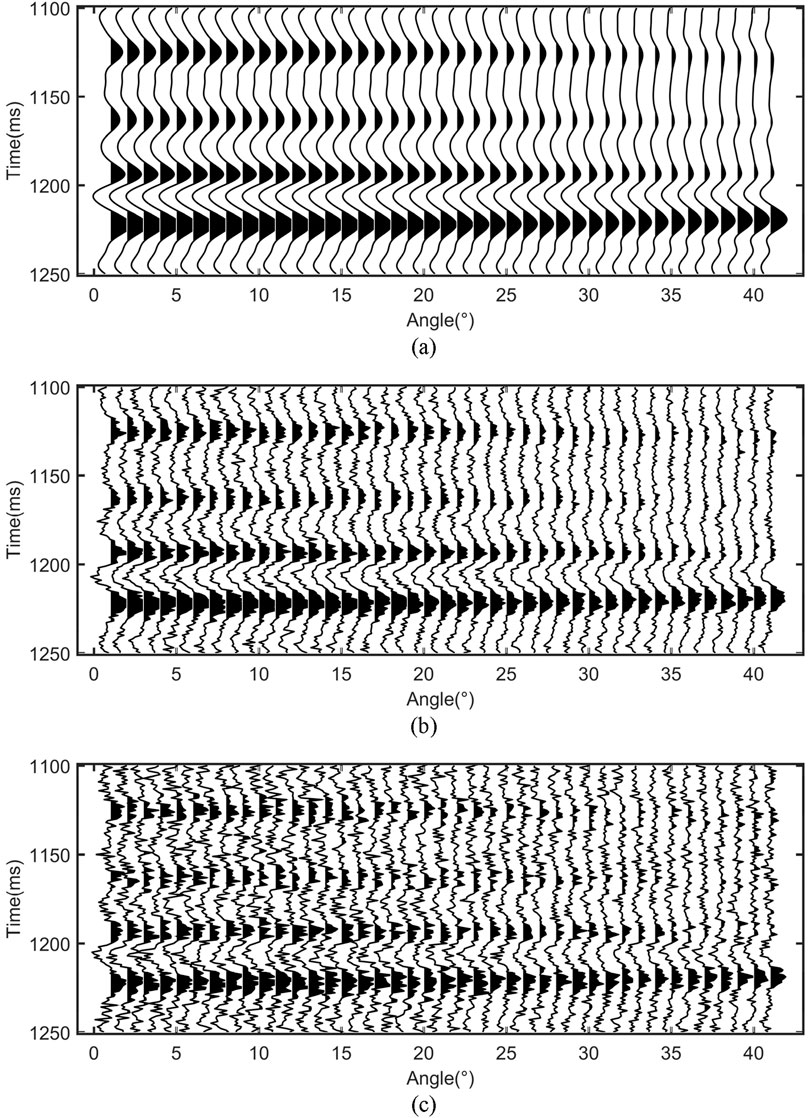
Figure 6. Synthetic angle gathers with different levels of noise: (A) without noise, (B) signal-to-noise ratio = 4, and (C) signal-to-noise ratio = 2.

Figure 7. Comparison among the real logs (black solid), inversion results by QACO (blue), and inversion results by ACO (green) for synthetic model II with different levels of noise: (A) without noise, (B) signal-to-noise ratio = 4, and (C) signal-to-noise ratio = 2. P-wave velocity, S-wave velocity, and density are shown from left to right. The upper and lower bounds of search windows are denoted by gray curves.
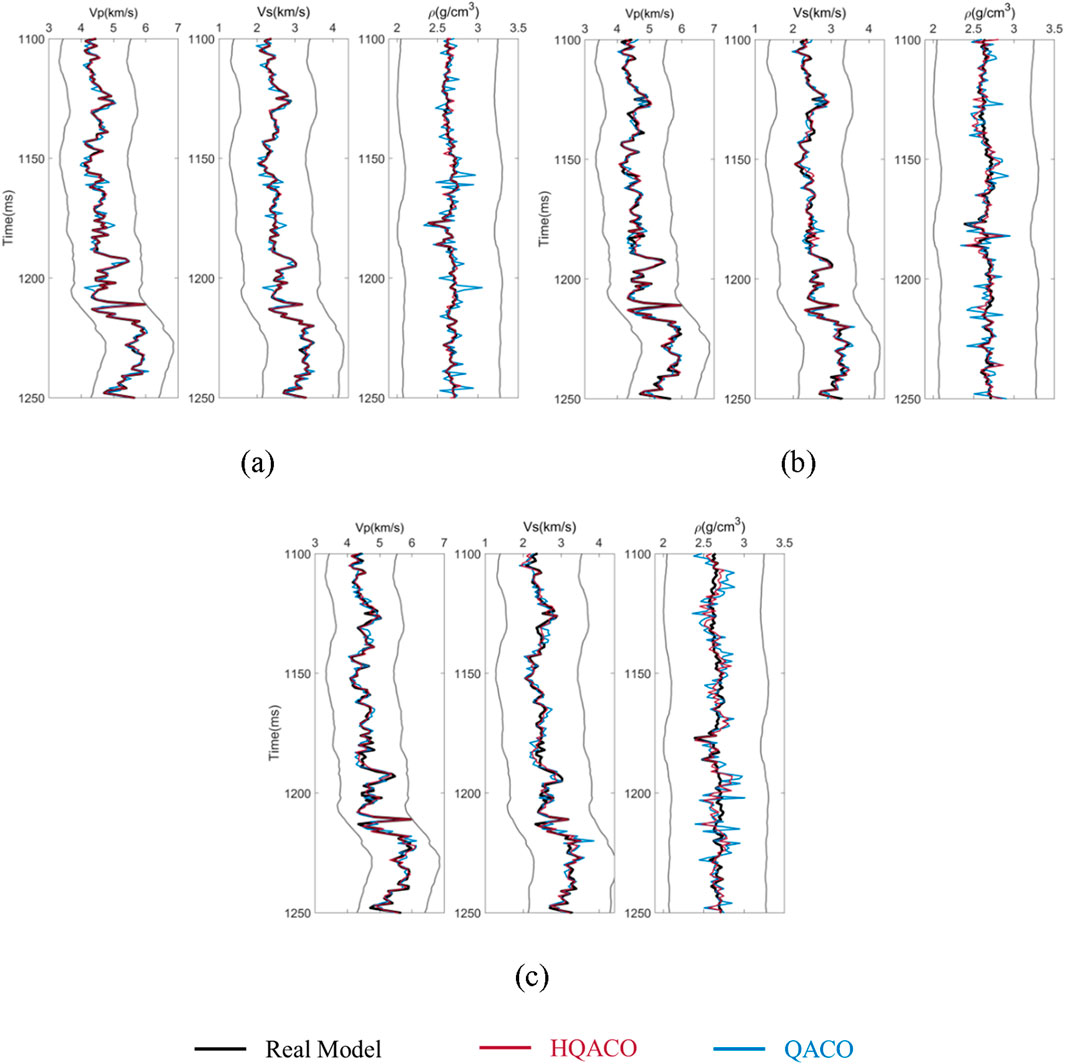
Figure 8. Comparison among the real logs (black solid), inversion results by HQACO (red), and inversion results by QACO (blue) for synthetic model II with different levels of noise: (A) without noise, (B) signal-to-noise ratio = 4, and (C) signal-to-noise ratio = 2. P-wave velocity, S-wave velocity, and density are shown from left to right. The upper and lower bounds of search windows are denoted by gray curves.

Figure 9. Residual between input seismic data and predicted seismograms with different methods when without noise: (A) ACO, (B) QACO, and (C) HQACO.

Figure 10. Residual between input seismic data and predicted seismograms with different methods when signal-to-noise ratio = 4: (A) ACO, (B) QACO, and (C) HQACO.
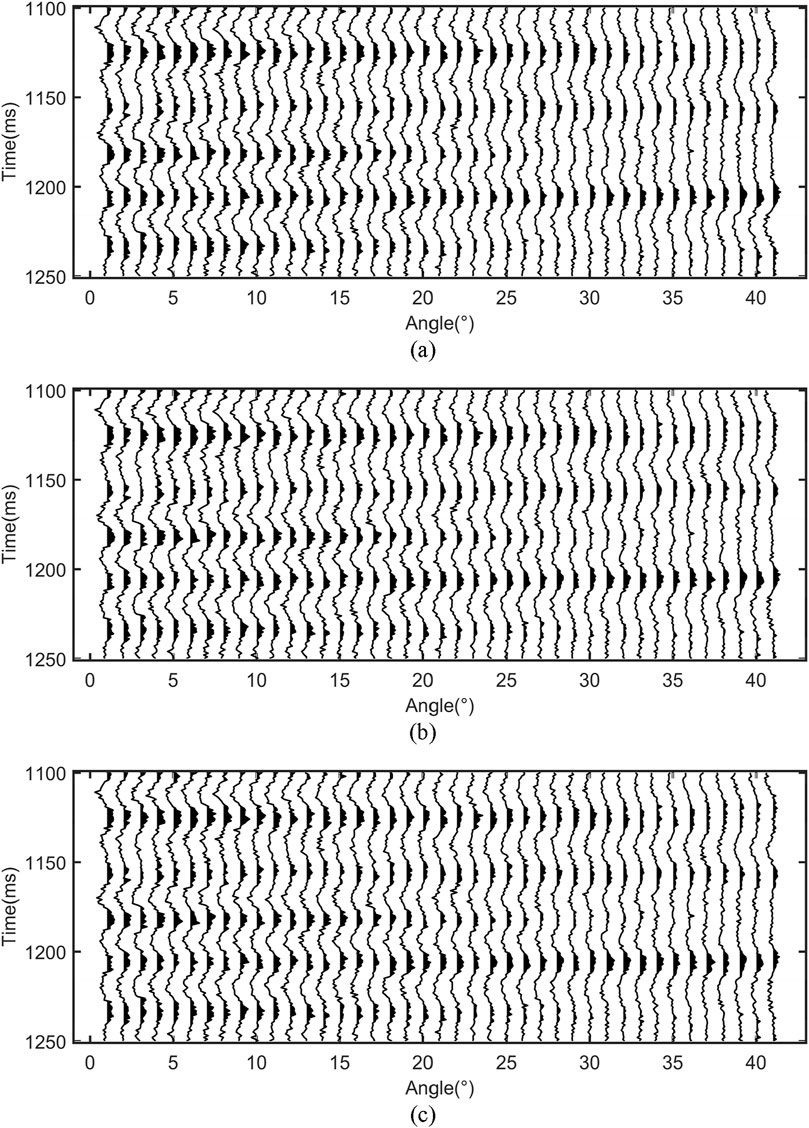
Figure 11. Residual between input seismic data and predicted seismograms with different methods when signal-to-noise ratio = 2: (A) ACO, (B) QACO, and (C) HQACO.
4 Discussion and conclusion
We propose a nonlinear AVO inversion method based on the exact Zoeppritz equation and apply it to the synthetic model. When dealing with high-contrast interfaces with far-offset information, the new inversion method based on the accurate Zoeppritz equation is sufficient to achieve the promising results. QACO shows greater global search competence and higher efficiency than ACO because the quantum qubit increases the population diversity and the quantum rotating gate is involved. HQACO, combining the quantum rotating gate with the self-adaptive rotating strategy and quantum gate, can adaptively update the search step and accelerate the convergence. All inversions use a dynamic search window, which can be constructed by combining the interpreted horizon with smoothed logs calibrated using seismic data. Inversion using dynamic search windows is more efficient than that using static search windows. Although it is recommended that special care must be taken in setting the search window range, in general, larger search windows require a larger computation time and have a greater likelihood of obtaining a global solution, whereas smaller search windows may miss the true solution. In conclusion, although the nonlinear inversion method based on the exact equations is time-consuming, HQACO is reliable in accuracy for reservoirs with strong contrast, long offset ranges, and noise energy using the exact Zoeppritz equation. The proposed method also significantly improves the inversion efficiency. The current quantum algorithm is developed in the current computer, whereas quantum computers promise computational improvement for a wide variety of applications, indicating that the algorithm should be designed for quantum computers to make possible further development of the efficiency of the inversion method. The proposed inversion method in conceptual models has been tested, and it can be applied in various geophysics problems and disciplines. With the recent breakthroughs in the construction of the universal quantum computer, future work will be devoted to incorporating multicomponent information, anisotropy, and complex wave propagation effects.
Data availability statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Author contributions
YC: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. JC: conceptualization, supervision, and writing–review and editing. HM: supervision and writing–review and editing. DF: writing–review and editing. CW: validation and writing–review and editing. CZ: writing–review and editing. MS: supervision and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The study was sponsored by the National Natural Science Foundation of China (42304134).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aleardi, M., and Mazzotti, A. (2017). 1D elastic full-waveform inversion and uncertainty estimation by means of a hybrid genetic algorithm–Gibbs sampler approach. Geophys. Prospect. 65 (1), 64–85. doi:10.1111/1365-2478.12397
Aleardi, M., Pierini, S., and Sajeva, A. (2019). Assessing the performances of recent global search algorithms using analytic objective functions and seismic optimization problems. Geophysics 84 (5), R767–R781. doi:10.1190/geo2019-0111.1
Buland, A., and Omre, H. (2003). Bayesian linearized AVO inversion. Geophysics 68 (1), 185–198. doi:10.1190/1.1543206
Cheng, J. W., Zhang, F., and Li, X. Y. (2022a). Seismic amplitude inversion for orthorhombic media based on a modified reflection coefficient approximation. Surv. Geophys. 43 (5), 1395–1433. doi:10.1007/s10712-022-09718-z
Cheng, J. W., Zhang, F., and Li, X. Y. (2022b). Nonlinear amplitude inversion using a hybrid quantum genetic algorithm and the exact zoeppritz equation. Petroleum Sci. 19 (3), 1048–1064. doi:10.1016/j.petsci.2021.12.014
Grover, L. K. (1996). “A fast quantum mechanical algorithm for database search,” in In Proceedings of the twenty-eighth annual ACM symposium on Theory of computing, Pennsylvania, Philadelphia, USA, May 22–24, 1996.
Han, K. H., and Kim, J. H. (2000). “Genetic quantum algorithm and its application to combinatorial optimization problem,” in Proceedings of the 2000 congress on evolutionary computation. CEC00 (Cat. No. 00TH8512), La Jolla, CA, USA, 16–19 July, 2000 (IEEE), 2, 1354–1360.
Han, K. H., Park, K. H., Lee, C. H., and Kim, J. H. (2001). “Parallel quantum-inspired genetic algorithm for combinatorial optimization problem,” in Proceedings of the 2001 congress on evolutionary computation (IEEE cat. No. 01TH8546), La Jolla, CA, USA, 16–19 July, 2000 (IEEE), 2, 1422–1429.
Hoos, H. H., and Stϋtzle, T. (2018). “Stochastic local search,” in Handbook of approximation algorithms and metaheuristics (Chapman and Hall/CRC), 297–307.
Kallel, L., Naudts, B., and Rogers, A. (2013). Theoretical aspects of evolutionary computing (Springer Science & Business Media).
Lahoz-Beltra, R. (2016). Quantum genetic algorithms for computer scientists. Computers 5 (4), 24. doi:10.3390/computers5040024
Layeb, A., and Saidouni, D. E. (2007). Quantum genetic algorithm for binary decision diagram ordering problem. Int. J. Comput. Sci. Netw. Secur. 7 (9), 130–135.
Li, T., and Mallick, S. (2015). Multicomponent, multi-azimuth pre-stack seismic waveform inversion for azimuthally anisotropic media using a parallel and computationally efficient non-dominated sorting genetic algorithm. Geophys. J. Int. 200 (2), 1136–1154. doi:10.1093/gji/ggu445
Liu, X., Cheng, J., Cai, Y., Mo, Q., Li, C., and Zu, S. (2022). Stochastic simulation of facies using deep convolutional generative adversarial network and image quilting. Mar. Petroleum Geol. 146, 105932. doi:10.1016/j.marpetgeo.2022.105932
Liu, X., Chen, X., Cheng, J., Zhou, L., Chen, L., Li, C., et al. (2023). Simulation of complex geological architectures based on multi-stage generative adversarial networks integrating with attention mechanism and spectral normalizatio. IEEE Trans. Geosci. Remote Sens. doi:10.1109/TGRS.2023.3294493
Liu, X., Li, J., Chen, X., Guo, K., Li, C., Zhou, L., et al. (2018). Stochastic inversion of facies and reservoir properties based on multi-point geostatistics. J. Geophys. Eng. 15 (6), 2455–2468. doi:10.1088/1742-2140/aac694
Lu, J., Yang, Z., Wang, Y., and Shi, Y. (2015). Joint PP and PS AVA seismic inversion using exact Zoeppritz equations. Geophysics 80 (5), R239–R250. doi:10.1190/geo2014-0490.1
Mallick, S. (1995). Model-based inversion of amplitude-variations-with-offset data using a genetic algorithm. Geophysics 60 (4), 939–954. doi:10.1190/1.1443860
Mallick, S., and Adhikari, S. (2015). Amplitude-variation-with-offset and prestack-waveform inversion: a direct comparison using a real data example from the Rock Springs Uplift, Wyoming, USA. Geophysics 80 (2), B45–B59. doi:10.1190/geo2014-0233.1
Moradi, S., Trad, D., and Innanen, K. A. (2018). “Quantum computing in geophysics: algorithms, computational costs, and future applications,” in SEG technical program expanded abstracts 2018 (Society of Exploration Geophysicists), 4649–4653. doi:10.1190/segam2018-2998507.1
Ostrander, W. J. T. (1984). Plane-wave reflection coefficients for gas sands at nonnormal angles of incidence. Geophysics 49 (10), 1637–1648. doi:10.1190/1.1441571
Russell, B. H., Gray, D., and Hampson, D. P. (2011). Linearized AVO and poroelasticity. Geophys. 76 (3), C19–C29. doi:10.1190/1.3555082
Sen, M. K., and Stoffa, P. L. (2013). Global optimization methods in geophysical inversion. Cambridge University Press.
Shuey, R. T. (1985). A simplification of the Zoeppritz equations. Geophysics 50 (4), 609–614. doi:10.1190/1.1441936
Smith, G. C., and Gidlow, P. M. (1987). Weighted stacking for rock property estimation and detection of gas. Geophys. Prospect. 35 (9), 993–1014. doi:10.1111/j.1365-2478.1987.tb00856.x
Stoffa, P. L., and Sen, M. K. (1991). Nonlinear multiparameter optimization using genetic algorithms: inversion of plane-wave seismograms. Geophysics 56 (11), 1794–1810. doi:10.1190/1.1442992
Zhang, F., and Li, X. (2013). Generalized approximations of reflection coefficients in orthorhombic media. J. Geophys. Eng. 10 (5), 054004. doi:10.1088/1742-2132/10/5/054004
Zhang, F., Zhang, T., and Li, X. Y. (2019). Seismic amplitude inversion for the transversely isotropic media with vertical axis of symmetry. Geophys. Prospect. 67 (9-Advances in Seismic Anisotropy), 2368–2385. doi:10.1111/1365-2478.12842
Zhou, L., Li, J., Chen, X., Liu, X., and Chen, L. (2017). Prestack AVA inversion of exact Zoeppritz equations based on modified Trivariate Cauchy distribution. J. Appl. Geophys. 138, 80–90. doi:10.1016/j.jappgeo.2017.01.009
Zoeppritz, K. (1919). On reflection and propagation of seismic waves. Gottinger Nachrichten, 1: 66–84.
Keywords: exact Zoeppritz equation, amplitude versus angle, nonlinear inversion, quantum computing, hybrid quantum ant colony optimization
Citation: Chen Y, Cheng J, Miao H, Feng D, Wang C, Zhang C and Song M (2024) Nonlinear amplitude versus angle inversion using hybrid quantum ant colony optimization and the exact Zoeppritz equation . Front. Earth Sci. 12:1483776. doi: 10.3389/feart.2024.1483776
Received: 20 August 2024; Accepted: 24 September 2024;
Published: 11 October 2024.
Edited by:
Qingchun Li, Chang’an University, ChinaReviewed by:
Lin Zhou, Hunan Provincial Key Laboratory of Shale Gas Resource Utilization, Hunan University of Science and Technology, ChinaSong JIn, China University of Geosciences Wuhan, China
Peng Lin, China University of Mining and Technology, Beijing, China
Copyright © 2024 Chen, Cheng, Miao, Feng, Wang, Zhang and Song. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mengxin Song, bXhzb25nQHBldHJvY2hpbmEuY29tLmNu
 Yuxing Chen
Yuxing Chen Jiwei Cheng
Jiwei Cheng Hongping Miao
Hongping Miao