Axisymmetric consolidation behavior of multilayered unsaturated soils with transversely isotropic permeability

Time-dependent consolidation behavior of unsaturated soils is a vital problem in the geotechnical engineering. With the aid of the Fredlund consolidation theory, this work further assumes the total stress of soils skeleton freely change, and extends the Fredlund consolidation theory to a Biot-type theory, establishing the fully-coupled equation model of multilayered unsaturated poroelastic media with transversely isotropic permeability. To convert the partial differential governing equation into ordinary differential equations, the integration transform technology is applied. Subsequently, the precise integration method is used to acquire the time-dependent consolidation solution of multilayered unsaturated media with transversely isotropic permeability in the transformed domain, which is further solved in the actual domain by the inverse Hankel transform. A verification examples is provided to compare the present results with the existing work in the literature, showing a great coincidence and proving the feasibility of the present solution. Finally, numerous numerical examples are presented to investigate the evolution of excess pore pressure and settlement under quasi-static loads, revealing the consolidation behavior of unsaturated soils. The results demonstrates that the ramping time, stratification, permeability, depth and $m_1^w$ have a significant effect on the consolidation behavior.

1 Introduction

Consolidation theory remains a key topic in geotechnical engineering. Originating from Biot’s work (Biot, 1941; Biot, 1955), which rigorously integrated pore pressure and settlement, lots of researchers (McNamee and Gibson, 1960; Schiffman and Fungaroli, 1965; Gibson et al., 1970; Booker and Randolph, 1984; Yue et al., 1994; Wang et al., 2023a; Wang et al., 2023b; Chen et al., 2005; Singh et al., 2007; Ai and Wang, 2008; Cai and Geng, 2009) have explored this complex issue. Their investigations typically assume geomaterial behaves as either an elastic half-space or a finite soil layer. In fact, natural geotechnical materials exhibit pronounced stratification due to prolonged and complex deposition processes, profoundly influencing their consolidation characteristics (Pan, 1989; Yue, 1996; Pan, 1997; Yue and Yin, 1998). Consequently, considering the layered characteristic in the consolidation analysis is quite significant. Booker and Small (Booker and Small, 1982; Booker and Small, 1987) firstly employed the finite layer method to explore the mechanical-hydraulic behavior of layered soils. Moreover, other researchers addressed this issue using the boundary element method (Aramaki, 1985; Dargush and Banerjee, 1991) and the transfer matrix method (Wang and Fang, 2001), the analytical layer-element method (Ai et al., 2011). In particularly, the analytical layer-element method only has the decaying exponential functions thin its stiffness matrix, mitigating the instability and the exponential overflow problem in the transfer matrix method. However, many existing studies fail to accurately model the comprehensive three-dimensional conditions that involve both vertical and tangential loads. Therefore, it is essential to expand this research to include three-dimensional scenarios for a more generalized understanding of consolidation problems. Vardoulakis and Harnpattanapanich (Vardoulakis and Harnpattanapanich, 1986; Harnpattanapanich and Vardoulakis, 1987) examined settlement along depth under external loads, while Senjuntichai and Rajapakse (Senjuntichai and Rajapakse, 1995) addressed the three-dimensional consolidation response of soil, providing precise solutions. Additionally, Pan (1999) derived fundamental solutions for layered poroelastic systems, and Ai and his colleagues (Ai et al., 2010; Ai and Zeng, 2012) explored non-axisymmetric consolidation solutions.

The above works assumes that the soil as the saturated medium. In fact, most of the soils on the earth are located in arid and semi-arid unsaturated zones, and the subgrade filler of railways and airport runways is also mostly unsaturated soil. Therefore, studying the consolidation characteristics of unsaturated soil under external loads is of great engineering significance. Early studies were limited to specific types of unsaturated soils, in which bubbles existed in a closed form in the liquid, ignoring the free flow effect of the two-phase fluid in the soil. To solve this problem, there are many works (Barden, 1965; Fredlund and Rahardjo, 1993; Loret and Khalili, 2000; Cao et al., 2024a; Cao et al., 2024b; Cao et al., 2023). Among them, Fredlund and Rahardjo (Fredlund and Rahardjo, 1993) used dual stress-strain state variables to define the contribution of the net stress and the matrix suction respectively, and then constructed the two-phase flow equation of unsaturated soils. Dakshanamurthy et al. (1984), Dakshanamurthy and Fredlund (1980) further proposed 2D and 3D consolidation models for unsaturated soils based on the assumption that the total stress of the soil skeleton remain unchanged.

Building on the governing equations for unsaturated soil consolidation, many investigators apply numerical or semi-analytical methods to study consolidation behavior. Ausilio and Conte (Ausilio et al., 2002) connected the displacement rate to the average degree of consolidation, utilizing Fourier transform to examine consolidation in unsaturated soils under both water-air coupled and uncoupled conditions. Qin and her cooperators (Qin et al., 2010; Wang et al., 2017a; Wang et al., 2017b) used analytical methods and combined different boundary conditions to study the one-dimensional unsaturated soil consolidation theory. Shan et al. (2012) used the transfer matrix method to discuss the distribution of pore water and air pressure of layered one-dimensional unsaturated soils. Ho et al. (2014) derived the governing equations of the one-dimensional consolidation model of unsaturated soil under single-sided and double-sided permeable boundaries, and proposed a theoretical solution method combining the eigenfunction method and Laplace transform. Based on previous work (Ho et al., 2014; Ho et al., 2015), Ho et al. (2016) further derived the uncoupled axisymmetric mathematical consolidation modelling of unsaturated soil. Huang and Li (2018) developed a plane strain consolidation model under bidirectional continuous permeable boundary conditions, solving it using Fourier transform and the method of separation of variables. Moradi et al. (2019) proposed a 1D multi-layer analytical model for unsaturated consolidation under partially permeable boundaries and time-varying loads, employing the differential quadrature method for the layered unsaturated soil system. Other researchers have also explored soil consolidation issues by incorporating non-ideal permeable boundaries. Tian et al. (2020) studied a 1D consolidation model of saturated soils under multi-stage loading conditions based on continuous drainage boundary conditions. Zong et al. (2020) pointed out that even if the external load is q₀, the pore pressure at the initial moment is smaller than q₀, based on a one-dimensional single-layer soil nonlinear consolidation model considering a continuous permeable boundary. Wang et al. (2019) utilized the eigenfunction method expansion and integration transform method to solve the 2D settlement-pore pressure distribution of unsaturated soil introducing the lateral semi-permeable drainage boundary (LSDB). Building upon a semi-permeable boundary (Wang et al., 2017a; Wang et al., 2017b), Wang et al. (2017c) also investigated the impact of time-varying loads on consolidation behaviors Niu et al. (2021) introduced a 1D consolidation model for unsaturated soils incorporating dynamic loaded scenarios. The partial differential equations (PDEs) were theoretically resolved via the eigenfunction expansion technique. Liu et al. (2022) explored the impact of exponential time-varying loads on consolidation characteristics, comparing these effects with those of constant loads.

In summary, current solutions for unsaturated consolidation problems predominantly focus on one-dimensional loading conditions, with limited research on two- or three-dimensional scenarios. It is particularly noteworthy that the above studies are all based on the assumption that the total stress remains unchanged during the consolidation process, so they can be regarded as a Terzaghi-type consolidation theory, that is, a non-coupled theory. In comparison, there are few studies based on the fully coupled consolidation theory (i.e., Biot-type consolidation theory) in which the total stress changes during the consolidation process. In addition, the stratification and transverse isotropy of permeability characteristics formed by natural soil deposition are often ignored in previous studies. Therefore, this paper utilizes Fredlund’s dual stress variable consolidation theory to investigate the fully coupled consolidation of layered unsaturated soil under variable loads, examining the influence of ramping time, the transverse isotropy of the permeability, the volume variation coefficient of pore water regarding net stress, depth and stratification on the time-dependent settlement, pore water pressure and pore air pressure distribution. Compared with the existing research, the innovation of this work can be drawn as follows: (1) A fully-coupled Fredlund consolidation model is proposed in this work, while the other work is limited to the non-coupled model based on the excessive assumption. (2) The transverse isotropy of permeability of soils is considered in the work, which is not included in the previous work. (3) The precise integration method is utilized to deal with these partial differential equations of the mathematical model, showing a great stability and robustness.

2 Methodology

2.1 Governing equations

In elasticity theory, the equilibrium differential equation ignoring body forces is:

$\frac{\partial {\sigma }_r}{\partial r}+\frac{\partial {\sigma }_{rz}}{\partial z}+\frac{{\sigma }_r-{\sigma }_{\theta }}{r}=0(\mathrm{1a})$

$\frac{\partial {\sigma }_{rz}}{\partial r}+\frac{\partial {\sigma }_z}{\partial z}+\frac{{\sigma }_{rz}}{r}=0(\mathrm{1b})$

where ${\sigma }_r$, ${\sigma }_{\theta }$, ${\sigma }_z$ are the normal stress in $r,\theta \text{\hspace{0.17em}and\hspace{0.17em}}z$ direction, ${\sigma }_{rz}$ is the shear stress in the r-z plane.

Based on Fredlund’s dual stress variable theory (Fredlund and Rahardjo, 1993), the linear elastic constitutive equation of unsaturated soils is given:

${\sigma }_r-u_a=2G\left(\frac{\partial u_r}{\partial r}+{\alpha }_s{\epsilon }_v\right)-\beta \left(u_a-u_w\right)(\mathrm{2a})$

${\sigma }_{\theta }-u_a=2G\left(\frac{u_r}{r}+{\alpha }_s{\epsilon }_v\right)-\beta \left(u_a-u_w\right)(\mathrm{2b})$

${\sigma }_z-u_a=2G\left(\frac{\partial u_z}{\partial z}+{\alpha }_s{\epsilon }_v\right)-\beta \left(u_a-u_w\right)(\mathrm{2c})$

${\sigma }_{rz}=G\left(\frac{\partial u_r}{\partial z}+\frac{\partial u_z}{\partial r}\right)(\mathrm{2d})$

where the volume stress is ${\epsilon }_v=\partial u_r/\partial r+u_r/r+\partial u_z/\partial z$, $u_r$ and $u_z$ are the displacement in $r\text{\hspace{0.5em}and\hspace{0.5em}}z$ direction; the matric suction is $p_c=u_a-u_w$; $u_w$ and $u_a$ are the excess pore water and air pressure; $\beta =m_2^s/m_1^s$, $m_1^s=3\left(1-2\mu \right)/E$ represents the coefficient of volume change of the soil skeleton regarding the net stress ${\sigma }_{mean}=\left({\sigma }_r+{\sigma }_{\theta }+{\sigma }_z\right)/3-u_a$; $m_2^s=3/H$ denotes the volume variation coefficient of the soil skeleton regarding the matric suction $p_c$; $E$ and $H$ denote the elastic modulus regarding the net stress ${\sigma }_{mean}$ and the matric suction $p_c$; $\mu$ is Poisson ratio.

It is assumed that two-phase flow in unsaturated soil is continuous. By introducing Darcy law and the constitutive relationship of pore water in Fredlund theory (Fredlund and Rahardjo, 1993), the seepage continuity equation of pore water with transversely isotropic permeability can be obtained as follows:

$\frac{m_1^w}{m_1^s}\frac{\partial {\epsilon }_v}{\partial t}+\left(m_2^w-m_1^w\beta \right)\frac{\partial }{\partial t}{p}_c=\frac{k_w^h}{{\gamma }_w}\left(\frac{\partial u_w}{\partial r}+\frac{u_w}{r}\right)+\frac{k_w^z}{{\gamma }_w}\frac{\partial u_w}{\partial z}(3)$

in which $m_1^w$ and $m_2^w$ are the volume variation coefficient of the pore water regarding the net stress ${\sigma }_{mean}$ and the matric suction $p_c$; $k_w$ and ${\gamma }_w$ are the permeability coefficient and the specific gravity。

Similarly, with the aid of Boyle law (Fredlund and Rahardjo, 1993) and the constitutive equation of the skeleton, the seepage continuity equation of the pore air with transversely isotropic permeability can also be obtained:

$\begin{array}{ll}\hfill \frac{m_1^a}{m_1^s}\frac{\partial {\epsilon }_v}{\partial t}+\left(m_2^a-m_1^a\beta \right)\frac{\partial }{\partial t}{p}_c& =\frac{k_a^h}{g{\rho }_a}\left(\frac{\partial u_a}{\partial r}+\frac{u_a}{r}\right)+\frac{k_a^z}{g{\rho }_a}\frac{\partial u_a}{\partial z}\hfill \\ \hfill & -\frac{u_{atm}n\left(1-S_r\right)}{{\left({\stackrel{⌢}{u}}_a\right)}^2}\frac{\partial u_a}{\partial t}\hfill \end{array}(4)$

where $m_1^a$ and $m_2^a$ are the volume variation coefficients of pore air regarding the net stress and the matrix suction (there is an intrinsic relationship $m_1^s=m_1^w+m_1^a$ and $m_2^s=m_2^w+m_2^a$); $k_a$ denotes the permeability coefficient of pore air; and $n$ represents the porosity and $S_r$ is the saturation degree; for ideal air, air density ${\rho }_a={\stackrel{⌢}{u}}_{a}M/RT$, where the average molar mass of the atmosphere is $M=0.029\text{kg}/\text{mol}$; air constant $R=8.314\mathrm{J}/\text{mol}\cdot \mathrm{K}$; $T$ is the absolute temperature; ${\stackrel{⌢}{u}}_a=u_a+u_a^0+u_{atm}$ represents the absolute air pressure. Given that the excess pore air pressure usually dissipates rapidly in the early stage of consolidation, its magnitude can be ignored compared to the atmospheric pressure, so we use instantaneous air pressure $u_a^0$ and atmospheric pressure $u_{atm}$ to describe absolute air pressure (Qin et al., 2010), i.e., ${\stackrel{⌢}{u}}_a=u_a+u_{atm}$.

Finally, the total volume flow rate $Q_{wz}$ of pore water and the total mass flow rate of pore air $Q_{az}$ along the depth direction from time 0 to time t are defined as:

$Q_{wz}=\underset{0}{\overset{t}{\int }}\frac{k_w^z}{{\gamma }_w}\frac{\partial u_w}{\partial z}dt(\mathrm{5a})$

$Q_{az}=\underset{0}{\overset{t}{\int }}\frac{k_a^z}{g}\frac{\partial u_a}{\partial z}dt(\mathrm{5b})$

Equations 1–5 constitute the mathematical governing equations of the fully-coupled consolidation for unsaturated soils. It is found that these equations are the partial differential equations (PDEs), hard to solve directly. Therefore, the Laplace-Hankel transform and the corresponding inverse transform in Equation 6 are introduced to simplify these PDEs into ordinary differential equations (ODEs) for solution:

${\overline{f}}^m\left(\xi ,z,s\right)=\underset{0}{\overset{\infty }{\int }}\underset{0}{\overset{\infty }{\int }}f\left(r,z,t\right)e^{-st}{J}_m\left(\xi r\right)rdtdr(\mathrm{6a})$

$f\left(r,z,t\right)=\frac{1}{2\mathrm{\pi }i}\underset{0}{\overset{\infty }{\int }}\underset{c-i\infty }{\overset{c+i\infty }{\int }}{\overline{f}}^m\left(\xi ,z,s\right)J_m\left(\xi r\right)\xi e^{st}dsd\xi (\mathrm{6b})$

in which, ${\overline{f}}^m\left(\xi ,z,s\right)$ denotes the corresponding function of $f\left(r,z,t\right)$ in the Laplace-Hankel domain; $s$ denotes the Laplace parameter regarding time $t$; $\xi$ is the Hankel transform parameter regarding coordinate r; $J_m\left(\xi r\right)$ is the m-order Bessel function.

2.2 Ordinary differential governing equations

In the Laplace transform domain, applying the 0th and 1st order Hankel transforms to Equations 2d, 2c respectively, we can obtain:

$\frac{\partial {\overline{u}}_r^1}{\partial z}=\frac{1}{G}{\overline{\sigma }}_{rz}^1+\xi {\overline{u}}_z^0(\mathrm{7a})$

$\frac{\partial {\overline{u}}_z^0}{\partial z}=\frac{1}{2G\left(1+{\alpha }_s\right)}{\overline{\sigma }}_z^0-\frac{{\alpha }_s\xi }{1+{\alpha }_s}{\overline{u}}_r^1-\frac{\beta }{2G\left(1+{\alpha }_s\right)}{\overline{u}}_w^0+\frac{\beta -1}{2G\left(1+{\alpha }_s\right)}{\overline{u}}_a^0(\mathrm{7b})$

Similarly, applying Laplace and 0th-order Hankel transforms to Equations 5a, 5b, we can obtain:

$\frac{\partial {\overline{u}}_w^0}{\partial z}=\frac{s{\gamma }_w}{k_w^z}{\overline{Q}}_{wz}^0(\mathrm{7c})$

$\frac{\partial {\overline{u}}_a^0}{\partial z}=\frac{sg}{k_a^z}{\overline{Q}}_{az}^0(\mathrm{7d})$

Substituting Equations 2a, 7b into Equation 1a and applying Laplace and first-order Hankel transforms, we obtain:

$\frac{\partial {\overline{\sigma }}_{rz}^1}{\partial z}=\frac{{\alpha }_s}{1+{\alpha }_s}\xi {\overline{\sigma }}_z^0+\frac{2G}{1-\mu }{\xi }^2{\overline{u}}_r^1+\frac{\beta }{1+{\alpha }_s}\xi {\overline{u}}_w^0+\frac{1-\beta }{1+{\alpha }_s}\xi {\overline{u}}_a^0(7e)$

Based on Equation 1b, the following equation in the Laplace and 0th-order Hankel domains can be acquired:

$\frac{\partial {\overline{\sigma }}_z^0}{\partial z}=-\xi {\overline{\sigma }}_{rz}^1(\mathrm{7f})$

In the Laplace and 0th-order Hankel transform domains, the water seepage continuity Equation 3 and Equations 7b, 7c are integrated to obtain:

$\frac{\partial {\overline{Q}}_{wz}^0}{\partial z}=A_{11}{\overline{u}}_w^0\left(z,\xi ,0\right)-A_{11}{\overline{u}}_a^0\left(z,\xi ,0\right)+A_{12}\xi {\overline{u}}_r^1+A_{13}{\overline{\sigma }}_z^0-A_{14}{\overline{u}}_w^0+A_{15}{\overline{u}}_a^0(\mathrm{7g})$

In the Laplace and 0th-order Hankel transform domains, the air flow continuity Equation 4 and Equations 7b, 7c are integrated to obtain:

$\begin{array}{ll}\hfill \frac{\partial {\overline{Q}}_{az}^0}{\partial z}& =\frac{u_{a0}M}{RT}\left[A_{21}{\overline{u}}_w^0\left(z,\xi ,0\right)-A_{21}{\overline{u}}_a^0\left(z,\xi ,0\right)+A_{22}\xi {\overline{u}}_r^1+A_{23}{\overline{\sigma }}_z^0-A_{24}{\overline{u}}_w^0\right]\hfill \\ \hfill & +A_{25}{\overline{u}}_a^0\hfill \end{array}(\mathrm{7h})$

where $A_{11}=m_2^w-m_1^w\beta$, $A_{12}=\frac{m_1^w}{m_1^s\left(1+{\alpha }_s\right)}$, $A_{13}=\frac{m_1^w}{2m_1^{s}G\left(1+{\alpha }_s\right)}$, $A_{14}=\frac{m_1^w\beta }{2m_1^{s}G\left(1+{\alpha }_s\right)}+A_{12}-\frac{k_w^h{\xi }^2}{s{\gamma }_w}$, $A_{15}=\frac{m_1^w\left(\beta -1\right)}{2m_1^{s}G\left(1+{\alpha }_s\right)}+A_{12}$, $A_{21}=m_2^a-m_1^a\beta$, $A_{22}=\frac{m_1^a}{m_1^s\left(1+{\alpha }_s\right)}$, $A_{23}=\frac{m_1^a}{2m_1^{s}G\left(1+{\alpha }_s\right)}$, $A_{24}=\frac{m_1^a\beta }{2m_1^{s}G\left(1+{\alpha }_s\right)}+A_{22}$, $A_{25}=\frac{u_{a0}M}{RT}\left[\frac{m_1^a\left(\beta -1\right)}{2m_1^{s}G\left(1+{\alpha }_s\right)}+A_{22}+\frac{u_{atm}n\left(1-S_r\right)}{{\left({\overline{u}}_a^0\right)}^2}\right]+\frac{k_a^h{\xi }^2}{sg{\rho }_a}$.

In Equations 7a–7h, the superscripts “0”and “1”represent that the variables have been processed by 0th-order or 1st-order Hankel transform.

Combination of the above equations leads to the following matrix expression:

$\frac{d}{dz}\left[\begin{array}{c}\mathbf{V}\left(z,\xi ,s\right)\\ \mathbf{U}\left(z,\xi ,s\right)\end{array}\right]=\left[\begin{array}{cc}{\mathbf{W}}_1& {\mathbf{W}}_2\\ {\mathbf{W}}_3& {\mathbf{W}}_4\end{array}\right]\cdot \left[\begin{array}{c}\mathbf{V}\left(z,\xi ,s\right)\\ \mathbf{U}\left(z,\xi ,s\right)\end{array}\right]+\left[\begin{array}{cc}\mathbf{0}& \mathbf{0}\\ {\mathbf{W}}_5& \mathbf{0}\end{array}\right]\cdot \left[\begin{array}{c}\mathbf{V}\left(z,\xi ,0\right)\\ \mathbf{U}\left(z,\xi ,0\right)\end{array}\right](8)$

in which, the generalized stress vector is $\mathbf{V}\left(z,\xi ,s\right)={\left[{\overline{\sigma }}_{rz}^1,{\overline{\sigma }}_z^0,{\overline{u}}_w^0,{\overline{u}}_w^0\right]}^{\mathrm{T}}$; the generalized displacement vector is $\mathbf{U}\left(z,\xi ,s\right)={\left[{\overline{u}}_r^1,{\overline{u}}_z^0,{\overline{Q}}_{wz}^0,{\overline{Q}}_{az}^0\right]}^{\mathrm{T}}$; and the coefficient matrices ${\mathbf{W}}_i\left(i=1-5\right)$ are given as follows:

$\begin{array}{ll}\hfill {\mathbf{W}}_1& =\left[\begin{array}{cccc}0& \frac{{\alpha }_s}{1+{\alpha }_s}\xi & \frac{\beta }{1+{\alpha }_s}\xi & \frac{1-\beta }{1+{\alpha }_s}\xi \\ -\xi & 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],\hfill \\ \hfill & {\mathbf{W}}_2=\left[\begin{array}{cccc}\frac{2G}{1-\mu }{\xi }^2& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& \frac{s{\gamma }_w}{k_w^z}& 0\\ 0& 0& 0& \frac{sg}{k_a^z}\end{array}\right],\hfill \\ \hfill & {\mathbf{W}}_3=\left[\begin{array}{cccc}\frac{1}{G}& 0& 0& 0\\ 0& \frac{1}{2G\left(1+{\alpha }_s\right)}& -\frac{\beta }{2G\left(1+{\alpha }_s\right)}& \frac{\beta -1}{2G\left(1+{\alpha }_s\right)}\\ 0& A_{13}& -A_{14}& A_{15}\\ 0& \frac{u_{a0}M}{RT}{A}_{23}& -\frac{u_{a0}M}{RT}{A}_{24}& \frac{u_{a0}M}{RT}{A}_{25}\end{array}\right],\hfill \\ \hfill & {\mathbf{W}}_4=\left[\begin{array}{cccc}0& \xi & 0& 0\\ -\frac{{\alpha }_s}{1+{\alpha }_s}\xi & 0& 0& 0\\ A_{12}\xi & 0& 0& 0\\ \frac{u_{a0}M}{RT}{A}_{23}\xi & 0& 0& 0\end{array}\right],\hfill \\ \hfill & {\mathbf{W}}_5=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& A_{11}& -A_{11}\\ 0& 0& \frac{u_{a0}M}{RT}{A}_{21}& -\frac{u_{a0}M}{RT}{A}_{21}\end{array}\right]\hfill \end{array}$

In terms of the time-varying loads (ramping loads and exponential loads) selected in this paper, the initial load magnitudes are all 0. Therefore, it can be assumed that the instantaneous generalized state vectors $\mathbf{V}\left(z,\xi ,0\right)=\mathbf{0}$, $\mathbf{U}\left(z,\xi ,0\right)=\mathbf{0}$ when applied by the external load.

2.3 Solution to the governing equation

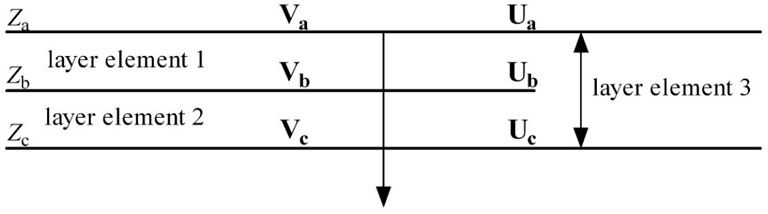
In the context of the two-point boundary value problem, the Precise integration method (PIM) introduced by Zhong (1994) stands out as an efficient and highly accurate technique widely utilized in various fields such as wave propagation, quasi-static analysis, and dynamic interaction studies. This section adopts the PIM for discretizing the ODE matrix along the depth dimension. In terms of a layered unsaturated soil with a depth L, the initial step of PIM is to dividing the model into 2^N micro layers, the length of each micro layers is L/2^N. Notably, within any adjacent micro layers, there exist four generalized state vectors, denoted as ${\mathbf{V}}_a,{\mathbf{V}}_b,{\mathbf{U}}_a\text{\hspace{0.17em}and\hspace{0.17em}}{\mathbf{U}}_b$.

In terms of adjacent micro layers given in Figure 1, four generalized state vectors between the upper and lower surface are established, respectively, i.e., ${\mathbf{V}}_a,{\mathbf{V}}_b,{\mathbf{U}}_a\text{\hspace{0.17em}and\hspace{0.17em}}{\mathbf{U}}_b$ found in micro layer 1 and ${\mathbf{V}}_c,{\mathbf{V}}_d,{\mathbf{U}}_c\text{\hspace{0.17em}and\hspace{0.17em}}{\mathbf{U}}_d$ found in micro layer 2. The continuity condition at the depth $z_b$ leads to ${\mathbf{V}}_b={\mathbf{V}}_c\text{\hspace{0.17em}and\hspace{0.17em}}{\mathbf{U}}_b={\mathbf{U}}_c$. Thus, there is indeed six generalized state vectors in the adjacent micro layers, i.e., ${\mathbf{V}}_a,{\mathbf{V}}_b,{\mathbf{V}}_c,{\mathbf{U}}_a,{\mathbf{U}}_b\text{\hspace{0.17em}and\hspace{0.17em}}{\mathbf{U}}_c$. The inherent relationship of the two micro layers has been given in Equations 9 and 10 (Ye et al., 2023):

Figure 1

Figure 1. The state vectors between the adjacent micro layers.

In terms of the layer element 1:

${\mathbf{V}}_b={\mathbf{F}}_1{\mathbf{V}}_a-{\mathbf{G}}_1{\mathbf{U}}_b(\mathrm{9a})$

${\mathbf{U}}_a={\mathbf{Q}}_1{\mathbf{V}}_a+{\mathbf{E}}_1{\mathbf{U}}_b(\mathrm{9b})$

Analogously, for the layer element 2:

${\mathbf{V}}_c={\mathbf{F}}_2{\mathbf{V}}_b-{\mathbf{G}}_2{\mathbf{U}}_c(\mathrm{10a})$

${\mathbf{U}}_b={\mathbf{Q}}_2{\mathbf{V}}_b+{\mathbf{E}}_2{\mathbf{U}}_c(\mathrm{10b})$

where ${\mathbf{F}}_i$, ${\mathbf{E}}_i$, ${\mathbf{Q}}_i$, ${\mathbf{G}}_i$ (i =1, 2) are four $4\times 4$ dimensional relational matrices. With the aid of Talor expansion, the series expression regarding the thickness $l$ can be achieved. In order to enhance computational efficiency while maintaining accuracy, higher-order terms beyond the fourth order are truncated. This approach optimizes the balance between computational complexity and numerical fidelity, and the we can have:

$\mathbf{F}\left(l\right)=\mathbf{I}+{\mathbf{F}}^{*}\left(l\right),{\mathbf{F}}^{*}\left(x\right)\approx {\mathbf{f}}_{1}l+{\mathbf{f}}_2{l}^2+{\mathbf{f}}_3{l}^3+{\mathbf{f}}_4{l}^4(\mathrm{11a})$

$\mathbf{E}\left(l\right)=\mathbf{I}+{\mathbf{E}}^{*}\left(l\right),{\mathbf{E}}^{*}\left(l\right)\approx {\mathbf{e}}_{1}l+{\mathbf{e}}_2{l}^2+{\mathbf{e}}_3{l}^3+{\mathbf{e}}_4{l}^4(\mathrm{11b})$

$\mathbf{Q}\left(l\right)\approx {\mathbf{\phi }}_{1}l+{\mathbf{\phi }}_2{l}^2+{\mathbf{\phi }}_3{l}^3+{\mathbf{\phi }}_4{l}^4(\mathrm{11c})$

$\mathbf{G}\left(l\right)\approx {\mathbf{g}}_{1}l+{\mathbf{g}}_2{l}^2+{\mathbf{g}}_3{l}^3+{\mathbf{g}}_4{l}^4(\mathrm{11d})$

where $\mathbf{I}$ is an $n\times n$ identity matrix, and ${\mathbf{f}}_i,{\mathbf{e}}_i,{\mathbf{\phi }}_i\text{\hspace{0.17em}and\hspace{0.17em}}{\mathbf{g}}_i$ are defined as:

$\begin{array}{ll}\hfill {\mathbf{f}}_1& ={\mathbf{W}}_1,{\mathbf{f}}_2=\frac{{\mathbf{W}}_1{\mathbf{f}}_1+{\mathbf{g}}_1{\mathbf{W}}_3}{2},{\mathbf{f}}_3=\frac{{\mathbf{W}}_1{\mathbf{f}}_2+{\mathbf{g}}_2{\mathbf{W}}_3+{\mathbf{g}}_1{\mathbf{W}}_3{\mathbf{f}}_1}{3},\hfill \\ \hfill & {\mathbf{f}}_4=\frac{{\mathbf{W}}_1{\mathbf{f}}_3+{\mathbf{g}}_3{\mathbf{W}}_3+{\mathbf{g}}_2{\mathbf{W}}_3{\mathbf{f}}_1+{\mathbf{g}}_1{\mathbf{W}}_3{\mathbf{f}}_2}{4}\hfill \end{array}(\mathrm{12a})$

$\begin{array}{ll}\hfill {\mathbf{e}}_1& =-{\mathbf{W}}_4,{\mathbf{e}}_2=\frac{{\mathbf{W}}_3{\mathbf{g}}_1-{\mathbf{e}}_1{\mathbf{W}}_4}{2},{\mathbf{e}}_3=\frac{{\mathbf{W}}_3{\mathbf{g}}_2+{\mathbf{e}}_1{\mathbf{W}}_3{\mathbf{g}}_1-{\mathbf{e}}_2{\mathbf{W}}_4}{3},\hfill \\ \hfill & {\mathbf{e}}_4=\frac{{\mathbf{e}}_1{\mathbf{W}}_3{\mathbf{g}}_2+{\mathbf{e}}_2{\mathbf{W}}_3{\mathbf{g}}_1+{\mathbf{W}}_3{\mathbf{g}}_3-{\mathbf{e}}_3{\mathbf{W}}_4}{4}\hfill \end{array}(\mathrm{12b})$

$\begin{array}{ll}\hfill {\mathbf{g}}_1& =-{\mathbf{W}}_2,{\mathbf{g}}_2=\frac{-{\mathbf{g}}_1{\mathbf{W}}_4+{\mathbf{W}}_1{\mathbf{g}}_1}{2},{\mathbf{g}}_3=\frac{-{\mathbf{g}}_2{\mathbf{W}}_4+{\mathbf{W}}_1{\mathbf{g}}_2+{\mathbf{g}}_1{\mathbf{W}}_3{\mathbf{g}}_1}{3},\hfill \\ \hfill & {\mathbf{g}}_4=\frac{{\mathbf{W}}_3{\mathbf{g}}_3+{\mathbf{g}}_1{\mathbf{W}}_3{\mathbf{g}}_2+{\mathbf{g}}_2{\mathbf{W}}_3{\mathbf{g}}_1-{\mathbf{g}}_3{\mathbf{W}}_4}{4}\hfill \end{array}(\mathrm{12c})$

$\begin{array}{ll}\hfill {\mathbf{\phi }}_1& =-{\mathbf{W}}_3,{\mathbf{\phi }}_2=-\frac{{\mathbf{W}}_3{\mathbf{f}}_1+{\mathbf{e}}_1{\mathbf{W}}_3}{2},{\mathbf{\phi }}_3=-\frac{{\mathbf{W}}_3{\mathbf{f}}_2+{\mathbf{e}}_2{\mathbf{W}}_3+{\mathbf{e}}_1{\mathbf{W}}_3{\mathbf{f}}_1}{3},\hfill \\ \hfill & {\mathbf{\phi }}_4=-\frac{{\mathbf{W}}_3{\mathbf{f}}_3+{\mathbf{e}}_3{\mathbf{W}}_3+{\mathbf{e}}_1{\mathbf{W}}_3{\mathbf{f}}_2+{\mathbf{e}}_2{\mathbf{W}}_3{\mathbf{f}}_1}{4}\hfill \end{array}(\mathrm{12d})$

Subsequently, we merge the adjacent micro layers into a new micro layer, termed as micro layer 3. The following expression is defined as follows:

${\mathbf{V}}_c={\mathbf{F}}_3{\mathbf{V}}_a-{\mathbf{G}}_3{\mathbf{U}}_c(\mathrm{13a})$

${\mathbf{U}}_a={\mathbf{Q}}_3{\mathbf{V}}_a+{\mathbf{E}}_3{\mathbf{U}}_c(\mathrm{13b})$

in which

${\mathbf{F}}_3={\mathbf{F}}_2{\left(\mathbf{I}+{\mathbf{G}}_1{\mathbf{Q}}_2\right)}^{-1}{\mathbf{F}}_1(\mathrm{14a})$

${\mathbf{E}}_3={\mathbf{E}}_1{\left(\mathbf{I}+{\mathbf{Q}}_2{\mathbf{G}}_1\right)}^{-1}{\mathbf{E}}_2(\mathrm{14b})$

${\mathbf{G}}_3={\mathbf{G}}_2+{\mathbf{F}}_2{\left({\mathbf{G}}_1^{-1}+{\mathbf{Q}}_2\right)}^{-1}{\mathbf{E}}_2(\mathrm{14c})$

${\mathbf{Q}}_3={\mathbf{Q}}_1+{\mathbf{E}}_1{\left({\mathbf{Q}}_2^{-1}+{\mathbf{G}}_1\right)}^{-1}{\mathbf{F}}_1(\mathrm{14d})$

Thus far, we have derived the expression for the state vector of the newly formed micro layer as given in Equations 11–14. It is important to note that the system was initially divided into 2^N micro layers. Consequently, each application of the merging operation to adjacent micro layers reduces the total count by half, resulting in 2^N−1 remaining micro layers, each sharing identical expressions. The discretized micro layers can be recombined into a new layer block, and the corresponding generalized state vector can also be obtained similarly.

Following these operations, the generalized state vectors of the layer blocks are determined using ${\mathbf{W}}_i\left(i=1-5\right)$ specified in Equation 8. Under external loading, the entire system is partitioned into three-layer blocks defined by loading plane $H_p$ and calculation plane $H_c$. Detailed procedures are elaborated in references (Ye et al., 2023). Upon incorporating boundary conditions, solutions for the unsaturated consolidation are obtained. Notably, the unsaturated medium model features a permeable top boundary for pore water and pore air, while the bottom is impermeable to both. Thus, we have ${\sigma }_w\left(r,0\right)={\sigma }_a\left(r,0\right)=0$ and $\frac{\partial {\sigma }_w\left(r,0\right)}{\partial z}=\frac{\partial {\sigma }_a\left(r,0\right)}{\partial z}=0$. In terms of the external load, we define the ramping loads and exponential loads as follows:

The ramping loads in the physical domain and transformed domain are given in Equation 15:

$q\left(z,r,t\right)=\left\{\begin{array}{l}\frac{q_{0}t}{t_0}0<t<t_0\\ q_{0}t\ge t_0\end{array}\right.0<r<r_0(\mathrm{15a})$

$q\left(z,\xi ,s\right)=\frac{q_0{r}_0\left(1-{\mathrm{e}}^{-s*t_0}\right)}{t_0\xi s^2}{J}_1\left(\xi r_0\right)(\mathrm{15b})$

The exponential loads in the physical domain and transformed domain are given in Equation 16:

$q\left(z,r,t\right)=q_0\left(1-{\mathrm{e}}^{-a*t}\right)0<r<r_0(\mathrm{16a})$

$q\left(z,\xi ,s\right)=\frac{q_0{r}_0}{\xi s}{J}_1\left(\xi r_0\right)-\frac{q_0{r}_0}{\xi \left(s+a\right)}{J}_1\left(\xi r_0\right)(\mathrm{16b})$

It is noteworthy that the solution obtained is situated in the transformed domain, while the actual solution in the physical domain still requires implementation through numerical inversion. The Laplace inverse transform adopts the Stehfest method (Stehfest, 1970), and its specific expression is given in Equation 17:

$f\left(t\right)=\frac{\ln 2}{t}{\displaystyle \sum _{i=1}^N}{V}_i\overline{f}\left(\frac{i\ln 2}{t}\right)(\mathrm{17a})$

$V_i={\left(-1\right)}^{N/2+1}\times {\displaystyle \sum _{k=\left(i+1\right)/2}^{\min \left(i,N/2\right)}}\frac{k^{N/2+1}\left(2k\right)!}{\left(N/2-k\right)!k!\left(k-1\right)!\left(i-k\right)!\left(2k-i\right)!}(\mathrm{17b})$

in which, the precision control variable N is set to 12.

Using the Hankel inverse transform, every two adjacent zeros of the Bessel function are grouped into sections, reducing the semi-infinite integral to 64 segments. Each segment is then evaluated using the 32-point Gauss-Legendre integration method, as detailed in reference (Ye et al., 2023). Following the numerical Laplace-Hankel inverse transformation, we can obtain the solution for the fully coupled consolidation of unsaturated soils under time-varying loads in the real domain.

2.4 Verification

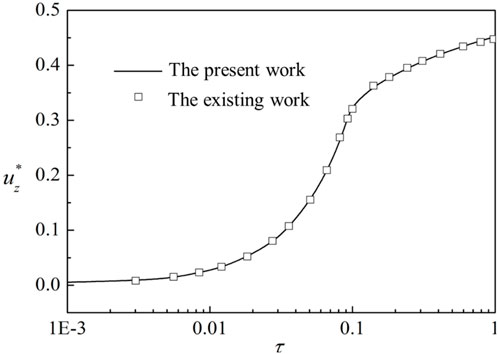
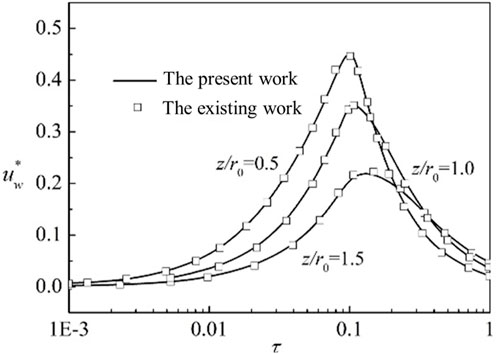
In view of the lack of fully coupled consolidation solution of axisymmetric unsaturated soil under variable load at present, this paper compares it with the consolidation solution of saturated soil under construction load in reference (Geng and Cai, 2009), and the results are shown in Figures 2, 3. By comparison, it can be seen that solution in this work is in good coincidence with solution in reference (Geng and Cai, 2009) in both settlement and pore pressure.

Figure 2

Figure 2. The variation of settlement against time under a ramp loading.

Figure 3

Figure 3. The variation of excess pore water pressure against time under a ramp loading.

3 Parametric analyses

3.1 The ramping time

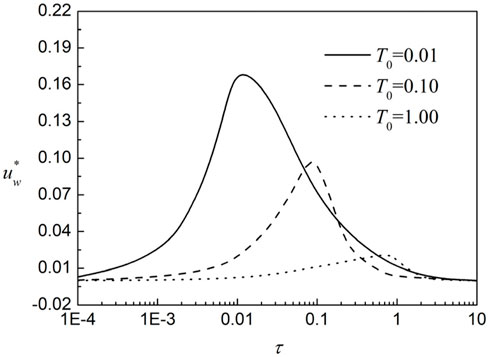
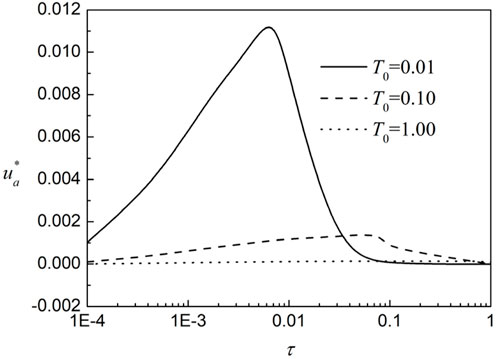
The subsequent analysis presents a series of numerical examples to examine the influence of ramping time $T_0$, the transverse isotropy of the permeability, the volume variation coefficient $m_1^s$ of pore water regarding the net stress ${\sigma }_{mean}$, and stratification on the flow-deformation characteristics of unsaturated soils through numerical examples. The calculation model is an unsaturated medium with the finite thickness 100 m. The surface of the medium is applied by a uniform vertical circular ramping load with a diameter $d_0=2r_0$ of and strength of $q_0$. The main parameters defining the original case are: porosity n=0.5, saturation degree $S_r=0.8$ Poisson’s ratio $\mu =1/3$, $m_1^s=0.25{\text{MPa}}^{-1}$, $m_2^s/m_1^s=0.4$, $m_1^w/m_1^s=0.2$, $m_2^w/m_1^s=0.8$, $k_w^h/k_w^z=1$, $k_a^h/k_a^z=1$. The dimensionless parameters of settlement and time are $u_z^{*}=u_z/m_1^s{q}_0{d}_0$ and $T=k_w^{z}t/m_1^s{\gamma }_w{r_0}^2$, respectively, while the dimensionless parameters of excess pore water and air pressure are $u_w^{*}=u_w/q_0$ and $u_a^{*}=u_a/q_0$, respectively, and the dimensionless construction time is $T_0=0.1$. In the following work, the calculation point of settlement is the origin, that is, r = 0, z = 0, and the calculation point of excess pore water and air pressure is r = 0, z = 0.5.

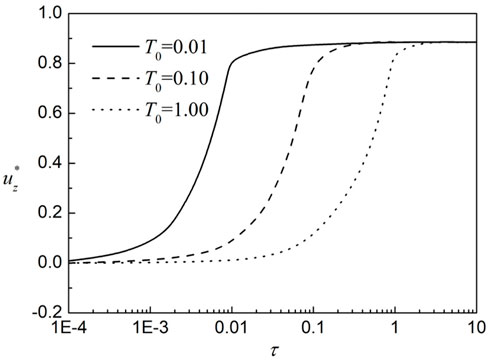
The influence of ramping time on the time-varying properties of unsaturated soil consolidation is discussed in the following. As can be seen from Figure 4: for different ramp times T₀, the final consolidation settlement is the same. Hence, the final settlement is not related to the ramp times. In the logarithmic coordinate system, most of the consolidation settlement occurs in the three sections of $\tau$ =0.001–0.01, 0.01–0.1, and 0.1-1, respectively. The less construction time T₀, the earlier time of the main settlement. For examples, the main settlement of the case $T_0=0.01$ appears when $\tau$ =0.001–0.01. When the dimensionless time is $\tau =T_0$, the settlement is basically stable, that is, most of the consolidation settlement is completed before the end of construction. Figure 5 depicts the varying law curve of excess pore water pressure over time under different load construction times T₀. It is shown in Figure 5, as the ramp time T₀ increases, the peak pore water pressure becomes lower and lower, and appears later and later. This is because the loading process is quite slow, and the pore pressure has been roughly dissipated when the construction is completed. Also, the peak excess pore water pressure is always found around the dimensionless construction time T₀. In terms of the pore air pressure dissipation curve in Figure 6, there is a significant value difference between it and the water pressure dissipation curve. The reason is that the air pressure dissipates very quickly, and most of the air has been completely discharged as the load increases. In addition, when $T_0=1$, the pore air pressure throughout the consolidation process is basically 0, so it is necessary to consider its existence only when the construction process is quite quick.

Figure 4

Figure 4. The variation of settlement against time with different ramp time T₀.

Figure 5

Figure 5. The variation of excess pore water pressure against time with different ramp time T₀.

Figure 6

Figure 6. The variation of excess pore air pressure against time with different ramp time T₀.

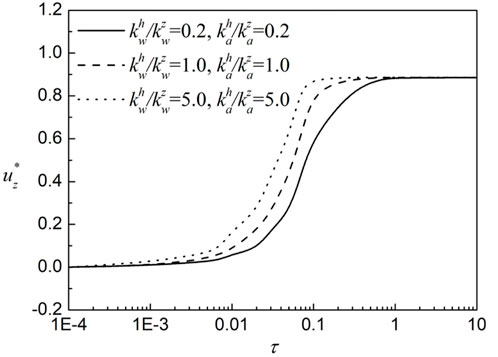
3.2 The transverse isotropy of the permeability

To investigate the influence of the transverse isotropy of the permeability on the flow-deformation behavior, four transverse isotropy coefficient cases $\frac{k_w^h}{k_w^z}=\frac{k_a^h}{k_z^z}=0.2,1,5$ are provided in this section, when $k_w^z$ and $k_a^z$ remain unchanged. Figures 7–9 show the variation of the settlement, the excess pore water and air pressure against the normalized time t. It is found from Figure 5 that the variation cure of case $k_w^h/k_w^z=5$ and $k_a^h/k_a^z=5$ is the earliest case to start the settlement and the earliest case to reach the final settlement. The larger the transverse isotropy coefficient $k_w^h/k_w^z$ and $k_a^h/k_a^z$, the faster the consolidation is completed. Meanwhile, the value of the final settlement is the same. In terms of the excess pore pressure, whether for the water pressure or the air pressure, the peak value decreases with increasing transversely isotropic coefficient. The reason is attributed to that the higher horizontal permeability of soils determines a smoother and more convenient drainage channel. The excess pore pressure of soils with a higher horizontal permeability is easier to dissipate under the external load. Hence, it is quite important to introduce the influence of the transversely isotropic permeability on the consolidation behavior of soils.

Figure 7

Figure 7. The variation of the settlement under different transversely isotropic permeability.

Figure 8

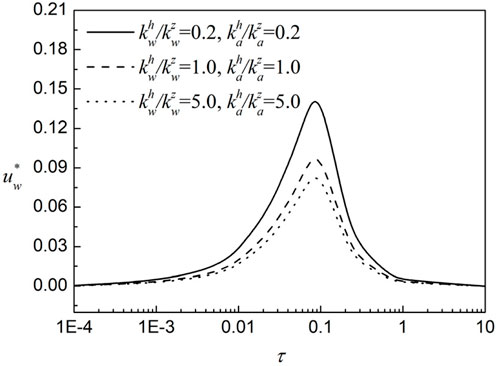
Figure 8. The variation of the excess pore water pressure under different transversely isotropic permeability.

Figure 9

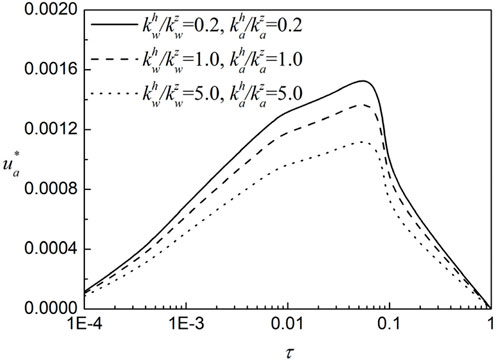
Figure 9. The variation of the excess pore air pressure under different transversely isotropic permeability.

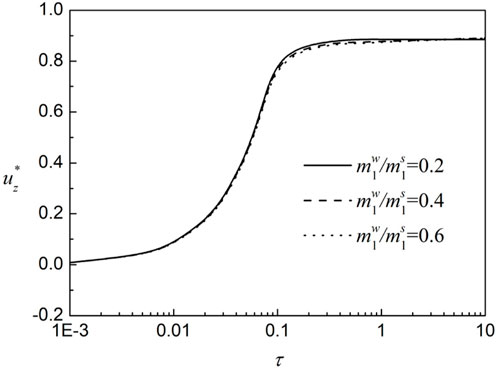
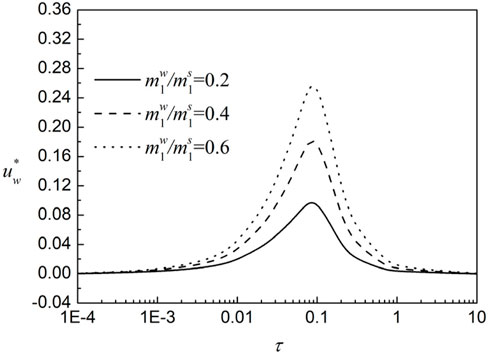
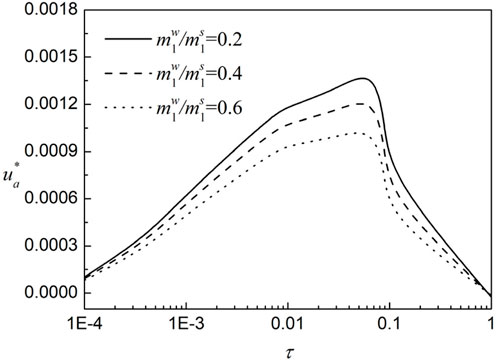
3.3 The volume variation coefficient of pore water regarding the net stress $m_1^w$

In order to discuss the effect of the volume variation coefficient of pore water regarding the net stress $m_1^w$ on the consolidation characteristics of unsaturated soil, the designed case is $m_1^w/m_1^s=0.2,0.4,0.6$, T₀=0.1, and the calculation results are shown in Figures 10–12. It is found in Figure 10 that the settlement in the unsaturated consolidation process is not greatly affected by $m_1^w$. The reason is that $m_1^w$ is defined in the constitutive equation of pore water to describe the volume change of pore water under net stress. In comparison, the volume change of pore water is negligible compared with the soil skeleton deformation. Hence, the influence of $m_1^w$ on the settlement of soils is negligible. Figure 11 depicts the pore water pressure dissipation curve regarding time $\tau$, and found that the change of $m_1^w$ will not affect the time when the peak value appears. Meanwhile, curves of three cases reach the peak value at almost the same time $\tau =T_0$. The larger the volume variation coefficient of pore water regarding the net stress $m_1^w$, the greater the excess pore water pressure generated thereby. It is noteworthy that the time of three cases when the excess pore water pressure appears and dissipates are basically consistent. Figure 12 shows the variation of the excess pore air pressure against time $\tau$. Relatively speaking, since the external load is borne more by the water in the unsaturated soils, the pore air pressure decreases with the increase of $m_1^w/m_1^s$, as shown in Figure 12. Similarly, the time of three cases that the excess pore air pressure reaches the peak remains basically consistent, which is occurred before T₀.

Figure 10

Figure 10. The variation of settlement against time with different $m_1^w.$

Figure 11

Figure 11. The variation of excess pore water pressure against time with different $m_1^w$.

Figure 12

Figure 12. The variation of excess pore air pressure against time with different $m_1^w$.

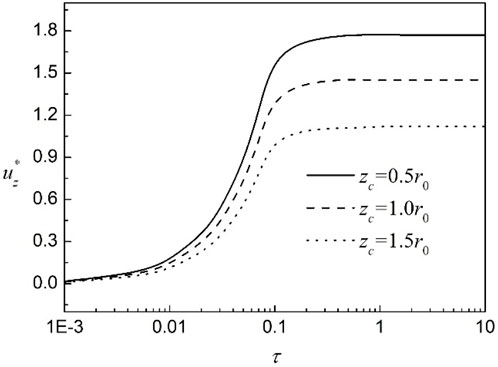
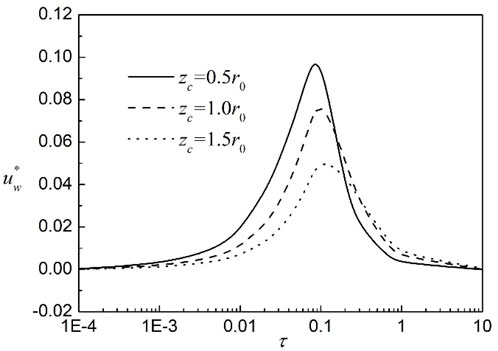
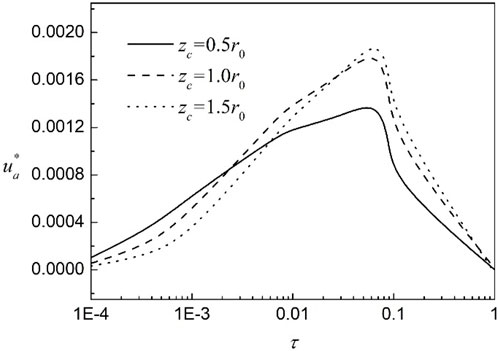
3.4 Calculation depth

The displacement and pore pressure shows a different trend along the depth. To describe the displacement development trend along the depth direction and the dissipation law of excess pore pressure and excess air pressure with time, the effect of calculation depth is discussed in this section. It can be seen from Figure 13 that the main development time of consolidation settlement is concentrated in this stage $\tau =0.01-0.1$ under the action of construction grading load, and after dimensionless time $\tau =T_0$, the settlement is basically stable, that is to say, most of the consolidation settlement will be completed before the end of construction. It is found that along the depth direction, the deeper the calculation point, the less the settlement. Meanwhile, when the construction load reaches the peak, the consolidation settlement basically does not develop. The peak value of pore water pressure also decreases with the increase of depth, and the peak value becomes later and later as shown in Figure 14. On the whole, they all rise to the peak with the increase of construction load, and then because the upper limit of load has been reached, the pore water pressure in the soil gradually dissipates completely with time. However, for the pore air pressure shown in Figure 15, there is a significant difference with the pore water pressure in magnitude. The reason is that compared with the pore water pressure, the air pressure dissipates quickly, and most of the air pressure caused by it has dissipated with the continuous increase of load. The closer to the surface, the smaller the peak pressure.

Figure 13

Figure 13. The variation of settlement against time along the depth.

Figure 14

Figure 14. The variation of excess pore water pressure against time along the depth.

3.5 Stratification

To illustrate the feasibility of the present solution to multilayered media, we constructed a multilayered soil with a soft interlayer (Case1) and compared it with a single-layer soil (Case 2) in which soil parameters, including modulus, permeability, and so on, were calculated by the weighted average method based on the parameters and thickness of layers in Case 1. The specific settlement, excess pore water and air pressure are shown in Figures 16–18. Parameters of the soil layer in Case 2 are the same as those in the original case except that the saturation is 0.73. Case 1 is a three-layer soil with a soft interlayer. The thickness ratio of each layer is 1:1:1, the ratio of the volume variation coefficient of the soil skeleton regarding the net stress (from top to bottom) is $m_1^{s1}:m_1^{s2}:m_1^{s3}=1:4:1$, and the saturation is 0.55, 0.78 and 0.86, respectively. The rest of the proportional relationship remains unchanged with reference to the that of Section 3.2. Meanwhile, the weighted average of the soil parameters of each layer in Case 1 regarding the layer thickness is exactly the single-layer soil parameters in Case 2. From the results, it is found that Case 1 with a soft interlayer is quite different from Case 2 in terms of settlement, pore water pressure and pore air pressure. Although there is a soft interlayer inside the case 1, soil properties of layers 1 and 3 in Case 2 are obviously weaker than those in Case 1. The reason is that the weighted average of the multi-layer soil parameters is consistent with that of the single-layer soil. The mechanics and permeability properties of the surface soil directly affect the evolution of the settlement and pore pressure dissipation within the soil. Therefore, the final steady-state settlement and peak excess pore pressure of Case 2 are significantly greater than those of Case 1. In fact, the settlement-pore pressure evolution law of the actual engineering must be combined with the soil layer parameter analysis obtained from the geology survey report. The results of this example are only to show the complexity of the flow-deformation consolidation law for layered unsaturated soils and prove the feasibility of the solution to the stratification in this work.

Figure 15

Figure 15. The variation of excess pore air pressure against time along the depth.

Figure 16

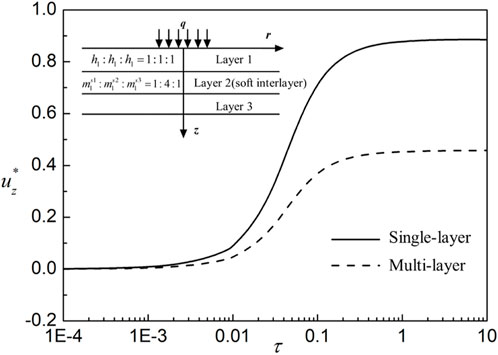
Figure 16. The variation of excess pore water pressure against time under multi-layered and single-layered cases.

Figure 17

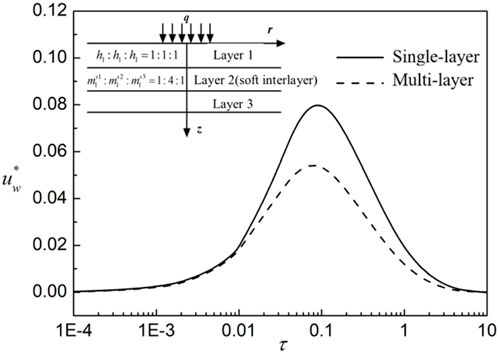
Figure 17. The variation of excess pore water pressure against time under multi-layered and single-layered cases.

Figure 18

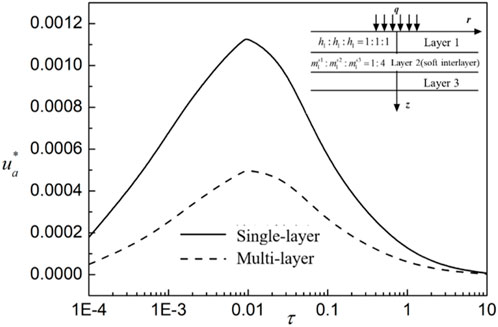
Figure 18. The variation of excess pore water pressure against time under multi-layered and single-layered cases.

4 Conclusion

Based on Fredlund’s dual stress variable theory, the fully-coupled axisymmetric consolidation governing equations of unsaturated soils is presented. With the aid of integration transform and precise integration method, proposed governing equations are solved, obtaining the solution in the actual domain. A series of numerical examples are provided to discuss the influence of the ramp time, $m_1^w$, and stratification. This work is expected to improve the fully-coupled consolidation theory, and revealed the time-dependent flow-deformation behavior of unsaturated media. Through the calculation result, the following conclusions can be obtained:

(1) Under time-varying loads, the dissipation rate of excess pore air pressure is significantly faster than that of excess pore water pressure, but its magnitude remains negligible in comparison.

(2) The ramping time T₀ does not affect the final steady-state settlement; it only influences deformation rates and alters pore pressure and air pressure dissipation during consolidation. A rapid loading velocity induce a surge of pore pressure.

(3) The volume variation coefficient of pore water regarding the net stress $m_1^w$ has no effect on the final consolidation settlement. However, reduced pore water compression leads to a notable increase in excess pore water pressure, though it does not affect the timing of the peak.

(4) The vertical displacement and excess pore water pressure along the depth shows a significant decrease, while the excess pore air pressure along the depth shows a unsignificant change.

(5) Stratification significantly influences the flow and deformation of unsaturated soils. Using a weighted average method to model multi-layer soil parameters in engineering analyses can result in substantial errors in the final settlement.

In the future work, we can further extend the axisymmetric condition to a three-dimensional condition. Meanwhile, the transverse isotropy of soil skeleton can also be considered in the future work to establish a more generalized consolidation model of unsaturated soils. Thea time-dependent soil-structure interaction investigation can also be considered based on the proposed model, which is meaningful for the long-time settlement prediction and control of underground structures in unsaturated soils, such as piles, plate and beam.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LS: Conceptualization, Formal Analysis, Methodology, Validation, Writing–original draft. BQ: Formal Analysis, Methodology, Visualization, Writing–review and editing. LL: Investigation, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Key Project of Natural Science Research Program of Anhui Provincial Education Department (No. 2023AH052494), and Open Foundation of Ma’ anshan Engineering Technology Research Center of Land Test evaluation and Restoration (No. TDJC24001).

Conflict of interest

Author LL was employed by China Construction Eighth Engineering Division Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ai, Z. Y., Cheng, Y. C., and Zeng, W. Z. (2011). Analytical layer-element solution to axisymmetric consolidation of multilayered soils. Comput. Geotech. 38 (2), 227–232. doi:10.1016/j.compgeo.2010.11.011

CrossRef Full Text | Google Scholar

Ai, Z. Y., and Wang, Q. S. (2008). A new analytical solution to axisymmetric Biot’s consolidation of a finite soil layer. Appl. Math. Mech.-Engl. 29 (12), 1617–1624. doi:10.1007/s10483-008-1209-9

CrossRef Full Text | Google Scholar

Ai, Z. Y., Wang, Q. S., and Han, J. (2010). Analytical solutions describing the consolidation of a multilayered soil under circular loading. J. Eng. Math. 66 (4), 381–393. doi:10.1007/s10665-009-9299-6

CrossRef Full Text | Google Scholar

Ai, Z. Y., and Zeng, W. Z. (2012). Analytical layer-element method for non-axisymmetric consolidation of multilayered soils. Int. J. Numer. Anal. Meth. Geomech. 36 (5), 533–545. doi:10.1002/nag.1000

CrossRef Full Text | Google Scholar

Aramaki, G. (1985). Application of the boundary element method for axisymmetric Biot's consolidation. Eng. Anal. 2 (4), 184–191. doi:10.1016/0955-7997(85)90002-5

CrossRef Full Text | Google Scholar

Ausilio, E., Connte, E., and Dente, G. (2002). “An analysis of the consolidation of unsaturated soils,” in Proceeding of the 3rd International Conference on Unsaturated Soils, London, 31 May 2021 (Recife), 239–251.

Google Scholar

Barden, L. (1965). Consolidation of compacted and unsaturated clays. Géotechnique 15 (3), 267–286. doi:10.1680/geot.1965.15.3.267

CrossRef Full Text | Google Scholar

Biot, M. A. (1941). General theory of three-dimensional consolidation. J. Appl. Phys. 12 (2), 155–164. doi:10.1063/1.1712886

CrossRef Full Text | Google Scholar

Biot, M. A. (1955). Theory of elasticity and consolidation for a porous anisotropic solid. J. Appl. Phys. 26 (2), 182–185. doi:10.1063/1.1721956

CrossRef Full Text | Google Scholar

Booker, J. R., and Randolph, M. F. (1984). Consolidation of a cross-anisotropic soil medium. Q. J. Mech. Appl. Math. 37 (3), 479–495. doi:10.1093/qjmam/37.3.479

CrossRef Full Text | Google Scholar

Booker, J. R., and Small, J. C. (1982). Finite layer analysis of consolidation II. Int. J. Numer. Anal. Meth. Geomech. 6 (2), 173–194. doi:10.1002/nag.1610060205

CrossRef Full Text | Google Scholar

Booker, J. R., and Small, J. C. (1987). A method of computing the consolidation behaviour of layered soils using direct numerical inversion of Laplace transforms. Int. J. Numer. Anal. Meth. Geomech. 11 (4), 363–380. doi:10.1002/nag.1610110405

CrossRef Full Text | Google Scholar

Cai, Y. Q., and Geng, X. Y. (2009). Consolidation analysis of a semi-infinite transversely isotropic saturated soil under general time-varying loadings. Comput. Geotech. 36 (3), 484–492. doi:10.1016/j.compgeo.2008.08.014

CrossRef Full Text | Google Scholar

Cao, Z., Jia, Y., Li, Z., and Du, F. (2023). Research on slurry diffusion and seepage law in mining overburden fractures based on CFD numerical method. Sci. Rep. 13 (1), 21302. doi:10.1038/s41598-023-48828-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, Z., Yang, X., Li, Z., Haung, C., Du, F., Wang, W., et al. (2024b). Fracture propagation and pore pressure evolution characteristics induced by hydraulic and pneumatic fracturing of coal. Sci. Rep. 14 (1), 9992. doi:10.1038/s41598-024-60873-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, Z., Yang, X., Zhang, P., Li, Z., Du, F., Wang, W., et al. (2024a). Experimental study on the fracture surface morphological characteristics and permeability characteristics of sandstones with different particle sizes. Energy Sci. Eng. 12 (7), 2798–2809. doi:10.1002/ese3.1768

CrossRef Full Text | Google Scholar

Chen, S. L., Zhang, L. M., and Chen, L. Z. (2005). Consolidation of a finite transversely isotropic soil layer on a rough impervious base. J. Eng. Mech. 131 (12), 1279–1290. doi:10.1061/(asce)0733-9399(2005)131:12(1279)

CrossRef Full Text | Google Scholar

Dakshanamurthy, V., and Fredlund, D. G. (1980). “Moisture and air flow in an unsaturated soil,” in Proceedings of the fourth international conference on expansive soils, Colorado, June 16-18, 1980 (Denver), 514–532.

Google Scholar

Dakshanamurthy, V., Fredlund, D. G., and Rahardjo, H. (1984). “Coupled three-dimensional consolidation theory of unsaturated porous media,” in Proceedings of the fifth international conference on expansive soils, Australia, 21-23 May 1984 (Adelaide), 99–103.

Google Scholar

Dargush, G. F., and Banerjee, P. K. (1991). A boundary element method for axisymmetric soil consolidation. Int. J. Solids Struct. 28 (7), 897–915. doi:10.1016/0020-7683(91)90007-3

CrossRef Full Text | Google Scholar

Fredlund, D., and Rahardjo, H. (1993). Soil mechanics for unsaturated soil. New York: John Wiley and Sons.

Google Scholar

Geng, X. Y., and Cai, Y. Q. (2009). Axisymmetric Biot consolidation of a semi-infinite isotropic saturated soil subjected to time-dependent loadings. Rock Soil Mech. 30 (8), 59–65. doi:10.16285/j.rsm.2009.08.039

CrossRef Full Text | Google Scholar

Gibson, R. E., Schiffman, R. L., and Pu, S. L. (1970). Plane strain and axially symmetric consolidation of a clay layer on a smooth impervious base. Q. J. Mech. Appl. Math. 23 (4), 505–520. doi:10.1093/qjmam/23.4.505

CrossRef Full Text | Google Scholar

Harnpattanapanich, T., and Vardoulakis, I. (1987). Numerical Laplace-Fourier transform inversion technique for layered soil consolidation problems, II. Gibson soil layer. Int. J. Numer. Anal. Meth. Geomech. 11 (1), 103–112. doi:10.1002/nag.1610110108

CrossRef Full Text | Google Scholar

Ho, L., Fatahi, B., and Khabbaz, H. (2014). Analytical solution for one-dimensional consolidation of unsaturated soils using eigenfunction expansion method. Int. J. Numer. Anal. Meth. Geomech. 38 (10), 1058–1077. doi:10.1002/nag.2248

CrossRef Full Text | Google Scholar

Ho, L., Fatahi, B., and Khabbaz, H. (2015). A closed form analytical solution for two-dimensional plane strain consolidation of unsaturated soil stratum. Int. J. Numer. Anal. Meth. Geomech. 39 (15), 1665–1692. doi:10.1002/nag.2369

CrossRef Full Text | Google Scholar

Ho, L., Fatahi, B., and Khabbaz, H. (2016). Analytical solution to axisymmetric consolidation in unsaturated soils with linearly depth-dependent initial conditions. Comput. Geotech. 74, 102–121. doi:10.1016/j.compgeo.2015.12.019

CrossRef Full Text | Google Scholar

Huang, M., and Li, J. (2018). Generalized analytical solution for 2D plane strain consolidation of unsaturated soil with time-dependent drainage boundaries. Comput. Geotech. 103, 218–228. doi:10.1016/j.compgeo.2018.07.012

CrossRef Full Text | Google Scholar

Liu, Y., Zheng, J., You, L., Lu, J., Cui, L., Yang, W., et al. (2022). An analytical solution for 2D plane strain consolidation in unsaturated soils with lateral and vertical semipermeable drainage boundaries under time-dependent loading. Int. J. Geomech. 22 (12), 06022032. doi:10.1061/(asce)gm.1943-5622.0002508

CrossRef Full Text | Google Scholar

Loret, B., and Khalili, N. (2000). A three-phase model for unsaturated soils. Int. J. Numer. Anal. Meth. 24 (11), 893–927. doi:10.1002/1096-9853(200009)24:11<893::aid-nag105>3.0.co;2-v

CrossRef Full Text | Google Scholar

McNamee, J., and Gibson, R. E. (1960). Plane strain and axially symmetric problem of the consolidation of a semi-infinite clay stratum. Q. J. Mech. Appl. Math. 13 (2), 210–227. doi:10.1093/qjmam/13.2.210

CrossRef Full Text | Google Scholar

Moradi, M., Keshavarz, A., and Fazeli, A. (2019). One dimensional consolidation of multi-layered unsaturated soil under partially permeable boundary conditions and time-dependent loading. Comput. Geotech. 107, 45–54. doi:10.1016/j.compgeo.2018.11.020

CrossRef Full Text | Google Scholar

Niu, J., Ling, D., Zhu, S., Gong, S., and Shan, Z. (2021). Solutions for one-dimensional consolidation of unsaturated soil with general boundary conditions subjected to time-dependent load. Int. J. Numer. Anal. Meth. Geomech. 45 (11), 1664–1680. doi:10.1002/nag.3219

CrossRef Full Text | Google Scholar

Pan, E. (1989). The static response of multilayered foundations to general surface loading and body force. Acta. Mech. Sin. 21 (3), 344–353.

Google Scholar

Pan, E. (1997). Static Green’s functions in multilayered half spaces. Appl. Math. Model. 21 (8), 509–521. doi:10.1016/s0307-904x(97)00053-x

CrossRef Full Text | Google Scholar

Pan, E. (1999). Green's functions in layered poroelastic half-spaces. Int. J. Numer. Anal. Meth. Geomech. 23 (13), 1631–1653. doi:10.1002/(sici)1096-9853(199911)23:13<1631::aid-nag60>3.0.co;2-q

CrossRef Full Text | Google Scholar

Qin, A., Sun, D., and Tan, Y. (2010). Analytical solution to one-dimensional consolidation in unsaturated soils under loading varying exponentially with time. Comput. Geotech. 37 (1), 233–238. doi:10.1016/j.compgeo.2009.07.008

CrossRef Full Text | Google Scholar

Schiffman, R. L., and Fungaroli, A. A. (1965). Consolidation due to tangential loads. Proc. 6th Int. Conf. Soil. Mech. Found. Eng. 1, 188–192.

Google Scholar

Senjuntichai, T., and Rajapakse, R. K. N. D. (1995). Exact stiffness method for quasi-statics of a multilayered poroelastic medium. Int. J. Solids Struct. 32 (11), 1535–1553. doi:10.1016/0020-7683(94)00190-8

CrossRef Full Text | Google Scholar

Shan, Z., Ling, D., and Ding, H. (2012). Exact solutions for one-dimensional consolidation of single-layer unsaturated soil. Int. J. Numer. Anal. Meth. Geomech. 36 (6), 708–722. doi:10.1002/nag.1026

CrossRef Full Text | Google Scholar

Singh, S. J., Rani, S., and Kumar, R. (2007). Quasi-static deformation of a poroelastic half-space with anisotropic permeability by two-dimensional surface loads. Geophys. J. Int. 170 (3), 1311–1327. doi:10.1111/j.1365-246x.2007.03497.x

CrossRef Full Text | Google Scholar

Stehfest, H. (1970). Algorithm 368: numerical inversion of Laplace transforms [D5]. Commun. ACM. 13 (1), 47–49. doi:10.1145/361953.361969

CrossRef Full Text | Google Scholar

Tian, Y., Wu, W., Jiang, G., Ei Naggar, M. H., Mei, G., Xu, M., et al. (2020). One-dimensional consolidation of soil under multistage load based on continuous drainage boundary. Int. J. Numer. Anal. Meth. Geomech. 44 (8), 1170–1183. doi:10.1002/nag.3055

CrossRef Full Text | Google Scholar

Vardoulakis, I., and Harnpattanapanich, T. (1986). Numerical Laplace-Fourier transform inversion technique for layered-soil consolidation problems, I. Fundamental solutions and validation. Int. J. Numer. Anal. Meth. Geomech. 10 (4), 347–365. doi:10.1002/nag.1610100402

CrossRef Full Text | Google Scholar

Wang, J., Shen, Q. S., Yuan, S., Wang, X. H., Shu, J. W., Zheng, J., et al. (2023b). A siphon drainage method for consolidation of soft soil foundation. Appl. Sci.-Basel. 13 (6), 3633. doi:10.3390/app13063633

CrossRef Full Text | Google Scholar

Wang, J. F., Yuan, M., Yin, X. X., Li, W. J., and Li, X. Y. (2023a). One-dimensional consolidation properties of soft clay under multi-stage loading. Appl. Sci.-Basel. 13 (18), 10340. doi:10.3390/app131810340

CrossRef Full Text | Google Scholar

Wang, J. G., and Fang, S. S. (2001). The state vector solution of axisymmetric Biot's consolidation problems for multilayered poroelastic media. Mech. Res. Commun. 28 (6), 671–677. doi:10.1016/s0093-6413(02)00218-5

CrossRef Full Text | Google Scholar

Wang, L., Sun, D., and Qin, A. (2017a). General semi-analytical solutions to one-dimensional consolidation for unsaturated soils. Appl. Math. Mech.-Engl. 38 (6), 831–850. doi:10.1007/s10483-017-2209-8

CrossRef Full Text | Google Scholar

Wang, L., Sun, D., Qin, A., and Xu, Y. (2017c). Semi-analytical solution to one-dimensional consolidation for unsaturated soils with semi-permeable drainage boundary under time-dependent loading. Int. J. Numer. Anal. Meth. Geomech. 41 (16), 1636–1655. doi:10.1002/nag.2694

CrossRef Full Text | Google Scholar

Wang, L., Sun, D., Qin, A., and Xu, Y. F. (2017b). Semi-analytical solution to one-dimensional consolidation for unsaturated soils with semi-permeable drainage boundary under time-dependent loading: semi-analytical Solution to Consolidation for Unsaturated Soil. Int. J. Geomech. 41, 1636–1655. doi:10.1002/nag.2694

CrossRef Full Text | Google Scholar

Wang, L., Xu, Y., Xia, X., and He, Y. (2019). Semi-analytical solutions of two-dimensional plane strain consolidation in unsaturated soils subjected to the lateral semipermeable drainage boundary. Int. J. Numer. Anal. Meth. Geomech. 43 (17), 2628–2651. doi:10.1002/nag.2986

CrossRef Full Text | Google Scholar

Ye, Z., Chen, Y., Kong, G., Chen, G., and Lin, M. G. (2023). 3D elastodynamic solutions to layered transversely isotropic soils considering the groundwater level. Comput. Geotech. 158, 105354. doi:10.1016/j.compgeo.2023.105354

CrossRef Full Text | Google Scholar

Yue, Z. Q. (1996). On elastostatics of multilayered solids subjected to general surface traction. Quart. J. Mech. Appl. Math. 49 (3), 471–499. doi:10.1093/qjmam/49.3.471

CrossRef Full Text | Google Scholar

Yue, Z. Q., Selvadurai, A. P. S., and Law, K. T. (1994). Excess pore pressure in a poroelastic seabed saturated with a compressible fluid. Can. Geotech. J. 31 (6), 989–1003. doi:10.1139/t94-113

CrossRef Full Text | Google Scholar

Yue, Z. Q., and Yin, J. H. (1998). Backward transfer-matrix method for elastic analysis of layered solids with imperfect bonding. J. Elast. 50 (2), 109–128. doi:10.1023/a:1007421014760

CrossRef Full Text | Google Scholar

Zhong, W. X. (1994). Precise time-integration method for structural dynamic equation. J. Dalian Univ. Tech. 34 (2), 131–136.

Google Scholar

Zong, M., Wu, W., Ei Naggar, M. H., Mei, G., Ni, P., and Xu, M. (2020). Analytical solution for one-dimensional nonlinear consolidation of double-layered soil with improved continuous drainage boundary. Eur. J. Envrion. Civ. En. 27 (8), 2746–2767. doi:10.1080/19648189.2020.1813207

CrossRef Full Text | Google Scholar