- College of Civil and Architectural Engineering, North China University of Science and Technology, Tangshan, Hebei, China
The earth pressure of slope retaining structure is one of the problems that are often encountered in geotechnical engineering but have not yet been fully understood and well solved. At present, there are still a lot of problems that need to be solved. For complex conditions such as stratified soil or containing ground water, the distribution law of earth pressure and the displacement mode of retaining structure need to be further studied. This paper summarizes the existing research on earth pressure of slope retain structures. According to the research methods, it is divided into three categories: research on the theoretical calculation method of earth pressure, research on earth pressure by model test, and research on earth pressure by numerical simulation. Focused discussions are carried out respectively, and the previous research results are summarized. At present, there are still a lot of problems that need to be solved in the research of earth pressure of slope retaining structure, and the calculation formula of earth pressure and the assumed fracture surface of earth are lack of experimental verification and engineering measurement.
1 Introduction
With the development of engineering construction, the problems encountered in geotechnical engineering are becoming more and more complex, which poses a challenge to classical soil mechanics and also a great test to geotechnical engineers. Earth pressure on retaining structures is a classical subject in soil mechanics. The traditional Rankine earth pressure theory and Coulomb earth pressure theory sometimes have large calculation errors due to too many assumptions and the limitation of applicable conditions. Many experts and scholars have carried out more in-depth research on the earth pressure on various forms of retaining structures. In this paper, the existing research on the earth pressure on retaining structures is summarized. And put forward some suggestions aim at that deficiency of the existing research. In theoretical investigations of earth pressure, and the simplified assumptions of the model should be as reasonable as possible, such as the form of soil sliding surface, the angle of soil fracture, and whether the rigidity of the assumed retaining structure meets the needs of the project. Numerical simulation of earth pressure can directly observe the distribution form of earth pressure, but there are certain requirements for grid division, and numerical simulation results are usually used to verify the test or theoretical results. The model test method can obtain the actual observation of displacement, stress and other data, and can intuitively study the displacement pattern of retaining wall, but the reasons for the different displacement patterns need to be further studied.
2 Study on theoretical calculation method of earth pressure
The derivation of earth pressure calculation method is an important way to study earth pressure. Many scholars have studied it and put forward a variety of calculation methods. This paper summarizes the existing calculation methods of earth pressure of slope retaining structure.
Based on the ultimate equilibrium theory and the assumption of plane sliding surface, Ma et al. (2008) deduced the Formula 1 for calculating the active earth pressure of the finite soil between two walls and the expression of the failure angle of the sliding surface of the soil by assuming that the soil is a rigid-plastic body, not considering the friction between the soil and the retaining structures, and considering the cohesion of the soil. The formula shows that the failure angle of sliding surface of finite soil is not a constant value 45° + φ/2, but a variable related to the calculation depth, soil internal friction angle, soil cohesion and finite soil width. It also points out that the active earth pressure of finite soil is less than Rankine active earth pressure, the Rankine earth pressure causes the calculated earth pressure to be greater than the actual value, resulting in unnecessary waste. The strength of active earth pressure of finite soil has a nonlinear distribution with depth.
Based on the equilibrium theory of sliding wedge, Li and Guo (2008) established a formula (Formula 2) for calculating the earth pressure of the finite soil between two walls, assuming that the soil is cohesive soil, considering the friction between the wall and the soil, considering the adhesion force behind the wall, and considering the uniform load on the top of the soil. The assumption that the soil is treated as a rigid body and the interaction between piles and soil is not taken into account can lead to biased calculation results and waste of materials in engineering design.
When the width of the finite soil is less than or equal to 0.5–0.75 times of the depth of the pit, the calculation model of the earth pressure of the finite soil should be considered. In addition, the author also noticed that when the depth of the foundation pit is greater than the depth of the basement of the adjacent building, the superposition of the finite soil above the depth of the foundation pit of the existing building and the semi-infinite soil below the depth of the foundation pit of the existing building needs further consideration.
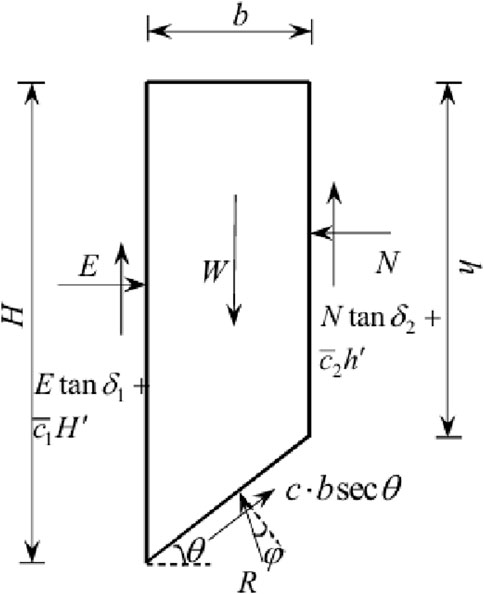
Wang et al. (2014) assumed that the sliding surface of the soil was a plane, considered the cohesion of the soil, and considered the normal and tangential interaction forces between the soil and the retaining wall and the foundation of the existing building. As shown in Figure 1, it is assumed that the earth pressure of finite soil is still distributed along the depth triangle. The calculation Formula 3 of finite soil pressure under this condition is obtained, and the results are compared with the finite element results, which confirms that this method is closer to the finite element solution. Wang Hongliang also pointed out the special situation when the cohesion between the retaining wall and the soil exceeds the gravity of the finite soil, and provided the applicable formula in this case. However, the angle of the sliding surface of the soil is simplified, and the fixed value of 45° + ϕ/2 is still used.
Among
Pang et al. (2009) based on the Coulomb earth pressure plane slip surface assumption, used the limit equilibrium method to derive the calculation formula of the passive earth pressure of the limited soil reserved in front of the wall when the central island method was used to excavate the foundation pit. The calculation results were compared with the finite element results, which showed that when the internal friction angle of the soil and the friction angle of the wall are small, the error was small, and the calculation formula met the engineering needs.
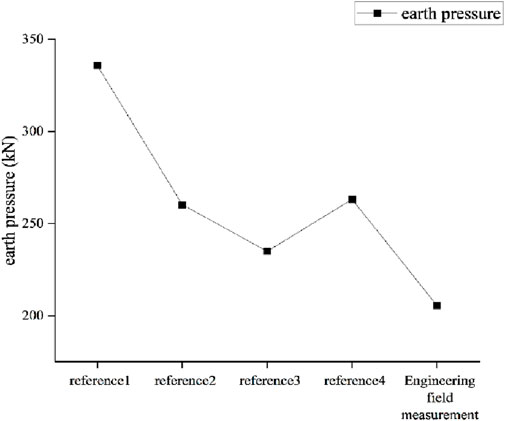
The study of theoretical calculation method of earth pressure is to establish an idealized model through appropriate simplified assumptions of engineering practice. According to the model, the calculation formula of earth pressure is obtained through theoretical derivation. When simplifying assumptions, it should be reasonable and as close as possible to the engineering practice. For example, the form of the assumed sliding surface of the soil should be verified by tests or retained by data provided by engineering measurements. As shown in Figure 2, the references from 1 to 4 are calculated and compared with the real-world data. It is shown that the reference 3 is approaching actual engineering values. That is to say the reference 3 is much more reasonable compared with another three references. Currently, the research assumes the retaining structure to be rigid, and the earth pressure law under the condition of the interaction between the retaining structure and the soil and the coordinated deformation can be further studied.
3 Study on earth pressure by numerical simulation method
With the development of computer technology, more and more attention has been paid to numerical simulation technology. Numerical simulation method can not only simulate the complex engineering environment, but also observe the failure mode intuitively, which is favored by researchers. However, this method has high requirements for the selection of parameters and the division of the grid. In some cases, the calculation results are deviated greatly because of the failure of convergence. At this time, other methods are needed to test the results.
Fan and Fang (2010) used the nonlinear finite element program PLAXIS to analyze the earth pressure of the rigid retaining wall near the stable rock surface from static to active conditions, and studied the acting position and distribution characteristics of the finite soil earth pressure between the rigid retaining wall and the stable rock surface. The effects of wall height and friction angle on the magnitude and location of earth pressure are also studied. The results show that the active earth pressure of finite soil is far less than the Coulomb earth pressure, and the active earth pressure position of finite soil is significantly higher than 1/3 of the wall height. The active earth pressure coefficient decreases and the active earth pressure position rises with the increase of the slope angle of the stable rock surface.
Wu et al. (2023) used FLAC3D software to establish a three-dimensional digital model of the retaining wall and the finite slope soil, simplify piles into beam elements and slopes into solid element sand verified the validity of the three-dimensional digital model through the change law of the inclination angle of the sliding plane of the finite slope soil and the change law of the passive earth pressure of the finite slope soil with the depth of the soil behind the wall. Then the model is used to simulate and analyze the influence of the parameters of retaining wall, such as soil parameters, slope angle and plaorm width on the earth pressure under the condition of translation. The simulation results show that with the increase of the plaorm width, the slope angle of the sliding surface of the finite slope decreases to zero at first and then increases gradually; the passive earth pressure presents a nonlinear distribution, and the active earth pressure presents a convex curve distribution.
Li and Zhou (2017) used the finite element analysis software ANSYS to study the earth pressure of the passive non-limit state of the translational extrusion of the retaining wall. The results show that the soil near the back of the wall forms a relative displacement area similar to an inverted trapezoid, and there are horizontal and vertical displacement differences between adjacent points in the area. The horizontal length of the relative displacement area (2 ∼ 3) is the height of the wall, and the larger the wall displacement is, the larger the relative displacement area is. The distribution of non-limit state passive earth pressure of retaining wall in translation mode is similar to a straight line. When the earth pressure transits from the static state to the passive limit state, the growth rate of the total value of the horizontal passive earth pressure gradually slows down, and its value is always less than the Coulomb passive earth pressure. The larger the friction angle of backfill is, the larger the passive earth pressure of non-limit state is.
The visual failure mode of finite soil and the distribution curve of earth pressure can be obtained by numerical simulation, aiding in deriving formulas for earth pressure calculation, and can also be engineering design and practical applications to verify its correctness.
4 Study on earth pressure of soil by model test method
The model test method is to use similar materials, reduce the actual project to a certain proportion, simulate the actual construction process, and monitor the soil pressure and other parameters. Through the model test, we can intuitively get valuable experimental phenomena, and many scholars have carried out related research.
Frydman and Keissar (1987) conducted centrifuge model tests on a rigid retaining wall near a vertical rigid boundary to observe the change of earth pressure behind the wall from static to active conditions. The retaining wall is made of aluminum, allowing the wall to rotate around its base. The test results show that the distribution of active earth pressure is not triangular. The active earth pressure coefficient decreases significantly with depth. The location of active earth pressure is more than one third of the wall height.
Fang and Ishibashi (1986) and Khosravi et al. (2013) carried out the model test of rigid retaining wall under the mode of translational movement. The results show that the distribution of earth pressure on the retaining wall is related to the mode of movement of the retaining wall, and the classical theory can not describe this phenomenon. The distribution of active earth pressure on retaining wall is parabolic in translation mode.
Cai (2020), Zhang et al. (2024) and Luo et al. (2022) studied the failure process and failure mode of active limit state of finite cohesionless soil with different widths in translational mode through the model test of movable retaining wall. The test results show that the compression of the soil width increases the inclination angle of the failure slip surface; when the soil width is small enough, the failure slip surface develops to the wall surface and then reflects to form the second slip surface, which develops to the soil surface. According to the different failure modes in the test results, the corresponding earth pressure calculation model is established, and the calculation method of the earth pressure of the finite width cohesionless fill under the translational displacement mode is derived according to the limit equilibrium method. The calculation results are compared with the existing test data to verify its applicability.
In addition, the slope gradient also has a significant impact on stability. Fang et al. (2022); Pipatpongsa et al. (2024); Fang et al. (2023) conduct a series of physical model experiments on arched slopes with different slope angles, a physical slope model under excavation is analysed through multi-field monitoring.
5 Conclusion and prospect
Due to the need of engineering, many experts and scholars have studied the earth pressure of slope retaining structure with different methods. The existing classical earth pressure theory can not meet the requirements of engineering safety and economy. How to calculate the earth pressure more accurately and reasonably has become an important and urgent subject. The paper provides a comprehensive review of existing research results based on three aspects: derivation of earth pressure calculation methods, investigation of earth pressure through model test methods, and study of earth pressure using numerical simulation methods, according to different research methodologies.
Through reading the literature, it is found that the existing research has the following shortcomings, In response to existing shortcomings, the following directions for follow-up research were identified.
(1) The delineation boundary between finite and semi-infinite soils is vague, and it is controversial how to correctly define finite soils; subsequent scholars can give the delineation conditions of finite and infinite soils and verify the correctness of the delineation conditions through experiments.
(2) The existing calculation methods based on Rankine semi-infinite soil pressure theory have the problems of insufficient calculation accuracy, too conservative and poor economy. In the future, when the theoretical study of earth pressure is conducted, efforts should be made to reduce the assumptions, improve the calculation accuracy, and increase the practical value of the calculation method. For the unavoidable simplified assumptions, the reasonableness and error of their assumptions should be supported by engineering real measurements or model tests.
(3) Existing studies using the limit equilibrium method assume that the soil sliding surface is planar, but there is a lack of engineering examples to verify, advanced multi-field monitoring system can be used to obtain the measured data, including the shape of the soil sliding surface, the angle of the sliding surface, and the effect of the change of the soil parameters on the soil sliding surface, in order to verify the reasonableness of the computational model.
(4) Most of the existing studies are aimed at homogeneous soil, without considering the impact of groundwater, and the earth pressure of heterogeneous soil and the existence of groundwater needs further study.
(5) The existing studies assume that the retaining structure is rigid, which is different from the actual situation. Subsequent scholars can consider the coordinated deformation between the retaining structure and the soil, which is closer to the actual situation.
Author contributions
YZ: Writing–original draft. HW: Conceptualization, Investigation, Methodology, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the 2023 Tangshan Basic Research Project (23130214E). Research on Digital Protection and Utilization of World Cultural Heritage Site Qing dong Mausoleum (ZD202120).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Cai, Y. L. (2020). Model test study on active earth pressure of retaining wall with limited space cohesionless backfill in translational movement mode. Highway 65 (05), 65–69.
Fan, C. C., and Fang, Y. S. (2010). Numerical solution of active earth pressures on rigid retaining walls built near rock faces. Comput. and Geotechnics 37 (7-8), 1023–1029. doi:10.1016/j.compgeo.2010.08.004
Fang, K., Miao, M. H., Tang, H. M., Dong, A., Jia, S., An, P., et al. (2022). Model test on deformation and failure behaviour of arching-type slope under excavation condition. Eng. Geol. 302, 106628–106717. doi:10.1016/j.enggeo.2022.106628
Fang, K., Miao, M. H., Tang, H. M., Jia, S., Dong, A., An, P., et al. (2023). Insights into the deformation and failure characteristic of a slope due to excavation through multi-field monitoring: a model test. Acta Geotech. 18 (18), 1001–1024. doi:10.1007/s11440-022-01627-0
Fang, Y. S., and Ishibashi, I. (1986). Static earth pressures with various wall movements. J. Geotechnical Eng. 112 (3), 317–333. doi:10.1061/(asce)0733-9410(1986)112:3(317)
Frydman, S., and Keissar, I. (1987). Earth pressure on retaining walls near rock faces. J. Geotechnical Eng. 113 (6), 586–599. doi:10.1061/(asce)0733-9410(1987)113:6(586)
Khosravi, M. H., Pipatpongsa, T., and Takemura, J. (2013). Experimental analysis of earth pressure against rigid retaining walls under translation mode. Géotechnique 63 (12), 1020–1028. doi:10.1680/geot.12.p.021
Li, F., and Guo, Y. C. (2008). Calculation and analysis of active earth pressure of finite soil mass in foundation pit engineering. Sci. Archit. (01), 15–18.
Li, Y. G., and Zhou, H. Z. (2017). Finite element analysis of non-limit state passive earth pressure of retaining wall in translation mode. Shanxi Water Sci. Technol. (04), 1–2 + 38.
Luo, Q., Huang, Y., Zhao, J. W., Guo, Z. R., Xiong, S. J., and Zhang, L. (2022). Centrifuge model test on soil fracture surface and earth pressure characteristics of balance weight retaining wall. Chin. J. Geotechnical Eng. 44 (11), 1968–1977.
Ma, P., Qin, S. Q., and Qian, H. T. (2008). Calculation of active earth pressure of finite soil. Chin. J. Rock Mech. Eng. (Suppl. 1), 3070–3074.
Pang, X. C., Liu, G. N., and Chen, X. S. (2009). Calculation method of passive earth pressure in front of central island wall of deep and large foundation pit. Railw. Constr. (05), 80–83.
Pipatpongsa, T., Fang, K., Leelasukseree, C., Chaiwan, A., and Chanwiset, N. (2024). Reverse toe sliding criteria of laterally confined low wall slope subjected to counterweight fill. Int. J. Rock Mech. Min. Sci. 175, 105683–105722. doi:10.1016/j.ijrmms.2024.105683
Wang, H. L., Song, E. X., and Song, F. Y. (2014). Calculation method of active earth pressure of finite soil adjacent to existing building foundation pit. Eng. Mech. 31 (04), 76–81.
Wu, S. C., Jia, W. S., Han, L. Q., and Liu, X. L. (2023). Study on the distribution law of earth pressure on retaining wall of finite sloping soil under the condition of translation. Min. Metallurgical Eng. 43 (05), 11–16.
Keywords: slope, retaining structure, earth pressure, numerical simulation, model test
Citation: Zhou Y and Wei H (2024) Review on the research progress of earth pressure on slope retaining structure. Front. Earth Sci. 12:1468607. doi: 10.3389/feart.2024.1468607
Received: 22 July 2024; Accepted: 27 August 2024;
Published: 18 September 2024.
Edited by:
Wen Nie, Jiangxi University of Science and Technology, ChinaCopyright © 2024 Zhou and Wei. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yijun Zhou, enlqZmNiQDEyNi5jb20=
 Yijun Zhou
Yijun Zhou Haobin Wei
Haobin Wei