- Centre for Hydrogeology and Geothermics, University of Neuchâtel, Neuchâtel, Switzerland
Introduction: The Stratigraphic Pile (SP) is one of the foundation of most geological studies. It represents, in a compact and practical way, a vertical succession of depositional events over geological time. Accurate definition of the SP is crucial for geological modeling, yet challenges arise when relying on borehole data in the absence of clear biostratigraphic indicators or chronostratigraphical data.
Methods: This manuscript introduces an algorithm designed to automatically determine the SP using borehole unit sequences. The algorithm also addresses the complexities associated with incomplete sedimentological records and subjective geological interpretations. The algorithm was tested on various datasets, taking into account differences in the number of boreholes and available information.
Results and Discussion: The efficiency of the algorithm was demonstrated through real-world applications, providing a basis for a comprehensive discussion of its advantages, limitations, and potential applications. The proposed methodology assumes that each borehole contains a single occurrence of a stratigraphic unit, taking into account possible interpretation errors and inconsistencies. The algorithm is capable of: automatically determining one or an ensemble of plausible stratigraphic sequences, identifying potential misinterpreted wells, quantifying the vertical relationships of the stratigraphic units, and assisting in the data preprocessing step and in building the geologic concept of the modeling area. In particular, this ensemble of SPs and identified inconsistencies provide valuable insights into the geological history and concepts for a particular area.
Conclusion: This research contributes to the refinement of geological modeling workflows and provides a valuable tool for automatic refinement of SP selection.
1 Introduction
The stratigraphic pile (SP), also often called parent sequence or stratigraphic sequence, is a major concept in the representation of sedimentary phenomena. It is defined as a vertical stack of distinct depositional events or stages, often called stratigraphic units, that have been deposited one on top of another over geological time. Crucially, the concept of time assumes a central role in defining these stratigraphic units. They are postulated to be bounded by isochronous surfaces (Boggs et al., 2012), underscoring the chronological order within the stratigraphic pile. Consequently, in the absence of tectonic activity, magmatic activity or sediment remobilization, a unit positioned above another is, by definition, younger.
Under normal circumstances, defining the SP is not a problem, as there is already a global geological time scale (Gradstein et al., 2020, GTS). However, its use depends on the success of correctly dating precise units and relating them to the different ages, epoch and era defined in the GTS. In the absence of clear biostratigraphic indicators or radiocarbon data, this task is difficult to achieve. Moreover, the GTS is defined at a coarse time scale where the finest type of unit is the stage, corresponding to periods of time generally lasting 1 million years. This is in many cases, it proves more practical to define stratigraphic units with time scales that are tailored to the specific local geological conditions. This approach becomes particularly relevant when dealing with Quaternary deposits. In such geological setting, stratigraphic units are often delineated based on regional glacial stages, a practice well-documented in the literature (Penck and Brückner, 1909; Schlüchter, 1989; Graf and Burkhalter, 2016; Buechi et al., 2018). These stratigraphies are often based on lithological features with a temporal notion (e.g.,Würmian moraines, Last Glacial Maximum retreating fluvioglacial deposits, interglacial between two glacial stages deposits, etc.). However, it is important to note that the identification of these units still involves a degree of subjectivity and is subject to the interpretation of geologists. As a result, there is often a level of uncertainty associated with such classifications. Mistaking two distinct moraines or river deposits with similar lithologies but deposited at different times could lead to inconsistent interpretations that do not align with the SP. This could cause significant issues in the geological modeling of these units.
In the special case where all the events forming the SP are present within a single borehole, the determination of the SP is straightforward. However, it is important to acknowledge that such complete sedimentological records are rarely encountered in practice. This scarcity of complete records primarily arises from the variability of sedimentological processes, including localized depositions and erosional events, which hinder the preservation of a comprehensive stratigraphic sequence, even on a local scale (Boggs et al., 2012).
The SP serves as a fundamental component in numerous geological modeling algorithms (e.g., Calcagno et al., 2008; Allard et al., 2021; Grose et al., 2021; de la Varga et al., 2019; Schorpp et al., 2022). Geological modeling typically follows a hierarchical workflow, beginning with the delineation of stratigraphic units using explicit or implicit surfaces. These units are then filled with facies using facies modeling algorithms, and finally, continuous values representing subsurface physical properties (e.g., porosity, hydraulic conductivity) are assigned to these facies (Pyrcz and Deutsch, 2014; Ringrose and Bentley, 2016; Wellmann and Caumon, 2018).
The first step in this hierarchical process, the delineation of stratigraphic units using the SP, is of paramount importance. Inconsistencies in boreholes compared to a given SP must be identified and excluded from the modeling process. This is because geological modeling methods rely on bounding surfaces that assume a certain spatial continuity. When boreholes are inaccurately labeled or when an inappropriate SP is used, it can significantly complicate the generation of these bounding surfaces, resulting in incoherent and unrealistic geological models.
To tackle some of these issues, Allard et al. (2021) have proposed a methodology based on a Markov Chain Monte Carlo (MCMC) algorithm. But, their approach assumes that units having similar lithologies and are indistinguishable, such as multiple events of gravels, sand, etc. Consequently, it becomes challenging to link a particular gravel event in a borehole to another in the SP. Using an MCMC approach and the likelihood of latent Gaussian fields, they proposed a method that samples plausible borehole configurations. However, it is important to note that this method requires prior knowledge of the SP, a challenge that the authors acknowledge remains unresolved.
If boreholes are in disagreement with the SP, a common solution is to exclude them from the dataset. This assumes that the boreholes have been falsely labeled and/or interpreted. However, it is important to verify the accuracy of the SP, as potentially important boreholes necessary for modeling could be mistakenly removed. It is possible that the interpreted units are actually lithofacies deposited over the same period of time, with potential local variations. Therefore, it may be more appropriate to consider these geological objects in terms of facies modeling rather than unit modeling. Various adapted algorithms, such as Sequential Indicator Simulation (Journel, 1989), Multiple-Point Statistics (Mariethoz et al., 2010), object-based (Wang et al., 2018) or process-based (Granjeon, 2014)), exist for this purpose.
Therefore, an accurate and appropriate determination of the SP is critical. To do so, several approaches can be employed. For example, one can view it as a topological problem (Thiele et al., 2016), where we want to determine the 1D topological graph that fully determines the temporal relations between the different stratigraphic units. In 1D, the graph nodes corresponds to the different units and the directed edges show the temporal relations between them (which unit is older than which one).
In this vein, we can note the impressive work of Jessell et al. (2021) who developed open tools (map2model and map2loop) to automate the process of data collection and data integration into 3D geological models from geological maps. Among the extracted data, their methodology can provide topological outputs such as the local stratigraphy (i.e. SP). To do so, they compile the stratigraphic relationships into a topological graph. To determine the relative age of each units, they rely on provided minimum and maximum ages of the units. However, such information is not often available, and as a consequence, they also allow the integration of more global stratigraphic information (national or regional database). After all this, it is not uncommon that uncertainties remain about the correct stratigraphic order (i.e., SP) and that a specific SP has to be arbitrarily chosen (among plausible ones). Note that despite the difficulty of their approach to propose a unique SP, this method can consider a wide range of geological contexts (faulted, folded, intrusive, etc.). However, the difficulty of proposing a single, most appropriate pile is still a clear limitation that could be alleviated by integrating additional information such as subsurface data.
Although the graph framework has proven to be convenient, we propose a simpler and more intuitive approach. Our goal is to determine the SP, within a given area, relying solely on borehole data. This SP consists of distinct stratigraphic units (i.e. no repetitions are allowed). To this end, we propose a matrix-based algorithm that allows a rapid proposal of several plausible SPs given a set of boreholes. The method is partly similar to the one proposed by Burns (1975), which summarizes geological events (units) in an event matrix showing the temporal relationships between them. Our method can also be seen as a topological approach since it is based on a matrix that shares some similarity with an adjacency matrix (which is another representation of a graph (Biggs, 1993; Thiele et al., 2016)). The matrix used in our approach is not strictly an adjacency matrix because it is not symmetrical. This has some advantages as we will show in the paper.
Our method assumes: that the sediments have been exposed to little or no tectonic activity (especially no inverse faults nor major folding events), that the sediments have not been significantly reorganized by sedimentary processes (e.g., turbidity flows), and that the boreholes are vertical or sub-vertical, with each borehole log containing only one or zero occurrences of each unit. Therefore, the use of inclined boreholes in this approach must be tempered because, depending on the local geology, it is possible that such boreholes may encounter the same unit more than once, especially if the unit boundaries are highly variable or exhibit spatial trends.
In addition, the method assumes that the data set may contain erroneous borehole interpretations and the existence of inconsistencies (e.g., where unit B is situated below unit A, contrary to expectations). In such cases, the pursuit of a single SP that is perfectly consistent with all the borehole data becomes unfeasible. Instead, our objective shifts toward establishing an ensemble of plausible SPs that can account for these variations and inconsistencies.
The paper is structured as follows:
Initially, we explain in details the algorithm to retrieve the SP. Subsequently, we test the algorithm on several datasets in order to confront it with different situations (more or less boreholes, more or less information in the boreholes). Finally, we apply the algorithm to real data and we engage in a comprehensive discussion that delves into the advantages, limitations, and perspectives associated with the used methodology and its potential fields of application.
2 Methodology
2.1 Notations and definitions
Let us first consider a list of distinct deposit events that is called the stratigraphic pile
Now consider a list of simplified boreholes
It is important to note that the presence of inconsistencies in the boreholes lead to multiple piles that can be inferred, where no pile is able to perfectly match all boreholes. Therefore, a proper method will not return just one pile
For practical reasons, we propose an alternative representation of the SP as a matrix
2.2 Algorithm
The algorithm’s core concept revolves around a sequential analysis of boreholes, where the entries of a matrix
To streamline the borehole analysis, we propose to focus on pairs of adjacent units within each borehole rather than examining the entire borehole at once. Each borehole is divided into
1. Update the Contact: This rule involves updating the direct contact between the units in the pair. For instance, if unit B is positioned above unit A, the entry
2. Propagation Upward: Under this rule, all known units located above the top unit of the pair are considered to be above the bottom unit of the pair. Consider two pairs of adjacent units,
3. Propagation Downward: Similar to rule 2, this rule posits that all known units situated below the bottom unit of the pair are also below the top unit of the pair.
By sequentially applying these rules to pairs of adjacent units within the boreholes, we iteratively refine our understanding of the SP, updating the matrix
Figure 1 is a representation how these rules work and how two boreholes are analyzed and integrated. First, an empty matrix of size
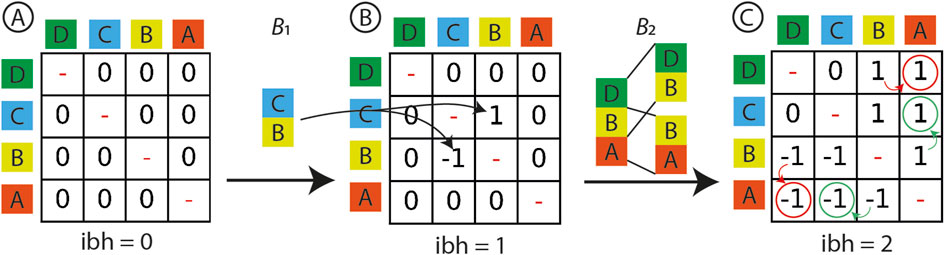
Figure 1. Schematic visualization of the algorithm applied to two boreholes derived from SP of four units at different steps (A–C). The pile is represented as a matrix of size k × k where each entry can be read as “the number of times the unit in row i is above the unit in column j”. The presence of a 0 indicates that the relative position of these two units is unknown. Black arrows are used to indicate an update of the contact (rule 1). Red arrows indicate a downward propagation (rule 3) while green ones indicate an upward propagation (rule 2). Black arrows are not shown in (C) for the sake of clarity.
It is important to note that during the update, it is necessary to ensure that a negative number is not increased or that a positive number is not decreased. Such updates would be in direct contradiction with the existing matrix, indicating that the analyzed borehole is inconsistent with the current SP. This is shown in Figure 2. In this example, the borehole

Figure 2. Inconsistent boreholes. (A) is the same starting point as in Figure 1. In this case, the borehole B2 is in direct contradiction with the pile M(1) in (B), which means that it cannot be added to pile M(1) (C). In such cases, a new empty pile is created M(2) and problematic borehole added to it (D).
Ultimately, each SP is assigned a score, calculated based on the percentage of boreholes that align with it. This can be done in several ways, such as retesting all boreholes for all piles once the piles have been determined, or keeping track of the number of boreholes used by each pile during the process.
A summary of all the different steps is given in Algorithm 1.
Once all matrix piles have been estimated, they can be back-transformed into their natural representation. The relationship between the two pile representations is simple. The position of each unit in the pile can be determined by counting the number of positive entries
As an illustration, the back transformation of the matrix shown in Figure 1C is made. Units B and A have respectively two and three positive entries which means that they are positioned in three and four positions of the pile. However, units C and D have both 0 positive entry (and two negative entries) which means that several positions are possible. These can be obtained by applying the previously introduced expressions, the possible positions range from
3 Results
3.1 Synthetic data application
Synthetic datasets are employed to demonstrate the algorithm theoretical capacity to deduce the SP based on a restricted set of boreholes. We consider two distinct scenarios.
1. Case 1: In this scenario, all boreholes originate from the same SP and are in concordance with each other.
2. Case 2: This scenario explores a situation where various SPs are employed to generate different sets of boreholes.
3. Case 3: In this scenario, all boreholes originate from the same SP but can be inconsistent.
The objective is twofold: to demonstrate the algorithm’s generability and to identify any anomalies or errors in the dataset. In the context of a SP comprising
3.1.1 Case one
Figure 3 presents two distinct synthetic sets, each comprising
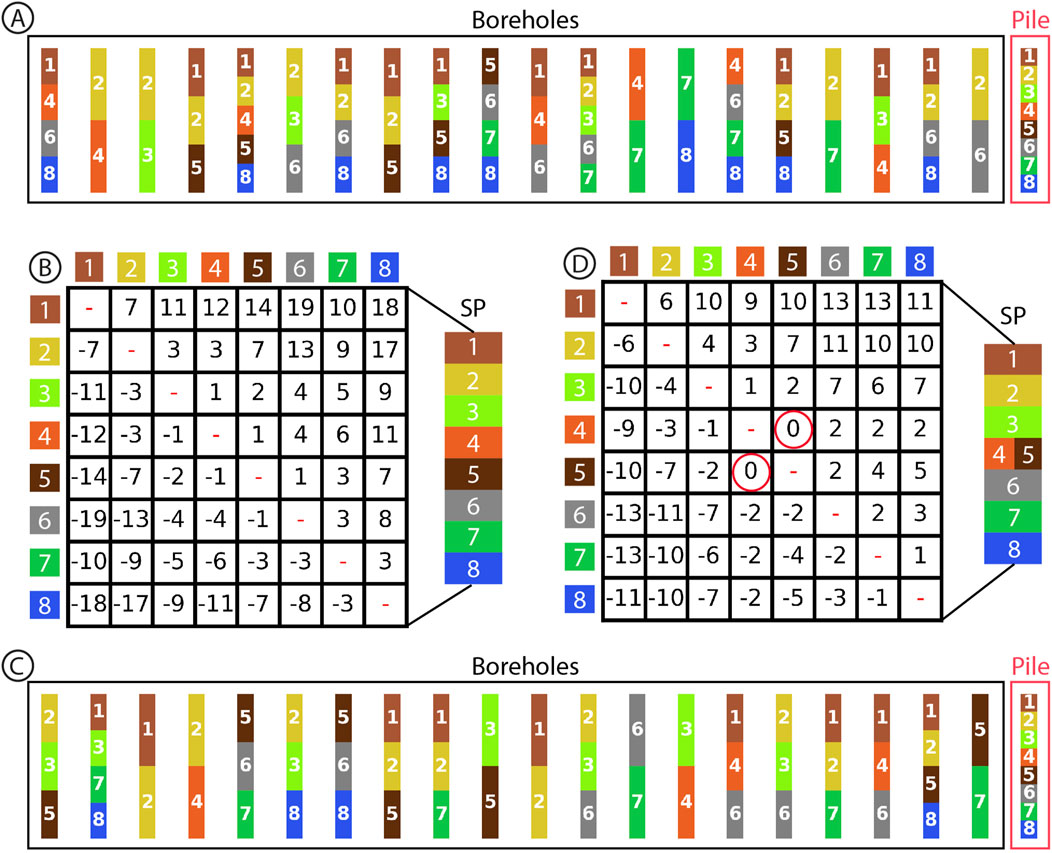
Figure 3. Stratigraphic Pile inference (B, D) from two synthetic datasets (A, C, respectively). The inferred piles (B, D) are shown beside the matrix in standard form. Red circles indicate an uninformed contact (entry equal to 0).
Considering the first set (Figure 3A), the resulting matrix, as obtained by applying Algorithm 1, is depicted in Figure 3B. Note that despite the relatively low number of boreholes (20) and the low probability of occurrence (0.3), the SP is accurately and entirely determined (no 0 entry).
Similar results were obtained with the second dataset (see Figure 3C). However, an undefined contact was observed this time (entries
Based on the previous results, we saw that with the same settings and parameters, two different sets of boreholes can give different results. It would be interesting to investigate the respective effect of
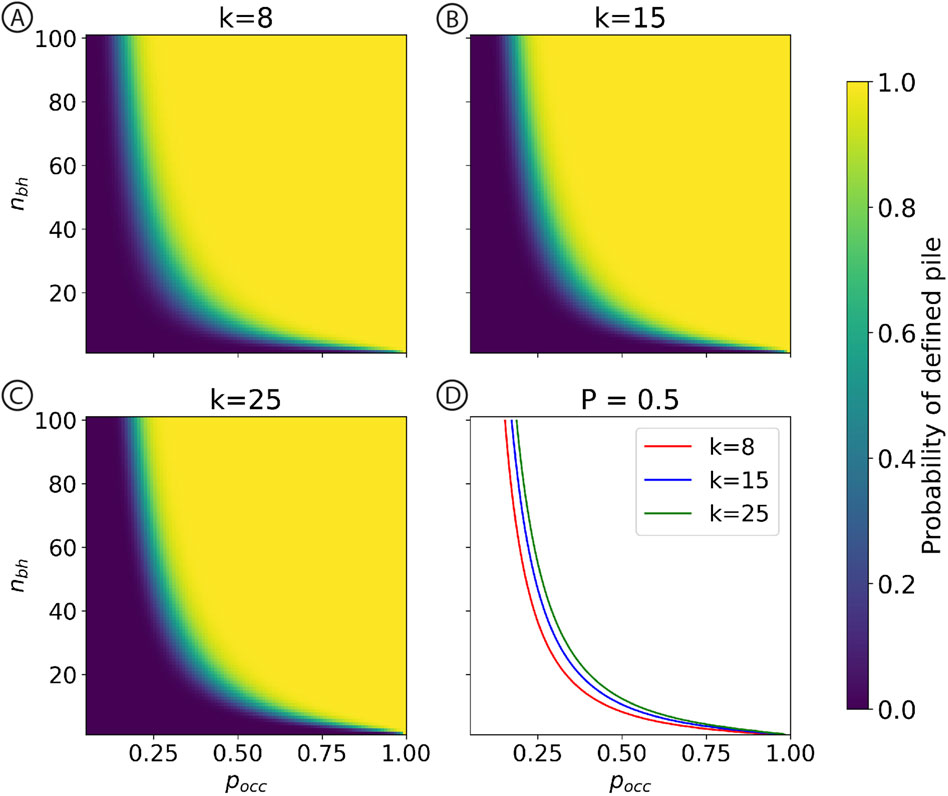
Figure 4. (A–C) Probabilities of getting a defined pile (no 0 entries) based on number of units in the pile
As expected the chances of identifying the input pile increases with
3.1.2 Case two
This second case investigates the effect of having boreholes that are not completely consistent with each other (i.e. generated using different SP). In fact, data are often inconsistent for a number of reasons such as potential errors in the data, units have been badly defined or the SP is locally varying. With this example, we show how to outline these problems. For this case, we use four different SPs (Figure 5A) and generated 80 boreholes, 50 with the first pile using

Figure 5. Second synthetic case results. (A): SP and parameters used to generate boreholes. Main pile is surrounded by red. The resulting SPs after the analysis of the 80 boreholes by Algorithm one are shown in (B) along with total number and proportions of boreholes in agreement with the pile. Main pile is surrounded by red.
The algorithm one found five resulting piles (Figure 5B), where the most probable one is also the main pile. This demonstrates that in this specific context, it is able to retrieve the main SP from which the boreholes originate. The other piles found are not identical to piles 2, three and four in Figure 5A, probably because there are fewer boreholes generated with these piles and also because they are less informative than the ones from the main pile. However, in these reconstructed piles, we can observe patterns of our own in Piles 2, three and 4. For example, in the second most probable pile, unit six is above unit 5, a relationship found in Piles two and 4. Or in the fourth most likely, unit two at the top of the pile is necessarily taken from a borehole in Pile 4.
3.1.3 Case three
For this case, the same pile of eight units was selected as in the previous cases, and a total of 100 boreholes were generated. The probability of occurrence of a unit is still 0.5. However, this time the boreholes also have a 20% chance of being mislabeled and therefore incorrect. In practice, this is done by randomly selecting two adjacent units in a borehole and inverting them, assuming that the geologist has mixed up the two units. The goal here is to test how the algorithm reacts when some of the boreholes are partially mislabeled.
The results are shown in Figure 6, where a total of nine piles have been identified by the algorithm. We can see that the most plausible pile is the correct one, with a score of 83% of the boreholes matching this pile, which is consistent with the 20% chance for a borehole to be mislabeled. The other piles have relatively high scores (
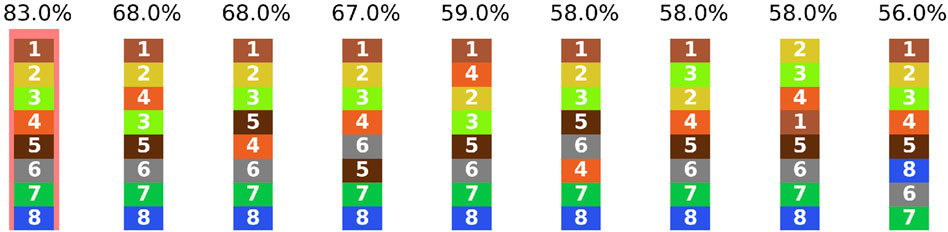
Figure 6. Third synthetic case results. It shows the SP that have been found after analysis of 100 boreholes generated based on the correct pile (leftmost pile), but which may contain errors in their interpretation.
3.2 Real data application
The study site is located in Switzerland, in the Alpine Rhine Valley (Figure 7A). It consists of a wide valley of about 230
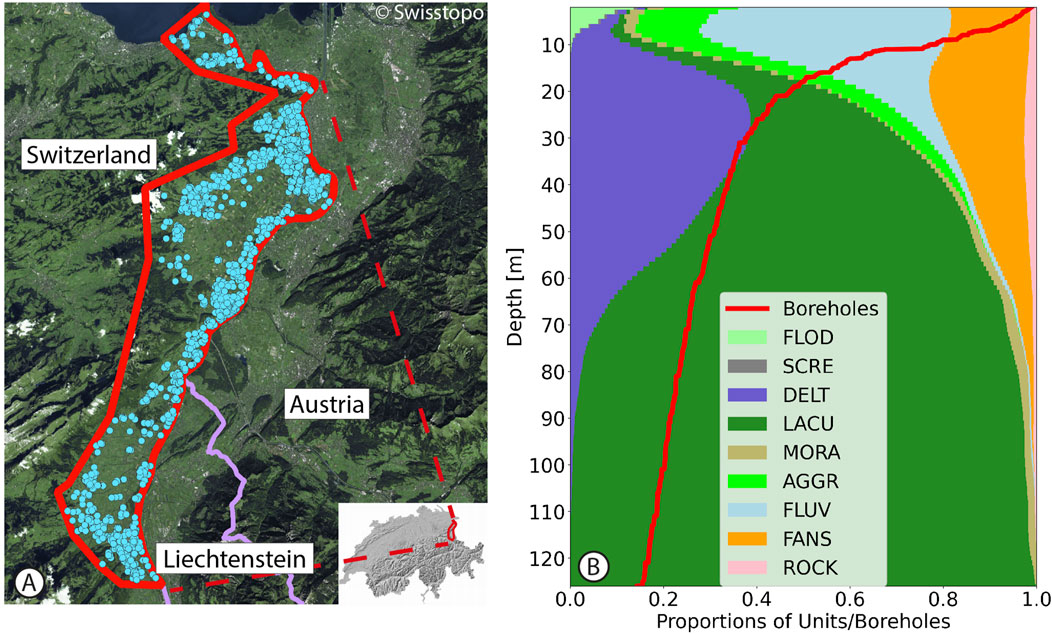
Figure 7. (A) the red area represents the geographical location of the Rhine Valley, situated at the boundary between Switzerland, Austria, and Liechtenstein. The blue dots on the map indicate the locations of the boreholes that have been collected and digitized by Swisstopo. (B) Evolution of unit proportions and proportions of boreholes reaching a certain depth. Note that data have not been declustered to estimate the proportions. ARTI unit was discarded from the analysis as it is only present on the first meters of depth.
The geology of this valley is a result of the Rhine river’s filling process. The oldest unit found is a moraine (MORA), which is typically associated with the Last Glacial Maximum. It generally follows the bedrock with a thickness of several meters and is generally observed on the sides of the valley. Above it we find lacustrine deposits (LACU) that are themselves below a unit composed of delta sediments (DELT). These two units composed most of the valley infill. Time order of younger sedimentological units is less clear, presuming that some of them were deposited synchronously. Regarding the river deposits, we have direct deposits from the Rhine bed (FLUV) that are mainly composed of gravels and sands, and aggradation deposits (AGGR) that present finer sediments. These river deposits are often covered by flood deposits (FLOD). Aside from the deposits from the Rhine river, we can also observe a significant number of alluvial fans from lateral valleys (FANS) and rock avalanche deposits (ROCK) that are very local and present in few boreholes. Recent scree deposits (SCRE) are sometimes observed but their proportion in relation to other units remains very low. Finally, soil and artificial deposits (ARTI) generally covers the units.
In total, there are 10 distinct stratigraphic units that have been identified, and their observed proportions in boreholes relative to depth are illustrated in Figure 7B. It is clear that the proportions of these units are not equally observed in the boreholes. While some units are quite prominent (LACU, DELT, FLUV), others are barely visible (e.g., MORA), and some are virtually absent, like SCRE, which indicates a poor spatial distribution.
The data were preprocessed and all boreholes that present several occurrences of the same unit were removed from the dataset ensuring that all boreholes can be analyzed with Algorithm 1. This reduces the total number of boreholes to 1481 (a reduction of about 5.6%). These multiple occurrences of units are always in pairs, where two units are intertwined. Most common pairs include, by occurrences, (AGGR, FLUV), (AGGR, FANS), (LACU, DELT) and (FLUV, FANS) while others are only observed one or 2 times.
The results of Algorithm one are shown in Figure 8A. For consistency not all the piles are shown here and only the five best over eight piles are presented and discussed.
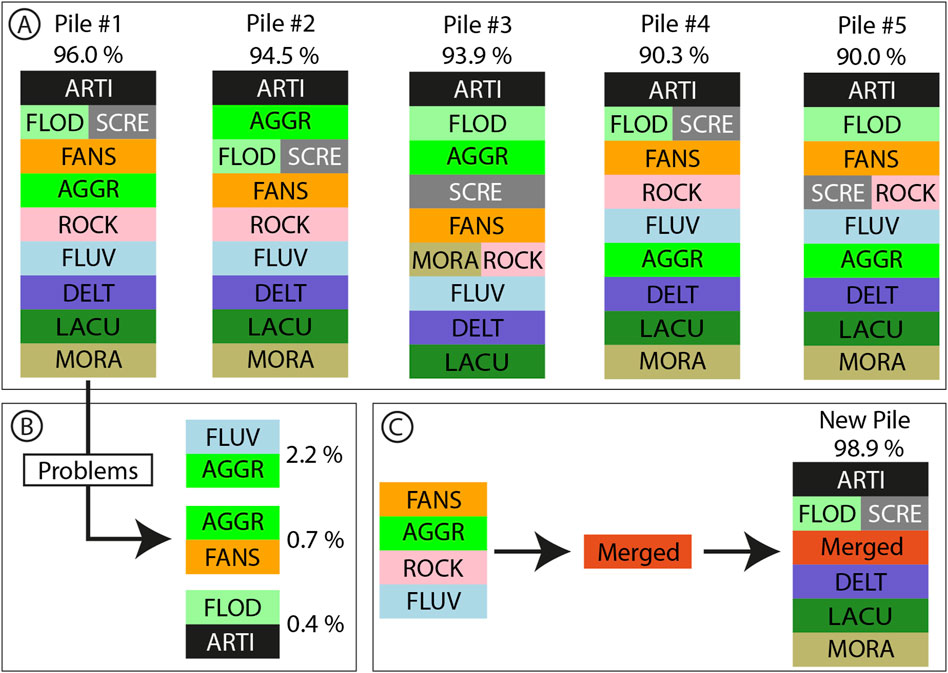
Figure 8. (A) Five most plausible SP found for the Alpine Rhine Valley using the algorithm. When two units are side by side it means that their relative position is unknown. Percentage indicates the number of consistent boreholes with this pile. (B) Inconsistent unit contacts observed in boreholes that are not in agreement with Pile #1 with proportions of boreholes concerned. (C) Proposition of merging some “units” into one stratigraphic unit to increase the number of boreholes in agreement.
We can note that despite the high number of boreholes, ambiguity still remains in the definition of the piles. Generally due to the relative position of FLOD and SCRE units. This can be explained by the scarcity of the SCRE unit occurrence in the boreholes, implying that these two units have not been observed together. This is not surprising as flood deposits are generally observed near the river (eastern side of the area). Scree deposits on the other hand, are located close to the relief (western side of the area).
All SPs exhibit a high level of agreement with boreholes, ranging from 90% to 96%. While there are notable similarities among the piles (e.g., the presence of DELT, LACU, MORA at the base and ARTI, FLOD at the top), there is also some variability. Specifically, the positions of FANS and AGGR shift in several instances, suggesting that these “units” might actually represent different lithofacies deposited during the same time interval. In certain piles, AGGR is found below FANS and FLUV, while in others, it is above them. FLUV is consistently located just above DELT, except in a few cases (#4 and #5) where AGGR lies in between. Additionally, ROCK consistently appears just above FLUV in all piles.
To quantify these discrepancies, an analysis of boreholes that do not align with a particular pile was conducted. Figure 8B displays the three most common unit contacts that conflict with pile #1. Approximately 2.2% of boreholes (32) show FLUV above AGGR, which is the primary source of disagreement with pile #1. The second most common discrepancy is AGGR above FANS, observed in 0.7% of boreholes (11). Interestingly, six boreholes (0.4%) exhibit FLOD above ARTI, which was unexpected. However, this observation should be interpreted cautiously, as more than 100 boreholes show the opposite arrangement (ARTI above FLOD), raising doubts about the authenticity of these six boreholes. The remaining conflicts are only observed in one or two boreholes and were consequently considered as irrelevant.
From these results, it makes sense to consider that the FLUV, FANS and AGGR deposits can be considered part of a single stratigraphic unit. These diverse lithological deposits may be interpreted as lithofacies, encompassing fluvial deposits on one end and episodically deposited alluvial cones on the other. In between, there are aggradation deposits associated with the river system. Consequently, consolidating these units into a single entity (as depicted in Figure 8C) would make sense. This operation raises the overall agreement with boreholes to nearly 99%. Furthermore, by merging these units, many boreholes that previously contained multiple occurrences of the same units would no longer exhibit such redundancy, particularly with respect to the FANS, AGGR, and FLUV units. The inclusion of unit ROCK in the merging was primarily driven by its consistent occurrence just above FLUV. Given that FLUV was merged, it logically follows that ROCK should be incorporated as well.
Importantly, the decision to merge units should always be driven by a valid geological concept that can elucidate why these three stratigraphic units are, in fact, not distinct. Merging implies that these three formations are heteropic (i.e., lithologically different but of the same age), which can have significant implications for their modeling process. Additionally, it is crucial to consider the number of boreholes affected by this merging. In this case, nearly 3% of the boreholes (45) became consistent with the pile. This number can serve as a justification for such a decision, suggesting that these boreholes may not have been inaccurately labeled.
4 Discussion
4.1 Summary of the method
The results presented, both synthetic and applied, demonstrate the ability of the algorithm to efficiently infer the SP or to determine problematic contacts when this is not possible. The algorithm’s success is highly dependent on the number of boreholes and the probability of occurrence of different units in the sedimentological records (i.e. in the boreholes). Determining the position of a rarely observed unit is more challenging. However, just because a unit is rare does not mean it can be neglected. Depending on their physical properties, they may have a significant impact on subsurface processes such as groundwater flow or contaminant transport. In such cases, the number of information about such units are scarce and does not allow the algorithm to find the clear position of the unit in the SP. Consequently, several pile configurations are possible. It may then be necessary to use stochastic and/or cross-validation methods to determine which pile is the most appropriate. Nevertheless, the algorithm has shown that it can still provide valuable information about such rare units. For example, in the applied case of the Rhine Valley, the SCRE unit is rare (present in 2%–3% of the boreholes), but has been clearly identified as a unit always present above most of the other units. Therefore, the final proposed piles are quite representative of the local stratigraphy, despite the scarcity of the unit.
In addition to its ability to determine the stratigraphic pile, this methodology offers the advantage of automatically identifying and quantifying potential errors in the data or the geological concept itself. Errors can be detected based on the frequency of occurrence. For instance, if unit B is observed above unit A in 100 boreholes, but in just one borehole, unit B is observed below unit A, it raises questions about the accuracy of the latter interpretation. However, if this observation is made in 20 boreholes, it becomes reasonable to question whether these two units are indeed of similar ages, implying that they might not be distinct stratigraphic units.
4.2 Merging units
The latter sentence brings about several conceptual questions, and it is important to recall that the aim of the present algorithm is to automatically find the sequence of stratigraphic units, which are differentiated by different ages of deposition. Under normal circumstances, this sequence is known and serves as the basis for the interpretation of the boreholes, interpretation that normally is expected to respect the pile. However, the boundary between units and facies is sometimes blurred, as it is easier (and more natural) to interpret a geological deposits based on its lithology (granulometry, structure, mineralogy, etc.) than its age. As a result, it is entirely possible that some boreholes could be misinterpreted, but also that the geological concept behind them (the stratigraphic pile) could be wrongly conceived. This is particularly true in the case of the Rhine Valley (Figures 7 and 8). In this case, many of the so-called stratigraphic units were, in fact, facies deposited over an identical time span. For example, we were able to show that, in the Rhein valley, the four units FANS, AGGR, ROCK, and FLUV make more sense, stratigraphically, grouped together than separated.
Note that the overall geological modeling process is particularly affected by such merging decisions. Without merging, a specific stratigraphic order must be chosen and each unit is then simulated independently. With the risk that many boreholes will be omitted because they do not respect the chosen SP, in order to avoid inconsistencies in the geological models. With merging, we can get away from having these units in a particular order and consider them as a whole chronostratigraphic unit. The units can then be delineated with additional geological studies to better capture their spatial arrangement and with adapted modeling methods (such as facies modeling methods, e.g., Alabert, 1989; Mariethoz et al., 2010). The advantage this time is that all boreholes can be included in the modeling process and a better representation of the subsurface heterogeneity can be obtained.
The choice of this grouping is also reinforced by the presence of a number of boreholes containing multiple occurrences of these same units. Such boreholes actually make no sense if these units are considered different, as an event that is supposed to occur within a single time span cannot be observed more than once. However, by considering them as part of a single unit, these problems disappear. In our case, it has enabled us to perform an initial stratigraphic analysis of the boreholes, to determine a plausible SP and to provide clues for rethinking the geological concept of certain units. In all cases, the question of whether units must be grouped or not, should be confirmed by additional studies or data. For example, one may conduct further geological studies to determine the relative age of the units (through more detailed analysis of the local stratigraphy) or to estimate their absolute age (if such data are available).
4.3 The three synthetic cases
The different synthetic cases presented are intended to represent different situations that may arise when a geological model is to be built from boreholes. The first case is not the most realistic because it assumes that all boreholes are perfectly labeled and that there is no spatial variation in the geology over the modeling area. Therefore, it serves more as a base case to validate the method. The second case explores the situation where multiple visions or concepts exist, represented by the different SPs reflected in the interpreted wells. The consequence is that it is not possible to find one single SP that fits all the boreholes. Such a situation is not unrealistic, as it is possible that the geological concept of the area has changed over time, resulting in differently interpreted wells. Or it may also be the result of spatially varying geology where the stratigraphy is locally different. In any cases, the proposed algorithm was able to retrieve the most dominant pile that matches the highest proportion of wells, but has difficulty to determine the others, probably due to the lack of generated boreholes from the other SPs. Finally, the third case examines the case of mislabeled or inconsistent boreholes and how well the algorithm performs with “noisy” data. Such a situation is quite common in practice (see Section 3.2), as boreholes are often interpreted by different people with different expertise and at different epochs. Note that such inconsistencies should not always be considered as simple “errors” in the interpretation of the data, but could also be the result of different lithostratigraphic units deposited during the same time period, as discussed above.
Additionally, it is important to note that the results obtained from synthetic examples should be treated with great caution. Indeed, the model assumed to generate the boreholes is very simple and based on a simple probability of presence or absence of the unit, largely missing the great complexity of sedimentological systems. Furthermore, some geological units may naturally occur less frequently, resulting in a lower likelihood of being encountered in borehole data. This lower likelihood adds to the algorithm’s challenge in accurately determining their positions in the stratigraphic sequence, as demonstrated in the specific case study.
4.4 Applications
This algorithm has direct applications, mainly providing piles for software that require them such as Geomodeller (Calcagno et al., 2008), GemPy (de la Varga et al., 2019), or ArchPy (Schorpp et al., 2022). However, the presented algorithm may pose challenges for Geomodeller and GemPy due to their ability to consider a wide range of geological settings, including folded or faulted environments, which contradict the assumptions made in the algorithm. Nevertheless, it can still be used if the polarity of the layers in each borehole can be determined. ArchPy is an ideal python module for Quaternary environments where folds or faults are absent. In terms of availability, the present algorithm has already been integrated into ArchPy’s GitHub repository1, as well as the synthetic examples of this study.
4.5 Limitations of the method
Despite its ability to easily analyze the stratigraphic relationships of a set of boreholes, the presented algorithm has several limitations that could be the focus of future research.
First, the method is limited to vertical or sub-vertical boreholes. but could be extended to incorporate some information from non-vertical boreholes. This is highly dependent on the geological context, but if the height of the geological interfaces is highly variable (even in the absence of tectonics), once a borehole is inclined, there is a possibility of having inconsistent boreholes (e.g. multiple occurrences of the same units, wrong order of units, etc.), which prevents their use with the present algorithm. Therefore, it is likely that the data obtained from such boreholes cannot be considered as a whole due to the potentially complex sequences of units that can be obtained from such non-vertical boreholes. Nevertheless, the data can still provide valuable information about the relative position of two units. Second, the method is restricted to chronostratigraphic units, only differentiated by their age. Unfortunately, it is quite common for geologists to describe units in terms of lithologies (lithostratigraphy), which can lead to cases that cannot be handled by the current algorithm. These include instances where the same units are present in multiple locations within a single borehole. In such cases, the relative position of the units is not readily discernible. Hence, it could be useful to have a solution to also determine the pile for such situations as pointed by Allard et al. (2020). The current matrix-based algorithm is unable to function effectively in this scenario. Consequently, alternative, more indirect approaches should be investigated. One could better explore the potential of topological and graph-based approaches such as the one proposed by Jessell et al. (2021). One other potential solution is the utilization of an optimization method, whereby a starting pile is progressively modified and updated until it aligns with the data from most of the boreholes.
In addition, sampling bias must also be considered when using this algorithm. For example, boreholes are often located near towns or villages and are typically drilled to relatively shallow depths. As a result, certain geological units may not be encountered or may be rarely encountered. This sampling bias can introduce limitations and significantly affect the performance of the algorithm, but as has been shown, it does not prevent the definition of a coherent SP for the Rhine Valley. In order to better understand the limitations of the method in real applications, these aspects should be further investigated.
5 Conclusion
Using a matrix approach and simple logical rules, the algorithm presented showed that it was capable of retrieving a stratigraphic pile (SP) given a limited set of boreholes. However, this greatly depends on the “completeness” of the boreholes and how a unit is likely to be recorded, as well as the total number of units in the SP. All in all, the algorithm and methodology presented in this research have a number of interesting benefits.
The limitations of the approach were also investigated. We found that the performance of the algorithm depends mainly on the number of boreholes
Finally, this tool should not only be seen as a simple tool for determining the stratigraphic pile, but rather as an aid in the pre-processing of geological data and in the construction of the geological conceptual model. Therefore, its applications are wide and diverse.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: http://www.github.com/randlab/ArchPy.
Author contributions
LS: Conceptualization, Methodology, Software, Writing–original draft, Writing–review and editing. JS: Methodology, Supervision, Validation, Writing–review and editing. PR: Funding acquisition, Methodology, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research is funded by the Swiss National Science Foundation under the contract 200020_182600/1 (PheniX project).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1http://www.github.com/randlab/ArchPy
References
Alabert, F. (1989). “Constraining description of randomly heterogeneous reservoirs to pressure test data: a Monte Carlo study,” in SPE annual technical Conference and exhibition (SPE), SPE–19600. doi:10.2118/19600-MS
Allard, D., Fabbri, P., and Gaetan, C. (2020). Modeling and simulating depositional sequences using latent Gaussian random fields. Math. Geosci. 53, 469–497. doi:10.1007/s11004-020-09875-0
Allard, D., Fabbri, P., and Gaetan, C. (2021). Modeling and simulating depositional sequences using latent Gaussian random fields. Math. Geosci. 53, 469–497. doi:10.1007/s11004-020-09875-0
Boggs, S. (2012). Principles of sedimentology and stratigraphy (biblioteca hernán malo gonzález). fourth edn.
Buechi, M. W., Graf, H. R., Haldimann, P., Lowick, S. E., and Anselmetti, F. S. (2018). Multiple quaternary erosion and infill cycles in overdeepened basins of the northern alpine foreland. Swiss J. Geosciences 111, 133–167. doi:10.1007/s00015-017-0289-9
Burns, K. (1975). Analysis of geological events. J. Int. Assoc. Math. Geol. 7, 295–321. doi:10.1007/bf02081703
Calcagno, P., Chilès, J.-P., Courrioux, G., and Guillen, A. (2008). Geological modelling from field data and geological knowledge: Part i. modelling method coupling 3d potential-field interpolation and geological rules. Phys. Earth Planet. Interiors 171, 147–157. doi:10.1016/j.pepi.2008.06.013
de la Varga, M., Schaaf, A., and Wellmann, F. (2019). GemPy 1.0: open-source stochastic geological modeling and inversion. Geosci. Model Dev. 12, 1–32. doi:10.5194/gmd-12-1-2019
Gradstein, F. M., Ogg, J. G., Schmitz, M. D., and Ogg, G. M. (2020). Geologic time scale 2020. Elsevier.
Graf, H. R., and Burkhalter, R. (2016). Quaternary deposits: concept for a stratigraphic classification and nomenclature—an example from northern Switzerland. Swiss J. Geosciences 109, 137–147. doi:10.1007/s00015-016-0222-7
Granjeon, D. (2014) “3d forward modelling of the impact of sediment transport and base level cycles on continental margins and incised valleys,” in From depositional systems to sedimentary successions on the Norwegian continental margin, 453–472doi. doi:10.1002/9781118920435.ch16
Grose, L., Ailleres, L., Laurent, G., and Jessell, M. (2021). Loopstructural 1.0: time-aware geological modelling. Geosci. Model Dev. 14, 3915–3937. doi:10.5194/gmd-14-3915-2021
Jessell, M., Ogarko, V., De Rose, Y., Lindsay, M., Joshi, R., Piechocka, A., et al. (2021). Automated geological map deconstruction for 3D model construction using map2loop 1.0 and map2model 1.0. Geosci. Model Dev. 14, 5063–5092. doi:10.5194/gmd-14-5063-2021
Journel, A. G. (1989) Fundamentals of geostatistics in five lessons, 8. Washington, DC: American Geophysical Union.
Mariethoz, G., Renard, P., and Straubhaar, J. (2010). The direct sampling method to perform multiple-point geostatistical simulations. Water Resour. Res. 46. doi:10.1029/2008WR007621
Pyrcz, M. J., and Deutsch, C. V. (2014). Geostatistical reservoir modeling. Oxford, United Kingdom: Oxford University Press.
Schlüchter, C. (1989). The most complete quaternary record of the Swiss Alpine Foreland. Palaeogeogr. Palaeoclimatol. Palaeoecol. 72, 141–146. doi:10.1016/0031-0182(89)90138-7
Schorpp, L., Straubhaar, J., and Renard, P. (2022). Automated hierarchical 3d modeling of quaternary aquifers: the ArchPy approach. Front. Earth Sci. 10. doi:10.3389/feart.2022.884075
Thiele, S. T., Jessell, M. W., Lindsay, M., Ogarko, V., Wellmann, J. F., and Pakyuz-Charrier, E. (2016). The topology of geology 1: topological analysis. J. Struct. Geol. 91, 27–38. doi:10.1016/j.jsg.2016.08.009
Volken, S., Preisig, G., and Gaehwiler, M. (2016). Geoquat: developing a system for the sustainable management, 3d modelling and application of quaternary deposit data. Swiss Bull. Appl. Geol. 21, 3–16. doi:10.5169/seals-658182
Wang, Y. C., Pyrcz, M. J., Catuneanu, O., and Boisvert, J. B. (2018). Conditioning 3d object-based models to dense well data. Comput. and Geosciences 115, 1–11. doi:10.1016/j.cageo.2018.02.006
Keywords: stratigraphic pile, automated pile, geostatistics, archpy, geological models
Citation: Schorpp L, Straubhaar J and Renard P (2024) An algorithm for identifying stratigraphic piles from interpreted boreholes. Front. Earth Sci. 12:1461658. doi: 10.3389/feart.2024.1461658
Received: 08 July 2024; Accepted: 13 September 2024;
Published: 26 September 2024.
Edited by:
Tianming Huang, Chinese Academy of Sciences (CAS), ChinaReviewed by:
Florian Wellmann, RWTH Aachen University, GermanyEmilson Leite, State University of Campinas, Brazil
Zhendong Cui, Institute of Geology and Geophysics (CAS), China
Copyright © 2024 Schorpp, Straubhaar and Renard. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ludovic Schorpp, bHVkb3ZpYy5zY2hvcnBwQHVuaW5lLmNo
 Ludovic Schorpp
Ludovic Schorpp Julien Straubhaar
Julien Straubhaar Philippe Renard
Philippe Renard