Heat and moisture transport characteristics in permafrost embankment under seasonal rainfall

The Tibetan Plateau has exhibited a discernible trend towards increased precipitation over the past 50 years. However, previous research predominantly focused on thermal stability of permafrost without the consideration of water flux boundary conditions, and therefore ignored the dynamics of water migration and its impacts on the embankment stability. To bridge this gap, a novel water-heat transfer model incorporating rainfall and water migration was developed and subsequently validated using monitored data. Comparative analyses were then conducted across three distinct rainfall intensities to investigate the variations in the moisture and temperature of superficial soil. Results indicate rainfall events exert a notable cooling effect during warm seasons but have little influence on cooling during cold seasons. By increasing the latent heat of evaporation, sensible heat and reducing the soil heat flux, rainfall results in embankment cooling, and the cooling effect correlates positively with rainfall intensity. Disregarding the water flux boundary conditions will overestimate the embankment temperature and underestimate the variation of water content, especially at the superficial soil. Rainfall results in a decline in water vapor flux and an increase in liquid water flux, which facilitates rapid downward transport and accumulation of liquid water. Despite the increased convective heat transfer of liquid water, the decrease in heat conduction, latent heat of evaporation and convective heat transfer of water vapor in the embankment is more pronounced. Rainfall changes the stability of permafrost embankment mainly by adjusting the energy distribution, which delays temperature increases in the underlying permafrost. When predicting the stability of permafrost, it is recommended to incorporate the water flux boundary conditions.

1 Introduction

The active layer in permafrost regions plays a crucial role in the exchange of water and energy between the atmosphere, ground, and permafrost (Woo et al., 2018; Cheng et al., 2019). This exchange has a significant impact on vegetation growth, the earth-air energy balance and permafrost stability (Bibi et al., 2018; Cao et al., 2021). The construction activities in permafrost regions have significantly altered the natural water and heat exchange processes. For instance, the use of asphalt pavement can accelerate the temperature rise in permafrost due to its ability to absorb heat and retard water evaporation (Jiang et al., 2018; Zhang TQ. et al., 2022). Additionally, rainfall, as a key source of recharge water in permafrost regions, has a notable influence on hydrothermal dynamics and surface energy characteristics (Mekonnen et al., 2021). Given the ongoing trend of warming and humidification, it is crucial to study the characteristics of water and heat transport in permafrost embankments, especially considering the effect of rainfall.

The research on the thermal stability of permafrost embankments has primarily focused on the impact of climate warming on permafrost temperature, and the migration of water within closed regions (without rainfall and evaporation) (Biskaborn et al., 2019; Zhang GF. et al., 2022). Under this background, human activities and meteorological factors have been identified as disruptors of the hydrothermal balance, ultimately leading to the permafrost degradation. In order to predict the water and heat state, scholars have developed various theoretical models, for instance, Yang et al. (2018) proposed a heat conduction model that overlooked the effects of convection, mass migration, and hydrothermal evaporation during permafrost melting. Similarly, Jiang et al. (2020) employed a combination of the first, second, and third boundary conditions to examine variations in the temperature field. According to the long-term monitoring data of different permafrost regions and the adherent layer theory, Li et al. (2020) proposed serials of numerical models to analyze the influences of climate warming, integral and two separated embankments and embankments on the permafrost zones. Although the thermal stability of permafrost embankments has been extensively studied, it is important to note that existing models have not considered the influence of rainfall and evaporation the on water-heat coupling process.

The pavement crack can serve as a pathway for water migration, consequently, the embankment is not a closed region (Hansson et al., 2005; Dan et al., 2011). Although asphalt pavement provides some resistance to water, it is vulnerable to cracking and damage from excessive load and water exposure. Previous studies have demonstrated that rainfall infiltration can increase soil water content and disrupt the water, heat balance within permafrost embankment (Philip and De Vries, 1957; Zhou et al., 2021). Moreover, rainfall can alter the thermal and physical properties of the soil (Qin et al., 2022) and accelerate permafrost degradation, leading to substantial uneven settlement of embankments (Liu et al., 2018; Peng et al., 2023). Due to the deep groundwater levels and low soil water content in arid areas, water vapor transport in unsaturated soil has been identified as the primary component of water migration (Zhang S. et al., 2016). Additionally, the evaporation process can consume a significant amount of evaporation latent heat (Zhou et al., 2023). Therefore, it is crucial to investigate the role of water vapor in the water and heat transport processes in unsaturated soil. Exploring the basic water and heat dynamics in embankment and their response to rainfall, is of paramount theoretical and practical importance for unraveling the mechanisms and devising effective strategies to mitigate the instability of permafrost embankments.

Considering the existing research landscape, the integration of rainfall and evaporation factors into the permafrost embankment model represents a notable advancement in the comprehension of water flux boundary conditions within humidified environments. This enhancement facilitates a more thorough examination of the water and heat transport dynamics within embankments, especially under four intensities of rainfall. The insights gained from this study have the potential to offer valuable theoretical guidance for embankment construction and disease prevention in permafrost regions.

2 Establishment of numerical model

2.1 Project profile

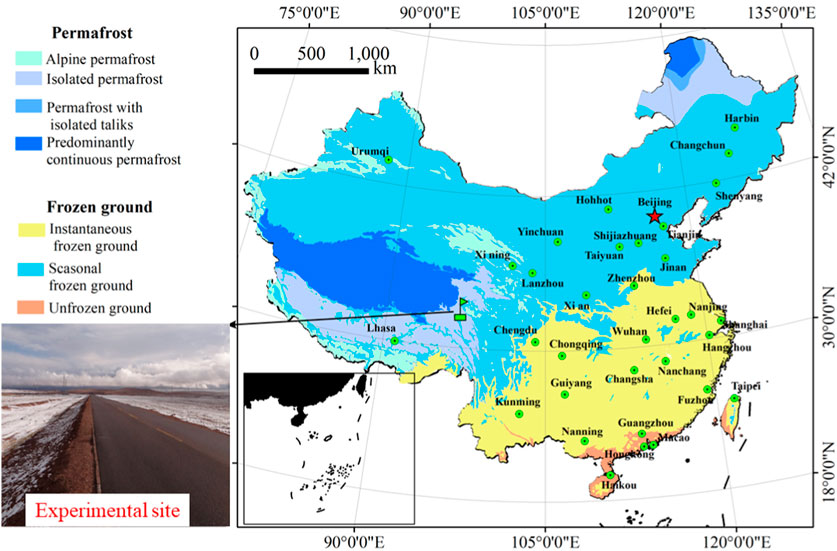
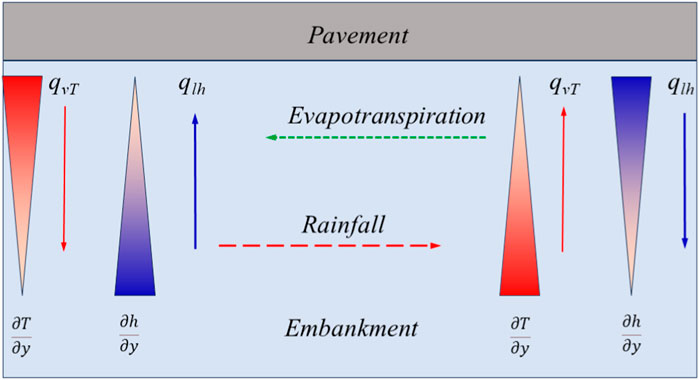
Taking the Erdaogao-Zhiduo highway in Qinghai Province as the research object (Figure 1). According to the geological and climatic conditions of the research area, the embankment model was established as follows: The height of the embankment is 3 m, and the width is 10 m, with a slope angle of 1:1.5. The overall width of the model is 30 m, and the depth of the model is 30 m. Under the surface, 0 m ∼ −2 m is gravelly soil, −2 m ∼ −3 m is silty clay and −3 m ∼ 30 m is a strongly weathered mudstone. The simulated embankment is a two-dimensional symmetric model, so the center line is taken as the axis, and half of the embankment is analyzed.

Figure 1

Figure 1. Location of the research area.

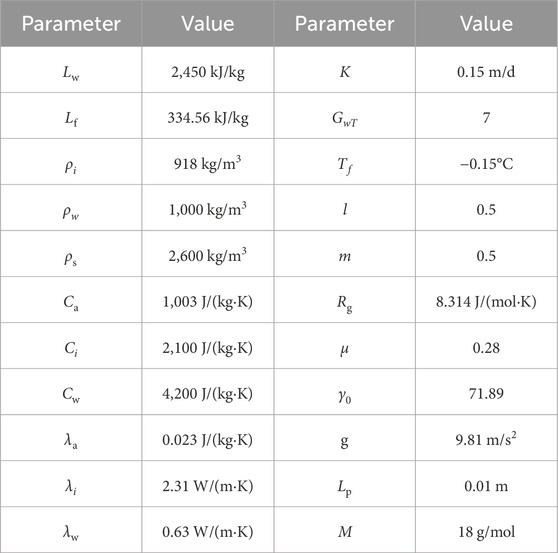
Reasonable model parameters are a prerequisite for accurate prediction. In this study, the parameters of the soil-freezing characteristic curve refer to experimental results. The parameters related to the temperature field refer to the experimental results of literature (Xu et al., 2010; Zhou, 2022). The model parameters are listed in Table 1.

Table 1

Table 1. Thermophysical parameters of different soils.

2.2 Theory model

2.2.1 Water migration

The movement of water in unsaturated soil occurs through two primary pathways: liquid water migration and water vapor migration. These movements are driven by water potential gradient, temperature gradient, liquid water hydraulic conductivity and vapor hydraulic conductivity. The variation of water content in the soil can be expressed as (Saito et al., 2006; Zhang et al., 2021),

$\frac{\partial \theta }{\partial t}+\frac{{\rho }_v}{{\rho }_w}\frac{\partial }{\partial }\left(n-{\theta }_l-{\theta }_i\right)=-\frac{\partial q_L}{\partial \mathrm{z}}-\frac{\partial q_V}{\partial \mathrm{z}}(1)$

The liquid water flux ($q_l$) and water vapor flux ($q_{\mathrm{v}}$) can be described by Equations 2, 3 (Saito et al., 2006):

$q_L=q_{Lh}+q_{LT}=K_{Lh}\left(\frac{\partial h}{\partial z}+1\right)+K_{LT}\frac{\partial T}{\partial z}(2)$

$q_V=q_{Vh}+q_{VT}=K_{Vh}\frac{\partial h}{\partial z}+K_{VT}\frac{\partial T}{\partial z}(3)$

where $\theta$ is total volumetric water content; ${\theta }_l$ and ${\theta }_i$ are volumetric water and ice content, respectively; $t$ is time; $h$ is pressure head; $z$ is vertical distance; $T$ is soil temperature; $K_{Lh}$ and $K_{LT}$ are the isothermal and thermal hydraulic conductivities for liquid water caused by $h$ and $T$; $K_{Vh}$ and $K_{VT}$ are the isothermal and thermal hydraulic conductivities for water vapor; ${\rho }_w$ is water density; ${\rho }_v$ is water vapor density.

According to previous studies, the hydraulic conductivity of liquid water $K_{Lh}$ can be obtained by the Van Genuchten model as shown in Equations 4, 5 (Banimahd and Zand-Parsa, 2013; Van Genuchten, 1980):

$K_{Lh}=K_s{S}_e^{0.5}{\left(1-{\left(1-S_e^{\frac{1}{m}}\right)}^m\right)}^2(4)$

$S_e=\frac{{\theta }_u-{\theta }_r}{{\theta }_s-{\theta }_r}(5)$

where $K_s$ is the hydraulic conductivity of saturated soil; $S_e$ is the effective saturation; ${\theta }_u$ is unfrozen water content; ${\theta }_s$ and ${\theta }_r$ are the saturated and residual water content, respectively.

The thermal hydraulic conductivity function ($K_{LT}$) can be calculated by Equation 6 (Banimahd and Zand-Parsa, 2013),

$K_{LT}=K_{Lh}\left(h{G}_{wT}\frac{1}{{\gamma }_0}\frac{d\gamma }{dT}\right)(6)$

where $G_{wT}$ is a gain factor; ${\gamma }_0$ is surface tension at 25°C; $\gamma$ is surface tension, which can be obtained from Equation 7 (Banimahd and Zand-Parsa, 2013),

$\gamma =75.6-0.1425T_c-2.38\times {10}^{-4}{T}_c^2(7)$

where $T_c$ is soil temperature in °C.

The parameters $K_{Vh}$ and $K_{VT}$ were described as Equations 8, 9 (Zhang et al., 2021; Nassar and Horton, 1997),

$K_{Vh}=\frac{D}{{\rho }_w}{\rho }_{sv}\frac{Mg}{R_{\mathrm{g}}T}{H}_r(8)$

$K_{VT}=\frac{D}{{\rho }_w}\eta H_r\frac{d{\rho }_{sv}}{dT}(9)$

where ${\rho }_{sv}$ is saturated water vapor density; $M$ is molecular weight of water; $g$ is gravitational acceleration; $R_{\mathrm{g}}$ is universal gas constant; $\eta$ is enhancement factor; $H_r$ is relative humidity; $D$ is the vapor diffusivity in soil, which can be calculated by Equation 10 (Banimahd and Zand-Parsa, 2013),

$D=\tau {\theta }_a{D}_a(10)$

where $\tau$ is tortuosity factor; ${\theta }_a$ is air-filled porosity; $D_a$ is the diffusivity of water vapor at temperature $T$. The variables $\tau$ and $D_a$ can be calculated by Equations 11, 12 (Millington and Quirk, 1961),

$\tau =\frac{{\theta }_a^{7/3}}{{\theta }_s^2}(11)$

$D_a=2.12\times {10}^{-5}{\left(\frac{T}{273.15}\right)}^2(12)$

The saturated vapor density (${\rho }_{sv}$) is a function of temperature, as shown in Equation 13 (Millington and Quirk, 1961),

${\rho }_{vs}=\frac{\exp \left(31.37-\frac{6014.79}{T}-7.92\times {10}^{3}T\right)}{{10}^{3}T}(13)$

The relative humidity was calculated from the pressure head exploiting the thermodynamic relationship between liquid water and water vapor, as present in Equation 14 (Zhang et al., 2021),

$H_r=\exp \left(\frac{hMg}{R_{\mathrm{g}}T}\right)(14)$

The enhancement factor can be obtained by Equation 15 (Cass et al., 1984),

$\eta =9.5+3\frac{\theta }{{\theta }_s}-8.5\exp \left\{-{\left[\left(1+\frac{2.6}{\sqrt{f_c}}\right)\frac{\theta }{{\theta }_s}\right]}^4\right\}(15)$

where $f_c$ is the mass fraction of clay in soil.

2.2.2 Heat transfer

The heat flow in this model is governed by energy conservation principle, and it can be described as the sum of heat conduction, liquid and vapor convection, and latent heat caused by phase change. This can be mathematically expressed as an equation that accounts for each of these contributing factors (Zhang et al., 2021; Banimahd and Zand-Parsa, 2013):

$\begin{array}{ll}\hfill C_p\frac{\partial T}{\partial t}-L_f{\rho }_i\frac{\partial {\theta }_i}{\partial t}+L_w{\rho }_w\frac{\partial {\theta }_v}{\partial t}& =\nabla \cdot \left[\lambda \nabla T\right]-q_L\nabla \left(C_{w}T\right)-q_V\nabla \left(C_{v}T\right)\hfill \\ \hfill & -L_w{\rho }_w\nabla q_V\hfill \end{array}(16)$

where $\lambda$ is the thermal conductivity of soil; $C_p$, $C_w$, $C_v$ are volumetric heat capacities of moist soil, liquid water, and water vapor, respectively; $L_w$ is the latent heat of evaporation; $L_f$ is latent heat of ice-water phase transition; ${\rho }_i$ is the ice density; ${\theta }_v$ is the volumetric vapor content.

The liquid water content was used as the variable to simultaneous Equations 1, 16. According to (Xu et al., 2010), the relationship between temperature and liquid water content is expressed by Equation 17

${\theta }_l=\left\{\begin{array}{l}{a}_0{\left|T-273.15\right|}^b,T<273.15\\ \theta ,T\ge 273.15\end{array}\right.(17)$

where $a_0$ and $b$ are fitting parameters.

2.2.3 Boundary conditions

2.2.3.1 Temperature boundary conditions

The air temperature is always simplified to a trigonometric function with an annual cycle (Lai et al., 2009; Zhang ML. et al., 2016). Considering the temperature increases $\Delta T$ in 1 year, the air temperature can be expressed as Equation 18,

$T_0=-4+\Delta T+273.15+A\sin \left(\frac{2\pi t}{365}-\frac{\pi }{2}\right)+\Delta T(18)$

where $A$ is the temperature amplitude; $\Delta T$ is the temperature rising amplitude.

According to the adherent layer theory, the temperature of the natural ground, embankment slope, and pavement can be expressed as Equations 19–21, respectively.

$T_0=-4+2.5+273.15+12\sin \left(\frac{2\pi t}{365}-\frac{\pi }{2}\right)+\Delta T(19)$

$T_1=-4+4.5+273.15+13\sin \left(\frac{2\pi t}{365}-\frac{\pi }{2}\right)+\Delta T(20)$

$T_2=-4+6.5+273.15+15\sin \left(\frac{2\pi t}{365}-\frac{\pi }{2}\right)+\Delta T(21)$

The bottom boundary is the heat flux, which is set at 0.03 W/m², and the left and right boundaries are adiabatic (Zhang ML. et al., 2016). The initial value for the natural site is the January 1 calculation after 50 years without embankment construction rainfall conditions.

The heat by rainfall infiltration can be expressed as (Wei et al., 2014):

$H=C_w{\rho }_{w}q\left(T_s-T_{rain}\right)(22)$

where $T_s$ is the surface temperature; $T_{rain}$ is the rainfall temperature. Rain temperature can be approximated using the wet-bulb temperature, which can be obtained from Equation 23 (Kollet et al., 2009):

$\begin{array}{l}{T}_{wet}=T_0\times (\arctan \left[0.151977{\left(H_r+8.313659\right)}^{0.5}\right]\\ +\arctan \left[T_0+H_r\right]-\arctan \left(H_r-1.676331\right)\\ +0.003918{H_r}^{1.5}\arctan \left(0.023H_r\right)-4.68)\end{array}(23)$

2.2.3.2 Water flux boundary conditions

In order to more accurately represent the water exchange between embankment and atmosphere, the coupled hydrothermal model introduces rainfall and evaporation. The water flux $Q$ was defined as the difference between the rainfall infiltration $v$ and the surface evaporation rate, which can be described as Equation 24 (Zhang ML. et al., 2016):

$Q=v-E/{\rho }_w(24)$

where $E$ is the surface evaporation rate.

According to the relationship between rainfall intensity and the hydraulic conductivity of pavement, rainfall infiltration can be categorized into two types: free infiltration and pressure infiltration. When the rainfall intensity is lower than the hydraulic conductivity, all the rainfall infiltrates into the soil. When the rainfall intensity exceeds the hydraulic conductivity, a portion of the rainfall accumulates at the surface and creates a water head, while the remaining portion results in surface runoff. Therefore, the rainfall infiltration can be mathematically expressed by Equation 25 (Nian et al., 2021),

$v=ki=\left\{\begin{array}{l}qq<K\\ K{i}_{p}q>K\end{array}\right.(25)$

where $q$ is the rainfall intensity; $i_p$ is the hydraulic gradient; $K$ is the hydraulic conductivity of pavement.

The thickness of the rainwater stabilization aggregation boundary is small, which is about 10⁻³ m. Therefore, the hydraulic gradient ($i_p$) can be expressed by Equation 26 (Nian et al., 2021):

$i_p=\left\{\begin{array}{l}\frac{{10}^{-3}}{L_{\mathrm{p}}}\left(q-K\right)*t\ge {10}^{-3}\\ \left(q-K\right)*\frac{t}{L_{\mathrm{p}}}\left(q-K\right)*t<{10}^{-3}\end{array}\right.(26)$

where $L_{\mathrm{p}}$ is the seepage length.

Equation 27 shows the definition of the surface evaporation rate (Zhang ML. et al., 2016),

$E=\frac{{\rho }_{vs}-{\rho }_{va}}{r_a+r_s}(27)$

where ${\rho }_{va}$ is atmospheric vapor density; $r_a$ is aerodynamic resistance; $r_s$ is soil resistance. The parameters $r_a$ and $r_s$ can be obtained by Equations 28, 29, respectively (Van Bavel and Hillel, 1976; Van de Griend and Owe, 1994),

$r_a=\frac{\ln \left(2.0/z_0\right)}{1.16u}(28)$

$r_s=10e^{100\left({\theta }_{\min }-{\theta }_{top}\right)}(29)$

where $u$ is wind speed at 2 m height; $z_0$ is surface roughness; ${\theta }_{top}$ and ${\theta }_{\min }$ are the soil water content of top layer and empirical minimum.

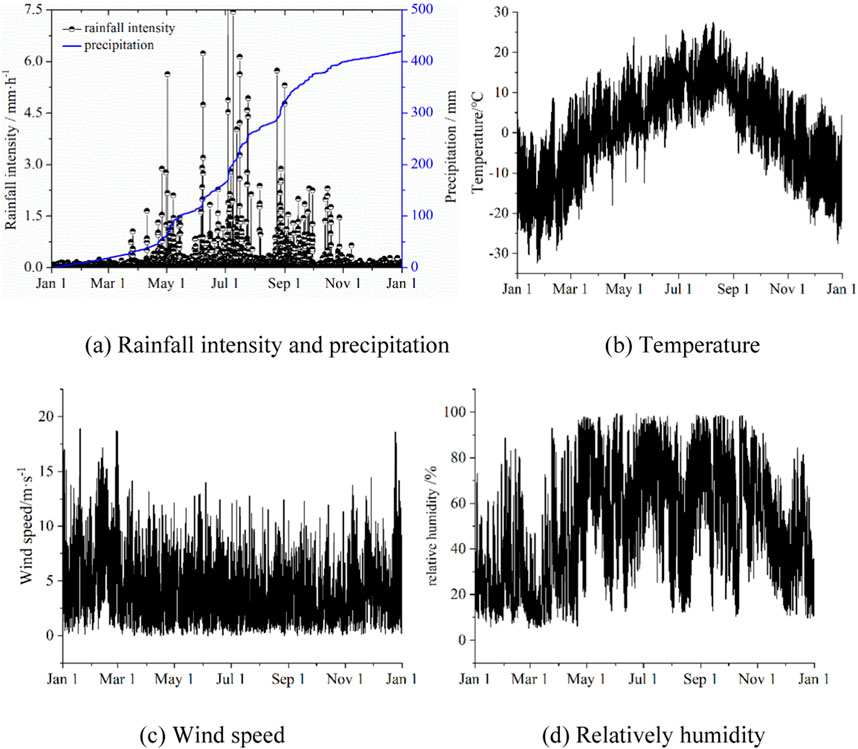
Figure 2 presents the basic meteorological results for the year 2023, which were used in the numerical model. It is evident that rainfall shows a distinct seasonal pattern, with higher amounts occurring in the warm season (April to October) and lower amounts in the cold season (October to April of the following year). Given the limited proportion of snowfall and the short duration of snow cover, this study exclusively focuses on analyzing the impact of rainfall boundary on the water and heat coupling process.

Figure 2

Figure 2. Basic meteorological monitoring for the year 2023.

The complex water-heating process was simulated using COMSOL Multiphysics software. To tackle this problem, two dependent variables were defined: $\theta$ for the water content and $T$ for the temperature. Then, the governing equations (Equations 1, 16) were represented in the form of partial differential equations (PDEs). Finally, input the model parameters into the model, the hydro-thermal coupled calculations can be performed. Despite the meteorological data, the numerical model necessitates supplementary parameters, as detailed in Table 2.

Table 2

Table 2. Model parameters.

2.3 Model verification

Figure 3 shows the variation of the measured and simulated unfrozen water content at four depths. The infiltration and evaporation of rainfall lead to significant fluctuations in the soil moisture content at 10 cm, and results in a larger bias between the measure and simulated results. In comparison, the soil moisture content exhibits less variation at depths of 25, 50, and 100 cm, and the model predictions show reduced deviation from the measured values. In generally, there is good agreement between the monitored data and the simulated results. At four distinct depths, the amount of unfrozen water in the melting stage is substantially more than that in the freezing stage. Because the temperature rises above freezing point from winter to spring, the amount of unfrozen water increases from the top to the bottom, reaching a maximum of roughly 0.15 m³/m³. During the warm season, the soil water content undergoes significant fluctuations, especially the shallow soil. According to statistical data on the volumetric water content of soil, the model’s performance, as evidenced by the statistical analysis (RMSE < 4.68% and MBE < 2.85%), effectively captures the water migration patterns within frozen soils under these conditions.

Figure 3

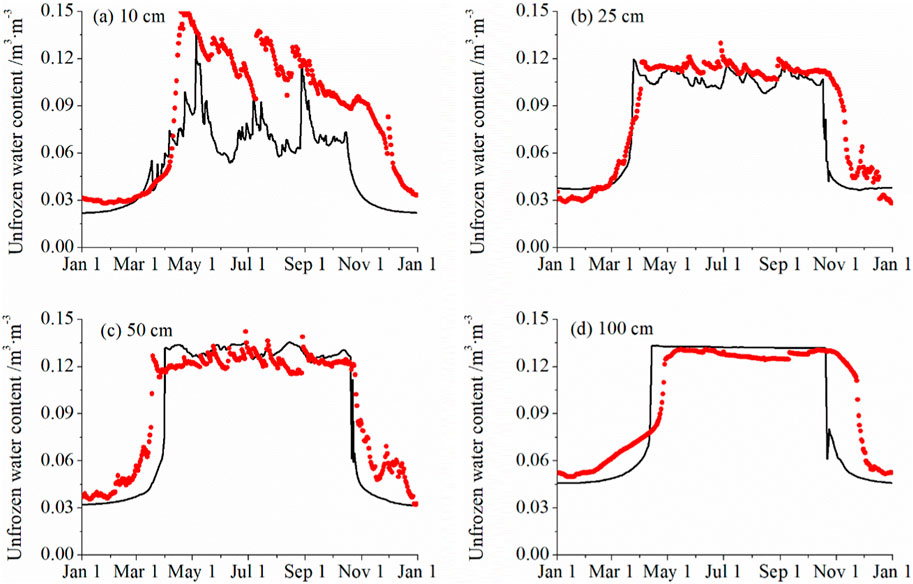
Figure 3. Comparison between the simulated and the measured unfrozen water content at four depths (The scatter points are the measured unfrozen water contents and the solid lines are the simulated results).

As observed in Figure 4, there is little difference between the measured and simulated temperatures. The end of July or the start of August mark the peak temperature of the soil. The temperature takes around 10 days to reach its maximum value when the depth goes from 5 to 100 cm. Additionally, when one descends deeper, the variation in soil temperature decreases to almost −3 °C/m. The root mean square error (RMSE) is less than 2.10°C and the maximum relative error (MBE) is less than 0.81°C. These results suggest that the proposed model is reasonably reliable at forecasting temperature variance in frozen soil.

Figure 4

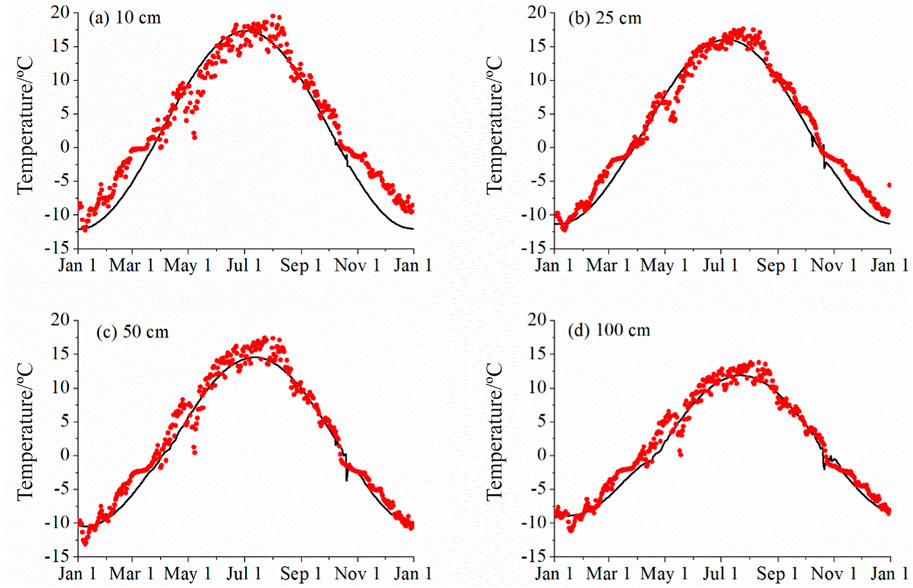
Figure 4. Comparison between the simulated and the measured temperature at four depths (The scatter points are the measured temperatures, and the solid line is the simulated result).

In this study, much attention should be paid to the variations of water and temperature in the embankment. Comparisons indicate that the water-heat coupling model is accurate when it considering the water flux boundary conditions. Consequently, the modified model can be applied to examine the how rainfall penetration affects the water and heat transportation within permafrost embankment. Thus, the water and heat response to four different rainfall intensities: none (0.0 R), half of the current rainfall (0.5 R), current rainfall (1.0 R), and 1.5 times the current rainfall (1.5 R) were examined in the following sections.

3 Results and analysis

3.1 Water content

Figure 5 illustrates the water content varies under four rainfall intensities. Notably, the total water content exhibits significant seasonal fluctuations at 2.5 m ∼ 3.0 m, while showing minimal change in 0 ∼ 2.5 m, regardless of rainfall intensity. This indicates that rainfall infiltration depth is about 0.5 m. Under rainfall intensities 0.0, 0.5, 1.0, and 1.5 R, the water content ranges within 2.5 ∼ 3.0 m are 0.07 ∼ 0.08 m³/m³, 0.05 ∼ 0.15 m³/m³, 0.07 ∼ 0.20 m³/m³ and 0.09 ∼ 0.20 m³/m³, respectively. Generally, water content increases with higher rainfall intensity. However, it is important to note that the water flux boundary condition is influenced by both rainfall and evaporation. When rainfall intensity is lower than the evaporation rate, soil water content decreases, as observed in the results on September 15 (Figures 5A, B). As the rainfall intensity increases from 1.0 to 1.5 R, the maximum water content remains almost constant, but the minimum water content increases with the rainfall intensity, and in July 15 the volumetric water content decreases from 0.18 to 0.13 m³/m³ (Figures 5C, D). This is because the infiltration rate of rainfall is also affected by the hydraulic conductivity of the pavement (Equation 22), when the rainfall intensity is greater than the hydraulic conductivity of the pavement, part of the rainfall will flow away as surface runoff, in other words, the maximum rate of rainfall infiltration is the hydraulic conductivity of the pavement, but the increase in rainfall intensity accelerates the rate of evaporation (Van Bavel and Hillel, 1976), which results in the volumetric water content at 1.5 R being lower than the volumetric water content at 1.0 R in July 15. Due to evaporation and occasional rainfall, the water content of superficial soil (2.5∼3.0 m) fluctuates significantly. In summary, the introduction of water flux boundary conduction leads to water redistribution and accelerates the water migration process, as evidenced by the observed variations in water content.

Figure 5

Figure 5. Variation of soil water content at different depths under four rainfall intensities.

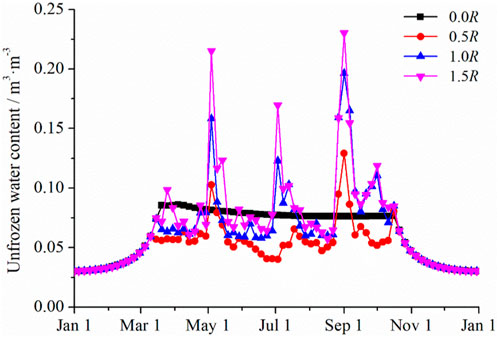
Figure 6 provides the variation of soil water content with time at a depth of 0.05 m beneath the top surface. It indicates that rainfall has little influence on the water content during the cold seasons, but it causes obvious fluctuation during the warm seasons, with the fluctuation amplitude increasing with rainfall intensities. For instance, when the rainfall intensity increases from 0.5 to 1.0 R, 1.5 R, the maximum water content in May increases from 0.10 to 0.16 m³/m³ and 0.23 m³/m³, respectively. It is noted that in arid and semi-arid regions, evaporation exceeds rainfall, leading to a decrease in soil water content below the initial value. Despite this, the total water content shows an increasing trend with the increase of rainfall from 0.5 to 1.0 R, 1.5 R in warm seasons, with average increments of about 5.50% and 14.27%, respectively. However, the increase in rainfall has little effect on the total water content in cold seasons. During the transition from winter to spring, there is a minimal change in soil water content due to the reduction in evaporation and precipitation. Overall, the results indicate that rainfall has a significant influence on soil water content in warm seasons, particularly in arid and semi-arid regions where evaporation is high.

Figure 6

Figure 6. Variation of water content with time under different rainfall intensities.

3.2 Water flux

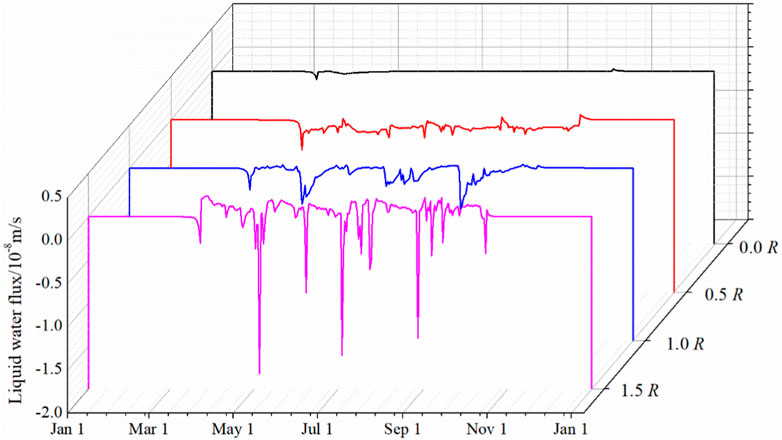
Figure 7 illustrates the variation of liquid water flux at a depth of 0.05 m under various rainfall intensities. All curves exhibit a similar trend: liquid water flux fluctuates greatly during the warm seasons but remains unchanged during cold seasons. This is due to the low hydraulic conductivity of frozen soil (lower than 10^–10 m/s), resulting in minimal liquid water migration. As soil temperature increases, the thawing of frozen soil facilitates the free penetration of rainfall, thereby enhancing water content. As shown in Figure 7, liquid water fluxes at 5 cm depth under rainfall intensities of 0.0, 0.5, 1.0 and 1.5 R are 0, −0.27 ∼ 0.04 (×10⁻⁸ m/s), −0.41 ∼ 0.06 (×10⁻⁸ m/s), −1.82 ∼ 0.24 (×10⁻⁸ m/s), respectively. The liquid water flux increases with higher rainfall intensity. Following Equations 1, 5, after rainfall penetration, both water content and water saturation increase, leading to an increase in hydraulic conductivity of liquid water and liquid water flux. However, this relationship is not linear. A higher moisture content corresponds to a larger evaporation coefficient, causing a more significant change in water content due to rapid evaporation after rainfall (Nian et al., 2021). Consequently, soil moisture content fluctuates significantly. In summary, increased rainfall accelerates the liquid water migration process during warm seasons.

Figure 7

Figure 7. Variation of liquid water flux at four rainfall intensities.

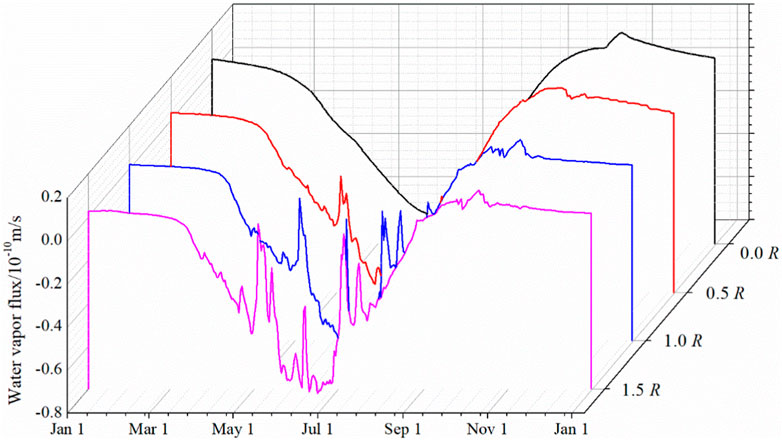
Figure 8 illustrates the water vapor flux at a 0.05 m depth under varying rainfall intensities. The four curves consistently show a pattern of significant variability in warm seasons, with flux values ranging from −0.82 to 0.18 (×10–10 m/s) (negative values indicating downward flux), and minimal fluctuations in cold seasons. Notably, the amplitude of fluctuations increases with larger rainfall intensity. Under conditions of 0.0, 0.5, 1.0, and 1.5 R, the water vapor flux ranged from −0.64 ∼ −0.45 (×10^–8 m/s) to −0.75 ∼ −0.26 (×10^–8 m/s), −0.76 ∼ −0.14 (×10⁻⁸ m/s) and −0.76 ∼ −0.08 (×10⁻⁸ m/s) in May, respectively. This reveals that larger rainfall intensity leads to a reduction in water vapor flux, primarily due to increased liquid water infiltration, which in turn decreases air volume and vapor diffusivity in the soil. Consequently, rainfall impedes downward water vapor migration, particularly in warmer conditions. Comparing Figures 7, 8, one observes that water vapor flux is significantly lower than liquid water flux in warm seasons, while its contribution to water migration is more substantial in cold seasons. In summary, an increase in rainfall leads to a rise in liquid water flux and a decline in water vapor flux, ultimately augmenting soil water content.

Figure 8

Figure 8. Variation of water vapor flux at different rainfall intensities.

3.3 Heat flux

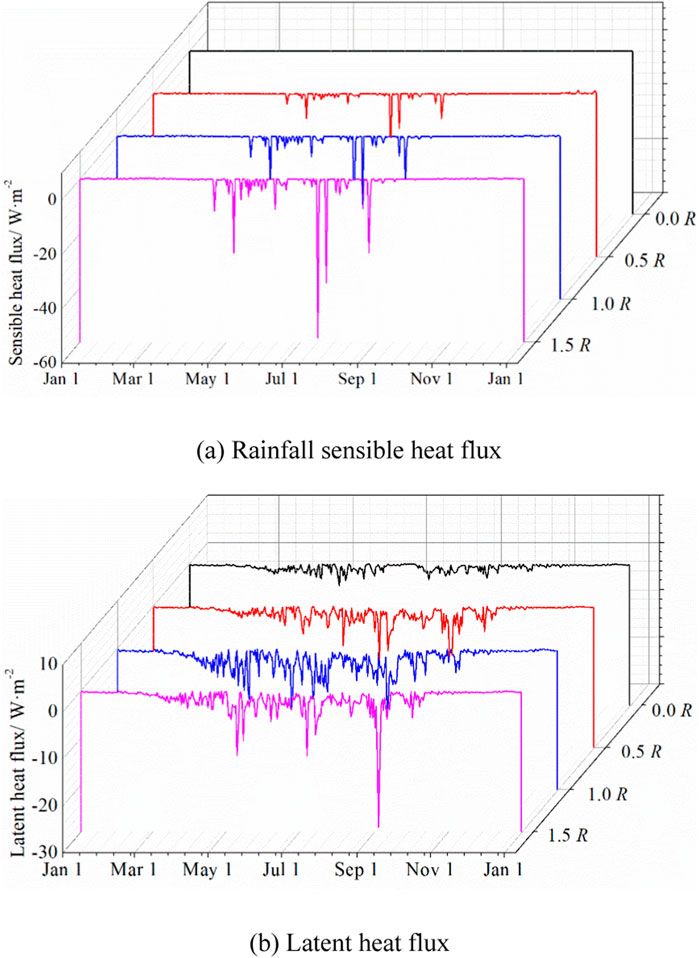
As shown in Figure 9A, rainfall sensible heat exhibits seasonal variations, characterized by consistently low values during cold seasons and fluctuations in warm seasons. A general upward trend in sensible heat flux is observed with increasing rainfall intensity. The average annual sensible heat flux rises from 111.6 to 208.7 W/m² and 288.1 W/m² when the rainfall intensity increases from 0.5 to 1.0 R and 1.5 R, respectively. This is due to the dependence of sensible heat on rainfall intensity and the temperature difference between rain and soil. In the cold season, these factors are relatively small, resulting in minimal variation in sensible heat across the three rainfall conditions. Conversely, during warm seasons, both the rainfall intensity and temperature difference are substantial, leading to higher sensible heat values. Furthermore, since the rainfall temperature is higher than the soil temperature, it acts as a cooling agent, reducing the soil temperature. During the freezing period, surface evaporation was minimal, and the disparities in latent heat among the three scenarios were insignificant. However, an upward trend in latent heat flux ensued with increased rainfall, particularly from April to October. During the period of concentrated rainfall in July, the increase in latent heat was not significant; instead, in September, there was a significant increase in latent heat. This is due to the fact that during the rainfall period, evaporation is hindered by the predominance of liquid water migration in the soil. After the rainfall, the evaporation rate increased due to the increase in soil water content. The latent heat flux increased from about 10 W/m² in July to 30 W/m² in September (Figure 9B). Notably, when the rainfall intensity rose from 0.0 to 0.5, 1.0, and 1.5 R, the annual mean latent heat flux increased by 42.77%, 67.89%, and 97.28%, respectively. According to the principle, when maintaining constant evaporation capacity, incorporating a water flux boundary condition can enhance both water content and evaporation heat flux. Consequently, the adoption of a closed boundary in the model leads to an overestimation of soil temperature.

Figure 9

Figure 9. Variation of heat flux with time under four different rainfall intensities.

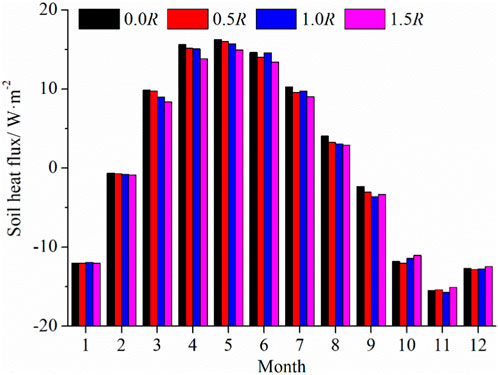
Figure 10 illustrates the monthly variations of soil heat flux at 0.05 m beneath the pavement. It shows that from January to February, the differences in soil heat flux under various conditions were less than 0.20 W/m²; from March to October, these differences gradually increased to 1.30 W/m²; and from October to December, they decreased below 0.20 W/m². Furthermore, the maximum soil heat flux under the four rainfall scenarios was 16.28,16.02, 15.69, and 14.93 W/m², respectively. When the rainfall intensity increased from 0R to 0.5, 1.0, and 1.5 R, the soil heat flux decreased by 0.26, 0.58, and 1.35 W/m², corresponding to reductions of 1.62%, 3.61%, and 8.28%, respectively. The data indicate that rainfall in the warm season has a more pronounced effect on reducing soil heat flux compared to equivalent rainfall in the cold season, and this reduction is positively correlated with the rainfall amount. Under the four temperature scenarios, the annual average soil heat flux is positive, suggesting that the surface absorbs more heat than it releases. However, it shows a decreasing trend, with the absorbed heat decreasing as rainfall increases. This trend slows down the degradation of permafrost and contributes to the stability of frozen ground.

Figure 10

Figure 10. Influence of rainfall intensity on monthly average heat flux.

3.4 Temperature

Figure 11 illustrates the soil temperature response at a depth of 0.05 m beneath the pavement. As seen, the temperature curves without rainfall exhibits a smoother profile, and there is no discernible difference between varying rainfall intensities during cold seasons; whereas temperatures under rainfall conditions exhibit fluctuations, and soil temperatures being consistently lower than non-rainfall conditions during the same period in warm seasons (Figure 11A). In July, the soil temperature drops by 0.36°C, 0.64°C, and 0.85°C under 0.5, 1.0, and 1.5 R rainfall intensities, respectively, while in January, the drops are 0.07°C, 0.07°C, and 0.06°C, respectively (Figure 11B). This indicates that rainfall can significantly cool the embankment in warm seasons, and the cooling effect positively related to rainfall intensity. Compared to warm seasons, rainfall contributes a lesser impact to cooling in cold seasons. The reduced cooling effect in colder seasons is due to smaller evapotranspiration and sensible heat fluxes (Figure 9), as well as the closer temperature proximity between rainfall and the soil, limiting the cooling influence at the boundary. The larger temperature difference between soil and rainfall can temporarily decrease soil heat conduction flux (Figure 10). Moreover, larger rainfall intensity leads to an increase in evapotranspiration and sensible heat, enhancing the heat transfer from the embankment to the air. Consequently, soil temperatures decline with escalating rainfall intensity.

Figure 11

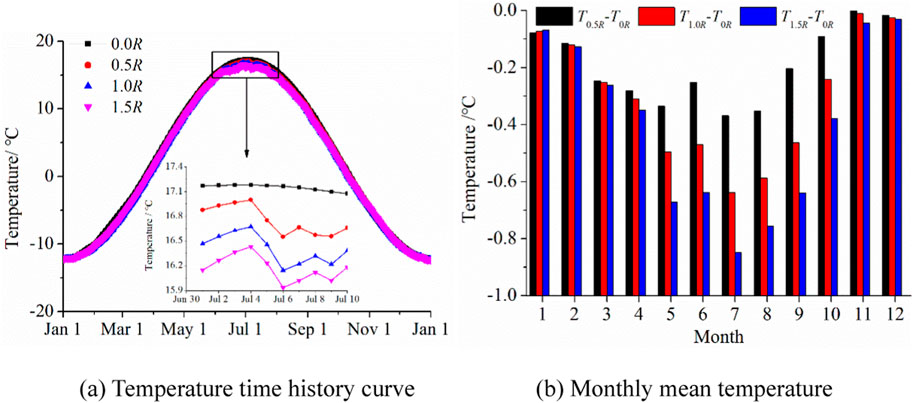
Figure 11. Influence of rainfall intensity on the soil temperature at 5 cm (T_0.0R is soil temperature without rainfall; T_0.5R is the soil temperature under the rain fall intensity 0.5 R; T_1.0R is the soil temperature under the rainfall intensity 1.0 R; T_1.5R is the soil temperature under the rainfall intensity 1.5 R).

4 Discussions

In the context of the ongoing humidification and warming, the impact of rising precipitation on permafrost dynamics has garnered significant attention in recent years (Magnússon et al., 2022). This study employed rainfall as the water flux boundary condition to investigate its influence on thermal-moisture dynamics within permafrost embankment. By comparing the open boundary (0.5, 1.0, 1.5 R) to a closed boundary (0.0 R), the results reveal that precipitation leads to a decline in superficial soil’s temperature, particularly in warm seasons. Consistent with observations at Fenghuoshan in permafrost regions (Wu et al., 2015; Cai et al., 2018), the findings underscored the enhanced cooling effect with increased rainfall. These results substantiate the logical and essential nature of incorporating water flux boundaries in the modeling of permafrost embankment’s thermal dynamics.

Figure 12 illustrates the distinct moisture transport mechanisms in the upper soil layer prior to and following rainfall. During the non-rainfall period in summer, the superficial soil exhibits a higher temperature and lower water content. Water vapor migrates downward due to the temperature gradient, while liquid water ascends driven by matric potential (Luo et al., 2020). Post-rainfall, the superficial soil cools down and water content rises, causing water vapor to ascend under the temperature gradient, and liquid water to descend under the matrix potential gradient. Notably, this post-rainfall migration direction contrasts with the pre-rainfall condition (Figure 12). It can be explained that rainfall infiltration increases the water content and permeability, and thereby promoting the migration of liquid water within the soil, and finally alters the distribution pattern of water (Li et al., 2012). As depicted in Figures 7, 8, liquid water flux significantly exceeds water vapor flux. Consequently, following rainfall, water moves downward and increases soil water content, which leads to a decrease in water vapor flux (Luo et al., 2016). This leads to substantial fluctuations in superficial soil moisture content during warm seasons. These factors collectively contribute to the phenomenon of rainfall accelerating the water migration process within the embankment.

Figure 12

Figure 12. Schematic of moisture transport in shallow soil before and after rainfall.

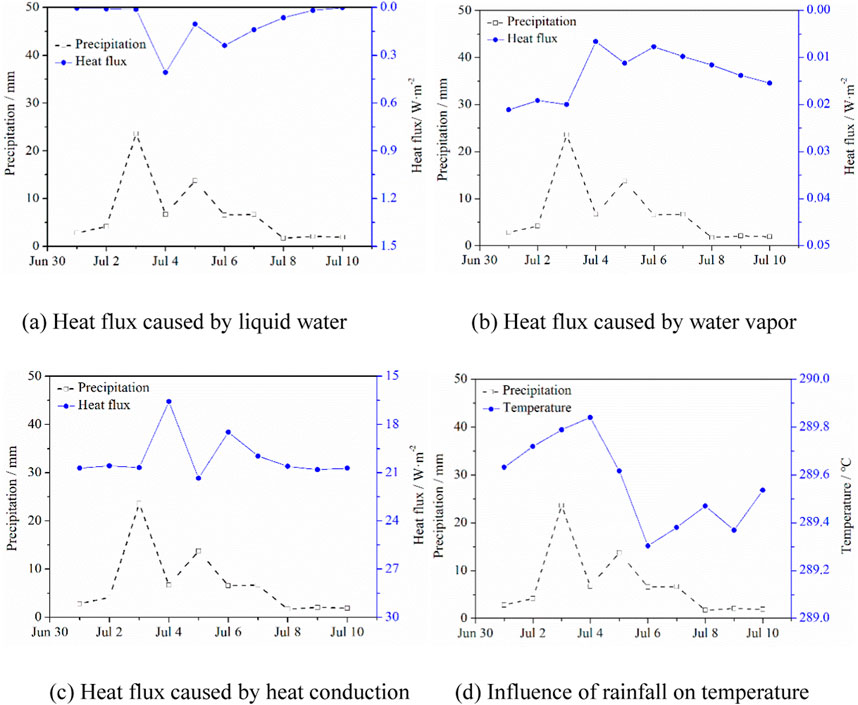
Water migration, involving liquid and vapor phases, often coexists with energy transfer, particularly including evaporation and phase change, which influences soil temperature dynamics (Chen et al., 2020). To elucidate this process, we examined relative energy data from July 1 to 10, focusing on significant rainfall events (Figure 13). On July 3, for instance, the average daily heat flux caused by conduction at 0.05 m dropped by 4.57 W/m², while the heat flux caused by liquid water increased by 0.38 W/m² and heat flux caused by water vapor decreased by 0.02 W/m². The substantial decrease in heat conduction indicates a dominant cooling effect (Figure 13D), as the magnitude of this decline surpasses the thermal convection boost from liquid water. Prior research suggests that rainfall temperatures are at least 3∼5°C lower than air temperatures, qualifying it as a cooling agent (Neumann et al., 2019). In warm seasons, the superficial soil temperature is higher than the rainfall temperature. Consequently, the superficial soil temperature decreases after rain. According to the results, the cooling effect is determined by both the rainfall intensity and the temperature difference between rainfall and soil. The cooling impact is influenced by both rainfall intensity and the temperature difference between soil and rainfall. As per Figure 2, summer receives over 80% of annual rainfall, resulting in a pronounced cooling effect due to the large temperature disparities. Seasonal rainfall variations thus impact the permafrost embankment’s temperature field by accelerating water migration and altering energy distribution patterns.

Figure 13

Figure 13. Variations of heat flux and temperature with rainfall (rainfall intensity 1.0 R).

The results indicate that rainfall can lower the temperature of the superficial soil. However, it also causes the superficial soil to undergo the dry-wet cycles, leading to a decrease in soil strength (Zhang et al., 2013). Besides, rainfall increases constantly is not beneficial to the stability of embankment. This is because rainfall can increase the soil water content, and it may uplift the groundwater level. A large number of engineering examples show that the soil will be saturated for a long time after the water infiltration into the embankment, and the embankment is prone to frost heave, settlement, and local collapse under the combined action of traffic load and freeze-thaw cycle (Jiang et al., 2023). Therefore, there is a rainfall balance point, so that rainfall is conducive to the thermal stability and protects the operation of the permafrost embankment.

5 Conclusion

Based on the established permafrost embankment water-heat coupling theory, the model was enhanced by incorporating rainfall and evaporation into water flux boundary condition. The reliability of the modified model was confirmed through validation with monitoring data from the Tibet Plateau. An analysis of water-heat transport under different boundary conditions led to the following key findings:

(1) The model incorporating the water flux boundary condition more accurately captures fluctuations in water content in warm seasons, whereas there is little difference in performance without the water flux boundary condition in cold seasons. It is advisable to employ the water flux boundary condition in numerical simulations of water-heat transfer within permafrost embankments.

(2) Rainfall influences the soil moisture to a depth of approximately 0.50 m. Summer rainfall rapidly impacts superficial soil moisture, but no significant accumulation occurs within the embankment. Increased rainfall intensity enhances liquid water flux and reduces water vapor flux, thereby accelerating the water migration process.

(3) Under humidification conditions, the decrease in heat conduction flux due to rainfall outweighs the increase in convective heat flux from liquid water. This results in a cooling effect that mitigates thermal disturbances within the embankment and alleviates the thermal disturbance of embankment on the underlying permafrost.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

ZW: Methodology, Writing–original draft, Writing–review and editing, Conceptualization, Resources. LW: Conceptualization, Formal Analysis, Methodology, Writing–original draft, Writing–review and editing. XW: Formal Analysis, Investigation, Writing–original draft, Writing–review and editing. FM: Funding acquisition, Methodology, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the Science and Technology Plan Project of Qinghai Province (2023-SF-125) and the Science Fund for Distinguished Young Scholars of Gansu Province (23JRRA615).

Conflict of interest

Author ZW was employed by Qinghai Guoluo Highway Engineering Construction Co., Ltd. Authors LW and XW were employed by Qinghai Provincial Traffic Control Construction Engineering Group Co., Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Banimahd, S. A., and Zand-Parsa, S. (2013). Simulation of evaporation, coupled liquid water, water vapor and heat transport through the soil medium. Agric. Water Manag. 130, 168–177. doi:10.1016/j.agwat.2013.08.022

CrossRef Full Text | Google Scholar

Bibi, S., Wang, L., Li, X. P., Zhou, J., Chen, D., and Yao, T. (2018). Climatic and associated cryospheric, biospheric, and hydrological changes on the Tibetan Plateau: a review. Int. J. Climatol. 38 (1), 1–17. doi:10.1002/joc.5411

CrossRef Full Text | Google Scholar

Biskaborn, B. K., Smith, S. L., Noetzli, J., Matthes, H., Vieira, G., Streletskiy, D. A., et al. (2019). Permafrost is warming at a global scale. Nat. Commun. 10, 264. doi:10.1038/s41467-018-08240-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Cai, H. C., Jin, L., Li, Y., Li, F., and Han, L. W. (2018). Influence of precipitation on permafrost in Fenghuo mountain region of Tibetan Plateau. J. China Railw. Soc. 40 (9), 104–110.

Google Scholar

Cao, W., Sheng, Y., Wu, J. C., Yaling, C., Erxing, P., and Leonid, G. (2021). Soil hydrological process and migration mode influenced by the freeze-thaw process in the activity layer of permafrost regions in Qinghai-Tibet Plateau. Cold Regions Sci. Technol. 184, 103236. doi:10.1016/j.coldregions.2021.103236

CrossRef Full Text | Google Scholar

Cass, A., Campbell, G., and Jones, T. (1984). Enhancement of thermal water vapor diffusion in soil. Soil Sci. Soc. Am. J. 48 (1), 25–32. doi:10.2136/sssaj1984.03615995004800010005x

CrossRef Full Text | Google Scholar

Chen, L., Fortier, D., McKenzie, J. M., and Sliger, M. (2020). Impact of heat advection on the thermal regime of roads built on permafrost. Hydrol. Process. 34 (7), 1647–1664. doi:10.1002/hyp.13688

CrossRef Full Text | Google Scholar

Cheng, G. D., Zhao, L., Li, R., Wu, X. D., Sheng, Y., Hu, G., et al. (2019). Characteristic, changes and impacts of permafrost on Qinghai-Tibet Plateau. Chin. Sci. Bull. 64 (27), 2783–2795. doi:10.1360/tb-2019-0191

CrossRef Full Text | Google Scholar

Dan, H. C., Li, L., and Li, L. (2011). Calculation for infiltration rate of flow in cracking asphalt pavement. J. Harbin Inst. Technol. 43 (6), 105–111.

Google Scholar

Hansson, K., Lundin, L. C., and Simkunek, J. (2005). Modeling water flow patterns in flexible pavements. Transp. Res. Rec. J. Transp. Res. Board, 1936, 133–141.

CrossRef Full Text | Google Scholar

Jiang, G. L., Wu, Q. B., and Zhang, Z. Q. (2018). Study on the differences of thermal moisture dynamics in the active layer of permafrost in different alpine ecosystems on the Tibet plateau. J. Glaciol. Geocryol. 40 (1), 7–17. doi:10.7522/j.issn.1000-0240.2017.0316

CrossRef Full Text | Google Scholar

Jiang, H. G., Huang, B. B., Ma, C. Y., Liu, Y. Y., Wang, K., and Yao, Z. Y. (2023). Moisture field of fine-soil subgrade with the influence of groundwater and rainfall. J. Shandong Univ. Eng. Sci. 53 (5), 74–82. doi:10.6040/j.issn.1672-3961.0.2022.093

CrossRef Full Text | Google Scholar

Jiang, Y. H., Li, G. S., Zhao, L. Y., Zhao, Y. Q., Duan, S. L., Zhang, W. D., et al. (2020). Temperature field study for permafrost subgrade with compound thermal boundaries. J. Inn. Mong. Univ. Nat. Sci. Ed. 51 (11), 649–657. doi:10.13484/j.nmgdxxbzk.20200614

CrossRef Full Text | Google Scholar

Kollet, S. J., Cvijanovic, I., Schüttemeyer, D., Maxwell, R. M., Moene, A. F., Bayer, P., et al. (2009). The influence of rain sensible heat and subsurface energy transport on the energy balance at the land surface. Vadose Zone J. 8 (4), 846–857. doi:10.2136/vzj2009.0005

CrossRef Full Text | Google Scholar

Lai, Y. M., Zhang, M. Y., and Li, S. Y. (2009). Theory and application of cold region engineering. Beijing: Science Press.

Google Scholar

Li, R., Zhao, L., Ding, Y. J., Wu, T., Xiao, Y., Du, E., et al. (2012). Temporal and spatial variations of the active layer along the Qinghai-Tibet Highway in a permafrost region. Chin. Sci. Bull. 57 (30), 4609–4616. doi:10.1007/s11434-012-5323-8

CrossRef Full Text | Google Scholar

Li, X. L., Ma, W., Mu, Y. H., Niu, Y. H., Huang, Y. T., and Chai, M. T. (2020). Influence of boundary conditions on the thermal stability of expressway constructed with an integral and two separated embankments in permafrost zones. J. Central South Univ. Sci. Technol. 51 (2), 420–431. doi:10.11817/j.issn.1672-7207.2020.02.01

CrossRef Full Text | Google Scholar

Liu, W. B., Yu, W. B., Fortier, R., Chen, L., Lu, Y., Zhang, M., et al. (2018). Thermal effect of rainwater infiltration into a replicated road embankment in a cold environmental chamber. Cold Regions Sci. Technol. 159, 47–57. doi:10.1016/j.coldregions.2018.12.008

CrossRef Full Text | Google Scholar

Luo, S. Q., Fang, X. W., Lu, S. H., Ma, D., Chang, Y., Song, M., et al. (2016). Frozen ground temperature trends associated with climate change in the Tibetan Plateau Three River Source Region from 1980 to 2014. Clim. Res. 67 (3), 241–255. doi:10.3354/cr01371

CrossRef Full Text | Google Scholar

Luo, Y., Zhang, J. M., Zhou, Z., Chikhotkin, V., Mi, M., and Shen, J. (2020). Evolution law of critical moisture content of soil cracking under rainfall-evaporation conditions. Rock Soil Mech. 41 (8), 2592–2600. doi:10.16285/j.rsm.2019.1465

CrossRef Full Text | Google Scholar

Magnússon, R. Í., Hamm, A., Karsanaev, S. V., Limpens, J., Kleijn, D., Frampton, A., et al. (2022). Extremely wet summer events enhance permafrost thaw for multiple years in Siberian tundra. Nat. Commun. 13, 1556. doi:10.1038/s41467-022-29248-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Mekonnen, Z. A., Riley, W. J., Grant, R. F., and Romanovsky, V. E. (2021). Changes in precipitation and air temperature contribute comparably to permafrost degradation in a warmer climate. Environ. Res. Lett. 16, 024008. doi:10.1088/1748-9326/abc444

CrossRef Full Text | Google Scholar

Millington, R., and Quirk, J. (1961). Permeability of porous solids. Trans. Faraday Soc. 57, 1200–1207. doi:10.1039/tf9615701200

CrossRef Full Text | Google Scholar

Nassar, I., and Horton, R. (1997). Heat, water, and solution transfer in unsaturated porous media: I--theory development and transport coefficient evaluation. Transp. Porous Media 27, 17–38. doi:10.1023/a:1006583918576

CrossRef Full Text | Google Scholar

Neumann, R. B., Moorberg, C. J., Lundquist, J. D., Turner, J. C., Waldrop, M. P., McFarland, J. W., et al. (2019). Warming effects of spring rainfall increase methane emissions from thawing permafrost. Geophys. Res. Lett. 46 (3), 1393–1401. doi:10.1029/2018gl081274

CrossRef Full Text | Google Scholar

Nian, G. Q., Chen, Z. H., Zhang, L. F., et al. (2021). Treatment of two boundary conditions for rainfall infiltration in slope and its application. Rock Soil Mech. 41 (12), 4105–4115.

Google Scholar

Peng, H., Wei, Y., Yuan, K., et al. (2023). Study on moisture migration rule and disaster mechanism of permafrost highway subgrade. J. Highw. Transp. Res. Dev. 40 (3), 42–50. doi:10.3969/j.issn.1002-0268.2023.03.006

CrossRef Full Text | Google Scholar

Philip, J., and De Vries, D. (1957). Moisture movement in porous materials under temperature gradients. Trans. Am. Geophys. Union 38 (2), 222–232. doi:10.1029/TR038i002p00222

CrossRef Full Text | Google Scholar

Qin, X. T., Cui, K., and Qing, Y. L. (2022). Study on rainfall infiltration law and mechanism of seasonal frozen soil slope under hydro-thermal coupling effect. China J. Highw. Transp. 35 (4), 87–98. doi:10.19721/j.cnki.1001-7372.2022.04.006

CrossRef Full Text | Google Scholar

Saito, H., Imnek, J., and Mohanty, B. P. (2006). Numerical analysis of coupled water, vapor, and heat transport in the vadose zone. Vadose Zone J. 5 (2), 784–800. doi:10.2136/vzj2006.0007

CrossRef Full Text | Google Scholar

Van Bavel, C., and Hillel, D. (1976). Calculating potential and actual evaporation from a bare soil surface by simulation of concurrent flow of water and heat. Agric. Meteorol. 17 (6), 453–476. doi:10.1016/0002-1571(76)90022-4

CrossRef Full Text | Google Scholar

Van de Griend, A. A., and Owe, M. (1994). Bare soil surface resistance to evaporation by vapor diffusion under semiarid conditions. Water Resour. Res. 30 (2), 181–188. doi:10.1029/93wr02747

CrossRef Full Text | Google Scholar

Van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44 (5), 892–898. doi:10.2136/sssaj1980.03615995004400050002x

CrossRef Full Text | Google Scholar

Wei, N., Dai, Y. J., Zhang, M. H., Zhou, L., Ji, D., Zhu, S., et al. (2014). Impact of precipitation-induced sensible heat on the simulation of land-surface air temperature. J. Adv. Model Earth Syst. 6 (4), 1311–1320. doi:10.1002/2014ms000322

CrossRef Full Text | Google Scholar

Woo, M. K., Kane, D. L., Carey, S. K., and Yang, D. (2018). Progress in permafrost hydrology in the new millennium. Permafr. Periglac. Process. 19 (2), 237–254. doi:10.1002/ppp.613

CrossRef Full Text | Google Scholar

Wu, Q. B., Hou, Y. D., Yun, H. B., and Liu, Y. (2015). Changes in active-layer thickness and near-surface permafrost between 2002 and 2012 in alpine ecosystems, Qinghai-Xizang (Tibet) Plateau, China. Glob. Planet. Change 124, 149–155. doi:10.1016/j.gloplacha.2014.09.002

CrossRef Full Text | Google Scholar

Xu, X. Z., Wang, J. C., and Zhang, L. X. (2010). Frozen soil physics. Beijing: Science press.

Google Scholar

Yang, K. F., Mu, Y. H., Ma, W., Bi, G. Q., Li, G. Y., and Mao, Y. C. (2018). The evolution law of ground temperature field in permafrost roadbed in Qinghai-Tibet plateau under climate warming. China Earthq. Eng. J. 40 (4), 734–744. doi:10.3969/j.issn.1000-0844.2018.04.0734

CrossRef Full Text | Google Scholar

Zhang, G. F., Nan, Z. T., Hu, N., Yin, Z., Zhao, L., Cheng, G., et al. (2022b). Qinghai-Tibet plateau permafrost at risk in the late 21st century. Earth’s Future 10 (6), 2022EF002652. doi:10.1029/2022ef002652

CrossRef Full Text | Google Scholar

Zhang, M. L., Wen, Z., Li, D. S., Chou, Y., Zhou, Z., Zhou, F., et al. (2021). Impact process and mechanism of summertime rainfall on thermal-moisture regime of active layer in permafrost regions of central Qinghai-Tibet Plateau. Sci. Total Environ. 796 (4), 148970. doi:10.1016/j.scitotenv.2021.148970

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, M. L., Wen, Z., Xue, K., and Chen, L. (2016b). A coupled model for liquid water, water vapor and heat transport of saturated–unsaturated soil in cold regions: model formulation and verification. Environ. Earth Sci. 75 (8), 701–719. doi:10.1007/s12665-016-5499-3

CrossRef Full Text | Google Scholar

Zhang, S., Teng, J. D., He, Z. Y., and Sheng, D. (2016a). Importance of vapor flow in unsaturated freezing soil: a numerical study. Cold Regions Sci. and Technol. 126, 1–9. doi:10.1016/j.coldregions.2016.02.011

CrossRef Full Text | Google Scholar

Zhang, T. Q., Yu, W. B., Lu, Y., and Chen, L. (2022a). Identification and correlation analysis of engineering environmental risk factors along the Qinghai-Tibet engineering corridor. Remote Sens. 14 (4), 908. doi:10.3390/rs14040908

CrossRef Full Text | Google Scholar

Zhang, Z. Q., Wu, Q. B., Wen, Z., Liu, Y. Z., and Lu, Z. J. (2013). Analysis of moisture accumulation process on frozen soil subgrade of asphalt pavement. China J. Highw. Transp. 26 (2), 1–6.

Google Scholar

Zhou, Z. X. (2022). The influence of rainfall in different seasons on thermal-moisture dynamics of permafrost active layer in the Qinghai-Tibet Plateau. Lanzhou: Lanzhou University of Technology.

Google Scholar

Zhou, Z. X., Zhou, F. X., Zhang, M. L., Lei, B. B., and Ma, A. J. (2023). Effects of seasonal rainfall characteristics on the hydrothermal state of permafrost active layer in the central Qinghai-Xizang (Tibet) Plateau. Plateau Meteorol. 42 (5), 1172–1181. doi:10.7522/j.issn.1000-0534.2023.00017

CrossRef Full Text | Google Scholar

Zhou, Z. X., Zhou, F. X., Zhang, M. L., Lei, B. B., and Ma, Z. (2021). Effect of increasing rainfall on the thermal-moisture dynamics of permafrost active layer in the central Qinghai-Tibet Plateau. J. Mt. Sci. 18 (11), 2929–2945. doi:10.1007/s11629-021-6707-5

CrossRef Full Text | Google Scholar