Tree-ring δ18O and δ2H stable isotopes reflect the global meteoric water line

Introduction: The Global Meteoric Water Line (GMWL) describes the linear relationship between stable hydrogen (δ²H) and oxygen (δ¹⁸O) isotopes in precipitation over large spatial scales and therefore represents a unique reference for water isotopic values. Although trees have the potential to capture the isotopic composition of precipitation, it remains unclear if the GMWL can be reconstructed from tree-ring stable isotopes, since δ¹⁸O and δ²H undergo in vivo physiological fractionation.

Methods: We analyze the tree rings δ¹⁸O and δ²H values from six regions along a latitudinal gradient from Spain to Greenland.

Results: The data show that the covariance between δ¹⁸O and δ²H closely follows the GMWL, which reflects the isotopic signature of large-scale precipitation patterns. We show that changes in regional tree-ring δ¹⁸O and δ²H values along wide latitudinal ranges are influenced by the isotopic composition of precipitation with temperature and latitude being the most significant drivers of spatial variation across the studied regions. In contrast, local tree-ring δ¹⁸O and δ²H values are mainly controlled by plant physiological fractionation processes that mask the isotopic signature of precipitation.

Conclusion: We conclude that covariance in tree-ring δ¹⁸O and δ²H reflects the GMWL at larger spatial scales, but not when evaluating them at individual sites.

Introduction

The isotopic composition of precipitation, represented by stable oxygen (δ¹⁸O) and hydrogen (δ²H) isotopes, is influenced by various factors such as temperature, the amount of precipitation, and relative humidity, as well as geographic elements such as latitude, altitude, and distance from the coast (Dansgaard, 1964; Gat, 1996; Bowen et al., 2019). Their relationship is globally defined by the Global Meteoric Water Line (GMWL), which is described by the equation δ²H = 8 δ¹⁸O + 10 (Craig, 1961) that primarily reflects the equilibrium fractionation factors between δ²H and δ¹⁸O in precipitation. These factors are influenced by evaporation processes (Dansgaard, 1964; Gat, 1996; Bowen et al., 2019) and vary at a local scale, leading to the Local Meteoric Water Lines (LMWL) that usually deviate from the GMWL (Lécuyer et al., 2020; Hatvani et al., 2023).

The GMWL provides a reference for the environmental and climatic interpretation of δ¹⁸O and δ²H values in a wide range of paleo proxy archives, including ice cores, speleothems, and lake sediments (Galewsky et al., 2016; Tappa et al., 2016; Pang et al., 2017; Ghadiri et al., 2020). The GMWL has demonstrated remarkable stability through time. Studies of European groundwaters have provided crucial evidence for this consistency, indicating stable atmospheric circulation patterns from the late Pleistocene through the Holocene (Rozanski, 1985).

Stable oxygen and hydrogen isotopes are preserved in the cellulose of living and relict tree rings, and their evaluation is used for climate reconstruction (Hafner et al., 2011; Nakatsuka et al., 2020; Büntgen et al., 2021; Nagavciuc et al., 2022; Xu et al., 2024) and eco-physiological studies (Cherubini et al., 2021; Lehmann et al., 2021; Holloway-Phillips et al., 2023; Vitali et al., 2023). The δ¹⁸O and δ²H isotopic values in cellulose, derived from soil water originally sourced from precipitation, are affected by fractionation processes occurring during pre-photosynthetic, photosynthetic, and post-carboxylation stages (Yakir, 1992; Roden et al., 2000). Thus, it is unclear if their final values in cellulose reflect those of the original precipitation water and if their mutual relationship corresponds to the GMWL. In fact, many factors affect the isotopic composition of cellulose. For example, transpiration enriches leaf water of both heavy isotopes (Roden et al., 2000), and carbonyl-water interactions during cellulose biosynthesis increase δ¹⁸O ratios (ε_o = 27‰) with values that are conserved in the analysed trees (Sternberg and DeNiro, 1983; Sternberg, 2009). Tree-ring δ¹⁸O records are widely used in paleoclimatic research as climate proxy (Siegwolf et al., 2022; Xu et al., 2024). In contrast, the δ²H ratio is decreased during cellulose biosynthesis compared to the leaf water (Cormier et al., 2018; Vitali et al., 2022) due to biological fractionation processes that are variable and differ between species (Arosio et al., 2020b). This, and the difficulty of their measurement (Roden et al., 2000; Cormier et al., 2018; Arosio et al., 2020a; Vitali et al., 2023), complicate the use of tree-ring δ²H values as a proxy archive, although they are potentially useful. One technical difficulty is that only the non-exchangeable, C-bound δ²H (referred to here as δ²Hn) carries climatic or physiological information, and thus, the exchangeable, oxygen-bound H must be subtracted from the measurements. In addition, the use of δ²Hn measures is complicated by uncertainties of hydrogen biological fractionation (Vitali et al., 2022). Moreover, there are inconsistencies between modelled and measured δ²H values (Waterhouse et al., 2002).

The uncertainties of the ability of tree-ring isotopes to faithfully preserve the original precipitation isotope signal is thus a major drawback for their utilization as proxy archives, even though they have the potential to provide broad geographical coverage. Initial efforts to relate δ²H and δ¹⁸O ratios to precipitation and to the GMWL have shown promise at regional scales (Lehmann et al., 2022; Churakova et al., 2023), but systematic studies at the hemispheric scale are still missing. The evaluation of δ¹⁸O and δ²Hn in the cellulose of a large number of samples collected at local and continental scales that cover extended time periods necessary in order to verify if they can be used to detect the GMWL and to identify the conditions for a reconstruction of the water cycle. Here, we show that we conduct study of δ¹⁸O and δ²Hn values in the tree-ring cellulose of living and subfossil wood samples from larch and non-larch conifers collected at six different sites across continental Europe, Iceland, and Greenland. The variations in δ¹⁸O and δ²Hn values between different sites and within each individual site were compared to understand the biological and physiological factors affecting the stable isotopes at different geographical scales.

Methods

Samples collection and stable isotope analysis

The δ¹⁸O and δ²Hn tree-ring cellulose data were analyzed from six sites across Spain, the European Alps, Iceland, and Greenland (Figure 1A; Table 1). While the datasets from Iceland and Greenland are unpublished, the Alpine arc data comes from the publicly available “Alpine Holocene Triple Tree Ring Isotope Record” (AHTTRIR) (Arosio et al., 2022), which comprises 202 trees at the tree line in the Swiss, Austrian, and Italian Alps, covering 46.03–47.03°N and 7.55–15.25°W. This dataset spans the last 9,000 years up to 2015 CE with a 5-year resolution. Analyses indicate a very low correlation (r < 0.2) between tree-ring width and isotopes in the Alpine dataset, confirming that favorable growing conditions (wider rings) do not significantly influence the 5-year average δ¹⁸O and δ²Hn values (Arosio et al., 2021). Greenland samples, with exceptionally narrow rings (mean 0.123 mm), were sectioned into 10-year blocks, while Icelandic wood was cut into annual slices. All samples underwent cellulose extraction (Ziehmer et al., 2018) and isotope analysis (Loader et al., 2015). The network spans six sites from 37°N to 80°N (Figure 1A), featuring larch and non-larch conifers. Samples from Spain and Iceland cover four centuries, the Alps span nine millennia, and Greenland’s wood extends over four centuries but predates the ¹⁴C dating limit by over 50 millennia (Table 1).

Figure 1

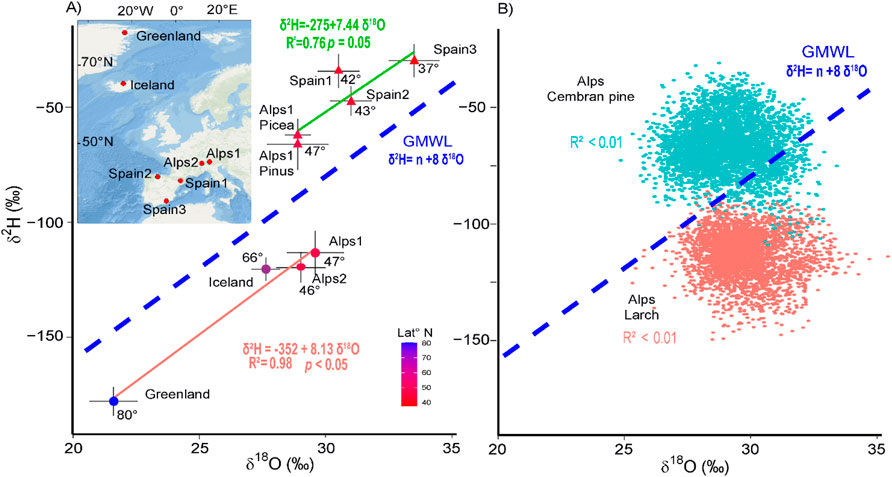
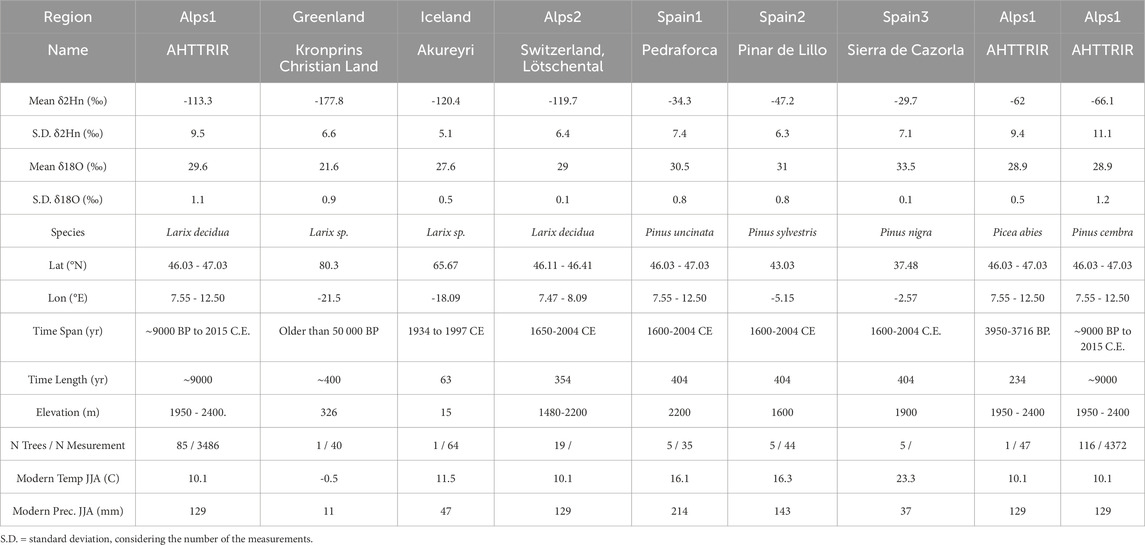
Figure 1. Comparison of δ¹⁸O and δ²H at continental and local scales. (A) plot of the δ¹⁸O and δ²H isotopic mean values for each site, the solid lines indicate linear regressions, the red line is for larch trees, and the green line is for pine and spruce trees. The dashed blue line represents the GMWL. For each region, the standard deviation is indicated, and linear regression fits, associated R values and p values for the two tree groups are shown. The number of trees for each site are: Alps (larch), 85; Greenland,1; Iceland, 1; Alps2, 19; Spain1, 5; Spain2, 5; Spain3, 5; Alps1 (Picea abies), 1; Alps1 (Pinus cembra), 116. The °N latitude is indicated by the colour of the points and expressed numerically (see Table 1 for details). The round dots are for larch trees, and the triangular dots are for pine and spruce trees. The inset shows sampling locations. (B) Scatter plot of tree-level δ²H and δ¹⁸O of the 85 larch trees (red) and 116 cembran pine trees (cyan), with the dotted blue line representing the GMWL.

Table 1

Table 1. Detailed characteristics of the sampling sites.

Isotope analysis and calibration

For the combined online measurements of δ¹³C, δ¹⁸O and δ²Hn, the samples were subjected to pyrolysis at temperatures exceeding 1,450°C in a Flash HT elemental analyzer to convert the cellulose to carbon monoxide and hydrogen (Leuenberger and Filot, 2007) following the method described in Filot et al. (2006). This high temperature is critical for decomposing the cellulose quantitatively into hydrogen and carbon monoxide, with the residue (partial carbon of the cellulose) (Leuenberger and Filot, 2007) collected in a graphite crucible. The resulting gases were separated via a 5 Å molecular sieve and analysed using a Thermo Delta XP or an Elementar/Isoprime mass spectrometer for δ¹³C and δ¹⁸O on CO and δ²Hn on H₂.

δ²Hn values are determined using an online equilibration technique described by Filot et al. (2006) and extended to a triple isotope method (COH) described by Loader et al. (2015). The specific procedure involves equilibrating the cellulose samples with water vapour of known δ²H values (close to VSMOW, variable in the range of −2 to +2‰ over years depending on the aliquot of internal water standards, calibrated against VSMOW with a precision of 0.5‰) at 110°C for 10 min using a continuous flow of helium carrier gas at 80 mL/min. The rate of equilibration was checked with different calibration waters in the range (−429.1 (Dome C) to +1 (Meerwasser) ‰) to cover a wide range of δ²H values as already used by Filot et al. (2006). The samples and standards are stored in a desiccator when not being analysed. This equilibration method was cross-calibrated with the nitration method using cellulose standards with known δ²Hn (Filot et al., 2006).

The mass spectrometric analysis involved the determination of isotope ratios of hydrogen and carbon monoxide, which were sequentially detected and measured after elution. This process included working gas pulses for both hydrogen and carbon monoxide, yielding raw delta values, which were converted in per mil (‰) deviations relative to Vienna Standard Mean Ocean Water (VSMOW) for hydrogen and oxygen as well as carbon based on the calibration procedure described below.

Calibration and quality control were integral to our methodology. A two-point calibration of the raw delta values obtained against our working gas was performed for all isotope ratios (Table 2). For hydrogen, we used Merck cellulose (−34.94‰ δ²H_total, and −70.9 δ²H_n) and IAEA-CH7 polyethylene standards (−100.3‰ for both δ²H_total, and δ²H_n as no exchangeable hydrogen is available). This calibration approach allows us to determine the offset and contraction/stretching of the scale relative to the international VSMOW-SLAP scale. These scale correction terms are independent of whether there are available exchangeable hydrogen atoms. To check for drift in the reference gas and to evaluate precision over time, we additionally used Wei Ming 101 cellulose (from WEI MING Pharmaceutical MFG) and/or IAEA-C3 cellulose (form IAEA) and IAEA-C6 sucrose (form IAEA) standards (Rozanski et al., 1992; Coplen et al., 2006). This led to the evaluation of the machine performance and the implementation of the necessary corrections to a linear drift. Furthermore, the inclusion of IAEA-CH7 specifically enabled quality control of the non-exchangeable hydrogen measurements, while the cellulose standards accounted for the exchangeable portion. For δ¹⁸O and δ¹³C, we used Merck and IAEA-C3 for the calibration, the corresponding values are given in Table 2. The system’s stability allowed for consistent and reliable data within the standard precision limits of ±0.3‰ for oxygen and ±3.0‰ for hydrogen.

Table 2

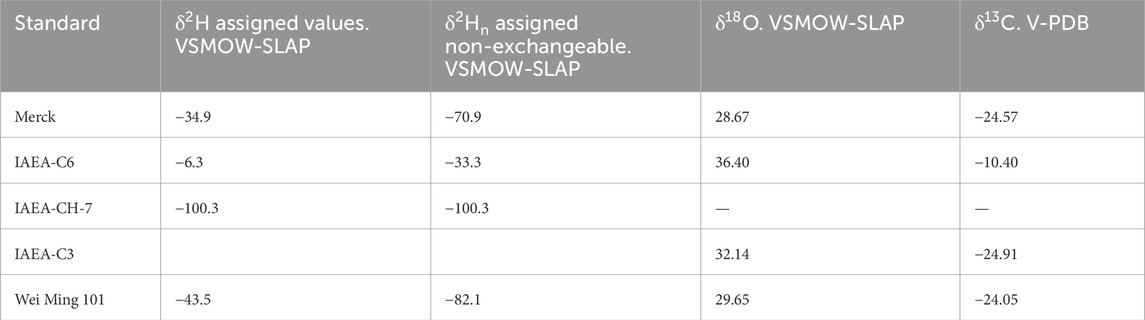
Table 2. Standard materials and assigned values: the values in bold were used for calibration. The other values were determined using these calibration values.

Tree-ring δ¹⁸O and δ²H data from three Spanish sites (Figure 1A; Table 1) were generated during the ISONET project (Treydte et al., 2006) and followed the methodology for δ¹⁸O detailed in Treydte (Treydte et al., 2014). The δ²Hn measurements were conducted using the technique described above. All samples in this study were measured for non-exchangeable, C-bound hydrogen from tree-ring cellulose (Filot et al., 2006; Loader et al., 2015).

All examined trees were absolutely dated with only one exception, the tree from Greenland, which was estimated to be older than 50,000 years. The fragmented remains of this tree were discovered within a glacier moraine at an elevation of 331 m asl, located more than 90 km away from the open sea.

Sea-level change correction for the alpine dataset

The δ²Hn and δ¹⁸O of the Alpine dataset were corrected for the effect of ice volume with a gradient obtained for δ¹⁸O (Fleitmann et al., 2009; Affolter et al., 2019) and converted to δ²H by multiplying it by a factor of eight, resulting in a gradient of −0.064‰ per meter of sea-level rise (Rozanski et al., 1982); as previously done for speleothem records from Switzerland (Affolter et al., 2019). The effect of ice volume correction on the Alpine database for δ²Hn and δ¹⁸O values is shown in Supplementary Figure S5. The other datasets do not require a correction as they are from the late Holocene period, where the correction is ineffective (Supplementary Figure S5). The Greenland sample has not been corrected for temperature because the growth temperature is unknown.

Larch oxygen isotope correction

The oxygen values of larch and non-larch trees are known to have similar values if they come from the same region and time, while those of hydrogen are known to be lower in larch than non-larch trees (Arosio et al., 2020b). Thus, we corrected all larch values based on the difference between the larch and non-larch species in the Alpine database (Figure 2, Supplementary Figures S2, S4-1, S5). The correction factor is −48.1‰.

Figure 2

Figure 2. Comparison of δ¹⁸O and δ²H of cellulose and precipitation. (A) Modelled δ¹⁸O and δ²H isotopic mean values (Bowen et al., 2005) of the JJA (June, July and August) precipitation from the linear regression fits, representing the LMWL, associated R values and p values, in light blue. Dashed blue line represents the GMWL. (B) Plot of δ¹⁸O and δ²H isotopic region mean values. The larch values (round shapes) have been corrected to overlap the non-larch values (triangular shapes). Linear regression fits, associated R values and p values are shown. Round dots are for larch trees, and triangular dots are for pine and spruce trees. The Greenland point (blue) was not taken into account in the linear regression.

Climate data

Monthly temperature and precipitation data were extracted from the Climatic Research Unit’s CRU TS4.03 dataset (Harris et al., 2020) for the period 1905-2002 at each study site.

Summer (JJA) and winter (DJA) seasonal means deviation for monthly precipitation hydrogen (δ²Hp) and oxygen (δ¹⁸Op) stable isotope values were calculated per site by extrapolating the monthly values from the gridded data defined by Bowen et al. (2005), using each site’s latitude, longitude, and altitude. The modelled data are based on precipitation measurements from 1960 to the present (Bowen et al., 2005).

Statistical analysis

To assess the variable’s dependency, a linear regression has been calculated (Figures 1, 2, 3; Supplementary Figures S1–S5) and associated with the P value and the Statistical power. The Statistical power is defined as one minus the probability of type II error (Greenland et al., 2016). The choice to use the average and standard deviation to represent the site values is based on the normal distribution of the isotopic values (Supplementary Figures S3A, B).

Figure 3

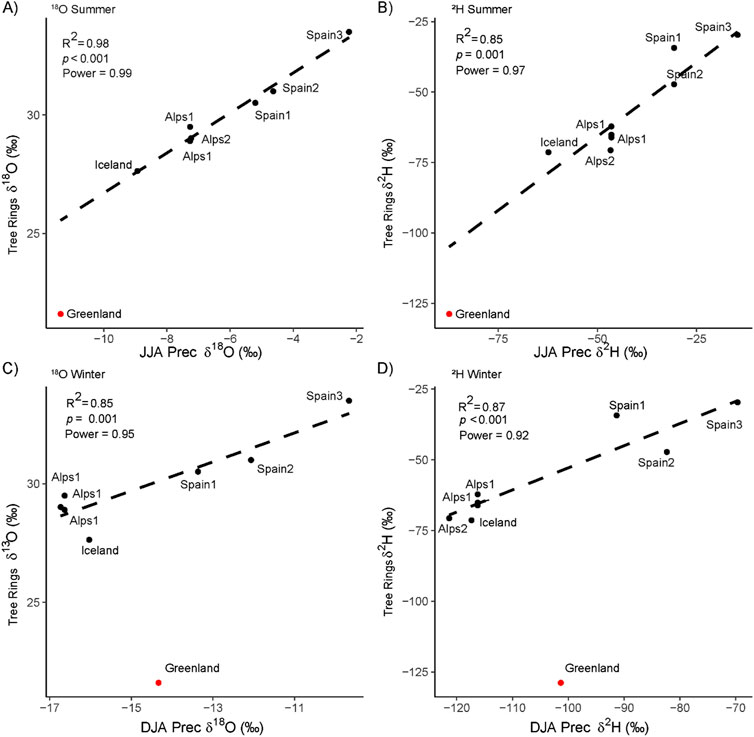
Figure 3. Seasonal modelled precipitation isotopic values vs. tree-ring isotopic values. Scatter plots of the correlation between isotopic measurements from tree rings and modelled precipitation during summer (JJA) and winter seasons (DJA). (A) Tree-ring δ¹⁸O (TR) versus summer δ¹⁸O precipitation, (B) Tree-ring δ²H versus summer δ²H precipitation, (C) Tree-ring δ¹⁸O versus winter δ¹⁸O precipitation, (D) Tree-ring δ²H versus winter δ²H precipitation. Each point represents a specific geographical location labelled accordingly. The lines of best fit are shown along with coefficient of determination (R²) and p-value, indicating the strength of the correlation. The Greenland point (red) was not taken into account in the linear regression.

To account for the uncertainty linked to the average of each region for δ²Hn and δ¹⁸O, we conducted a Monte Carlo simulation with 10,000 iterations whereby the linear model was fitted to δ²Hn and δ¹⁸O incorporating the uncertainty by randomly adding the standard deviation of both isotopes.

The inferred mean linear regression is 8.03 for larch and 6.64 for the non-larch group (Supplementary Figure S1.1). The same analysis was carried out for all regions together but with the correction for larch and not including the Greenland sample, with a mean linear regression of 8.19 (Supplementary Figures S1.2). To show the uncertainty generated from the Monte Carlo simulation, we calculated the distribution density of the simulated slopes and intercepts (Supplementary Figures S1.2B, C), simulated values and all linear interpolations (Supplementary Figure S1.2C).

The relationships between the isotope data (δ²Hn and δ¹⁸O) and geographical/climatic variables were analysed using two approaches: 1) linear regression between each isotope and each individual variable (Supplementary Figure S2, Supplementary Figure S4.1) and 2) multivariate regression analysis incorporating all variables simultaneously, excluding the Greenland sample (Supplementary Table S1).

All the data analysis was performed in R version 4.3.2.

Results

Species-specific analysis at continental scale

Our network is mostly focused over Europe and covers a large part of the Northern Hemisphere from the south of Spain to northern Greenland, across a range of time periods, and it shows that the slope of the linear interpolation of the regional averages of tree-ring δ¹⁸O and δ²H parallels that of the GMWL (Figure 1A) and the LMWL (Figure 2B). It is important to note that the GMWL has remained stable throughout the Holocene, providing a consistent reference for isotopic studies across this geological epoch (Rozanski, 1985). In contrast, we observe no relationship between δ¹⁸O and δ²Hn at the single site level (Figure 1B). An analysis of the Alpine dataset shows that the isotopes present a normal t-distribution (McCarroll and Loader, 2004) (Supplementary Figure S3), supporting the use of mean values and standard deviations for the representations of our datasets.

Larch was shown to have δ²Hn values different from those of non-larch conifers, in agreement with the previous study (Arosio et al., 2020b). Thus, δ¹⁸O and δ²Hn data were initially analysed separately. The linear regression of the means of their δ¹⁸O and δ²Hn values was statistically significant (Figure 1A, p < 0.05, R² = 0.98 and slope = 8.13, power = 0.80, n = 4). This was confirmed by a Monte Carlo analysis, which includes the uncertainty of averages through the use of standard deviation. It produced a regression δ¹⁸O vs. δ²Hn with a similar slope (mean = 8.03, first quartile = 6.85 and third quartile = 9.01) (Supplementary Figure S1.1C). Importantly, the 8.13 slope value is close to that of the GMWL (Craig, 1961) (8.0), and to that of the LMWL (7.9 calculated with the modelled precipitation values) (Figure 2A). The linear regression of the δ¹⁸O and δ²Hn mean values of the non-larch was also significant but only marginally (p = 0.054, R² = 0.76 and slope = 7.46, power = 0.54, n = 5), confirmed by Monte Carlo simulations that produced a similar slope value (mean = 6.64, first quartile = 4.67 and third quartile = 8.23) (Supplementary Figure S1.1B). Thus, the linear regression analysis of the δ¹⁸O-δ²Hn mean values of all the sites was statistically significant (Figure 1A) and aligned with the GMWL (Figure 1A) and the LMWL (Figure 2). However, the intercepts of the larch (−358‰) and of non-larch (−275‰) linear regressions differed remarkably from that of the GMWL (+10) (Craig, 1961), because of the isotopic fractionation occurring in trees. Their different intercepts could be explained as the δ¹⁸O in cellulose is ∼27‰ higher than that of leaf/precipitation water, while the δ²Hn was shown to be −171‰ after photosynthetic and +158‰ at post-photosynthetic steps (Lehmann et al., 2022) and differ in larch and non-larch conifers (Arosio et al., 2020b).

Larch correction and continental analysis

The regression lines of larch and non-larch trees have very similar slopes, indicating that the difference between larch and non-larch values is roughly constant among different sites. The use of the two species together is possible but only by correcting the larch samples (Figure 2B, Supplementary Figure S1.2). After correction and considering all the regions together, the linear regression produced a slope value of 8.2 (p < 001, R² = 0.79, n = 8, power = 0.91, mean of 8.19 with a Monte Carlo analysis) (Figure 2B; Supplementary Figure S2). This value is similar to that of the regressions adjusted for the simulated isotopic precipitation values of the same sites (Figure 2A), which are 7.9 and 8.0 for the LMWL and the GMWL (Craig, 1961), respectively. Of note, we excluded the Greenland sample for the statistical analysis of Figure 2B, because it lacks an exact dating and its sea-level correction; moreover, its rather low values may affect the linear interpolation. Nevertheless, it remains an interesting verification sample.

Figure 2B shows that the mean values of all sites are well aligned on the regression line, except Spain1, which has higher δ²Hn values than Spain 2. This difference cannot be explained by climatic or geographical effects (Table 1), or isotopic value of precipitation (Figure 2A), and we attributed the increased δ²Hn values to physiological stress at Spain 1 that may increase autotrophic metabolism and affect isotopic fractionation (Cormier et al., 2018) (Figure 4).

Figure 4

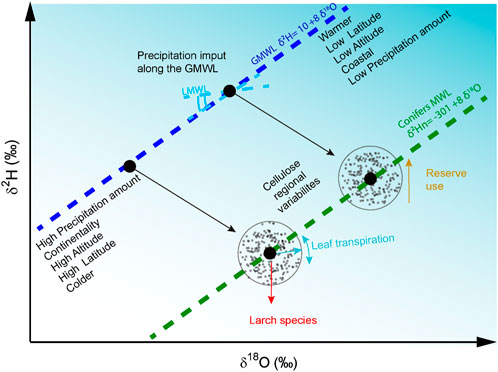
Figure 4. Scheme of the factors affecting tree-ring δ²H and δ¹⁸O and the GMWL. Incoming precipitation generally falls around the GMWL, described by the equation δ²H = 8 * δ¹⁸O+ 10. The range of precipitation isotope ratios at a given location is strongly related to its temperature, elevation, and continentality. The slope of 8.0 reflects the relative equilibrium fractionation factors between δ²H and δ¹⁸O and defines the GMWL. At the leaf or needle level, transpiration occurs along a line (light blue), the slope of which is controlled by the relative humidity (Lehmann et al., 2022). Biological fractionation of both isotopes can modify the isotopic values of leaf water. Hydrogen isotopic values can be enriched by reserve uses (Cormier et al., 2018) and have lower values in larch species compared to other conifers (Arosio et al., 2020b).

Seasonal, geographical, and present climatic influence

After excluding the Greenland sample, we found that the relationship between the mean regional summer temperatures and the mean regional isotopic values for both δ²H and δ¹⁸O was significant (p < 0.01 R² = 0.85 and 0.83 for both δ¹⁸O and δ²Hn respectively) (Supplementary Figures S4-1A, B). In contrast, summer precipitation amounts do not seem to be a representative parameter of the regional tree-ring δ²Hn and δ¹⁸O, as the correlation is not significant (Supplementary Figures S4-1C, D). We conclude that temperature was the primary factor driving the variations observed in both δ²H and δ¹⁸O mean values across the different regions.

In addition, we found a strong significant correlation between the regional tree-ring δ¹⁸O and δ²Hn (larch corrected) and the modelled summer isotope precipitation values (Bowen et al., 2005; IAEA/WMOA, 2006; Bowen, 2012), while the correlation with winter isotope precipitation values was weaker, especially for δ¹⁸O (Figure 3). The correlation between tree-ring δ²Hn and precipitation δ²Hp is lower than that between tree-ring δ¹⁸O and δ¹⁸Op (Figure 3). This difference is likely caused by the higher biological fractionation of δ²Hn, which can dampen the seasonal climate signal. However, since hydrogen and oxygen come from the same water sources, the seasonal δ²H should reflect the summer seasonality as δ¹⁸O does. The correlations between tree-ring isotopes and the summer temperatures are similar(δ¹⁸O) or higher (δ²Hn) than those between model precipitation isotopes and temperatures (Supplementary Figures S4-1, S4-2).

The stronger summer δ¹⁸O signal is probably due to the high altitude (>1,000 m) (Spain and the Alps) or the high latitude (Greenland and Iceland) of the sampling sites, where tree growth occurs only in the summer season (Moser et al., 2010) and depends on δ¹⁸O of summer precipitation (Szymczak et al., 2020). This contrasts with lowland broadleaved trees, the leaf water of which reflects the winter δ¹⁸O precipitation stored in the soil (Allen et al., 2019). Note that the Greenland sample was excluded from this analysis since it comes from another interglacial stage where temperatures and precipitation amounts are unknown.

The relationship of δ²Hn and δ¹⁸O with latitude showed significant negative regression slopes (p < 0.01 for both isotopes, R² = 0.88 for δ¹⁸O and R² = 0.81 for δ²Hn) (Figures 1A, 2A; Supplementary Figures SA, B). This agrees with the known temperature-controlled isotope fractionation in precipitation caused by poleward air mass transport that carries lower δ²Hn and δ¹⁸O values at higher latitude sites (Dansgaard, 1964). The altitude effect was not statistically significant (R² = 0.4, p = 0.08 for δ¹⁸O; R² = 0.4, p = 0.09 for δ²Hn) (Supplementary Figures S2C, D), possibly because of the limited altitudinal range of our data (Kern et al., 2014).

A multivariate regression analysis confirms that a key driver of spatial δ¹⁸O and δ²Hn variation is summer temperatures and that the δ²Hn values are also significantly related to δ²Hn summer precipitation, latitude, and altitude (Supplementary Table S1).

Analysis of individual trees

In the sections above, we considered the mean values of the different regions, but it is also important to analyse the isotopic variation in the individual sites. We focused on our largest database, the Alps1 sites. In the larch and non-larch trees of the dataset, the correlations between the two isotopes were statistically non-significant (Figure 1B). The low correlation (R² < 0.1) remained even after the normalisation of all trees (Supplementary Figure S3A), and also when considering the mean value of the different sites (R² < 0.1) (Supplementary Figure S3B). Thus, the low correlation is intrinsic to the trees and is not due to the merging of trees from the same region, with mean R² < 0.25 for all larch and R² < 0.2 for all cembra pine (Supplementary Figure S3C).

Greenland sample

The Greenland sample was found at an altitude of 313 m a.s.l and 90 km from the ocean, indicating in situ growth during an interglacial phase when the climate in Greenland was warm. Now there are no trees nearby. Nevertheless, the Greenland sample falls remarkably close to the linear regression line for the region (shown by the red dot in Figure 2B).

Discussion

Species-specific analysis at continental scale

Present work analyses six sites covering a large part of the Northern Hemisphere from the south of Spain to northern Greenland, across a range of time periods. Our data show that the δ¹⁸O and δ²Hn means of regions exhibit a covariance that follows the GMWL, indicating that the tree-ring isotopes capture the regional value of precipitation isotopes, although with a difference between larch and non-larch conifers (Figure 1A).

The consistent offsets of the larch and non-larch linear regressions from the GMWL across the entire dataset suggest a nearly constant difference in the isotopic fractionation of the two groups during the processes of cellulose formation (Figure 1A). This suggests that large-scale systematic physiological effects on isotope fractionation do not occur over the large spatial and temporal range of our data, although there are exceptions, such as the deviation observed at Spain 1 attributed to metabolic fractionation (Figure 2B).

Larch correction and continental analysis

From the regression of the means of δ²Hn and δ¹⁸O, using all the samples corrected, we obtained a slope value close to 8, which is very close to the slope of the GMWL (Craig, 1961). Similar recent study reported slightly different results with a δ²Hn and δ¹⁸O slope value of 10, higher than the expected 8.0 for the GMWL or 7.8 for the LMWL (Supplementary Figure S9 in the appendix of Vitali et al. (2022)). The work was based on the ISONET dataset (Vitali et al., 2022) that contains conifers and oak trees of high and low altitudes and different δ²Hn measurement systems that may cause variability in tree-ring δ¹⁸O and δ²Hn (Kern et al., 2014; Allen et al., 2019). This may explain the difference from our study, which contains only high altitude/latitude conifers and uses the same δ²Hn measurement system. The precipitation signal appears coherent across our network and reflects the regional summer isotopic precipitation signal (Figure 2).

Seasonal, geographical, and present climatic influence

The δ²H and δ¹⁸O values of local precipitation are primarily influenced by regional-scale processes (Rozanski et al., 1982), which include geographical and climatic factors such as temperature, precipitation, latitude, continentality, and altitude (Craig, 1961; Ingraham, 1998). Given that this study employs what is likely one of the largest datasets available for continental-scale isotopic analysis, it enables a deeper investigation into the geographical and climatic factors driving tree rings isotopic variation. Our findings demonstrate that regional tree-ring δ²Hn and δ¹⁸O mean values reflect these continental precipitation isotopic variations, with temperature and latitude emerging as dominant drivers. The seasonal investigation points to regional tree-ring δ²Hn and δ¹⁸O values as predominantly reflecting summer precipitation isotopic patterns, suggesting that temperature and latitude significantly influence spatial variation. The globally coherent nature of the water cycle during the Common Era (Konecky et al., 2023) further supports the capacity of tree-ring δ²Hn and δ¹⁸O measurements to capture geographic isotopic shifts across different time periods.

This finding may be important for archaeological studies (Bernabei et al., 2019), as well as for tracing the origin of Arctic driftwood (Hellmann et al., 2013). However, this is partially limited by the difference between larch and non-larch conifers and possibly other species. Another potential confounding factor is that at high latitudes and under certain climatic conditions, the active permafrost with low δ²H and δ¹⁸O values can contribute to the tree water supply (Kirdyanov et al., 2024).

The main limitation of this study is the small and variable sample sizes across regions due to the scarcity of δ²Hn measurements. Strengths include wide spatial dataset coverage, exclusive use of conifer species, and consistent δ¹⁸O and δ²Hn measurement systems. Notably, an ancient Greenland sample, excluded from statistical analyses due to its uniqueness, was used for verification.

Analysis of individual trees

We found an absence of correlation if a single site is analysed; this absence of correlation is intrinsic to the trees and is not due to the merging of trees from the same region (Figure 1B). This cannot be explained by the relatively small spatial range or variation in the LMWL values in the European Alps (between 7.84 and 8.29) (Flaim et al., 2013; Hürkamp et al., 2019) or by the different sampling sites or offsets between trees. More likely, it is due to temporal variations of δ¹⁸O and δ²Hn in response to climate and weather conditions, which include leaf transpiration, soil condition and rooting variation. These factors influence the fractionation of tree-ring δ¹⁸O variations can retain temperature or hydroclimate signals utilized by paleoclimatic studies (McCarroll and Loader, 2004; Nagavciuc et al., 2019; Yang et al., 2021). However, they are masked in the continental analysis by averaging the regional tree-ring isotopic values. From this analysis, we conclude that the low correlation between δ¹⁸O and δ²Hn at the local level is due to the temporal variations of isotope fractionations rather than database heterogeneity.

Greenland sample

The Greenland sample is not used for the correlation analysis as it is not dated. Nevertheless, its proximity to the Conifers MWL (shown by the red dot in Figure 2B) could indicate that it experienced similar hydrological conditions and biological δ²Hn fractionations. However, the sample has lower δ²Hn and δ¹⁸O values compared to the present precipitation isotopic values (Figure 3), which can be interpreted as being due to a lower temperature than nowadays (Supplementary Figures S4-1A, B), or that the tree used melting ice water that has lower δ²H and δ¹⁸O values.

Conclusion

Our network analysis reveals that regional tree-ring δ¹⁸O and δ²Hn averages align with the GMWL, influenced by geographic and climatic gradients of summer precipitation isotopes. When site variance in δ¹⁸O and δ²H precipitation is large, the isotopic precipitation signal dominates, driven primarily by temperature and latitude. Effective reconstruction of these relationships requires multi-century regional averaging. Thus, tree-ring isotope variability can trace the geographic origin of living and relict wood on a hemispheric scale during interglacial phases. In contrast, short-term and local isotopic changes decouple the two isotopes due to distinct biological fractionation effects (Holloway-Phillips et al., 2023). The information obtained in this work is summarized in Figure 4. Precipitation δ²H and δ¹⁸O vary globally following the GMWL with local variations (LMWL). This global variation is reflected in the δ²Hn and δ¹⁸O of tree rings, which allow the identification of a European conifer MWL with a slope of about 8 and an intercept of −301‰ (Figure 4). Tree species diversity must also be taken into account as in our case by applying a larch correction. Of note, this global-continental variation can only be detected using data covering >300 years of length. For shorter time periods at local levels, the two isotopes no longer show a significant covariance but carry distinct climatic or physiological information, which may be exploited in climate reconstructions.

Data availability statement

The Alpine datasets are available on Pangaea https://doi.org/10.1594/PANGAEA.941604. The Greenland datasets are going to be deposited in PANGEA and will be publicly available. Inquiries can be directed to the corresponding author.

Author contributions

TA: Conceptualization, Investigation, Data curation, Formal analysis, Writing–original draft, Writing–review and editing. UB: Writing–original draft, Writing–review and editing. KN: Resources, Investigation, Writing–review and editing. GEM: Resources, Writing–review and editing. MS: Resources, Writing–review and editing. TP: Resources, Writing–review and editing. MPS: Writing–review and editing. EG: Writing–review and editing. LAH: Writing–review and editing. IH: Resources, Writing–review and editing. TB: Visualization, Writing–review and editing. ML: Conceptualization, Resources, Investigation, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research has been supported by the Swiss National Science Foundation (grant nos. SNF P500PN 210716, SNF 200021L_144255 and SNF 200020_172550) and the Austrian Science Fund (grant no. I-1183-N19). The Greenland sample was collected during fieldwork funded by the Austrian Science Fund. This research (the Greenland fieldwork) was funded in whole by the Austrian Science Fund (FWF) (Grant DOI 10.55776/Y1162). For open access purposes, the author has applied a CC BY public copyright licence to any author accepted manuscript version arising from this submission. The Greenland government is thanked for permission to undertake this fieldwork (KNNO Expedition Permit C-19-32; Scientific Survey Licence VU-00150; Greenland National Museum and Archives 2019/01).

Acknowledgments

We are grateful to Peter Nyfeler for lab assistance.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2024.1440064/full#supplementary-material

SUPPLEMENTARY FIGURE S1.1Linear regression using a 1000-time Monte Carlo simulation: a) the linear regression of larch (red) and non-larch group (cyan) separately, b) the frequency of the coefficient values for Monte Carlo simulation of the linear regression of the non-larch group, the vertical line is the mean slope value. c) the frequency of the coefficient values for Monte Carlo simulation of the linear regression of larch group, the vertical line is the mean slope value.

SUPPLEMENTARY FIGURE S1.2Linear regression using a 1000-time Monte Carlo simulation adding the uncertainty to both isotopes: A) the linear regression of all species but with the correction for the larch species, excluding the Greenland sample in red; B) the frequency of the slope values for Monte Carlo simulation of the linear regression, the vertical line is the mean slope value. C) all the linear regressions of the Monte Carlo simulation, and the simulated points in gray, the Greenland sample was not considered, D) the frequency of the intercept values for the Monte Carlo simulation of the linear regression, the vertical line is the mean slope value.

SUPPLEMENTARY FIGURE S2Geographical variables vs. tree-ring isotopic values. Linear regression latitude (°N) and elevation (m) vs. cellulose δ¹⁸O and δ²H isotope value by region, with linear regression fits and associated R² values. The Greenland point (red) has not been taken into account in the linear regression. A) latitude °N vs. cellulose δ¹⁸O. B) latitude °N vs. cellulose δ²H. C) elevation (m) vs. cellulose δ¹⁸O. D) elevation (m) vs. cellulose δ²H.

SUPPLEMENTARY FIGURE S3Scatter plot of tree-mean δ²Hn and δ¹⁸O and R² of all the trees of the Alpine database. A) Scatter plot of tree-level δ²H and δ¹⁸O of the 85 larch trees (red, LADE) and 116 cembran pine trees (cyan, PICE). Along the top and right margins of the scatter plot, there are density plots that show the distribution of the δ¹⁸O and δ²H values for both species. B) Scatter plot of tree-level δ²H and δ¹⁸O of the 85 larch trees (red, LADE) and 116 cembran pine trees (cyan, PICE), after the normalisation of the mean for each tree in both isotopes. Along the top and right margins of the scatter plot, there are density plots that show the distribution of the δ¹⁸O and δ²H values for both species. C) Scatter plot of tree-level δ²H and δ¹⁸O of the mean value of 85 larch trees (red, LADE) and 116 cembran pine trees (cyan, PICE). D) Box plot showing the R2 of the δ²Hn and δ¹⁸O correlation, for 85 larch (red, LADE) tree) and 116 cembran pine trees (cyan, PICE) of the Alpine database.

SUPPLEMENTARY FIGURE S4-1Climate variables vs. tree-ring δ¹⁸O and δ²Hn values. Linear regression between mean isotope value by region and mean seasonal climate variable by region, with linear regression fits and associated R² values. A) JJA temperature (1905–2002 CE) vs. cellulose δ¹⁸O. B) JJA precipitation (1905–2002 CE) vs. cellulose δ¹⁸O. C) JJA temperature vs. cellulose δ²H. D) JJA precipitation vs. cellulose δ²H. The Greenland point (red) has not been taken into account in the linear regression.

SUPPLEMENTARY FIGURE S4-2Climate variables vs. modelled precipitation δ¹⁸O and δ²H values. Linear regression between mean isotope value by region and mean seasonal climate variable by region, with linear regression fits and associated R² values. A) JJA temperature (1905–2002 CE) vs. cellulose δ¹⁸O. B) JJA precipitation (1905–2002 CE) vs. cellulose δ¹⁸O. C) JJA temperature vs. cellulose δ²H. D) JJA precipitation vs. cellulose δ²H. The Greenland point (red) has not been taken into account in the linear regression.

SUPPLEMENTARY FIGURE S5 Alpine δ¹⁸O and δ²Hn tree-ring isotope values Correction effect. Before using the Alpine database, which covers the last 9,000 years, δ¹⁸O and δ²Hn were corrected for the effect of ice volume with a gradient obtained for δ¹⁸O (Fleitmann et al., 2009; Affolter et al., 2019), converted by a factor of eight to δ²H of −0.064‰ per-meter of sea-level rise (Rozanski et al., 1982); previously done in speleothems from Switzerland(Affolter et al., 2019). Non-corrected values are shown in black, corrected values are shown in red.

SUPPLEMENTARY TABLE S1Multivariate analysis for δ¹⁸O and δ²Hn. Multivariate regression model results of predicting tree-ring δ¹⁸O (top) and δ²Hn (bottom) values based on climate variables. Listed are model coefficient estimates, standard errors, t-values, and p-values indicating statistical significance.

References

Affolter, S., Häuselmann, A., Fleitmann, D., Edwards, R. L., Cheng, H., and Leuenberger, M. (2019). Central Europe temperature constrained by speleothem fluid inclusion water isotopes over the past 14,000 years. Sci. Adv. 5, eaav3809. doi:10.1126/sciadv.aav3809

PubMed Abstract | CrossRef Full Text | Google Scholar

Allen, S. T., Kirchner, J. W., Braun, S., Siegwolf, R. T., and Goldsmith, G. R. (2019). Seasonal origins of soil water used by trees. Hydrology Earth Syst. Sci. 23, 1199–1210. doi:10.5194/hess-23-1199-2019

CrossRef Full Text | Google Scholar

Arosio, T., Ziehmer, M., Nicolussi, K., Schluechter, C., Thurner, A., Österreicher, A., et al. (2022). Alpine Holocene triple tree ring isotope record. PANGAEA. Available at: https://doi.pangaea.de/10.1594/PANGAEA.941604.

Google Scholar

Arosio, T., Ziehmer, M. M., Nicolussi, K., Schlüchter, C., and Leuenberger, M. (2020a). Alpine Holocene tree-ring dataset: age-related trends in the stable isotopes of cellulose show species-specific patterns. Biogeosciences 17, 4871–4882. doi:10.5194/bg-17-4871-2020

CrossRef Full Text | Google Scholar

Arosio, T., Ziehmer-Wenz, M. M., Nicolussi, K., Schlüchter, C., and Leuenberger, M. (2020b). Larch cellulose shows significantly depleted hydrogen isotope values with respect to evergreen conifers in contrast to oxygen and carbon isotopes. Front. Earth Sci. 8, 579. doi:10.3389/feart.2020.523073

CrossRef Full Text | Google Scholar

Arosio, T., Ziehmer-Wenz, M. M., Nicolussi, K., Schlüchter, C., and Leuenberger, M. C. (2021). Investigating masking effects of age trends on the correlations among tree ring proxies. Forests 12, 1523. doi:10.3390/f12111523

CrossRef Full Text | Google Scholar

Bernabei, M., Bontadi, J., Rea, R., Büntgen, U., and Tegel, W. (2019). Dendrochronological evidence for long-distance timber trading in the Roman Empire. PloS one 14, e0224077. doi:10.1371/journal.pone.0224077

PubMed Abstract | CrossRef Full Text | Google Scholar

Bowen, G. J. (2012). The online isotopes in precipitation calculator.

Google Scholar

Bowen, G. J., Cai, Z., Fiorella, R. P., and Putman, A. L. (2019). Isotopes in the water cycle: regional-to global-scale patterns and applications. Annu. Rev. Earth Planet. Sci. 47, 453–479. doi:10.1146/annurev-earth-053018-060220

CrossRef Full Text | Google Scholar

Bowen, G. J., Wassenaar, L. I., and Hobson, K. A. (2005). Global application of stable hydrogen and oxygen isotopes to wildlife forensics. Oecologia 143, 337–348. doi:10.1007/s00442-004-1813-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Büntgen, U., Urban, O., Krusic, P. J., Rybníček, M., Kolář, T., Kyncl, T., et al. (2021). Recent European drought extremes beyond Common Era background variability. Nat. Geosci. 14, 190–196. doi:10.1038/s41561-021-00698-0

CrossRef Full Text | Google Scholar

Cherubini, P., Battipaglia, G., and Innes, J. L. (2021). Tree vitality and forest health: can tree-ring stable isotopes Be used as indicators? Curr. For. Rep. 7, 69–80. doi:10.1007/s40725-021-00137-8

CrossRef Full Text | Google Scholar

Churakova, O. V., Porter, T. J., Zharkov, M. S., Fonti, M. V., Barinov, V. V., Taynik, A. V., et al. (2023). Climate impacts on tree-ring stable isotopes across the Northern Hemispheric boreal zone. Sci. Total Environ. 870, 161644. doi:10.1016/j.scitotenv.2023.161644

PubMed Abstract | CrossRef Full Text | Google Scholar

Coplen, T. B., Brand, W. A., Gehre, M., Gröning, M., Meijer, H. A. J., Toman, B., et al. (2006). New guidelines for δ¹³ C measurements. Anal. Chem. 78, 2439–2441. doi:10.1021/ac052027c

PubMed Abstract | CrossRef Full Text | Google Scholar

Cormier, M.-A., Werner, R. A., Sauer, P. E., Gröcke, D. R., Leuenberger, M. C., Wieloch, T., et al. (2018). 2H-fractionations during the biosynthesis of carbohydrates and lipids imprint a metabolic signal on the δ2H values of plant organic compounds. New Phytol. 218, 479–491. doi:10.1111/nph.15016

PubMed Abstract | CrossRef Full Text | Google Scholar

Craig, H. (1961). Isotopic variations in meteoric waters. Science 133, 1702–1703. doi:10.1126/science.133.3465.1702

PubMed Abstract | CrossRef Full Text | Google Scholar

Dansgaard, W. (1964). Stable isotopes in precipitation. tellus 16, 436–468. doi:10.1111/j.2153-3490.1964.tb00181.x

CrossRef Full Text | Google Scholar

Filot, M. S., Leuenberger, M., Pazdur, A., and Boettger, T. (2006). Rapid online equilibration method to determine the D/H ratios of non-exchangeable hydrogen in cellulose. Rapid Commun. Mass Spectrom. An Int. J. Devoted Rapid Dissem. Up-to-the-Minute Res. Mass Spectrom. 20, 3337–3344. doi:10.1002/rcm.2743

PubMed Abstract | CrossRef Full Text | Google Scholar

Flaim, G., Camin, F., Tonon, A., and Obertegger, U. (2013). Stable isotopes of lakes and precipitation along an altitudinal gradient in the Eastern Alps. Biogeochemistry 116, 187–198. doi:10.1007/s10533-013-9855-z

CrossRef Full Text | Google Scholar

Fleitmann, D., Cheng, H., Badertscher, S., Edwards, R. L., Mudelsee, M., Göktürk, O. M., et al. (2009). Timing and climatic impact of Greenland interstadials recorded in stalagmites from northern Turkey. Geophys. Res. Lett. 36, 2009GL040050. doi:10.1029/2009GL040050

CrossRef Full Text | Google Scholar

Galewsky, J., Steen-Larsen, H. C., Field, R. D., Worden, J., Risi, C., and Schneider, M. (2016). Stable isotopes in atmospheric water vapor and applications to the hydrologic cycle. Rev. Geophys. 54, 809–865. doi:10.1002/2015rg000512

PubMed Abstract | CrossRef Full Text | Google Scholar

Gat, J. R. (1996). Oxygen and hydrogen isotopes in the hydrologic cycle. Annu. Rev. Earth Planet. Sci. 24, 225–262. doi:10.1146/annurev.earth.24.1.225

CrossRef Full Text | Google Scholar

Ghadiri, E., Affolter, S., Brennwald, M. S., Fleitmann, D., Häuselmann, A. D., Cheng, H., et al. (2020). Estimation of temperature–altitude gradients during the Pleistocene–Holocene transition from Swiss stalagmites. Earth Planet. Sci. Lett. 544, 116387. doi:10.1016/j.epsl.2020.116387

CrossRef Full Text | Google Scholar

Greenland, S., Senn, S. J., Rothman, K. J., Carlin, J. B., Poole, C., Goodman, S. N., et al. (2016). Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations. Eur. J. Epidemiol. 31, 337–350. doi:10.1007/s10654-016-0149-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Hafner, P., Robertson, I., McCarroll, D., Loader, N. J., Gagen, M., Bale, R. J., et al. (2011). Climate signals in the ring widths and stable carbon, hydrogen and oxygen isotopic composition of Larix decidua growing at the forest limit in the southeastern European Alps. Trees 25, 1141–1154. doi:10.1007/s00468-011-0589-z

CrossRef Full Text | Google Scholar

Harris, I., Osborn, T. J., Jones, P., and Lister, D. (2020). Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. data 7, 109. doi:10.1038/s41597-020-0453-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Hatvani, I. G., Smati, A. E., Erdélyi, D., Szatmári, G., Vreča, P., and Kern, Z. (2023). Modeling the spatial distribution of the meteoric water line of modern precipitation across the broader Mediterranean region. J. Hydrology 617, 128925. doi:10.1016/j.jhydrol.2022.128925

CrossRef Full Text | Google Scholar

Hellmann, L., Tegel, W., Eggertsson, Ó., Schweingruber, F. H., Blanchette, R., Kirdyanov, A., et al. (2013). Tracing the origin of Arctic driftwood. JGR Biogeosciences 118, 68–76. doi:10.1002/jgrg.20022

CrossRef Full Text | Google Scholar

Holloway-Phillips, M., Cernusak, L. A., Nelson, D. B., Lehmann, M. M., Tcherkez, G., and Kahmen, A. (2023). Covariation between oxygen and hydrogen stable isotopes declines along the path from xylem water to wood cellulose across an aridity gradient. New Phytol. 240, 1758–1773. doi:10.1111/nph.19248

PubMed Abstract | CrossRef Full Text | Google Scholar

Hürkamp, K., Zentner, N., Reckerth, A., Weishaupt, S., Wetzel, K.-F., Tschiersch, J., et al. (2019). Spatial and temporal variability of snow isotopic composition on Mt. Zugspitze, Bavarian Alps, Germany. J. Hydrology Hydromechanics 67, 49–58. doi:10.2478/johh-2018-0019

CrossRef Full Text | Google Scholar

IAEA/WMO, A (2006). “Global network of isotopes in precipitation,” in The GNIP database.

Google Scholar

Ingraham, N. L. (1998). “Isotopic variations in precipitation,” in Isotope tracers in catchment hydrology (Elsevier), 87–118. Available at: https://www.sciencedirect.com/science/article/pii/B9780444815460500100 (Accessed February 19, 2024).

CrossRef Full Text | Google Scholar

Kern, Z., Kohán, B., and Leuenberger, M. (2014). Precipitation isoscape of high reliefs: interpolation scheme designed and tested for monthly resolved precipitation oxygen isotope records of an Alpine domain. Atmos. Chem. Phys. 14, 1897–1907. doi:10.5194/acp-14-1897-2014

CrossRef Full Text | Google Scholar

Kirdyanov, A. V., Saurer, M., Arzac, A., Knorre, A. A., Prokushkin, A. S., Churakova, O. V., et al. (2024). Thawing permafrost can mitigate warming-induced drought stress in boreal forest trees. Sci. Total Environ. 912, 168858. doi:10.1016/j.scitotenv.2023.168858

PubMed Abstract | CrossRef Full Text | Google Scholar

Konecky, B. L., McKay, N. P., Falster, G. M., Stevenson, S. L., Fischer, M. J., Atwood, A. R., et al. (2023). Globally coherent water cycle response to temperature change during the past two millennia. Nat. Geosci. 16, 997–1004. doi:10.1038/s41561-023-01291-3

CrossRef Full Text | Google Scholar

Lécuyer, C., Bojar, A.-V., Daux, V., and Legendre, S. (2020). Geographic variations in the slope of the δ2H–δ18O meteoric water line over Europe: a record of increasing continentality, 507. 10.1144/SP507-2020-68: Geological Society, London, Special Publications.

Google Scholar

Lehmann, M. M., Schuler, P., Cormier, M.-A., Allen, S. T., Leuenberger, M., and Voelker, S. (2022). “The stable hydrogen isotopic signature: from source water to tree rings,” in Stable isotopes in tree rings: inferring physiological, climatic and environmental responses (Cham: Springer International Publishing), 331–359.

CrossRef Full Text | Google Scholar

Lehmann, M. M., Vitali, V., Schuler, P., Leuenberger, M., and Saurer, M. (2021). More than climate: hydrogen isotope ratios in tree rings as novel plant physiological indicator for stress conditions. Dendrochronologia 65, 125788. doi:10.1016/j.dendro.2020.125788

CrossRef Full Text | Google Scholar

Leuenberger, M. C., and Filot, M. S. (2007). Temperature dependencies of high-temperature reduction on conversion products and their isotopic signatures. Rapid Comm. Mass Spectrom. 21, 1587–1598. doi:10.1002/rcm.2998

PubMed Abstract | CrossRef Full Text | Google Scholar

Loader, N. J., Street-Perrott, F. A., Daley, T. J., Hughes, P. D. M., Kimak, A., Levanic, T., et al. (2015). Simultaneous determination of stable carbon, oxygen, and hydrogen isotopes in cellulose. Anal. Chem. 87, 376–380. doi:10.1021/ac502557x

PubMed Abstract | CrossRef Full Text | Google Scholar

McCarroll, D., and Loader, N. J. (2004). Stable isotopes in tree rings. Quat. Sci. Rev. 23, 771–801. doi:10.1016/j.quascirev.2003.06.017

CrossRef Full Text | Google Scholar

Moser, L., Fonti, P., Büntgen, U., Esper, J., Luterbacher, J., Franzen, J., et al. (2010). Timing and duration of European larch growing season along altitudinal gradients in the Swiss Alps. Tree Physiol. 30, 225–233. doi:10.1093/treephys/tpp108

PubMed Abstract | CrossRef Full Text | Google Scholar

Nagavciuc, V., Ionita, M., Kern, Z., McCarroll, D., and Popa, I. (2022). A ∼700 years perspective on the 21st century drying in the eastern part of Europe based on δ18O in tree ring cellulose. Commun. Earth and Environ. 3, 277. doi:10.1038/s43247-022-00605-4

CrossRef Full Text | Google Scholar

Nagavciuc, V., Ionita, M., Perșoiu, A., Popa, I., Loader, N. J., and McCarroll, D. (2019). Stable oxygen isotopes in Romanian oak tree rings record summer droughts and associated large-scale circulation patterns over Europe. Clim. Dyn. 52, 6557–6568. doi:10.1007/s00382-018-4530-7

CrossRef Full Text | Google Scholar

Nakatsuka, T., Sano, M., Li, Z., Xu, C., Tsushima, A., Shigeoka, Y., et al. (2020). A 2600-year summer climate reconstruction in central Japan by integrating tree-ring stable oxygen and hydrogen isotopes. Clim. Past 16, 2153–2172. doi:10.5194/cp-16-2153-2020

CrossRef Full Text | Google Scholar

Pang, Z., Kong, Y., Li, J., and Tian, J. (2017). An isotopic geoindicator in the hydrological cycle. Procedia Earth Planet. Sci. 17, 534–537. doi:10.1016/j.proeps.2016.12.135

CrossRef Full Text | Google Scholar

Roden, J. S., Lin, G., and Ehleringer, J. R. (2000). A mechanistic model for interpretation of hydrogen and oxygen isotope ratios in tree-ring cellulose. Geochimica Cosmochimica Acta 64, 21–35. doi:10.1016/s0016-7037(99)00195-7

CrossRef Full Text | Google Scholar

Rozanski, K. (1985). Deuterium and oxygen-18 in European groundwaters—links to atmospheric circulation in the past. Chem. Geol. Isot. Geosci. Sect. 52, 349–363. doi:10.1016/0168-9622(85)90045-4

CrossRef Full Text | Google Scholar

Rozanski, K., Sonntag, C., and Münnich, K. O. (1982). Factors controlling stable isotope composition of European precipitation. Tellus 34, 142–150. doi:10.1111/j.2153-3490.1982.tb01801.x

CrossRef Full Text | Google Scholar

Rozanski, K., Stichler, W., Gonfiantini, R., Scott, E. M., Beukens, R. P., Kromer, B., et al. (1992). The IAEA 14C intercomparison exercise 1990. Radiocarbon 34, 506–519. doi:10.1017/s0033822200063761

CrossRef Full Text | Google Scholar

Siegwolf, R. T., Brooks, J. R., Roden, J., and Saurer, M. (2022). “Stable isotopes in tree rings: inferring physiological,” in Climatic and environmental responses.

Google Scholar

Sternberg, L., and DeNiro, M. J. (1983). Isotopic composition of cellulose from C3, C4, and CAM plants growing near one another. Science 220, 947–949

PubMed Abstract | CrossRef Full Text | Google Scholar

Sternberg, L. L. O. (2009). Oxygen stable isotope ratios of tree-ring cellulose: the next phase of understanding. New. Phytologist. 181, 553–562

CrossRef Full Text | Google Scholar

Szymczak, S., Barth, J., Bendix, J., Huneau, F., Garel, E., Häusser, M., et al. (2020). First indications of seasonal and spatial variations of water sources in pine trees along an elevation gradient in a Mediterranean ecosystem derived from δ18O. Chem. Geol. 549, 119695. doi:10.1016/j.chemgeo.2020.119695

CrossRef Full Text | Google Scholar

Tappa, D. J., Kohn, M. J., McNamara, J. P., Benner, S. G., and Flores, A. N. (2016). Isotopic composition of precipitation in a topographically steep, seasonally snow-dominated watershed and implications of variations from the global meteoric water line. Hydrol. Process. 30, 4582–4592. doi:10.1002/hyp.10940

CrossRef Full Text | Google Scholar

Treydte, K., Boda, S., Graf Pannatier, E., Fonti, P., Frank, D., Ullrich, B., et al. (2014). Seasonal transfer of oxygen isotopes from precipitation and soil to the tree ring: source water versus needle water enrichment. New Phytol. 202, 772–783. doi:10.1111/nph.12741

PubMed Abstract | CrossRef Full Text | Google Scholar

Treydte, K., Schleser, G. H., Esper, J., Andreu, L., Bednarz, Z., Berninger, F., et al. (2006). Climate signals in the European isotope network ISONET. TRACE-Tree Rings Archaeol. Climatol. Ecol. 5. Available at: https://hdl.handle.net/20.500.12259/47260 (Accessed October 25, 2023).

Google Scholar

Vitali, V., Martínez-Sancho, E., Treydte, K., Andreu-Hayles, L., Dorado-Liñán, I., Gutierrez, E., et al. (2022). The unknown third–Hydrogen isotopes in tree-ring cellulose across Europe. Sci. Total Environ. 813, 152281. doi:10.1016/j.scitotenv.2021.152281

PubMed Abstract | CrossRef Full Text | Google Scholar

Vitali, V., Peters, R. L., Lehmann, M. M., Leuenberger, M., Treydte, K., Büntgen, U., et al. (2023). Tree-ring isotopes from the Swiss Alps reveal non-climatic fingerprints of cyclic insect population outbreaks over the past 700 years. Tree Physiol. 43, 706–721. doi:10.1093/treephys/tpad014

PubMed Abstract | CrossRef Full Text | Google Scholar

Waterhouse, J. S., Switsur, V. R., Barker, A. C., Carter, A. H. C., and Robertson, I. (2002). Oxygen and hydrogen isotope ratios in tree rings: how well do models predict observed values? Earth Planet. Sci. Lett. 201, 421–430. doi:10.1016/s0012-821x(02)00724-0

CrossRef Full Text | Google Scholar

Xu, C., Huang, R., An, W., Zhao, Q., Zhao, Y., Ren, J., et al. (2024). Tree ring oxygen isotope in Asia. Glob. Planet. Change 232, 104348. doi:10.1016/j.gloplacha.2023.104348

CrossRef Full Text | Google Scholar

Yakir, D. (1992). Variations in the natural abundance of oxygen-18 and deuterium in plant carbohydrates. Plant, Cell and Environ. 15, 1005–1020. doi:10.1111/j.1365-3040.1992.tb01652.x

CrossRef Full Text | Google Scholar

Yang, B., Qin, C., Bräuning, A., Osborn, T. J., Trouet, V., Ljungqvist, F. C., et al. (2021). Long-term decrease in Asian monsoon rainfall and abrupt climate change events over the past 6,700 years, Proc. Natl. Acad. Sci. U. S. A. Long-term decrease Asian monsoon rainfall abrupt Clim. change events over past 6,700 years. 118, e2102007118, doi:10.1073/pnas.2102007118

CrossRef Full Text | Google Scholar

Ziehmer, M. M., Nicolussi, K., Schlüchter, C., and Leuenberger, M. (2018). Preliminary evaluation of the potential of tree-ring cellulose content as a novel supplementary proxy in dendroclimatology. Biogeosciences 15, 1047–1064. doi:10.5194/bg-15-1047-2018

CrossRef Full Text | Google Scholar