Entropic control on the desorption of oil molecular droplets in water from kerogen surface

Understanding the thermodynamics of interfacial interactions between oil and kerogen is imperative for developing technologies aimed at improving hydrocarbon recovery in reservoirs, especially in unconventional shale, which retains abundant hydrocarbons in a non-porous medium. The temperature effect on the interactions of a light oil molecular cluster with kerogen was investigated using molecular dynamics simulation. Non-polar and polar light oil droplets were modeled with clusters of 30 octane molecules and 30 octanethiol molecules in water, respectively. Kerogen was modeled with a molecular fragment from a mature type II kerogen. The potential of mean force calculations was performed at constant volume and temperature via umbrella sampling at temperatures in 300–500 K range, comparable to the reservoir temperatures of common shale plays. The results show that the free energy of desorption of oil droplets scales linearly with temperature and has a strong negative temperature dependence, suggesting a significant entropic contribution to the free energy and underscoring the fundamental basis of the thermal stimulation technique for improved oil recovery. The simulations suggest that single molecules cannot represent the interactions of an oil droplet with the kerogen surface. The internal dynamics within the droplets play an important role in the strong temperature dependence of the free energy. The calculated free energy, contact angle, and surface tension of oil droplets are comparable with observations and provide an improved understanding of the interfacial interactions between the multicomponent fluid and kerogen. Such agreement demonstrates the reliability of the method and molecular models for modeling the complex interfacial interaction system. The results present a thermodynamic understanding and molecular details of the temperature effect on the oil interactions with kerogen, providing valuable insight into strategies for unconventional oil recovery.

1 Introduction

Petroleum is a major energy source, and crude oil is a strategic resource (Blackwill et al., 2014; Belu Mănescu and Nuño, 2015; Behar and Ritz, 2017). Current technology can yield up to 30%–60% of the original oil in place, leaving up to 70% of crude oil in a reservoir (Thomas, 2008; Lake et al., 2014). For unconventional reservoirs, the fraction of oil recovered is even lower. A large fraction of unrecovered oil is retained in the porous media of minerals and organic materials in the rock, especially for formations where most unrecovered oil is adsorbed at the surfaces of the nanoporous network of materials such as kerogen (Curtis, 2002; Zhang et al., 2012; Mastalerz et al., 2012; Psarras et al., 2017). The intermolecular interactions at the interfaces play an important role in confining the oil-containing fluid and preventing the oil molecules from being recoverable (Kirby, 2010; Wang, 2014). Thus, the thermodynamics of fluid-surface interactions is critical for understanding how the physical conditions and fluid composition impact oil properties, which are essential for developing strategies for recovering unconventional shale oil (Javadpour et al., 2007; Anovitz and Cole, 2015; Salahshoor et al., 2018).

Oil recovery technologies have used heat to enhance recovery, including steam injection, hot water flooding, and in situ combustion (Butler, 1991). The temperature effect induced by thermal stimulation on the properties of the fluid and the interfaces may play a critical role in unconventional oil recovery. These techniques were originally designed to recover conventional hydrocarbons, especially heavy oil, by reducing viscosity. Recent studies based on reservoir modeling and laboratory observations show that thermal stimulation can be economically viable in improving oil recovery from unconventional shale (Egboga et al., 2017; Chen et al., 2018). In these models, fluid properties, such as viscosity, density, and compressibility, are based on experimental values (Chen et al., 2013; Sanchez-Rivera et al., 2015). Fluid properties influenced by fluid-surface interactions at the molecular scale are not explicitly included in the models used to describe fluid transport. It is not clear how the thermal stimulations alter the fluid-surface interactions that dominate oil recovery efficiency. As a result, this simplified treatment of fluid properties in reservoir modeling could affect model accuracy by not explicitly including interfacial interactions, especially for fluid in the abundant nanopores of kerogen-rich shale, where the fraction of the fluid affected by surfaces increases as pore size decreases (Zhang et al., 2020). Interfacial interactions within nanopores necessitate an atomistic-scale treatment. Using molecular dynamics simulation, Wang et al. (2015) evaluated the temperature effect on the density distribution of octane in a kerogen slit (with graphene surface used as a model for the kerogen surface) at temperatures ranging from 333 K to 393 K (Wang et al., 2015). They observed up to a 2% reduction in the number of adsorbed octane molecules at elevated temperatures. Recently, using similar methods, Yang et al. (2020) examined the temperature effect on the adsorption of hydrocarbon mixtures at the surfaces of a kerogen slit (with a functionalized surface as the model) at temperatures ranging from 280 K to 400 K. They observed a linear reduction in the number of oil molecules confined within the slit as a function of temperature (Yang et al., 2020). Although both findings support the reduction of oil adsorption in confined spaces, they were based on phenomenological observations using molecular dynamics simulations, and the thermodynamics of the interfacial interactions and the energetics contributing to increased recovery by thermal stimulation remain unexplored.

Desorption of oil molecules from the surfaces of shale is a thermodynamic process. Knowledge of free energy is essential for understanding both the equilibrium and the kinetics of the process. Although a thermal stimulus for improving oil recovery is well-known and long-practiced, fundamental questions remain. For instance, how does temperature affect the free energy of desorption? What are the enthalpy and entropy contributions to the free energy? Answers to questions like these can provide a fundamental understanding of thermal stimulation techniques. It has been shown that the entropic contribution to the adsorption free energy is important for understanding the adsorption kinetics of organic molecules on oxide and metal surfaces (Campbell and Sellers, 2012). The entropy of adsorption for alkane and alcohol molecules on several metal oxide surfaces can be predicted from their gas-phase entropy. For zeolite framework structures, the entropy of adsorption can be predicted from a single material descriptor, the occupiable volume available for hydrocarbon molecules (Campbell and Sellers, 2012; Dauenhauer and Abdelrahman, 2018). Given the similarity between molecular adsorption at solid surfaces and oil adsorption at kerogen surfaces, we hypothesized that the entropic contribution to the free energy of oil adsorption at kerogen surfaces is significant in influencing the temperature effect on the free energy of the desorption of oil molecules from the kerogen surface.

In the present study, we focus on the temperature effect on the free energy of interactions between light oil molecules and kerogen surfaces over the temperature range of 300 K–500 K. The enthalpy and entropy contributions to the free energy are estimated. The effect of molecular polarity (polar vs. non-polar oil) and molecular clustering (oil droplet vs. single oil molecule) on desorption free energy is taken into consideration. In addition, the correlation between the free energy and contact angles of oil droplets is explored to understand the wettability of kerogen surfaces by oil droplets. Quantifying the relationships between free energy, temperature, and contact angle provides a thermodynamic basis for understanding the wettability of kerogen by oil and the effect of thermal stimulations for recovering hydrocarbon fluid confined in the nanoporous medium of shale.

2 Computational methods

2.1 Molecular models

Two types of interfacial systems were investigated: a single oil molecule and an oil droplet (modeled as a cluster of 30 molecules) in water at the kerogen surface (Figure 1). The size of the simulation box, the number of water molecules, and the kerogen slab thickness are tabulated in Table 1. The input structures of water, the oil molecules, the oil clusters, and the kerogen surface were taken from our previous study on modeling adsorption at the kerogen surface (Zhang et al., 2020). Preparations of the interfacial systems are described in the next section. Crude oil is a complex mixture primarily composed of hydrocarbons and can vary significantly in composition depending on its source. The major component in light crude oil is typically alkanes. Hydrocarbons with eight carbon atoms are one of the most abundant compounds in crude oil (Furimsky, 2015), especially in the Bakken formation, primarily located in North Dakota and Montana (Han and Gu, 2014). Therefore, n-octane (C₈H₁₈) was selected to model a light oil compound. Given that sulfur is among the most abundant elements in crude oil aside from carbon and hydrogen (Liu et al., 2010; Demirbas et al., 2015), octanethiol (C₈H₁₇SH) was used as a model for sulfur-containing oil (a polar oil molecule) to study the effect of molecular polarity on desorption. The oil droplets were prepared using 30 molecules of octane and octanethiol to model the non-polar and polar oil droplets, respectively. For kerogen, there are four basic types in shale, including algal kerogen (type I), mixed kerogen (type II), terrestrial kerogen (type III), and inertinite kerogen (type IV), defined by their origin and composition, including their H/C ratio. The most commonly found kerogen in sedimentary rock is mixed kerogen (type II kerogen), which forms in marine environments and is associated with productive source rocks for oil and gas. For this study, a simplified molecular fragment (C₂₂H₁₃ON) was employed to model thermally mature type II kerogen (Collell et al., 2014). More complex and realistic oil molecular models and different types of kerogen models will be the subject of future study. A kerogen slab was built with 511 molecules of the kerogen fragment. The assembled kerogen slab has an H/C ratio of 0.59 and an O/C ratio of 0.05, which is consistent with the definition of type II kerogen. The density of the final prepared model after an extended equilibration process for kerogen is 1.15 g/cm³, close to the low end of the experimental data: 1.18–1.89 g/cm³ (Nwachukwu and Barker, 1985; Okiongbo et al., 2005; Ward, 2010; Jagadisan et al., 2017).

Figure 1

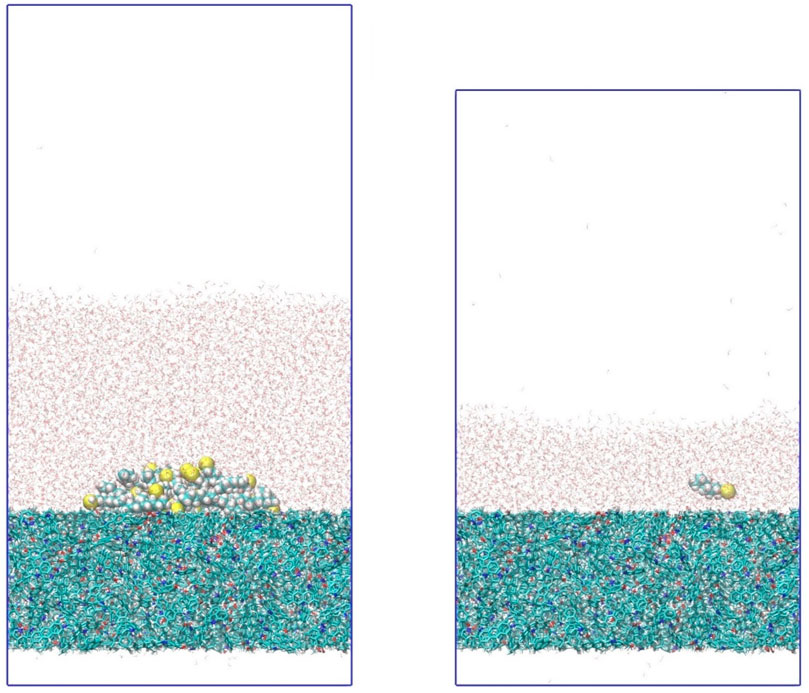
Figure 1. Simulation snapshot of a polar oil droplet (left) and a single polar oil molecule (right) in water on kerogen surfaces. Each simulation box contains water, oil, and kerogen molecules. Different types of molecules are depicted with different styles for visual clarity. White represents hydrogen; green, carbon; yellow, sulfur; blue nitrogen; and red, oxygen.

Table 1

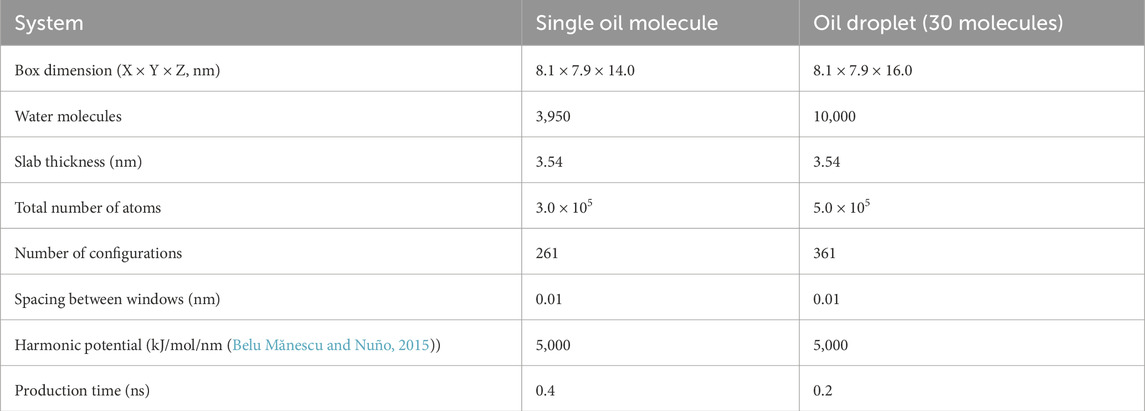
Table 1. Specification of simulation systems: box size, number of water molecules, kerogen slab thickness, total number of atoms, number of configurations for umbrella sampling, the spacing between windows, harmonic potential, and production time.

Because the kerogen surface is an aperiodic system and structurally flexible during molecular dynamics, an increase in temperature can roughen the surface. High roughness can lead to technical difficulties in locating the surface plane and constraining the distance between the molecules and the surface in umbrella sampling, which creates challenges in reliably calculating the potential of mean force for desorption. Thus, the kerogen surfaces were fixed by constraining the positions of all kerogen atoms in all directions (X, Y, and Z). However, the rigid surfaces may introduce an artificial effect on the dynamics of interfacial interactions by altering momentum transfer across the interface, which can induce a systematic error in the calculated desorption free energy. To estimate the error caused by using a rigid kerogen surface, we compared the free energy of desorption of a single polar oil molecule calculated without fixing the kerogen surface at relatively low temperatures (200 K–400 K) to values calculated with a fixed kerogen surface at the same temperatures. As shown in Supplementary Figure S1, the free energies calculated with a fixed kerogen surface are consistently overestimated by a constant, ∼3–6 kJ/mol, independent of temperature across the investigated range. This result suggests that a rigid surface can be used to calculate the temperature dependence of the free energy of adsorption, with the absolute free energy shifted by approximately +4.5 kJ/mol.

For water molecules, there is a collection of molecular models. Although there is not a single water model that can produce all water properties accurately (Guillot, 2002; Jorgensen and Tirado-Rives, 2005), most water models can produce water properties qualitatively well (Guillot, 2002). Nonetheless, we compared several common water models by replicating the calculation of the free energy profile for the desorption of a single polar oil molecule in water at the kerogen surface. Some of the common water models we tested include simple point charge models (SPC, SPC/F, and SPC/E) and the transferable intermolecular potential series (TIP3P, TIP4P-Ew, and TIP5P-E). The calculated results and performance details are compared in Supplementary Figure S2 and Supplementary Table S1. Different water models produced noticeable differences in the free energy profile, with the desorption free energy ranging from ∼19 to 30 kJ/mol. The highest desorption energy was produced by the TIP4P-Ew model and the lowest desorption energy by SPC/F (López-Lemus et al., 2008). However, they all share qualitatively similar profiles., This study used the SPC/F water model for its simplicity and computational efficiency (Toukan and Rahman, 1985; Dang and Pettitt, 1987; Lobaugh and Voth, 1997; Wu et al., 2006). The SPC/F model is also adopted in the CLAYFF force field (Cygan et al., 2004), which has been extensively used to describe aqueous solution interactions with mineral surfaces (Cygan et al., 2021; Kalinichev et al., 2007; Wang et al., 2006). The parameters of the SPC/F potential used in this study are listed in Supporting Text 1. We anticipate that using different water models will not alter how the desorption free energy responds to temperature change, although the absolute values of free energy may change.

The OPLS-AA force field was employed to describe the organic molecules, including octane, octanethiol, and kerogen (Jorgensen et al., 1996), which is compactible with the water model used in this study. The molecular geometries and dipole moments described by this force field are in agreement with results from density functional theory calculations, as shown in Supplementary Tables S1, S2. The density, diffusion coefficient, and interfacial energy between octane and water at ambient conditions using the OPLS-AA potentials are consistent with the literature (Jorgensen et al., 1996; Ghahremanpour et al., 2022). While the potentials for the individual subsystems have been developed and well-tested, the interactions between them have yet to be fully developed. Following the practice in molecular dynamics simulations of complex systems (Yang et al., 2020) for the present study, the short-range non-bonded interaction parameters between the oil molecules, kerogen, and water were calculated using the combination rule based on geometric averages. Using the combination rule has produced reasonable results, as demonstrated recently by our previous study and other computational studies in the literature (Zhang et al., 2020; Yang et al., 2020), and consistent with experimental observations.

2.2 Preparation of the interfacial system

Procedures for the preparation of the interfacial systems were reported in our previous publication (Zhang et al., 2020) and are summarized here with additional details. Before the potential of mean force calculations using umbrella sampling were carried out, the systems were carefully prepared and extensively equilibrated in multiple stages, with each steps carefully monitored for equilibration. The entire interfacial system consists of two subsystems: the fluid subsystem of oil and water and the surface subsystem of kerogen. Each subsystem was equilibrated separately before they were merged. After merging, the entire system was equilibrated again. For the kerogen surface subsystem, 511 model kerogen molecules were initially randomly inserted into a simulation supercell with a targeted density of 1.25 g/cm³. The system was run for about 0.5 ns in the NVT ensemble at 3000 K, then gradually quenched from 3000 K to 500 K in NVT ensemble about 0.5 nsThis was followed by an NPT run to adjust the system stress at temperatures from 500K to 300 K and pressures set to 1 bar in multiple steps, for a total of more than 1.0 ns The resulting density is 1.15 g/cm³ at 300 K and 1 bar. Finally, the kerogen surface was created by inserting a space between two kerogen slabs, followed by a stabilization and relaxation at 300 K for about 0.5 ns in the NVT ensemble. For the water and oil subsystem, oil molecules were equilibrated for up to 0.25 ns in the NVT ensemble before being immersed in water. After immersion in water, the oil and water subsystem was equilibrated in the NPT ensemble at 300 K and 1 bar for about 0.5 ns, followed by equilibration in the NVT ensemble at 300 K for about 0.5 ns After two subsystems were merged, as shown in Figure 1, additional equilibration simulations were performed in the NVT ensemble for up to 1–2 ns in multiple steps, depending on the temperature. All equilibration processes were closely monitored at each step by tracking instantaneous properties and their fluctuations, including temperature, stress tensor, density, potential energy, and kinetic energy. If at any point the system behaved abnormally, preparation would be started from the beginning. Equilibrium was observed once the instantaneous properties converged with reasonable fluctuations around their means. After the entire system was equilibrated, simulations were carried out in the NVE ensemble for 0.5–1.0 ns while the center of mass of the oil molecules or molecular clusters constrained at different distances along the desorption path, normal to the kerogen surface, to generate the independent initial configurations for each of the umbrella sampling windows.

2.3 Molecular dynamics simulation

Molecular dynamics (MD) simulations were carried out with GROMACS (Berendsen et al., 1995; Lindahl et al., 2001; Van Der Spoel et al., 2005; Hess et al., 2008; Pronk et al., 2013; Páll et al., 2015; Abraham et al., 2015). The potential of mean force profile of oil desorption was computed using umbrella sampling. All MD simulations were performed in the canonical ensembles (NVT) with the following settings: periodic boundary conditions, a time step of 1.0 fs, fast smooth particle-mesh Ewald (SPME) for electrostatic interactions with an interpolation order of 4, a relative strength of the Ewald-shifted direct potential of 10⁻⁵, a 0.12 nm fourierspacing, the Verlet cutoff-scheme, and the Nosé–Hoover extended ensemble for temperature coupling. Five different temperatures were investigated: 300 K, 350 K, 400 K, 450 K, and 500 K. This temperature range was based on the reported data of common shale reservoir temperature ranging from 305 K to 436 K (Yu and Sepehrnoori, 2014). As shown in Figure 1, slab models were used, with a single molecule and molecular cluster fully immersed in water molecules, and with a sufficient gap between the other kerogen surface and water to prevent the surface effect from another surface (Figure 1). Despite the presence of the gap, oil molecules and droplets in all simulations remained fully submerged in water. No phase changes were observed during these simulations. The pressure of the system remained approximately constant (Supplementary Table S4).

2.4 Umbrella sampling and weighted histogram analysis method (WHAM)

All systems were initially equilibrated in multiple steps with extensive equilibration before the free energy calculation, as described in the previous section, “Preparation of the interfacial system”. For umbrella sampling, the center of mass of the oil molecules (droplets) or the oil molecule (single molecule) was constrained at a distance along the reaction coordinate. However, they were not constrained to the surface and could freely interact with various surface sites. Thus, different surface sites on the kerogen surface were sampled, according to the nature of each site. The energies obtained represent statistical averages of the interactions across all the surface sites. Umbrella sampling can be conducted with different numbers of windows, leading to two different approaches: a large number of narrow windows with a short simulation for each window, or a smaller number of wider windows with a long simulation for each window. We extensively tested the effect of the window count, ranging from 20 to over 500, and the umbrella sampling length ranging, from 0.2 ns to 5.0 ns, on statistical errors and the computational efficiency. Our test simulations showed that shorter umbrella sampling simulations with a larger number of narrow windows were more computationally efficient and produced acceptable errors compared to longer simulations with fewer, wider windows. Umbrella sampling with 261 and 361 windows, each with an independent initial configuration, was used for the single molecule and molecular clusters, respectively (Table 1). The large number of windows significantly reduced the equilibration time for the umbrella sampling, as each window was spaced only 0.01 nm from its neighboring windows along the desorption path. Each simulation was run for an additional 0.1 ns in the NVT ensemble to allow the system to relax and reach equilibrium. Data were then collected for 0.2 ns and 0.1 ns in the NVT ensemble for a single molecule and the molecular cluster, respectively, for analysis. The umbrella sampling simulation settings for each system were carefully tested before production runs, and the parameters are shown in Table 1. Upon the completion of the umbrella sampling simulations, WHAM analysis was performed to compute the potential of mean force and to estimate errors. The errors were calculated using Bayesian bootstrapping, with each bootstrapping consisting of 10 bootstraps. Examination of the errors and convergence in the WHAM analysis confirmed that the 0.1 ns equilibration and 0.1–0.2 ns umbrella sampling duration were adequate to produce a reliable free energy profile with acceptable errors.

2.5 Data visualization and analysis

The simulation data was visualized by VMD (Humphrey et al., 1996). VMD was also used to analyze the surface area of interfaces and the quantity of adsorbed atoms on the surface through Tcl/tk scripting (Supporting Text 2). The surface area was calculated using both the geometric and solvent-accessible surface area (SASA) algorithms with different probe radii. Oil atoms within 0.36 nm of the kerogen surface were counted as the first layer adsorbate atoms, considering the maximum range of short-range non-bonded interactions is approximately 0.36 nm in these simulations. The contact angles of oil droplets were measured from MD snapshots by Fiji ImageJ (version 1.52p, open source) (Rueden et al., 2017) using the contact angle plugin developed by Marco Brugnara. The circle best-fit algorithm was applied. The reported surface areas and contact angles are averages over the trajectories from the simulations at the free energy minimum or in the adsorbed state. The contact angle measurements are listed in Supplementary Table S3 of the supporting information, with additional information in Supplementary Figures S3, S4.

3 Results and discussion

3.1 Effect of temperature on the free energy of desorption

The free energy of desorption of oil droplets is shown in Figure 2 and Table 2, and it was calculated as the energy difference between the adsorbed state at the minimum of the potential of mean force profile and the desorbed state at the plateau of the profile. As temperature increases, the desorption free energy decreases in an approximately linear fashion for both the polar and non-polar oil droplets. The free energy is related to the enthalpy (heat of desorption) and entropy by:

$∆G\left(T\right)=∆H–T∆S(1)$

where ∆G (kJ/mol) is the free energy of desorption, ∆H (kJ/mol) is the enthalpy, T is the temperature (K), and ∆S (kJ/mol/K) is the entropic contribution to free energy. Both the heat and entropy of adsorption are insensitive to temperature over a moderate temperature range, as suggested by a recent study. (Bhan et al., 2008) Since the temperature ranges in this study and those in the reservoirs are small (less than a factor of 2)⁵³, Equation 1 can then be used to calculate ∆H and ∆S by linear fitting of the calculated free energy. Although in general such an assumption of constant enthalpy and entropy is an approximation for a small temperature range, the estimated values provide interesting insights into the interplay between enthalpy and entropy.

Figure 2

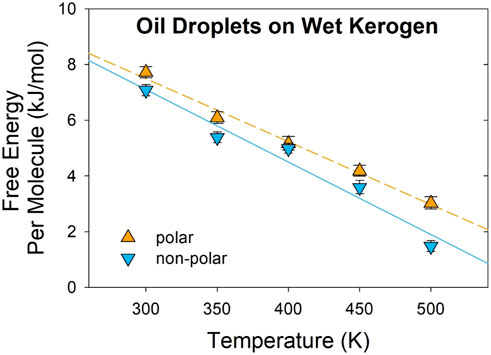
Figure 2. Temperature effect on the free energy of oil droplets on kerogen surfaces. The orange triangles (pointing upwards) represent the free energy per molecule of a polar oil droplet, while the blue triangles (pointing downwards) denote the free energy of a non-polar droplet. Standard errors are illustrated with error bars. Lines are guides for the eyes.

Table 2

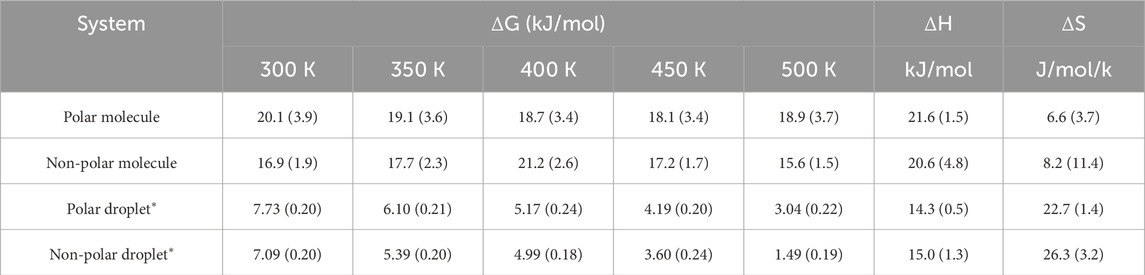
Table 2. Free energy of desorption (∆G), enthalpy (∆H), and entropy (∆S) at different temperatures. Numbers in parentheses are estimated errors. * The ∆G, ∆H, and ∆S of oil droplets are normalized as per molecule for comparison.

As listed in Table 2, the estimated enthalpy of desorption ∆H is +14.3 ± 0.5 kJ/mol and +15.0 ± 1.3 kJ/mol per molecule for polar and non-polar droplets, respectively. The entropy of desorption ∆S is + 22.7 ± 1.4 J/mol/K and + 26.3 ± 3.2 J/mol/K per molecule for the polar and non-polar oil droplets, respectively. The positive enthalpy suggests that oil droplet desorption from kerogen is an endothermic process. The magnitude of ΔH is a quantitative measure of the strength of the binding between the adsorbate (i.e., oil) and the adsorbent (i.e., kerogen surface) (Myers, 2002; Karavias and Myers, 1991). In comparison with the molecular adsorption of hydrocarbon molecules in zeolite framework structures, the calculated ΔH values are at the lower end of the adsorption enthalpy range, from +15 kJ/mol for alkanes in chabazite zeolite to +80 kJ/mol in Ferrierite zeolite, (Dauenhauer and Abdelrahman, 2018), suggesting a weaker interaction between the oil droplets and kerogen surface compared to the alkanes adsorption in the zeolite framework. The comparable ΔH values between polar and non-polar droplets suggest a similar strength of binding with the kerogen surface. This is largely because the kerogen surface exhibits both hydrophobic and hydrophilic molecular groups that have similar interactions with either octane or octanethiol droplets.

The positive ΔS values suggest that the oil molecules gain entropy upon desorption, indicating that the oil molecules are less constrained with increased randomness and disorder in the desorbed state than in the adsorbed state. As suggested in a previous study, for a short-chain alkane with fewer than ten carbons, surface adsorption has no impact on the vibrational freedom of the molecules (Campbell and Sellers, 2012). Since the oil molecules octane and octanethiol have eight carbons, it is expected that the change in the entropy of desorption can be mostly attributed to the translational and rotational freedom. The small but statistically significant difference in ΔS between octane (26.3 J/mol/k) and octanethiol (22.7 J/mol/K) suggests that the octane droplet gains more entropy after desorption than octanethiol, largely because of the more hydrophobic nature of the molecule in water. It is interesting to note that the calculated ∆H and ∆S values for the oil droplets follow the trend of the relationship between enthalpy and entropy in other molecular adsorption processes, which is established for alkanes in zeolite framework structures (Dauenhauer and Abdelrahman, 2018). This result implies that the surface adsorption process of the oil droplets at the kerogen surface behaves similarly to molecular adsorptions confined within the internal structure of zeolites (Dauenhauer and Abdelrahman, 2018).

As Figure 2 and Table 2 suggest, increasing temperature reduces the desorption free energy and promotes the release of oil molecules from the surface. Such an understanding highlights the fundamental basis for oil recovery technologies that apply thermal stimulations such as steam injection, hot water flooding, and in situ combustion (Butler, 1991). Because ΔS exerts a temperature effect on the desorption free energy, understanding the entropy associated with the desorption of oil molecules in water or brine at reservoir conditions may provide important clues for improving the effectiveness of the thermal stimulation in oil recovery. In addition, as demonstrated in a previous study, there is a strong positive correlation between the adsorption entropy of molecules at the MgO surface and the entropy of the gas-phase molecule (Butler, 1991); therefore, exploring the gas-phase entropy of oil molecules may provide valuable insight into developing thermal oil recovery technology.

3.2 Effect of molecular clustering on the interfacial interactions

To understand how a molecular cluster affects the desorption free energy, the desorption of a single oil molecule in water at the kerogen surface was investigated for comparison. The free energy is plotted in Figure 3, and the enthalpy and entropy are listed in Table 2. ∆H and ∆S were calculated by linear fitting using Equation 1. The enthalpy of desorption, ∆H, is 21.6 (1.5) kJ/mol and 20.6 (4.8) kJ/mol for polar and non-polar molecules, respectively, which is approximately 40% higher than the ΔH of oil droplets. The entropy of desorption, ∆S, is 6.6 (3.7) J/mol/K and 8.2 (11.4) J/mol/K for the polar and non-polar oil molecules, respectively, which is about three times lower than the ΔS of oil droplets. The errors in entropy and enthalpy are relatively large because the small system of a single oil molecule is more susceptible to statistical errors than the larger system of an oil droplet (30 oil molecules) (Frenkel and Berend, 2002). Considering the errors in the calculations, both ∆H and ∆S are statistically indistinguishable between the polar and non-polar molecules.

Figure 3

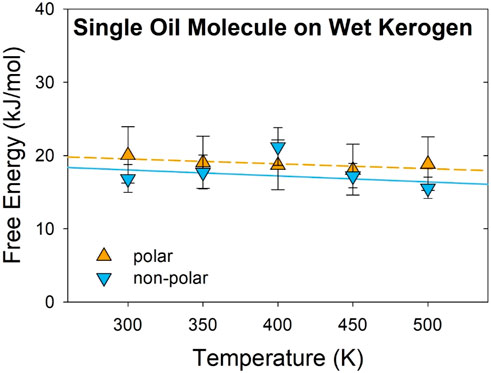
Figure 3. Temperature effect on the free energy of single oil molecules on kerogen surfaces. The orange triangles (pointing upwards) represent the polar oil, while the blue triangles (pointing downwards) denote the non-polar oil. Standard errors are illustrated with error bars. Lines are guides for the eyes.

The positive ∆H indicates that the desorption of oil molecules is endothermic, similar to that of oil droplets. The higher ∆H value for the single oil molecules compared to oil droplets per molecule is largely due to the fact that a fraction of the oil molecules in a droplet do not interact directly with the kerogen surface, leading to a lower ∆H value per molecule. This result suggests that the desorption free energy of a single molecule cannot be linearly scaled to a cluster of molecules or a droplet. The reduction in desorption enthalpy for oil droplets indicates that they are easier to desorb than single oil molecules.

As shown in Figure 3, the free energy of a single oil molecule is less sensitive to temperature with smaller ∆S values (7–8 J/mol/K) than those of the droplets (23–26 J/mol/K) (Figure 2; Table 2). The calculated ∆S values for single oil molecules are about 1 R (gas constant, 8.314 J/mol/K), whereas the ∆S values for oil droplets are about 3 R. This significant difference highlights a dramatic gain in entropy for the oil droplets after being desorbed from the kerogen surface, which is largely attributed to the increased degree of freedom of the oil molecules in the cluster. This result suggests that the thermodynamics of the desorption of a single oil molecule cannot be used to describe the desorption of an oil droplet. In addition, the result emphasizes that the entropic contribution to the free energy is significant for the desorption of oil droplets, which supports the hypothesis of this study that temperature significantly affects on the free energy because of the high entropy associated with the desorption.

3.3 Effect of polarity of oil molecules on the interfacial interactions

Overall, the molecular polarity makes no significant difference in desorption free energy, entropy, or enthalpy except for a moderate difference in the desorption entropy of oil droplets (26.3 ± 3.2 J/mol/K for octane vs 22.7 ± 1.4 J/mol/K for octanethiol). This difference is related to the less directional interactions (less restriction in translational and rotational mobility) due to the more hydrophobic nature of octane molecules compared to the dipole-dipole interaction in octanethiol molecules. This similarity in the desorption enthalpy originates from that fact that the kerogen surface is heterogeneous and contains both polar (e.g., hydroxyl -OH and amine -NH) and non-polar functional groups. In addition, water molecules (hydrophilic) at the interface compete with the oil molecules to interact with the kerogen surface. As a result, the interactions of octane and octanethiol molecules with the surface are similar. Our previous simulations of the adsorption of a single oil molecule on wet and dry kerogen surfaces show that water alters the energetics of oil-kerogen interactions (Zhang et al., 2020). On dry kerogen, a polar oil molecule requires nearly twice as much free energy to desorb from the kerogen surface as a non-polar one. On kerogen with water, water molecules take part in the surface interactions, suppressing the interaction energetics of both polar and non-polar oil (Zhang et al., 2020). This result indicates that fluid composition can complicate the oil-surface interactions. This complexity suggests that the interactions between different components need to be reasonably described in molecular models to reliably simulate more realistic hydrocarbon systems with multiple chemical components (oil, water, and electrolyte), a subject of future studies.

3.4 Contact angle, free energy, and surface tension

The calculated contact angles of the polar and non-polar oil clusters on the kerogen surfaces are plotted in Figure 4. All the values are less than 90°. Therefore, the kerogen surface can be considered oil-wet at temperatures ranging from 300 K to 500 K. As temperature increases, the contact angles increase (Figure 4), which is consistent with the decrease in desorption free energy as a function of temperature as shown in Figure 2. This is a result of the positive entropy of desorption of the droplets from the kerogen surface (Table 2). The calculated contact angle of the polar oil droplet is systematically smaller than that of the non-polar oil by an average of ∼4° over the temperature range, from 48° to 64° for the polar oil and 50°–74° for the non-polar oil. This difference suggests that the kerogen surface is slightly more wettable by the polar oil droplet than by the non-polar oil droplet. Note that the kerogen wettability depends on its type, as the surface properties are largely controlled by its composition. Special attention has been paid to ensuring that the configurations used to calculate contact angles correspond to the free energy minimum of the system (Drelich, 2019). The reported contact angles should be free from the complications often caused by contact angle hysteresis in experimental observations, i.e., the difference between advancing and receding contact angles due to the presence of metastable states (Drelich, 2019; Makkonen, 2017).

Figure 4

Figure 4. Temperature effect on the contact angle of polar and non-polar oil droplets in water on kerogen surfaces. The orange triangles (pointing upwards) represent the polar oil, while the blue triangles (pointing downwards) denote non-polar oil. Standard errors are illustrated with error bars. Lines are guides for the eyes.

Because interfacial free energy and contact angle are closely related, it would be interesting to connect interfacial free energy and contact angle with surface tension. Note that interfacial free energy and contact angle are calculated independently in our simulations. Surface tension (γ) is the surface free energy (F) per surface area (a), defined by Equation 2 as (Zisman and Fowkes, 1964; Ip and Toguri, 1994; Hung et al., 2015):

${\gamma }_{i-j}=\left(\partial F/\partial a_{i-j}\right)(2)$

$dF={\gamma }_{i-j}\bullet d{a}_{i-j}(3)$

where i and j denote the 2 contacting phases in the simulations, including water, kerogen surface, and oil.

It is reasonable to assume that the surface area of kerogen remains constant since all the umbrella sampling simulations were performed at equilibrium. The contact angle (θ) of the oil droplet on the kerogen surface in the three-phase system can be described by Young’s equation (Das and Binder, 2010; Seveno et al., 2013).

$\mathrm{\gamma }{}_{\text{water}-\text{kerogen}}–\mathrm{\gamma }{}_{\text{oil}-\text{kerogen}}=\mathrm{\gamma }{}_{\text{oil}-\text{water}}\bullet cos\theta (4)$

By applying Equation 3 to each of the subsystems of the interfacial system, recognizing the two states (desorbed and adsorbed) of the system with different interfacial areas between water and oil while conserving the surface area, and combining them with Equation 4, the desorption energy (∆F) can then be expressed as:

$∆F=\gamma {}_{\mathrm{o}\mathrm{i}\mathrm{l}-\mathrm{water}\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}\bullet \left(a{}_{\mathrm{o}\mathrm{i}\mathrm{l}-\text{water},\mathrm{f}\mathrm{r}\mathrm{e}\mathrm{e}}–a{}_{\mathrm{o}\mathrm{i}\mathrm{l}-\text{water},\mathrm{a}\mathrm{d}\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{b}\mathrm{e}\mathrm{d}}+a{}_{\mathrm{o}\mathrm{i}\mathrm{l}-\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{g}\mathrm{e}\mathrm{n},\mathrm{a}\mathrm{d}\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{b}\mathrm{e}\mathrm{d}}\bullet cos\theta \right)(5)$

where a_i-j is the surface area. A detailed description of the derivation of Equation 5 is provided in Supporting Text 3. At a given temperature, using the calculated free energy (∆F, Table 2); the calculated contact angle (θ, Supplementary Table S3); and the estimated interfacial areas (a_i-j, Supplementary Table S5) from the MD simulations, Equation 5 can be used to estimate the surface tension of the oil-water interface. However, estimating the surface area of a molecular cluster is not straightforward. Since the contact angle is directly measured based on the geometry of the molecular cluster adsorbed at the surface, it is reasonable to use the geometric surface area, which can be calculated based on the geometry of the adsorbed droplet. The geometric area has indeed been used in molecular modeling of surface wettability (Yan et al., 2011; Hung et al., 2015). However, due to the relatively small number of molecules (∼800 atoms) in the clusters, the surface of the oil droplets in this study is not smooth, especially at elevated temperatures. Increasing temperature leads to noticeable changes in the surface morphology as a result of deviations from an ideal spherical shape. Therefore, the surface areas (Supplementary Table S5) were estimated based on both the geometric area and solvent-accessible surface area (SASA). As a result, the averages as well as the upper and lower bounds were calculated and plotted in Figure 5.

Figure 5

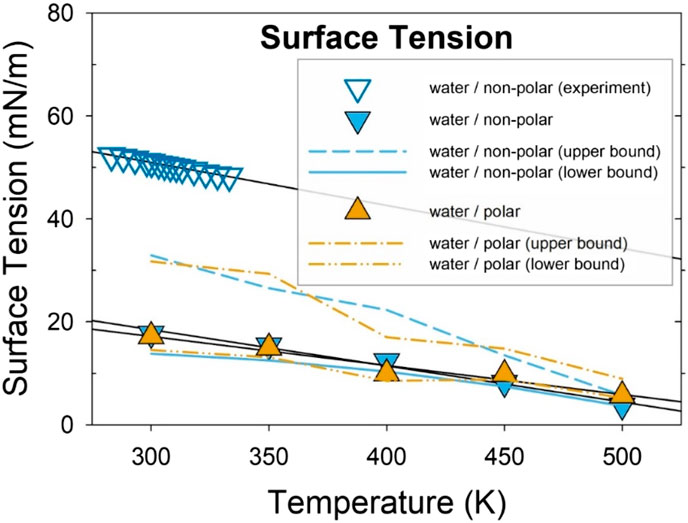
Figure 5. Calculated surface tension of water-oil as a function of temperature. The orange triangles (pointing upwards) represent the surface tension of water/polar oil; the blue triangles (pointing downwards) denote the surface tension of water/non-polar oil; and the hollow blue triangles (pointing downwards) stand for experiments at atmospheric pressure (Zeppieri et al., 2001). Estimated upper and lower bounds mark the high and low surface tensions calculated with different methods of surface area estimation. Lines are guides for the eyes.

As shown in Figure 5, the calculated surface tension decreases as a function of temperature, in agreement with the experimental results regarding temperature dependence (Zeppieri et al., 2001). However, the calculated interfacial tension value between the droplets and water (∼18 mN/m) is about 33 mN/m lower than, or about a third of the experimental result (51.0 mN/m) at 300 K (Zeppieri et al., 2001), or computational results from our simulation (55.4 ± 0.5 mN/m) and from the literature (53.45 ± 0.34) (Jorgensen et al., 1996). If the flat interface measured in the experiment is the same as the curved interface between the droplet and water examined in this study, the interfacial tension values should match. The difference is likely caused by the nanometer-size geometry of the droplets (∼2 nm, 30 molecules). It is well documented that the surface tension of a liquid depends on the radius of the droplet (de Miguel and Rubí, 2021; Lu and Jiang, 2005; Xue et al., 2011; Wang et al., 2016). Since the oil droplets are relatively small and their size is only about 2 nm (1 nm in radius), the curvature has a significant effect on the surface tension. For microdroplets, as the radius of a droplet falls below 30–50 nm, especially below 10 nm (Lu and Jiang, 2005; Xue et al., 2011; Wang et al., 2016), the surface tension shows a major drop from the value of a flat interface. For instance, the estimated surface tension of n-C₈H₁₈ is reduced by ∼32% (∼7 mN/m) for a ∼1 nm radius droplet from the bulk value (∼21.6 mN/m, Figure 6 in reference 71, regarding surface tension of octane). (Wang et al., 2016) Considering this size effect and using the same magnitude of reduction by radius, the surface tension calculated from the MD simulations for the 1 nm radius droplet at 300 K is scaled to be ∼56 mN/m for a flat interface, which is in good agreement with the experimentally measured surface tension of ∼51.0 mN/m at 300 K (Figure 5). It is interesting to note that the slope of the calculated surface tension as a function of temperature for nanometer droplets is similar to that of bulk surface tension from the experimental data (Figure 5).

3.5 Concluding remarks and implications

Molecular dynamics simulations were applied to investigate the temperature effects on the interactions of light oil molecules in water with the kerogen surface. The free energy, enthalpy, and entropy of desorption, the contact angle of oil droplets, and surface tension were calculated. The results show that the desorption free energy of oil molecules from the kerogen surface is a negative linear function of temperature. This relationship provides a thermodynamic basis for understanding thermal stimulation techniques for improved oil recovery. The simulations show that single molecules cannot represent an oil droplet in the process of oil desorption from the kerogen surface. The free energy of desorption of the droplets is strongly dependent on temperature, while the free energy of the individual molecules is only slightly dependent on temperature. The main driver for the temperature effect on the desorption free energy is the entropy of desorption of oil molecules from the kerogen surface. The internal dynamics and interactions between oil molecules within the droplets play an important role in the strong temperature dependence of the free energy. As part of the internal dynamics, the shape of the droplets in water changes dynamically and the magnitude of these changes depends on the temperature, reflecting the entropic contribution to the desorption free energy. In general, because the entropy of molecular adsorption is closely related to the molecular gas-phase entropy, exploring the gas-phase entropy of oil molecules found in a given reservoir may provide important clues to tailor technologies for thermally induced oil recovery.

Surface wettability of reservoir rock materials by oil molecules is important for oil recovery. The results on the correlation between the free energy and contact angles of oil droplets improve the understanding of the wettability of the kerogen surface. The calculated contact angle of octane on a mature type II kerogen model is ∼50°–75°, which is considered moderately wetting. However, the surface properties of kerogen depend on its composition and different types of kerogens are expected to have different wettability. As the H/C ratio decreases from type II to type III, the surface hydrophobicity decreases. It is expected that type III kerogen will have a larger contact angle and the surface will become poorly wetting, especially in high-maturity samples. In addition to organic matter like kerogen, there are minerals such as clays, carbonate, quartz and feldspar. These inorganic materials are considered hydrophilic and have poor wettability by oil molecules unless the surfaces are altered. As demonstrated in this study, quantifying the relationships between free energy, temperature, and contact angle provides a thermodynamic basis to understand the wettability of kerogen by oil and the effects of thermal stimulation for recovering hydrocarbon fluid confined in the nanoporous medium of shale.

Reasonable predictions of oil-water interfacial tension and its temperature dependence from the simulations show that our molecular models are reasonable and the methods are robust. With future development of models for kerogen (and different types) and oil molecules, the methodology is capable of modeling multiphase hydrocarbon-bearing fluid interactions with reservoir rock materials. The results will provide a fundamental understanding of the thermodynamics of the fluid in nanoconfined spaces in shale.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

ZZ: Data curation, Formal Analysis, Investigation, Methodology, Project administration, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. AS: Data curation, Formal Analysis, Investigation, Software, Writing–review and editing. JW: Conceptualization, Funding acquisition, Project administration, Resources, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231. Portions of this research were conducted with high-performance computational resources provided by the Louisiana Optical Network Infrastructure (http://www.loni.org) and high-performance computing resources provided by Louisiana State University (http://www.hpc.lsu.edu).

Acknowledgments

The authors would like to thank Dipta Ghosh from Louisiana State University for meaningful discussions. JW is grateful for the support from the Charles L. Jones Endowed Professorship in Geology & Geophysics at Louisiana State University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2024.1434431/full#supplementary-material

References

Abraham, M. J., Murtola, T., Schulz, R., Páll, S., Smith, J. C., Hess, B., et al. (2015). GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 1–2, 19–25. doi:10.1016/j.softx.2015.06.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Anovitz, L. M., and Cole, D. R. (2015). Characterization and analysis of porosity and pore structures. Rev. Mineralogy Geochem. 80 (1), 61–164. doi:10.2138/rmg.2015.80.04

CrossRef Full Text | Google Scholar

Behar, A., and Ritz, R. A. (2017). OPEC vs US shale: analyzing the shift to a market-share strategy. Energy Econ. 63, 185–198. doi:10.1016/j.eneco.2016.12.021

CrossRef Full Text | Google Scholar

Belu Mănescu, C., and Nuño, G. (2015). Quantitative effects of the shale oil revolution. Energy Policy 86, 855–866. doi:10.1016/j.enpol.2015.05.015

CrossRef Full Text | Google Scholar

Berendsen, H. J. C., van der Spoel, D., and van Drunen, R. (1995). GROMACS: a message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 91 (1), 43–56. doi:10.1016/0010-4655(95)00042-E

CrossRef Full Text | Google Scholar

Bhan, A., Gounder, R., Macht, J., and Iglesia, E. (2008). Entropy considerations in monomolecular cracking of alkanes on acidic zeolites. J. Catal. 253 (1), 221–224. doi:10.1016/j.jcat.2007.11.003

CrossRef Full Text | Google Scholar

Blackwill, R. D., Sullivan, O., and America’s Energy Edge, M. L. (2014). The geopolitical consequences of the shale revolution. Foreign Aff. 93 (2), 102–114.

Google Scholar

Butler, R. M. (1991). Thermal recovery of oil and bitumen. Englewood Cliffs, N.J: Prentice Hall.

Google Scholar

Campbell, C. T., and Sellers, J. R. V. (2012). The entropies of adsorbed molecules. J. Am. Chem. Soc. 134 (43), 18109–18115. doi:10.1021/ja3080117

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, C., Balhoff, M., and Mohanty, K. K. (2013). “Effect of reservoir heterogeneity on improved shale oil recovery by CO2 huff-n-puff,” in All days; SPE: the woodlands, Texas, USA. SPE-164553-MS. doi:10.2118/164553-MS

CrossRef Full Text | Google Scholar

Chen, J.-H., Georgi, D. T., and Liu, H.-H. (2018). Electromagnetic thermal stimulation of shale reservoirs for petroleum production. J. Nat. Gas Sci. Eng. 59, 183–192. doi:10.1016/j.jngse.2018.08.029

CrossRef Full Text | Google Scholar

Collell, J., Galliero, G., Gouth, F., Montel, F., Pujol, M., Ungerer, P., et al. (2014). Molecular simulation and modelisation of methane/ethane mixtures adsorption onto a microporous molecular model of kerogen under typical reservoir conditions. Microporous Mesoporous Mater. 197, 194–203. doi:10.1016/j.micromeso.2014.06.016

CrossRef Full Text | Google Scholar

Curtis, J. B. (2002). Fractured shale-gas systems. AAPG Bull. 86 (11), 1921–1938. doi:10.1306/61EEDDBE-173E-11D7-8645000102C1865D

CrossRef Full Text | Google Scholar

Cygan, R. T., Greathouse, J. A., and Kalinichev, A. G. (2021). Advances in clayff molecular simulation of layered and nanoporous materials and their aqueous interfaces. J. Phys. Chem. C 125 (32), 17573–17589. doi:10.1021/acs.jpcc.1c04600

CrossRef Full Text | Google Scholar

Cygan, R. T., Liang, J.-J., and Kalinichev, A. G. (2004). Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. J. Phys. Chem. B 108 (4), 1255–1266. doi:10.1021/jp0363287

CrossRef Full Text | Google Scholar

Dang, L. X., and Pettitt, B. (1987). Simple intramolecular model potentials for water. J. Phys. Chem. 91 (12), 3349–3354. doi:10.1021/j100296a048

CrossRef Full Text | Google Scholar

Das, S. K., and Binder, K. (2010). Does Young’s equation hold on the nanoscale? A Monte Carlo test for the binary Lennard-Jones fluid. EPL 92 (2), 26006. doi:10.1209/0295-5075/92/26006

CrossRef Full Text | Google Scholar

Dauenhauer, P. J., and Abdelrahman, O. A. (2018). A universal descriptor for the entropy of adsorbed molecules in confined spaces. ACS Cent. Sci. 4 (9), 1235–1243. doi:10.1021/acscentsci.8b00419

PubMed Abstract | CrossRef Full Text | Google Scholar

de Miguel, R., and Rubí, J. M. (2021). Gibbs thermodynamics and surface properties at the nanoscale. J. Chem. Phys. 155 (22), 221101. doi:10.1063/5.0072533

PubMed Abstract | CrossRef Full Text | Google Scholar

Demirbas, A., Alidrisi, H., and Balubaid, M. A. (2015). API gravity, sulfur content, and desulfurization of crude oil. Petroleum Sci. Technol. 33 (1), 93–101. doi:10.1080/10916466.2014.950383

CrossRef Full Text | Google Scholar

Drelich, J. W. (2019). Contact angles: from past mistakes to new developments through liquid-solid adhesion measurements. Adv. Colloid Interface Sci. 267, 1–14. doi:10.1016/j.cis.2019.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Egboga, N. U., Mohanty, K. K., and Balhoff, M. T. (2017). A feasibility study of thermal stimulation in unconventional shale reservoirs. J. Petroleum Sci. Eng. 154, 576–588. doi:10.1016/j.petrol.2016.10.041

CrossRef Full Text | Google Scholar

Frenkel, D., and Berend, S. (2002). “Statistical errors,” in Understanding molecular simulation: from algorithms to applications (San Diego: Elsevier), 525–532. doi:10.1016/B978-012267351-1/50023-7

CrossRef Full Text | Google Scholar

Furimsky, E. (2015). Properties of tight oils and selection of catalysts for hydroprocessing. Energy fuels. 29 (4), 2043–2058. doi:10.1021/acs.energyfuels.5b00338

CrossRef Full Text | Google Scholar

Ghahremanpour, M. M., Tirado-Rives, J., and Jorgensen, W. L. (2022). Refinement of the optimized potentials for liquid simulations force field for thermodynamics and dynamics of liquid alkanes. J. Phys. Chem. B 126 (31), 5896–5907. doi:10.1021/acs.jpcb.2c03686

PubMed Abstract | CrossRef Full Text | Google Scholar

Guillot, B. (2002). A reappraisal of what we have learnt during three decades of computer simulations on water. J. Mol. Liq. 101 (1–3), 219–260. doi:10.1016/S0167-7322(02)00094-6

CrossRef Full Text | Google Scholar

Han, L., and Gu, Y. (2014). Optimization of miscible CO₂ water-alternating-gas injection in the Bakken formation. Energy fuels. 28 (11), 6811–6819. doi:10.1021/ef501547x

CrossRef Full Text | Google Scholar

Hess, B., Kutzner, C., van der Spoel, D., and Lindahl, E. (2008). GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 4 (3), 435–447. doi:10.1021/ct700301q

PubMed Abstract | CrossRef Full Text | Google Scholar

Humphrey, W., Dalke, A., and Schulten, K. (1996). VMD: visual molecular dynamics. J. Mol. Graph. 14 (1), 33–38. doi:10.1016/0263-7855(96)00018-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Hung, S.-W., Hsiao, P.-Y., Chen, C.-P., and Chieng, C.-C. (2015). Wettability of graphene-coated surface: free energy investigations using molecular dynamics simulation. J. Phys. Chem. C 119 (15), 8103–8111. doi:10.1021/jp511036e

CrossRef Full Text | Google Scholar

Ip, S. W., and Toguri, J. M. (1994). The equivalency of surface tension, surface energy and surface free energy. J. Mater. Sci. 29 (3), 688–692. doi:10.1007/BF00445980

CrossRef Full Text | Google Scholar

Jagadisan, A., Yang, A., and Heidari, Z. (2017). Experimental quantification of the impact of thermal maturity on kerogen density. Petrophysics 58 (06), 603–612.

Google Scholar

Javadpour, F., Fisher, D., and Unsworth, M. (2007). Nanoscale gas flow in shale gas sediments. J. Can. Petroleum Technol. 46 (10). doi:10.2118/07-10-06

CrossRef Full Text | Google Scholar

Jorgensen, W. L., Maxwell, D. S., and Tirado-Rives, J. (1996). Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 118 (45), 11225–11236. doi:10.1021/ja9621760

CrossRef Full Text | Google Scholar

Jorgensen, W. L., and Tirado-Rives, J. (2005). Potential energy functions for atomic-level simulations of water and organic and biomolecular systems. Proc. Natl. Acad. Sci. 102 (19), 6665–6670. doi:10.1073/pnas.0408037102

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalinichev, A. G., Wang, J., and Kirkpatrick, R. J. (2007). Molecular dynamics modeling of the structure, dynamics and energetics of mineral–water interfaces: application to cement materials. Cem. Concr. Res. 37 (3), 337–347. doi:10.1016/j.cemconres.2006.07.004

CrossRef Full Text | Google Scholar

Karavias, F., and Myers, A. L. (1991). Isosteric heats of multicomponent adsorption: thermodynamics and computer simulations. Langmuir 7 (12), 3118–3126. doi:10.1021/la00060a035

CrossRef Full Text | Google Scholar

Kirby, B. J. (2010). Micro- and nanoscale fluid mechanics: transport in microfluidic devices. New York: Cambridge University Press.

Google Scholar

Lake, L. W., Johns, R., and Rossen, B. (2014). Fundamentals of enhanced oil recovery. 2nd ed. SPE: Richardson.

Google Scholar

Lindahl, E., Hess, B., and van der Spoel, D. (2001). GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Model. 7 (8), 306–317. doi:10.1007/s008940100045

CrossRef Full Text | Google Scholar

Liu, P., Shi, Q., Chung, K. H., Zhang, Y., Pan, N., Zhao, S., et al. (2010). Molecular characterization of sulfur compounds in Venezuela crude oil and its SARA fractions by electrospray ionization fourier transform ion cyclotron resonance mass spectrometry. Energy fuels. 24 (9), 5089–5096. doi:10.1021/ef100904k

CrossRef Full Text | Google Scholar

Lobaugh, J., and Voth, G. A. (1997). A quantum model for water: equilibrium and dynamical properties. J. Chem. Phys. 106 (6), 2400–2410. doi:10.1063/1.473151

CrossRef Full Text | Google Scholar

López-Lemus, J., Chapela, G. A., and Alejandre, J. (2008). Effect of flexibility on surface tension and coexisting densities of water. J. Chem. Phys. 128 (17), 174703. doi:10.1063/1.2907845

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, H. M., and Jiang, Q. (2005). Size-dependent surface tension and tolman’s length of droplets. Langmuir 21 (2), 779–781. doi:10.1021/la0489817

PubMed Abstract | CrossRef Full Text | Google Scholar

Makkonen, L. (2017). A thermodynamic model of contact angle hysteresis. J. Chem. Phys. 147 (6), 064703. doi:10.1063/1.4996912

PubMed Abstract | CrossRef Full Text | Google Scholar

Mastalerz, M., He, L., Melnichenko, Y. B., and Rupp, J. A. (2012). Porosity of coal and shale: insights from gas adsorption and SANS/USANS techniques. Energy fuels. 26 (8), 5109–5120. doi:10.1021/ef300735t

CrossRef Full Text | Google Scholar

Myers, A. L. (2002). Thermodynamics of adsorption in porous materials. AIChE J. 48 (1), 145–160. doi:10.1002/aic.690480115

CrossRef Full Text | Google Scholar

Nwachukwu, J. I., and Barker, C. (1985). Variations in kerogen densities of sediments from the orinoco delta, Venezuela. Chem. Geol. 51 (3–4), 193–198. doi:10.1016/0009-2541(85)90131-7

CrossRef Full Text | Google Scholar

Okiongbo, K. S., Aplin, A. C., and Larter, S. R. (2005). Changes in type II kerogen density as a function of maturity: evidence from the kimmeridge clay formation. Energy fuels. 19 (6), 2495–2499. doi:10.1021/ef050194+

CrossRef Full Text | Google Scholar

Páll, S., Abraham, M. J., Kutzner, C., Hess, B., and Lindahl, E. (2015). “Tackling exascale software challenges in molecular dynamics simulations with GROMACS,” in Solving software challenges for exascale. Editors S. Markidis, and E. Laure (Cham: Lecture Notes in Computer Science; Springer International Publishing), 8759, 3–27. doi:10.1007/978-3-319-15976-8_1

CrossRef Full Text | Google Scholar

Pronk, S., Páll, S., Schulz, R., Larsson, P., Bjelkmar, P., Apostolov, R., et al. (2013). GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 29 (7), 845–854. doi:10.1093/bioinformatics/btt055

PubMed Abstract | CrossRef Full Text | Google Scholar

Psarras, P., Holmes, R., Vishal, V., and Wilcox, J. (2017). Methane and CO ₂ adsorption capacities of kerogen in the eagle ford shale from molecular simulation. Acc. Chem. Res. 50 (8), 1818–1828. doi:10.1021/acs.accounts.7b00003

PubMed Abstract | CrossRef Full Text | Google Scholar

Rueden, C. T., Schindelin, J., Hiner, M. C., DeZonia, B. E., Walter, A. E., Arena, E. T., et al. (2017). ImageJ2: ImageJ for the next generation of scientific image data. BMC Bioinforma. 18 (1), 529. doi:10.1186/s12859-017-1934-z

CrossRef Full Text | Google Scholar

Salahshoor, S., Fahes, M., and Teodoriu, C. (2018). A review on the effect of confinement on phase behavior in tight formations. J. Nat. Gas Sci. Eng. 51, 89–103. doi:10.1016/j.jngse.2017.12.011

CrossRef Full Text | Google Scholar

Sanchez-Rivera, D., Mohanty, K., and Balhoff, M. (2015). Reservoir simulation and optimization of huff-and-puff operations in the bakken shale. Fuel 147, 82–94. doi:10.1016/j.fuel.2014.12.062

CrossRef Full Text | Google Scholar

Seveno, D., Blake, T. D., and De Coninck, J. (2013). Young’s equation at the nanoscale. Phys. Rev. Lett. 111 (9), 096101. doi:10.1103/PhysRevLett.111.096101

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomas, S. (2008). Enhanced oil recovery - an overview. Oil and Gas Sci. Technol. - Rev. IFP 63 (1), 9–19. doi:10.2516/ogst:2007060

CrossRef Full Text | Google Scholar

Toukan, K., and Rahman, A. (1985). Molecular-dynamics study of atomic motions in water. Phys. Rev. B 31 (5), 2643–2648. doi:10.1103/PhysRevB.31.2643

CrossRef Full Text | Google Scholar

Van Der Spoel, D., Lindahl, E., Hess, B., Groenhof, G., Mark, A. E., and Berendsen, H. J. C. (2005). GROMACS: fast, flexible, and free. J. Comput. Chem. 26 (16), 1701–1718. doi:10.1002/jcc.20291

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Kalinichev, A. G., and Kirkpatrick, R. J. (2006). Effects of substrate structure and composition on the structure, dynamics, and energetics of water at mineral surfaces: a molecular dynamics modeling study. Geochimica Cosmochimica Acta 70 (3), 562–582. doi:10.1016/j.gca.2005.10.006

CrossRef Full Text | Google Scholar

Wang, S., Feng, Q., Javadpour, F., Xia, T., and Li, Z. (2015). Oil adsorption in shale nanopores and its effect on recoverable oil-in-place. Int. J. Coal Geol. 147–148, 9–24. doi:10.1016/j.coal.2015.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, S., Javadpour, F., and Feng, Q. (2016). Confinement correction to mercury intrusion capillary pressure of shale nanopores. Sci. Rep. 6 (1), 20160. doi:10.1038/srep20160

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y. (2014). Nanogeochemistry: nanostructures, emergent properties and their control on geochemical reactions and mass transfers. Chem. Geol. 378–379, 1–23. doi:10.1016/j.chemgeo.2014.04.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Ward, J. (2010). Kerogen density in the marcellus shale. Soc. Petroleum Eng. doi:10.2118/131767-MS

CrossRef Full Text | Google Scholar

Wu, Y., Tepper, H. L., and Voth, G. A. (2006). Flexible simple point-charge water model with improved liquid-state properties. J. Chem. Phys. 124 (2), 024503. doi:10.1063/1.2136877

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, Y.-Q., Yang, X.-C., Cui, Z.-X., and Lai, W.-P. (2011). The effect of microdroplet size on the surface tension and tolman length. J. Phys. Chem. B 115 (1), 109–112. doi:10.1021/jp1084313

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, Y. Y., Gao, N., and Barthlott, W. (2011). Mimicking natural superhydrophobic surfaces and grasping the wetting process: a review on recent progress in preparing superhydrophobic surfaces. Adv. Colloid Interface Sci. 169 (2), 80–105. doi:10.1016/j.cis.2011.08.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y., Liu, J., Yao, J., Kou, J., Li, Z., Wu, T., et al. (2020). Adsorption behaviors of shale oil in kerogen slit by molecular simulation. Chem. Eng. J. 387, 124054. doi:10.1016/j.cej.2020.124054

CrossRef Full Text | Google Scholar

Yu, W., and Sepehrnoori, K. (2014). Simulation of gas desorption and geomechanics effects for unconventional gas reservoirs. Fuel 116, 455–464. doi:10.1016/j.fuel.2013.08.032

CrossRef Full Text | Google Scholar

Zeppieri, S., Rodríguez, J., and López de Ramos, A. L. (2001). Interfacial tension of alkane + water systems. J. Chem. Eng. Data 46 (5), 1086–1088. doi:10.1021/je000245r

CrossRef Full Text | Google Scholar

Zhang, T., Ellis, G. S., Ruppel, S. C., Milliken, K., and Yang, R. (2012). Effect of organic-matter type and thermal maturity on methane adsorption in shale-gas systems. Org. Geochem. 47, 120–131. doi:10.1016/j.orggeochem.2012.03.012

CrossRef Full Text | Google Scholar

Zhang, Z., Liu, H., and Wang, J. (2020). Energetics of interfacial interactions of hydrocarbon fluids with kerogen and calcite using molecular modeling. Energy fuels. 34, 4251–4259. doi:10.1021/acs.energyfuels.0c00053

CrossRef Full Text | Google Scholar

Zisman, W. A. (1964). “Relation of the equilibrium contact angle to liquid and solid constitution,” in Contact angle, wettability, and adhesion. Editor F. M. Fowkes (WASHINGTON, D.C.: Advances in Chemistry; AMERICAN CHEMICAL SOCIETY), 43, 1–51. doi:10.1021/ba-1964-0043.ch001

CrossRef Full Text | Google Scholar