- 1School of Civil Engineering, Henan Polytechnic University, Jiaozuo, China
- 2Gongqing Institute of Science and Technology, Gongqingchengshi, China
- 3State Key Laboratory of Earthquake Dynamics, Institute of Geology, China Earthquake Administration, Beijing, China
- 4Institute of Mountain Hazards and Environment, Chinese Academy of Sciences and Ministry of Water Resources, Chengdu, Sichuan, China
- 5Key Laboratory of Lower Yellow River Channel and Estuary Regulation, Ministry of Water Resources, Yellow River Institute of Hydraulic Research, Yellow River Conservancy Commission, Zhengzhou, China
To overcome the reliance on large samples and high-quality data in existing evaluation methods, while also improving evaluation efficiency and accuracy, this paper proposes a method for rapid landslide hazard assessment. This method utilizes existing research findings and specific analytical techniques for the study area to conduct rapid assessments. Taking the landslide in Yongxing Town, Mingshan Area, Ya’an City, Sichuan Province as an example, the Analytic Hierarchy Process (AHP) is combined with the Information Value (IV) method, Certainty Factor (CF) method, and Frequency Ratio (FR) method from previous studies, The AHP-IV and AHP-FR methods assess the study area as a moderately hazardous zone, while the AHP-CF method assesses it as a slightly hazardous zone. Affected by the strong 2013 Lushan earthquake, the landslide in the study area caused permanent damage. Field investigation results show that the landslide hazard in the study area is moderate, and the AHP-IV and AHP-FR methods are more consistent with the actual field results. The AHP-CF method, due to not considering the water system factor and having certain errors in its discrimination method, leans towards a safer assessment, The results of the three evaluation methods are somewhat consistent.
1 Introduction
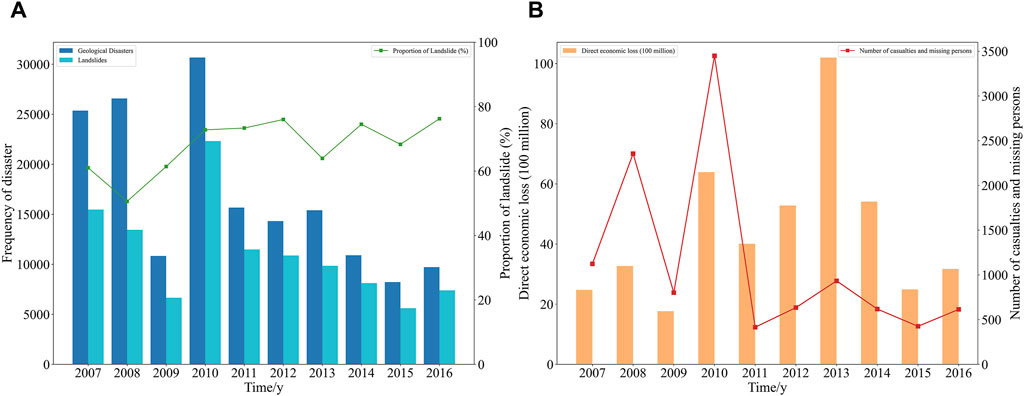
China, with its vast territory and complex geological environment, frequently experiences various geological disasters, causing significant economic losses and casualties. According to the “National Geological Disaster Bulletin” for 2007–2016, there are over 8,000 geological disasters in China each year, with landslide disasters occurring more than 5,000 times annually (Figure 1A). Landslides account for over 50% of geological disasters. As shown in the proportion of landslides in geological disasters over the past decade, landslides account for as much as 76%. The direct economic losses and casualties caused by geological disasters in China in recent years are shown in Figure 1B. Annually, landslides in China cause direct economic losses of about 4.446 billion yuan and 1,073 casualties. In recent years, China has experienced several major landslide events: In 1989, a torrential rain triggered the Xikou landslide, causing direct economic losses of over 6 million yuan and 221 casualties, making it the largest landslide disaster in China in the late 1980s; in September 2011, thousands of gentle slope landslides occurred in Nanjiang County, Sichuan, severely affecting villages and farmland; in September 2014, a gentle slope landslide occurred in Xiangjiaping, Jiangkou Town, leveling an entire residential area; the “6·24” major landslide in Maoxian, Sichuan in 2017 resulted in 83 casualties; in November 2018, a gentle slope landslide in Yutai Village, Toutuo Town, Chongqing, posed a huge threat to local residents and construction projects in progress (Zhu, 2022).
In the study of landslide hazard assessment (Cheng et al., 2024; Marín-Rodríguez et al., 2024), two research methods have been widely applied: one is the empirical rule analysis method based on expert knowledge, and the other is the data-driven statistical regression analysis method. The first type, empirical rule analysis, is characterized by its simplicity and independence from data samples. By utilizing expert knowledge to compare the relationships between various factors one by one, it can also effectively reduce human error and achieve relatively accurate and reliable hazard analysis. Among these, the Analytical Hierarchy Process (AHP) has been widely applied, which involves selecting typical landslide predisposing environmental factors and triggering factors based on expert experience, and determining the contribution weights of different factors before conducting an overlay analysis assessment (Feizizadeh and Blaschke, 2014; Mandal and Mandal, 2018). Wu et al. used the AHP to compile a landslide susceptibility map for Gangu County, China, providing an important reference for geological disaster management and risk assessment (Wu et al., 2016) Sandeep Panchal et al. applied the AHP for landslide disaster assessment on National Highway 5 in India, determining the weights of each factor through a hierarchical structure and pairwise comparison matrix, and generated a landslide hazard distribution map (Panchal and Shrivastava, 2022). Chunhung Wu et al. combined rainfall and six site factors, and through the AHP, obtained landslide susceptibility assessment results for different areas in central Taiwan and mapped the susceptibility distribution (Wu and Chen, 2009).
The advantage of the second type, statistical regression analysis lies in its ability to reveal relationships between variables and to make predictions and inferences. By calculating parameters and conducting significance tests, the importance of influencing factors can be determined. Additionally, statistical regression analysis is highly interpretable, explaining the impact of independent variables on dependent variables, which aids in further exploring the relationships between variables. Among these, Lee et al. used the Frequency Ratio (FR) and Logistic Regression (LR) to assess landslide susceptibility in the Selangor area of Malaysia, comparing the applicability of these two methods in landslide susceptibility mapping (Lee and Pradhan, 2007). Shraban Sarkar used the Information Value (IV) method for landslide susceptibility assessment in parts of the Darjeeling Himalayas (Sarkar et al., 2013). Zhang et al. optimized the Frequency Ratio method and applied it to landslide susceptibility assessment in the Caiyuan Basin in the southeast mountainous region of China (Zhang et al., 2020). Bai used the Logistic Regression method to analyze landslide susceptibility in the Youfang River basin (Bai et al., 2015). Xing used a modified LR method to assess the susceptibility of rainfall-induced landslides (Xing et al., 2021). Abdo employed both the Frequency Ratio and Statistical Index methods to analyze the impact of different factors on landslide susceptibility, proposing corresponding susceptibility distribution maps and suggestions (Abdo, 2022). Wang et al. evaluated landslide hazard in Wen County, northwest China, using the IV, Weights-of-Evidence (WOE), and Certainty Factor (CF) methods (Wang et al., 2019). Chen et al. compared the application of the Frequency Ratio model, Statistical Index model, and Weights-of-Evidence model in landslide susceptibility mapping, providing a basis for comparison and selection in landslide susceptibility assessment (Chen et al., 2016a).
The advantage of the first type, empirical rule analysis is very extensive, but its weight assignment relies on the subjective judgment of decision-makers, making it highly subjective. The advantage of the second type, statistical regression analysis, which starts from the statistical information of a large amount of data, is highly objective. However, mathematical statistical models have limitations in precisely expressing the nonlinear relationship between factors and landslide hazards (Chen et al., 2021). To further enhance the accuracy of landslide hazard assessment, some scholars have combined empirical rule analysis with statistical regression analysis. Chen et al. used the AHP and CF methods to map landslide susceptibility in the Baozhong area of Baoji City, China (Chen et al., 2016b). Ionut Cristi Nicu applied the AHP, FR, and Statistical Index methods for landslide susceptibility assessment (Nicu, 2018). Guoliang Du et al. compared the effects of the AHP-IV and LR-IV methods in the susceptibility distribution map of the Himalayan convergence zone in China (Du et al., 2019).
Statistical regression analysis requires a large sample size and high-quality data. Landslide data are often limited and exhibit spatial and temporal unevenness, which may lead to inaccuracies or significant biases in the results of statistical regression analysis. When studying individual landslides, researchers often do not use this method due to its high data requirements. Today, for regional landslide hazard assessments, many researchers have applied statistical regression analysis to obtain evaluation results. If the results of previous studies can be appropriately applied when studying individual landslides, it can overcome the drawbacks of data requirements in statistical regression analysis and significantly improve the efficiency of landslide hazard assessment. If the first type of empirical rule analysis method based on expert knowledge is also applied, the accuracy of landslide hazard assessment can be enhanced.
This article focuses on the landslide in Yongxing Town, Mingshan Area, Ya’an City, Sichuan Province. By selecting statistical regression analysis results from similar areas, it obtains the IV, CF, and FR values. It combines previous research results with the AHP method in empirical rule analysis, using AHP-IV, AHP-CF, and AHP-FR methods to assess the landslide hazard in Yongxing Town. The AHP-IV and AHP-FR methods assess the landslide in the study area as moderately hazardous, which is more consistent with field survey results. The AHP-CF method, due to not considering factors such as rainfall and distance from water system, and having errors in its discrimination method, assesses the area as slightly hazardous, leaning towards less safe assessment.
2 Overview of the study area
2.1 Basic characteristics
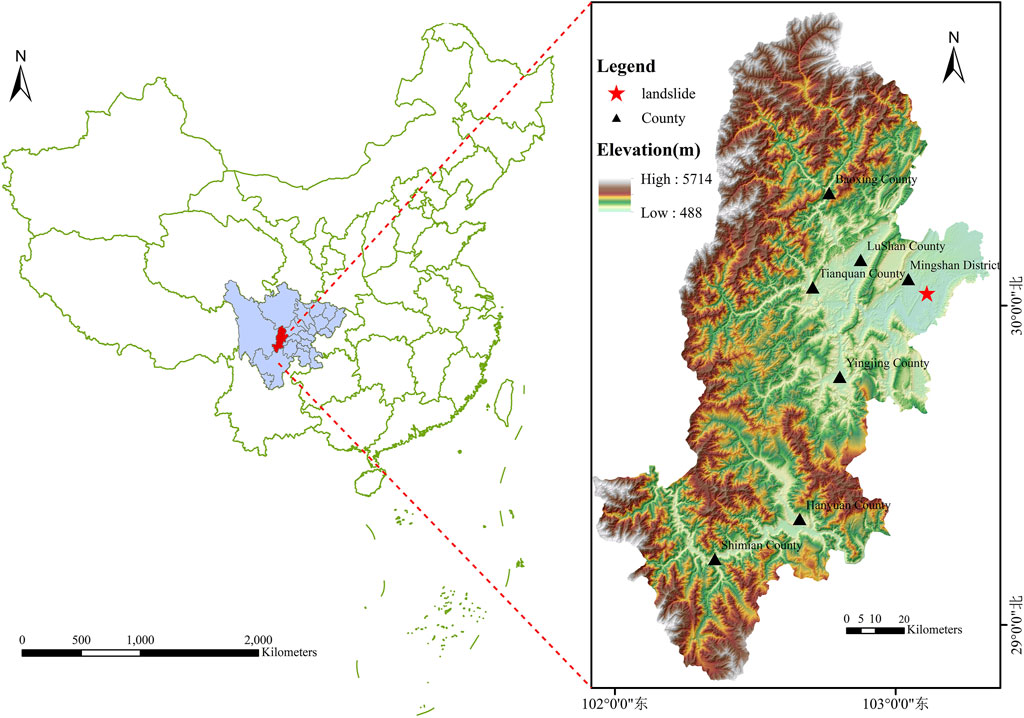
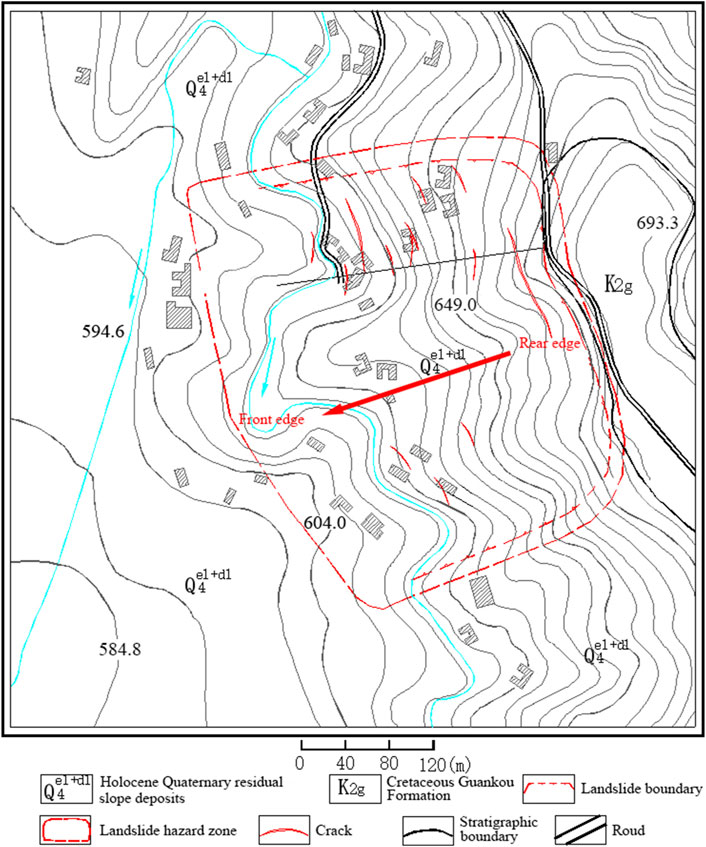
The landslide is located on the south side of the Mingshan-Cheling County Road in Huacheng Village, Yongxing Town, Mingshan Area, Ya’an City, Sichuan Province, with coordinates at East Longitude 103°09′41″ and North Latitude 30°02′51″ (Figure 2). The landslide has an irregular planar shape, mainly sliding along two gullies. The rear edge of the landslide is below a steep slope formed by bedrock ridges, with an elevation of 665 m, while the front edge is at the foot of the slope with an elevation of 615 m, bounded on both sides by bedrock ridges. The landslide has a length of 250 m, an average width of about 500 m, an average thickness of about 4.0 m, covering an area of 125,000 square meters and a volume of 500,000 cubic meters, classified as a medium-sized traction-type soil landslide.
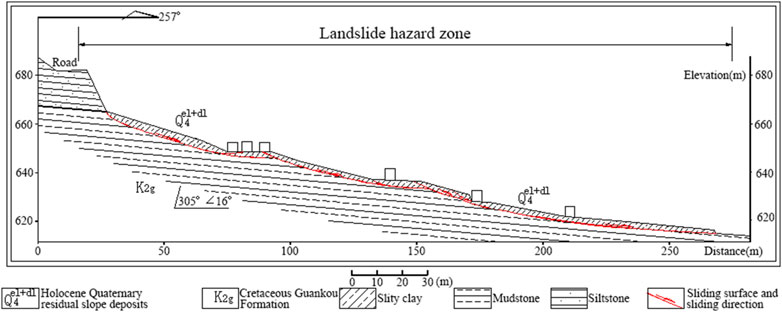
The landslide is located to the east of Group 2 of Huacheng Village in Yongxing Town. The rear edge of the slope is formed by a bedrock ridge, 3–30 m high with a slope of 30°–60°, forming the rear boundary of the landslide. The middle part of the slope forms a ridge, with gullies on both sides. The rear edge of the gully has a slope of about 15°–18° and a width of about 50–60 m. Near the middle ridge, the slope is gentler at 8°–12°. The middle part of the gully is relatively gentle, with a slope of about 12°–14° and a width of 50–60 m, with some areas flattened for housing construction. The middle front edge of the terrain is steeper, with a slope of about 14°–18° and a width of 30–50 m, with some parts forming steep steps of 3–5 m due to cutting. The front edge of the terrain is gentler, with a slope of about 11°–13° and a width of about 80 m. The landslide slope faces 257°, underlain by mudstone and siltstone of the Cretaceous Guankou Formation, with rock layer attitude 305°∠16°, forming a dip-slope (Figure 3).
The landslide mass consists of Quaternary residual slope deposit fine clay
2.2 Deformation and damage characteristics
The landslide first occurred in 2001, with deformation mainly distributed in the gullies on both sides, causing effects such as cracking of residential walls and ground fissures, leading to the relocation of 12 households with 56 villagers. The landslide undergoes slow creep annually, particularly intensifying during heavy rain. Current landslide deformations include subsidence at the front edge, with farm roads and house foundations sinking 10–30 cm (Figure 5A), causing cracks in roads and houses; cracking of houses in the middle, with ground fissures opening 1–5 cm wide and extending 2–10 m; partial slumping at the steep step behind the houses in the middle-front, compressing the houses; and in the middle-rear part of the landslide, partial collapse of the slope, house cracking with openings of 0.5–3 cm (Figure 5B), extending 1–3 m, and ground bulging.
2.3 Impact of earthquakes on landslides
Newmark’s method (Newmark, 1965) is commonly used to determine the stability of slopes under seismic activity. Its main principle is that under the coupled effect of seismic acceleration, the slope undergoes instantaneous displacement along the sliding surface, accumulating continuously. When the applied peak seismic acceleration exceeds the critical acceleration of the slope, a landslide is triggered. This is determined by performing a double integration of the difference between these two accelerations to obtain the cumulative displacement value (Jibson, 2007; Roy et al., 2016; Ma and Xu, 2019). If the cumulative displacement is small, the slope will recover after the seismic activity stops, without suffering damage. However, if the cumulative displacement exceeds the critical displacement, the slope is considered to have suffered permanent damage (Wang et al., 2010).
When using the Newmark method, it is necessary to obtain both the critical acceleration of the slope and the peak seismic acceleration. The critical acceleration of a slope is the minimum seismic acceleration needed to overcome shearing resistance of the soil and initiate sliding under seismic activity. It reflects the maximum acceleration the slope can withstand and is an inherent parameter of the slope (Li and Su, 2021). The critical acceleration of a slope is related to the material composition of the slope, its geometric shape, and factors such as the cohesion, friction angle, density and the slope angle (Wang and Lin, 2010) The more loose the slope material and the steeper the slope angle, the smaller the magnitude of critical acceleration required to generate large movements and the poorer the seismic resistance; conversely, for materials with good cohesion, the critical acceleration is larger, and the seismic resistance is better (Qiu et al., 2024). The critical acceleration of a slope needs to be determined for specific slopes through repeated experiments and is unknown for most cases (Maharjan et al., 2021). According to field survey results, the overall stability of the landslide in the study area is poor, and the slope is steep. Referring to the research results from Wang et al. (2010), a critical acceleration of 0.1 g (98
However, in earthquakes that occur in mainland China, there is some uncertainty in the direction of the earthquake fault and the orientation of the long and short axes of the isoseismal lines. To consider the relationship between the orientation of the long and short axes of the isoseismal lines and the azimuth of the seismic impact point, the peak accelerations along the long and short axes are calculated separately, and their geometric mean is used as the reference value for the peak acceleration at the seismic impact point (He et al., 2023). The calculation process is given by Eq. 3.
In Eqs 1–3:
Based on the principles of the Newmark method, it is known that when the peak ground acceleration of an earthquake exceeds the critical acceleration of a slope, it will cause permanent damage to the slope. Earthquake data were obtained from the National Earthquake Science Data Center. Calculations show that the peak ground acceleration caused by the severe “4.20” Lushan earthquake in 2013 in this study area was 183.11
3 Research methods
Numerous scholars in China and abroad have conducted a series of studies on landslide risk assessment (Qiu et al., 2022). Among them, empirical rule analysis based on expert experience and knowledge, and statistical regression analysis based on a large amount of data and statistical information, have been widely applied. Empirical rule analysis can select landslide disaster-causing factors and quantify their weights, offering intuitive and interpretable results. Statistical regression analysis reveals the relationships between variables, enabling prediction and inference. However, empirical rule analysis is highly subjective and statistical regression analysis struggles to precisely express the non-linear relationship between factors and landslide risks. This paper adopts a combination of both methods, using the Analytical Hierarchy Process (AHP) in empirical rule analysis combined with the Information Value Method, Certainty Factor Method, and Frequency Ratio Method from statistical regression analysis. Specifically, it employs AHP-IV, AHP-CF, and AHP-FR methods to assess landslide risk in Yongxing Town, Mingshan District, Ya’an City.
3.1 Analytical Hierarchy Process
The Analytical Hierarchy Process (AHP), developed in the 1970s by the American operations researcher Saaty (1977), has evolved over the years into a mature methodology. Its basic principle is to decompose the elements of the evaluation system’s alternative solutions into levels such as objectives, criteria, and plans, and then conduct qualitative and quantitative decision-making analysis. This method is characterized by mathematizing the decision-making process of decision-makers using a limited amount of quantitative information, based on in-depth analysis of the influencing factors and internal relationships of complex decision making problems. This provides a convenient decision-making tool for complex problems having multiple objectives, multiple criteria, or unstructured characteristics (Vaidya and Kumar, 2006).
The application of AHP generally involves the following three steps:
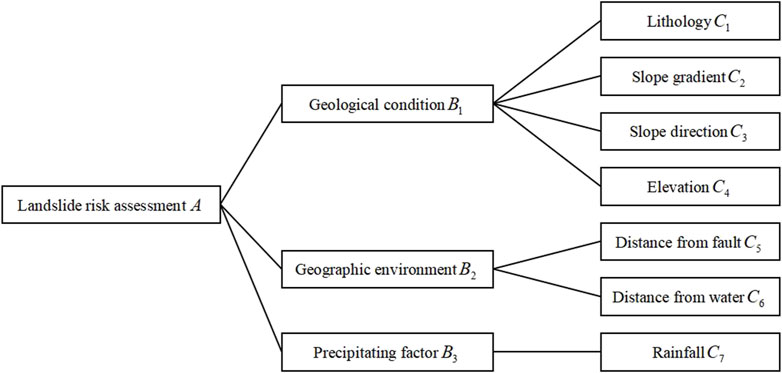
(1) Establishing a hierarchical structure model. This includes the goal layer, criteria layer, and plan layer (Figure 7).
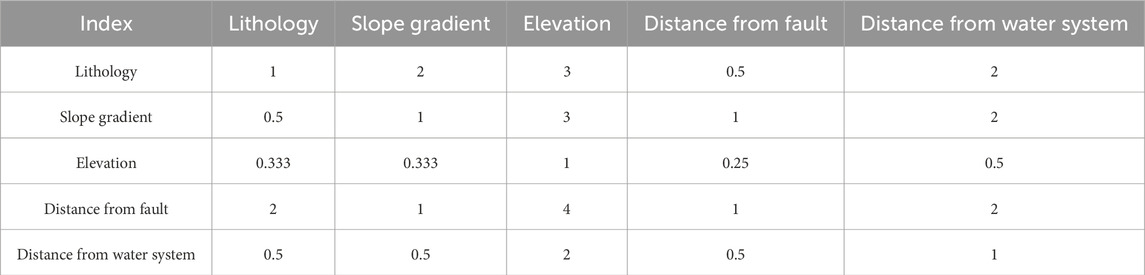
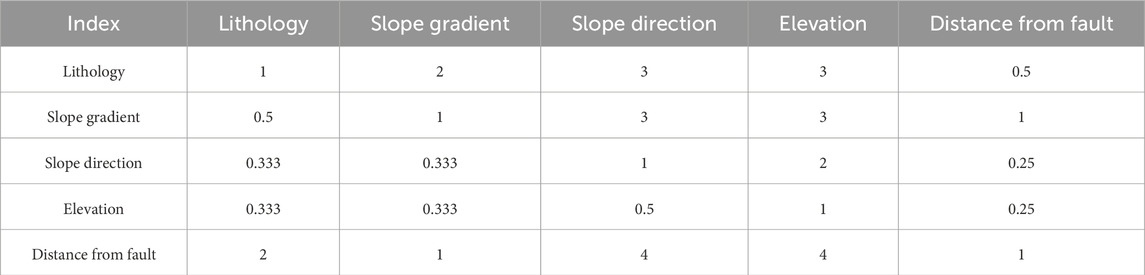
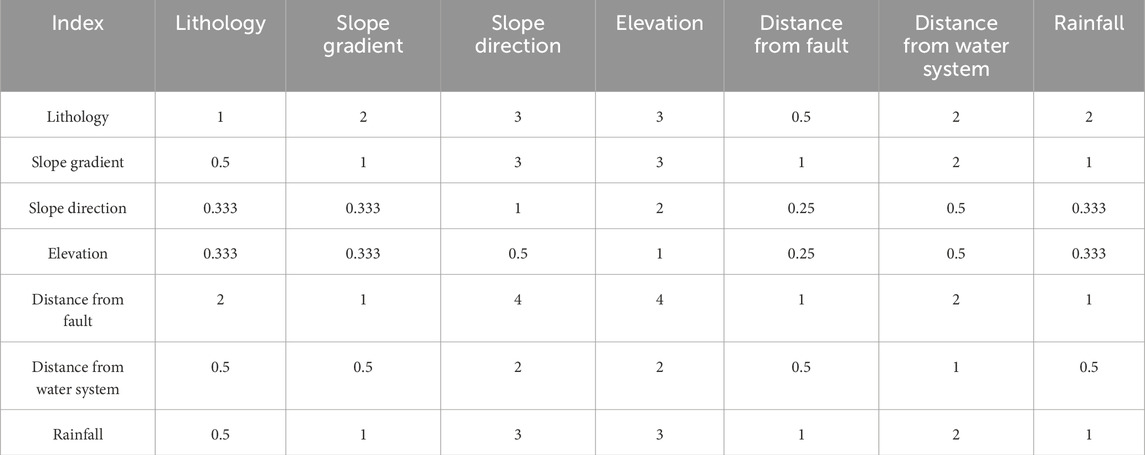
(2) Constructing a judgment matrix. Constructing the judgment matrix is a key step in AHP decision-making. Starting from the goal layer, each element within the same layer is compared pairwise to determine their relative importance (Table 1).
(3) Consistency test. To ensure the reliability of the matrix, the consistency of the judgment matrix is tested by calculating its consistency index:
where
3.2 Information Value method
The Information Value (IV) method, introduced in 1948 by the American mathematician and founder of information theory, Shannon, in his paper “A Mathematical Theory of Communication,” employs probability theory and logical methods to derive the formula for calculating information value (Shannon, 1948). In the 1980s, Professor Yan Tongzhen first introduced information theory into landslide disaster prediction research (Yin, 1988), and later it was widely applied by experts and scholars in the field of disaster assessment. The concept of information prediction suggests that the occurrence of a landslide disaster is related to the quantity and quality of information obtained during the prediction process and is measured by the amount of information. The greater the information value, the more conducive it is to the occurrence of a disaster (Sharma et al., 2015). The calculation of information value can be expressed by the following formula:
where
Where
3.3 Certainty Factor method
The Certainty Factor (CF) method is a common method for assessing landslide susceptibility, based on the probability function of landslide occurrence. It calculates the certainty factor of the evaluation factor using the following formula:
Where
The range of
3.4 Frequency Ratio method
The Frequency Ratio (FR) method calculates the probability of landslides occurring for each influencing factor within different grading intervals, analyzing the spatial relationship between the distribution of landslides and the gradation of each influencing factor. The frequency ratio is the ratio of the area where landslides occur in a particular grading interval of an influencing factor to the total landslide area of the study area, and the ratio of the area under that grade to the total area of the study area (Solaimani et al., 2013; Panchal and Shrivastava, 2021) The formula and calculation process of the frequency ratio are as follows:
In the formula:
Methods such as AHP, IV, CF, and FR are applicable for evaluating the impact of various factors on outcomes, each with its unique advantages and limitations. AHP is easy to understand and suitable for complex decisions, but it may be influenced by subjective biases; IV is simple to operate and effective for large data sets, but it relies on the quality of the data; CF is intuitive and effective for rapid analysis, but it can distort results when factor correlations are high; FR effectively analyzes the relationship between event frequency and factors, but it requires extensive historical data. The choice of method should consider the research needs and data conditions comprehensively to ensure the accuracy and practicality of the evaluation results.
4 Selection of evaluation factors
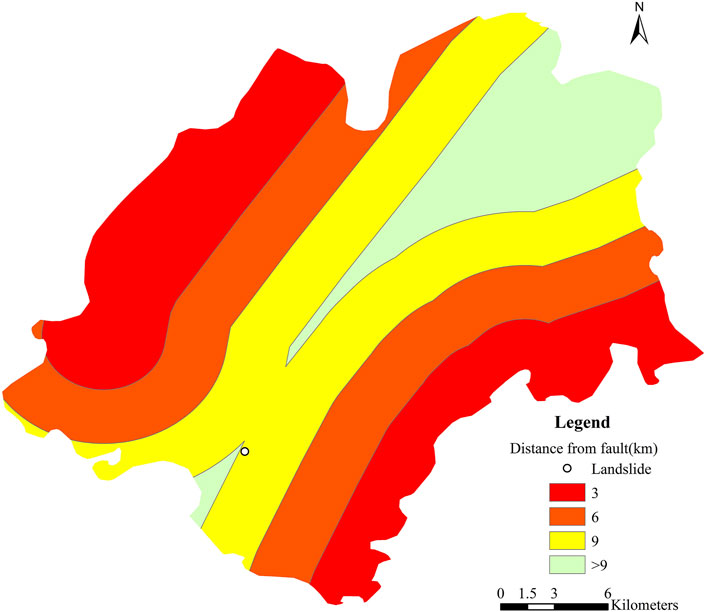
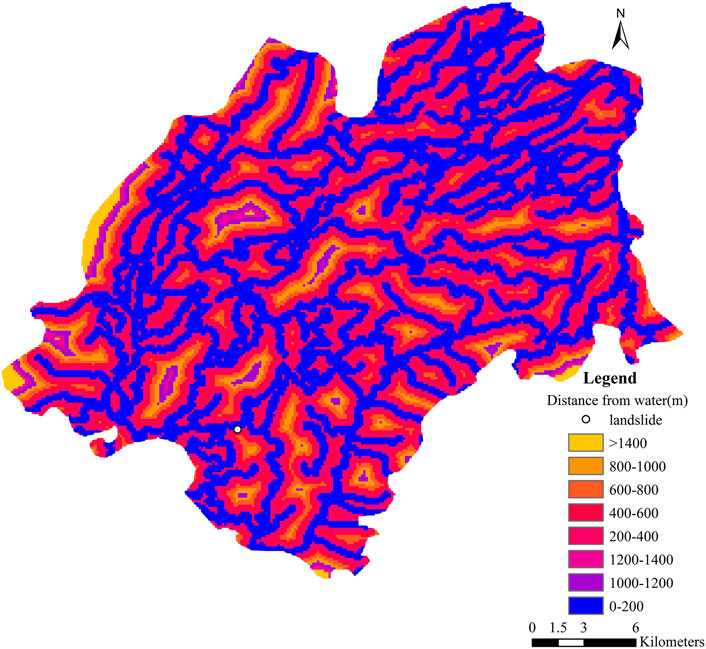
The selection of evaluation factors is fundamental to landslide risk assessment. Choosing and analyzing these factors is key to quantifying the occurrence and evolution of landslides. By considering different evaluation factors, one can gain deeper insights into the potential risks and evolutionary trends of landslides. This paper comprehensively evaluates landslide risks in the study area using seven evaluation factors: lithology, slope, aspect, elevation, distance from faults, distance from hydrological systems, and rainfall. The data on lithology, slope, aspect, and elevation are obtained from field survey results. The distance from faults is indicated in Figure 6, the distance from hydrological systems is shown in Figure 8, and rainfall data is available from the Mingshan District annals.
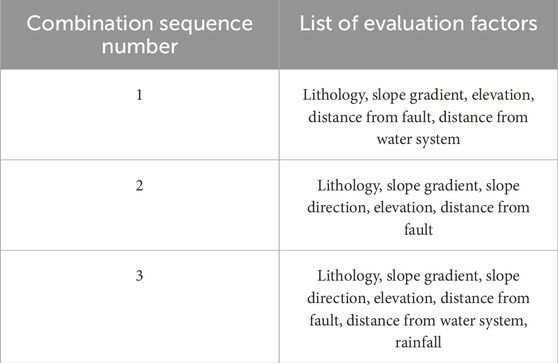
The selection of evaluation factors is subjective, and the combination of single evaluation factors is limited. Based on the analysis of landslide formation mechanisms and previous research experience (Liu et al., 2024; Qiu et al., 2024; Ye et al., 2024), this paper selects three types of combinations of evaluation factors (Table 3). By using multiple combinations of different evaluation factors and comprehensively considering various factors, a more thorough understanding and assessment of landslide risks are achieved. Such an integrated evaluation approach helps to reduce the subjectivity and one-sidedness of single-factor evaluations, enhancing the reliability and accuracy of the assessment results. By comparing results from different combinations, the relative importance of each evaluation factor in different contexts can be explored, thus providing more targeted suggestions and decision-making support for landslide prevention and disaster management.
5 Landslide risk assessment
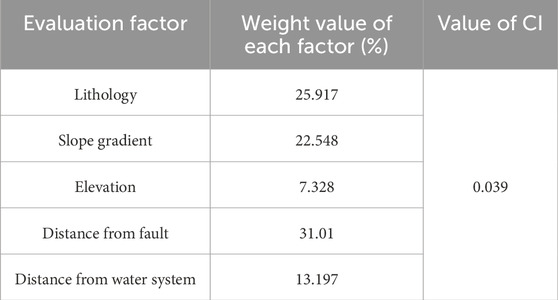
5.1 Determining the weight of evaluation factors using the Analytical Hierarchy Process (AHP)
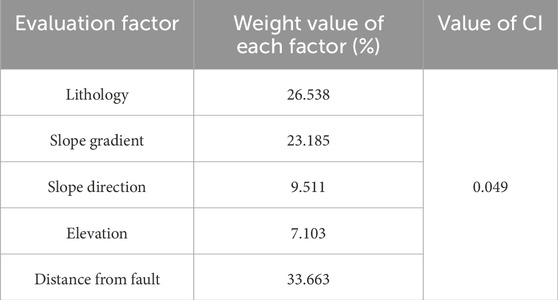
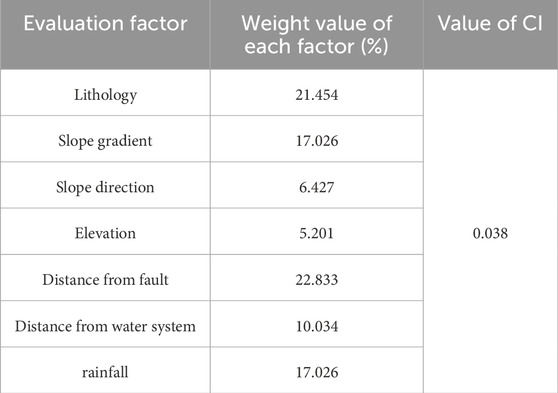
(1) The results of pairwise comparisons of evaluation factors were obtained through expert argumentation, Constructing the judgment matrix (Tables 4–6):
(2) Result verification (refer to Eq. 4 for the calculation method):
5.2 AHP-IV method
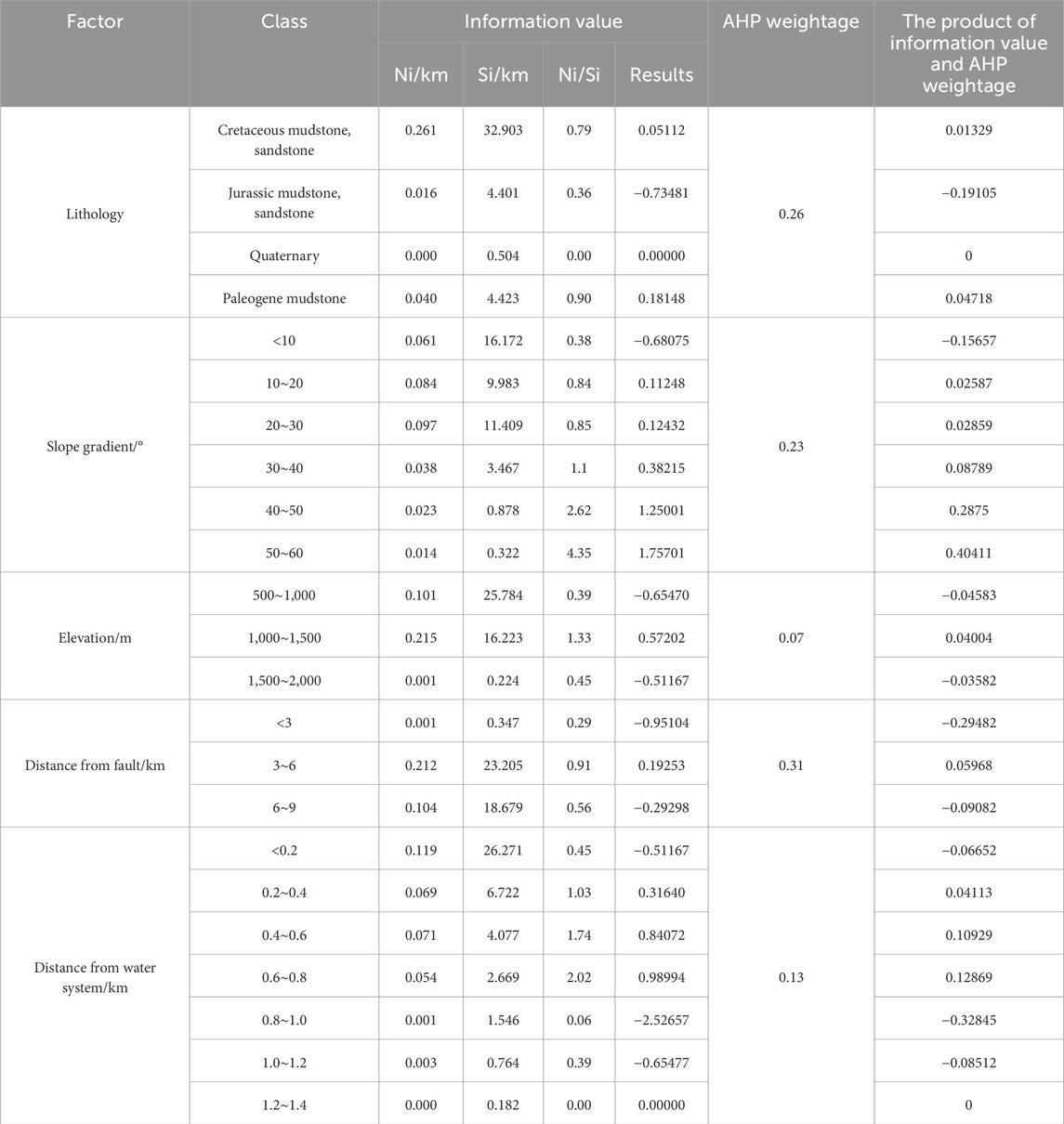
Some scholars have used the Information Value method for landslide risk assessment (Sarkar et al., 2013; Zhang et al., 2014; Du et al., 2019; Wang et al., 2019). This paper combines the information values from the article by Zhang et al. (2014) with the weights of the AHP method, by selecting relevant factors (see Table 3) and conducting overlay analysis, the information value of each factor category is calculated. Then, these information values are multiplied by the weights from the Analytic Hierarchy Process (AHP) and aggregated to assess the landslide susceptibility of specific locations, with the detailed calculation process shown in Table 10, refer to Eqs 5, 6 for the calculation method.
5.3 AHP-CF method
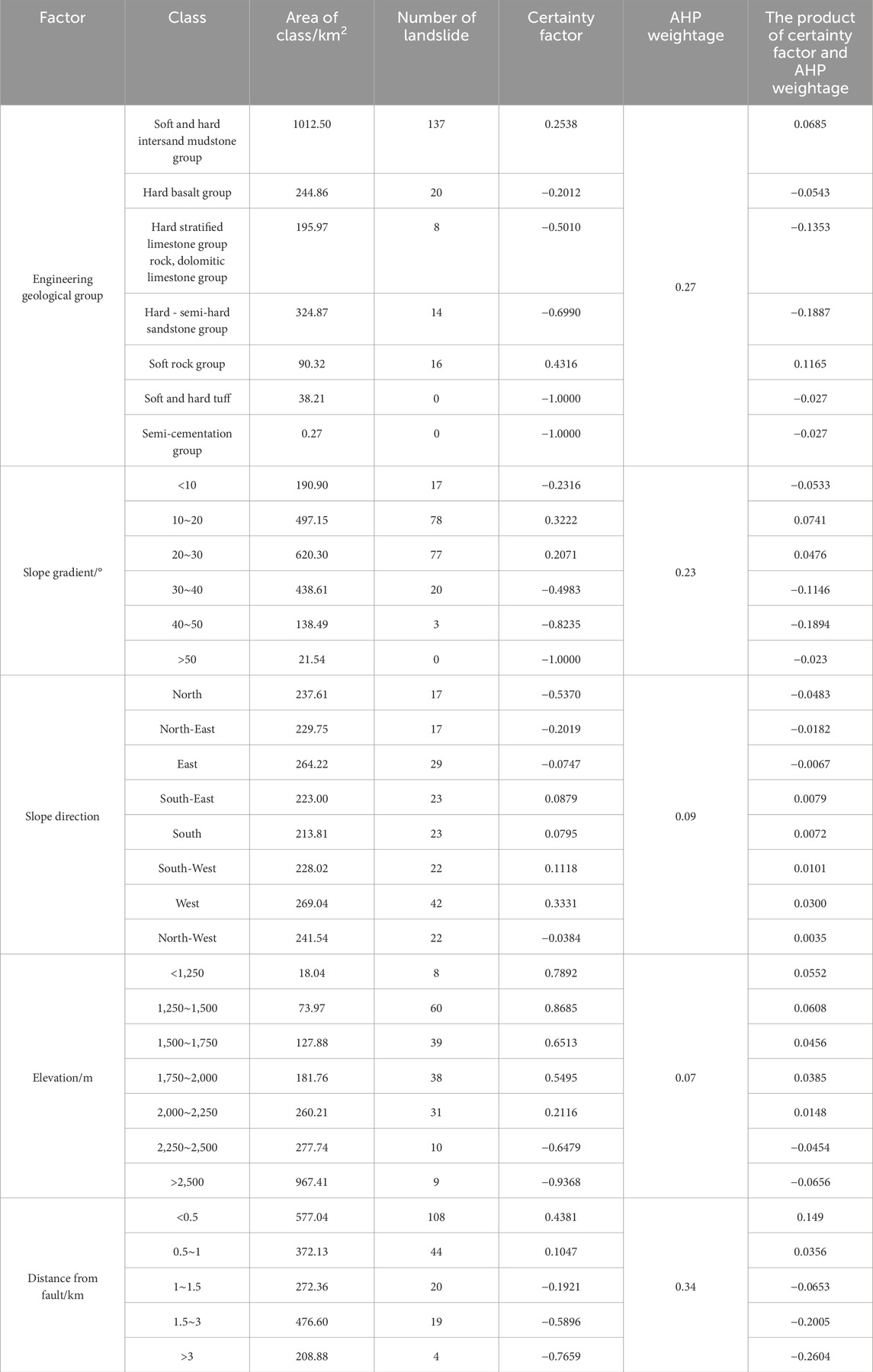
Some scholars have used the Certainty Factor method for landslide risk assessment (Chen et al., 2016b; Wang et al., 2019; Xiong et al., 2022) This paper combines the certainty factor values from the article by Xiong et al. (2022) with the weights of the AHP method, by analyzing the spatial distribution of factors related to landslides (see Table 3), the certainty coefficients of these factors are calculated. Then, these certainty coefficient values are multiplied by the weights from the Analytic Hierarchy Process (AHP) and aggregated to assess the landslide susceptibility of specific locations, with the detailed calculation process shown in Table 11, refer to Eq. 7 for the calculation method.
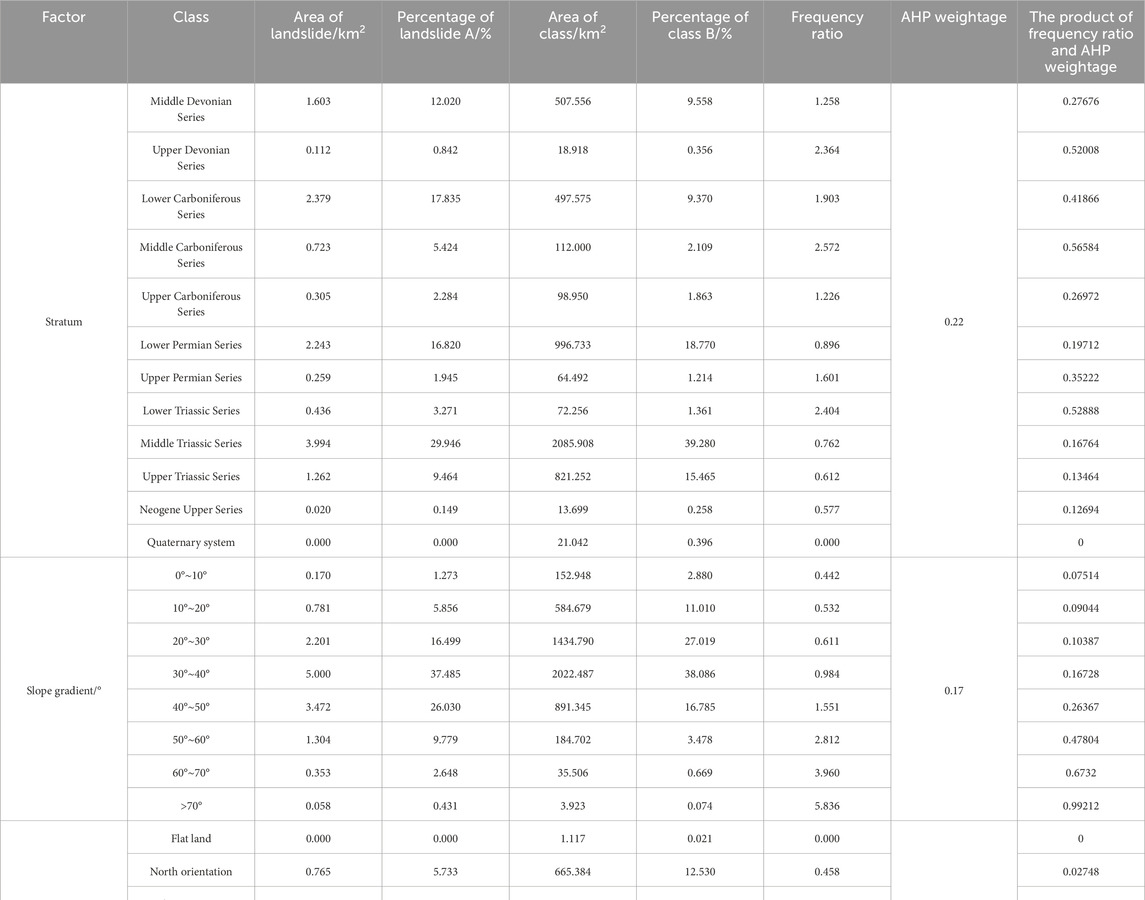
5.4 AHP-FR method
Some scholars have used the Frequency Ratio method for landslide risk assessment (Lee and Pradhan, 2007; Chen et al., 2016a; Nicu, 2018; Zhang et al., 2020; Zhang et al., 2020; Abdo, 2022). This paper combines the frequency ratio values from the article by Zhang Qiukai (Zhang et al., 2020) with the weights of the AHP method, by analyzing the classification of factors related to landslides (see Table 3), the frequency ratio for each factor category is calculated. Then, these frequency ratios are multiplied by the weights from the Analytic Hierarchy Process (AHP) and aggregated to assess the landslide susceptibility of specific locations, with the detailed calculation process shown in Table 12, refer to Eq. 8 for the calculation method.
5.5 Evaluation results
The calculation results and risk identification methods of the three approaches are shown in Table 13.
6 Results and discussion
6.1 Results analysis
The AHP-IV and AHP-FR methods classify the area as a moderate-risk zone, while the AHP-CF method assesses it as a low-risk zone.
The landslide in question first occurred in 2001, causing damage to 12 residential houses. It has been sliding annually in recent years, particularly during the “4.20” Lushan earthquake in 2013, where the peak ground acceleration caused by the earthquake was greater than the critical acceleration of the landslide, resulting in permanent damage. Field investigations reveal that the stability of landslide is currently poor. Under the action of rainfall, it is highly susceptible to overall sliding. The assessments of the AHP-IV and AHP-FR methods, categorizing the area as a moderate-risk zone, align more closely with the actual situation. The AHP-CF method, assessing it as a low-risk zone, shows some variance from the other two methods’ results. This discrepancy mainly arises from two aspects: Firstly, the AHP-CF method did not consider rainfall and proximity to the water source as evaluation factors for this landslide, even though both are significant influence factors. Rainfall increases pore water pressures in the soil, leading to a reduction in effective stress and reduced shear strength, thus triggering landslides. Areas close to water systems often have higher groundwater levels and hence lower effective stresses, thus increasing the probability of landslides. The exclusion of these factors in the AHP-CF method leads to an “apparently” safer assessment of the study area. Secondly, the judgment method of the AHP-CF method is derived from the inherent nature of the CF method itself. Applying the results of this study directly into it may introduce certain errors.
To improve the accuracy of the AHP-CF method for landslide risk assessment, the following improvements can be made: Firstly, more comprehensive evaluation factors should be selected, considering hydrological factors like rainfall and proximity to the water system. Secondly, the judgment method of the AHP-CF method should be adjusted according to the actual situation, to be better align with the reality of the study area, thereby enhancing the accuracy of the assessment. Finally, integrating other assessment methods, such as AHP-IV and AHP-FR, and considering various factors, the AHP-CF method can be continuously optimized.
6.2 Discussion
The geographical and geological conditions of different study areas may significantly vary. Directly applying the results of one study to another area may not yield safe evaluations. This paper, while using previous research results, uses the AHP method to better adapt these results to the current study area. However, the judgment of the AHP-IV approach is derived from the Information Value (IV) values cited in the original article, which did not use the AHP. Therefore, directly applying the AHP-IV method’s evaluation results to the cited article’s IV evaluation method can lead to a certain errors. The same applies to the judgment results of the AHP-FR method. The judgment of the AHP-CF method, derived from the inherent nature of the CF method, allows for only a general judgment, and its accuracy remains to be verified. Nevertheless, the evaluation results of all three methods show high consistency and align with the actual conditions of the landslide in the study area. Therefore, despite some errors, the evaluation results are still considered reasonable.
Landslide risk assessment has always been a hot topic in the field of geological disaster research. To improve evaluation efficiency and accuracy, this paper proposes a rapid method for landslide risk assessment. This method comprehensively considers various factors such as geological conditions, geographical environment, and triggering factors. It utilizes existing research conclusions and study methods specific to the study area for quick calculation and evaluation. The method involves the following steps (Figure 9):
(1) Collect data on geological disasters in the study area, including geological conditions, geographical environment, and triggering factors.
(2) Summarize the basic characteristics of the landslide.
(3) Choose targeted methods for analysis based on the basic characteristics of the landslide.
(4) Use suitable research results from similar areas.
(5) Establish a comprehensive evaluation method based on targeted evaluation methods and previous research findings.
(6) Apply the comprehensive evaluation method, combined with the basic characteristics of the landslide, to assess its risk.
Currently, for regional landslide risk assessment, many researchers have applied statistical regression analysis to obtain evaluation results. If appropriate previous research results are applied to individual landslide studies, it can overcome the shortcomings of statistical regression analysis in terms of data requirements and greatly improve the efficiency of landslide risk assessment. For example, in this study, after seven data including lithology, slope, aspect, elevation, distance from faults, distance from hydrological systems, and rainfall were easy to obtain, we can make a rapid assessment of landslide risk.
It is important to note that when applying previous research results to different study areas, the accuracy of landslide risk assessment needs to be verified. To enhance accuracy, this paper selected research results from three similar areas and combined them with the AHP method. Ultimately, the three evaluation results showed high consistency, thus considered reasonable. However, due to the lack of an appropriate judgment method, the research results of this method may still contain some errors.
7 Conclusion
Through the landslide risk evaluation, the risks associated with the landslides in the study area were assessed, leading to the following conclusions.
(1) The study employed three landslide risk assessment methods: AHP-IV, AHP-CF, and AHP-FR. Both AHP-IV and AHP-FR methods assessed the study area as a moderate-risk zone, while the AHP-CF method rated it as a low-risk area.
(2) Field investigation results classified the landslide risk in the study area as moderate. When these findings were combined with the cumulative displacement caused by earthquakes in the surrounding areas, the assessments of the AHP-IV and AHP-FR methods, categorizing the area as a moderate-risk zone, were found to be more consistent with the actual situation. The AHP-CF method, which assessed the area as low-risk, was analyzed for its error sources, and suggestions for improvement were proposed.
(3) The study proposed a rapid method for landslide risk assessment. This method takes into account various factors including geological conditions, geographical environment, and triggering factors. It utilizes existing research findings and methods tailored to the study area to quickly evaluate landslide risk.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
NH: Investigation, Writing–review and editing. XG: Formal Analysis, Methodology, Writing–original draft. WZ: Conceptualization, Writing–review and editing. LX: Conceptualization, Writing–original draft. FG: Supervision, Writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is Sponsored by State Key Laboratory of Earthquake Dynamics (Project No. LED2023B02); the Fundamental Research Funds for the Universities of Henan Province (Grant No. NSFRF240624); and the National key R&D program (Grant No. 2023YFF080020602).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdo, H. (2022). Assessment of landslide susceptibility zonation using frequency ratio and statistical index: a case study of Al-Fawar basin, Tartous, Syria. Int. J. Environ. Sci. Technol. 19, 2599–2618. doi:10.1007/s13762-021-03322-1
Bai, S.-B., Lu, P., and Wang, J. (2015). Landslide susceptibility assessment of the Youfang catchment using logistic regression. J. Mt. Sci. 12, 816–827. doi:10.1007/s11629-014-3171-5
Chen, W., Chai, H., Sun, X., Wang, Q., Ding, X., and Hong, H. (2016a). A GIS-based comparative study of frequency ratio, statistical index and weights-of-evidence models in landslide susceptibility mapping. Arabian J. Geosciences 9, 204–216. doi:10.1007/s12517-015-2150-7
Chen, W., Li, W., Chai, H., Hou, E., Li, X., and Ding, X. (2016b). GIS-based landslide susceptibility mapping using analytical hierarchy process (AHP) and certainty factor (CF) models for the Baozhong region of Baoji City, China. Environ. Earth Sci. 75, 63–14. doi:10.1007/s12665-015-4795-7
Chen, Z., Song, D. Q., Juliev, M., and Pourghasemi, H. R. (2021). Landslide susceptibility mapping using statistical bivariate models and their hybrid with normalized spatial-correlated scale index and weighted calibrated landslide potential model. Environ. Earth Sci. 80, 324. doi:10.1007/s12665-021-09603-9
Cheng, Y. X., Gan, Y., Shi, C. M., Huo, A. D., Pei, Y. H., Song, Y., et al. (2024). A critical analysis of geological hazard risk assessment including future perspectives. Sustainability 16, 3701. doi:10.3390/su16093701
Du, G., Zhang, Y., Yang, Z., Guo, C., Yao, X., and Sun, D. (2019). Landslide susceptibility mapping in the region of eastern Himalayan syntaxis, Tibetan Plateau, China: a comparison between analytical hierarchy process information value and logistic regression-information value methods. Bull. Eng. Geol. Environ. 78, 4201–4215. doi:10.1007/s10064-018-1393-4
Feizizadeh, B., and Blaschke, T. (2014). An uncertainty and sensitivity analysis approach for GIS-based multicriteria landslide susceptibility mapping. Int. J. Geogr. Inf. Sci. 28, 610–638. doi:10.1080/13658816.2013.869821
He, N., Qu, X., Yang, Z., Xu, L., and Gurkalo, F. (2023). Disaster mechanism and evolution characteristics of landslide–debris-flow geohazard chain due to strong earthquake—a case study of niumian gully. Water 15, 1218. doi:10.3390/w15061218
Jibson, R. W. (2007). Regression models for estimating coseismic landslide displacement. Eng. Geol. 91, 209–218. doi:10.1016/j.enggeo.2007.01.013
Kadapa, H. (2024). A comprehensive framework for landslide risk assessment of archaeological sites in Gujarat, India. Egypt. J. Remote Sens. Space Sci. 27, 41–51. doi:10.1016/j.ejrs.2024.01.002
Kayastha, P., Dhital, M. R., and De Smedt, F. (2013). Application of the analytical hierarchy process (AHP) for landslide susceptibility mapping: a case study from the Tinau watershed, west Nepal. Comput. Geosciences 52, 398–408. doi:10.1016/j.cageo.2012.11.003
Lee, S., and Pradhan, B. (2007). Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 4, 33–41. doi:10.1007/s10346-006-0047-y
Li, C., and Su, L. J. (2021). Influence of critical acceleration model on assessments of potential earthquake-induced landslide hazards in Shimian County, Sichuan Province, China. Landslides 18, 1659–1674. doi:10.1007/s10346-020-01578-1
Liu, Y., Qiu, H. J., Kamp, U., Wang, N. L., Wang, J. D., Huang, C., et al. (2024). Higher temperature sensitivity of retrogressive thaw slump activity in the Arctic compared to the Third Pole. Sci. Total Environ. 914, 170007. doi:10.1016/j.scitotenv.2024.170007
Ma, S. Y., and Xu, C. (2019). Applicability of two Newmark models in the assessment of coseismic landslide hazard and estimation of slope-failure probability: an example of the 2008 wenchuan mw 7.9 earthquake affected area. J. Earth Sci. 30, 1020–1030. doi:10.1007/s12583-019-0874-0
Maharjan, S., Gnyawali, K. R., Tannant, D. D., Xu, C., and Lacroix, P. (2021). Rapid terrain assessment for earthquake-triggered landslide susceptibility with high-resolution DEM and critical acceleration. Front. Earth Sci. 9. doi:10.3389/feart.2021.689303
Mandal, B., and Mandal, S. (2018). Analytical hierarchy process (AHP) based landslide susceptibility mapping of Lish river basin of eastern Darjeeling Himalaya, India. Adv. Space Res. 62, 3114–3132. doi:10.1016/j.asr.2018.08.008
Marín-Rodríguez, N. J., Vega, J., Zanabria, O. B., Gonz Lez-Ruiz, J. D., and Botero, S. (2024). Towards an understanding of landslide risk assessment and its economic losses: a scientometric analysis. Landslides. doi:10.1007/s10346-024-02272-2
Newmark, N. M. (1965). Effects of earthquakes on dams and embankments. Geotechnique 15, 139–160. doi:10.1680/geot.1965.15.2.139
Nicu, I. C. (2018). Application of analytic hierarchy process, frequency ratio, and statistical index to landslide susceptibility: an approach to endangered cultural heritage. Environ. Earth Sci. 77, 79. doi:10.1007/s12665-018-7261-5
Panchal, S., and Shrivastava, A. K. (2021). A comparative study of frequency ratio, shannon's entropy and analytic hierarchy process (AHP) models for landslide susceptibility assessment. Isprs Int. J. Geo-Information. 10, 603. doi:10.3390/ijgi10090603
Panchal, S., and Shrivastava, A. K. (2022). Landslide hazard assessment using analytic hierarchy process (AHP): a case study of National Highway 5 in India. Ain Shams Eng. J. 13, 101626. doi:10.1016/j.asej.2021.10.021
Qiu, H. J., Su, L. L., Tang, B. Z., Yang, D. D., Ullah, M., Zhu, Y. R., et al. (2024). The effect of location and geometric properties of landslides caused by rainstorms and earthquakes. Earth Surf. Process. Landforms. doi:10.1002/esp.5816
Qiu, H. J., Zhu, Y. R., Zhou, W. Q., Sun, H. S., He, J. Y., and Liu, Z. J. (2022). Influence of DEM resolution on landslide simulation performance based on the Scoops3D model. Geomatics Nat. Hazards Risk 13, 1663–1681. doi:10.1080/19475705.2022.2097451
Roy, R., Ghosh, D., and Bhattacharya, G. (2016). Influence of strong motion characteristics on permanent displacement of slopes. Landslides 13, 279–292. doi:10.1007/s10346-015-0568-3
Saaty, T. L. (1977). A scaling method for priorities in hierarchical structures. J. Math. Psychol. 15, 234–281. doi:10.1016/0022-2496(77)90033-5
Sarkar, S., Roy, A. K., and Martha, T. R. (2013). Landslide susceptibility assessment using information value method in parts of the Darjeeling Himalayas. J. Geol. Soc. India 82, 351–362. doi:10.1007/s12594-013-0162-z
Shannon, C. E. (1948). A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423. doi:10.1002/j.1538-7305.1948.tb01338.x
Sharma, L. P., Patel, N., Ghose, M. K., and Debnath, P. (2015). Development and application of Shannon's entropy integrated information value model for landslide susceptibility assessment and zonation in Sikkim Himalayas in India. Nat. Hazards 75, 1555–1576. doi:10.1007/s11069-014-1378-y
Solaimani, K., Mousavi, S. Z., and Kavian, A. (2013). Landslide susceptibility mapping based on frequency ratio and logistic regression models. Arabian J. Geosciences 6, 2557–2569. doi:10.1007/s12517-012-0526-5
Vaidya, O. S., and Kumar, S. (2006). Analytic hierarchy process: an overview of applications. Eur. J. Operational Res. 169, 1–29. doi:10.1016/j.ejor.2004.04.028
Wang, K. L., and Lin, M. L. (2010). Development of shallow seismic landslide potential map based on Newmark's displacement: the case study of Chi-Chi earthquake, Taiwan. Environ. Earth Sci. 60, 775–785. doi:10.1007/s12665-009-0215-1
Wang, Q. Q., Guo, Y. H., Li, W. P., He, J. H., and Wu, Z. Y. (2019). Predictive modeling of landslide hazards in Wen County, northwestern China based on information value, weights-of-evidence, and certainty factor. Geomatics Nat. Hazards Risk 10, 820–835. doi:10.1080/19475705.2018.1549111
Wang, X., Nie, G., and Wang, D. (2010). Research on relationship between landslides and peak ground accelerations induced by Wenchuan earthquake. Chin. J. Rock Mech. Eng. 29, 82–89.
Wu, C.-H., and Chen, S.-C. (2009). Determining landslide susceptibility in Central Taiwan from rainfall and six site factors using the analytical hierarchy process method. Geomorphology 112, 190–204. doi:10.1016/j.geomorph.2009.06.002
Wu, Y., Li, W., Liu, P., Bai, H., Wang, Q., He, J., et al. (2016). Application of analytic hierarchy process model for landslide susceptibility mapping in the Gangu County, Gansu Province, China. Environ. Earth Sci. 75, 422–511. doi:10.1007/s12665-015-5194-9
Xing, X., Wu, C., Li, J., Li, X., Zhang, L., and He, R. (2021). Susceptibility assessment for rainfall-induced landslides using a revised logistic regression method. Nat. Hazards 106, 97–117. doi:10.1007/s11069-020-04452-4
Xiong, X., Wang, C., Bai, Y., Tie, Y., Gao, Y., and Li, G. (2022). Comparison of landslide susceptibility assessment based on multiple hybrid models at county level: a case study for Puge County, Sichuan Province. Chin. J. Geol. Hazard Control 33, 114–124.
Yang, D. D., Qiu, H. J., Ye, B. F., Liu, Y., Zhang, J. J., and Zhu, Y. R. (2023). Distribution and recurrence of warming-induced retrogressive thaw slumps on the central qinghai-tibet plateau. J. Geophys. Research-Earth Surf. 128. doi:10.1029/2022jf007047
Ye, B. F., Qiu, H. J., Tang, B. Z., Liu, Y., Liu, Z. J., Jiang, X. Y., et al. (2024). Creep deformation monitoring of landslides in a reservoir area. J. Hydrology 632, 130905. doi:10.1016/j.jhydrol.2024.130905
Yin, K. (1988). Statistical prediction model for slope instability of metamorphosed rocks. Proc. 5th Int. Symposium Landslides 1988, 1269–1272.
Yu, Y., and Wang, Y. (2004). Attenuation relations for horizontal peak ground acceleration and response spectrum in northeastern Tibetan plateau region. Acta Seismol. Sin., 591–600.
Zhang, D., Chang, M., Ma, G., Jia, T., and Zhou, Z. (2014). The hazard assessment of geological disasters by “4.20” Lushan earthquake in Longmen town of ya’an, Sichuan province, China. J. Geol. Hazards Environ. Preserv. 25, 16–21.
Zhang, Q., Ling, S., Li, X., Sun, C., Xu, J., and Huang, T. (2020a). Comparison of landslide susceptibility mapping rapid assessment models in Jiuzhaigou County, Sichuan province, China. Chin. J. Rock Mech. Eng. 39, 1595–1610.
Zhang, Y., Lan, H., Li, L., Wu, Y., Chen, J., and Tian, N. (2020b). Optimizing the frequency ratio method for landslide susceptibility assessment: a case study of the caiyuan basin in the Southeast mountainous area of China. J. Mt. Sci. 17, 340–357. doi:10.1007/s11629-019-5702-6
Keywords: hazard assessment, analytic hierarchy process, information value method, certainty factor method, Frequency Ratio method, peak ground acceleration
Citation: He N, Gao X, Zhong W, Xu L and Gurkalo F (2024) A method for rapidly assessing landslide hazard—taking the landslide in Yongxing town, Mingshan area as an example. Front. Earth Sci. 12:1429346. doi: 10.3389/feart.2024.1429346
Received: 08 May 2024; Accepted: 04 June 2024;
Published: 01 July 2024.
Edited by:
Haijun Qiu, Northwest University, ChinaReviewed by:
Qi Xing, Sichuan University of Science and Engineering, ChinaXinghua Zhu, Chang’an University, China
Copyright © 2024 He, Gao, Zhong, Xu and Gurkalo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei Zhong, emhvbmd3ZWlAaW1kZS5hYy5jbg==
 Na He
Na He Xinhang Gao1
Xinhang Gao1 Wei Zhong
Wei Zhong Linjuan Xu
Linjuan Xu Filip Gurkalo
Filip Gurkalo