Comparison and analysis for prediction accuracy of true triaxial rock strength criterion

To verify the predictive accuracy of existing strength criteria on true triaxial strength experimental data, understand the characteristics of different strength criteria, and provide a basis for selecting strength criteria for engineering applications, ten commonly used rock strength criteria were selected and divided into MC and HB types. The distribution characteristics of the yield surfaces and yield curves of different criteria were compared and analyzed in the principal stress space and the π plane. Afterwards, based on the least absolutely deviation method, these ten strength criteria were used to predict 32 sets of true triaxial rock strength experimental data. The results showed that the range of undetermined parameters for MC type strength criteria was small and easy to determine, while the range of undetermined parameter for HB type criteria was large and difficult to determine the search range, in addition, the fitting process may not converge. The fitting accuracy of strength criteria for true triaxial experimental data depends on the sensitivity of rock strength to the intermediate principal stress. PH and GP criteria are the most sensitive to changes of the intermediate principal stress, followed by MWC and ML criteria, MGC and ZZ criteria, MCJP and HBWW criteria. PH and GP criteria overestimate the effect of the intermediate principal stress, resulting in the largest prediction errors, while the other three-dimensional strength criteria have high prediction accuracy and no significant differences. The research results can provide scientific basis for engineering design, geological hazard prediction, and mineral resource development.

1 Introduction

Rock strength criteria serve as crucial theoretical foundation and scientific basis for issues such as underground tunnel design and wellbore stability prediction. With the continuous advancement of deep earth engineering by Sinopec, the exploration and development efforts for deep-seated oil and gas resources have gradually intensified, leading to a comprehensive enhancement in the exploration and development capabilities of deep-seated resources. Consequently, there is an urgent need for further research on the failure characteristics and strength of deep-seated rocks (Cai et al., 2021; Fengjiao et al., 2023; Hoek and Brown,1980; Hoek and Brown, 2019; Jiang and Pietruszczak, 1988). The Mohr-Coulomb (MC) criterion, due to its clear concept, and the Hoek-Brown (HB) criterion, owing to its high fitting accuracy to experimental data and the convenience of strength parameters obtaining, are widely used. However, current MC and HB criteria cannot accurately characterize the nonlinear characteristics of rock failure under high confining pressures, besides, debates regarding the influence of intermediate principal stresses on strength have persisted alongside their applications (Kim and Lade, 1984; Lade and Duncan, 1975; Pan and Hudson, 1988).

For centuries, mechanics researchers have conducted extensive studies on the yield and failure of materials under multiaxial stress states. The study of strength criteria began with metallic materials (Priest and Hunt, 2005; Warnke and Warnke, 1975; Wiebols and Cook, 1968). In 1864, Tresca proposed that when the maximum shear stress within the material reaches its limit, the material enters a plastic state and begins to yield. This criterion forms a regular hexagon on the π plane and a hexagonal cylinder in the principal stress space. In 1913, von-Mises proposed the von-Mises criterion using the circumscribed circle of Tresca’s criterion on the π plane to replace the yield curve of Tresca’s criterion. However, these two criteria, being based on metallic materials, did not reflect the influence of hydrostatic pressure on yield and could not be applied to the yield and failure of rock-like materials under triaxial compression or tension stress states. Rock strength criteria are theories used to determine whether rocks will yield or fail under different stress states, which are commonly used to predict the ultimate strength of rocks under different stress conditions (You, 2010; You, 2011; Zhang et al., 2024; Zhang et al., 2017a; Zhang et al., 2017b). Currently, the most commonly used and influential criterion is the Mohr-Coulomb criterion. However, the MC criterion does not consider the influence of intermediate principal stress, only describing the ultimate strength of rocks under triaxial compression stress states, and it has six singular points on the π plane, making numerical calculations inconvenient. Recognizing that rock failure is mainly controlled by deviatoric stress, Drucker and Prager improved the von-Mises criterion and proposed the Drucker-Prager (DP) criterion. The DP criterion is a conical surface in the principal stress space and a circle in the π plane. However, the DP criterion cannot describe the differences in strength of rocks on different meridians, nor can it fully coincide with triaxial tensile and triaxial compressive points on the π plane. The DP criterion contains two material strength parameters. Depending on the position of the ultimate trace of the DP criterion on the π plane and the triaxial compressive or triaxial tensile strength points of the MC criterion, four sets of relationships between strength parameters of DP criterion and strength parameters of MC criterion can be obtained, namely, the elongated cone, compressive cone, intermediate cone, and tangent cone. The DP criterion considers the influence of hydrostatic pressure, which is more suitable for rock and soil materials than the von-Mises criterion. However, different forms of the DP criterion can result in material strength differences of 3–4 times. This discrepancy poses risks in engineering, leading to the general belief that the DP criterion overestimates the strengthening effect of intermediate principal stress on rock strength and should be used with caution in rock and soil engineering (Zhang et al., 2013; Zhou et al., 2018; Zhou, 1994).

To address the deficiencies of the MC and DP criteria, Lade and Duncan proposed the Lade-Duncan criterion in 1975 and 1977. However, it was only applicable to weakly bonded sandy soils. From 1977 to 1979, Lade revised the Lade-Duncan criterion, and established the well-known Modified Lade criterion. The Modified Lade criterion considers the influence of intermediate principal stress and forms a smooth curve on the π plane, which overcomes the shortcomings of the classical MC criterion and presents broad application prospects. The only drawback is that the ultimate trace line of the Modified Lade criterion on the π plane only intersects with the MC criterion in the triaxial compression state, overestimating rock strength in the triaxial tension state. Strength criteria based on two parameters of cohesion and internal friction angle can be uniformly classified as MC-type strength criteria, such as the DP criterion, ML criterion, Mogi-Coulomb (MGC) criterion, and Modified Wiebol-Cook (MWC) criterion. Another classic strength criterion is the Hoek-Brown (HB) criterion, established by Hoek and Brown in 1980. Similar to the MC criterion, the HB criterion can distinguish between triaxial tensile and compressive strength, which exhibits nonlinear characteristics on the meridional plane. In the region of tensile stress and high confining stress, the HB criterion can better reflect the failure characteristics of rocks than the MC criterion. The HB criterion contains two undetermined parameters reflecting rock properties m) and rock structure (s). For intact rock cores, s is generally assumed to be 1. To compensate for the deficiencies of the HB criterion, scholars at home and abroad have established various modified HB criteria. Voigt (1901) found through experiments that the test results did not correspond with the Mohr-Coulomb (MC) strength theory, leading him to believe that “the strength problem is very complex, and it is impossible to provide a single theory that can be effectively applied to various materials.” In 1953, Timoshenko reiterated Voigt’s conclusion. Mendelson, a plasticity mechanic, pointed out in 1968 that “seeking a more accurate theory, especially because it must be more complex, seems to be a futile task.” Fan (1998) mentioned in his work that there are two unresolved challenges in the study of rock strength theory. One is the failure to consider the influence of shear stress on all faces except the maximum shear stress within the rock, and the other is the inability to unify various criteria into one failure criterion. This is known as the Voigt-Timoshenko problem. Thanks to the proposal of the double shear stress element and Drucker’s postulate, Yu proposed the Unified Strength Theory in 1991, which marked a milestone in the resolution of the Voigt-Timoshenko problem. This theory is based on Drucker’s convex postulate for the yield surface and the material parameters have clear physical meanings. It is a piecewise linear function of the intermediate principal stress and can reflect the effect of intermediate principal stress on rock-like materials and the difference in triaxial tensile and compressive strengths. It fills the gap between single shear strength theory (Mohr-Coulomb criterion) and double shear strength theory. By changing the material parameter b reflecting the effect of intermediate principal stress, it can linearly approximate the majority of strength criteria. Xiaoping et al. (2008) believed that the Unified Strength Theory encompasses and approximates all existing and possible strength theories with a simple mathematical expression. Single shear, double shear strength theories, and other failure criteria between them are all special cases or linear approximations of the Unified Strength Theory.

Mogi (1967) conducted extensive work on the influence of intermediate principal stress on rock failure, finding that the increase in strength with the increase in intermediate principal stress is proportional to the minimum principal stress and less than the minimum principal stress. With the increase in the intermediate principal stress, the angle between the failure surface and the maximum principal stress significantly decreases. Al-Ajmi Zimmerman (2005) proposed the MGC criterion, which can predict the strength of rocks under multiaxial stress states well. Sriapai et al. (2013) tested the true triaxial compressive strength of Maha Sarakhan salt rock and found that within the applied stress range, the elastic parameters of salt rock tend to be independent of σ₂. Compared with Mogi, ML, and 3D HB criteria, the MWC criterion best describes the influence of σ₂ on the strength of salt rock. Rahimi and Nygaard (2015) used 13 failure criteria to predict the collapse pressure of wellbore, and the results showed that the predictions of ML, MWC, and MGC were most consistent with the actual wellbore instability accidents. Colmenares and Zoback (2002) studied the fitting effects of MC, HB, ML, MWC, exponential Mogi criterion, and DP criterion on true triaxial rock strength experimental data based on the least squares method. The results showed that MWC and ML had good fitting effects for most data sets, especially for hard rocks. After the research of Colmenares and Zoback, many famous three-dimensional strength criteria emerged, and the research only introduced five sets of true triaxial strength data, which means that the studied strength models and experimental data are limited. Bahrami et al. (2017) compared 11 strength criteria through 14 sets of true triaxial strength experimental data and found that ML had the best consistency with experimental data.

The above studies all used the least squares method to fit the undetermined parameters in the strength criteria, exaggerating the influence of individual abnormal data points, leading to the deviation of the fitting line from the majority of normal data sets. Moreover, the number of experimental data used for validation in the above studies is limited, and there is no unified opinion on which failure criterion to choose. The selection of rock strength criteria is a key step in determining whether the wellbore is stable or not, and some scholars believe that the choice of strength criteria is more important than the study of strength criteria themselves. Considering that the actual failure criteria should achieve a balance between accuracy and simplicity, this study selected five commonly used Mohr-Coulomb type criteria and 5 Hoek-Brown type criteria, analyzed the yield surfaces in principal stress space and the yield lines in the π plane of these 10 criteria, and then used the method of least linear to fit 32 sets of true triaxial rock strength experimental data, evaluating the fitting accuracy of the three-dimensional rock strength criteria selected in this study and their response characteristics to intermediate principal stress.

2 The existing criteria

2.1 Criterion for the strength of the MC type

The Mohr-Coulomb criterion is widely accepted due to its clear conceptual framework, simplicity in form, and its ability to ensure the safety of geotechnical engineering predictions. It is expressed as follows in Eq. 1,

${\sigma }_1=\frac{1+\sin {\phi }_o}{1-\sin {\phi }_o}{\sigma }_3+\frac{2c_o\cos {\phi }_o}{1-\sin {\phi }_o}(1)$

Where, c_o represents the cohesion, measured in MPa, and φ_o represents the internal friction angle, measured in degrees.

Assuming that the normal stress on the failure plane is independent of the second principal stress, Al-Ajmi and Zimmerman discovered a linear relationship in 2005 that effectively fits the octahedral shear stress τ_oct with the mean normal stress σ_m,2 in the space of true triaxial test data points. They established the well-known Mogi-Coulomb criterion, which is expressed as Eqs 2, 3,

${\tau }_{\text{oct}}=a+b{\sigma }_{m,2}(2)$

$\left\{\begin{array}{l}{\sigma }_{m,2}=\frac{{\sigma }_1+{\sigma }_3}{2}\\ {\tau }_{oct}=\frac{1}{3}\sqrt{{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_1-{\sigma }_3\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2}\end{array}\right.(3)$

The coefficients a and b are as shown in Eq. 4,

$\left\{\begin{array}{l}a=\frac{2\sqrt{2}}{3}{c}_o\cos {\varphi }_o\\ b=\frac{2\sqrt{2}}{3}\sin {\varphi }_o\end{array}\right.(4)$

Ewy (1999) introduced a coefficient S reflecting the influence of cohesion on rock yielding and failure in the Lade criterion, establishing the modified Lade criterion , which is shown as Eqs 5, 6,

$I_1^{″3}/I_3^{″}=\eta +27(5)$

$\left\{\begin{array}{l}{I}_1^{″}=\left({\sigma }_1+S\right)+\left({\sigma }_2+S\right)+\left({\sigma }_3+S\right)\\ I_3^{″}=\left({\sigma }_1+S\right)\left({\sigma }_2+S\right)\left({\sigma }_3+S\right)\end{array}\right.(6)$

The relationship between the material parameters S and η in the modified Lade criterion and the cohesion and internal friction angle is as shown in Eq. 7,

$\left\{\begin{array}{l}S=\frac{c_o}{\tan {\varphi }_o}\\ \eta =\frac{4{\tan }^2{\varphi }_o\left(9-7\sin {\varphi }_o\right)}{1-\sin {\varphi }_o}\end{array}\right.(7)$

Zhou proposed a nonlinear strength criterion, which is an extension of the external Drucker-Prager criterion. Due to its similarity to the Wiebols-Cook criterion, the strength criterion established by Zhou is called the Modified Wiebols-Cook (MWC) criterion, as shown in Eq. 8,

$\left\{\begin{array}{l}\sqrt{J_2}=A+B{J}_1+C{J}_1^2\\ J_1=\left({\sigma }_1+{\sigma }_2+{\sigma }_3\right)/3\\ J_2=\left[{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_1-{\sigma }_3\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2\right]/6\end{array}\right.(8)$

In the equation, J₁ represents the mean effective confining pressure, measured in MPa, and J₂ represents the second stress invariant. The coefficients A, B and C can be expressed as Eq. 9,

$\left\{\begin{array}{l}C=\frac{\sqrt{27}}{2C_1+\left(q-1\right){\sigma }_3-C_0}\left(\frac{C_1+\left(q-1\right){\sigma }_3-C_0}{2C_1+\left(2q-1\right){\sigma }_3-C_0}-\frac{q-1}{q+1}\right)\\ B=\frac{\sqrt{3}\left(q-1\right)}{q+2}-\frac{C}{3}\left[2C_0+\left(q+2\right){\sigma }_3\right]\\ A=\frac{C_0}{\sqrt{3}}-\frac{C_0}{3}B-\frac{C_0^2}{9}C\end{array}\right.(9)$

In the above equation, q, C₀ and C₁ have relationships with cohesion and internal friction angle as shown in Eq. 10,

$\left\{\begin{array}{l}{C}_0=2c_o\cos {\varphi }_o/\left(1-\sin {\varphi }_o\right)\\ q=\frac{1+\sin {\varphi }_o}{1-\sin {\varphi }_o}\\ C_1=\left(1+0.6\tan {\varphi }_o\right)C_0\end{array}\right.(10)$

Using the variables, i.e., $\left(\xi ,r,\theta \right)$ in the π-plane, the Mohr-Coulomb (MC) criterion expressed in terms of principal stresses can be transformed into the form shown in Eq. 11:

$\left\{\begin{array}{l}{r}_{MC}-g_{MC}\left(\frac{2\sqrt{2}\sin {\varphi }_0}{3-\sin {\varphi }_0}\xi +\frac{2\sqrt{6}{\mathrm{c}}_0\cos {\varphi }_0}{3-\sin {\varphi }_0}\right)=0\\ g_{MC}=\frac{3-\sin {\varphi }_0}{\left(3-\sin {\varphi }_0\right)\cos \theta +\sqrt{3}\left(1+\sin {\varphi }_0\right)\sin \theta }\end{array}\right.(11)$

In the equation, g_MC represents the Lode angle shape function of the Mohr-Coulomb (MC) criterion on the π-plane. Lee et al. replaced g_MC with the Lode angle shape function g_JP, proposed by Jiang and Pietruszczak, to establish a new strength criterion called the MCJP criterion. The Lode angle shape function g_JP is as shown in Eq. 12,

$g_{JP}\left(\theta \right)=\frac{\left(\sqrt{1+f}-\sqrt{1-f}\right)k}{k\sqrt{1+f}-\sqrt{1-f}+\left(1-k\right)\sqrt{1-f\cos 3\theta }}(12)$

In whihc, θ represents the Lode angle in degrees, and k represents the ratio of triaxial tensile strength to triaxial compressive strength, as shown in Eq. 13:

$k=\left(3-\sin {\phi }_o\right)/\left(3+\sin {\phi }_o\right)(13)$

Research indicates that as k approaches 0.5, the Lode angle shape function proposed by Jiang and Pietruszczak on the π-plane transforms into a curved triangular pyramid shape. When k approaches 1, the function on the π-plane becomes circular in shape. Additionally, as f approaches 1, the function on the π-plane becomes a smooth and convex curve.

It can be observed that the strength parameters of the aforementioned five criteria are both cohesion and internal friction angle. This study categorizes them as MC type strength criteria. In the three-dimensional stress space, the yield surface of this type of criterion is plotted, as shown in Figure 1. For comparison purposes, with the same cohesion and internal friction angle, the yield criteria of this type are plotted on the same hydrostatic pressure plane (π-plane), as illustrated in Figure 2. Analysis reveals that the meridians of the MC-type criteria undergo linear changes with increasing hydrostatic pressure, while the shape of the yield curve on the π-plane remains unchanged with varying hydrostatic pressure. The yield surface of the MC criterion forms a hexacone, and the MGC criterion degenerates into the MC criterion under triaxial tensile and compressive stress states. Thus, the triaxial tensile and compressive meridians of the MGC criterion coincide with those of the MC criterion, but the MGC criterion exhibits concavity at the triaxial tensile stress state. The yield surfaces of ML, MWC, and MCJP criteria form surface cones, complying with Drucker’s postulate. On the π-plane, their yield curves are smooth and convex, facilitating application in numerical calculations. However, ML and MWC criteria do not coincide with the MC criterion at the triaxial tensile stress state. The yield surface of the MCJP criterion forms a curved triangular pyramid, and both the triaxial compressive and triaxial tensile meridians coincide with the MC criterion, exhibiting smoothness and convexity characteristics. Additionally, MC-type strength criteria cannot reflect the nonlinear characteristics of rocks under high confining pressures, and the fitting accuracy to true triaxial strength experimental data remains to be verified.

Figure 1

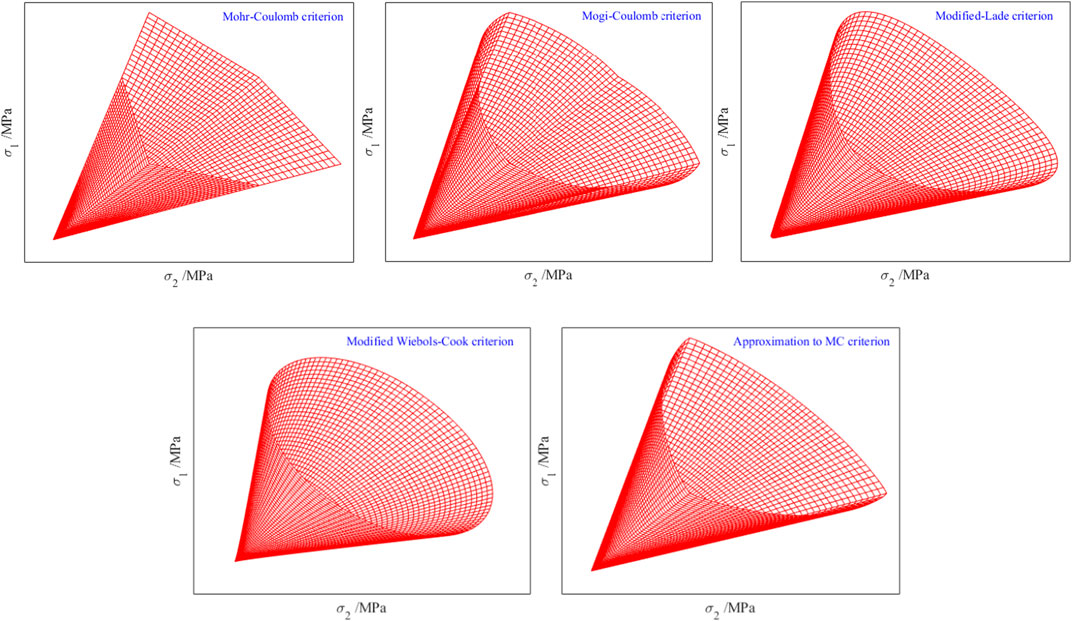
Figure 1. Distribution characteristics of MC type strength criterion on surface of principal stress space.

Figure 2

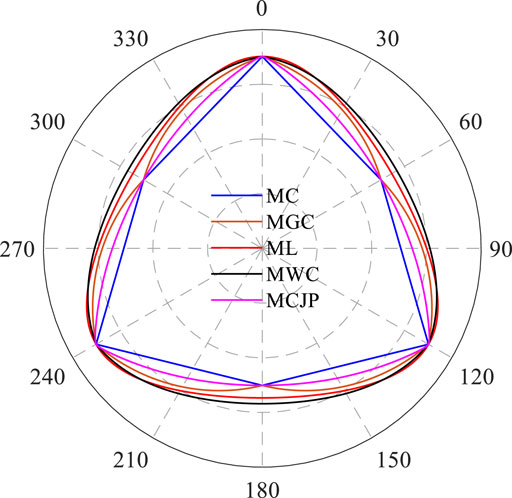
Figure 2. The distribution characteristics of the yield curve of MC-type strength criteria in the π-plane.

2.2 Criterion for the strength of the HB type

In 1980, Hoek and Brown proposed the well-known Hoek-Brown (HB) empirical criterion for intact rock, as shown in Eq. 14:

${\sigma }_1-{\sigma }_3=\sqrt{m_i{\sigma }_c{\sigma }_3+{\sigma }_c^2}(14)$

In the equation, $m_i$ represents the material parameter describing intact rock properties, and ${\sigma }_c$ represents the uniaxial compressive strength of the rock, typically obtained through laboratory experiments.

In 1988, Pan and Hudson proposed the Pan-Hudson (PH) criterion based on the average of the inner and outer circles of the Hoek-Brown criterion. It is expressed as follows in Eq. 15,

$\frac{3}{{\sigma }_c}{J}_2+\frac{\sqrt{3}}{2}{m}_i\sqrt{J_2}-\frac{m_i{I}_1}{3}={\sigma }_c(15)$

Based on the principle that the Drucker-Prager (DP) criterion and the Hoek-Brown (HB) criterion should yield the same uniaxial compressive strength under uniaxial compression stress state, Priest (2005) proposed the generalized Priest criterion, expressed as follows in Eq. 16,

$\frac{3}{{\sigma }_c}{J}_2+\frac{\sqrt{3}}{3}{m}_i\sqrt{J_2}-\frac{m_i{I}_1}{3}=s{\sigma }_c(16)$

Based on extensive experimental data, the Hoek-Brown (HB) criterion has demonstrated good fitting accuracy for rock strength under triaxial compressive stress states. Therefore, according to the HB criterion, the yield curve on the π-plane should coincide with the HB criterion under triaxial compressive stress states. Following the assumption of the Mogi-Coulomb (MGC) criterion that the normal stress on the failure plane is independent of the second principal stress, Zhang and Zhu (2007) established the Zhang-Zhu (ZZ) criterion, as shown in Eq. 17,

$\frac{3}{{\sigma }_c^2}{J}_2+\frac{m_i}{2\sqrt{3}}\left(3+2\sin \theta \right)\frac{\sqrt{J_2}}{{\sigma }_c}-\left(\frac{m_i{I}_1}{3{\sigma }_c}+1\right)=0(17)$

When the hydrostatic pressure is fixed, on the π-plane, the distances from the hydrostatic pressure axis to the yield curve of the Hoek-Brown (HB) criterion can be obtained separately under triaxial compressive and triaxial tensile stress states, as shown in Eq. 18,

$\left\{\begin{array}{l}{r}_c=\frac{1}{3\sqrt{6}}\left(-m{\sigma }_c+\sqrt{m^2{\sigma }_c^2+12\sqrt{3}m{\sigma }_c\xi +36{\sigma }_c^2}\right)\\ r_t=\frac{2}{3\sqrt{6}}\left(-m{\sigma }_c+\sqrt{m^2{\sigma }_c^2+3\sqrt{3}m{\sigma }_c\xi +9{\sigma }_c^2}\right)\end{array}\right.(18)$

Therefore, the ratio of triaxial tensile strength to triaxial compressive strength according to the Hoek-Brown (HB) criterion is expressed as shown in Eq. 19,

$k\left(\xi \right)=\frac{-2m{\sigma }_c+2\sqrt{m^2{\sigma }_c^2+3\sqrt{3}m{\sigma }_c\xi +9{\sigma }_c^2}}{-m{\sigma }_c+\sqrt{m^2{\sigma }_c^2+12\sqrt{3}m{\sigma }_c\xi +36{\sigma }_c^2}}(19)$

To eliminate the six singular points of the Hoek-Brown (HB) criterion on the π-plane and meet the convexity requirement, Lee et al. (2012) replaced the Lode angle shape function of the HB criterion with the one proposed by Willam and Warnke (Eq. 20). This modification resulted in a smooth and convex three-dimensional HB strength criterion,

$\begin{array}{l}{g}_{ww}\left(\theta \right)=\\ \frac{2\left(1-k^2\right)\cos \left(\theta -\left(\pi /3\right)\right)+\left(2k-1\right)\sqrt{4\left(1-k^2\right){\cos }^2\left(\theta -\left(\pi /3\right)\right)+5k^2-4k}}{4\left(1-k^2\right){\cos }^2\left(\theta -\left(\pi /3\right)\right)+{\left(2k-1\right)}^2}\end{array}(20)$

When the hydrostatic pressure value is fixed, on the π-plane, the distance from the hydrostatic pressure axis to any point on the yield curve of the three-dimensional Hoek-Brown (HB) criterion after Lee’s modification can be expressed as shown in Eq. 21,

$r_{HBWW}-g_{ww}\left(\theta \right)r_c=0(21)$

The strength parameters of the HB, PH, GP, ZZ, and HBWW criteria are all based on rock mass properties and uniaxial compressive strength. In this study, these criteria are classified as HB-type strength criteria. By taking the same strength parameters, the yield surfaces of these criteria in three-dimensional stress space and their yield curves on the π-plane are plotted, as shown in Figures 3, 4, respectively.

Figure 3

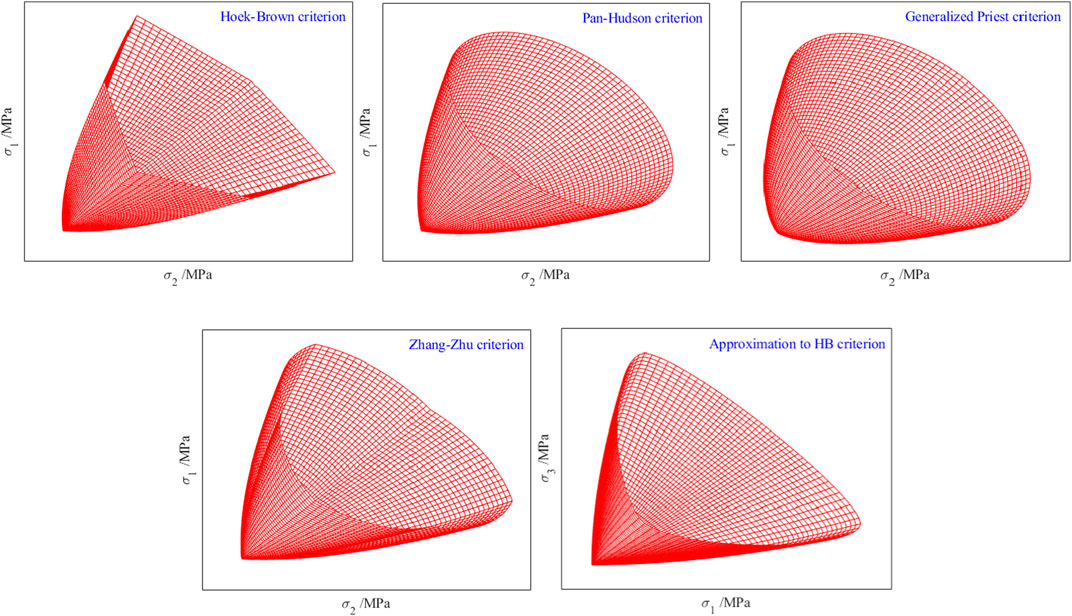
Figure 3. The distribution characteristics of the surface of HB-type strength criteria in principal stress space.

Figure 4

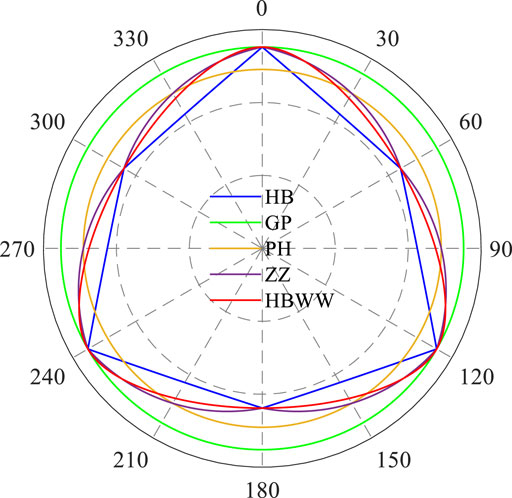
Figure 4. The distribution characteristics of the yield curves of HB-type strength criteria in the π-plane.

Analysis reveals that the meridians of this type of strength criteria exhibit nonlinear characteristics with increasing hydrostatic pressure, reflecting the nonlinear behavior of rock strength under high confining pressures. Consequently, the shapes of the yield curves on the π-plane change with increasing hydrostatic pressure. The HB criterion forms a hexagon on the π-plane, exhibiting six inflection points. The yield curve of the PH criterion is a smooth and convex circle, but it does not coincide with the HB criterion at points of triaxial tensile and compressive stress state, suggesting a need for further research on its fitting accuracy to true triaxial rock strength experimental data. The yield curve of the GP criterion is also smooth and convex, forming a perfect circle. It coincides with the HB criterion under triaxial compressive stress states but overestimates rock strength under triaxial tensile stress states. The ZZ criterion coincides with the HB criterion under both triaxial compressive and tensile stress states and considers the influence of intermediate principal stress on strength. It has been recommended by the International Society for Rock Mechanics and Engineering (ISRM). However, the yield curve of the ZZ criterion exhibits concavity at states of triaxial tensile stress, failing to meet the requirement of smooth and convex curves. The HBWW criterion is a smooth approximation function of the HB criterion. It coincides with the HB criterion at both triaxial tensile and compressive stress states, meeting the requirement of smooth and convex. The fitting results of Lee (Lee et al., 2012) using this criterion on eight sets of true triaxial rock strength experimental data indicate that the modified HB criterion has high predictive accuracy, but it is fitting performance with more experimental data remains to be verified.

Comparing the two types of strength criteria, it can be observed that the yield surfaces of different criteria all exhibit triaxial symmetry. Under low hydrostatic pressure, the yield surfaces close, but as the hydrostatic pressure increases, the opening gradually enlarges, reflecting the characteristic of rocks being more compressible than tensile resistant. HB-type strength criteria better reflect the nonlinear yielding and failure characteristics of rocks under high confining pressures. ML, MWC, MCJP, GP, PH, and HBWW criteria all meet the requirement of smooth and convex curves. However, GP and PH criteria cannot distinguish between the differences in triaxial tensile and compressive strength. Both the MGC and ZZ criteria assume that the normal stress on the failure plane is independent of the second principal stress. In triaxial tensile and compressive stress states, both criteria degenerate into the MC and HB criteria. However, there exist singular points on the π-plane, and the yield curves exhibit concavity at points of triaxial tensile and compressive stress.

3 Data and fitting method

3.1 Triaxial rock strength data

Rock true triaxial strength testing equipment is still relatively uncommon, making experiments challenging. Although a considerable number of true triaxial tests have been conducted domestically and internationally over the past few decades, a major limitation in studying rock properties under three-dimensional stress is still the lack of sufficient true triaxial test data to validate theoretical and empirical rock failure models. Previous validation studies of three-dimensional rock strength criteria have often been limited by the incompleteness of selected strength criteria or by the scarcity of true triaxial strength experimental data used for validation, leading to potentially incomplete or biased research conclusions. This study has compiled 32 sets of true triaxial strength experimental data from existing literature, as shown in Table 1.

Table 1

Table 1. Summary table of true triaxial rock strength test data.

3.2 Data fitting method

In 2002, Colmenares and Zoback conducted a systematic study on the prediction accuracy of five sets of true triaxial strength experimental data using the least squares method. The results indicated that the Mogi-Lade (ML) and Mogi-Coulomb (MWC) criteria performed well in predicting the strength of rocks highly influenced by intermediate principal stress, while the Mohr-Coulomb (MC) and Hoek-Brown (HB) criteria performed better in predicting the strength of rocks less affected by intermediate principal stress. It is worth noting that at the time, criteria such as the Mogi-Greenwood-Coulomb (MGC) and Zhang-Zhu (ZZ) criteria had not yet been proposed, and these were not included in the comparison study conducted by Comenares and Zoback. Additionally, Comenares and Zoback utilized the least squares method in their study, which minimizes the sum of squared errors as the objective function. However, it has been demonstrated that this method is more sensitive to outliers, and a small number of outliers can lead to fitting results deviating from the majority of normal data trends. Therefore, Yeo and Lee recommended using the least absolute deviations method to determine the undetermined parameters in the strength criteria. This method minimizes the sum of absolute errors as the objective function, reducing the influence of individual outlier data points on the fitting results and ensuring that the fitted curve lies within the region of the majority of normal data sets. In this study, based on the least absolute deviations method, the objective function for fitting the experimental data is expressed as shown in Eq. 22,

$D_{abs}=\min \left\{\sum {}_{i=1}^N\left|{\sigma }_i^p-{\sigma }_i^m\right|\right\}/N(22)$

In the equation, ${\sigma }_i^m,{\sigma }_i^p$ represent the true triaxial rock strength test value and the predicted value for the ith dataset, respectively, where i denotes the ith dataset and N denotes the total number of experiments. A smaller value of $D_{abs}$ indicates higher fitting accuracy. Using MATLAB numerical analysis software, based on the principle of least absolute deviations, programs were developed to fit the above 10 types of rock strength criteria to the 32 sets of true triaxial rock strength experimental data.

4 Results and discussion

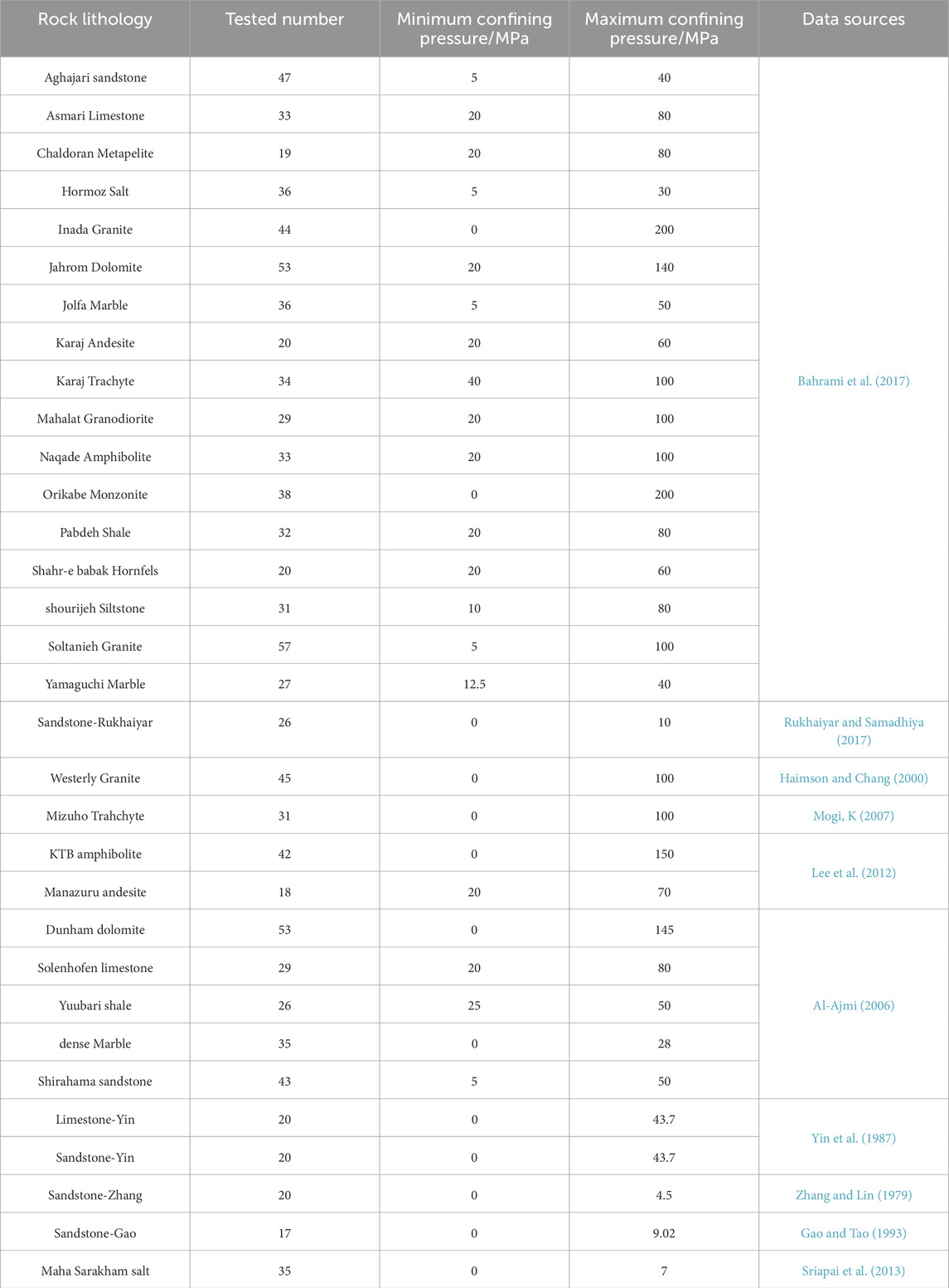
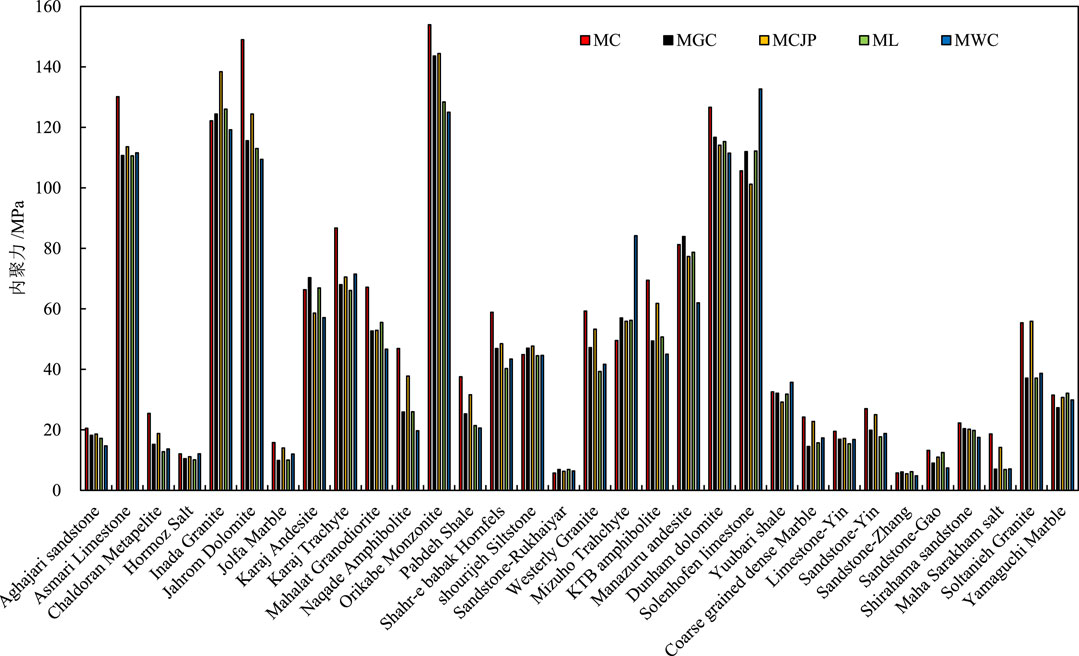
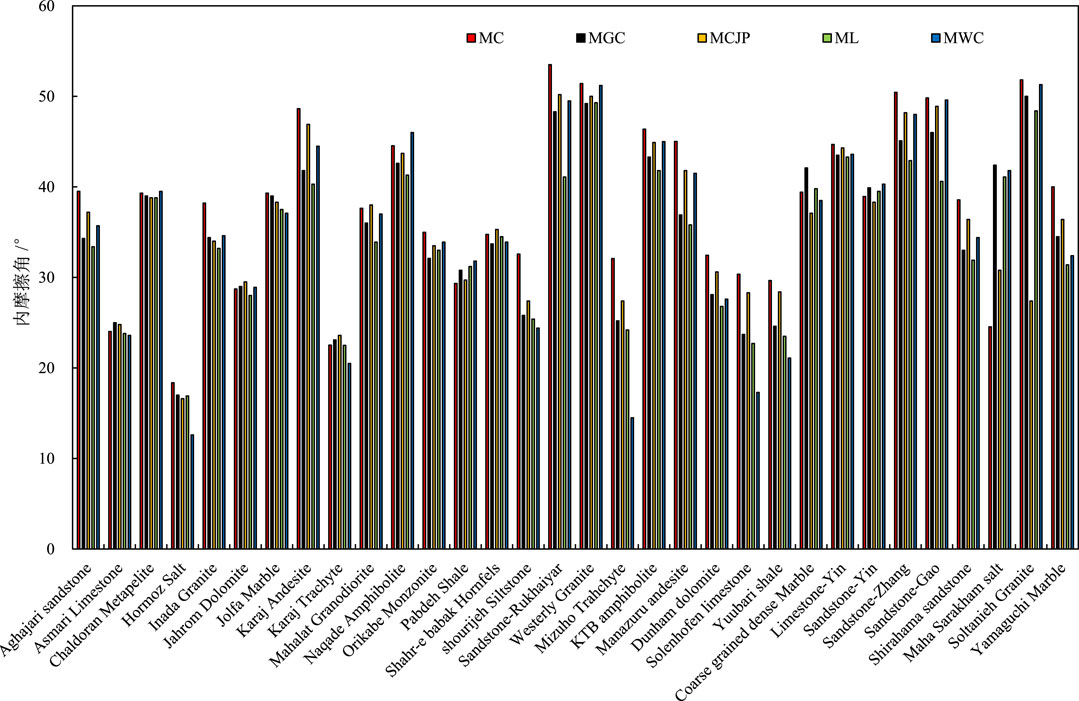
Based on the least absolute deviations method, the cohesive strength and internal friction angle for MC-type strength criteria are fitted and shown in Figure 5 and Figure 6, respectively. Additionally, the uniaxial compressive strength and rock mass parameter for HB-type strength criteria are fitted and displayed in Figure 7 and Figure 8, respectively.

Figure 5

Figure 5. Fitting results of cohesive strength for MC-type strength criteria.

Figure 6

Figure 6. Fitting results of friction angle for MC-type strength criteria.

Figure 7

Figure 7. Fitting results of uniaxial compressive strength for HB-type strength criteria.

Figure 8

Figure 8. Fitting results of rock mass parameter for HB-type strength criteria.

Analysis reveals significant differences in cohesive strength among different rock types. For instance, the cohesive strength obtained from fitting for Sandstone-Rukhaiyar and Sandstone-Zhang is less than 10 MPa, while for Asmari Limestone, Jahrom Dolomite, and Orikabe Monzonite, it exceeds 130 MPa. The internal friction angles of different rock types are distributed between 0° and 60°, facilitating the determination of the search range during the fitting process.

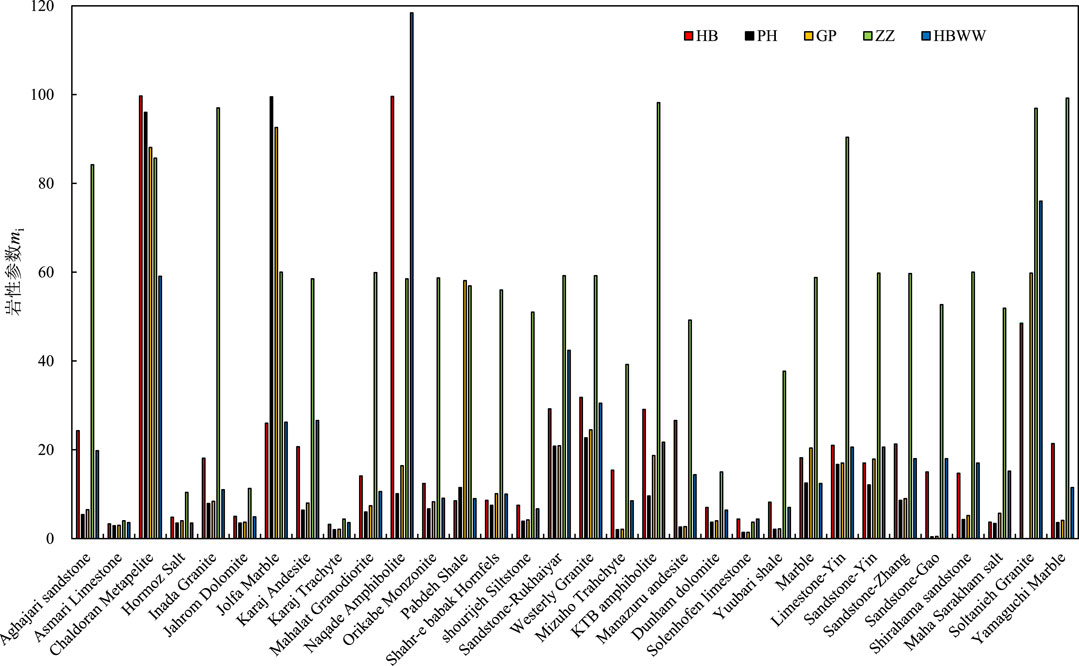
For intact rock, in HB-type strength criteria, the rock structure parameter s is set to 1. The uniaxial compressive strength σ_c and the rock mass parameter m_i are treated as undetermined parameters. Analyzing the fitting results yields the following conclusions, firstly, significant variations exist in the undetermined parameters obtained by different HB-type strength criteria for the same set of experimental data. Determining the fitting range for undetermined parameters is challenging. Secondly, some experimental data do not converge during the fitting process, with rock mass parameters exceeding empirical ranges and uniaxial compressive strengths being too low, making it difficult to determine the optimal fitting parameters.

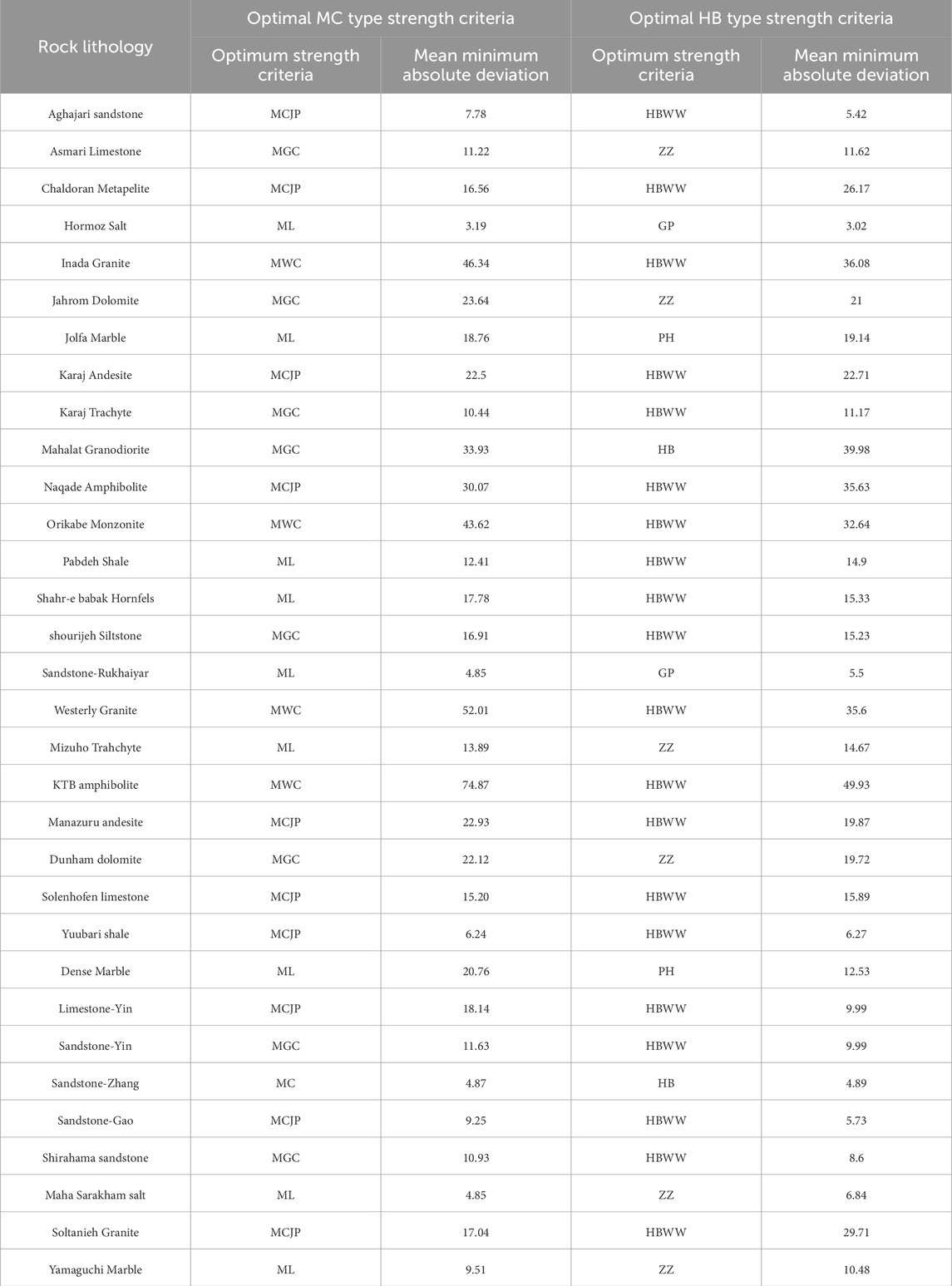
To compare the fitting effects of MC-type and HB-type strength criteria for true triaxial rock strength criteria, the MC-type and HB-type strength criteria with the smallest fitting errors for each set of experimental data, along with their corresponding average minimum absolute errors, are listed in Table 2. Underscores in the table indicate the strength criteria with the highest fitting accuracy for each dataset and their corresponding average minimum absolute deviations.

Table 2

Table 2. Comparison of prediction performance between MC-type and HB-type strength criteria.

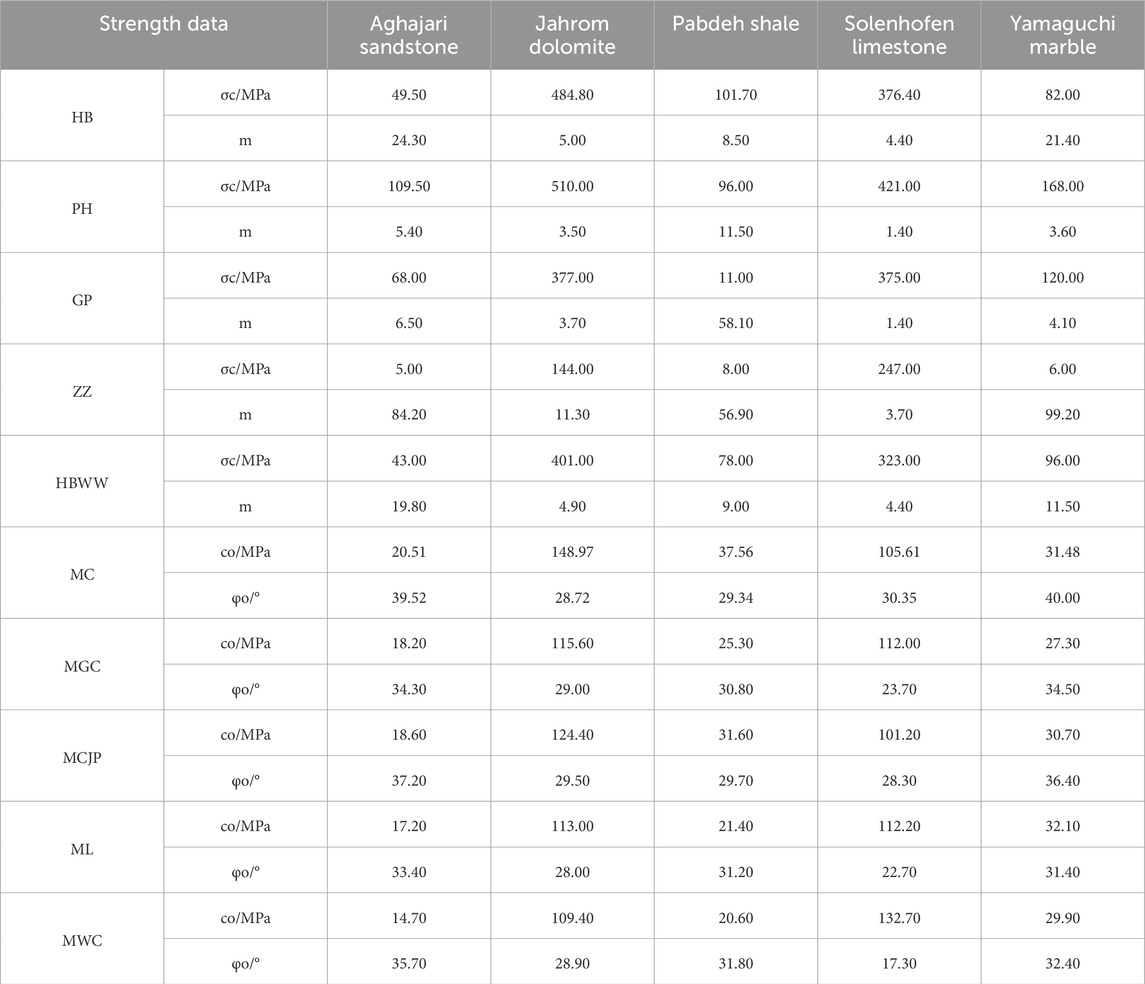
Among the 32 sets of true triaxial rock strength data, MC-type strength criteria exhibit the highest fitting accuracy for 16 sets of experimental data, while for the remaining 16 sets, HB-type strength criteria demonstrate higher predictive accuracy. Specifically, HBWW criteria provide the best predictive performance across different rock types and have the widest applicability. To compare the predictive trends of rock strength with intermediate principal stress using MC-type and HB-type strength criteria, the envelopes of predicted strengths for five sets of experimental data (Aghajari sandstone, Jahrom Dolomite, Pabdeh Shale, Solenhofen limestone, and Yamaguchi Marble) are plotted on the σ₁-σ₂ principal stress plane alongside their corresponding strength criteria predictions, as shown in Figure 9.

Figure 9

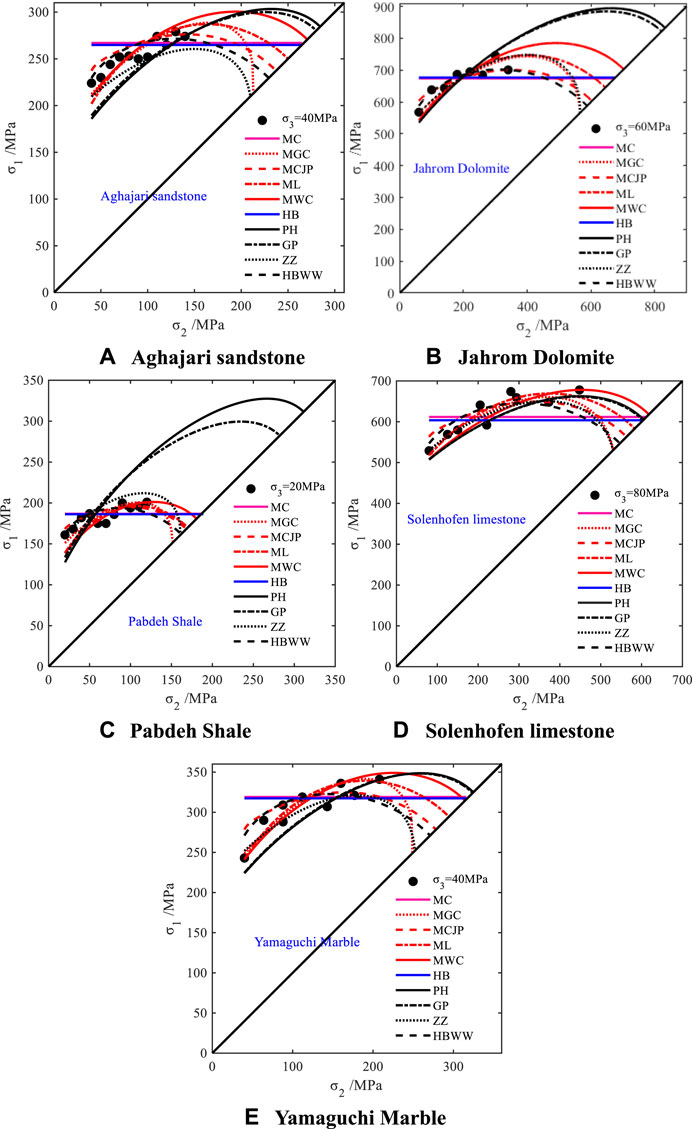
Figure 9. Comparison of different strength criteria for fitting experimental data on the σ1-σ2 principal stress plane.

At the same time, the fitting parameters of the rock strength criteria selected in this paper to the strength of the five different types of rock in Figure 9 are given, as shown in Table 3.

Table 3

Table 3. Strength parameters for different types of rocks.

From Figure 9, it can be observed that PH criteria and GP criteria are the most sensitive to changes in intermediate principal stress, followed by MWC criteria and ML criteria. The predictive results of MGC criteria and ZZ criteria exhibit similar trends with changes in intermediate principal stress. MCJP criteria and HBWW criteria are the least sensitive to changes in intermediate principal stress, and their predicted strength variations show similar trends. On the other hand, the predictive trends of strength with changes in intermediate principal stress for MC criteria and HB criteria largely overlap. Since rocks typically experience triaxial stress states (σ₁>σ₂>σ₃), criteria based solely on maximum and minimum principal stresses, such as MC criteria, cannot fully reflect rock failure under true triaxial stress conditions. Undoubtedly, intermediate principal stress significantly influences rock failure. The failure strength increases with increasing intermediate principal stress, and then decreases as the intermediate principal stress further increases. Therefore, increasing or decreasing the intermediate principal stress may both lead to rock failure.

5 Conclusion

Based on the study, the following conclusions can be drawn, firstly, MC and HB criteria ignore the influence of intermediate principal stress on rock strength. PH and GP criteria overestimate the influence of intermediate principal stress, resulting in large prediction errors. The remaining three-dimensional rock strength criteria have prediction errors within an acceptable range. The concept of undetermined parameters in MC-type strength criteria is simple and clear, making it easy to determine the search range during fitting. However, the parameter variation range for HB-type criteria is large, making it difficult to determine the search range, and non-convergence may occur during the fitting process. Secondly, both three-dimensional MC-type and HB-type strength criteria reflect the trend of rocks increasing and then decreasing in strength with increasing intermediate principal stress. Increasing or decreasing intermediate principal stress may both lead to rock failure. There is no significant difference in the predictive accuracy of three-dimensional rock strength criteria for true triaxial rock strength, in addition, none of the three-dimensional rock strength criteria demonstrate a clear advantage in predicting the strength of experimental data. Thirdly, the predictive accuracy of three-dimensional rock strength criteria depends on the sensitivity of the studied rock strength to the changing of intermediate principal stress. PH and GP criteria are thr most sensitive to in the changing of intermediate principal stress, followed by MWC and ML criteria. The predictive results of MGC and ZZ criteria exhibit similar trends with changes in intermediate principal stress. MCJP and HBWW criteria are the least sensitive to in the changing of intermediate principal stress, and their predicted strength variation trends are similar. The predictive trends of strength with changes in intermediate principal stress for MC and HB criteria largely overlap. The study of rock mechanics characteristics, especially strength characteristics, is helpful to provide support for underground rock engineering, meet the needs of engineering construction, and promote the development of the discipline.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

SH: Conceptualization, Investigation, Software, Writing–original draft, Writing–review and editing. HC: Data curation, Methodology, Supervision, Writing–original draft. LC: Formal Analysis, Project administration, Validation, Writing–original draft, Writing–review and editing. FY: Formal Analysis, Project administration, Validation, Writing–original draft. MZ: Funding acquisition, Resources, Visualization, Writing–original draft.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors SH, HC, and FY were employed by Sinopec Northwest Oilfield Branch. Author LC was employed by Sino Science and Technology Co., Ltd. Author MZ was employed by Sinopec Research Institute of Petroleum Engineering Co., Ltd., SINOPEC.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2024.1416979/full#supplementary-material

References

Al-Ajmi, A. (2006). Wellbore stability analysis based on a new true-triaxial failure criterion. KTH.

Google Scholar

Al-Ajmi, A. M., and Zimmerman, R. W. (2009). A new well path optimization model for increased mechanical borehole stability. J. Petroleum Sci. Eng. 69 (1-2), 53–62.

CrossRef Full Text | Google Scholar

Bahrami, B., Mohsenpour, S., Miri, M. A., and Mirhaseli, R. (2017). Quantitative comparison of fifteen rock failure criteria constrained by polyaxial test data. J. Petroleum Sci. Eng. 159, 564–580. doi:10.1016/j.petrol.2017.09.065

CrossRef Full Text | Google Scholar

Cai, W., Zhu, H., Liang, W., Zhang, L., and Wu, W. (2021). A new version of the generalized Zhang–Zhu strength criterion and a discussion on its smoothness and convexity. Rock Mech. Rock Eng. 54 (8), 4265–4281. doi:10.1007/s00603-021-02505-z

CrossRef Full Text | Google Scholar

Colmenares, L. B., and Zoback, M. D. (2002). A statistical evaluation of intact rock failure criteria constrained by polyaxial test data for five different rocks. Int. J. Rock Mech. Min. Sci. 39 (6), 695–729. doi:10.1016/s1365-1609(02)00048-5

CrossRef Full Text | Google Scholar

Ewy, R. T. (1999). Wellbore-stability predictions by use of a modified Lade criterion. SPE Drill. Complet. 14 (02), 85–91. doi:10.2118/56862-pa

CrossRef Full Text | Google Scholar

Fan, Q. N., and Yin, Y. J. (2004). Mechanics of materials [D]. Tsinghua University Press Limited.

Google Scholar

Fengjiao, W., He, X., Liu, Y., Meng, X., and Liu, L. (2023). Mechanism of low chemical agent adsorption by high pressure for hydraulic fracturing-assisted oil displacement technology: a study of molecular dynamics combined with laboratory experiments. Langmuir 39 (46), 16628–16636. doi:10.1021/acs.langmuir.3c02634

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Y., and Tao, Z. (1993). Examination and analysis of true triaxial compression testing of strength criteria of rock. J. Geotechnical Eng. 15 (4), 26–32.

Google Scholar

Haimson, B., and Chang, C. (2000). A new true triaxial cell for testing mechanical properties of rock, and its use to determine rock strength and deformability of Westerly granite. Int. J. Rock Mech. Min. Sci. 37 (1-2), 285–296. doi:10.1016/s1365-1609(99)00106-9

CrossRef Full Text | Google Scholar

Hoek, E., and Brown, E. T. (1980). Empirical strength criterion for rock masses. J. geotechnical Eng. Div. 106 (9), 1013–1035. doi:10.1061/ajgeb6.0001029

CrossRef Full Text | Google Scholar

Hoek, E., and Brown, E. T. (2019). The Hoek–Brown failure criterion and GSI–2018 edition. J. Rock Mech. Geotechnical Eng. 11 (3), 445–463. doi:10.1016/j.jrmge.2018.08.001

CrossRef Full Text | Google Scholar

Jiang, J., and Pietruszczak, S. (1988). Convexity of yield loci for pressure sensitive materials. Comput. Geotechnics 5 (1), 51–63. doi:10.1016/0266-352x(88)90016-x

CrossRef Full Text | Google Scholar

Kim, M. K., and Lade, P. V. (1984). Modelling rock strength in three dimensions. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 21 (1), 21–33. Pergamon. doi:10.1016/0148-9062(84)90006-8

CrossRef Full Text | Google Scholar

Lade, P. V., and Duncan, J. M. (1975). Elastoplastic stress-strain theory for cohesionless soil. J. Geotechnical Eng. Div. 101 (10), 1037–1053. doi:10.1061/ajgeb6.0000204

CrossRef Full Text | Google Scholar

Lee, Y. K., Pietruszczak, S., and Choi, B. H. (2012). Failure criteria for rocks based on smooth approximations to Mohr-Coulomb and Hoek–Brown failure functions. Inter. J. Rock Mech. Mining Sci. 56, 146–160

CrossRef Full Text | Google Scholar

Mogi, K. (2007). Experimental rock mechanics. United Kingdom: Taylor and Francis Group London.

Google Scholar

Pan, X. D., and Hudson, J. A. (1988). A simplified three dimensional Hoek-Brown yield criterion. ISRM Int. Symp. OnePetro. doi:10.1016/0148-9062(89)90069-7

CrossRef Full Text | Google Scholar

Priest, S., and Hunt, S. (2005). “Application of a new three-dimensional yield criterion for argillaceous rocks,” in Proceedings of the 40th US symposium on rock mechanics (American Rock Mechanics Association).

Google Scholar

Priest, S. D. (2005). Determination of shear strength and three-dimensional yield strength for the Hoek-Brown criterion. Rock Mech. Rock Eng. 38 (4), 299–327. doi:10.1007/s00603-005-0056-5

CrossRef Full Text | Google Scholar

Rahimi, R., and Nygaard, R. (2015). Comparison of rock failure criteria in predicting borehole shear failure. Inter. J. Rock Mech. Mining Sci. 79, 29–40

CrossRef Full Text | Google Scholar

Rukhaiyar, S., and Samadhiya, N. K. (2017). Strength behaviour of sandstone subjected to polyaxial state of stress. Int. J. Min. Sci. Technol. 27 (6), 889–897. doi:10.1016/j.ijmst.2017.06.022

CrossRef Full Text | Google Scholar

Sriapai, T., Walsri, C., and Fuenkajorn, K. (2013). True-triaxial compressive strength of Maha Sarakham salt. Int. J. Rock Mech. Min. Sci. 61, 256–265. doi:10.1016/j.ijrmms.2013.03.010

CrossRef Full Text | Google Scholar

Voigt, J. U., Pedrizzetti, G., Lysyansky, P., Marwick, T. H., Houle, H., Baumann, R., et al. (2015). Definitions for a common standard for 2D speckle tracking echocardiography: consensus document of the EACVI/ASE/Industry Task Force to standardize deformation imaging. Eur. Heart J. Cardiovasc. Imaging 16 (1), 1–11

PubMed Abstract | CrossRef Full Text | Google Scholar

Warnke, K. W. E., and Warnke, E. P. (1975). “Constitutive model for triaxial behaviour of concrete,” in Proc. Concrete struc. Subjected to triaxial stresses, int. Ass. For bridge and structural engineering (Zurich), 1–30.

Google Scholar

Wiebols, G. A., and Cook, N. G. W. (1968). An energy criterion for the strength of rock in polyaxial compression. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 5 (6), 529–549. Pergamon. doi:10.1016/0148-9062(68)90040-5

CrossRef Full Text | Google Scholar

Yin, G., He, L., Xian, X., et al. (1987). The experimental study of the influence of engineering stress changes on strength characteristics of rocks. J. Geotechnical Eng. 9 (2), 20–28.

Google Scholar

Zhou, X, Qian, Q, and Yang, H. (2008). Strength criterion of deep rock mass [J]. Chin. J. Rock Mech. Eng. 27 (1), 117–123.

Google Scholar

You, M. (2010). Three independent parameters to describe conventional triaxial compressive strength of intact rocks. J. Rock Mech. Geotechnical Eng. 2 (4), 350–356. doi:10.3724/SP.J.1235.2010.00350

CrossRef Full Text | Google Scholar

You, M. (2011). Comparison of the accuracy of some conventional triaxial strength criteria for intact rock. Int. J. Rock Mech. Min. Sci. 5 (48), 852–863. doi:10.1016/j.ijrmms.2011.05.006

CrossRef Full Text | Google Scholar

Zhang, B., Pan, Z., Cao, L., Xie, J., Chu, S., Jing, Y., et al. (2024). Measurement of wellbore leakage in high-pressure gas well based on the multiple physical signals and history data: method, technology, and application. Energy Sci. Eng. 12 (01), 4–21. doi:10.1002/ese3.1619

CrossRef Full Text | Google Scholar

Zhang, J., and Lin, T. (1979). Stress conditions and the variation of rupture characteristics of a rock as shown by triaxial stress. Acta Mech. Sin. (2), 103–104. doi:10.6052/0459-1879-1979-2-1979-015

CrossRef Full Text | Google Scholar

Zhang, L., and Zhu, H. (2007). Three-dimensional Hoek-Brown strength criterion for rocks. J. Geotechnical Geoenvironmental Eng. 133 (9), 1128–1135. doi:10.1061/(asce)1090-0241(2007)133:9(1128)

CrossRef Full Text | Google Scholar

Zhang, M., Liang, L., and Liu, X. (2017a). Impacts of rock anisotropy on horizontal wellbore stability in Shale reservoir. Appl. Math. Mech. 38 (3), 295–309. doi:10.21656/1000-0887.370155

CrossRef Full Text | Google Scholar

Zhang, M., Liang, L., and Liu, X. (2017b). Impact analysis of different rock shear failure criteria to wellbore collapse pressure. Chin. J. Rock Mech. Eng. 36 (S1), 372–378.

Google Scholar

Zhang, Q., Zhu, H., and Zhang, L. (2013). Modification of a generalized three-dimensional Hoek–Brown strength criterion. Int. J. Rock Mech. Min. Sci. 59, 80–96. doi:10.1016/j.ijrmms.2012.12.009

CrossRef Full Text | Google Scholar

Zhou, J., He, S., Tang, M., Huang, Z., Chen, Y., Chi, J., et al. (2018). Analysis of wellbore stability considering the effects of bedding planes and anisotropic seepage during drilling horizontal wells in the laminated formation. J. Petroleum Sci. Eng. 170, 507–524. doi:10.1016/j.petrol.2018.06.052

CrossRef Full Text | Google Scholar

Zhou, S. (1994). A program to model the initial shape and extent of borehole breakout. Comput. Geosciences 20 (7-8), 1143–1160. doi:10.1016/0098-3004(94)90068-x

CrossRef Full Text | Google Scholar