Thermomechanical coupling seepage in fractured shale under stimulation of supercritical carbon dioxide

As a waterless fracturing fluids for gas shale stimulation with low viscosity and strong diffusibility, supercritical CO₂ is promising than the water by avoiding the clay hydration expansion and reducing reservoir damage. The permeability evolution influenced by the changes of the temperature and stress is the key to gas extraction in deep buried shale reservoirs. Thus, the study focuses on the coupling influence of effective stress, temperature, and CO₂ adsorption expansion effects on the seepage characteristics of Silurian Longmaxi shale fractured by supercritical CO₂. The results show that when the gas pressure is 1–3 MPa, the permeability decreases significantly with the increase in gas pressure, and the Klinkenberg effects plays a predominant role at this stage. When the gas pressure is 3–5 MPa, the permeability increases with the increase in gas pressure, and the influence of effective stress on permeability is dominant. The permeability decreases exponentially with the increase in effective stress. The permeability of shale after the adsorption of CO₂ gas is significantly lower than that of before adsorption; the permeability decreases with the increase in temperature at 305.15 K–321.15 K, and with the increase in temperature, the permeability sensitivity to the temperature decreases. The permeability is closely related to supercritical CO₂ injection pressure and volume stress; when the injection pressure of supercritical CO₂ is constant, the permeability decreases with the increase in volume stress. The results can be used for the dynamic prediction of reservoir permeability and gas extraction in CO₂-enhanced shale gas development.

Highlights

• Discussed evolution of permeability of Silurian Longmaxi shale after fracturing by supercritical carbon dioxide

• Analyzed slippage factor in seepage process under coupling conditions of the temperature and effective stress

• Constructed a THM coupled permeability model of fractured shale by newly defined effective stress coefficient

1 Introduction

With the increasing demand for energy in our country, the domestic energy resource shortage is becoming more serious. The degree of dependency on natural gas is close to 30%, which seriously threatens energy safety. Shale gas is one of the most realistic replacement resources for conventional oil and gas resources, judging by the current global nonrenewable energy exploration and development analysis. Shale gas refers to unconventional natural gas occurring in organic-matter-rich mud shale and its intercalation, which exists in an adsorbed or free state and is mainly composed of methane. The potential of shale gas resources in China is enormous, and the technical recovery capacity is 25 trillion square meters. The national 13th Five-Year Plan for Shale Gas Development (2016–2020) clearly states that shale gas production will reach 30 billion m³ by 2020 and 80–100 billion m³ by 2030. Therefore, developing shale gas efficiently is of great strategic significance for fully optimizing and developing China’s energy structure and resources.

The study of gas permeability in the reservoirs is vital for gas disasters (Yin et al., 2009; Li et al., 2023), and gas productivity under stimulation by supercritical carbon dioxide (Yang et al., 2022). Understanding the seepage and permeability characteristics of shale under the coupling action of multiphyisical fields is helpful in exploring the migration law of shale gas in natural shale reservoirs. Therefore, it is necessary to study the seepage and permeability characteristics of shale after fracturing. Many scholars at home and abroad have carried out to that effect, including Liu et al. (Liu et al., 2016; Liu, 2017) who conducted numerical research and analysis on the fractal of directional permeability of gas-producing shale fracture network.

The others of consider the Klinkenberg effects in predicting and measuring shale permeability (Firouzi et al., 2014; Moghaddam and Jamiolahmady, 2016; Li et al., 2017a). Li et al. used the self-developed multifunctional true triaxial fluid–solid coupling experimental machine to study shale permeability under true triaxial stress (Li et al., 2016). The research results show that the experimental data match various anisotropic permeability models to a high degree, and the machine has the advantage of reflecting the permeability changes caused by each principal stress increment. Song Wenhui et al. studied the apparent permeability of shale reservoirs rich in organic matter (Song et al., 2016). Duan et al. used Langmuir isothermal adsorption equation to establish a mathematical model of dual media fracturing well seepage (Duan et al., 2011). Wu et al. established the seepage model of shale gas in matrix pores from the matrix’s nanopore scale (Wu et al., 2015). Li et al. argued that the desorption of adsorbed gas and free gas in matrix pores should be considered simultaneously in the dual matrix model of shale gas seepage (Li et al., 2013). Zhang et al. used the Boltzmann lattice method to calculate the permeability of shale gas (Zhang et al., 2014). Cheng et al. proposed a calculation method for shale porosity, inherent permeability, and apparent permeability based on the shale pore structure image (Cheng et al., 2022a). Sun et al. and Chen et al. used the pulse method to measure the fracture permeability of coal shale and fitted and analyzed the established effective stress permeability model (Chen et al., 2014; Sun et al., 2014). The analysis results show that the model can better describe the relationship between reservoir fracture permeability and pore pressure in the process of shale gas exploitation. Chen et al. studied the sensitivity of gas shale permeability to confining pressure and the influence of confining pressure on gas shale permeability (Cheng et al., 2022b). Zhang et al. proposed that microfractures are the key to improving shale permeability (Zhang et al., 2015a; Zhang et al., 2015b). In addition, the stress-sensitive and fluids viscosity is the key to the gas flow in shale reservoirs (Su et al., 2022; Zhang et al., 2024).

With the increase in effective stress, micro fractures close, and shale permeability decreases exponentially. Supercritical CO₂ fracturing also involves the influence of the CO₂ and shale interaction on the permeability of shale after fracturing. In addition to the characteristics of multiscale and ultralow porosity, the seepage mechanism of shale gas is also different from that of conventional natural gas (Li et al., 2013), which has the characteristics of dual medium seepage. Many influencing factors affect seepage law of shale. Among them, temperature has an impact on the permeability of shale and is a factor that cannot be ignored (Teng et al., 2016).

From the literature review, most of the current research on shale gas permeability is still at the stage of numerical simulation and theoretical model analysis, and the experimental research is relatively scarce and mainly focuses on the flow law of shale gas (CH₄) in the shale layer. There is not much research on either the change law of reservoir permeability after fracturing fluid injection during the fracturing process or the factors affecting permeability. In this paper, the Silurian Longmaxi formation shale in southern Sichuan is taken as the research object in the supercritical CO₂ fracturing shale experiment conducted using the self-developed experimental device. The purpose of the study is to obtain the fractured shale specimen and carry out experimental research on the influence of volume stress, temperature, gas pressure, and CO₂ adsorption expansion effects on the permeability characteristics of shale. The study explores the coupling relationship between the stress field, temperature field, and shale permeability and analyzes the seepage law of fractured shale under the condition of multifield coupling, providing a scientific basis for the dynamic prediction of reservoir permeability and shale gas productivity prediction in CO₂-enhanced shale gas development.

2 Research object and research method

2.1 Geological characteristics of the study area

The shale of the Longmaxi Formation is widely distributed in southern Sichuan and belongs to the Late Ordovician to Early Silurian period. The lower part of the Wufeng Formation is mainly composed of large sets of black shale interbedded with several sets of thin volcanic ash sedimentary layers. Topped with limestone or marl, the Hernantebe fauna is rich in fossils. The lower part of the Longmaxi Formation is black and grayish-black thin-layered shale where massive shale laminae fractures are developed. The upper part is grey-green and yellow-green shale mixed with sandy shale, sometimes with siltstone or argillaceous limestone, and the sand content increases from bottom to top, forming an upward-increasing coarser sedimentary sequence. The Sichuan region’s five mountains—the dragon stream group formed in Huaxia and Yangtze plates—touch each other. After the Middle Ordovician, the Yangtze plate entered the tectonic evolution stage of the Foreland Basin, and the southern Sichuan area was a part of the Yangtze Foreland Basin. In the early Silurian, the extrusion from the southeast to northwest direction was strengthened, and the southern Sichuan area was continuously uplifted. The Leshan-Longnusi paleo-uplift was gradually expanded, the sea area was narrowed, the seawater became shallower, and the sedimentary differentiation was intensified. During this period, the Upper Yangtze region was sandwiched between the Leshan-Longnusi paleo-uplift and Qianzhong–Xuefeng paleo-uplift, forming a semi occluded stagnant sea basin.

2.2 Experimental equipment and specimen preparation

The shale specimens were taken from the outcrop of the Silurian Longmaxi Formation in the southern Sichuan Basin. The average shale thickness in this block is 100–500 m, and the burial depth is 1.5–4 km. It mainly comprises dark gray and black silty shale, carbonaceous shale, siliceous shale, and argillaceous siltstone. The organic carbon content of shale is 0.35%–18.4%, the average value is 2.52%, the thermal maturity is 1.8%–3.6%, the brittle mineral content is 47.6%–74.1%, and the average brittle mineral content is 56.3%. Before the percolation experiment, the basic physical and chemical parameters and mineral composition (XRD) tests were carried out on the shale specimens. The experimental results indicated that the total organic carbon (TOC) and the maximum vitrinite reflectance (R.o.) contents of the outcrop shale are 4.18% and 2.36%, respectively. These values are favorable for the formation and exploitation of shale gas (TOC ≥ 2%, 3% ≥ R. o.≥ 1%). The basic physical parameters and mineral composition of representative shale specimen Y-1 are shown in Table 1 (Liu, 2017).

Table 1

Table 1. Basic physical parameters and mineral composition of the Y-1 shale specimen.

We selected homogeneous rock bedding development specimens cut in size 200 mm × 200 mm × 200 mm cubic. Sinkholes of 15 mm in diameter and 110 mm in length were drilled in the specimen along the direction of the central vertical bedding plane. Special steel quality chemical adhesive and the filler tube fixed to the center of the specimen in the sinkhole were used to simulate the wellbore fracturing. A fluid injection tube was used for hole sealing in the length of 90 mm; a 20 mm section of the hole in the center of the specimen was left open. Natural air drying of shale surfaces using plastic wrapping reduced the effects of long-time exposure to air on a large number of bedding slits, the specimens collection details can be found in Table 2 (Liu, 2017).

Table 2

Table 2. Basic parameters of the specimens collection.

The migration of shale gas in the fracturing process is the key to shale gas development. The seepage experiment with fractured shale is carried out using the self-developed, supercritical CO₂ fracturing and permeability enhancement experimental device on the shale gas reservoir. The specimen used in the seepage test is obtained after supercritical CO₂ fracturing. The specific experimental steps are as follows: 1) the physical properties of the supercritical CO₂ are sensitive to changes in temperature; therefore, in the fracturing experiments, CO₂ temperature and the temperature of the specimen need to be strictly controlled. To simulate the high-temperature shale reservoir conditions, an incubator was first used to heat the specimen for 24 h before the experiment to ensure that the specimen was uniformly heated to the target temperature. In the fracturing experiment, a temperature control box was used to control the target temperature, and the fracturing fluid line, acoustic emission connection line, and jack tubing were connected to external equipment through special metal pipe channels. Specimen No. 2 was fractured with liquid CO₂ and did not need to be heated. 2) The specimen was put into the loaded three-bearing pressure chamber, and 8 AE probes were attached to the four surfaces of the specimen in an oblique diagonal arrangement to test whether the sensors were correctly installed and sensitive. After the pressure chamber of three bearings was capped, the three-way principal stress was applied to the specimen at a speed of 2 MPa/min. The line heater was set to the target temperature, and the fracturing fluid flowed through the line heater. After that, the fracturing fluid injection pump was connected to the injection line and the simulation wellbore. The pipes near the wellbore inlet were kept warm by winding heating belts. 3) The acoustic emission testing and the pressure and temperature data collection systems were open. After the injection pump was filled with CO₂ or water, the injection pump was turned on to inject high-pressure CO₂ or water at a flow rate of 30 ml/min. The pressure increased continuously until the specimens broke. When the pressure dropped to zero, the injection pump was turned off. The No. 5 fracturing shale specimen was selected to conduct the seepage test of fractured shale.

2.3 Experimental Scheme Design

The temperature of the stratum is related to its depth. The deeper the stratum is, the closer it is to the core and the higher the temperature. The depth of the shale rock is about 1400 m–1800 m, and the temperature is approximately 309.15 K–321.15 K. The experimental scheme was based on previous studies and the study procedure was shown in Figures 1, 2 (Zhou et al., 2016; Liu et al., 2017a, 2017b; Liu, 2017). Five temperature values of 309.15 K, 312.15 K, 315.15 K, 318.15 K, and 321.15 K were selected. Under the condition of fixed average surrounding rock stress, the seepage experiments with the above five equal gradient temperatures were carried out to test the influence of the equal gradient temperature on the permeability of fractured shale.

Figure 1

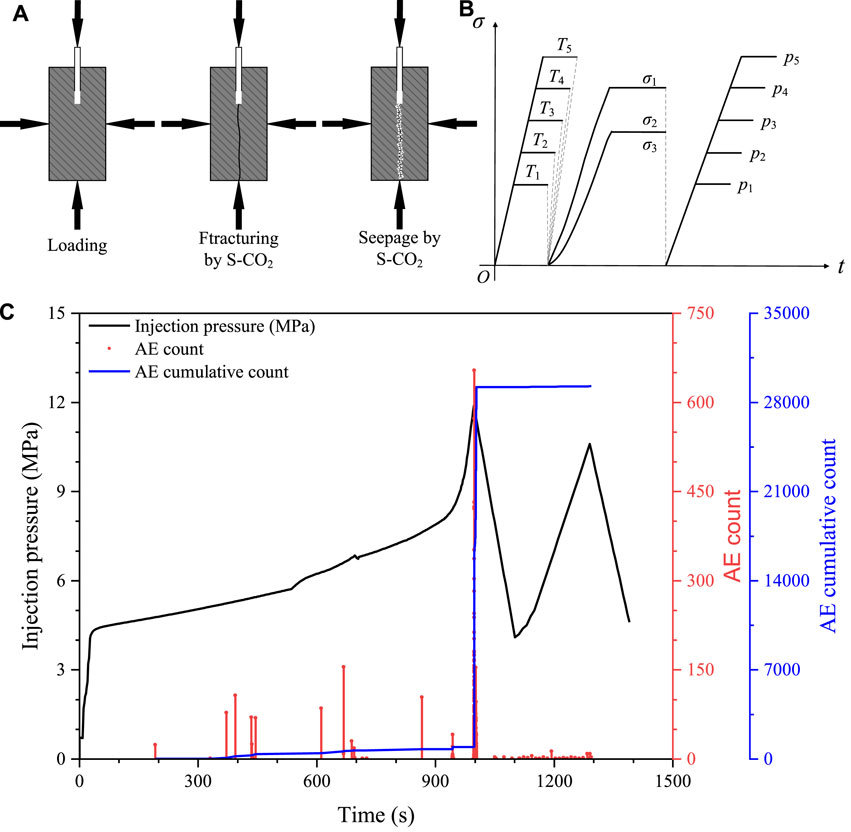
Figure 1. Experiment workflow and injection process: (A) specimen made by supercritical carbon dioxide injection fracturing; (B) stress path; and (C) injection curve.

Figure 2

Figure 2. Schematic diagram of structure principle and photos of experiment equipment.

The existing in situ stress test data show that the vertical in situ stress is not always greater than the horizontal in situ stress, which is closely related to tectonic stress. If there is the effect of horizontal tectonic stress, the three-dimensional in situ stress will be equal at some points with a large burial depth. Generally, the vertical stress $\left({\sigma }_1\right)$ and horizontal stress (${\sigma }_2$, ${\sigma }_3$) increase with the increase in ground depth. According to Dinic’s algorithm: ${\sigma }_2={\sigma }_3=\frac{\nu }{1-\nu }{\sigma }_1$, ${\sigma }_1=\overline{\gamma }H$, where H is the ground depth (m), $\overline{\gamma }$ is the average value of rock bulk density above ground depth (kN·m^-3), and ν is Poisson's ratio. According to structural geology (Li et al., 2013), Poisson's ratio ν for shale is 0.20–0.40, and the natural unit weight of shale is 23.0–26.2 kN·m^-3. In this paper, $\nu$ =0.25, $\overline{\gamma }$ =23 kN·m^-3, and ${\sigma }_2{=\sigma }_{3}7.6\mathrm{H}$, $\overline{{\sigma }_i}$ (i=1, 2, 3) ≥ 12.7H (where $\overline{{\sigma }_i}$ (i=1, 2, 3) is the average in situ stress) were used to design the loading value of in situ stress, specifically ${\sigma }_2={\sigma }_3\ge 7.5$ MPa, $\overline{{\sigma }_i}$ (i =1, 2, 3) ≥ 8.5, 9.5, 10.5, 11.5, 12.5 MPa

In the seepage stage, when the pressure of CO₂ gas injected for 3 h is constant, it is considered that the adsorption equilibrium has been reached. In the adsorption stage, the gas is continuously injected for 24 h, then absorbed for 24 h, the CO₂ adsorption equilibrium has reached for a total of 48 h. The single variable method was used to study the adsorption effect, effective stress, temperature, and gas pressure on shale seepage. Axial pressure was taken as confining pressure greater than the CO₂ fluid pressure during the whole experiment. The same shale test specimens, after supercritical CO₂ fracturing, were divided into three groups to carry out shale seepage tests successively. Five different gas pressure points (1, 2, 3, 4, and 5 MPa) were set. According to the design requirements that the axial pressure and confining pressure be greater than the air pressure and the previous in situ stress-loading value, this experiment designed five groups of different stress-loading values; axial pressure = confining pressure = 8.5, 9.5, 10.5, 11.5, and 12.5 MPa.

The experiment adopted the principle of a single variable, according to which, when one of the factors is studied as an independent variable, the other factors remain constant. This paper studies the influence of adsorption, effective stress, temperature, and gas pressure on permeability according to the designed ground temperature and ground stress gradient. In this experiment, the single variable method is used to study the effects of adsorption effect, effective stress, temperature, and gas pressure on the characteristics of CO₂ permeation into shale. Throughout the experiment, axial pressure = confining pressure > CO₂ fluid pressure is assumed. After supercritical CO₂ fracturing(Φ100 mm × 200 mm cylinder specimen), the same shale specimens are divided into three groups to carry out the shale seepage experiment. The specific experimental scheme is described in Figure 2.

To test the influence of the adsorption effects on permeability, the temperature was constant at 315.15 K, and the specific experimental steps were as follows: 1) Place the shale specimen coated with silica gel into the triaxial chamber, place the triaxial chamber into the thermostatic bath, set the temperature of the experiment to 305.15 K, and keep the oil temperature of the thermoplastic tube outside the specimen consistent with that of the thermostatic oil bath; 2) Alternately load the confining pressure and axial pressure to 2.0 MPa, and vacuum for 12 h with a vacuum pump to remove the air from the pores of shale specimens; 3) Load the test piece (axial pressure and confining pressure are alternately loaded to 8.5 MPa); 4) Close the gas outlet, fill the shale test piece with CO₂ gas (the injection pressure is 1 MPa), continue to inject for 24 h, then close the air inlet, and let CO₂ continue to adsorb in the shale for 24 h. After it is considered that the CO₂ adsorption has reached equilibrium, the gas outlet can be opened and collect flow and other data; 5) Repeat step 4, and conduct the seepage experiment of CO₂ gas pressure under the conditions of 2 MPa, 3 MPa, 4 MPa, and 5 MPa. According to the flow under different gas pressures, the permeability is calculated by Darcy’s law seepage formula. In addition, without CO₂ adsorption, CO₂ gas with different pressures (1, 2, 3, 4, and 5 MPa) is directly introduced. Under the same axial pressure and confining pressure experimental conditions, shale permeability is tested as a comparative experiment after CO₂ adsorption equilibrium.

To test the influence of effective stress on permeability, the experimental temperature value was constant at 305.15 K, and the volume stress was set to 25.5, 28.5, 31.5, 34.5, and 37.5 MPa. The specific experimental steps are as follows: 1) Place the pressure chamber into a constant temperature oil bath, set the temperature of the experiment to 305.15 K, and carry out the next experiment when the temperature reaches a stable level; 2) Alternately load the confining pressure and axial pressure to 2.0 MPa, vacuum the system with a vacuum pump for 12 h, and close the outlet valve; 3) Load the axial pressure and confining pressure to 8.5 MPa, open the inlet valve, supply CO₂ gas with a gas pressure of 1 MPa to the test piece, and open the outlet valve; the pressure at the outlet end is constant at 0.1 MPa. Collect the flow value after the flow is stable; 4) Then, adjust the gas pressure under the same conditions, conduct the seepage experiment under the gas pressure of 2 MPa, and collect various data; 5) After the CO₂ percolation experiment under the same volume stress and different osmotic pressure is completed, vacuum the system, change the volume stress, repeat steps 3) and 4), and continue the experiment under the next volume stress.

To test the influence of temperature and gas pressure on permeability, the confining and axial pressures were constant at 8.5 MPa, and the volume stress was constant at 25.5 MPa. Seepage experiments under different CO₂ gas pressures (1, 2, 3, 4, and 5 MPa) and different temperature conditions (305.15 K, 309.15 K, 313.15 K, 317.15 K, and 321.15 K) were carried out. First, the temperature is kept at a constant value, and the seepage experiment under different CO₂ pressure is carried out. After the experiment is completed, the temperature is increased to the next temperature point, and then the CO₂ seepage experiment is conducted under the same conditions as the previous temperature.

The specimen of the percolation test is the shale specimen obtained after supercritical CO₂ fracturing. Supercritical CO2 fracturing has produced macroscopic visible artificial cracks in the specimen, and the formation of a certain pore fracture network provides a channel for percolation. The experiment adopts the steady-state method to test the shale permeability and calculates the permeability of the test piece under different conditions according to Darcy's law. The calculation Formula (1) is

$k=\frac{2p_{a}Q\mu L}{A\left(p_i^2-p_o^2\right)}(1)$

Where the $k$ is permeability, the Q is the gas flow, the $p$ is atmospheric pressure, the L is the length of the specimen, the $\mu$ is the viscosity coefficient of gas, the A is the cross-sectional area of the specimen, the $p_i$ is the inlet gas pressure, and the $p_o$ is the outlet gas pressure, the gas outlet is connected to the atmosphere, so that the $p_o$ is equal to the atmospheric pressure 101.82 kPa.

3 Permeability evolution of fractured shale under the coupling conditions of temperature and stress

3.1 Influence of adsorbed gas on shale permeability

The permeability evolution in fractured shale before and after CO₂ adsorption is shown in Figure 3, according to Liu (2017). It can be considered that the shale specimen did not adsorb CO₂ before the test or the amount of CO₂ adsorbed was the minimal. After the shale specimens adsorbed with CO₂ and was saturated, the shale specimens were used to measure the permeability under different pore pressures. Under the same pore pressure, the permeability of shale after CO₂ adsorption is significantly lower than that of before adsorption. This is due to the expansion deformation effect caused by adsorption, which leads to the narrowing of the seepage channel and thus reduces the permeability.

Figure 3

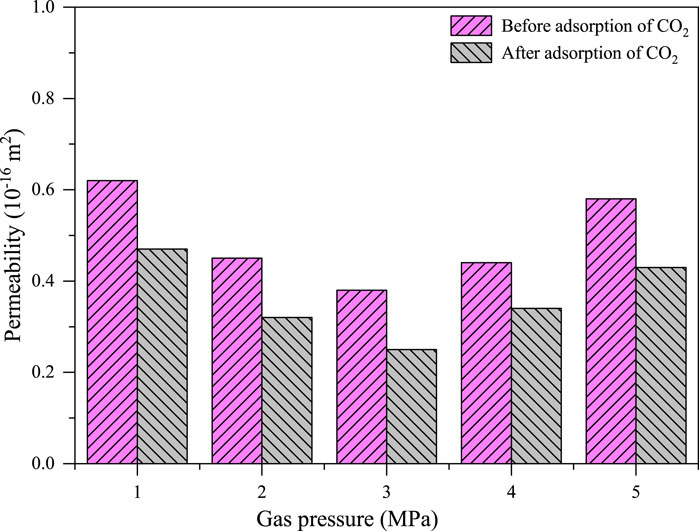
Figure 3. Permeability evolution of fractured shale specimens before and after adsorption of CO₂ gas.

In addition, the effective stress and the Klinkenberg effects together effect on the shale permeability and cause the minimum permeability during the change of the pore pressure. When the pressure exceeds 3 MPa, the effective stress decreases with the increase in gas pressure, leading to increased shale permeability. Therefore, at this stage, the permeability increases with the increase in gas pressure. When the pressure is lower than 3 MPa, the effective stress increases with the decrease in gas pressure, which will reduce the permeability of shale, but at the same time, due to the Klinkenberg effects of the gas in the pores, the permeability will increase with the decrease in pore pressure. According to the experimental results, when the pressure is lower than 3 MPa, the permeability of shale generally increases with the decrease in gas pressure, indicating that at this stage, the Klinkenberg effects plays a leading role in shale permeability.

According to the previous analysis of shale’s mercury intrusion pore structure, the pore size distribution of shale has multiple peak characteristics; different pore size distributions correspond to different pore structure characteristic lengths, and different values of characteristic lengths correspond to different flow mechanisms. Therefore, the seepage of fluid in shale also presents different flow mechanisms resulting from the multiscale structure characteristics of its pore fracture. In shale gas production, the effective radius of pores is lower than the true radius because of the gas adsorption; however, with the desorption of adsorbed gas, the effective radius gradually increases, which leads to a change in the gas flow mechanism. When the experimental temperature is 305.15 K, the average pore pressure is 1.0 MPa. In the CO₂ seepage fractured shale experiment, the diameter of CO₂ gas molecules was 0.33 nm, and the characteristic length of shale pores was replaced by the average pore size of shale. The average pore size was 9.6 nm, obtained from the previous pore size distribution, and the calculated Knudsen diffusion coefficient was 0.068, leading to the conclusion that there is a slippage effect in the seepage of the fractured shale specimen under the experimental conditions.

3.2 Influence of temperature on shale permeability

Under the conditions of equal confining and axial pressures and volume stress of 25.5 MPa, the relationship curve between shale permeability and gas pressure under different temperature conditions (305.15 K–321.15 K) is shown in Figure 4, according to Liu (2017), and the fitted exponential function relationship is shown in Table 3. The permeability has a negative exponential relationship with temperature. The higher the temperature, the lower the permeability. However, with the increase in temperature, the rate of permeability reduction slows down, indicating that the sensitivity of permeability to temperature decreases with the increase in temperature. The influence of temperature on shale specimens is such that, with the increase in temperature, the volume of shale particles expands, resulting in the reduction in pore fracture space and permeability channel, which leads to the reduction in permeability. This can be explained by the relationship between particle volume expansion strain and porosity presented in and Kozeny–Carman’s relationship between permeability and porosity (Chen et al., 2014).

Figure 4

Figure 4. Effect of temperature on permeability at a volume stress of 25.5 MPa.

Table 3

Table 3. Fitting equation of permeability and temperature.

However, it can be seen from Figure 5 that under different gas pressure conditions, there are notable differences in the rate of permeability reduction with the increase in temperature. The rate of permeability reduction in the temperature range of 313.15 K–321.15 K is significantly lower than in the range of 305.15 K–313.15 K, which is due to the role of temperature and volume stress. The increase in temperature will increase the expansion of the shale matrix, and the volume stress will limit the expansion of pores and fissures of shale. Within the limited pore and fissure volume, the expansion volume of the shale matrix caused by temperature is limited. Therefore, shale permeability decreases with the increase in temperature, but the reduction rate slows down. In the study, the temperature sensitivity coefficient is introduced and shown in Eq. 2, where CT equals the temperature sensitivity coefficient, k₀ is the initial value of permeability; △k is the change difference in permeability caused by temperature change, and △T is the temperature change difference before and after (Zhang et al., 2015b).

$C_T=-\frac{1}{k_0}\frac{\Delta k}{\Delta T}(2)$

Figure 5

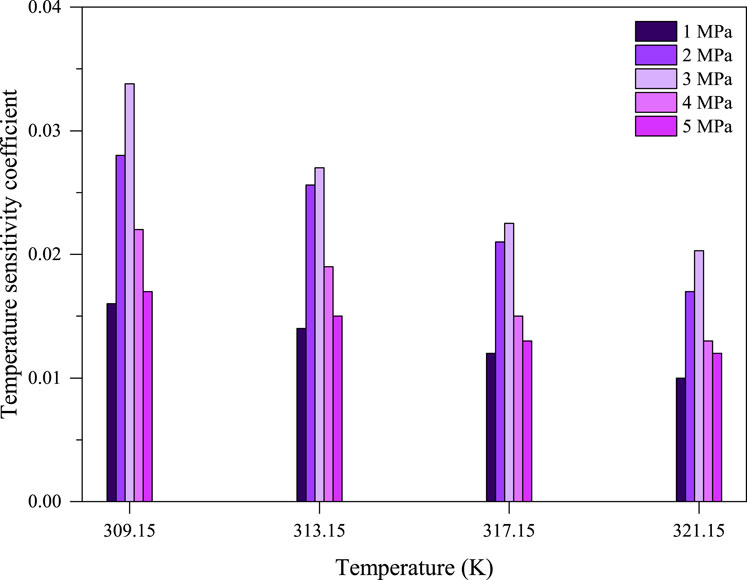
Figure 5. Changes of the temperature sensitivity coefficient with the temperature under different pore pressures.

In the study, the temperature of 305.15 K is taken as the initial value of permeability. According to the collecting experimental data and Eq. 1, the permeability at different temperatures and pore pressures are calculated, as shown in Table 3. According to Eq. 2 and collecting data, the relationship between temperature sensitivity coefficient and temperature under different pore pressures is presented in Figure 5, according to Liu (2017).

As can be seen from Figure 5, first, under constant volume stress, the temperature sensitivity coefficients under different pore pressures gradually decrease with the increase in temperature, which indicates that the shale permeability also becomes less sensitive with the increase in temperature. Although the increase in temperature will increase the expansion deformation of the shale, the compression of the existing volume stress will limit the deformation of the shale specimen, so the expansion deformation of the shale matrix also has a certain limit. Since the increase in the expansion deformation of the shale matrix decreases with the increase in temperature, the decrease in permeability with the increase in temperature will also continue to decrease; that is, the sensitivity of permeability to temperature will worsen. Second, at the same temperature, the temperature sensitivity coefficient initially increases and then decreases with the increase in the pore pressure. When the gas pressure is 1–3 MPa, the greater the pore pressure is, the greater the temperature sensitivity coefficient is. This is because at 1–3 MPa, the gas pressure is relatively low, mainly because the effective stress caused by the gas pressure plays a leading role. With the increase in the gas pressure, the effective stress decreases, and the blocking effect of the confining pressure on the expansion of the shale matrix heated to the inner pore space decreases. Therefore, the temperature sensitivity increases with the increase in the pore pressure. However, when the gas pressure exceeds 3 MPa, the pore pressure increases. And, the pore pressure plays a leading role. The CO₂ fluid existing in the pore fissures of shale will also produce a compression constraint effect on the shale matrix, which will produce a thermal effect on the temperature and hinder the expansion of the shale matrix into the pore fissure space. Therefore, the smaller the expansion of the shale matrix caused by the same temperature change, the smaller the value of the temperature sensitivity coefficient and the lower the sensitivity of shale permeability to temperature.

3.3 Influence of volume stress and average effective stress on shale permeability

The law of CO₂ permeability changing with volume stress is shown in Figure 6, according to Liu (2017). The permeability increases with the volume stress. The increase in permeability decreases a negative exponential function. When the volume stress reaches a certain value, the permeability curve finally becomes gentle, and the permeability tends to a fixed value, indicating a threshold for shale permeability. This value can be obtained according to the negative exponential relationship between permeability and volume stress. When the volume stress increases to infinity, the permeability is infinitely close to 0.25 × 10⁻¹⁶ m². The effective stress is generally considered as the difference between in situ stress and fluid pressure, and the average effective stress, as shown in Formula 3, can be used to replace the calculation (Xu et al., 2011).

${\sigma }_{\mathrm{e}}=\frac{1}{3}\left({\sigma }_1+2{\sigma }_3\right)-\frac{1}{2}\left(p_i+p_o\right)(3)$

Figure 6

Figure 6. Variation of the permeability with the volume stress in fractured shale specimens.

Where the $p_i$ and $p_o$ are the gas pressure at the inlet and outlet, the ${\sigma }_1$ and ${\sigma }_3$ is the maximum principal stress and confining pressure, respectively.

The relationship between the permeability and average effective stress is shown in Figure 7, according to Liu (2017). The permeability of the shale specimen changes with the average effective stress in a negative exponential function; that is, the permeability decreases with the increase in the average effective stress. This change is mainly due to the compression deformation effect of effective stress on shale. When the effective stress increases, the pores and fissures are compressed and closed, resulting in a decrease in the permeability of the shale specimens.

Figure 7

Figure 7. Permeability evolution with effective stress in fractured shale specimens.

3.4 Influence of gas pressure on shale permeability

The experimental study on the influence of gas pressure on shale permeability is carried out according to the designed temperature and pore pressure. The relationship between the permeability and pore pressure at 305.15 K–321.15 K under the volume stress of 25.5 MPa are shown in Figure 8, according to Liu (2017). It can be seen from that under the same effective stress and temperature conditions, when the CO₂ gas pressure increases from 1 MPa to 2 MPa, the permeability decreases significantly, which is due to the more significant Klinkenberg effects under lower pressure conditions. When the temperature is constant when the gas pressure is 1–3 MPa, the permeability decreases significantly with the increase in pore pressure. When the pore pressure exceeds 3 MPa, the permeability rises with the increase in pore pressure. This is similar to the trend in coal rock permeability decreasing in power function with the increase in pore pressure under the conditions of low pore pressure (0.3–2.05 MPa) obtained by the study (Peng et al., 2009). It is generally believed that when the pore pressure is relatively low, the Klinkenberg effects in the gas seepage decreases with increasing pore pressure (Klinkenberg et al., 1941; Xu et al., 2013; Yu et al., 2013; Liu et al., 2017b; Cheng, 2022c). According to the experimental results of this study, the reason for the change in permeability with pore pressure is that the change in permeability is affected by both effective stress and the Klinkenberg effects. When the pressure is 1–3 MPa, the influence of the Klinkenberg effects on permeability is greater than that of the effective stress. Therefore, when the pressure is 1–3 MPa, the permeability decreases with the increase in pore pressure. When the gas pressure is 3–5 MPa, the effective stress decreases with the increase in gas pressure. In a word, the effect of effective stress on permeability is dominant increasing the permeability with the increase in pore pressure.

Figure 8

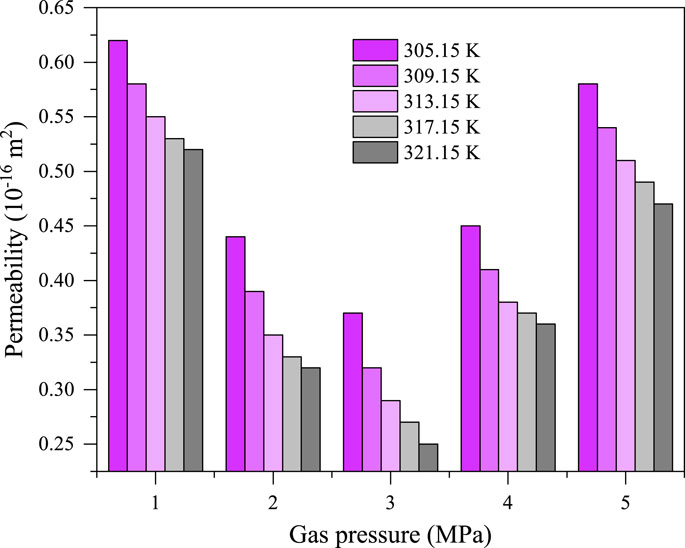
Figure 8. Effects of pore pressure on permeability of fractured shale specimens at a volume stress of 25.5 MPa.

4 Discussion and future research

4.1 Influence of temperature-pressure coupling conditions on slippage factor

The changes of the reservoir stress and temperature will cause the deformation of the fracture, and directly change the fracture aperture and affect the seepage characteristics of the fractured rock mass. That is, the crack expands along the direction of the maximum principal stress. This indicates that hydraulic fractures provide a better seepage channel by communicating with natural fractures, and further affect the seepage performance of natural fractures in the shale gas reservoirs. The permeability at a certain buried depth of shale reservoir is jointly affected by in situ stress and temperature, and its relationship can be written as Eq. 4 by Xuefu Xian.

$k=k_0\exp \left({\alpha }_{T}T-C_v{\sigma }_{\mathrm{e}}\right)(4)$

Where the ${\sigma }_{\mathrm{e}}$ is the average effective stress, the $C_v$ is the volume compressibility coefficient of the shale, according to the study by Li (2003), it can be calculated with the formula $C_v=\frac{\varphi }{\left(1-\varphi \right)}\cdot \frac{3\left(1-2\nu \right)}{E}$, the T is the reservoir temperature, the ${\alpha }_T$ is the coefficient of thermal expansion, and the $k_0$ is the permeability of shale at conditions of the room temperature and 1 atmosphere pressure (293.15 K, 101.325 kPa), which is related to the structure of the shale. Formula (4) shows that when the effects of the stress field and temperature field on permeability are comprehensively considered, the permeability of the underground rock mass at a certain burial depth can be considered affected by the coupling effect of the stress field and the temperature field, where the permeability is not a simple numerical superposition of the two fields. The permeability evolution with the reservoir temperature is shown in Figure 9, which present a downward trend. The change of temperature contributed to the gas adsorption, induces the thermal stress and thermoplastic strengthening, and thus can cause the deformation or compression (Zhu et al., 2011; Wang et al., 2014; Shang et al., 2019). The lower the permeability of porous media, the smaller the pore pressure difference, and the more obvious the slippage effect. As the temperature rises, the slip factor tends to increase, while the permeability decreases, as shown in Eq. 5.

$k=k_0\left(1+\frac{b}{p}\right)\Delta \sigma C_f(5)$

Figure 9

Figure 9. Permeability evolution with the reservoir temperature.

The temperature increase in shale reservoirs can influence both the Klinkenberg effects and the slippage factor, shown in Figure 10, according to Liu (2017). The Klinkenberg effects refers to the phenomenon in which the measured gas permeability of a shale reservoir increases with increasing pressure, but deviates from Darcy’s law at low pressure, due to the slip flow of gas molecules near the surface of the pore walls. The Klinkenberg effects is related to the slippage factor, as both are influenced by the degree of slip flow occurring within the pore structure of the shale. A temperature increase can increase the gas viscosity within the pores, thereby reducing the degree of slip flow, which can result in a reduction of the Klinkenberg effects. The slippage factor is the minimum force required for sliding to occur within the rock, or the coefficient of friction. As mentioned previously, an increase in temperature can reduce the coefficient of friction within the rock, thereby decreasing the slippage factor. However, when the temperature increases to a certain degree, the viscosity of the fluids within the rock may also decrease, which can increase the slippage factor. Overall, the effect of temperature on the Klinkenberg effects and slippage factor in shale reservoirs is complex and can depend on several factors, such as the mineralogy and porosity of the rock, the type of fluids presents, and the type of stress within the rock. It is important to consider these factors when studying the impact of temperature on the Klinkenberg effects and slippage factor in shale reservoirs.

Figure 10

Figure 10. Slippage factor of shale at different temperatures.

The Klinkenberg effects can be used to increase gas production in shale gas development in the following ways. One way to utilize the Klinkenberg effects to increase gas production in shale gas development is through gas injection. By injecting a gas with a lower viscosity than the reservoir gas, such as nitrogen or carbon dioxide, the viscosity of the gas within the pore structure can be reduced, which can increase the degree of slip flow and reduce the threshold pressure required for gas production. This technique is called “low-salinity gas flooding” or “slip-enhanced gas recovery.” Another way to utilize the Klinkenberg effects to increase gas production in shale gas development is through reservoir characterization. By accurately characterizing the pore structure of the shale reservoir, engineers can determine the degree of slip flow within the pore structure and design production strategies that take advantage of this effect. For example, production rates can be optimized by targeting zones with higher degrees of slip flow. Hydraulic fracturing is a process used to create fractures within the shale formation to increase the surface area available for gas production. The Klinkenberg effects can be used in the design of hydraulic fracturing by selecting fluids and proppants that can reduce the viscosity of the fluid within the fractures, thereby increasing the degree of slip flow and reducing the threshold pressure required for gas production. Thus, utilizing the Klinkenberg effects to increase gas production in shale gas development requires a thorough understanding of the properties of the reservoir and the pore structure within the shale. By designing production strategies that take advantage of this effect, engineers can optimize production rates and increase the overall recovery of gas from the reservoir.

4.2 Temperature-stress coupled permeability model of fractured shale

This section will discuss the effects of temperature, porosity, in situ stress, pore fluid, and shale formation in combination with the mechanism concept diagram. Changes in factors such as temperature and stress affect the closure and connectivity of rock pores and fractures, thereby changing the porosity of shale, which in turn may affect the permeability of shale. From the definition of porosity, the porosity of shale ϕ is the ratio of the pore volume $V_p$ to the total shale volume $V$, as shown in Eq. 6.

$\varphi =\frac{V_p}{V}(6)$

It is assumed that the seepage process of shale occurs not only in macroscopic fractures, but also in a small number of connected pores in the matrix, that is, the equivalent vug-fracture seepage. The pore volume change caused by temperature and pressure coupling factors is composed of initial pore volume, pore deformation, and fracture space change caused by fracture compression; then, considering the change of temperature and pressure conditions, the overall pore volume change is as follows, Eq. 7.

$V_p=V_{p0}+\Delta V_p+\Delta V_f(7)$

The total deformation of the shale influenced by temperature and stress can be expressed by Eq. 8.

$V{=V}_0+\Delta V(8)$

Thus, when the formation temperature rises from T₀ to T, the porosity can be expressed by Eq. 9.

${\varphi }_T=\frac{V_p}{V}(9)$

If it combines Eqs 7 and 8, and substitute into Eq. 9, the porosity at temperature of T can be expressed by Eqs 10–13.

${\varphi }_T=\frac{V_{p0}+∆V_p+∆V_f}{V_0+∆V}(10)$

The formula (10) is divided by $V_0$ at the same time, we can get Eq. 11.

${\varphi }_T=\frac{\frac{V_{p0}}{V_0}+\frac{\Delta V_p}{V_0}+\frac{\Delta V_f}{V_0}}{1+\frac{\Delta V}{V_0}}(11)$

The initial porosity of shale is ${\varphi }_0=V_{p0}/V_0$, so that Eq. 11 can be expressed by Eq. 12.

${\varphi }_T=\frac{{\varphi }_0+\frac{\Delta V_p}{V_0}+\frac{\Delta V_f}{V_0}}{1+\frac{\Delta V}{V_0}}(12)$

The volume deformation of shale is ${\epsilon }_v=\Delta V/V_0$, so Eq. 12 can be expressed as Eq. 13.

${\varphi }_T=\frac{{\varphi }_0+\frac{\Delta V_p}{V_0}+\frac{\Delta V_f}{V_0}}{1+{\epsilon }_v}(13)$

Among them, due to stress compression and temperature rise, the deformation of fractures and pores (or matrix) in shale can be determined by Eqs 14 and 15, respectively.

$\frac{\Delta V_f}{V_0}=-\frac{1}{K_f}\left(\Delta \sigma -\alpha \Delta p\right)(14)$

$\frac{\Delta V_p}{V_0}=-\frac{1}{K}\left(\Delta \sigma -\beta \Delta p\right)+3{\epsilon }_T(15)$

And the ${\epsilon }_T={\alpha }_T\Delta T$, thus, the porosity of shale at the temperature of T can be expressed by Eq. 16.

${\varphi }_T=\frac{{\varphi }_0-\frac{1}{K_f}\left(\Delta \sigma -\alpha \Delta p\right)-\frac{1}{K}\left(\Delta \sigma -\beta \Delta p\right)+3{\alpha }_T∆T}{1+{\epsilon }_v}(16)$

After considering a series of temperature effects such as thermal expansion, thermal cracking, and the influence of temperature on shale adsorption expansion, the volumetric strain of shale can be expressed according to literature (Li et al., 2020), as shown in Eq. 17.

${\epsilon }_v=-\frac{1}{K}\left(\Delta \sigma -\alpha \Delta p\right)+{\epsilon }_s+{\epsilon }_{Tp}+{\epsilon }_e(17)$

Usually the Biot coefficient is 1, but some studies have shown that the Biot coefficient is not 1 in specific cases (Mao et al., 2018; Li et al., 2019). According to the research (Skempton, A. 1984; Zhou et al., 2009), the effective stress coefficient can be expressed by Eq. 18.

$\alpha =1-\frac{C_s}{C}\left(0\le \alpha \le 1\right)(18)$

The fracture compression coefficient $C_f$ is defined by Eq. 19 and Eq. 20, respectively.

$C_f=\frac{\delta }{{\delta }_{\max }}(19)$

$C_f=\frac{1}{K_f}(20)$

And Eq. 21 can be obtained by combining these two Equations.

${\delta }_{\max }=K_f\delta (21)$

Eq. 18 shows that the case where the Biot coefficient α is not equal to 1 due to fracture compression is worth further exploring. From the literature (Chen et al., 2021), the study newly defined a Biot coefficient for the deep shale formation, as shown in Eq. 22.

$\alpha =\begin{array}{cc}\frac{1}{1+\frac{{\sigma }_n-p}{K_{n0}{K}_f\delta }}& \end{array}{\sigma }_n>p\text{\hspace{1em}or\hspace{1em}}\alpha =\begin{array}{cc}1& {\sigma }_n<p\end{array}(22)$

Where the $K_{n0}$ is the initial normal stiffness.

To accurately characterize the effective stress coefficient in pores (or matrix), this study newly defines the effective stress coefficient β of pores in shale, that is, the proportion of connected pores participating in the diffusion and seepage process to the total pore volume, which can be measured by MRI and other methods. When the connectivity of all pores is 100%, it is considered that the effective stress coefficient of the pores is 1, otherwise $\beta \subseteq \left(0,1\right)$. Thus, if the permeability satisfied $k=k_0{\left({\varphi }_T/{\varphi }_0\right)}^3$, the permeability can be expressed by Eq. 23. The permeability evolution with effective stress and temperature difference are displayed in Figure 11.

$k=k_0{\left[\frac{{\varphi }_0-\frac{1}{K_f}\left(\Delta \sigma -\alpha \Delta p\right)-\frac{1}{K}\left(\Delta \sigma -\beta \Delta p\right)+3{\alpha }_T∆T}{\left(1+{\epsilon }_v\right){\varphi }_0}\right]}^3(23)$

Figure 11

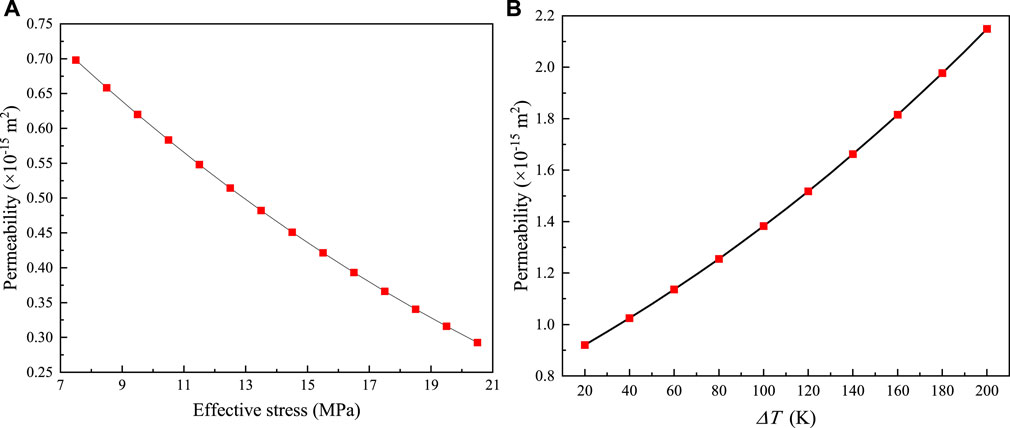
Figure 11. Relationship between permeability and (A): effective stress, (B): temperature difference.

4.3 Implications for shale gas extraction in southwestern China

4.3.1 Shale gas extraction influenced by reservoir temperature

The potential application and engineering value of shale gas extraction in southwestern China. Supercritical carbon dioxide fracturing shale forms hydraulic fractures, which connect natural fractures and shale pores to form seepage channels. At the same time, carbon dioxide enters the pores and fractures of shale, displaces the methane gas adsorbed in shale, and forms an industrial gas flow that enters the wellbore and is discharged to the surface production system, the stimulation process of shale formation is shown in Figure 12. Based on the previous studies, the permeability increases with temperature, and decrease with effective stress. High temperature not only promotes methane desorption, but also increases reservoir permeability, which is beneficial for gas production. However, as the gas pressure changes, the permeability is not only related to the effective stress, but also influenced by the gas slip effect. Also, the gas slippage effect varies at different temperatures.

Figure 12

Figure 12. Schematic diagram of shale gas extraction by supercritical carbon dioxide stimulation.

As the depth of shale gas development increases, the ground temperature will further increase. With the increase of temperature and formation stress, deep shale undergoes plastic deformation in which organic matter pores and clay mineral pores are compressed and micro-fractures are closed under pressure, and elastic deformation in which brittle mineral pores and rock skeleton particles are compressed (Sun et al., 2023). Although the increase in formation temperature has little effect on the strength of the rock mass in the range of about 400°C, it can further promote the desorption of methane in the shale, thereby improving the gas production efficiency; the elevated formation temperature often also causes the rock mass to expansion and deform, increase the viscosity of the gas and reduce the permeability of the shale reservoir; in addition, the temperature rise of the formation will accelerate the thermal movement of the water molecules in the shale reservoir, reduce the viscosity of the liquid water, thereby increasing the fluidity of the liquid water and accelerating chemical reaction rate of the water molecules and hydrophilic minerals in shale reservoirs affects the fracturing effect of shale reservoirs and the drainage of shale gas.

The research shows that when the reservoir temperature and stress are both at a lower level, the reservoir in situ stress plays a leading role in the shale adsorption capacity; when the temperature and in situ stress are both at a greater level, the reservoir temperature plays a leading role in the shale adsorption capacity (Yu et al., 2018). Generally speaking, the effect of adsorption swelling deformation on shale gas permeability is small, so the influence of adsorption swelling deformation can be ignored in the specific permeability model, as shown in Eq. 17. This is because shale gas mainly penetrates into the wellbore through pores and fractures, while the adsorption expansion deformation mainly affects the microscopic pore structure, and has little effect on fractures.

4.3.2 Shale gas extraction influenced by reservoir microstructure

The shale reservoirs are rich of complex fracture network both before the stimulation and after the stimulation by hydraulic fracturing or supercritical water/CO₂ jet (Wang et al., 2015; Huang et al., 2018; Wang et al., 2018; Yang et al., 2022; Huang et al., 2023). Using RFPA^2D-FLOW, a system for rock failure process analysis, seven shale models with different angles of natural fracture or fissure, such as the bedding planes, joints, and the mini faults, etc., were established, and their fracture processes were numerically simulated. The fracturing process of shale with prefabricated fractures can be divided into three stages: linear deformation, yield deformation, and complete failure. Peak stress under various fractures dips with increasing angles and presents first increases and then a trend change, except when the fissure angle turns into 75°. While the fissure angle is 45°, the maximum stress peak is at 42.34 MPa. Because of the strong brittleness and poor ductility of shale, the stress falls vertically parallel to the stress coordinate axis after the specimen stress reaches the peak value. The elastic modulus and compressive strength of shale have significant anisotropy. When the fissure angle is 45°, the stress peak and compressive strength of the specimen reach the maximum value. When the fissure angle is 0°, the peak stress and compressive strength of the specimen reach the minimum value. When the fissure angle is 75°, the elastic modulus is the largest. When the fissure angle turns into 90°, the elastic modulus of the specimen is the smallest. Under the coupled action of seepage stress, shale exhibits four failure modes: oblique, X-type, λ-type, and collapse. The failure of shale specimens is mainly a tensile failure, and some subtle cracks occur in the specimens, leading to stress redistribution in the specimens. In the later failure process of the specimens, shear failure also occurs. When the fissure angle is 90°, the crack on the right side of the fissure is mainly caused by shear failure, while the crack on the left side of the prefabricated crack is mainly caused by tensile failure. The cracks at other angles are primarily caused by tensile failure but are also accompanied by a small number of cracks generated by shear failure.

4.4 Limitations and prospect

The study focusses on the evolution of shale permeability under the coupling conditions of temperature and stress; and constructed a temperature-stress coupled permeability model of fractured shale by newly defined Biot effective stress coefficient. However, the temperature set in the test is not enough to simulate the temperature of shale reservoirs at a depth of more than ∼1800 m. For example, the geothermal gradient in the Jiaoshiba shale reservoir area ranges from 297.15 K to 305.15 K per kilometer, and the measured bottomhole temperatures reach 371.91 K (2,860 m), 370.57 K (2,890 m) and 371.01 K (3,100 m), respectively (Li et al., 2017b). Deep shale gas reservoirs with a burial depth greater than 3,500 m are important strategic replacement reservoirs for shale gas exploration and development in the Sichuan Basin (He et al., 2021). As the burial depth of the reservoir increases, the temperature of the formation is also increasing, and the parameters such as the thermal conductivity of the shale, such as Figure 13 (Kang, 2008), will also change slightly, which may affect the values of the parameters related to the permeability and further affect the shale gas drainage. In the next step of research, it is necessary to set parameters such as temperature and pressure as the environmental conditions of the formation below 3,500 m buried depth, so as to improve the pertinence of the research.

Figure 13

Figure 13. Thermal conductivity of shale at different reservoirs temperatures.

Future research needs to rely on the current popular basic theory of artificial intelligence and closely combine basic physical and mechanical experiments to accelerate the inversion of physical and mechanical parameters of fast deep shale reservoirs. To use the machine learning method to build a shale permeability model under the coupling of temperature and stress, such as dual-porosity medium model considering influence of desorption hysteresis effects (Chu et al., 2024a; Chu et al., 2024b), the machine learning-based models should be based on a large amount of experimental data and field observation data, and thus, the proper machine learning algorithms should be used to establish shale permeability models under the coupling of temperature and stress. For example, to further study the seepage mechanics of shale containing fractures and its anisotropy (Li et al., 2021; Li et al., 2022), using algorithms such as neural networks, decision trees, and support vector machines to establish the nonlinear relationship between temperature and stress on shale permeability, and predicting the change law of shale permeability. It should be noted that all these methods require a large amount of experimental data and field observation data to verify the reliability of the model. In addition, shale permeability is influenced by multiple factors, and building an accurate model requires the consideration of the complex relationship between various influencing factors. To build a shale permeability model under the coupling of temperature and stress using machine learning methods, the following basic steps can be taken. Firstly, Data collection and preparation is the prerequisite. Collect and prepare relevant datasets, including temperature, stress, and shale permeability data. These data should be labeled and cleaned for use in the machine learning model. And then extracting the features from in situ and typical engineering. Based on the dataset, select appropriate features, and perform feature engineering. Feature selection techniques, such as Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA), can be used to improve model accuracy and robustness. Based on datasets and features extraction, the model can be selected and constructed for deep leaning. Choose a suitable machine learning algorithm to build the model based on the characteristics of the dataset. Commonly used algorithms include Support Vector Machines (SVM), Neural Networks (NN), Random Forest (RF), and Decision Trees (DT), among others. Naturally, the model training and optimization is the key to get the balance of the data noise and inevitable event. Then the model can be optimized by training the chosen machine learning algorithm using the dataset to improve the model’s performance by adjusting the algorithm’s parameters. Cross-validation techniques can be used for model training and validation to avoid overfitting. Thus, the newly constructed and trained model can be evaluated by using a testing dataset and select the best-performing model for deployment. Before deployment, the model needs to be optimized and adjusted for better performance and in situ engineering applications. In future research, building a shale permeability model under the coupling of temperature and stress using machine learning methods requires needs to be continually adjusted and optimized to achieve better predictive performance based on in situ shale gas extraction engineering.

5 Conclusion

Supercritical CO₂ fracturing is used to make the fractured shale specimen. The study carried out the experimental exploration on the influence of effective stress, temperature, and CO₂ adsorption expansion effects on the features of the permeability evolution of Silurian Longmaxi shale. The study explored the coupling effects of the stress field and temperature field on the shale permeability and got the seepage law of fractured shale. The results are as follows. 1) When the gas pressure is 1–5 MPa, the shale permeability is affected by the combined action of the Klinkenberg effects and effective stress. The dominant factors of permeability change are different in different gas pressure ranges. When the gas pressure is 1–3 MPa, the permeability decreases significantly with the increase in gas pressure, and the Klinkenberg effects plays a leading role at that time. When the gas pressure is 3–5 MPa, the permeability increases with the increase in gas pressure, and the effect of effective stress on permeability is dominant at that time; 2) The permeability of fractured shale decreases exponentially with the increase in effective stress; The permeability of shale after adsorption of CO₂ gas is significantly lower than before the adsorption, which is due to the expansion deformation effect caused by adsorption, resulting in the narrowing of seepage channel and the reduction in permeability; 3) The relationship curve between the permeability of fractured shale and temperature shows that the permeability of shale decreases with the increase at 305.15 K–321.15 K, mainly because the volume expansion caused by temperature reduces the channel space of seepage. With the increase in temperature, the sensitivity of permeability to temperature decreases. Shale permeability is closely related to supercritical CO₂ injection pressure and volume stress. When the injection pressure of supercritical CO₂ is constant, the permeability of shale decreases with the increase in volume stress.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

GL: Funding acquisition, Investigation, Methodology, Resources, Writing–original draft. DS: Conceptualization, Data curation, Investigation, Supervision, Visualization, Writing–review and editing. PC: Data curation, Writing–review and editing. YZ: Data curation, Writing–review and editing. JL: Data curation, Writing–review and editing. JL: Data curation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the program for Natural Science Foundation of Hunan Province (No. 2021JJ40028).

Conflict of interest

Author YZ was employed by Sinohydro Bureau 8 Co., Ltd., POWERCHINA.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, T., Feng, X. T., Yang, C., Cao, W., and Liu, X. (2014). Research on confining pressure sensitivity and anisotropy for gas shale permeability. J. Min. Saf. Eng. 31 (4), 639–642. (In Chinese). doi:10.13545/j.issn1673-3363.2014.04.024

CrossRef Full Text | Google Scholar

Cheng, H., Wei, J., and Cheng, Z. (2022b). Study on sedimentary facies and reservoir characteristics of Paleogene sandstone in Yingmaili block, Tarim basin. Geofluids 2022, 1445395. doi:10.1155/2022/1445395

CrossRef Full Text | Google Scholar

Cheng, H., Ma, P., Dong, G., Zhang, S., Wei, J., Qi, Q., et al. (2022a). Characteristics of carboniferous volcanic reservoirs in beisantai oilfield, junggar basin. Math. Problems Eng. 2022, 7800630. doi:10.1155/2022/7800630

CrossRef Full Text | Google Scholar

Cheng, H., Yang, D., Lu, C., Qin, Q., and Cadasse, D. (2022c). Intelligent oil production stratified water injection technology. Wirel. Commun. Mob. Comput. 2022, 1–7. doi:10.1155/2022/3954446

CrossRef Full Text | Google Scholar

Chu, P., Xie, H., Gao, M., Li, C., Shang, D., Liu, Q., et al. (2024a). Influence of desorption hysteresis effects on coalbed methane migration and production based on dual-porosity medium model incorporating hysteresis pressure. Comput. Geotechnics 165, 105893. doi:10.1016/j.compgeo.2023.105893

CrossRef Full Text | Google Scholar

Chu, P., Xie, H., Li, C., Liu, Q., Lu, Z., and Lu, J. (2024b). Mechanism of desorption hysteresis in coalbed methane: insights from microscopic pore properties and adsorption theory. Phys. Fluids 36, 012004. doi:10.1063/5.0184321

CrossRef Full Text | Google Scholar

Duan, Y., Wei, M., Li, J., and Tang, Y. (2011). Shale gas seepage mechanism and fractured wells’ production evaluation. J. Chongqing Univ. 34 (4), 62–66. (In Chinese).

Google Scholar

Firouzi, M., Alnoaimi, K., Kovscek, A., and Wilcox, J. (2014). Klinkenberg effect on predicting and measuring helium permeability in gas shales. Int. J. Coal Geol. 123 (2), 62–68. doi:10.1016/j.coal.2013.09.006

CrossRef Full Text | Google Scholar

He, Z., Nie, H., and Jiang, T. (2021). Challenges and countermeasures of effective development with large scale of deep shale gas in Sichuan Basin. Reserv. Eval. Dev. 11 (2), 135–145. (In Chinese). doi:10.13809/j.cnki.cn32-1825/te.2021.02.001

CrossRef Full Text | Google Scholar

Huang, M., Kang, Y., Wang, X., Hu, Y., Cai, C., Liu, Y., et al. (2018). Experimental investigation on the rock erosion characteristics of a self-excited oscillation pulsed supercritical CO₂ jet. Appl. Therm. Eng. 139, 445–455. doi:10.1016/j.applthermaleng.2018.05.014

CrossRef Full Text | Google Scholar

Huang, M., Wu, L., Su, D., Zhao, Z., and Zhang, M. (2023). Enhancing gas production in low-permeability natural gas hydrate reservoirs by the axial water jet slotting and grouting in vertical wellbores. Gas Sci. Eng. 118, 205088. doi:10.1016/j.jgsce.2023.205088

CrossRef Full Text | Google Scholar

Kang, J. (2008). Research on thermal cracking of rocks and its application. Dalian: Dalian University of Technology Press. (In Chinese).

Google Scholar

Klinkenberg, L. J. (1941). The permeability of porous media to liquids and gases. Drill. Prod. Pract. 2 (2), 57–73. doi:10.5510/OGP20120200114

CrossRef Full Text | Google Scholar

Li, B., Gao, Z., Yang, K., Li, J., Ren, C., Xu, J., et al. (2020). Study on coal adsorption-permeability model under the coupling of temperature and pore pressure. Chin. J. Rock Mech. Eng. 39 (4), 668–681. (In Chinese). doi:10.1016/S0016-2361(99)00269-0

CrossRef Full Text | Google Scholar

Li, C., and Zhu, S. (2019). Discussion of dual effective stresses in porous media—analysis on the paper of Re-recognition of dual effective stresses and the comprehensive effect. Petroleum Sci. Bull. 04, 414–429. (In Chinese). doi:10.3969/j.issn.2096-1693.2019.04.037

CrossRef Full Text | Google Scholar

Li, C. (2003). The relationship between rock compressibility and porosity. China Offshore Oil Gas Geol. 17 (5), 354–358. (In Chinese).

Google Scholar

Li, C., Rao, S., Hu, S., Wang, J., Wei, Z., Huang, Q., et al. (2017b). Present-day geothermal field of the Jiaoshiba shale gas area in southeast of the Sichuan basin, SW China. Chin. J. Geophys. 60 (2), 617–627. (In Chinese). doi:10.6038/cjg20170216

CrossRef Full Text | Google Scholar

Li, J., and Li, B. (2021). Modeling of anisotropic coal permeability under the effects of matrix-fracture interaction. J. Nat. Gas Sci. Eng. 93, 104022. doi:10.1016/j.jngse.2021.104022

CrossRef Full Text | Google Scholar

Li, J., Li, B., Lu, J., Duan, S., and Gao, Z. (2022). Evolution of fracture permeability and its compressibility in proppant-supported shale. J. Nat. Gas Sci. Eng. 105, 104713. doi:10.1016/j.jngse.2022.104713

CrossRef Full Text | Google Scholar

Li, J., and Sultan, A. S. (2017a). Klinkenberg slippage effect in the permeability computations of shale gas by the pore-scale simulations. J. Nat. Gas Sci. Eng. 48, 197–202. doi:10.1016/j.jngse.2016.07.041

CrossRef Full Text | Google Scholar

Li, M., Yin, G., Jiang, Xu, Cao, J., and Song, Z. (2016). Permeability evolution of shale under anisotropic true triaxial stress conditions. Int. J. Coal Geol. 165, 142–148. doi:10.1016/j.coal.2016.08.017

CrossRef Full Text | Google Scholar

Li, X., Li, Q., Wang, Y., Liu, W., Hou, Di, Zheng, W., et al. (2023). Experimental study on instability mechanism and critical intensity of rainfall of high-steep rock slopes under unsaturated conditions. Int. J. Min. Sci. Technol. 33 (10), 1243–1260. doi:10.1016/j.ijmst.2023.07.009

CrossRef Full Text | Google Scholar

Li, Y., Li, Y., Luo, P., and Zhao, J. (2013). Study on seepage mechanism and productivity of shale gas. Fault-Block Oil Gas Field 20(2), 186–190. (In Chinese). doi:10.6056/dkyqt201302013

CrossRef Full Text | Google Scholar

Liu, G. (2017). Supercritical CO₂ fracturing of shale and its permeability variation under multi-field coupling conditions. Dissertation, Chongqing: Chongqing University. (In Chinese).

Google Scholar

Liu, G., Xian, X., Zhou, J., Zhang, L., Liu, Q., Zhao, Y., et al. (2017b). Experimental study on the supercritical CO₂ fracturing of shale. J. China Coal Soc. 42 (3), 694–701. doi:10.13225/j.cnki.jccs.2016.0604

CrossRef Full Text | Google Scholar

Liu, G., Xian, X., Zhou, J., Zhao, Y., Yin, H., Guo, Y., et al. (2017a). Dynamic permeability change of supercritical CO₂ fractured shale and its influencing factors. J. China Coal Soc. 42 (10), 2670–2678. (In Chinese). doi:10.13225/j.cnki.jccs.2017.0262

CrossRef Full Text | Google Scholar

Liu, R., Yu, L., and Jiang, Y. (2016). Fractal analysis of directional permeability of gas shale fracture networks: a numerical study. J. Nat. Gas Sci. Eng. 33 (33), 1330–1341. doi:10.1016/j.jngse.2016.05.043

CrossRef Full Text | Google Scholar

Mao, X., Liu, Y., Feng, Y., Zheng, W., and Liu, S. (2018). Re-recognition of dual effective stresses and the comprehensive effect. Petroleum Sci. Bull. 04, 390–398. (In Chinese). doi:10.3969/j.issn.2096-1693.2018.04.035

CrossRef Full Text | Google Scholar

Moghaddam, R. N., and Jamiolahmady, M. (2016). Fluid transport in shale gas reservoirs: simultaneous effects of stress and slippage on matrix permeability. Int. J. Coal Geol. 163, 87–99. doi:10.1016/j.coal.2016.06.018

CrossRef Full Text | Google Scholar

Peng, S., Xu, J., Tao, Y., and Cheng, M. (2009). Coefficient of sensitiveness between permeability and effective pressure of coal samples. Journal of Chongqing University, 303–307. (In Chinese).

Google Scholar

Shang, X., Wang, J. G., Zhang, Z., and Gao, F. (2019). A three-parameter permeability model for the cracking process of fractured rocks under temperature change and external loading. Int. J. Rock Mech. Min. Sci. 123, 104106. doi:10.1016/j.ijrmms.2019.104106

CrossRef Full Text | Google Scholar

Skempton, A. W. (1984). Effective stress in soils, concrete and rocks. Sel. Pap. soil Mech. 1032 (3), 106–118. doi:10.1680/sposm.02050.0014

CrossRef Full Text | Google Scholar

Song, W., Yao, J., Li, Y., Sun, H., Zhang, L., Yang, Y., et al. (2016). Apparent gas permeability in an organic-rich shale reservoir. Fuel 181, 973–984. doi:10.1016/j.fuel.2016.05.011

CrossRef Full Text | Google Scholar

Su, Y., Xu, J., Wang, W., Wang, H., and Zhan, S. (2022). Relative permeability estimation of oil−water two-phase flow in shale reservoir. Petroleum Sci. 19 (3), 1153–1164. doi:10.1016/j.petsci.2021.12.024

CrossRef Full Text | Google Scholar

Sun, C., Nie, H., Su, H., Du, W., Lu, T., Chen, Y., et al. (2023). Porosity, permeability and rock mechanics of Lower Silurian Longmaxi Formation deep shale under temperature-pressure coupling in the Sichuan Basin, SW China. Petroleum Explor. Dev. 50 (1), 85–98. (In Chinese). doi:10.1016/s1876-3804(22)60371-9

CrossRef Full Text | Google Scholar

Sun, H., Yao, J., Zhang, L., Wang, C., Sun, Z., Yan, Y., et al. (2014). A computing method of shale permeability based on pore structures. J. China Univ. Petroleum 38 (02), 92–98. (In Chinese). doi:10.3969/j.issn.1673-5005.2014.02.014

CrossRef Full Text | Google Scholar

Teng, T., Wang, J. G., Gao, F., Ju, Y., and Jiang, C. (2016). A thermally sensitive permeability model for coal-gas interactions including thermal fracturing and volatilization. J. Nat. Gas Sci. Eng. 32, 319–333. doi:10.1016/j.jngse.2016.04.034

CrossRef Full Text | Google Scholar

Wang, C., Feng, J., Liu, J., Wei, M., Wang, C., and Gong, B. (2014). Direct observation of coal gas interactions under thermal and mechanical loadings. Int. J. Coal Geol. 131, 274–287. doi:10.1016/j.coal.2014.06.021

CrossRef Full Text | Google Scholar

Wang, W., Su, Y., Sheng, G., Cossio, M., and Shang, Y. (2015). A mathematical model considering complex fractures and fractal flow for pressure transient analysis of fractured horizontal wells in unconventional reservoirs. J. Nat. Gas Sci. Eng. 23, 139–147. doi:10.1016/j.jngse.2014.12.011

CrossRef Full Text | Google Scholar

Wang, W., Su, Y., Zhang, Q., Xiang, G., and Cui, S. (2018). Performance-based fractal fracture model for complex fracture network simulation. Petroleum Sci. 15 (1), 126–134. doi:10.1007/s12182-017-0202-1

CrossRef Full Text | Google Scholar

Wu, J., Chang, Y., Liang, T., Guo, X., and Chen, X. (2015). Shale gas flow model in matrix nanoscale pore. Nat. Gas. Geosci. 26 (3), 575–579. (In Chinese). doi:10.11764/j.issn.1672-1926.2015.03.0575

CrossRef Full Text | Google Scholar

Xu, J., Cao, J., Li, B., Zhou, T., Li, M., and Liu, D. (2013). Experimental study on the response law of coal permeability to pore pressure change. Chin. J. Rock Mech. Eng. 32 (02), 225–230. (In Chinese).

Google Scholar

Xu, J., Zhang, D., Peng, S., Nie, W., Wang, L., and Chen, Y. (2011). Experimental research on impact of temperature on seepage characteristic of coal containing methane under triaxial stress. Chin. J. rock Mech. Eng. 30 (S1), 2730–2735. (In Chinese).

Google Scholar

Yang, H., Zhao, Y., Zhang, X., Liu, G., Du, X., Shang, D., et al. (2022). Supercritical CO₂ fracturing with different drilling depths in shale. Energy Sources, Part A Recovery, Util. Environ. Eff. 44 (4), 10603–10622. doi:10.1080/15567036.2019.1673850

CrossRef Full Text | Google Scholar

Yin, G., Li, X., Zhao, H., Li, X., and Jing, X. (2009). Experimental study of effect of gas pressure on gas seepage of outburst coal. Chin. J. Rock Mech. Eng. 28 (4), 697–702. (In Chinese). doi:10.1016/j.jrmge.2022.05.013

CrossRef Full Text | Google Scholar

Yu, Y., Zhang, H., Zhang, C., Hao, Z., and Wang, L. (2013). Effects of temperature and stress on permeability of standard coal briquette specimen. J. China Coal Soc. (06), 936–941. doi:10.13225/j.cnki.jccs.2013.06.029

CrossRef Full Text | Google Scholar

Yu, C, Zhou, X., Fang, G., Wang, S., and Yu, Z. (2018). Adsorptivity of shale under the formation temperature and pressure: a case of Longmaxi Formation in northeastern Chongqing. Lithol. Reserv. 30 (6), 10–17. (In Chinese). doi:10.12108/yxyqc.20180602

CrossRef Full Text | Google Scholar

Zhang, H., Liu, W., and Zhu, L. (2015a). Fracture permeability model and experiments of shale gas reservoirs. Rock Soil Mech. 36 (3), 719–729. doi:10.16285/j.rsm.2015.03.016

CrossRef Full Text | Google Scholar

Zhang, L., Yao, J., Sun, H., and Sun, Z. (2014). Permeability calculation in shale using lattice Boltzmann method. J. China Univ. Petroleum 38 (01), 87–91. doi:10.3969/j.issn.1673-5005.2014.01.013

CrossRef Full Text | Google Scholar

Zhang, Q., Wang, W., Su, Y., Chen, W., Lei, Z., Li, L., et al. (2024). A semi-analytical model for coupled flow in stress-sensitive multi-scale shale reservoirs with fractal characteristics. Petroleum Sci. 21 (1), 327–342. doi:10.1016/j.petsci.2023.10.003

CrossRef Full Text | Google Scholar

Zhang, W., Wang, Q., Yang, X., Duan, Q., Ye, J., Li, X., et al. (2015b). Porosity and permeability of paleozoic mudstone and shale in the Yangtze block. Nat. Gas. Geosci. 26 (8), 1534–1539. doi:10.11764/j.issn.1672-1926.2015.08.1534

CrossRef Full Text | Google Scholar

Zhao, Z., Chen, S., Chen, Y., and Yang, Q. (2021). On the effective stress coefficient of single rough rock fractures. Int. J. Rock Mech. Min. Sci. 137, 104556. doi:10.1016/j.ijrmms.2020.104556

CrossRef Full Text | Google Scholar

Zhou, J., Liu, G., Jiang, Y., Xian, X., Liu, Q., Zhang, D., et al. (2016). Supercritical carbon dioxide fracturing in shale and the coupled effects on the permeability of fractured shale: an experimental study. J. Nat. Gas Sci. Eng. 36, 369–377. doi:10.1016/j.jngse.2016.10.005

CrossRef Full Text | Google Scholar

Zhou, J., Xian, X., Jiang, Y., Li, X., and Jiang, D. (2009). A permeability model considering the effective stress and coal matrix shrinking effect. J. Southwest Petroleum Univ. Sci. Technol. Ed. 31 (01), 4-8+181–182. doi:10.3863/j.issn.1674-5086.2009.01.002

CrossRef Full Text | Google Scholar

Zhu, W. C., Wei, C. H., Liu, J., Qu, H. Y., and Elsworth, D. (2011). A model of coal-gas interaction under variable temperatures. Int. J. Coal Geol. 86, 213–221. doi:10.1016/j.coal.2011.01.011

CrossRef Full Text | Google Scholar