Research on optimization of grouting treatment for underground mining goaf collapse based on 3-dimensional simulation

The collapse of goaf is one of the most serious geological disasters in cities where underground mineral resources are mined. The ground subsidence caused by the goaf limits the social and economic development of the area, while also endangering the safety of residents and property near the mining area. At present, support and grouting treatment methods are commonly used for the treatment of goaf. The cost of support treatment is relatively high, and it is difficult to control the collapse of the deeper goaf. Grouting treatment is suitable for conducting detailed investigations of underground spaces. The cost of complete grouting is high, and the timing of grouting termination is difficult to control. This paper aims to explore the optimization of grouting efficiency in the treatment of underground subsidence in goaf areas using the reserved pillar mining method. Through the stability calculation of the goaf pillars and roof, it can be concluded that the goaf pillars are unstable pillars under current conditions and are prone to damage under load interference. At present, surface subsidence has occurred in the goaf and requires treatment. Consider the comparison between the collapse control effect under different grouting rates and the complete grouting, and ultimately select the condition of 90% grouting rate to achieve the control effect. This conclusion can provide a certain theoretical reference basis for the treatment of similar goaf collapse, and has certain practical significance.

1 Introduction

According to statistics, there are more than 110,000 non coal mines in China. The extraction of many solid minerals results in millions of cubic meters goaf every year. Failure to deal with goaf effectively makes it still have the hidden danger of ground deformation. Large-scale surface collapse may occur at anytime, which seriously endangers the surrounding environment and the safety of people’s property.

The existence of goaf seriously affects the geological environment of the area, mainly in the following. The collapse of the goaf destroys the surface crop land and affects the agricultural ecology. In plain area, water will accumulate due to concentrated deformation of the goaf. And in arid mountainous area, the goaf will destroy the surface water system and aggravate the problem of water shortage. The ground deformation caused by mining will produce landslides, which pose a great threat to the industrial and civil buildings near the hillside.

The research on the ground deformation of goaf can be traced back to 1838, Gonot put forward the hypothesis of “vertical line theory” of mining subsidence by investigating the surface subsidence accident in Liege. Then many scholars have put forward many hypotheses, such as “normal theory”, “second-class line theory”, “natural slope theory”, “circular arch theory”, “zoning theory”, etc. (Gotsev et al., 2003; Stokes et al., 2003; Ting et al., 2012; Wang XY. et. al, 2017; Zegzulka et al., 2023), which jointly open people’s cognition of overburden movement and ground deformation in goaf, and have their geometric theoretical models in different researches. Those researches made the study of goaf stability more systematic and intuitive. The research on the ground deformation of goaf intersected with many adjacent disciplines, infiltrates and complemented each other, gradually evolved into a comprehensive discipline (Xu et al., 2023). According to the long-term research, mining collapse has many characteristics, such as latent, transforming, progressive and sudden. The main influencing factors of surface collapse can be divided into natural geological environment factors and artificial mining activity factors (Wang et al., 2015). The influence radius of surface deformation is related to the depth of coal seam, and the mining method also determines the scale of collapse deformation (Zhang and Yang, 2016). At present, the research of goaf stability focuses on the mechanism and mechanical behavior of roof strata movement and ground deformation (Wang W. et. al, 2017). The research methods can be divided into phenomenological research of goaf deformation and theoretical model research of mechanical mechanism method (Lou et al., 2014). The former is based on the monitoring data of ground deformation in goaf. In the analysis of the data, such as statistical probability integral, section function and other methods are used to summarize the law of surface deformation and failure, and then analyze the change of strata in the mining area (Yavuz, 2004). The other method is based on various mechanical principles and methods. It is applied to goaf analysis. Based on the assumption of continuous medium of rock mass, the mechanical mechanism of rock mass in goaf is studied. Based on the above research, the movement law of overlying strata is analyzed, and the surface deformation model is deduced (Xu et al., 2013). For the complicated geological conditions and influencing factors in actual mining engineering, there is no consistent mechanical model, which is generally applicable to all mining subsidence analysis (Wang et al., 2022). The deformation of underground rock mass determines the characteristics of surface deformation, so the study of rock mass deformation is particularly important in underground mining deformation. The study of rock deformation laws in underground space has become more mature. Yu et al. proposed a numerical model for rock deformation based on microstructure, based on elastic damage mechanics and thermoelastic theory (Yu et al., 2015). Zhu et al. tested the mineral composition of old sandstone in Shanxi Ruineng Coal Mine to elucidate the softening mechanism of rocks after water absorption (Zhu et al., 2021. Yin et al. studied the high-temperature shear mechanical properties and shear dilation deformation characteristics of underground rock masses under different initial normal stresses (Yin et al., 2021).

On the basis of theoretical research on ground deformation of goaf, the methods for stability analysis of goaf can be divided into four types: prediction method, analytical method, semi prediction and semi analysis method and numerical simulation method (Li XB. et. al, 2019; Li PX. et. al, 2019). Each method has its own emphasis and is applicable to the analysis of different problems (Yang et al., 2015). This paper employs the numerical simulation analysis method, which possesses advantages such as high accuracy, speed and efficiency, intuitive visualization, flexibility, and comprehensiveness. These advantages render numerical analysis methods an indispensable and vital tool for the stability evaluation of underground goafs.

To solve the problem of ground deformation in goaf, two methods can be adopted, namely, early design mining method for prevention and late treatment for deformation and damage control (Sergey et al., 2012). The early design mining methods include protective pillar method, strip mining method, pillar mining method, etc. (Guo et al., 2011) This method needs to select an appropriate mining retention ratio in the mining process to achieve the economic benefits of mining while ensuring the stability of the ground. However, it is difficult to ensure the long-term stability of the reserved part, and it is easy to cause multiple collapse accidents due to local damage. The filling methods for goaf treatment can be divided into many types according to the different filling materials, so they have strong adjustability. The filling material can turn waste into treasure. This method has the effect of safety and environmental protection, and is the first choice for goaf treatment. Filling method can be combined with other methods for joint treatment, such as caving filling method and reinforcement filling method, to meet the governance needs of different goaf areas (Xuan and Xu, 2017). By changing the stress distribution of surrounding rock, the filling method can effectively control the deformation of rock stratum and surface, which is applicable to the treatment of goafs under buildings and structures and some goafs that do not allow large deformation (Zhang et al., 2019) Various buildings and traffic facilities can be built above the goaf after filling method treatment (Li et al., 2012).

The existing methods for evaluating the deformation of goaf have their own focuses and shortcomings. For the complex geological conditions and influencing factors in actual mining engineering, there is no consistent mechanical model that is universally applicable to all mining subsidence analysis. In order to reuse the land resources in the goaf and put it into urban construction again, it is necessary to solve the problem of ground deformation and utilization. Under the premise of economic benefit and safety development, and in order to build a project to meet the planning needs, it is full of value to conduct in-depth and systematic research on the ground deformation and control measures of goaf. The existing methods for controlling the collapse of goaf are generally a combination of support and grouting measures. However, this method of controlling goaf collapse has its limitations. Support treatment cannot effectively prevent the collapse and deformation caused by deep mining pits. The problem with grouting lies in its cost, sometimes with a large underground space and high cost of complete filling, and the termination of grouting cannot be effectively controlled. This paper explores the effectiveness of pit collapse control under incomplete grouting conditions and reserved pillar mining methods.

The phosphate mine goaf studied in this paper is located in Lianyungang China. The existence of goaf seriously restricts the optimal use of land and the development of city. The potential geological disasters threaten the safety of life and property of nearby residents. The treatment of the goaf has practical engineering application significance. At the same time, it can be used as a reference for the analysis and treatment of many goafs that have not been treated. It can provide guidance for the follow-up goaf treatment engineering, and has theoretical significance for the deformation and failure mode, stability analysis method and treatment effect evaluation of goaf.

2 Present situation of collapse deformation in phosphate mine

2.1 Surface collapse

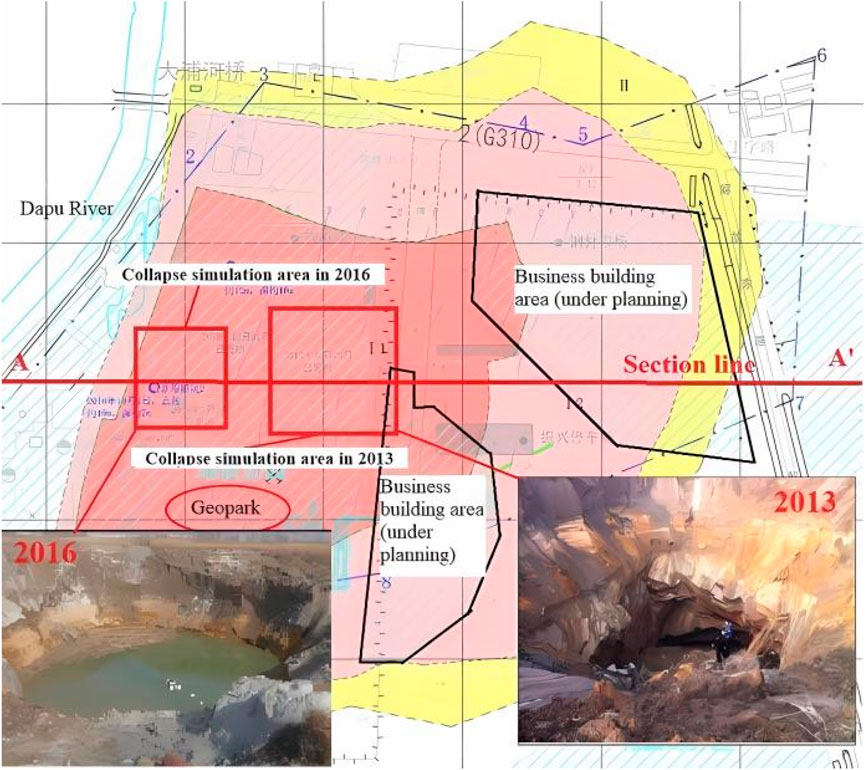
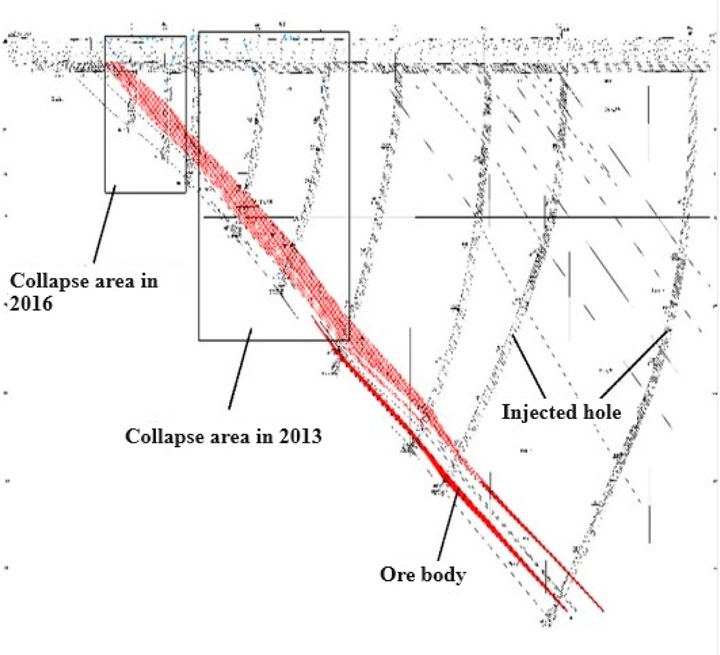
A phosphate mine was designed to be mined in 1966 and closed after a major collapse accident in 2016, with the deepest mining depth of is 440 m underground. On 25 December 2013, affected by underground mining and surrounding construction activities, the overlying strata of the old tunnel collapsed, forming a collapse pit in the upper part of the goaf. The collapse pit is funnel-shaped, with a maximum diameter of about 100 m and a depth of more than 50 m. On 4 March 2016, surface collapse occurred in the middle section, forming an inverted dome collapse pit with a long axis of about 130 m and a short axis of about 100 m, with a collapse area of about 9,400 square meters. On 31 December 2016, a ground collapse occurred about 70 m to the south of the phosphate rock pile in the mining area, and the diameter of the collapse pit was about 100 m. The collapse pits shown in Figure 1. The area circled in red represents the range of impact of collapse deformation. In addition to the formation of collapse pits, cracks have also appeared on the surface and walls of buildings within the scope of collapse impact. Shown as Figure 2. The Quaternary strata in the study area are mainly composed of loose sediments such as terrestrial and marine sand, silty clay, etc., with a thickness of 20.2–34.0 m. According to the exposure of drilling on site, the underlying bedrock strata in the study area are granite mixed with gneiss of Qishan Formation, phosphorus bearing marble of Jinping Formation and dolomitic plagioclase gneiss of Yuntai Formation. Four ore bodies were mined for phosphate ore, with a main strike of 13°, a dip direction of about 103°, and a dip angle of about 39°. Different stages of mining were carried out using collapse method, open pit method, explosive force transportation method, and stage mining room method. The overall mining was stopped in 2016.

Figure 1

Figure 1. Goaf area and collapse pit.

Figure 2

Figure 2. Cracks on the ground and buildings

2.2 Ground deformation

Due to the excavation of underground mine room, the upper ground is deformed, and the range of surface movement is called surface movement basin. Since the mining of the phosphate mine, with the expansion of goaf area, the area and maximum subsidence value of the mobile basin were increasing. At that time, there was only one maximum subsidence point in the center of the basin. The old collapse pit had been backfilled, and no obvious large cracks were found in the site. The fracture strikes in the north of this section are 147–162°and in the south are 50°–75°, which are caused by typical tension.

3 Geological modeling of goaf

3.1 Geologic model

The surface range of the model selected in this paper is shown in Figure 1. The schematic diagram of model section A-A ‘is shown in Figure 3.

Figure 3

Figure 3. Schematic diagram of model section A-A′.

The original data of three-dimensional finite element calculation model of phosphorite goaf was directly imported into Rhino6.0 from ItasCad, and then imported into ABAQUS in the form of. sat file for modeling. The model is shown in Figure 4A. The three-dimensional finite element software ABAQUS is used to simulate the ground settlement of phosphorus mine goaf. In the field of geotechnical engineering, ABAQUS has irreplaceable analytical advantages compared to other numerical software, and it contains a large number of constitutive models of rock and soil materials. In addition to rich material models, there are also various types of units that can be used to solve various structural problems. In engineering applications, some functions of ABAQUS can facilitate the excavation and backfilling process of rock and soil, and can also automatically generate initial stress for coupled simulation of seepage and stress of fluid solids.

Figure 4

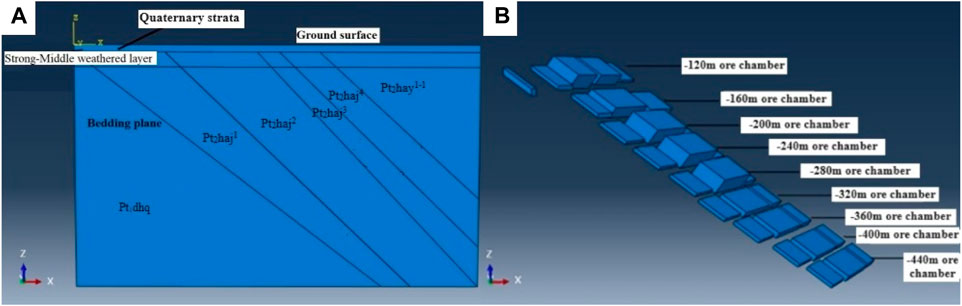
Figure 4. Numerical model [(A) Three-dimensional calculation model; (B) Calculation model of chamber].

From top to bottom, the horizontal strata are Quaternary strata, strongly weathered rock strata and moderately weathered rock strata. From top right to bottom left are the first member of the lower Yuntai formation of Haizhou group (Pt₂hay^1-1), the fourth member of Jinping formation of Haizhou group (Pt₂haj⁴), the third member of Jinping formation of Haizhou group (Pt₂haj³), the second member of Jinping formation of Haizhou group (Pt₂haj²), the first member of Jinping formation of Haizhou group (Pt₂haj¹) and Qushan formation of Donghai group (Pt₁dhq).

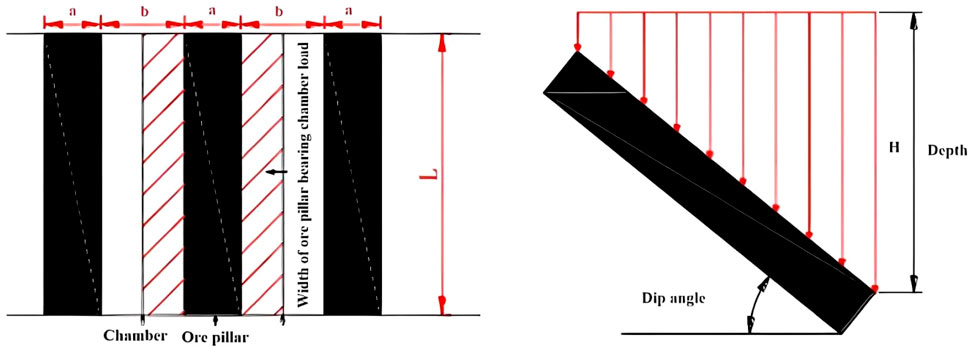
The underground mining chambers are irregular hexahedrons in the actual situation, and the regular hexahedrons of the same scale are used in the model establishment to simplify the calculation. The overall distribution of the chambers is from −120 m to −440 m in depth. The chambers are thin on both sides, and are thick in the middle. The overall size of the model is 1000m × 1000m × 600m, that is, the surface area is one square kilometer, and the calculated depth is 600 m. The chambers formed by mining are generally distributed between the two strata, and the inclination angle of the chambers is roughly consistent with that of the strata. After mining, the rock between the two chambers is the pillar, and the pillar bears the rock pressure after the stress release, shown as Figure 4B.

3.2 Material parameters and boundary conditions

The physical and mechanical parameters of rock mass were obtained by rock mass mechanical tests on samples of different rock strata and ore bodies. Uniaxial compression test, shear test and tensile test were adopted. The parameters are shown in Table 1.

Table 1

Table 1. Numerical simulation of rock and soil strength parameters in goaf.

In the three-dimensional finite element model, according to the actual engineering situation, different boundary conditions are set up to realize the settlement of goaf. The displacement and rotation angle of the bottom of the model are fixed in X, Y and Z directions. On the left and right sides of the model, that is, the East and west sides of the actual stratum, X direction displacement and rotation angle are fixed. Y direction displacement and rotation angle are fixed on the front and back sides of the model, that is, the north and south sides of the actual stratum.

The top surface of the model is a free surface boundary condition, and there is no fixed displacement and rotation angle in three directions. In this calculation, the main displacement is the vertical displacement in Z direction, that is, the main land subsidence and the vertical displacement of the ground.

4 Analysis of pillar stability

In the mining of the phosphate mine, the pillar was reserved to bear the load of the upper strata. When the load strength of the pillar exceeds the bearing capacity, it may be damaged, making the upper roof partially suspended. It will be easy to produce chain reaction when the roof pressure is transferred to other pillars, which leads to the failure of the pillars in turn.

Therefore, it is necessary to calculate the bearing capacity of the pillars and the relationship between the load and the stability of the pillars. The evaluation of pillar stability is based on the stability coefficient. The calculation formula of mining stability coefficient is as follows Eq. 1.

$K_Z=P_U/P_Z(1)$

where: K_Z: Stability coefficient; P_U: Ultimate load of rock pillars, kN; P_Z: Actual load on rock column, kN.

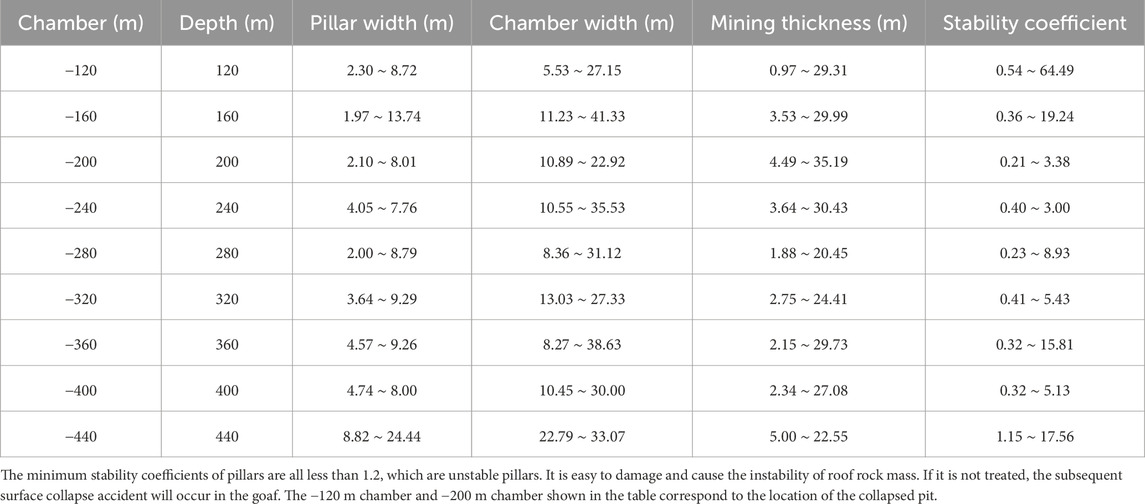
According to the regulations of the safety stability coefficient of mining pillars, when the value reaches between 1.2 and 2.0, it can be said that the mining pillars in the site are basically stable. When the value is greater than 2.0, the pillars of the site reach stability. If the value is less than 1.2, the pillars of the site are considered unstable.

The pillar setting in the goaf of the phosphate mine is special, and the loading condition of the pillar is shown in Figure 5.

Figure 5

Figure 5. Pillar loading mode.

According to the load bearing mode, the load formula of pillar section is as follows Eq. 2.

$P_Z={\gamma }_{0}H\cos \alpha \left(a+b\right)L(2)$

where: ${\gamma }_0$: Average weight of overlying strata, kN/m³; H: Buried depth of rock pillar, m; a: Width of retaining rock column, m; b: Width of mining chamber, m; L: Length of retaining rock column, m.

Because the pillar height in the middle section of each layer is the highest, the mining thickness is the largest, and it is most likely to be damaged, so only the pillar stability coefficient in the middle section of each layer needs to be calculated. The specific calculation results are shown in Table 2.

Table 2

Table 2. Pillar safety factors.

5 Historical deduction and prediction analysis of goaf subsidence

5.1 Establishment of three-dimensional finite element model

At present, the goaf is in the state of no backfilling. In this simulation, taking this as the initial state, the numerical simulation of excavation without backfill is carried out firstly. The initial geostress in the research area is mainly based on the self-weight stress position, and geostress is applied through self-weight.

The numerical analysis is divided into two steps. The first step is to calculate the self-weight stability of the stratum in the original state, and record the stress as the initial stress field. The second step is to excavate the mine chamber under this stress condition, and analyze the stratum settlement after excavation. When calculating the historical ground settlement of the goaf, the calculation steps are set to stop the calculation when the maximum settlement and deformation range of the ground settlement reach the current actual situation. And then the continuous deformation of the goaf ground under the current conditions is simulated. Grouting filling type and parameters are shown in Table 3.

Table 3

Table 3. Grouting filling type and parameters.

5.2 Simulation of historical deformation

When establishing the model, solid units are selected to simulate the underground rock mass, and the parameters of each layer of rock and soil mainly come from the material strength parameters obtained from on-site measurements and indoor experiments. The underground rock mass is set as an elastic-plastic model and simulated using the Mohr Coulomb yield model built-in in the software.

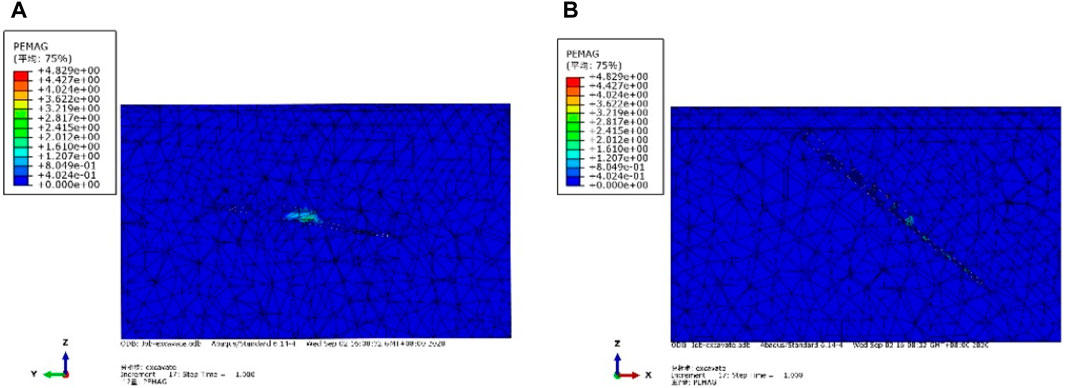
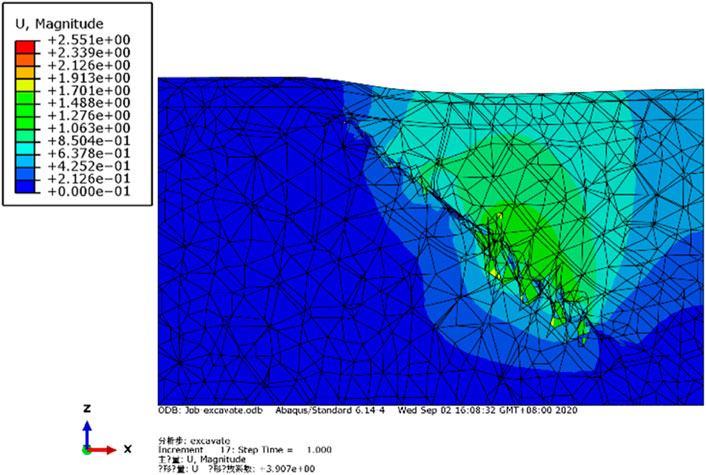
Submit the calculation task under the above calculation conditions, and output results are analyzed by finite element method. The distribution of current plastic zone in goaf is shown in Figure 6. The plastic zone is mainly distributed in the pillars between the excavation parts of the mine house and the rock mass between the adjacent mine houses at different depths. The overall scale of the plastic zone is small and it does not reach the connection. The mine house will not collapse, and only a small part of the blocks will be deformed and fall off.

Figure 6

Figure 6. Current plastic zone in Goaf [(A) Front view; (B) Side view].

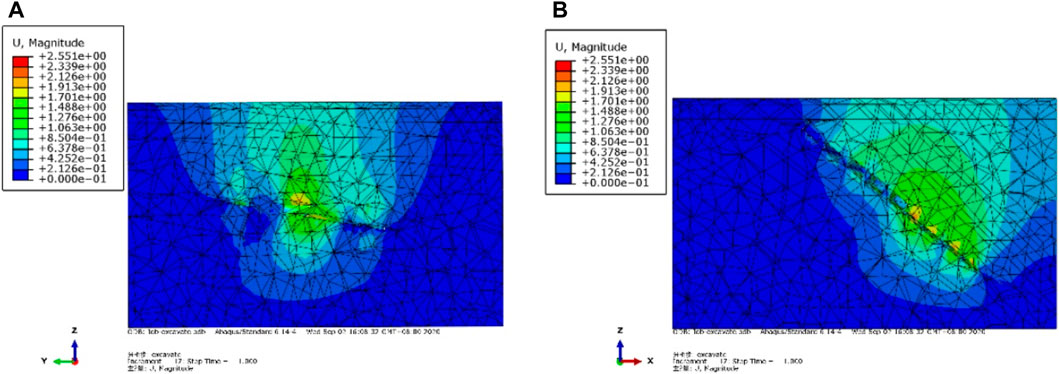
According to the displacement nephogram, the displacement values on the surface are distributed in concentric circles. The maximum displacement at the surface is 0.638 m, which is above the mine house from - 120 m to - 400 m depth. According to the east-west and North-South cross-sections, the maximum displacement change occurs at the room with a depth of 280 m, that is, the deformation or shedding of some blocks occurs at the top corner of the room after excavation. The deformation of the room at 280 m is the most obvious under the action of in situ stress.

The vertical displacement nephogram of the surface and both sides shows that the vertical displacement of the surface is nearly elliptical. A large scale of land subsidence occurred in this area. It is basically consistent with the actual range of building cracks. On the z-direction displacement nephogram of the cross sections on both sides, the top of the mine room moves downward due to the self-weight stress of the overlying rock mass, and the bottom of the mine room heaves upward due to the release of excavation stress. The calculated range of land subsidence is small, but the settlement is relatively large, which has a significant impact on the upper buildings. Figure 7 shows the total deformation diagram of the calculation model under the condition of goaf, that is, the changes of various parts in the actual stratum. The results show that the strata change is consistent with the settlement data of the actual project.

Figure 7

Figure 7. Total displacement at current surface of goaf.

5.3 Analysis of collapse control measures

According to the collapse history calculation and current situation analysis results, if the collapse pit is not treated, the collapse disaster in the region will further occur. The requirement of treatment is to eliminate the hidden danger of geological disaster caused by ground collapse. Ensure the safety of roads around the site and completely eliminate the hazard of ground subsidence in the goaf. The site after goaf treatment can meet the requirements of Geological Park, office building and other engineering construction planned in the later stage.

The method of grouting and filling is used to control the mining subsidence in the goaf of phosphate mine. The treatment method is to use the filling material as the geological filling material for phosphate rock mining and fill the mined room. This method can maintain the self-strength of the surrounding rock and the support capacity of the remaining pillars, and prevent the instability or local collapse of the overburden or roadway in the stope.

Grouting body interacts with ore pillar and surrounding rock to form support system to limit displacement of surrounding rock. This changes the stress state of overburden and support system in the stope, reduces the stress difference in surrounding rocks, and relatively improves the strength and bearing capacity of surrounding rocks after mining, thus restricting the movement and alleviating the deformation. At the same time, the stress concentration caused by overburden movement is transferred to the depth of the floor through the filling support system. Therefore, grouting filling can effectively prevent the overall destabilization of overburden rock and significantly reduce the settlement of goaf ground.

Treatment measures to achieve green environmental protection, economic and practical purpose of grouting filling in Phosphate Mine Goaf. According to the principle of material selection for waste utilization and local sampling, the filling materials are mainly tailings sand, fly ash, cement and additives.

In the actual construction process, it is very difficult and expensive to achieve full filling and grouting due to the excessive depths of phosphate rock mining, irregular arrangement of ore rooms and the influence of underground pressure and aquifer. In the treatment of room-pillar method, the strength of pillar plays a decisive role in the stability of goaf, so the treatment of goaf can be realized when grouting body accounts for a certain proportion of the room volume. The calculation formula of grouting filling quantity in goaf is as follows Eq. 3.

$Q_g=\frac{\tau ·s·M·N·n·\eta }{c·\mathit{cos}\alpha }(3)$

where: Q_g is total filling volume of grouting for goaf treatment, m³; τ is grout coefficient of losses; s is area of goaf treatment, m²; M is average mining thickness of ore bed, m; N is Recovery rate of ore bed, %; η is filling coefficient of grouting fluid; c is stone rate of grouting fluid, %; α is dip angle of strata, °.

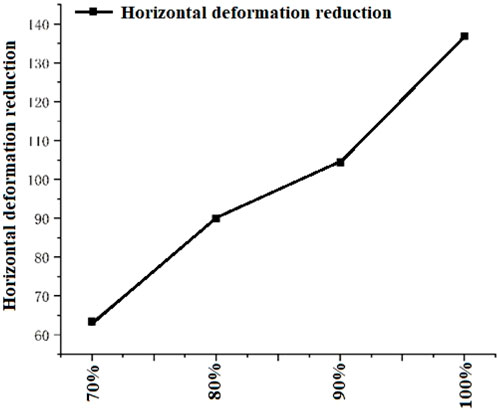
The volume of the mine room to be treated in the phosphate mine goaf is about 800,000 m³. Change the grouting fluid filling system while other parameters remain unchanged. The filling coefficient of grouting fluid is set as 70%, 80%, 90% and 100% respectively in the numerical analysis. Through numerical simulation, the ground deformation and stress distribution of goaf under different grouting filling rates are simulated, and the treatment effects under different grouting filling rates are comprehensively compared and analyzed.

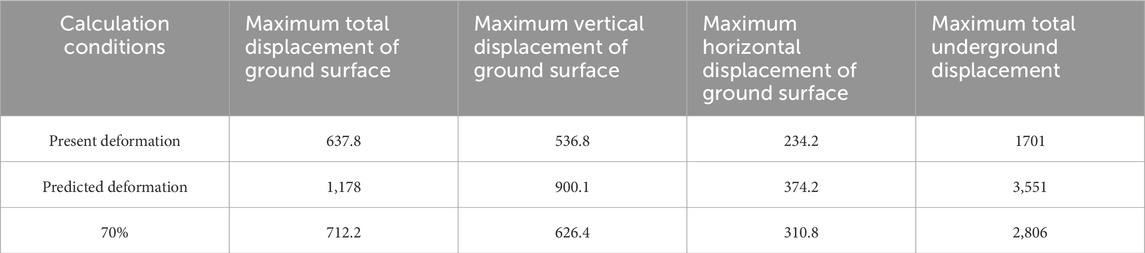
The simulation results of displacement under different conditions are shown in Table 4 and Figures 8–12. The treatment effect of different grouting schemes in vertical and horizontal directions will gradually increase with the increase of grouting amount. The vertical settlement reduction and horizontal displacement reduction are the most significant under the condition of complete grouting and filling. The settlement reduction effect under 90% grouting filling rate is close to that of full grouting filling. Overall, the complete grouting and filling treatment not only meets the design requirements, but also has the best effect. This scheme should be preferred without considering the construction difficulty. Based on actual economic benefits, it can be considered to reduce the amount of grouting appropriately to save costs. From the perspective of controlling surface settlement deformation and collapse damage, 90% of the grouting results are close to the complete grouting results, which can effectively control the vertical deformation of the ground.

Table 4

Table 4. Deformation calculation results (mm).

Figure 8

Figure 8. Total displacement of current section of goaf. (A) Front view; (B) Side view.

Figure 9

Figure 9. Current total deformation diagram of goaf.

Figure 10

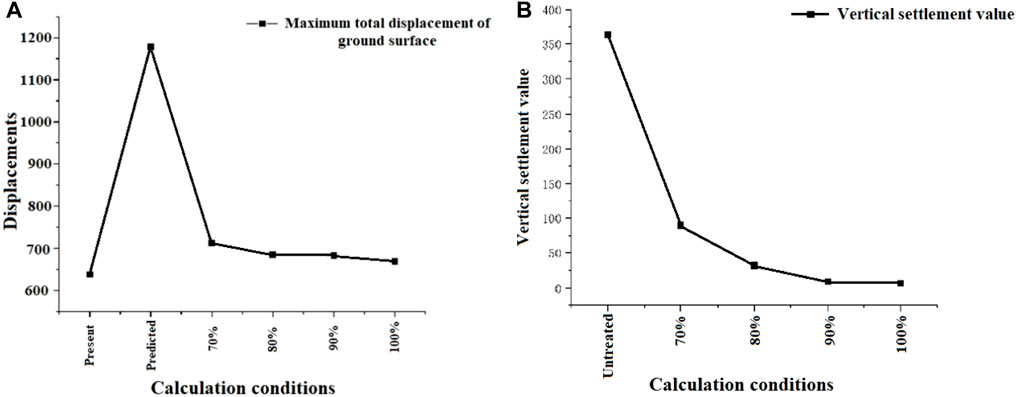
Figure 10. (A) Maximum total displacement of ground surface; (B) Added value of vertical settlement (mm).

Figure 11

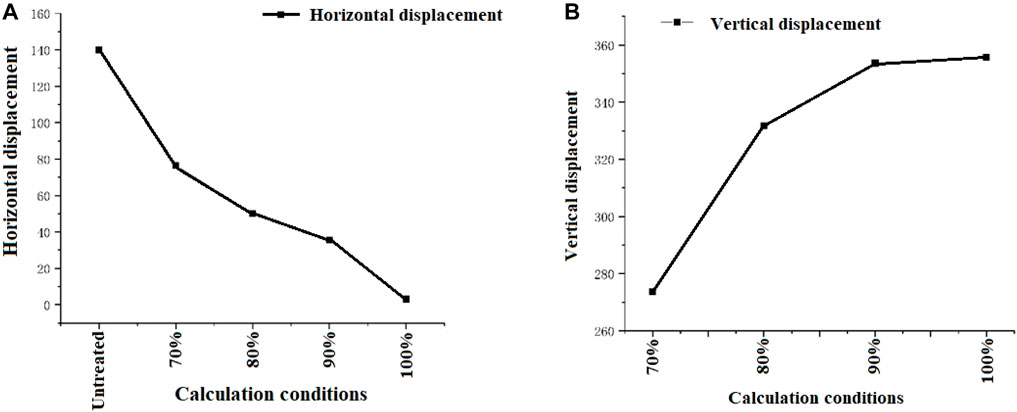
Figure 11. (A) Increase value of horizontal deformation (mm); (B) Control effect of vertical deformation (mm).

Figure 12

Figure 12. Horizontal deformation control effect (mm).

6 Conclusion

This paper analyzes the treatment effect a phosphate mine under different grouting filling rates, and compares the settlement results of goaf deformation under different calculation conditions. Following conclusions were achieved.

(1) Analyzing the method of mining reserved pillars, it was found that without treatment and filling, the mine cave would collapse, which is basically consistent with the actual collapse area. After grouting treatment, the bearing capacity of the mine pillar has been improved, the load capacity has been reduced, and the strength is sufficient to bear the overlying rock load without further damage. The goaf after treatment will undergo continuous deformation mainly due to settlement.

(2) Compared to the absence of grouting and filling treatment, each treatment plan has a relatively significant effect on reducing settlement in the goaf, and the effect of reducing deformation increases with the increase of grouting volume. When complete grouting and filling is achieved, the vertical and horizontal deformation of the goaf ground decreases the most. When designing grouting for collapsed mines, starting from the current stage, the ground deformation of the goaf decreases with the increase of grouting filling rate.

(3) The goaf is planned to be treated with grouting, with grouting volume ranging from 70% to 100%. According to simulation results, the total maximum ground displacement, maximum vertical ground deformation, maximum horizontal ground deformation, and maximum underground displacement all decrease with the increase of grouting volume. When the grouting filling amount reaches 100%, the total ground displacement is only 30 mm, and the vertical deformation is only 7.5 mm, which meets the design requirements. There is no settlement space inside the mining room, and the effect of subsequent building loads on the treatment area is not significant.

(4) Compared with the ground deformation in the goaf without grouting treatment, the ground settlement under the conditions of 90% grouting amount and complete grouting both meet the design requirements of the upper building load. The vertical reduction effect of the ground under 90% grouting amount is similar to that of complete grouting. Considering the construction difficulty and funding of governance measures, a grouting rate of 90% can also meet the design requirements of subsequent buildings. For the mining method of reserved pillars, if the mining plan is not reasonable, the goaf may collapse. The design of incomplete grouting can save construction costs and reduce construction difficulty, but it is necessary to explore and study the grouting filling rate. This conclusion can provide certain guidance for the treatment of goaf collapse.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author contributions

LT: Writing–original draft. XX: Writing–review and editing. CS: Writing–review and editing. ZL: Writing–review and editing. XL: Writing–original draft, Writing–review and editing. MD: Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study is supported by the Research Fund of National Natural Science Foundation of Shandong Province of China (NSFC) (Grant No. ZR2022ME188), Jinan City “new university 20” research leader studio project (Grant No. 20228108), and the project of Slope safety control and disaster prevention technology innovation team of “Youth Innovation Talent Introduction and Education Plan” of Shandong Colleges and universities [Grant No. Lu Jiao Ke Han (2021) No. 51].

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Gotsev, D. V., Kovalev, A. V., and Sporykhin, A. N. (2003). Stable equilibrium of the multilayer lining of a vertical mine opening in elastoplastic rock mass. Int. Appl. Mech. 39, 286–291. doi:10.1023/A:1024462218891

CrossRef Full Text | Google Scholar

Guo, W. B., Hou, Q. L., and Zou, Y. F. (2011). Relationship between surface subsidence factor and mining depth of strip pillar mining. Trans. Nonferrous Metals Soc. China 21, s594–s598. doi:10.1016/S1003-6326(12)61646-X

CrossRef Full Text | Google Scholar

Li, L., Hao, G., Wu, K., and Li, R. (2012). New viewpoint of foundation stability of newly building upon goaf. Energy Procedia 17, 1717–1723. doi:10.1016/j.egypro.2012.02.303

CrossRef Full Text | Google Scholar

Li, P. X., Yan, L. L., and Yao, D. H. (2019b). Study of tunnel damage caused by underground mining deformation: calculation, analysis, and reinforcement. Adv. Civ. Eng. 2019, 1–18. doi:10.1155/2019/4865161

CrossRef Full Text | Google Scholar

Li, X. B., Wang, D. Y., Li, C. J., and Liu, Z. X. (2019a). Numerical simulation of surface subsidence and backfill material movement induced by underground mining. Adv. Civ. Eng. 2019, 1–17. doi:10.1155/2019/2724370

CrossRef Full Text | Google Scholar

Lou, S. H., Yang, B., and Luo, Z. Q. (2014). Three-dimensional information acquisition and visualization application in goaf. Procedia Eng. 84, 860–867. doi:10.1016/j.proeng.2014.10.507

CrossRef Full Text | Google Scholar

Sergey, S., Nicolas, O., and Benoît, S. (2012). Ground deformation associated with post-mining activity at the French-German border revealed by novel InSAR time series method. Int. J. Appl. Earth Observations Geoinformation 23, 142–154. doi:10.1016/j.jag.2012.12.008

CrossRef Full Text | Google Scholar

Stokes, T. E., Hocking, G. C., and Forbes, L. K. (2003). Unsteady free-surface flow induced by a line sink. J. Eng. Math. 47, 137–160. doi:10.1023/A:1025892915279

CrossRef Full Text | Google Scholar

Ting, C. H., Sivakugan, N., Read, W., and Shukla, S. K. (2012). Analytical method to determine vertical stresses within a granular material contained in right vertical prisms. Int. J. geomechanics 12 (1), 74–79. doi:10.1061/(ASCE)GM.1943-5622.0000110

CrossRef Full Text | Google Scholar

Wang, F. T., Zhang, C., Zhang, X. G., and Song, Q. (2015). Overlying strata movement rules and safety mining technology for the shallow depth seam proximity beneath a room mining goaf. Int. J. Min. Sci. Technol. 25 (1), 139–143. doi:10.1016/j.ijmst.2014.12.007

CrossRef Full Text | Google Scholar

Wang, T. L., Chen, C. X., Xia, K. Z., Zhang, C. Q., Wang, Y., and Liu, X. T. (2022). Ground surface deformation in the hanging wall of the jinshandian underground iron mine in China. Front. Earth Sci. 10, 1–16. doi:10.3389/feart.2022.909466

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W., Jiang, T., and Wang, Z. (2017b). A analytical model for cover stress re-establishment in the goaf after longwall caving mining. J. South. Afr. Inst. Min. Metallurgy 117 (7), 670–683. doi:10.17159/2411-9717/2017/v117n7a9

CrossRef Full Text | Google Scholar

Wang, X. Y., Wang, T. T., Wang, Q., Liu, X. M., Li, R. Z., and Liu, B. J. (2017a). Evaluation of floor water inrush based on fractal theory and an improved analytic hierarchy process. Mine Water Environ. 36, 87–95. doi:10.1007/s10230-016-0407-3

CrossRef Full Text | Google Scholar

Xu, N. X., Kulatilake, PHSW, Tian, H., Wu, X., Nan, Y. H., and Wei, T. (2013). Surface subsidence prediction for the WUTONG mine using a 3-D finite difference method. Comput. Geotechnics 48, 134–145. doi:10.1016/j.compgeo.2012.09.014

CrossRef Full Text | Google Scholar

Xu, Z. C., Xu, W., Zhu, Z. H., and Zhao, J. Y. (2023). Research on monitoring and stability evaluation of ground subsidence in gypsum mine goaf. Front. Environ. Sci. 04, 1–20. doi:10.3389/fenvs.2022.1097874

CrossRef Full Text | Google Scholar

Xuan, D. Y., and Xu, J. L. (2017). Longwall surface subsidence control by technology of isolated overburden grout injection. Int. J. Min. Sci. Technol. 27, 813–818. doi:10.1016/j.ijmst.2017.07.014

CrossRef Full Text | Google Scholar

Yang, Z. Q., Zhai, S. H., Gao, Q., and Li, M. H. (2015). Stability analysis of large-scale stope using stage subsequent filling mining method in Sijiaying iron mine. J. Rock Mech. Geotechnical Eng. 7 (1), 87–94. doi:10.1016/j.jrmge.2014.11.003

CrossRef Full Text | Google Scholar

Yavuz, H. (2004). An estimation method for cover pressure re-establishment distance and pressure distribution in the goaf of longwall coal mines. Int. J. Rock Mech. Min. Sci. 41 (2), 193–205. doi:10.1016/S1365-1609(03)00082-0

CrossRef Full Text | Google Scholar

Yin, Q., Wu, J. Y., Zhu, C., He, M. C., Meng, Q. X., and Jing, H. W. (2021). Shear mechanical responses of sandstone exposed to high temperature under constant normal stiffness boundary conditions. Geomech. Geophys. Geo-Energy Geo-Resources 7 (2), 35. doi:10.1007/s40948-021-00234-9

CrossRef Full Text | Google Scholar

Yu, Q. L., Ranjith, P. G., Liu, H. Y., Yang, T. H., Tang, S. B., Tang, C. A., et al. (2015). A mesostructure-based damage model for thermal cracking analysis and application in granite at elevated temperatures. ROCK Mech. ROCK Eng. 48 (6), 2263–2282. doi:10.1007/s00603-014-0679-5

CrossRef Full Text | Google Scholar

Zegzulka, J., Marsik, F., Necas, J., Hlosta, J., Zurovec, D., and Ivan, I. (2023). Thermodynamic theory of the most energy-efficient natural repose angle. Continuum Mech. Thermodyn. 35, 393–412. doi:10.1007/s00161-023-01184-1

CrossRef Full Text | Google Scholar

Zhang, J. X., Sun, Q., Fourie, A., Ju, F., and Dong, X. J. (2019). Risk assessment and prevention of surface subsidence in deep multiple coal seam mining under dense above-ground buildings: case study. Hum. Ecol. Risk Assess. Int. J. 25 (6), 1579–1593. doi:10.1080/10807039.2018.1471579

CrossRef Full Text | Google Scholar

Zhang, X., and Yang, M. (2016). Influence of dip angle of coal bed to the voidage distribution at goaf area. J. Resi. Sci. Tech. 13 (7).

Google Scholar

Zhu, C., He, M. C., Jiang, B., Qin, X. Z., Yin, Q., and Zhou, Y. (2021). Numerical investigation on the fatigue failure characteristics of water-bearing sandstone under cyclic loading. J. Mt. Sci. 18 (12), 3348–3365. doi:10.1007/s11629-021-6914-0

CrossRef Full Text | Google Scholar