Seismic attenuation and stress on the San Andreas Fault at Parkfield: are we critical yet?

The Parkfield transitional segment of the San Andreas Fault (SAF) is characterized by the production of frequent quasi-periodical M6 events that break the very same asperity. The last Parkfield mainshock occurred on 28 September 2004, 38 years after the 1966 earthquake, and after the segment showed a ∼22 years average recurrence time. The main reason for the much longer interevent period between the last two earthquakes is thought to be the reduction of the Coulomb stress from the M6.5 Coalinga earthquake of 2 May 1983, and the M6 Nuñez events of June 11th and 22 July 1983. Plausibly, the transitional segment of the SAF at Parkfield is now in the late part of its seismic cycle and current observations may all be relative to a state of stress close to criticality. However, the behavior of the attenuation parameter in the last few years seems substantially different from the one that characterized the years prior to the 2004 mainshock. A few questions arise: (i) Does a detectable preparation phase for the Parkfield mainshocks exist, and is it the same for all events? (ii) How dynamically/kinematically similar are the quasi-periodic occurrences of the Parkfield mainshocks? (iii) Are some dynamic/kinematic characteristics of the next mainshock predictable from the analysis of current data? (e.g., do we expect the epicenter of the next failure to be co-located to that of 2004?) (iv) Should we expect the duration of the current interseismic period to be close to the 22-year “undisturbed” average value? We respond to the questions listed above by analyzing the non-geometric attenuation of direct S-waves along the transitional segment of the SAF at Parkfield, in the close vicinity of the fault plane, between January 2001 and November 2023. Of particular interest is the preparatory behavior of the attenuation parameter as the 2004 mainshock approached, on both sides of the SAF. We also show that the non-volcanic tremor activity modulates the seismic attenuation in the area, and possibly the seismicity along the Parkfield fault segment, including the occurrence of the mainshocks.

1 Introduction

An important seismological question is whether detectable preparatory phases exist and can be observed before major earthquakes. In case of a positive response, the next question would be whether the same preparatory phase is common to all mainshocks, and many recent studies went deep into these issues. For example, Bletery and Nocquet (2023) analyzed the very final moments of the seismic cycle on a set of 90 earthquakes (M7); they found that a ∼2-hour-long exponential acceleration characterizes the slip before the ruptures, suggesting that large earthquakes start with a precursory phase of slip. Other recent laboratory observations focused on the nucleation process: for example, Bolton et al. (2023) pointed to key differences in the nucleation process of slow and fast labquakes, showing that the evolution in space and time of the foreshock activity is linked to fault slip velocity, similar to the increase and coalescence of foreshocks/seismic activity that occur prior to large crustal earthquakes (Dodge et al., 1996; Bouchon et al., 2011; Kato et al., 2016; 2012; Chen and Shearer, 2013; Brodsky and Lay, 2014; Sugan et al., 2014; Ellsworth and Bulut, 2018; Yoon et al., 2019; Ben-Zion and Zaliapin, 2020; Cattania and Segall, 2021).

Another important study on laboratory earthquakes is the one by Vasseur et al. (2017), who documented systematic evidence for a detectable preparatory phase to failure in rock samples during laboratory experiments, showing that an accurate prediction of the time of occurrence of the catastrophic failure of the sample was possible in most cases, and that its accuracy depended on the typical inter-flaw distance of the material that was being probed. They showed that there are materials with few defects (e.g., glass) for which the time of occurrence of the catastrophic failure is inherently unpredictable. This is because in a sample with a dense distribution of defects, cracks can connect adjacent defects when the material is under stress, and the process of catastrophic failure is at the end of a somewhat smooth coalescence of a myriad of individual cracks. A very homogeneous material, on the contrary, is characterized by a small number of defects, and for a crack to connect two distant flaws the sample needs to undergo a large stress that may easily surpass its very strength.

But how can we go from the centimetric laboratory scale to the tens or the hundreds of kilometers of a large crustal mainshock? Assuming that such a scaling operation is feasible, during the latter portion of the seismic cycle we expect that crustal rocks are subjected to a dramatic process of coalescence of suitably oriented cracks within the volume that immediately surrounds the fault plane. As a consequence, we expect substantial changes in crack density, with spatial and temporal fluctuations of the population of cracks of different dimensions, which would significantly impact the permeability of rocks, the anelastic attenuation of seismic waves, and possibly any deep non-volcanic tremors in an area (NVT), when they exist (Nadeau and Dolenc, 2005; Nadeau and Guilhem, 2009).

Although we think that detecting the exponential slip acceleration observed by Bletery and Nocquet (2023) would be very useful in practice, monitoring the evolution of other physical parameters during the entire earthquake cycle, in absence of slip, could provide a deeper understanding of the evolution of the stress on the fault, and, more generally, on the physics of earthquakes and faulting. One of such parameters of interest is the non-geometric attenuation: $Q_S^{-1}\left(t,f\right)$.

If we want to use anelastic attenuation to monitor stress changes and crack coalescence within crustal rocks, we need to understand the role of crustal fluids in seismic attenuation. In fact, pore fluids in crustal rocks define the anelastic attenuation of seismic waves (O’Connell and Budiansky, 1977), and more importantly they may dominate the evolution of the strength of a fault during the latest portion of its seismic cycle through diffusion (Sibson, 2009; Lucente et al., 2010; Scholtz, 2019; Malagnini et al., 2022). The variability of anelastic attenuation over time is dominated by the fluctuations of rock’s bulk permeability (Malagnini and Parsons, 2020), and can be used to study interesting aspects of single- and multi-mainshock seismic sequences (Malagnini et al., 2022; Lucente et al., 2010; D’Amico et al., 2010).

Previous work by Malagnini et al. (2019) and Malagnini and Parsons (2020) demonstrated that fluctuations of non-geometric crustal attenuation (not including site-related effects) are intimately related to crustal rocks’ bulk permeability, and thus to the state of stress they undergo. The cited authors explored the following causal relationships: (i) between perturbations of stress (tectonic, seasonal, tidal) and perturbations of $Q_S^{-1}$, that is: $\delta \left(Q_S^{-1}\left(t,f\right)\right)$, and (ii) between shaking-induced changes in rock bulk permeability and perturbations $\delta \left(Q_S^{-1}\left(t,f\right)\right)$. Such damage and healing processe were noted by Kelly et al. (2013), and processes of removal/redeposition of colloidal deposits in rock pores and cracks may also be influential (Roeloffs, 1998; Liu and Manga, 2009).

About relationships of the kind (i) listed above, the modeling effort undertaken by Johnson et al. (2017) about hydrospheric, thermal, and tidal loading cycles on the faults of California allowed Malagnini and co-workers to interpret the specific spectral peaks of the attenuation time histories, and, more importantly, to indirectly estimate the extreme sensitivity of seismic attenuation to stress changes. About relationships of the second kind (ii), their interpretation was based on the studies by Brodsky, Manga, and co-workers (e.g., Brodsky et al., 2003; Manga and Brodsky, 2006; Liu and Manga, 2009; Manga et al., 2012), and were also backed by results of numerical experiments (Barbosa et al., 2019).

Our hypothesis is that the changes in rock bulk permeability that take place during the pre-critical stage of the seismic cycle (dilatancy) must have detectable signatures on the anelastic contribution to the total seismic attenuation. It is conceivable that the increased permeability along the very fault plane under subcritical conditions (Townend and Zoback, 2000) allows pore pressure to diminish immediately below the fault, at the upper limit of NVT depths (in Central California, tremor activity characterizes a planar patch at depths between 10 and 40 km, see Guilhem and Nadeau, 2012). Pore pressure diminution at NVT depths would correspond to a decrease in NVT, and to an upward pore fluid migration that would take place along the fault plane. In turn, the latter could weaken the fault segment studied here, and facilitate the occurrence of a mainshock. In what follows we will try to substantiate this hypothesis by looking for correlations between $Q_S^{-1}$ and NVT activity.

When the fault belongs to a system like the one responsible for the 2016 sequence of Amatrice-Visso-Norcia (Central Italy), a major issue about recognizing the signature of criticality on seismic attenuation is represented by its geometric complexity. In fact, multiple individual structures of such a system could go critical one after the other, and fail in a cascade of multiple mainshocks, each one with its own preparatory phase, shaking-induced damage, and healing phase, with all these phenomena partially overlapping in time.

2 Materials and methods

2.1 Technique

The technique used in this study is made of two distinct parts. First, there is the calculation of the average attenuation parameter as a function of frequency $\left({<Q}_S^{-1}\left(f\right)>\right)$ and the maximization of the signal-to-noise ratio by using the peak values of narrowband-filtered time histories instead of the corresponding Fourier amplitudes. Both parts are described in detail in Supplementary Appendix SA, as well as the computation of the variability of the attenuation parameter as a function of time $\left(\delta \left(Q_S^{-1}\left(t,f\right)\right)\right)$.

2.2 The Parkfield transitional segment of the San Andreas Fault: characteristics and data set

To avoid the complications of a fault system like that of the Central Apennines, we chose the transitional segment of the San Andreas Fault (SAF) at Parkfield because of its very simple geometry and behavior. In facts, the Parkfield fault segment is a vertical, relatively isolated stretch of a strike-slip fault that produces frequent quasi-periodical M6 events that break the very same asperity and contains deeper NVT just beneath the seismogenic zone.

The Parkfield transitional segment of the SAF connects the creeping section of the SAF, to the NW, to its locked section to the SE (see map in Figure 1A). The latter was responsible for the 7.9 1857 Fort Tejon earthquake (Sieh, 1978a; b; Agnew and Sieh, 1978). Due to a pseudo-regularity of its seismic cycle, the transitional segment of the SAF underwent several mainshocks with an average recurrence time of ∼22 years, including the 1966 earthquake. This stretch of the SAF has been thoroughly studied and instrumented, starting in the mid 1980s, with the goal of gathering data from short distances from the nucleation region of the next M6 earthquake. Bakun and McEvilly (1984) proposed that such M6 characteristic earthquakes would repeat every 22 years, nucleate at a common hypocenter, and always rupture the same fault area, releasing the same amount of energy. Map in Figure 1A shows the 2004 earthquake.

Figure 1

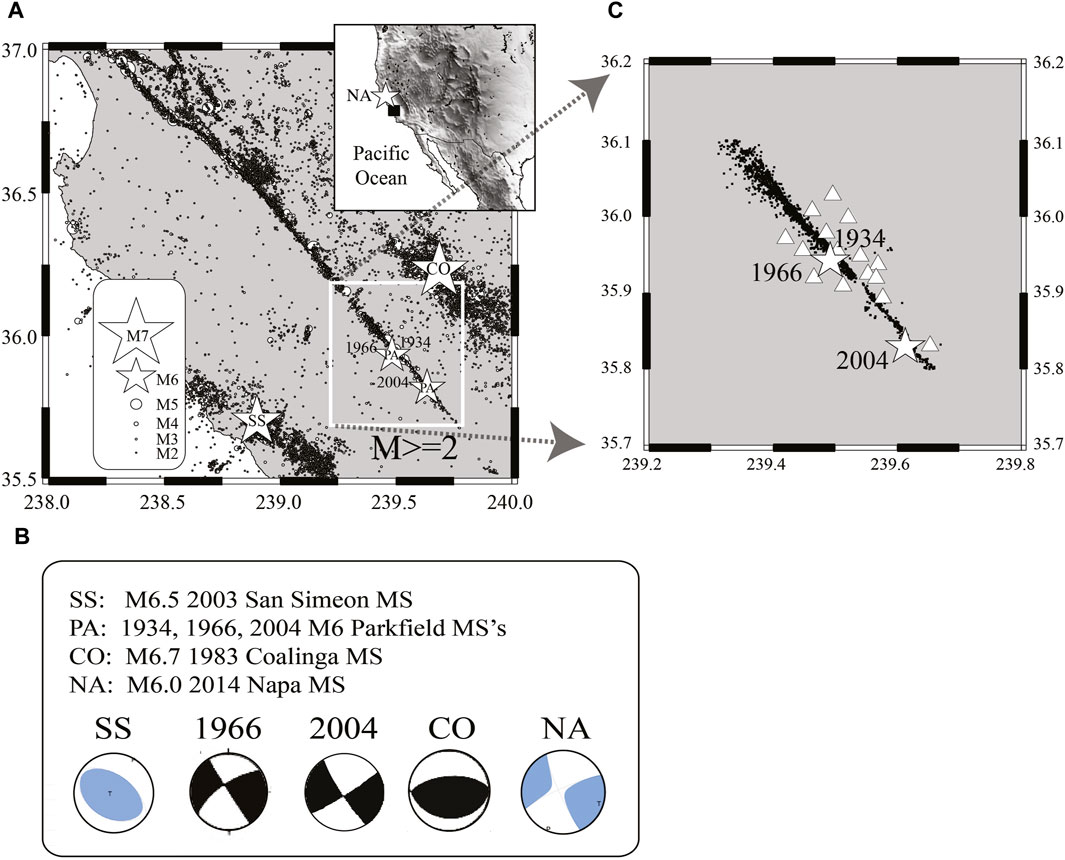
Figure 1. (A) map of the region, showing the background seismicity and four mainshocks of specific interest in this study (white stars), whose focal mechanisms are indicated in (B). The four mainshocks are the following: i) the 2003 M6.5 San Simeon earthquake, ii) the 1966 M6 Parkfield mainshock, iii) the 2004 M6 Parkfield mainshock, and iv) the 1983 M6.8 Coalinga event. Focal mechanisms in B are provided by the United State Geological Survey (USGS). (C) i) black dots: epicentral locations of the SAF earthquakes used in this study; ii) white triangles: seismic stations of the HRSN. The frame of C is outlined in white in the regional map (A), and the white stars of the 1966 (upper) and 2004 (lower) mainshocks.

The importance of the quasi-periodical Parkfield earthquakes was widely acknowledged, and the area was heavily instrumented with a state-of-the-art seismic network. The High-Resolution Seismic Network (HRSN, see https://ncedc.org/hrsn/, and map in Figure 1C) was installed to closely monitor the Parkfield asperity, Spudich and Oppenheimer (1986) recognized its capability of electively distinguish and reject energy coming from unwanted azimuths, eliminating the complications due to scattered energy, and making it possible to analyze high-frequency ground motions (1–100 Hz) in terms of rupture behavior. Because of their signal-to-noise ratios, only waveforms from the borehole stations of the HRSN are used in this paper.

2.2.1 Seismic data from earthquakes of the transitional segment

The interest in the Parkfield transitional segment of the SAF was also driven by the idea that seismologists would have collected signals from the final stage of its seismic cycle (Bakun et al., 2005; Kagan, 1997; Mileti and Fitzpatrick, 1992; Roeloffs, E., & Langbein, 1994; Bakun and Lindh, 1985). Although the HRSN was shut down between June 1998 and early 2001, due to lack of funding, it luckily recorded seismic data during the occurrence of the 28 September 2004 M6 mainshock and kept working in continuous mode up to present days.

Data from the HRSN allowed researchers to see the occurrence of entire families of repeating earthquakes (Nadeau et al., 1995; Nadeau and Johnson, 1998; Beeler et al., 2001), which were used as a network of creep meters at depth to estimate deep fault slip rates (Nadeau and McEvilly, 1999) and the scaling of earthquake stress drop, in the hypothesis that the entire earthquake slip of each repeater was released seismically (Nadeau and Johnson, 1998). The predictability of individual repeating earthquakes was studied by Zechar and Nadeau (2012), the triggering and interaction processes involving families of repeating sequences at Parkfield were studied by Nadeau et al. (1995) and Chen et al. (2013), and the triggering and interaction processes involving families of repeating sequences at Parkfield were studied by Chen et al. (2013). Finally, the scaling of geodetically based estimates of seismic stress drop has been reevaluated by Malagnini et al. (2007) and used to infer the scaling of peak and average seismic stress drops on extended fault surfaces.

Because of its scientific interest (from the quasi-periodical nature of its mainshocks, to the presence of repeating earthquakes, the existence of deep non-volcanic tremor (NVT), etc.), and because it was so heavily instrumented, the Parkfield transitional segment of the SAF was investigated thoroughly, and many issues were discussed: from the possibility of remotely-triggered changes in the fault properties due to a distant earthquake (Taira et al., 2009), to the indirect evaluation of the strength of the asperity that is responsible for the M6 mainshocks from a statistical analysis of the seismic catalog (Sebastiani and Malagnini, 2020).

The study by Sebastiani and Malagnini is of particular interest for our discussion. The authors considered the variance of the spatial center of the daily seismic activity along the transitional segment of the SAF at Parkfield, calculated on a moving time window. They observed an initial linear growth of the variance and interpreted it as due to an increasing frictional engagement of the two sides of the SAF. During the first part of the seismic cycle, the frictional engagement outside the asperity goes up to a maximum value, then an erosional process of the coupled area of the fault takes over (like what was documented by Mavrommatis et al., 2017 about the case of the Tohoku-Oki giant earthquake of 2011), and linearly reduced the amount of coupled fault surface. As the coupled area reduces in size, the stress is transferred onto the adjacent asperity, leading to failure. Growth and decay of the variance are pseudo-periodically modulated between a common low value and the increasing (growing phase) or decreasing (decreasing phase) peak values.

After being halted due to a stress perturbation from the 1983 Coalinga earthquake (e.g., see Figure 5 of Toda and Stein, 2002), the process promptly resumed a virtually unchanged increasing trend. The stable and regular decrease of the variance started in early 1988 allowed a very accurate retrospective prediction of the time of occurrence of the 2004 main shock. Based on the analysis of the variance of daily seismic activity along the SAF calculated on a moving time window, Sebastiani and Malagnini (2020) forecasted the occurrence of the next mainshock in mid-2024. Updates of their forecast are issued every two-three month; because the accuracy of the forecast linearly increases with time as the next earthquake approaches (their Figure 2), they expect that their most recent time window (7-day width in early 2024) to represent a final estimate.

Figure 2

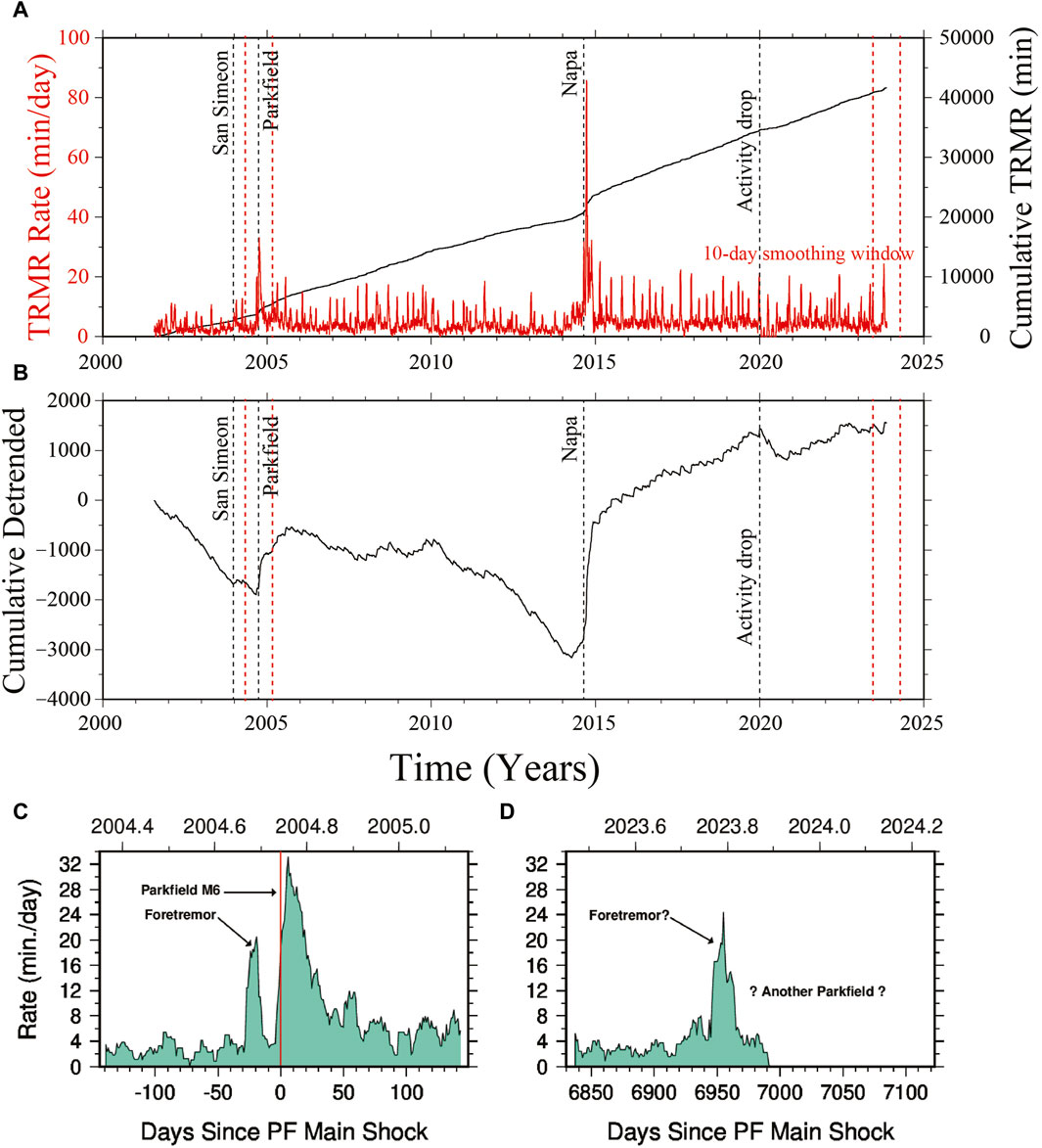
Figure 2. (A) In red, the long term rate of non-volcanic tremor NVT (∼8,500 days) smoothed using a 10-day window (min/day); in black, the cumulative tremor activity (min). (B) The detrended cumulative tremor activity. Indicated in (A, B) (black dashed lines) are the times of occurrence of the following events: the M6.5 San Simeon, the M6 Parkfield, and the M6 Napa. All these earthquakes perturbed the tremor activity at Parkfield. The fourth vertical black dashed line marks the position of a significant drop in the NVT activity, which seems to correspond to a drop in the variance of the attenuation parameter on the Pacific side of the SAF (see Supplementary Figure 6S2). (C) Rate of tremor 10-day smoothed (minutes/day) in the 293-day (9.7-month) 7-month time windows: 7 May 2004 - 24 February 2005. (D) Rate of tremor 10-day smoothed (minutes/day) in the time window 13 Jun 2023 - 1 April 2024. Bracketing dates of the two time windows of (C, D) are indicated in (A, B) by vertical dashed red lines.

Right before the 2004 mainshock, the attenuation parameter calculated by Malagnini et al. (2019) in the immediate vicinity to the transitional segment of the SAF at Parkfield showed some monotonic variations at high frequency, which they interpreted to be stress-induced, and which it occurred during the very last portion of the seismic cycle (the pre-critical state). Their interpretation of the relationship between stress and attenuation was strengthened by the signature left on seismic attenuation by the tensile normal stress change (unclamping, see Johanson and Burgmann, 2010) that was suddenly induced by the M6.5 San Simeon earthquake on the transitional segment of the SAF at Parkfield.

This study repeats the time-domain attenuation analysis performed by Malagnini et al. (2019) on a much larger data set that spans the time window 2001–2023. For the time window 2001–2020 we exclusively use waveforms from repeating earthquakes from a catalog provided by Li et al. (2023), while for the time window 2020–2023 we analyze seismic waveforms from regular earthquakes (no repeaters) from the NCSS catalog (https://ncedc.org/ncedc/catalog-search.html). The map in Figure 1C shows the spatial distribution of the microearthquakes and of the seismic stations used in this study. The total number of earthquakes used here is N_evt=6,851, for a total number of waveforms N_wave=225,557. The subset of non-repeaters is made of N_nr=727 earthquakes, and the subset of waveforms from the time window 2020–2023 is N_{wave_nr}=21,237.

Due to the effective co-location of repeating earthquakes belonging to the same cluster, and to their minimal location errors (at least relative to one another), the use of repeaters contributes to the increase of the signal-to-noise (S/N) ratio of spectral amplitudes. The catalog of all the earthquakes used in this study is provided in the Supplementary Material.

2.2.2 Non-volcanic tremors

An interesting additional observation is the 10-day smoothed rate of non-volcanic tremor (NVT) collected along the transitional segment of the SAF (Guilhem and Nadeau, 2012). The long-term NVT rate (∼8,500 days, updated through 15 November 2023) is plotted in red in Figure 2A, the cumulative NVT is plotted in black, and its detrended version is shown in Figure 2B. About 30-day prior to the 2004 Parkfield event a significant NVT foretremor was observed (Nadeau and Guilhem, 2009; Guilhem and Nadeau, 2012). Prior to this foretremor, a relatively quiescent period of ∼120-day of NVT activity was also observed (Figure 2C).

A similar quiescent period also precedes the proposed foretremor of the next possible Parkfield M6 (Figure 2D). This 120-day quiescence is unusual for the majority of NVT episodes throughout the long-term NVT catalog (Figure 2A). The two pairs of dashed red vertical lines in Figures 2A, B correspond to the time windows of Figures 2C, D.

Other studies have shown marked relationships of NVT to the seismic cycle. For example, Brenguier et al. (2008) found that NVT activity in the Parkfield area in California reveals that large earthquakes induce long-term perturbations in the San Andreas fault zone including NVT activity. The 2003 San Simeon and 2004 Parkfield earthquakes induced an increased NVT activity along the San Andreas fault. After the Parkfield earthquake, NVT activity remained elevated for more than 3 years and decayed over time, similarly to afterslip derived from GPS (Global Positioning System) measurements (Brenguier et al., 2008; Figure 3). These observations indicate that NVT activity is related to co-seismic damage in the shallow layers and to deep co-seismic stress change and postseismic stress relaxation within the San Andreas fault zone.

Figure 3

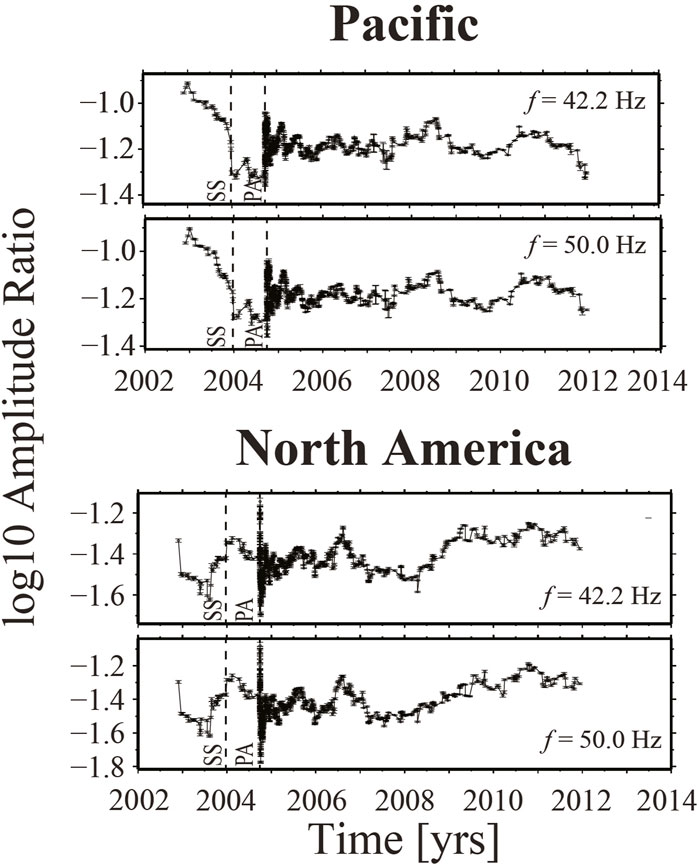
Figure 3. (Results from Malagnini et al., 2019). Logarithms of total attenuation experienced by direct S waves along the transitional segment of the SAF at Parkfield, between 4 and 12 km of hypocentral distance. Data points shown here are assimilable to the log10 of spectral amplitude ratios at the indicated central frequencies of 42.2 and 50.0 Hz. Total attenuation increases towards increasingly negative numbers. Attenuation is calculated on the two opposite sides of the SAF: Pacific side at the top, North American side at the bottom. Indicated by SS and PA are the times of occurrence of the 22 December 2003 M6.5 San Simeon earthquake, and the 28 September 2004 M6.0 Parkfield mainshock.

Another example of NVT behavior relative to the seismic cycle of smaller quakes is also evident. Guilhem and Nadeau (2012) showed in their Figure 5 that earthquakes above M2.6 are essentially absent during NVT episodes but that just after the episodes, the frequency of quakes above M2.6 are significantly accelerated.

2.3 Are we critical yet? some questions

The abstract states four intriguing questions about the earthquake cycles that were observed at Parkfield, with a special interest in the current one, and about the dynamic and kinematic characteristics of the next mainshock. In what follows we will try to give an answer to each one of them.

2.3.1 Question (i): does a detectable preparation phase for the Parkfield mainshocks exist?

Figure 2A suggests the presence of an anomaly in the tremor rate at Parkfield, which we call foretremor, between 15 and 30 days before the 2004 mainshock. A similar anomaly (another foretremor?) seems to characterize the tremor rate in recent weeks (Figure 2B). Observations shown in Figure 2 are intriguing, although we cannot produce solid proof of the recent anomaly being a foretremor.

Figure 3 (modified from Malagnini et al., 2019) shows the behavior of total attenuation between the hypocentral distances of 12 and 4 km. Plots are relative to the latest portion of the earthquake cycle that ended with the 2004 mainshock of 28 September 2004: they show the logarithms of the ratios between spectral amplitudes taken at the two specific hypocentral distances of 12 and 4 km (the more such logarithms are negative, the stronger the attenuation).

Whereas the total attenuation increases on the Pacific side of the SAF, with an instantaneous increase at the occurrence of the San Simeon earthquake, an opposite trend characterizes the North American side of the fault. Malagnini et al. (2019) explained this behavior with a cartoon (their Figure 5), in which it is evident that, at least in terms of seismic attenuation, the interseismic period on the two sides of the SAF are somehow opposite, with the Pacific side of the SAF characterized by an increasing extensional stress with respect to its North American counterpart. The latter shows only a step-like decrease in correspondence to the San Simeon event, because its attenuation time history must be thought of in terms of the coupling existing with the opposite (Pacific) side of the SAF.

A complete graphic description of the seismic attenuation in the entire frequency band investigated here (2–50 Hz), in the time window between 01/01/2001 and 01/01/2005, is given in Figure 4 (Pacific side of the SAF on the left, North American side of the SAF on the right). The Figure provides 3-D plots of the anomalies of the attenuation parameter $\delta \left(Q_S^{-1}\left(t,f\hspace{0.17em}\right)\right)$ as a function of time and frequency), with respect to the time-averaged attenuation parameter calculated in the time window between 01/01/2001 and 09/28/2004 (the day of the occurrence of the Parkfield mainshock).

Figure 4

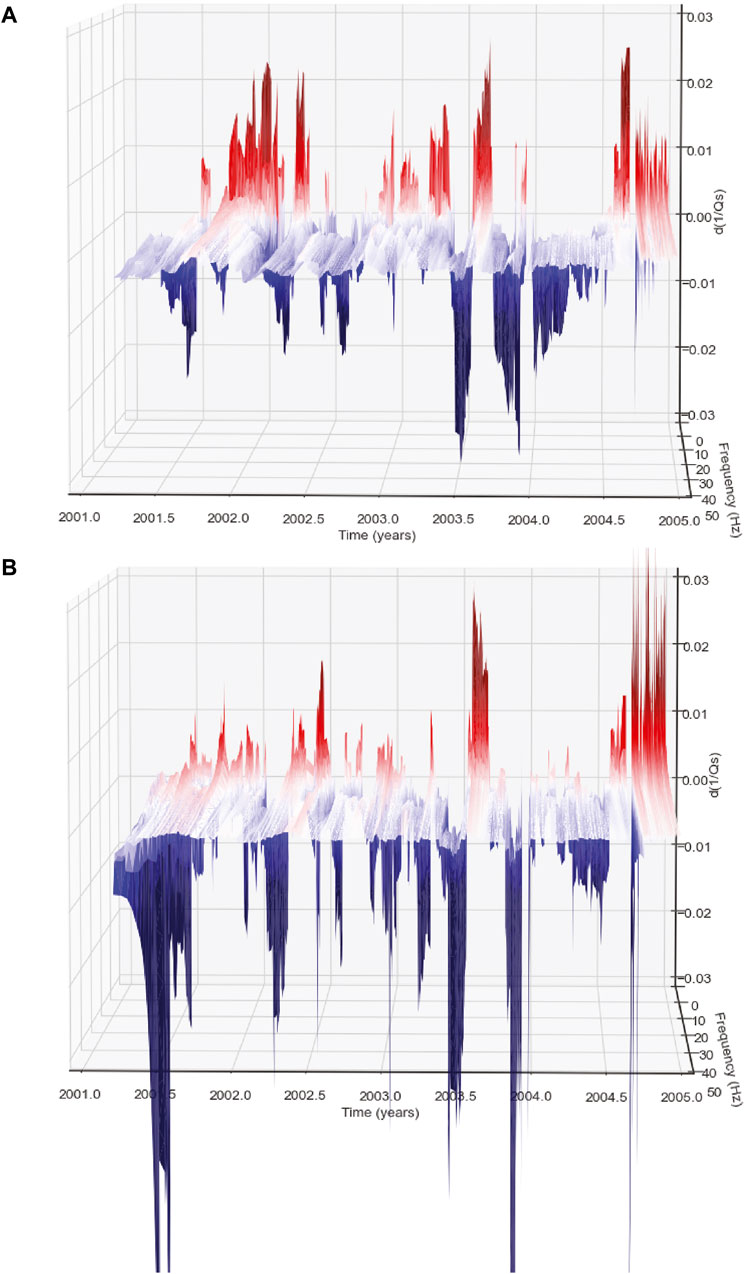
Figure 4. Variations of the attenuation parameter as a function of time, $\left(\delta \left(Q_S^{-1}\left(t,f\right)\right)\right)$, in the time window 01/01/2001–01/01/2005. Anomalies are computed with respect to the average attenuation parameter ${〈\delta \left(Q_S^{-1}\left(t,f\right)\right)〉}_t$ calculated between 01/01/2004 and 28/09/2004 (the occurrence of the Parkfield mainshock). (A) Pacific side; (B) North American side. The North America side of the fault is characterized by a low-frequency (2–5 Hz) deep negative anomaly that starts around the spring of 2003, gradually reaches a zero value around the beginning of June 2004, and has a sharp acceleration that culminates right before the mainshock. We note that a very similar pattern characterizes the anomalies of the opposite, Pacific side of the fault. The post-mainshock time history is characterized by relatively large, positive and negative swings of the attenuation parameter around the pre-mainshock time-averaged value.

With Figure 5 we try to extract more specific information on two frequency bands at the two ends of the investigated spectrum: 2–5 and 30–50 Hz. The quantities shown in Figure 5 are the stacked attenuation values that were calculated in the central frequencies contained in the mentioned bands (in Table 1, the investigated central frequencies grouped in the band named “Low” are the ones that were used to obtain the 2–5 Hz stacked and across-frequency averaged time history, and those in the band named “High” are the ones used to obtain the 30–50 Hz stacked and across-frequency averaged time history). Of great interest is the bifurcation of the stacked attenuation time histories (Low and High frequency bands) that can be observed starting a couple of months before the 28 September 2004, Parkfield mainshock.

Figure 5

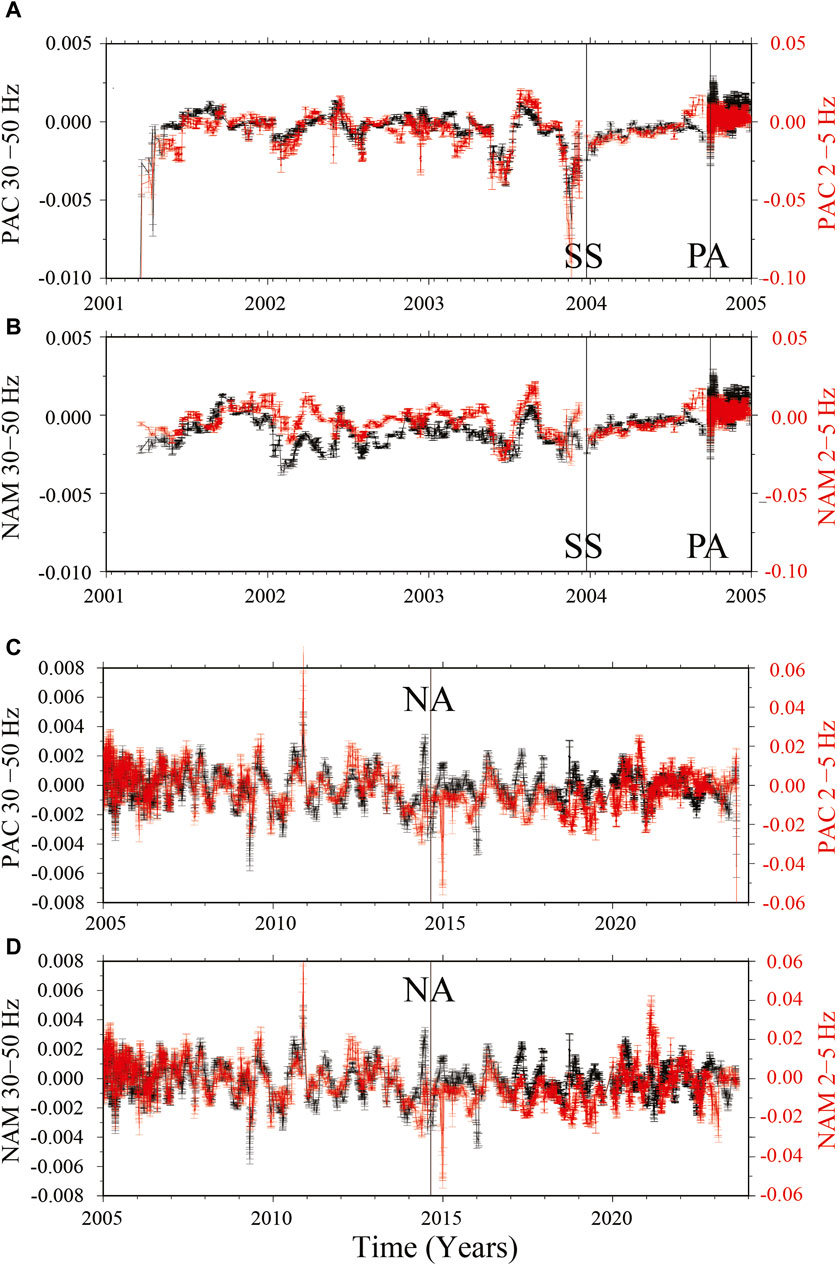
Figure 5. Stacked-averaged estimates of time histories of the variation of the attenuation parameter $\left(\delta \left(Q_S^{-1}\left(t,f\right)\right)\right)$ in two frequency bands: 2.0–5.0 Hz (black, left scale) and 30–50 Hz (red, right scale). In (A, B), the stacked-averaged values of the attenuation parameter are plotted in a 3-year time window (01/01/2002 through 01/01/2005), whereas (C, D) show the stacked-averaged attenuation time histories between 01/01/2005 and the fall of 2023. In each pair of panels, (A–D), the upper plot is relative to the attenuation parameter on the Pacific side of the SAF, the lower plot to the North American side of the SAF. It is clear the effect of the 2003 San Simeon earthquake, which was described in detail by Malagnini et al. (2019). SS, PA and NA indicate, respectively, the occurrences of the San Simeon, Parkfield, and Napa earthquakes. Supplementary Figure S1 shows the same information for two intermediate frequency ranges: 5–10 and 12–26 Hz, where no splitting is observed before the 2004 earthquake.

Table 1

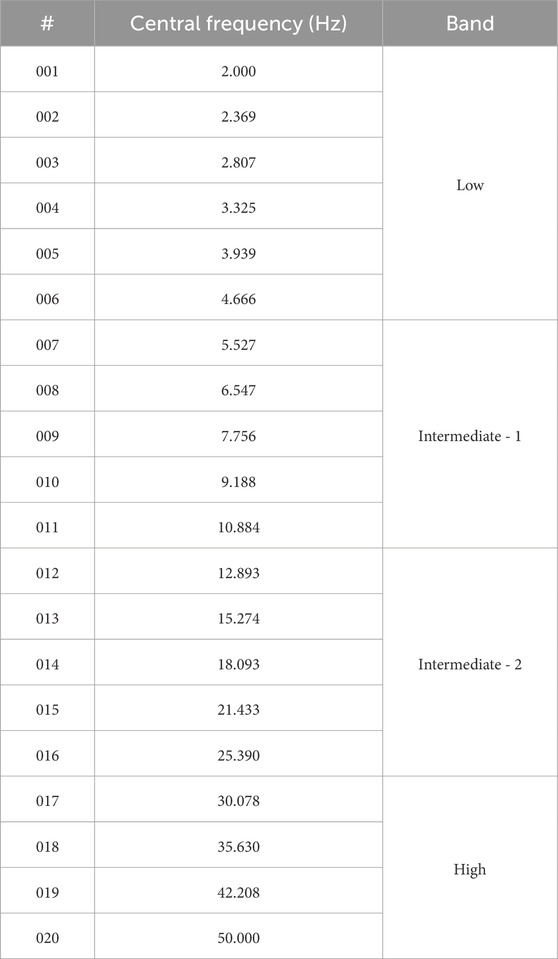
Table 1. Left column: “name” of the specific central frequency, as it enters the regression code. Central column: central frequency in Hz. Right column: partition of the available spectrum. Low- and High-frequencies are investigated in the main text. Results from the “Intermediate” bands are shown in the Supplementary Material.

At the time of the mainshock, the bifurcations of Figure 5 show a rebound effect on both frequency bands, on both sides of the SAF. Such a phenomenon, if we do not consider the effects of damage, which is especially effective at low frequencies, indicates a tendency for the crack density distribution at low frequencies (2–5 Hz) to move towards a crack density more suitable to an early stage of the seismic cycle.

Following Sebastiani and Malagnini (2020), who provided a forecast for the next Parkfield mainshock via the analysis of the variability of the variance of the daily center of the seismic activity along the transitional segment of the SAF in the time window between 1973 and late 2019, we look at the variability of the variance of the attenuation anomalies as a function of time.

Variances are computed over subsequent subsets of attenuation anomalies. Subsets are obtained as follows: after a number of samples is chosen (e.g., 40), we look at the longest time window needed to gather 40 subsequent data points, then we apply that length to all the time windows that we analyze.

In each time window we randomly choose a subset of 40 data points to be used to compute the variance. We randomly choose 10% of data points to be eliminated from each subset and do multiple estimates of variance by looping through this bootstrap step of the analysis several times (10). We finally average all variance determinations. Time windows are moved, one data point at a time, toward more recent times. The analysis done without applying the bootstrapping/averaging technique yields very similar results. In Figure 6 plot the average variances, normalized by the length of the time window. We point out that a single estimate of variance does not differ much from what we present here.

Figure 6

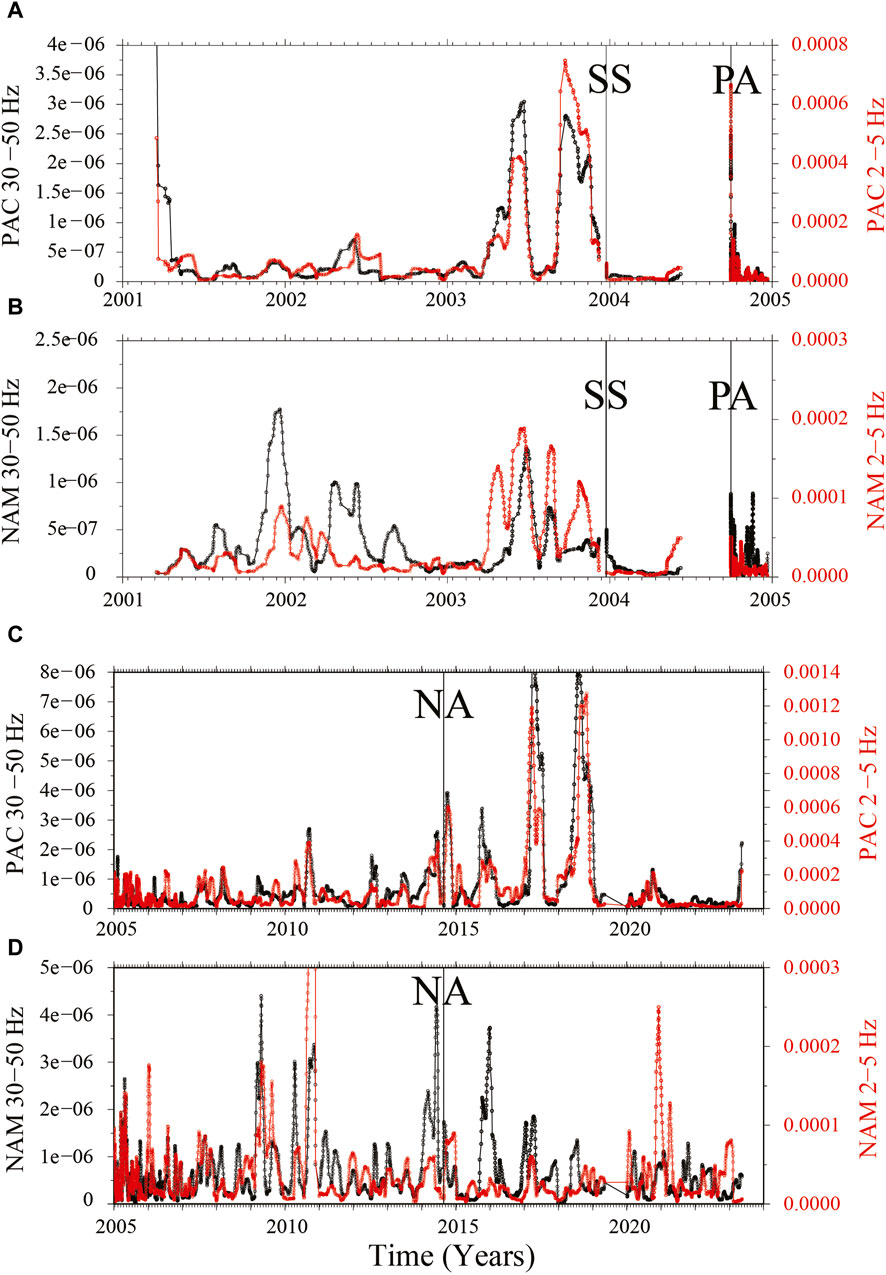
Figure 6. Variance of the stacked attenuation time histories of Figure 5 calculated on adjacent subsets of 40 data points. Note that (A, B), at the end of the previous seismic cycle, the San Simeon earthquake completely shuts off the variance of the attenuation time histories on both sides of the fault. Before being shut-off, variance is characterized by an increasing trend on the Pacific side of the fault (the entire year 2003). During the current cycle (C, D), in the decade 2010–2020, an increasing trend is observed on the variance on the Pacific side of the SAF. The different time scales available before and after the main earthquake of 2004 do not allow a fair comparison, although the peak amplitudes of the variance time histories in the two periods are quite similar, as well as the amplitudes of the variance past San-Simeon earthquake, and of that past the year 2021. SS, PA and NA indicate, respectively, the occurrences of the San Simeon, Parkfield, and Napa earthquakes. Supplementary Figure S2 shows a plot of the variance in two intermediate frequency ranges: 5–10 and 12–26 Hz. Comparing this Figure with Figure 2 we see a correspondence between the variance drop and a significant reduction of tremor activity in 2020, suggesting that the seismic attenuation (and possibly the main seismic activity) is modulated by the NVT rate.

It is crucial to state that the attenuation time histories showed here in Figures 4–6, are causal with respect to the three earthquakes indicated therein: San Simeon, Parkfield, and Napa (all these events induced changes of various kinds along the transitional segment of the SAF (Nadeau and McEvilly, 2004; Malagnini et al., 2019). The time histories of the attenuation parameter were separated in different segments divided by the three major events, in such a way no acausal effects, with respect to the three earthquakes, are allowed in our results.

What emerges from the visual inspection of Figures 5, 6 is the following:

1. In the pre-mainshock time window (Figure 5), a splitting is observed on both sides of the SAF: the stacked attenuation parameter at low-frequency (2–5 Hz) increases starting about 6 weeks before the 2004 mainshock, whereas the stacked attenuation parameter at high frequency (30–50 Hz) diminishes. This behavior is particularly interesting since it documents the signature of the very final stage of the seismic cycle. To our knowledge, no other cases of a similar phenomenon are documented in the scientific literature.

2. Another interesting feature of the stacked time histories on both sides of the SAF, and in both frequency bands, is the reduction of the amplitudes of the fluctuation that can be observed during the previous time history, which could also be the signature of a longer portion of the preparation phase of the 2004 mainshock. The same feature is described in Figures 6A, B, where we show the variance of the stacked attenuation time histories as a function of time. The dramatic drop of variance observed after the San Simeon earthquake clearly documents the reduction of the fluctuations experienced by the attenuation anomalies right after the San Simeon earthquake.

2.3.2 Question (ii): how dynamically/kinematically similar are the quasi-periodic occurrences of the Parkfield mainshocks?

The question is: when compared to the final stage of the previous seismic cycle of this segment of the SAF, do we see a similar attenuation time history, or attenuation variance, during the current final stage of the seismic cycle? Having defined the signature of the final stage of the seismic cycle of the Parkfield transitional segment of the SAF at points n. One and two in the previous paragraph, we can try to compare the “preparation phase” to the 2004 mainshock to the observations of seismic attenuation done in the time window between 01/01/2005 and present.

The stacked and averaged attenuation time histories of Figures 5C, D show that, differently from what happened in the pre-2004 mainshock time window (between the time of occurrence of the San Simeon earthquake and that of the 2004 Parkfield mainshock), a reduction of the amplitudes of the anomalies of the attenuation parameter $\delta \left(Q_S^{-1}\left(t,f\hspace{0.17em}\right)\right)$ as a function of time is observed only on the Pacific side of the SAF at Parkfield. The current reduction of the fluctuation amplitudes (which is confirmed by the analysis of the variance given in Figures 6C, D) is thus different from the one that ended the previous seismic cycle. Two alternative interpretations: (i) we are not yet in the final stage of the seismic cycle; (ii) if the next mainshock will not share the same nucleation zone of the 2004 mainshock (for example, it will nucleate in the same area of the 1966 event, See Figure 1), the differences between Figures 5A–D, 6A–D are related to the different nucleation zone.

We conclude that trying to answer Question (ii) is impossible. However, given also the results by Sebastiani and Malagnini (2020), our preferred hypothesis is that the next mainshock will not have the same hypocentral location of the 2004 one: for example, it could be close to that of 1966.

2.3.3 Question (iii): are some dynamic/kinematic characteristics of the next mainshocks predictable?

An important dynamic/kinematic characteristic of all Parkfield mainshocks is the location of their nucleation. Given the fact that the two epicenters of the 1966 and 2004 mainshocks were on the opposite ends of the Parkfield asperity, where do we expect the epicenter of the next failure to be located? Whereas it is possible that the hypocenters of the Parkfield main shocks have the tendency to randomly alternate between the two ends of the transitional segment of the SAF, our answer to Question (iii) is negative.

2.3.4 Question (iv): should we expect the duration of the current interseismic period to be close to the 22-year “undisturbed” average value?

The past seismic cycle was substantially perturbed in two different instances: (i) the occurrence of the M6.5 Coalinga earthquake of 2 May1983 and of the M6 Nuñez events of June 11th and 22 July 1983 reduced the Coulomb stress on the transitional segment of the SAF (Toda and Stein, 2002; Sebastiani and Malagnini, 2020), and (ii) the occurrence of the M6.5 22 December 2003 San Simeon earthquake increased the Coulomb stress on the same fault segment. Whereas the Coalinga-Nuñez effect is thought to be responsible for the anomalous duration of the previous seismic cycle (38 years), the San Simeon earthquake accelerated the transitional segment of the SAF toward criticality. During the current seismic cycle, no static/dynamic stress has been applied to the transitional segment by earthquakes in its proximity.

Recently, Sebastiani & Malagnini (2020) analyzed the variability of the variance of the daily position of the center of the seismicity that occurs along the transitional segment of the SAF and produced a forecast for the occurrence of the next Parkfield mainshock. Their “prediction”, based on the observation of the cyclic behavior of the variance variability along the fault segment, was for mid-2004. In their paper, Sebastiani and Malagnini produced a retrospective forecast of the 2004 Parkfield mainshock and showed that the accuracy of their forecast linearly improved as the time of the mainshock approached. Because of the evolution of the accuracy of their results, after the publication of their paper Sebastiani and Malagnini started providing a group of colleagues with somewhat regular updates of their forecast, and their results have been relatively consistent with their original forecast.

Although the Napa earthquake (Figure 5) influenced the nucleation of repeating earthquakes, and nonvolcanic tremor (NVT) (Nadeau, 2015; Peng et al., 2015: see cumulative curve of tremor activity below in Figure 2) along the transitional segment of the SAF, it did not appreciably perturb the seismic attenuation in the area. Interestingly, the Napa earthquake was about 300 km away from Parkfield.

In summary, we do not expect the current seismic cycle to be substantially different from its “undisturbed” time duration of 22 years. Our interpretation of the current situation is corroborated by a hint given by the “flattening” of the time histories of the attenuation parameter in both frequency bands (2–5 and 30–50 Hz) that is observed since 2020 along the Pacific side of the SAF (Figures 5C, 6C). Based on the information provided above, our answer to question (iv) is positive: we expect the duration of the current seismic cycle to be “regular” (i.e., close to the 22-year average value).

2.3.5 Why does the bifurcation appear just once?

An important question, at least partially unrelated with the set of four questions listed above, is the following: In the hypothesis that we are at the end of the current seismic cycle, why the bifurcation observed right before the 2004 mainshock (Figures 5A, B) is still missing at the end of 2023 (Figures 5C, D)?. One possible explanation is that the mainshock is more than 6–8 weeks away. Another possible explanation is that the next mainshock will have a different hypocentral location, and the splitting seen in Figures 5A,B is related to the volume surrounding the nucleation of the 2004 earthquake.

3 Discussion

Our understanding of the phenomena described in this study is based on the hypothesis that the fluctuations $\delta \left(Q_S^{-1}\left(t,f\right)\right)$, and those of deep NVT activity, provide information about the state of stress of the crustal rocks that are in the immediate vicinity of the fault surface and for the NVT deep below the seismogenic zone, especially about how they evolve over time. The correlation between 1/Q and the stress acting on the fault was investigated in detail by Malagnini and Parsons (2020), and by Malagnini et al. (2022), who related the variability of $Q_S^{-1}$ to that of the bulk permeability of crustal rocks.

Within the limits of our hypothesis, a preparatory phase for the Parkfield mainshocks could be detected based on the observation of changing NVT activity and of some monotonic variations of the attenuation parameter. The idea is that the crack population within crustal rocks has a specific (yet unknown) statistical distribution of dimensions, and that its characteristics vary as a function of time following the fluctuations of the stress acting upon the investigated volume.

In an initial stage in which the crustal rocks gradually undergo an increasing deviatoric stress from an unstressed initial state, the crack density is expected to grow (e.g., Scholz, 2019), the rock bulk permeability is expected to increase, and the same is true for the attenuation parameter. In a later stage of the seismic cycle, when the fault reaches a subcritical stress level, crack coalescence becomes the dominant phenomenon: some cracks would grow and coalesce, forming the structure where the catastrophic fracture will eventually take place. The phenomenon of fracture coalescence was studied by Bolton et al. (2023), who recorded acoustic emissions (AE) in lab samples under stress and concluded that a transition from pervasive to localized deformation must occur within the sample in the lead-up to failure.

In general, the strain localization produced by crack coalescence would relax the deviatoric stress away from the volume in which coalescence takes place, so that the volume surrounding the growing fracture would go into compaction, with a substantial reduction of crack density (Scholz, 2019). It is conceivable that the unknown crack distribution would change dramatically during the whole process of crack coalescence and growth of the macroscopic fracture, and such changes would be drastic for the portion of the crack population characterized by some preferred lengths and orientations, with the longer cracks contributing the most to the process. It is conceivable that these processes are linked to the activity rate changes observed by the NVT, at least partially.

The clear bifurcations shown by $\delta \left(Q_S^{-1}\left(t,f\right)\right)$ in two frequency bands in Figures 5A, B right before the Parkfield manshock tell us that the crack population within different frequency bands reacts in two opposite ways to the stress reaching a subcritical level. In fact, after a 7 months-long time window, started on 22 December 2003, of smooth monotonic increase of $\delta \left(Q_S^{-1}\left(t,f\right)\right)$, the 30–50 Hz stack shows a decreasing attenuation (starting in the month of July 2004), whereas the 2–5 Hz stack shows an opposite trend of increasing attenuation. In both cases, the July-September 2004 fluctuations that lead to the bifurcations of Figures 5A, B are much larger than the standard errors of the individual data points of $\delta \left(Q_S^{-1}\left(t,f\right)\right)$. We point out that since our dataset can only yield information about the crustal volume in the immediate vicinity to the fault plane, our estimates of $\delta \left(Q_S^{-1}\left(t,f\right)\right)$ may primarily be used as a proxy to fault strength.

Below 5 Hz the wavefield sampled in this study is dominated by surface waves (see Supplementary Figure S3). This makes the bifurcation even more interesting, because long wavelengths from surface waves (0.2–1.5 km) do not sample a deeper portion of the crust than the 30–50 Hz short wavelengths (20–60 m) from direct S-waves. In fact, it is just the opposite, and the increased attenuation in the 30–50 Hz band is partially influenced by the deeper portion of the SAF, where the nucleation of the 2004 earthquake took place, and just above the wide area where the NVT activity takes place. In fact, the total attenuation is the integral of the local attenuation experienced along the entire travel path. If the increased attenuation for low-frequency seismic waves is the result of crack opening and interconnection related to strain localization through the crack coalescence phenomenon, the decreasing attenuation in the high-frequency band is likely the result of the closing cracks in the 20–60 m length range, as the stress localizes on the growing (will-be) catastrophic fracture and relaxes elsewhere.

Likely, the bifurcations seen in Figures 5A, B between the low- and the high-frequency estimates of the stacked attenuation on both sides of the SAF mark the transition of the Parkfield’s asperity to criticality, when the coalescence of cracks gradually evolves into a catastrophic fracture (Scholz, 2019). The 2–5 Hz band describes the attenuation at wavelengths between 0.2 and 1.5 km, which likely represent the minimum crack lengths participating in the coalescence that takes place along the SAF.

From Figures 5A, B we see that the splitting between the low- and the high-frequencies is common to both sides of the SAF in the 6–8 weeks before the Parkfield mainshock. Moreover, the estimates of the attenuation parameter on the Pacific side of the SAF in the two frequency bands (2–5 and 30–50 Hz) fluctuate synchronously, whereas on the North American side of the SAF the two frequency bands show a more irregular behavior, with asynchronous fluctuations. These differences are the results of the different fluctuations of two subsets of cracks with specific average lengths in the general crack population and are likely due to the structural differences existing between the crust on the two sides of the SAF. Finally, a synchronous behavior characterizes both sides of the SAF in the two intermediate frequency bands of 5–10 and 12–26 Hz, where the bifurcations are not observed (Supplementary Figure S1), indicating that all the action (coalescence/compaction due to stress localization/relaxation) is confined within the two extreme bands of the available spectrum.

Another interesting feature is that the San Simeon earthquake produces a change in all the time histories of the stacked $\delta \left(Q_S^{-1}\left(t,f\right)\right)$, regardless of the presence of bifurcations: they all suddenly become smooth, with a tendency for a monotonic trend of increasing attenuation parameter. Our hypothesis is that the time window that starts with the occurrence of the San Simeon earthquake and ends at the onset of bifurcation (July 2004) contains the first part of the crack coalescence process, where the drastic reduction of $\delta \left(Q_S^{-1}\left(t,f\right)\right)$ observed on both sides of the SAF is the signature of stress localization in a very narrow volume along the fault surface. We argue that the pre-critical state is marked by the onset of the bifurcation: it starts when the crack coalescence (stress localization) is strong enough to allow compaction away from the growing fracture, where the stress that acts within the narrow volume surrounding the macroscopic fracture can relax.

About the differences between the time histories $\delta \left(Q_S^{-1}\left(t,f\right)\right)$ on the two sides of the SAF, we point out that the SAF at Parkfield puts in contact two very different geological structures, with granite on the west and the metamorphosed Franciscan formation on the east. However, at the end of a period of smoother variability of the attenuation parameters, the same bifurcation appears on both sides of the SAF, reinforcing our hypothesis of stress localization and volume compaction.

3.1 The current situation

From the visual inspection of Figures 6C, D, we cannot find signs about the Parkfield asperity having reached its critical state yet, even though a phase similar to the one started by the San Simeon earthquake seems to emerge in February-April 2021 only on the Pacific side of the fault, with smoother time histories of the stacked $\delta \left(Q_S^{-1}\left(t,f\right)\right)$. A plausible explanation of the fact that no clear signs of criticality can currently be pointed out, unlike during the last 9 months of the previous seismic cycle, is that in December 2003 the San Simeon earthquake gave a dramatic step-like push to the Parkfield segment of the SAF (Johanson and Burgmann, 2010) that forced the system to suddenly transition to its pre-critical state. At the end of the current seismic cycle, on the contrary, the path toward criticality is still driven by smooth tectonic loading.

A significant drop in the variance of the attenuation parameter is observed in Figure 6C, starting in mid-2021, like the drop shown by Figures 6A, B after the San Simeon earthquake. The difference with the current situation may be due to the absence of a step-like external push toward failure, and the next Parkfield mainshock may still be imminent. Finally, we note that between 2001 and the end of 2003 the variance of the attenuation parameter went up significantly, before dropping at the end of 2003, in coincidence with the occurrence of the San Simeon earthquake. A somehow similar increase in variance started in 2011 and lasted roughly until the beginning of 2020. Finally, in mid-2021 the variance of the attenuation parameter on the Pacific side of the SAF went down to very small values and never recovered its level ever since.

4 Conclusive remarks

This study aims at the recognition of the pre-critical state of the transitional segment of the SAF at Parkfield, in the hypothesis that the fluctuations of the attenuation parameter represent a proxy for the stress conditions in the crustal volume crossed by an active fault. We argue that, along the fault segment under scrutiny, the signature of the pre-critical state of the 2004 mainshock is represented by the variations in opposite directions of the low- and the high-frequency attenuation parameters as a function of time (low-frequency attenuation increases sharply, high-frequency attenuation decreases). The bifurcations are observed on both sides of the fault, and last 6–8 weeks. The pre-critical state of the Parkfield asperity emerges after a period of smooth variability of the attenuation parameter that lasts for about 1 year.

The bifurcation of the stacked seismic attenuation is the result of the different trends followed by the populations of cracks in the two ranges of frequency at both ends of the available spectrum: 2–5 and 30–50 Hz. To interact with the seismic energy, cracks’ lengths must form permeability structures with dimensions comparable to the wavelengths carried by the seismic radiation: 400–1,500 m for the 2–5 Hz band, and 60–100 m for the 30–50 Hz band. Cracks in the permeability structures whose dimensions are comparable to the short-wavelength radiation tend to close because crack coalescence causes strain localization into the macroscopic fracture, and compaction and stress relaxation in the surrounding volume. The long-wavelength radiation, on the contrary, gets more attenuated because the longer cracks that dominate the coalescence process increase the bulk permeability in the volume immediately around the fault plane by enhancing their aperture and interconnection. Finally, the 2–5 Hz band is dominated by surface waves that sample a shallower crustal structure than the direct S-waves of the 30–50 Hz band.

Another important property of the attenuation parameter in 2004 is the sudden reduction of its variance ${\sigma }^2\left[\delta \left(Q_S^{-1}\left(t,f\right)\right)\right]$ on both sides of the SAF, starting right after the occurrence of the San Simeon earthquake. A similar reduction of 2 [(1/Q)] can be observed starting at the beginning of 2021 on the sole Pacific side of the fault. If we currently are at the end of the seismic cycle, the fact that the attenuation signature is different from what observed in 2004 may be due to one, two, or all the three following reasons:

1. The sudden drop in variance in 2004, which occurred on both sides of the SAF, was due to a dramatic acceleration in the process of crack coalescence from the stress push from the San Simeon earthquake. Once the coalescence is mature, further changes in stress would not change the permeability structure, resulting in smoother time histories. Nothing like that occurred recently, and it is possible that the variance will go down gradually on both sides of the SAF in the next few months, following a gradual increase in the tectonic load.

2. The preparation phase of the next earthquake is going to result in a nucleation like the one of the 1966 earthquake. If this is the case, the attenuation signature may be different from what we observed in 2004, depending on the hypocentral location of the next earthquake.

3. The drop in variance observed in 2020–2021 on the Pacific side of the SAF seems to correspond to a substantial drop in the NVT activity (Figure 2), suggesting that NVT plays an important role in modulating seismic attenuation. If the latter shows a precursory behavior, then it is likely that the NVT activity modulates the main seismic activity of the transitional segment of the SAF, and an important property of the NVT activity during the 2004 sequence is the precursory quiescence of about 120-day, and the subsequent foretremor leading up to a Parkfield mainshock. If we currently are at the end of the seismic cycle, a quiescence followed by a possible foretremor episode, like that of the 2004 Parkfield mainshock, may result from the changing conditions of crack growth and its attenuation properties.

About the intertwined behavior of $\delta \left(Q_S^{-1}\left(t,f\right)\right)$ and the NVT activity, it is possible that the increased permeability along the very fault plane under subcritical conditions allows pore pressure to diminish at NVT depth (in our case, this would correspond to the observed decrease in NVT activity that starts in 2020), and to an upward pore fluid migration along the fault plane. In turn, the latter may weaken the fault and facilitate the occurrence of the mainshock. Within the limits of this hypothesis, monitoring the fluctuations of NVT activity along the SAF would be useful in recognizing the pre-critical state of the fault.

The quiet period preceding the 2004 mainshock is consistent with our idea of upward fluid migration, and with the twofold role of the latter: (i) a lower pore pressure at NVT depth that inhibits the tremor activity; (ii) the increased pore-fluid pressure upward that lowers the fault strength and facilitates the nucleation of the mainshock. Likely, the pre-mainshock variability of the attenuation parameter is small due to the stabilizing action of strain localization upon $\delta \left(Q_S^{-1}\left(t,f\right)\right)$. What causes a foretremor (i.e., a sharp increase in NVT with limited duration, occurring after a quiet period) is not clear, and the time lag between a foretremor and the mainshock may correspond to the diffusion time needed to reach a sufficient pore-fluid pressure along the fault. Consistently with our hypothesis, larger events (that primarily occur above the tremor zone) do not occur during the actual times of most tremor episodes. Rather, there is a definite tendency for the larger events to occur after the tremor episodes by a few days throughout the longer-term period (Figure 5 of Guilhem and Nadeau, 2012; Supplementary Figure S4 of the Supplementary Material of the same paper).

In the next few months (or years) the Parkfield segment of the SAF will provide most of the answers to our questions. In the meantime, it may be worthwhile applying our technique on different tectonic settings characterized by more complex fault geometries and ongoing NVT activity. Aside from more advanced theoretical developments and laboratory experiments on seismic attenuation at increasing differential stresses, the most important ingredient for a successful use of attenuation and NVT information would be the use of data from dense seismic networks equipped with borehole sensors, recording at high sampling rate (250–500 sps for borehole stations; max 200 sps for surface instruments, see Malagnini et al., 2021).

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://www.ncedc.org.

Author contributions

LM: Conceptualization, Data curation, Formal Analysis, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing. RN: Data curation, Formal Analysis, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing. TP: Formal Analysis, Methodology, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. LM was partially supported by funds from the Departmental Project NEMESIS, awarded by the Istituto Nazionale di Geofisica e Vulcanologia (INGV), and partially by internal funds from INGV Sezione di Roma 1.

Acknowledgments

LM is deeply grateful to Prof. Douglas Dreger, from the Berkeley Seismological Laboratory of the University of California Berkeley (BSL), for his warm hospitality and for sharing his office space with him for almost 2 decades, and to all the faculties and staff at BSL. For RMN, office space and computer facilities were provided by BSL. We are particularly thankful to Dr. Taka’aki Taira, who provided a rich catalog of repeating earthquakes. A special thanks goes to Dr. Daniele Melini and to his group “Laboratorio di Geofisica Computazionale”, who impeccably run the INGV High-Performance Computers.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2024.1349425/full#supplementary-material

References

Agnew, D., and Sieh, K. (1978). A documentary study of the felt effects of the great California earthquake of 1857. Seismol. Soc. Am. Bull. 68, 1717–1729.

Google Scholar

Akinci, A., Malagnini, L., Herrmann, R. B., Pino, N. A., Scognamiglio, L., and Eyidogan, H. (2001). High-frequency ground motion in the Erzincan region, Turkey: inferences from small earthquakes. Bull. Seismol. Soc. Am. 91 (6), 1446–1455. doi:10.1785/0120010125

CrossRef Full Text | Google Scholar

Bakun, W., and McEvilly, T. (1984). Recurrence models and Parkfield, California, earthquakes. J. Geophys. Res. 89, 3051–3058. doi:10.1029/jb089ib05p03051

CrossRef Full Text | Google Scholar

Bakun, W. H., Aagaard, B., Dost, B., Ellsworth, W. L., Hardebeck, J. L., Harris, R. A., et al. (2005). Implications for prediction and hazard assessment from the 2004 Parkfield earthquake. Nature 437, 969–974. doi:10.1038/nature04067

PubMed Abstract | CrossRef Full Text | Google Scholar

Bakun, W. H., and Lindh, A. G. (1985). The Parkfield, California, earthquake prediction experiment. Science 229 (4714), 619–624. doi:10.1126/science.229.4714.619

PubMed Abstract | CrossRef Full Text | Google Scholar

Barbosa, N. D., Hunziker, J., Lissa, S., H Saenger, E., and Lupi, M. (2019). Fracture unclogging: a numerical study of seismically induced viscous shear stresses in fluid saturated fractured rocks. J. Geophys. Res. Solid Earth 124 (11), 11705–11727. doi:10.1029/2019JB017984

CrossRef Full Text | Google Scholar

Beeler, N. M., Lockner, D. L., and Hickman, S. H. (2001). A simple stick-slip and creep-slip model for repeating earthquakes and its implication for microearthquakes at Parkfield. Bull. Seismol. Soc. Am. 91 (6), 1797–1804. doi:10.1785/0120000096

CrossRef Full Text | Google Scholar

Ben-Zion, Y., and Zaliapin, I. (2020). Localization and coalescence of seismicity before large earthquakes. Geophys. J. Int. 223, 561–583. doi:10.1093/gji/ggaa315

CrossRef Full Text | Google Scholar

Bletery, Q., and Nocquet, J.-M. (2023). The precursory phase of large earthquakes. Science 381 (6655), 297–301. doi:10.1126/science.adg2565

PubMed Abstract | CrossRef Full Text | Google Scholar

Bolton, D. C., Marone, C., Saffer, D., and Trugman, D. T. (2023). Foreshock properties illuminate nucleation processes of slow and fast laboratory earthquakes. Nat. Commun. 14, 3859. doi:10.1038/s41467-023-39399-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouchon, M., Karabulut, H., Aktar, M., Özalaybey, S., Schmittbuhl, J., and Bouin, M. P. (2011). Extended nucleation of the 1999 M w 7.6 Izmit earthquake. Science 331, 877–880. doi:10.1126/science.1197341

PubMed Abstract | CrossRef Full Text | Google Scholar

Brenguier, F., Campillo, M., Hadziioannou, C., Shapiro, N. M., Nadeau, R. M., and Larose, E. (2008). Postseismic relaxation along the san Andreas Fault at Parkfield from continuous seismological observations. Science 321, 1478–1481. doi:10.1126/science.1160943

PubMed Abstract | CrossRef Full Text | Google Scholar

Brodsky, E. E., and Lay, T. (2014). Recognizing foreshocks from the 1 April 2014 Chile earthquake. Science 344, 700–702. doi:10.1126/science.1255202

PubMed Abstract | CrossRef Full Text | Google Scholar

Brodsky, E. E., Roeloffs, E., Woodcock, D., Gall, I., and Manga, M. (2003). A mechanism for sustained groundwater pressure changes induced by distant earthquakes. J. Geophys. Res. 108 (B8), 2390. doi:10.1029/2002JB002321

CrossRef Full Text | Google Scholar

Cartwright, D. E., and Longuet-Higgins, M. S. (1956). The statistical distribution of the maxima of a random function. Proc. R. Soc. A 237, 212–232.

Google Scholar

Cattania, C., and Segall, P. (2021). Precursory slow slip and foreshocks on rough faults. J. Geophys. Res. Solid Earth 126, e2020JB020430. doi:10.1029/2020jb020430

CrossRef Full Text | Google Scholar

Chen, K. H., Bürgmann, R., and Nadeau, R. M. (2013). Do earthquakes talk to each other? Triggering and interaction of repeating sequences at Parkfield. J. Geophys. Res. Solid Earth 118 (1), 165–182. doi:10.1029/2012jb009486

CrossRef Full Text | Google Scholar

Chen, X., and Shearer, P. M. (2013). California foreshock sequences suggest aseismic triggering process. Geophys. Res. Lett. 40, 2602–2607. doi:10.1002/grl.50444

CrossRef Full Text | Google Scholar

O’Connell, R. J., and Budiansky, B. (1977). Viscoelastic properties of fluid-saturated cracked solids. J. Geophys. Res. 82 (36), 5719–5735.

Google Scholar

D'Amico, S., Koper, K. D., Herrmann, R. B., Akinci, A., and Malagnini, L. (2010). Imaging the rupture of the Mw 6.3 April 6, 2009 L'Aquila, Italy earthquake using back-projection of teleseismic P-waves. Geophys. Res. Lett. 37 (3). doi:10.1029/2009gl042156

CrossRef Full Text | Google Scholar

Dodge, D. A., Beroza, G. C., and Ellsworth, W. L. (1996). Detailed observations of California foreshock sequences: implications for the earthquake initiation process. J. Geophys. Res. Solid Earth 101, 22371–22392. doi:10.1029/96jb02269

CrossRef Full Text | Google Scholar

Ellsworth, W. L., and Bulut, F. (2018). Nucleation of the 1999 Izmit earthquake by a triggered cascade of foreshocks. Nat. Geosci. 11, 531–535. doi:10.1038/s41561-018-0145-1

CrossRef Full Text | Google Scholar

Guilhem, A., and Nadeau, R. M. (2012). Episodic tremors and deep slow-slip events in Central California. EPSL 357-358, 1–10. doi:10.1016/j.epsl.2012.09.028

CrossRef Full Text | Google Scholar

Johanson, I. A., and Burgmann, R. (2010). Coseismic and postseismic slip from the 2003 San Simeon earthquake and their effects on backthrust slip and the 2004 Parkfield earthquake. J. Geophys. Res. 115, B07411. doi:10.1029/2009JB006599

CrossRef Full Text | Google Scholar

Johnson, C. W., Fu, Y., and Burgmann, R. (2017). Stress models of the annual hydrospheric, atmospheric, thermal, and tidal loading cycles on California faults: perturbation of background stress and changes in seismicity. J. Geophys. Res. Solid Earth 122 (10), 625. doi:10.1002/2017JB014778

CrossRef Full Text | Google Scholar

Kagan, Y. Y. (1997). Statistical aspects of Parkfield earthquake sequence and Parkfield prediction experiment. Tectonophysics 270 (3-4), 207–219. doi:10.1016/s0040-1951(96)00210-7

CrossRef Full Text | Google Scholar

Kato, A., Fukuda, J. I., Nakagawa, S., and Obara, K. (2016). Foreshock migration preceding the 2016 M_w 7.0 Kumamoto earthquake, Japan. Geophys. Res. Lett. 43, 8945–8953. doi:10.1002/2016gl070079

CrossRef Full Text | Google Scholar

Kato, A., Obara, K., Igarashi, T., Tsuruoka, H., Nakagawa, S., and Hirata, N. (2012). Propagation of slow slip leading up to the 2011 Mw9.0 Tohoku-Oki earthquake. Science 335, 705–708. doi:10.1126/science.1215141

PubMed Abstract | CrossRef Full Text | Google Scholar

Kelly, C. M., Rietbrock, A., Faulkner, D. R., and Nadeau, R. M. (2013). Temporal changes in attenuation associated with the 2004 M6.0 Parkfield earthquake. J. Geophys. Res. Solid Earth 118, 630–645. doi:10.1002/jgrb.50088

CrossRef Full Text | Google Scholar

Li, Y., Bürgmann, R., and Taira, T. (2023). Spatiotemporal variations of surface deformation, shallow creep rate, and slip partitioning between the San Andreas and southern Calaveras Fault. J. Geophys. Res. Solid Earth 128, e2022JB025363. doi:10.1029/2022JB025363

CrossRef Full Text | Google Scholar

Liu, W., and Manga, M. (2009). Changes in permeability caused by dynamic stresses in fractured sandstone. Geophys. Res. Lett. 36, L20307. doi:10.1029/2009GL039852

CrossRef Full Text | Google Scholar

Lucente, F. P., De Gori, P., Margheriti, L., Piccinini, D., Di Bona, M., Chiarabba, C., et al. (2010). Temporal variation of seismic velocity and anisotropy before the 2009 MW 6.3 L’Aquila earthquake. Italy, Geol. 38, 1015–1018. doi:10.1130/G31463.1

CrossRef Full Text | Google Scholar

Malagnini, L., Dreger, D. S., Bürgmann, R., Munafò, I., and Sebastiani, G. (2019). Modulation of seismic attenuation at Parkfield, before and after the 2004 M6 earthquake. J. Geophys. Res. Solid Earth 124, 5836–5853. doi:10.1029/2019JB017372

CrossRef Full Text | Google Scholar

Malagnini, L., Dreger, D. S., Nadeau, R. M., Munafò, I., and Cocco, M. (2021). On the heterogeneity of the earthquake rupture. Geophys. J. Int. 225 (3), 1771–1781. doi:10.1093/gji/ggaa528

CrossRef Full Text | Google Scholar

Malagnini, L., Herrmann, R. B., and Di Bona, M. (2000). Ground motion scaling in the Apennines (Italy). Bull. Seism. Soc. Am. 90, 1062–1081. doi:10.1785/0119990152

CrossRef Full Text | Google Scholar

Malagnini, L., Mayeda, K., Uhrhammer, R., Akinci, A., and Herrmann, R. B. (2007). A regional ground-motion excitation/attenuation model for the San Francisco region. Bull. Seismol. Soc. Am. 97 (3), 843–862. doi:10.1785/0120060101

CrossRef Full Text | Google Scholar

Malagnini, L., and Parsons, T. (2020). Seismic attenuation monitoring of a critically stressed San Andreas fault. Geophys. Res. Lett. 47. doi:10.1029/2020GL089201

CrossRef Full Text | Google Scholar

Malagnini, L., Parsons, T., Munafò, I., Mancini, S., Segou, M., and Geist, E. L. (2022). Crustal permeability changes inferred from seismic attenuation: impacts on multi-mainshock sequences. Front. Earth Sci. 10, 963689. doi:10.3389/feart.2022.963689

CrossRef Full Text | Google Scholar

Manga, M., Beresnev, I., Brodsky, E. E., Elkhoury, J. E., Elsworth, D., Ingebritsen, S. E., et al. (2012). Changes in permeability caused by transient stresses: field observations, experiments, and mechanisms. Rev. Geophys. 50, RG2004. doi:10.1029/2011RG000382

CrossRef Full Text | Google Scholar

Manga, M., and Brodsky, E. (2006). Seismic triggering of eruptions in the far field: volcanoes and geysers. Annu. Rev. Earth Planet. Sci. 34, 263–291. doi:10.1146/annurev.earth.34.031405.125125

CrossRef Full Text | Google Scholar

Mavrommatis, A. P., Segall, P., and Johnson, K. M. (2017). A physical model for interseismic erosion of locked fault asperities. J. Geophys. Res. 122 (10), 8326–8346. doi:10.1002/2017jb014533

CrossRef Full Text | Google Scholar

Mileti, D. S., and Fitzpatrick, C. (1992). The causal sequence of risk communication in the Parkfield earthquake prediction experiment. Risk Anal. 12 (3), 393–400. doi:10.1111/j.1539-6924.1992.tb00691.x

CrossRef Full Text | Google Scholar

Nadeau, R. M. (2015). Ambient tremor activity triggered by the 24 august 2014, M6.0 south Napa earthquake in the parkfield-cholame region of California. Seismol. Res. Lett. 86 (2B), 635.

Google Scholar

Nadeau, R. M., and Dolenc, D. (2005). Non-volcanic tremors deep beneath the san Andreas fault. Science 307, 389. doi:10.1126/science.1107142

PubMed Abstract | CrossRef Full Text | Google Scholar

Nadeau, R. M., Foxall, W., and McEvilly, (1995). Clustering and periodic recurrence of microearthquakes on the san Andreas Fault at Parkfield, California. Science 267 (5197), 503–507. doi:10.1126/science.267.5197.503

PubMed Abstract | CrossRef Full Text | Google Scholar

Nadeau, R. M., and Guilhem, A. (2009). Nonvolcanic tremor evolution and the san Simeon and Parkfield, California, earthquakes. Science 325, 191–193. doi:10.1126/science.1174155

PubMed Abstract | CrossRef Full Text | Google Scholar

Nadeau, R. M., and Johnson, L. R. (1998). Seismological studies at Parkfield VI: moment release rates and estimates of source parameters for small repeating earthquakes. Bull. Seismol. Soc. Am. 88 (3), 790–814. doi:10.1785/bssa0880030790

CrossRef Full Text | Google Scholar

Nadeau, R. M., and McEvilly, T. V. (1999). Fault slip rates at depth from recurrence intervals of repeating microearthquakes. Science 285, 718–721. doi:10.1126/science.285.5428.718

PubMed Abstract | CrossRef Full Text | Google Scholar

Nadeau, R. M., and McEvilly, T. V. (2004). Periodic pulsing of characteristic microearthquakes on the san Andreas Fault. Science 303 (5655), 220–222. doi:10.1126/science.1090353

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, Z., Shelly, D. R., and Ellsworth, W. L. (2015). Delayed dynamic triggering of deep tremor along the Parkfield-Cholame section of the San Andreas Fault following the 2014 M6.0 South Napa earthquake. Geophys. Res. Lett. 42, 7916–7922. doi:10.1002/2015GL065277

CrossRef Full Text | Google Scholar

Raoof, M., Herrmann, R. B., and Malagnini, L. (1999). Attenuation and excitation of three-component ground motion in Southern California. Bull. Seism. Soc. Am. 89, 888–902. doi:10.1785/bssa0890040888

CrossRef Full Text | Google Scholar

Roeloffs, E., and Langbein, J. (1994). The earthquake prediction experiment at Parkfield, California. Rev. Geophys. 32 (3), 315–336. doi:10.1029/94rg01114

CrossRef Full Text | Google Scholar

Roeloffs, E. A. (1998). Persistent water level changes in a well near Parkfield, California, due to local and distant earthquakes. J. Geophys. Res. 103 (B1), 869–889. doi:10.1029/97jb02335

CrossRef Full Text | Google Scholar

Scholz, C. (2019). The mechanics of earthquakes and faulting. Cambridge: Cambridge University Press. doi:10.1017/9781316681473

CrossRef Full Text | Google Scholar

Sebastiani, G., and Malagnini, L. (2020). Forecasting the next Parkfield mainshock on the san Andreas Fault (California). J. Ecol. Nat. Resour. 4. issue 3. doi:10.23880/jenr-16000218

CrossRef Full Text | Google Scholar

Sibson, R. H. (2009). Rupturing in overpressured crust during compressional inversion—the case from NE Honshu, Japan. Tectonophysics 473, 404–416. doi:10.1016/j.tecto.2009.03.016

CrossRef Full Text | Google Scholar

Sieh, K. (1978a). Central California foreshocks of the great 1857 earthquake. Seismol. Soc. Am. Bull. 68, 1731–1749.

Google Scholar

Sieh, K. (1978b). Slip along the san Andreas Fault associated with the great 1857 earthquake. Seismol. Soc. Am. Bull. 68, 1421–1428.

Google Scholar

Spudich, P., and Oppenheimer, D. (1986). “Dense seismograph array observations of earthquake rupture dynamics,” in Earthquake source mechanics. Editors S. Das, J. Boatwright, and C. H. Scholz doi:10.1029/GM037p0285

CrossRef Full Text | Google Scholar

Sugan, M., Kato, A., Miyake, H., Nakagawa, S., and Vuan, A. (2014). The preparatory phase of the 2009 Mw 6.3 L'Aquila earthquake by improving the detection capability of low-magnitude foreshocks. Geophys. Res. Lett. 41, 6137–6144. doi:10.1002/2014gl061199

CrossRef Full Text | Google Scholar

Taira, T. A., Silver, P. G., Niu, F., and Nadeau, R. M. (2009). Remote triggering of fault-strength changes on the San Andreas fault at Parkfield. Nature 461 (7264), 636–639. doi:10.1038/nature08395

PubMed Abstract | CrossRef Full Text | Google Scholar

Toda, S., and Stein, R. S. (2002). Response of the San Andreas fault to the 1983 Coalinga-Nuñez earthquakes: an application of interaction-based probabilities for Parkfield. J. Geophys. Res. 107 (B6). ESE 6-1-ESE 6-16. doi:10.1029/2001jb000172

CrossRef Full Text | Google Scholar

Townend, J., and Zoback, M. (2000). How faulting keeps the crust strong. Geology 28 (5), 399–402. doi:10.1130/0091-7613(2000)28<399:hfktcs>2.0.co;2

CrossRef Full Text | Google Scholar

Vasseur, J., Wadsworth, F. B., Heap, M. J., Main, I. G., Lavalle, Y., and Dingwell, D. B. (2017). Does an inter-flaw length control the accuracy of rupture forecasting in geological materials? Earth Planet. Sci. Lett. 475, 181–189. doi:10.1016/j.epsl.2017.07.011

CrossRef Full Text | Google Scholar

Yoon, C. E., Yoshimitsu, N., Ellsworth, W. L., and Beroza, G. C. (2019). Foreshocks and mainshock nucleation of the 1999 M_<i>w</i> 7.1 hector mine, California, earthquake. J. Geophys. Res. Solid Earth 124, 1569–1582. doi:10.1029/2018jb016383

CrossRef Full Text | Google Scholar

Zechar, J. D., and Nadeau, R. M. (2012). Predictability of repeating earthquakes near Parkfield, California. Geophys. J. Int. 190 (1), 457–462. doi:10.1111/j.1365-246x.2012.05481.x

CrossRef Full Text | Google Scholar