Snowfall deposition in mountainous terrain: a statistical downscaling scheme from high-resolution model data on simulated topographies

One of the primary causes of non-uniform snowfall deposition on the ground in mountainous regions is the preferential deposition of snow, which results from the interaction of near-surface winds with topography and snow particles. However, producing high-resolution snowfall deposition patterns can be computationally expensive due to the need to run full atmospheric models. To address this, we developed two statistical downscaling schemes that can efficiently downscale near-surface, low-resolution snowfall data to fine-scale snow deposition accounting for the effect of preferential deposition in mountainous regions. Our approach relies on a comprehensive, model database generated using 3D wind fields from an atmospheric model and a preferential deposition model on several thousand simulated topographies covering a broad range in terrain characteristics. Both snowfall downscaling schemes rely on fine-scale topographic scaling parameters and low-resolution wind speed as input. While one scheme, referred to as the “wind scheme”, further necessitates fine-scale vertical wind components, a second scheme, referred to as the “aspect scheme”, does not require fine-scale temporal input. We achieve this by additionally downscaling near-surface vertical wind speed solely using topographic scaling parameters and low-resolution wind direction. We assess the performance of our downscaling schemes using an independent subset of the model database on simulated topographies, model data on actual terrain, and spatially measured new snow depth obtained through a photogrammetric drone survey following a snowfall event on previously snow-free ground. While the assessments show that our downscaling schemes perform well (relative errors ≤ ±3% with modeled and ≤ ±6% with measured snowfall deposition), they also demonstrate comparable results to benchmark downscaling models. However, our schemes notably outperform the benchmark models in representing fine-scale patterns. Our downscaling schemes possess several key features, including high computational efficiency, versatility enabled by the comprehensive model database, and independence from fine-scale temporal input data (aspect scheme), indicating their potential for widespread applicability. Therefore, our downscaling schemes for near-surface snowfall and vertical wind speed can be beneficial for various applications at fine grid resolutions such as in atmospheric and climate sciences, snow hydrology, glaciology, remote sensing, and avalanche sciences.

1 Introduction

In mountainous regions, snowfall is subject to dynamic alterations across spatial and temporal scales, leading to substantial spatial variability in the accumulated snow on the ground. This poses a significant challenge for applications that require accurate high-resolution spatial snow depth distributions in mountainous terrain, such as in avalanche forecasting (Schweizer et al., 2003; Bellaire and Jamieson, 2013), avalanche hazard mapping (Harvey et al., 2018; Bühler et al., 2022a), for glacier mass balances (Dadic et al., 2010a; Farinotti et al., 2010; Mott et al., 2019), in large-scale monitoring products based on remote sensing (Gascoin et al., 2019), in water resource management or for snow-melt forecasts (Bavay et al., 2009; Griessinger et al., 2019). As temperatures rise, the probability of having precipitation falling as rain instead of snow also rises. However, evidence strengthened that climate change has resulted in a notable increase in heavy precipitation events across many regions, with further intensification projected in the future (IPCC, 2023). Furthermore, despite a predicted decrease in snowfall fraction, midwinter mean and heavy snowfall may experience slight snowfall increases in the future (Frei et al., 2018). As such, the accurate representation of high-resolution spatial snowfall patterns is becoming increasingly relevant for establishing natural hazard protection measures. This is particularly salient given that extreme precipitation events in winter could potentially become more localized in the future (Yang et al., 2023).

The interplay between snowfall, wind flow, and topography acts on mountain-range, ridge and slope scale (Mott et al., 2018). At the mountain-range scale, the accumulated snow on the ground is mainly driven by orographic precipitation. One example is the forced dynamical lifting of air masses, which rises from elevation differences. Indeed, elevation has often been found to be a main explanatory variable for spatial snow depth in mountainous terrain (Seyfried and Wilcox, 1995; Grünewald and Lehning, 2011; Lehning et al., 2011; Kirchner et al., 2014; Helbig and van Herwijnen, 2017). At the much smaller spatial scale of ridges and slopes, heterogeneous snowfall deposition acts across ridges and slopes due to near-surface wind-topography-particle interactions in the absence of snow redistribution and sublimation (Föhn and Meister, 1983; Lehning et al., 2008). Lehning et al. (2008) introduced this process as preferential snowfall deposition and attributed it to increased wind speeds and updraft on the windward side of ridges versus reduced wind speeds and downdraft on the leeward side. In a case study using Weather Research and Forecasting (WRF) large-eddy modelings, preferential snowfall deposition was estimated in a 50 m horizontal grid to increase the accumulated snow on the lee side of mountains locally by up to 10% (Gerber et al., 2019). These findings provide important insights into the complex interplay between atmospheric conditions, topography, and snow particles.

High-resolution three-dimensional (3D) topography-wind-snow particle interactions have been extensively studied using advanced atmospheric models at fine spatial scales of only a few tens of meters (e.g., Mott and Lehning, 2010; Mott et al., 2014; Gerber et al., 2017; Vionnet et al., 2017; Wang and Huang, 2017; Gerber et al., 2019). However, these high-resolution models require huge computational power and detailed atmospheric input information that is not accessible to many applications. Therefore, low-order models or statistical and dynamical downscaling approaches can be valuable in creating high-resolution snowfall maps in mountainous terrain. A recent example of a dynamical downscaling model is from Reynolds et al. (2023). They developed a High-resolution variant of Gutmann et al. (2016)’s Intermediate Complexity Atmospheric Research (ICAR) model, named HICAR, which features changes to the advection scheme and the wind solver. The new wind solver incorporates the effects of topography on the 3D wind flow field by using empirical terrain parameters, which allow HICAR to simulate complex topographic flow features (Reynolds et al., 2023). By employing this approach, 3D characteristic snowfall patterns at the ridge-scale can be replicated much faster than using a conventional atmospheric model. However, since dynamical downscaling involves running computationally intensive models, with the target to predict the atmospheric state in 3D at increasingly higher resolutions (nesting approach), statistical downscaling offers a computationally even faster solution through simplified relationships between high and low-resolution data and requires less input data. In order to derive these simplified relationships, descriptor variables are sought by analyzing high-resolution databases. The significance of high-resolution snow maps in mountainous areas has led to extensive research in statistically describing spatial snow depth distribution. Empirical relationships have been established with terrain parameters (e.g., Grünewald et al., 2013; Helbig et al., 2015; Skaugen and Melvold, 2019; Helbig et al., 2021) or with horizontal wind speed maps and terrain parameters such as shelter or exposure to prevailing winds (e.g., Purves et al., 1998; Winstral et al., 2002; Winstral and Marks, 2002). Several snow cover shaping processes can be described simultaneously through these statistical descriptions. Dadic et al. (2010b) introduced a statistical approach to characterize only preferential snow deposition on glaciers using both high-resolution vertical and horizontal mean wind speed maps. This parameterization was based on case studies conducted in a glacierized catchment, where Dadic et al. (2010a) identified significant correlations between measured high-resolution snow deposition maps and modelled vertical and horizontal mean wind speed maps. Despite its benefits, statistical downscaling can, however, have lower accuracy and known problems of extrapolation compared to dynamical downscaling. This may originate from a limited descriptive (observation) database or insufficient process descriptions, which will ultimately restrict the applicability. In summary, the choice of the most suitable approach depends on various factors such as the intended application, available input data, and computational resources.

In the following, we present a computationally efficient, potentially widely applicable method that statistically downscales low-resolution near-surface snowfall to high-resolution preferentially deposited snowfall in mountainous terrain. Thus, we focus on spatial snowfall deposition drivers through the wind and topography, neglecting redistribution. In Section 2.1, we describe how we first generated a large, diverse fine-scale snowfall database using the snow transport module of Alpine3D (A3D) driven by a large ensemble of atmospheric model ARPS (Advanced Regional Prediction System) wind fields on simulated topographies (Helbig et al., 2017). Several thousand model runs, under controlled weather conditions, allowed us to generate a database for fine-scale preferred snowfall deposition on a broad range of topographic characteristics. Section 3 details how we derived high-resolution downscaling factors for the low-resolution snowfall input by merging physical-based understanding in the data-driven, statistical analysis. In Section 3.2, we introduce two statistical downscaling models that emulate fine-scale distributed snowfall on topography using fine-scale terrain parameters and low-resolution near-surface wind data as input. In one scheme, fine-scale vertical wind speed is utilized. In the other scheme, we replace it with downscaled vertical wind speed, which does not require fine-scale temporal input. Besides evaluating the downscaling schemes with a model test data set on simulated topographies (Section 4.1), we assess performances with both model data and an acquired snowfall data set derived from optical imagery recorded by an unmanned aerial system (UAS) recorded optical imagery at Latschüelfurgga, Davos, Switzerland (Section 4.2).

2 Data

In this section, we present our extensive spatial model database for preferred snowfall deposition on simulated topographies. This database enabled us to create statistical downscaling methods for low-resolution near-surface snowfall. We further present a new data set of snow depth measurements obtained through UAS observations in a real mountainous setting and also describe the fine-scale ARPS-A3D preferred snowfall deposition modelings in the same environment. We assess the performance of our downscaling schemes using both data sets on actual terrain as well as with an independent subset of the model database (test data set).

2.1 Model database for fine-scale preferred snowfall deposition on simulated topographies

Figure 1 shows our recipe to derive the fine-scale snowfall database by (A) Generating simulated topographies, (B) Generating 3D wind fields and (C) Generating the snowfall database using (A) and (B). The following three paragraphs describe each step in more detail.

FIGURE 1

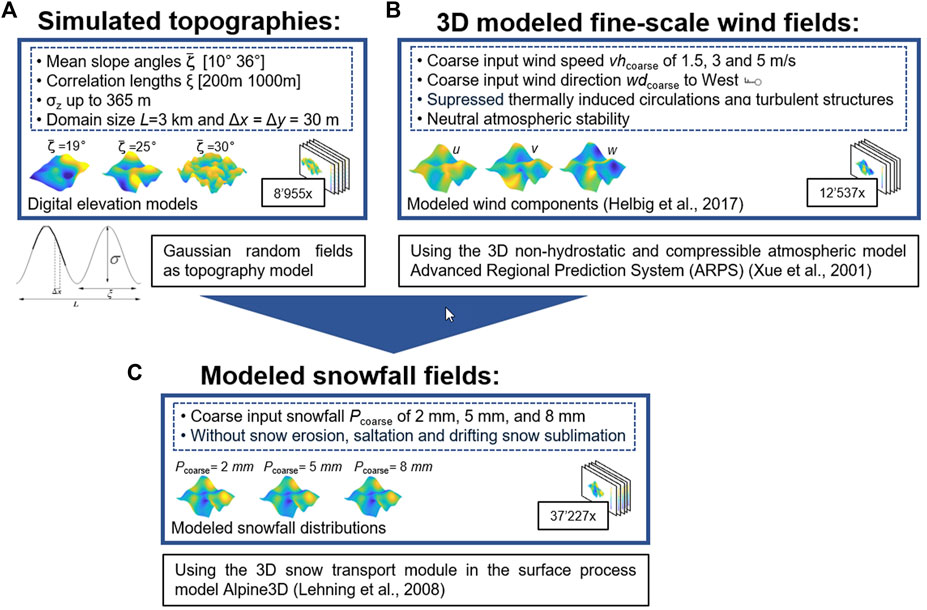
FIGURE 1. Workflow for generating the spatial snowfall and vertical wind speed database: (A) illustrates the ensemble of simulated topographies, (B) provides details on how to generate spatial 3D wind fields, and (C) demonstrates how (A) and (B) were combined to emulate preferential spatial deposition of snowfall. Numbers in squares indicate the number of performed model runs per workflow step.

Simulated topographies were used instead of actual topographies to encompass a wider range of terrain characteristics (see Figure 1A). If actual topographies were used, the number of terrain characteristics that could be described would be limited, thereby restricting the richness of the underlying model development data set. To generate simulated topographies, specifically digital elevation models (DEMs) with varying terrain elevations z, isotropic and stationary Gaussian random fields (GRFs) were employed. We chose GRF as simulated topography models because Gaussian statistics were found to effectively describe the geometrical aspects of realistic topographies across a wide range of mountainous terrain (Helbig and Löwe, 2012). The prescribed Gaussian covariance allowed the variation of the characteristic height (standard deviation σ_z) and width (correlation length ξ) of topographic features within the model domain for a fixed spatial mean slope. We selected five spatial mean slope angles $\bar{\zeta }$ (10°, 19°, 25°, 30°, and 36°). Nine σ_z, ξ-combinations were specified per $\bar{\zeta }$, and each combination was implemented with 199 realizations, resulting in an ensemble of about 8,955 simulated DEMs. Our choice of topographic features enabled us to generate a diverse ensemble of representative topographies in mountainous regions, encompassing a wide range of realistic mean slopes and typical geometries of topographic features (compare the values in Table 1 in Helbig and Löwe (2012) and in Helbig and Löwe (2014)). Slope angles ζ were determined from the partial derivatives ∂_xz and ∂_yz in orthogonal directions via ${\tan }^2\zeta ={({\partial }_{\text{x}}z)}^2+{({\partial }_{\text{y}}z)}^2$. A terrain parameter μ is associated with the mean square slope by $2{\mu }^2=\stackrel{̄}{{({\partial }_{\text{x}}z)}^2+{({\partial }_{\text{y}}z)}^2}=\overline{{\tan }^2\zeta }$. We note that μ is further related to σ_z and ξ via $\mu =\sqrt{2}{\sigma }_{\text{z}}/\xi$ since our isotropic Gaussian covariance implies a joint probability density for the partial derivatives that factorize into two Gaussians with standard deviation μ (Löwe and Helbig, 2012). The domain size L of the squared DEMs L x L was fixed at 3 km, and the horizontal resolution, or grid cell size, was set at Δx = Δy =30 m, resulting in 100 × 100 (N × N) sized DEMs. For more technical details regarding the generation of simulated topographies, please consult Helbig and Löwe (2012).

TABLE 1

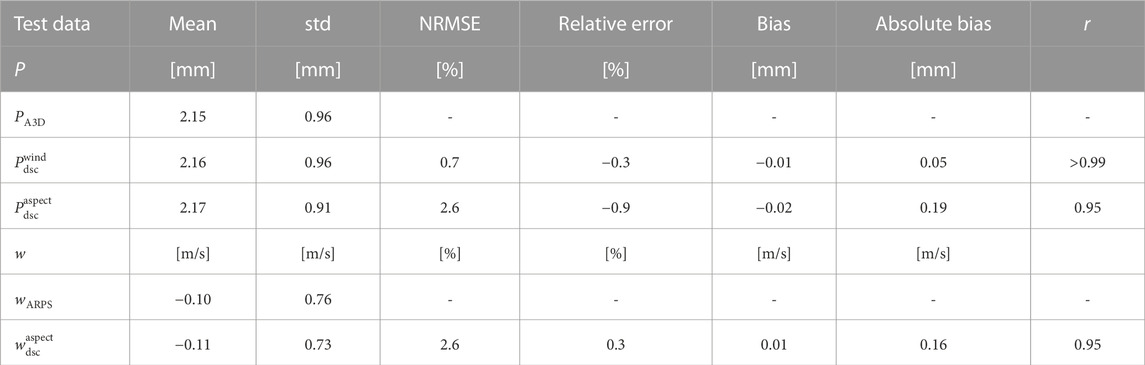
TABLE 1. Performance of downscaled snowfall with ARPS-A3D modeled snowfall (P_A3D) and downscaled vertical wind speed with ARPS modeled vertical wind speed w_ARPS on the test data set generated on simulated topographies. $P_{\text{dsc}}^{\text{wind}}$ and $P_{\text{dsc}}^{\text{aspect}}$ represent downscaled snowfall using the wind and aspect scheme, respectively. $w_{\text{dsc}}^{\text{aspect}}$ represents downscaled vertical wind speed using the aspect scheme.

2.1.1 3D fine-scale wind fields on simulated topographies

The ensemble of simulated topographies was used to generate 3D fine-scale wind fields in diverse mountainous terrain (Figure 1B). These wind fields were computed using the 3D nonhydrostatic and compressible atmospheric model ARPS (Xue et al., 2000; 2001). ARPS can emulate dominant wind-topography interactions, including sheltering, ridge-acceleration, separation, channelling, and recirculation (Raderschall et al., 2008), and reproduces well measured wind field characteristics (Chow et al., 2006; Raderschall et al., 2008; Zhou and Chow, 2011).

In this study, we used ARPS wind fields generated on simulated topographies as described in Helbig et al. (2017) and additional ARPS wind fields. To extend the ARPS wind data set, we maintained the controlled weather conditions as in Helbig et al. (2017), focusing solely on the mechanic wind-topography interactions. To achieve this, we suppressed thermally induced circulations by neglecting radiation effects and by assuming neutral atmospheric stability. We further prevented the development of turbulent structures by running ARPS for a rather short integration time of 30 s allowing the mean flow field to adapt to the local topography (Mott et al., 2010). The constant aerodynamic roughness length was set to 0.01 m across the entire model domain to mimic a uniform snow-covered mountain surface (Manes et al., 2008). We initialized ARPS with an inflow wind direction from the west, a spatially homogeneous wind speed, and neutral atmospheric stability. Using spatially homogeneous fine-scale input is equivalent to applying a single coarse-scale (low-resolution) input value. Three coarse-scale wind speed values were selected to initiate ARPS, representing typical free-stream near-surface wind conditions observed during snowfall events with preferential deposition (e.g., Dadic et al., 2010a; Mott and Lehning, 2010; Groot Zwaaftink et al., 2011; Vionnet et al., 2017; Wang and Huang, 2017).

• with 3 m/s on all simulated topographies (8,955 topographies) [data set as in Helbig et al. (2017)].

• with 5 m/s on topographies with $\bar{\zeta }$ of 19° (1,791 topographies) [data set as in Helbig et al. (2017)].

• with 1.5 m/s on topographies with $\bar{\zeta }$ of 19° (1,791 topographies) (data set extension).

We extended the wind database from Helbig et al. (2017) to include wind fields with an initial coarse wind speed value of 1.5 m/s, employing the same topographies as those used for the larger coarse-scale wind speed of 5 m/s. This extension allowed us to identify scaling factors for fine-scale deposited snowfall across a range of near-surface horizontal wind speed values. We use 3D ARPS wind fields to compute fine-scale preferentially deposited snowfall using the snow transport module of the A3D model. However, for the development of the downscaling schemes, we utilize near-surface ARPS wind speeds from the first layer above the ground, with an average depth of 2.95 m above the ground. The horizontal wind speed vh is computed as $vh={(u^2+v^2)}^{1/2}$, where u and v are the directional components. Out of 12,537 initiated ARPS model runs, 12,409 (99%) remained numerically stable. Based on the analysis of ARPS near-surface wind fields from Helbig et al. (2017), LeToumelin et al. (2023) found that topographies with higher spatial mean slope angles lead to overall lower local wind speeds and wider wind speed distributions due to increased momentum drag of the steeper topographies. Local wind speed accelerations in the data set were up to four times the initial wind speed of 3 m/s, while deceleration reduced wind speed to nearly zero. Angular deviations from the initial west inflow direction increased for topographies with spatial mean slope, ranging locally from 0° to 82° (Figures 1, 2 in LeToumelin et al. (2023)). Besides local ridge acceleration and deceleration on windward and leeward slope sides, the ARPS wind flow on Gaussian topographies thus displayed characteristic adjustments in response to the local terrain.

FIGURE 2

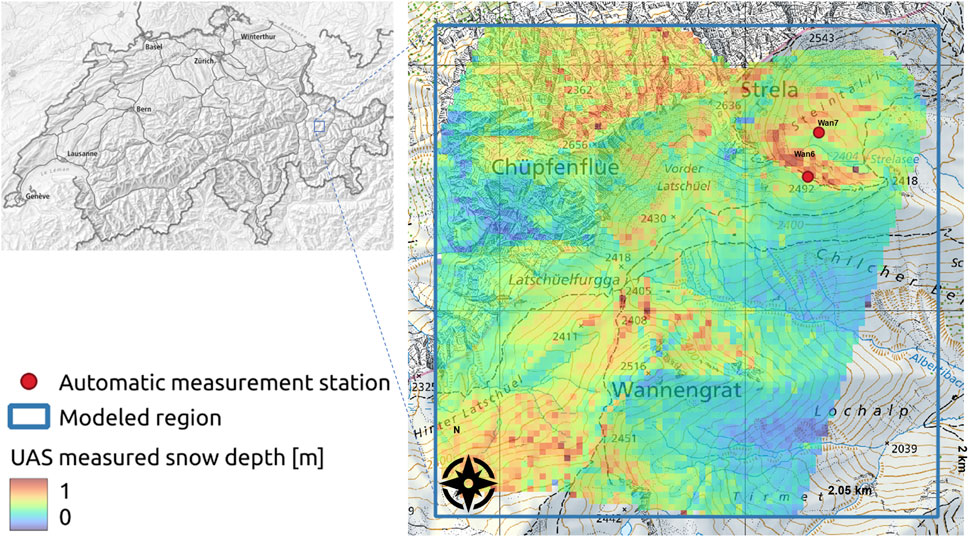
FIGURE 2. Overview of the Latsch region in eastern Switzerland, showing snow depth data derived from UAS and aggregated to a 25 m grid cell resolution (colored area) as well as the positions of the AWS stations Wan6 and Wan7 (red points), and the modeled region (blue square). The national map is sourced from Swisstopo (©swisstopo).

2.1.2 Snowfall database

We produced fine-scale fields of preferentially deposited snowfall by using the snow transport module of the A3D model (Lehning et al., 2006) driven with the 3D ARPS wind fields (see Figure 1C). A3D is a surface process model in a modular structure with the main module being the snow-cover module SNOWPACK (Lehning et al., 1999; Bartelt and Lehning, 2002; Lehning et al., 2002a; b). All modules are driven by MeteoIO, a meteorological data pre-processing library for handling the input (Bavay and Egger, 2014). To focus solely on preferential snowfall, we only used the suspension scheme within the snow transport module of A3D and prevented any erosion, saltation, and drifting snow sublimation from occurring (implemented as described in Doorschot and Lehning, 2002; Lehning et al., 2008; Clifton and Lehning, 2008; Groot Zwaaftink et al., 2011). Our model setup is similar to that of Lehning et al. (2008); Mott and Lehning (2010); Mott et al. (2010, 2014), who conducted A3D runs that excluded erosion and saltation processes in the snow transport model. Their results demonstrated the significant impact of preferential deposition on snow distribution and further depicted measured spatial patterns well. It is worth noting that drifting snow sublimation occurs only during strong wind events and in regions with unsaturated air (Groot Zwaaftink et al., 2013). In contrast, preferential deposition does not require high wind speeds but does require saturated air.

To mimic conditions of saturated, cold air and avoid snow melt, we initialized our modelings with −5°C air and ground surface temperature, 100% relative humidity, no incoming shortwave radiation and a fixed longwave radiation value. We used a longwave radiation value of 280 W/m², equivalent to the annual mean all-sky longwave radiation recorded in Davos, Switzerland (1995–1998) (Marty, 2001). The surface was snow-free at the start of each model run. We calculated preferential snow deposition using A3D for each ARPS wind field. However, we additionally initiated each wind field with three different snowfall values (P), specifically 2, 5, and 8 mm. All A3D input variables are distributed uniformly across the model domain. It is worth noting that the spatially homogeneous distribution is akin to applying a single coarse-scale model input value, which is why we denote this input with the subscript “coarse”, such as P_coarse. To ensure the validity of our A3D setup, we ran the model for three hourly time steps, which confirmed that the resulting snowfall distributions were identical. We therefore used data from one time step for further analysis. To minimize biases caused by conversion with a snow density formula, we refrained from converting deposited snowfall precipitation to snow depth within the A3D model. Modelled preferentially deposited snowfall is therefore snow water equivalent (SWE).

To ensure the formation of mean wind flow features with minimal boundary effects and avoid using unrealistic ARPS wind speeds generated at the domain boundaries, we followed the methodology of Helbig et al. (2017) by restricting our analysis of the 100 × 100 model domain to an inner area of 69 × 79 grid cells. The resulting model domain had a mean length L of 2,220 m, with smaller dimensions of L_x = 2070 m and L_y = 2,370 m, as opposed to the larger 3 km × 3 km DEM domain. We further removed local wind and snowfall data if (a) p < 0, (b) vh < 0.5 m/s, (c) ζ ≥ 60° (steep slopes), or (d) less than three topographic features were captured per domain (L/ξ < 3). The latter criterion ensures that the relevant processes in a domain were well represented. We excluded steep slopes from the analysis to prevent the propagation of numerical inaccuracies originating from the ARPS wind fields into the computation of preferentially deposited snowfall. These inaccuracies arise in ARPS from utilizing the terrain-following vertical coordinate system on steep slope angles where large grid aspect ratios result at the surface and translate in the momentum equations, as outlined by Lundquist et al. (2010). A3D was run with 12,409 valid wind fields for each of the three coarse snowfall input values, producing 12,240 valid snowfall fields per input (99%). After post-processing, approximately 166 million individual valid snowfall values (83%) remained for all three low-resolution wind speed and snowfall values.

2.2 Measured, spatial continuous snow depth data in eastern Switzerland

We collected snowfall data in a small alpine catchment above Davos in the eastern Swiss Alps using a WingtraOne unmanned aerial system (UAS), which uses the VTOL (vertical take-off and landing) and latest post processing kinematics (PPK) technology and is equipped with a 42 megapixel Sony RX1R II camera. Two UAS flights were performed at an average height of 216 m above terrain and an overlap of 60% across- and 80% along track: once in summer (17 September 2020) when there was no snow, and again a day after the first significant snowfall (28 October 2020). We utilized 3,485 optical images to create digital surface models (DSM) through photogrammetric processing. By subtracting the summer DEM from the winter DSM, we derived spatial new snow depth, as in Bühler et al. (2017); Eberhard et al. (2021). The acquired area above Davos (referred to in the following as “Latsch”) covers about 3.6 km² at a 10 cm horizontal grid cell resolution (Figure 2). The PPK positioning accuracy (x = 2.39 cm, y = 4.71 cm and z = 9.68 cm) was assessed at three independently measured check points. We ignored snow depth data less than 0 m or greater than 3 m and aggregated summer and winter DEM’s from 10 cm grid cell resolution to a 25 m grid resolution. The UAS acquisition took place on 28 October, around noon, after a snowfall event that lasted from the morning of 26 October to noon on 27 October 2020 (data is available from Bühler et al. (2022b)).

2.3 Modeled preferential snowfall deposition in eastern Switzerland

We evaluate downscaled near-surface snowfall for the October 2020 event in the Latsch area with measured (Section 2.2) as well as modeled preferred snowfall deposition. As model input, we employed meteorological data from automatic weather stations (AWS) in the area (Wan6 and Wan7 in Figure 2), as well as model output from the COSMO (Consortium for Small-Scale Modeling) numerical weather prediction model (MeteoSwiss). AWS measured hourly values were derived from 10-min intervals of data, including flat field snow depth measurements from a SR50 sonic distance sensor at Wan7 and wind direction measurements from a Young wind vane at Wan6. Hourly horizontal near-surface wind speeds were obtained from the COSMO-1E ensemble forecasting system (analysis) after applying bias correction (Winstral et al., 2019) and averaging for the two coarse inflow grid cell values. For the modeling purposes, we employed the UAS-acquired summer DEM with a 25 m horizontal grid cell resolution.

We followed the approach of prior studies that used ARPS-A3D modeling to examine snow transport and deposition processes (e.g., Mott and Lehning, 2010; Groot Zwaaftink et al., 2011; 2013). Instead of computing an ARPS wind field for every time step, these studies illustrated that a few wind fields are sufficient for characterizing the predominant mean flow characteristics in the area during an event. Here, to model the entire snowfall event, we identified five representative sub-snowfall events from the cumulative snowfall distribution at Wan7, based on its quantiles. This reduced the 28 h event period to five time steps that encompassed the dominant weather patterns of the entire event period. For each sub-event period, we determined the mean near-surface wind speed, most frequent wind direction, and sum of snowfall, which were applied spatially homogeneously as input for ARPS (wind) and the A3D snow transport module (snowfall) (Figure 3). We further utilized the same spatially uniform meteorological inputs for saturated, cold air to initialize the snow transport module of A3D, applied the same setup for A3D and ARPS and post-processing techniques, as used in the modelings on simulated topographies.

FIGURE 3

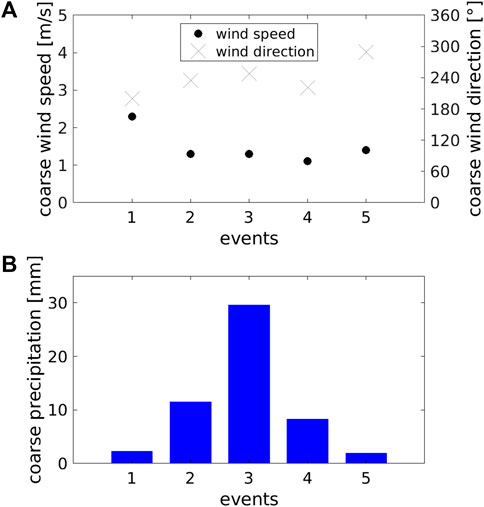
FIGURE 3. Coarse-scale meteorological input for each of the five sub-events of the October 2020 snowfall event in the Latsch region (Figure 2): (A) Wind speed (bias-corrected COSMO) and wind direction (Wan6), and (B) Total snowfall (identified from measured snow depth changes at Wan7).

We used a constant new snow density value of 110 kg/m³ for all conversions between snow depth and snowfall for the event in the Latsch region. This value was obtained by manually measuring the 24 h new snow amounts and SWE at the nearby observer station at the SLF Weissfluhjoch field site on the morning of October 27th. Wan7 recorded a total of 48.73 cm of new snow during the event period, which, when converted using the snow density value, amounts to a total snowfall of 53.6 mm SWE.

3 Methods

In the previous section, we presented our vast, diverse database for fine-scale snowfall and all wind components that is suitable for training statistical models using machine learning techniques. In this section, we introduce our two downscaling schemes for low-resolution snowfall, solely utilizing near-surface meteorology and terrain characteristics. Instead of letting the computer identify the relevant relationships in the data, we decided to integrate some physical and empirical process understanding in a regression-based, data-driven downscaling scheme approach. We therefore begin this section, by identifying scaling factors for fine-scale deposited snowfall and vertical wind speed. These fine-scale downscaling factors capture the dominant unresolved processes in low-resolution deposited snowfall within mountainous regions. Our variable naming convention going forward is: Coarse-scale variables are labeled with a “coarse” subscript, while fine-scale variables have no scale indicator. Fine-scale variables originating from models are labeled with their respective model name as a subscript: modeled with ARPS (“ARPS”), with Alpine3D (“A3D”) or with a downscaling model (“dsc”).

3.1 Identification of scaling factors

To identify the primary downscaling factors crucial for accurately emulating fine-scale deposited snowfall in mountainous regions, we analyzed the entire snowfall model database. In this analysis, we considered previously discovered correlations with vertical wind speed (Lehning et al., 2008; Dadic et al., 2010a) and local terrain characteristics (Winstral et al., 2002, e.g.). Grouping modeled deposited snowfall P_A3D according to coarse snowfall P_coarse and plotting it as a function of normalized vertical wind speed w_ARPS, reveals that deposited snowfall scales linearly with coarse snowfall P_coarse (compare Figures 4A–C). We confirm that snowfall scales best with vertical wind speed. The negative correlation between modeled deposited snowfall P_A3D and vertical wind speed w_ARPS (Figure 4) becomes stronger with increasing coarse horizontal wind speed vh_coarse, suggesting non-linear dependencies (compare Figures 4D–F). Moreover, we observe an increased spatial variability in deposited snowfall as wind speed increases, as evidenced by the broader distributions for the extreme vertical wind speed quantiles in Figure 4 and the broader distribution widths of deposited snowfall with increasing vh_coarse in Figures 4D–F. The Pearson correlation values r obtained were 0.7 for P_A3D and P_coarse, and −0.63 for P_A3D and w_ARPS.

FIGURE 4

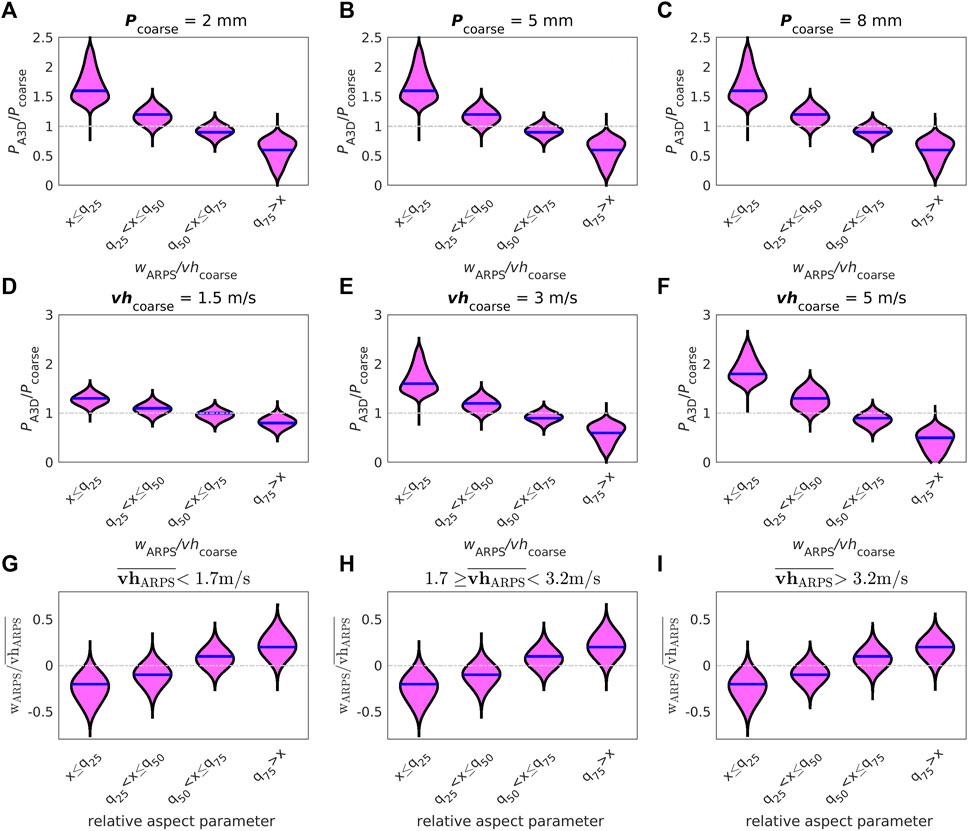
FIGURE 4. Modeled values from the full data set (test+training): (top) and (middle) for snowfall P_A3D and (bottom) for ARPS modeled vertical wind speed w_ARPS. (top) for vh_coarse = 3 m/s and a coarse-scale snowfall P_coarse = input value of (A) 2 mm, (B) 5 mm and (C) 8 mm. (middle) for P_coarse = 2 mm, spatial mean slope angles of 19° and a coarse-scale horizontal wind speed vh_coarse value of (D) 1.5 m/s, (E) 3 m/s and (F) 5 m/s (bottom) for P_coarse = 2 mm, spatial mean slopes of 19° and an ARPS modeled spatial mean horizontal wind speed $\overline{v{h}_{\text{ARPS}}}$ value being (G) $<$ 1.7 m/s, (H) 1.7 $\ge \overline{v{h}_{\text{ARPS}}}<$ 3.2 m/s and (I) $\overline{v{h}_{\text{ARPS}}}>$ 3.2 m/s. Normalized snowfall data is binned according to w/vh_coarse quantiles with q₂₅=−0.2, q₅₀=0 and q₇₅=0.1 and normalized vertical wind speed according to quantiles of the relative aspect parameter Δψ with q₂₅=−45° and q₅₀=0, q₇₅=45. The top and bottom edges of each violin represent distances 1.5 times the interquartile range from the median. Outliers beyond these limits are not shown.

To achieve our objective of developing a versatile and broadly applicable downscaling scheme, we further sought to identify static fine-scale downscaling factors for the primary scaling variable in preferential snowfall deposition: the vertical wind speed. We found that a terrain aspect angle relative to coarse wind direction together with the slope angle can well depict the typical behavior of vertical wind speed in mountainous terrain, with positive vertical wind speeds (updraft) on the windward side of mountains and negative (downdraft) on the lee side. We determine the relative aspect parameter of the terrain using the following steps (see Data availability statement for a public script): First, we convert all angles to the compass system, where 0° represents north and the count goes clockwise. Second, we calculate the angular deviations between the terrain aspect ψ and the coarse wind direction wd_coarse, setting wd_coarse as new 0°. In simpler terms, we determine the rotation angle needed to align the terrain aspect with the coarse wind direction. We then convert the resulting values such that they range from 0° to 180°, where 0°–90° correspond to windward terrain slopes, and 90°–180° correspond to slopes on the lee side of mountains. Finally, we obtained a relative terrain aspect parameter (Δψ) by subtracting these angular deviations from 90°, resulting in values ranging from −90° to 0° for slopes more on the lee side and from $>0°$ to 90° for more windward oriented slopes. Thus, Δψ mimics the behavior of vertical wind speed as also evidenced by its strong correlation (r = 0.8) with the modeled vertical wind speed, w_ARPS. Correlation between w_ARPS and the relative aspect parameter Δψ slightly decreases with increasing $\overline{v{h}_{\text{ARPS}}}$ (compare Figures 4G–I). Correlation between w_ARPS and Δψ decreases similarly, though slightly less, with increasing vh_coarse [not shown]. P_A3D and w_ARPS also scale weakly with μ (correlations of 0.15 and −0.19, respectively).

3.2 Downscaling schemes

Due to the observed linear relationship between deposited snowfall and low-resolution input P_coarse, we limited the data used for model development to one P_coarse of 2 mm, which represents approximately one-third of the entire database. We partitioned the model database randomly into 80% for training the statistical downscaling models and 20% for testing, and repeated this process 10 times.

We compute downscaled snowfall P_dsc by applying a locally varying downscaling factor X_dsc to modify coarse-scale snowfall P_coarse in each fine-scale grid cell:

$P_{\text{dsc}}=P_{\text{coarse}}{X}_{\text{dsc}}.(1)$

We developed two nonlinear statistical downscaling factors by using the identified scaling factors for P_coarse and w. The underlying functions of both downscaling factors were motivated by considering the observed behavior in our database, particularly near limit values of scaling variables, and by drawing on insights from previously reported process understanding. All downscaling models were derived by fitting robust M-estimators using iterated reweighted least squares, which were implemented in the R v3.6.0 statistical programming language (R Core Team, 2019) and its robustbase v0.93-6 package (Maechler et al., 2020).

3.2.1 Wind scheme

First, we introduce a “wind scheme”, in which X_dsc is a function of local vertical wind speed w and local slope parameter μ:

$P_{\text{dsc}}^{\text{wind}}=P_{\text{coarse}}{X}_{\text{dsc}}^{\text{wind}}\left(w,\mu \right).(2)$

$X_{\text{dsc}}^{\text{wind}}(w,\mu )$ in Eq. 2 is:

$X_{\text{dsc}}^{\text{wind}}\left(w,\mu \right)=\text{erfc}{\left(\text{a}w\left(w+|w|\right)\right)}^{\text{b}}\left(1-\text{c}w+\text{d}{w}^3\right)\left(1+\text{e}{\mu }^{\text{f}}\right),(3)$

with the complementary error function erfc(), w in m/s and constant parameters a = 0.4825 (±2e-04), b = 0.03418 (±2e-05), c = 0.592003 (±1e-06), d = 0.004452 (±1e-06), e = 0.24714 (±1e-05) and f = 2.24223 (±7e-05). The 95% confidence intervals for the fit parameters are provided in parentheses.

3.2.2 Aspect scheme

Second, we introduce an “aspect scheme”, in which X_dsc is now a function of downscaled vertical wind speed $w_{\text{dsc}}^{\text{aspect}}$ and local slope parameter μ:

$P_{\text{dsc}}^{\text{aspect}}=P_{\text{coarse}}{X}_{\text{dsc}}^{\text{aspect}}\left(w_{\text{dsc}}^{\text{aspect}},\mu \right).(4)$

For $X_{\text{dsc}}^{\text{aspect}}(w_{\text{dsc}}^{\text{aspect}},\mu )$, we use Eq. 3 but replace w with $w_{\text{dsc}}^{\text{aspect}}$ to maintain the same downscaling factor as in the wind scheme, i.e., $X_{\text{dsc}}^{\text{aspect}}(w_{\text{dsc}}^{\text{aspect}},\mu )=X_{\text{dsc}}^{\text{wind}}(w_{\text{dsc}}^{\text{aspect}},\mu )$. As fine-scale near-surface vertical wind speed w is frequently not available, we developed a downscaling scheme for w. To achieve this, we followed the approach used here for downscaling snowfall (Eq. 1) but used fine-scale ARPS modeled wind speed from the training database, specifically at the P_A3D locations. Downscaled vertical wind speed w_dsc is computed by modifying the spatial mean of local horizontal wind speeds $\overline{vh}$ with a locally varying downscaling factor Y_dsc. We modify $\overline{vh}$, rather than vh_coarse, to account for the wind drag over unresolved complex topography. This adjustment can be thought of as including the influence of the surrounding terrain before implementing local modifications. We introduce a vertical wind speed downscaling “aspect scheme”, where Y_dsc is a function of the local relative terrain aspect parameter Δψ (terrain aspect ψ relative to coarse-scale wind direction wd_coarse) and local slope parameter μ:

$w_{\text{dsc}}^{\text{aspect}}=\overline{vh}{Y}_{\text{dsc}}^{\text{aspect}}\left(\mathrm{\Delta }\psi ,\mu \right).(5)$

$Y_{\text{dsc}}^{\text{aspect}}(\mathrm{\Delta }\psi ,\mu )$ is:

$Y_{\text{dsc}}^{\text{aspect}}\left(\mathrm{\Delta }\psi ,\mu \right)=\left[{\text{a}}^{\prime }-{\text{b}}^{\prime }\left(\mathrm{\Delta }\psi \right)+{\text{c}}^{\prime }\text{erf}\left({\text{d}}^{\prime }\left(\mathrm{\Delta }\psi \right)\right)\right]\left({\text{e}}^{\prime }+{\mu }^{{\text{f}}^{\prime }}\right),(6)$

with constant parameters are a’ = −0.087122 (±5e-06), b’ = 0.4788 (±9e-04), c’ = 2.068 (±2e-03), d’ = 0.6298 (±3e-04), e’ = −0.046577 (±5e-06) and f’ = 0.72451 (±2e-05). The 95% confidence intervals for the fit parameters are again provided in parentheses.

If local vh is unavailable to calculate the spatial mean of horizonal wind speeds $\overline{vh}$, a subgrid parameterization for $\overline{vh}$ can be used. A subgrid parameterization for horizontal wind speed (vh_sgp) approximates the unresolved topographic drag for coarse resolution horizontal wind speed vh_coarse (e.g., Beljaars et al., 2004; Rontu, 2006; Jimenez and Dudhia, 2012; Helbig et al., 2017). The subgrid parameterization from Helbig et al. (2017) scales a vh_coarse with a subgrid topographic scaling factor $X_{\text{sgp}}^{\text{topo}}$, which depends on the characteristic width of topographic features ξ per model domain size L and mean squared slope μ in the coarse grid cell. $X_{\text{sgp}}^{\text{topo}}$ was developed using largely the same ARPS wind data as used in the present study, resulting in:

$v{h}_{\text{sgp}}=\overline{vh}=v{h}_{\text{coarse}}{X}_{\text{sgp}}^{\text{topo}}\left(L/\xi ,\mu \right).(7)$

For $X_{\text{sgp}}^{\text{topo}}$, Helbig et al. (2017) used the subgrid sky view factor, i.e., $X_{\text{sgp}}^{\text{topo}}=F_{\text{sky,sbg}}(L/\xi ,\mu )$, which can be parameterized as in Helbig and Löwe (2014). We can thus approximate $\overline{vh}$ with vh_sgp (Eq. 7) when computing $w_{\text{dsc}}^{\text{aspect}}$ (Eq. 5), which additionally enables snowfall downscaling via Eq. 4 without relying on fine-scale horizontal wind speed data. With this, our downscaling schemes exhibit a modular character, providing flexibility for enhancing or replacing individual model components.

3.3 Performance measures

We use various performance measures to evaluate the downscaling schemes against modelings or measurements. These include relative error measures such as bias error (modeled-downscaled), relative error (bias/coarse input value), and Pearson correlation coefficient r to assess correlation. We also calculate absolute error measures, including the normalized root-mean-square error (NRMSE) (normalized by the data range) and absolute bias.

4 Results

4.1 Performance on model test data set

We begin the assessment of our downscaling schemes by evaluating the performances using the model test data set, which was generated on simulated topographies.

4.1.1 Downscaled snowfall on simulated topographies

Modeled and downscaled snowfall show good agreement on our test data set (Table 1), with similar means and standard deviations. Relative and absolute errors for the wind scheme are below 1%, while for the aspect scheme they are lower than 3%. Overall, the wind scheme performs slightly better than the aspect scheme.

To further scrutinize the model performances, we computed relative errors for groups of normalized vertical wind speed (w_ARPS/vh_coarse) and slope angle, which were determined based on the 0.25, 0.5, and 0.75 quantiles (q25, q50, q75) of the corresponding distribution. Relative errors in downscaled snowfall increase at the largest and lowest vertical wind speeds (Figure 5), with increasing slope angles (Supplementary Figure S3) and with coarse horizontal wind speed [not shown]. These findings align with observing the largest relative errors occurring for the largest positive and negative vertical wind speeds (Figure 5). As steep slopes tend to have the largest up- and downdrafts, especially on windward or leeward-facing slopes, the largest relative errors are concentrated on such steep terrain.

FIGURE 5

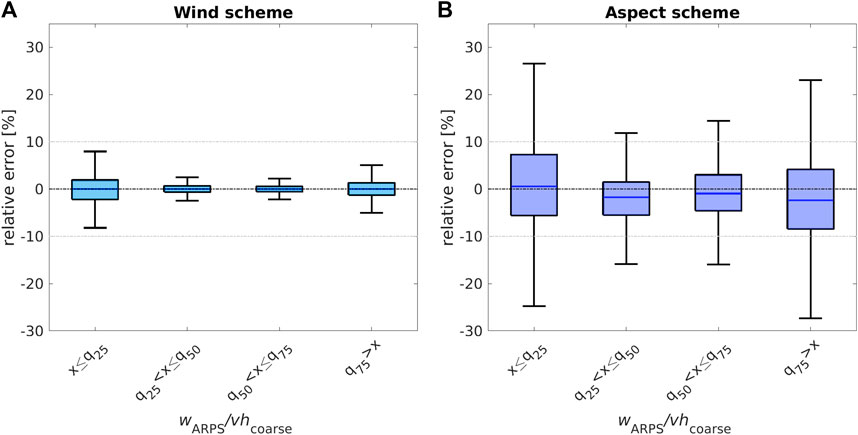
FIGURE 5. Relative errors between ARPS-A3D modeled and downscaled snowfall for our test data set as a function of normalized ARPS modeled vertical wind speeds w_ARPS/vh_coarse quantiles with q₂₅=−0.2, q₅₀=0 and q₇₅=0.1. (A): $P_{\text{dsc}}^{\text{wind}}$ (wind scheme) and (B): $P_{\text{dsc}}^{\text{aspect}}$ (aspect scheme).

While both downscaling schemes have an overall similar error distribution across the entire vertical wind speed distribution, relative errors of the aspect scheme are clearly larger and more scattered, especially for the largest and lowest vertical wind speeds. Similarly, relative errors of the aspect scheme are larger and more scattered across the entire slope angle distribution. However, the interquartile range of all relative errors for both schemes is mostly lower than 10%, with median relative errors lower than 5% for the entire vertical wind speed as well as slope angle distribution (Figure 5, Supplementary Figure S3).

4.1.2 Downscaled vertical wind speed on simulated topographies

Modeled and downscaled vertical wind speed show very good agreement on our test data set (Table 1). The means and standard deviations are very similar, with relative and absolute errors below 3%. The overall performance of downscaled vertical wind speed is very similar to that of the aspect scheme for snowfall (see Table 1).

We again analyzed model performances in more detail by computing relative errors for groups of normalized vertical wind speed (w_ARPS/vh_coarse) and slope angle derived from the 0.25, 0.5, and 0.75 quantiles of the corresponding distribution. Relative errors for downscaled vertical wind speed increase for the largest and lowest vertical wind speeds (Figure 6A) and with increasing slope angles (Figure 6B). We observe similar distributions of the relative errors for downscaled vertical wind speed to that observed for downscaled snowfall, especially with the aspect scheme for snowfall. The interquartile range of all relative errors is again lower than 10%, and the median errors are lower than 5% for the entire vertical wind speed and slope angle distribution (Figure 6).

FIGURE 6

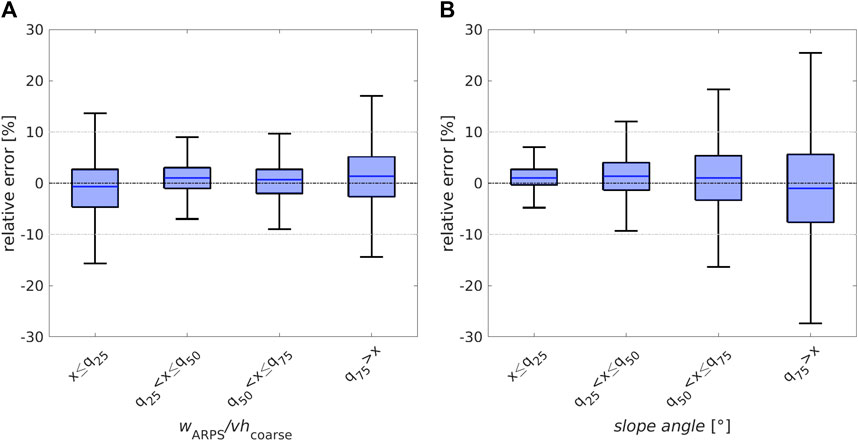
FIGURE 6. Relative errors between ARPS modeled (w_ARPS) and downscaled $(w_{\text{dsc}}^{\text{aspect}})$ vertical wind speed for our test data set as a function of (A) normalized ARPS modeled vertical wind speeds w_ARPS/vh_coarse quantiles with q₂₅=−0.2, q₅₀=0 and q₇₅=0.1 and (B) slope angle quantiles with q₂₅=11°, q₅₀=17° and q₇₅=25°.

4.2 Performance on real topography in eastern Switzerland

Following the presentation of performances on simulated topographies, this section showcases assessments conducted on an actual topography in eastern Switzerland. We assess the performance of all downscaling schemes using model data and, for the snowfall downscaling schemes, actual measurements of new snow depth. We further evaluate the performances with previous downscaling methods, which serve as a benchmark for our schemes. We chose a commonly used statistical method for downscaling snowfall that utilizes the Sx parameter (Winstral et al., 2002) with maximum search distance of 300 m as suggested in (Schirmer et al., 2011). We adopt the implementation used in MeteoIO (Bavay and Egger, 2014), a meteorological data preprocessing library. We use a deep learning approach called “DEVINE” (LeToumelin et al., 2023) for vertical wind speed.

4.2.1 Downscaled snowfall on real topography

Comparing measured snow depth with modeled and downscaled snow depth, we observe overall similar magnitudes and no significant biases. The closest agreement is among modeled and all downscaled snow depths. Despite this, the benchmark downscaling scheme clearly produces less detailed spatial deposition patterns (Figure 7), a result which has been previously reported (Schirmer et al., 2011).

FIGURE 7

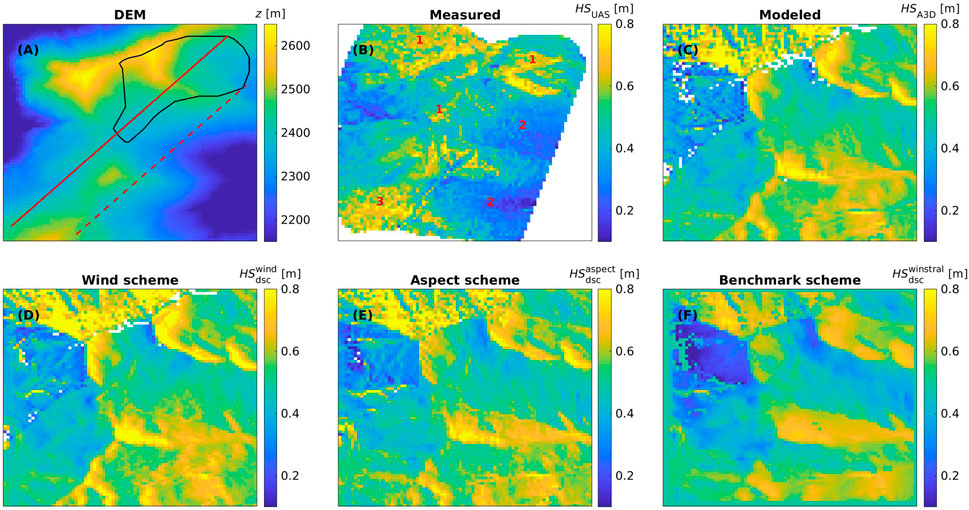
FIGURE 7. Spatial images for the Latsch region site: (A) DEM, (B) HS_UAS (measured), (C) HS_A3D (modeled), (D) $H{S}_{\text{dsc}}^{\text{wind}}$ (downscaled), (E) $H{S}_{\text{dsc}}^{\text{aspect}}$ (downscaled) and (F) $H{S}_{\text{dsc}}^{\text{winstral}}$ (downscaled). Modeled and downscaled snowfall was converted to HS using observed, spatially constant snow density. Note that spatial data here is presented without post-processing (Section 2.1.2), but excludes data (shown in white) where HS < 0, as discussed in Section 5.

However, there were some local differences between the measurements and modeled and all downscaled patterns (marked by 1–3 in Figure 7B). These can be attributed to (1) avalanche deposits (seen on images from automatic camera nearby; Supplementary Figure S1) where measurements show more snow at the bottom of the slopes and less snow in the starting zones, (2) lower elevation terrain where less snow was measured than modeled possibly due to rapid snow settlement and snow melt (local energy balance impacts) on the day of the UAS flight (maximum AWS measured air temperature of 7° at Wan6 on 28 October), and (3) north/northeast-facing slopes that remain shaded and where measurements show more snow as there was still snow from a previous snowfall (confirmed by images from automatic camera; Supplementary Figure S2). Our model chain and the downscaling schemes obviously do not account for these intricate processes.

Along two cross sections through the Latsch region (red lines in Figure 7A), all downscaling schemes exhibit the closest agreement with the modeled snow deposition, demonstrating NRMSE and relative errors ranging between 7% and 15%, and −3% and 5%, respectively. The measurements differ considerably from both the model and downscaling schemes, with larger NRMSE and relative errors ranging between 25% and 31%, and −12% and −4%, respectively (Figure 8). One cross section (solid line) passes through north/northeast-facing slopes (area “3”, Figure 7A) and an avalanche deposition zone (area “1”), where measured snow depth is greater than modeled and downscaled snow (Figure 8A at 0–400 m and 400–700 m). The second cross section (dashed line) passes through areas with slightly lower terrain elevations (area “2”), where we believe that local energy balance processes caused warmer ground and hence lower snow depth than the amount model and downscaling schemes predict (Figure 8B at 200–500 m and 700–1,200 m). The benchmark downscaling scheme locally produces lower snow deposition compared to the other downscaling models along the transects. This is reflected in differences in the relative error of 5.1% as opposed to 0.1% and −2.5%, particularly noticeable on windward and leeward sides of slopes (e.g., Figure 8A at 1,200–1,400 m and in (B) at 300–600 m and 1,200–1,500 m). This may be attributed to the smoother deposition patterns of the benchmark scheme.

FIGURE 8

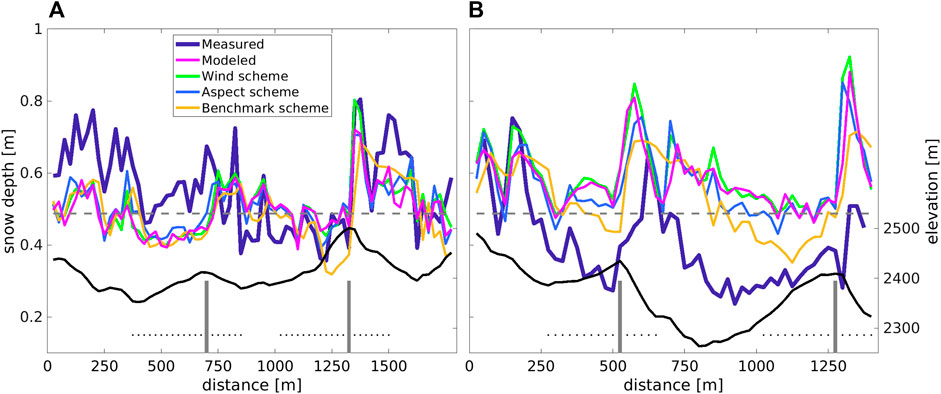
FIGURE 8. Two cross sections for measured, modeled and downscaled deposited snow depth HS through the Latsch region (see Figure 7A): (A) Along the red solid line and (B) Along the red dashed line. MeteoIO/Winstral is the benchmark downscaling scheme. The gray dashed lines mark the event total snowfall, i.e., the sum of coarse-scale snowfall input. The gray vertical lines indicate the ridges where we have estimated contributions of preferential snowfall deposition; corresponding cross-ridge distances are delineated by the dotted lines (see Section 5)

We now focus our analysis on the subarea within the black outline in Figure 7A to evaluate preferential snowfall deposition patterns. All spatial means and standard deviations closely match measured snow data (Table 2). While medians from all downscaling schemes clearly agree best with the model, only the distributions from the wind and aspect scheme closely resemble the model (Figure 9). In contrast, the distribution from the benchmark scheme is broader and less balanced around the median, consistent with observed smoother spatial patterns (Figures 7, 8). Measured snow deposition has the lowest median and skews toward lower values, resulting in overall larger errors with the model and all downscaling schemes (Table 2). Some of these discrepancies may be attributed to using a single uniform snow density for converting snowfall to new snow depth, which does not account for spatio-temporal variations in snow density during a 28-h event. To address this, we evaluated performance against modeled snow deposition, leading to consistent reductions in relative and absolute errors for the wind and aspect scheme, and partial improvements for the benchmark scheme (values in parentheses in Table 2). Next, we compared the performance of the downscaling schemes on real and simulated topographies by pooling snowfall data from all five events. This analysis revealed that the wind and aspect schemes performed only slightly worse on real topography compared to simulated topographies (maximum 4% larger errors; see Table 2 vs. 1). This and that some of the five sub-event snowfall amounts in the Latsch region were larger than in the model database on simulated topographies, confirm that the downscaling schemes work well, even for larger snowfall values.

TABLE 2

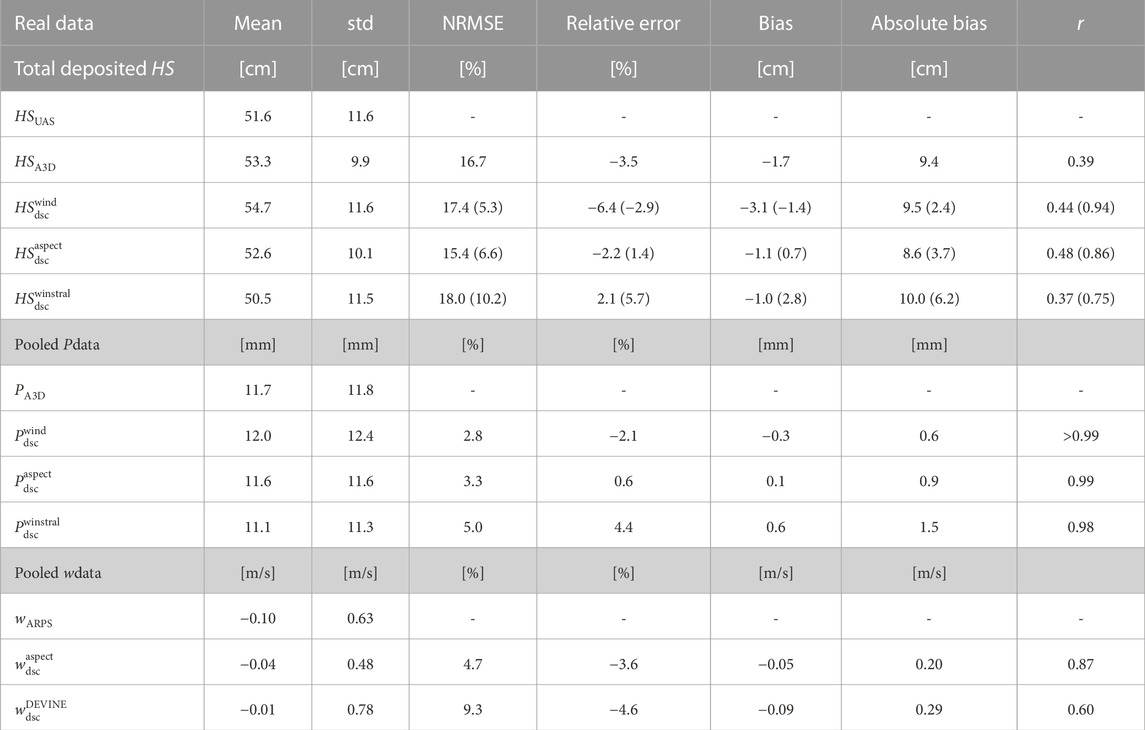
TABLE 2. Performance measures are assessed for a specific subarea of the real topography, as illustrated in Figure 7A, and for vertical wind speed, as depicted in Figure 11: (1) Total deposited HS: Downscaled deposited snow depth using the wind, aspect and the benchmark downscaling scheme ($H{S}_{\text{dsc}}^{\text{wind}}$, $H{S}_{\text{dsc}}^{\text{aspect}}$, $H{S}_{\text{dsc}}^{\text{winstral}}$). Evaluations are with measured snow depth HS_UASand in parentheses with ARPS-A3D modeled snow depth HS_A3D. (2) Pooled Pdata: Pooled Pdata from all 5 snowfall events. Evaluations are with ARPS-A3D modeled snowfall (P_A3D). (3) Pooled wdata: Pooled wdata from all 5 events. $w_{\text{dsc}}^{\text{aspect}}$and $w_{\text{dsc}}^{\text{DEVINE}}$represent downscaled vertical wind speed using the aspect and the benchmark downscaling scheme, respectively. Evaluations are with ARPS modeled vertical wind speed w_ARPS.

FIGURE 9

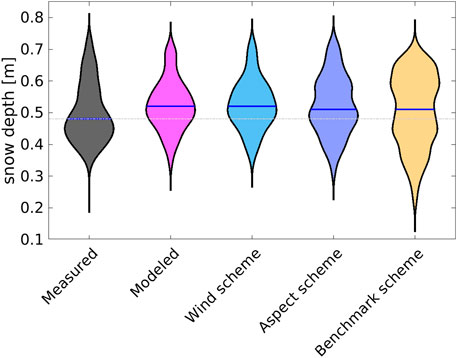
FIGURE 9. Comparison of measured, modeled, and downscaled deposited snow depth statistics for the Latsch region site (black outline in Figure 7A). The plot displays the median values (indicated by a blue line within the violin) and density distributions (violin shape). The top and bottom edges of each violin represent distances 1.7 times the interquartile range from the median. Outliers beyond these limits are not shown. MeteoIO/Winstral is the benchmark downscaling scheme.

Relative errors, for groups of normalized vertical wind speed (w_ARPS/vh_coarse) derived from q25, q50 and q75 of the distribution, increase from wind to aspect to benchmark schemes, as shown in Figure 10. Although relative errors of wind and aspect scheme are larger in the real environment, they are still in similar orders of magnitude compared to those on simulated topographies (Figures 10A, B versus Figure 5), which is reassuring. Interestingly, the aspect scheme has the most balanced relative errors around zero across all wind speeds, resulting in the lowest overall relative error and bias compared to the wind and benchmark scheme (Table 2). Relative errors increase only slightly at the largest and lowest wind speeds, which was more pronounced for the test data set.

FIGURE 10

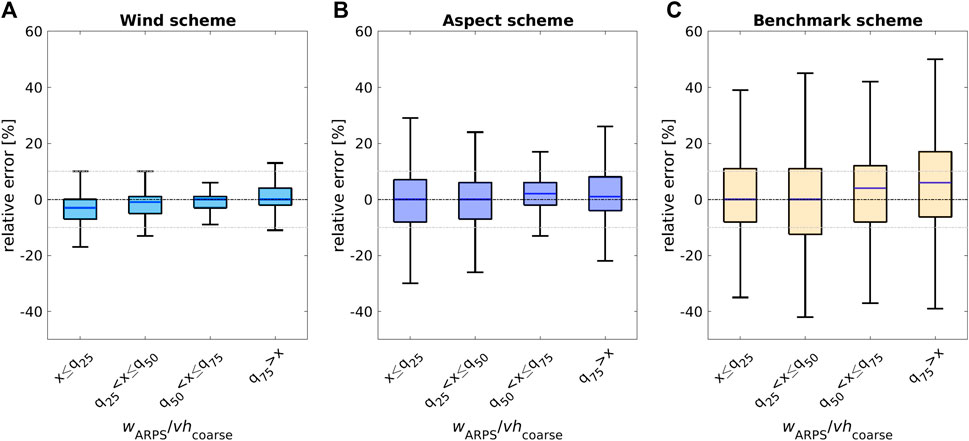
FIGURE 10. Relative errors between ARPS-A3D modeled and downscaled snowfall (for the five sub-events pooled) for the subarea of the Latsch region site (see Figure 7A) as a function of normalized ARPS modeled vertical wind speeds w_ARPS/vh_coarse quantiles with q₂₅=−0.2, q₅₀=−0.1 and q₇₅=0.1. (A): $P_{\text{dsc}}^{\text{wind}}$ (wind scheme), (B): $P_{\text{dsc}}^{\text{aspect}}$ (aspect scheme) and (C) $P_{\text{dsc}}^{\text{winstral}}$ (MeteoIO/Winstral as benchmark scheme).

4.2.2 Downscaled vertical wind speed on real topography

Downscaled and ARPS-modeled vertical wind speeds show similar magnitudes and spatial patterns in the Latsch region (Figure 11). However, downscaled vertical wind speeds from the benchmark scheme, DEVINE, (LeToumelin et al., 2023), produce smoother spatial patterns (Figure 11C). Comparing modeled and downscaled vertical wind speeds along a cross-section through the area (red line in Figure 11A) confirms these observations. The benchmark scheme displays a smoother pattern and differs more from modeled values in the up/downdrafts across the largest ridge of the cross-section (800–1,050 m in Figure 12).

FIGURE 11

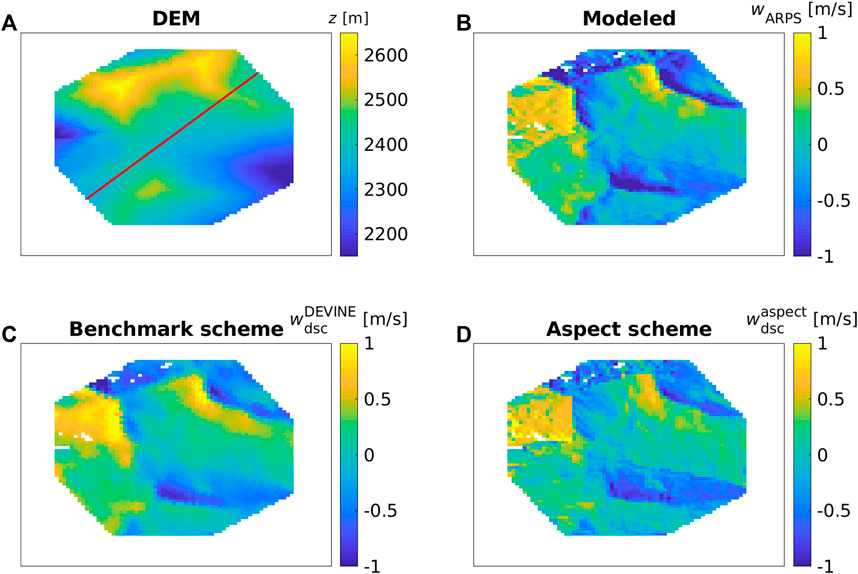
FIGURE 11. Spatial images for a subarea of the Latsch region site for the vertical wind speed w evaluations: (A) DEM, (B) w_ARPS (modeled), (C) $w_{\text{dsc}}^{\text{DEVINE}}$ (downscaled) and (D) $w_{\text{dsc}}^{\text{aspect}}$ (downscaled). DEVINE is the benchmark downscaling scheme. All w are for the second sub-snowfall event generated with vh_coarse of 1.3 m/s and wd_coarse of 235° (see Figure 3). Note, that for all w evaluations in the Latsch region, only terrain with slope angles ≥60° was removed (shown in white).

FIGURE 12

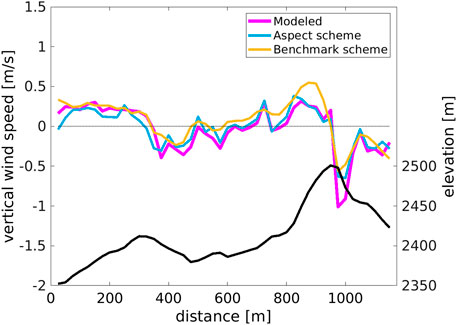
FIGURE 12. Cross section for modeled and downscaled vertical wind speed through the Latsch region site along the solid red line shown in Figure 11A. DEVINE is the benchmark downscaling scheme. All w are for the second sub-snowfall event generated with vh_coarse of 1.3 m/s and wd_coarse of 235°.

Relative errors for both downscaling schemes increase for lower vertical wind speeds in the groups of normalized vertical wind speed (w_ARPS/vh_coarse) derived from q25, q50, and q75 of the distribution (Figure 13). Though the aspect scheme exhibits sign reversal for upwind w (windward), and the benchmark scheme does not, both schemes show unbalanced relative errors around zero. However, the aspect scheme slightly outperforms the benchmark scheme for the entire vertical wind speed distribution, resulting in lower overall relative and absolute errors ($<$ 5%) compared to the benchmark scheme (≤9%) (Table 2). Despite the larger relative errors for the aspect scheme in a real environment than on the simulated topographies (Figures 13 versus 6A), the overall errors are only 2% higher (Tables 1, 2), which is reassuring.

FIGURE 13

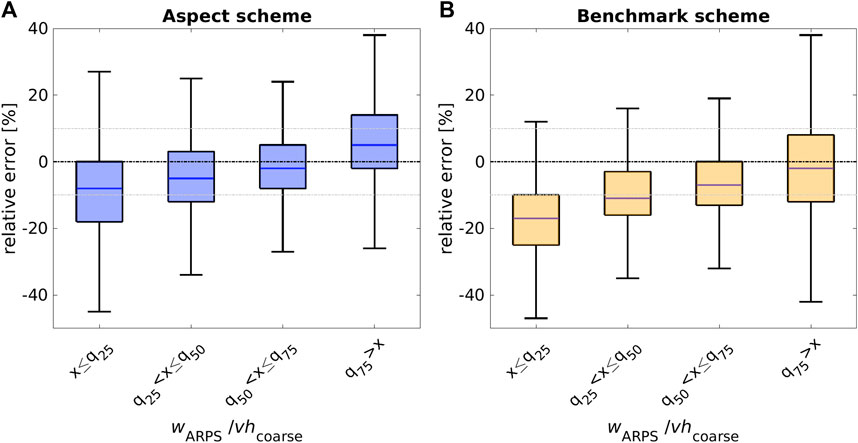
FIGURE 13. Relative errors between ARPS modeled and downscaled vertical wind speed for the Latsch region site shown in Figure 11A as a function of normalized ARPS modeled vertical wind speeds w_ARPS/vh_coarse quantiles with q₂₅=−0.3, q₅₀=−0.1 and q₇₅=0.2. (A): $w_{\text{dsc}}^{\text{aspect}}$ (downscaled) and (B) $w_{\text{dsc}}^{\text{DEVINE}}$ (downscaled with benchmark scheme DEVINE).

5 Discussion

To evaluate the aspect scheme performances for snowfall and vertical wind speed, we used the spatial mean horizontal wind speed from ARPS $(\overline{v{h}_{\text{ARPS}}})$ instead of the subgrid parameterization for $\overline{vh}$ as proposed in Eq. 7, to focus solely on the aspect scheme performances. However, utilizing a subgrid parameterization for $\overline{vh}$ completes the aspect downscaling schemes for vertical wind speed (Eqs 5, 6) and snowfall (Eq. 4) by providing a downscaling approach that does not rely on fine-scale wind data. This makes the aspect schemes ideal for applications where fine-scale wind data is typically unavailable, such as hazard mapping, glacier mass balance calculations, or wind resource assessments.

Obtaining high-quality spatial snowfall data sets in mountainous regions is challenging due to several limiting criteria that must be met before, during, and after the snowstorm. These include a prior snow-free ground, intermediate wind conditions for preferential deposition, and quick accessibility to the region after the storm to avoid snow settling, drifting snow, and avalanches altering the deposited snow distribution. Many of these criteria were met; erosion, saltation, and drifting snow sublimation had negligible or none contributions during and after the event. Despite having to balance some of the other criteria like pre-existing snow on north-facing slopes and avalanches, we assembled an independent spatial snowfall data set that allowed us to show that our downscaling schemes replicate preferentially deposited snow on a real topography.

Our downscaling schemes for snowfall are designed to capture preferential deposition. Thus, they can not accurately represent the very fine-scale distribution of new snow depth driven by snow redistribution processes (via wind or avalanches). Furthermore, distinct differences in local meteorological conditions during a snowfall cannot be captured (see Figure 7B or Figure 8B). In contrast, the downscaling schemes effectively provide spatial snowfall input for fine-scale (modeling) applications in mountainous regions.

To quantify the contribution of preferential snowfall deposition on spatial variations in snow depth, we employed the methodology from Gerber et al. (2019) to estimate the increase in leeward snowfall deposition due to preferential deposition. They calculated this effect on the lee side of an eastern Swiss mountain ridge, finding it to be approximately 10% when comparing the largest leeward deposition to the mean snow accumulation across the ridge. Applying this method to A3D-modeled snowfall deposition across four ridges with cross-ridge distances as shown in Figure 8 (gray bars and dotted lines) yielded values ranging from 15% to 18%. Notably, to ensure comparability, we used mean leeward deposition instead of the maximum, given our finer model grid cell resolution (25 m versus 50 m), which could lead to steeper local topographic features and thus more localized topography-flow-particle interactions. As our model suggests a somewhat greater contribution of preferential snowfall deposition compared to the 10% reported in Gerber et al. (2019), we discuss potential explanations: 1) Complex topography-preferential deposition interactions: Prior studies (e.g., Lehning et al., 2008; Mott et al., 2010; Mott et al., 2014; Vionnet et al., 2017; Wang and Huang, 2017; Comola et al., 2019) highlight the intricate relationship between topography and preferential deposition. In our extensive model database, covering diverse topographic characteristics, we identified scaling factors causing significant local variations in spatial snowfall deposition. This variability, supported by a 45% coefficient of variation (spatial standard deviation to spatial mean ratio, see Table 1), could explain disparities with Gerber et al. (2019). Notably, our mountain ridges feature smaller elevation differences (60–150 m) compared to the ridge in Gerber et al. (2019) (about 700 m). 2) Atmospheric stability effects: Wang and Huang (2017) and Comola et al. (2019) point out that snowfall deposition patterns are further influenced by atmospheric stability, which affects local wind flows. We employed neutral atmospheric stability for simulating 3D ARPS wind fields to compute preferential snowfall deposition with A3D, while the events simulated by Gerber et al. (2019) were characterized by a weakly stable atmosphere. Our choice may have led to higher local preferential snowfall deposition on the lee sides due to reduced flow blocking under neutral stability. This aligns with the concept that preferential deposition increases on the leeward slope with intensified flow advection, as pointed out by Wang and Huang (2017) and confirmed by LES model experiments in Comola et al. (2019). In summary, our preferential snowfall deposition patterns, featuring maxima on the lee side of the mountain, are consistent with LES modeling results on a Gaussian hill using inertialess particles, effectively representing inertial dendritic crystals, as demonstrated by Comola et al. (2019).

Statistical downscaling is a valuable tool for a computationally efficient generation of detailed snow and wind data. However, the accuracy depends on the quality of the statistical algorithms, finding the dominant scaling factors, and the quality of the training data for deriving the relationships. We developed a conventional statistical, regression-based method and incorporated some physical and empirical process understanding. Nevertheless, our approach performed similar to or even better than benchmark schemes, particularly in describing fine-scale patterns (see Figures 7, 8; and Figures 11, 12). Promising alternatives to our approach are physics-based machine and deep learning approaches (Vadyala et al., 2022). To ensure reliable and transferable relationships, we created a diverse training data set by running an atmospheric model and a preferential deposition model on simulated topographies under controlled atmospheric conditions. This approach avoids introducing issues like data sparsity and biases, and allows for a systematic search for scaling factors. While our training dataset covers preferentially deposited snowfall across diverse topographies, we simulated snowfall for a single atmospheric state—saturated, cold air, a common condition during winter snowfall events. Consequently, the predictability of our downscaling schemes under different conditions remains uncertain, and systematic investigations into how preferential deposition changes under different atmospheric conditions are currently lacking. In general, a modeled training database can only be as good as the underlying model physics. Both applied models have shown good performance in mountainous terrain and compared to observations (e.g., Raderschall et al., 2008; Mott et al., 2010; Mott and Lehning, 2010). However, some model limitations exist and are discussed in the following.

In our model database, we identified grid cells showing negative snowfall deposition (1.7%). These negative values may have resulted from inaccuracies in the mass balance of the wind flow fields and/or the snow transport module of A3D. Mass balance inaccuracies in wind flow fields could be due to the ARPS model setup (such as boundary conditions) or numerically unstable flow fields, as we observed in model domains L with a rather large characteristic width of topographic features ξ (low L/ξ ratio) such that the flow only insufficiently adapted to the topography (Helbig et al., 2017). Handling terrain-following coordinates over fine-scale topography can also introduce spatial discretization uncertainties that increase with slope angles (Lundquist et al., 2010). On the other hand, the suspension scheme in the snow transport module may have introduced mass balance inaccuracies if the solution did not converge fast enough. Overall, mass balance inaccuracies in our model database may have resulted in erroneous absolute snowfall values. We therefore refrained from applying a normalization correction in our snowfall downscaling schemes. While such a correction may ensure the conservation of the total snowfall in the model domain, it might also exacerbate inaccuracies in absolute snowfall values. We assessed the modeled mass balance by comparing the spatial sums of total modeled snowfall to input (∑_iP_A3D,i/∑_iP_coarse,i). The model overestimated the input mass balance by 8% for the test data set on simulated topographies and by 11% on the actual topography. This overestimation may have contributed to the larger modeled deposited snow depth compared to the measured values on the actual topography (Figure 9). However, uncertainties also arise from applying a spatio-temporal constant snow density when converting snowfall to snow depth as well as that the measured new snow depth distribution was also altered by other snow processes than preferential snowfall deposition. It is thus difficult to assess the exact reasons for the differences between measured new snow depth and modeled deposited snowfall (Table 2). However, it is reassuring, that the model and both our snowfall downscaling schemes emulate fine-scale measured deposition patterns similar than a benchmark downscaling scheme for snowfall (Figure 7).

6 Summary and conclusion

In this study, we developed two computationally efficient statistical downscaling schemes that emulate high-resolution preferential snowfall deposition in mountainous terrain. We trained both schemes using a comprehensive model data set of deposited snowfall and near-surface wind on simulated topographies under controlled atmospheric conditions. To generate fine-scale 3D wind fields, we utilized the atmospheric model ARPS, which we then used to drive the snow transport module of the Alpine3D surface process model to derive the fine-scale snowfall data set. Both downscaling schemes rely on low-resolution, near-surface snowfall and wind speed as well as high-resolution terrain parameters as input. The “wind scheme” requires an additional input of high-resolution vertical wind speeds, while the “aspect scheme” can function without any fine-scale temporal input by also relying on low-resolution wind directions.

Both downscaling schemes performed well compared to the model test data set on simulated topographies, with relative errors of less than −1%. An evaluation with a snow depth data set measured in eastern Switzerland revealed similar magnitudes and spatial patterns for both schemes, except in areas where other processes came into play, such as in avalanche deposition zones, in regions with existing snow cover, or where the ground was warmer (see discussion and Figure 7). In contrast, the benchmark downscaling scheme, which was the MeteoIO implementation (Bavay and Egger, 2014) based on the statistical method utilizing the Sx parameter (Winstral and Marks, 2002), produced much less fine-scale spatial snowfall deposition patterns. To avoid the need for high-resolution time-dependent input in the aspect snowfall scheme, we further developed a downscaling scheme for vertical wind speed that performed well on our test data set with absolute and relative errors of less than ±3%. In comparison to the benchmark downscaling model DEVINE, which is a deep learning model for all wind components (LeToumelin et al., 2023), our aspect downscaling scheme for vertical wind speed emulated ARPS-modeled vertical wind speed on a real topography similar but with improved fine-scale patterns. The overall good performance on both real and simulated topographies, as well as with measurements and benchmark downscaling models, confirms the effectiveness of this approach. In fact, by developing a statistical approach on a process-based, fine-scale model database and integrating physical understanding, we created relevant key features for the downscaling schemes, including high computational efficiency, versatility, and the ability to cope without fine-scale temporal input data, all of which favor their broad applicability. Emerging physics-based machine or deep learning approaches provide promising alternatives in the future (Vadyala et al., 2022).

Although preferential deposition for snowfall is only one process in shaping the spatial snow depth distribution in mountainous terrain, it generates significant spatial variation dictated by the interaction of local terrain features with wind and snow particles during a snowfall event. These patterns of preferential snowfall deposition offer valuable insights into fine-scale snow distributions, which are essential for applications in snow hydrology, glaciology, avalanche sciences, atmospheric and climate sciences, as well as remote sensing. Particularly our aspect downscaling schemes have the potential to generate fine-scale snowfall and fine-scale vertical wind speed fields efficiently without requiring expensive fine-scale modelings. This capability could be especially useful for long-term analyses or large-scale studies in mountainous terrain, such as in modeling snow distributions for glacier or ice mass balances (e.g., Oerlemans et al., 2009), in satellite snow data-acquisitions (e.g., Gascoin et al., 2019), in wind resource assessments, in extreme snowfall projections (Quante et al., 2021), for climate impact or dust deposition studies (Di Mauro et al., 2019). The latter could be particularly interesting given recent Saharan dust outbreaks that covered large mountainous regions in Europe, which were well-documented (Meinander et al., 2022; Dumont et al., 2023; Helbig, 2023).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

NH: Conceptualization, Data curation, Investigation, Methodology, Software, Validation, Project administration, Funding acquisition, Visualization, Writing–original draft, Writing–review and editing. RM: Conceptualization, Methodology, Validation, Writing–review and editing. YB: Conceptualization, Resources, Investigation, Data curation, Validation, Writing–review and editing. LLT: Software, Investigation, Data curation, Validation, Writing–review and editing. ML: Conceptualization, Validation, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. NH was funded by the WSL Institute for Snow and Avalanche Research SLF through an internal innovative project fund. This fund was supplemented with funding from RAMMS (ramms.slf.ch). Open access funding by Swiss Federal Institute for Forest, Snow and Landscape Research (WSL).

Acknowledgments

NH thanks Perry Bartelt for his interest in the study and support. We would like to thank Franziska Gerber for valuable content discussions as well as the two anonymous referees for their valuable suggestions. We thank the Federal Office of Meteorology and Climatology (MeteoSwiss) for providing COSMO data.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1308269/full#supplementary-material

References

Bartelt, P., and Lehning, M. (2002). A physical SNOWPACK model for the Swiss avalanche warning Part I: numerical model. Cold Reg. Sci. Technol. 35, 123–145. doi:10.1016/s0165-232x(02)00074-5

CrossRef Full Text | Google Scholar

Bavay, M., and Egger, T. (2014). MeteoIO 2.4.2: a preprocessing library for meteorological data. Geosci. Model Dev. 7, 3135–3151. doi:10.5194/gmd-7-3135-2014

CrossRef Full Text | Google Scholar

Bavay, M., Lehning, M., Jonas, T., and Löwe, H. (2009). Simulations of future snow cover and discharge in alpine headwater catchments. Hydrol. Process. 23, 95–108. doi:10.1002/hyp.7195

CrossRef Full Text | Google Scholar

Beljaars, A. C. M., Brown, A. R., and Wood, N. (2004). A new parametrization of turbulent orographic form drag. Q. J. R. Meteorol. Soc. 130, 1327–1347. doi:10.1256/qj.03.73

CrossRef Full Text | Google Scholar

Bellaire, S., and Jamieson, B. (2013). Forecasting the formation of critical snow layers using a coupled snow cover and weather model. Cold. Reg. Sci. Technol. 94, 37–44. doi:10.1016/j.coldregions.2013.06.007

CrossRef Full Text | Google Scholar

Bühler, Y., Adams, M. S., Stoffel, A., and Boesch, R. (2017). Photogrammetric reconstruction of homogenous snow surfaces in alpine terrain applying near-infrared UAS imagery. Int. J. Remote Sens. 38, 3135–3158. doi:10.1080/01431161.2016.1275060

CrossRef Full Text | Google Scholar

Bühler, Y., Bebi, P., Christen, M., Margreth, S., Stoffel, L., Stoffel, A., et al. (2022a). Automated avalanche hazard indication mapping on a statewide scale. Nat. Hazards Earth Syst. Sci. 22, 1825–1843. doi:10.5194/nhess-22-1825-2022

CrossRef Full Text | Google Scholar

Bühler, Y., Stoffel, A., and Salzmann, C. M. (2022b). Photogrammetric drone data latschuelfurgga. EnviDat. doi:10.16904/envidat.374

CrossRef Full Text | Google Scholar

Chow, F. K., Weigel, A. P., Street, R. L., Rotach, M. W., and Xue, M. (2006). High-resolution large-eddy simulations of flow in a steep alpine valley. Part I: methodology, verification, and sensitivity experiments. J. Appl. Meteorol. Climatol. 45, 63–86. doi:10.1175/jam2322.1

CrossRef Full Text | Google Scholar

Clifton, A., and Lehning, M. (2008). Improvement and validation of a snow saltation model using wind tunnel measurements. Earth Surf. Process. Landforms 33, 2156–2173. doi:10.1002/esp.1673

CrossRef Full Text | Google Scholar

Comola, F., Giometto, M. G., Salesky, S. T., Parlange, M. B., and Lehning, M. (2019). Preferential deposition of snow and dust over hills: governing processes and relevant scales. J. Geophys. Res. Atmos. 124, 7951–7974. doi:10.1029/2018JD029614

CrossRef Full Text | Google Scholar

Dadic, R., Mott, R., Lehning, M., and Burlando, P. (2010a). Wind influence on snow depth distribution and accumulation over glaciers. J. Geophys. Res. Earth Surf. 115. doi:10.1029/2009JF001261

CrossRef Full Text | Google Scholar

Dadic, R., Mott, R., Lehning, M., and Burlando, P. (2010b). Parameterization for wind–induced preferential deposition of snow. Hydrol. Process. 24, 1994–2006. doi:10.1002/hyp.7776

CrossRef Full Text | Google Scholar

Di Mauro, B., Garzonio, R., Rossini, M., Filippa, G., Pogliotti, P., Galvagno, M., et al. (2019). Saharan dust events in the european alps: role in snowmelt and geochemical characterization. Cryosphere 13, 1147–1165. doi:10.5194/tc-13-1147-2019

CrossRef Full Text | Google Scholar

Doorschot, J., and Lehning, M. (2002). Equilibrium saltation: mass fluxes, aerodynamic entrainment, and dependence on grain properties. Boundary-Layer Meteorol. 104, 111–130. doi:10.1023/A:1015516420286

CrossRef Full Text | Google Scholar

Dumont, M., Gascoin, S., Réveillet, M., Voisin, D., Tuzet, F., Arnaud, L., et al. (2023). Spatial variability of saharan dust deposition revealed through a citizen science campaign. Earth Syst. Sci. Data Discuss. 2023, 1–31. doi:10.5194/essd-2023-16

CrossRef Full Text | Google Scholar

Eberhard, L. A., Sirguey, P., Miller, A., Marty, M., Schindler, K., Stoffel, A., et al. (2021). Intercomparison of photogrammetric platforms for spatially continuous snow depth mapping. Cryosphere 15, 69–94. doi:10.5194/tc-15-69-2021

CrossRef Full Text | Google Scholar

Farinotti, D., Magnusson, J., Huss, M., and Bauder, A. (2010). Snow accumulation distribution inferred from time-lapse photography and simple modelling. Hydrol. Process. 24, 2087–2097. doi:10.1002/hyp.7629

CrossRef Full Text | Google Scholar

Föhn, P. M. B., and Meister, R. (1983). Distribution of snow drifts on ridge slopes: measurements and theoretical approximations. Ann. Glaciol. 4, 52–57. doi:10.3189/S0260305500005231

CrossRef Full Text | Google Scholar

Frei, P., Kotlarski, S., Liniger, M. A., and Schär, C. (2018). Future snowfall in the Alps: projections based on the EURO-CORDEX regional climate models. Cryosphere 12, 1–24. doi:10.5194/tc-12-1-2018

CrossRef Full Text | Google Scholar

Gascoin, S., Grizonnet, M., Bouchet, M., Salgues, G., and Hagolle, O. (2019). Theia Snow collection: high resolution operational snow cover maps from Sentinel-2 and Landsat-8 data. Earth Syst. Sci. Data 493, 493–514. doi:10.5194/essd-11-493-2019

CrossRef Full Text | Google Scholar

Gerber, F., Lehning, M., Hoch, S. W., and Mott, R. (2017). A close-ridge small-scale atmospheric flow field and its influence on snow accumulation. J. Geophys. Res. Atmos. 122, 7737–7754. doi:10.1002/2016JD026258

CrossRef Full Text | Google Scholar

Gerber, F., Mott, R., and Lehning, M. (2019). The importance of near-surface winter precipitation processes in complex alpine terrain. J. Hydrometeor. 20, 177–196. doi:10.1175/JHM-D-18-0055.1

CrossRef Full Text | Google Scholar

Griessinger, N., Schirmer, M., Helbig, N., Winstral, A., Michel, A., and Jonas, T. (2019). Implications of observation-enhanced energy-balance snowmelt simulations for runoff modeling of alpine catchments. Adv. Water Resour. 133, 103410. doi:10.1016/j.advwatres.2019.103410

CrossRef Full Text | Google Scholar

Groot Zwaaftink, C. D., Löwe, H., Mott, R., Bavay, M., and Lehning, M. (2011). Drifting snow sublimation: a high-resolution 3-D model with temperature and moisture feedbacks. J. Geophys. Res. 116, D16107. doi:10.1029/2011JD015754

CrossRef Full Text | Google Scholar

Groot Zwaaftink, C. D., Mott, R., and Lehning, M. (2013). Seasonal simulation of drifting snow sublimation in alpine terrain. Water Resour. Res. 49, 1581–1590. doi:10.1002/wrcr.20137

CrossRef Full Text | Google Scholar

Grünewald, T., and Lehning, M. (2011). Altitudinal dependency of snow amounts in two small alpine catchments: can catchment-wide snow amounts be estimated via single snow or precipitation stations? Ann. Glaciol. 52, 153–158. doi:10.3189/172756411797252248

CrossRef Full Text | Google Scholar

Grünewald, T., Stötter, J., Pomeroy, J., Dadic, R., Moreno Banos, I., Marturia, J., et al. (2013). Statistical modelling of the snow depth distribution in open alpine terrain. Hydrol. Earth Syst. Sci. 17, 3005–3021. doi:10.5194/hess-17-3005-2013

CrossRef Full Text | Google Scholar

Gutmann, E., Barstad, I., Clark, M., Arnold, J., and Rasmussen, R. (2016). The intermediate complexity atmospheric research model (icar). J. Hydrometeorol. 17, 957–973. doi:10.1175/JHM-D-15-0155.1

CrossRef Full Text | Google Scholar

Harvey, S., Schmudlach, G., Bühler, Y., Dürr, L., Stoffel, A., and Christen, M. (2018). “Avalanche terrain maps for backcountry skiing in Switzerland,” in Proceedings of the international snow science workshop (Austria: Innsbruck), 1625–1631.

Google Scholar

Helbig, N. (2023). Snowfall downscaling source code to calculate the relative terrain aspect parameter. EnviDat. doi:10.16904/envidat.435

CrossRef Full Text | Google Scholar

Helbig, N., Bühler, Y., Eberhard, L., Deschamps-Berger, C., Gascoin, S., Dumont, M., et al. (2021). Fractional snow-covered area: scale-independent peak of winter parameterization. Cryosphere 15, 615–632. doi:10.5194/tc-15-615-2021

CrossRef Full Text | Google Scholar

Helbig, N., and Löwe, H. (2012). Shortwave radiation parameterization scheme for subgrid topography. J. Geophys. Res. 117. doi:10.1029/2011JD016465

CrossRef Full Text | Google Scholar

Helbig, N., and Löwe, H. (2014). Parameterization of the spatially averaged sky view factor in complex topography. J. Geophys. Res. 119, 4616–4625. doi:10.1002/2013JD020892

CrossRef Full Text | Google Scholar

Helbig, N., Mott, R., van Herwijnen, A., Winstral, A., and Jonas, T. (2017). Parameterizing surface wind speed over complex topography. J. Geophys. Res. 121, 651–667. doi:10.1002/2016JD025593

CrossRef Full Text | Google Scholar

Helbig, N., and van Herwijnen, A. (2017). Subgrid parameterization for snow depth over mountainous terrain from flat field snow depth. Water Resour. Res. 53, 1444–1456. doi:10.1002/2016WR019872

CrossRef Full Text | Google Scholar

Helbig, N., van Herwijnen, A., Magnusson, J., and Jonas, T. (2015). Fractional snow-covered area parameterization over complex topography. Hydrol. Earth Syst. Sci. 19, 1339–1351. doi:10.5194/hess-19-1339-2015

CrossRef Full Text | Google Scholar

IPCC (2023). “Climate change 2023: synthesis report. A report of the intergovernmental panel on climate change,” in Contribution of working groups I, II and III to the sixth assessment report of the intergovernmental panel on climate change. Editors H. Lee, and J. Romero (Geneva, Switzerland: IPCC).

Google Scholar

Jimenez, P. A., and Dudhia, J. (2012). Improving the representation of resolved and unresolved topographic effects on surface wind in the WRF model. J. Appl. Meteorol. Climatol. 51, 300–316. doi:10.1175/jamc-d-11-084.1

CrossRef Full Text | Google Scholar

Kirchner, P. B., Bales, R. C., Molotoch, N. P., Flanagan, J., and Guo, Q. (2014). LiDAR measurement of seasonal snow accumulation along an elevation gradient in the southern Sierra Nevada, California. Hydrol. Earth Syst. Sci. 18, 4261–4275. doi:10.5194/hess-18-4261-2014

CrossRef Full Text | Google Scholar

Lehning, M., Bartelt, P., Brown, B., and Fierz, C. (2002b). A physical SNOWPACK model for the Swiss avalanche warning Part III: meteorological forcing, thin layer formation and evaluation. Cold Reg. Sci. Technol. 35, 169–184. doi:10.1016/s0165-232x(02)00072-1

CrossRef Full Text | Google Scholar

Lehning, M., Bartelt, P., Brown, B., Fierz, C., and Satyawali, P. (2002a). A physical SNOWPACK model for the Swiss avalanche warning Part II: snow microstructure. Cold Reg. Sci. Technol. 35, 147–167. doi:10.1016/s0165-232x(02)00073-3

CrossRef Full Text | Google Scholar

Lehning, M., Bartelt, P., Brown, B., Russi, T., Stöckli, U., and Zimmerli, M. (1999). Snowpack model calculations for avalanche warning based upon a new network of weather and snow stations. Cold Reg. Sci. Technol. 30, 145–157. doi:10.1016/s0165-232x(99)00022-1

CrossRef Full Text | Google Scholar

Lehning, M., Grünewald, T., and Schirmer, M. (2011). Mountain snow distribution governed by an altitudinal gradient and terrain roughness. Geophys. Res. Lett. 38. doi:10.1029/2011gl048927

CrossRef Full Text | Google Scholar

Lehning, M., Löwe, H., Ryser, M., and Raderschall, N. (2008). Inhomogeneous precipitation distribution and snow transport in steep terrain. Water Resour. Res. 44. doi:10.1029/2007WR006545

CrossRef Full Text | Google Scholar

Lehning, M., Völksch, I., Gustafsson, D., Nguyen, T., Stähli, M., and Zappa, M. (2006). ALPINE3D: a detailed model of mountain surface processes and its application to snow hydrology. Hydrol. Process. 20, 2111–2128. doi:10.1002/hyp.6204

CrossRef Full Text | Google Scholar

LeToumelin, L., Gouttevin, I., Helbig, N., Galiez, C., Roux, M., and Karbou, F. (2023). Emulating the adaptation of wind fields to complex terrain with deep-learning. Artif. Intell. Earth Syst. 2, 1–39. doi:10.1175/AIES-D-22-0034.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Löwe, H., and Helbig, N. (2012). Quasi-analytical treatment of spatially averaged radiation transfer in complex terrain. J. Geophys. Res. 17. doi:10.1029/2012JD018181

CrossRef Full Text | Google Scholar

Lundquist, K., Chow, F. K., and Lundquist, J. K. (2010). An immersed boundary method for the weather research and forecasting model. Mon. Weather Rev. 138, 796–817. doi:10.1175/2009MWR2990.1

CrossRef Full Text | Google Scholar

Maechler, M., Rousseeuw, P., Croux, C., Todorov, V., Ruckstuhl, A., Salibian-Barrera, M., et al. (2020). robustbase: basic Robust Statistics. R package version 0.93-6.

Google Scholar

Manes, C., Guala, M., Löwe, H., Bartlett, S., Egli, L., and Lehning, M. (2008). Statistical properties of fresh snow roughness. Water Resour. Res. 44, 1–9. doi:10.1029/2007wr006689

CrossRef Full Text | Google Scholar

Marty, C. A. (2001). Surface radiation, cloud forcing and greenhouse effect in the alps. Ph.D. thesis, ETHZ Zurich, Switzerland and Physikalisch-Meteorologisches Observatorium Davos. Switzerland: World Radiation Center Davos.

Google Scholar

Meinander, O., Alvarez Piedehierro, A., Kouznetsov, R., Rontu, L., Welti, A., Kaakinen, A., et al. (2022). Saharan dust transported and deposited in Finland on 23 February 2021. Vienna, Austria: EGU General Assembly. 23–27 May 2022. EGU22-4818. doi:10.5194/egusphere-egu22-4818

CrossRef Full Text | Google Scholar

Mott, R., and Lehning, M. (2010). Meteorological modeling of very-high resolution wind fields and snow deposition for mountains. J. Hydrometeorol. 11, 934–949. doi:10.1175/2010jhm1216.1

CrossRef Full Text | Google Scholar

Mott, R., Schirmer, M., Grünewald, T., and Lehning, M. (2010). Understanding snow-transport processes shaping the mountain snow-cover. Cryosphere 4, 545–559. doi:10.5194/tc-4-545-2010

CrossRef Full Text | Google Scholar

Mott, R., Scipión, D., Schneebeli, M., Dawes, N., Berne, A., and Lehning, M. (2014). Orographic effects on snow deposition patterns in mountainous terrain. J. Geophys. Res.-Atmos. 119, 1419–1439. doi:10.1002/2013JD019880

CrossRef Full Text | Google Scholar

Mott, R., Vionnet, V., and Grünewald, T. (2018). The seasonal snow cover dynamics: review on wind-driven coupling processes. Front. Earth Sci. 6. doi:10.3389/feart.2018.00197

CrossRef Full Text | Google Scholar

Mott, R., Wolf, A., Kehl, M., Kunstmann, H., Warscher, M., and Grünewald, T. (2019). Avalanches and micrometeorology driving mass and energy balance of the lowest perennial ice field of the Alps: a case study. Cryosphere 13, 1247–1265. doi:10.5194/tc-13-1247-2019

CrossRef Full Text | Google Scholar

Oerlemans, J., Giesen, R., and Van Den Broeke, M. (2009). Retreating alpine glaciers: increased melt rates due to accumulation of dust (vadret da morteratsch, Switzerland). J. Glaciol. 55, 729–736. doi:10.3189/002214309789470969

CrossRef Full Text | Google Scholar

Purves, R. S., Barton, J. S., Mackaness, W. A., and Sugden, D. E. (1998). The development of a rule-based spatial model of wind transport and deposition of snow. Ann. Glaciol. 26, 197–202. doi:10.3189/1998AoG26-1-197-202

CrossRef Full Text | Google Scholar

Quante, L., Willner, S. N., Middelanis, R., and Levermann, A. (2021). Regions of intensification of extreme snowfall under future warming. Sci. Rep. 11, 16621. doi:10.1038/s41598-021-95979-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Raderschall, N., Lehning, M., and Schär, M. (2008). Fine-scale modeling of the boundary layer wind field over steep topography. Water Resour. Res. 44. doi:10.1029/2007WR006544

CrossRef Full Text | Google Scholar

R Core Team (2019). R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing.

Google Scholar

Reynolds, D. S., Gutmann, E., Kruyt, B., Haugeneder, M., Jonas, T., Gerber, F., et al. (2023). The high-resolution intermediate complexity atmospheric research (hicar v1.0) model enables fast dynamic downscaling to the hectometer scale. Geosci. Model Dev. Discuss. 2023, 1–30. doi:10.5194/gmd-2023-16

CrossRef Full Text | Google Scholar

Rontu, L. (2006). A study on parametrization of orography-related momentum fluxes in a synoptic-scale NWP model. Tellus 58A, 69–81. doi:10.3402/tellusa.v58i1.14752

CrossRef Full Text | Google Scholar

Schirmer, M., Wirz, V., Clifton, A., and Lehning, M. (2011). Persistence in intra-annual snow depth distribution: 1. Measurements and topographic control. Water Resour. Res. 47. doi:10.1029/2010wr009426

CrossRef Full Text | Google Scholar

Schweizer, J., Jamieson, J., and Schneebeli, M. (2003). Snow avalanche formation. Rev. Geophys. 41, 1016. doi:10.1029/2002RG000123

CrossRef Full Text | Google Scholar

Seyfried, M. S., and Wilcox, B. P. (1995). Scale and the nature of spatial variability: field examples having implications for hydrologic modeling. Water Resour. Res. 31, 173–184. doi:10.1029/94WR02025

CrossRef Full Text | Google Scholar

Skaugen, T., and Melvold, K. (2019). Modeling the snow depth variability with a high-resolution lidar data set and nonlinear terrain dependency. Water Resour. Res. 55, 9689–9704. doi:10.1029/2019WR025030

CrossRef Full Text | Google Scholar

Vadyala, S. R., Betgeri, S. N., Matthews, J. C., and Matthews, E. (2022). A review of physics-based machine learning in civil engineering. Results Eng. 13, 100316. doi:10.1016/j.rineng.2021.100316

CrossRef Full Text | Google Scholar

Vionnet, V., Martin, E., Masson, V., Lac, C., Naaim-Bouvet, F., and Guyomarc’h, G. (2017). High-resolution large eddy simulation of snow accumulation in alpine terrain. J. Geophys. Res. Atmos. 122, 11. doi:10.1002/2017jd026947

CrossRef Full Text | Google Scholar

Wang, Z., and Huang, N. (2017). Numerical simulation of the falling snow deposition over complex terrain. J. Geophys. Res. Atmos. 122, 980–1000. doi:10.1002/2016JD025316

CrossRef Full Text | Google Scholar

Winstral, A., Elder, K., and Davis, R. E. (2002). Spatial snow modeling of wind-redistributed snow using terrain-based parameters. J. Hydrometeorol. 3, 524–538. doi:10.1175/1525-7541(2002)003<0524:ssmowr>2.0.co;2

CrossRef Full Text | Google Scholar

Winstral, A., Magnusson, J., Schirmer, M., and Jonas, T. (2019). The bias-detecting ensemble: a new and efficient technique for dynamically incorporating observations into physics-based, multilayer snow models. Water Resour. Res. 55, 613–631. doi:10.1029/2018WR024521

CrossRef Full Text | Google Scholar

Winstral, A., and Marks, D. (2002). Simulating wind fields and snow redistribution using terrain-based parameters to model snow accumulation and melt over a semi-arid mountain catchment. Hydrol. Process. 16, 3585–3603. doi:10.1002/hyp.1238

CrossRef Full Text | Google Scholar

Xue, M., Droegemeier, K. K., and Wong, V. (2000). The Advanced Regional Prediction System (ARPS) - a multi-scale, non-hydrostatic atmospheric simulation and prediction model. Part I: model dynamics and verification. Meteorol. Atmos. Phys. 75, 161–193. doi:10.1007/s007030070003

CrossRef Full Text | Google Scholar

Xue, M., Droegemeier, K. K., Wong, V., Shapiro, A., Brewster, K., Carr, F., et al. (2001). The Advanced Regional Prediction System (ARPS) - a multi-scale, non-hydrostatic atmospheric simulation and prediction tool. Part II: model physics and applications. Meteorol. Atmos. Phys. 76, 143–165. doi:10.1007/s007030170027

CrossRef Full Text | Google Scholar

Yang, L., Franzke, C. L. E., and Duan, W. (2023). Evaluation and projections of extreme precipitation using a spatial extremes framework. Int. J. Climatol. 43, 3453–3475. doi:10.1002/joc.8038

CrossRef Full Text | Google Scholar

Zhou, Y., and Chow, F. K. (2011). Large-eddy simulation of the stable boundary layer with explicit filtering and reconstruction turbulence modeling. J. Atmos. Sci. 68, 2142–2155. doi:10.1175/2011JAS3693.1

CrossRef Full Text | Google Scholar