Binary structure constrained gravity inversion based on seismic first arrival travel time data

Gravity exploration method is one of the important methods for deep mineral resource exploration, but gravity data inversion has limited resolution ability in the vertical direction. In order to improve the vertical resolution of gravity data inversion, we propose a binary structure constrained gravity inversion method based on seismic first arrival travel time data. This method effectively reconstructs a density model with high vertical resolution by transferring the structural information of a high-resolution velocity model reconstructed by seismic data inversion to gravity data inversion through the binary structure constrained technique. This strategy eliminates the need to integrate both gravity and seismic methods into a single inversion framework, avoiding both the difference in convergence speeds between the two methods, as well as getting rid of the complexity associated with calculating structural coupling terms. Theoretical simulations show that the fuzzy c-means cluster analysis technique can accurately extract the target region of the velocity model reconstructed by seismic data inversion. Under the constraint of seismic structural information, the resolution of reconstructed density model is much higher than that of separate gravity data inversion, which proves that high resolution seismic information can improve the vertical resolution of gravity data inversion. Compared with the traditional cross-gradient joint inversion, the binary structure constrained gravity inversion method can further improve the resolution of the density model, especially in the reconstruction of the anomaly interface, which verifies that the method has certain effectiveness.

1 Introduction

Gravity exploration is characterized by great depth, low cost and high efficiency, and has been widely used in the study of the internal structure of the earth’s crust and the exploration of the distribution of deep minerals and oil and gas resources (Guillen and Menichetti, 1984; Li and Oldenburg, 1998; Nabighian et al., 2005; Nabighian et al., 2010; Afshar et al., 2018; Yan et al., 2020; Ming et al., 2021). Gravity anomaly information is a comprehensive reflection of all density information of the stratum from top to bottom, so much so that the vertical resolution is not high, and only by stripping away the influence of the surface and shallow layers can the information of the specified destination layer be obtained. However, seismic data have high vertical resolution, which enables good stratification and provides reliable stratigraphic information. Therefore, high resolution seismic method can provide more accurate vertical structural information for gravity methods and reduce the multi-resolution of gravity data inversion. However, how to incorporate these high precision structural information into gravity data inversion has been a challenging task for geophysicists.

In recent years, in order to improve the density resolution of gravity inversion, a large number of joint inversion studies of gravity data and other geophysical data have been carried out, and at present the joint inversion methods are mainly classified into two main categories, one of which is the structural coupling method, and the structural coupling joint inversion aims to improve the structural similarity between different models by defining the metrics of the model structure and minimizing the structural differences between the two models. The joint inversion results obtained based on the structural coupling method show high structural consistency, and the cross-gradient is a representative of this type of method, which has been widely used in the joint inversion of gravity and other geophysical data (Fregoso and Gallardo, 2009; Moorkamp et al., 2011; Pak et al., 2017; Gross, 2019; Zhang et al., 2020; Tavakoli et al., 2021). Subsequently, the structural coupling method was further improved, structural coupling functions such as Gramian determinant (Zhdanov et al., 2012), dot product function (Molodtsov et al., 2011) and cosine dot product gradient function (Zhang et al., 2022) are proposed. The idea of the above functions is to obtain a subsurface model with higher structural consistency, but the constraint effect of this coupling method is relatively weak (Lelievre et al., 2012).

The other is the rock physical coupling method, which is used to improve the linear or nonlinear correlation between different physical parameters by incorporating some statistical rock physical information into the deterministic inversion. When there is a physical parameter relationship, the relationship can be used to constrain different physical parameter inversion methods, and the strength of this constraint is much higher than that of the structural coupling method (Niwlawn and Jacobsen, 2000; Afnimar et al., 2002; Moorkamp et al., 2011; Heincke et al., 2017). When the relationship equation of physical property parameters does not exist, the statistical petrophysical information can also be integrated into the deterministic inversion objective function through the fuzzy clustering related function, and the known statistical petrophysical information can be used to infer the physical properties of the unknown region (Lelievre et al., 2009; Carter McAuslan et al., 2015; Sun and Li, 2016; Rongzhe et al., 2023). This type of coupling has stronger constraints than structural coupling, but is weaker than the case where physical parameter relationships exist. The petrophysical-based coupling method is totally dependent on the completeness and accuracy of the petrophysical information, which shows some limitations.

The above coupling-based joint inversion method can improve the vertical resolution of the density model to a certain extent. However, the implementation of this strategy needs to consider the integration of different methods, and there is bound to be the problem of inconsistent data convergence rate of different methods, which directly affects the constraints on the model parameters, and the results of the joint inversion reconstruction may not be in line with the expectations. At the same time, it is also necessary to consider the relative weights between different data sets, the size of the weights may depend on the quality of different data and the sensitivity of the model parameters, etc. Only by adjusting the appropriate weight factors to balance the relationship between the various items can ensure that the joint inversion of the convergence of the stability. In addition, it is also necessary to consider the effect of the order of magnitude difference of different model parameters, different model parameters have different order of magnitude, if they are coupled directly, it will affect the coupling effect of different model parameters and the inversion results. Therefore, the synchronized joint inversion is a relatively complicated inversion algorithm.

How to quickly reconstruct a high-precision density model, we utilize the velocity model reconstructed from seismic data as the spatial constraint information to constrain the gravity inversion, and propose a new binary structure constrained gravity inversion method based on seismic data, and this method does not need to fuse seismic and gravity into a joint inversion framework. First, the subsurface velocity model was obtained by inverting the seismic first arrivals travel time data; Secondly, the velocity model is divided into target and background regions by fuzzy c-means analysis technique to form a binary constraint model, where all the cells in the target region are set as 1 and all the cells in the background region are set as 0. Then, under the constraint of binary constraint model, the Gaussian Newton method is used to optimize the objective function of gravity data inversion. Finally, we verify the effectiveness and accuracy of the new algorithm by theoretical simulation.

The remainder of the paper is organized in the following order. Section 2 introduces the traditional inversion principle and the gravity inversion principle based on binary constraints. Section 3 analyzes the effectiveness of the binary structure constraint gravity inversion method and compares it with the cross-gradient structure constraint. Finally, Section 4 concludes the paper.

2 Inversion methods

2.1 Single inversion algorithm

The inversion problem can be understood as the search for a physical parameter model that matches the actual subsurface conditions while satisfying the data misfit requirements. In order to avoid problems such as instability and multiple solutions caused by solving pathological inverse problems, the inverse equations are usually solved by the Tikhonov and Arsenin. (1977) regularization method. First, we construct the gravity and seismic first arrival travel time inversion objective functions containing the data misfit term and the model constraint term, respectively, with the following expressions:

$\mathrm{\Phi }\left({\mathbf{m}}_1\right)={‖{\mathbf{W}}_{d1}\left({\mathbf{d}}_1-{\mathbf{f}}_1\left({\mathbf{m}}_1\right)\right)‖}^2+{\alpha }_1\cdot {‖{\mathbf{W}}_{m1}\left({\mathbf{m}}_1-{{\mathbf{m}}_1}_{ref}\right)‖}^2(1)$

${\mathrm{\Phi }}_2\left({\mathbf{m}}_2\right)={‖{\mathbf{W}}_{d2}\left({\mathbf{d}}_2-{\mathbf{f}}_2\left({\mathbf{m}}_2\right)\right)‖}^2+{\alpha }_2\cdot {‖{\mathbf{W}}_{m2}\left({\mathbf{m}}_2-{\mathbf{m}}_{2ref}\right)‖}^2(2)$

Where, ${\mathbf{f}}_1\left({\mathbf{m}}_1\right)$ and ${\mathbf{f}}_2\left({\mathbf{m}}_2\right)$ represent the gravity and seismic forward response, respectively; ${\mathbf{m}}_1$ and ${\mathbf{m}}_2$ represent density and velocity models, respectively; ${\mathbf{d}}_1$ and ${\mathbf{d}}_2$ represent observational data for gravity and seismic, respectively; ${\mathbf{W}}_{d1}$ and ${\mathbf{W}}_{d2}$ represent the diagonal inverse matrices of gravity and seismic data noise errors, respectively; ${\mathbf{W}}_{m1}$ and ${\mathbf{W}}_{m2}$ represent the gravity and seismic model smoothing matrices, respectively; ${\mathbf{m}}_{1ref}$ and ${\mathbf{m}}_{2ref}$ represent reference models for density and velocity models, respectively; ${\alpha }_1$ and ${\alpha }_2$ represent the regularization factors for gravity and seismic methods, respectively.

For the gravity method (Singh, 2002), the forward response expression is a linear equation which can be expressed as:

${\mathbf{f}}_1\left({\mathbf{m}}_1^{k+1}\right)={\mathbf{A}}_1\cdot {\mathbf{m}}_1^{k+1}(3)$

For the seismic first arrival travel time method (Vidale, 1988), the forward response expression is a nonlinear equation, and the nonlinear problem needs to be transformed into a linear problem in the inverse solution process.

$\mathbf{f}\left({\mathbf{m}}_2^{k+1}\right)\cong \mathbf{f}\left({\mathbf{m}}_2^k\right)+{\mathbf{A}}_2^k\left({\mathbf{m}}_2^{k+1}-{\mathbf{m}}_2^k\right)(4)$

Where, A₁ and A₂ represent the Jacobi matrices for gravity and seismic methods, respectively. k represents the number of inversion iterations.

By taking the extremes of the inverse objective function Eq. 1 and Eq. 2 respectively. We are able to obtain the expression of the Gaussian Newton method model for the k+1 iteration.

For the gravity method, the model expression for the Gaussian Newton method for the k+1 iteration is given below:

${\mathbf{m}}_1^{k+1}={\mathbf{m}}_1^k+{\left[{\mathbf{A}}_1^{\mathrm{T}}{\mathbf{W}}_{d1}^{\mathrm{T}}{\mathbf{W}}_{d1}{\mathbf{A}}_1+{\alpha }_1\cdot {\mathbf{W}}_{m1}^{\mathrm{T}}{\mathbf{W}}_{m1}\right]}^{-1}\times \left[\begin{array}{l}{\mathbf{A}}_1^{\mathrm{T}}{\mathbf{W}}_{d1}^{\mathrm{T}}{\mathbf{W}}_{d1}\left({\mathbf{d}}_1-{\mathbf{A}}_1{\mathbf{m}}_1^k\right)\\ +{\alpha }_1\cdot {\mathbf{W}}_{m1}^{\mathrm{T}}{\mathbf{W}}_{m1}\left({\mathbf{m}}_1^k-{\mathbf{m}}_{1ref}^k\right)\end{array}\right](5)$

For the seismic first arrival travel time method, the model expression for the Gaussian Newton method for the k+1 iteration is given below:

${\mathbf{m}}_2^{k+1}={\mathbf{m}}_2^k+{\left[{\left({\mathbf{A}}_2^k\right)}^{\mathrm{T}}{\mathbf{W}}_{d2}^{\mathrm{T}}{\mathbf{W}}_{d2}{\mathbf{A}}_2^k+{\alpha }_2\cdot {\mathbf{W}}_{m2}^{\mathrm{T}}{\mathbf{W}}_{m2}\right]}^{-1}\times \left[\begin{array}{l}{\left({\mathbf{A}}_2^k\right)}^{\mathrm{T}}{\mathbf{W}}_{d2}^{\mathrm{T}}{\mathbf{W}}_{d2}\left({\mathbf{d}}_2-{\mathbf{A}}_2^k{\mathbf{m}}_2^k\right)\\ +{\alpha }_1\cdot {\mathbf{W}}_{m2}^{\mathrm{T}}{\mathbf{W}}_{m2}\left({\mathbf{m}}_2^k-{\mathbf{m}}_{2ref}^k\right)\end{array}\right](6)$

Gravity inversion usually produces skinning effect, which leads to the phenomenon that inverted anomalies are concentrated at the surface, in order to ameliorate the effect of skinning effect, we add a depth-weighted matrix to the smoothing constraint matrix (Li and Oldenburg, 1996).

2.2 The binary structure constrained gravity inversion base on seismic data

We firstly execute the seismic first arrival travel time inversion, and obtain the velocity model by solving the Gaussian Newton optimization of the objective function using Eq 6. The velocity model reconstructed from the seismic inversion is used as the guided model, and the fuzzy c-means clustering technique (Windham, 1982) is utilized for the extraction of target regions from the guided model. The extraction process is as follows:

We give the expression for the FCM objective function as follows:

${\mathrm{\Phi }}_{\text{FCM}}={\displaystyle \sum _{i=1}^M}{\displaystyle \sum _{j=1}^C}{u}_{ij}^q{‖m_i-v_j‖}_2^2,(7)$

$0\le u_{ij}\le 1,(8)$

${\displaystyle \sum _{k=1}^C}{u}_{ij}=1,(9)$

Where, $m_i$ indicates the i model cell, M indicates the number of model cells, C indicates the number of clusters, $v_j$ indicates the clustering center of the jth cluster, q indicates fuzzy coefficients, usually set to 2, $u_{ij}$ indicates the class affiliation of the i model cell to class j clusters, the membership is between [0, 1].

In Eq 7, the model cell m_i is known, we need to find the membership matrix u_i and the clustering centers v_ij. Take the partial derivatives of the FCM objective function with respect to the membership and the clustering center respectively, i.e. $\frac{\partial {\mathrm{\Phi }}_{\text{FCM}}}{\partial v_j}=0$, $\frac{\partial {\mathrm{\Phi }}_{\text{FCM}}}{\partial u_{ij}}=0$, the final membership and clustering center can be obtained by the iterative form, which is expressed as follows:

$u_{ij}=\frac{{‖m_i-v_j‖}^2}{{\sum }_{j=1}^C{‖m_i-v_j‖}^2}.(10)$

$v_j=\frac{{\sum }_{i=1}^M{u}_{ij}^q{x}_i}{{\sum }_{i=1}^M{u}_{ij}^q},(11)$

$\mathbf{m}={\left(\begin{array}{c}{m}_1\\ m_2\\ \cdot \cdot \cdot \\ m_M\end{array}\right)}_{M\times 1},{\mathbf{u}}_j={\left[\begin{array}{cccc}{u}_{1j}^q& & & \\ & u_{2j}^q& & \\ & & \cdot \cdot \cdot & \\ & & & u_{Mj}^q\end{array}\right]}_{M\times M},{\mathbf{v}}_j={\left(\begin{array}{c}{v}_j\\ v_j\\ \cdot \cdot \cdot \\ v_j\end{array}\right)}_{M\times 1}(13)$

In summary, the solution process of the FCM technique can be summarized in the following steps:

1) Initialize the membership matrix u with a random number between 0 and 1 such that it satisfies Eq 8 and initialize the cluster centers v;

2) Calculate the objective function Eq 7, if the objective function is less than the preset threshold, then end the clustering iteration; if it is greater than the threshold, then continue the iteration;

3) Calculate the membership matrix u Eq 10 and the clustering center v Eq 11, then return to step 2) to continue the iteration.

The above FCM technique extracts the classification of the speed model to obtain the clustering center ${\mathrm{v}}_j$, and then calculates the absolute value of the difference between the clustering center ${\mathrm{v}}_j$ and the background value of the speed model m_2b ((| $v_j$-m_2b|), and takes the minimum value as the threshold ξ. Then, when | $m_i$-m_2b| < ξ (i = 1, 2,···, M), set Q_i = 0, and the others set Q_i = 1, here Q is called the binary constrained model matrix, and it is a matrix consisting of only 0 and 1, $\mathrm{Q}={\left[Q_1,Q_2,\cdots ,Q_M\right]}_{M\times 1}^{\mathrm{T}}$.

Finally, under the binary constraint, the gravity inversion calculation involves only the model parameters corresponding to the target region, and the model cells of other regions can be directly populated by the background model parameters, and the density model update equation after the binary constraint can be obtained by using the Gaussian Newton method to optimize the solution of the inversion objective function of the gravity data (Eq 1):

${\mathbf{m}}_1^{k+1}={\mathbf{m}}_1^k+{\left[{\mathbf{A}}_1^{\mathrm{T}}{\mathbf{W}}_{d1}^{\mathrm{T}}{\mathbf{W}}_{d1}{\mathbf{A}}_1+{\alpha }_1\cdot {\mathbf{W}}_{m1}^{\mathrm{T}}{\mathbf{W}}_{m1}\right]}^{-1}\times \left[\begin{array}{l}{\mathbf{A}}_1^{\mathrm{T}}{\mathbf{W}}_{d1}^{\mathrm{T}}{\mathbf{W}}_{d1}\left({\mathbf{d}}_1-{\mathbf{A}}_1{\mathbf{m}}_1^k\right)\\ +{\alpha }_1\cdot {\mathbf{W}}_{m1}^{\mathrm{T}}{\mathbf{W}}_{m1}\left({\mathbf{m}}_1^k-{\mathbf{m}}_{1ref}^k\right)\end{array}\right](14)$

${\mathbf{m}}_1^{k+1}=\text{diag}\left(\mathbf{Q}\right)\cdot {\mathbf{m}}_1^{k+1}(15)$

The density model is subjected to binary constraints at each iteration until the data misfit meets the desired value or the number of iterations is maximized, thus ending the computation and obtaining the inversion results.

3 Numerical examples

3.1 Analysis of the effectiveness of a binary structure constrained gravity inversion method based on seismic data

In this section, we perform separate gravity inversion and gravity inversion with binary structure constraints based on seismic data to verify the accuracy of the proposed algorithm through comparative analysis. We design a combined model, which consists of three anomalies of different sizes, the real velocity and density models are shown in Figure 1.

FIGURE 1

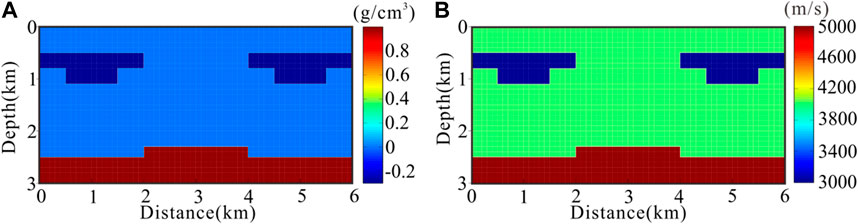
FIGURE 1. The first synthetic model including three targets with different size and burial depths. (A) The real density model; (B) The real velocity model.

The theoretical model has a background area of 6 km × 3 km, a background velocity of 4000 m/s, and a background density of 0 g/cm³. The shallow anomalies located in the upper left and upper right of the model are both 2 km × 0.6 km, with velocities of 3000 m/s and densities of −0.3 g/cm³, while the deep anomalies located in the lower part of the model are 6 km × 2.2 km, with velocities of 5000 m/s and densities of 1 g/cm³. The seismic method is to bury the seismic sources at a depth of 50 m below the ground, with a total of 9 sources, and place two sets of equipment containing 15 receivers in the left and right wells at 1.5 km and 4.5 km, respectively, with a spacing of 200 m. The gravity has a total of 30 observation points, which are uniformly distributed on the survey line from 0 to 6 km. The number of subsurface grid sections is 70 × 30 for both seismic and gravity methods.

Two strategies are used for the reconstruction of the density model, one is the separate gravity inversion and the other is the gravity inversion based on the binary structural constraints of the seismic data. The initial velocity and density models set in the inversion calculation are both background models.

Firstly, the separate gravity inversion (Grv_sep) is performed, and the inversion is stopped after 10 iterations, and the reconstructed density model is shown in Figure 2A. The reconstructed density model from the separate gravity inversion has only a general outline, and shows large deviations in the anomaly ranges in both the deep and shallow parts, especially in the density physical values. Despite the good convergence performance of the inversion, the anomaly shape and boundary are poorly recovered and the vertical resolution is more limited. Secondly, we perform gravity inversion based on binary structure constraints (Grv_bs_joint). The velocity model obtained from seismic inversion is divided into target region and background region by FCM technique to form a binary constraint model, where all the model cells in the target region are set to 1 and all the model cells in the background region are set to 0. Then, under the constraints of the binary constraint model, the objective function of the gravity data inversion is optimized and solved using Gaussian Newton method. The seismic inversion is stopped after 8 iterations and the velocity model obtained is shown in Figure 2B. The binary constraint model obtained based on the extraction of the target region by FCM technique is shown in Figure 2C. The gravity inversion with binary structure constraints is stopped after 10 iterations and the density model obtained is shown in Figure 2D.

FIGURE 2

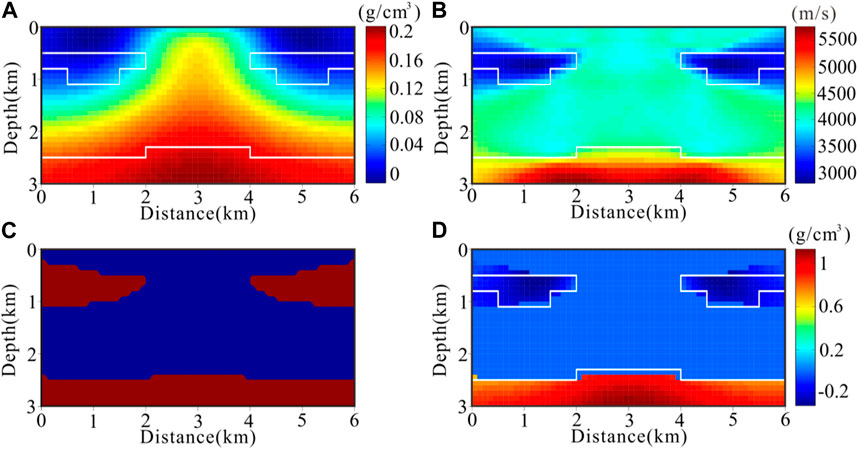
FIGURE 2. The reconstruction density model of different methods for the first synthetic model. (A) Separate gravity inversion results; (B) Separate seismic inversion results; (C) Binary constraint model; (D) Binary structured constrained gravity inversion results.

In Figure 2B, the seismic inversion results show strong vertical resolution ability, which can effectively distinguish deep and shallow anomalous areas. It is more reliable to take the velocity model as the a priori information. In Figure 2C, the target area extraction results based on the FCM technique are also more accurate, and the size range of the target area matches the seismic inversion results. In Figure 2D, the gravity inversion with binary structure constraints has a better match with the real model in terms of the shape size and density value of the anomalies, and the boundary of the anomalous body is more clearly portrayed, with a greater improvement in the resolution in the vertical direction.

We also determine the quality of the reconstructed inversion model by introducing the model root-mean-square error (RMSE), defined as:

$\text{RMSE}=\sqrt{{\displaystyle \sum _{i=1}^M}{\left(m_i^{true}-m_i^{inv}\right)}^2/M}(16)$

Where, $m_i^{ture}$ is the real model physical property value of the ith cell; $m_i^{inv}$ is the inversion model physical property value of the ith cell.

We calculated the root-mean-square error between the reconstructed density model and the real density model as shown in Table 1. From these values, it can be seen that the root-mean-square error of the model obtained by the binary structure constrained gravity inversion algorithm is smaller than that obtained by separate gravity inversion method. This indicates that the resolution of the density model reconstructed by the binary structure constrained gravity inversion algorithm is higher than separate gravity inversion method.

TABLE 1

TABLE 1. Root-mean-square errors between reconstructed and real models for different gravity inversion algorithms(RMSE).

3.2 Comparative analysis of binary constraints and cross-gradient structural constraints

In this section, we verify the effectiveness of the proposed algorithm by comparing and analyzing the reconstruction ability of binary structure constraints and cross-gradient structure constraints on the density model. We design a rectangular combination of two rectangular bodies of different sizes, the real density model is shown in Figure 3A, and the real velocity model is shown in Figure 3B.

FIGURE 3

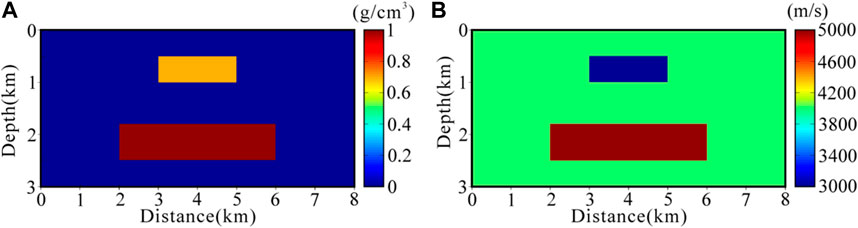
FIGURE 3. The second synthetic model including two targets with different size and burial depths. (A) The real density model; (B) The real velocity model.

The background region has a size of 8 km × 3 km and background velocities and densities of 4000 m/s and 0 g/cm³, respectively. The target region contains two rectangular anomalies, the upper rectangle has a size of 2 km × 0.5 km and velocities and densities of 3000 m/s and 0.7 g/cm³, respectively. The size of the lower rectangle is 4 km × 0.7 km, and the velocities and densities are 5000 m/s and 1 g/cm³, respectively. The gravity has a total of 29 observation points, which are uniformly distributed on the survey line of 0–8 km. We dissect the model into 80×30 horizontal and vertical cells, each of size 100×100 m.

We directly use the real velocity model as the a priori structural information, and then reconstruct the density model by separate inversion, cross-gradient joint inversion, and binary structure constrained inversion. In all inversion methods, the initial density model is the background density model.

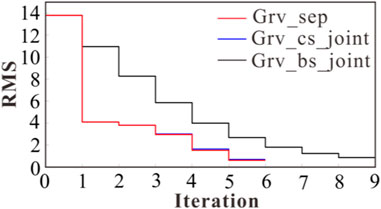
We first perform a separate gravity data inversion. The separate inversion is stopped after 5 iterations and the reconstructed density model is shown in Figure 5A. The final misfit of gravity data is 0.624, as shown by the red solid line in Figure 6. As expected, the reconstructed density model does not clarify the location and geometry of the target, and the anomaly boundaries are not clear enough to distinguish the upper and lower anomalies, which is usually due to the limited vertical resolution of the gravity data. In the iteration of the cross-gradient joint inversion algorithm, we fixed the velocity model in each iteration and structured the constrained density model by the cross-gradient function (Grv_cs_joint). The algorithm was stopped after 5 iterations, which took about 21.4 s. The reconstructed density model is shown in Figure 5B. The final misfit of gravity data is 0.699, as shown by the blue solid line in Figure 6. We find that the density model obtains a structural constraint effect at the boundary of the velocity model anomalies and can recover the sharp boundary of the two rectangular anomalies, but the structural constraint effect is poor outside the target region, mainly due to the fact that there is no gradient change of the velocity value of the velocity model outside the target region, and the value of the cross-gradient in the region is always zero, which leads to the cross-gradient function not acting as structural constraints, and thus a pseudoanomaly occurs outside the rectangular anomalies. Therefore, there is a false anomaly outside the rectangular anomaly, which is structurally different from the real density model. This phenomenon also shows that the cross-gradient joint inversion algorithm should be used with caution when there is a big difference in the convergence speed of different geophysical methods.

In the binary structure constrained gravity inversion algorithm, we abandon the traditional threshold method to distinguish the background region and the target region, but through the FCM clustering technique to extract the target region of the real velocity model, we set the number of clusters C = 2, and constantly update the clustering center, and finally the target region and the background region are divided into two categories, the red region is the target region, and the blue region is the background region, as shown in Figure 4. We use the acquired target region as the a priori structural information for the gravity inversion. Meanwhile, the gravity inversion is computed only in the target domain, and the background domain is kept unchanged. The algorithm stops after 8 iterations and takes about 11.9 s. The reconstructed density model is shown in Figure 5C. The final misfit of gravity data is 0.873, as shown by the black solid line in Figure 6. We find that the reduction of the inversion solution space reduces the gravity inversion multiplicity, resulting in a reconstructed density model that is closer to the real model. Compared with the cross-gradient constrained joint inversion algorithm, more accurate values of spatial geometry and physical parameters of the anomalies are obtained, which improves the vertical resolution of the gravity inversion. Meanwhile, the computation time is reduced because of the lower dimensionality of the reconstructed parameters and the elimination of the structural coupling terms between different model parameters.

FIGURE 4

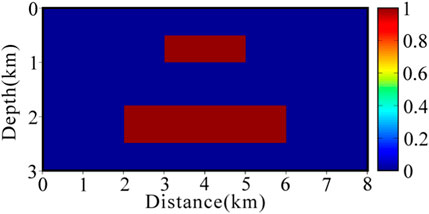
FIGURE 4. The binary constraint model obtained based on the extraction of the target region by FCM technique.

FIGURE 5

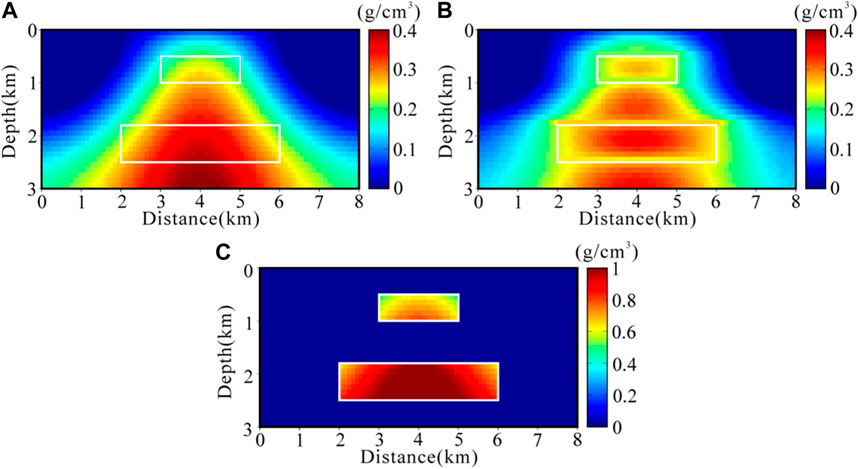
FIGURE 5. The reconstruction density model of different methods for the second synthetic model. (A) Separate gravity inversion results; (B) Cross-gradient joint inversion results; (C) Binary structured constrained gravity inversion results.

FIGURE 6

FIGURE 6. Gravity data inversion data misfit iteration curves.

We also determine the quality of the reconstructed inversion image by introducing the model root-mean-square error. We calculated the root-mean-square error between the reconstructed density model and the real density model as shown in Table 2. From these values, it can be seen that the root-mean-square error of the model obtained by the binary structure constrained gravity inversion algorithm is smaller than that obtained by other algorithms. This indicates that the resolution of the density model reconstructed by the binary structure constrained gravity inversion algorithm is higher than that of other conventional methods.

TABLE 2

TABLE 2. Root-mean-square errors between reconstructed and real models for different gravity inversion algorithms(RMSE).

4 Conclusion

We develop a binary structure constrained gravity inversion algorithm based on seismic first arrival travel time data. The fuzzy c-means clustering technique is used to extract the target region of the velocity guided model, and the obtained target region is used as the gravity inversion region. Two synthetic examples are used to analyze the accuracy and effectiveness of the binary structure constrained gravity inversion method. Our results show that the cross-gradient structurally constrained joint inversion does not reconstruct the density model well when the reference model is fixed, and the method is more suitable for joint inversion calculations of two geophysical methods with similar convergence speeds to try to avoid too large a difference in convergence speeds. The binary structure constrained gravity inversion only performs the inversion calculation in the target region, which effectively reduces the dimension of the inversion solution space, and thus reduces the inversion multisolution. Compared with the separate gravity inversion and the cross-gradient joint inversion, the proposed method obtains more accurate values of spatial geometry and physical parameters of the anomalies, which further improves the vertical resolution of gravity inversion. The algorithm proposed in this paper is not only applicable to gravity method, but also can be extended to magnetic and electromagnetic methods, which can effectively improve the resolution of magnetization and resistivity model reconstruction.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XD: Writing–original draft, Writing–review and editing. RZ: Writing–original draft, Writing–review and editing. JZ: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the Science and Technology Development Plan Project of Jilin Province, China under Grant YDZJ202201ZYTS491.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Afnimar, A., Koketsu, K., and Nakagawa, K. (2002). Joint inversion of refraction and gravity data for the three-dimensional topography of a sediment-basement interface. Geophys. J. Int. 151 (1), 243–254. doi:10.1046/j.1365-246x.2002.01772.x

CrossRef Full Text | Google Scholar

Afshar, A., Norouzi, G., Moradzadeh, A., and Riahi, M. (2018). Application of magnetic and gravity methods to the exploration of sodium sulfate deposits, case study: garmab mine, Semnan, Iran. J. Appl. Geophys. 159, 586–596. doi:10.1016/j.jappgeo.2018.10.003

CrossRef Full Text | Google Scholar

Carter-McAuslan, A., Lelievre, P. G., and Farquharson, C. G. (2015). A study of fuzzy c-means coupling for joint inversion, using seismic tomography and gravity data test scenarios. Geophysics 80 (1), W1–W15. doi:10.1190/geo2014-0056.1

CrossRef Full Text | Google Scholar

Fregoso, E., and Gallardo, L. A. (2009). Cross-gradients joint 3D inversion with applications to gravity and magnetic data. Geophysics 74 (4), L31–L42. doi:10.1190/1.3119263

CrossRef Full Text | Google Scholar

Gross, L. (2019). Weighted cross-gradient function for joint inversion with the application to regional 3-D gravity and magnetic anomalies. Geophys. J. Int. 217 (3), 2035–2046. doi:10.1093/gji/ggz134

CrossRef Full Text | Google Scholar

Guillen, A., and Menichetti, V. (1984). Gravity and magnetic inversion with minimization of a specific functional. Geophysics 49 (8), 1354–1360. doi:10.1190/1.1441761

CrossRef Full Text | Google Scholar

Heincke, B., Jegen, M., Moorkamp, M., Hobbs, R. W., and Chen, J. (2017). An adaptive coupling strategy for joint inversions that use petrophysical information as constraints. J. Appl. Geophys. 136, 279–297. doi:10.1016/j.jappgeo.2016.10.028

CrossRef Full Text | Google Scholar

Lelievre, P. G., Farquharson, C. G., and Hurich, C. A. (2012). Joint inversion of seismic traveltimes and gravity data on unstructured grids with application to mineral exploration. Geophysics 77 (1), K1–K15. doi:10.1190/geo2011-0154.1

CrossRef Full Text | Google Scholar

Lelievre, P. G., Oldenburg, D. W., and Williams, N. C(2009). Integrating geological and geophysical data through advanced constrained inversions. Explor. Geophys. Melb. 40 (4), 334–341. doi:10.1071/eg09012

CrossRef Full Text | Google Scholar

Li, Y., and Oldenburg, D. W. (1998). 3-D inversion of gravity data. Geophysics 63 (1), 109–119. doi:10.1190/1.1444302

CrossRef Full Text | Google Scholar

Li, Y., and Oldenburg, D. W. (1996). 3-D inversion of magnetic data. Geophysics 61 (2), 394–408. doi:10.1190/1.1443968

CrossRef Full Text | Google Scholar

Ming, Y., Niu, X., Xie, X., Han, Z., Li, Q., and Sun, S. (2021). Application of gravity exploration in urban active fault detection. IOP Conf. Ser. Earth Environ. Sci. 660 (1), 012057. doi:10.1088/1755-1315/660/1/012057

CrossRef Full Text | Google Scholar

Molodtsov, D., Kashtan, B., and Rostov, Y. (2011). Joint inversion of seismic and magnetotelluric data with structural constraint based on dot product of image gradients. Seg. Tech. Program Expand. Abstr. 30 (1), 740–744. doi:10.1190/1.3628184

CrossRef Full Text | Google Scholar

Moorkamp, M., Heincke, B., Jegen, M., Roberts, A. W., and Hobbs, R. W. (2011). A framework for 3-D joint inversion of MT, gravity and seismic refraction data. Geophys. J. Int. 184 (1), 477–493. doi:10.1111/j.1365-246x.2010.04856.x

CrossRef Full Text | Google Scholar

Nabighian, M. N., Ander, M. E., Grauch, V. J. S., Hansen, R. O., LaFehr, T. R., Li, Y., et al. (2010). “Gravity exploration methods; 75th anniversary historical development of the gravity method in exploration,” in Geophysical references series. Editor S. Fomel (Tulsa, OK: Society of Exploration Geophysicists), 113–139.

Google Scholar

Nabighian, M. N., Ander, M. E., Grauch, V. J. S., Hansen, R. O., LaFehr, T. R., Li, Y., et al. (2005). Historical development of the gravity method in exploration. Geophysics 70 (6), 63ND–89ND. doi:10.1190/1.2133785

CrossRef Full Text | Google Scholar

Niwlawn, L., and Jacobsen, B. H. (2000). Integrated gravity and wide-angle seismic inversion for two-dimensional crustal modelling. Geophys. J. Int. 140 (1), 222–232. doi:10.1046/j.1365-246x.2000.00012.x

CrossRef Full Text | Google Scholar

Pak, Y., Tonglin, L., and Kim, G. (2017). 2D data-space cross-gradient joint inversion of MT, gravity and magnetic data. J. Appl. Geophys. 143, 212–222. doi:10.1016/j.jappgeo.2017.05.013

CrossRef Full Text | Google Scholar

Rongzhe, Z., Tonglin, L., Cai, L., Haoyuan, H., Xingguo, H., and Vatankah, S. (2023). Geophysical joint inversion based on mixed structural and rock-physics coupling constraints. Geophysics 88 (2), K27–K37. doi:10.1190/geo2021-0795.1

CrossRef Full Text | Google Scholar

Singh, B. (2002). Simultaneous computation of gravity and magnetic anomalies resulting from a 2-D object. Geophysics 67 (3), 801–806. doi:10.1190/1.1484524

CrossRef Full Text | Google Scholar

Sun, J., and Li, Y. (2016). Joint inversion of multiple geophysical data using guided fuzzy c-means clustering. Geophysics 81 (3), ID37–ID57. doi:10.1190/geo2015-0457.1

CrossRef Full Text | Google Scholar

Tavakoli, M., Nejati Kalateh, A., Rezaie, M., Gross, L., and Fedi, M. (2021). Sequential joint inversion of gravity and magnetic data via the cross-gradient constraint. Geophys. Prospect. 69 (7), 1542–1559. doi:10.1111/1365-2478.13120

CrossRef Full Text | Google Scholar

Tikhonov, A. N., and Arsenin, V. Y. (1977). Solutions of ill-posed problems. Toronto: Wiley.

Google Scholar

Vidale, J. E. (1988). Finite-difference calculation of travel times. Bull. Seismol. Soc. Am. 78 (6), 2062–2076.

Google Scholar

Windham, M. P. (1982). Cluster validity for the fuzzy c-means clustering algorithrm. IEEE Trans. pattern analysis Mach. Intell. 4 (4), 357–363. doi:10.1109/tpami.1982.4767266

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, J., Lü, Q., Qi, G., Fu, G., Zhang, K., Lan, X., et al. (2020). A 3D geological model constrained by gravity and magnetic inversion and its exploration implications for the world-class zhuxi tungsten deposit, south China. Acta Geol. Sin. (Beijing) 94 (6), 1940–1959. doi:10.1111/1755-6724.14602

CrossRef Full Text | Google Scholar

Zhang, R., Li, T., Deng, X., Huang, X., and Pak, Y. (2020). Two-dimensional data-space joint inversion of magnetotelluric, gravity, magnetic and seismic data with cross-gradient constraints. Geophys. Prospect. 68 (2), 721–731. doi:10.1111/1365-2478.12858

CrossRef Full Text | Google Scholar

Zhang, R., Li, T., and Liu, C. (2022). Joint inversion of multiphysical parameters based on a combination of cosine dot-gradient and joint total variation constraints. IEEE Trans. geoscience remote Sens. 60, 1–10. doi:10.1109/tgrs.2021.3071498

CrossRef Full Text | Google Scholar

Zhdanov, M. S., Gribenko, A., and Wilson, G. (2012). Generalized joint inversion of multimodal geophysical data using Gramian constraints. Geophys. Res. Lett. 39 (9), 51233. doi:10.1029/2012gl051233

CrossRef Full Text | Google Scholar