
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 29 December 2023
Sec. Geohazards and Georisks
Volume 11 - 2023 | https://doi.org/10.3389/feart.2023.1295672
The occurrence of over-excavation or under-excavation in tunnel construction poses significant safety risks. Moreover, there is currently no automatic estimation method available for real-time estimation of earthwork excavation, particularly in the case of shield tunnels. In this study, we tracked the excavation process of Chengdu Metro Line 19, acquired tunneling parameters and earthwork excavation data using various sensors, and subsequently proposed an automatic estimation method that combines Bayesian optimization (BO) and gradient boosting regression tree (GBRT) algorithm. The results of our case study indicate that the BO-GBRT model improves the performance of earthwork excavation estimation, reducing the residual after each calculation with a root mean square error (RMSE) of 1.712 and mean absolute error (MAE) of 1.331. Furthermore, compared to other machine learning methods, the proposed BO-GBRT model demonstrates superior estimation performance. Additionally, the importance distribution of input parameters reveals that propulsion pressure, foam pressure, and rotation speed are the most critical factors affecting earthwork excavation. Overall, the proposed automatic estimation method shows great promise as a tool for efficiently estimating earthwork excavation in shield tunnel construction.
Urban railway systems have been rapidly developed to mitigate the increasingly serious traffic problem in developing countries (Zhang et al., 2020; Qin et al., 2022). Most of the metro tunnels are constructed using shield machines because these machines save in labor, allow for high-quality construction, and generate small disturbance (Yan et al., 2021). During the shield tunnel construction, the amount of earthwork excavation determines the degree of disturbance to the surrounding stratum (Lu et al., 2015; Koopialipoor et al., 2019a). Exceeding the designated range of earthwork excavation, either through over-excavation or under-excavation, can have detrimental effects such as damage to nearby structures or surface deformations (Song et al., 2019). These consequences subsequently lead to increased construction costs, slower progress rates, and higher post-construction maintenance expenses (Verma et al., 2018; Foderà et al., 2020). Unlike the drill-and-blast method, the shield tunneling technique occupies a significant portion of the tunnel face, making direct measurement of tunnel over-excavation and under-excavation challenging (Jian et al., 2022). Given these circumstances, the development of an automatic estimation method for accurately assessing the earthwork excavation quantity in shield tunnels becomes crucial for safe construction.
At the construction site, some engineers have attempted to monitor the earthwork excavation amount of shield machine by arranging equipment. Dong et al. (2018) monitors real-time dynamic information of the muck discharge by installing a belt weighing device in the shield machine. Gong et al. (2021) proposed a real-time muck analysis system for assistant intelligence TBM tunneling, which can measure the mass and volume flow of the muck by installing a belt scale and a scanner to monitor the stability of the rock mass on the tunnel face. In fact, construction workers often adopt the hook scale metering system to calculate the earthwork excavation amount. Some achievements have been made in in-site monitoring of engineering, but there are still some limitations, such as the serious lag effect of weighing outside the tunnel and the measurement accuracy of the belt scale is easily affected by belt tension and soil viscosity factors. Moreover, in-site monitoring methods can only serve as a reference after construction and cannot timely remind machine operators whether there is over-excavation or under-excavation. The amount of earthwork excavation for each ring still depends on the subjective experience of the machine operator.
Recently, the machine learning (ML) methods have attracted much attention because it can mine the inherent laws behind the data by relying on good autonomous learning and analysis ability (Huang et al., 2021). Various ML methods have been developed and applied to tunnel construction, such as tunneling parameters optimization (Afradi et al., 2019; Gao et al., 2021; Kong et al., 2022; Song and Xia, 2022), shield attitude forecast (Wang et al., 2019; Zhou et al., 2019; Xiao et al., 2021; Xiao et al., 2022a; Huang et al., 2022), and stratigraphic identification (Zhao et al., 2019; Liu et al., 2020; Yang et al., 2022). For more comprehensive details, one may refer to the relevant review papers by Song et al. (2023) and Li et al. (2023). Especially in the field of drill-and-blast method excavation, some scholars have attempted to use ML methods to predict and discriminate the over-excavation and under-excavation. For example, Lu et al. (2015) used fisher discrimination analysis, conjugate gradient, and support vector machine (SVM) methods to predict and discriminate tunnel overbreak. Koopialipoor et al. (2019b), Koopialipoor et al. (2019c) adopted a variety of neural network technologies for over-excavation prediction, and demonstrated that their developed models can predict earthwork excavation with high degree of accuracy. From above analysis, ML methods have achieved good results in tunnel automation construction, which provides technical support for this study to establish an automatic estimation method for shield tunnel earthwork excavation amount using the ML methods and massive operation data.
The primary contribution of this study lies in the pioneering application of ML methods in the domain of shield tunneling excavation estimation. By establishing a correlation between excavation parameters and earthwork amount, the findings can offer valuable insights for optimizing shield machine parameters and ensuring safe tunnel construction. Specifically, leveraging a substantial dataset of shield excavation and earthwork excavation records from Chengdu Metro Line 19, we propose an ML-based automatic estimation method for earthwork amount. This approach combines Bayesian optimization (BO) with the gradient boosting regression tree (GBRT) algorithm. Additionally, three ML models are utilized to compare and analyze the accuracy of earthwork excavation estimation. Moreover, the significance of input parameters is assessed to determine the influence of excavation-related factors on earthwork amount estimation.
Based on in-situ tunneling data, combined with ML method and feedback control strategies, automatic estimation method for earthwork excavation can be implemented. This will be superior to machine operators setting tunnel parameters solely based on subjective experience. The whole automatic estimation process can be divided into four steps, as shown in Figure 1.
Step 1:. By tracking the in-site tunneling process, collect the shield tunnel earthwork excavation data and EPB tunneling data, and ultimately form a database for estimating earthwork excavation amount.
Step 2:. Establish an earthwork excavation estimation model based on ML algorithm, and estimate earthwork excavation information when the machine operator provides preset parameters.
Step 3:. Use the estimation model to estimate the earthwork excavation amount to assist shield tunneling. When the design requirements are not met, the machine operator will intervene in real-time to control the earthquake excavation; When the design requirements are met, tunneling according to the preset parameters.
Step 4:. Accompanied by excavation, obtain the tunneling data and earthwork excavation information again, update the database, and then repeat steps 2 and 3.
The foundation of the implementation framework is to obtain in-site tunneling data, and the core of the implementation framework is to establish an estimation model based on ML algorithm. In the following content, we will provide a detailed introduction to the ML model used.
In existing ML algorithms, gradient boosting method can fully consider the weight of each learner with the characteristics of high accuracy and stable estimation results (Jiang et al., 2022). Therefore, we adopt the gradient boosting regression tree algorithm as the basic training algorithm for the evaluation model, and on this basis, we propose a Bayesian optimization estimation model (BO-GBRT).
GBRT is an iterative decision tree-based regression algorithm based on boosting strategy (Friedman, 2001). Its basic idea is: first, the decision tree is used as the basic learner, and the residual of the previous round of learners (the gradient value of the loss function) is adopted to train the current round of learners. Then, the weights of the training set are updated, and then iterate continuously until the expected residual or the set maximum number of iterations are reached. Finally, these trained learners are integrated into a robust learner. GBRT algorithm is widely adopted in various scenarios for its strong interpretation, fast estimation speed, and the ability to combine multiple influencing factors freely (Wu et al., 2021; Zhang et al., 2022).
Given the training dataset D = {(x1, y1), (x2, y2), …, (xm, ym)} and loss function L (x, f(x)), the process of establishing GBRT model is as follows (Zhang et al., 2022):
Step 1:. Initialize the first weak learner with the training set:
Step 2:. For m = 1, 2, …, M, generate M regression trees iteratively:
1) For i =1, 2, …, N, calculate the negative gradient of the loss function of the mth regression tree and regard it as the estimate of the residual:
2) Build a regression tree to fit rmi and generate the leaf node region of the mth regression tree Rmj (j=1, 2,…, Jm), where J is the number of leaf nodes of the mth regression tree.
3) For j=1, 2, …, Jm, calculate the best fit value for each leaf node:
where yi is the observed value of sample xi of the jth leaf node;
4) Update the current round model as:
where I is a function. If the sample xi is on Rmj, I=1; otherwise, I=0.
Step 3:. Iteration until the expected number of base learners is reached, and the final strong learner is:
GBRT supports many different loss functions for regression. In this study, the loss function is squared error.
BO is an iterative algorithm proposed by Snoek et al. (2012), which is widely used in hyperparameter optimization issues. It mainly includes two parts: surrogate model and acquisition function (Cui and Yang, 2018). On the one hand, BO usually adopts Gaussian process (GP) as the surrogate model of the objective function modeling, for its flexibility and tractability. GP is an extension of the multi-dimensional Gaussian distribution on the infinite dimensional stochastic process, represented by the mean and covariance functions. Theoretically, it can achieve countless multi-layer neural network fitting (Gu et al., 2020). On the other hand, choose appropriate acquisition function to match the surrogate model is important in the practical hyperparameter optimization problem. The common acquisition functions include the probability of improvement (PI), expected improvement (EI), and upper confidence bound (UCB). Among them, the UCB function balances the mean and variance by weighting and is selected as the acquisition function in this study, which is defined as (Archetti and Candelieri, 2019):
where
Figure 2 shows the modeling process of the BO-GBRT model. First, preprocess the data based on the characteristics of the earthwork excavation dataset, including effective data extraction, feature selection, and dataset segmentation. Then, the BO-GBRT model is trained using the training dataset. In this stage, according to the hyperparameters search range of the GBRT algorithm, the BO algorithm works by defining a probabilistic model that estimates the relationship between hyperparameters and model performance, using an acquisition function to balance exploration and exploitation. The objective function, which measures model performance based on a chosen metric, is evaluated for a set of hyperparameters, with the probabilistic model being updated iteratively until the best set of hyperparameters is identified. Then constantly update, iterate, and calculate to get a GP model that closer to the true distribution of the objective function. When the iteration reaches the maximum number, stop updating the model and output the optimal hyperparameter combination result. Finally, the BO-GBRT model of earthwork excavation estimation with optimal hyperparameter combination is obtained.
The layout of the study area is shown in Figures 3A. The research data was collected from Chengdu Metro Line 19, China. The study section starts from New Wharf Street Station and is laid along Ningbo Road, passing through several roads, bridges, and residential areas, finally arriving at Honglian Village South Station. The excavation diameter of the tunnel is 8.64 m and the buried depth of the bottom plate is 16.4∼50 m and the buried depth of the top plate is 8∼41.5 m. The starting and ending mileages of the study section are 98732 and 100967, and the total excavation length is 2.235 km.
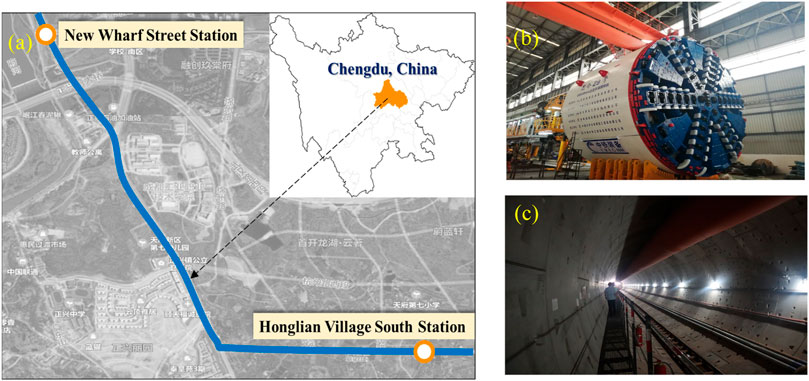
FIGURE 3. Study section of Chengdu Metro Line 19: (A) layout of the study area; (B) EPB shield machine; (C) completed shield tunnel.
The two representative soil strata of the tunnel site are moderately weathered mudstone and sandstone, and the remaining upper overburden layers include miscellaneous fill, silty clay, fine sand, pebble, and strongly weathered mudstone. The excavation equipment of the section is the earth pressure balance (EPB) shield machine, which recorded 530 tunneling parameters at 1Hz acquisition frequency, such as advance rate, cutterhead thrust, and rotation speed, providing a solid data basis for establishing an estimation model.
There are multiple ground buildings within the research section, and the disturbance generated during the EPB shield machine construction will cause deformation or damage to the existing buildings on the ground. Therefore, according to the safety control requirements of the project, in-site engineers are particularly concerned about the over-excavation and under-excavation phenomenon, and recorded the earthwork excavation amount through a high-precision hook scale metering (HSM) system. As shown in Figures 4C, the high-precision HSM system is installed in the control room of the gantry crane, paired with components such as the cinder box (Figures 4A) and gantry crane (Figures 4B), and can achieve a maximum weighing capacity of 60 t and an accuracy of 0.01 t. The engineer manually records the excavation amount of the earthwork and keep it in the form of paper documents (Figures 4D).

FIGURE 4. Process of obtaining earthwork excavation amount data: (A) shield tunnel cinder box; (B) gantry crane; (C) control room; (D) paper record file.
Through in-site tracking records, the author team recorded a total of 409 sets of earthwork excavation data for cinder boxes, with corresponding ring numbers ranging from 131 to 172, an average value of 31.33 t, a maximum value of 37.04 t, and a minimum value of 23.82 t. These data are adopted as target values for the BO-GBRT model, and 530 tunneling parameters within the 131 to 172 ring range are used as input values for the BO-GBRT model.
Unlike manually recorded earthwork excavation data, EPB tunneling data has obvious characteristics such as large data volume, complex features, and low value density (Xiao et al., 2022b). Therefore, this section mainly analyzes the preprocessing of EPB tunneling data.
The shield machine is not advancing forward all the time in a day, and there are many invalid tunneling data, as shown in Figures 5A. The first step of effective data extraction is to eliminate invalid tunneling data and extract effective tunneling section. Effective tunneling section refers to the complete rock boring process of the shield machine, usually including free running, loading, boring, and unloading. According to the excavation law of Chengdu Metro, the rotation speed is taken as the judging feature of the effective tunneling section. The rotation speed greater than zero is valid tunneling, and less than or equal to zero is invalid tunneling. Additionally, it is recommended to demolish the tunneling section that has a length shorter than 0.1 m and a tunneling time less than 60 s. It is often observed that the data distribution of tunneling sections with limited lengths and durations lacks orderliness, which poses challenges for subsequent data modeling endeavors (Xue et al., 2019). Finally, we filter out the tunneling sections shown in Figures 5B.
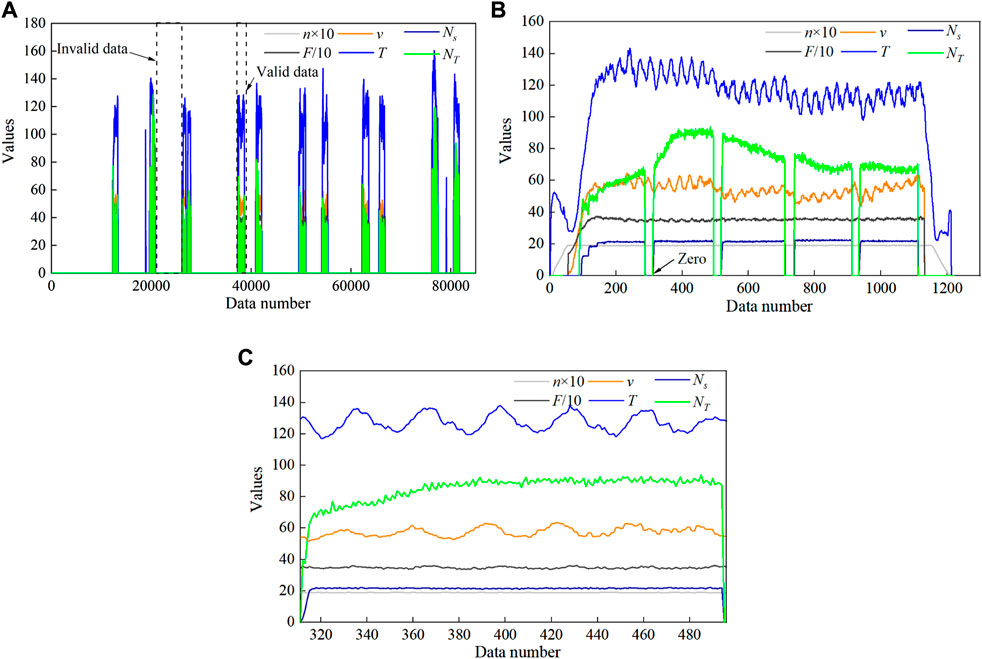
FIGURE 5. Effective data extraction from massive shield tunneling data: (A) raw data for 1 day; (B) effective tunneling section; (C) tunneling section corresponding to one cinder box.
Further, it is necessary to screen out the tunneling data matching with a single cinder box on the basis of effective tunneling section. According to the in-site construction arrangement, the machine operator will temporarily reduce the rotation speed of the screw machine (Ns) to zero to suspend the tunneling process. This time varies from 10 s to 20 s. Therefore, based on the characteristic of Ns, the effective tunneling section is further divided into single section corresponding to single cinder box, and the representative result is shown in Figures 5C. Finally, 409 groups of tunneling data corresponding to the earthwork excavation amount are screened, and the average tunneling time and tunneling length of each cinder box are 180.8 s and 149.3 mm, respectively.
The core of realizing the earthwork excavation estimation is to grasp the key tunneling parameters that directly affect the earthwork excavation. Parameters surely unrelated to the earthwork excavation, such as motor temperature and oxygen content, will be excluded. During the construction of Chengdu Metro, the propulsion system is the main tunneling force for the earthwork excavation, and the cutterhead system is the main rotary force for the earthwork excavation (Ates et al., 2014; Leng et al., 2020). In addition, additives such as foam or bentonite are added to increase the fluidity and water resistance of the muck during excavation. Representative parameters include the advance rate, propulsion pressure, rotation speed, cutterhead torque, foam pressure, bentonite pump outlet pressure, and central scouring pressure, etc.
Therefore, in this study, thirty average values of advance rate (v), cutterhead thrust (F), propulsion pressure (PA∼PF), rotation speed (n), cutterhead torque (T), foam pressure (FP1∼FP12), bentonite pump outlet pressure (BP1∼BP3), and central scouring pressure (SP1∼SP5) are adopted as the input parameters of the model. Nine reconstruction parameters (the difference between the first and end of tunneling section), propulsion displacement (DA∼DF), current ring cumulative of foam mixture (FM), bentonite (BT), and cutterhead spray (CS), are also adopted as the model inputs. Moreover, the boring time (t) of a tunneling section is also added as an input feature, which determines the boring length and affects the amount of earthwork excavation.
Further, we checked the correlation of these forty input parameters by Pearson correlation coefficient (PCC) method (Benesty et al., 2009). As presented in Figures 6A, six groups of propulsion displacement (DA∼DF), twelve groups of foam pressure (FP1∼FP12), and five groups of central scouring pressure (SP1∼SP5) all have high correlations in the same attribute. In view of these redundant parameters, each group only retains one set of parameters that are highly correlated with earthwork excavation. Finally, a total of twenty parameters are used for this analysis.
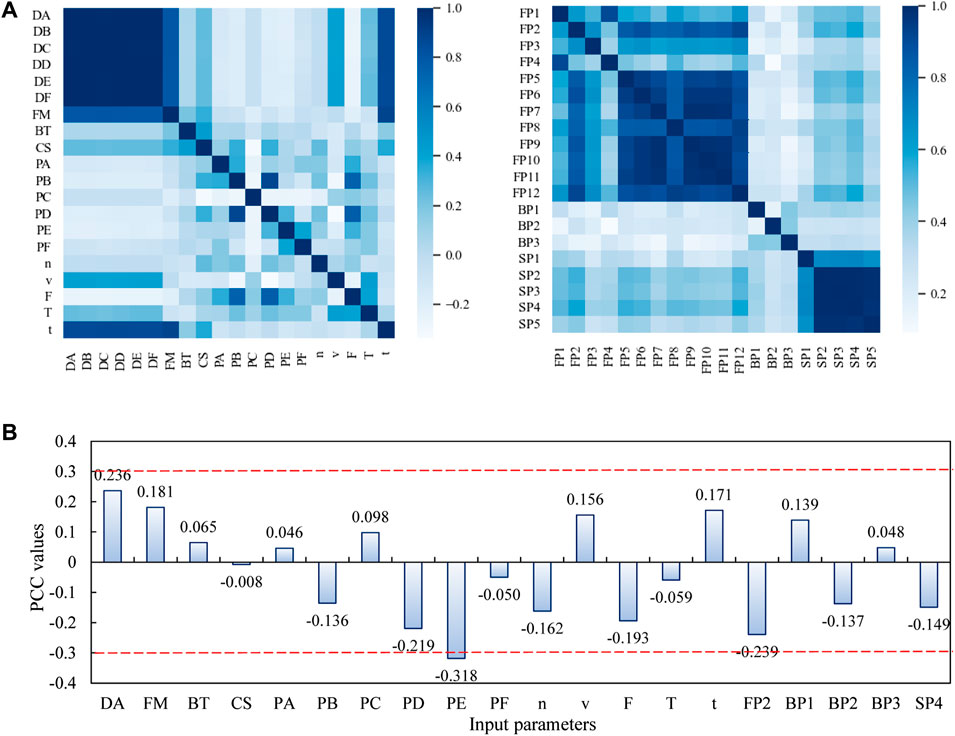
FIGURE 6. PCC values of the input parameters for the earthwork excavation. (A) forty input parameters; (B) twenty input parameters.
The ultimate datasets include 409 monitored earthwork excavation amount points and 20 tunneling parameters, recording the output and input parameters of each cinder box. Figures 6B presented the correlations between earthwork excavation amount and 20 tunneling parameters. It is found that the correlation between input parameters and output parameters is weak, and the absolute values of PCC are all less than 0.3. The parameter with the smallest PCC is the current ring cumulative of cutterhead spray (CS), which is only −0.008. The findings reveal that the earthwork excavation weakly correlates to twenty input variables, and a simple linear relationship between variables is not existed.
In this study, 409 sets of earthwork excavation amount and the corresponding shield tunneling parameters are adopted as the datasets for BO-GBRT model. Datasets of similar scale have been widely used in other previous scenarios, and the model application effect is good (Mottahedi et al., 2018; Xue et al., 2019; Yin et al., 2022). To develop intelligent model for predicting earthwork excavation, the established database should be divided into training and test datasets. According to Swingler (1996) (Swingler, 1996), the best model developments and model evaluations can be obtained using a combination of percentage values of (80, 20). Therefore, 328 datasets (80% of the data) randomly sampled from the database are used for model development and the remaining 81 datasets (20% of the data) are adopted for model evaluation. Table 1 presented the statistical description of parameters in training set and test set.
The datasets of this study contain a variety of parameters with different dimensions. If the normalization process is not carried out before entering the model, the estimation accuracy of the model will be vulnerable affected by the singular data. Therefore, the standardization method expressed in Eq. 7 is applied to the input dataset to eliminate the impact of different characteristics scales.
where
The important link in the estimation model establishment process is to select the optimal hyperparameter combination through the BO algorithm. The parameters involved in GBRT algorithm mainly include n_estimators, learning rate, min_samples_split, max_features, and max_depth. These parameters determine the accuracy and training time of the estimation model. Taking parameter n_estimators as an example, Figure 7 shows the changes in root mean square error (RMSE) and mean absolute error (MAE) of the model under different n_estimators numbers in the training and test sets. The RMSE and MAE values of the training set decrease dramatically with the increasing number of n_estimators, and the errors are almost equal to zero when the number of n_estimators exceed 1000 (Figure 7A). Moreover, for the low number of n_estimators, the RMSE and MAE values of the test set decline with the increase in the number of n_estimators (Figure 7B), which refers to the mitigation of underfitting. When the decision tree exceeds 300, the RMSE and MAE values tend to saturate (Figure 7B). According to the development laws of RMSE and MAE, it can find the best n_estimators is within the range of 300∼1000. Finally, the optimal depth value solved by the BO algorithm is 438. Similarly, other hyperparameters selections of BO-GBRT model are listed in Table 2.
In this section, we compare the estimation results of SVM, Adaptive boosting (AdaBoost), and Random forest (RF) algorithms with the BO-GBRT model. To ensure a good comparison between the models, these three model hyperparameters are also optimized using the BO algorithm, and the optimal hyperparameters for each model are shown in Table 3. We choose the MAE, RMSE, and residual error (Re) as the evaluation indicators of the four ML models. The calculation formulas of the three indicators are as follows:
where
These ML models are implemented using the Scikit-learn toolbox in Python 3.7. The entire test process is trained and optimized on a computer equipped with a Windows 64-bit operating system, Intel Core i7-7700k 4.20 GHz 8-core CPU with 32 GB RAM.
Table 4 list the estimation results of the four models in terms of RMSE, MAE, and R2. The results indicate that the BO-GBRT model outperformed the other three models in terms of earthwork excavation volume, achieving the smallest values for both RMSE and MAE as well as higher R2 values, both in the training and testing sets. Additionally, the BO-GBRT model has fully learned the data characteristics of the training set, the RMSE and MAE values are close to zero. The RMSE and MAE values of the test set are also the smallest, 1.712 and 1.331, respectively. Concurrently, considering the training time, it illustrates the superiority of the BO-GBRT model in predicting the scenarios of earthwork excavation amount, which can meet the requirements of real-time estimation of projects.
Figure 8 illustrates the results of measured and estimated earthwork excavation amount by BO optimization models. Regarding the test set, the BO-GBRT model virtually better captures the evolution of the earthwork excavation amount. Re appear to be randomly distributed around zero. Figure 9 represents the distribution curves of the measured and estimated earthwork excavation amount. The estimation values of the BO-GBRT model are most similar to the measured earthwork excavation amount distribution curve, and the estimated range basically covers the actual scope (i.e., 28∼36 t). Figure 10 shows the comparison of the measured and estimated earthwork excavation amount. It can be seen that the estimated and measured earthwork excavation amount of the four models are basically distributed around the 1:1 line.
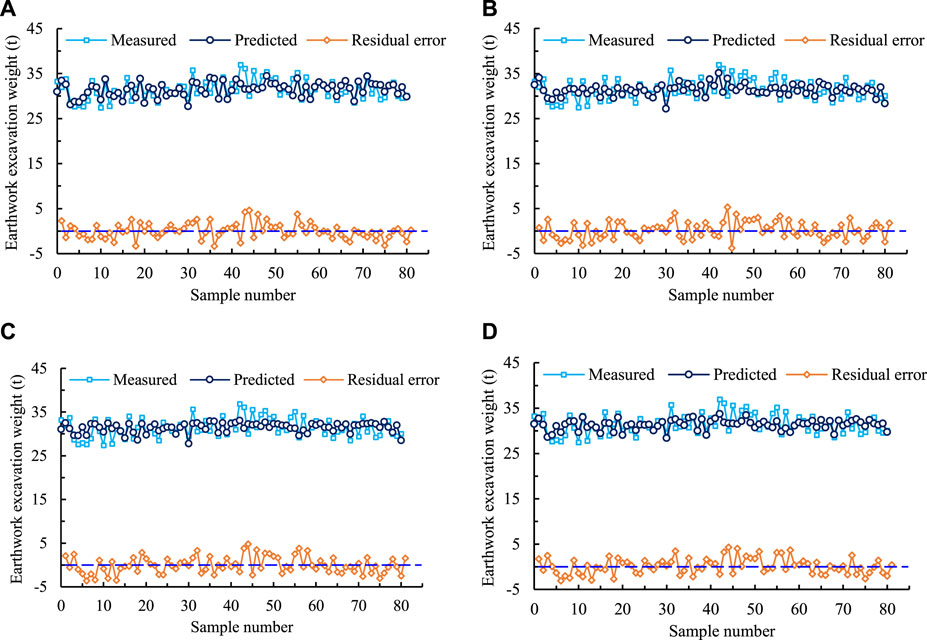
FIGURE 8. Measured and estimated earthwork excavation amount: (A) BO-GBRT; (B) BO-SVM; (C) BO-AdaBoost; (D) BO-RF.
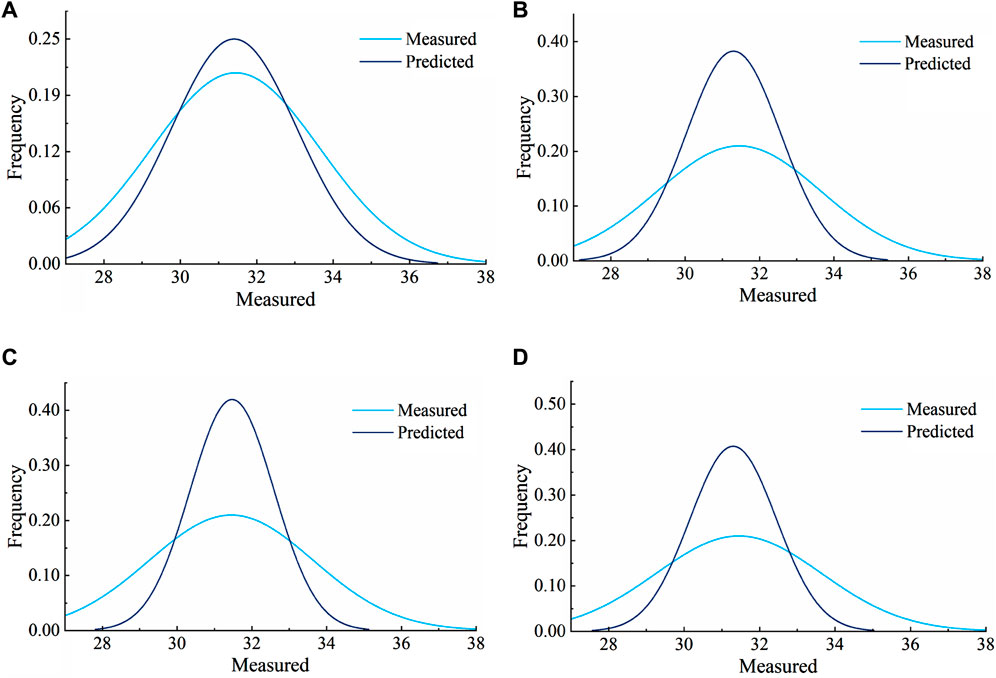
FIGURE 9. Distribution curves of the measured and estimated earthwork excavation amount: (A) BO-GBRT; (B) BO-SVM; (C) BO-AdaBoost; (D) BO-RF.
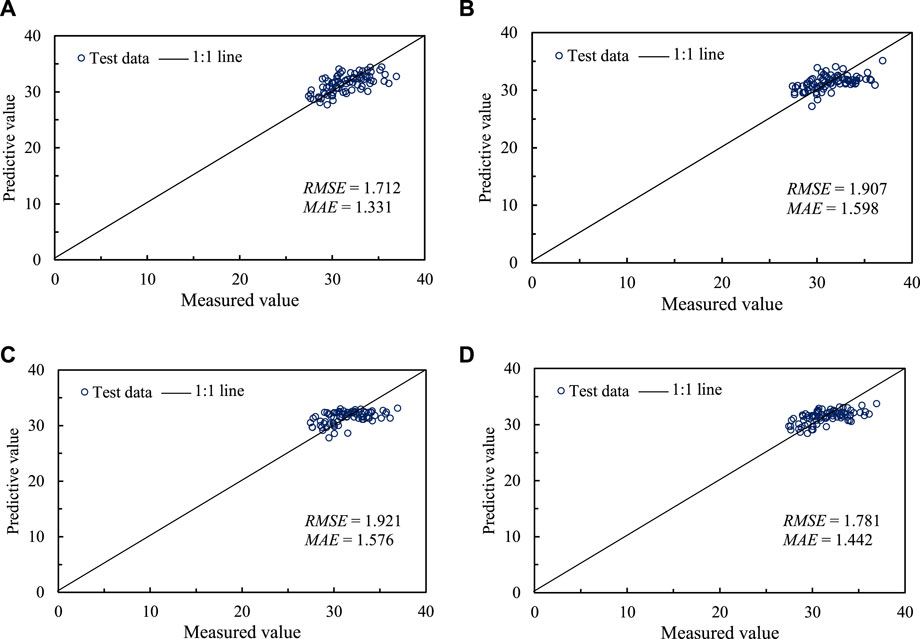
FIGURE 10. Comparison of the measured and estimated earthwork excavation amount: (A) BO-GBRT; (B) BO-SVM; (C) BO-AdaBoost; (D) BO-RF.
The anticipated results show that the estimation effect of the four Bayesian optimized models is similar and all have good estimation effect. However, considering the evaluation indicators of RMSE, MAE, Re, and the distribution curves of the measured and estimated values, the proposed BO-GBRT model can better estimate the earthwork excavation amount during shield tunnel excavation.
In order to evaluate the impact of input features on earthwork excavation amount, this section uses the GBRT to obtain the feature importance. The principle of this method is to evaluate the importance of each input variable by comparing the variable importance measure (VIM) of the Gini index calculated by the decision trees (Otchere et al., 2022). The main calculation formula of VIM is as follows:
where
If there are n decision trees in GBRT model, then:
The value range of VIM is 0∼1. The higher the VIM value, the greater the influence of the input parameters on the earthwork excavation amount.
The importance of the input parameters for earthwork excavation amount is displayed in Figure 11. The longer the bar corresponding to the input parameter, the importance contributions to the earthwork excavation amount. From Figure 11, the importance of predictive variables shows that PE, FP2, and n, namely, the propulsion pressure, foam pressure, and rotation speed, are the most critical factors affecting the earthwork excavation amount. The results indicate that propulsion pressure and foam pressure are the parameters that have a greater impact on the earthwork excavation amount. In the future, more applications will be conducted in different strata or different EPB shield tunnels to reveal the influence of tunneling parameters on the earthwork excavation amount.
The amount of earthwork excavation directly determines whether the shield tunnel is over-excavation or under-excavation, and further affects the stability of the tunnel face. Conventional methods are lag measurement and cannot guide the excavation process in real time. And data-driven methods have been successfully applied in many scenarios, as Phoon et al. (2022) stated, “In the era of Industry 4.0, data-driven analytics is likely to be more effective than physics in site characterization and it is a natural extension of current practice.” Data-driven techniques excel at extracting valuable information from extensive datasets. This study employs the data-driven GBRT algorithm to address the complexities and uncertainties inherent in the environment. Notably, through engineering practice, an initial set of 40 input parameters was determined, which was then reduced to 20 dimensions using data-driven methods. This reduction in parameters significantly enhances the computational efficiency of the ML model.
This study proposes a preliminary framework and implementation method of automatic estimation for earthwork excavation, integrating data acquisition, model construction, feedback control, and iterative updating. Through simple engineering training, in-site workers can choose the optimal tunneling parameters to avoid over-excavation or under-excavation. However, the in-site construction environment is complex, with diverse geological conditions and many uncertain factors. To truly guide the construction site, the proposed method must be closely integrated with the in-site environment and continuously optimized and upgraded in practice. Currently, this project has reached its conclusion, but we eagerly anticipate future opportunities to further validate the effectiveness of the model using specific engineering examples. Therefore, our forthcoming endeavors will concentrate on other shield tunneling projects, while also striving to expand the scope of the database in terms of diverse formations and equipment considerations. Furthermore, the subsequent phase of this work will also emphasize the evaluation of updated optimization algorithms to comprehensively compare their efficacy in estimating the amount of earthwork excavation.
The key factor in the construction of an EPB shield machine is to achieve balance between the internal and external chamber pressures. Through control of operational parameters, excavation amounts for each tunneling section can be kept within a reasonable range, thereby reducing the impact on the surrounding strata. This study addresses issues surrounding delayed and imprecise estimation of shield tunnel earthwork excavation, proposing a BO-GBRT model for automatic estimation. The main conclusions are as follows:
(1) The proposed method utilizes data collected by HSM system and EPB shield machines, with validation conducted using the Chengdu Metro project. Results demonstrate that the BO-GBRT model is an effective tool for estimating the excavation volume of shield tunnel earthwork.
(2) Compared to other machine learning methods, the BO-GBRT model significantly improves performance, with residual errors reduced as evidenced by RMSE of 1.712 and MAE of 1.331.
(3) Importance analysis indicates that propulsion pressure, foam pressure, and rotation speed are the most influential features in earthwork excavation.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
YC: Conceptualization, Investigation, Writing–review and editing. HX: Data curation, Software, Validation, Writing–original draft, Writing–review and editing. MH: Conceptualization, Methodology, Writing–original draft. LF: Software, Writing–original draft. QX: Validation, Writing–review and editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was supported by the Program of Shenzhen Key Laboratory of Green, Efficient and Intelligent Construction of Underground Metro Station (Grant No. ZDSYS20200923105200001), National Natural Science Foundation of China (Grant No. 52079150), and Three Type Talents of China Institute of Water Resources and Hydropower Research (Grant No. GE0145B042022).
Author YC was employed by Power China Railway Construction Investment Group Co., Ltd. Authors MH and QX were employed by Power China Southern Construction Investment Group Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors declare that this study received funding from the Core Research Project of Power Construction Corporation of China (Grant No. DJ-HXGG-2021-01). The funder had the following involvement in the study: data collection, interpretation of data, and the decision to submit it for publication.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Afradi, A., Ebrahimabadi, A., and Hallajian, T. (2019). Prediction of the penetration rate and number of consumed disc cutters of tunnel boring machines (TBMs) using artificial neural network (ANN) and support vector machine (SVM)—case study: beheshtabad water conveyance tunnel in Iran. Asian J. Water, Environ. Pollut. 16 (1), 49–57. doi:10.3233/ajw190006
Ates, U., Bilgin, N., and Copur, H. (2014). Estimating torque, thrust and other design parameters of different type TBMs with some criticism to TBMs used in Turkish tunneling projects. Tunn. Undergr. Space Technol. 40, 46–63. doi:10.1016/j.tust.2013.09.004
Benesty, J., Chen, J., Huang, Y., and Cohen, I. (2009). “Pearson correlation coefficient,” in Noise reduction in speech processing (Berlin, Heidelberg: Springer), 1–4.
Cui, J., and Yang, B. (2018). Survey on Bayesian optimization methodology and applications. J. Softw. 29 (10), 3068–3090. (in Chinese) doi:10.13328/j.cnki.jos.005607
Dong, L., Zhu, K., and Xiao, H. (2018). Application of dynamic monitoring system of belt dregs in slagging control of shield. Constr. Technol. 47 (1), 572–575
Faramarzi, A., Heidarinejad, M., Mirjalili, S., and Gandomi, A. H. (2020). Marine Predators algorithm: a nature-inspired metaheuristic. Expert Syst. Appl. 152, 113377. doi:10.1016/j.eswa.2020.113377
Foderà, G. M., Voza, A., Barovero, G., Tinti, F., and Boldini, D. (2020). Factors influencing overbreak volumes in drill-and-blast tunnel excavation. A statistical analysis applied to the case study of the Brenner Base Tunnel–BBT. Tunn. Undergr. Space Technol. 105, 103475. doi:10.1016/j.tust.2020.103475
Friedman, J. H. (2001). Greedy function approximation: a gradient boosting machine. Ann. statistics 29, 1189–1232. doi:10.1214/aos/1013203451
Gao, B., Wang, R., Lin, C., Guo, X., Liu, B., and Zhang, W. (2021). TBM penetration rate prediction based on the long short-term memory neural network. Undergr. Space 6 (6), 718–731. doi:10.1016/j.undsp.2020.01.003
Gong, Q., Zhou, X., Liu, Y., Han, B., and Yin, L. (2021). Development of a real-time muck analysis system for assistant intelligence tbm tunnelling. Tunn. Undergr. Space Technol. 107, 103655. doi:10.1016/j.tust.2020.103655
Gu, T., Xu, G., Li, W., Li, J., Wand, Z., and Luo, J. (2020). Intelligent house price evaluation model based on ensemble LightGBM and Bayesian optimization strategy. J. Comput. Appl. 40 (9), 2762–2767. (in Chinese) doi:10.11772/.issn.1001-9081.2019122249
Huang, H., Chang, J., Zhang, D., Zhang, J., Wu, H., and Li, G. (2022). Machine learning-based automatic control of tunneling posture of shield machine. J. Rock Mech. Geotechnical Eng. 14 (4), 1153–1164. doi:10.1016/j.jrmge.2022.06.001
Huang, M. Q., Ninić, J., and Zhang, Q. B. (2021). BIM, machine learning and computer vision techniques in underground construction: current status and future perspectives. Tunn. Undergr. Space Technol. 108, 103677. doi:10.1016/j.tust.2020.103677
Jian, F., Zhou, X., and Sheng, J. (2022). Analysis and application of over and under excavation of tunnel based on 3d laser point cloud data. Sci. Technol. innovation 2022 (11), 145–148. (in Chinese).
Jiang, S., Li, J., Zhang, S., Gu, Q., Lu, C., and Liu, H. (2022). Landslide risk prediction by using GBRT algorithm: application of artificial intelligence in disaster prevention of energy mining. Process Saf. Environ. Prot. 166, 384–392. doi:10.1016/j.psep.2022.08.043
Jones, D. R. (2001). A taxonomy of global optimization methods based on response surfaces. J. Glob. Optim. 21 (4), 345–383. doi:10.1023/a:1012771025575
Kong, X., Ling, X., Tang, L., Tang, W., and Zhang, Y. (2022). Random forest-based predictors for driving forces of earth pressure balance (EPB) shield tunnel boring machine (TBM). Tunn. Undergr. Space Technol. 122, 104373. doi:10.1016/j.tust.2022.104373
Koopialipoor, M., Ghaleini, E. N., Haghighi, M., Kanagarajan, S., Maarefvand, P., and Mohamad, E. T. (2019c). Overbreak prediction and optimization in tunnel using neural network and bee colony techniques. Eng. Comput. 35 (4), 1191–1202. doi:10.1007/s00366-018-0658-7
Koopialipoor, M., Ghaleini, E. N., Tootoonchi, H., Jahed Armaghani, D., Haghighi, M., and Hedayat, A. (2019a). Developing a new intelligent technique to predict overbreak in tunnels using an artificial bee colony-based ANN. Environ. Earth Sci. 78 (5), 165–214. doi:10.1007/s12665-019-8163-x
Koopialipoor, M., Jahed Armaghani, D., Haghighi, M., and Ghaleini, E. N. (2019b). A neuro-genetic predictive model to approximate overbreak induced by drilling and blasting operation in tunnels. Bull. Eng. Geol. Environ. 78 (2), 981–990. doi:10.1007/s10064-017-1116-2
Leng, S., Lin, J. R., Hu, Z. Z., and Shen, X. (2020). A hybrid data mining method for tunnel engineering based on real-time monitoring data from tunnel boring machines. IEEE Access 8, 90430–90449. doi:10.1109/access.2020.2994115
Li, J. B., Chen, Z. Y., Li, X., Jing, L. J., Zhangf, Y. P., Xiao, H. H., et al. (2023). Feedback on a shared big dataset for intelligent TBM Part I: feature extraction and machine learning methods. Underground Space.
Liu, Q., Wang, X., Huang, X., and Yin, X. (2020). Prediction model of rock mass class using classification and regression tree integrated AdaBoost algorithm based on TBM driving data. Tunn. Undergr. Space Technol. 106, 103595. doi:10.1016/j.tust.2020.103595
Lu, Z., Wu, L., and Bo, L. (2015). Optimization of tunnel overbreak prediction based on geological parameter analyses. Mod. Tunn. Technol. 52 (03), 189–192+204. (in Chinese). doi:10.13807/j.cnki.mtt.2015.03.026
Mottahedi, A., Sereshki, F., and Ataei, M. (2018). Overbreak prediction in underground excavations using hybrid ANFIS-PSO model. Tunn. Undergr. Space Technol. 80, 1–9. doi:10.1016/j.tust.2018.05.023
Otchere, D. A., Ganat, T. O. A., Ojero, J. O., Tackie-Otoo, B. N., and Taki, M. Y. (2022). Application of gradient boosting regression model for the evaluation of feature selection techniques in improving reservoir characterisation predictions. J. Petroleum Sci. Eng. 208, 109244. doi:10.1016/j.petrol.2021.109244
Phoon, K. K., Ching, J., and Shuku, T. (2022). Challenges in data-driven site characterization. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 16 (1), 114–126. doi:10.1080/17499518.2021.1896005
Qin, C., Shi, G., Tao, J., Yu, H., Jin, Y., Xiao, D., et al. (2022). An adaptive hierarchical decomposition-based method for multi-step cutterhead torque forecast of shield machine. Mech. Syst. Signal Process. 175, 109148. doi:10.1016/j.ymssp.2022.109148
Snoek, J., Larochelle, H., and Adams, R. P. (2012). Practical bayesian optimization of machine learning algorithms. Adv. neural Inf. Process. Syst. 25.
Song, Z., Mao, J., Tian, X., Zhang, Y., and Wang, J. (2019). Optimization analysis of controlled blasting for passing through houses at close range in super-large section tunnels. Shock Vib. 2019, 1–16. doi:10.1155/2019/1941436
Song, Z., and Xia, Z. (2022). Carbon emission reduction of tunnel construction machinery system based on self-organizing map-global particle swarm optimization with multiple weight varying models. IEEE Access 10, 50195–50217. doi:10.1109/access.2022.3173735
Song, Z., Yang, Z., Huo, R., and Zhang, Y. (2023). Inversion analysis method for tunnel and underground space engineering: a short review. Appl. Sci. 13 (9), 5454. doi:10.3390/app13095454
Swingler, K. (1996). Applying neural networks: a practical guideBurlington, Massachusetts, United States: Morgan Kaufmann.
Verma, H. K., Samadhiya, N. K., Singh, M., Goel, R. K., and Singh, P. K. (2018). Blast induced rock mass damage around tunnels. Tunn. Undergr. Space Technol. 71, 149–158. doi:10.1016/j.tust.2017.08.019
Wang, P., Kong, X., Guo, Z., and Hu, L. (2019). Prediction of axis attitude deviation and deviation correction method based on data driven during shield tunneling. IEEE Access 7, 163487–163501. doi:10.1109/access.2019.2952649
Wu, W., Wang, J., Huang, Y., Zhao, H., and Wang, X. (2021). A novel way to determine transient heat flux based on GBDT machine learning algorithm. Int. J. Heat Mass Transf. 179, 121746. doi:10.1016/j.ijheatmasstransfer.2021.121746
Xiao, H., Chen, Z., Cao, R., Cao, Y., Zhao, L., and Zhao, Y. (2022a). Prediction of shield machine posture using the GRU algorithm with adaptive boosting: a case study of Chengdu Subway project. Transp. Geotech. 7, 100837. doi:10.1016/j.trgeo.2022.100837
Xiao, H., Xing, B., Wang, Y., Yu, P., Liu, L., and Cao, R. (2021). Prediction of shield machine attitude based on various artificial intelligence technologies. Appl. Sci. 11 (21), 10264. doi:10.3390/app112110264
Xiao, H. H., Yang, W. K., Hu, J., Zhang, Y. P., Jing, L. J., and Chen, Z. Y. (2022b). Significance and methodology: preprocessing the big data for machine learning on TBM performance. Underground Space 7 (04), 680–701.
Xue, Y., Li, Z., Qiu, D., Zhang, L., Zhao, Y., Zhang, X., et al. (2019). Classification model for surrounding rock based on the PCA-ideal point method: an engineering application. Bull. Eng. Geol. Environ. 78 (5), 3627–3635. doi:10.1007/s10064-018-1368-5
Yan, T., Shen, S. L., Zhou, A., and Lyu, H. M. (2021). Construction efficiency of shield tunnelling through soft deposit in Tianjin, China. Tunn. Undergr. Space Technol. 112, 103917. doi:10.1016/j.tust.2021.103917
Yang, H., Song, K., and Zhou, J. (2022). Automated recognition model of geomechanical information based on operational data of tunneling boring machines. Rock Mech. Rock Eng. 55 (3), 1499–1516. doi:10.1007/s00603-021-02723-5
Yin, X., Gao, F., Wu, J., Huang, X., Pan, Y., and Liu, Q. (2022). Compressive strength prediction of sprayed concrete lining in tunnel engineering using hybrid machine learning techniques. Underground Space 7 (05), 928–943.
Zhang, D., Shen, Y., Huang, Z., and Xie, X. (2022). Auto machine learning-based modelling and prediction of excavation-induced tunnel displacement. J. Rock Mech. Geotechnical Eng. 14, 1100–1114. doi:10.1016/j.jrmge.2022.03.005
Zhang, P., Wu, H. N., Chen, R. P., Dai, T., Meng, F. Y., and Wang, H. B. (2020). A critical evaluation of machine learning and deep learning in shield-ground interaction prediction. Tunn. Undergr. Space Technol. 106, 103593. doi:10.1016/j.tust.2020.103593
Zhao, J., Shi, M., Hu, G., Song, X., Zhang, C., Tao, D., et al. (2019). A data-driven framework for tunnel geological-type prediction based on TBM operating data. IEEE Access 7, 66703–66713. doi:10.1109/access.2019.2917756
Zhou, C., Xu, H., Ding, L., Wei, L., and Zhou, Y. (2019). Dynamic prediction for attitude and position in shield tunneling: a deep learning method. Automation Constr. 105, 102840. doi:10.1016/j.autcon.2019.102840
Keywords: shield tunnel, earthwork excavation, data preprocessing, Bayesian optimization, automatic estimation, intelligent construction
Citation: Cao Y, Xiao H, He M, Fan L and Xu Q (2023) Estimation method of earthwork excavation using shield tunneling data -- a case study of Chengdu Metro. Front. Earth Sci. 11:1295672. doi: 10.3389/feart.2023.1295672
Received: 17 September 2023; Accepted: 30 November 2023;
Published: 29 December 2023.
Edited by:
Manoj Khandelwal, Federation University Australia, AustraliaReviewed by:
Han Du, Tsinghua University, ChinaCopyright © 2023 Cao, Xiao, He, Fan and Xu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Haohan Xiao, eGlhb2hoQGl3aHIuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.