An improved Burgers creep model of coal based on fractional-order

The instability and destruction of various types of coal pillars left in deep underground mining are frequently attributed to cumulative creep deformation exceeding the permissible limit, with high in situ stress playing a critical role in this phenomenon. To understand the complicated creep behavior of coal, triaxial compression creep tests were conducted. It has been proven that the coal specimens subjected to high confining pressure exhibit typical three-stage creep characteristics. Furthermore, with the increase in confining pressure, the creep threshold value increases while the creep threshold coefficient decreases. By fitting the creep strain-time results, an improved Burgers creep model based on fractional-order was proposed. This model can describe the primary, secondary, and tertiary stages and reflect the nonlinear behavior, contributing to the understanding of the long-term stability evaluation of deep coal pillars.

1 Introduction

In underground coal mining, various coal pillars are often left under surface buildings and around main entries. These pillars remain in place for an extended period, and their long-term stability is critical for the movement of the overburden and the protection of surface structures (Zhang et al., 2023a). In most cases, the failure of coal mass is not primarily due to insufficient strength but rather instability caused by long-term accumulation of creep deformation beyond the limit before reaching ultimate failure.

With the increasing mining depth, the in situ stress is greatly increased. In this case, coal undergoes a transition from brittle to ductile behavior, posing challenges for stability control in underground engineering(Zhang et al., 2022; Zhang et al., 2023b). One of the main challenges is the influence of rheological properties of the rock mass and the prominent creep deformation characteristics of coal pillars. These challenges are particularly pronounced in deep mines where the effects of creep are more significant. For entries with a long service life in deep mines, such as rise or dip entries, their long-term stability is directly related to mine safety and production. When determining the width of protected coal pillars, the time effect should be taken into consideration. Therefore, studying the creep behaviors of coal under high in situ stress, especially the triaxial creep behaviors, holds certain importance in the stability control of deep coal pillars.

In recent years, there have been many research achievements on the creep behaviors and constitutive models of rocks. For example, by adjusting the combination of units, improved creep models and corresponding constitutive equations are proposed. Some scholars have also improved some units or unit parameters in existing creep models so that the model can describe the tertiary stage. Recent studies have developed various creep models for rocks and minerals. Li and Yin (2021) modified the Nishihara model by incorporating an accelerating element to characterize sandstone creep. Similarly, Yan et al. (2023) established a creep model for hard flint limestone. However, Liu et al. (2017) and Shao et al. (2023) adopted an improved damage Nishihara model to simulate creep in their materials. Multi-stage creep tests on sandstone by Hou et al. (2019) led to a model with elastic, viscous and damage components. For high soft rocks, Ping et al. (2016) combined improved Burgers, Hookean and Saint Venant elements. Fractal derivative theory was applied by Yin et al. (2023) to develop a viscoelastic-plastic creep model with damage. Wu et al. (2020) and Lyu et al. (2021) used fractional Maxwell approaches, Abel dashpots and damage factors for salt rock and other materials. Li et al. (2017) compared Burgers, Nishihara and extended Nishihara models for coal under varying gas conditions. Other recent work includes modified Burgers (Ran et al., 2021) and pore pressure-based (Zhang et al., 2023c) models. Short-term nonlinear creep with damage was analyzed by Yang et al. (2015) using the Burgers equation. Zhang et al. (2019) introduced a negative elastic modulus and a non-Newtonian component into the classical Nishihara model based on the theoretical analysis of the experimental results. Cheng et al. (2020) established a creep hardening damage model considering the viscosity damage factor of coal. In summary, a range of improved constitutive relationships have been proposed through integrating additional elements and mechanisms.

Through existing literature, it is known that the research scope of rock rheology is wide. Researchers, based on traditional sciences such as material mechanics, fracture damage mechanics, elastoplastic theory, and rheological principles, analyze existing rheological models, or develop improved mechanical models based on test data. However, most of the literature studying the creep constitutive relationship of rocks has focused on rock and soil materials such as sandstone, shale, mudstone, soil, and filling materials. There are relatively few studies involving the creep constitutive relationships of coal, and many issues remain unclear, particularly regarding coal’s triaxial creep constitutive relationships.

This paper conducted triaxial compression creep tests on coal, by fitting the test results, the adaptability of Burgers equation was verified. Then an improved Burgers creep model based on fractional-order was proposed, which can describe the primary, secondary and tertiary stages of triaxial creep of coal specimens and reflect nonlinear behaviors.

2 Triaxial compression creep test of coal

2.1 Specimen preparation

The coal specimens tested in this work were extracted from the No. 3 seam at Yangcheng Coal Mine, Jining City, Shandong Province, China. This coal seam ranges between 5.54 and 7.78 m thick with a bulk density of 1.35 kN/m³. Intact coal blocks lacking substantial joints were chosen for specimen preparation (Liu et al., 2023; Liu and Li, 2023). Vertical coring techniques were utilized to obtain cylindrical specimens, which were processed to standard dimensions (diameter × height = 50 × 100 mm) based on International Society of Rock Mechanics (ISRM) recommended practice(ISRM, 1978; Bieniawski and Bernede, 1979; ISRM, 1983). This ensured consistent sample geometry and conditions across the testing program.

2.2 Apparatus

The traditional triaxial compression (σ₂ = σ₃) creep test of the coal specimens was conducted using the TOP INDUSTRIE STAC 600-600 multifunctional rock triaxial testing system (Figure 1). This testing system can perform uniaxial compression, traditional triaxial compression tests, as well as uniaxial and triaxial compression creep tests on rocks. It enables the investigation of the short-term and long-term deformation and strength properties of rocks, as well as the evolution of permeability properties during the deformation process of rocks.

FIGURE 1

FIGURE 1. Multi-function rock triaxial testing system.

2.3 Triaxial compression creep test plan

2.3.1 Loading mode

The loading methods for creep tests on coal specimens generally include single-step loading, stepwise loading, and cyclic loading/unloading. For different applied stress levels, single-step loading requires conducting separate tests for each specimen, which clearly consumes more time, demands a larger number of coal specimens, and imposes higher requirements on the testing equipment. Due to the significant variability among coal specimens, the use of single-step loading is not advisable. On the other hand, stepwise loading involves testing the same coal specimen, with the next applied stress level loaded after the specimen reaches stable creep deformation at the previous stress level. Compared to single-step loading, stepwise loading effectively mitigates the impact of specimen variability on test results (Tan and Kang, 1980).

2.3.2 Applied stress level

The magnitude of the applied stress is typically set between 12.5% and 80% (Griggs, 1939) of the compressive strength. The triaxial compressive strength of the coal specimens at different confining pressures (0 MPa, 5 MPa, 10 MPa, and 15 MPa) is as follows: 10.2 MPa, 12.3 MPa, 14.5 MPa, and 17.8 MPa, respectively. Based on the results of compression tests on the specimens, the applied stress was divided into five levels at 40%, 50%, 60%, 70%, and 80% of their respective compressive strengths.

2.3.3 Test duration

To avoid excessive equipment consumption, it is not possible to load for too long test duration. At the same time, the triaxial compression strength of the coal specimens is relatively low, so the creep time for each applied stress level was determined to be 6 h. This duration allows for the manifestation of creep characteristics within a short period of time.

2.3.4 Test design

As shown in Table 1, a uniaxial compression creep test and three triaxial compression creep tests were designed for coal specimens under different confining pressures (5 MPa, 10 MPa, and 15 MPa).

TABLE 1

TABLE 1. Design of uniaxial and triaxial creep compression tests of coal specimens.

2.4 Test results

2.4.1 Macroscopic deformation characteristics

Figures 2–5 show the creep deformation results of each coal specimen under different confining pressures (0 MPa, 5 MPa, 10 MPa, and 15 MPa), ε₁, ε₃, and ε_v represent axial strain, circumferential strain, and volumetric strain, respectively.

FIGURE 2

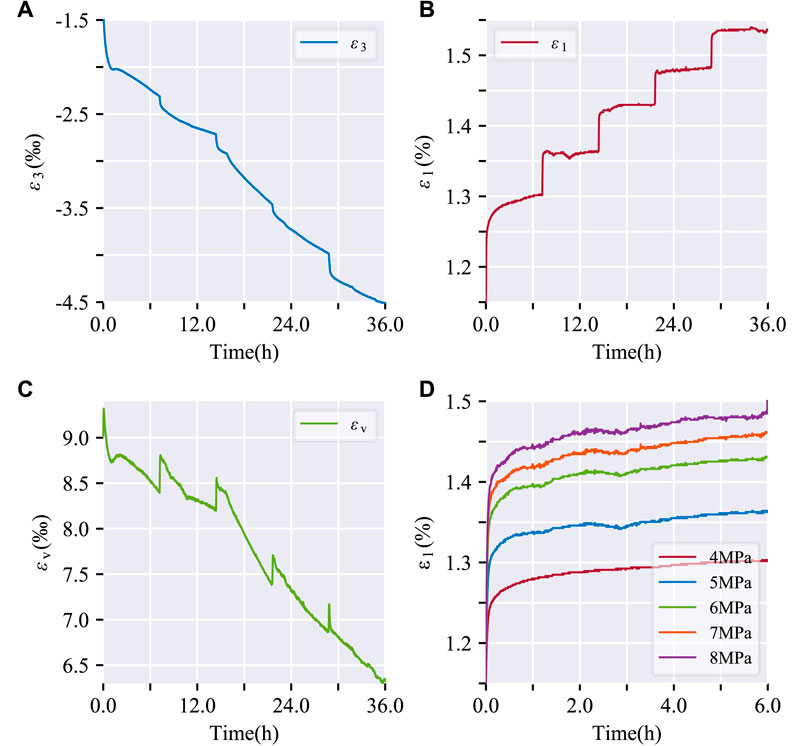
FIGURE 2. Strain-time curves of coal specimen (No.UCC1) under uniaxial compression creep. (A) diametric strain over time; (B) axial strain over time; (C) volumetric strain over time; (D) axial strain over time at different applied stress level.

FIGURE 3

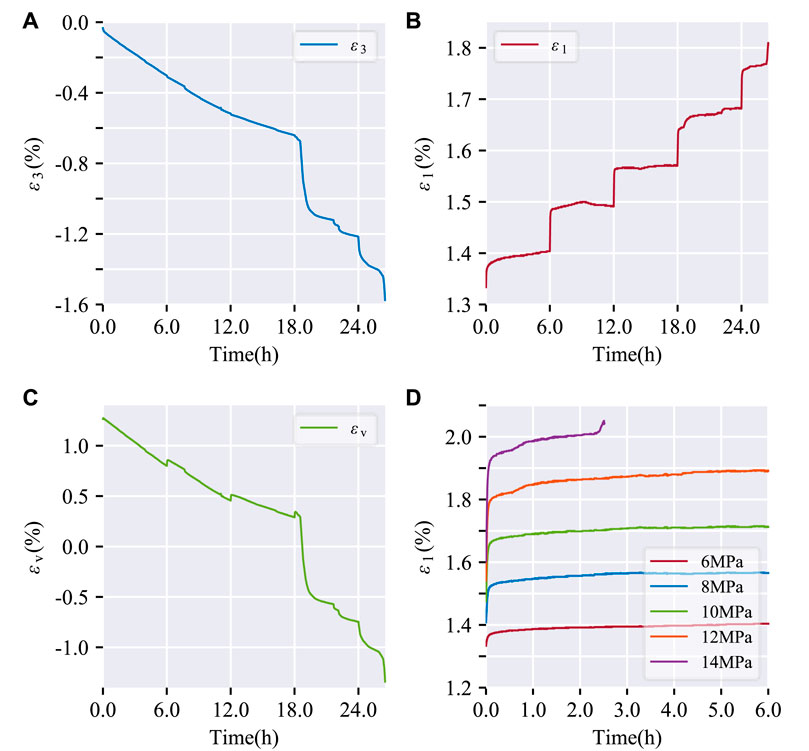
FIGURE 3. Strain-time curves of coal specimen (No.TCC1) under triaxial compression creep (σ₃=5 MPa). (A) diametric strain over time; (B) axial strain over time; (C) volumetric strain over time; (D) axial strain over time at different applied stress level.

FIGURE 4

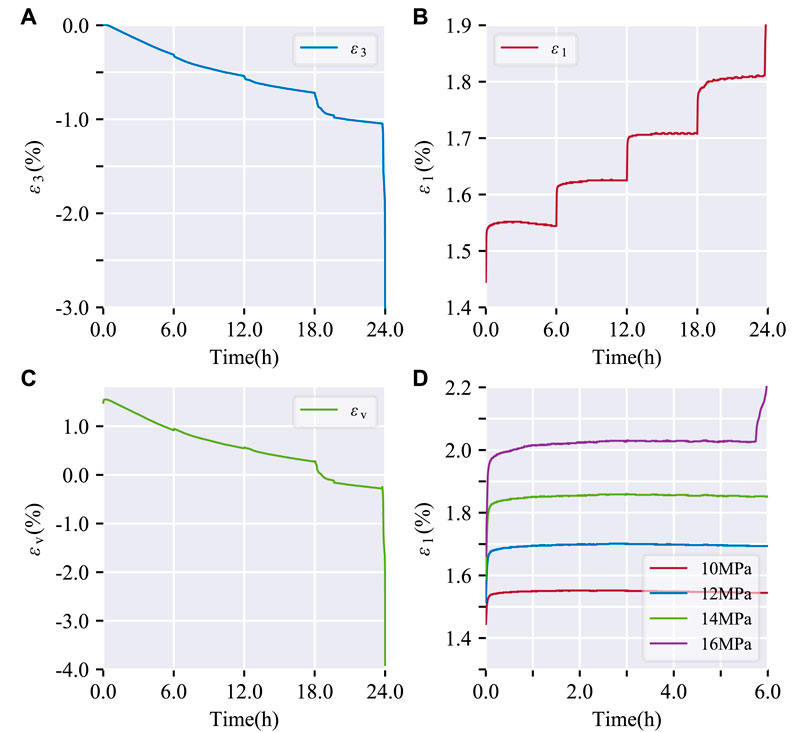
FIGURE 4. Strain-time curves of coal specimen (No.TCC2) under triaxial compression creep (σ₃=10 MPa). (A) diametric strain over time; (B) axial strain over time; (C) volumetric strain over time; (D) axial strain over time at different applied stress level.

FIGURE 5

FIGURE 5. Strain-time curves of coal specimen (No.TCC3) under triaxial compression creep (σ₃=15 MPa). (A) diametric strain over time; (B) axial strain over time; (C) volumetric strain over time; (D) axial strain over time at different applied stress level.

From Figures 2–5, it can be observed that the diametric strain-time curve, axial strain-time curve, and volumetric strain-time curve all exhibit a stepped pattern. The circumferential strain, axial strain, and volumetric strain increase continuously with the prolongation of loading time, indicating a clear creep behavior of the coal specimens.

Uniaxial creep tests displayed stable time-dependent deformation without tertiary creep (Figure 2D). Under triaxial conditions, moderate stress levels induced stable creep with distinguishable primary and secondary regimes (Figures 3D, 4D, 5D). However, the highest stress state resulted in unstable tertiary creep characterized by acceleration after secondary creep. Coal specimen No.TCC3 exemplified the stress-controlled transition at 20 MPa–below this axial level, the creep rate gradually declined and stabilized over time. Beyond 20 MPa, significant creep rate increase emerged following the secondary stage, indicative of tertiary creep onset.

2.4.2 Creep strength characteristics

It can be seen from Section 2.4.1 that there are obvious stress thresholds during the deformation process of coal specimens, such as the minimum stress level for creep deformation, and the stress level where tertiary creep occurs. Table 2 shows the calculated results of the creep strength characteristics parameters.

TABLE 2

TABLE 2. Calculation results of creep strength characteristics parameters for coal specimens.

(1) Coal specimens exhibit a creep threshold under varying confining pressures. Below this threshold axial stress, no creep occurs. At the threshold stress, significant creep phenomena emerge, with distinct primary and secondary creep stages observed. Furthermore, increasing confining pressure elevates the creep threshold continuously for two reasons: first, higher confinement corresponds to greater uniaxial strength, necessitating larger applied creep stresses; second, stronger circumferential constraints impose a larger threshold for creep initiation.

(2) In terms of the creep threshold coefficient, the values are 0.50, 0.47, 0.63 and 0.64 under 0 MPa, 5 MPa, 10 MPa and 15 MPa confining pressures, respectively, which are lower than the general creep threshold coefficient for rocks.

(3) Regarding the creep strength, the creep strength of coal specimens under different confining pressures is less than their uniaxial compressive strength, exhibiting significant creep characteristics. Under 0 MPa, 5 MPa, 10 MPa, and 15 MPa confining pressures, the creep strengths are 0.78, 0.74, 0.65, and 0.56 times the corresponding uniaxial compressive strengths, decreasing with increasing confining pressure.

(4) At the final stress level, tertiary creep occurred under 5 MPa, 10 MPa, and 15 MPa confining pressures, resulting in considerable deformation that severely weakened the mechanical properties of the coal specimens, leading to unstable failure.

3 Improved Burgers creep model based on fractional-order

The previous section conducted triaxial compression creep tests on coal. From the creep curves, it can be observed that coal exhibits mechanical behaviors such as elasticity and plasticity. Therefore, it is feasible to approximate the creep characteristics of coal using abstract mechanical models and establish its constitutive relationship.

3.1 Fitting of the Burgers model

Based on Li’s research Li et al. (2017), it was determined that the Burgers model provides a superior representation of the three stages of the creep process in coal compared to other models. Consequently, the Burgers model was chosen for fitting. The Burgers model consists of Maxwell and Voigt-Kelvin elements connected in series, as depicted in Figure 6. The constitutive relationship for creep of this model is presented in Equation 1.

$\epsilon =\frac{\sigma }{k_2}+\frac{\sigma }{{\eta }_2}+\frac{\sigma }{k_1}\left(1-e^{-\frac{k_1}{{\eta }_1}t}\right)(1)$

where k₁, k₂ are the stiffness of the springs in the Maxwell and Voigt-Kelvin model, respectively; η₁, η₂ are the viscosity coefficients of the dashpots in the Maxwell and Voigt-Kelvin model, respectively.

FIGURE 6

FIGURE 6. Burgers model.

The fitting curve of the Burgers model is shown in Figure 7. It can be observed that the Burgers model exhibits instantaneous deformation and a primary creep stage. It includes a linear term, allowing it to reflect steady creep characteristics. However, a limitation of the model is that it has only one inflection point and cannot capture accelerated creep behavior.

FIGURE 7

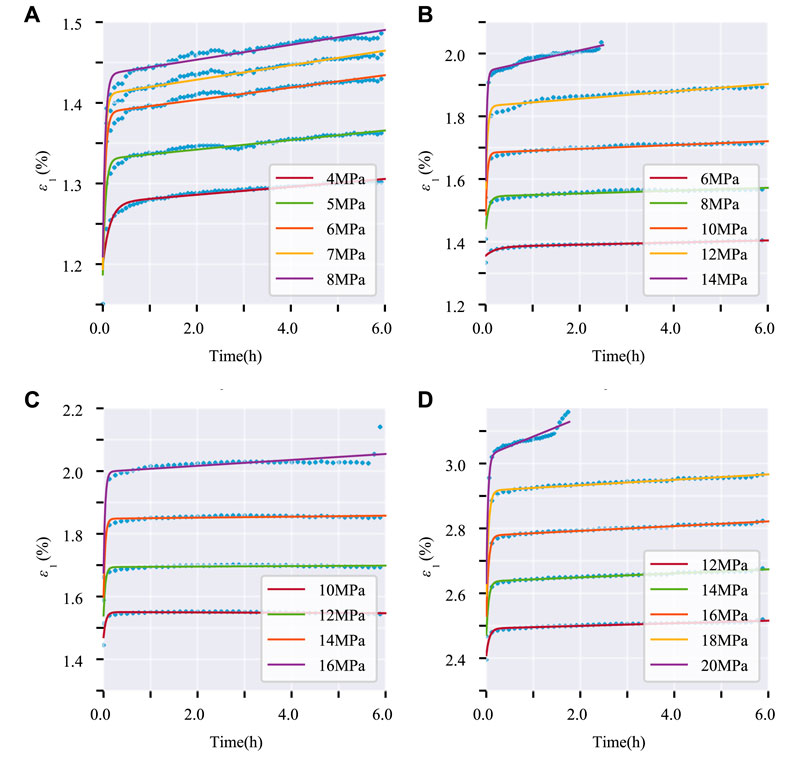
FIGURE 7. Burgers model fitting. (A) axial creep curve fitting; (B) triaxial creep curve fitting (σ₃=5 MPa); (C) triaxial creep curve fitting (σ₃=10 MPa); (D) triaxial creep curve fitting (σ₃=15 MPa).

3.2 Fractional-order improved Burgers model

As mentioned in Section 3.1, the main limitation of the Burgers model is its inability to capture tertiary creep behavior in coal specimens. The Newtonian unit in the model has purely linear and extremely viscous characteristics, making it difficult to reflect the nonlinear creep features of coal specimens. Therefore, improving the Burgers model is necessary.

3.2.1 Introduction to fractional calculus

In classical calculus, the German mathematician Leibniz used dⁿy(x)/dxⁿ (where n is a positive integer) to represent derivatives of different orders. Fractional-order calculus (non-integer calculus) directly extends integer-order calculus (Hassouna et al., 2022), where n is expanded from positive integers to fractions, complex numbers, and other levels.

Hence, when n ∈(0,1), it indicates the medium’s properties lie between those of an ideal solid and fluid. As shown in Figure 8, in fractional-order models, the Abel dashpot in fractional-order models represents this behavior (Koeller, 1984), with the constitutive relationship:

$\sigma \left(t\right)=\eta \frac{{\mathrm{d}}^n\epsilon }{\mathrm{d}{t}^n}(2)$

where n is the order, n∈(0,1); η is the viscosity coefficient of the Abel dashpot.

FIGURE 8

FIGURE 8. Abel dashpot.

3.2.2 Fractional-order Burgers model

The one-dimensional fractional-order Burgers model comprises fractional-order Maxwell and Voigt-Kelvin elements connected in series (Figure 9). The governing creep equation is:

$\epsilon =\frac{\sigma }{k_2}+\frac{\sigma }{{\eta }_2}\cdot \frac{t^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\frac{\sigma }{k_1}\left[1-E_{\alpha }\left(-{\left(\frac{k_1}{{\eta }_1}t\right)}^{\alpha }\right)\right](3)$

where α, β are the orders of the Abel dashpot in the fractional-order Maxwell and Voigt-Kelvin model, respectively. E_α represents the single-parameter Mittag-Leffler function in fractional-order calculus, and Γ(1+β) denotes the Gamma Function.

FIGURE 9

FIGURE 9. Fractional-order Burgers model.

As observed in Figure 10, the fractional-order Burgers model can accurately capture the nonlinear characteristics of coal specimens during the primary and secondary creep stages. The fitting results are more precise, as exemplified under 6 MPa axial stress (Figure 10B). The experimental data largely falls within the 95% confidence interval.

FIGURE 10

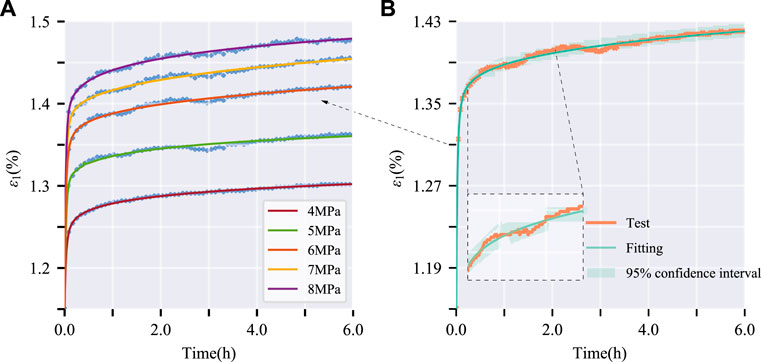
FIGURE 10. Fitting of uniaxial creep curve based on fractional-order Burgers model. (A) Fitting curve at different applied stress level; (B) Zoomed in fitting curve at 6 MPa applied stress level.

Underground coal formations are mostly subjected to a triaxial stress state. Therefore, it is necessary to extend the fractional-order Burgers model from one-dimensional to three-dimensional to reflect the creep characteristics of coal more accurately. The creep equation for the three-dimensional fractional-order Burgers model is given by:

${\epsilon }_1=\begin{array}{l}\frac{{\sigma }_1+2{\sigma }_3}{9K}+\frac{{\sigma }_1-{\sigma }_3}{3G_2}+\frac{{\sigma }_1-{\sigma }_3}{3{\eta }_2}\cdot \frac{t^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}\\ +\frac{{\sigma }_1-{\sigma }_3}{3G_1}\left[1-E_{\alpha }\left(-{\left(\frac{k_1}{{\eta }_1}t\right)}^{\alpha }\right)\right]\end{array}(4)$

where K is the volumetric modulus of the coal specimen, G₁, G₂ are the shear modulus of the Abel dashpot in the fractional-order Maxwell and Voigt-Kelvin model, respectively.

The triaxial creep response was modeled using a 3D fractional-order Burgers formulation. As shown in Figure 11, good agreement was obtained between the primary and secondary creep stages experimentally observed for coal specimens and the theoretical fit. The nonlinear creep behavior was effectively captured within a 95% confidence interval under representative conditions of 15 MPa confinement and 18 MPa axial stress. However, limitations were evident under sustained loading approaching failure, where the model deviated from measured tertiary creep characterized by accelerating strain accumulation.

FIGURE 11

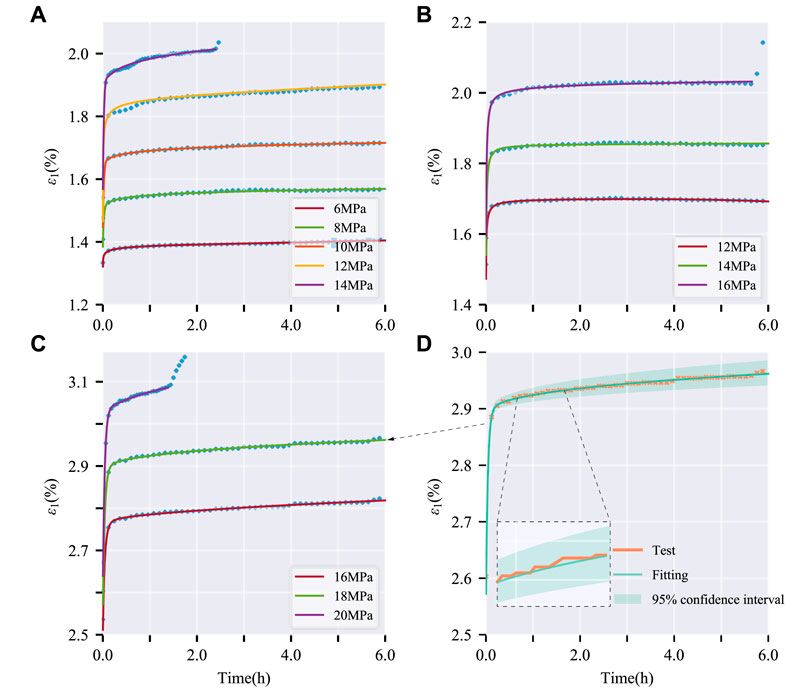
FIGURE 11. Fitting of triaxial creep curve based on fractional-order Burgers model. (A) σ₃=5 MPa; (B) σ₃=10 MPa; (C) σ₃=15 MPa; (D) Zoomed in fitting curve at 18MPa applied stress level.

3.2.3 Improved fractional-order Burgers model

3.2.3.1 Property of Abel dashpot

From the constitutive equation of the Abel dashpot (Eq. 2), the creep equation can be derived as follows:

$\epsilon =\frac{\sigma }{\eta }\cdot \frac{t^n}{\mathrm{\Gamma }\left(1+n\right)}(5)$

In this study, with a reference condition of σ = 15 MPa and ξ = 3 GPa s, the characteristics of strain with respect to the order n in the Abel dashpot are discussed. As shown in Figure 12, changing the order of the Abel dashpot results in different curves. When the order n is less than 1.0, the curve exhibits a concave shape. When the order n is greater than 1.0, the creep curve shows a convex shape, resembling a tertiary creep curve. Therefore, an Abel dashpot with an order greater than 1.0 can be used to reflect the tertiary creep characteristics of the coal specimen.

FIGURE 12

FIGURE 12. Abel dashpot creep curves at different orders. (A) 0.10 < n < 0.25; (B) n > 1.

3.2.3.2 Improved fractional-order ideal viscoplastic model

From the results of the triaxial compression creep tests, it can be observed that prior to the final stage of stress loading, the coal specimen undergoes primary creep and then enters the stage of secondary creep. Only after a certain period following the final loading stage does the coal specimen exhibit tertiary creep. This indicates two conditions must be met for tertiary creep to occur: first, the applied stress level magnitude must exceed the threshold for tertiary creep; second, the loading time must reach the initiation time for tertiary creep. In the presence of Coulomb elements, the fractional viscoplastic model exhibits distinct behavior. When the applied stress level is below the critical stress value (σ_s), the model initially experiences rapid deformation, which then gradually stabilizes over time. Conversely, when the applied stress level exceeds the critical stress value (σ_s), the fractional viscoplastic model enters an unstable creep phase, clearly fulfilling the first condition for tertiary creep. However, it's important to note that this model lacks time-related components, and therefore, it does not satisfy the second condition for tertiary creep as per the requirements of fractional viscoplastic models.

3.2.3.3 Improved fractional-order Burgers model

In order to capture the tertiary creep characteristics of the coal specimen, as shown in Figure 13, an additional “switch” unit is introduced into the fractional-order ideal viscoplastic model. The tertiary creep only occurs when the loading time reaches the initiation time for tertiary creep (t_a) and the applied stress level exceeds the critical stress level. When t > t_a, the constitutive equation for fractional-order ideal viscoplastic model can be derived as follows:

$\epsilon =\frac{\sigma -{\sigma }_{\mathrm{s}}}{\eta }\cdot \frac{{\left(t-t_{\mathrm{a}}\right)}^{\gamma }}{\mathrm{\Gamma }\left(1+\gamma \right)}(6)$

where, γ is the order of the Abel dashpot in the fractional-order ideal viscoplastic model, γ >1.0; t_a is the initiation time for tertiary creep; σ_s is the initiation applied stress level for tertiary creep.

FIGURE 13

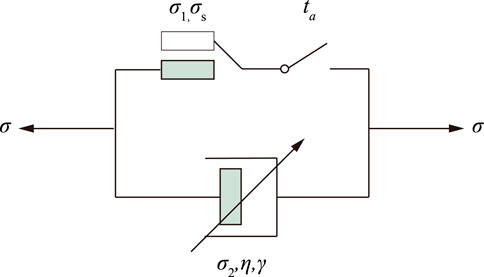
FIGURE 13. Improved fractional-order ideal viscoplastic model. σ₁ is the stress on the Coulomb element, and σ₂ is the stress on the Abel dashpot.

An enhanced fractional-order Burgers model was developed by incorporating an improved fractional-order viscoelastic component, as illustrated in Figure 14.

FIGURE 14

FIGURE 14. Improved fractional-order Burgers model.

In a uniaxial stress state, when t < t_a, the creep equation is given by:

$\epsilon =\frac{\sigma }{k_2}+\frac{\sigma }{{\eta }_2}\cdot \frac{t^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\frac{\sigma }{k_1}\left[1-E_{\alpha }\left(-{\left(\frac{k_1}{{\eta }_1}t\right)}^{\alpha }\right)\right](7)$

In a uniaxial stress state, when t ≥ t_a and σ ≥ σ_s, the creep equation is given by:

$\epsilon =\frac{\sigma }{k_2}+\frac{\sigma }{{\eta }_2}\cdot \frac{t^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\frac{\sigma }{k_1}\left[1-E_{\alpha }\left(-{\left(\frac{k_1}{{\eta }_1}t\right)}^{\alpha }\right)\right]+\frac{\sigma -{\sigma }_{\mathrm{s}}}{{\eta }_3}\cdot \frac{{\left(t-t_{\mathrm{a}}\right)}^{\gamma }}{\mathrm{\Gamma }\left(1+\gamma \right)}(8)$

In a triaxial stress state, based on Eq. 7, when t ≥ t_a and σ₁-σ₃ < σ_s, we have:

${\epsilon }_1=\frac{{\sigma }_1+2{\sigma }_3}{9K}+\frac{{\sigma }_1-{\sigma }_3}{3G_2}+\frac{{\sigma }_1-{\sigma }_3}{3{\eta }_2}\cdot \frac{t^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\frac{{\sigma }_1-{\sigma }_3}{3G_1}\left[1-E_{\alpha }\left(-{\left(\frac{k_1}{{\eta }_1}t\right)}^{\alpha }\right)\right](9)$

In a triaxial stress state, based on Eq. 8, when t ≥ t_a and σ₁-σ₃ ≥ σ_s, we have:

${\epsilon }_1=\frac{{\sigma }_1+2{\sigma }_3}{9K}+\frac{{\sigma }_1-{\sigma }_3}{3G_2}+\frac{{\sigma }_1-{\sigma }_3}{3{\eta }_2}\cdot \frac{t^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\frac{{\sigma }_1-{\sigma }_3}{3G_1}\left[1-E_{\alpha }\left(-{\left(\frac{k_1}{{\eta }_1}t\right)}^{\alpha }\right)\right]+\frac{{\sigma }_1-{\sigma }_3-{\sigma }_{\mathrm{s}}}{3{\eta }_3}\cdot \frac{{\left(t-t_{\mathrm{a}}\right)}^{\gamma }}{\mathrm{\Gamma }\left(1+\gamma \right)}(10)$

3.2.3.4 Parameter identification of improved fractional-order Burgers creep model

According to Eqs 7–10, the improved fractional-order Burgers model has a total of 13 parameters: α, β, γ, k₁, k₂, K, G₁, G₂, η₁, η₂, η₃, t_a, and σ_s. These parameters can be roughly divided into two categories:

The first parameter group comprises values readily obtained from experimental creep tests. Examples are the volumetric modulus K, the initiation time t_a for tertiary creep onset, and the critical applied stress σ_s inducing instability.

The second group contains parameters derived by model optimization to experimental data. Examples include the order of Abel dashpots (α, β, γ), viscosity coefficients (η₁, η₂, η₃), spring stiffness values (k₁, k₂), and shear moduli of springs (G₁, G₂).

Fitting of the triaxial creep curve of coal specimens was carried out using Eq. 10, and the results are shown in Figure 15 below.

FIGURE 15

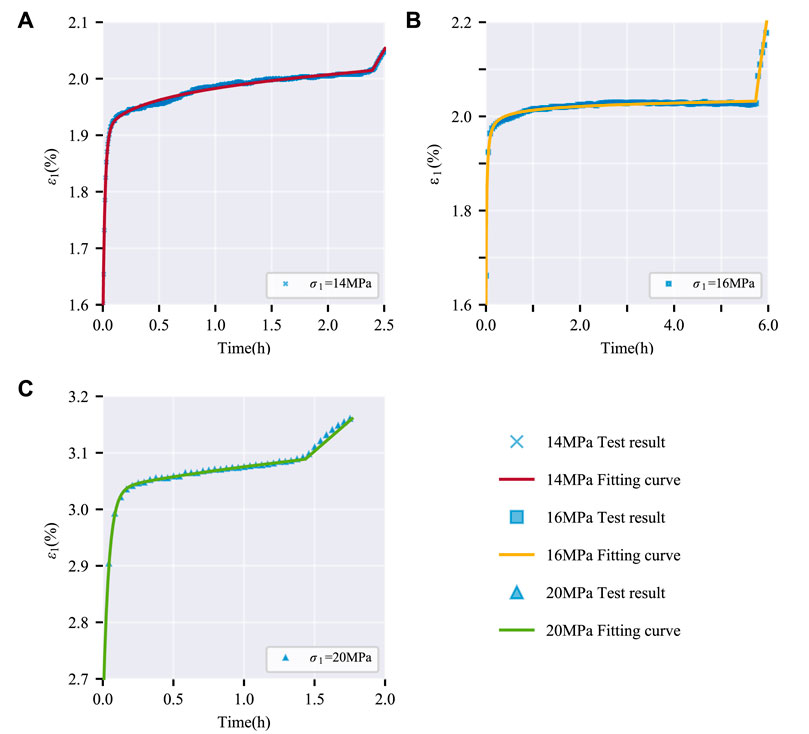
FIGURE 15. Tertiary creep curve fitting of improved fractional-order Burgers model. (A) σ₃=5 MPa; (B) σ₃=10 MPa; (C) σ₃=15 MPa.

Model calibration was conducted by fitting Eq. 10 to experimental triaxial creep curves obtained for the coal specimens, with results depicted in Figure 15.

The triaxial creep response modeled by the enhanced fractional Burgers formulation showed good agreement with experimental coal data across the entire creep process, as evidenced in Figure 15. In particular, the nonlinear primary and tertiary creep regimes were well captured, demonstrating adaptability of the improved model.

4 Discussion

This work implemented triaxial creep testing on coal specimens and developed an enhanced fractional-order Burgers formulation capable of representing primary, secondary and tertiary creep regimes. The nonlinear creep-time behavior was well characterized, improving constitutive modeling of coal creep with implications for deep coal pillar stability assessments. Compared to traditional creep models, the tertiary stage was better captured by the modified approach. Limitations remain, as damage mechanisms and stress-dependent effects were not incorporated, while the physical basis of the accelerating component requires further elucidation.

5 Conclusion

The creep-time curve of the coal specimen exhibits typical three-stage characteristics, namely primary creep, secondary creep, and tertiary creep stages. At higher confining pressures, the duration of the applied stress level corresponding to tertiary creep is shorter.

Through curve fitting procedures, the adaptability of the Burgers model to the test results was validated. The Burgers model demonstrated capacity to adequately characterize the primary and secondary creep regimes in triaxial creep tests on coal specimens. However, a limitation was evident in the model’s inability to capture tertiary creep phenomena.

In response to the restrictions of the Burgers model, this study presents an enhanced fractional-order Burgers creep model, which has been expanded from one dimension to three dimensions. In order to better account for the acceleration tendencies observed in the triaxial creep behavior of coal samples, the fractional-order ideal viscoplastic model was adapted with the inclusion of a time-dependent switching mechanism. This modified model effectively captures the complete triaxial creep progression in coal, demonstrating substantial fitting capability and accurately portraying the nonlinear attributes inherent to coal specimen triaxial creep.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

YY: Writing–original draft, Funding acquisition, Writing–review and editing. GH: Writing–original draft, Writing–review and editing. YZ: Writing–review and editing, Data curation, Formal Analysis. LY: Data curation, Formal Analysis, Writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Natural Science Foundation of Shandong Provincial (Grant Nos. ZR2022ME195).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bieniawski, Z. T., and Bernede, M. J. (1979). Suggested methods for determining the uniaxial compressive strength and deformability of rock materials. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 16, 138–140. doi:10.1016/0148-9062(79)91451-7

CrossRef Full Text | Google Scholar

Cheng, Q., Li, H., Huang, B., and Zhao, X. (2020). Creep hardening damage constitutive model of coal with fracture proppant. J. Geophys. Eng. 17, 1026–1036. doi:10.1093/jge/gxaa061

CrossRef Full Text | Google Scholar

Griggs, D. (1939). Creep of rocks. J. Geol. 47, 225–251. doi:10.1086/624775

CrossRef Full Text | Google Scholar

Hassouna, M., El Kinani, E. H., and Ouhadan, A. (2022). “Chapter thirteen - fractional calculus: applications in rheology,” in Fractional order systems. Editors A. G. Radwan, F. A. Khanday, and L. A. Said (Cambridge, Massachusetts, United States: Academic Press), 513–549.

CrossRef Full Text | Google Scholar

Hou, R. B., Zhang, K., Tao, J., Xue, X., and Chen, Y. (2019). A nonlinear creep damage coupled model for rock considering the effect of initial damage. Rock Mech. Rock Eng. 52, 1275–1285. doi:10.1007/s00603-018-1626-7

CrossRef Full Text | Google Scholar

ISRM (1978). Suggested methods for determining the strength of rock materials in triaxial compression. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 15, 47–51. doi:10.1016/0148-9062(78)91677-7

CrossRef Full Text | Google Scholar

ISRM (1983). Suggested methods for determining the strength of rock materials in triaxial compression: revised version. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 20, 285–290. doi:10.1016/0148-9062(83)90598-3

CrossRef Full Text | Google Scholar

Koeller, R. C. (1984). Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 51, 299–307. doi:10.1115/1.3167616

CrossRef Full Text | Google Scholar

Li, X. C., Yang, C. L., Ren, T., Nie, B., Zhao, C., Liu, S., et al. (2017). Creep behaviour and constitutive model of coal filled with gas. Int. J. Min. Sci. Technol. 27, 847–851. doi:10.1016/j.ijmst.2017.07.017

CrossRef Full Text | Google Scholar

Li, X. F., and Yin, Z. X. (2021). Study of creep mechanical properties and a rheological model of sandstone under disturbance loads. Processes 9, 1291. doi:10.3390/pr9081291

CrossRef Full Text | Google Scholar

Liu, H. Z., Xie, H. Q., He, J. D., Xiao, M. L., and Zhuo, L. (2017). Nonlinear creep damage constitutive model for soft rocks. Mech. Time-Dependent Mater, 21, 73–96. doi:10.1007/s11043-016-9319-7

CrossRef Full Text | Google Scholar

Liu, S. M., and Li, X. L. (2023). Experimental study on the effect of cold soaking with liquid nitrogen on the coal chemical and microstructural characteristics. Environ. Sci. Pollut. Res. 30, 36080–36097. doi:10.1007/s11356-022-24821-9

CrossRef Full Text | Google Scholar

Liu, S., Sun, H., Zhang, D., Yang, K., Li, X., Wang, D., et al. (2023). Experimental study of effect of liquid nitrogen cold soaking on coal pore structure and fractal characteristics. Energy 275, 127470. doi:10.1016/j.energy.2023.127470

CrossRef Full Text | Google Scholar

Lyu, C., Liu, J. F., Ren, Y., Liang, C., and Liao, Y. (2021). Study on very long-term creep tests and nonlinear creep-damage constitutive model of salt rock. Int. J. Rock Mech. Min. Sci. 146, 104873. doi:10.1016/j.ijrmms.2021.104873

CrossRef Full Text | Google Scholar

Ping, C., Wen, Y. D., Wang, Y. X., Haiping, Y., and Bingxiang, Y. (2016). Study on nonlinear damage creep constitutive model for high-stress soft rock. Environ. Earth Sci. 75, 900. doi:10.1007/s12665-016-5699-x

CrossRef Full Text | Google Scholar

Ran, H. Y., Guo, Y. X., Feng, G. R., Qi, T., and Du, X. (2021). Creep properties and resistivity-ultrasonic-AE responses of cemented gangue backfill column under high-stress area. Int. J. Min. Sci. Technol. 31, 401–412. doi:10.1016/j.ijmst.2021.01.008

CrossRef Full Text | Google Scholar

Shao, Y. W., Suo, Y. L., Xiao, J., Bai, Y., and Yang, T. (2023). Creep characteristic test and creep model of frozen soil. Sustainability 15, 3984. doi:10.3390/su15053984

CrossRef Full Text | Google Scholar

Tan, T. K., and Kang, W. F. (1980). Locked in stresses, creep and dilatancy of rocks, and constitutive equations. Rock Mech. 13, 5–22. doi:10.1007/BF01257895

CrossRef Full Text | Google Scholar

Wu, F., Gao, R. B., Liu, J., and Li, C. (2020). New fractional variable-order creep model with short memory. Appl. Math. Comput. 380, 125278. doi:10.1016/j.amc.2020.125278

CrossRef Full Text | Google Scholar

Yan, Q., Qin, S. F., Sang, X. F., Luo, Z., and Liang, M. (2023). Research on creep characteristics of loading and unloading of hard Flint limestone. Front. Mater, 10. doi:10.3389/fmats.2023.1177733

CrossRef Full Text | Google Scholar

Yang, S. Q., Xu, P., and Ranjith, P. G. (2015). Damage model of coal under creep and triaxial compression. Int. J. Rock Mech. Min. Sci. 80, 337–345. doi:10.1016/j.ijrmms.2015.10.006

CrossRef Full Text | Google Scholar

Yin, Q., Zhao, Y., Gong, W. M., Dai, G., Zhu, M., Zhu, W., et al. (2023). A fractal order creep-damage constitutive model of silty clay. Acta Geotech. 18, 3997–4016. doi:10.1007/s11440-023-01815-6

CrossRef Full Text | Google Scholar

Zhang, F. M., Zhang, D. F., and Huang, S. J. (2023a). Creep characteristics and creep model of coal based on pore water pressure. Processes 11, 638. doi:10.3390/pr11020638

CrossRef Full Text | Google Scholar

Zhang, J. C., Li, X. L., Qin, Q. Z., Wang, Y., and Gao, X. (2023b). Study on overlying strata movement patterns and mechanisms in super-large mining height stopes. Bull. Eng. Geol. Environ. 82, 142. doi:10.1007/s10064-023-03185-5

CrossRef Full Text | Google Scholar

Zhang, J., Li, B., Zhang, C., and Li, P. (2019). Nonlinear viscoelastic–plastic creep model based on coal multistage creep tests and experimental validation. Energies 12, 3468. doi:10.3390/en12183468

CrossRef Full Text | Google Scholar

Zhang, Z. B., Wang, E. Y., Li, N., Zhang, H., Bai, Z., and Zhang, Y. (2023c). Research on macroscopic mechanical properties and microscopic evolution characteristic of sandstone in thermal environment. Constr. Build. Mater, 366, 130152. doi:10.1016/j.conbuildmat.2022.130152

CrossRef Full Text | Google Scholar

Zhang, Z. B., Wang, E. Y., Zhang, H. T., Bai, Z., and Chen, X. (2022). Research on nonlinear variation of elastic wave velocity dispersion characteristic in limestone dynamic fracture process. Fractals 31, 2350008. doi:10.1142/S0218348X23500081

CrossRef Full Text | Google Scholar