- Research Institute of Petroleum Exploration and Development-Northwest, PetroChina, Lanzhou, China
Carbonate reservoirs exhibit complex pore structure, which significantly affects the elastic properties and seismic response, as well as the prediction of physical parameters. As one of the main factors impacting fluid prediction, pore structure parameter directly involves in few inversion methods. In order to directly predict pore structure parameter in inversion, a novel quantitative reflection coefficient formula is proposed, that integrate Russell's poroelasticity theory with Sun's petrophysical model. This formula separates fluid bulk modulus from porosity and pore structure parameter, allowing for accurate determination of pore-fluid distribution through Bayesian framework. Both theoretical model analysis and multi-component digital core experiments of carbonates validate the importance of pore structure parameter on fluid identification. The practical application of carbonate reservoirs in Sichuan Basin demonstrates that the proposed fluid factor, eliminating the prediction illusion caused by heterogeneity in porosity and pore structure parameter within strata, provides more precise and reliable predictions compared to the Russell fluid factor. Furthermore, the similarity between the Russell fluid factor obtained directly from the Russell approximation and the Russell fluid factor calculated indirectly from the proposed method confirms the stability and accuracy of the new reflection coefficient formula.
1 Introduction
With the advancement of exploration and development technology, the targets of exploration and development are becoming increasingly intricate. There has been a decline in reserves and grades of both oil and gas, with a growing proportion of low porosity and low permeability. In terms of carbonate reservoirs, predicting reservoirs is much challenging due to their deep burial depth and weak seismic responses. Moreover, they exhibit strong heterogeneity and significant variations in physical properties and thickness over short distances, as well as complex pore types. All these characteristics contribute to heightened difficulty in identifying oil and gas within them. Therefore, one of the current challenges in geophysics lies in effectively identifying fluids within target reservoirs with complex porous media.
The effect of porosity and pore types on the effective elastic properties of reservoirs is very critical in hydrocarbon prediction. A study conducted by Sun et al. (1997) showed that the variations in the pore aspect ratio can lead to changes in wave velocity exceeding 2000 m/s or more. Currently, significant advancements have been achieved in the research of pore structure parameters. For example, Zimmerman (1986) and Kachanov et al. (1994) examined the influence of two- and three-dimensional pore shape on elastic properties, respectively. Berryman (1999) derived approximate analytical expressions for the elastic parameters of dry/saturated fractured rock based on DEM theory. Jiang et al. (2012) proposed a new petrophysical modeling method using the Gassmann equation and Eshelby–Walsh ellipsoidal fracture theory to extract a parameter characterizing variations in the pore structure, thereby demonstrating its profound influence on the elastic properties of the rock. Deng et al. (2015) provided an analytical expression for the initial minimum aspect ratio of soft pores based on poroelasticity theory and extended the “squirt flow” model based on the characteristic aspect ratio by adding soft pores iteratively to analyze the influence of complex pore distribution on the squirt flow and its possible velocity dispersion characteristics. Wang et al. (2016) established a pore-scale numerical simulation method for elastic wave propagation in porous media based on the extraction of the pore structure parameter from digital core images in view of the complex pore structure and significant heterogeneity of carbonate rocks, verified its reliability with natural core data, and quantitatively analyzed the effect of carbonate pore structures on the propagation velocity and the scattering attenuation of elastic waves. He et al. (2012) proposed a unified expression by consolidating various petrophysical models for porous media, including Pride, Geertsma, and Keys-Xu, aiming to establish a more universal application across different rock types. Subsequently, He et al. (2018) further emphasized the significance of the pore aspect ratio as a fundamental benchmark due to the ambiguous physical definition and inconsistent quantitative representation of the pore structure parameter. These studies collectively indicate that the current research on the pore structure parameter primarily focuses on small-scale cores and logs but lacks applicability for fluid prediction at the seismic scale.
In the past few decades, there has been significant advancement in the fluid identification technology of seismic reservoirs, from a “qualitative” approach based on seismic amplitude anomaly in the 1980s to a “quantitative” method relying on the fluid factor in the present stage. With the development of a prestack seismic inversion, the fluid sensitive terms have evolved from assessing the relative variation in elastic parameters to presently recognizing physical parameters with distinct petrophysical significance. Biot (1941) and Gassmann (1951) both proposed the construction methods of the fluid factor for porous fluid-saturated rocks. Russell et al. (2003) and Russell et al. (2011) used the Biot–Gassmann theory to refine the Aki–Richards approximation under saturated fluid conditions and introduced the fluid factor, which can be directly involved in seismic fluid detection. Yin et al., (2014) derived a seismic reflection coefficient formula that incorporates porosity by combining the Russell approximation with the Nur model. Du et al. (2019) then extended this formula to PP–PS joint inversions, which further improves the fluid prediction in heterogeneous reservoirs but does not consider the pore structure parameter. Zong et al. (2012) and Zong et al. (2015) established a direct relationship among fluid factors and P- and S-wave moduli based on the petrophysical model of porous elastic media to obtain a new Zoeppritz approximation formula based on the P- and S-wave moduli, which circumvents the issue related to accurately determining density fluid factor calculation and has been successfully applied in an exploration area in eastern China. Sun, et al. (2015) proposed a novel fracture fluid factor that can simultaneously detect fracture development and fluid properties by combining P-wave anisotropic fracture prediction and Russell fluid factor into the Cartesian coordinate system in order to address the challenge of fluid identification in anisotropy, which achieved promising application in igneous areas. Sun et al. (2016) employed sequential Gaussian simulation and Metropolis sampling algorithm based on Bayesian’s theoretical framework to directly estimate the Russell fluid factor, which enhanced the accuracy of fluid factor identification. Although substantial developments have been made in recent years regarding the algorithms of fluid prediction, the issue of fluid prediction under non-homogeneous conditions still faces challenges such as strong multi-solution and less precise prediction. This can be attributed to the omission of pore structure parameters in the widely used Gassmann fluid equation for bidirectional media containing fluid, making it complicated and challenging to accurately quantify the impact of pore structure. Fan et al. (2019) and Zong et al. (2019) introduced the squirt flow model into an inversion, along with the relevant parameters of the pore structure, making an initial step toward integrating the pore structure parameter in seismic reservoir prediction. Li et al. (2021) also proposed a new method combining the pore structure with the Bayesian non-linear simultaneous inversion of physical parameters, further improving the importance and involvement of the pore structure in the reservoir prediction. However, the aforementioned methods including pore structures can only be obtained in an indirect way. In other words, traditional physical parameters are first calculated, and then, specific petrophysical theories are employed to derive the pore structure and other fluid parameters. This approach does not directly incorporate the pore structure parameter as the factor in the inversion process of seismic reflection coefficient. Therefore, it is imperative to further study the inversion method of the pore structure from indirect to direct inversions in order to streamline the procedure, while improving the inversion accuracy.
In order to mitigate the impact of complex pore structure on fluid prediction in carbonate reservoirs, a novel inversion method is proposed that integrates Sun’s petrophysical model and Russell’s poroelasticity theory to derive a decoupled reflection coefficient formula for fluid bulk modulus
2 Methods
Establishing a direct mathematical relationship between theoretical or empirical petrophysical models and expressions of seismic reflection coefficients is the key to quantitative characterization of fluid prediction involving the pore structure.
2.1 Poroelasticity theory
First, one of the widely used quantitative formulas of seismic response for fluid identification is Biot–Gassmann theory (Krief et al., 1990), which elucidates the pore/fluid interaction in homogeneous porous media and defines the functional relationship between seismic velocity and fluid. Its corresponding formula is shown as follows:
where
where
In addition, by substituting the fluid factor
where
2.2 Reflection coefficient formula for decoupling porosity and pore structure parameter
Second, in terms of petrophysics, Sun (2000) proposed a petrophysical model based on Biot theory, introducing the pore structure parameter
It is worth noting that the pore structure parameter
According to the derivation by Han et al. (2004), it can be concluded that
It can be found by comparing formula 9, 4that
The exponential term in formula 10 poses challenges for numerical analysis, and therefore, it can be expanded by the Taylor series as follows:
The selection of different orders in approximation (12) can be tailored to meet different accuracy requirements. To achieve the decoupling of
where
3 Accuracy analysis
For verifying the rationality of the proposed reflection coefficient in formula 13 for decoupling the pore structure parameter
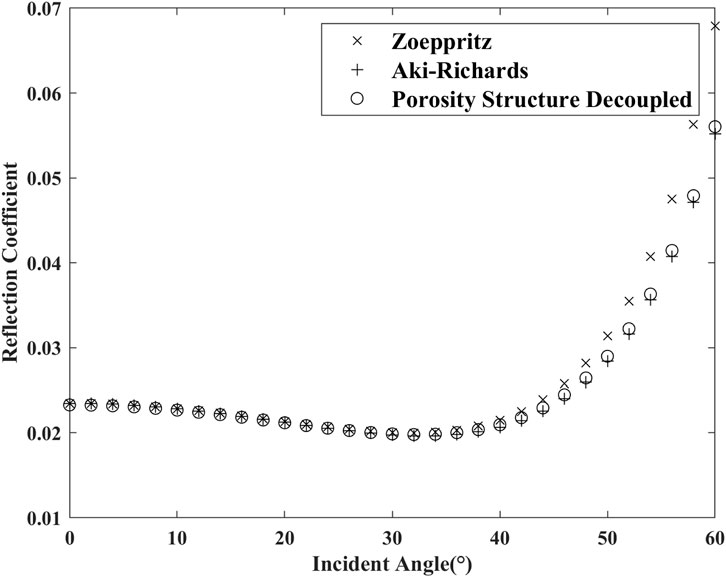
FIGURE 1. Accuracy comparison of reflection coefficients among the Zoeppritz formula (×), Aki–Richard formula (+), and proposed formula of decoupling the pore structure (○).
4 Importance of the pore structure
It should be noted that there are five terms to be solved in the proposed approximation (13), including porosity
A two-layer model with the same basic elastic parameters (
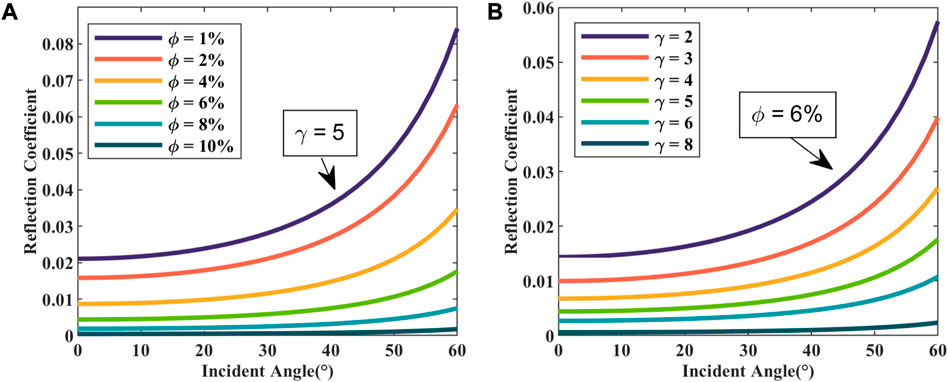
FIGURE 2. Contribution of porosity
5 Inversion for decoupling the pore structure
5.1 Bayesian framework
The solution of the proposed method, as indicated by formula 13, involves five parameters to be solved for. This places higher demands on the stability and accuracy of the inversion compared to the traditional AVO method, which typically require only three parameters. The proposed formula requires the association of
where
For simplicity of expression, formula 14 can be reformulated as follows:
where
The solution of formula 15 provides the five parameters; however, it suffers from severe ill-posedness in practical applications. Therefore, based on the Bayesian framework, the issue of well-posedness can be effectively improved by introducing the prior information of the model parameters into the regularization of inversion. Thus, the posterior probability density distribution of model parameters
where
The prestack seismic gathers in actual data contain a certain level of noise. Assuming that the noise is uncorrelated with a mean value of 0, following the likelihood function of the Gaussian distribution, thus, the likelihood function of noise can be expressed as follows:
where
The prior distribution of the model parameters can be either univariate or multivariate. Considering that five involved parameters, which have certain correlation, need to be obtained by the proposed method, the selection of multivariate distribution can effectively mitigate the ill-conditioning issue. While Gaussian distribution only provides consistent weighting coefficients, which may impact the sparsity of inversion results, Cauchy distribution can yield non-consistent weighting coefficients with sparsity effects and greater geological significance. Therefore, the multivariate Cauchy distribution is adopted as the prior distribution for the model parameters, with its specific formula given as follows:
where
By substituting formulas 17, 18 into Formula 16, the posterior probability density of model parameters can be obtained as follows:
After the algebraic transformation of Formula 20, the objective function
where
5.2 Decorrelation method
The statistical correlation between elastic parameters is widely recognized as a major factor contributing to the instability of the prestack inversion. The proposed method involves five parameters, out of which three parameters (fluid bulk modulus
The decorrelation method is illustrated using a three-parameter dataset as an example, since it involves five parameters in the proposed inversion, which is not convenient for figuring. As shown in Figure 3A, the sequences x, y, and z exhibit significant correlation, and their covariance matrix is expressed as follows:
where
where
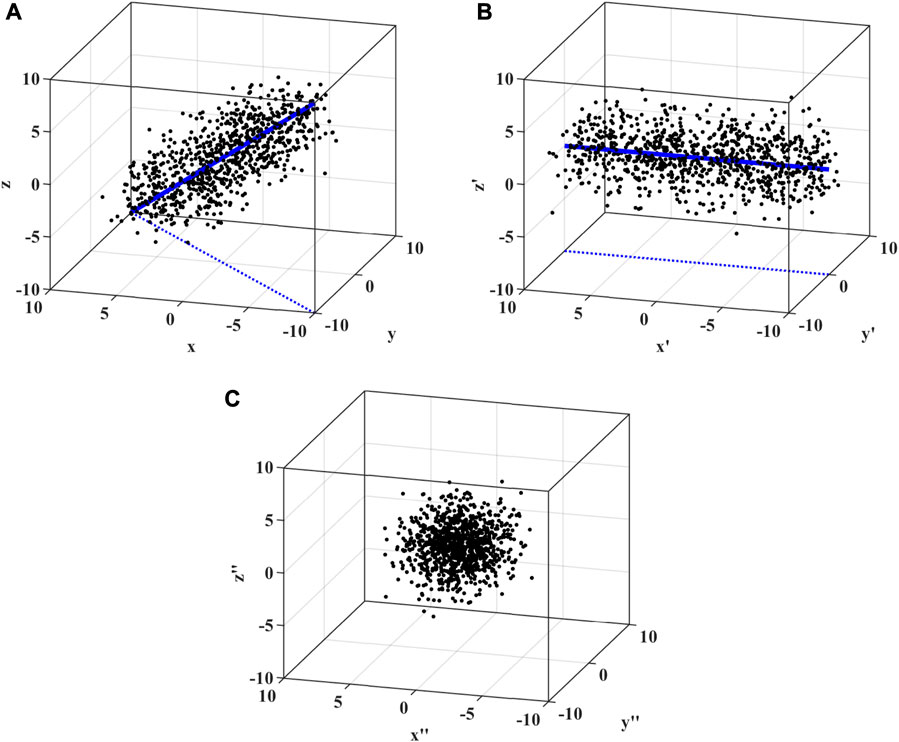
FIGURE 3. Decorrelation example: (A) original data with correlation, (B) data with weak correlation, and (C) white data.
According to the aforementioned method, one of the covariance matrices
The covariance matrix can be extended to two
where
6 Synthetic data test
The proposed inversion of decoupling porosity
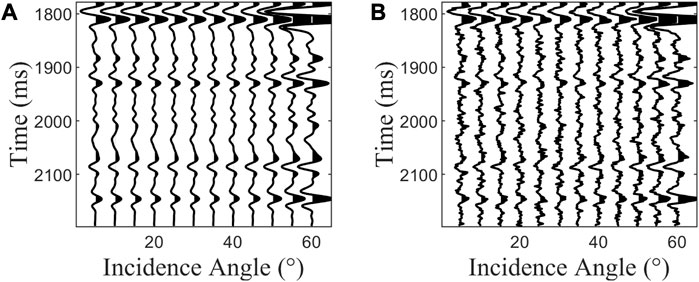
Figures 5A, B show the inversion results without and with noise, respectively, displaying the three direct inversion parameters of fluid bulk modulus
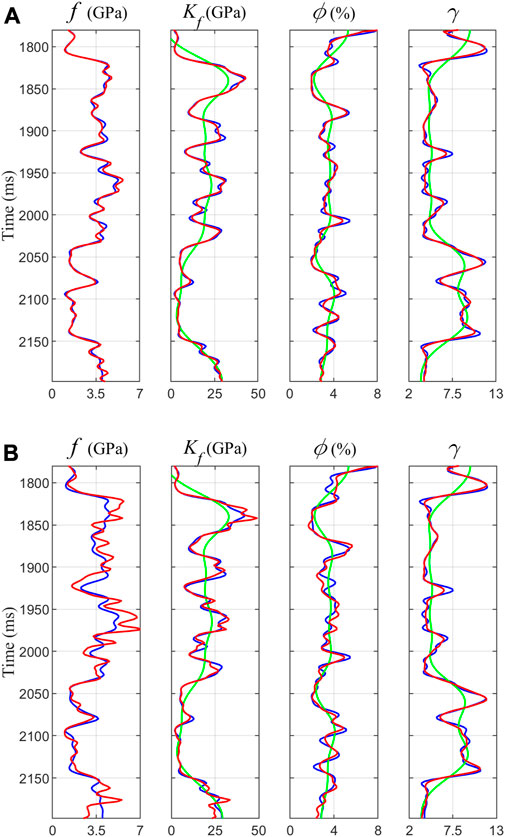
FIGURE 5. Inversion results from the synthetic data without noise (A) and with noise of S/N=2 (B) (the green line indicates the low-frequency data, the blue line indicates the model data, and the red line indicates the inversion data).
7 Actual data application
The well data from an exploration area in the Sichuan Basin is utilized to validate the feasibility and applicability of the proposed prestack inversion technique for decoupling both pore structure parameter
7.1 Digital core analysis
Before fluid detection, component analysis and simulation of different pore shapes were conducted on a total of seven cores from three wells in various formations to construct multi-component digital core models for evaluating the influence of the pore structure in this working area. Figure 6A shows a gray-scale slice obtained through a CT scan depicting the actual core. Based on the analysis of the actual core, the multi-component digital core was constructed, as shown in Figure 6B. The digital core comprised two dominant minerals: dolomite (light-colored) and quartz (dark-colored), and the dark-colored component also containing 7% kaolinite. As numerous previous studies have demonstrated the effect of porosity
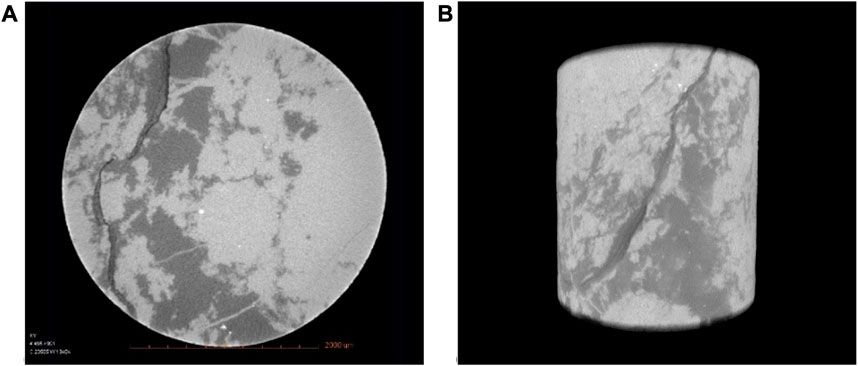
FIGURE 6. Core analysis. (A) Gray-scale slice of core using a CT scan; (B) digital core image (he light-colored component is dolomite, and the dark-colored component is 93% quartz and 7% kaolinite).
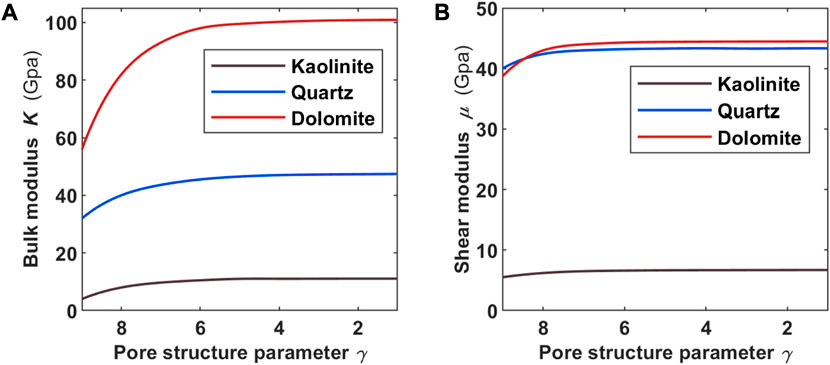
FIGURE 7. Impact of the pore structure parameter
7.2 Fluid prediction
Reservoir analysis is initially performed on the well data, using the same well in the anti-noise experiment, as shown in Figure 8. Among the three logged carbonate gas-bearing reservoirs (highlighted by red and blue boxes in Figure 8), Russell fluid factor
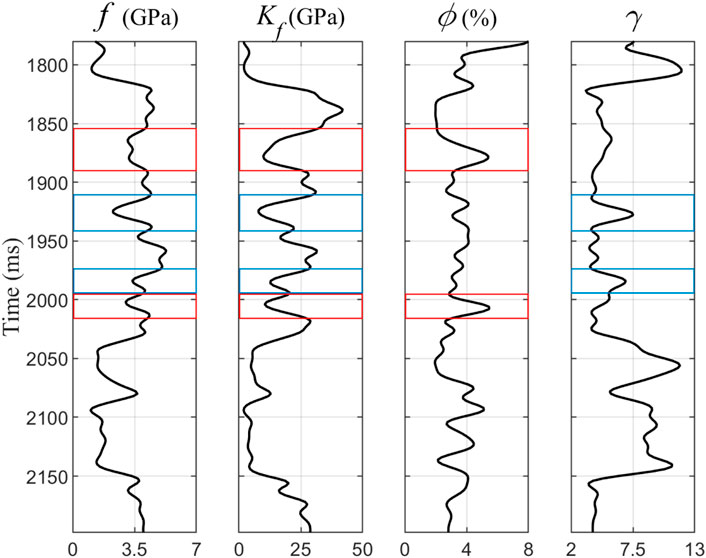
FIGURE 8. Factor analysis of affecting reservoir identification (reservoirs in the red boxes are controlled by porosity
Second, both the proposed inversion and Russell’s
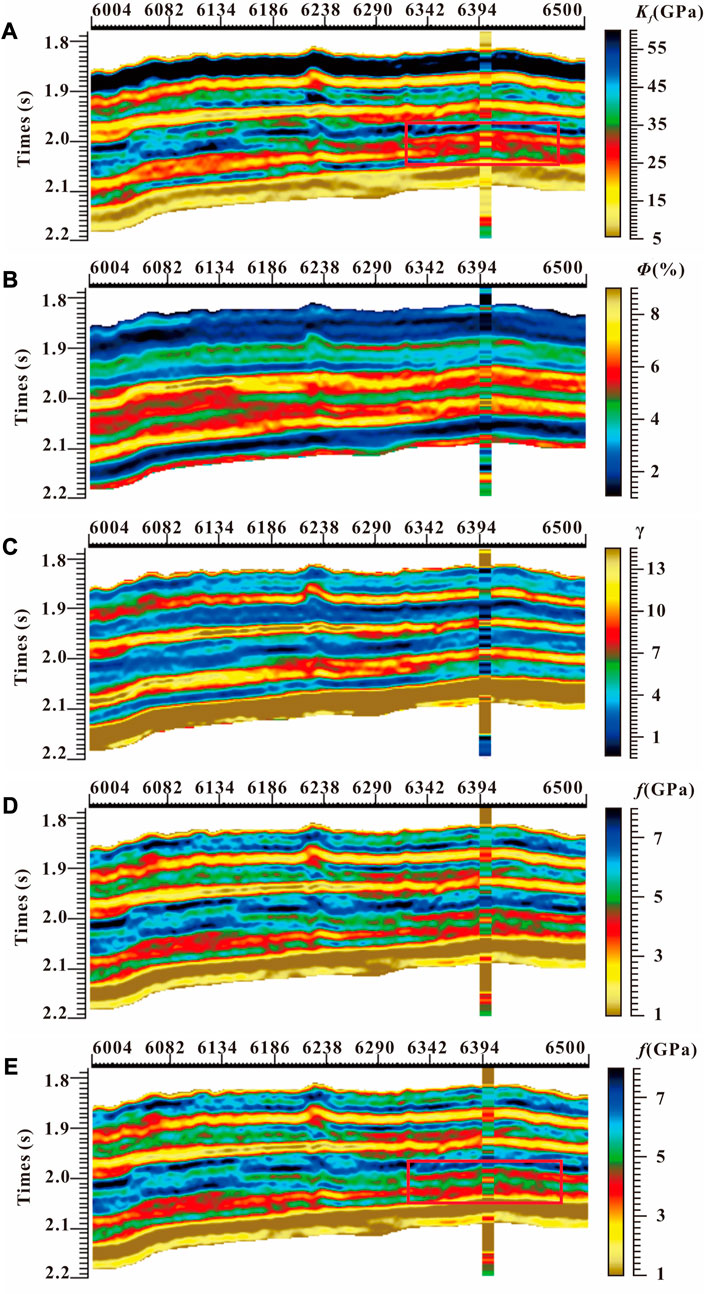
FIGURE 9. Inversion profile of fluid bulk modulus
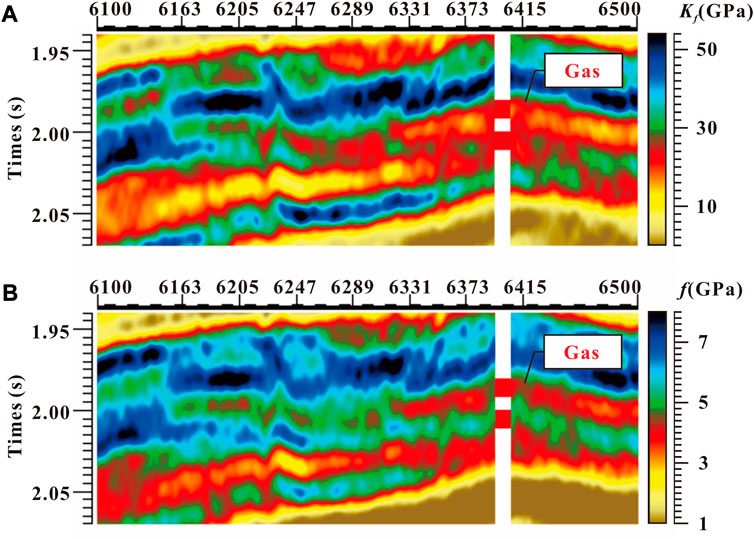
FIGURE 10. Magnified partial profiles of fluid bulk modulus
8 Conclusion
The pore structure parameter
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
RH: methodology and writing-original draft. EW: conceptualization and project administration. WW: methodology and visualization. GY: data curation and formal analysis. XZ: validation and writing-review and editing. WZ: investigation and formal analysis. DH: conceptualization and investigation.
Funding
This work was funded by the Key Technology Research Project of CNPC, grant number 2021ZG03, and the Science and Technology Project of Petrochina, grant number 2022DJ8004.
Conflict of interest
Authors RH, EW, WW, GY, XZ, WZ, and DH were employed by PetroChina.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Backus, G., and Gilbert, F. (1968). The resolving power of gross Earth data. Geophys. J. Int. 16 (2), 169–205. doi:10.1111/j.1365-246x.1968.tb00216.x
Berryman, J. G. (1999). Origin of Gassmann’s equations. GEOPHYSICS 64 (5), 1627–1629. doi:10.1190/1.1444667
Biot, M. A. (1941). General theory of three-dimensional consolidation. J. Appl. Phys. 12 (2), 155–164. doi:10.1063/1.1712886
Chen, J. J., and Yin, X. Y. (2007). Three-parameter AVO waveform inversion based on Bayesian theorem. Chin. J. Geophys. 50 (4), 1251–1260. doi:10.1007/s11442-007-0020-2
Deng, J., Zhou, H., Wang, H., Zhao, J., and Wang, S. (2015). The influence of pore structure in reservoir sandstone on dispersion properties of elastic waves. Chin. J. Geophys. 58 (9), 3389–3400. doi:10.6038/cjg20150931
Du, B., Yang, W., Zhang, J., Yong, X., Gao, J., and Li, H. (2019). Matrix-fluid decoupling-based joint PP-PS wave seismic inversion for fluid identification. GEOPHYSICS 84 (3), R477–R487. doi:10.1190/geo2017-0376.1
Fan, X., Zhang, G., and Zhang, J. (2019). Prediction method of pore structure parameters of tight sandstone. Seg. Tech. Program Expand. Abstr. 89, 3678–3682. doi:10.1190/segam2019-3199837.1
Gassmann, F. (1951). Über die elastizitat poroser medien: vierteljahrschrift der naturforschenden. Gesellshaft 96, 1–23.
Han, D., and Batzle, M. L. (2004). Gassmann’s equation and fluid-saturation effects on seismic velocities. GEOPHYSICS 69 (2), 398–405. doi:10.1190/1.1707059
He, X., He, Z., Wang, X., Xiong, X., and Jiang, L. (2012). Rock skeleton models and seismic porosity inversion. Appl. Geophys. 9 (3), 349–358. doi:10.1007/s11770-012-0345-1
He, X., Lin, K., Zhang, Z., and He, Z. (2018). Quantitative comparison of the influence of porosity and pore structure on reservoir characteristics. Geophys. Prospect. Petroleum 57 (2), 179–185.
Jiang, L., Wen, X., Zhou, D., He, Z., and He, X. (2012). The constructing of pore structure factor in carbonate rocks and the inversion of reservoir parameters. Appl. Geophys. 9 (2), 223–232. doi:10.1007/s11770-012-0333-5
Kachanov, M., Tsukrov, I., and Shafiro, B. (1994). Effective moduli of solids with cavities of various shapes. Appl. Mech. Rev. 47 (1S), S151–S174. doi:10.1115/1.3122810
Krief, M., Garat, J., Stellingwerff, J., and Ventre, J. (1990). A petrophysical interpretation using the velocities of P and S waves. Log. Anal. 31, 355–369.
Li, H., Zhang, J., Pan, H., and Gao, Q. (2021). Nonlinear simultaneous inversion of pore structure and physical parameters based on elastic impedance. Sci. China Earth Sci. 64 (6), 977–991. doi:10.1007/s11430-020-9773-8
Russell, B. H., Gray, D., and Hampson, D. P. (2011). Linearized AVO and poroelasticity. GEOPHYSICS 76 (3), C19–C29. doi:10.1190/1.3555082
Russell, B. H., Hedlin, K., Hilterman, F. J., and Lines, L. R. (2003). Fluid-property discrimination with AVO: A biot-gassmann perspective. GEOPHYSICS 68 (1), 29–39. doi:10.1190/1.1543192
Sun, R., Yin, X., Wang, B., and Zhang, G. (2016). A direct estimation method for the Russell fluid factor based on stochastic seismic inversion. Chin. J. Geophys. 59 (3), 1143–1150. doi:10.6038/cjg20160334
Sun, W., He, Z., Li, Y., Zhang, F., and Zhou, Y. (2015). A new factor of fluid-filled fractures and its application. Chin. J. Geophys. 58 (7), 2536–2545. doi:10.6038/cjg20150728
Sun, Y. (2000). Core-log-seismic integration in hemipelagic marine sediments on the eastern flank of the Juan de Fuca Ridge. Proc. Ocean Drill. Program, Sci. Results 168, 21–23. doi:10.2973/odp.proc.sr.168.009.2000
Sun, Y., and Goldberg, D. (1997). Effects of aspect ratio on wave velocities in fractured rocks. Seg. Tech. Program Expand. Abstr. 67, 925–928. doi:10.1190/1.1886170
Wang, F., Bian, H., Zhang, Y., Duan, C., and Chen, G. (2016). Hilbert-Huang transform combined with smoothed pseudo Wigner-Ville time-frequency distribution to identify reservoir fluid properties. Geophys. Prospect. Petroleum 55 (6), 851–860. doi:10.3969/j.issn.1000-1441.2016.06.010
Wang, W., Li, G., Yu, X., Yang, W., Wang, W., Feng, L., et al. (2017). A meta-analysis of adenosine A2A receptor antagonists on levodopa-induced dyskinesia in vivo. Seg. Tech. Program Expand. Abstr. 87, 702–706. doi:10.3389/fneur.2017.00702
Yin, X., and Zhang, S. (2014). Bayesian inversion for effective pore-fluid bulk modulus based on fluid-matrix decoupled amplitude variation with offset approximation. GEOPHYSICS 79 (5), R221–R232. doi:10.1190/geo2013-0372.1
Zhang, T., Sun, Y., Tian, J., Lu, L., Qin, F., Zhao, X., et al. (2018b). Two-parameter prestack seismic inversion of porosity and pore-structure parameter of fractured carbonate reservoirs: part 2 - applications. Interpretation 6 (4), SM9–SM17. doi:10.1190/int-2018-0019.1
Zhang, T., and Sun, Y. (2018a). Two-parameter prestack seismic inversion of porosity and pore structure parameter of fractured carbonate reservoirs: part 1 — methods. Interpretation 6, 1–SM8. doi:10.1190/int-2017-0219.1
Zhao, J., Pan, J., Hu, Y., Li, J., Liu, X., Li, C., et al. (2021a). Digital rock physics-based studies on effect of pore types on elastic properties of carbonate reservoir Part 1: imaging processing and elastic modelling. Chin. J. Geophys. 64 (2), 656–669. doi:10.6038/cjg2021O0228
Zhao, J., Pan, J., Hu, Y., Li, J., Liu, X., Li, C., et al. (2021b). Digital rock physics-based studies on effect of pore types on elastic properties of carbonate reservoir Part 2: pore structure factor characterization and inversion of reservoir. Chin. J. Geophys. 64 (2), 670–671. doi:10.23736/S0026-4806.20.06558-1
Zimmerman, R. W. (1986). Compressibility of two-dimensional cavities of various shapes. J. Appl. Mech. 53 (3), 500–504. doi:10.1115/1.3171802
Zong, Z., and Wang, Y. (2019). Amplitude variation with angle inversion for fluid discrimination with the consideration of squirt flow. Seg. Tech. Program Expand. Abstr. 89, 734–738. doi:10.1190/segam2019-3216431.1
Zong, Z., Yin, X., and Wu, G. (2012). AVO inversion and poroelasticity with P- and S-wave moduli. GEOPHYSICS 77 (6), N17–N24. doi:10.1190/geo2011-0214.1
Keywords: fluid prediction, pore structure parameter, fluid factor, porosity, carbonate
Citation: He R, Wang E, Wang W, Yan G, Zheng X, Zhao W and He D (2023) Bayesian fluid prediction by decoupling both pore structure parameter and porosity. Front. Earth Sci. 11:1269597. doi: 10.3389/feart.2023.1269597
Received: 30 July 2023; Accepted: 29 August 2023;
Published: 15 September 2023.
Edited by:
Xintong Dong, Jilin University, ChinaReviewed by:
Xiangbo Gong, Jilin University, ChinaShiqi Dong, Changjiang River Scientific Research Institute (CRSRI), China
Copyright © 2023 He, Wang, Wang, Yan, Zheng, Zhao and He. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Run He, aGVfcnVuNzMyQDEyNi5jb20=
 Run He
Run He Enli Wang
Enli Wang Wanjin Zhao
Wanjin Zhao