Wide azimuth seismic data processing technology and application: a case study of tight gas reservoirs in western China

As the difficulty of oil and gas field exploration and development increases both domestically and internationally, onshore exploration targets have gradually shifted from the shallow to the deep and from conventional oil and gas reservoirs to unconventional ones. Particularly in the exploration and development of unconventional oil and gas horizontal wells, there is an increasing demand for higher precision and quality of seismic data to better identify formation lithology, rock fractures, and improve the characterization of reservoirs, reservoir positioning, and connectivity. Wide-azimuth seismic exploration possesses significant technical advantages in addressing exploration challenges such as lithologic exploration, small fault imaging, and detailed characterization of oil and gas reservoirs. Wide azimuth seismic data reduces blind spots in seismic acquisition and improves the imaging accuracy of small faults. Notably, there exist distinct anisotropic characteristics in fault areas and fractured reservoirs. Wide azimuth seismic data is particularly advantageous for studying amplitude variation with variations in amplitude with offset (AVO), incident angle (AVA), or azimuth (AVAZ), as well as velocity with azimuth (VVA). These variations aid in identifying faults, fractures, and changes in formation lithology. As the focus of oil and gas exploration gradually shifts to complex lithological reservoirs and unconventional oil and gas reservoirs, narrow azimuth seismic exploration has been gradually replaced by wide azimuth exploration. However, as observation azimuth increases, challenges related to velocity variations with azimuth, azimuth-related traveltime differences, and azimuth-related anisotropy arise. Based on wide-azimuth seismic data from tight gas reservoirs in western China, this study conducted wide-azimuth anisotropic velocity analysis, OVT domain data regularization processing, OVT domain prestack time/depth migration, and horizontally transverse isotropy (HTI) azimuth anisotropy correction techniques. After applying specialized processing to the wide-azimuth seismic data, significant improvements were observed in the S/N and resolution of the target layer. The delineation of fractures related to hydrocarbon sources also became more distinct. These advancements not only provided high-quality results for high-fidelity, high-resolution imaging of tight gas reservoirs but also provided azimuth volume corresponding to fast and slow wave velocities for seismic data interpretation, facilitating velocity variation with azimuth (VVAZ) fracture detection and AVO analysis research.

1 Introduction

Unconventional reservoirs, influenced by the inherent anisotropy of subsurface media, exhibit variations in seismic attributes such as amplitude, velocity, and polarization direction as seismic waves propagate through the formations. The seismic response characteristics of fracture-type reservoirs differ among different azimuthal observation systems, showcasing azimuthal anisotropy (Thomsen, 1986; Rüger and Tsvankin, 1995; Rüger, 1998). Parallel fractures and interbedded thin layers can generate transversely isotropic (TI) properties. Parallel fractures often align nearly vertically, with their symmetry axis being horizontal, and are thus referred to as horizontally transverse isotropy (HTI). Interbedded thin layers are commonly oriented horizontally, with their symmetry axis in the vertical direction, giving rise to vertically TI (VTI). The combination of parallel fractures and interbedded thin layers results in orthorhombic media. Both HTI media and orthorhombic anisotropic media belong to azimuthal anisotropy (AA) (Rüger, 1997).

For unconventional reservoirs with high angle fractures, such as shale oil and gas as well as tight oil and gas formations, they can be effectively considered as HTI media with a horizontal symmetry axis. The seismic exploration data of fractured reservoirs often exhibit the influence of HTI anisotropy, which is primarily manifested in variations of seismic wave amplitude, velocity, and phase with changes in the azimuth of the survey lines (Rüger, 1998; Yuan and Wang, 2020). In fractured reservoirs, there are vertical fractures present above the target layer due to the existence of formation pressure. These approximately vertical fractures introduce anisotropic characteristics in the propagation of seismic waves. Such formations with these characteristics are referred to as HTI media, exhibiting distinct HTI azimuthal anisotropy. This anisotropy causes periodic changes in seismic wave amplitude, impedance, velocity, and travel time with variations in the azimuth of the survey lines (Thomsen, 2010). Additionally, it results in AVO characteristics that increase or decrease with the incidence angle. The AVO features are important for the characterization of fine channels and the detection of gas and serve as crucial factors in the exploration of gas-bearing tight reservoirs within channel sand bodies.

Wide-azimuth seismic data can be used to detect underground fractures that exhibit directional alignment. In an anisotropic medium, both parallel and perpendicular fractures display amplitude variations with azimuthal angle, allowing for the prediction of fractures through the study of amplitude variations (Thomsen, 1988). When seismic waves propagate through HTI anisotropic media, the travel time is shortest and the energy is strongest when the compressional waves propagate along the direction of the fractures. As the angle between the seismic wave propagation direction and the fracture orientation increases, the travel time becomes longer and the energy weakens. The longest travel time and weakest energy occur when seismic waves propagate perpendicular to the fracture direction. Due to the azimuthal anisotropy of HTI media, seismic attributes such as amplitude, impedance, velocity, and travel time exhibit periodic changes with azimuth. Additionally, AVO can increase or decrease with the incidence angle (Swan, 2012). If the issue of velocity variation with azimuth is not addressed, and only a single average velocity is used for normal moveout (NMO) correction, it becomes challenging to flatten all gathers across the range of azimuth angles, and the objective of coherent stacking cannot be achieved (Davison et al., 2011; Tsvankin, 1997a; Tsvankin, 1997b). Therefore, an analysis of velocity considering anisotropy and HTI anisotropy correction is crucial.

In the study of HTI azimuthal anisotropy, Tsvankin and Thomsen (1994) provided NMO velocity expressions for horizontal reflection planes of P and S waves within the symmetric plane of HTI media. Building upon the similarity between the seismic velocity equations in the symmetric plane of HTI media and the velocity equations in VTI media, Rüger and Tsvankin (1995) extended Thomsen’s anisotropy parameters to HTI media. They derived precise expressions for NMO velocity of horizontal interface reflections under arbitrary anisotropy strengths and conducted parameter inversion, establishing relationships between NMO velocity and the principal axis direction, vertical velocity, and anisotropy parameters. If rocks can be approximated as horizontally homogeneous media when subjected to horizontal and vertical stress fields, Gray and Head (2000) used the prestack seismic amplitudes with incidence angle and azimuth (AVAZ) analysis method to solve the Ruger equation and estimate the azimuthal anisotropy parameters that lead to azimuthal variations of AVAZ. This method was applied for fracture orientation and fracture density detection. Based on the analysis of the sensitivity of AVO to NMO velocity errors, Swan (2001) proposed a velocity picking method to mitigate the influence of NMO stretch distortion.

The Offset Vector Tile (OVT) concept was initially proposed by Vermeer (1998) based on a cross-shaped arrangement. In 1999, Cary introduced the concept of Common Offset Vector (COV) into the three-dimensional domain, extending the idea of grouping 2D common offset traces. In 2000, Vermeer discussed the processing method based on the OVT domain, leading to the gradual development of OVT domain processing research (Vermeer, 2000). Calvert et al. (1949), Schapper et al. (2009). Anisotropy velocities and offset vector tile prestack-migration processing of the Durham Ranch 3D, northwest Colorado. The Leading Edge, 28 (11):1,352–1,361) analyzed data processed in the OVT domain and found that it effectively preserved azimuthal information, providing azimuthal attributes for subsequent interpretation. Stein et al. (2010) conducted OVT domain processing analysis on wide-azimuth data and suggested that the processed data could be utilized for better fracture prediction in reservoirs. Schapper et al. (2009) demonstrated the improved capability of OVT-domain prestack time migration in analyzing anisotropic velocities using processed 3D field data.

Acquisition of seismic data with wide azimuth will not only multiply the acquisition cost, but also change the linear characteristics of the shot regular noise of the far array due to the increase of the number of traces in the middle and far offset, showing an approximate hyperbolic characteristic distribution, which is not conducive to the suppression of regular noise of wide azimuth seismic data. Although it is beneficial for velocity analysis and multiple suppression, due to the influence of anisotropy, the frequency and resolution of the stack data are reduced, which is not conducive to high-resolution imaging of thin reservoirs and small fractures.

Based on wide-azimuth seismic data acquired from tight gas reservoirs in western China, this study conducted wide-azimuth anisotropic velocity analysis, OVT domain data regularization processing, OVT domain prestack time/depth migration, and HTI azimuth anisotropy correction techniques. The comprehensive technique effectively addressed the issues of gather distortion, non-linearity, and incoherent stacking caused by azimuthal anisotropy. Additionally, the processing approach provided azimuth volumes corresponding to fast and slow wave velocities, which facilitated interpretations such as VVAZ fracture detection and AVO analysis.

2 Theory and method

2.1 Anisotropic velocity analysis of wide azimuth seismic data

The term anisotropy in seismic exploration typically refers to velocity anisotropy, which refers to the variation of seismic wave velocities with angle. Traditional velocity analysis methods are generally based on the assumption of hyperbolic events. However, due to the presence of anisotropy, the travel time of reflected waves no longer satisfy the hyperbolic condition. Conventional velocity analysis methods are not suitable for meeting the accuracy requirements of wide-azimuth velocity analysis (Lu et al., 1998). Therefore, it is necessary to use velocity analysis that considers anisotropy to process and interpret seismic data (Alkhalifah and Tsvankin, 1995).

Compared to isotropic media, the travel time curve in HTI media is no longer a standard hyperbola (Alkhalifah, 1997). If we still calculate travel time in HTI media based on conventional hyperbolic assumptions, errors will occur, particularly at large offsets (Berryman, 1979). This deviation caused by the choice of travel time curve will have a greater impact and affect the accuracy of velocity analysis. In the process of generating velocity spectra, the absence of accurate travel time information from far-offset traces will lead to a decrease in the accuracy of the spectra for the available traces. This deviation discussed here precisely reflects the velocity azimuthal anisotropy characteristic of HTI media. Significant HTI anisotropy characteristics exist in fault zones and fractured reservoirs. Conventional (narrow-azimuth) exploration may weaken or overlook the effectiveness of exploration parallel to the fractures. On the other hand, wide-azimuth exploration significantly improves the ability to identify fracture development zones.

Tsvankin (1995) and Bakulin et al. (2000) deduced a formula for calculating the P-wave NMO velocity in HTI media at any azimuth angle as follow:

$V_{nmo}^2=V_{vert}^2\frac{1+A}{1+A{\sin }^2\alpha }(1)$

where, $V_{vert}$ is the P-wave velocity when seismic waves propagate vertically downward, $\alpha$ is the angle between the seismic wave propagation path and the crack, $A$ is anisotropic parameter of HTI media, and $A=2{\delta }^{\left(v\right)}$.

When the seismic wave propagation path is parallel to the crack, i.e., $\alpha =0^o$, the P-wave NMO velocity can be expressed as:

$V_{nmo}^2=V_{vert}^2\left(1+A\right)(2)$

When the seismic wave propagation path is parallel to the crack, i.e., $\alpha ={90}^o$, the P-wave NMO velocity can be simplified into:

$V_{nmo}^2=V_{vert}^2(3)$

Therefore, Eq. 1 can be converted into

$V_{nmo}^2=\frac{V_{nmo1}^2{V}_{nmo2}^2}{V_{nmo1}^2{\sin }^2\alpha +V_{nmo2}^2{\cos }^2\alpha }(4)$

The above equation can be written in an elliptical form:

$\frac{V_{nmo}^2{\cos }^2\alpha }{V_{nmo1}^2}+\frac{V_{nmo}^2{\sin }^2\alpha }{V_{nmo2}^2}=1(5)$

where, $V_{nmo1}$ is the NMO correction velocity parallel to the fracture, and $V_{nmo2}$ is the NMO correction velocity perpendicular to the fracture. From Eq. 5, it can be observed that it represents the polar form of an elliptical equation, indicating that the NMO velocity of compressional waves exhibits an elliptical distribution with respect to the observation azimuth. This allows for the prediction of compressional wave azimuthal anisotropy for fracture detection. Additionally, by utilizing the characteristics of wide-azimuth data in 3D seismic surveys, the compressional wave NMO velocities can be extracted for different azimuths. Based on the attribute values, an ellipse can be fitted, where the ratio of the major and minor axes represents the magnitude of the azimuthal anisotropy intensity and the density of fractures at the sampling point. The direction of fracture development is indicated by the major axis (or minor axis) of the ellipse, which can be determined through imaging logging and coring in real data. The azimuthal anisotropy gradient exhibits a cosine (or elliptical) variation pattern with respect to the azimuth, and as the anisotropy intensity increases, the eccentricity of the ellipse also increases. Therefore, by analyzing the variation characteristics of azimuthal AVO gradients, it is possible to predict the intensity and direction of fracture development.

2.2 OVT domain processing technology based on wide azimuth data

Wide-azimuth data forms the basis for OVT domain processing, which was developed to meet the research requirements of wide-azimuth seismic data (Cary, 1999). OVT is a subset of data in a crossline and inline arrangement, divided into small rectangular sections based on equal shot and receiver distances. Each of these small rectangles is an OVT offset vector tile. Through OVT domain processing, the migrated data retains azimuthal information, providing a solid foundation for prestack inversion and the study of anisotropy. It offers significant advantages in fracture prediction, characterization of reservoir heterogeneity, fluid identification, and other aspects. Figure 1 illustrates the workflow of OVT domain processing for wide-azimuth seismic data.

FIGURE 1

FIGURE 1. OVT domain processing flow of wide azimuth data.

OVT domain data processing technology provides high-quality seismic data with rich information for structural interpretation. Currently, this technology has been successfully applied in multiple blocks, yielding favorable results. The following aspects demonstrate its effectiveness:

1) By conducting azimuthal stacking on OVT domain gathers, multiple azimuthal data volumes are obtained. Through analysis and comparison of these volumes, the azimuthal stack with the highest sensitivity to fractures in different orientations is selected, enabling precise identification and characterization of fracture sets.

2) When the propagation direction is perpendicular to the fracture strike, the amplitude is minimized. This amplitude difference increases with larger offset distances. The amplitude attribute varies with azimuth, with stronger amplitudes indicating the direction of fracture strikes and weaker amplitudes indicating vertical fracture orientations. The ratio of amplitude differences in these two directions reflects the density of fractures. A higher ratio indicates greater fracture density, while a lower ratio indicates lower fracture density.

3) As seismic waves propagate in an anisotropic medium, P-waves travel along the direction of fracture development, resulting in the shortest travel time and strongest energy. As the propagation direction deviates from the fracture strike angle, the travel time increases, and the energy weakens. When P-waves propagate perpendicular to the fracture direction, the energy is weakest. Travel time azimuthal anisotropy can be utilized for fracture prediction.

4) When seismic waves propagate parallel to the fracture medium, no dispersion phenomena are observed. However, dispersion phenomena can be observed when waves propagate in the vertical fracture direction. Frequency azimuthal anisotropy can be utilized for fracture prediction.

2.2.1 Data regularization processing technology in OVT domain based on wide azimuth data

Wide-azimuth data serves as the foundation for OVT domain processing. OVT refers to a subset of data in a cross-line arrangement, divided based on source-receiver offset distances. Due to the irregular distribution of source and receiver locations during acquisition, the azimuthal distribution within each data unit is uneven, resulting in non-uniform spatial coverage, irregular sampling, and migration noise issues. These factors degrade the imaging quality. Conventional data regularization techniques typically interpolate data in the common offset domain, using seismic data from different azimuths to compute interpolation factors. This method generally yields satisfactory results for areas with minor azimuthal anisotropy or narrow-azimuth data. However, for wide-azimuth data with significant structural dip or strong azimuthal anisotropy, the interpolation results are often unsatisfactory. Compared to common offset gathers, the OVT domain gathers have inherent advantages that make them more suitable for data regularization techniques. Within the OVT domain, the seismic data used for interpolation factors have fixed source-receiver offset ranges and azimuths. As a result, they exhibit better data similarity, allowing for more accurate interpolation factor determination and achieving superior interpolation results.

Based on the traditional matching pursuit Fourier interpolation (MPFI) method, this paper utilizes the advantages of wide-azimuth OVT domain data to propose an improved MPFI method. The improved method incorporates low-frequency information without spurious frequencies as a constraint, effectively suppressing spurious frequency components in high frequencies. As a result, both frequency leakage and spurious frequency issues are simultaneously addressed, effectively mitigating the impact of data irregularities. The proposed method significantly improves the signal-to-noise ratio (S/N) of seismic data and achieves higher fidelity compared to traditional regularization methods.

The basic idea of the MPFI algorithm is to estimate the unknown frequency spectrum in the Fourier domain using the known non-uniform spatial sampling information in the space-time domain, and then use the conventional inverse Fourier transform to transform the estimated frequency spectrum back to the corresponding space-time domain of a given regular grid, thereby completing the reconstruction process of seismic data. The principle of non-uniform discrete Fourier transform can be expressed as follow (Xu and Zhang, 2005; Xu and Zhang, 2010):

The continuous one-dimensional spatial Fourier forward transform can be expressed as:

$\overline{P}\left(k,\omega \right)={\int }_{-\infty }^{+\infty }P\left(x,\omega \right)e^{jkx}dx(6)$

where, $x$ is spatial variable, $k$ is spatial frequency, $\omega$ is instantaneous angular frequency, $P\left(x,\omega \right)$ and $\overline{P}\left(k,\omega \right)$ are spatial domain data and spatial frequency domain data. The inverse transformation of the above formula can be obtained as:

$P\left(x,\omega \right)={\int }_{-\infty }^{+\infty }\overline{P}\left(k,\omega \right)e^{jkx}dk(7)$

The discrete Fourier transform of Eq. 6 can be expressed as:

$\overline{P}\left(k,\omega \right)={\displaystyle \sum _{n=0}^{N-1}}P\left(n\Delta x,\omega \right)e^{jkn\Delta x}\Delta x(8)$

For irregular sampling data, the following formula can be used to obtain spatial Fourier transform data:

$\overline{P}\left(k,\omega \right)={\displaystyle \sum _{n=0}^{N-1}}P\left(x_n,\omega \right)e^{jkn\Delta x}\Delta x_n(9)$

where, $\Delta x_n=\left(x_{n+1}-x_{n-1}\right)/2$, and $x_n$ is the sampling point of data.

The algorithm principle for Fourier reconstruction data regularization under irregular sampling grid conditions can be expressed as follows:

For time-frequency slices $f\left(x\right)$, there are $M$ spatial points, and a total of $N$ wavenumber coefficients, defined as:

${\mathrm{\Phi }}_{M\times N}=\left[\begin{array}{ccc}{e}^{i{k}_1{x}_1}& \cdots & e^{i{k}_N{x}_1}\\ e^{i{k}_1{x}_2}& \cdots & e^{i{k}_N{x}_2}\\ ⋮& \cdots & ⋮\\ e^{i{k}_1{x}_M}& \cdots & e^{i{k}_N{x}_M}\end{array}\right]=\left[\begin{array}{ccc}{\varphi }_1& \cdots & {\varphi }_N\end{array}\right](10)$

The Fourier transform can be expressed as:

$\begin{array}{ccc}f=\mathrm{\Phi }F& & F={\mathrm{\Phi }}^{H}f\end{array}(11)$

Assume $j$ represents the number of iterations, the spectrum estimation process can be expressed as:

$F^j\left(p\right)=\underset{-N/2\le k\le N/2}{\max }\left(f^j,{\varphi }_k^H\right)(12)$

$F^{j+1}=F^j-F^j\left(p\right){\mathrm{\Phi }}^H{\varphi }_p(13)$

When dealing with irregular sampling, frequency leakage occurs due to the violation of the orthogonality condition. It can be observed that the basic idea of this method is to reduce the energy leakage between different wave numbers. The specific approach is to iteratively apply discrete Fourier transform (DFT) and its inverse transform, extracting the maximum energy for each frequency in each iteration to reconstruct the Fourier coefficients without leakage. Then, based on the estimated discrete Fourier transform, interpolation is performed to the desired output positions, gradually minimizing the spectral leakage during the reconstruction of the orthogonal basis.

The improved MPFI method is based on the original anti leakage Fourier interpolation algorithm mentioned above. Before selecting the component with the maximum energy, it applies a smaller weight to the Fourier spectrum of the higher frequency band, and applies a larger weight to the real signal to achieve the purpose of anti aliasing. This is also the advantage of the improved MPFI compared to previous methods.

The specific implementation steps of the improved MPFI regularization method are as follows:

1) Perform DFT on seismic data;

2) Calculate the weight (a priori value) for the Fourier spectrum and apply the weight to the full frequency band of the spectrum;

3) Select the Fourier spectral component with the weighted maximum energy;

4) Add the Fourier spectral component (unweighted) to the “estimated spectrum”;

5) Perform inverse Fourier transform on the Fourier spectral component (unweighted), and outputting the iterative result according to the input position;

6) Subtract the iteration result from the original input data;

7) Repeat steps 1) to 6) until the set number of iterations is reached or Eq. 3 reaches the set value;

8) Figure 2 is the seismic stack section before and after the improved MPFI regularization, we can also clearly see that after the MPFI 5-D regularization processing, the co-phase axis continuity is enhanced, the diffraction characteristics of tight sand are clearer, the signal-to-noise ratio and resolution have been greatly improved and the missing data acquisition part has been significantly improved.

FIGURE 2

FIGURE 2. (A) The Stack section before MPFI, (B) the Stack section after improved MPFI.

2.2.2 OVT domain prestack time/depth migration technology based on wide azimuth

At present, the commonly used pre-stack migration method is common-offset domain migration. Due to the influence of the acquisition system, the coverage of different offset distances within each common midpoint (CMP) bin is uneven. Near and far offsets have lower coverage, while middle-offsets have higher coverage. In actual seismic data, there are often noticeable gaps in common-offset gathers for near and far offsets. This situation often results in an amplitude imbalance phenomenon in the migrated common reflection point (CRP) gathers, which cannot accurately reflect the subsurface geological conditions.

Wide-azimuth data forms the basis for OVT domain processing. The OVT is a natural extension of the crossline gathers and represents a subset of data in a work area. Each OVT tile is a single coverage profile, similar to a three-dimensional post-stack data volume. It is obtained by dividing the crossline gathers into equal intervals based on the offset and receiver line distances. Through OVT domain processing, the pre-stack migrated gather data retains azimuthal information, and the energy distribution is more consistent for near and far offsets. This not only provides a solid data foundation for pre-stack inversion but also establishes a basis for the study of anisotropy and AVO analysis. It offers significant advantages in predicting fractures, characterizing reservoir heterogeneity, and identifying fluid properties (Schapper et al., 2009).

The advantages of OVT domain pre-stack migration over conventional migration are as follows: 1) Each subset in the OVT domain is assigned a unique index based on its position relative to the center of the crossline gathers. Subsets with the same index represent OVT bodies with the same range of offset and azimuth. This forms a COV (Common Offset Vector) volume. The migrated gather data retains azimuth and offset information, which is crucial for azimuthal and AVO analysis (Rüger, 1996; Rüger, 2002). 2) Within each OVT domain gather, the seismic traces have approximately the same offset and azimuth. Pre-stack migration is performed for each OVT element within the near, middle, and far offset ranges (Swapper et al., 2009; Su et al., 2021). The consistency of energy distribution across the offset ranges ensures that the gathered data retains its quality and avoids the “noise” characteristics associated with azimuthal anisotropy in traditional common-offset domains. This significantly improves the imaging accuracy of fractures and weak interbed reflections. 3) The regularization and noise suppression processing in the OVT domain ensure uniform coverage and centralization of the elements. This theoretically reduces the problem of curved traveltime/depth in pre-stack migration and preserves the amplitude relationships of common reflection point gathers. It facilitates reservoir prediction and fracture detection related to azimuth on common reflection point gathers.

Figure 3 is the conventional pre-stack migration CRP gathers and OVT-domain pre-stack migration spiral gathers. It can be seen that after OVT migration, the near-mid-far offset energy relationship is more consistent and the fidelity is better. It contains azimuth information, which is conducive to the research of AVAZ inversion. The azimuthal anisotropy is more obvious, which is conducive to the study of fracture prediction.

FIGURE 3

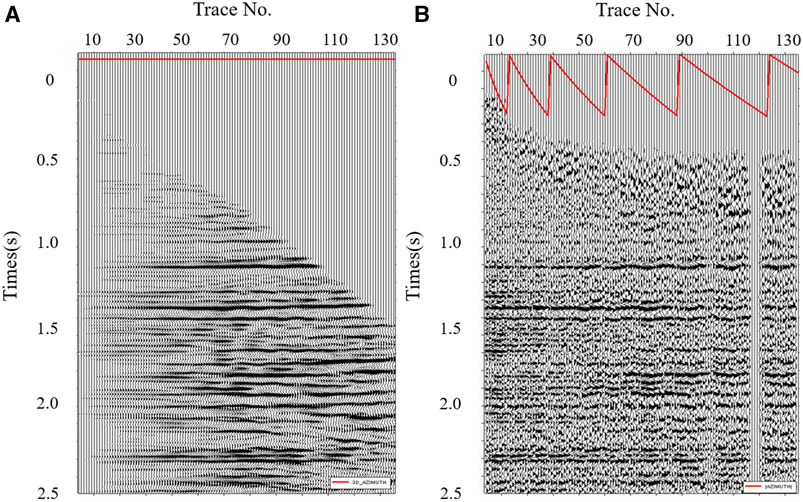
FIGURE 3. Comparison of conventional migration prestack CRP gather (A) and OVT domain prestack migration spiral gather (B).

Figure 4 shows a comparison of OVT-domain pre-stack time migrated profiles for different reflection angles. It can be observed that the profiles enable better analysis of AVO response characteristics of sand bodies and identification of fracture features for different reflection angles.

FIGURE 4

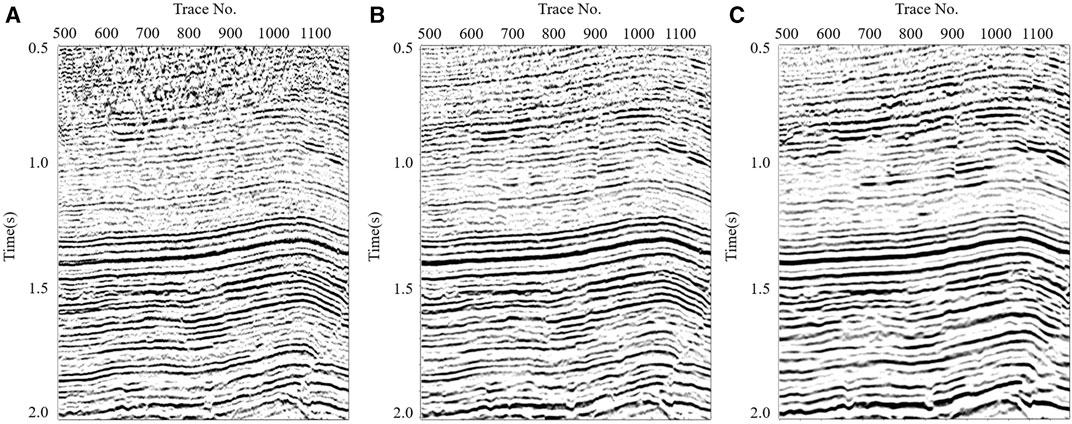
FIGURE 4. Comparison of prestack time migration profile in OVT domain (A) Angle of reflection 0–12°,(B) Angle of reflection 10–22°,(C) Angle of reflection 20–36°.

2.3 HTI media azimuth anisotropy correction technology

Obvious azimuth anisotropy often exists in fractured and unconventional reservoirs. Due to the existence of anisotropy, the amplitude, wave impedance, velocity and travel time of seismic elastic wave change periodically with the change of azimuth of measured line, and also increase or decrease with the increase of incident Angle (depending on different formation conditions), which is known as AVO characteristics. Therefore, the characteristics of P-wave velocity, travel time, amplitude and wave impedance in HTI media changing with the azimuth of the survey line and changing with the incident angle are studied. By fitting the ellipse, the development intensity (elliptic curvature) and direction (elliptic symmetry axis direction) of cracks are predicted. The existence of fractures will cause abnormal seismic amplitude, which is the physical mechanism of AVO technology (Grechka and Tsvankin, 1998; Xu and Tsvankin, 2007; Canning and Malkin, 2008).

The existence of fractures will cause abnormal seismic amplitude, which is the physical mechanism of AVO technology (Jenner, 2002; Zeng et al., 2021). The seismic exploration technology of lithologic oil and gas reservoirs is analyzed and identified by using the variation characteristics of amplitude with shot-receiver distance. According to the meaning and correlation of AVO attributes, intersection analysis is carried out to achieve the purpose of bright spot identification, oil and gas detection, fracture prediction and lithologic identification (Su et al., 2020; Zeng et al., 2022). Shuey (1985) proposed a simplified reflection coefficient equation under the premise of isotropic media and small percentage change in elastic properties, as following:

$R\left(\theta \right)\approx R\left(0\right)+\left[A_{0}R\left(0\right)+\frac{\Delta \sigma }{{\left(1-\sigma \right)}^2}\right]{\sin }^2\theta +\frac{\Delta V_P}{2V_P}\left(t{g}^2\theta -{\sin }^2\theta \right)(14)$

Where,

$\begin{array}{c}{A}_0=B-2\left(1+B\right)-\frac{1-2\sigma }{1-\sigma }\\ B=\frac{\Delta V_P/V_P}{\Delta V_P/V_P+\Delta \rho /\rho }\\ R\left(0\right)=\frac{1}{2}\left(\Delta V_P/V_P+\Delta \rho /\rho \right)\end{array}$

$V_P$, $\Delta V_P$, $\rho$, $\Delta \rho$, $\sigma$, $\Delta \sigma$ are the average and difference of the P-wave velocity, density and poisson ratio of the upper and lower media.

When there is azimuthal anisotropy, the AVO response varies with the source-detector azimuth and the equation in HTI media can be expressed as (Wang, 1999):

$R\left(\theta ,\varphi \right)=R\left(0\right)+\frac{1}{2}\left\{\frac{\Delta V_P}{V_P}-{\left(\frac{2V_S}{V_P}\right)}^2\frac{\Delta G}{G}\left[\Delta \gamma +2{\left(\frac{2V_S}{V_P}\right)}^2\Delta \omega \right]{\cos }^2\varphi \right\}{\sin }^2\theta (15)$

Where, $G=\rho V_S^2$, $\Delta G$ is the difference between the average vertical shear modulus of the upper and lower media, and $\Delta \omega$ and $\Delta \gamma$ are the difference between the shear wave splitting parameter and the Thomsen anisotropy coefficient, respectively. It can be seen that if there is no azimuthal anisotropy, the AVO response in all directions should be the same. When azimuthal anisotropy exists, the AVO response will change with the variation of the source-detector azimuth. For anisotropic media, the direct expression of the AVO gradient will depend on the azimuth. In other words, the intercept P related to a small incident angle is hardly affected by azimuthal anisotropy, while the gradient G at a large incident angle will vary with the angle between the fracture and the observed azimuth.

According to Rüger (1997), when $\theta <{25}^{。}$ for HTI media, a simplified reflection coefficient can be approximated as

$R\left(\theta ,\varphi \right)=P+G\left(\varphi ,\beta \right){\sin }^2\theta (16)$

Where, $\theta$ is the reflection angle, $\varphi$ is azimuth angle, $P$ is the intercept, $\beta$ is the fracture orientation angle, and $G$ is the gradient which is effected by $\Delta \sigma$.

Theoretically, $G$ is composed of two parts: isotropic part $G_{iso}$ and anisotropic part $G_{aniso}$.

Then assuming $G_1=G_{iso}$, $G_2=G_{aniso}+G_1$

$R\left(\theta ,\varphi \right)=P+\left[G_1{\sin }^2\left(\varphi -\beta \right)+G_2{\cos }^2\left(\varphi -\beta \right)\right]{\sin }^2\theta (17)$

According to Grechka and Tsvankin (1998), Grechka and Tsvankin (1999), Bakulin et al. (2000), Grechka and Tsvankin (1999), in HTI media, the gradient is equivalent to the NMO velocity as expressed:

$\frac{1}{v_{nmo}^2\left(\varphi \right)}={\lambda }_1{\cos }^2\left(\varphi -\beta \right)+{\lambda }_2{\sin }^2\left(\varphi -\beta \right)(18)$

Where ${\lambda }_1$ and ${\lambda }_2$ are slowness along the major axes of symmetry.

And according to Swan (2012), the relative NMO velocity error can be expressed as follow:

$\frac{\Delta v}{v\left(\varphi \right)}=\frac{\Delta v}{v_1}{\cos }^2\left(\varphi -\beta \right)+\frac{\Delta v}{v_2}{\sin }^2\left(\varphi -\beta \right)(19)$

The two components $\Delta v/v_1$, $\Delta v/v_2$ are along the fractures and perpendicular to the fractures, respectively.

The workflow of the automatic residual anisotropic velocity analysis technique can be expressed as follow:

1) Perform automatic residual velocity analysis on the OVT gathers that acquired by prestack depth migration, and pick up the velocity of each sample in the depth domain.

2) According to the picked velocity, we can obtain the anisotropy parameters and calculate the value of $\Delta v/v_1$ and $\Delta v/v_2$.

3) Smooth $\Delta v/v_1$ and $\Delta v/v_2$ to avoid the abnormal value in the velocity field.

4) Calculate the residual moveout in the depth domain or the time domain.

5) Apply residual anisotropic NMO correction and finally we can obtain flatten gathers and a high-resolution profile.

Figure 5 (a) is the profile of $\Delta v/v_2-\Delta v/v_1$ , (b) is the azimuth profile of slow wave, (c) is the profile of $\Delta \mathit{v}/{\mathit{v}}_{\mathbf{2}}$ slow wave. Tight gas reservoirs in channel sand, with strong heterogeneity, developed small faults and oil-source faults. HTI anisotropy technique can be used to flatten the gather which is useful to the analysis of AVO and also can be used for high-fidelity and amplitude-preserving processing of seismic data. As shown in Figures 6, 7, after azimuthal anisotropy correction, the event is flatter and the velocity focusing is better, the in-phase stacking makes the seismic resolution greatly improved, and at the same time, the weakly reflected energy between layers is further strengthened. By this way, seismic data is more effective to reflect the abnormal reflection of the shallow channel. The internal small faults are clear and the AVO response characteristics of the prestack gather are obvious and reliable, which provides a good foundation for later characterization of the river channel and gas detection.

FIGURE 5

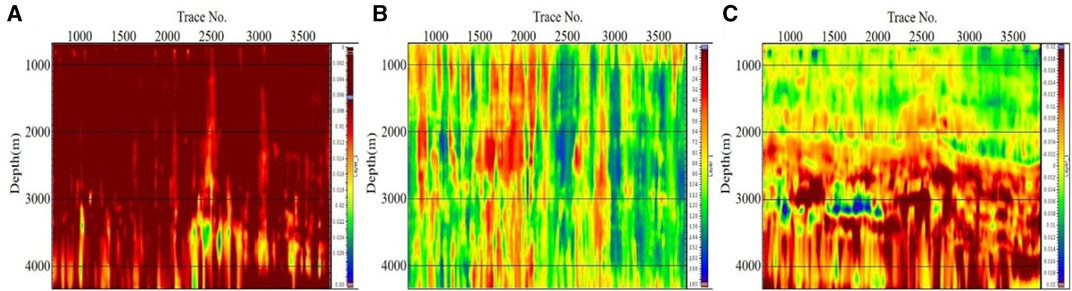
FIGURE 5. (A) The profile of $\mathbf{\Delta }\mathit{v}/{\mathit{v}}_{\mathbf{1}}-\mathbf{\Delta }\mathit{v}/{\mathit{v}}_{\mathbf{2}}$, (B) is the azimuth profile of slow wave, (C) is the profile of $\mathbf{\Delta }\mathit{v}/{\mathit{v}}_{\mathbf{2}}$ slow wave. It can be seen from the figure that where cracks and fractures develop, the difference will appear obvious anomalies.

FIGURE 6

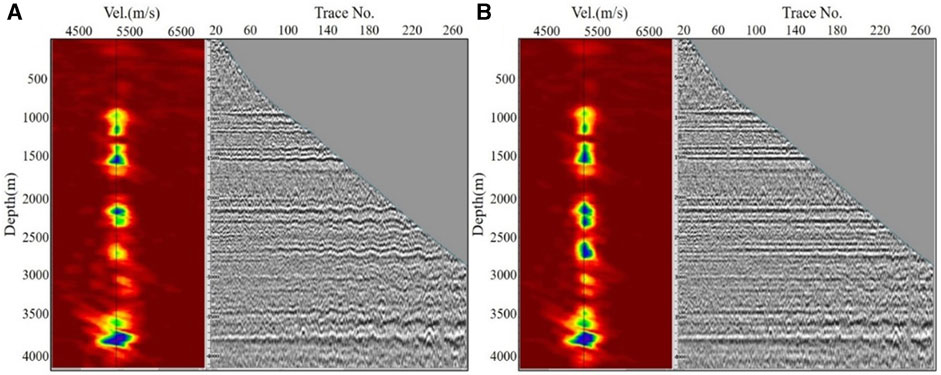
FIGURE 6. (A) Before azimuthal anisotropy correction. (B) After azimuthal anisotropy correction. After azimuthal anisotropy correction, the event is flatter and the velocity focusing is better.

FIGURE 7

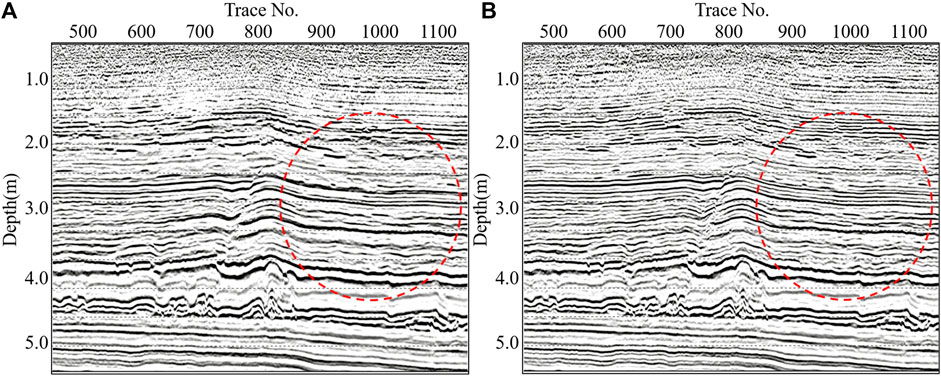
FIGURE 7. (A) PSTM before azimuthal anisotropy correction. (B) PSTM after azimuthal anisotropy correction. After HTI anisotropy correction, the in-phase stacking makes the seismic resolution greatly improved.

3 Examples

The northern slope of the central Sichuan uplift is the main favorable exploration fields. The S-Y research work area in the Sichuan Basin has a full coverage area of 2052.1 km², and belongs to low hilly and mountainous landform. The terrain fluctuates slightly and the relative elevation is small, but the local elevation changes greatly. The altitude is generally around 350–720 m. As shown in Figure 8, the low-lying areas of the work area are mostly along the banks of the Fujiang River and Zijiang River, and the terrain in the north of the work area is relatively high. The structural location of the S-Y work area in the Sichuan Basin is located in the Yilong tectonic group in the gentle uplift structural area of the central Sichuan Basin. The faults and fractures in this area are relatively developed, and two types of hydrocarbon source faults are developed. Normal faults are developed in the Shaximiao Formation, with small fault spacing and short extension distance. The pressure of gas reservoirs is controlled by the development degree of hydrocarbon source faults. With the development of hydrocarbon source faults in the Xujiahe Formation, the higher the pressure of the gas reservoir, the higher the pressure of the lower sand body where the same fault communicates.

FIGURE 8

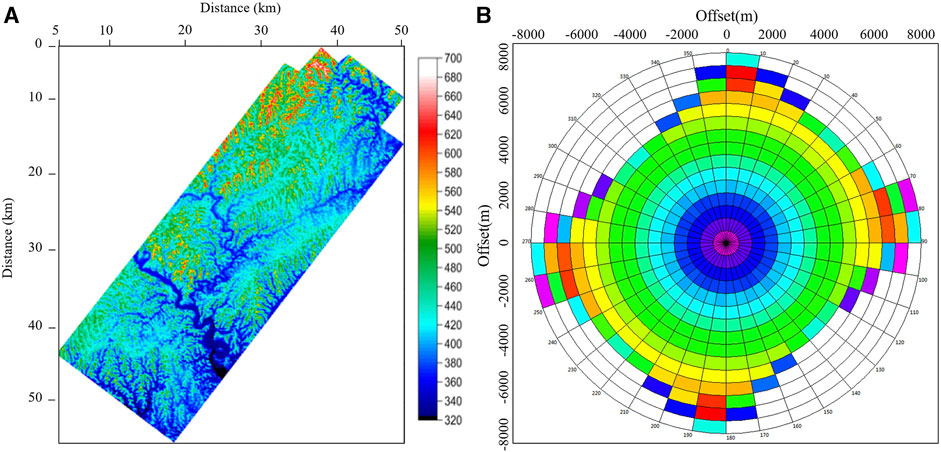
FIGURE 8. (A) The surface elevation map of the work area. (B) Rose diagram of observation system. The elevation of S-Y block is generally about 350–720 m and the local elevation changes greatly. It can be seen from the rose diagram that the work area belongs to wide azimuth acquisition.

The formation and enrichment of tight sandstone gas reservoirs in Shaximiao Formation in S-Y 3D working area are mainly controlled by high-quality hydrocarbon sources, high-quality channel sand bodies and source faults. In the research area, the lithology of the Jurassic Shaximiao Formation is dominated by purplish red mudstone with light gray lumps of fine-medium sandstone, with a thickness of 800–2200 m. The fluvial-lake sedimentary system is mainly developed, and the meander river delta plain and front fluvial-facies are mainly microfacies. The bottom-up sedimentation has a certain inheritance, and the provenance is mainly from the north section of Longmen Mountain and Micang-Daba. The development of source rocks, the development of small high-angle faults in the Jurassic and the complex relationship between faults and sand body are favorable areas for exploration and development of tight sandstone gas reservoirs. The 23 stage channel sand bodies in Shaximiao Formation are longitudinally superimposed, the reservoir is highly heterogeneous, the wave impedance difference between the thin channel sand bodies and the surrounding rocks is small, the seismic response characteristics of the reservoirs are not obvious, and the seismic prediction of the reservoirs and hydrocarbons is difficult. Therefore, it is necessary to carry out research on high-fidelity and high-resolution imaging of channel sand body, high-precision imaging and prediction of fault, fault distribution characteristics and the relationship between sand body configuration.

As can be seen from Figure 9, the signal to noise ratio of the section processed for tight sandstone gas reservoirs in narrow channels is higher. The seismic response characteristics of gas bearing sand bodies have been further highlighted, and the imaging of small faults is clearer and more reliable. High-quality processed data is provided for fine interpretation of sand bodies, fracture prediction, AVO analysis, and oil and gas detection.

FIGURE 9

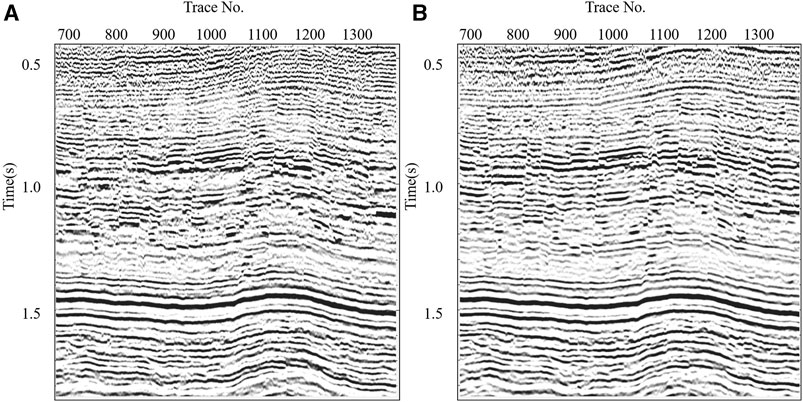
FIGURE 9. (A) Is the conventional processing prestack time migration profile. (B) is the wide azimuth data OVT domain prestack time migration profile. After OVT domain processing and HTI anisotropic correction, the signal-to-noise ratio and resolution of seismic profile have been significantly improved, the boundary of tight sand body is clearer, and the small fractures are more clearly characterized.

Figure 10 (a) shows the root mean square amplitude attribute map of the original processing data, and (b) shows the root mean square amplitude attribute map of the new processed data. It can be seen that the new processed data is more clear and reliable in terms of fine portrayal of river channels, with a higher fidelity.

FIGURE 10

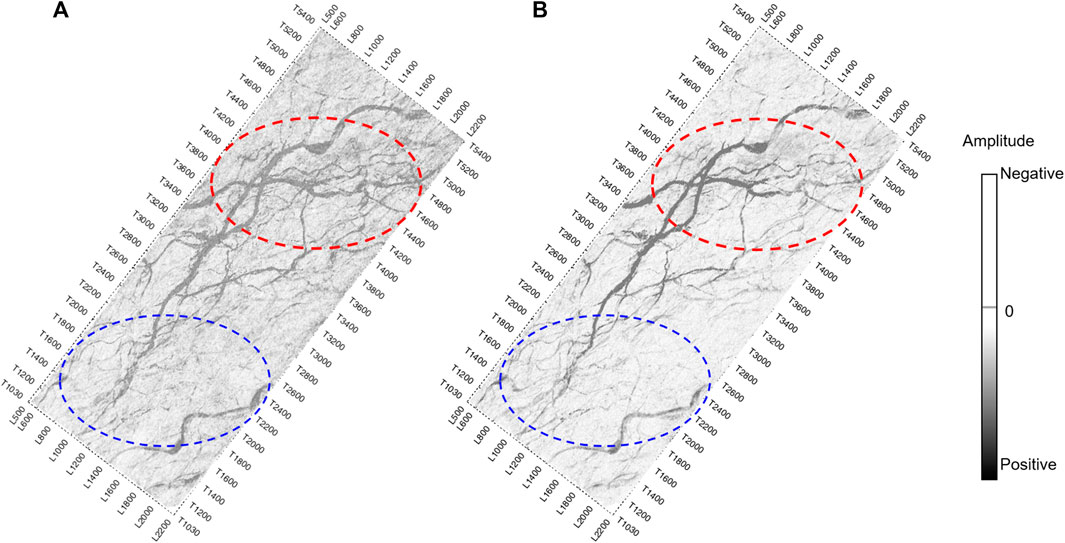
FIGURE 10. (A) shows the root mean square amplitude plane attribute map of the original processing result data, and (B) shows the root mean square amplitude plane attribute map of the new processed data.

Figure 11 (a) shows the coherent attribute map of the original processed data, and (b) shows the coherent attribute map of the wide-azimuth processing data. It can be seen that the faults are clearer and more continuous after the wide-azimuth data processing, making it easier for the fine interpretation of the faults.

FIGURE 11

FIGURE 11. (A) shows the coherent attribute map of the original processed data, and (B) shows the coherent attribute map of the wide-azimuth processing data.

4 Conclusion

A comprehensive technologies including anisotropic velocity analysis, data extraction in the OVT domain data regularization processing, prestack time/depth migration in OVT domain, and HTI correction, have been developed. The resolution of thin tight gas sand reservoir in the newly processed profile is higher, and the faults are clearer, which well demonstrate the advantages of wide azimuth seismic data processing technology.

On the basis of wide azimuth seismic data, OVT prestack migration gathers preserve azimuth information, which can better detect azimuth anisotropy in the data. Conducting HTI correction effectively solves the problem of different phase stacking caused by azimuth anisotropy, and greatly improves resolution and interlayer weak reflection energy.

Wide azimuth seismic data is more conducive to studying AVO, AVA, AVAZ, VVA, and the identification of faults, fractures. The integrated technology of wide azimuth seismic acquisition, processing, and interpretation is one of the directions for the exploration development of thin layers, fractures, and unconventional oil and gas reservoirs.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

HZ: Formal Analysis, Methodology, Project administration, Writing–original draft, Writing–review and editing. QS: Methodology, Project administration, Writing–review and editing. HM: Methodology, Writing–review and editing. HuL: Formal Analysis, Investigation, Methodology, Writing–review and editing. HaL: Formal Analysis, Writing–review and editing. DW: Data curation, Investigation, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article from CNPC Prospective Research Project “Research on deep and ultra-deep geological structure and tectonic style” (2021DJ0201). The funder was not involved in the study design, collection, analysis, processing of data, interpretation of data, the writing of this article, or the decision to submit it for publication.

Acknowledgments

Thanks to the support of Geophysical Research Project of PetroChina Oil and Gas and New Energy Company “Research on Full Frequency Processing Method of Thin Reservoirs and Research on Target Fine Characterization Technology” (2022KT1503).

Conflict of interest

HZ, QS, HM, HuL, HaL, and DW were employed by the company PetroChina.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alkhalifah, T. (1997). Velocity analysis using nonhyperbolic moveout in transversely isotropic media. Geophysics 62 (6), 1839–1854. doi:10.1190/1.1444285

CrossRef Full Text | Google Scholar

Alkhalifah, T., and Tsvankin, I. (1995). Velocity analysis for transversely isotropic media. Geophysics 60 (5), 1550–1566. doi:10.1190/1.1443888

CrossRef Full Text | Google Scholar

Bakulin, A., Grechka, V., and Tsvankin, I. (2000). Estimation of fracture parameters from reflection seismic data—Part I: HTI model due to a single fracture set. Geophysicals 65 (6), 1788–1802. doi:10.1190/1.1444863

CrossRef Full Text | Google Scholar

Berryman, J. G. (1979). Long wave elastic anisotropy in transversely isotropic media. Geophysics 44 (5), 896–917. doi:10.1190/1.1440984

CrossRef Full Text | Google Scholar

Calvert, A., Jenner, E., Jefferson, R., Bloor, R., Adams, N., Ramkhelawan, R., et al. (1949). Preserving azimuthal velocity information: experiences with cross-spread noise attenuation and offset vector tile preSTM. Seg. Tech. Program Expand. Abstr. 27 (1), 207. doi:10.1190/1.3054789

CrossRef Full Text | Google Scholar

Canning, A., and Malkin, A. (2008). “Removing NMO/migration stretch effects for improved AVO analysis,” in 7thConference and Exposition on Petroleum Geophysics, Hyderabad, 14-16 Jan, 2008.

Google Scholar

Cary, P. W. (1999). Common-offset-vector gathers: an alternative to cross-spreads for wide-azimuth 3-D surveys. Seg. Tech. Program Expand. Abstr. 18 (1), 1496. doi:10.1190/1.1820804

CrossRef Full Text | Google Scholar

Davison, C., Ratcliffe, A., Grion, S., Johnston, R., Duque, C., Neep, J., et al. (2011). “Azimuthal velocity uncertainty: estimation and application,” in Seg technical program expanded (SAN Antonio, United States: Society of Exploration Geophysicists). doi:10.1190/1.3627743

CrossRef Full Text | Google Scholar

Gray, D., and Head, K. (2000). Fracture detection in Manderson Field: a 3-D AVAZ case history. Lead. Edge 19 (11), 1214–1221. doi:10.1190/1.1438508

CrossRef Full Text | Google Scholar

Grechka, V., and Tsvankin, I. (1998). 3-D description of normal moveout in anisotropic inhomogeneous media. Geophysics 63, 1079–1092. doi:10.1190/1.1444386

CrossRef Full Text | Google Scholar

Grechka, V., and Tsvankin, L. (1999). 3-D moveout velocity analysis and parameter estimation for orthorhombic media. Geophysics 64 (3), 820–837. doi:10.1190/1.1444593

CrossRef Full Text | Google Scholar

Jenner, E. (2002). Azimuthal AVO: methodology and data examples. Lead. Edge 21, 782–786. doi:10.1190/1.1503184

CrossRef Full Text | Google Scholar

Lu, L., Chen, J., and Chen, W. D. (1998). “Anisotropic velocity analysis and moveout: a practical approach,” in SEG technical program expanded abstracts (New Orleans, United States: Society of Exploration Geophysicists), 1487–1490. doi:10.1190/1.1820193

CrossRef Full Text | Google Scholar

Rüger, A. (1996). “Reflection coefficients and azimuthal AVO analysis in anisotropic media,”. Doctoral Thesis (Colorado: Colorado School of Mines).

Google Scholar

Rüger, A. (1997). P-wave reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry. Geophysics 62, 713–722. doi:10.1190/1.1444181

CrossRef Full Text | Google Scholar

Rüger, A. (1998). Variation of P-wave reflectivity with offset and azimuth in anisotropic media. Geophysics 63 (3), 935–947. doi:10.1190/1.1444405

CrossRef Full Text | Google Scholar

Rüger, A. (2002). Reflection coefficients and azimuthal AVO analysis in anisotropic media. Tulsa: Society of Exploration Geophysicists. doi:10.1190/1.9781560801764.ch6

CrossRef Full Text | Google Scholar

Rüger, A., and Tsvankin, I. (1995). “Azimuthal variation of AVO response for fractured reservoirs,” in Seg technical program expanded abstracts (Houston: Society of Exploration Geophysicists), 1103–1106. doi:10.1190/1.1887623

CrossRef Full Text | Google Scholar

Schapper, S., Jefferson, R., Calvert, A., and Williams, M. (2009). Anisotropic velocities and offset vector tile prestack-migration processing of the Durham Ranch 3D, Northwest Colorado. Lead. Edge 28 (11), 1352–1361. doi:10.1190/1.3259614

CrossRef Full Text | Google Scholar

Shuey, R. T. (1985). A simplification of the Zoeppritz equations. Geophysics 50 (50), 609–614. doi:10.1190/1.1441936

CrossRef Full Text | Google Scholar

Stein, J. A., Boyer, S., Hellman, K., and Weigant, J. (2010). “Application of POCS interpolation to exploration,” in SEG technical program expanded abstracts (Colorado: Society of Exploration Geophysicists). doi:10.1190/1.3513590

CrossRef Full Text | Google Scholar

Su, Q., Zeng, H., Meng, H., Qie, S., Zhang, X., and Liu, H. (2020). “Application of HTI anisotropy correction for wide-azimuth seismic data: a case study of tight gas exploration in Sichuan Basin, China,” in SEG international exposition and annual meeting (Houston: Society of Exploration Geophysicists). doi:10.1190/segam2020-3427291.1

CrossRef Full Text | Google Scholar

Su, Q., Zeng, H., Tian, Y., Li, H., Lyu, L., and Zhang, X. (2021). High-resolution seismic processing technique with broadband, wide-azimuth, and high-density seismic data—a case study of thin-sand reservoirs in eastern China. Interpretation 9 (3), T833–T842. doi:10.1190/int-2020-0107.1

CrossRef Full Text | Google Scholar

Swan, H. W. (2012). Automatic compensation of AVO background drift. Lead. Edge 26 (12), 1528–1536. doi:10.1190/1.2821938

CrossRef Full Text | Google Scholar

Swan, W. H. (2001). Velocities from amplitude variations with offset. Geophysics 66, 1735–1743. doi:10.1190/1.1487115

CrossRef Full Text | Google Scholar

Thomsen, L. (1986). Weak elastic anisotropy. Geophysics 51 (10), 1954–1966. doi:10.1190/1.1442051

CrossRef Full Text | Google Scholar

Thomsen, L. (1988). Reflection seismology over azimuthally anisotropic media. Geophysics 53 (3), 304–313. doi:10.1190/1.1442464

CrossRef Full Text | Google Scholar

Thomsen, L. (2010). Elastic anisotropy due to aligned cracks in porous rock. Geophys. Prospect. 43 (6), 805–829. doi:10.1111/j.1365-2478.1995.tb00282.x

CrossRef Full Text | Google Scholar

Tsvankin, I. (1995). Normal moveout from dipping reflectors in anisotropic media. Geophysics 60 (1), 268–284. doi:10.1190/1.1443755

CrossRef Full Text | Google Scholar

Tsvankin, I. (1997a). Anisotropic parameters and P-wave velocity for orthorhombic media. Geophysics 62 (4), 1292–1309. doi:10.1190/1.1444231

CrossRef Full Text | Google Scholar

Tsvankin, I. (1997b). Reflection moveout and parameter estimation for horizontal transverse isotropy. Geophysics 62 (2), 614–629. doi:10.1190/1.1444170

CrossRef Full Text | Google Scholar

Tsvankin, I., and Thomsen, L. (1994). Nonhyperbolic reflection moveout in anisotropic media. Geophysics 59 (8), 1290–1304. doi:10.1190/1.1443686

CrossRef Full Text | Google Scholar

Vermeer, G. J. O. (1998). Creating image gathers in the absence of proper common-offset gathers. Explor. Geophys. 29 (4), 636–642. doi:10.1071/eg998636

CrossRef Full Text | Google Scholar

Vermeer, G. J. O. (2000). Processing with offset-vector-slot gathers. Seg. Tech. Program Expand. Abstr. 19 (1), 2484. doi:10.1190/1.1816134

CrossRef Full Text | Google Scholar

Wang, Y. H. (1999). Approximations to the Zoeppritz equations and their use in AVO analysis. Geophysics 64 (6), 1920–1927. doi:10.1190/1.1444698

CrossRef Full Text | Google Scholar

Xu, S., Zhang, Yu, and Lambaré, G. (2010). Antileakage Fourier transform for seismic data regularization in higher dimensions. Geophysics 75 (6), 113–120. doi:10.1190/1.3507248

CrossRef Full Text | Google Scholar

Xu, S., Zhang, Yu, Pham, D., and Lambaré, G. (2005). Anti-leakage Fourier transform for seismic data regularization. Geophysics 70 (4), 87–95. doi:10.1190/1.1993713

CrossRef Full Text | Google Scholar

Xu, X., and Tsvankin, I. (2007). A case study of azimuthal AVO analysis with anisotropic spreading correction. Lead. Edge 26 (12), 1552–1561. doi:10.1190/1.2821942

CrossRef Full Text | Google Scholar

Yuan, S. Y., Wang, J. H., Liu, T., and Xie, T. (2020). 6D phase-difference attributes for wide-azimuth seismic data interpretation. Geophysics 85 (6), 37–49. doi:10.1190/geo2019-0431.1

CrossRef Full Text | Google Scholar

Zeng, H., Wang, X., Su, Q., Yundong, Y., Huan, L., Huijie, M., et al. (2021). Research and application of mixed sources high-precision matching processing technology in the complex obstacle area in western China. Oil Geophys. Prospect. 56 (3), 476–484. doi:10.13810/j.cnki.issn.1000-7210.2021.03.006

CrossRef Full Text | Google Scholar

Zeng, H. H., Su, Q., Meng, H. J., Yang, G. G., Qie, S. H., and Liu, H. (2022). “Hti medium azimuthal anisotropy correction technology and application of wide azimuth seismic data,” in 83rd EAGE Annual Conference & Exhibition, Madrid, June 6-9, 2022, 1–5.

CrossRef Full Text | Google Scholar