Numerical simulations of pure quasi-P-waves in orthorhombic anisotropic media

Wang, Hao; Huang, Jianping; Yang, Jidong; Shen, Yi

doi:10.3389/feart.2023.1261033

ORIGINAL RESEARCH article

Front. Earth Sci., 19 October 2023

Sec. Solid Earth Geophysics

Volume 11 - 2023 | https://doi.org/10.3389/feart.2023.1261033

This article is part of the Research Topic Advances of New Technologies in Seismic Exploration View all 22 articles

Numerical simulations of pure quasi-P-waves in orthorhombic anisotropic media

Hao Wang*

Jianping Huang

Jidong Yang

Yi Shen

School of Geosciences, China University of Petroleum (East China), Qingdao, China

The accurate simulation of anisotropic media is critical in seismic imaging and inversion. In recent years, some scholars have dedicated efforts to the study of precise elastic waves in anisotropic media; however, it is easy to separate P-wave and S-wave from elastic wave fields in isotropic media but difficult to separate them in anisotropic media. To address this issue, others have proposed pseudo-pure-wave equations based on the theory of wave-mode separation, but shear wave interference still exists. Therefore, we derived the first-order pure quasi-P-wave equation with no shear wave component in orthorhombic anisotropic media (ORT) which is common in the Earth’s crust and has very important research value. The presence of a pseudodifferential operator in the equation poses a challenge for solving. In order to solve the pure wave equation, we decomposed the original pseudodifferential operator into an elliptic differential operator and a scalar operator, both of which are easily solvable. In addition, we extended the equation from ORT media to tilted ORT (TORT) media. The example results indicate that our pure quasi-P-wave equation can yield a more stable and accurate P-wave field. The pure wave equation we propose can be applied in reverse time migration (RTM), the least squares RTM (LSRTM), and even the full waveform inversion (FWI).

1 Introduction

With the growing complexity of targets in oil and gas exploration, precise high-resolution imaging technology has emerged as a vital tool, offering robust technical support and emphasizing the significance of accounting for underground media anisotropy (Chen et al., 2010; Fowler et al., 2010; Du et al., 2015). Various migration and inversion imaging methods have been developed based on anisotropic media, including Vertical Transverse Isotropy media (VTI) (S. Sun et al., 2022), (C. Luo et al., 2022), (R. Bloot et al., 2012), tilted TI (TTI) media (Han Q et al., 2022), and orthorhombic anisotropic media (ORT) media. However, certain challenges emerge when using the original elastic wave equation for forward numerical simulations. This may result in a complex algorithm and significant computational costs, especially given the current hardware limitations (Du and Qin, 2009; Cheng J B et al., 2013). Furthermore, the separation of elastic wave fields using wavefield separation techniques faces several challenges in anisotropic media (Dellinger J and Etgen J, 1990; Cheng J and Fomel S, 2014). As a result, scholars from various countries have recently devoted themselves to the study of single-mode wave propagation, such as the quasi-P-wave. Broadly speaking, anisotropic numerical simulations of single-mode waves can be categorized into two main types of methods. The first approach is based on the acoustic approximation proposed by Alkhalifah T (1998), and the core idea of this acoustic approximation is to set the shear wave velocity along each anisotropic symmetry axis to zero. Subsequently, he (Alkhalifah T, 2000) derived a fourth-order wave equation for TI media within the framework of the acoustic approximation and this equation was proven to be challenging to solve. Following this, other researchers decomposed this high-order linear partial differential equation into lower-order forms that are more easily solvable. Applying these simplified equations to wavefield simulation and RTM can enhance computational efficiency (Zhou H et al., 2006; Du X et al., 2008; Fowler PJ et al., 2010). However, when using these simplified equations for numerical simulations, several issues may arise, including potential wavefield interference caused by pseudo-shear waves (Grechka et al., 2004) and the possibility of numerical instability when the anisotropic symmetry axis undergoes abrupt changes (Fletcher et al., 2009; Duveneck and Bakker, 2011; Zhang et al., 2011). The second method is based on the pure P-wave equation, thereby fundamentally eliminating interference from shear waves. In this regard, Klie and Toro (2001) employed a previous version of the acoustic equation to eliminate an analytical artifact in Alkhalifah’s solution. Pestana et al. (2011) and Chu et al. (2013) introduced a new equation that contains intricate pseudo-differential operators, with all of its model parameters being separable. This equation can be solved using the pseudospectral method, but computational efficiency decreases when dealing with complex anisotropic parameters. The dispersion relation for decoupled qP and qSV waves was introduced under the assumption of the acoustic approximation in VTI media (Liu et al., 2009). This approach has proven to be effective in solving the equation when the anisotropic parameter model remains relatively stable. Cheng et al. (2013) derived a pseudo-pure wave equation based on the theory of elastic wave separation. By isolating the scalar-mode wave from pseudo-pure-mode wave equations, residual shear wave components were successfully eliminated (Cheng et al., 2014). Section 3.1 (Example 1) showcases the results of forward wave field simulations using the pseudo-pure P-wave equation in ORT. Based on different theories, Sheng and Zhou (2014) derived a new pure qP wave equation applicable to TTI media. Their approach presents a broadly adaptable solution for handling pseudo-differential operators.

To simplify the algorithms for numerical simulation in anisotropic media, approximations for the phase and group velocities of qP waves have found widespread use. Many approximate algorithms have been introduced previously to meet the numerical simulation requirements for various purposes. Dellinger and Etgen (1990) presented two consecutive continuous scalar anisotropic approximations expressed directly as rational polynomials. Alkhalifah and Tsvankin (1995) recommended performing velocity analysis by inversely deducing the dependency of P-wave moveout velocities on the ray parameter in TI media. Tsvankin (1996) examined the p-wave velocity and summarized its sign in TI media. Fomel (2004) and Fomel et al. (2013) put forward the approximation approach for three-dimensional anisotropic media on the basis of previous studies. Qi et al. (2014) and Qi et al. (2015) simplified the P-wave phase velocity by an elliptic approximation and they further elucidated the correlation between elastic coefficients and Thomsen-type parameters of ORT media. Zhang et al. (2022) systematically clarified the approximation of P-, S1- and S2- wave reflection coefficients in ORT. Guo et al. (2019), Guo et al. (2021), and Li et al. (2023) proposed theoretical models for rock effective elastic properties in the TI media, and these models provide the basis to link fracture properties to seismic attributes.

In this article, we have derived the dispersion equation for pure qP waves in ORT media. Instead of employing the exact dispersion relation presented by Tsvankin (1997), we utilized the phase velocity equation for pure qP waves introduced by Qi and Stovas (2016) to simplify the expression of the equation. This choice was driven by the goal of significantly decreasing the computational workload in ORT media. Importantly, the simplified phase velocity approximation remains highly accurate for acoustic or elastic ORT media characterized by strong anisotropy. After that, we deconstruct the pseudo-differential operator in the aforementioned dispersion equation into an elliptic differential operator and a scalar operator. This equation became easy to solve using this method and the wave field simulated in this way will have more balanced amplitudes, as demonstrated in the work by Sheng et al. (2015). Notably, when the differential operator is substituted with a Laplacian operator, following the approach by Sheng and Zhou (2014), the equation exhibits an improved tolerance to directional errors. Lastly, we extend the equation from ORT media to TORT media, to better simulate real geological stratum media.

2 Materials and methods

To reduce algorithm complexity, we start from the last of the three formulas: the GMA-type approximate formula, the Fomel approximation, and the simplified Fomel approximation for ORT media proposed by Qi and Stovas (2016). All the formulas are accurate for elastic or acoustic orthorhombic media with strong anisotropy and the simplified one reduces the steps of the algorithm but has no effect on the final result. The simplified phase velocity in ORT media has the following form:

v_{p}^{2} (θ, φ) = \frac{1}{2} v_{p 0}^{2} (\cos^{2} θ + α (φ) \sin^{2} θ) + \frac{1}{2} v_{p 0}^{2} \sqrt{{(\cos^{2} θ + α (φ) \sin^{2} θ)}^{2} + 4 β (φ) \cos^{2} θ \sin^{2} θ} (1)

With α (φ) = \frac{1}{2} (r_{2} ξ_{2}^{2} \cos^{2} φ + r_{1} ξ_{1}^{2} \sin^{2} φ) + \frac{1}{2} \sqrt{{(r_{2} ξ_{2}^{2} \cos^{2} φ + r_{1} ξ_{1}^{2} \sin^{2} φ)}^{2} + \frac{1}{ξ_{3}^{2}} r_{1} r_{2} ξ_{1}^{2} ξ_{2}^{2} \sin^{2} (2 φ)} (2)

β (φ) = r_{1} \sin^{2} φ + r_{2} \cos^{2} φ - α (φ) (3)

And all the parameters are defined as:

\begin{array}{c} r_{1} \equiv 1 + 2 δ^{(1)}, r_{2} \equiv 1 + 2 δ^{(2)}, ξ_{1} \equiv \sqrt{1 + 2 η^{(1)}} ξ_{2} \equiv \sqrt{1 + 2 η^{(2)}}, ξ_{3} \equiv \sqrt{1 + 2 η^{(3)}} \\ η^{(1)} \equiv (ε^{(1)} - δ^{(1)}) / (1 + 2 δ^{(1)}), η^{(2)} \equiv (ε^{(2)} - δ^{(2)}) / (1 + 2 δ^{(2)}), η^{(3)} \equiv \frac{ε^{(1)} - ε^{(2)} - δ^{(3)} (1 + 2 ε^{(2)})}{(1 + 2 ε^{(2)}) (1 + 2 δ^{(3)})} \end{array} (4)

where $θ$ is phase angle measured from the vertical axis ( $z - axis$ ) ranges from $0$ to $π$ and $φ$ is azimuthal angles measured from the $x - axis$ between 0 and $2 π$ , $v_{p}$ is the p-wave phase velocity along the axis of symmetry, $ε^{(1)} ε^{(2)} δ^{(1)} δ^{(2)} δ^{(3)}$ are Thomsen (1986) anisotropic parameters.

We bring the following relationship function into Eq. 1,

\sin θ \cos φ = \frac{v_{p} (θ, φ) k_{x}}{ω}, \sin θ \sin φ = \frac{v_{p} (θ, φ) k_{y}}{ω}, \cos θ = \frac{v_{p} (θ, φ) k_{z}}{ω} (5)

So we get the dispersion equation in ORT media as:

ω^{2} = \frac{1}{2} v_{p 0}^{2} [M (k) + \sqrt{M^{2} (k) + P (k)}] (6)

Where $k = (k_{x}, k_{y}, k_{z}) M (k) = k_{z}^{2} + Q (k_{x}, k_{y})$

P (k) = 4 [r_{1} k_{y}^{2} + r_{2} k_{x}^{2} - Q (k_{x}, k_{y})] k_{z}^{2}

Q (k_{x}, k_{y}) = \frac{1}{2} [r_{2} ξ_{2}^{2} k_{x}^{2} + r_{1} ξ_{1}^{2} k_{y}^{2} + \sqrt{{(r_{2} ξ_{2}^{2} k_{x}^{2} + r_{1} ξ_{1}^{2} k_{y}^{2})}^{2} + 4 \frac{1}{ξ_{3}^{2}} r_{1} r_{2} ξ_{1}^{2} ξ_{2}^{2} k_{x}^{2} k_{y}^{2}}] (7)

Where $k_{x} k_{y} k_{z}$ denotes the P-wave wavenumber in their axis ( $x - axis$ ; $y - axis$ ; $z - axis$ ) and $ω$ denotes angular frequency. $v_{p 0}$ is vertical velocity.

At this time, the dispersion equation is still hard to solve. We use the elliptic differential operator method proposed by Sheng et al. (2015) to solve the equation. First, we rewrite Eq. 5 into the format:

\begin{array}{c} ω^{2} = \frac{1}{2} v_{p 0}^{2} [M (k) + \sqrt{M^{2} (k) + P (k)}] \\ = \frac{1}{2} v_{p 0}^{2} [M (k) + M (k) \sqrt{1 + P (k) / M^{2} (k)}] \\ = v_{p 0}^{2} M (k) \frac{1}{2} [1 + \sqrt{1 + P (k) / M^{2} (k)}] \end{array} (8)

We define $S_{e} = \frac{1}{2} [1 + \sqrt{1 + P (k) / M^{2} (k)}]$ and $S_{e}$ is the elliptic scalar. In order to further solve the equation, we bring Eq. 4 into Eq. 8:

\begin{array}{c} ω = v_{p 0}^{2} [k_{z}^{2} + Q (k_{x}, k_{y})] S_{e} \\ = v_{p 0}^{2} \{k_{z}^{2} + \frac{1}{2} [r_{2} ξ_{2}^{2} k_{x}^{2} + r_{1} ξ_{1}^{2} k_{y}^{2} + \sqrt{{(r_{2} ξ_{2}^{2} k_{x}^{2} + r_{1} ξ_{1}^{2} k_{y}^{2})}^{2} + 4 \frac{1}{ξ_{3}^{2}} r_{1} r_{2} ξ_{1}^{2} ξ_{2}^{2} k_{x}^{2} k_{y}^{2}}]\} S_{e} \end{array} (9)

Then we rewrite Eq. 9 into the first order form, and the first order pure qP-wave equation of ORT media can be defined as:

\begin{array}{c} \partial_{t} u = v_{0}^{2} \{\partial_{z} (p_{z}) + \frac{1}{2} [r_{2} ξ_{2}^{2} \partial_{x} (p_{x}) + r_{1} ξ_{1}^{2} \partial_{y} (p_{y}) + \sqrt{{[r_{2} ξ_{2}^{2} \partial_{x} (p_{x}) + r_{1} ξ_{1}^{2} \partial_{y} (p_{y})]}^{2} + 4 \frac{1}{ξ_{3}^{2}} r_{1} r_{2} ξ_{1}^{2} ξ_{2}^{2} \partial_{x} (p_{x}) \partial_{y} (p_{y})}]\} S_{e} \\ \partial_{t} p_{x} = \partial_{x} u, \partial_{t} p_{y} = \partial_{y} u, \partial_{t} p_{z} = \partial_{z} u \end{array} (10)

In order to ensure the stability of the equation, we introduce the self-conjugate differential operator in the rotating coordinate system according to Zhang et al. (2011) and Bube et al. (2012) in tilted media. Finally, the first-order pure qP-wave equation of TORT media can be derived as

\begin{align} \partial_{t} u = v_{0}^{2} \{G_{z}^{T} (p_{z}) + \frac{1}{2} [r_{2} ξ_{2}^{2} G_{x}^{T} (p_{x}) + r_{1} ξ_{1}^{2} G_{y}^{T} (p_{y}) + \sqrt{{[r_{2} ξ_{2}^{2} G_{x}^{T} (p_{x}) + r_{1} ξ_{1}^{2} G_{y}^{T} (p_{y})]}^{2} + 4 \frac{1}{ξ_{3}^{2}} r_{1} r_{2} ξ_{1}^{2} ξ_{2}^{2} G_{x}^{T} (p_{x}) G_{y}^{T} (p_{y})}]\} \\ S_{e} \partial_{t} p_{x} = G_{x} u, \partial_{t} p_{y} = G_{y} u, \partial_{t} p_{z} = G_{z} u \end{align} (11)

Where

\begin{array}{l} G_{x} = (\cos φ \cos θ \cos α - \sin φ \sin α) \frac{\partial}{\partial x} + (\sin φ \cos θ \cos α + \cos φ \sin α) \frac{\partial}{\partial y} - (\sin θ \cos α) \frac{\partial}{\partial z} \\ G_{y} = (- \cos φ \cos θ \sin α - \sin φ \cos α) \frac{\partial}{\partial x} + (- \sin φ \cos θ \sin α + \cos φ \cos α) \frac{\partial}{\partial y} + (\sin θ \sin α) \frac{\partial}{\partial z} \\ G_{z} = (\cos φ \sin θ) \frac{\partial}{\partial x} + (\sin φ \sin θ) \frac{\partial}{\partial y} + (\cos θ) \frac{\partial}{\partial z} \\ G_{x}^{T} = \frac{\partial}{\partial x} (\cos φ \cos θ \cos α - \sin φ \sin α) + \frac{\partial}{\partial y} (\sin φ \cos θ \cos α + \cos φ \sin α) - \frac{\partial}{\partial z} (\sin θ \cos α) \\ G_{y}^{T} = \frac{\partial}{\partial x} (- \cos φ \cos θ \sin α - \sin φ \cos α) + \frac{\partial}{\partial y} (- \sin φ \cos θ \sin α + \cos φ \cos α) + \frac{\partial}{\partial z} (\sin θ \sin α) \\ G_{z}^{T} = \frac{\partial}{\partial x} (\cos φ \sin θ) + \frac{\partial}{\partial y} (\sin φ \sin θ) + \frac{\partial}{\partial z} (\cos θ) \end{array}

3 Numerical tests

3.1 Example 1

In order to verify the correctness of the pure qP wave equation derived in this paper of ORT and TORT anisotropic media. Firstly, we extend the pseudo-pure P-wave equation of Cheng et al. (2013) to ORT media and remove residual shear wave components in wavefields, then compared these results with ours’. All three models’ parameters are shown in Table 1. Model 1 is used by the pseudo-pure wave simulation. The parameters $θ$ , $φ$ , $α$ are set as 0, and $γ^{(1)}$ and $γ^{(2)}$ are anisotropy parameters of shear waves in model 1. Figures 1A–C are the three components of pseudo-pure qP-wave fields, where X, Y, and Z represent inline, crossline, and depth slices of the snapshots in each picture. The outermost wave corresponds to the qP wave, the innermost wave corresponds to the qSH wave and the middle corresponds to the qSV wave. As can be seen in the first three Figures, the shear wave energy is also strong when the shear wave anisotropy is strong in each component. The fourth picture represents the summation of three components, obviously, the qP-wave energy is highlighted and the qS-wave energy is eliminated from each other, but there is still residual qS-wave energy. Figures 2A–C respectively are two horizontal and vertical components of divergence, polarization projection and deviation operators in the wavenumber domain of ORT media. Figure 2D shows the separated qP wavefield snapshots after correction of the polarization deviations. Comparing Figures 1D, 2D, it can be seen that the qS-wave component is almost completely eliminated in the corrected qP-wave fields, leaving only a little energy which may be due to the complexity of orthogonal anisotropy or the selection of anisotropy parameters. The pure qP-waves field snapshots of ORT and TORT anisotropic media are shown in Figure 3. Figure 3A uses model 2 and Figure 3B uses model 3. The distinction between Model 1 and Model 2 and 3 lies in the fact that, in Model 2 and 3, all three parameters $V_{s 0}$ , $γ^{(1)}$ , and $γ^{(2)}$ , representing shear waves, were set to 0. The shape of each component of qP-wave in Figures 2D, 3A is completely consistent which also verifies the correctness of the equation we derived indirectly, moreover, there is no shear wave energy at all and the amplitude is relatively balanced in Figure 3A. We can see that the wave field value does not appear unstable or wrong and there is no obvious dispersion in Figure 3B, although we designed a large dip angle parameter in model 3. Eq. 11 in tilted medium can also simulate the results well and the algorithm is stable and reliable. Comparing the two figures, it can be found that the wave field of the x-z plane is the most sensitive to the large dip parameter, and the other two planes have less influence.

TABLE 1

TABLE 1. Orthotropic parameter values in Thomsen form.

FIGURE 1

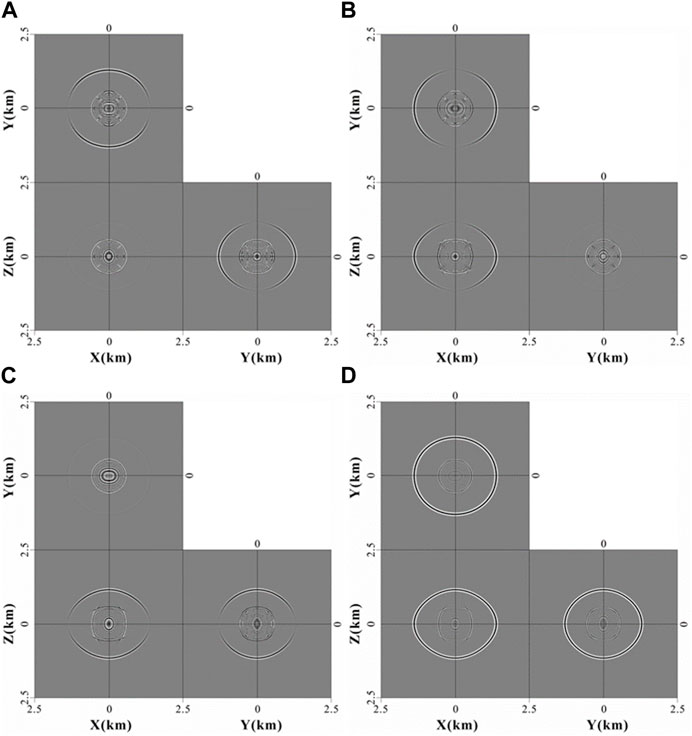
FIGURE 1. Wavefield modeling in ORT media. (A–C) are two horizontal and one vertical component of pseudo-pure qP-wave fields. (D) is the summation of three components.

FIGURE 2

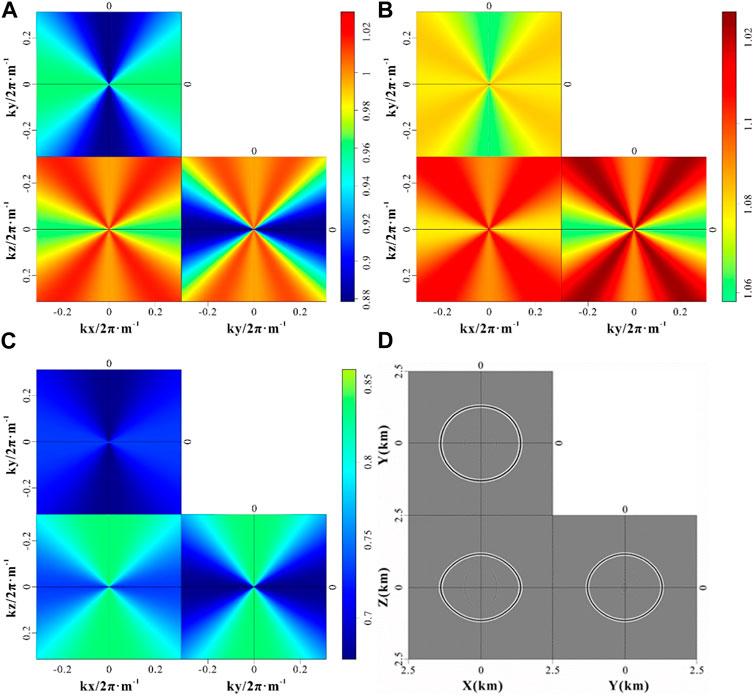
FIGURE 2. Wavenumber domain divergence, polarization projection, and deviation operators in ORT $(c)$ media and the separated qP wavefield snapshots. (A) represents two horizontal and vertical components of the divergence operator. (B) is two horizontal and vertical components of the polarization projection operator. (C) represents two horizontal and vertical components of the projection deviation operator. (D) is the separated qP wavefield snapshots after correction of the polarization deviations.

FIGURE 3

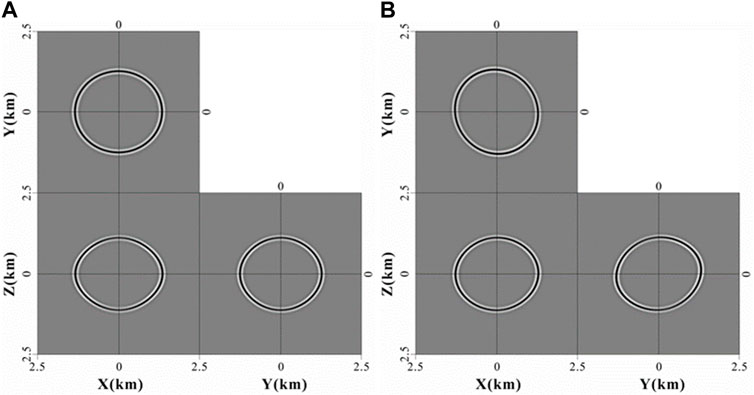
FIGURE 3. The pure qP-waves fields snapshots in ORT and TORT anisotropic media. (A) represents two horizontal and vertical components of snapshots in ORT. (B) is two horizontal and vertical components of snapshots in TORT.

The length, width, and height of all the models contain 300 sampling points, and the sampling interval is 25. The source wavelet is Rick wavelet, with a dominant frequency of 25 Hz. The source point is located in the center of the model. All wavefield snapshots are at the time t = 500ms.

3.2 Example 2

In order to test the applicability of the algorithm, we used the modified actual anisotropic parameter fields for numerical simulation. Because each parameter field is constant and does not change in Example 1, the anisotropic parameter field is variable in space in the actual seismic data processing or simulation, so just completing Example 1 is not enough to prove the reliability of the method. Figures 4A–I shows nine anisotropic parameter fields. The inline has 1,220 sampling points, the crossline has 195 sampling points, and the z-axis contains 1,510 sampling points. The x-axis and y-axis have the same sampling interval is 25, and the z-axis is 10. The source wavelet is Rick wavelet, with a dominant frequency of 25 Hz. The source point is in the surface of the model. Figure 4J shows the wavefield snapshots of the real model at the time t = 2,500 ms. Figure 4K represents a three-dimensional shot record and the length of record t is 2,000 ms. Figures 4J, K have relatively clear wave fields, and it can be seen that the wave field changes with the change of space in the anisotropic parameters.

FIGURE 4

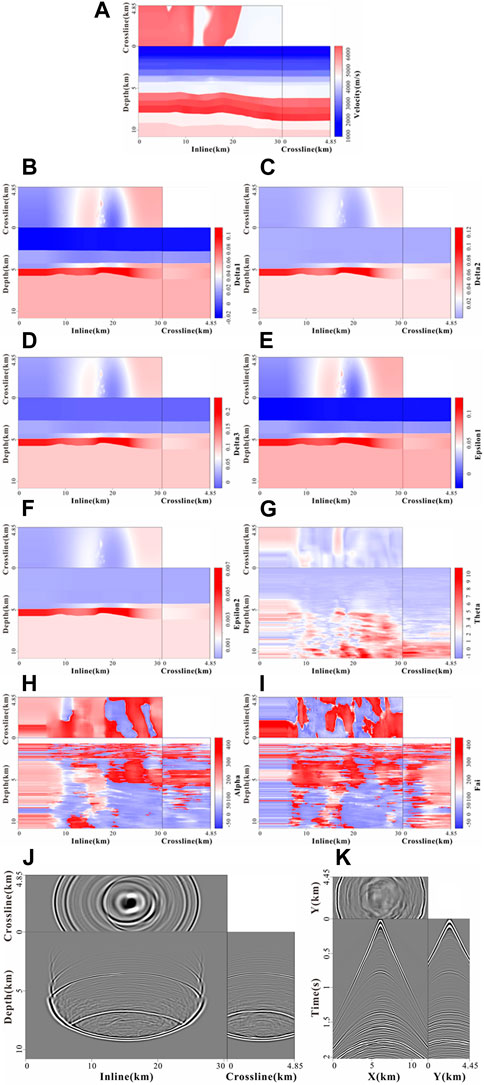
FIGURE 4. The pure qP-waves forward simulation with the modified actual anisotropic parameter field in ORT media. (A–I) respectively are $V_{p 0}$ , $δ^{(1)}$ , $δ^{(2)}$ , $δ^{(3)}$ , $ε^{(1)}$ , $ε^{(2)}$ , $θ$ , $α$ , and $φ$ . (J) represents two horizontal and vertical components of snapshots at 2,500 ms. (K) is the shot record and the length is 2,000 ms.

4 Conclusion

We derived a first-order pure qP-wave equation of ORT and extended the equation to TORT media. The problem of solving pseudo-differential operators is solved by using anelliptic approximation method. The differential operator is replaced by an elliptic differential operator instead of a Laplacian operator, so the pure qP-wave equation could simulate a more stable and balanced amplitude P-wave field. It can be seen from Example 1 that the equation we derived is correct, furthermore, there is no shear wave energy and Eq. 11 can also simulate a stable wave field under a large dip angle. The accuracy of our equation is relatively high and meets the accuracy of the current actual production based on the results in Example 2. In subsequent research, we are going to apply the equation to the RTM and simulate seismic wave fields using equations without approximation in orthotropic media.

Data availability statement

The datasets presented in this study can be obtained by contacting the corresponding author directly at: MTUyNzUyNjY5NjBAMTYzLmNvbQ==.

Author contributions

HW: Writing–original draft. JH: Writing–review and editing. JY: Investigation, Writing–review and editing. YS: Investigation, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study is supported by the Marine S&T Fund of Shandong Province for Pilot National Laboratory for Marine Science and Technology (Qingdao) (No. 2021QNLM020001), the Major Scientific and Technological Projects of Shandong Energy Group (No. SNKJ2022A06R23), the Funds of Creative Research Groups of China (No. 41821002), National Natural Science Foundation of China Outstanding Youth Science Fund Project (Overseas) (No. ZX20230152), the Major Scientific and Technological Projects of CNPC (No. ZD2019-183-003).

Acknowledgments

This work was carried out at China University of Petroleum (East China).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alkhalifah, T. (1998). Acoustic approximations for processing in transversely isotropic media. Geophysics 63 (2), 623–631. doi:10.1190/1.1444361