Crustal heterogeneity effects on coseismic deformation: numerical simulation of the 2008 MW 7.9 Wenchuan earthquake

Coseismic deformation of large earthquakes causes significant property damages and fatalities, which requires quantitative research of multiple disciplines such as geodesy, geological investigation, seismic tomography, and seismic dislocation theory. The finite element method accounts for material heterogeneity and geometric complexity, making it suitable for studying the coseismic deformation of large earthquakes. This paper develops a parallel elastic finite element program that utilizes split nodes and high-performance parallel computing technology on the FELAC software platform to study the coseismic deformation of large earthquakes. We verify the accuracy of the parallel elastic finite element program by comparing its results with the analytical solutions from seismic dislocation theory for four ideal earthquake cases. Finally, we established parallel elastic finite element models to study the coseismic deformation of the 2008 Wenchuan earthquake. The simulation results are consistent with the GPS and InSAR data. Coseismic surface deformation results are significantly influenced by medium regional heterogeneity with different layered structures besides the Longmenshan fault. The finite element program lay the foundation for the inversion of the coseismic fault rupture process based on the heterogeneous medium model and complex geometric model.

1 Introduction

Coseismic deformation by large earthquakes offers insights into the elastic properties of Earth’s medium. It arises from the sudden release and modification of strain energy along the fault, causing significant losses in terms of property and human lives. The complexity of coseismic deformation induced by the 2008 M_W 7.9 Wenchuan earthquake has been accurately captured through Global Positioning System (GPS) and Interferometric Synthetic Aperture Radar (InSAR) data. This study employs a series of parallel elastic finite element models to examine the influence of crustal medium variations on the coseismic deformation caused by the Wenchuan earthquake.

The study of coseismic deformation has matured, with well-established theoretical frameworks providing analytical and semi-analytical solutions rooted in seismic dislocation theory. Steketee (1958) initially proposed analytical dislocation solutions in semi-infinite elastic space, which were later extended by Okada (1985, 1992) to include both surface and internal coseismic deformation in three-dimensional semi-infinite elastic space. Sun et al. (1996, 2009) made significant advancements in coseismic dislocation theory specifically for the spherical layered earth model. Wang et al. (2003) developed the program EDGRN/EDCMP for coseismic deformation calculation in elastic or layered elastic Earth media. Additionally, USGS introduced the Coulomb 3.3 software (Toda et al., 2011) based on seismic dislocation theory in homogenous semi-infinite elastic space, which was widely applied in the calculation of coseismic deformation and the analysis of seismic hazard change. While commonly employed for forward calculation of coseismic deformation, the accuracy of the calculation results strongly depends on simple geometry and material model, which hinders the accurate acquisition of coseismic deformation calculations for complex geometric and material cases. Large earthquakes frequently occur at plate boundaries and interplate block edges, characterized by significant lateral variations in the medium. Practical scenarios necessitate the development of numerical simulation methods that account for the complex geometry and transverse heterogeneity of materials in coseismic deformation calculation.

Satellite geodesy, facilitated by recent advancements in space observation technology, has proven pivotal in observing and documenting surface deformation caused by large earthquakes, both coseismic and postseismic. Massonet et al. (1993) conducted a pioneering study using InSAR data to capture the coseismic deformation of the M_W 7.3 Landers earthquake in Southern California. GPS and InSAR technologies have become prevalent tools to observe crustal deformation by large earthquakes. Numerous studies have employed a combination of InSAR and GPS data to investigate coseismic and postseismic deformation resulting from various earthquakes, such as the 2001 Ms 8.1 eastern Kunlun earthquake (Wan et al., 2008), the 2001 M_W 7.8 Kokoxili earthquake (Tu et al., 2016; Zhao et al., 2018), the 2008 M_W 7.9 Wenchuan earthquake (Wan et al., 2017), the 2011 M_W 9.0 Tohoku-Oki earthquake (Wang M. et al., 2011), and the M_W 7.8 Gorkha, Nepal earthquake (Sreejith et al., 2016). Previous studies have employed geodetic inversion techniques to estimate interseismic and coseismic slips for various seismic events (Tong et al., 2010; Ozawa et al., 2012). While image processing techniques effectively extract deformation characteristics from observed data, these interpretations primarily offer insights into observation results and do not comprehensively reveal specific earthquake mechanisms.

The finite element method (FEM) is extensively employed for numerical analysis of coseismic deformation. Freed and Lin (2001) utilized a viscoelastic finite element model to calculate coseismic and postseismic Coulomb stress changes associated with the 1992 Landers earthquake sequence, providing a valuable understanding of the delayed triggering of the 1999 Hector Mine earthquake. Zhang et al. (2015) employed a 3D finite element program based on the equivalent physical force method of seismic dislocation to investigate coseismic deformation in a spherical Earth model. Hu et al. (2012) and Wang et al. (2021) adopted the finite element method to analyze both coseismic and postseismic deformation of the 2008 Wenchuan earthquake. In addition, Hu et al. (2004) investigated postseismic deformation using a 3D viscoelastic Burgers FEM model for notable earthquakes, including the 1960 giant Chile earthquake, the 2004 giant Sumatra earthquake (Hu and Wang, 2012), and the 2012 M_W 8.6 Indian Ocean earthquake (Hu et al., 2016). Luo and Liu (2010, 2018) utilized a three-dimensional viscoelastoplastic finite element model to calculate coseismic and postseismic Coulomb stress changes caused by the 2008 Wenchuan earthquake. Viscoelastic element models have also been applied to significant earthquakes, such as the 2004 M_W 9.2 Sumatra–Andaman, 2005 M_W 8.7 Nias, and 2007 M_W 8.4 Bengkulu earthquakes (Wiseman et al., 2015), as well as the 1964 M_W 9.2 Alaska earthquake (Suito and Freymueller, 2009). Numerical methods offer valuable tools for constructing realistic models of complex problems, allowing for scientific explanations grounded in mechanical mechanisms.

In this study, we developed a parallel finite element program based on the PFELAC 2.2 software platform (Element Computing Technology Co., Ltd, 2018a; Element Computing Technology Co., Ltd, 2018b; Xu et al., 2022) to precisely simulate coseismic displacement and stress fields associated with large earthquakes. To achieve this, we employed the split nodes technique (Melosh and Raefsky, 1981) and high-performance parallel computing technology. The surface coseismic displacement field and stress field at a half fault depth were validated against analytical or semi-analytical solutions provided by EDGRN/EDCMP (Wang et al., 2003) and Coulomb 3.3 (Toda et al., 2011) for four fault models: pure strike-slip, normal, reverse, and oblique thrust faults. Furthermore, by manipulating the transverse elastic moduli of the model, we quantitatively assessed the effects of medium heterogeneity on coseismic deformation. We calculated the coseismic deformation of the 2008 Wenchuan earthquake using the finite fault inversion model proposed by Wan et al. (2017) and compared it with observed geodetic GPS and InSAR data. The developed model captures the impact of crustal heterogeneity on the coseismic deformation of the 2008 Wenchuan earthquake.

2 Method and model

2.1 Elastic finite element formula

Formula (1) represents the virtual work principle in the 3D elastic finite element method, stating that the strain energy’s virtual work is the sum of the virtual work of the body force and the virtual work of the traction force (Hu, 2009; Hu et al., 2009; 2012).

${\int }_V{\delta \mathit{\epsilon }}^{\mathrm{T}}\bullet \mathit{\sigma }dV={\int }_V{\delta \mathit{u}}^{\mathrm{T}}\bullet \mathit{f}dV+{\int }_{\mathrm{\Gamma }}{\delta \mathit{u}}^{\mathrm{T}}\bullet \mathit{T}\mathrm{d}\mathrm{\Gamma }(1)$

where $\mathit{\sigma }$ and $\mathit{\epsilon }$ represent the column vector form of stress and strain tensors, respectively, with $\mathit{\sigma }={\left\{{\sigma }_{xx}{\sigma }_{yy}{\sigma }_{zz}{\sigma }_{yz}{\sigma }_{xz}{\sigma }_{xy}\right\}}^{\mathrm{T}}$ and $\mathit{\epsilon }={\left\{{\epsilon }_{xx}{\epsilon }_{yy}{\epsilon }_{zz}{\gamma }_{yz}{\gamma }_{xz}{\gamma }_{xy}\right\}}^{\mathrm{T}}$ (engineering strain). The column vectors $\mathit{f}={\left\{f_x{f}_y{f}_z\right\}}^{\mathrm{T}}$ and $\mathit{T}={\left\{T_x{T}_y{T}_z\right\}}^{\mathrm{T}}$ represent the body force in the study area $V$ and traction force on the boundary $\mathrm{\Gamma }$, respectively. $\delta \mathit{u}={\left\{\delta \mathrm{u}\delta \mathrm{v}\delta \mathrm{w}\right\}}^{\mathrm{T}}$ denotes the virtual displacement, and ${\delta \mathit{\epsilon }=\left\{\delta {\epsilon }_{xx}\delta {\epsilon }_{yy}\delta {\epsilon }_{zz}\delta {\gamma }_{yz}\delta {\gamma }_{xz}\delta {\gamma }_{xy}\right\}}^{\mathrm{T}}$ represents the virtual strain.

The 3D elastic constitutive equation is given by (Hu, 2009; Hu et al., 2009; 2012)

$\mathit{\sigma }=\mathit{D}\mathit{\epsilon }(2)$

The elastic matrix D can be expressed as

$\mathit{D}=fact\ast \left[\begin{array}{c}\begin{array}{ccc}1-\mathrm{p}\nu & \mathrm{p}\nu & \mathrm{p}\nu \\ \mathrm{p}\nu & 1-\mathrm{p}\nu & \mathrm{p}\nu \\ \mathrm{p}\nu & \mathrm{p}\nu & 1-\mathrm{p}\nu \end{array}\\ \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\end{array}\begin{array}{c}\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\\ \begin{array}{ccc}0.5-\mathrm{p}\nu & 0& 0\\ 0& 0.5-\mathrm{p}\nu & 0\\ 0& 0& 0.5-\mathrm{p}\nu \end{array}\end{array}\right](3)$

where $fact=\frac{\text{pe}}{\left(1+\mathrm{p}\nu \right)\left(1-2\ast \mathrm{p}\nu \right)}$. The parameters pe and pν correspond to Young’s modulus and Poisson’s ratio, respectively.

To calculate coseismic displacement and stress, we employ the splitting nodes technique to convert coseismic dislocation on faults into a load vector. In this case, there are no body forces ($\mathit{f}={\left\{f_x{f}_y{f}_z\right\}}^{\mathrm{T}}$) or traction forces (${\mathit{T}=\left\{T_x{T}_y{T}_z\right\}}^{\mathrm{T}}$). Instead, we introduce the initial strain ${\mathit{\epsilon }}_0={\left\{{\epsilon }_{xx0}{\epsilon }_{yy0}{\epsilon }_{zz0}{\gamma }_{yz0}{\gamma }_{xz0}{\gamma }_{xy0}\right\}}^{\mathrm{T}}$, obtained from the splitting coseismic dislocation on faults. Consequently, we derive the finite element formula (4) as follows (Hu, 2009; Hu et al., 2009; 2012):

${\int }_V{\delta \mathit{\epsilon }}^{\mathrm{T}}\bullet \mathit{\sigma }dV={\int }_{\mathit{V}}{\delta \mathit{\epsilon }}^{\mathrm{T}}\bullet {\mathit{\sigma }}_{\mathbf{0}}dV(4)$

Expanding Formula (4), we have (Hu, 2009; Hu et al., 2009; 2012):

$\begin{array}{c}{\int }_V(fact\ast \left(1-\mathrm{p}\nu \right)\ast {\epsilon }_{xx}\delta {\epsilon }_{xx}+fact\ast \mathrm{p}\nu {\ast \epsilon }_{yy}\delta {\epsilon }_{xx}+fact\ast \mathrm{p}\nu \ast {\epsilon }_{zz}\delta {\epsilon }_{xx}+fact\ast \mathrm{p}\nu \ast {\epsilon }_{xx}\delta {\epsilon }_{yy}+fact\ast \hfill \\ \left(1-\mathrm{p}\nu \right)\ast {\epsilon }_{yy}\delta {\epsilon }_{yy}+fact\ast \mathrm{p}\nu \ast {\epsilon }_{zz}\delta {\epsilon }_{yy}+fact\ast \mathrm{p}\nu \ast {\epsilon }_{xx}\delta {\epsilon }_{zz}+fact\ast \mathrm{p}\nu \ast {\epsilon }_{yy}\delta {\epsilon }_{zz}+fact\ast \hfill \\ \left(1-\mathrm{p}\nu \right)\ast {\epsilon }_{zz}\delta {\epsilon }_{zz}+shear\ast fact\ast {\gamma }_{yz}\delta {\gamma }_{yz}+shear\ast fact\ast {\gamma }_{xz}\delta {\gamma }_{xz}+shear\ast fact\ast {\gamma }_{xy}\delta {\gamma }_{xy})\hfill \\ dV={\int }_V(fact\ast \left(1-\mathrm{p}\nu \right)\ast {\epsilon }_{xx0}\delta {\epsilon }_{xx}+fact\ast \mathrm{p}\nu {\ast \epsilon }_{yy0}\delta {\epsilon }_{xx}+fact\ast \mathrm{p}\nu \ast {\epsilon }_{zz0}\delta {\epsilon }_{xx}+fact\ast \mathrm{p}\nu \ast {\epsilon }_{xx0}\delta {\epsilon }_{yy}\hfill \\ +fact\ast \left(1-\mathrm{p}\nu \right)\ast {\epsilon }_{yy0}\delta {\epsilon }_{yy}+fact\ast \mathrm{p}\nu \ast {\epsilon }_{zz0}\delta {\epsilon }_{yy}+fact\ast \mathrm{p}\nu \ast {\epsilon }_{xx0}\delta {\epsilon }_{zz}+fact\ast \mathrm{p}\nu \ast {\epsilon }_{yy0}\delta {\epsilon }_{zz}\hfill \\ +fact\ast \left(1-\mathrm{p}\nu \right)\ast {\epsilon }_{zz0}\delta {\epsilon }_{zz}+shear\ast fact\ast {\gamma }_{yz0}\delta {\gamma }_{yz}+shear\ast fact\ast {\gamma }_{xz0}\delta {\gamma }_{xz}+shear\ast fact\ast {\gamma }_{xy0}\delta {\gamma }_{xy})dV\hfill \end{array}(5)$

where $shear=0.5-\mathrm{p}\nu$. In the subsequent section, we will discuss the computation of the initial strain ${\mathit{\epsilon }}_0={\left\{{\epsilon }_{xx0}{\epsilon }_{yy0}{\epsilon }_{zz0}{\gamma }_{yz0}{\gamma }_{xz0}{\gamma }_{xy0}\right\}}^{\mathrm{T}}$, obtained from the distribution of coseismic dislocation $∆\mathit{U}={\left.\left\{∆\right.U∆V∆W\right\}}^{\mathrm{T}}$ on seismogenic faults using the splitting nodes technique.

2.2 Splitting nodes technique

The splitting nodes technique, pioneered by Melosh and Raefsky (1981), offers a straightforward approach to calculate coseismic displacement and stress, as outlined in formulas (4) and (5). The underlying principle of the splitting nodes technique is depicted in Figure 1 (Melosh and Raefsky, 1981).

FIGURE 1

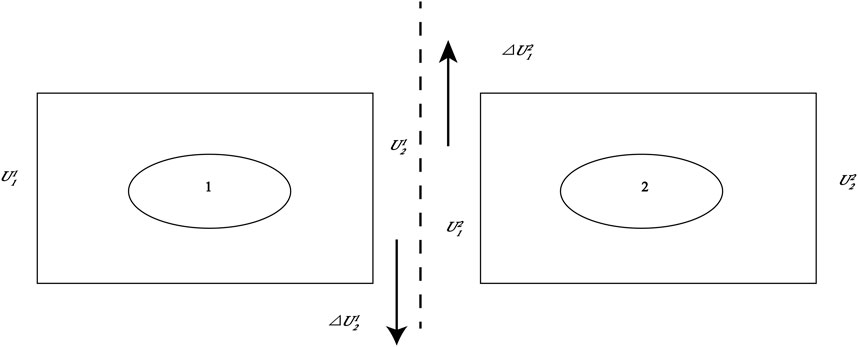
FIGURE 1. One-dimensional fault model illustrating the splitting nodes technique (adapted from Melosh and Raefsky, 1981). Elements 1 and 2, with U as the displacement, are positioned adjacent to the seismogenic fault. The superscript denotes the element number, while the subscript indicates the node number of the element. ΔU represents the total dislocation of an earthquake.

The relationship between the nodal displacement of the element and the global nodal displacement is given by (Melosh and Raefsky, 1981):

$U_1^1=U_1,U_2^1=U_1^2=U_2,U_2^2=U_3(6)$

where the displacement $U_2^1=U_1^2=U_2$ consists of two components: the average displacement $\overline{U}$ and the half dislocation $\Delta U/2=\Delta U_2^1=-\Delta U_1^2$.

The global finite element equations of elements 1 and 2 are expressed as follows (Melosh and Raefsky, 1981):

$\left[\begin{array}{ccc}{\mathrm{K}}_{11}^1& {\mathrm{K}}_{12}^1& 0\\ {\mathrm{K}}_{21}^1& {\mathrm{K}}_{22}^1+{\mathrm{K}}_{11}^2& {\mathrm{K}}_{12}^2\\ 0& {\mathrm{K}}_{21}^2& {\mathrm{K}}_{22}^2\end{array}\right]\left[\begin{array}{c}{U}_1\\ U_2\\ U_3\end{array}\right]=\left[\begin{array}{c}{F}_1-{\mathrm{K}}_{12}^1\Delta U_2^1\\ F_2-{\mathrm{K}}_{22}^1\Delta U_2^1-{\mathrm{K}}_{11}^2\Delta U_1^2\\ F_3-{\mathrm{K}}_{21}^2\Delta U_1^2\end{array}\right](7)$

The term $\left[\mathrm{K}\right]$ represents the global stiffness matrix, [U] denotes the global nodal displacement vector, while [F] corresponds to the global load vector.

Formula (7) expresses the determination of the coseismic load vector, which is caused by the three-dimensional coseismic dislocation $∆\mathit{U}={\left\{∆u∆v∆w\right\}}^{\mathrm{T}}$ on the seismogenic faults.

2.3 Parallel technology

We developed a parallel elastic finite element program based on the virtual work principle (formulas (4), (5)) and the splitting nodes technique (formula (7)), utilizing the PFELAC 2.2 software platform (Element Computing Technology Co., Ltd., 2018a, 2018b; Xu et al., 2022). The parallel computation employed the domain decomposition method, consisting of a master process and a series of sub-processes. The master process is responsible for the assembling of the global stiffness matrix and global load vector, as well as the parallel solution of the system of super-sized linear equations. The subprocesses calculated the element stiffness matrix and element load vector. This research analyzed coseismic deformations by four different-type earthquakes using parallel finite element programs. The developed finite element programs were validated with results from Coulomb 3.3 and EDGRN/EDCMP to assess their accuracy.

3 Program testing

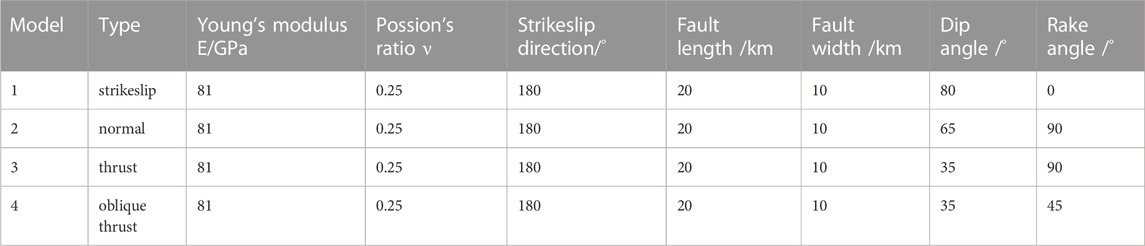
To validate our 3D elastic parallel finite element method (FEM) programs, we tested with four ideal earthquake models: pure strike-slip, normal, thrust, and oblique thrust faults, and compared the results with analytical solutions. The parameters for each model are listed in Table 1. Our finite element model has dimensions of 200 km × 200 km × 50 km, adequately encompassing the fault dimensions. The seismogenic fault is positioned at the center of the model and has a length of 20 km and a width of 10 km, extending to the surface. The FEM model employed a homogeneous, elastic, and isotropic material, with a uniform dislocation of 1 m assigned to the pure strike-slip, normal, and thrust faults, respectively. In the FEM model of the oblique thrust fault, the strike-slip and thrust dislocation components were both $\sqrt{2}/2$ m. We compared the coseismic displacements and stresses obtained from our FEM models with those from the Coulomb 3.3 and EDGRN/EDCMP programs to validate our 3D elastic parallel finite element method (FEM) programs. This study focuses on comparing the FEM simulations and the results by EDGRN/EDCMP and Coulomb 3.3 specifically for Model 4 (oblique thrust fault). The comparison for Models 1, 2, and 3 (pure strike-slip, normal, and thrust faults) is available in the Appendix.

TABLE 1

TABLE 1. The geometry and material parameters of four earthquake fault models.

Figure 2 compares surface coseismic displacement fields (u, v, w) of Model 4 (oblique thrust fault) with those by the Coulomb 3.3 program. The horizontal surface coseismic displacement (u, v) and vertical surface coseismic displacement (w) exhibit an asymmetric pattern for both the FEM model and the Coulomb 3.3 program. The overall patterns of the three coseismic surface displacement components are highly similar between the FEM model and the Coulomb 3.3 program.

FIGURE 2

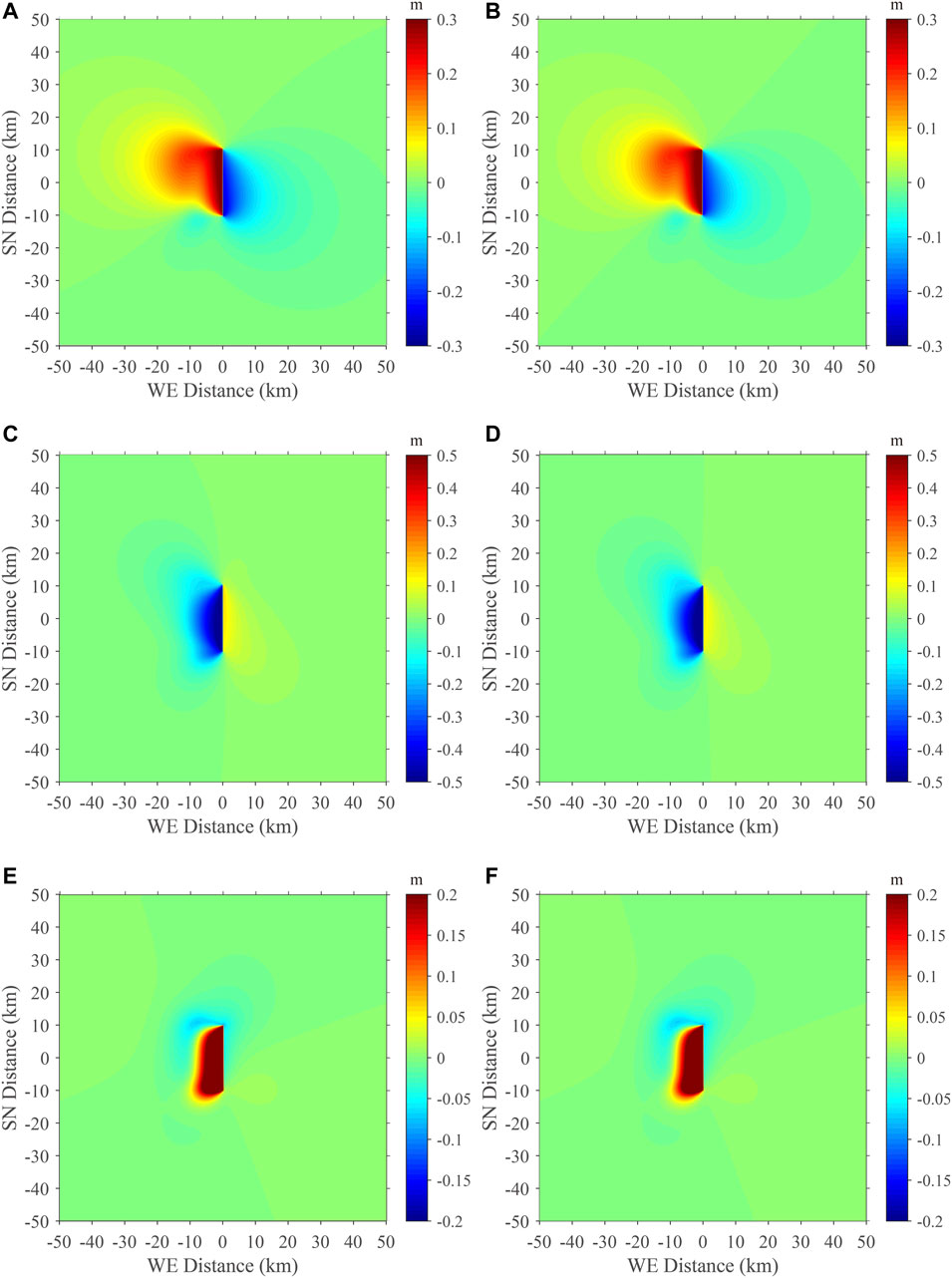
FIGURE 2. Comparison of the coseismic surface displacements Model 4 (oblique thrust fault) between the FEM model and Coulomb 3.3 program. Left column: u, v, and w components by the FEM (panels A, C, E). Right column: u, v, and w components by Coulomb 3.3 program (panels B, D, F).

Figure 3 illustrates the coseismic stress field (${\mathrm{\sigma }}_{xx},{\sigma }_{yy},{\sigma }_{zz},{\sigma }_{xy},{\mathrm{\sigma }}_{yz},{\sigma }_{xz}$) at the half fault depth between the FEM model and the Coulomb 3.3 program for Model 4 (oblique thrust fault). The left column shows the FEM results, while the right column displays the results from the Coulomb 3.3 program. Both normal stresses (${\mathrm{\sigma }}_{xx},{\sigma }_{yy},{\sigma }_{zz}$)and shear stresses (${\sigma }_{xy},{\mathrm{\sigma }}_{yz},{\sigma }_{xz}$) exhibit asymmetry. The patterns of six coseismic stress components by the FEM and the program Coulomb 3.3 are highly similar.

FIGURE 3

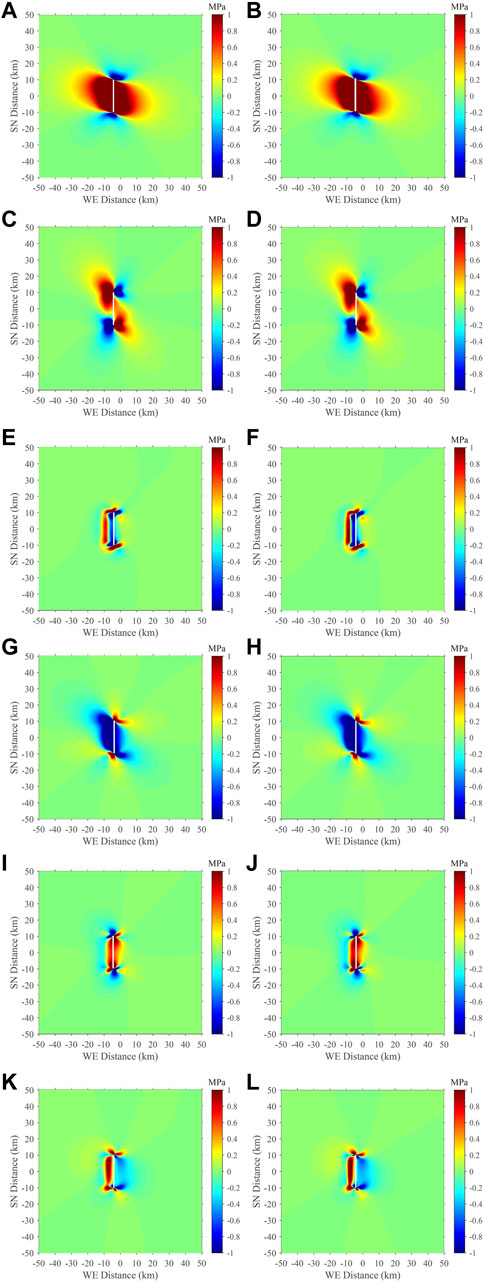
FIGURE 3. Comparison of coseismic stress at half fault depth between the FEM and Coulomb 3.3 program. Left column: FEM results for ${\mathrm{\sigma }}_{xx},{\sigma }_{yy},{\sigma }_{zz},{\sigma }_{xy},{\mathrm{\sigma }}_{yz},{\sigma }_{xz}$. Right column: Coulomb 3.3 program results for ${\mathrm{\sigma }}_{xx},{\sigma }_{yy},{\sigma }_{zz},{\sigma }_{xy},{\mathrm{\sigma }}_{yz},{\sigma }_{xz}$., The x-axis label represents the eastward direction, while the y-axis label represents the northward direction.

In Figure 4, we compare the surface coseismic displacements along a profile, passing the midpoint of the surface trace of the fault outcrop, perpendicular to the strike-slip direction using the FEM model, Coulomb 3.3, and EDGRN/EDCMP programs for Model 4 (oblique thrust). The three components exhibit highly similar patterns, with minor discrepancies that could be attributed to the sparse mesh grid of the FEM model.

FIGURE 4

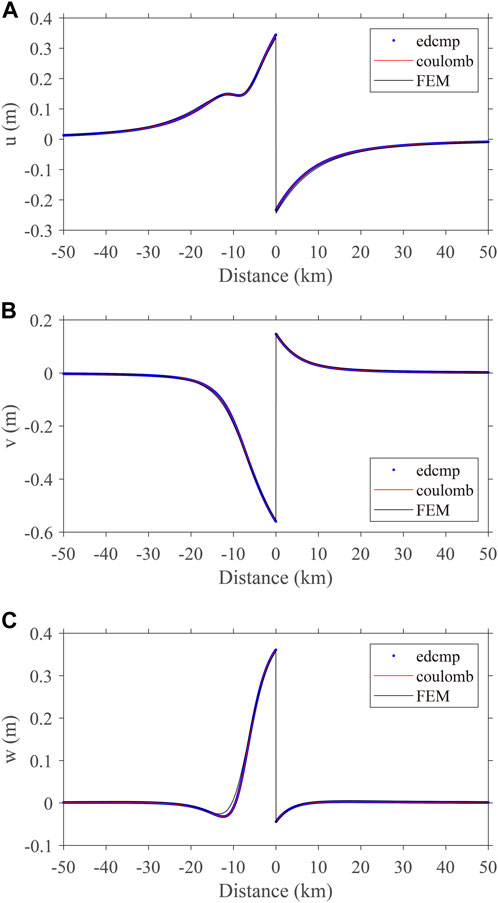
FIGURE 4. Comparison of surface coseismic displacement along a profile, passing the midpoint of the surface trace of the fault outcrop, perpendicular to the strike-slip direction using the FEM model, Coulomb 3.3, and EDGRN/EDCMP programs for Model 4 (oblique thrust fault). The x-axis represents the eastward direction, and the y-axis represents the displacement components.

By comparing the coseismic surface displacement (Figures 2, 4) and coseismic stress (Figure 3) of Model 4, we have validated the accuracy and reliability of our 3D elastic parallel FEM programs. Additionally, in the Appendix section, we have conducted similar tests for the remaining three models (pure strike-slip, normal, and thrust faults).

In this paper, a set of parallel finite element programs to study the coseismic deformation of large earthquakes is developed on the PFELAC software platform based on the domain decomposition parallel finite element technique and the split node method. This parallel finite element program can take into account the complex geometry of the originating faults, the complexity of the coseismic rupture process, the strong topographic relief, and the material inhomogeneity of the Earth’s medium in the transverse and longitudinal directions. Due to the use of the domain decomposition parallel finite element technique, the node number of finite element meshes can reach ten million, which guarantees the calculation accuracy of the coseismic displacement and stress fields in the study area. On this basis, we can also calculate the coseismic Coulomb stress changes on the major faults around a large earthquake based on this parallel finite element program, which can be used to evaluate the seismic hazard changes on the major faults after a large earthquake. We can also quantitatively analyze the inhomogeneous distribution of coseismic stress drop on the main earthquake fault plane, which can be used to judge the range of aftershock distribution on the main earthquake fault plane.

4 Case study: the coseismic deformation of the 2008 M_W 7.9 Wenchuan earthquake

The 2008 M_W 7.9 Wenchuan earthquake occurred in the Longmen Shan fault zones, which include the Beichuan fault, the Wenchuan-Maowen fault, and the Pengguan fault (Shen et al., 2009; Figure 5). The Longmen Shan fault zones, with a length of >300 km, predominantly strike in the NE-SW direction. Their well-constrained geometry is based on geological surveys (Xu et al., 2008), precise aftershock positioning (Huang et al., 2008; Liu et al., 2019), seismic tomography (Lei and Zhao, 2009; Liu et al., 2009), and deep seismic reflection profiles (Guo et al., 2013). The Longmen Shan fault zones are one of the longest rupture zones observed in interplate thrust earthquakes (Xu et al., 2008). The Longmen Shan fault zones exhibit significant variations in topography and crustal structure, with an elevation difference of around 4 km between the Qinghai-Tibetan Plateau and the Sichuan Basin, and variations in crustal thickness by tens of kilometers (Liu et al., 2015; 2018). Tomographic studies reveal significant structural differences in the media on both sides of the Longmen Shan fault zones (Lei and Zhao, 2016), providing direct evidence of medium heterogeneity within and around the fault zones through observed variations in seismic velocities. The jelly sandwich model of the Qinghai-Tibet Plateau (Bürgmann and Dresen, 2008) implies vertical stratification, indicating significant medium heterogeneity in the adjacent regions to the fault zones. We will introduce the 3D parallel elastic finite element models to provide valuable insights into the impact of medium heterogeneity on the coseismic deformation of the 2008 M_W 7.9 Wenchuan earthquake.

FIGURE 5

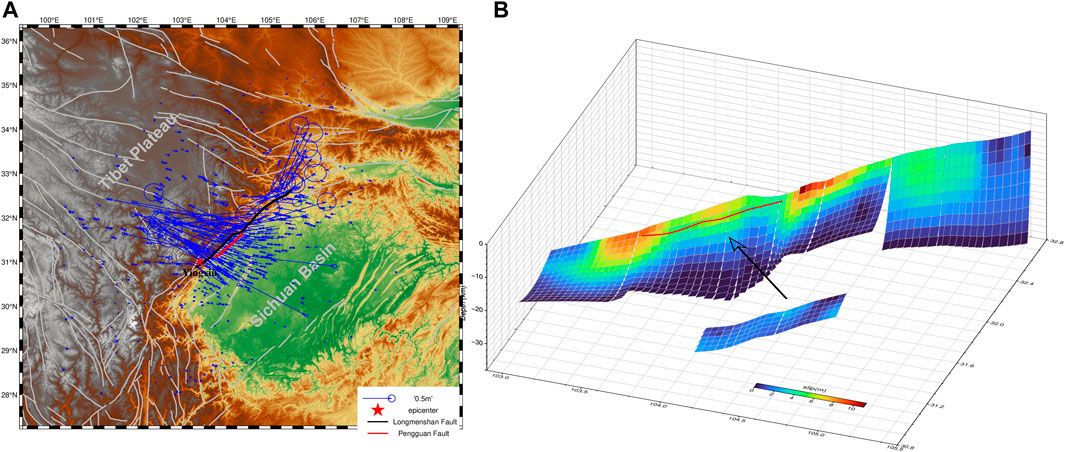
FIGURE 5. The tectonic background and coseismic dislocation distribution of the 2008 M_W 7.9 Wenchuan earthquake. (A) Tectonic background: blue arrows denote coseismic GPS data, gray lines represent the main active faults, black and red lines denote the Beichuan fault, the Wenchuan-Maowen fault, and the Pengguan fault. The red star denotes the epicenter of the 2008 Wenchuan earthquake. (B) Coseismic dislocation distribution of the 2008 M_W 7.9 Wenchuan earthquake (Wan et al., 2017).

The steep slopes surrounding the Longmen Shan fault zones limit the number of GPS observation points. After the 2008 Wenchuan earthquake, the China Crustal Observation Network project team initially provided data from 122 GPS observation points, which was later increased to 158 points by Shen et al. (2009). Wang Q. et al. (2011) contributed additional coseismic and postseismic deformation data. Wang et al. (2021) conducted an analysis of long-term deformation observations and identified a deceleration trend in the GPS velocity field from northwest to southeast when using the fault zones as a boundary. The strain rate field exhibited significant variations across the fault zones in the presence of continuous deformation fields obtained through GPS velocity interpolation. Localized abrupt changes in strain rate along the Longmen Shan fault zones can be attributed to significant variations in medium properties, corresponding to complex stress distribution. The Japan Aerospace Exploration Agency (JAXA) and the European Space Agency (ESA), using GPS and InSAR data revealed that the 2008 M_W 7.9 Wenchuan earthquake predominantly involved thrust-slip motion, with a moderate strike-slip component. The coseismic deformation of the 2008 Wenchuan earthquake reflects the opposing displacements on either side of the fault zones and the consequent shortening of the crust. The observed coseismic displacements were comparatively larger in the Songpan-Ganzi region than those in the Sichuan Basin. The difference can be explained by theoretical models indicating a weaker crustal medium in the Qinghai-Tibet Plateau than that in the Sichuan Basin and the special geometry of the fault zones. In our numerical simulation, we employed seismic tomography (Lei and Zhao, 2009; Liu et al., 2009) and deep seismic reflection profiles (Guo et al., 2013) to construct a finite element model of the coseismic deformation induced by the 2008 Wenchuan earthquake.

The coseismic vertical displacement of the 2008 Wenchuan earthquake is significant, yet direct measurements of this component remain limited. Based on direct topographic measurements, previous studies revealed the following coseismic vertical displacement patterns during the 2008 Wenchuan earthquake: (1) The Yingxiu-Beichuan rupture zone experienced vertical displacements ranging from 0.2 to 11 m, with an average of 2–4 m. The maximum displacement of 11 m occurred on the eastern side of Beichuan town, marking the highest coseismic vertical displacement within the surface rupture zone (Li et al., 2008; Dong and Chen, 2009). (2) The Hanwang rupture zone exhibited vertical displacements ranging from 0.5 to 4 m, with the highest point at Shaba Village, Jiulong Town, Mianzhu City, reaching approximately 4 m (Li et al., 2008). (3) The Xiaoyudong rupture zone demonstrated vertical displacements ranging from 0.2 to 3 m, with an average of 1–1.5 m (Li et al., 2008). Previous studies utilized first-class precision level measurement to determine the coseismic vertical displacement components of the Wenchuan earthquake along specific level routes. The findings revealed that: (1) The western hanging wall of the main rupture zone in the Longmen Shan Central Rupture predominantly experienced significant coseismic uplift. The vertical displacement decreases rapidly with distance from the fault. The highest uplift, approximately 4.7 m, was observed at the Beiyun 1 level point in Beichuan town. (2) The maximum vertical sinking occurred within the Beichuan-Guixi fault valley, with a coseismic sinking of approximately 0.6 m (Wang et al., 2010; Dong et al., 2012).

Several research teams have focused on surface rupture and quantified the coseismic dislocation distribution of the 2008 Wenchuan earthquake (Xu et al., 2010; Zhang et al., 2011; Tan et al., 2015). Previous studies employed various approaches, such as joint inversion of InSAR and GPS data (Tong et al., 2010; Xu et al., 2010) and Okada’s static elastic dislocation model (Bai et al., 2012), to characterize the fault’s coseismic rupture. However, these models have limitations in accounting for the heterogeneity of the medium in the Longmen Shan fault zones. To overcome this limitation, we adopted Wan’s (2017) coseismic rupture model, which incorporates the layered structure of the medium and the spatial complexity of the fault rupture plane.

In this study, we utilized a large finite element model with dimensions of 1,000 km*1,000 km*100 km to comprehensively compare with fault sizes. Two parallel finite element models, Model A and Model B, were constructed based on the coseismic dislocation inversion model proposed by Wan et al. (2017). Model A represents a uniform medium with Young’s modulus of 8.1E10 Pa and Poisson’s ratio of 0.25. Conversely, Model B incorporates heterogeneity by including different material properties in seven vertically divided layers, as derived from Wan et al. (2017). Furthermore, there are significant horizontal variations in the medium on both sides of the fault zones.

Figure 6 illustrates the coseismic surface displacements of Model B and the absolute residuals of the coseismic surface displacements by Model A and Model B, respectively. The results confirm that the 2008 Wenchuan earthquake is predominantly characterized by thrust slip, with a moderate component of strike-slip motion. The simulated coseismic vertical displacements reveal significant uplift exceeding 4 m in the western hanging wall of the Longmen Shan fault zones, consistent with the first-class precision level measurements (Figure 6C; Wang et al., 2010; Dong et al., 2012). These simulated vertical displacements align with findings from first-class precision level and direct topographic measurements, indicating a sharp decrease with increasing distance from the fault (Figure 6C; Li et al., 2008; Dong and Chen, 2009; Wang et al., 2010; Dong et al., 2012). The absolute residuals of Models A and B exceed 8 cm, highlighting the significance of accounting for the vertical and transverse heterogeneity of the medium. The comparison of simulated coseismic horizontal displacements and GPS data is shown in Figure 7.

FIGURE 6

FIGURE 6. The coseismic surface displacements of Model B and the absolute residuals of the coseismic surface displacements by Model A and Model (B). Panels (A-C) represent the u, v, w components of the coseismic surface displacements of Model B, respectively. Panels (D-F) show the absolute residuals of the coseismic surface displacements (u, v, w) by Model A and Model (B).

FIGURE 7

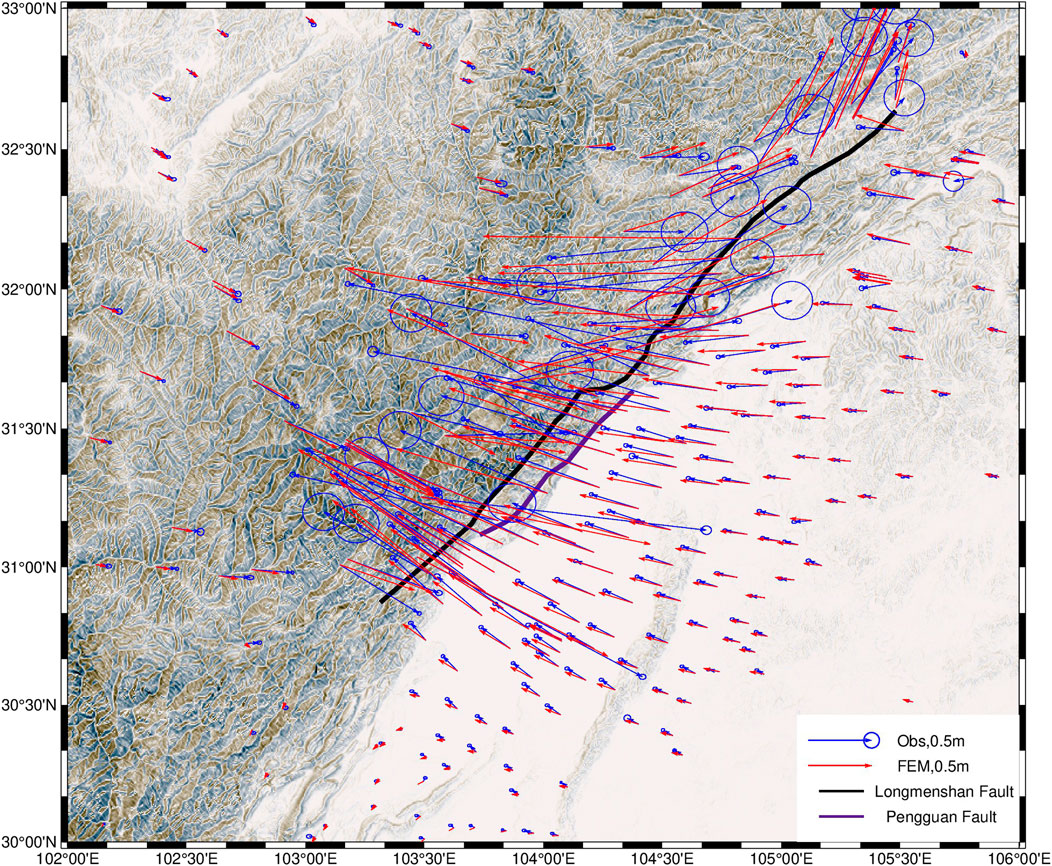
FIGURE 7. A comparison between the coseismic surface deformation predicted by Model B and the corresponding GPS data.

Figure 7 compares the coseismic surface deformation by Model B with GPS observation data. The root mean square error (RMSE) between the east component of the finite element model and GPS data is 7.98 cm, while for the north component, it is 5.61 cm. The GPS observation data uncertainty is quantified by RMSE values of 1.56 cm (east component) and 1.81 cm (north component). The finite element computation results demonstrate coherence with the actual characteristics of coseismic surface deformation.

Figure 8 compares the coseismic deformation between Model B and InSAR data. The left column represents the results of Model B, while the right column shows the InSAR data. Figures 8A, B present the ascending Line Of Sight (LOS) displacement with a root mean square error (RMSE) of 11.0 cm. Figures 8C, D display the descending LOS displacement with an RMSE of 9.11 cm. By employing the complex rupture model proposed by Wan et al. (2017), Model B demonstrates consistency with both GPS and InSAR data.

FIGURE 8

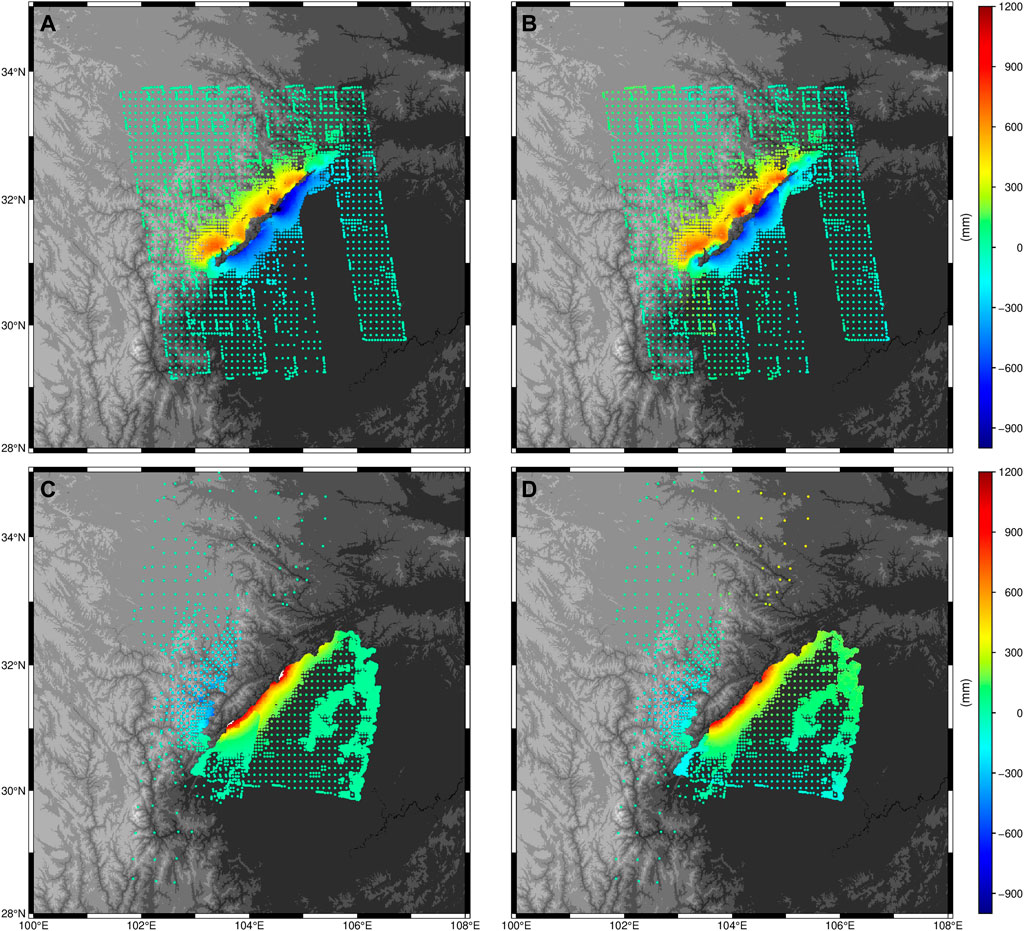
FIGURE 8. A comparison of the coseismic surface deformation by Model B and InSAR data. (A) LOS ascending displacement by Model B; (B) LOS ascending displacement by InSAR data; (C) LOS descending removal by Model B; (D) LOS descending displacement by InSAR data.

5 Discussion

We have developed a parallel elastic finite element program with the splitting nodes technique for accurate computation of coseismic displacement and stress fields by large earthquakes. To validate the effectiveness and accuracy of our FEM program, we conducted a comparative analysis of four earthquake cases using results from programs EDGRN/EDCMP and Coulomb 3.3 based on seismic dislocation theory. The parallel elastic finite element method offers advantages in handling geometric complexity, material heterogeneity, and complex boundary conditions. Utilizing this method, we can calculate Coulomb stress changes (∆CFS) on major fault planes our parallel elastic finite element method to determine coseismic displacement and stress fields, to assess the alteration in seismic hazard following significant earthquakes (Toda et al., 2008).

Three theoretical models (Model 1, Model 2, and Model 3) were developed to quantitatively investigate the impact of different medium variations on the distribution of coseismic deformation. In all models, a vertical complete strike-slip fault with a 1 m pure strike-slip dislocation is present at the center. The Poisson’s ratio is uniformly set to 0.25 for all three models. The Young’s modulus values on the left and right sides of the fault are described as Ea and Eb, respectively. The sum of Ea and Eb remains constant throughout the models, with specific values assigned as follows: Ea=Eb=8.1E10 Pa (Model 1); Ea=2 Eb=10.8E10 Pa (Model 2); Eb=2Ea=10.8E10 Pa (Model 3). Figure 9 presents the coseismic surface deformations of the three models. The results demonstrate that in Model 1, where Young’s modulus of the media on both sides of the fault is equal (Model 1), strict symmetry is observed in the surface coseismic displacements on both sides of the fault. However, in models (Model 2 and Model 3) with a doubling difference in Young’s modulus of the media on each side of the fault, the symmetry of the surface coseismic displacements between the two fault segments is lost. The segment with a lower Young’s modulus exhibits larger assigned displacement, while the segment with a higher Young’s modulus has smaller assigned displacement. Nevertheless, the overall distribution characteristics of total deformation remain unaffected. Li and Huang (2011) conducted numerical simulations and found a positive correlation between the vertical component of the seismic coseismic displacement field and the shear modulus, while the horizontal component showed a negative correlation. This indicates the importance of considering lateral variations in the medium, which can be determined quantitatively through seismic tomography imaging and deep seismic reflection profiles when analyzing the coseismic deformation of major earthquakes.

FIGURE 9

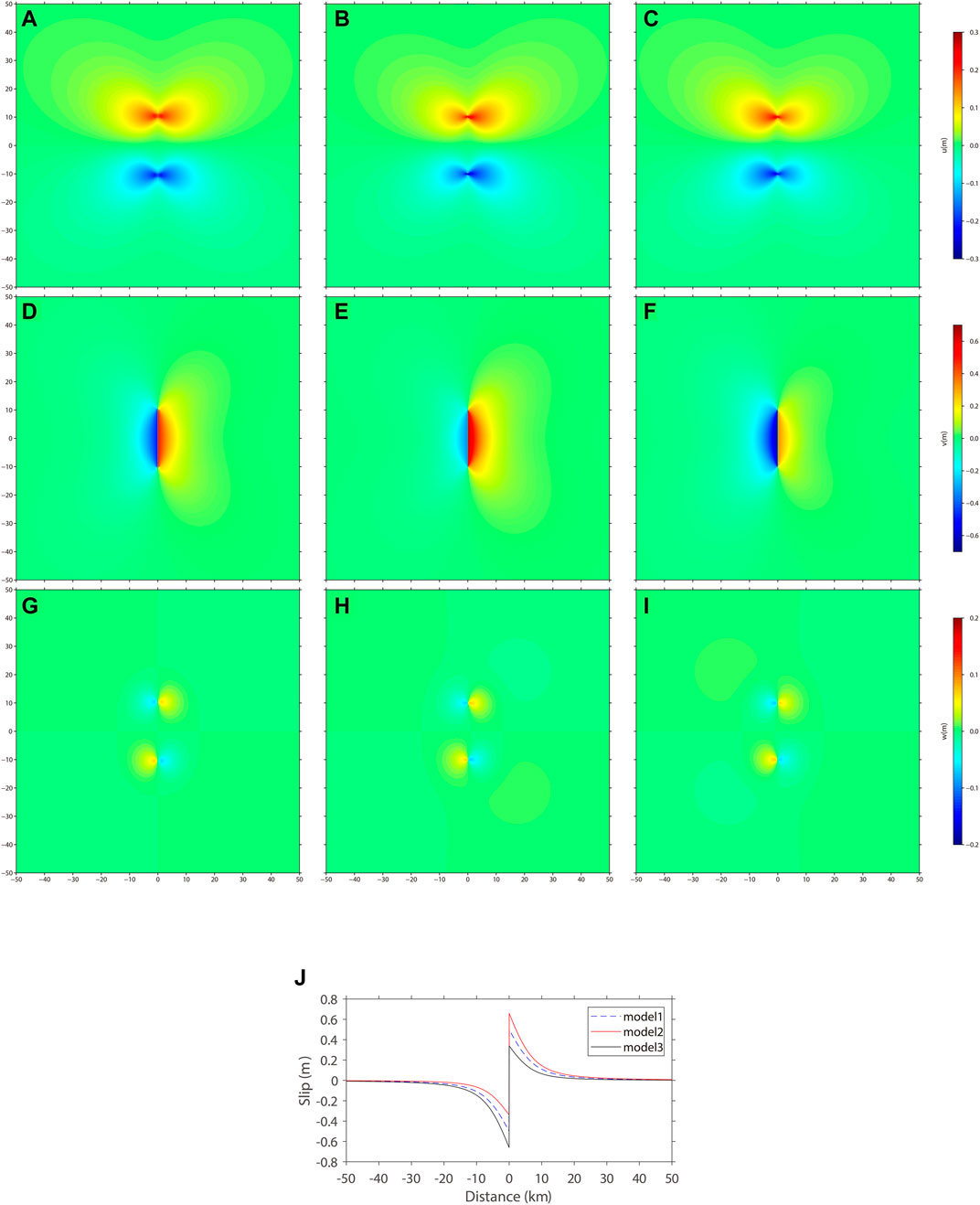
FIGURE 9. Comparison of the surface coseismic deformation results for the three theoretical models. (A, D, G): u v w by Model 1; (B, E, H): u v w by Model 2; (C, F, I): u v w by Model 3; (J): displacement component v comparison along a surface profile by Model 1, 2, and 3.

The asymmetry of the surface coseismic distribution of an ideal fault may be caused both by the inhomogeneity of the material on both sides of the fault (Figure 9) and by the geometric complexity of the fault. The Longmen Shan faults exhibit a spade-like structure. Xu and Xu (2015) investigated models with different dip angles and material parameters, revealing greater coseismic deformation in the hanging wall than in the foot wall Quantitative analysis is required to understand the influence of fault morphology on coseismic deformation. Our findings inform future inversion studies in the coseismic rupture of large earthquakes, highlighting the importance of considering fault geometry and media differences on the inversion results.

6 Conclusion

We have developed a 3D parallel elastic finite element program using split nodes and high-performance parallel computing. To validate its accuracy, we compared the program’s results for four ideal earthquake cases with analytical solutions from seismic dislocation theory. Our program investigates the media inhomogeneity in the lateral and depth directions on both sides of the main fault, complementing existing homogeneous models. This development lays the groundwork for future inversion studies of coseismic fracture processes based on inhomogeneous models. Using the program, we analyzed the coseismic deformation of the 2008 Wenchuan earthquake, obtaining results consistent with previous research and GPS data. This demonstrates the program’s suitability for complex geometry and inhomogeneous media in coseismic deformation analysis.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

MS: Conceptualization, Methodology, Visualization, Formal analysis, Writing–original draft, Writing–review and editing. SM: Writing–original draft, Writing–review and editing. CH: Conceptualization, Methodology, Supurvision, Writing–review and editing, Funding acquision, Project administration. YS: Conceptualization, Formal analysis, Writing–original draft, Writing–review and editing.

Funding

This research was supported by the National Science Foundation of China (42074117) and the Fundamental Research Funds for the Central Universities (E2ET0413X2).

Acknowledgments

Professors Yongen Cai, Yuanze Zhou, and Pengpeng Huangfu gave some constructive suggestions on the numerical simulations. Dr. Bojing Zhu and Dunyu Liu polished the manuscript. The finite element modeling was carried out by the software PFELAC of version 2.2.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1245677/full#supplementary-material

References

Bai, Y., Xu, X.-W., Xu, J., and Zhou, B. (2012). The spatial distribution of displacement fields in 2008 Wenchuan earthquake. Prog. Geophys. (in Chinese) 27 (1), 29–31. doi:10.6038/j.issn.1004-2903.2012.01.004

CrossRef Full Text | Google Scholar

Bürgmann, R., and Dresen, G. (2008). Rheology of the lower crust and upper mantle: evidence from rock mechanics, geodesy and field observations. Annual Review of Earth and Planetary Sciences 36 (1), 531–567. doi:10.1146/annurev.earth.36.031207.124326

CrossRef Full Text | Google Scholar

Dong, Y., and Chen, C. (2009). Character of coesimic vertical displacement near Beichuan during Wenchuan MS 8.0 earthquake. Journal of Geodesy and Geodynamics (in Chinese) 29 (6), 28–31. doi:10.14075/j.jgg.2009.06.017

CrossRef Full Text | Google Scholar

Dong, Y., Luo, S., Han, Y., and Chen, C. (2012). Co- and post-seismic vertical displacements of Wenchuan M_S 8.0 earthquake near Beichuan. Acta Seismologica Sinica (in Chinese) 34 (5), 611–620. doi:10.3724/SP.J.1246.2011.00029

CrossRef Full Text | Google Scholar

Element Computing Technology Co. Ltd (2018b). Parallel architecture of FELAC (in Chinese), 8–14.

Google Scholar

Element Computing Technology Co., Ltd (2018a). Fundamentals and applications of finite element analysis of FELAC, 48–59. (in Chinese).

Google Scholar

Freed, A. M., and Lin, J. (2001). Delayed triggering of the 1999 Hector Mine earthquake by viscoelastic stress transfer. Nature 411, 180–183. doi:10.1038/35075548

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, X., Gao, R., Randy Keller, G., Xu, X., Wang, H., and Li, W. (2013). Imaging the crustal structure beneath the eastern Tibetan Plateau and implications for the uplift of the Longmen Shan range. Earth and Planetary Science Letters 379, 72–80. doi:10.1016/j.epsl.2013.08.005

CrossRef Full Text | Google Scholar

Hu, C. (2009). A new method to study earthquake triggering and continuous evolution of stress field. Beijing: Ph.D. Dissertation: Peking University.

Google Scholar

Hu, C., Cai, Y., and Wang, Z. (2012). Effects of large historical earthquakes, viscous relaxation, and tectonic loading on the 2008 Wenchuan earthquake. Journal of Geophysical Research Solid Earth 117 (B06410). doi:10.1029/2011jb009046

CrossRef Full Text | Google Scholar

Hu, C., Zhou, Y., Cai, Y., and Wang, C. (2009). Study of earthquake triggering in a heterogeneous crust using a new finite element model. Seismological Research Letters 80 (5), 799–807. doi:10.1785/gssrl.80.5.799

CrossRef Full Text | Google Scholar

Hu, Y., Bürgmann, R., Banerjee, P., Feng, L., Hill, E. M., Ito, T., et al. (2016). Asthenosphere rheology inferred from observations of the 2012 Indian Ocean earthquake. Nature 538, 368–372. doi:10.1038/nature19787

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, Y., and Wang, K. (2012). Spherical-earth finite element model of short-term postseismic deformation following the 2004 Sumatra earthquake. Journal of Geophysical Research Solid Earth 117 (B05404). doi:10.1029/2012jb009153

CrossRef Full Text | Google Scholar

Hu, Y., Wang, K., He, J., Klotz, J., and Khazaradze, G. (2004). Three-dimensional viscoelastic finite element model for postseismic deformation of the great 1960 Chile earthquake. Journal of Geophysical Research 109 (B12403). doi:10.1029/2004jb003163

CrossRef Full Text | Google Scholar

Huang, Y., Wu, J. P., Zhang, T. Z., and Zhang, D. N. (2008). Relocation of the M8.0 Wenchuan earthquake and its aftershock sequence. Science in China Series D Earth Sciences 51 (12), 1703–1711. doi:10.1007/s11430-008-0135-z

CrossRef Full Text | Google Scholar

Huang, Z., Su, W., Peng, Y., Zheng, Y., and Li, H. (2003). Rayleigh wave tomography of China and adjacent regions. Journal of Geophysical Research Solid Earth 108 (B2), 2073. doi:10.1029/2001jb001696

CrossRef Full Text | Google Scholar

Lei, J., and Zhao, D. (2009). Structural heterogeneity of the longmenshan fault zone and the mechanism of the 2008 wenchuan earthquake (M_S 8.0). Geochemistry, Geophysics, Geosystems 10, Q10010. doi:10.1029/2009gc002590

CrossRef Full Text | Google Scholar

Lei, J., and Zhao, D. (2016). Teleseismic p-wave tomography and mantle dynamics beneath Eastern Tibet. Geochemistry, Geophysics, Geosystems 17, 1861–1884. doi:10.1002/2016gc006262

CrossRef Full Text | Google Scholar

Li, F., and Huang, J. (2011). Numerical simulation of influences of medium heterogeneity and dip of fault on coseismic displacement. Journal of Geodesy and Geodynamics (in Chinese) 31 (5), 52–60. doi:10.3969/j.issn.1671-5942.2011.05.012

CrossRef Full Text | Google Scholar

Li, H., Fu, X., Woerd, J., Si, J., Wang, Z., Hou, L., et al. (2008). Co-seisimic surface rupture and dextra-slip oblique thrusting of the M_S 8.0 Wenchuan Earthquake. Acta Geologica Sinica (in Chinese) 82 (12), 1623–1643. doi:10.3321/j.issn:0001-5717.2008.12.002

CrossRef Full Text | Google Scholar

Liu, C., Dong, P., Zhu, B., and Shi, Y. (2018). Stress shadow on the southwest portion of the Longmen Shan Fault impacted the 2008 Wenchuan earthquake rupture. Journal of Geophysical Research Solid Earth 123, 9963–9981. doi:10.1029/2018jb015633

CrossRef Full Text | Google Scholar

Liu, C., Zhu, B.-J., Yang, X.-L., and Shi, Y.-L. (2015). Crustal rheology control on earthquake activity across the eastern margin of the Tibetan Plateau: insights from numerical modelling. Journal of Asian Earth Sciences 100, 20–30. doi:10.1016/j.jseaes.2015.01.001

CrossRef Full Text | Google Scholar

Liu, Q., Li, Y., Chen, J., Guo, B., Li, S., Wang, J., et al. (2009). Wenchuan M_S 8.0 earthquake: preliminary study of the S-wave velocity structure of the crust and upper mantle. Chinese Journal of Geophysics (in Chinese) 52 (2), 309–319. doi:10.6038/j.issn.0001-5733.2012.08.008

CrossRef Full Text | Google Scholar

Liu, X., Wu, J., Liang, C., Qian, Q., and Du, P. (2019). The latest seismicity characteristics and significance in Longmenshan Fault Zone. Chinese Journal of Geophysics (in Chinese) 62 (4), 1312–1322. doi:10.6038/cjg2019M0283

CrossRef Full Text | Google Scholar

Luo, G., and Liu, M. (2010). Stress evolution and fault interactions before and after the 2008 great Wenchuan earthquake. Tectonophysics 491, 127–140. doi:10.1016/j.tecto.2009.12.019

CrossRef Full Text | Google Scholar

Luo, G., and Liu, M. (2018). Stressing rates and seismicity on the major faults in eastern Tibetan Plateau. Journal of Geophysical Research Solid Earth 123 (10), 968–986. doi:10.1029/2018jb015532

CrossRef Full Text | Google Scholar

Massonnet, D., Rossi, M., Carmona, C., Adragna, F., Peltzer, G., Feigl, K., et al. (1993). The displacement field of the Landers earthquake mapped by radar interferometry. Nature 364, 138–142. doi:10.1038/364138a0

CrossRef Full Text | Google Scholar

Melosh, H. J., and Raefsky, A. (1981). A simple and efficient method for introducing faults into finite element computations. Bulletin of the Seismological Society of America 71 (5), 1391–1400. doi:10.1785/bssa0710051391

CrossRef Full Text | Google Scholar

Okada, Y. (1985). Surface deformation due to shear and tensile faults in a half-space. Bulletin of the Seismological Society of America 75 (4), 1135–1154. doi:10.1785/bssa0750041135

CrossRef Full Text | Google Scholar

Okada, Y. (1992). Internal deformation due to shear and tensile faults in a half-space. Bulletin of the Seismological Society of America 82 (2), 1018–1040. doi:10.1785/bssa0820021018

CrossRef Full Text | Google Scholar

Ozawa, S., Nishimura, T., Munekane, H., Suito, H., Kobayashi, T., Tobita, M., et al. (2012). Preceding, coseismic, and postseismic slips of the 2011 Tohoku earthquake, Japan. Journal of Geophysical Research Solid Earth 117, B07404. doi:10.1029/2011jb009120

CrossRef Full Text | Google Scholar

Shen, Z.-K., Sun, J., Zhang, P., Wan, Y., Wang, M., Bürgmann, R., et al. (2009). Slip Maxima at fault junctions and rupturing of barriers during the 2008 Wenchuan earthquake. Nature Geoscience 2, 718–724. doi:10.1038/ngeo636

CrossRef Full Text | Google Scholar

Sreejith, K. M., Sunil, P. S., Agrawal, R., Saji, A. P., Ramesh, D. S., and Rajawat, A. S. (2016). Coseismic and early postseismic deformation due to the 25 April 2015, M_W 7.8 Gorkha, Nepal, earthquake from InSAR and GPS measurements. Geophysical Research Letters 43, 3160–3168. doi:10.1002/2016gl067907

CrossRef Full Text | Google Scholar

Steketee, J. A. (1958). On Volterra's dislocations in a semi-infinite elastic medium. Canadian Journal of Physics 36, 192–205. doi:10.1139/p58-024

CrossRef Full Text | Google Scholar

Suito, H., and Freymueller, J. T. (2009). A viscoelastic and afterslip postseismic deformation model for the 1964 Alaska earthquake. Journal of Geophysical Research Solid Earth 114 (B11404). doi:10.1029/2008jb005954

CrossRef Full Text | Google Scholar

Sun, W., Okubo, S., Fu, G., and Araya, A. (2009). General formulations of global co-seismic deformations caused by an arbitrary dislocation in a spherically symmetric Earth model-applicable to deformed earth surface and space-fixed point. Geophysical Journal International 177, 817–833. doi:10.1111/j.1365-246x.2009.04113.x

CrossRef Full Text | Google Scholar

Sun, W., Okubo, S., and Vaníček, P. (1996). Global displacements caused by point dislocations in a realistic Earth model. Journal of Geophysical Research Solid Earth 101 (B4), 8561–8577. doi:10.1029/95jb03536

CrossRef Full Text | Google Scholar

Tan, H., Wu, G., Xuan, S., Yang, G., Fan, W., and Shen, C. (2015). Wenchuan M_S 8.0 earthquake coseismic slip distribution inversion. Geodesy and Geodynamics 6 (3), 173–179. doi:10.1016/j.geog.2015.05.001

CrossRef Full Text | Google Scholar

Toda, S., Lin, J., Meghraoui, M., and Stein, R. S. (2008). 12 May 2008 M = 7.9 Wenchuan, China, earthquake calculated to increase failure stress and seismicity rate on three major fault systems. Geophysical Research Letters 35 (L17305). doi:10.1029/2008gl034903

CrossRef Full Text | Google Scholar

Toda, S., Stein, R. S., Sevilgen, V., and Lin, J. (2011). Coulomb 3.3 graphic-rich deformation and stress-change software for earthquake, tectonic, and Volcano Research and teaching-user guide. Open-File Report. doi:10.3133/ofr20111060

CrossRef Full Text | Google Scholar

Tong, X., Sandwell, D. T., and Fialko, Y. (2010). Coseismic slip model of the 2008 Wenchuan earthquake derived from joint inversion of interferometric synthetic aperture radar, GPS, and field data. Journal of Geophysical Research 115, B04314. doi:10.1029/2009jb006625

CrossRef Full Text | Google Scholar

Tu, H.-W., Wang, R.-J., Diao, F.-Q., Zhang, Y., Wan, Y.-G., and Jin, M.-P. (2016). Slip model of the 2001 Kunlun mountain M_S 8.1 earthquake by SDM: joint inversion from GPS and InSAR Data. Chinese Journal of Geophysics (in Chinese) 59 (6), 404–413. doi:10.1002/cjg2.20245

CrossRef Full Text | Google Scholar

Wan, Y., Shen, Z.-K., Bürgmann, R., Sun, J., and Wang, M. (2017). Fault geometry and slip distribution of the 2008 M_W 7.9 Wenchuan, China earthquake, inferred from GPS and insar measurements. Geophysical Journal International 208, 748–766. doi:10.1093/gji/ggw421

CrossRef Full Text | Google Scholar

Wan, Y., Shen, Z.-K., W, M., Zhang, Z.-S., Gan, W.-J., Wang, Q.-L., et al. (2008). Coseismic slip distribution of the 2001 Kunlun mountain pass west earthquake constrained by GPS and InSAR data. Chinese Journal of Geophysics 51, 753–764. doi:10.1002/cjg2.1268

CrossRef Full Text | Google Scholar

Wang, M., Li, Q., Wang, F., Zhang, R., Wang, Y. Z., Shi, H. B., et al. (2011a). Far-field coseismic displacements associated with the 2011 Tohoku-Oki earthquake in Japan observed by Global Positioning System. Chinese Science Bulletin 56 (23), 2419–2424. doi:10.1007/s11434-011-4588-7

CrossRef Full Text | Google Scholar

Wang, M., Shen, Z. K., Wang, Y. Z., Bürgmann, R., Wang, F., Zhang, P. Z., et al. (2021). Postseismic deformation of the 2008 Wenchuan earthquake illuminates lithospheric rheological structure and dynamics of Eastern Tibet. Journal of Geophysical Research Solid Earth 126. doi:10.1029/2021jb022399

CrossRef Full Text | Google Scholar

Wang, Q., Qiao, X., Lan, Q., Freymueller, J., Yang, S., Xu, C., et al. (2011b). Rupture of deep faults in the 2008 Wenchuan earthquake and uplift of the Longmen Shan. Nature Geoscience 4, 634–640. doi:10.1038/ngeo1210

CrossRef Full Text | Google Scholar

Wang, Q., Cui, D., Zhang, X., Wang, W., and Liu, J. (2010). Studies on surface vertical deformation of the Longmenshan and the Wenchuan M_S 8.0 earthquake. Recent Developments in World Seismology (in Chinese) 6, 11–12. doi:10.3969/jissn.0235-4975.2010.06.010

CrossRef Full Text | Google Scholar

Wang, R., Martin, F. L., and Roth, F. (2003). Computation of deformation induced by earthquakes in a multi-layered elastic crust—fortran programs EDGRN/EDCMP. Computers and Geosciences 29, 195–207. doi:10.1016/s0098-3004(02)00111-5

CrossRef Full Text | Google Scholar

Wiseman, K., Bürgmann, R., Freed, A. M., and Banerjee, P. (2015). Viscoelastic relaxation in a heterogeneous earth following the 2004 sumatra–andaman earthquake. Earth and Planetary Science Letters 431, 308–317. doi:10.1016/j.epsl.2015.09.024

CrossRef Full Text | Google Scholar

Working Group of the Crustal Motion Observation Network of China Project (2008). Coseismic displacement field of the 2008 Ms 8.0 Wenchuan earthquake determined by GPS. Sci. China (Ser. D) (in Chinese) 38 (10), 1195–1206. doi:10.3321/j.issn:1006-9267.2008.10.003

CrossRef Full Text | Google Scholar

Xu, B., and Xu, C. (2015). Numerical simulation of influences of the Earth Medium’s lateral heterogeneity on co- and post-seismic deformation. Geodesy and Geodynamics 6 (1), 46–54. doi:10.1016/j.geog.2014.11.001

CrossRef Full Text | Google Scholar

Xu, C., Liu, Y., Wen, Y., and Wang, R. (2010). Coseismic slip distribution of the 2008 M_W 7.9 Wenchuan earthquake from joint inversion of GPS and InSAR Data. Bulletin of the Seismological Society of America 100, 2736–2749. doi:10.1785/0120090253

CrossRef Full Text | Google Scholar

Xu, M., Li, H., Song, Z., Xu, Q., Zhang, X., Fu, P., et al. (2022). An electric-thermal-solid physical fields coupling calculation based on FELAC platform, 2022. IEEE 5th International Conference on Electronics Technology, 532–536. doi:10.1109/ICET55676.2022.9825404

CrossRef Full Text | Google Scholar

Xu, X., Wen, X., Ye, J., Ma, B., Chen, J., Zhou, R., et al. (2008). The M_S 8.0 Wenchuan earthquake surface ruptures and seismogenic structure. Seismology and Geology (in Chinese) 30 (3), 597–629. doi:10.3969/j.issn.0253-4967.2008.03.003

CrossRef Full Text | Google Scholar

Zhang, B., Zhang, H., and Shi, Y. (2015). Equivalent-body force approach on modeling elastic dislocation problem using finite method. Chinese Journal of Geophysics (in Chinese) 58 (05), 1666–1674. doi:10.6038/cjg20150518

CrossRef Full Text | Google Scholar

Zhang, G., Qu, C., Shan, X., Song, X., Zhang, G., Wang, C., et al. (2011). Slip distribution of the 2008 Wenchuan M_S 7.9 earthquake by joint inversion from GPS and InSAR measurements: a resolution test study. Geophysical Journal International 186, 207–220. doi:10.1111/j.1365-246x.2011.05039.x

CrossRef Full Text | Google Scholar

Zhao, D., Qu, C., Shan, X., Bürgmann, R., Gong, W., and Zhang, G. (2018). Spatiotemporal evolution of postseismic deformation following the 2001 M_W 7.8 Kokoxili, China, earthquake from 7 years of Insar Observations. Remote Sensing 10, 1988. doi:10.3390/rs10121988

CrossRef Full Text | Google Scholar