Evolution of residual strain and strain energy in rocks under various types of uniaxial cyclic loading-unloading

In the process of roadway excavation, the rock mass around the roadway is often subjected to cyclic loads, and the rock mechanical properties and strain energy evolution under cyclic loads are obviously different from those under compression, so it is urgent to carry out research on rock mechanical properties and strain energy evolution under cyclic loads. This study aims to investigate the evolution of residual strain and strain energy in rocks under uniaxial cyclic loading-unloading experiments (UCLUE). Four types of rocks, namely coal, white sandstone, red sandstone, and granite, were subjected to uniaxial compression experiments (UCE) and various uniaxial cyclic loading-unloading experiments (UEACLUE). The findings are as follows: analysis of UEACLUE revealed a gradual decrease in residual strain with an increasing number of cycles, leading to its eventual disappearance. However, if the cyclic loading-unloading (CLU) was continued beyond this point, the rocks displayed a reappearance of residual strain. The number of cycles required to eliminate residual strain was found to be inversely proportional to the peak strength of the rocks, while directly proportional to the upper limit value of UCLUE. Among the different stages of the uniaxial cyclic loading and unloading test, the plastic stage of white sandstone exhibited the largest disparity in dissipated strain energy, followed by the plastic stage of red sandstone, with coal displaying the smallest difference. Analysis of dissipated strain energy in the four types of uniaxial cyclic loading and unloading tests revealed differences of 0.00348 mJ▪mm⁻³, 0.03488 mJ▪mm⁻³, 0.02763 mJ▪mm⁻³, and 0.01619 mJ▪mm⁻³ in the plastic stage for the respective rock types. Furthermore, examination of the input strain energy density (ISED) and dissipated strain energy density (DSED) during the CLU process showed a linear relationship between these variables. Additionally, the investigation of ISED and DSED in other types of UCLUE demonstrated adherence to the cyclic-linear dissipation law (CLDL). The study of mechanical properties and strain energy evolution under CLU is of positive significance for the development of rock fatigue damage and rock damage mechanics.

1 Introduction

The mechanical properties and evolution of strain energy in rock masses subjected to CLU present distinct characteristics in comparison to those under UCE (Yang et al., 2018; Arora et al., 2019; Stavropoulou et al., 2021). To achieve a comprehensive understanding of the failure mechanism and ensure the long-term stability of rock masses, it is crucial to investigate the mechanical properties and strain energy evolution specifically under CLU conditions. Extensive research conducted by various scholars has yielded substantial achievements in the study of mechanical properties under UCLUE. Liu et al. (2022) studied the mechanical properties of rock under triaxial multistage CLU, and the results showed that the elastic modulus, damping ratio, and damping coefficient of the sample generally reduced with the increase of the cycle. Liu et al. (2018) used random sinusoidal waves simplified from Wenchuan seismic waves to study the mechanical properties of rock mass with discontinuous joints. Ding et al. (2022) conducted UCLUE experiments on coal mass and found that the mechanical behavior of coal mass showed cyclic hysteresis under cyclic load, and the failure mode was more serious. Meng et al. (2021) conducted rock experiments under CLU, and the research results showed that the stress-strain curve of rock under CLU showed a hysteretic effect, and discussed the evolution law of strength, deformation characteristics, and expansion characteristics with the change of confining pressure. He et al. (2015) and He et al. (2017) used CLU experiments to analyze rock deformation and strain energy characteristics and studied rock damping ratio and damping coefficient under different conditions. In the research of rock damping under CLU, Liu et al. (2008) and Liu et al. (2010) studied the damping and damping coefficient of triaxial CLU experiment and proposed that these increase linearly with the increasing of cyclic load cycles. Zhang et al. (2011) found that the hysteresis ring was not a closed ring by analyzing the hysteresis ring in the conventional triaxial experiment of rocks, and redefined the calculation method of the hysteresis ring. Chang et al. (2019) conducted a study on the mechanical properties of rock-concrete subjected to cyclic loads. The results revealed the occurrence of three typical failure modes, namely, shear cracking, tensile cracking, and combined shear and wing cracking, in all specimens subjected to cyclic and static loads. Guo et al. (2022) performed impact dynamics tests on rock-concrete materials, providing a detailed analysis of failure modes, mechanical properties, and energy dissipation characteristics, thereby contributing to the existing research on the dynamics of rock-concrete materials. Ali et al. (2016) investigated the shear mechanism of rock joints under pre-peak cyclic load and identified two categories of influences: shrinkage and degeneration. Momeni et al. (2015) examined the effect of cyclic loads on the mechanical properties of granite and observed that fatigue damage analysis under different load levels indicated crack nucleation during a significant portion of the fatigue life span, with crack growth occurring under higher stress levels. Manoj and Petroš (2009) found that the microstructure of rock specimens has an impact on the fatigue characteristics of rock under dynamic cyclic loads. Yoshinaka et al. (1997) investigated the change in pore pressure and related failure modes through triaxial cyclic load tests on soft rock. Some scholars have studied the mechanical properties of rocks under unilateral unloading under true triaxial compression and analyzed their failure forms (Liu et al., 2020a; Liu et al., 2023).

The study of strain energy evolution in rocks is a prominent topic in rock mechanics, garnering significant attention from scholars both domestically and internationally, resulting in extensive research and fruitful outcomes (Xie et al., 2005; Xie et al., 2008). Investigations into the strain energy evolution of rocks primarily focus on understanding the laws governing strain energy under UCE, conventional triaxial loading, impact loads, and the distribution of strain energy throughout the loading process (Justo et al., 2018; Rashidi Moghaddam et al., 2018). ZHANG and GAO (2012a), ZHANG and GAO (2012b), and ZHANG and GAO (2015) analyzed the strain energy of red sandstone by examining the elastic strain energy at each unloading point. They further explored nonlinear theories of rock behavior. Meng et al. (2015) utilized strain energy calculation formulas to study the dissipation and accumulation of strain energy in rocks, considering factors such as size effect and loading rate. They obtained strain energy data from rock UCE experiments conducted with various sizes and loading rates. Building upon the study of strain energy evolution under UCE, Gong et al. (2018), Gong et al. (2019a), and Gong et al. (2019b) conducted uniaxial loading-unloading experiments to investigate strain energy accumulation and dissipation throughout the entire loading process. They proposed linear rules governing strain energy storage and dissipation, contributing to the theoretical understanding of rock strain energy evolution. Additionally, they improved the calculation formula for the peak strain energy impact index and established a rockburst tendency criterion based on the residual elastic strain energy index (the difference between pre-peak elastic strain energy density and post-peak failure strain energy density). Through an examination of the elastic properties of rocks in UCLUE, Liu et al. (2020b) observed that the elastic strain energy of rocks remained constant. Furthermore, Liu et al. (2021) postulated that the load at each unloading point in uniaxial fractional loading-unloading experiments was equal to that in UCE. They then proposed a method for analyzing the strain energy law in UCE.

The existing studies primarily focus on the damping characteristics and strain energy evolution of rocks under UCLUE. However, there is a relative dearth of research on the residual strain of rock mass and its internal relationship with different forms of energy. Investigating the internal relationship between residual strain and strain energy during UCLUE is crucial for effectively preventing and predicting rock fatigue damage and dynamic disasters. Therefore, it is imperative to conduct investigations to explore the correlation between the residual strain of rock masses and strain energy under UCLUE.

2 UCLUE method and curve analysis

2.1 UCE curve analysis

The experimental study involved four materials: coal, white sandstone, red sandstone, and granite. Both UCLUE and UCE were conducted using the RMT-150B rock mechanics test system.

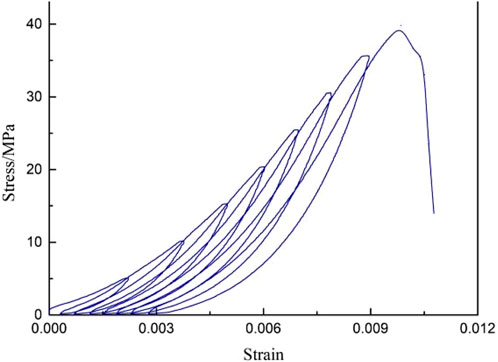
In accordance with internationally recognized standards in rock mechanics, standard rock specimens were prepared using cutting and polishing techniques. These procedures were performed to meet the specified dimensional requirements for precise and dependable testing. Figure 1 provides a visual representation of the specimens. The uniaxial compressive strength values for coal, white sandstone, red sandstone, and granite are 10.24, 39.40, 60.94, and 80.71 MPa, respectively. Additionally, the elastic moduli for the four rocks are 5.01, 9.72, 10.22, and 19.21 GPa, respectively. The corresponding peak strains for each rock are 0.05930, 0.01038, 0.00773, and 0.00915, respectively. Figure 2 illustrates the stress-strain curves of the investigated rocks, showcasing the correlation between applied stress and resulting strain for each rock type. These curves enable the visualization of the different stages experienced during the loading process. Specifically, the stress-strain curve can be divided into three distinct stages based on the rate of stress-strain growth: compaction, elastic, and plastic stages. During the compaction stage, the strain growth rate increases in relation to the applied stress. The elastic stage is characterized by a linear stress-strain relationship. Finally, in the plastic stage, the strain growth rate gradually diminishes as the stress increases.

FIGURE 1

FIGURE 1. Four rock samples. (A) Coal sample. (B) White sandstone sample. (C) Red sandstone sample. (D) Granite sample.

FIGURE 2

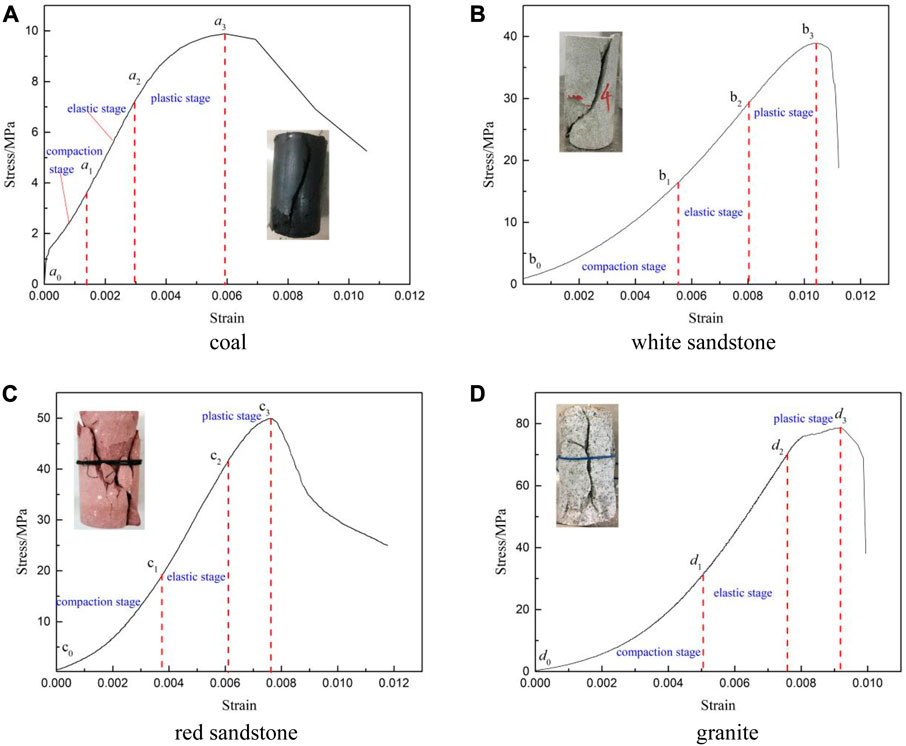
FIGURE 2. Uniaxial compression curve of rock. (A) Coal. (B) White sandstone. (C) Red sandstone. (D) Granite.

2.2 Analysis of UEACLUE curve

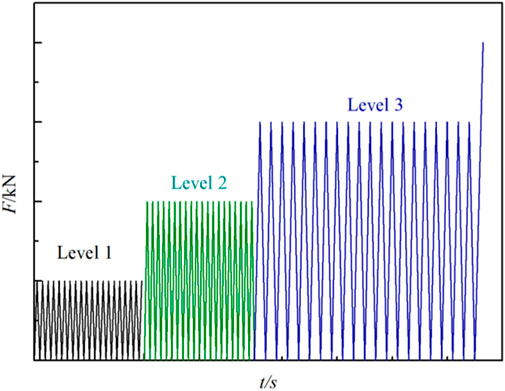
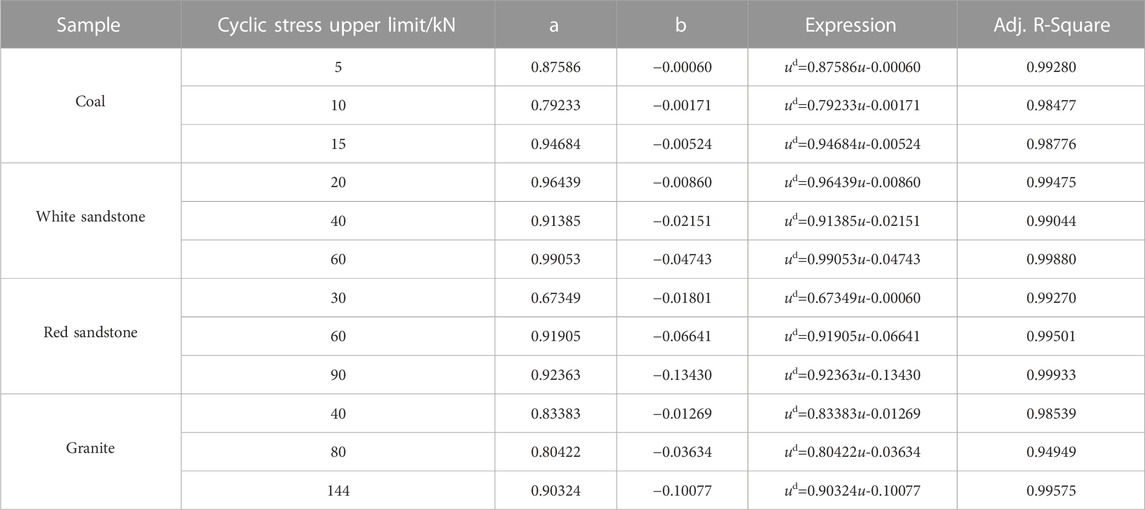
In order to facilitate the analysis of residual strain in the UEACLUE experiments for different rock specimens, it is assumed that the upper stress limits for each type of rock are within the load range corresponding to the compaction stage, elastic stage, and plastic stage. The lower stress limits are set to 0. The upper limits for coal in the uniaxial cyclic loading and unloading tests are 5, 10, and 15 kN, respectively. For sandstone, the upper limits are 20, 40, and 60 kN, respectively. Red sandstone has upper limits of 30, 60, and 90 kN in the single-axis cyclic loading and unloading tests. As for granite, the upper limits are 40, 80, and 144 kN, respectively. The loading rate for the experiments is set at 0.5 kN/s, and a total of 20 cycles are conducted. Following the completion of the cyclic loading and unloading process, the specimens are not subjected to any further experiment.

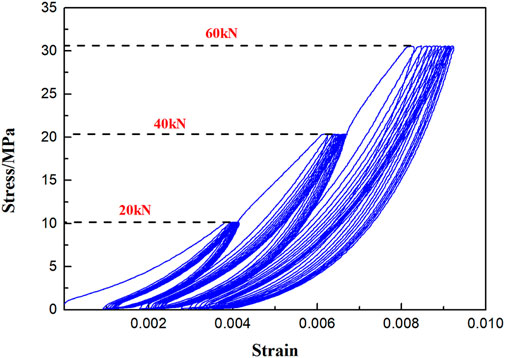
From the visual representation presented in Figure 3, it is evident that the loading stress-strain path of sandstone under cyclic load is different from the unloading stress-strain. In particular, the nonlinearity of the unloading curve indicates that the rock has the hysteretic effect, and the initial loading-unloading will produce large residual strain. The residual strains has produced by the first loading-unloading of coal are 7 × 10⁻⁵, 4.89 × 10⁻⁴, and 6.36 × 10⁻⁴, respectively. The residual strains produced by the first loading-unloading of white sandstone are 9.3 × 10⁻⁴, 1.77 × 10⁻³, and 2.3 × 10⁻³, respectively. The residual strains produced by the first loading-unloading of red sandstone are 1.1 × 10⁻³, 2.02 × 10⁻³, and 2.63 × 10⁻³, respectively. The residual strains produced by the first loading-unloading of granite are 3.1 × 10⁻⁴, 4.11 × 10⁻⁴, and 4.8 × 10⁻⁴, respectively. The residual strain of the four rock types exhibits a positive correlation with the upper limit of the applied uniaxial cyclic loading and unloading stress. This correlation demonstrates that cracks can develop in the rock during the elastic stage, while the subsequent propagation of cracks remains stable. Notably, high-strength rocks exhibit relatively lower levels of residual strain during the initial loading and unloading processes.

FIGURE 3

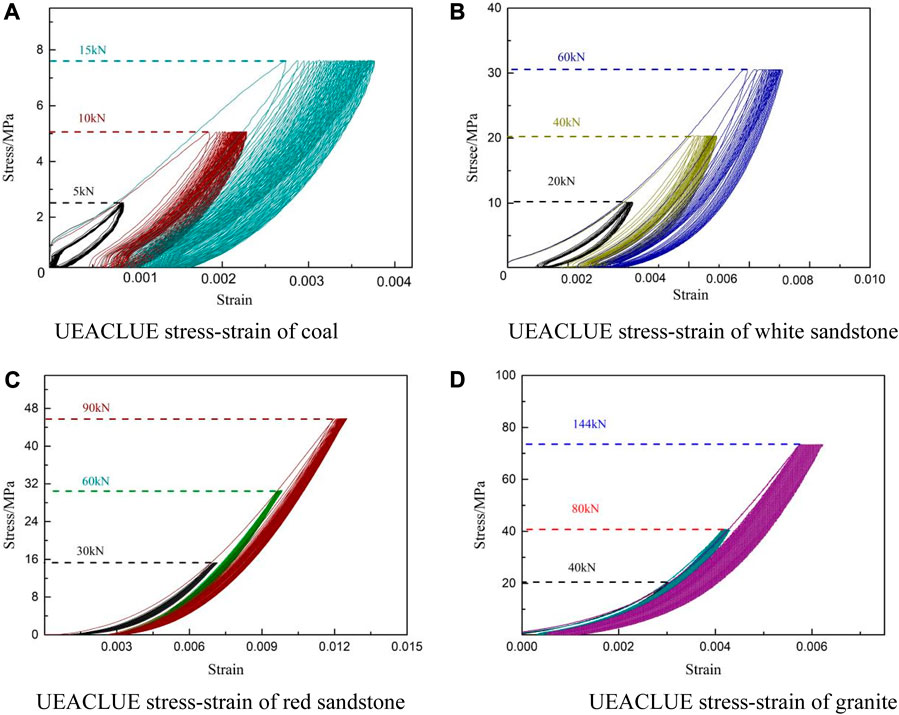
FIGURE 3. UEACLUE stress-strain of four rock. (A) UEACLUE stress-strain of coal. (B) UEACLUE stress-strain of white sandstone. (C) UEACLUE stress-strain of red sandstone. (D) UEACLUE stress-strain of granite.

3 The evolution law of rock residual strain

3.1 Uniaxial cyclic loading-unloading experiment

Figure 4 illustrates the gradual reduction in residual strain observed for the four rock types as the cycle number increases during the experiment. Eventually, a point is reached where a non-residual strain phenomenon is observed.

FIGURE 4

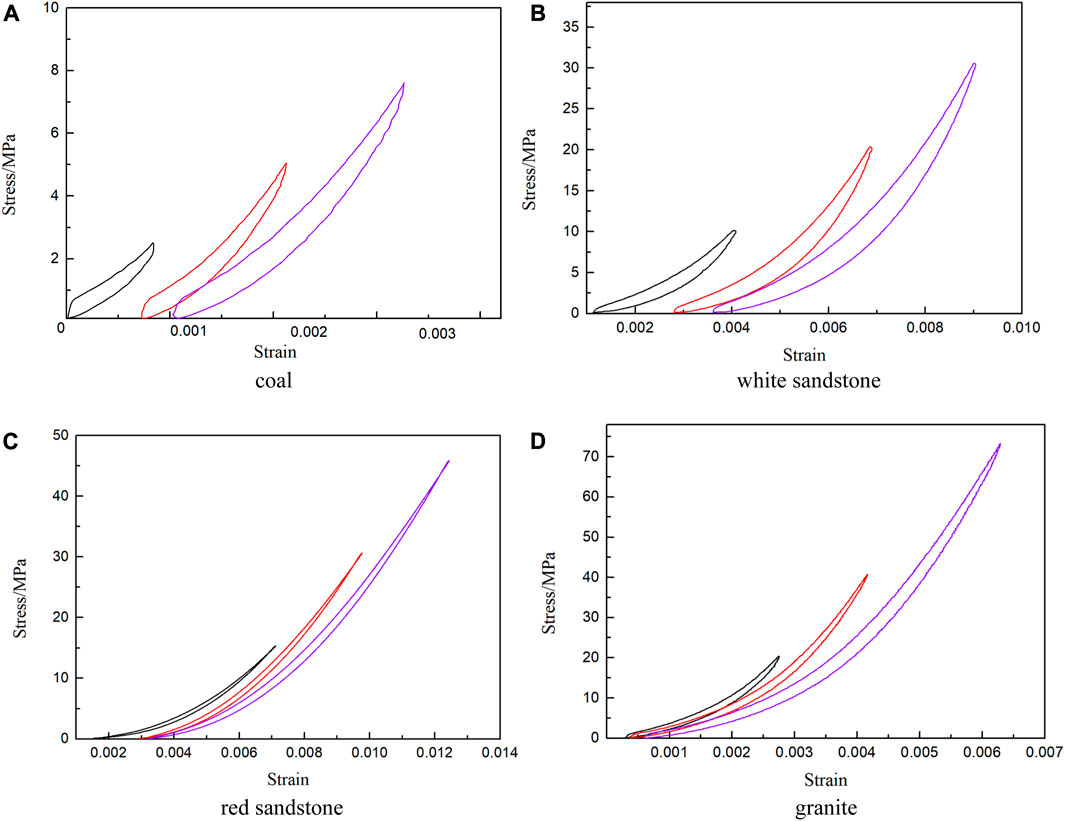
FIGURE 4. Non-residual strain of the four rocks. (A) Coal. (B) White sandstone. (C) Red sandstone. (D) Granite.

The UEACLUE yielded distinct stress limits at which non-residual strain phenomena all will occurred for different rock types. Specifically, the coal sample exhibited non-residual strain at the 8th, 14th, and 15th cycles in the compaction, elastic, and plastic stages, respectively. Likewise, white sandstone demonstrated non-residual strain at the 7th, 12th, and 14th cycles in the compaction, elastic, and plastic stages, respectively. Similarly, for red sandstone, the stress limit was observed at the 6th, 10th, and 10th cycles in the compaction, elastic, and plastic stages, respectively. Finally, granite displayed non-residual strain at the 5th, 7th, and 8th cycles in the compaction, elastic, and plastic stages, respectively.

During the experimental procedure, the residual strain of the rocks exhibited a gradual decrease until reaching a state of non-residual strain. However, if the loading-unloading process was continued beyond this point, the residual strain reappeared. The occurrence of the non-residual strain phenomenon was found to be directly related to the applied stress, showing a proportional relationship. Among the four types of rocks investigated in this study, it was observed that higher-strength rocks experienced fewer occurrences of the non-residual strain phenomenon during the UEACLUE experiments.

3.2 Uniaxial variable upper cyclic loading limit experiment

To further investigate the non-residual strain phenomenon in sandstone under UEACLUE, a series of uniaxial variable upper cyclic loading limit experiments were conducted. The experiments consisted of three grades, each consisting of 20 cycles, with the upper limit values of CLU set at 20, 40, and 60 kN, respectively. The experiments followed a lower limit of 0 and a loading rate of 0.5 kN/s. At the end of each cycle, the sample was compressed until failure. Figure 5 illustrates the stress paths observed during the experiments.

FIGURE 5

FIGURE 5. Uniaxial variable upper cyclic loading limit experiment stress paths.

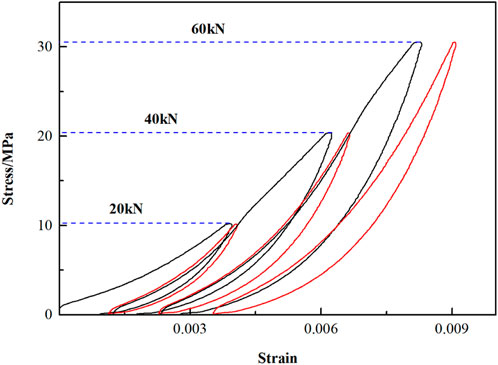
Figures 6, 7 show the curve of stress-strain and non-residual strain in the uniaxial equal amplitude cyclic loading experiment. In the uniaxial equal amplitude cyclic loading experiment of sandstone, the residual strains produced in the first cycle of the first stage, second stage and third stage are 1.34 × 10⁻³, 0.55 × 10⁻³, and 0.44 × 10⁻³, respectively. After the non-residual strain phenomenon of rock appears in the first stage of CLU, residual strain will appear again if the loading-unloading experiment has continued. The second stage and third stage cycles have the same evolution law, indicating that after the occurrence of non-residual strain phenomenon, if the upper limit of CLU stress has increased, residual strain phenomenon will appear again. To sum up, in the UCLUE, after the non-residual strain phenomenon of rock appears, increasing the upper limit value of UCLUE stress and continue to carrying out CLU, the rock will appear non-residual strain again.

FIGURE 6

FIGURE 6. Uniaxial equal amplitude cyclic loading experiment.

FIGURE 7

FIGURE 7. Non-residual strain.

4 Rock strain energy evolution

4.1 Strain energy calculation method

Based on the principles of thermodynamics, it is observed that when the rock is subjected to loading, a certain amount of strain energy is stored within the rock and can be reversed under specific conditions. This stored energy is referred to as elastic strain energy. However, during the loading process, another portion of the strain energy is dissipated and cannot be reversed. This dissipated energy is known as dissipative strain energy.

The relationship is as follows (Meng et al., 2015):

$\mathit{u}={\mathit{u}}^{\mathit{d}}+{\mathit{u}}^{\mathit{e}}$

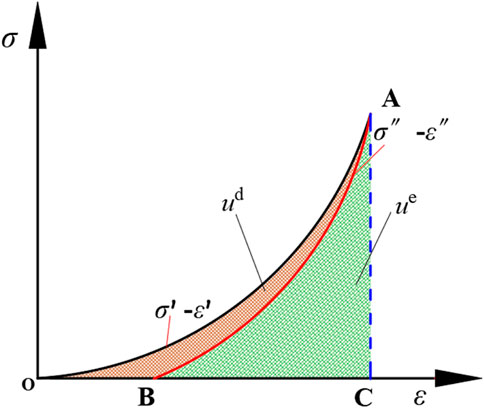
Where u is the total strain energy density generated by the work of external load on the rock specimen; u^e is the elastic strain energy density stored in the rock; u^d is the DSED. The distribution has shown in the Figure 8.

FIGURE 8

FIGURE 8. Schematic diagram of strain energy.

As shown in Figure 8, the area under the unloading curve represents the elastic strain energy u^e, and the area enclosed by the loading curve, unloading curve, and horizontal coordinate represents the dissipated strain energy u^d of the rock.

${\mathit{u}}^{\mathit{d}}={\displaystyle \underset{\mathbf{0}}{\overset{\mathit{\epsilon }}{\int }}}{\mathit{\sigma }}^{\prime }\mathit{d}{\mathit{\epsilon }}^{\prime }-{\displaystyle \underset{{\mathit{\epsilon }}^{″}}{\overset{\mathit{\epsilon }}{\int }}}{\mathit{\sigma }}_{\mathbf{1}}^{″}\mathit{d}{\mathit{\epsilon }}_{\mathbf{1}}^{″}$

${\mathit{u}}^{\mathit{e}}={\displaystyle \underset{{\mathit{\epsilon }}^{″}}{\overset{\mathit{\epsilon }}{\int }}}{\mathit{\sigma }}_{\mathbf{1}}^{″}\mathit{d}{\mathit{\epsilon }}_{\mathbf{1}}^{″}$

Where ε is axial strain; σ' and ε' represent loading stress and strain. σ" and ε" represent unloading stress and strain. Figure 8 shows the stress-strain curve of rock under axial load σ₁. The total ISED of the experimenting machine is u, the DSED is u^d, and the elastic strain energy density is u^e.

4.2 Strain energy dissipation evolution under cyclic load

Using the strain energy analysis method, the stress-strain curve obtained from the UCLUE is integrated.

As depicted in Figure 9. In the UEACLUE, the DSED of rock decreases non-linearly as the number of cycles increases, the strain energy dissipation increasing when the number of cycles is the same with the increase of the upper limit value of UCLUE. The DSED produced by the first loading-unloading of rock is much greater than that produced by the subsequent loading-unloading. Previous studies have suggested that a strong correlation between DSED and the generation of damage in rocks. By understanding the evolution law of DSED, it is possible to establish a theoretical foundation for more precise assessments of rock fatigue damage. By comparing the dissipative energy generated by uniaxial cyclic loading and unloading of four kinds of rocks, it can be seen that in the plastic stage, the dissipative strain energy-cycle curve of coal evolves in an approximate horizontal direction with the increase of cycle times after the 7th cycle, while the dissipative strain energy curve of sandstone fluctuates to a certain extent with the increase of cycle times. The dissipative strain energy of granite and red sandstone in plastic stage decreases linearly with the increase of cycle times. The dissipative strain energy of the four kinds of rocks in the compaction stage, elastic stage and plastic stage is inversely proportional to the peak strength. In the cycle process of the compaction stage, the dissipative strain energy density of coal, red sandstone and white sandstone fluctuates little, while that of granite fluctuates greatly. In the comparison of dissipative strain energy of the four rocks, it can be found that the dissipative strain energy of the white sandstone in the elastic stage has little difference with that of the plastic stage, which indicates that the dissipative strain energy of the sandstone in the elastic stage is relatively large, while the dissipative strain energy of the other three rocks increases significantly from the elastic stage to the plastic stage. In the uniaxial cyclic loading and unloading test of coal, the maximum difference of dissipated strain energy density generated by each cyclic loading and unloading is 0.00348 mJ·mm⁻³. In the uniaxial cyclic loading and unloading test of white sandstone, the maximum difference of dissipated strain energy density produced by each cyclic loading and unloading is 0.03488 mJ·mm⁻³. In the uniaxial cyclic loading and unloading test of red sandstone, the maximum difference of dissipated strain energy density produced by each cyclic loading and unloading is 0.02763 mJ·mm⁻³. In the uniaxial cyclic loading and unloading test of granite, the maximum difference of dissipated strain energy density produced by each cycle loading and unloading is 0.01619 mJ·mm⁻³.

FIGURE 9

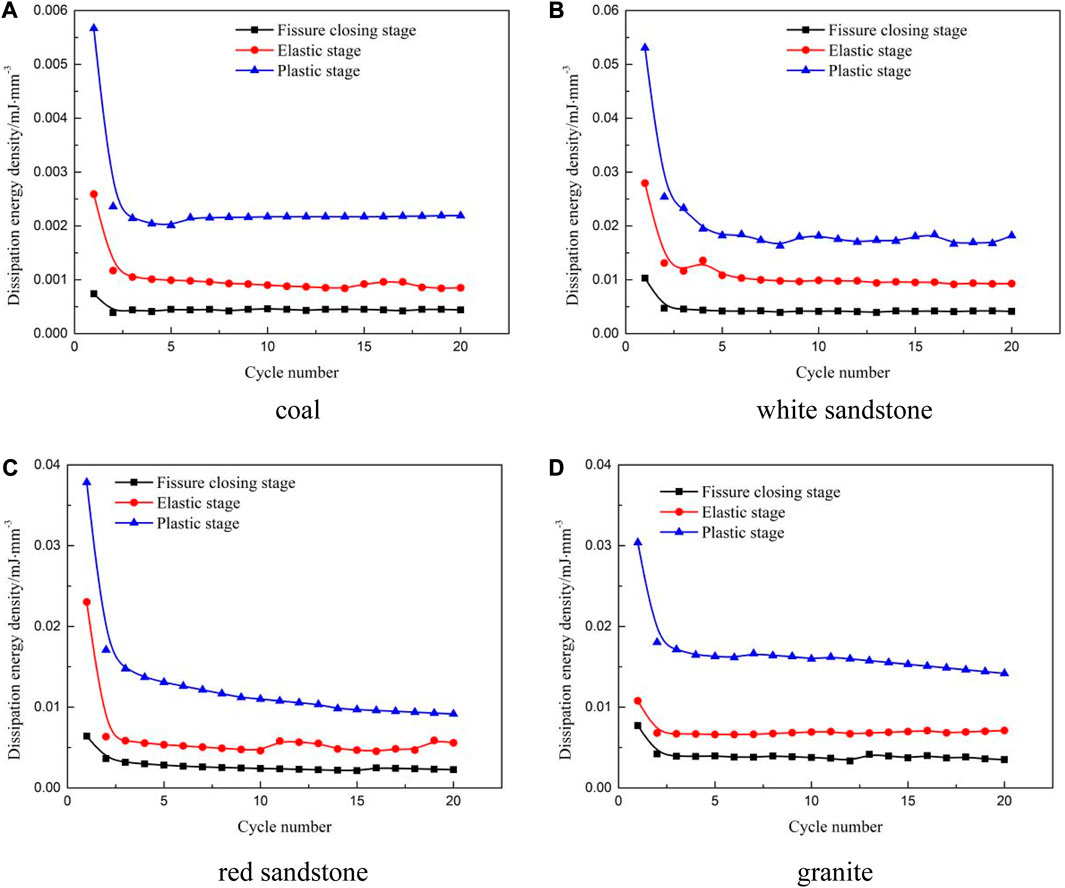
FIGURE 9. Curves of rock strain energy dissipation and cycle numbers under UEACLUE. (A) Coal. (B) White sandstone. (C) Red sandstone. (D) Granite.

4.3 Cyclic-linear dissipation law (CLDL)

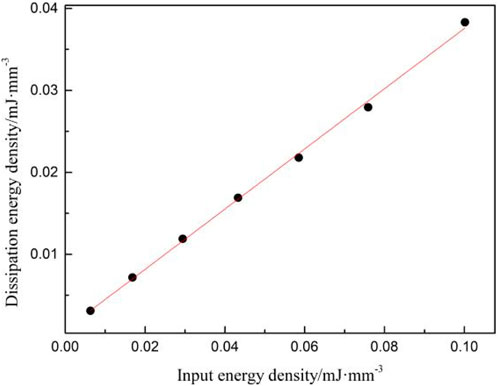
Through a comprehensive investigation of the quantitative relationship between DSED and ISED, a linear functional relationship between the two has been established. This finding confirms the existence of a CLDL in rocks.

${\mathit{u}}^{\mathit{d}}=\mathit{a}\mathit{u}+\mathit{b}$

Where ɑ and b represent the fitting parameters in the linear functional relationship between DSED and ISED. The fitting results for white sandstone are exemplified and illustrated in Figure 10.

FIGURE 10

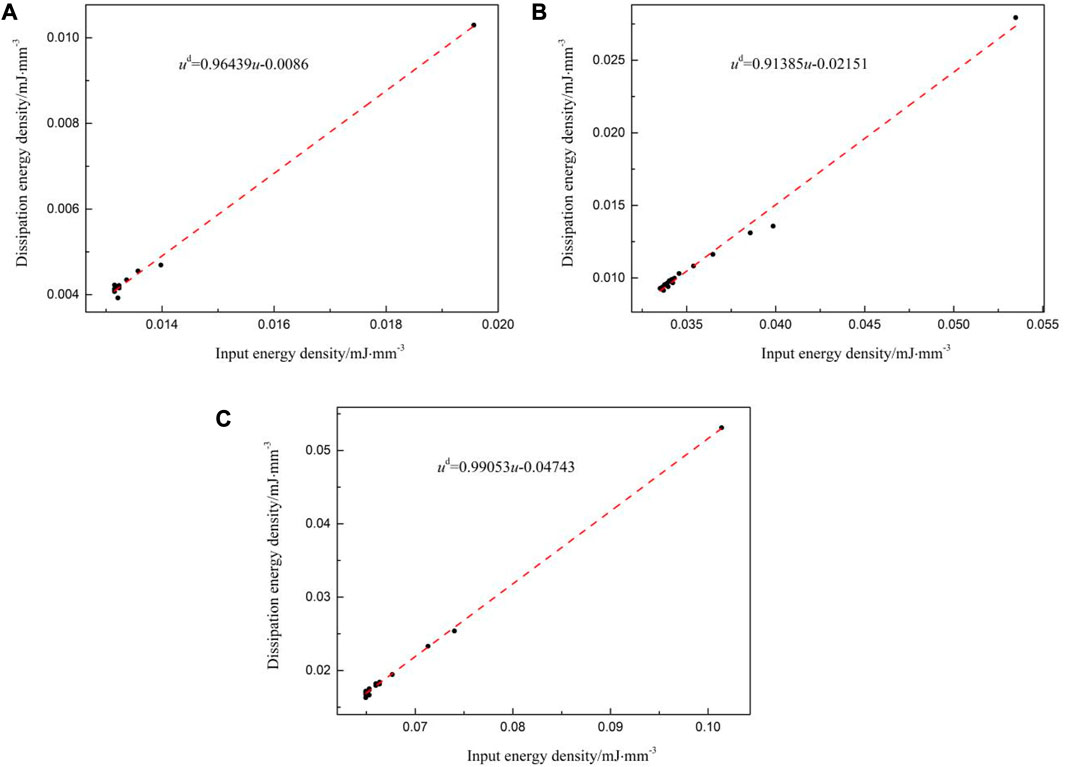
FIGURE 10. (A) is the fitting result of the compaction stage, (B) is the fitting result of the elastic stage, and (C) is the fitting result of the plastic stage.

Figure 10 presents the fitting results for white sandstone as an example. Based on Table 1 and Figure 10, the input strain energy and dissipated strain energy of the four types of rocks were fitted during the experiment. The fitting correction coefficients for all four types of rocks are above 0.98, indicating a good fitting effect. It indicates that there is a linear functional relationship between the input strain energy and dissipated strain energy of rocks under UEACLUE, which is independent of the load level of CLU. Based on the cyclic - linear dissipation law, it is evident that the evolution trend of dissipation strain energy is consistent with that of input strain energy during experiment.

TABLE 1

TABLE 1. Fitting results of CLDL.

5 Application range of CLDL

5.1 Uniaxial variable upper and lower cyclic loading limit experiment

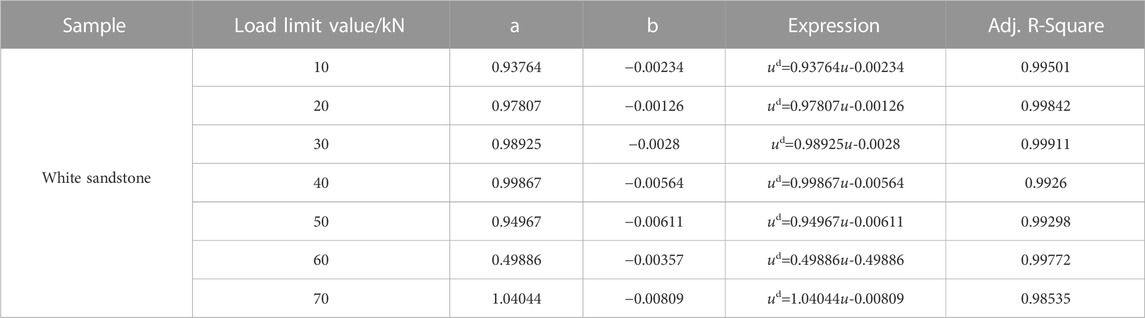
To validate the aforementioned hypothesis, a uniaxial variable upper and lower with constant amplitude (UVULCLUE) experiment was conducted using the RMT-150B apparatus. The experiment consisted of multiple stages, with each stage characterized by different upper and lower limits of cyclic loading. In the first stage, the upper limit was set at 10 kN, while the lower limit was 0. After completing 20 cycles in the first stage, the experiment progressed to the second stage, where the upper limit was increased to 20 kN, while the lower limit remained the same as the previous stage’s upper limit. The difference between the upper limit values of cyclic loading and unloading stress of adjacent grades is 10 kN. “Stress path of UVULCLUE” as shown in Figure 11A.

FIGURE 11

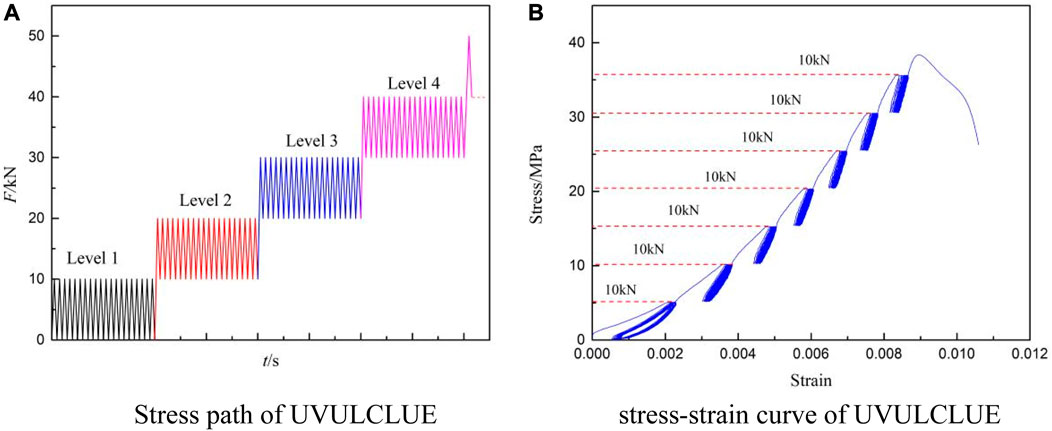
FIGURE 11. Uniaxial variable upper and lower cyclic loading limit experiment. (A) Stress path of UVULCLUE. (B) Stress-strain curve of UVULCLUE.

As shown in Figure 11B. In the UVULCLUE, the residual strain of 0.55 × 10⁻³ is generated by the initial loading-unloading in the first stage cycle, which is larger than that generated by other cycles in the first stage cycle, indicating that the initial loading-unloading is caused by the compaction of the internal defects in the sandstone, resulting in a more residual strain than that in other cycles. The residual strain of the rocks from Grade 2 to Grade 7 under initial loading are 2.18 × 10⁻³, 0.99 × 10⁻³, 0.55 × 10⁻³, 0.73 × 10⁻³, 0.38 × 10⁻³, and 0.35 × 10⁻³, respectively.

The strain energy evolution law of UVULCLUE has shown in Table 2. The strain energy calculated at the beginning of the second stage of the UVULCLUE is the strain energy density within the load range of the second level cycle. In other words, the ISED, DSED, and elastic strain energy density of the second level cycle is the strain energy density under 10–20 kN, rather than the strain energy density of the rock under 20 kN.

TABLE 2

TABLE 2. Fitting results.

The quantitative relationship between the DSED and the total ISED was investigated respectively in the UVULCLUE, and it was found that there was also a linear functional relationship between them. It shows that the CLDL not only applies to UEACLUE, but also applies to other types of CLU experiments, which introduces a novel perspective on the evolution of strain energy in rock during loading-unloading.

5.2 Uniaxial stage loading-unloading experiment

Uniaxial stage loading-unloading adopts the loading-unloading method of increasing load. The loading stage of the experiment is 10 kN, that is, 0→10→0→20→0→30 kN. The uniaxial stage loading-unloading curve as depicted in Figure 12.

FIGURE 12

FIGURE 12. Uniaxial stage loading-unloading curve.

The phenomenon of “hardening” in rock specimens under loading-unloading, where the peak load exceeds the uniaxial compressive strength, has been observed consistently in previous studies. For instance, Zuo et al. (2011) investigated the cyclic load behavior of coal and rock mass, while You and Su (2008) studied marble specimens. Building upon the findings of these researchers, it is believed that the “hardening” phenomenon is attributed to the presence of cracks within the rock specimens. Local contact stress between these cracks is significantly higher than the stress induced by axial compression loading. As a result, the specimens exhibit substantial strain and even localized failure under axial load. Debris formed during the loading-unloading process may detach and fill adjacent cracks, thereby increasing friction and enhancing the bearing capacity of the rock. It is important to note that “hardening” should not be confused with an increase in overall strength, which encompasses tensile, compressive, shear, and torsional resistance. Instead, “hardening” primarily refers to the augmentation of friction and bearing capacity.

As shown in Figure 13. The relationship between the ISED and the DSED with the increase of the unloading level in uniaxial stage loading-unloading is analyzed. And a linear functional relationship between the DSED and the ISED is obtained. When the input strain energy increases, the strain energy dissipating also increases in the same proportion. Meng et al. (2015) believed that the strain and failure of rock is a process of the generation, expansion, connection, penetration, and sliding of micro-cracks within the rock. Strain energy needs to be absorbed to generate new fractured surfaces, while the sliding friction between fractured surfaces dissipates strain energy. In other words, the strain energy density absorbed by rocks is a linear function of the sliding friction strain energy density between fractured surfaces. To sum up, the CLDL applies to various loading-unloading methods in this manuscript and is able to better reflect the strain energy evolution law during the loading-unloading process of rocks.

FIGURE 13

FIGURE 13. Linear energy storage law.

6 Discussion

Based on the hypothesis proposed regarding the “hardening” phenomenon in rock specimens, several important implications can be derived. Firstly, it is crucial to consider the presence and behavior of cracks in rock specimens when studying their mechanical response under loading-unloading conditions. The high local contact stress between cracks highlights the significance of crack initiation, propagation, and interaction in determining the overall deformation and failure characteristics of the rock.

Secondly, the formation of debris and its subsequent filling between cracks should be taken into account. The accumulation of debris can enhance the frictional contact between cracks, leading to an increase in the bearing capacity of the rock. This phenomenon implies that the mechanical behavior of rocks is not solely governed by the intrinsic properties of the rock material, but also influenced by the interactions and interplay between cracks and debris.

Furthermore, the “hardening” phenomenon challenges the conventional understanding that loading and unloading inherently result in damage to rock mass. Instead, it suggests that under certain conditions, cyclic loading and unloading can actually contribute to the strengthening of rock specimens. This finding underscores the need for a more comprehensive and nuanced understanding of the fatigue and damage processes in rocks, considering the complex interrelationships among stress, deformation, crack evolution, and debris behavior.

Overall, this hypothesis provides a framework for further investigations into the underlying mechanisms of the “hardening” phenomenon and opens up avenues for exploring innovative approaches to enhance the mechanical properties and stability of rock materials.

7 Conclusion

By analyzing the mechanical characteristics and strain energy evolution in UCLUE, we have identified the evolution law of residual strain in rock mass under loading-unloading conditions. Furthermore, through the analysis of strain energy evolution, we have discovered the CLDL. To validate the applicability of the CLDL, we have conducted studies using two additional loading-unloading schemes. The results obtained from these studies are as follows:

(1) In the process of UEACLUE, the residual strain of rock gradually decreases until non-residual strain occurs. If the loading-unloading continues, the residual strain will appear again. In the process of UEACLUE, the occurrence times of non-residual strain phenomenon is proportional to the upper limit value of UEACLUE. Among the four kinds of rocks in this paper, the higher the strength of the rocks, the fewer the occurrence cyclic numbers of non-residual strain phenomenon in the UEACLUE.

(2) In the UCLUE, after the non-residual strain phenomenon of rock occurs, increasing the upper limit value of UCLUE stress and continuing to carry out CLU, the non-residual strain phenomenon of rock will appear again.

(3) The presence of cracks in rock specimens leads to high local contact stress between the cracks, exceeding the stress under axial compression loading. This results in significant strain and even local failure phenomena in the specimens under axial load, with the formation of debris that can fall off and fill nearby cracks. The debris filling between the cracks enhances friction and increases the load-bearing capacity of the rock.

(4) In terms of the different stages of uniaxial cyclic loading and unloading tests, the largest dissipated strain energy difference was observed in the plastic stage of white sandstone, followed by the plastic stage of red sandstone, and the smallest in the plastic stage of coal. By analyzing the dissipated strain energy from four types of uniaxial cyclic loading and unloading tests, it was observed that the dissipated strain energy differences within the same group varied as follows: 0.00348, 0.03488, 0.02763, and 0.01619 mJ·mm⁻³.

(5) By analyzing the dissipated strain energy and input strain energy in uniaxial cyclic loading and unloading test, there is a linear relationship between ISED and DSED of CLU. The applicability of the CLDL has been verified by other loading-unloading experiment schemes. A new law of rock strain energy evolution in UCLUE is found.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

ZL: Conceptualization, methodology, data curation, and writing-original draft preparation. XL: Data curation, writing-reviewing and editing, supervision. All authors contributed to the article and approved the submitted version.

Funding

This study was funded by a grant from the Anhui University Graduate Scientific Research Project (No. YJS20210387).

Acknowledgments

The authors are very grateful to the reviewers for carefully reading the manuscript and providing valuable suggestions. Thanks to Dr. Matloob Sundas for the revision and polish of the language of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

UCLUE, uniaxial cyclic loading-unloading experiment; UCE, uniaxial compression experiment; UEACLUE, uniaxial equal amplitude cyclic loading-unloading experiments; CLU, cyclic loading-unloading; ISED, input strain energy density; DSED, dissipated strain energy density; CLU, cyclic loading-unloading; ULUE, uniaxial loading-unloading experiment; CLDL, cyclic-linear dissipation law; UVULCLUE, uniaxial variable upper and lower with constant amplitude.

References

Ali, F., Moradian, Z., Rivard, P., and Ballivy, G. (2016). Shear mechanism of rock joints under pre-peak cyclic loading condition. Int. J. Rock Mech. Min. Sci. 83, 197–210. doi:10.1016/j.ijrmms.2016.01.009

CrossRef Full Text | Google Scholar

Arora, K., Chakraborty, T., and Rao, K. S. (2019). Experimental study on stiffness degradation of rock under uniaxial cyclic sinusoidal compression loading. Rock Mech. Rock Eng. 52, 4785–4797. doi:10.1007/s00603-019-01835-3

CrossRef Full Text | Google Scholar

Chang, X., Guo, T., Lu, J., and Wang, H. (2019). Experimental study on rock-concrete joints under cyclically diametrical compression. Geomechanics Eng. 17 (6), 553–564. doi:10.12989/gae.2019.17.6.553

CrossRef Full Text | Google Scholar

Ding, Z. W., Jia, J. D., Tang, Q. B., and Li, X. F. (2022). Mechanical properties and energy damage evolution characteristics of coal under cyclic loading and unloading. Rock Mech. Rock Eng. 55, 4765–4781. doi:10.1007/s00603-022-02884-x

CrossRef Full Text | Google Scholar

Gong, F., Yan, J., and Li, X. (2018). A new criterion of rock burst proneness based on the linear energy storage law and the residual elastic energy index. Chin. J. Rock Mech. Eng. 37, 1993–2014. (in Chinese). doi:10.13722/j.cnki.jrme.2018.0232

CrossRef Full Text | Google Scholar

Gong, F., Yan, J., Luo, S., and Li, X. (2019a). Investigation on the linear energy storage and dissipation laws of rock materials under uniaxial compression. Rock Mech. Rock Eng. 52, 4237–4255. doi:10.1007/s00603-019-01842-4

CrossRef Full Text | Google Scholar

Gong, F. Q., Yan, J. Y., Li, X. B., and Luo, S. (2019b). A peak-strength strain energy storage index for rock burst proneness of rock materials. Int. J. Rock Mech. Min. Sci. 117, 76–89. doi:10.1016/j.ijrmms.2019.03.020

CrossRef Full Text | Google Scholar

Guo, T., Liu, K., Ma, S., Yang, J., Xiang, L., Zhou, K., et al. (2022). Dynamic fracture behavior and fracture toughness analysis of rock-concrete bi-material with interface crack at different impact angles. Constr. Build. Mater. 356, 129286. doi:10.1016/j.conbuildmat.2022.129286

CrossRef Full Text | Google Scholar

He, M., Chen, Y., Li, N., and Zhu, C. (2015). Deformation and energy characteristics of sandstone subjected to uniaxial cyclic loading. J. China Coal Soc. 40, 1805–1812. (in Chinese). doi:10.13225/j.cnki.jccs.2014.1226

CrossRef Full Text | Google Scholar

He, M., Li, N., Chen, Y., and Zhu, C. (2017). Damping ratio and damping coefficient of rock under different cyclic loading conditions. Rock Soil Mech. 38, 2531–2538. (in Chinese). doi:10.16285/j.rsm.2017.09.009

CrossRef Full Text | Google Scholar

Justo, J., Castro, J., and Cicero, S. (2018). Energy-based approach for fracture assessment of several rocks containing U-shaped notches through the application of the SED criterion. Int. J. Rock Mech. Min. Sci. 110, 306–315. doi:10.1016/j.ijrmms.2018.07.013

CrossRef Full Text | Google Scholar

Liu, J., Xie, H., Jin, X., Zhou, H., Zhou, J., Fu, C., et al. (2008). Experimental study on damping characteristics of rock under cyclic loading. Chin. J. Rock Mech. Eng. 197, 712–717. (in Chinese). doi:10.3321/.issn:1000-6915.2008.04.009

CrossRef Full Text | Google Scholar

Liu, J., Xu, J., Li, Q., and Li, G. (2010). Experimental research on damping paramerers of rock under cyclic loading. Chin. J. Rock Mech. Eng. 29 (5), 1036–1041. (in Chinese).

Google Scholar

Liu, Y., Dai, F., Feng, P., and Xu, N. W. (2018). Mechanical behavior of intermittent jointed rocks under random cyclic compression with different loading parameters. Soil Dyn. Earthq. Eng. 113, 12–24. doi:10.1016/j.soildyn.2018.05.030

CrossRef Full Text | Google Scholar

Liu, C., Zhao, G., Xu, W., Meng, X. r., Huang, S. j., Zhou, J., et al. (2020a). Experimental investigation on failure process and spatio-temporal evolution of rockburst in granite with a prefabricated circular hole. J. Central South Univ. 27 (10), 2930–2944. doi:10.1007/s11771-020-4519-3

CrossRef Full Text | Google Scholar

Liu, Z., Wang, W., Luo, J., and Miao, G. (2020b). Method of energy evolution of rock under uniaxial compression test. J. China Coal Soc. 45, 3131–3139. (in Chinese). doi:10.13225/j.cnki.jccs.2019.1067

CrossRef Full Text | Google Scholar

Liu, Z., Zhao, G., Meng, X., Zhang, R., Cheng, X., Dong, C., et al. (2021). Analysis of creep energy evolution of red sandstone based on linear energy storage law. J. Central South Univ. Technol. 52, 2748–2760. (in Chinese). doi:10.11817/j.issn.1672-7207.2021.08.021

CrossRef Full Text | Google Scholar

Liu, H., Pengfei, B., Xin, L., Wei, Y., and Wang, M. (2022). Mechanical properties and energy dissipation characteristics of phyllite under triaxial multi-stage cyclic loading-unloading conditions. Chin. J. Rock Mech. Eng. 43, 265–274+281. (in Chinese). doi:10.16285/j.rsm.2021.1352

CrossRef Full Text | Google Scholar

Liu, C., Zhao, G., Xu, W., Meng, X., Liu, Z., Cheng, X., et al. (2023). Experimental study on failure characteristics of single-sided unloading rock under different intermediate principal stress conditions. Int. J. Min. Sci. Technol. 33 (3), 275–287. doi:10.1016/j.ijmst.2022.12.005

CrossRef Full Text | Google Scholar

Manoj, N., and Petroš, V. (2009). Fatigue and dynamic energy behaviour of rock subjected to cyclical loading. Int. J. Rock Mech. Min. Sci. 46 (1), 200–209. doi:10.1016/j.ijrmms.2008.05.002

CrossRef Full Text | Google Scholar

Meng, Q., Han, L., Pu, H., Wen, S., and Li, H. (2015). Experimental on the effect of strain rate and size on the energy accumulation and dissipation of rock. J. China Coal Soc. 40, 2386–2398. (in Chinese). doi:10.13225/j.cnki.jccs.2014.1771

CrossRef Full Text | Google Scholar

Meng, Q., Liu, J. F., Ren, L., Pu, H., and Chen, Y. l. (2021). Experimental study on rock strength and deformation characteristics under triaxial cyclic loading and unloading conditions. Rock Mech. Rock Eng. 54, 777–797. doi:10.1007/s00603-020-02289-8

CrossRef Full Text | Google Scholar

Momeni, A., Karakus, M., Khanlari, G. R., and Heidari, M. (2015). Effects of cyclic loading on the mechanical properties of a granite. Int. J. Rock Mech. Min. Sci. 77, 89–96. doi:10.1016/j.ijrmms.2015.03.029

CrossRef Full Text | Google Scholar

Rashidi Moghaddam, M., Ayatollahi, M. R., and Berto, F. (2018). Rock fracture toughness under mode II loading: A theoretical model based on local strain energy density. Rock Mech. Rock Eng. 51, 243–253. doi:10.1007/s00603-017-1319-7

CrossRef Full Text | Google Scholar

Stavropoulou, E., Dano, C., and Boulon, M. (2021). Shear response of wet weak carbonate rock/grout interfaces under cyclic loading. Rock Mech. Rock Eng. 54, 2791–2813. doi:10.1007/s00603-021-02406-1

CrossRef Full Text | Google Scholar

Xie, H., Peng, R., Ju, Y., and Zhou, H. (2005). On energy analysis of rock failure. Chin. J. Rock Mech. Eng. 24, 2603–2608. (in Chinese). doi:10.3321/j.issn:1000-6915.2005.15.001

CrossRef Full Text | Google Scholar

Xie, H., Yang, J., Li, L., and Peng, R. (2008). Energy mechanism of deformation and failure of rocks. Chin. J. Rock Mech. Eng. 27, 1729–1739. (in Chinese). doi:10.3321/j.issn:1000-6915.2008.09.001

CrossRef Full Text | Google Scholar

Yang, Y., Duan, H., and Xing, L. (2018). Fatigue deformation and energy evolution of coal under uniaxial cyclic loading. J. Basic Sci. Eng. 26, 154–167. (in Chinese). doi:10.16058/j.issn.1005-0930.2018.01.014

CrossRef Full Text | Google Scholar

Yoshinaka, R., Tran, T. V., and Osada, M. (1997). Mechanical behavior of soft rocks under triaxial cyclic loading conditions. Int. J. Rock Mech. Min. Sci. 34, 354.e1–354.e14. doi:10.1016/S1365-1609(97)00243-8

CrossRef Full Text | Google Scholar

You, M., and Su, C. (2008). Experimental study on strengthening of marble specimen in cyclic loading of uniaxial or pseudo-triaxial compression. Chin. J. Solid Mech. 29 (1), 66–72. (in Chinese). doi:10.19636/j.cnki.cjsm42-1250/o3.2008.01.010

CrossRef Full Text | Google Scholar

Zhang, Z., and Gao, F. (2012a). Research on nolinnear characteristics of rock energy. Chin. J. Rock Mech. Eng. 31, 1198–1207. (in Chinese). doi:10.3969/j.issn.1000-6915.2012.06.015

CrossRef Full Text | Google Scholar

Zhang, Z., and Gao, F. (2012b). Expriment research on energy evolution of red sandstone samples under uniaxial compression. Chin. J. Rock Mech. Eng. 31, 953–962. (in Chinese). doi:10.3969/j.issn.1000-6915.2012.05.012

CrossRef Full Text | Google Scholar

Zhang, Z., and Gao, F. (2015). Experimental investigation on the energy evolution of dry and water-saturated red sand-stones. Int. J. Min. Sci. Technol. 25, 383–388. doi:10.1016/j.ijmst.2015.03.009

CrossRef Full Text | Google Scholar

Zhang, Y., Jiang, X., Yang, H., and Chen, S. (2011). Effect of confining pressure on evolution law of hysteresis loop of sandstone under cyclic loading. Chin. J. Rock Mech. Eng. 30, 320–325. (in Chinese).

Google Scholar

Zuo, J-P., Xie, H., Meng, B., and Liu, J. (2011). Experimental research on loading-unloading behavior of coal-rock combination bodies at different stress levels. Rock Soil Mech. 32, 1287–1296. (in Chinese). doi:10.16285/j.rsm.2011.05.028

CrossRef Full Text | Google Scholar