Study on the consolidation behavior of horizontal drainage foundation under complex aquifer formation conditions in karst regions

Introduction: The consolidation behavior of horizontal drainage foundation under complex aquifer conditions in karst areas is a hot topic in the field of geotechnical engineering.

Methods: This paper presents a modified piecewise-linear model for plane-strain consolidation. In this model, the distributed drainage boundary was used to describe the drainage performance of soil layer boundaries, and the UH model considering the time effect was selected to reflect soil’s rheological property. Through comparison with existing research, the validity of the calculation model in this paper was verified. Then several examples were used to analyze the consolidation behavior of the foundation under the combined action of rheological effect and distributed drainage boundaries.

Results and discussion: Numerical studies show that the phenomenon of the increase of excess pore pressure exists in the foundation of the distributed drainage boundary after considering the rheology in the early stage of consolidation. Moreover, the larger the secondary consolidation coefficient and the initial over-consolidation parameter, or the smaller the pave rate and the thickness-width ratio, the above phenomenon is more obvious. In terms of the dissipation of the pore water pressure, the larger the secondary consolidation coefficient and the initial over-consolidation parameter, the slower the pore pressure dissipation, and the smaller the pave rate or the thickness-width ratio can achieve the above effects. In terms of the impact on settlement, the above-mentioned parameters are consistent, that is, the larger the corresponding parameter, the larger the corresponding settlement value.

1 Introduction

In recent years, engineering safety protection has become a hot topic in geotechnical engineering. To achieve this goal, scholars have conducted corresponding research work from different perspectives. For example, many scholars (Liu and Li, 2023a; Liu et al., 2023b; Liu et al., 2023c) explored the mechanical properties of rock or soil through experimental methods, in order to provide valuable basic data for engineering safety development. In addition, some scholars (Gao et al., 2023; Zhang et al., 2023a; Li et al., 2023; Zhang et al., 2023b) studied the working mechanism of rock or soil from a theoretical perspective. It is worth noting that the drainage and consolidation of foundation in karst areas is a branch of the above research. Among many drainage consolidation methods, laying horizontal drainage bodies has become the focus of attention in recent years. In this regard, many scholars (Nagahara et al., 2004; Liu, 2008; Chen et al., 2016a) carried out related research. Some scholars have conducted research on horizontal drainage materials (i.e., sand cushion (Nagahara et al., 2004; Chai et al., 2014), geotextiles (Chen et al., 2016b), and some scholars (Liu, 2008; Xu and Lei, 2016; Xu and Lei, 2017) conducted corresponding discussions on the optimization of horizontal drainage. Among them, the optimization of drainage channels has attracted the attention of many scholars. Regarding the optimization problem of the drainage channel, it can be attributed to the drainage boundary problem in the consolidation process in essence (Chen et al., 2020b). In this regard, highly recognized drainage boundaries include completely permeable boundaries (Terzaghi et al., 1996), mixed drainage boundaries (Gray, 1944), semi-permeable boundaries (Liu and Lei, 2013) and continuous drainage boundaries (Mei et al., 2022). It is worth noting that the above-mentioned research work is based on the full deployment of drainage bodies. Relevant studies (Chen et al., 2020a; Chen et al., 022b) have shown that most of the drainage process of foundation is concentrated in the early stage of consolidation, and it is not obvious in the middle and late stages of consolidation which the engineers are concerned about. In order to solve this problem, some scholars (Fan and Mei, 2016) proposed a method of distributed horizontal drainage. Since this method was proposed, scholars have started from a theoretical perspective to discuss the consolidation problem under the distributed drainage boundary. Some scholars have successively discussed the consolidation of single-layer (Chen et al., 2020b) and multi-layer foundations (Chen et al., 2020a) under distributed drainage boundaries based on Terzaghi’s consolidation theory, and some scholars (Yao et al., 2019) applied Biot’s consolidation theory to explore the distributed drainage boundary problem. However, the above researches ignore the inherent characteristics of the soft soil, that is, the nonlinear of deformation, especially the rheological characteristics.

Many experiments (Zhou and Chen, 2006; Joseph, 2014; Gui et al., 2015; Chen et al., 2016a) show that the deformation process of cohesive soil has significant rheological characteristics. To reflect this characteristic, scholars have proposed many constitutive relations. Among them, one type is composed of component models, which include Kelvin model (Wang et al., 2017), Nishihara model (Yan et al., 2017), Voigt model (Liu et al., 2015), Merchant model (Ding et al., 2022), and so on. The other is based on elastic-viscoplastic theory, such as the EVP model (Zhou et al., 2020) and the UH constitutive model considering time effects (Yao et al., 2020). In order to observe the effect of rheological properties on the consolidation process, scholars successively introduced the above constitutive model into the classic Terzaghi consolidation equation, and analyzed the consolidation behavior of soil considering the rheological effect. However, most of these studies are based on the classic Terzaghi consolidation theory. When solving related problems, users need to construct corresponding partial differential equations according to corresponding conditions. Moreover, the complexity of partial differential equations will be further strengthened according to the increase of consideration factors. This undoubtedly adds a lot of difficulty to the solution process. In order to optimize the consolidation calculation process, Fox and Beries. (1997) proposed a piecewise-linear consolidation method. This method does not require the construction of complex partial differential equations, and has a modular feature. At present, this method has been used by many scholars to study consolidation problems. For example, considering the multi-layered nature of the soil (Fox et al., 2014), the viscosity of the soil (Liu et al., 2020), the soil’s structure (Shi et al., 2021), and the permeability of soil’s boundary (Liu et al., 2021).

In view of the existing research status, this paper presents a modified plane-strain consolidation model, called MPSC model, based on piecewise-linear consolidation method (Deng and Zhou, 2016a; Deng and Zhou, 2016b). In MPSC model, the distributed drainage boundary (Fan and Mei, 2016) is used to reflect the drainage state of the soil, and the UH constitutive model considering the time effect (Yao et al., 2020) is used to describe the deformation process of the soil. By comparing with existing researches, the validity of the model in this paper is verified. Then, some calculation examples are applied to analyze the influence of the rheological properties of the soil under the distributed drainage boundary on the consolidation process.

2 Model description

2.1 Distributed drainage boundary

Relevant research (Chen et al., 2020a; Chen et al., 2020b) has showed that the drainage volume in the middle and late stages of consolidation that engineers were concerned about was less. In order to achieve the purpose of drainage and resource conservation, scholars (Fan and Mei, 2016) proposed the method of distributing drainage bodies. The corresponding schematic diagram is shown in Figure 1. Among them, Figure 1A is a model diagram of distributed drainage boundary, and Figure 1B is a characteristic element obtained based on symmetry.

FIGURE 1

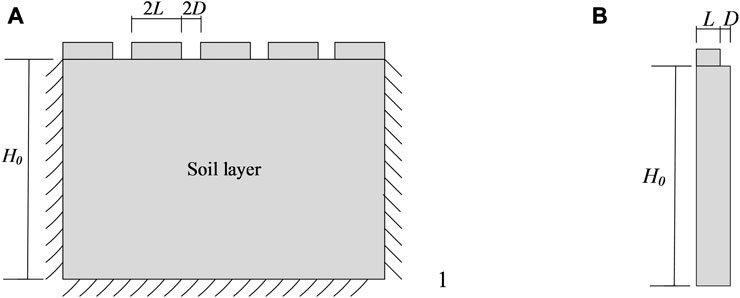
FIGURE 1. The model for the distributed drainage boundary: (A) the diagram of distributed drainage boundary; (B) the characteristic element.

In Figure 1A, the drainage material is arranged on the top surface of the foundation at equal intervals. Among them, the width of the paved area is 2L, and the distance between adjacent paved areas (that is, the unpaved area) is 2D. In this way of laying the drainage body, the pore water in the foundation first flows horizontally from the undistributed area to the distributing area, and then flows vertically within the distributing area, and finally drains out of the foundation. In essence, the problem of ground consolidation under the distributed drainage boundary (Fan and Mei, 2016) can be attributed to the plane strain problem.

2.2 Basic assumption

When establishing the MPSC model, the following assumptions are introduced here:

a.The soil is always saturated, and soil particles and pore water will not be compressed.

b.The deformation of the soil only occurs in the vertical direction, and it can be described by the UH constitutive model considering the time effect (Yao et al., 2020).

c.The top surface of the soil is a drainage surface, and can be described by distributed drainage boundaries (Fan and Mei, 2016), and other boundaries are impervious.

d.The flow of pore water in the soil conforms to Darcy’s law.

2.3 MPSC model

When studying the consolidation process of distributed drainage boundary foundations, scholars (Yao et al., 2019; Chen et al., 2020b) usually choose the characteristic element (i.e., Figure 1B) for modeling. Among them, the width of the characteristic element includes two parts: a paved area with a width of L and a unpaved area with a width of D. Similar to the existing research, the MPSC model also uses the above method, and the schematic diagram is shown in Figure 2. As shown in Figure 2A, the thickness of the soil layer is H₀, and it is always in saturated state (i.e., the height of the static water surface is always H_w). At the initial moment (see Figure 2A), the soil layer is divided into $R_i\times R_j$ elements. Among them, the horizontal direction is $R_i$ elements of equal width (d); the vertical direction is $R_j$ elements of equal thickness (L₀). In the analysis, the center point of the element is used as the research object. In order to facilitate the calculation of the position of the corresponding element, z coordinate system with the positive direction upward is established here, and the coordinates of the center point of the element (i.e., $z_{i,j}^t$) and the coordinates of the right vertex of the element (i.e., $z_{c,i,j}^t$) are given. Among them, $z_{c,i,j}^t$ is related to the cross-sectional area of the element (i.e., $A_{i,j}^t$), and the corresponding relationship is shown in Eq. 1. Moreover, $z_{i,j}^t$ and the thickness of the consolidated element (i.e., $L_{i,j}^t$) are related to $z_{c,i,j}^t$, and the corresponding relationship is shown in Eqs 2, 3. At the initial moment (see Figure 2A), the soil layer has been consolidated and stabilized under the original load q₀ and its own weight. When the new load $\Delta q$ is applied, the soil layer enters a new consolidation stage (see Figure 2B). During the consolidation process, the deformation only occurs in the vertical direction, and the width of element in the horizontal direction is always the same. Regarding the drainage surface of the foundation, it is assumed that only the top surface is drained, and it can be described by a distributed drainage boundary. That is to say, the paved area is drainage area, and the corresponding hydraulic gradient is not equal to 0; the unpaved area is undrained area, and the corresponding hydraulic gradient is 0.

$z_{c,i,j}^t=z_{c,i-1,j}^t+z_{c,i,j-1}^t-z_{c,i-1,j-1}^t+\frac{A_{i,j}^t-\left(z_{c,i-1,j}^t-z_{c,i-1,j-1}^t\right)d}{d/2}(1)$

$z_{i,j}^t=\frac{z_{c,i-1,j}^t+z_{c,i-1,j-1}^t+z_{c,i,j}^t+z_{c,i,j-1}^t}{4}(2)$

$L_{i,j}^t=\frac{z_{c,i-1,j}^t-z_{c,i-1,j-1}^t+z_{c,i,j}^t-z_{c,i,j-1}^t}{2}(3)$

FIGURE 2

FIGURE 2. Geometry for MPSC model: (A) initial configuration; (B) during consolidation.

2.4 Total stress of element

Regarding the plane-strain consolidation problem, (Deng and Zhou, 2016a; Deng and Zhou, 2016b) carried out corresponding research based on the piecewise-linear method. With reference to the research of Deng et al. (2016a), Deng et al. (2016b), the total stress of the corresponding element can be expressed as:

${\sigma }_{i,j}^t=\left(H_w-\frac{z_{c,i-1,Rj}^t+z_{c,i,Rj}^t}{2}\right){\gamma }_w+q_0+\Delta q+\frac{A_{i,j}^t{\gamma }_{i,j}^t}{2d}+{\displaystyle \sum _{n=j+1}^{Rj}}\frac{A_{i,n}^t{\gamma }_{i,n}^t}{d}(4)$

Where ${\gamma }_w$ represents the specific gravity of water; ${\gamma }_{i,j}^t\left[=\left[G_s+e_{i,j}^t){\gamma }_w\right]/\left(1+e_{i,j}^t\right)\right]$ represents the saturated weight for element (i, j). The parameter $G_s$ is the specific gravity of soil particles. Based on previous research (Fox et al., 1997) on piecewise-linear consolidation methods, the value of $G_s$ can be defined as follows: when the self-weight of the soil is not considered, $G_s$ = 1; when the self-weight of the soil is considered, the magnitude of $G_s$ depends on the category of the soil.

2.5 Constitutive relationship

In MPSC model, it is assumed that the deformation of the soil has rheological characteristics, and the UH constitutive model considering the time effect (Yao et al., 2013; Hu and Yao, 2015) can be used to describe the above-mentioned characteristics of the soil. Regarding the UH constitutive model considering the time effect (Yao et al., 2013; Hu and Yao, 2015), existing studies (Liu et al., 2020) have introduced it into the one-dimensional consolidation process for corresponding discussion. Among them, the relationship between effective stress and void ratio can be expressed by Eqs 5, 6). Regarding the seepage process, it is considered that the seepage process is isotropic. And, the process conforms to Darcy’s law.

${{\sigma }^{\prime }}_{i,j}^{t+\Delta t}=\frac{{{\sigma }^{\prime }}_{i,j}^t}{1-\frac{\left(e_{i,j}^t-e_{i,j}^{t+\Delta t}\right)\ln 10-C_{\alpha }{\left(R_{i,j}^t\right)}^{\alpha }\Delta t}{C_s+\frac{\left(C_c-C_s\right)M^4}{M_f^4}}},{{\sigma }^{\prime }}_{i,j}^{t+\Delta t}>{{\sigma }^{\prime }}_{i,j}^t(5)$

${{\sigma }^{\prime }}_{i,j}^{t+\Delta t}=\frac{C_s{{\sigma }^{\prime }}_{i,j}^t}{C_s-\left[\left(e_{i,j}^t-e_{i,j}^{t+\Delta t}\right)\ln 10-C_{\alpha }{\left(R_{i,j}^t\right)}^{\alpha }\Delta t\right]},{{\sigma }^{\prime }}_{i,j}^{t+\Delta t}\le {{\sigma }^{\prime }}_{i,j}^t(6)$

Where $C_c,C_s$ and $C_{\alpha }$ are the compression index, the swelling index and the secondary consolidation coefficient, respectively; $\Delta t$ is the time increment; M、 $M_f$ are the stress ratio at the critical state and the potential failure stress ratio, respectively. $R_{i,j}^t$ is the over-consolidation parameter of the corresponding element at time t. The corresponding expressions for the above parameters are as follows:

$M=6\sin \phi /\left(3-\sin \phi \right)(7)$

$M_{\mathrm{f}}=6\left[\sqrt{\chi /R\left(1+\chi /R\right)}-\chi /R\right](8)$

$R={\sigma }^{\prime }/{\sigma }_0^{\prime }\exp \left[-\ln 10{\epsilon }_{\mathrm{v}}^{\mathrm{p}}\left(1+e_0\right)/\left(C_{\mathrm{c}}-C_s\right)\right](9)$

Where $\chi =M^2/\left[12\left(3-M\right)\right]$; $\phi$ is the effective internal friction angle of the soil; ${\sigma }_0^{\prime }$ is the initial effective stress adapted to the initial void ratio e₀; It is worth noting that R₀ is the initial value of the over-consolidation parameter R, and it has a reciprocal relationship with the over-consolidation ratio OCR; ${\epsilon }_v^p$ is plastic deformation.

2.6 Seepage process and settlement

After solving the total stress and effective stress, the corresponding pore pressure can be expressed as:

$u_{i,j}^t={\sigma }_{i,j}^t-\sigma {\prime }_{i,j}^t(10)$

For the seepage process, Figure 3 shows a schematic diagram of the seepage flow. It can be seen from Figure 3 that the seepage process is divided into vertical seepage and horizontal seepage. First, the vertical seepage process is introduced here. Among them, the vertical equivalent permeability coefficient can be expressed as:

$K_{zs,i,j}^t=\frac{k_{z,i,j+1}^t{k}_{z,i,j}^t\left(L_{i,j+1}^t+L_{i,j}^t\right)}{L_{i,j+1}^t{k}_{z,i,j}^t+L_{i,j}^t{k}_{z,i,j+1}^t}(11)$

Where $k_{z,i,j}^t$ is the vertical permeability coefficient, and its relation to void ratio can be described by e-lgk (Liu et al., 2020).

$e=e_0-C_k\lg \left(k_0/k\right)(12)$

Where $C_k$ is the permeability index, which can reflect the speed of change of the permeability coefficient with void ratio.

FIGURE 3

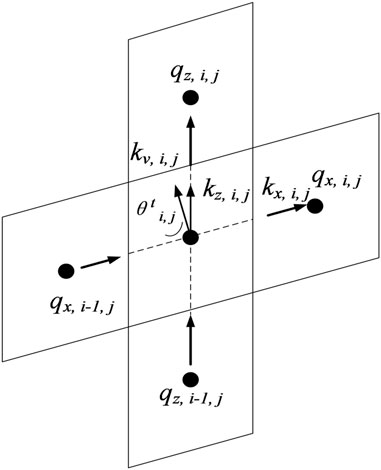
FIGURE 3. Fluid flow between contiguous elements (Deng and Zhou, 2016a).

For the upper and lower boundaries, the equivalent permeability coefficients are defined as $k_{zs,i,Rj}^t\left[=k_{v,i,Rj}^t\right]$ and $k_{zs,i,0}^t\left[=k_{z,i,1}^t\right]$.

In addition to the permeability coefficient, the vertical hydraulic gradient is

$i_{z,i,j}^t=\frac{h_{i,j+1}^t-h_{i,j}^t}{z_{i,j+1}^t-z_{i,j}^t}(13)$

Where $h_{i,j}^t$ is the head of element (i, j) at time t, which is composed of two parts, namely the head generated $\left[u_{i,j}^t/{\gamma }_w\right]$ by the pore pressure and the position head $z_{i,j}^t$.

In the paper, the boundary of the top surface of the soil layer can be described by distributed drainage boundary conditions, which is composed of paved area and unpaved area. In unpaved area, the top boundary of the soil layer is impervious, that is, the vertical component of the hydraulic gradient is 0. In paved area, the vertical component of the corresponding hydraulic gradient can be expressed by Eq. 14, namely:

$i_{z,i,Rj}^t=\frac{2\left(H_{\mathrm{w}}-h_{i,Rj}^t\right)}{L_{i,Rj}^t\sin {\theta }_{i,Rj}^t}(14)$

For horizontal seepage, the corresponding hydraulic gradient and equivalent permeability coefficient can be expressed as:

$i_{x,i,j}^t=\frac{h_{i+1,j}^t-h_{i,j}^t}{\sqrt{d^2+{\left(z_{i+1,j}^t-z_{i,j}^t\right)}^2}}(15)$

$K_{xs,i,j}^t=\frac{2k_{x,i,j}^t{k}_{x,i+1,j}^t}{k_{x,i+1,j}^t+k_{x,i,j}^t}(16)$

Where $k_{x,i,j}^t$ is horizontal permeability coefficient, which is equal to the vertical permeability coefficient $k_{z,i,j}^t$.

Then, the flow at the boundary of the element in the corresponding direction can be expressed as:

$q_{x,i,j}^t=-K_{xs,i,j}^t{i}_{x,i,j}^t\left(z_{c,i,j}^t-z_{c,i,j-1}^t\right)\sin {\theta }_{i,j}^t(17)$

$q_{z,i,j}^t=-K_{zs,i,j}^t{i}_{z,i,j}^{t}d(18)$

After solving the corresponding flow, related indicators (i.e., the area $A_{i,j}^{t+\Delta t}$, void ratio $e_{i,j}^{t+\Delta t}$, top surface settlement $S_i^{t+\Delta t}$, Average settlement $S_{avg}^{t+\Delta t}$ ) of the corresponding element at time $t+\Delta t$ can be expressed as:

$A_{i,j}^{t+\Delta t}=A_{i,j}^t+\left(q_{x,i-1,j}^t+q_{z,i,j-1}^t-q_{x,i,j}^t-q_{z,i,j}^t\right)\Delta t(19)$

$e_{i,j}^{t+\Delta t}=\frac{A_{i,j}^{t+\Delta t}\left(1+e_{0,i,j}\right)}{A_{0,i}}-1(20)$

$S_i^{t+\Delta t}=H_0-z_{c,i,Rj}^{t+\Delta t}(21)$

$S_{avg}^{t+\Delta t}=\frac{{\displaystyle \sum _{i=1}^{Ri}}{S}_i^{t+\Delta t}}{Ri}(22)$

Where $A_{0,j}$ is the cell cross-sectional area at the initial moment; $e_{0,i,j}$ is the void ratio of the corresponding element at the initial moment, which is judged according to the initial stress.

In order to observe the dissipation of pore pressure in the foundation, the calculation formula of excess pore pressure is given here, namely:

$u_{ex,i,j}^t=u_{i,j}^t-u_{0,i,j}(23)$

Where $u_{0,i,j}$ is the pore pressure of the corresponding element at the initial moment.

Then, the average excess pore pressure in the foundation can be expressed as:

$u_{ex,avg}^t=\frac{{\displaystyle \sum _{i=1}^{Ri}}{\displaystyle \sum _{j=1}^{Rj}}d{L}_{i,j}^t{u}_{ex,i,j}^t}{\left(L+D\right)H_0}(24)$

3 Model verification

3.1 Comparison considering the rheological effect of soil

In order to simulate the rheology of soil, many scholars have proposed corresponding constitutive relations. Among them, Yao et al. (2013) proposed the UH model considering the time effect. Later, Hu and Yao, (2015) introduced its one-dimensional form into the classic Terzaghi consolidation theory and studied the effect of rheology on the consolidation process. In order to verify the validity of the MPSC model in this paper, the case provided by Hu and Yao, (2015) is used for comparison. When making comparison, the MPSC model needs to be degenerated into a one-dimensional form. The specific method is: the number of horizontal units is 1, and the top drainage boundary is a completely permeable boundary. What’s more, the values of other parameters are: the soil thickness H₀=1m, H_w=1m, $G_s$ =1.0, q₀=10kPa, e₀=0.53, $\Delta q$ =90 kPa. Regarding the constitutive model, the corresponding parameter value is as follows: $C_c$ =0.0217, $C_s$ =0.0131, M =1.112, R₀=0.95. For the secondary consolidation coefficient, the corresponding values are 0.5 $C_{\alpha }$, $C_{\alpha }$ and 2 $C_{\alpha }$. Among them, $C_{\alpha }$ =0.0108. Regarding the seepage process, Darcy’s law is considered to be applicable, and the permeability coefficient k=3.63 × 10^-7 m/min and remains unchanged.

Figure 4 shows the comparison results of the average consolidation degree U_P obtained by Hu and Yao, (2015) and MPSC model in this paper. By comparing the data in Figure 4, it is found that the maximum error between the calculated results of the two methods is 2.6%. That is to say, the calculation results in this paper can better match the results of Hu and Yao, (2015). This also indicates that the calculation model in this paper is effective for the rheological consolidation calculation process.

FIGURE 4

FIGURE 4. Comparison results of the average consolidation degree U_P under rheological effect.

3.2 Comparison under distributed drainage boundary

In order to optimize the layout of horizontal drainage bodies, scholars (Fan and Mei, 2016) proposed the distributed drainage boundary. Existing studies (Yao et al., 2019; Chen et al. (2020a), Chen et al. (2020b) have shown that the boundary can achieve the purpose of drainage and resource utilization. In previous studies, Chen et al. (2020b) used analytical solutions to explore the influence of the width-thickness ratio Q on the pore pressure dissipation process under the linear elastic constitutive relationship. Among them, time is expressed in a dimensionless way, and the corresponding expression is

$T_{\mathrm{v}}=\frac{C_{v}t}{{H_0}^2}=\frac{k\left(1+e_0\right)}{a{\gamma }_{\mathrm{w}}{H_0}^2}t(25)$

Where a is the compression factor; e₀ is the initial void ratio.

In order to verify the correctness of the MPSC model in this paper, the above case is selected for comparison. When making comparison, the flow process of water in soil pores conforms to Darcy’s law, and the UH model considering the time effect in MPSC model needs to replaced by the elastic constitutive relationship (i.e., $\Delta e=a\Delta p$) as Chen et al. (2020b). Additionally, the other conditions set in this paper in the comparison are consistent with those used by Chen et al. (2020b). The comparison results are shown in Figure 5, and the maximum error between the calculated results of the two methods is 3.4%. This indicates that the MPSC model is capable of simulating soil consolidation problems under distributed drainage boundary conditions.

FIGURE 5

FIGURE 5. Comparison of U_P under distributed drainage boundary.

4 Analysis of the consolidation behaviour

In this section, the consolidation behavior of the foundation under the combined action of the distributed drainage boundary and the rheological effect is analyzed. Among them, the indicators describing the consolidation process of the foundation include the average excess pore pressure $u_{ex,avg}$ and the average settlement $S_{avg}$. In the analysis, the dimensionless time is used to reflect the consolidation process, namely:

$T_{\mathrm{v}}=\frac{{\sigma }_0{k}_0\left(1+e_0\right)\ln 10}{C_{\mathrm{c}}{\gamma }_{\mathrm{w}}{H_0}^2}t(26)$

Where ${\sigma }_0$ is the reference stress, and $e_0$ and $k_0$ are the reference void ratio and reference permeability coefficient corresponding to ${\sigma }_0$. In addition, the values of the parameters in the analysis are as follows: H₀=6m, H_w=6m, $G_s$ =2.75, L+D=6 m (i.e., horizontal width), $C_c$ =0.45, $C_s$ =0.1, $C_k$ =0.6, $C_{\alpha }$ =0.012, R₀=0.9, M =0.5665, the pave rate W=0.5, the thickness-width ratio Q=5.0. Regarding the load, the original load on the top of the soil is $q_0$ =100kPa, the new load $\Delta q$ =100kPa, e₀=1.0, k₀=2.0×10^-7 m/min. It is worth noting that when analyzing the influence of related parameters on consolidation properties, the corresponding parameters can be changed.

4.1 Influence of the pave rate on consolidation behavior

In the study of distributed drainage boundary, the pave rate W is a key parameter. Generally, the pave rate refers to the ratio of the width of the paving drainage body to the total width of the soil layer. In this case, the pave rate W is taken as 0.1, 0.5 and 0.8 in sequence. Figure 6 shows the effect of the pave rate W on the average excess pore pressure $u_{ex,avg}$. It can be found from this figure that at the initial stage of consolidation (such T_v=0.001), the average excess pore pressure $u_{ex,avg}$ is greater than the applied load (i.e., new load $\Delta q$). This is a phenomenon that has not been discovered by existing studies (Fan and Mei, 2016; Yao et al., 2019; Chen et al., 2020b) under distributed drainage boundary. Regarding the cause of this phenomenon, most one-dimensional studies (Hu and Yao, 2015; Liu et al., 2020) attribute it to rheological effects. Besides, when the boundary is a distributed drainage boundary (that is, the pave rate W is less than 1.0), the pore pressure curve is always above the full-distribution drainage boundary. This shows that the pave rate can delay the dissipation of pore pressure in the foundation. Moreover, the degree of delay will increase as the pave rate decreases. For example, at T_v = 0.4, the average excess pore pressure $u_{ex,avg}$ with the pave rates of 0.1, 0.5 and 0.8 are 95.01 kPa, 68.18 kPa, and 46.28 kPa, respectively. However, when the pave rate is 0.8, the pore pressure curve will gradually approach the pore pressure curve at the boundary of the completely arranged drainage body. This also shows that reasonable laying of horizontal drainage materials can achieve the effect of both drainage and resource conservation.

FIGURE 6

FIGURE 6. Influence of pave rate W on average excess pore pressure.

Figure 7 shows the influence of the pave rate W on the average settlement $S_{avg}$. On the whole, the smaller the pave rate, the smaller the settlement at the same time. For instance, at T_v = 0.2, when the pave rate is 0.1, 0.5 and 0.8, the values of $S_{avg}$ are 0.072 m, 0.156 m, 0.226 m, respectively. Moreover, they are respectively 0.28 times, 0.61 times, and 0.88 times of the corresponding settlement under the full-distributed drainage boundary. In other words, to reach the same value of settlement, the greater the pave rate, the shorter the time consumed. Taking $S_{avg}$ = 0.3 m as an example, the time required for the pave rate equal to 0.8 when the settlement value is reached is only 0.26 times the pave rate equal to 0.1.

FIGURE 7

FIGURE 7. Influence of pave rate W on average settlement.

4.2 Influence of thickness-width ratio Q on consolidation

In addition to the pave rate, the thickness-width ratio Q is also an important parameter in the study of distributed drainage boundaries. In this case, the thickness-to-width ratio is 1, 2, and 6 respectively to carry out the corresponding research. Figure 8 shows the effect of Q on $u_{ex,avg}$. Similar to the above results, after considering the effect of thickness-to-width ratio, the average pore pressure dissipation curve is also located above the pore pressure curve of the full-distributed drainage boundary. This also means that the thickness-to-width ratio can also delay the dissipation of pore pressure. Moreover, the smaller the thickness-to-width ratio, the more obvious the above-mentioned delay effect. For example, when T_v= 0.5, the average excess pore pressure when the thickness-to-width ratio is 1 is still 1.42 times the corresponding pore pressure when the value of Q is 6. It can be seen that the influence of the thickness-to-width ratio on the dissipation of pore water pressure cannot be ignored.

FIGURE 8

FIGURE 8. Influence of thickness-width ratio Q on average excess pore pressure.

Figure 9 shows the thickness-to-width ratio on the average settlement $S_{avg}$. It can be found from this figure that the ratio mainly affects the middle and late stages of consolidation. And, as the thickness-to-width ratio decreases, the value of settlement at the same time is smaller. For example, when T_v = 0.3, the settlement when the thickness-to-width ratio is equal to 1 is only 0.73 times the corresponding settlement when the thickness-to-width ratio is equal to 6. Furthermore, it can be found from the figure that the corresponding curves considering the thickness-to-width ratio are all located above the settlement curve of the full-distribution drainage boundary. In other words, the settlement process of the foundation after considering the thickness-to-width ratio will be slower than the settlement process under the full-distributed drainage boundary.

FIGURE 9

FIGURE 9. Influence of thickness-width ratio Q on average settlement.

4.3 Influence of secondary consolidation coefficient on consolidation behavior

The rheological properties of cohesive soil is an important feature that distinguishes it from other soils. The existing researches (Liu et al., 2020; Zhou et al., 2020) indicate that the coefficient of secondary consolidation is an important indicator for describing the rheological characteristics of soil. Based on this, with the secondary consolidation coefficient $C_{\alpha }$ as the representative, the influence of the rheology on the consolidation process under the distributed drainage boundary is analyzed here. In the analysis, the value of $C_{\alpha }$ is taken as 0.006, 0.012, and 0.018 in sequence.

Figure 10 shows the effect of the secondary consolidation coefficient on the average excess pore pressure. It can be found from this figure that the greater the secondary consolidation coefficient, the greater the peak average of the excess pore pressure. For example, the peak of the pore pressure when $C_{\alpha }$ = 0.018 is 1.23 times the corresponding peak of $C_{\alpha }$ =0.006. The above phenomenon has been discovered by scholars (Hu and Yao, 2015; Liu et al., 2020) in one-dimensional consolidation analysis. Moreover, scholars (Hu and Yao, 2015; Liu et al., 2020) have also provided corresponding explanations, that is, the rheological characteristics of soil cause obstruction in the discharge of pore water in the soil.

FIGURE 10

FIGURE 10. Influence of secondary consolidation coefficient on average excess pore pressure.

Figure 11 shows the effect of secondary consolidation coefficient on the average settlement $S_{avg}$. It can be seen from this figure that the larger the secondary consolidation coefficient (that is, the stronger the rheological effect), the larger the value of settlement at the same time. For example, at T_v =1.0, with the increase of the secondary consolidation coefficient, the value of the average settlement is 0.334 m, 0.391 m, 0.443 m, respectively. From this result, the settlement when the secondary consolidation coefficient is equal to 0.018 is 1.33 times the settlement when the secondary consolidation coefficient is 0.006. It can be seen that the rheological effect has a significant influence on the settlement of the distributed drainage boundary foundation. Besides, it can also be seen from Figure 11 that the greater the secondary consolidation coefficient, the greater the slope of the end of the deformation curve, and the longer it takes for the settlement of the foundation to reach a stable state. From the above analysis, it can be seen that it is very necessary to accurately measure the secondary consolidation coefficient of soil when predicting the settlement of soil in practical engineering.

FIGURE 11

FIGURE 11. Influence of secondary consolidation coefficient on the average settlement.

4.4 Influence of the initial over-consolidation state on consolidation behavior

The over-consolidation of soil is an important branch of consolidation research. In the UH model considering the time effect (Yao et al., 2013; Hu and Yao, 2015; Liu et al., 2020), the initial over-consolidation parameter R₀ reflect the initial over-consolidation state of the soil. In the study, the initial over-consolidation parameter R₀ is 0.3, 0.6 and 0.9 in turn. Figure 12 shows the effect of the parameter R₀ on the average excess pore pressure. From this figure, the initial over-consolidation state has significant effect on the dissipation process of the excess pore pressure in the distributed drainage boundary foundation. On the whole, the larger the value of R₀ (that is, the weaker the initial over-consolidation state), the slower the average pore pressure will dissipate. For example, at T_v = 0.2, with the increase of R₀, the corresponding average pore pressures are 28.62 kPa, 58.60 kPa and 88.25 kPa. In other words, when it dissipates to the same pore pressure value, the stronger the initial over-consolidation of the soil, the shorter the time it takes. For example, when the average excess pore pressure dissipates to 52 kPa, the dimensionless time taken when the initial over-consolidation parameters are 0.3, 0.6, and 0.9 are 0.10, 0.26, and 0.60, respectively.

FIGURE 12

FIGURE 12. Influence of initial over-consolidation parameter R₀ on average excess pore pressure.

Figure 13 shows the influence of the parameter R₀ on average settlement. Figure 13 shows that the initial over-consolidation state of the soil has a significant impact on the settlement process of the foundation. For the same moment, the smaller the initial over-consolidation parameter R₀, the smaller the corresponding average settlement. For example, when the dimensionless time T_v = 1, as the initial over-consolidation parameter increases, the corresponding settlement values are 0.129 m, 0.281 m, and 0.389 m. It can be seen that the settlement at this moment when the initial over-consolidation parameter is 0.9 is 3.02 times the corresponding settlement when the initial over-consolidation parameter is 0.3. In addition, it can also be seen from the figure that the stronger the degree of initial over-consolidation, the shorter the time it takes for the foundation to enter a stable state. For example, when the dimensionless time T_v is equal to 1, the foundation has reached a stable state when the initial over-consolidation parameter is equal to 0.3, but the deformation of the foundation when the initial over-consolidation parameter is equal to 0.6 and 0.9 is still in progress. This also indicates that preloading is an effective method to reduce post construction settlement.

FIGURE 13

FIGURE 13. Influence of initial over-consolidation parameter R₀ on average settlement.

5 Conclusion

Considering soil’s rheology and the distributed drainage boundary, this paper presents a modified piecewise-linear model for plane-strain consolidation. By comparing with the existing research, the validity of the consolidation model in this paper was verified. Finally, several calculation examples were used to discuss the consolidation behavior of the foundation under the combined action of distributed drainage boundaries and rheological effects. The main conclusions are as follows:

1. After considering the rheological behavior of the soil, there is an increase in pore pressure in the soil layer. Moreover, other factors (i.e., the initial over-consolidation parameter, the pave rate and the thickness-to-width ratio) can have a further impact on above phenomenon.

2. Distributed drainage boundaries can delay the consolidation process of soil. Moreover, reasonable selection of the pave rate and the thickness-to-width ratio can achieve the purpose of consolidation drainage and resource saving.

3. With the increase of rheological effect, the dissipation of pore pressure of distributed drainage boundary foundation slows down at the same time, but the process of foundation settlement speeds up.

4. The larger initial over-consolidation parameter, the slower the pore pressure dissipation in the distributed drainage boundary foundation, but the faster the foundation settlement.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization: YX, JZ; Methodology: ZL; Writing and editing: YX, JZ; Verification and editing: PC. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by the National Natural Science Foundation of China (Grant No. 51578511), and the support is gratefully acknowledged. All the authors are highly thankful to the reviewers for their fruitful comments to improve the quality of the paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chai, J. C., Horpibulsuk, S., Shen, S. L., and Carter, J. P. (2014). Consolidation analysis of clayey deposits under vacuum pressure with horizontal drains. Geotext. Geomembranes 42 (5), 437–444. doi:10.1016/j.geotexmem.2014.07.001

CrossRef Full Text | Google Scholar

Chen, Y. T., Wang, G. J., Meng, F. Q., and Xu, Y. (2016a). Application and analysis of the geotextile composite cushion in the ground improvement of the new dredger fill. Chin. J. Geotech. Eng. 38 (S1), 169–172. doi:10.11779/CJGE2016S1032

CrossRef Full Text | Google Scholar

Chen, Z. B., Kong, Q. P., Zhu, J. G., and Zhang, S. F. (2016b). Experimental study on behavior of secondary consolidation of soft soils considering upper soil layers’ stress under repeated cyclic loading. J. Cent. South Univ. Sci. Tech. 47 (10), 3507–3514. doi:10.11817/j.issn.1672-7207.2016.10.030

CrossRef Full Text | Google Scholar

Chen, Z., Ni, P. P., Chen, Y. F., and Mei, G. X. (2020b). Plane-strain consolidation theory with distributed drainage boundary. Acta Geotech. 15 (2), 489–508. doi:10.1007/s11440-018-0712-z

CrossRef Full Text | Google Scholar

Chen, Z., Zhang, F., Chen, Y. F., Hu, S. W., Mei, G. X., Zhang, H., et al. (2020a). Pituitary-derived circular RNAs expression and regulatory network prediction during the onset of puberty in landrace × yorkshire crossbred pigs. Eng. Mech. 37 (1), 135–144. doi:10.3389/fgene.2020.00135

CrossRef Full Text | Google Scholar

Deng, A., and Zhou, Y. D. (2016a). Modeling electroosmosis and surcharge preloading consolidation I: Model formulation. J. Geotech. Geoenviron. 142 (2), 04015093. doi:10.1061/(ASCE)GT.1943-5606.0001417

CrossRef Full Text | Google Scholar

Deng, A., and Zhou, Y. D. (2016b). Modeling electroosmosis and surcharge preloading consolidation II: Validation and simulation results. J. Geotech. Geoenviron. 142 (2), 04015094. doi:10.1061/(ASCE)GT.1943-5606.0001418

CrossRef Full Text | Google Scholar

Ding, P., Xu, R. Q., Zhu, Y. H., and Wen, M. J. (2022). Fractional derivative modelling for rheological consolidation of multilayered soil under time-dependent loadings and continuous permeable boundary conditions. Acta Geotech. 17, 2287–2304. doi:10.1007/S11440-021-01417-0

CrossRef Full Text | Google Scholar

Fan, H. B., and Mei, G. X. (2016). Finite element consolidation analysis with distributed drainage boundaries in homogeneous ground. J. PLA. Univ. Sci. Tech. 17 (5), 438–444. doi:10.12018/j.issn.1009-3443.20160519002

CrossRef Full Text | Google Scholar

Fox, P. J., and Berles, J. D. (1997). CS2: A piecewise-linear model for large strain consolidation. Int. J. Numer. Anal. Metall. 21 (7), 453–475. doi:10.1002/(SICI)1096-9853(199707)21:7<453::AID-NAG887>3.0.CO;2-B

CrossRef Full Text | Google Scholar

Fox, P. J., Pu, H. F., and Berles, J. D. (2014). CS3: Large strain consolidation model for layered soils. J. Geotech. Geoenviron. 140 (8), 04014041. doi:10.1061/(ASCE)GT.1943-5606.0001128

CrossRef Full Text | Google Scholar

Gao, Y., Yu, Z., Chen, W., Yin, Q., Wu, J., and Wang, W. (2023). Recognition of rock materials after high-temperature deterioration based on SEM images via deep learning. J. Mater Res. Technol. 25, 273–284. doi:10.1016/j.jmrt.2023.05.271

CrossRef Full Text | Google Scholar

Gray, H. (1944). Simultaneous consolidation of contiguous layers of unlike compressible soils. Trans. ASCE 70 (2), 149–166.

Google Scholar

Gui, Y., Yu, Z. H., Liu, H. M., Cao, J., and Wang, Z. C. (2015). Secondary consolidation properties and mechanism of plateau lacustrine peaty soil. Chin. J. Geotech. Eng. 37 (08), 1390–1398. doi:10.11779/CJGE201508005

CrossRef Full Text | Google Scholar

Hu, J., and Yao, Y. P. (2015). One-dimensional consolidation analysis of UH model considering time effect. J. B. Univ. Aeronaut. Astronaut. 41 (8), 1492–1498. doi:10.13700/j.bh.1001-5965.2014.0583

CrossRef Full Text | Google Scholar

Joseph, P. G. (2014). Viscosity and secondary consolidation in one-dimensional loading. Geotech. Res. 1 (3), 90–98. doi:10.1680/gr.14.00008

CrossRef Full Text | Google Scholar

Li, X. L., Zhang, X. Y., Shen, W. L., Wang, Y., Qin, Q., Lu, X., et al. (2023). Abutment pressure distribution law and support analysis of super large mining height face. Int. J. Env. Res. Pub He 20 (2), 227. doi:10.3390/ijerph20010227

CrossRef Full Text | Google Scholar

Liu, J. C., and Lei, G. H. (2013). One-dimensional consolidation of layered soils with exponentially time-growing drainage boundaries. Comput. Geotech. 54 (10), 202–209. doi:10.1016/j.compgeo.2013.07.009

CrossRef Full Text | Google Scholar

Liu, J. C., Lei, G. H., and Wang, X. D. (2015). One-dimensional consolidation of visco-elastic marine clay under depth-varying and time-dependent load. Mar. Georesour. Geotec. 33 (4), 337–347. doi:10.1080/1064119X.2013.877109

CrossRef Full Text | Google Scholar

Liu, J. F. (2008). Requirements of thickness of sand mats for consolidation method. Chin. J. Geotech. Eng. 30 (3), 366–371. doi:10.3321/j.issn:1000-4548.2008.03.010

CrossRef Full Text | Google Scholar

Liu, S. M., and Li, X. L. (2023a). Experimental study on the effect of cold soaking with liquid nitrogen on the coal chemical and microstructural characteristics. Environ. Sci. Pollut. R. 30 (3), 36080–36097. doi:10.1007/s11356-022-24821-9

CrossRef Full Text | Google Scholar

Liu, S. M., Sun, H. T., Zhang, D. M., Yang, K., Li, X., Wang, D., et al. (2023c). Experimental study of effect of liquid nitrogen cold soaking on coal pore structure and fractal characteristics. Energy 275 (7), 127470. doi:10.1016/j.energy.2023.127470

CrossRef Full Text | Google Scholar

Liu, S. M., Sun, H. T., Zhang, D. M., Yang, K., Wang, D., Li, X., et al. (2023b). Nuclear magnetic resonance study on the influence of liquid nitrogen cold soaking on the pore structure of different coals. Phys. Fluids 35 (1), 012009. doi:10.1063/5.0135290

CrossRef Full Text | Google Scholar

Liu, Z. Y., Zhang, J. C., Duan, S. Q., Xia, Y. Y., and Cui, P. L. (2020). A consolidation modelling algorithm based on the unified hardening constitutive relation and Hansbo's flow rule. Comput. Geotech. 117, 103233. doi:10.1016/j.compgeo.2019.103233

CrossRef Full Text | Google Scholar

Liu, Z. Y., Zhang, J. C., Yang, C. Y., and Xu, C. Y. (2021). Piecewise-linear model for one-dimensional consolidation considering Non-Darcian flow under continuous drainage boundary. Int. J. Geomech. 21 (5), 06021011. doi:10.1061/(ASCE)GM.1943-5622.0002017

CrossRef Full Text | Google Scholar

Mei, G. X., Feng, J. X., Xu, M. J., and Ni, P. P. (2022). Estimation of interface parameter for one-dimensional consolidation with continuous drainage boundary conditions. Int. J. Geomech. 22 (3), 04021292. doi:10.1061/(ASCE)GM.1943-5622.0002300

CrossRef Full Text | Google Scholar

Nagahara, H., Fujiyama, T., Ishiguro, T., and Ohta, H. (2004). FEM analysis of high airport embankment with horizontal drains. Geotext. Geomembranes 22 (1), 49–62. doi:10.1016/S0266-1144(03)00051-7

CrossRef Full Text | Google Scholar

Shi, J. S., Ling, D. S., and Niu, J. J. (2021). SCS: A one-dimensional piecewise-linear large strain consolidation model for structured soils. Int. J. Numer. Anal. Metall. 45 (17), 2541–2564. doi:10.1002/nag.3276

CrossRef Full Text | Google Scholar

Terzaghi, K., Peck, R. B., and Mesri, G. (1996). Soil mechanics in engineering practice. New York, NY, USA: John Wiley and Sons, 229–231.

Google Scholar

Wang, L., Sun, D. A., Li, P. C., and Xie, Y. (2017). Semi-analytical solution for one-dimensional consolidation of fractional derivative viscoelastic saturated soils. Comput. Geotech. 83, 30–39. doi:10.1016/j.compgeo.2016.10.020

CrossRef Full Text | Google Scholar

Xu, L. D., and Lei, G. H. (2016). Effect of horizontal sand drainage cushion on consolidation efficiency of natural ground. J. Hehai Univ. Nat. Sci. 44 (1), 78–83. doi:10.3876/j.issn.1000-1980.2016.01.013

CrossRef Full Text | Google Scholar

Xu, L. D., and Lei, G. H. (2017). Effect of sand blanket on efficiency of ground consolidation with prefabricated vertical drains and its design method. J. Cent. South. Univ. Sci. Tech. 48 (4), 1035–1043. doi:10.11817/j.issn.1672−7207.2017.04.025

CrossRef Full Text | Google Scholar

Yan, B. Q., Guo, Q. F., Ren, F. H., and Cai, M. F. (2017). Modified Nishihara model and experimental verification of deep rock mass under the water-rock interaction. Int. J. Rock. Mech. Min. 83, 104250–104339. doi:10.1016/j.ijrmms.2020.104250

CrossRef Full Text | Google Scholar

Yao, R. D., Ni, P. P., Mei, G. X., and Zhao, Y. L. (2019). Numerical analysis of surcharge preloading consolidation of layered soils via distributed sand blankets. Mar. Georesour. Geotec. 37 (8), 902–914. doi:10.1080/1064119X.2018.1506529

CrossRef Full Text | Google Scholar

Yao, Y. P., Huang, J., Zhang, K., and Cui, G. Z. (2020). Numerical back-analysis of creep settlement of airport high fill. Rock Soil Mech. 41 (10), 3395–3404+3414. doi:10.16285/j.rsm.2020.0402

CrossRef Full Text | Google Scholar

Yao, Y. P., Kong, L. M., and Hu, J. (2013). An elastic-viscous-plastic model for over-consolidated clays. Sci. China Technol. Sc. 56 (2), 441–457. doi:10.1007/s11431-012-5108-y

CrossRef Full Text | Google Scholar

Zhang, J. C., Li, X. L., Qin, Q. Z., Wang, Y. B., and Gao, X. (2023b). Study on overlying strata movement patterns and mechanisms in super-large mining height stopes. B Eng. Geol. Environ. 82 (3), 142. doi:10.1007/s10064-023-03185-5

CrossRef Full Text | Google Scholar

Zhang, L. B., Shen, W. L., Li, X. L., Wang, Y., Qin, Q., Lu, X., et al. (2023a). Abutment pressure distribution law and support analysis of super large mining height face. Int. J. Env. Res. Pub He 20 (1), 227. doi:10.3390/ijerph20010227

CrossRef Full Text | Google Scholar

Zhou, F. X., Wang, L. Y., and Liu, H. B. (2020). A fractional elasto-viscoplastic model for describing creep behavior of soft soil. Acta Geotech. 16 (1), 67–76. doi:10.1007/s11440-020-01008-5

CrossRef Full Text | Google Scholar

Zhou, Q. J., and Chen, X. P. (2006). Test study on properties of secondary consolidation of soft soil. Rock Soil Mech. 27 (3), 404–408. doi:10.16285/j.rsm.2006.03.014

CrossRef Full Text | Google Scholar