- 1School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an, China
- 2Key Laboratory of Geotechnical and Underground Space Engineering of Shaanxi Province, Xi’an, China
- 3China Railway 20th Bureau Group First Engineering Co., Ltd., Suzhou, China
In the process of constructing double-track subway tunnels in shallow buried loess areas, the interaction of double-track tunnels is significantly influenced by the net distance and the cross-section size, which is challenging to control the surface settlement. Therefore, the surface settlement prediction is essential while constructing double-track subway tunnels in shallow buried loess areas. The paper analyzed the surface settlement law of shallow buried double-track tunnels in loess areas through theoretical research and numerical simulation. The research results show that with the decrease of the net distance, the surface settlement superimposed curve was double V shape -W shape - single V shape. When the superimposed curve is double V shape and W shape, the Peck formula was used to calculate the surface settlement curve of the single-track tunnel, then superimposed to obtain the final surface settlement curve. When the superimposed surface settlement curve was V shape, based on the Peck formula, the formula for predicting the surface settlement suitable for symmetry and asymmetry was established. The net distance ratio and the area ratio were defined, and considering the tunnel’s interaction, the value and position of the maximum were corrected. Then numerical tests were carried out 16 times with different net distance ratios and area ratios, to determine the parameters of increments and position offsets of the maximum regarding the net distance ratio and the area ratio. Finally, two engineering were conducted for verifying the rationality and applicability exhibited by the prediction formula. The prediction formula served for predicting the surface settlement of double-track subway tunnels in shallow buried loess areas. Which can reduce construction risks and assure the safety of buildings above the ground.
1 Introduction
Loess can be broadly found in western China (He et al., 2013; Song et al., 2021; Xue et al., 2023a), during the implementation of the Western Development Strategy, the number of subway tunnels has increased in loess areas. Subway tunnels in loess areas are generally in the form of double-track (Ding, 2019; Song et al., 2020; Su et al., 2020; Xue et al., 2023b), affected by the occupied space and adjacent buildings, the forms of loess subway tunnels are gradually increasing. The double-track subway tunnel in shallow buried loess areas is affected by the tunnel burial depth, tunnel clearance and surrounding rock, and the construction is difficult to carry out (Chapman et al., 2004; Feng and Yu, 2019; Fan et al., 2021). The original equilibrium state of the stratum will be changed during the excavation, which brings risks to the safety of buildings above the ground (Zhou et al., 2021; Cao et al., 2023; Chen et al., 2023; Xue et al., 2023c).
A lot of previous studies focus on the laws of surface settlement resulting from the excavation of double-track tunnels (DTT) in loess areas. Based on the modified random medium theory, Han and Su (2022) used the standard transformation principle to obtain the polar coordinate expression of the analytical formula, and the research results could serve for predicting the surface settlement resulting from the construction of loess tunnels with arbitrary cross-section. She et al. (2015) summarized the characteristics exhibited by the surface longitudinal settlement trough resulting from the subway tunnel excavation, analyzed the surface displacement release rate and the largest slope of the surface longitudinal settlement, and proposed a prediction method for surface longitudinal settlement. Han and Wang (2012) analyzed the monitoring data of the Chaoyang Gate—KangFu Road tunnel of Xi’an subway Line 1, and studied the longitudinal and transverse surface settlement laws of tunnel excavation in loess areas, then the Peck formula served for establishing the surface settlement prediction model of the excavation of subway tunnels. Zhang et al. (2017) built a 3D elastoplastic model and studied the surface settlement law of DTT in loess areas under different net distances, the research results will serve for optimizing the net distance of double-track subway tunnels in loess areas. He et al. (2012) summarized the monitoring data of the surface settlement in the process of constructing DTT in saturated soft loess areas, and studied the laws regarding the maximum settlement as well as the ground loss rate. Suwansawat and Einstein (2007) calculated the surface settlement resulting from the single-track tunnel (STT) excavation using the Gaussian formula, and superimposed two curves to obtain the final surface settlement curve. Since the interaction between tunnels is not considered, the calculation results are largely different from the monitoring data. Oack (2014) calculated the ground settlement of the first excavation tunnel by using the Peck formula, and calculated the surface settlement of the second excavation tunnel by using the modified Gaussian curve, followed by superimposing the surface settlement of the above two tunnels for obtaining the final surface settlement. Mahmutoğlu (2011) analyzed factors affecting the surface settlement of double-track symmetric tunnels in shallow buried areas, and found the association of the settlement trough change with the surrounding rock disturbance. Hunt (2005) studied the law of surface settlement resulting from DTT excavation through numerical simulation, considering the impact of the second excavation tunnel construction, and corrected the surface settlement curve. Zhou et al. (2021) studied the influencing mechanism regarding DTT excavation by using the Peck formula, for the disturbance resulting from the first excavation tunnel, the disturbance correction factor was input for deriving the prediction formula for the surface settlement resulting from DTT construction. Li (2014) analyzed the factors that caused the surface settlement by tunnel excavation in loess areas, and established a calculation model for surface settlement by using random medium theory. Song et al. (2022) conducted a study on the construction sequence of shallow buried tunnels with small spacing asymmetric section in loess areas, to control the surface settlement, the large-section tunnel should be excavated first. Jiang (2022) optimized the construction parameters of the double side heading method in shallow buried loess subway tunnels, and the result shows that increasing the spacing between the tunnel faces can reduce surface settlement, and the surface settlement curve is a single V-shape after excavation.
Taken together, there are more studies on the surface settlement resulting from double-track subway tunnel excavation in loess areas, but there is a lack of comprehensive research on the symmetry and net distance on the effect of the surface settlement. The paper first analyzes the mechanism of the surface settlement in double-track subway tunnels in shallow buried loess areas, then establishes a surface settlement prediction formula suitable for symmetric and asymmetric double-track subway tunnels in shallow buried loess areas, determines the parameters of increment and position offset of the maximum on surface settlement regarding the net distance ratio and the area ratio. Finally, the reliability of the prediction formula is proved through the application and monitoring comparison of actual projects, and the application sphere of the prediction formula is discussed.
2 Surface settlement mechanisms and prediction formula for double-track subway tunnels
2.1 Peck formula
The Peck formula and the random medium theory are commonly used methods for predicting surface settlement, the Peck formula is simpler and easier to calculate than the random medium theory, in order to increase the practicality of the prediction formula, the paper studied the surface settlement based on the Peck formula, the Peck formula is Eqs 1, 2.
Where S(x) is the surface settlement value at any point of the surface settlement curve, Smax is the maximum of the surface settlement, x is the horizontal distance between the calculated point and the origin, i is the settlement trough width, R is the tunnel diameter, η is the ground loss rate.
2.2 Analysis of surface settlement mechanism
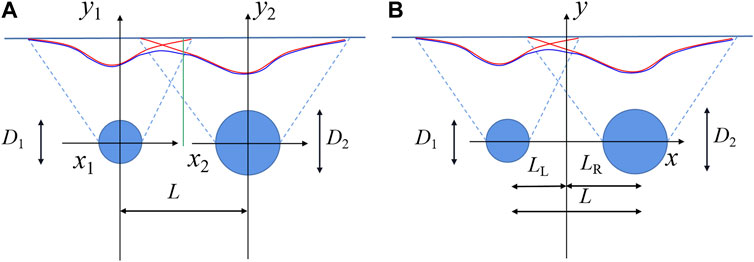
Figure 1 displays the surface settlement curves with the net distance of double-track subway tunnels in shallow buried loess areas, where Di is the tunnel diameter (the value of i is 1, 2) and Lj is the net distance of the tunnel (the value of j is 1, 2, 3, 4, 5, and 6). According to Figure 1A, when the tunnel section is symmetric, two settlement curves do not affect each other when the tunnel net distance is L1, the surface settlement curve is a double V shape, and the Peck formula can serve for calculating the curve and obtaining the maximum of settlement.
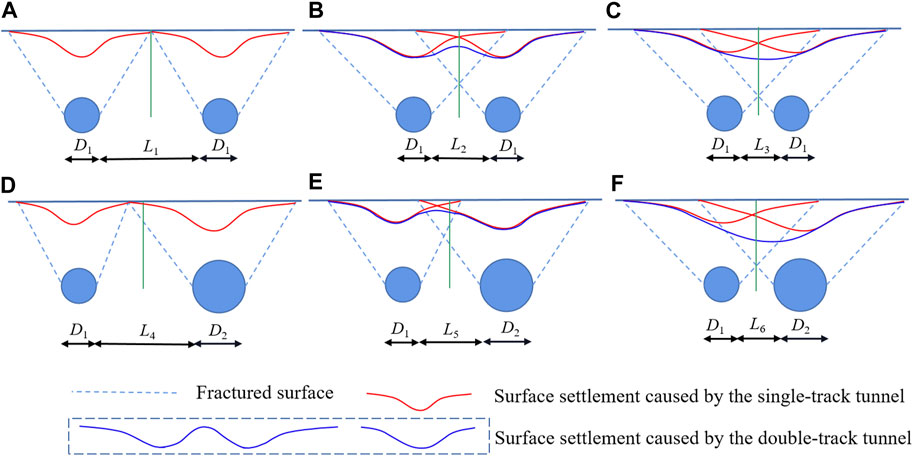
FIGURE 1. Surface settlement mechanism: (A) The net distance of the tunnel is L1, (B) The net distance of the tunnel is L2, (C) The net distance of the tunnel is L3, (D) The net distance of the tunnel is L4, (E) The net distance of the tunnel is L5, (F) The net distance of the tunnel is L6.
According to the research on the law of the surface settlement regarding DTT influenced by the net distance (Chen et al., 2014; Lu et al., 2019), as Lj decreases, the superimposed surface settlement curve is a W shape and the tunnel interaction is small, which is displayed in Figure 1B. The superimposed part has no influence on the value and the position of the maximum, so the surface settlement curve can be obtained by the superposition of the Peck formula. In Figure 1C, when Lj continues to decrease, the tunnel exhibits a large interaction, which changes the value and position of the maximum, the superimposed surface settlement curve is a single V shape, and the surface settlement curve conforms to the normal distribution. Therefore, for double-track symmetric subway tunnels in shallow buried loess areas, with the decrease of Lj, the surface settlement superimposed curve is double V shape -W shape - single V shape. From Figures 1D–F, the surface settlement mechanism of double-track asymmetric subway tunnels is the same as that of double-track symmetric subway tunnels in shallow buried loess areas. When the surface settlement curve is double V shape and W shape, the Peck formula can be used to calculate the single-track tunnel settlement curve and superimposed to obtain the final surface settlement curve. When the surface settlement curve is a single V shape, the surface settlement is normally distributed.
2.3 Establishment of the prediction formula
From the results in Section 2.2, the surface settlement curve can be superimposed by the Peck formula when it is double V shape and W shape. The tunnel center is the coordinate origin when calculating the surface settlement, so the surface settlement curve from the STT cannot be superimposed directly (Song et al., 2018; Yin et al., 2022). In Figure 2A, the formula for the surface settlement in single-track tunnels is Eqs 3, 4.
Where SL(x) is the value at any point of the surface settlement curve of the left tunnel, Smaxl is the maximum of the surface settlement result of the left tunnel, x1 is the horizontal distance between the calculated point and the origin in the left tunnel coordinate system, iL is the settlement trough width of the left tunnel.
Where SR(x) is the value at any point of the surface settlement curve of the right tunnel, SmaxR is the maximum of the surface settlement result of the right tunnel, x2 is the horizontal distance between the calculated point and the origin in the right tunnel coordinate system, and iR is the settlement trough width of the right tunnel.
In Figure 2B, taking the intersection of the tunnel circle center line and the central axis as the origin, a new coordinate system is established. Translate and superimpose the coordinate axis of Eqs 3, 4 to obtain Eq. 5. When both a and b are 0.5, Eq. 5 can superimpose the surface settlement curve for the double-track symmetric tunnel, when a ≠ b, Eq. 5 can superimpose the surface settlement curve for the double-track asymmetric tunnel.
Where S(x) is the value at any point of the superimposed surface settlement curve, a is the LL/L, b is the LR/L, L denotes the horizontal distance between the center of the left and right tunnels, LL denotes the horizontal distance between the central axis of the new coordinate system and the central axis of the left tunnel, LR denotes the horizontal distance between the central axis of the new coordinate system and the central axis of the right tunnel.
When the superimposed surface settlement curve is a single V shape, the maximum of the surface settlement is resulting from the superimposed settlement curve, and the interaction cannot be neglected. Since the surface settlement curve exhibits a normal distribution, it is assumed that the superimposed surface settlement curve is a modified form of Peck formula, and Eq. 5 is rewritten as Eq. 6.
Where
When the surface settlement superimposed curve is a single V shape, the value and position of the maximum will be changed by the tunnel interaction. Specific to DTT, the area difference and the net distance are important factors affecting the surface settlement, so m is defined as the net distance of the tunnel/small section tunnel diameter, and n is the area of the large section tunnel/small section tunnel area. Using
Where
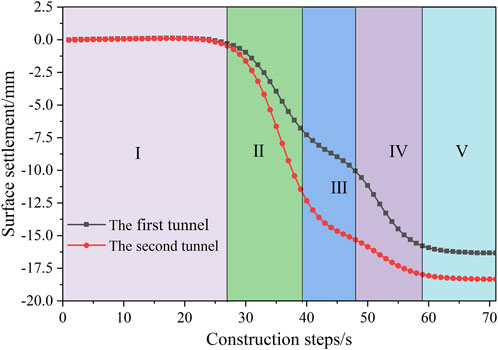
It is necessary to obtain the surface settlement value resulting from the STT excavation before the surface settlement curve is superimposed (Ou et al., 2019). According to Figure 3, the surface settlement during the excavation of DTT falls into five stages: the initial stage of excavation (I)—the stage of the first excavation near the characteristic surface (II)—the stage of the first excavation away from the characteristic surface, the second excavation near the characteristic surface (III)—the stage of the second excavation near the characteristic surface (Ⅳ)—the stage of the second excavation away from the characteristic surface (Ⅴ). Since the second tunnel is not yet excavated upon the excavation of the first tunnel, the surface settlement value at the upper extent of the first tunnel at the end of Stage II is taken as the value of surface settlement resulting from the separate excavation regarding the first tunnel. As the excavation of the first tunnel affected the surface settlement in the second tunnel’s upper part, the variation in the surface settlement in the part at the end of Stage IV and Stage II is taken as the value of surface settlement resulting from the separate excavation regarding the second tunnel.
3 Parameters analysis of prediction formula
3.1 Scheme of numerical simulation
In order to determine f(m,n) and w(m,n) in Eq. (7), the paper compares the surface settlement curve after superposition and completion of excavation through the numerical test, and establishes the equation for increment and position offset of the surface settlement maximum at different m and n, the control variables method is used for the 16 tests, with only m and n changed during the simulation. m is taken as 1, 2, 3, and 4, and n is taken as 1, 2, 3, and 4 for each value of m. In order to control the surface settlement (Wang, 2017; Lu et al., 2019; Zheng and Wu, 2019), the large section tunnel was excavated first in the numerical test, and the results of the numerical test are valid when the superimposed surface settlement curve is a single V shape.
3.2 Finite element mesh and model parameters
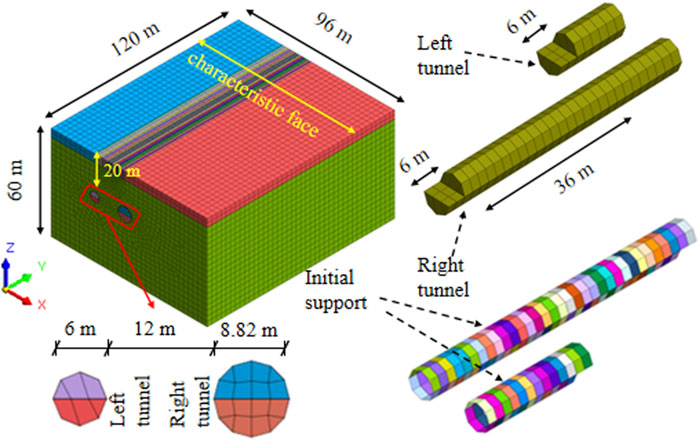
The paper used MIDAS/GTS software to establish a 3D numerical model, the majority of single-track subway tunnels are around 6 m in diameter (Yang, 2017), so the diameter of the small cross-section tunnel is taken as 6 m. Figure 4 illustrates the model (with m is 2 and n is 2), the large section tunnel has a diameter of 8.80 m. Given to which degree the tunnel excavation influences the surrounding rock (Yang, 2017; Lu et al., 2019; Yu et al., 2019), the lengths of the X, Y, and Z direction are 96 m, 120 m, and 60 m respectively, where the Y direction stands for the tunnel excavation direction. The small section tunnel has a burial depth of 20 m. The distance between the excavation faces is 36 m and the step method is adopted for tunnel excavation. The surrounding boundaries of the model are set as horizontal constraints, and the bottom boundary is set as horizontal and vertical constraints.
For eliminating the way the model boundary influences the simulation results (Li et al., 2020; Wei et al., 2023), 100 m away from the initial excavation face is selected as the characteristic face. The soil parameters, the burial depth of the small section tunnel, the construction method, the support measures, and the distance between the excavation faces are kept consistent during the 16 tests.
The surrounding rock adopts the Mohr-Coulomb model and is simulated with 3 D solid element (Xiang et al., 2020; Zhang et al., 2021; Hu et al., 2023), the initial support adopts elastic model and is simulated with 2 D plate element. Table 1 lists the material parameters.
3.3 Simulation process
The excavation footage in the simulation process is 2 m, the upper step of the right tunnel is excavated first, then applying the initial support for the upper step. The distance between the upper and lower steps is 6 m, and then excavating the lower step and applying the initial support for the lower step, the left tunnel undergoes the same excavation process as the right tunnel, and the distance between the upper steps of the left and right tunnels is always 36 m.
3.4 Analysis of simulation results
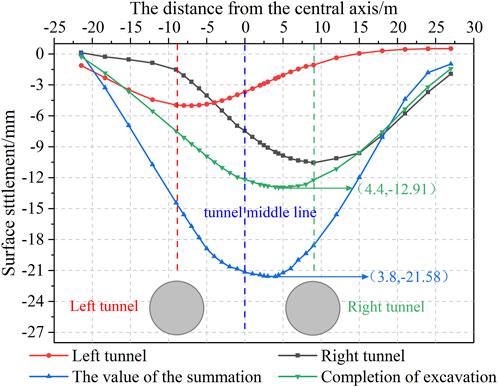
Figure 5 shows the surface settlement change curve in the process of excavation (with m is 2 and n is 1). From Figure 5, there is a symmetric surface settlement curve regarding STT excavation at the tunnel center. The surface settlement maximum after superposition is 12.91 mm, located 4.4 m to the right of the central axis. After excavation, the maximum value is 21.58 mm, which is 3.8 m on the right of the central axis. The increment is 8.67 mm and the position offset is 0.5 m of maximum on the surface settlement, which shows the interaction of tunnels has a greater influence on the value of the maximum and a smaller influence on the position of the maximum.
The simulation is continued according to the method in Figure 5, the final settlement curve and the superimposed settlement curve are compared to obtain all the maximum increments and position offsets, the simulation results are shown in Tables 2, 3.
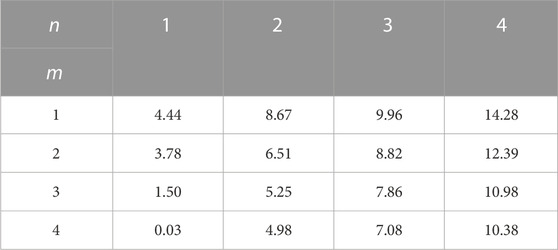
Figure 6 shows the results of data fitting in Tables 2, 3, the value increments and position offsets of surface settlement maximum regarding different m and n are fitted. Figure 6A shows the surface after fitting the 16 maximum value increments, the value increment of the maximum increases with the increase in n for a certain m, as n becomes larger, the effect of large section tunnel on small section tunnel becomes more pronounced. For a given n, the weakened interaction between the left and right tunnels, the increment of the maximum decreases with the increase in m. When n is fixed, the largest change in the maximum increment is 14.28 mm, when m is fixed, the Largest change in the maximum increment is 10.38 mm, which shows that the maximum increment is greatly influenced by m and n. The increments are fitted and the fitted expression is f(m,n)=−0.1706m2−0.0844n2−0.0993 m n+2.3651 m−3.2524 n−3.8213, the fitting degree is 0.9721 and the fit is good.
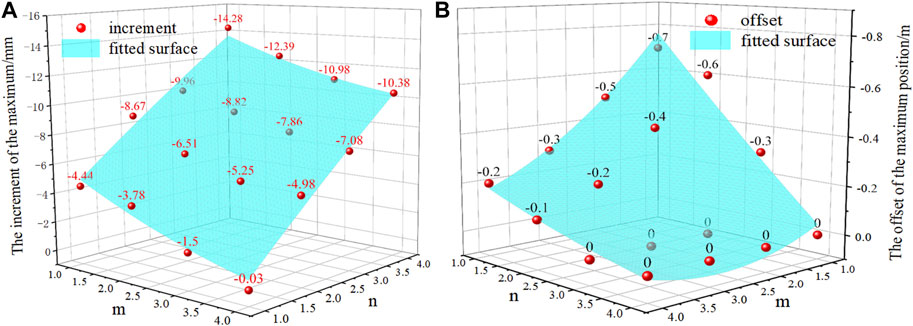
FIGURE 6. Fitting of the surface settlement maximum: (A) Increment of the value, (B) Offset of the position.
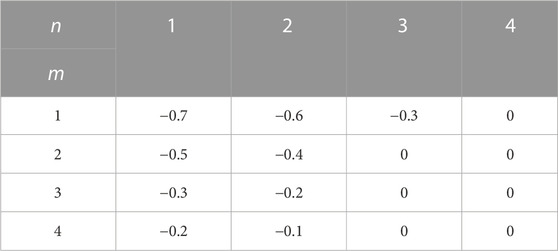
Figure 6B shows the surface after fitting the 16 maximum position offsets. From Figure 6B, when n is 1 and 2, the maximum position offset can be influenced by m in the same way as the maximum increment change law, when n belongs to 3–4 and m belongs to 1–4, the position offset is 0. When n is 1 and m is 1, the position offset is 0.7 m, which indicates that the maximum position offset is slightly influenced by m and n. The position offsets of the maximum are fitted and the fitted expression is w(m,n)=−0.0313m2−0.0063n2−0.0590 m n+0.4113 m+0.3313 n−1.4125, the fitting degree is 0.9120 and the fit is good.
4 Verification of engineering
4.1 Double-track symmetric subway tunnel
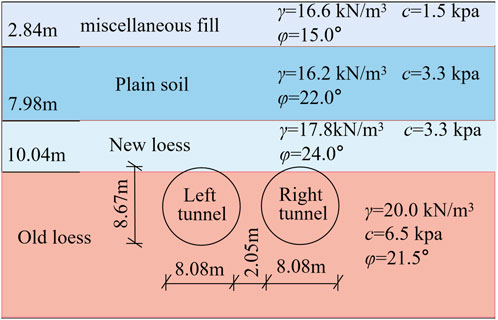
A double-track symmetric subway tunnel of Xi’an Subway Line 3 is located underground on Jinhua North Road, Xi’an, The mileage of the left tunnel is ZDK31+443.908 to ZDK31+503.908, and the mileage of the right tunnel is YDK31+443.965 to YDK31+503.965. The dimension is 8.08 m
The tunnel radius, internal friction angle, and tunnel burial depth are substituted into the Peck formula. The internal friction angle of various geology is calculated by the weighted average method (Hu et al., 2012), and the surface loss rate is taken as 4% for acquiring the surface settlement curve regarding the STT excavation (Han et al., 2007). The two surface settlement curves are superimposed and fitted, then the value of the maximum is corrected by using f(0.25,1) = −12.41 mm, and the position offset of the maximum is corrected by using w(0.25,1) = −0.53 m.
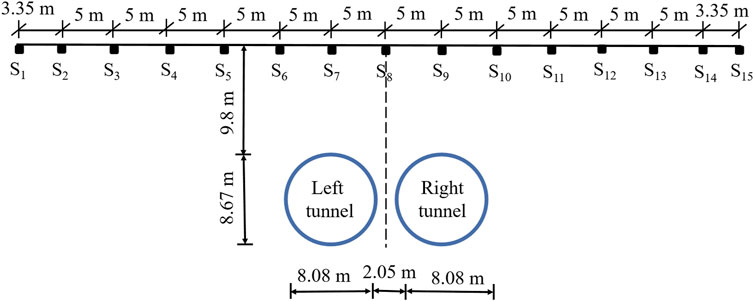
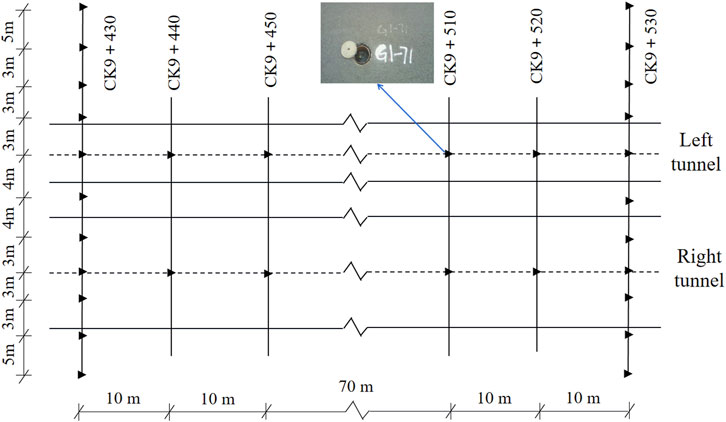
The distance between adjacent monitoring sections along the excavation direction is 5 m, and the lateral arrangement of the monitoring sections is shown in Figure 8, the distance between the monitoring points of the main influence area is 5 m, and the distance between the monitoring points of the secondary influence area is 3.35 m.
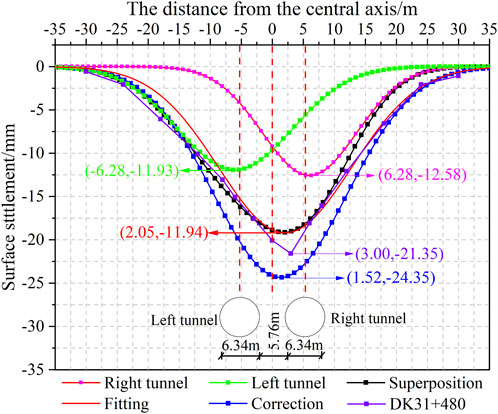
Comparing the superposed surface settlement curve with the monitoring data (DK31 + 480), the results displayed in Figure 9, the surface settlement maximum after superposition is 11.94 mm, which is located at 2.05 m to the right of the central axis. The corrected surface settlement curve and the monitoring data are both single V shape, and the largest values are 24.35 mm and 21.35 mm respectively, with a difference of 3 mm. The maximum is located at 1.52 m and 3 m on the right side of the central axis, and the difference is 1.48 m, which proves the reliability exhibited by the formula in predicting the surface settlement regarding double-track symmetric subway tunnels in shallow buried loess areas.
4.2 Double-track asymmetric subway tunnel
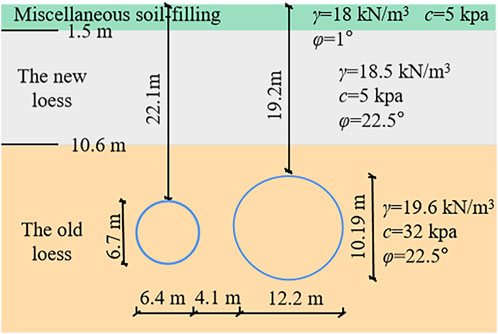
Xi’an Subway Line 4 Yannan Fourth Road Station ∼ Datang Furongyuan Fourth Road Station is mainly along the Furong West Road in Yanta District. A 246-meter double-track asymmetric subway tunnel in shallow buried loess areas is built at the southern end of Datang Furongyuan. The mileage is CK9 + 358.100 to CK9 + 619.325, the geological conditions are miscellaneous fill, new loess, and old loess from top to bottom. The sizes of the right and left tunnels are 12.2 m
The surface settlement curve regarding the STT can be obtained according to the method in Section 4.1. After fitting the superimposed settlement curve, f(0.68,2.72)= −10.70 mm is used to correct the fitted maximum value, and w(0.68,2.72)= −0.40 m is used to correct the fitted maximum position. Surface settlement monitoring points are arranged as shown in Figure 11, the distance between adjacent monitoring sections along the excavation direction is 10 m. Most of the monitoring sections are set up with 2 points and a few with 11 points. In order to fully reflect the final surface settlement caused by the tunnel excavation, the monitoring sections CK9+430 and CK9+530 are selected for analysis.
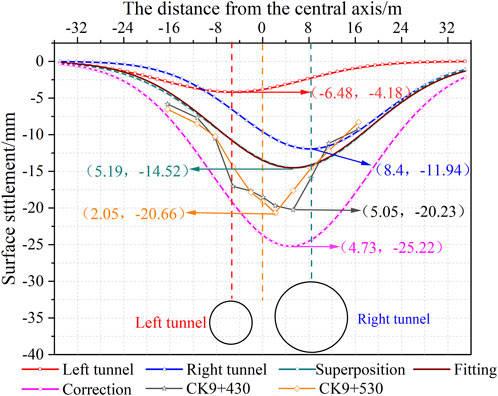
Compare the final surface settlement curve and the monitoring data to get Figure 12. In Figure 12, the maximum value of the superimposed surface settlement is 14.52 mm, located at 5.19 m to the right of the central axis. The corrected surface settlement prediction curve and the monitoring data are single V shape, and the largest corrected surface settlement is 25.22 mm, with an increment of 73.69%, the maximum is located at 4.73 m to the right of the tunnel central axis. The largest surface settlements are 20.66 mm and 20.23 mm in the two monitoring sections respectively, and the locations are 2.05 m and 5.05 m. The corrected surface settlement prediction curve is slightly different from the maximum monitoring data, and the maximum location is in the middle of the maximum locations in the two monitoring sections, which proves the reliability of the prediction formula for predicting surface settlement in double-track asymmetric subway tunnels in shallow buried loess areas.
5 Discussion
Based on the International Tunneling Association (ITA) classification criteria for the tunnel section area, when the left tunnel has a diameter of 6 m and n of 4, the right tunnel is an extra large section tunnel. Thus, in this section, only m is analyzed and studied to determine the applicable range of m when n is 1–4. From the discussion in Section 2.3, the prediction formula is applicable to double-track subway tunnels in shallow buried loess areas where the superimposed surface settlement curve is a single V shape, Therefore, the applicable standard of the formula is that the surface settlement superimposed curve is a single V shape.
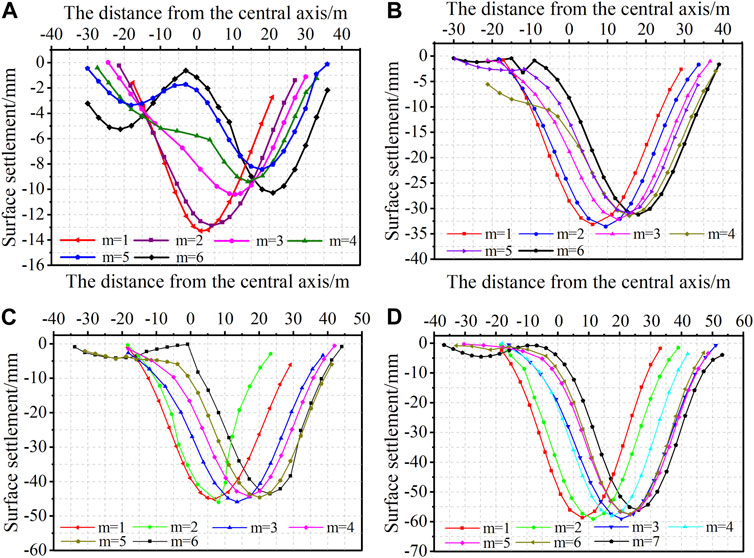
Figure 13 shows the variation of the superimposed surface settlement curve with increasing m for different n. For double-track symmetric subway tunnels in shallow buried loess areas, it can be seen from Figure 13A that the superimposed curve is a single V shape when m is 1, 2, 3, 4, W shape when m is 5, and double V shape when m is 6. This indicates that for double-track symmetric subway tunnels in shallow buried loess areas, the applicable range of m is 1–4.
For double-track asymmetric subway tunnels in shallow buried loess areas, Figures 13B–D show that when n is 2, 3 and m is 1,2,3,4, the superimposed curve is a single V shape, the superimposed curve is a W shape when m is 5, and the superimposed curve is a double V shape when m is 6. When n is 4, m is 1–5, the superimposed curve is single a V shape, when m is 6, the superimposed curve is a W shape, when m is 7, the superimposed curve is a double V shape. The application range of the formula is that when n is 2–3, m is 1–4, and when n is 4, m is 1–5.
The results of the analysis in Figure 13 show that for a certain n, as m increases, the surface settlement superimposed curve changes in a single V shape—W shape—double V shape trend, this indicates the surface settlement mechanism in loess areas is the same for double-track symmetric subway tunnels and double-track asymmetric subway tunnels, which validates the conclusions in Section 2.2.
The prediction formula proposed in the paper is simple in form and easy to take values, and can predict the surface settlement for shallow buried double-track tunnels in loess areas, which is more practical. However, the diameter, the burial depth, and the section shape of the small cross-section tunnel are fixed, which limits the applicability of the prediction formula. Therefore, in the future, the tunnel diameter, the burial depth, and the cross-section shape should be considered to increase the applicability of the prediction formula.
6 Conclusion
The paper examines the surface settlement mechanism regarding double-track subway tunnels in shallow buried loess areas, and divides the superimposed curve of surface settlement into double V shape, W shape, and single V shape. Then the prediction formula is built and relevant parameters are determined by using numerical tests. Finally, the prediction formula is applied to shallow buried double-track subway tunnels project in shallow loess areas. Data monitoring serves for verifying the prediction formula’s reliability and the application range of the prediction formula is discussed. The study has four main four conclusions.
(1) The surface settlement mechanism in loess areas is the same for double-track symmetric subway tunnels and double-track asymmetric subway tunnels. When the superimposed curve of the surface settlement regarding double-track subway tunnels in shallow buried loess areas is double V shape and W shape, the interaction between the left and right tunnels can be ignored, and the Peck formula serves for calculating the surface settlement curve resulted from the single-track tunnel excavation, and then superimposing the surface settlement curve to obtain the final surface settlement curve.
(2) When the superimposed surface settlement curve of double-track subway tunnels in shallow buried loess areas is a single V shape, the net distance ratio and the area ratio are defined. According to the Peck formula, the value and position of the maximum are corrected by considering the interaction of the tunnel, and the final surface settlement expression of double-track subway tunnels in shallow buried loess areas is obtained. Through 16 numerical tests, the parameters on the surface settlement regarding the net distance ratio and the area ratio in the expression are determined.
(3) The formula is applied in symmetric and asymmetric subway tunnels in shallow buried loess areas, which verifies the formula’s rationality and the accuracy of the parameters. Then the scope of application of the formula is discussed. The research results show that when the area ratio is 1 and the net distance ratio is 1–3, the prediction formula is suitable for double-track symmetric subway tunnels in shallow buried loess areas. When the area ratio is 2–3, the net distance ratio is 1–4, the area ratio is 4 and the net distance ratio is 1–5, the prediction formula is suitable for double-track asymmetric subway tunnels in shallow buried loess areas.
(4) The prediction formula served for predicting the surface settlement of double-track subway tunnels in shallow buried loess areas, which can reduce construction risks and ensure the safety of buildings above ground. However, the diameter, the burial depth, and the cross-section shape of the small-section tunnel are fixed. In actual engineering, there has a major difference in terms of the diameter, the burial depth, and the cross-section shape of the tunnel, the predictions in the paper have some limitations. Therefore, the variation of the diameter, the burial depth, and the cross-section shape of the tunnel should be considered, which will be the focus of the prediction modification.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
SW conceived and designed the methods, completed the numerical model. ZS provided the guide of monitoring and theoretical research for the study, and economically supported the project. XT and YS completed data analysis, and the writing of paper manuscript. YZ provided the monitoring materials and completed the data collection. All authors contributed to the article and approved the submitted version.
Funding
This study was supported by the Provincial Natural Science Foundation of Shaanxi (No. 2021JM-373) and the Science and Technology Innovation Team of Shaanxi Innovation Capability Support Plan (No. 2020TD005).
Conflict of interest
Author YS was employed by China Railway 20th Bureau Group First Engineering Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Cao, P., Hu, X. B., Liu, E. L., and Guo, H. Y. (2023). Mechanical properties and numerical simulation analysis on large deformation of Jiangluling Carbonaceous Shale Tunnel. Front. Earth Sci. 2023 (11), 1125410. doi:10.3389/feart.2023.1125410
Chapman, D. N., Rogers, C., and Hunt, D. (2004). Predicting the settlements above twin tunnels constructed in soft ground. Tunn. Undergr. Sp. Tech. 19 (4-5), 78–380. doi:10.1016/j.tust.2004.02.008
Chen, C. L., Zhao, C. L., Wei, G., and Ding, Z. (2014). Prediction of soil settlement induced by double-line shield tunnel based on Peck formula. Rock Soil Mech. 35 (08), 2212–2218. doi:10.16285/j.rsm.2014.08.024
Chen, Y., Tan, L. X., Xiao, N., Liu, K. W., Jia, P. J., and Zhang, W. (2023). The hydro-mechanical characteristics and micro-structure of loess enhanced by microbially induced carbonate precipitation. Geomech. ENERGY ENVIR 34, 100469. doi:10.1016/j.gete.2023.100469
Ding, Z. Y. (2019). Research on ground surface settlement and control induced by double-line tunnels construction. Xi’an: Xi’an University of Science and Technology.
Fan, S. Y., Song, Z. P., Tian, X. X., Wang, K. M., and Zhang, Y. W. (2021). Tunnel deformation and stress response under the bilateral foundation pit construction - a case study. Arch. Civ. Mech. Eng. 21 (3), 1–19. doi:10.1007/s43452-021-00259-7
Feng, H. J., and Yu, R. G. (2019). Numerical analysis of influence of double - line tunnel shield tunneling on ground surface settlement. J. Railw. Eng. Soc. 36 (3), 78–83. doi:10.3969/j.issn.1006-2106.2019.03.014
Han, D., and Su, S, Q. (2022). Prediction of surface settlement caused by construction of shallow-buried and under-excavated subway tunnel in loess stratum. Urb Rd Bdg F C 5 (11), 168–170+177+21. doi:10.16799/j.cnki.csdqyfh.2022.11.045
Han, R. M., and Wang, Y. Z. (2012). Analysis and prediction for ground subsidence of subway tunnel built in saturated soft loess. Urb Rpd Rail Transit 25 (2), 74–78. doi:10.3969/j.issn.1672-6073.2012.02.019
Han, X., Li, N., and Jamie, R. S. (2007). An adaptability study of Gaussian equation applied to predicting ground settlements induced by tunneling in China. Rock Soil Mech. 28 (01), 23–28+35. doi:10.3969/j.issn.1000-7598.2007.01.005
He, L. C., Wang, M. S., and Li, Y. J. (2013). Supporting technology for shallow large-span neighborhood loess tunnel. Rock Soil Mech. 34 (S2), 306–310. doi:10.16285/j.rsm.2013.s2.048
He, N. N., Li, P., Shao, S. J., Li, J. K., and Jiao, Y. Y. (2012). Ground settlement monitoring above Xi'an Metro tunnel through the saturated soft loess. J. Earth Sci. Environ. 34 (1), 96–103. doi:10.3969/j.issn.1672-6561.2012.01.013
Hu, B., Liu, Y. L., Tang, H. M., and Xu, H. Q. (2012). Research on ground subsidence due to tunnel excavation in huquan-mingdu section of wuhan subway. Chin. J. Rock Mech. Eng. 31 (05), 908–913. doi:10.3969/j.issn.1000-6915.2012.05.006
Hu, Z. N., Zhang, J., Wang, Y. G., and Wang, Y. F. (2023). Mechanical behaviors of surrounding rock and supporting structure of shallowburied unsymmetrical pressure tunnel crossing soil–rock interface. Front. Earth Sci. 10, 1113430. doi:10.3389/feart.2022.1113430
Hunt, D. (2005). Predicting the ground movements above twin tunnels constructed in London Clay. Birmingham: University of Birmingham.
Jiang, Z. L. (2022). Optimization of construction parameters for the double sidewall guide trench method in shallow buried metro tunnels in loess areas. Railw. Eng. 62 (03), 126–131. doi:10.3969/j.issn.1003-1995.2022.03.28
Li, C. L., Wu, K., Qin, S., and Shao, Z. S. (2020). Theoretical investigation to the effect of bolt reinforcement on tunnel viscoelastic behavior. Arab. J. Sci. Eng. 45 (5), 3707–3718. doi:10.1007/s13369-019-04215-9
Li, M. (2014). Study and prediction the surface settlement in the loess strata during shield construction. Xi’an: Xi’an University of Science and Technology.
Lu, J., Yao, A. J., Zheng, X., Zhang, J. T., and Tian, T. (2019). Study on the law and computational method of ground surface settlement induced by double-line tunnel excavation. Chin. J. Rock Mech. Eng. 38 (S2), 3735–3747. doi:10.13722/j.cnki.jrme.2019.0630
Mahmutoğlu, Y. (2011). Surface subsidence induced by twin subway tunnelling in soft ground conditions in Istanbul. B Eng. Geol. Environ. 70 (1), 115–131. doi:10.1007/s10064-010-0289-8
Ocak, I. (2014). A new approach for estimating the transverse surface settlement curve for twin tunnels in shallow and soft soils. Environ. Earth Sci. 72 (7), 2357–2367. doi:10.1007/s12665-014-3145-5
Ou, X. D., Luo, B. X., Jiang, J., Qin, Jinxi., and Yang, S. N. (2019). Study on prediction model of surface settlement of shield double-ine tunnel in nanning metro. J Guangxi Univ (Nat Sci Ed). 44 (04), 1010–1020. doi:10.13624/j.cnki.issn.1001-7445.2019.1010
Qi, W. Q., Yang, Z. Y., Jiang, Y. S., Shao, X. K., Yang, X., and He, Q. (2021). Structural deformation of existing horseshoe-shaped tunnels by shield overcrossing. Ksce J. Civ. Eng. 25 (2), 735–749. doi:10.1007/s12205-020-0599-8
She, F. T., Wang, Y. X., and Zhang, Y. (2015). Surface longitudinal settlement induced by subway tunneling in loess and its prediction analysis method. Rock Soil Mech. 36 (S1), 287–292. doi:10.16285/j.rsm.2015.S1.049
Song, Z. P., Liu, Y, L., and Zhang, Y. W. (2021). Research and prospect of demarcation of deep and shallow buried in loess tunnel. Hazard Control Tunn Undergr Eng 3 (2), 1–15. doi:10.19952/j.cnki.2096-5052.2021.02.01
Song, Z. P., Li, S. H., Zhang, X. G., Wang, J. B., and Wang, Tao. (2018). Study on strata settlement regular pattern inducedby tunnel construction based on Peck formula. Xi' Univ. Arch. Tech. (Nat Sci Ed). 50 (02), 190–195. doi:10.15986/j.1006-7930.2018.02.006
Song, Z. P., Tian, X. X., Li, H., Zhang, Y., W., and Zhou, G. N. (2020). Numerical analysis and application of the construction method for the small interval tunnel in the turn line of metro. Sci. Progress-Uk 103 (3), 0036850420932067. doi:10.1177/0036850420932067
Song, Z. P., Wang, S. Y., Su, C. S., Pan, H. W., and Wei, S. F. (2022). Optimization of construction scheme for shallow buried tunnel with small spacing asymmetric section in loess stratum. J. Xi' Univ. Arch. Tech. (Nat Sci Ed). 54 (5), 646–656. doi:10.15986/j.1006-7930.2022.05.002
Su, K., Zhang, Y. J., Cui, J. P., and Li, C. A. (2020). Installation time of ground support during tunnel excavation: A novel graph methodology. Ksce J. Civ. Eeg 24 (12), 3866–3874. doi:10.1007/s12205-020-1079-x
Suwansawat, S., and Einstein, H. H. (2007). Describing settlement troughs over twin tunnels using a superposition technique. J. Geotech. Geoenviron 133 (4), 445–468. doi:10.1061/(asce)1090-0241(2007)133:4(445)
Wang, T. (2017). Study on construction optimization and deformation control of shallow buried large span small spacing tunnel in loess areas. Xi’an: Xi’an University of Architecture and Technology.
Wei, J. J. (2018). The law of surrounding rock and ground surface deformation in loess tunnel construction. Sci Tech Eng. 18 (11), 287–292. doi:10.3969/j.issn.1671-1815.2018.11.045
Wei, S., Hong, Z. L., Yang, M., Li, N., and Tan, T. X. (2023). Impact of subway shield tunnel construction on deformation of existing utility tunnel. Front. Earth Sci. 11, 1104865. doi:10.3389/feart.2023.1104865
Xiang, L., Wang, F., Jin, B. C., Wang, B., Tian, C. M., and Ou, Y. (2020). Surrounding rock pressure of loess deep large-diameter shield tunnel. Chin. Civ. Eng. J. 53 (S1), 112–118. doi:10.15951/j.tmgcxb.2020.s1.019
Xue, Y., Liu, J., Liang, X., Li, X., Wang, S. H., Ma, Z. Y., et al. (2023b). Influence mechanism of brine-gas two-phase flow on sealing property of anisotropic caprock for hydrogen and carbon energy underground storage. Int. J. HYDROGEN ENERG 48(30): 11287–11302. doi:10.1016/j.ijhydene.2022.05.173
Xue, Y., Liu, S., Chai, J., Liu, J., Ranjith, P. G., Cai, C. Z., et al. (2023a). Effect of water-cooling shock on fracture initiation and morphology of high-temperature granite: Application of hydraulic fracturing to enhanced geothermal systems. Appl. ENERG 337, 120858. doi:10.1016/j.apenergy.2023.120858
Xue, Y., Ranjith, P. G., Gao, F., Zhang, Z. Z., and Wang, S. H. (2023c). Experimental investigations on effects of gas pressure on mechanical behaviors and failure characteristic of coals. J. ROCK Mech. Geotech. 15 (2), 412–428. doi:10.1016/j.jrmge.2022.05.013
Yang, Z. D. (2017). Study on shield tunnel section size for Tianjin metro new line. Mod. Urt (10), 47–50.
Yin, G. M., Fu, H. L., Hou, W. Z., and Yang, S. S. (2022). Introduction of several methods of value of Peck formula parameters. J. Railw. Sci. Eng. 19 (07), 2015–2022. doi:10.19713/j.cnki.43-1423/u.T20210810
Yu, S., Jiang, X. H., Wang, D. L., Xu, T., Kong, Y., Cui, C., et al. (2019). RBCK1 promotes p53 degradation via ubiquitination in renal cell carcinoma. Mod. Tunn. Technol. 56 (S2), 254–262. doi:10.1038/s41419-019-1488-2
Zhang, T., Zhou, H., Lai, J. X., Wang, K., and Feng, Z. H, (2017). Optimization of clearance of tunnel in xi'an metro constructed with double shield TBM. Road. Mach. Constr. Mech. 34 (10), 78–83. doi:10.3969/j.issn.1000-033X.2017.10.011
Zhang, Y. T., Sun, X. L., Yang, B., and Sun, Y. J. (2021). Influence of local expansion on safety of tunnel support. Tunn. Constr. 41 (S2), 306–312. doi:10.3973/j.issn.2096-44982021.S2.039
Zhang, Z. Y., Zhao, C. Y., Long, P., Zhang, X. H., and Lei, M. F. (2022). Research on the stability of shallow-buried large cross-section tunnel by construction method conversion. Front. Earth Sci. 10, 37. doi:10.3389/feart.2022.831169
Zheng, X. X., and Wu, S. S. (2019). Research on deformation control of asymmetric neighborhood large-span shallow buried city tunnel. Tech Hwy Trans. 35 (03), 94–99. doi:10.13607/j.cnki.Gljt.2019.03.016
Zhou, P. Y., Wang, J. B., Song, Z. P., Cao, Z. L., and Pei, Z. M. (2022). Construction method optimization for transfer section between cross passage and main tunnel of metro station. Front. Earth Sci. 10, 183. doi:10.3389/feart.2022.770888
Keywords: prediction, surface settlement, double-track, subway tunnels, shallow buried, peck formula
Citation: Wang S, Song Z, Tian X, Sun Y and Zhang Y (2023) Prediction for the surface settlement of double-track subway tunnels for shallow buried loess based on peck formula. Front. Earth Sci. 11:1219544. doi: 10.3389/feart.2023.1219544
Received: 09 May 2023; Accepted: 15 June 2023;
Published: 26 June 2023.
Edited by:
Yi Xue, Xi’an University of Technology, ChinaReviewed by:
Pengpeng Ni, Sun Yat-Sen University, ChinaKun Fang, China University of Geosciences Wuhan, China
Zhengzheng Cao, Henan Polytechnic University, China
Copyright © 2023 Wang, Song, Tian, Sun and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhanping Song, c29uZ3pocHl0QHhhdWF0LmVkdS5jbg==
 Shuangyuan Wang
Shuangyuan Wang Zhanping Song
Zhanping Song Xiaoxu Tian
Xiaoxu Tian Yinhao Sun
Yinhao Sun Yuwei Zhang
Yuwei Zhang