Sensitivity limits for strain detection of hypothetical remote fluid-induced earthquakes (Mw ≥ 4): a case study in Taiwan

Capturing and quantifying the timing of remotely triggered earthquakes and understanding the physical processes responsible for this delay represent major challenges in earthquake forecasting. In this study, we propose a physical framework for the integration of borehole strainmeter observations for the investigation of remote triggering of moderate to large earthquakes (M_w ≥ 4) in Taiwan. Based on the time-delay computation between regional events and global earthquakes, we establish a selection of earthquakes showing fault zone properties (hydraulic diffusivity and nucleation length) that may be compatible with a magnitude-dependent fluid-induced nucleation process. Using theoretical fault zones parameters, we calculate the evolution of fluid pressure transiting along the nucleation region under the assumption of a one-dimensional, homogeneous poroelastic medium. Pore pressure levels reached before earthquake rupture are ranging from about 0.02 kPa to 3 kPa in the case of teleseismic wave-induced elastic pressure ranging from 0.15 kPa to 27.3 kPa. To compute the time-dependent evolution of deformation generated by a remote diffusing pressure front, we model the nucleation region using the analogue volcano source represented by a horizontal circular crack, and calculate synthetic dilatation at the strainmeter location from displacements using a finite-difference approach. In general, predictions are about two to four orders of magnitude smaller than observations (∼ 10^–5 to 10^–3 nϵ). Therefore, this suggests that detection of pore pressure-related deformation would have required change of volume in the nucleation region that is at least one order of magnitude larger than for the hypothetical cases considered here. The study represents the first attempt to analyze strain time-series for detecting pre-earthquake strain anomalies related to fluid-induced earthquakes and illustrates the challenge for detecting and characterizing intermediate-to far-field earthquake precursors caused by fluid flow in active regions.

1 Introduction

Seismic waves from large earthquakes induce ephemeral dynamic stress perturbations over large distances (Huang et al., 2004). Despite leaving no permanent stress changes once they pass, seismic waves are capable of triggering earthquakes at distances far beyondthe aftershock region (Hill, 2008; Brodsky and van der Elst, 2014; Miyazawa et al., 2021). Remote dynamic triggering is a rare ($<$ 2% of the time) (Pankow and Kilb, 2020) but ubiquitous phenomena (Velasco et al., 2008), and the number of evidence keeps growing since the first observations of entensive earthquake triggering in the United States following the 1992 moment magnitude (M_w) 7.3 Landers earthquake (Hill et al., 1993) and the 2002 M_w 7.9 Denali Fault earthquake (Gomberg et al., 2004). In general, dynamically triggered earthquakes occur subsequent to the passage of the surface waves (Hill, 2008; Velasco et al., 2008) with periods of 15–20 s, since they dominate gound motion in the far field (waves with smaller periods tend to be scattered and attenuated) (van der Elst and Brodsky, 2010). However, the optimal conditions for triggering remain unknown and the latter represents likely a complex combination of wave characteristics (e.g., peak amplitude, duration) and local environment (fault types and geometry and wave incidence angle) (Parsons et al., 2014). If long-lasting (hundred of seconds) dynamic perturbations at moderate to high strain level ($>$ 100 nϵ or equivalently ∼ 3 kPa) may be an efficient combination for triggering (Pollitz et al., 2012; Johnson and Bürgmann, 2016), peak strain level of teleseismic waves represents a key contribution to long-range triggering (van der Elst and Brodsky, 2010) and critically stressed faults can also rupture under strain level that is near the background noise (∼ 2 nϵ) (van der Elst and Brodsky, 2010; Miyazawa et al., 2021) [Supplementary Figure S1 in the Electronic Supplement shows a case of remote triggering at very low regional strain in Central Greece (Bernard et al., 2006; Canitano et al., 2013)].

Establishing a temporal relationship between two events is simple because seismicity is produced continuously in active tectonic regions. More challenging is to establish temporal and spatial causation between two distant earthquakes. The longer the delay between the mainshock and the posited event, the more difficult to connect them. This delay, which represents a fundamental characteristics of remote triggering, may be difficult to explain by a simple Coulomb failure model only (e.g., Belardinelli et al., 2003). Conversely, a small, or the absence of delay between two events does not necessarily imply remote triggering, as still remains the possibility of coincidental occurrence of events. Indeed, Parsons et al. (2014) found that as many as five earthquakes with M_w ≥ 6 can occur purely by chance on any given day, for example. Since most of observed remote triggering cases concern microearthquakes and tectonic tremors (Peng et al., 2009; Peng et al., 2011; Gonzalez-Huizar et al., 2012), the magnitude range of the triggered earthquakes is still subject to debate. Many studies report the very rare occurrence of moderate to large earthquakes (M_w ≥ 5) remotely triggered hours to days following large teleseisms (M_w ≥ 7) (Parsons and Velasco, 2011; Johnson et al., 2015) while O’Malley et al. (2018) found that higher magnitude earthquakes occur more often than smaller events within 3 days following the passage of seismic waves. In Taiwan, detection of triggered microseismicity and tectonic tremors has also been reported (Chao et al., 2011; Sun et al., 2015), but whether larger events were triggered has not been demonstrated yet. Remote triggering is generally established using statistically significant variations in earthquake rate coincident with the passage of seismic waves (e.g., Johnson and Bürgmann, 2016; Yao et al., 2021). However, going beyond rate changes as the sole indicator for remote triggering (Pankow and Kilb, 2020) is essential for capturing and quantifying the timing of the triggered earthquakes and understanding the physical processes responsible for this delay whose remain major challenges in earthquake forecasting (Brodsky and van der Elst, 2014).

In this study, we propose a physical framework for the integration of borehole strainmeter time-series for the investigation of remote triggering of moderate to large earthquakes (M_w ≥ 4) in Taiwan. We first analyze the time-delay between any regional event with M_w ≥4 from 2000 to 2022 and the global earthquake with M_w ≥ 7 that precedes it (Supplementary Section S1; Supplementary Figure S2 in the Electronic Supplement) and then establish a selection of regional earthquakes based on a magnitude-dependent fluid-induced nucleation framework (Parsons et al., 2017). We then investigate pre-earthquake strain signals and propose an approach to compute far-field dilatation induced by an overpressure front diffusing in a fracture. Finally, we discuss the limitations faced for strain detection of the precursory phase related to hypothetical remote fluid-induced earthquakes.

2 Event selection based on a fluid-induced nucleation model

Among the diverse mechanisms proposed to explain delayed remote triggering of earthquakes with all magnitudes (Parsons, 2005; Peng et al., 2011; Shelly et al., 2011), a mechanism in particular shows that delays observed in the case of triggered earthquakes are likely not randomly distributed but are rather proportional to the event magnitudes (Parsons et al., 2017). The mechanism relies on the fact that dynamic straining from seismic waves can break a fluid seal previously blocked into a fault zone (Brodsky et al., 2003) which then releases overpressurized fluid that progressively invades the fault region. Pore fluid infiltration reduces clamping normal stress (strength is reduced with increasing pore pressure) and thus helps promote failure according to the Coulomb failure criteria. Only critically stressed faults are hydraulically conductive (Barton et al., 1995) and thus prone to fluid-induced triggering. As such a process implies fluid flow through a fault zone, a delay is required before failure conditions are met. This fluid transit time increases with earthquake magnitude since the latter is directly proportional to the dimensions of the fault rupture (Kanamori, 1977). Besides, earthquake magnitude also scales with the critical nucleation dimension (2L_c, in meter) which represents the size of the smaller asperity where rupture may initiate (Ohnaka, 2000):

$2L_c=\sqrt[3]{10^{-9}{M}_0}(1)$

where M₀ represents the scalar seismic moment (in N.m). The critical nucleation dimension represents the minimum transit distance for a fluid to induce an earthquake of a given magnitude, and measures 0.1 km to about 1.5 km for a magnitude range between 4 and 6.5, for example. Fluid transit from a highly pressurized source through a porous medium follows a diffusion behavior (Malagnini et al., 2012):

$r=2.32\sqrt{Dt}(2)$

where r is the distance from the pressure source, t is time and D is the hydraulic diffusivity.

Since the time-delay between a transient stressing of the Earth’s crust and the eventual occurrence of remote earthquakes may be diagnostic of their nucleation process (Parsons et al., 2017), we establish a regional earthquake selection that may be compatible with a possible fluid-induced nucleation model. We retain the regional events for which estimated time-delays may be consistent with commonly observed fault zone diffusivity values (typically D ∼ 10^–2 to 10 m².s⁻¹) (Parsons et al., 2017; Guo et al., 2021). We extend our selection to a delay of approximately 1 week to include some of the largest events (M_w ≥ 6.4) from the preliminary selection (Supplementary Section S1). We estimate maximum trough-to-peak dilatation of the Rayleigh wave using the waveform similarity between dilatation ϵ_v and the vertical component of the seismic acceleration a_z (Canitano, 2020):

${ϵ}_v=\left(\frac{0.12T_c}{\pi V_r}\right)\left(\frac{1-2\gamma }{\gamma }\right)a_z(3)$

where T_c is the Rayleigh wave main period (T_c = 15 s), γ denotes the Poisson’s ratio (γ = 0.25) and V_r the Rayleigh wave phase velocity (V_r = 4 km.s⁻¹). A good waveform coherence is observed between signals (Supplementary Figure S3) while amplitude discrepancies (about 10%–15%) may be related to uncertainties in the borehole strainmeter calibration protocol (Canitano et al., 2018). We consider a Rayleigh wave trough-to-peak strain amplitude of 2 nϵ as limit and we adjust the delay by estimating the time-difference between the arrival time of the Rayleigh wave with maximum amplitude at the strong-motion station and the regional event onset (Figure 1). Maximum Rayleigh wave amplitude ϵ_m associated with the retained 22 regional events are ranging from 5 nϵ to about 900 nϵ with epicentral distances from about 1,400 km to 18,000 km (Supplementary Figure S3; Table 1). Regional events are showing delays ranging from about 20 min to 6 days and M_w from 4.12 to 6.80 (Table 2). Figure 2A presents the retained earthquakes integrated in a magnitude-dependent critical nucleation model.

FIGURE 1

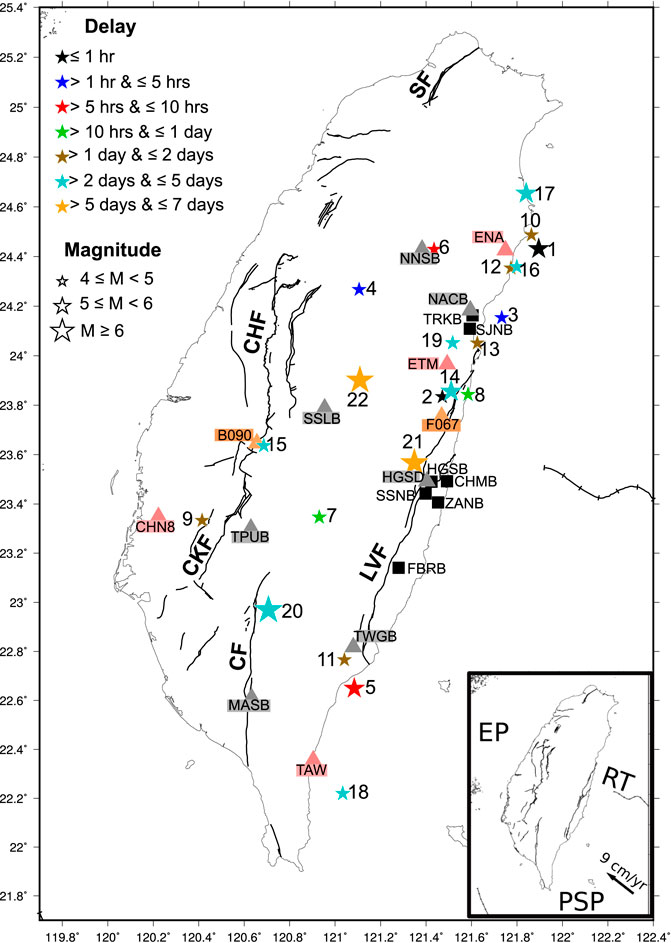
FIGURE 1. Location, magnitude and delay associated with the retained events. Triangles denote strong-motion stations (Broadband Array for Seismology in Taiwan (BATS) Institute of Earth Sciences, Academia Sinica (1996), Taiwan Strong Motion Instrumentation Program (TSMIP) and Central Weather Bureau Seismic Network (CWBSN) are shown in gray, orange and pink, respectively) used for estimating peak dynamic strain and black squares show borehole strainmeters used for analyzing strain changes (11 events). LVF: Longitudinal Valley fault; CF: Chaochou fault; SF: Shanchiao fault; CHF: Chelungpu fault; CKF: Chukou fault. (Inset) Geodynamic framework of Taiwan (RT: Ryukyu trench; EP: Eurasian plate; PSP: Philippine Sea plate). The black arrow indicates the relative motion between the PSP and the EP.

TABLE 1

TABLE 1. Characteristics of the mainshocks (M_w ≥ 7) preceding the retained regional events.

TABLE 2

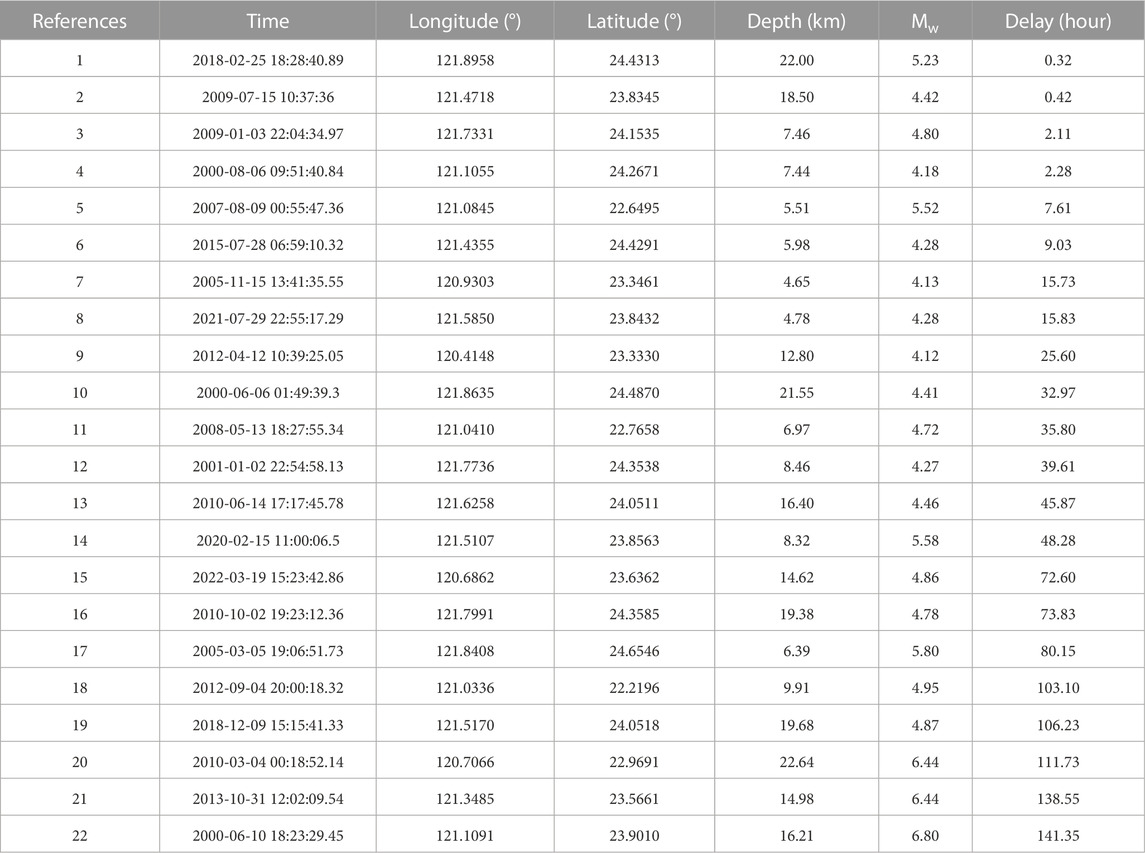
TABLE 2. Regional earthquakes (M_w ≥ 4 with depth ≤25 km) integrated in a fluid-diffusion nucleation model. Events are listed by increasing time-delay.

FIGURE 2

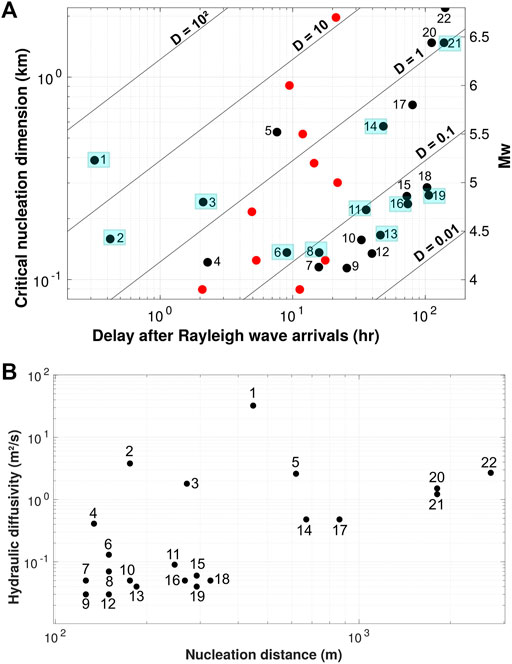
FIGURE 2. (A) Magnitude-dependent nucleation dimension (2L_c) versus time-delay for the target earthquakes (black dots). The red dots show remotely triggered earthquakes from Parsons et al. (2017). Events for which precursory deformation changes are investigated are outlined by a blue shaded box. Fault zones diffusion rates (Eq. 2) are plotted for diffusivity values ranging from 10^–2 to 10² m² s⁻¹. (B) Theoretical nucleation distance versus fault hydraulic diffusivity for the retained regional earthquakes (Table 2).

3 Investigation of pre-earthquake strain anomalies

We investigate pre-earthquake anomalies using Sacks-Evertson (Sacks et al., 1971) borehole strainmeter sensors. Given their very high sensitivity at short-to intermediate-period (minutes to weeks), strainmeters represent a powerful tool to search for crustal strain transients, including anomalies preceding earthquakes (Amoruso and Crescentini, 2010; Canitano et al., 2015). We process the 1-min sampling strain time-series [see Canitano et al. (2018); Canitano et al. (2021) for details] for stations located at a maximum distance of about 50 km from our target events (11 events). Other events are either too far from operating stations ($>$ 80 km) or occurred prior to the network deployment. Figure 3 and Supplementary Figure S4 present the temporal evolution of dilatation over a time-span of minutes to days preceding regional events.

FIGURE 3

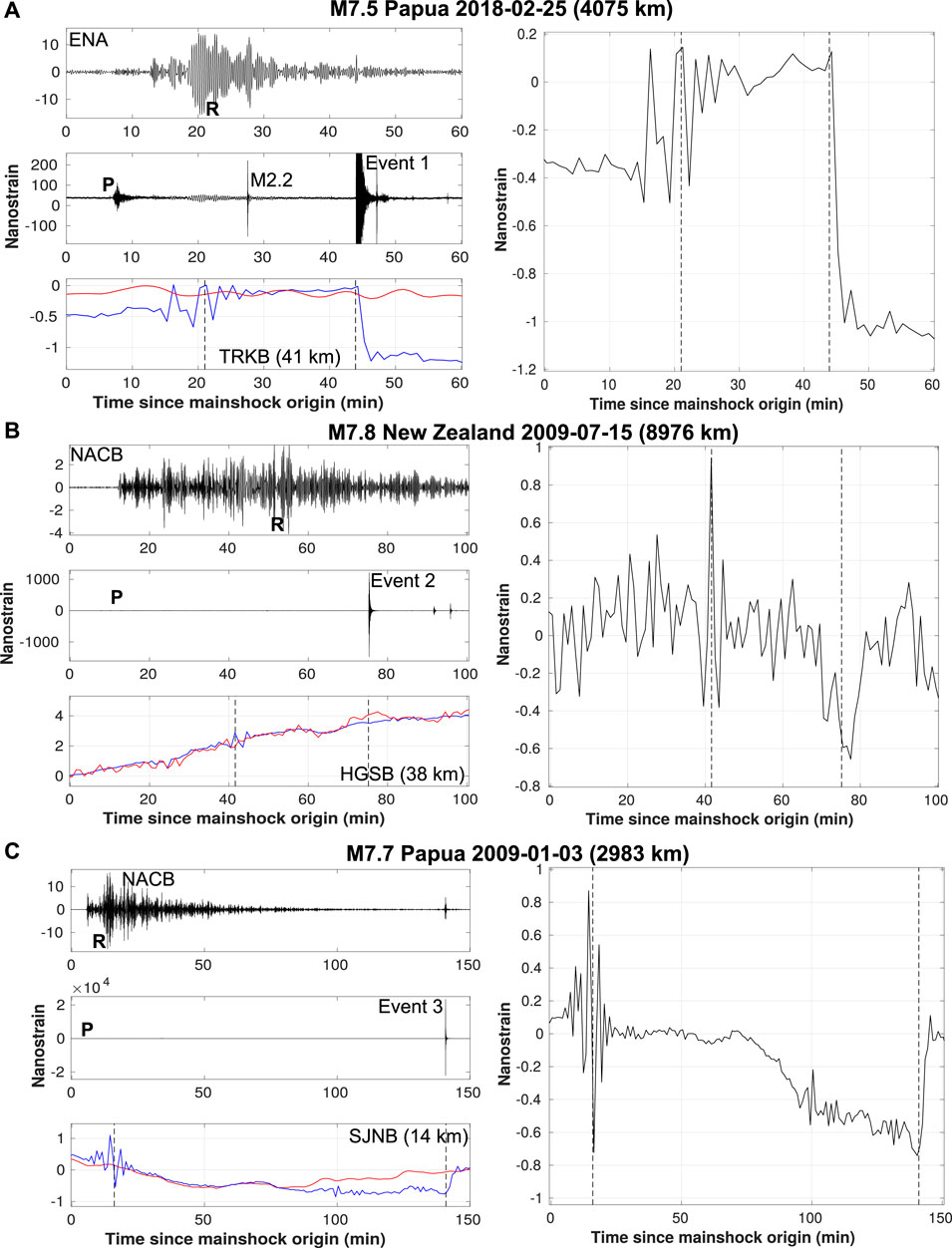
FIGURE 3. Investigation of pre-earthquake anomalies in borehole strain data related to regional earthquakes occurring shortly following the passing of Rayleigh waves (≤2 h) from global events: (A) 25 February 2018 M_w 5.23 earthquake (event 1), (B) 15 July 2009 M_w 4.42 earthquake (event 2) and (C) 3 January 2009 M_w 4.80 earthquake (event 3). (Left) From top to bottom: dilatation estimated from converted vertical seismic acceleration signal bandpassed between 10 and 25 s (R denotes Rayleigh waves with maximum amplitude) and raw signal (P denotes P-wave arrivals), respectively and dilatation recorded by borehole strainmeter (blue curve) and air pressure-induced dilatation (red curve). (Right) Residual dilatation signal (i.e., corrected for air pressure-induced strain). Vertical black dashed lines depict the arrivals of Rayleigh waves with maximum amplitude and the regional event onset, respectively. Strain expansion is positive.

In general, dilatation level after correction of external perturbations ranges from approximately 10^–1 to 5.10^–1 nϵ at the period of minutes to hours and then increases to about 1 nϵ at a daily period to a tens of nanostrain at the period of a few days. For events 1 and 2, which occurred during the passage of surface waves from global earthquakes, we observe no pre-rupture strain variations at remote strainmeters (40 km away). Event 3 (M_w 4.80) possibly represents the most favorable case for detecting subnanometric near-source strain variations (Figure 3C). It occurred at shallow depth (7 km), about 14 km away from SJNB station, and 2 h following the Rayleigh wave arrivals of a M_w 7.7 earthquake in Papua. Strain variations are strongly correlated with atmospheric pressure for about 45–50 min after the Rayleigh wave arrivals (15 min after the mainshock origin time), then suddenly the correlation breaks, suggesting the possible detection of an other source of deformation. We observe a gradual expansion starting about 1 h preceding the regional earthquake with a total deformation of about −7.10^–1 nϵ, well above the short-period strain noise of approximately 10^–1 nϵ. For event 11, large pore pressure variations ($>$ 25 kPa) induced by the intense Rayleigh wave straining in southern LV (about 1 μϵ) following the 2008 Eastern Sichuan earthquake may be expected. However, we find no evidence of pre-earthquake variations, which illustrates the complexity for detecting subnanometric deformation at periods larger than 12–24 h because signals are also impacted by environmental perturbations, especially rainfall (Hsu et al., 2015; Mouyen et al., 2017), and by low tidal strain noise remaining after correction (∼ 0.5-1 nϵ) (Supplementary Figure S4). Finally, strain contraction of −10 nϵ and −20 nϵ are observed hours to days preceding event 16 and event 21, respectively, and are analyzed in the next section.

4 Connecting strain observations to transient pressure anomalies

To connect the strain observations to potential transient pressure anomalies, we follow a two-step approach. In a first step, we calculate the temporal variation of the theoretical pore pressure induced in the fracture by the passing seismic waves. In a second step, we compute the time-dependent evolution of dilatation generated by a remote diffusing pressure front at the sensor location.

4.1 Theoretical pressure induced in the fracture by elastic waves

The evolution of pore pressure P in the fracture in the case of a one-dimensional (1-D), semi-infinite, isotropic, homogeneous poroelastic medium, is given by (Duoxing et al., 2015):

$P\left(x,t\right)=P_m\left[1-erf\left(\frac{x}{2\sqrt{Dt}}\right)\right](4)$

where P_m represents trough-to-peak stress of seismic waves (obtained through ϵ_m for Hooke’s law), erf is the error function, x is the distance in the fracture, t is transit time and D is the hydraulic diffusivity. Pore pressure at x = 0 (i.e., before fluid initiates transit) is equal to seismic wave elastic pressure (P(x = 0, t) = P_m) and estimates range from 0.15 kPa to 27.3 kPa. To estimate the pressure level at the time of the rupture, that is when the fluid has transited along the entire nucleation region (x = 2L_c), we estimate the nucleation length for each event (Eq. 1) and then calculate hydraulic diffusivity using the nucleation length and the estimated time-delay (or transit time) following Eq. 2. Theoretical diffusivity factors range from 0.03 to 30 m².s⁻¹ for nucleation distances 2L_c of about 0.13–2.7 km (Figure 2B) and are generally consistent with estimates from Feng et al. (2021). Pore pressure levels before rupture occurs are ranging from about 0.02 kPa to 3 kPa (Figure 4).

FIGURE 4

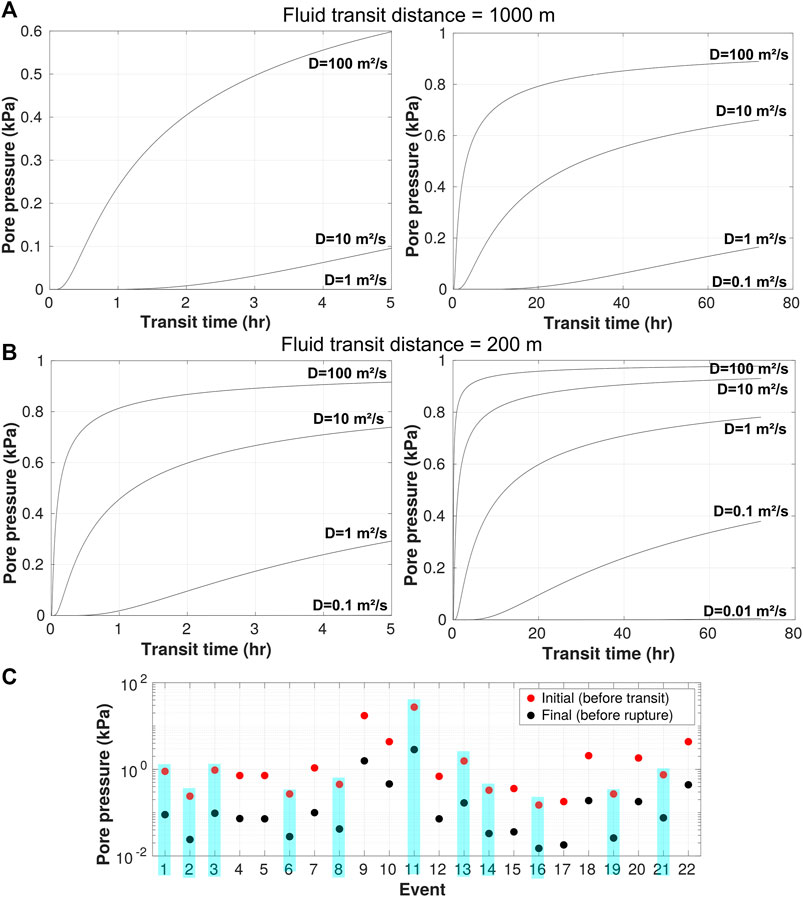
FIGURE 4. Evolution of pore pressure in the fracture resulting from an unitary elastic wave overpressure (1 kPa) as a function of hydraulic diffusivity: (A) fluid-transit distance of 1 km and (B) fluid-transit distance of 200 m. (C) Estimate of initial (before fluid transit) and final (before rupture) pore pressure level in the fracture with respect to the maximum seismic wave elastic pressure for observed time-delays (Table 2) and for fluid-transit distances and diffusion factors given by the magnitude-dependent nucleation model (Figure 2). Events for which precursory deformation changes are investigated are outlined by a blue shaded box.

4.2 Dilatation computation at strainmeter sites

Full and accurate modeling of crustal deformation induced by a pressure front propagating in an heterogeneous fault zone is a complex problem. To compute the time-dependent evolution of dilatation generated by a remote diffusing pressure front, we adopt some simplifications. We model the nucleation region using the analogue volcano source represented by a horizontal circular crack in a semi-infinite elastic solid. The three dimensional (3-D) displacements generated by a sill-like source in a semi-infinite, elastic half-space subjected to the time-dependent pressure change P(t) (Eq. 4), are expressed as (Fialko et al., 2001):

$\begin{array}{ll}\hfill U_E\left(t\right)& \hfill =a\frac{P\left(t\right)}{G}{U}_r\frac{X}{R}\\ \hfill U_N\left(t\right)& \hfill =a\frac{P\left(t\right)}{G}{U}_r\frac{Y}{R}\\ \hfill U_Z\left(t\right)& \hfill =-a\frac{P\left(t\right)}{G}{U}_z\end{array}(5)$

where a represents the characteristic crack dimension (here taken as the nucleation distance 2L_c), G is the half-space rigidity (G = 30 GPa), X = $\frac{x-x_0}{a}$ and Y = $\frac{y-y_0}{a}$ are dimensionless distances with respect to the characteristic crack dimension where (x₀, y₀, z₀) and (x, y, z) are the coordinates of the center of the crack and of the observation point in an E-N-Z referential, respectively, and R (= $\sqrt{X^2+Y^2}$) represents the source-station radial distance. U_r and U_z represent the radial and vertical displacements as detailed in Fialko et al. (2001). We simulate the 3-D displacements using dMODELS software (MATLAB-based) (Battaglia et al., 2013) and estimate the temporal evolution of synthetic dilatation at the strainmeter location from displacements using the finite-difference approach proposed by Canitano et al. (2017).

A remarkable property of the 1-D pore pressure equation is that the hydraulic diffusivity represents the only factor that controls the pore pressure dynamics in the fracture (Shapiro et al., 2018). In particular, D controls the pore pressure rise-time (Figure 4); the greater the diffusivity, the earlier dilatation changes induced in the crust by a pressure front diffusing in the fracture can be detected. The temporal evolution of the synthetic dilatation generated by a remote overpressure front based on the theoretical parameters related to a fluid-induced nucleation mechanism (Figure 2B) is shown in Figure 5. In general, predictions underestimate the observations by at least two to four orders of magnitude. Namely, no predicted signal is expected to be $>\sim$ 10^–2 nϵ which represents the strainmeter nominal resolution. Therefore any precursory signal, if occurred in our earthquake selection, would have remained undetected.

FIGURE 5

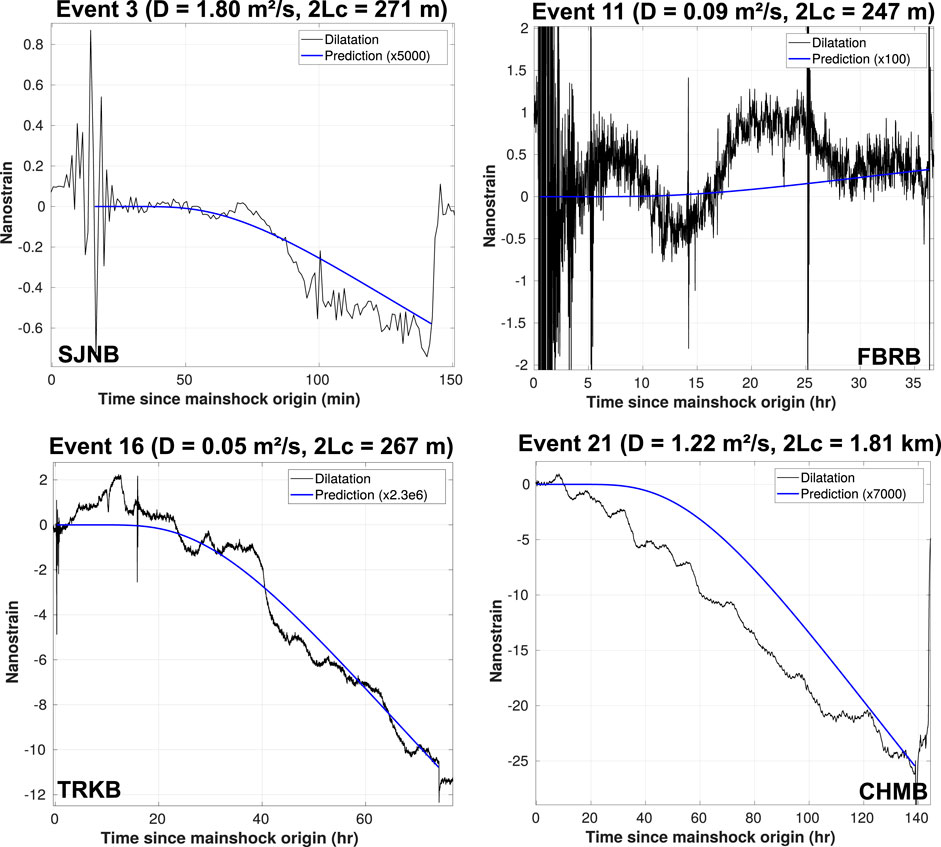
FIGURE 5. Example of temporal evolution of synthetic dilatation at the strainmeter location computed from 3-D displacements generated by a remote overpressure front in a fracture. The onset time of predictions is scaled with the arrival of Rayleigh waves with maximum amplitude at the station. For comparison, amplitude of the predicted signal is magnified to match the strain level observed before rupture.

5 Discussion

The detection of crustal strain anomalies and their characterization as earthquake precursors is a complex problem (Bernard, 2001). Although the quality of the data and of the applied corrections play an important role in monitoring strain transients (e.g., the detection level), complexities are mainly related to the transient source characteristics and to the source-station distance (quasi-static deformation decreases with a factor of 1/R²). In particular, the detection capability strongly depends of the strength of the source of deformation. Here, the latter is controlled by the size of the nucleation region (which depends of the earthquake magnitude) and by the pressure gradient, which is determined by the fracture hydraulic diffusivity and by the elastic wave pressure. We consider the volume change ΔV in the crack fracture resulting from a uniform pressure gradient ΔP as a proxy for the source strength. For an incompressible fluid, it is expressed as:

$\mathrm{\Delta }V=-4\pi \left(1-\nu \right)\frac{\mathrm{\Delta }P}{G}{a}^3\underset{0}{\overset{1}{\int }}t\varphi \left(t\right)dt(6)$

where ϕ function is the solution of the Fredholm equation of the second kind (Fialko et al., 2001; Battaglia et al., 2013). Figure 6 presents the theoretical volume change in the fracture for earthquakes with magnitude ranging from 4 to 7. To detect the precursory phase of a remote fluid-induced earthquake at a subdaily period within a few kilometer radius from the source requires a source volume that is about 5–10 times larger than for the hypothetical cases considered in this study. Since strain measurement noise increases with period (Crescentini et al., 1997), this would require monitoring crustal deformation with a station located near a large regional earthquake that occurred shortly following a large teleseismic event; a configuration that is highly unlikely. Therefore, to improve our understanding of remote earthquake triggering in Taiwan, the protocol adopted here should be combined with a more conservative approach that relies on the search of earthquakes with a wide range of magnitudes following large global events.

FIGURE 6

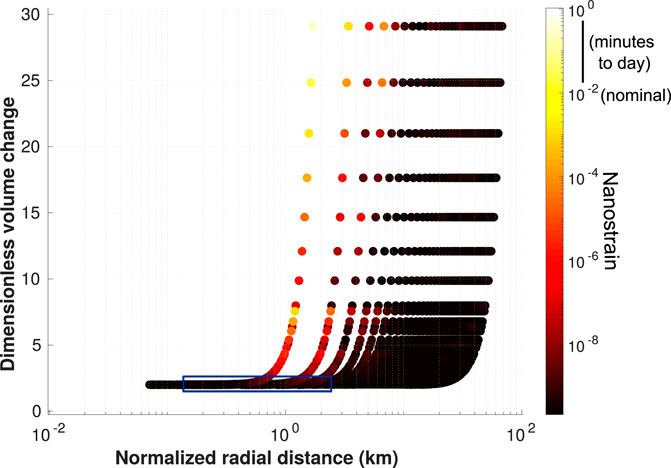
FIGURE 6. Theoretical volume change in the fracture ΔV/(a³ΔP/G) as a function of the source-station radial distance R/(z₀/a) estimated for earthquakes with magnitude ranging from 4 (a = 0.1 km) to 7 (a = 3 km). The blue region outlines the range where our observations fall. Strain levels associated with the analyzed hypothetical remote fluid-induced earthquakes are at least two to three orders of magnitude lower than the strainmeter nominal resolution (about 10^–2 nϵ).

Since it controls the dilatation level during computation, the incident-wave strain level may also represent a critical parameter for detection of fluid-induced seismicity. However, the effect of dynamic peak strain on triggered seismicity is not well understood (Brodsky and van der Elst, 2014), and a large strain perturbation doesn’t necessarily imply remote triggering, and vice versa (Parsons et al., 2014). The 2008 M_w 7.9 Eastern Sichuan earthquake, which generated strong regional ground motions due to pronounced rupture directivity effects (Kurahashi and Irikura, 2010), has induced dynamic stress over Taiwan about twice larger than any other great teleseismic earthquake (e.g., the 2011 M_w 9.0 Tohoku and the 2012 M_w 8.6 Sumatra events). Although, the event triggered seismicity in northern China (Peng et al., 2010), it had little to no impact on the seismicity in Taiwan (Chao et al., 2011), at least during the first days following the wave passing (Section 3). Recently, field (Bonini, 2020) and laboratory (Zheng, 2018; Jin et al., 2021) observations have shown that pore pressure induced in a fluid-filled fracture by a seismic wave can be amplified relative to the incident-wave pressure [up to three orders of magnitude (Zheng, 2018)]. This transient pore fluid amplification would suggest that even seismic waves with insignificant stress levels can induce substantial overpressure in fault zones. Besides, this also implies that fluid level can remain high after transiting in the fracture, therefore favoring nucleation in case of delayed triggering or inducing large normal stress unclamping in case of instantaneous (or nearly-instantaneous) triggering. Such a process may also favor detection at remote distances of transient events that generate little regional deformation, as analyzed here. For example, in the case of event 3 (Figure 5), we observe that the pore pressure rise-time and temporal evolution in the fracture is well predicted for station SJNB (nearby station TRKB was shutted off), but the strain level is underestimated by about three orders of magnitude. Although the analyze of a pressure amplification mechanism in the fault zone is beyond the scope of this study, we cannot rule out that such a process may be at play for some cases. On the other hand, moderate strain changes observed for events 16 and 21 are too large to reflect a transient deformation and likely represent the contraction response due to rainfall loading (Canitano et al., 2021), which illustrates the impracticability for detecting precursory strain during environmental disturbances.

Finally, we recognize that our analogue volcano deformation model is by no means complex enough to reflect the far-field deformation caused by fluid flow in active regions, but it provides a preliminary framework for the integration of borehole dilatation observations for the search of precursory signals associated with remote fluid-induced earthquakes (Parsons et al., 2017). A more elaborated model of fault valving (Zhu et al., 2020), integrating fluid-driven aseismic creeep (Shelly et al., 2011; Cebry et al., 2022) and seismicity (Shapiro et al., 2018), combined with a multidisciplinary geophysical monitoring is fundamental for enhancing detection and characterization of precursory phenomena in Taiwan (Fu et al., 2020) or in other active regions (Delorey et al., 2015).

6 Conclusion

We develop a protocol to integrate high-resolution borehole strain measurements for the investigation of remote triggering of moderate to large earthquakes (M_w ≥ 4) in Taiwan. The physical framework is compatible with a magnitude-dependent fluid-induced nucleation process where the nucleation region is simplified using the analogue volcano source represented by a horizontal circular crack. We observe that theoretical evolution of dilatation generated by a remote diffusing pressure front in a semi-infinite, elastic half-space is two to four orders of magnitude smaller than observations (∼ 10^–5 to 10^–3 nϵ). This suggests that detection of pore pressure-related deformation would have required change of volume in the nucleation region that is at least one order of magnitude larger than for the hypothetical cases considered here. The study represents the first attempt to analyze strain time-series for detecting pre-earthquake strain anomalies related to fluid-induced earthquakes and illustrates the challenge for detecting and characterizing intermediate-to far-field earthquake precursors caused by fluid flow in active regions.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This research is supported by the Ministry of Science and Technology grant MOST 111-2116-M-001-018.

Acknowledgments

I am thankful to Associate Editor Giovanni Martinelli and two reviewers for their constructive comments allowing to improve the manuscript. I am grateful to Alan Linde, Selwyn Sacks, and the support staff of the Carnegie Institution of Washington for the construction, installation, and maintenance of the dilatometers. I would like to thank Hsin-Ming Lee who has collected the strainmeter data, Ya-Ju Hsu and Zhigang Peng for insightful comments and Pascal Bernard for providing MOK strainmeter data (CRL, Greece). This is the contribution of the Institute of Earth Sciences, Academia Sinica, IESAS2414.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1213577/full#supplementary-material

References

Amoruso, A., and Crescentini, L. (2010). Limits on earthquake nucleation and other pre-seismic phenomena from continuous strain in the near field of the 2009 L’Aquila earthquake. Geophys. Res. Lett.37. doi:10.1029/2010GL043308

CrossRef Full Text | Google Scholar

Barton, C. A., Zoback, M. D., and Moos, D. (1995). Fluid flow along potentially active faults in crystalline rock. Geology23 (8), 683–686. doi:10.1130/0091-7613(1995)023<0683:ffapaf>2.3.co;2

CrossRef Full Text | Google Scholar

Battaglia, M., Cervelli, P. F., and Murray, J. R. (2013). dMODELS: A MATLAB software package for modeling crustal deformation near active faults and volcanic centers. J. Volcanol. Geotherm. Res.254, 1–4. doi:10.1016/j.jvolgeores.2012.12.018

CrossRef Full Text | Google Scholar

Belardinelli, M. E., Bizzarri, A., and Cocco, M. (2003). Earthquake triggering by static and dynamic stress changes. J. Geophys. Res.108 (B3), 2135. doi:10.1029/2002jb001779

CrossRef Full Text | Google Scholar

Bernard, P. (2001). From the search of ’precursors’ to the research on ’crustal transients. Tectonophysics338, 225–232. doi:10.1016/s0040-1951(01)00078-6

CrossRef Full Text | Google Scholar

Bernard, P., Lyon-Caen, H., Briole, P., Deschamps, A., Boudin, F., Makropoulos, K., et al. (2006). Seismicity, deformation and seismic hazard in the Western rift of corinth: New insights from the corinth rift laboratory (CRL). Tectonophysics426, 7–30. doi:10.1016/j.tecto.2006.02.012

CrossRef Full Text | Google Scholar

Bonini, M. (2020). Investigating earthquake triggering of fluid seepage systems by dynamic and static stresses. Earth Sci. Rev.210, 103343. doi:10.1016/j.earscirev.2020.103343

CrossRef Full Text | Google Scholar

Brodsky, E. E., Roeloffs, E., Woodcock, D., Gall, I., and Manga, M. (2003). A mechanism for sustained groundwater pressure changes induced by distant earthquakes. J. Geophys. Res.108, 2390. doi:10.1029/2002JB002321

CrossRef Full Text | Google Scholar

Brodsky, E. E., and van der Elst, N. J. (2014). The uses of dynamic earthquake triggering. Annu. Rev. Earth Planet. Sci.42, 317–339. doi:10.1146/annurev-earth-060313-054648

CrossRef Full Text | Google Scholar

Canitano, A., Bernard, P., Linde, A. T., and Sacks, S. (2013). Analysis of signals of a borehole strainmeter in the Western rift of Corinth, Greece. J. Geod. Sci.3 (1), 63–76. doi:10.2478/jogs-2013-0011

CrossRef Full Text | Google Scholar

Canitano, A., Hsu, Y. J., Lee, H. M., Linde, A. T., and Sacks, S. (2017). A first modeling of dynamic and static crustal strain field from near-field dilatation measurements: Example of the 2013 M_w 6.2 ruisui earthquake, taiwan. J. Geod.91 (1), 1–8. doi:10.1007/s00190-016-0933-6

CrossRef Full Text | Google Scholar

Canitano, A., Hsu, Y. J., Lee, H. M., Linde, A. T., and Sacks, S. (2015). Near-field strain observations of the october 2013 ruisui, taiwan, earthquake: Source parameters and limits of very-short term strain detection. Earth Planets Space67, 125. doi:10.1186/s40623-015-0284-1

CrossRef Full Text | Google Scholar

Canitano, A., Hsu, Y. J., Lee, H. M., T Linde, A., and Sacks, S. (2018). Calibration for the shear strain of 3-component borehole strainmeters in eastern Taiwan through Earth and ocean tidal waveform modeling. J. Geod.92 (3), 223–240. doi:10.1007/s00190-017-1056-4

CrossRef Full Text | Google Scholar

Canitano, A., Mouyen, M., Hsu, Y. J., Linde, A. T., Sacks, S., and Lee, H. M. (2021). Fifteen years of continuous high-resolution borehole strainmeter measurements in eastern taiwan: An overview and perspectives. GeoHazards2 (3), 172–195. doi:10.3390/geohazards2030010

CrossRef Full Text | Google Scholar

Canitano, A. (2020). Observation and theory of strain-infrasound coupling during ground-coupled infrasound generated by Rayleigh waves in the Longitudinal Valley (Taiwan). Bull. Seismol. Soc. Am.110 (6), 2991–3003. doi:10.1785/0120200154

CrossRef Full Text | Google Scholar

Cebry, S. L., Ke, C. Y., Shreedharan, S., Marone, C., Kammer, D. S., and McLaskey, G. C. (2022). Creep fronts and complexity in laboratory earthquake sequences illuminate delayed earthquake triggering. Nat. Comm.13, 6839. doi:10.1038/s41467-022-34397-0

CrossRef Full Text | Google Scholar

Chao, K., Peng, Z., Wu, C., Tang, C. C., and Lin, C. H. (2011). Remote triggering of non-volcanic tremor around Taiwan. Geophys. J. Int.188 (1), 301–324. doi:10.1111/j.1365-246x.2011.05261.x

CrossRef Full Text | Google Scholar

Crescentini, L., Amoruso, A., Fiocco, G., and Visconti, G. (1997). Installation of a high-sensitivity laser strainmeter in a tunnel in central Italy. Rev. Sci. Instru.68, 3206–3210. doi:10.1063/1.1148268

CrossRef Full Text | Google Scholar

Delorey, A. A., Chao, K., Obara, K., and Johnson, P. A. (2015). Cascading elastic perturbation in Japan due to the 2012 M_w 8.6 Indian Ocean earthquake. Sci. Adv.1, e1500468. doi:10.1126/sciadv.1500468

PubMed Abstract | CrossRef Full Text | Google Scholar

Duoxing, Y., Qi, L., and Lianzhong, Z. (2015). Propagation of pore pressure diffusion waves in saturated porous media. J. Appl. Phys.117, 134902. doi:10.1063/1.4916805

CrossRef Full Text | Google Scholar

Feng, K. F., Huang, H. H., Hsu, Y. J., and Wu, Y. M. (2021). Controls on seasonal variations of crustal seismic velocity in Taiwan using single-station cross-component analysis of ambient noise interferometry. J. Geophys. Res. Solid Earth126. doi:10.1029/2021JB022650

CrossRef Full Text | Google Scholar

Fialko, Y., Khazan, Y., and Simons, M. (2001). Deformation due to a pressurized horizontal circular crack in an elastic half-space, with applications to volcano geodesy. Geophys. J. Int.146, 181–190. doi:10.1046/j.1365-246x.2001.00452.x

CrossRef Full Text | Google Scholar

Fu, C. C., Lee, L. C., Ouzounov, D., and Jan, J. C. (2020). Earth’s outgoing longwave radiation variability prior to M ≥ 6.0 earthquakes in the Taiwan area during 2009-2019. Front. Earth Sci.8, 364. doi:10.3389/feart.2020.00364

CrossRef Full Text | Google Scholar

Gomberg, J., Bodin, P., Larson, K., and Dragert, H. (2004). Earthquake nucleation by transient deformations caused by the M = 7.9 Denali, Alaska, earthquake. Nature427, 621–624. doi:10.1038/nature02335

PubMed Abstract | CrossRef Full Text | Google Scholar

Gonzalez-Huizar, H., Velasco, A. A., Peng, Z., and Castro, R. (2012). Remote triggered seismicity caused by the 2011, M9.0 Tohoku-Oki, Japan earthquake. Geophys. Res. Lett.39. doi:10.1029/2012GL051015

CrossRef Full Text | Google Scholar

Guo, H., Brodsky, E. E., Goebel, T. H. W., and Cladouhos, T. T. (2021). Measuring fault zone and host rock hydraulic properties using tidal responses. Geophys. Res. Lett.48 (13). doi:10.1029/2021GL093986

CrossRef Full Text | Google Scholar

Hill, D. P. (2008). Dynamic stresses, Coulomb failure, and remote triggering. Bull. Seismol. Soc. Am.98, 66–92. doi:10.1785/0120070049

CrossRef Full Text | Google Scholar

Hill, D. P., Reasenberg, P. A., Michael, A., Arabaz, W. J., Beroza, G., Brumbaugh, D., et al. (1993). Seismicity remotely triggered by the magnitude 7.3 Landers, California, earthquake. Science260 (5114), 1617–1623. doi:10.1126/science.260.5114.1617

PubMed Abstract | CrossRef Full Text | Google Scholar

Hsu, Y. J., Chang, Y. S., Liu, C. C., Lee, H. M., Linde, A. T., Sacks, S., et al. (2015). Revisiting borehole strain, typhoons, and slow earthquakes using quantitative estimates of precipitation-induced strain changes. J. Geophys. Res. Solid Earth120 (6), 4556–4571. doi:10.1002/2014jb011807

CrossRef Full Text | Google Scholar

Huang, F., Jian, C., Tang, Y., Xu, G., Deng, Z., and Chi, G. (2004). Response changes of some wells in the mainland subsurface fluid monitoring network of China, due to the September 21, 1999, Ms7.6 Chi-Chi Earthquake. Tectonophysics390, 217–234. doi:10.1016/j.tecto.2004.03.022

CrossRef Full Text | Google Scholar

Institute of Earth Sciences, Academia Sinica (1996). Broadband Array in taiwan for Seismology. Taiwan: Institute of Earth Sciences, Academia Sinica. Other/Seismic Network. doi:10.7914/SN/TW

CrossRef Full Text | Google Scholar

Jin, Y., Dyaur, N., and Zheng, Y. (2021). Laboratory evidence of transient pressure surge in a fluid-filled fracture as a potential driver of remote dynamic earthquake triggering. Seismic Rec.1, 66–74. doi:10.1785/0320210015

CrossRef Full Text | Google Scholar

Johnson, C. W., and Bürgmann, R. (2016). Delayed dynamic triggering: Local seismicity leading up to three remote M ≥ 6 aftershocks of the 11 April 2012 M8.6 Indian Ocean earthquake. J. Geophys. Res. Solid Earth121, 134–151. doi:10.1002/2015JB012243

CrossRef Full Text | Google Scholar

Johnson, C. W., Bürgmann, R., and Pollitz, F. F. (2015). Rare dynamic triggering of remote M ≥ 5.5 earthquake from global catalog analysis. J. Geophys. Res. Solid Earth120, 1748–1761. doi:10.1002/2014JB011788

CrossRef Full Text | Google Scholar

Kanamori, H. (1977). The energy release in great earthquakes. J. Geophys. Res.82, 2981–2987. doi:10.1029/jb082i020p02981

CrossRef Full Text | Google Scholar

Kurahashi, S., and Irikura, K. (2010). Characterized source model for simulating strong ground motions during the 2008 Wenchuan earthquake. Bull. Seismol. Soc. Am.100, 2450–2475. doi:10.1785/0120090308

CrossRef Full Text | Google Scholar

Malagnini, L., Lucente, F. P., De Gori, P., Akinci, A., and Munafo, I. (2012). Control of pore fluid pressure diffusion on fault failure mode: Insights from the 2009 L’Aquila seismic sequence. J. Geophys. Res.117, B05302. doi:10.1029/2011JB008911

CrossRef Full Text | Google Scholar

Miyazawa, M., Brodsky, E. E., and Guo, H. (2021). Dynamic earthquake triggering in southern California in high resolution: Intensity, time decay, and regional variability. AGU Adv.2, e2020AV000309. doi:10.1029/2020av000309

CrossRef Full Text | Google Scholar

Mouyen, M., Canitano, A., Chao, B. F., Hsu, Y. J., Steer, P., Longuevergne, L., et al. (2017). Typhoon-induced ground deformation. Geophys. Res. Lett.44 (21), 11,004–11,011. doi:10.1002/2017gl075615

CrossRef Full Text | Google Scholar

Ohnaka, M. (2000). A physical scaling relation between the size of an earthquake and its nucleation zone size. Pure Appl. Geophys.157, 2259–2282. doi:10.1007/pl00001084

CrossRef Full Text | Google Scholar

O’Malley, R. T., Mondal, D., Goldfinger, C., and Behrenfeld, M. J. (2018). Evidence of systematic triggering at teleseismic distances following large earthquakes. Sci. Rep.8, 11611. doi:10.1038/s41598-018-30019-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Pankow, K. L., and Kilb, D. (2020). Going beyond rate changes as the sole indicator for dynamic triggering of earthquakes. Sci. Rep.10, 4120. doi:10.1038/s41598-020-60988-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Parsons, T. (2005). A hypothesis for delayed dynamic earthquake triggering. Geophys. Res. Lett.32, L04302. doi:10.1029/2004gl021811

CrossRef Full Text | Google Scholar

Parsons, T., Malagnini, L., and Akinci, A. (2017). Nucleation speed limit on remote fluid-induced earthquakes. Sci. Adv.3, e1700660. doi:10.1126/sciadv.1700660

PubMed Abstract | CrossRef Full Text | Google Scholar

Parsons, T., Segou, M., and Marzocchi, W. (2014). The global aftershock zone. Tectonophysics618, 1–34. doi:10.1016/j.tecto.2014.01.038

CrossRef Full Text | Google Scholar

Parsons, T., and Velasco, A. A. (2011). Absence of remotely triggered large earthquakes beyond the mainshock region. Nat. Geosci.4, 312–316. doi:10.1038/ngeo1110

CrossRef Full Text | Google Scholar

Peng, Z., Vidale, J. E., Wech, A. G., Nadeau, R. M., and Creager, K. C. (2009). Remote triggering of tremor along the san andreas fault in central California. J. Geophys. Res.114, B00A06. doi:10.1029/2008JB006049

CrossRef Full Text | Google Scholar

Peng, Z., Wang, W., Chen, Q. F., and Jiang, T. (2010). Remotely triggered seismicity in north China following the 2008 M_w 7.9 Wenchuan earthquake. Earth Planets Space62, 893–898. doi:10.5047/eps.2009.03.006

CrossRef Full Text | Google Scholar

Peng, Z., Wu, C., and Aiken, C. (2011). Delayed triggering of microearthquakes by multiple surface waves circling the Earth. Geophys. Res. Lett.38, L04306. doi:10.1029/2010gl046373

CrossRef Full Text | Google Scholar

Pollitz, F. F., Stein, R. S., Sevilgen, V., and Bürgmann, R. (2012). The 11 April 2012 east Indian Ocean earthquake triggered large aftershocks worldwide. Nature490, 250–253. doi:10.1038/nature11504

PubMed Abstract | CrossRef Full Text | Google Scholar

Sacks, S., Suyehiro, S., Evertson, D. W., and Yamagishi, Y. (1971). Sacks-Evertson strainmeter, its installation in Japan and some preliminary results concerning strain steps. Pap. Meteorol. Geophys.22, 707–712. doi:10.2183/pjab1945.47.707

CrossRef Full Text | Google Scholar

Shapiro, N. M., Campillo, M., Kaminski, E., Vilotte, J. P., and Jaupart, C. (2018). Low-frequency earthquakes and pore pressure transients in subduction zones. Geophys. Res. Lett.45. doi:10.1029/2018GL079893

CrossRef Full Text | Google Scholar

Shelly, D. R., Peng, Z., Hill, D. P., and Aiken, C. (2011). Triggered creep as a possible mechanism for delayed dynamic triggering of tremor and earthquakes. Nat. Geosci.4, 384–388. doi:10.1038/ngeo1141

CrossRef Full Text | Google Scholar

Sun, W. F., Peng, Z., Lin, C. H., and Chao, K. (2015). Detecting deep tectonic tremor in Taiwan with a dense array. Bull. Seismol. Soc. Am.105 (3), 1349–1358. doi:10.1785/0120140258

CrossRef Full Text | Google Scholar

van der Elst, N. J., and Brodsky, E. E. (2010). Connecting near-field and far-field earthquake triggering to dynamic strain. J. Geophys. Res.115, B07311. doi:10.1029/2009JB006681

CrossRef Full Text | Google Scholar

Velasco, A. A., Hernandez, S., Parsons, T., and Pankow, K. (2008). Global ubiquity of dynamic earthquake triggering. Nat. Geosci.1, 375–379. doi:10.1038/ngeo204

CrossRef Full Text | Google Scholar

Wessel, P., and Smith, W. H. F. (1998). New, improved version of generic mapping tools released. Eos Trans. AGU79, 579. doi:10.1029/98EO00426

CrossRef Full Text | Google Scholar

Yao, D., Peng, Z., Kaneko, Y., Fry, B., and Meng, X. (2021). Dynamic triggering of earthquakes in the North Island of New Zealand following the 2016 M_w 7.8 Kaikoura earthquake. Earth Planet. Sci. Lett.557, 116723. doi:10.1016/j.epsl.2020.116723

CrossRef Full Text | Google Scholar

Zheng, Y. (2018). Transient pressure surge in a fluid-filled fracture. Bull. Seismol. Soc. Am.108, 1481–1488. doi:10.1785/0120170230

CrossRef Full Text | Google Scholar

Zhu, W., Allisson, K. L., Dunham, E. M., and Yang, Y. (2020). Fault valving and pore pressure evolution in simulations of earthquake sequences and aseismic slip. Nat. Comm.11, 4883. doi:10.1038/s41467-020-18598-z

PubMed Abstract | CrossRef Full Text | Google Scholar