High-resolution modeling of meander neck cutoffs: laboratory and field scales

Meandering rivers are distinguished by their characteristic sinuosity, which is subject to modulation through channel cutoff, resulting in the formation of oxbow lakes within the abandoned meander loops. Throughout the evolutionary course of a river, these cutoffs establish a connection between the channel and floodplain systems, both crucial to maintaining the dynamic equilibrium of the river system. Nonetheless, the interactive dynamic between the channel and floodplain and its influence on the transient behavior of the channel’s morphodynamics during a cutoff event are frequently reduced to simplistic representations in computational models. This study introduces a comprehensive numerical model that elucidates the adaptive processes of bed and planform during and subsequent to the inception of cutoff and oxbow lakes. The model is assessed through its application to a laboratory scale cutoff, before being employed to a real-world meandering river, specifically the Ucayali River in Peru, in order to gain understanding into channel development and the intricate patterns of planform dynamics following cutoff events. The model is able to capture the main modes of planform migration, translation and expansion for the case of the bend in the Ucayali River. During the neck cutoff, the model simulates the progression of erosional and depositional waves traveling in upstream and downstream directions respectively, underscoring the importance of incorporating both hydrodynamic and morphodynamic factors in characterizing the river dynamics associated with meander cutoffs.

1 Introduction

Meandering rivers are pervasive worldwide, providing corridors for navigation, delivering resources for industry, agriculture and urban water use. They interact with their valleys through floods and bank migration. Despite human alteration of rivers, natural erosion and deposition processes remain a dominant factor changing most fluvial systems (Syvitski and Kettner, 2011), thereby altering their floodplains. The morphodynamics ofriver migration generated by the interaction of water flow, sediment transport, erosion and sedimentation, is characterized by two repeating planform changing processes. One process is the short-term increase of sinuosity via meander elongation with downstream migration (sometimes upstream) of meander loops. The second process is the reduction of sinuosity with intermittent, long-term occurrence of channel cutoffs, where the flow bypasses the meander loop by a shorter path with the subsequent formation of an abandoned reach (Camporeale et al., 2008). An example of the effect of such processes is illustrated by the reconstruction of the scrollbars and paleochannel of different ages distributed along the floodplain (following Rojas et al. (2023)’s methodology) of the Ucayali River shown in Figure 1. Notice the change in local sinuosity from 2.24 to 1.75 in the region where a cutoff occurred in 2014–2015 (determined from the satellite images from 2006 to 2017, when the bend was finally abandoned). It shows that bend expansion and translation were the primary modes for cutoff formation. During the lifetime of a meandering river, where migration and cutoffs interact in space and time, dynamic-equilibrium conditions occur and morphometrics (such as sinuosity, lateral migration rates, and rate of cutoff occurrence) reach their statistical steady-states (Gutierrez et al., 2014; Vermeulen et al., 2016; Ruben-Dominguez et al., 2021; Ielpi et al., 2023). Given the recurring and profound social-ecological impacts caused by the occurrence of channel cutoffs in meandering rivers (Abad et al., 2022; Nagel et al., 2022), fluvial geomorphologists have developed theories and tools to help explain this process (Stølum, 1996; Edwards and Smith, 2002; Camporeale et al., 2005). Yet, a predictive model of channel cutoff has not been sufficiently developed to simulate the interaction between rivers and related alluvial floodplains (Camporeale et al., 2007).

FIGURE 1

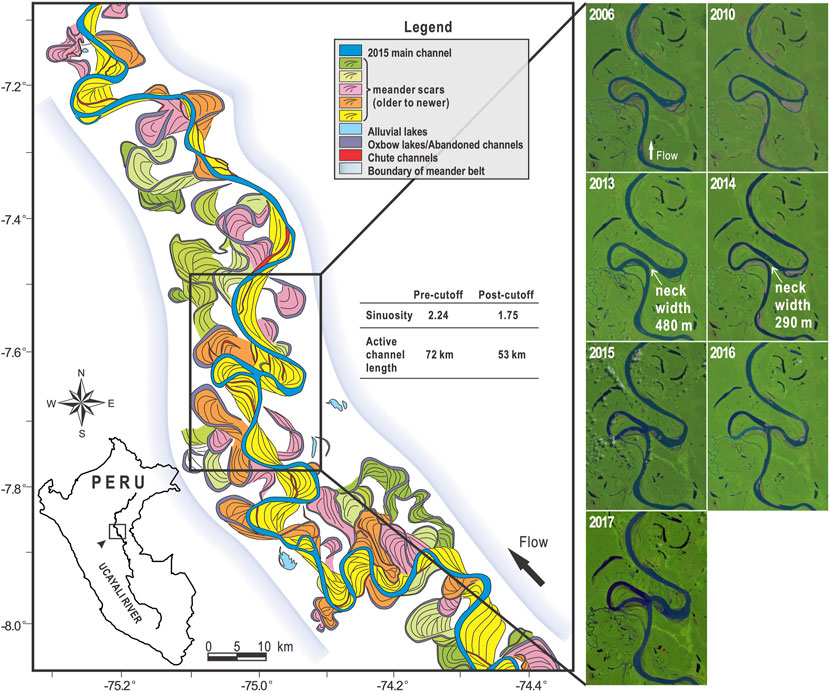
FIGURE 1. Multi-stage (modern and ancient) meander cutoffs along the Ucayali River, Peru (7°38′2.15″ S, 75°0′2.10″ W, affecting towns such as Santa Maria, Tumbes, San Roque, Monte de Cion, and others). The reconstruction of paleochannels was performed following Rojas et al. (2023)’s methodology. Notice that the Ucayali River is dynamic inside of the geologic valley. Seven Landsat imageries (from 2006 to 2017) of the central river bend are shown, at where a cutoff occurred in 2014–2015. The maximum migration rate during this period was over 200 m/year.

Cutoffs are sporadic events. They may be triggered by hydrologic events (Turnipseed et al., 2021), or when the sinuosity of the channel attains a critical condition (Stølum, 1996; Hooke, 2004). Cutoffs govern different aspects of river and floodplain morphology, limiting channel sinuosity and determining sedimentary deposits through channel migration and avulsion on the floodplain (Ielpi et al., 2020). Two types of cutoffs are typically identified: chute cutoffs, which develop over the floodplain with an incised chute channel that bypasses the meander during large floods (Camporeale et al., 2008; Turnipseed et al., 2021), and neck cutoffs. Meander neck cutoffs are defined as the shorter path the river follows during an incision through the neck of a meander (Tower, 1904), and occur when the upstream and downstream banks of the meander migrate into one another until the bank collapses, creating a shorter path and forming an oxbow lake. Recently, two main modes of neck cutoff have been identified; mode 1) is related to low frequency, medium to high magnitude floods, cutting through the neck; and mode 2) is related to low to medium flow, with progressive bank erosion and intermittent bank collapse (Li et al., 2022). Cutoffs limit geometrical complexity by removing older meanders by shortening the channel length, stabilizing mean river geometry around a statistically steady state (geometrical role); and act as a noise generator that limits the deterministic space-time dynamics of meander migration (dynamical role) (Camporeale et al., 2008). A conceptual model for long-term neck cutoff evolution (Richards and Konsoer, 2020), considers four main stages: 1) the active meander stage occurs before the cutoff development; 2) neck cutoff stage is characterized by the deevelopment of a shorter path while the old bend remains active; 3) the lacustrine stage involves the plugging of the input and output of the old bend; 4) the terrestrialized stage marks the filling of the oxbow lake with sediment. Depending on local hydrogeomorphic conditions, some of the abandoned channels remain connected or not the main channel Rojas et al. (2023). Accelerated erosion and increased sediment supply have been noted downstream of cutoffs (Howard and Knutson, 1984; Zinger et al., 2011). Thus, a key response of the system to the disturbance is the formation of a sediment erosional wave traveling upstream and a sediment depositional wave traveling downstream from the cutoff point. This phenomenon has been observed both in an experimental setting (Han and Endreny, 2014a), and in the field (Hooke, 1995; Abad et al., 2012).

Sustainable river management and restoration planning require spatiotemporal modeling of channels (Pannone and De Vincenzo, 2022), and cutoffs need to be accounted for long-term meandering evolution (Bogoni et al., 2017). Several river evolution models have successfully represented the statistical properties of river sinuosity, as well as pool and point bar development (Sun et al., 1996; Howard, 1996; Darby et al., 2002; Lancaster and Bras, 2002; Abad and Garcia, 2006; Seminara, 2006; Crosato, 2008; Frascati and Lanzoni, 2010; Motta et al., 2012b,a; Asahi et al., 2013; Schwenk et al., 2015; Bogoni et al., 2017; Sylvester et al., 2019). A common framework of meandering modeling focuses on the evolution of the river centerline. This framework is based on geomorphological evidence, indicating that the erosion of the concave bank balanced by deposits in the opposite bank, and the width remains constant during the migration process (Camporeale et al., 2008). For simplicity and long-term simulation, these models handle cutoff processes with a geometric scheme for the active reach. The scheme tracks the planimetric distance between the external banks of two meander bends. When the centerline of the bends gets closer than a specified distance, typically the channel width, it is assumed that the cutoff occurs, and the loop is deleted from the simulation (Howard and Knutson, 1984). Pannone and De Vincenzo (2022) proposed a 1D theoretical model for meander growth and death, when tested with field data, the results had agreement with the time elapses of the real cutoff. Geometrical schemes of cutoff neglect the spatially and temporally elaborate in-channel cutoff sequence reported by field studies such as Kiss and Sipos (2015) in Hungary, Gay et al. (1998) in the Power River (Montana, United States), Micheli and Larsen (2011) in the Sacramento River (California, United States), Richards and Konsoer (2020) in the White River (Arkansas, United States), and Abad et al. (2022) in the Ucayali River (Loreto, Peru). Based on these field studies, identified precursors to cutoff include channel widening, bar development, and slope steepening. The geometric schemes also neglect paleo-channels, which influence surficial lithology and later can serve for inference of paleo-ecology and paleo-climate, and are therefore helpful in long-term reproduction or prediction of river evolution and sediment budgets (Todd and Went, 1991; Sylvia and Galloway, 2006; Davidson and North, 2009; Constantine et al., 2014; Rojas et al., 2023). A physically-based model was proposed by Asahi et al. (2013) based on numerical models flow, bed evolution, and bank erosion; however, it still ignored the complex hydrodynamic and sediment deposition processes that happen during the cutoff stage [stage 2 described before (Richards and Konsoer, 2020)].

There are processes of river meandering that morphodynamic models ignore, such as the period where the old bend is still active transporting water and developing aggradation, flow variability, influence of riparian vegetation, overbank processes (Camporeale et al., 2008). To address the lack of some of these processes, a new model is presented that solves numerically the free surface flow equations, the Exner equation, and the bank erosion and accretion processes. This model is coupled with a sub-model designed for cutoff scenarios, thereby enabling the characterization of post-cutoff morphodynamics. Two cases are analyzed for validation purposes focusing on the sediment load variation after the cutoff and the morphodynamics of the cutoff stage, where the old bend is still active. The first case used experimental cutoff data derived from a controlled laboratory environment (Han and Endreny, 2014a). The second case, was set to replicate the Ucayali River’s cutoff event shown in Figure 1.

2 Methods

The meander cutoff model comprises three main processes: i) the initial mesh generation and the assignment of the initial river bank lines; ii) the computation of the two-dimensional depth-averaged hydrodynamics with the model TELEMAC-2D (Lang, 2013). Additionally, the model calculates sediment transport and bed evolution using SISYPHE (Tassi and Villaret, 2014); and iii) the channel migration, cutoff detection, and mesh continuous adaption, which are performed using the submodel MEANDRE (Langendoen et al., 2016).

2.1 Initialization of computational mesh and river bank lines

The initial mesh generation divides the computation domain into two regions. The first is the channel region, where the mesh has a higher spatial resolution since it is where key morphodynamic processes occur. The maximum size of the triangular elements in the channel region, d_s is defined as d_s = b/5, where b is the river channel half-width. The second region is the floodplain region, where a coarser resolution is used, with a size of triangular elements, d_f between 3d_s and 5d_s to reduce computational effort. The mesh size transition between the two regions is progressively increased to minimize numerical instability.

The initial river bathymetry and floodplain topography are mapped onto the initial mesh within the framework of a Cartesian coordinate system. In cases where digital elevation model (DEM) data for the floodplain is not accessible, an alternative method for defining the valley slope, S_v, is based on the equation S_v = S_c ⋅Ω, where S_c is the longitudinal channel slope and Ω is the channel sinuosity. The initial demarcation of the river bank lines is required to separate the channel and floodplain domains. These bank lines are subject to dynamic modifications enacted by the channel migration submodel.

2.2 Hydrodynamics and bed morphodynamics

TELEMAC-2D and SISYPHE are mature open-source models developed by EDF-R&D (France). More details about TELEMAC-2D and SISYPHE can be found in the two manuals by Lang (2013) and Tassi and Villaret (2014), respectively. We will briefly introduce the governing equations of the two models below.

TELEMAC-2D solves the two-dimensional time-dependent shallow water equations (Eqs. 1–3) using the h-type finite element method (Lang, 2013) for spatial discretization. The mass and momentum conservation equations are:

$\frac{\partial h}{\partial t}+\mathbf{U}\cdot \nabla h+h\nabla \cdot \mathbf{U}=Sr{c}_h(1)$

$\frac{\partial u}{\partial t}+\mathbf{U}\cdot \nabla u=Sr{c}_x-g\frac{\partial H}{\partial x}+\frac{1}{h}\nabla \cdot \left(h{v}_t\nabla u\right)(2)$

$\frac{\partial v}{\partial t}+\mathbf{U}\cdot \nabla v=Sr{c}_y-g\frac{\partial H}{\partial y}+\frac{1}{h}\nabla \cdot \left(h{v}_t\nabla v\right)(3)$

where h is the water depth; t is the time; U = (u, v) is the depth-averaged velocity vector in Cartesian (x- and y-direction) coordinates, respectively; Src_h, Src_x and Src_y are the source/sink terms in mass and momentum conservation (bottom roughness is wrapped into the two terms Src_x and Src_y); g is the gravitational acceleration; H is the water surface elevation; ν_t is the turbulent eddy viscosity. We used a k-ϵ model averaged over the vertical for turbulence closure in the 2D model utilized in this work (Hervouet, 2007).

SISYPHE computes the sediment transport (as bedload and suspended load for non-cohesive or cohesive sediments) and the evolution of the riverbed (Tassi and Villaret, 2014). Among several classical bedload transport formulae, the Meyer-Peter-M$\ddot{\mathrm{u}}$ller formula (Eq. 4) was selected for validation of the cases analyzed herein.

${\mathrm{\Phi }}_b=\left\{\begin{array}{ccc}\hfill & 0\hfill & \hfill \mathrm{i}\mathrm{f}{\theta }^{\prime }⩽0.047\\ \hfill 8& {\left({\theta }^{\prime }-0.047\right)}^{3/2}\hfill & \hfill \mathrm{i}\mathrm{f}{\theta }^{\prime }>0.047\end{array}\right.(4)$

where Φ_b is the non-dimensional sand transport rate and θ′ is the Shields parameter.

The Exner equation (Eq. 5) is used in the SISYPHE model to solve bed evolution:

$\frac{\partial z_b}{\partial t}=-\frac{1}{1-\lambda }\nabla \cdot {\mathbf{Q}}_{\mathbf{b}}(5)$

where z_b is the bed elevation; t is the time; λ is the material porosity; Q_b = (Q_bx, Q_by) is the vector of unit sediment discharges in x- and y-direction, respectively.

The formulation of Soulsby (1997) and Talmon et al. (1995) was used to correct the magnitude and the direction of the bed load transport, respectively, and Engelund’s formula to evaluate the deviation of sediment transport and the depth-averaged flow due to secondary flow.

The computation of the flow field is performed by TELEMAC-2D and the computation of Exner equation is addressed by SISYPHE. Flow field and bed morphology have different time scales; hydraulic perturbations occur faster than the bed evolution processes. For that reason, the computation of flow and bed evolution can be decoupled. Once the flow variables are solved, they are passed to SISYPHE to solve bedload and bed evolution.

2.3 Channel migration and cutoff detection

Planform channel migration occurs by fluvial erosion and bank geotechnical processes causing bank retreat, and by depositional processes then produce bank advance (Parker et al., 2011). Here MEANDRE is used (Langendoen et al., 2016) to solve bank erosion and accretion as expressed by Eqs. 6, 7:

$E=\left\{\begin{array}{ccc}\hfill & M_e\left(\frac{\tau }{{\tau }_{ce}}-1\right)\hfill & \hfill \mathrm{i}\mathrm{f}\tau >{\tau }_{ce}\\ \hfill & 0\hfill & \hfill \mathrm{i}\mathrm{f}\tau ⩽{\tau }_{ce}\end{array}\right.(6)$

$A=\left\{\begin{array}{ccc}\hfill & M_a\left(1-\frac{\tau }{{\tau }_{ca}}\right)\hfill & \hfill \mathrm{i}\mathrm{f}\tau <{\tau }_{ca}\\ \hfill & 0\hfill & \hfill \mathrm{i}\mathrm{f}\tau ⩾{\tau }_{ca}\end{array}\right.(7)$

where E and A are the bank erosion and accretion rates [m/s], respectively; M_e and M_a are the erosion-rate and accretion-rate coefficient (m/s), respectively; τ is the shear stress exerted by the flow on the banks; τ_ce is the critical shear stress for erosion of the material on the banks, on the other hand, τ_ca is a conceptual parameter equivalent to critical shear stress, on the contrary applied for accretion. The relation between the two previous critical shear stresses is important since their net effect is the widening or narrowing of the channel. Typically, we let M_e = M_a and τ_ce = τ_ca to maintain a dynamically uniform channel width. M_e, M_a, τ_ce, and τ_ca are model calibration parameters in MEANDRE, and they are typically chosen to match the observed channel migration rates in the study river through an analysis of multi-year remotely-sensed images.

Besides the flow field and bed evolution, bank migration (planform dynamics) is involved in the morphological evolution of rivers and it has the largest time scale. The algorithm proposed for the erosion and accretion processes also has a different coupling period from bed morphology and flow field computations. During the step of the computation of the erosion and accretion rates, we can obtain the migration distances of the river through Eq. 8. The migration of the banks determined by d, triggers adaptation of the elements of the mesh and reconfiguration of its topology (adaptation of nodes and reconfiguration of elements of the mesh).

$\mathbf{d}=\left\{\begin{array}{cc}\hfill E\cdot \mathrm{\Delta }t\cdot {\mathbf{e}}_{\mathbf{n}}& \mathrm{e}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\hfill \\ \hfill A\cdot \mathrm{\Delta }t\cdot {\mathbf{e}}_{\mathbf{n}}& \mathrm{a}\mathrm{c}\mathrm{c}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\hfill \end{array}\right.(8)$

where d is the migration vector; Δt is time step in the model; and e_n is the unit vector normal to the bank.

Previous studies have proposed an algorithm for detecting imminent cutoffs in numerical modeling (e.g., Sun et al., 1996; Camporeale et al., 2005). In this study, we utilized a modified version of Camporeale et al. (2005)’s algorithm, which uses the outer-bank line instead of the channel centerline and optimizes the sweeping range. These modifications significantly reduce iteration times compared to enumerating all nodes to calculate their distances and locate the minimum distance that identifies an imminent cutoff. The algorithm is briefly described below (Figure 2):

1. The outer-bank lines are discretized at equal length intervals (d_s in Figure 2) and n nodes that are sorted onto a uniform square grid board. The size of each cell is exactly equal to the threshold distance of cutoff d_c, where d_c is set to be equal to 2d_s in our model, i.e., 20% channel width or 0.4b.

2. Approximately n operations are needed to traverse all outer-bank nodes. From upstream to downstream, when a node (P_i in Figure 2) is being examined, except for the cell that P_i is in (namely the center cell), only five cells contain nodes and will be swept. In other words, for the case illustrated in Figure 2, standing at the center cell, the five cells to be traversed are the west, east, southwest, south, and southeast cells.

3. Then, all nodes within the center cell are swept to identify if a node exists that fulfills two conditions, first, a Cartesian distance to node P_i lower than d_c, and second, streamwise distance between these two nodes larger than 5d_c. Then the same search statements are executed in the five nearby cells.

4. If the node fulfills the conditions to trigger a cutoff, the two nodes where a cutoff occurs are recorded and both the oxbow lake and the new shortened channel are formed.

FIGURE 2

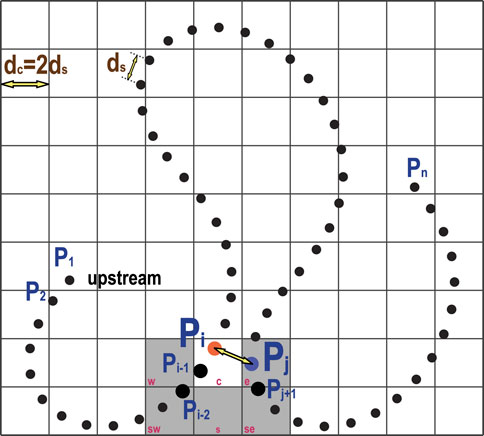
FIGURE 2. Schematic of the cutoff detection algorithm: an outer-bank line is discretized into a finite number of nodes, P₁, P₂, …, P_n; an arbitrary node, P_i (orange node), is being scanned for possible cutoff; the distance between P_i and P_j (blue node) is found less than d_c, as well as the streamwise distance of these two nodes are larger than 5d_c, indicating a cutoff has been detected.

Integrating the above algorithm, the model can detect incipient cutoffs. As described in earlier sections, the present model uses an irregular mesh based on triangular elements for the main channel and the floodplain; thus, it is crucial to keep track of the bank lines during meander evolution. Therefore, we define a binary variable to track the channel–floodplain regions. For the initial mesh, all channel nodes are given the value of 0, and all floodplain nodes are given the value of 1. The boundaries of “0 region” and “1 region” are two polylines representing the left and right bank lines (see Figure 3A). After several time steps, especially at the moment of cutoff, the “0 region” will be enlarged and forms a new left bank line or a right bank line (see Figure 3B). Next, the model will continuously run using the new configurations. Flow velocities in the newly-formed oxbow lake will reduce when time advances; thus, the “1 region” will gradually shrink and eventually form a new channel (see the process in Figures 3C–F).

FIGURE 3

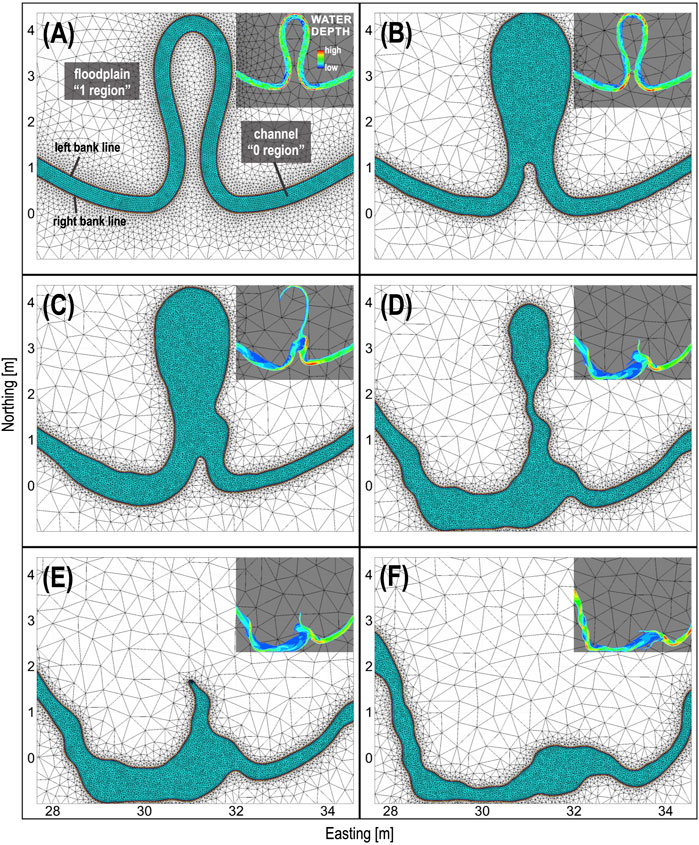
FIGURE 3. A demonstration of mesh adaptation for pre-cuotoff (A), cutoff (B,C), and post-cutoff (D–F) condition. Notice that the finer mesh along the main channel is maintained during the transitional stage of the cutoff process. Herein, the water depth (sub-panels) is shown only when flow velocity magnitude is above a tolerance (1e-3 m/s).

2.4 Relevant timescales and computation strategy

Three categories of physical processes are involved: hydraulics, sediment transport/bed evolution, and migration of the river banks. Each of them has different timescales and for that reason, different time steps can be used for the numerical solution of the flow field, the bed evolution, and the computation of the migration of banks. The decoupling of the hydraulics and bed evolution is handled internally by SISYPHE. The time step is specified in term of multiples of the time used for the hydraulics (one, two or three orders of magnitude are typically utilized). The time step for the migration of the banks is managed by MEANDRE; the time step for the migration of the banks is set as several times the time step used to evolve the river bed. In cases where local processes are acting (e.g., bank collapse) at different rates than reach-averaged rates, a coupling between the different modules has to be accounted for.

3 Results

3.1 Modeling Han and Endreny’s laboratory cutoff experiment

The validation of the methodology formulated here was performed first using the results of the experiment of Han and Endreny (2014a); they utilized a physical model to simulate the development of a cutoff. The experiment was set in a mobile bed river table (3.66 m × 1.83 m × 0.2 m) where the water surface and riverbed were periodically monitored before, during and after the cutoff development. The water surface and riverbed configuration were measured at a sub-millimeter scale at various meander evolution stages: M3 was the initial stage; M4 was the pre-cutoff stage; M5 was at cutoff; M6 was 5 h after cutoff; all the mentioned stages are depicted in Figure 4A. The experiment used an 80 mL/s constant rate input of water into the river table’s upper reservoir while draining the lower reservoir from a fixed elevation orifice weir crest. The river had an average channel width and depth of 80 mm and 25 mm, respectively, a valley slope of 1.8%, a sediment size D₅₀ of 0.2 mm with 10% talc powder to create cohesivity, a mean velocity of 0.04 m/s, a Reynolds number of 3200, a Froude number of 0.05, an average boundary shear stress of 0.18 Pa and the bed material had a critical shear stress of 0.15 Pa. The river water surface and riverbed digital elevation model (DEM) data during the experiment were obtained from post-processing stereo-pair images (Han and Endreny, 2014b).

FIGURE 4

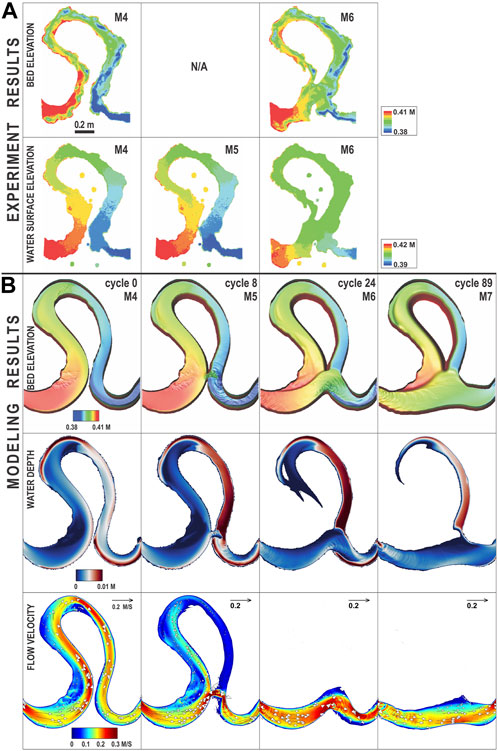
FIGURE 4. Modeling results compared against experiment results. Flow is from left to right. (A) Experiment results (bed elevation and water surface elevation). M4-M6 are temporal stages. Note that the bed elevation data at M5 was not captured to avoid the potential interference of draining the river. (B) Modeling results (bed elevation, water depth, and flow velocity). Cycle = 0, 8 and 24 correspond to M4, M5, and M7 in the experiment, and cycle = 89 refers to the formation of the new straight channel after cutoff, which is an extension of the experiment. For simplicity the floodplain topography is not shown.

The cutoff modeling approach described herein was utilized to simulate this experiment and the results of flow velocity, bed shear stress, water depth and bed topography are shown in Figure 4B for the experimental meander stages M4, M5 and M6, which corresponded with the model Cycle 0, 8 and 24. A cycle is a single timestep where the river banks are adapted by the processes of bank erosion and accretion, and the mesh is generated again if necessary for a better representation of the river banks position. The model also simulated beyond M6 (Cycle 89), corresponding to a stage when the cutoff had transitioned to its lowest sinuosity. The water depth and velocity vectors at M5 (also shown at Figure 4) capture the development of the cutoff breaching the channel outer banks, and the changes in water depth between the stages M5 and M7 capture the transition from oxbow lake to paleo-channel. During cutoff, shear stresses increased in the cutoff region; these larger shear stresses then spatially expanded and cut a deeper, straighter channel through the meander neck, which resulted in their decrease.

The model simulated the post-cutoff sequence through Cycle 89 to track activity in the upstream erosional and downstream depositional processes, extending beyond M7, after the laboratory experiment terminated. This additional tracking allowed us to outline a conceptual model of the development of the longitudinal bed profile during and after the cutoff (Figure 5), which is based on the river geometry and other bend wavelengths and amplitudes found during cutoff evolution (Gutierrez and Abad, 2014; Gutierrez et al., 2014). The first stage of the conceptual model involves the conditions just before the cutoff, with the channel planform and longitudinal bed profile described in Figure 5A, where S_e denotes the equilibrium streamwise slope. The next stage is the development of the cutoff (Figure 5B), where the longitudinal bed profile is modified with a reach of slope, S_AB, where the shorter length of the new channel compared to the pre-cutoff conditions produced a larger slope. The next stage is indicated in Figures 5C, D; the channel tends to return to an equilibrium bed profile by triggering an erosional wave traveling upstream and a depositional wave traveling downstream, as indicated in Figure 5C, and depicted in the bed longitudinal profile; this process also promotes planform migration (Abad et al., 2012). A fundamental part of the conceptual model is the erosional and depositional waves (Figure 5C); the erosional wave moves upstream, incising the bed, and the depositional wave moves downstream, depositing the sediment eroded from the upstream area. This process helps the development of the oxbow lake with the definition of the new left bank line, as identified in Figure 5D. Moreover, the deposition of sediments downstream contributes to plugging the outlet of the oxbow lake.

FIGURE 5

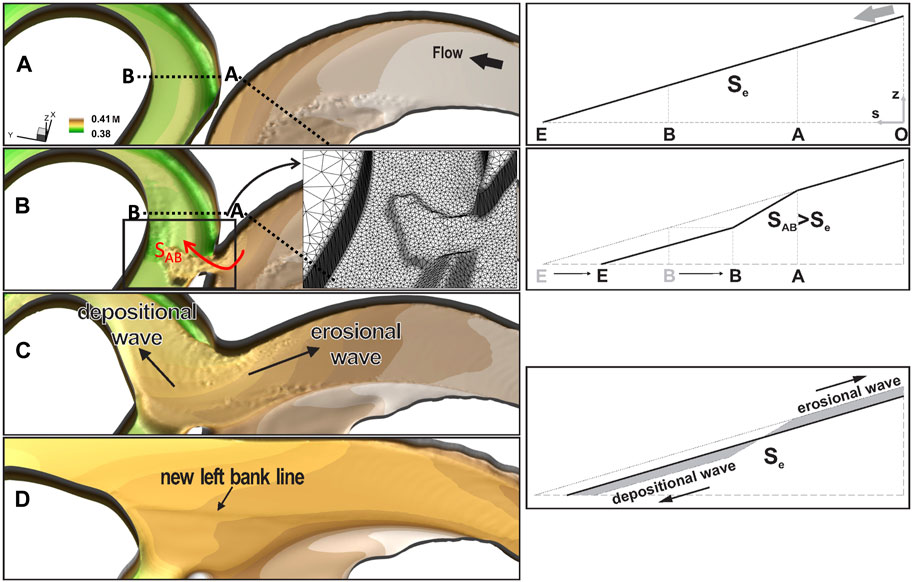
FIGURE 5. 3D view of bed morphology: (A) pre-cutoff condition, (B) connectivity between the bends is initiated, (C) the erosional and depositional waves are propagated, (C) to (D) width and bed adjustment take place. The quality of the mesh (along the main channel and the floodplain) is maintained during the transitional cutoff process. Vertical exaggeration is 2. The conceptual model of morphological response after cutoff: i) profile before cutoff, ii) profile right after cutoff, iii) the river tends to return to equilibrium conditions by producing erosional (upstream) and depositional (downstream) waves (Abad et al., 2012).

The evolution of bed shear stress and bedload for the numerical modeling of Han and Endreny (2014a)’s cutoff experiment is shown in Figure 6. Bed shear stress increases after the cutoff, first locally near the neck, and upstream and downstream of it (see M5 and M6 in Figure 6A). After the meander loop is abandoned, the shear stress in the new shorter reach is larger than before the cutoff (compare M4 to M7 in Figure 6A). Note that after the cutoff, the downstream reach widens, because of the increased shear stress. Bedload upstream and downstream the cutoff increases to a peak (by cycle 30), and then gradually decreases (Figure 6B). The increment is larger downstream the cutoff. After the meander loop has been abandoned, and the reach of the cutoff has been straightened, bedload is larger than before the cutoff.

FIGURE 6

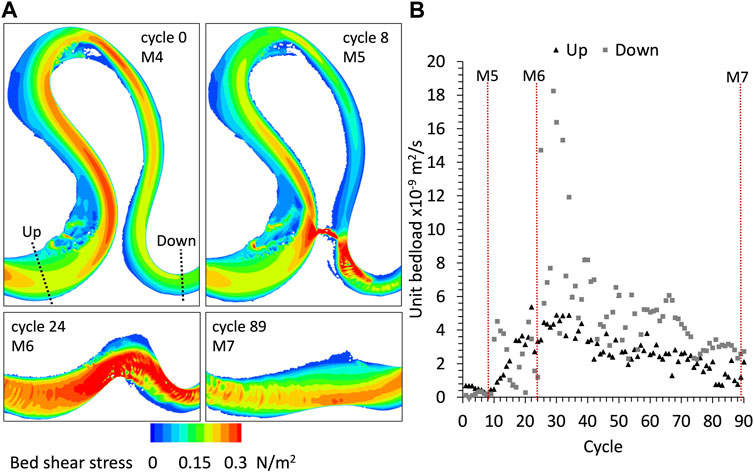
FIGURE 6. Analysis of sediment transport computed for Han and Endreny (2014a)’s experiment modeling: (A) bed shear stress, (B) evolution of unit sediment transport computed by the model before and after the cutoff.

3.2 Modeling a cutoff in the Ucayali River

Following the model application in the laboratory scale, we conducted the simulation on a natural cutoff in the Ucayali River. In the satellite imagery provided by the Landsat Missions, a massive number of cutoffs, oxbow lakes, scroll bars, and paleo-channels can be observed along the Ucayali River (see the example reach illustrated in Figure 1). A cutoff event that occurred between 2014 and 2015 was considered for modeling with the approach presented in this study. The cutoff was located approximately 200 km downstream of Pucallpa City, eastern Peru. From the satellite imagery of 2006, 2010, 2013, 2014, 2015, 2016, and 2017, it was determined that the channel banks migrated at approximately 50–200 m/yr (see Figure 1). To set up the cutoff model based on the 2013 river geometry, several assumptions were made: 1) Since the goal was to reproduce the main physical processes of the cutoff (bank migration, riverbed erosion and sedimentation), the initial river geometry was considered of constant width of 800 m instead of the spatially varying river widths. The width was eventually self-adjusted during the simulation; 2) Due to the limitation of available data, the initial river bathymetry was obtained from a synthetic riverbed topography model proposed by Li and García (2021), which represents the morphodynamic bed equilibrium configuration around river bends. The computed bed topography was validated against the measured cross-sectional profiles. Similar to the channel width, the bed evolution will self-adjust the bathymetry during modeling; 3) The topography on the floodplain was not considered in this study. Hence, instead of applying local DEM data as the initial floodplain topography, the initial floodplain topography was modeled as an inclined plane with a constant valley slope; 4) A constant flow discharge of 12,000 m³/s (annual mean) was imposed as boundary condition at the inlet; 5) For the sediment boundary condition, a model of recirculating boundary condition was presented by Mendoza et al. (2016), where the volume of sediment measured at the outlet is fed back at the inlet. In such conditions, the sediment transport is at the dynamic equilibrium state, with oscillations caused by the development of bedforms. However, for the case of the Ucayali River, equilibrium conditions were set at the inlet sediment boundary condition, since after the neck cutoff, the sediment would have been fed at the inlet, something not necessarily true when only one cutoff is simulated.

Figure 7 shows the modeled migration of the banks between 2013 and 2017 in the analyzed reach; at Cycle 35, the cutoff was initiated. An abrupt drop in flow velocity is observed at the bend, that is, being abandoned. In Cycle 60 of the simulation, which corresponds chronologically to the satellite imagery of 2015, an oxbow lake was fully formed since the velocity is zero although the oxbow is still not infilled. There is a coincidence in the development of bars when comparing the modeling results; the bars marked with a to c indicated in the results of cycle 60 illustrated in Figure 7, are similar to the ones observed from the satellite imagery of 06/2015. During Cycle 100 the simulation developed a large bar just downstream of the cutoff point, which reconfigures the flow distribution and promotes bank erosion in front of such bar. This is also observed in the satellite imagery (image of 2017 in Figure 7). After the cutoff developed, the new shortened channel will progressively self-adjust to a new meander bend, whose channel sinuosity will gradually increase due to channel migration, same as the rest of the upstream and downstream bends (Figure 8). The simulation took 120 h for the Ucayali River in a high-performance cluster using 32 cores of computation. The channel (floodplain) was discretized using triangular elements with maximum size of 50 m (250 m) edge length.

FIGURE 7

FIGURE 7. The Ucayali River. Modeling results compared against Landsat imageries, flow goes from left to right. Modeled bed elevation, flow velocity and water depth are shown at the initial condition (Oct. 2013), Cycle #35 (cutoff initiation, no satellite imagery available), Cycle #60 (Jun. 2015) and Cycle #100 (Apr. 2017).

FIGURE 8

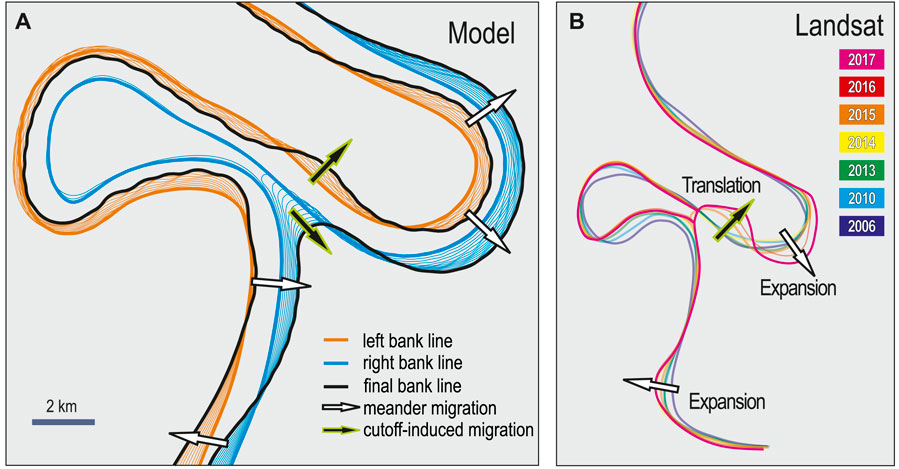
FIGURE 8. The Ucayali River. Simulated bank line migration [in (A)] agrees with the trend of the Landsat imageries-derived centerline migration [in (B)]. Hollow arrows indicate the regular migration patterns without cutoff impact: translation and expansion. Solid arrows indicate the cutoff-induced channel migration: channel widening, shortened waterway formation and oxbow lake sedimentation.

The process of bed evolution also determines how the cutoff bend interacts temporarily with the flow before being completely abandoned. Such interaction is observed in the modeled flow velocity and bed elevation (Figure 7), where the velocity after the cutoff gradually diminished while the original bed was aggrading. The abandonment of the original bend occurs progressively. For instance, Turnipseed et al. (2021) showed the case of a neck cutoff in the White River, Arkansas, where during a bank full event the original meander still captured 51% of the flow 1 year after the cutoff.

4 Discussion

4.1 Model novelties/advantages and limitations

4.1.1 Novelties/advantages

Asahi et al. (2013) have presented numerical simulations of river meandering processes for steady (bankfull) and unsteady flow discharges considering the conceptual model presented by Parker et al. (2011). The simulated hydraulic conditions were typical of laboratory experiments. Turnipseed et al. (2021) described the numerical simulation of early stages of cutoff along the White River (channel width: 150 m, mean annual discharge: 750 m³/s) in Arkansas, United States. The computational domain (mesh) at these stages were predefined using field measurements, thus no simulation of the cutoff process was presented. The present study validates the computational results against both laboratory-based experiments and at the field scale considering one of the most dynamic rivers in the world, the Ucayali River (Schwenk and Foufoula-Georgiou, 2016; Lopez Dubon and Lanzoni, 2019; Abad et al., 2022). The Ucayali River presents migration rates from 50 to 200 m/yr, channel width of 800 m, and a mean annual discharge of 12,000 m³/s. According to Asahi et al. (2013) when using a constant flow discharge, planform patterns did not evolve towards more complex shapes, but attained low sinuosities without developing cutoffs. Conversely, under unsteady flows, higher sinuosities bends formed. In our study, the initial planform is that observed just prior to a neck cutoff, with the well developed secondary circulation driven by channel axis curvature and topographic steering (Seminara, 2006). The high-resolution mesh used along the main channel and repeated remeshing of the eroded floodplain allowed to reproduce the complex erosional and depositional patterns observed in the laboratory and in the field during the various phases of the cutoff (see videos in the Supplemental material S1).

Long-term simulations (from hundreds of years to geologic time scales) were usually performed with linearized models (Sun et al., 1996, 2001; Camporeale et al., 2005; Frascati and Lanzoni, 2010; Schwenk et al., 2015) computing in a simplified manner river migration and cutoff processes, and their interactions with the river valley. These models in general neglect erosional and depositional waves due to cutoff occurrence (Abad et al., 2012), the stage of cutoff where the old bend is still active capturing part of the flow (Richards and Konsoer, 2020), the bedform modulation of bank stability due to bedform migration (Abad et al., 2013), flow variability (hydrographs) possibly leading to inundation of the floodplain (Simon et al., 2020), floodplain heterogeneities. The model presented here can account for sediment waves after cutoff, large scale bedform modulation (bar dynamics), and flow variation. The model has been shown to reproduce successfully neck cutoff dynamics at both the laboratory timescale (few tens of hours) and in the field. In this latter case, the simulated time period is typical of short-term river evolution (a few years). Longer evolution periods however require a computational cost, that is, too heavy even for a modern high-performance computing platform.

4.1.2 Limitations

Horizontal and vertical heterogeneity of floodplain material is not accounted for in the present model. The rate of bank retreat in rivers, however depends on the interaction of forcing factors (shear stress exerted by the flow and bank instability) with the resistance to erosion and geomechanical properties of the bank material. In the present modeling framework, we have simplified the bank erosion/accretion processes and ignored the bank collapse events. Horizontal (floodplain soils of different properties) and vertical (layers of soils of different properties) heterogeneities may have important effects on the dynamics of meandering rivers (Motta et al., 2012b; Motta et al., 2014; Bogoni et al., 2017; Zhao et al., 2021). In addition, repeated bank collapses can produce a catch-up behavior (outer bank collapse and subsequent inner bank accretion) as shown by Zhao et al. (2021).

4.2 Complex morphodynamic processes

The morphodynamic processes prior, during and after cutoff processes involve several complex patterns which can be addressed by the present modeling framework.

Paleochannels and river migration: As observed in Figure 1, during the lifetime of a river, both recent geomorphic features (e.g., scroll bars and oxbow lakes) and ancient geomorphic features (e.g., paleochannels and terraces) are found. The floodplain is usually characterized of fine sediment deposits and vertical layers of heterogenous soils (Abad et al., 2022), vegetation responding to river dynamics, differentiated elevations throughout the floodplain, and complex connectivity due to the existence of dry and wet paleochannels (Rojas et al., 2023), a required ingredient for preservation of the stratigraphic record in fluvial meander-belt deposits (Durkin et al., 2017).

Forced and migrating free bars: the coexistence of forced and free bars in meandering channels (Tubino and Seminara, 1990) is typical of meandering rivers. After cutoff, the channel develops a low sinuosity (less curvature forcing), and free migrating bars can interact with bars forced by channel enlargements (Luchi et al., 2010) as those produced by a neck cutoff (Figure 7). In addition the migration of both large scale (bars) and small scale (dunes) bedforms produces a modulation of the shear stresses exerted on the outer bank and, hence, on bank erosion (Abad et al., 2013).

4.3 Detailed monitoring of large scale processes

Recently, detailed field measurements in cutoffs were performed along different rivers; White River, Arkansas (United States) (Richards et al., 2018; Richards and Konsoer, 2020; Turnipseed et al., 2021), Wabash River, Indiana and Illinois (United States) (Zinger et al., 2011), Huallaga River, Loreto (PERU) (Valverde et al., 2023). However, still a need for more detailed high-resolution hydrogeomorphic characterization of the different phases during pre-, cutoff, and post-cutoff conditions, including those of traveling sediment waves. In Amazonian rivers, cutoffs occur in a timescale dependent of the river characteristics, but the Ucayali River is one of most dynamic rivers where little hydrogeomorphic data is available (Abad et al., 2022). In order to improve river modeling at these large and very active systems, more detailed river data is needed, not just to understand the physical processes, but also to calibrate sediment transport equations, since, along these rivers, sediment fluxes are dependent on planform conditions (including influence of tributaries), flow variability and bedforms activity (Abad et al., 2022; Abad et al., 2023; Valverde et al., 2023).

5 Conclusion

The present research introduces a computational model capable of predicting the transitional hydrodynamics and morphodynamics associated with a meander neck cutoff, considering the temporary interaction with the reach undergoing abandonment. The model was validated by means of a laboratory-controlled mobile bed experiment and an actual cutoff observed in the Ucayali River. It is shown to effectively reproduce cutoff dynamics and evaluate non-local morphological effects beyond the constraints of existing linear models, such as bar formation, sediment wave evolution, and two-dimensional flow field structure. The results of the model show widening of the cutoff cross-section, with the consequent formation of forced bars, adaptation of the main channel bed through upstream and downstream sediment waves, formation of oxbow lakes, and preservation of the resulting paleo-channel in the floodplain. In summary, the model demonstrates efficient cutoff detection and channel adaptation capabilities, thereby highlighting the importance of considering both hydrodynamics and morphodynamics for describing meander cutoff temporal evolution. The study also describes the need to develop physics-based simplified models for incorporating local effects of neck cutoffs into the long term river migration models.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/ZhiLiHydro/NeckCutoffModeling.

Author contributions

Conceptualization: ZL, AM, and JA; methods: ZL and AM. Experiment data: TE and BH; computational resources, EC and RD; formal analysis: ZL and AM; data curation: ZL and AM; interpretation and discussion, ZL, AM, JA, TE, BH, EC, and RD; writing–original draft preparation, ZL and AM; review and editing, JA, TE, BH, EC, and RD; visualization, ZL and AM; supervision, JA; funding acquisition, JA. All authors contributed to the article and approved the submitted version.

Funding

JA thanks partial funding from Gordon and Betty Moore Foundation (Grant GBMF7711), OTCA (Contract ANA/623/2021).

Acknowledgments

JA thanks long-term collaborations with the Directorate of Navigation and Hydrography of the Peruvian Navy, Senamhi-Peru (Marco Paredes), Yangtze University-China (Jingfu Shan), and UNAM-Mexico that nurture research ideas. The authors also thank the editors and three reviewers for their insightful comments and suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1208782/full#supplementary-material

References

Abad, J. D., and Garcia, M. H. (2006). RVR meander: A toolbox for re-meandering of channelized streams. Comput. Geosci. 32, 92–101. doi:10.1016/j.cageo.2005.05.006

CrossRef Full Text | Google Scholar

Abad, J. D., Peralta, B., Paredes, J., Frias, C., Gutierrez, R., and Montoro, H. (2012). The meandering ucayali river, a cyclic adaptation of cutoff and planform migration. San Jose, Costa Rica. River Flow, September 5-7.

Google Scholar

Abad, J. D., Frias, C. E., Buscaglia, G. C., and Garcia, M. H. (2013). Modulation of the flow structure by progressive bedforms in the kinoshita meandering channel. Earth Surf. Process. Landforms 38, 1612–1622. doi:10.1002/esp.3460

CrossRef Full Text | Google Scholar

Abad, J. D., Mendoza, A., Arceo, K., Torres, Z., Valverde, H., Medina, G., et al. (2022). Planform dynamics and cut-off processes in the lower ucayali river, peruvian amazon. Water 14, 3059. doi:10.3390/w14193059

CrossRef Full Text | Google Scholar

Abad, J. D., Motta, D., Guerrero, L., Paredes, M., Kuroiwa, J. M., and Garcia, M. (2023). Hydrogeomorphology of asymmetric meandering channels: experiments and field evidence. Water Resour. Res. 59, e2022WR033904. doi:10.1029/2022wr033904

CrossRef Full Text | Google Scholar

Asahi, K., Shimizu, Y., Nelson, J., and Parker, G. (2013). Numerical simulation of river meandering with self-evolving banks. J. Geophys. Res. Earth Surf. 118, 2208–2229. doi:10.1002/jgrf.20150

CrossRef Full Text | Google Scholar

Bogoni, M., Putti, M., and Lanzoni, S. (2017). Modeling meander morphodynamics over self-formed heterogeneous floodplains. Water Resour. Res. 53, 5137–5157. doi:10.1002/2017wr020726

CrossRef Full Text | Google Scholar

Camporeale, C., Perona, P., Porporato, A., and Ridolfi, L. (2005). On the long-term behavior of meandering rivers. Water Resour. Res. 41. doi:10.1029/2005wr004109

CrossRef Full Text | Google Scholar

Camporeale, C., Perona, P., Porporato, A., and Ridolfi, L. (2007). Hierarchy of models for meandering rivers and related morphodynamic processes. Rev. Geophys. 45. doi:10.1029/2005rg000185

CrossRef Full Text | Google Scholar

Camporeale, C., Perucca, E., and Ridolfi, M. L. (2008). Significance of cutoff in meandering river dynamics. J. Geophys. Res. 113, F01001–F01011. doi:10.1029/2006JF000694

CrossRef Full Text | Google Scholar

Constantine, J. A., Dunne, T., Ahmed, J., Legleiter, C., and Lazarus, E. D. (2014). Sediment supply as a driver of river meandering and floodplain evolution in the amazon basin. Nat. Geosci. 7, 899–903. doi:10.1038/ngeo2282

CrossRef Full Text | Google Scholar

Crosato, A. (2008). Analysis and modelling of river meandering. Ph.D. thesis. Delft University of Technology.

Google Scholar

Darby, S. E., Alabyan, A. M., and Van de Wiel, M. J. (2002). Numerical simulation of bank erosion and channel migration in meandering rivers. Water Resour. Res. 38, 2-1–2-21. doi:10.1029/2001wr000602

CrossRef Full Text | Google Scholar

Davidson, S. K., and North, C. P. (2009). Geomorphological regional curves for prediction of drainage area and screening modern analogues for rivers in the rock record. J. Sediment. Res. 79, 773–792. doi:10.2110/jsr.2009.080

CrossRef Full Text | Google Scholar

Durkin, P. R., Hubbard, S. M., Holbrook, J., and Boyd, R. (2017). Evolution of fluvial meander-belt deposits and implications for the completeness of the stratigraphic record. GSA Bull. 130, 721–739. doi:10.1130/B31699.1

CrossRef Full Text | Google Scholar

Edwards, B. F., and Smith, D. H. (2002). River meandering dynamics. Phys. Rev. E 65, 046303. doi:10.1103/physreve.65.046303

PubMed Abstract | CrossRef Full Text | Google Scholar

Frascati, A., and Lanzoni, S. (2010). Long-term river meandering as a part of chaotic dynamics? a contribution from mathematical modelling. Earth Surf. Process. Landforms 35, 791–802. doi:10.1002/esp.1974

CrossRef Full Text | Google Scholar

Gay, G. R., Gay, H. H., Gay, W. H., Martinson, H. A., Meade, R. H., and Moody, J. A. (1998). Evolution of cutoffs across meander necks in powder river, Montana, USA. Earth Surf. Process. Landforms 23, 651–662. doi:10.1002/(sici)1096-9837(199807)23:7<651::aid-esp891>3.0.co;2-v

CrossRef Full Text | Google Scholar

Gutierrez, R. R., and Abad, J. D. (2014). On the analysis of the medium term planform dynamics of meandering rivers. Water Resour. Res. 50, 3714–3733. doi:10.1002/2012wr013358

CrossRef Full Text | Google Scholar

Gutierrez, R. R., Abad, J. D., Choi, M., and Montoro, H. (2014). Characterization of confluences in free meandering rivers of the amazon basin. Geomorphology 220, 1–14. doi:10.1016/j.geomorph.2014.05.011

CrossRef Full Text | Google Scholar

Han, B., and Endreny, T. A. (2014a). Detailed river stage mapping and head gradient analysis during meander cutoff in a laboratory river. Water Resour. Res. 50, 1689–1703. doi:10.1002/2013wr013580

CrossRef Full Text | Google Scholar

Han, B., and Endreny, T. A. (2014b). River surface water topography mapping at sub-millimeter resolution and precision with close range photogrammetry: laboratory scale application. IEEE J. Sel. Top. Appl. Earth Observations Remote Sens. 7, 602–608. doi:10.1109/jstars.2014.2298452

CrossRef Full Text | Google Scholar

Hervouet, J.-M. (2007). “Hydrodynamics of free surface flows,” in Modeling with the finite element method (France: John Wiley & Sons).

CrossRef Full Text | Google Scholar

Hooke, J. (1995). River channel adjustment to meander cutoffs on the River Bollin and River Dane, northwest England. Geomorphology 14, 235–253. doi:10.1016/0169-555X(95)00110-Q

CrossRef Full Text | Google Scholar

Hooke, J. (2004). Cutoffs galore!: occurrence and causes of multiple cutoffs on a meandering river. Geomorphology 61, 225–238. doi:10.1016/j.geomorph.2003.12.006

CrossRef Full Text | Google Scholar

Howard, A., and Knutson, T. (1984). Sufficient conditions for river meandering: A simulation approach. Water Resour. Res. 20, 1659–1667. doi:10.1029/WR020i011p01659

CrossRef Full Text | Google Scholar

Howard, A. D. (1996). “Modeling channel evolution and floodplain morphology,” in Floodplain processes, 15–62.

Google Scholar

Ielpi, A., Lapôtre, M., Finotello, A., and Ghinassi, M. (2020). Planform-asymmetry and backwater effects on river-cutoff kinematics and clustering. Earth Surf. Process. Landforms 46, 357–370. doi:10.1002/esp.5029

CrossRef Full Text | Google Scholar

Ielpi, A., Viero, D. P., Lapôtre, M. G. A., Graham, A., Ghinassi, M., and Finotello, A. (2023). How is time distributed in a river meander belt? Geophys. Res. Lett. 50, e2022GL101285. doi:10.1029/2022gl101285

CrossRef Full Text | Google Scholar

Kiss, T., and Sipos, G. (2015). “Mártély lake: an oxbow of the lower tisza river,” in Landscapes and landforms of Hungary (Springer), 271–277.

CrossRef Full Text | Google Scholar

Lancaster, S. T., and Bras, R. L. (2002). A simple model of river meandering and its comparison to natural channels. Hydrol. Process. 16, 1–26. doi:10.1002/hyp.273

CrossRef Full Text | Google Scholar

Lang, P. (2013). Telemac-2D user’s manual. Tech. rep., EDF R&D

Google Scholar

Langendoen, E. J., Mendoza, A., Abad, J. D., Tassi, P., Wang, D., Ata, R., et al. (2016). Improved numerical modeling of morphodynamics of rivers with steep banks. Adv. Water Resour. 93, 4–14. doi:10.1016/j.advwatres.2015.04.002

CrossRef Full Text | Google Scholar

Li, Z., and García, M. H. (2021). pyRiverBed: A Python framework to generate synthetic riverbed topography for constant-width meandering rivers. Comput. Geosci. 152, 104755. doi:10.1016/j.cageo.2021.104755

CrossRef Full Text | Google Scholar

Li, Z., Gao, P., and Wu, Z. (2022). Processes of neck cutoff and channel adjustment affected by seeding herbaceous vegetation and variable discharges. Catena 208, 105731–105811. doi:10.1016/j.catena.2021.105731

CrossRef Full Text | Google Scholar

Lopez Dubon, S., and Lanzoni, S. (2019). Meandering evolution and width variations: A physics-statistics-based modeling approach. Water Resour. Res. 55, 76–94. doi:10.1029/2018WR023639

CrossRef Full Text | Google Scholar

Luchi, R., Zolezzi, G., and Tubino, M. (2010). Modelling mid-channel bars in meandering channels. Earth Surf. Process. Landforms 35, 902–917. doi:10.1002/esp.1947

CrossRef Full Text | Google Scholar

Mendoza, A., Abad, J., Langendoen, E., Wang, D., Tassi, P., and Abderrezzak, K. (2016). The management of pain associated with wound care in severe burn patients in Spain. J. Hydraulic Eng. 143, 1–10. doi:10.1061/(ASCE)HY.1943-7900.0001208

PubMed Abstract | CrossRef Full Text | Google Scholar

Micheli, E., and Larsen, E. (2011). River channel cutoff dynamics, sacramento river, California, USA. River Res. Appl. 27, 328–344. doi:10.1002/rra.1360

CrossRef Full Text | Google Scholar

Motta, D., Abad, J. D., Langendoen, E. J., and Garcia, M. H. (2012a). A simplified 2D model for meander migration with physically-based bank evolution. Geomorphology 163, 10–25. doi:10.1016/j.geomorph.2011.06.036

CrossRef Full Text | Google Scholar

Motta, D., Abad, J. D., Langendoen, E. J., and Garcia, M. H. (2012b). The effects of floodplain soil heterogeneity on meander planform shape. Water Resour. Res. 48. doi:10.1029/2011wr011601

CrossRef Full Text | Google Scholar

Motta, D., Langendoen, E. J., Abad, J. D., and García, M. H. (2014). Modification of meander migration by bank failures. J. Geophys. Res. Earth Surf. 119, 1026–1042. doi:10.1002/2013JF002952

CrossRef Full Text | Google Scholar

Nagel, G. W., de Moraes Novo, E. M. L., Martins, V. S., Campos-Silva, J. V., Barbosa, C. C. F., and Bonnet, M. P. (2022). Impacts of meander migration on the amazon riverine communities using landsat time series and cloud computing. Sci. Total Environ. 806, 150449. doi:10.1016/j.scitotenv.2021.150449

PubMed Abstract | CrossRef Full Text | Google Scholar

Pannone, M., and De Vincenzo, A. (2022). On the prediction of the characteristic times of river meander cutoff sequence: theoretical model and comparison with laboratory and field observations. Water Resour. Res. 58, 1–20. doi:10.1029/2021WR031661

CrossRef Full Text | Google Scholar

Parker, G., Shimizu, Y., Wilkerson, G. V., Eke, E. C., Abad, J. D., Lauer, J. W., et al. (2011). A new framework for modeling the migration of meandering rivers. Earth Surf. Process. Landforms 36, 70–86. doi:10.1002/esp.2113

CrossRef Full Text | Google Scholar

Richards, D., and Konsoer, K. (2020). Morphologic adjustments of actively evolving highly curved neck cutoffs. Earth Surf. Process. Landforms 45, 1067–1081. doi:10.1002/esp.4763

CrossRef Full Text | Google Scholar

Richards, D., Konsoer, K., Turnipseed, C., and Willson, C. (2018). “Characterising three-dimensional flow through neck cutoffs with complex planform geometry,” in Fluvial meanders and their sedimentary products in the rock record (John Wiley Sons, Ltd), 273–295. doi:10.1002/9781119424437.ch11

CrossRef Full Text | Google Scholar

Rojas, T. V., Abad, J. D., Roque, W., Latrubesse, E., and Shan, J. (2023). Free and underfit-scavenger river dynamics dominate the large amazonian pacaya-samiria wetland structure. Front. Environ. Sci. 11, 1082619. doi:10.3389/fenvs.2023.1082619

CrossRef Full Text | Google Scholar

Ruben-Dominguez, L., Naito, K., Gutierrez, R., Szupiany, R., and Abad, J. D. (2021). Meander statistics toolbox (mstat): a toolbox for geometry characterization of bends in large meandering channels. SoftwareX 14, 100674. doi:10.1016/j.softx.2021.100674

CrossRef Full Text | Google Scholar

Schwenk, J., and Foufoula-Georgiou, E. (2016). Meander cutoffs nonlocally accelerate upstream and downstream migration and channel widening. Geophys. Res. Lett. 43, 12437–12445. doi:10.1002/2016gl071670

CrossRef Full Text | Google Scholar

Schwenk, J., Lanzoni, S., and Foufoula-Georgiou, E. (2015). The life of a meander bend: connecting shape and dynamics via analysis of a numerical model. J. Geophys. Res. Earth Surf. 120, 690–710. doi:10.1002/2014jf003252

CrossRef Full Text | Google Scholar

Seminara, G. (2006). Meanders. J. Fluid Mech. 554, 271–297. doi:10.1017/s0022112006008925

CrossRef Full Text | Google Scholar

Simon, C., Langendoen, E., Abad, J. D., and Mendoza, A. (2020). On the governing equations for horizontal and vertical coupling of one- and two-dimensional open channel flow models. J. Hydraulic Res. 58, 709–724. doi:10.1080/00221686.2019.1671507

CrossRef Full Text | Google Scholar

Soulsby, R. (1997). Dynamics of marine sands. London: Thomas Telford.

Google Scholar

Stølum, H. H. (1996). River meandering as a self-organization process. Science 271, 1710–1713. doi:10.1126/science.271.5256.1710

CrossRef Full Text | Google Scholar

Sun, T., Meakin, P., Jøssang, T., and Schwarz, K. (1996). A simulation model for meandering rivers. Water Resour. Res. 32, 2937–2954. doi:10.1029/96wr00998

CrossRef Full Text | Google Scholar

Sun, T., Meakin, P., and Jøssang, T. (2001). A computer model for meandering rivers with multiple bed load sediment sizes: 2. Computer simulations. Water Resour. Res. 37, 2243–2258. doi:10.1029/2000WR900397

CrossRef Full Text | Google Scholar

Sylvester, Z., Durkin, P., and Covault, J. A. (2019). High curvatures drive river meandering. Geology 47, 263–266. doi:10.1130/G45608.1

CrossRef Full Text | Google Scholar

Sylvia, D. A., and Galloway, W. E. (2006). Morphology and stratigraphy of the late quaternary lower brazos valley: implications for paleo-climate, discharge and sediment delivery. Sediment. Geol. 190, 159–175. doi:10.1016/j.sedgeo.2006.05.023

CrossRef Full Text | Google Scholar

Syvitski, J. P., and Kettner, A. (2011). Sediment flux and the anthropocene. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 369, 957–975. doi:10.1098/rsta.2010.0329

PubMed Abstract | CrossRef Full Text | Google Scholar

Talmon, A. M., Struiksma, N., and Vanmierlo, M. C. L. M. (1995). Laboratory measurements of the direction of sediment transport on transverse alluvial-bed slopes. J. Hydraulic Res. 33, 495–517. doi:10.1080/00221689509498657

CrossRef Full Text | Google Scholar

Tassi, P., and Villaret, C. (2014). Sisyphe v6.3 user’s manual. Tech. rep., EDF R&D.

Google Scholar

Todd, S. P., and Went, D. J. (1991). Lateral migration of sand-bed rivers: examples from the devonian glashabeg formation, sw ireland and the cambrian alderney sandstone formation, channel islands. Sedimentology 38, 997–1020. doi:10.1111/j.1365-3091.1991.tb00368.x

CrossRef Full Text | Google Scholar

Tower, W. (1904). The development of cut-off meanders. Bull. Am. Geogr. Soc. 36, 589–599. doi:10.2307/197978

CrossRef Full Text | Google Scholar

Tubino, M., and Seminara, G. (1990). Free–forced interactions in developing meanders and suppression of free bars. J. Fluid Mech. 214, 131–159. doi:10.1017/S0022112090000088

CrossRef Full Text | Google Scholar

Turnipseed, C., Konsoer, K., Richards, D., and Willson, C. (2021). Numerical modeling of two-dimensional hydrodynamics in a highly curving and actively evolving neck cutoff under different hydrologic conditions. Water Resour. Res. 57, 1–14. doi:10.1029/2020WR027329

CrossRef Full Text | Google Scholar

Valverde, H., Abad, J., Guerrero, L., Estrada, Y., and Frias, C. (2023). Hydrogeomorphic characterization of the huallaga river for the peruvian amazon waterway. J. Waterw. Port, Coast. Ocean Eng. In review.

Google Scholar

Vermeulen, B., Hoitink, A. J. F., Zolezzi, G., Abad, J. D., and Aalto, R. (2016). Multiscale structure of meanders. Geophys. Res. Lett. 43, 3288–3297. doi:10.1002/2016GL068238

CrossRef Full Text | Google Scholar

Zhao, K., Lanzoni, S., Gong, Z., and Coco, G. (2021). A numerical model of bank collapse and river meandering. Geophys. Res. Lett. 48, e2021GL093516. doi:10.1029/2021gl093516

CrossRef Full Text | Google Scholar

Zinger, J., Rhoads, B., and Best, J. (2011). Extreme sediment pulses generated by bend cutoffs along a large meandering river. Nat. Geosci. 4, 675–678. doi:10.1038/ngeo1260

CrossRef Full Text | Google Scholar