Analysis of flood control risk in floodwater utilization considering the uncertainty of flood volume and peak

Introduction: A design flood is a hypothetical flood used for the design of reservoirs and other hydrologic engineering infrastructures. Among many hydrological properties of a design flood, flood volume and peak can significantly affect the safety of reservoir operation. However, the uncertainty of flood volume and peak has rarely been considered in the risk analysis of reservoir operation regarding floodwater utilization.

Methods: In this paper, a general risk analysis framework that integrates the Monte Carlo sampling method and the most likely event selection method is proposed to calculate the risk of operating a single reservoir. By generating a large amount of stochastic bivariate flood data, the most likely design values were selected for a given return period. The probability of the maximum water level exceeding the current design flood level was calculated based on the simulation of flood control operation under various floodwater utilization schemes.

Results: The model is applied to the Shagou reservoir in the Shuhe River basin, China. The results show that the design flood volume and flood peak obtained by the bivariate joint return are 7.59% and 8.22% higher than those from univariate frequency analysis, respectively; the joint return period of bivariate design value spans from 10a to 1000a compared to the historical data; and the flood control risk at Shagou reservoir is 0.29 under current flood control operations based on the uncertainty of flood volume and peak.

Discussion: Moreover, the marginal benefit may contain floodwater utilization and a transmission risk effect between different node projects in the flood control system.

1 Introduction

With continuous economic development and population growth, the demand for water resources is becoming increasingly intense, and scarcity of water resources is among the major factors restricting social progress (Chen et al., 2016; Chang et al., 2017). To alleviate water resource shortages, various floodwater utilization models have been recently developed and demonstrated to be effective in many studies (Ding et al., 2017; Meng et al., 2018; Liu et al., 2019; Wang et al., 2019). According to the floodwater utilization concept (Wallington and Cai, 2020; Wang et al., 2020), floodwater utilization strategies can only be implemented if the risks are controlled within an acceptable range. As one of the major and effective engineering measures for floodwater utilization, reservoirs are built for multiple purposes, including flood control, water supply, and other functions. Moreover, floods are among the most frequent, widespread, and devastating natural disasters in the context of climate change and human activities (Wu et al., 2020); thus, flood control risks are particularly important for reservoir flood control operations. Therefore, the scientific assessment of flood control risk in floodwater utilization operations is important for flood management in reservoirs.

The risk analysis of floodwater utilization is a fundamental issue in flood management, engineering design, and area planning. Because the uncertainty factors lead to deviations between the calculated deterministic results and the actual occurrence and the risks involved in flood control decision making (Xiong and Qi, 2010; Delenne et al., 2012; Simonovic and Arunkumar, 2016; Ocio et al., 2017; Chen et al., 2019), various uncertainties have been discussed in the estimations of floodwater utilization in past years, including meteorological and hydrological forecast uncertainties, hydraulic uncertainties and human operation uncertainty (Melching, 1992; Cloke and Pappenberger, 2009; Dong, 2009; Diao and Wang, 2010; Wu et al., 2011; Kriauciuniene et al., 2013; Tung and Wong, 2014; Yan et al., 2014; Ocio et al., 2017). Due to significant concerns regarding design flood estimation under a specific return period for reservoir flood management, the study of its uncertainty has received much research attention from hydrologists (Parkes and Demeritt, 2016; Nakamura and Oki, 2018; Brunner and Sikorska-Senoner, 2019; Guo et al., 2020). Notably, design floods are generally defined by several features that are correlated with uncertainty (Dung et al., 2015; Daneshkhah et al., 2016; Guo et al., 2020), such as flood peak, flood volume, and regional flood composition. Hence, analysis of bivariate design floods characterized by correlated flood volumes and peaks reveals its advantage over traditional analysis of univariate design floods. In recent years, numerous frameworks have been developed to estimate uncertainties in bivariate design floods in various flood control systems (Zhang and Singh, 2007c; Yan et al., 2014; Fan et al., 2016; Ozga-Zielinski et al., 2016; Yin et al., 2018b; Xiong et al., 2019; Guo et al., 2020; Huang et al., 2020). The application of the copula-based methodology has been of growing interest in bivariate design floods. Various uncertainties in copula-based design flood estimation are discussed (Malekmohammadi et al., 2009; Serinaldi, 2013; Michailidi and Bacchi, 2017; Liu et al., 2018; Guan et al., 2022), including model uncertainty, parameter uncertainty, and sampling uncertainty. In particular, the sampling uncertainty of flood volume and peak is high in bivariate design floods, influencing the selection of model structure and parameters. The floodwater utilization approach is devised based on the analysis of flood control risk caused by various uncertainties. Analyzing the frequency curve of flood control reservoir capacity is necessary to balance risks and benefits considering the uncertainty of flood volume and peaks in the selection of floodwater utilization schemes.

However, to the best of our knowledge, there are few studies on the flood control risk of floodwater utilization from a sampling uncertainty perspective. More importantly, apart from a few papers, flood volume and peak and their impacts on flood control risk have not been systematically estimated in the literature. Towards this goal, here we propose an integrated model that employs the Monte Carlo sampling method and the most likely event selection method to estimate the probability of the maximum water level exceeding the current design flood level.

The remainder of this paper is structured as follows. Section 2 describes the Shagou reservoir of the Shuhe River in the Huaihe River Basin in China, which is chosen as the study domain. Section 3 introduces the research framework. Section 4 presents the computational process and the results. Section 5 discusses the impacts of flood control operations on flood control risk. Section 6 provides the conclusions of this study.

2 Case study

2.1 Study area

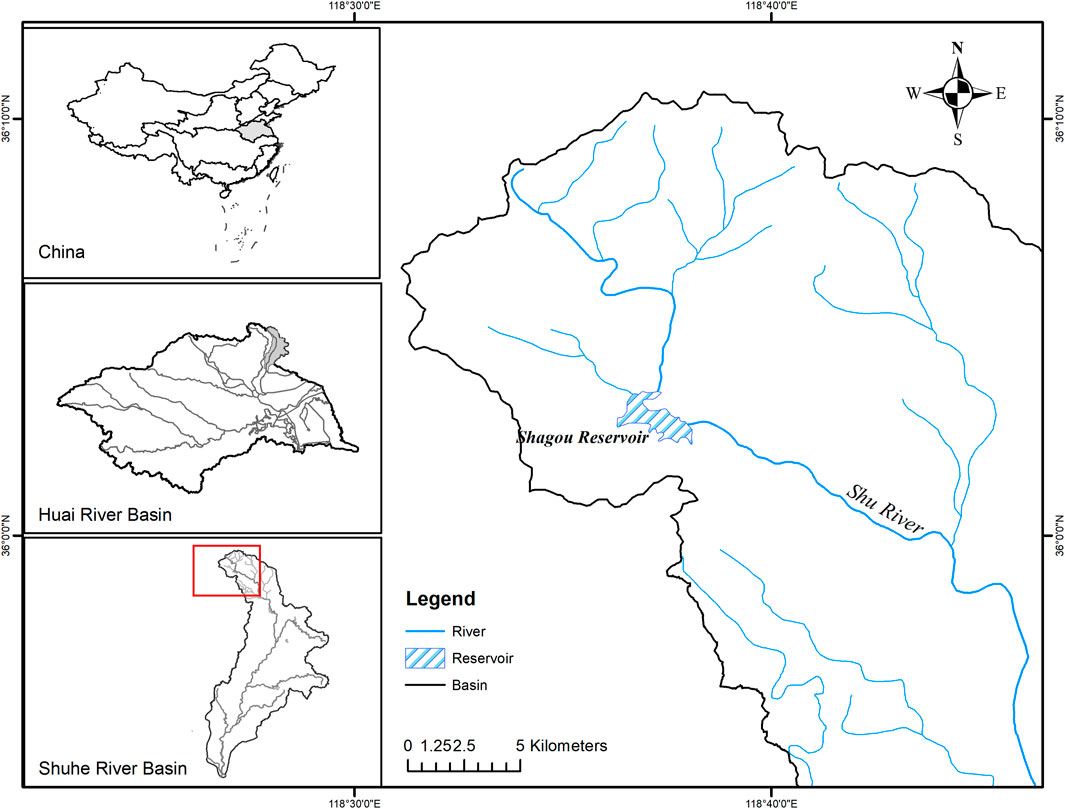
The Shagou reservoir is located upstream of the Shuhe River in the Huaihe River Basin in China, with a control basin area of 164 km², as shown in Figure 1. The average annual precipitation is 745 mm, and flood season (from June to September) accounts for approximately 74% of the annual precipitation. In the current flood control operation, the flood-limited water level of the Shagou reservoir is 231.5 m, and the maximum control outflow is 500 m³/s under the given return period $T$ =20a. In this paper, the Shagou reservoir is taken as the research object to discuss the flood control risk in floodwater utilization considering the uncertainty of flood volume and peak.

FIGURE 1

FIGURE 1. Sketch map of the Shagou reservoir in the Shu River basin, China.

2.2 Data

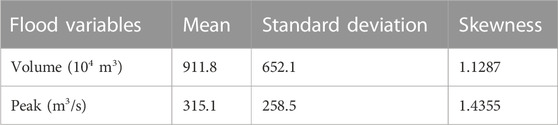
The annual maximum 72 h flood volume and corresponding flood peak observed in 1964–2013 are utilized to represent the flood characterization in the Shagou reservoir. The data are provided by the Yi-Shu-Si River Basin Administration, which is responsible for the unified management of major rivers (including the Shuhe River), lakes, hubs and other projects in the Yishusi Basin. The statistical results of flood volume and flood peak are shown in Table 1.

TABLE 1

TABLE 1. Statistical features of flood variables from 1964 to 2013.

According to the statistics of historical flood data, the highest annual maximum flood volume is 3.115 m³⨯10⁷ m³, which is approximately 3.5 times the multiyear average, and the lowest annual maximum is 70.4 m³⨯10⁴ m³. Similarly, the highest annual maximum flood peak is 1,190 m³/s, which is approximately 3.7 times the multiyear average, and the lowest annual maximum is 3.92 m³/s. The annual flood change is dramatic, and floodwater utilization is necessary for local regional water management. When the range of flood volume is [2,070, 2,204] ⨯10⁴ m³, the flood peak range is [315, 994] m³/s. Obvious uncertainty exists between flood volume and peak, which may have an adverse effect on flood control operation. Estimating the flood control risk caused by the flood volume and peak uncertainty in the Shagou reservoir is important for flood control operation decision making in floodwater utilization management.

3 Materials and methods

3.1 Joint distribution of flood variables based on copulas

Multivariate distribution construction using copulas has been well developed in the past years (Sklar, 1959; Shaked and Joe, 1998; Sancetta and Satchell, 2004). A bivariate joint distribution can be expressed by a copula function and its corresponding marginal distributions. A copula is a function that links two marginal distribution functions to construct a multivariate distribution function. Sklar’s theorem states that if $F_{XY}\left(x,y\right)$ is a bivariate distribution function of 2 correlated random variables $X$ and $Y$ the respective marginal distributions $F_X\left(x\right)$ and $F_Y\left(y\right)$, it is possible to write a cumulative distribution function (CDF) with two single marginal distributions as follows:

$F_{XY}\left(x,y\right)=C_{\theta }\left[F_X\left(x\right),F_Y\left(y\right)\right](1)$

where $\theta$ is the copula parameter. If these marginal distributions are continuous, a unique copula function $C\left(\bullet \right)$ exists (Sraj et al., 2015).

There are many classes of copula functions, such as Archimedean copulas, elliptical copulas and Plackett copulas (Plackett, 1965; Fang et al., 2002). Archimedean copulas are popular because they can be easily constructed and are capable of capturing a wide range of dependence structures with several desirable properties, such as symmetry and associativity (Nelson, 2006; Hofert, 2008). The widely used bivariate Archimedean family copulas include the Clayton Copula, Frank Copula, and Gumbel-Hougaard (GH) Copula, with a parameter $\theta$, as shown in Table 2. The copula parameter $\theta$ is usually estimated by the maximum likelihood method (Strupczewski et al., 2001). Therefore, the joint distribution function based on the copula method can be derived when the marginal distribution functions of variables are determined (Zhang and Singh, 2007a).

TABLE 2

TABLE 2. Types of Clayton, Frank and GH copulas.

In current studies, root mean square error (RMSE) (Zhang and Singh, 2006), Akaike’s information criterion (AIC) (Zhang and Singh, 2007b) and Nash-Sutcliffe efficiency ($E_{ns}$) (Xu et al., 2017) are usually employed to measure the goodness of fit of the joint distribution.

3.2 Joint return period

In conventional univariate analysis, the return period is usually used to represent the average time interval of a specific design flood, which is also a method used to measure the magnitude of floods. Within the copula-based framework, various definitions of the joint return period have been proposed, such as OR, AND, Kendall, dynamic, and structure-based return periods (Shiau, 2003; De Michele et al., 2005; Salvadori et al., 2011; Yin et al., 2018a). In this paper, the OR case ($T_{or}$) is adopted to describe the flood occurrence and can be expressed as follows:

$T_{or}=\frac{\mu }{1-F\left(q,w\right)}=\frac{\mu }{1-C_{\theta }\left[F_Q\left(q\right),F_W\left(w\right)\right]}(2)$

where $\mu$ is the mean interarrival time between two consecutive events (in the case of annual maxima $\mu$ =1 year), and $F\left(q,w\right)=P\left(q\ge Q,w\ge W\right)$ is depicted by a copula function $C_{\theta }\left[F_Q\left(q\right),F_W\left(w\right)\right]$; $F_Q\left(q\right)$ and $F_W\left(w\right)$ denote the marginal distribution functions Q and W, respectively.

3.3 Most-likely event selection

According to Eq. 2, in the bivariate case, infinite possible combinations of Q and W can be selected for a given joint return period $T_{or}$, which have the same joint probability. The different likelihood of each combination must be considered to select appropriate design scenarios (Salvadori et al., 2011; Xiong et al., 2020). Based on Sklar’s theorem, all the possible compositions of flood volume and peak differ in terms of their probability of occurrence, which can be measured by the value of the joint PDF (Salvadori et al., 2011; Gräler et al., 2013; Guo et al., 2018). The most likely flood event $\left[q^{*}\left(t\right),w^{*}\left(t\right)\right]$ of all possible events at a given joint return period $T_{or}$ can be obtained by the following formula:

$\left\{\begin{array}{l}\left[q^{*}\left(t\right),w^{*}\left(t\right)\right]=\arg \max f\left(q,w\right)=c_{\theta }\left[F_Q\left(q\right),F_W\left(w\right)\right]\bullet f_Q\left(q\right)\bullet f_W\left(w\right)\\ C_{\theta }\left[F_Q\left(q\right),F_W\left(w\right)\right]=1-\frac{1}{T_{or}}\end{array}\right.(3)$

where $f\left(q,w\right)$ is a nonstationary joint PDF of q and w; $C\left(\bullet \right)$ is the density function of the copula for nonstationary data series; and $f_Q\left(q\right)$ and $f_W\left(w\right)$ are the marginal PDFs.

3.4 Flood control risk

Generally, the risk is simplified and defined as the probability of occurrence of a risk event (Sun et al., 2018; Li et al., 2022). In this paper, the flood control risk for the reservoir is defined as the probability of the highest level over the design flood level and can be expressed as follows:

$R=P\left({\mathrm{H}}_m>{\mathrm{H}}_d\right)=\frac{m}{n}(4)$

where ${\mathrm{H}}_m$ is the highest reservoir level in the flood control operation, ${\mathrm{H}}_d$ is the design flood level of the reservoir, $m$ is the number of times that the highest water level exceeds the design water level in stochastic simulations, and $n$ is the total number of stochastic simulations.

3.5 General framework of risk estimation

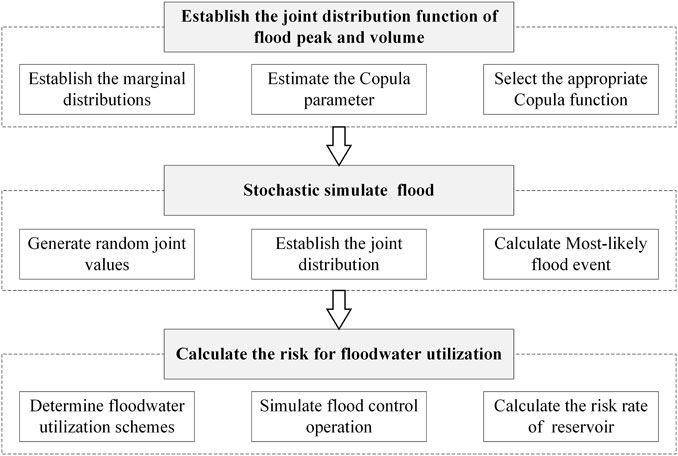
In this research, the framework of estimating flood control risk with the flood uncertainty of flood volume and peak is proposed based on the Monte Carlo sampling method and the most likely event selection method. It can be divided into three steps, which are shown in Figure 2.

FIGURE 2

FIGURE 2. Flowchart of the proposed framework.

Step 1: Establish the joint distribution function. Based on the observed flood volume and peak data with k-samples, the marginal distributions $F_X\left(x\right)$ and $F_Y\left(y\right)$ and the probability density functions $f_X\left(x\right)$ and $f_Y\left(y\right)$ are established, respectively. The copula functions can be estimated by using the historical flood series. According to the goodness of fit of the joint distribution, the optimal copula function is selected to construct the joint distribution function of flood volume and peak.

Step 2: Stochastic simulation of the flood. Based on the multilevel Monte Carlo method (Giles, 2008; Brodie, 2013; Clare et al., 2022), $n$ sets of bivariate data with k-samples are randomly generated. Based on the generated flood series, the joint distribution function is constructed for each set. The most likely method is employed to select the appropriate $\left(q,w\right)$ under the given $T_{or}$.

Step 3: Calculate the risk. According to the engineering and hydrological characteristics, various design floodwater utilization schemes have been developed. The design flood hydrograph can be obtained by $n$ sets of $\left(q,w\right)$ and typical floods. Taking $n$ sets of flood hydrographs as input data, the simulation of flood control operation is carried out, and the flood control risk can be calculated by Eq. 4.

4 Results

4.1 Parameter estimation for the marginal distributions

In this paper, the Pearson type III (P-III) distribution, which is recommended by the Chinese Ministry of Water Resources (Wang et al., 2015; Peng et al., 2017; Gao et al., 2018), was employed to obtain the single marginal distribution of flood volume and flood peak. The parameters of the P-III distribution were estimated by the moment method (Hosking, 1990) and are shown in Table 3. The K-S test ($D_n$) is employed to describe how well the distributions fit the flood data. With K-S’s critical value $D_{0.05}=\frac{1.36}{\sqrt{50}}=0.1923$, the $D_n$ of flood volume and peak are both 0.0980. Therefore, flood volume data and flood peak data both failed to reject the P-III distribution.

TABLE 3

TABLE 3. Parameters of P-III in flood volume and peak.

4.2 Joint distribution function based on the copula function

For the flood data, Clayton, Frank and G-H Copula were used to establish the joint distribution. RMSE, AIC and $E_{ns}$ were obtained to measure the goodness of joint distribution as shown in Table 4. The empirical joint probabilities were estimated for the flood data by using the Gringorten formula (Gringorten, 1963; Du et al., 2019). The smaller the RMSE and AIC are, the better the joint distribution is. The larger $E_{ns}$ is, the better the joint distribution is. Based on the above measurement principles, the results indicated that the best-fitted joint distribution is the G-H copula function with the parameter 1.8890 in the Shagou reservoir flood volume and peak. Then, the structure of the joint distribution function of the historical flood volume and peak was determined.

TABLE 4

TABLE 4. Results of copula parameter and goodness of fit.

4.3 Most-likely design values

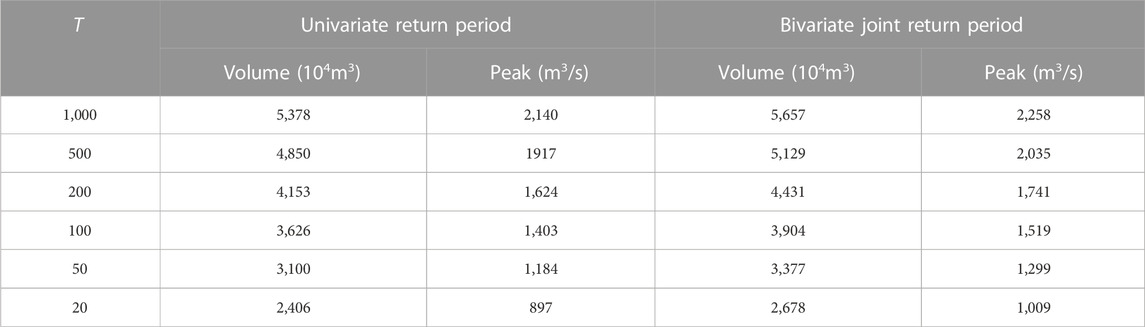
According to the bivariate joint distribution of historical flood data, the most likely method was employed to obtain the bivariate flood volume and peak for a given joint return period $T_{or}$. The comparison of design flood values under the bivariate joint return period and univariate return period is shown in Table 5.

TABLE 5

TABLE 5. Design flood values under different return periods.

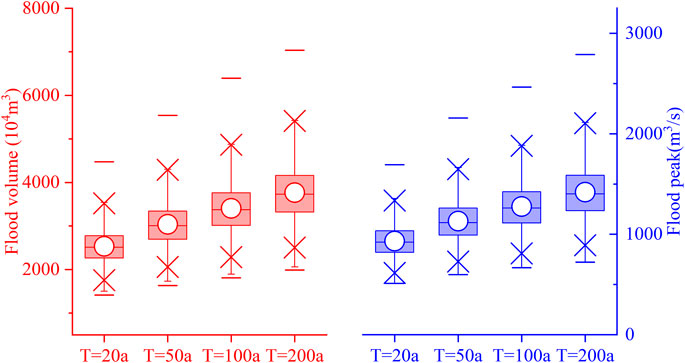
The results show that the flood volume and peak obtained by the bivariate joint return for a given joint return period $T_{or}$ are larger than the values obtained by the univariate return period. As shown in Table 5, the design flood volume for the univariate return period is 7.59% more than that for the bivariate joint return period, and the design flood peak for the univariate return period is 8.22% more than that for the bivariate joint return period. The value of flood volume and peak for joint return period $T_{or}=100\mathrm{a}$ will make a larger return period in the respective univariate frequency analysis, which is nearly 144 a. Considering the correlation between flood volume and peak, multivariable flood events can be described more reasonably and may demonstrate a new theoretical basis for flood control operations.

4.4 Stochastic flood simulation

Based on the joint distribution function of flood volume and peak, the multilevel Monte Carlo method was employed to generate bivariate design data. Considering the number of historical flood data, 50 samples are randomly generated in each set. In the same way, the joint distribution was constructed, and the most likely design values were obtained. The number of stochastic simulation sets is 10,000 in this paper and the design flood values based on the stochastically simulated flood for given $T_{or}$ are shown in Figure 3. The statistics of bivariate design data under different bivariate joint return periods are shown in Figure 4.

FIGURE 3

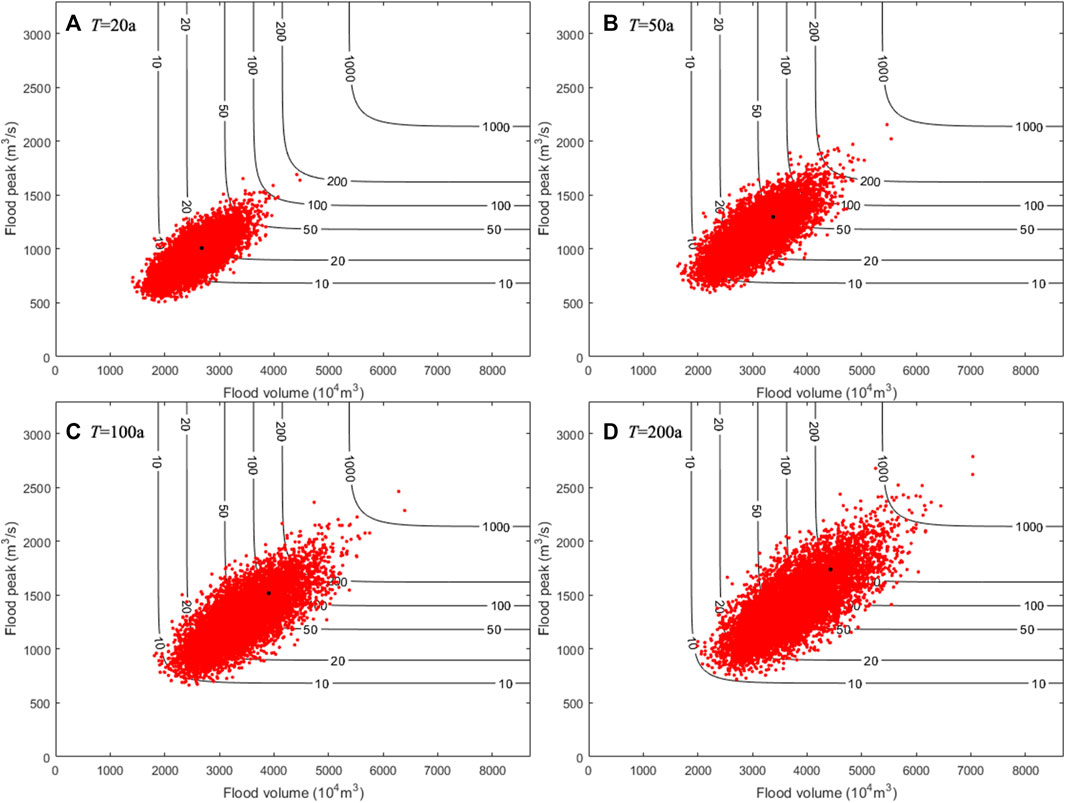
FIGURE 3. Design flood values under different stochastic simulations (the black point indicates that the value was obtained by historical data): (A) T = 20a; (B) T =50a; (C) T =100a; (D) T=200a.

FIGURE 4

FIGURE 4. Box-plots of bivariate design data under different bivariate joint return periods.

The results reveal that the generated design flood values are scattered around the most likely design value calculated based on historical flood data. As the bivariate joint return period increases, the generated design values also increase. For the $T_{or}=20\mathrm{a}$, the range of flood volume and flood peak is [1,412, 4,476] ⨯10⁴ m³ and [509, 1,692] m³/s, respectively. And for the $T_{or}=200\mathrm{a}$ the range of flood volume and flood peak is [1990, 7,036] ⨯10⁴ m³ and [721, 2,788] m³/s, respectively. The Shagou reservoir is designed with the univariate return period T=100a, and the joint return period of the simulated joint design value spans from 10a to 1000a compared to the historical data under the same bivariate joint return period $T_{or}=100\mathrm{a}$. The joint design value is related to the economy of engineering construction and the reliability of flood control operation for reservoirs. If a small joint design value is adopted, the scale of the reservoir will be small, which is not conducive to providing its own benefits and may lead to a huge loss of life and property in flood control. The uncertainty of flood volume and peak should be given more attention in the field of floodwater utilization.

4.5 Flood control risk of reservoir

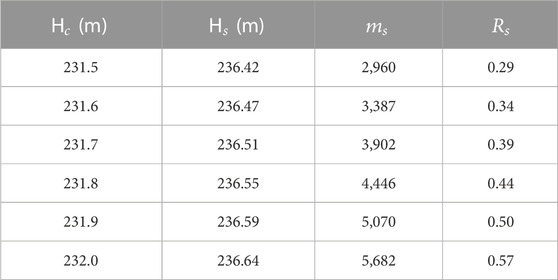
As mentioned in Section 2.1, the Shagou reservoir was designed with the standard T=100a, and the corresponding design flood water level is 233.13 m, which was obtained by univariate flood volume frequency analysis. In the current scheduling rules, the water level is limited to 231.5 m in the flood season. The essence of floodwater utilization is transferring more floodwater into ordinary water resources in the flood season for use in the non-flood season, where the flood-limited water level plays an important role. In recent years, numerous studies have been carried out to scientifically raise the flood-limited water level in the flood season without decreasing flood control standards or damaging the ecological environment of rivers (Li et al., 2010; Liu et al., 2015; Chang et al., 2017; Xie et al., 2018; Ye et al., 2019; Wang et al., 2020). In this paper, according to the current operation, the flood-limited water level is designed to be from 231.5 m to 232.0 m with an interval of 0.1 m to indicate various floodwater utilization schemes.

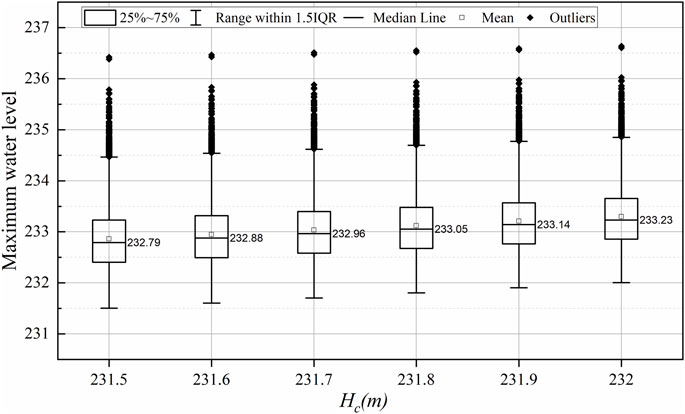
The flood in August 1974 was selected as a typical flood, and various flood hydrographs were obtained by using the design bivariate design value in Section 4.4. By simulating the current flood control operation, the maximum water level (${\mathrm{H}}_s$), the count of the maximum water level exceeding the current design water level ($m_s$), and the flood control risk ($R_s$) were calculated under different flood-limited water levels (${\mathrm{H}}_c$), which are shown in Table 6. The statistical results of the maximum water level are shown in Figure 5 under different flood-limited water levels.

TABLE 6

TABLE 6. Flood control risk statistics under different flood-limited water levels.

FIGURE 5

FIGURE 5. Statistical results of the maximum water level under various flood-limited water levels.

In the flood control operation of a reservoir, the flood-limited water level is considered to be the initial water level in a flooding process. With the initial water level rise, the maximum water level in the flood control operation process will also increase accordingly. According to the statistical results, the averages of the maximum water levels are all less than the design water level of 233.13 m under flood utilization with flood-limited water levels of 231.5, 231.6, 231.7 and 231.8 m. With the increase in flood-limited water level, the counts of the maximum water level exceeding the current design water level similarly increased. When the flood-limited water level increased from 231.5 m to 232, ${\mathrm{H}}_c$ and $R_s$ nearly doubled. The flood control risk increased with the rising flood-limited water level, and the benefit of floodwater utilization grew correspondingly. Assuming that the water level of the reservoir can be kept at the flood-limited water level when the flood season ends, the benefit growth rate and risk growth rate can be calculated quantitatively compared to the current operation and are shown in Figure 6.

FIGURE 6

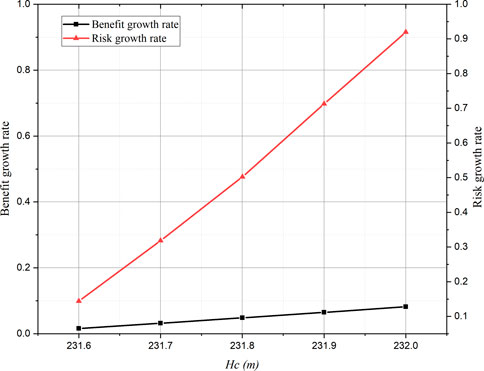
FIGURE 6. Increased water resources and flood control risk under various floodwater utilization schemes.

The results reveal that different increased rates occurred between benefit and risk with the same increased flood-limited water level. In particular, the growth rates of benefit and risk are 0.08% and 91% with ${\mathrm{H}}_c$ =232.0 compared to the current operation, respectively. Achieving a lower benefit increment brings a greater risk increment to water management, which shows that the marginal benefit may be contained in floodwater utilization.

5 Discussion

Flood control operations have a certain impact on reservoir flood control risk. As an important indicator of flood control operation, the maximum control outflow ($Q_c$) and the maximum water level in the flooding process are directly related (Ding et al., 2015; Moridi and Yazdi, 2017; Zhao et al., 2017). In this section, different maximum control outflows of the reservoir were set, representing the corresponding flood control operation, and the corresponding flood control risk was calculated based on the steps in Section 3. According to the current maximum control outflow of 500 m³/s, flood control operations with maximum control outflows of 450 and 500 m³/s were set, and the simulation of reservoir flood control was carried out with the design bivariate value in Section 4.4. Based on various flood control operations, the maximum water level of the reservoir was calculated, and the flood control risk was obtained, as shown in Table 7.

TABLE 7

TABLE 7. Flood control risk under different maximum control outflows.

In flood operations, with the increase in the maximum control outflow of the reservoir, more floods are released downstream. For the upstream reservoir, the less flood control storage is needed, the lower the flood control risk is in flood control operation. In this paper, the maximum control outflow has a strong impact on flood control risk. In particular, with the maximum control outflow increasing to 550 from 500 m³/s, the reduction in flood control risk will be 48%. In the field of floodwater utilization, many studies aim at risk decision-making for transforming some amount of floodwater into ordinary water resources without decreasing flood control standards (Li et al., 2010; Ye et al., 2019; Wang et al., 2022). The reduction of flood control risk is favorable for floodwater utilization, however, the flood control risk of the upstream reservoir affects the flood control risk of the downstream reservoir through changes in discharge control. In the flood control system, there is a risk transmission effect in different flood control projects.

6 Conclusion

Considering the influence of the uncertainty of flood volume and peak, the estimation of flood control risk is discussed in this paper. Taking the reservoir as the study object, the Monte Carlo sampling method and the most likely event selection method were employed to develop a general framework and then applied to the Shagou reservoir in the Shuhe River basin, China. The main conclusions can be summarized as follows:

(1) The proposed framework can estimate the flood control risk considering the uncertainty of flood volume and peak. For flood control risk with an uncertain distribution of random variables, the stochastic simulation has certain advantages. At present, the framework can be used with a single reservoir in the flood control risk of flood control systems. The calculation of flood control risk under cascade reservoirs and parallel reservoirs will continue to be studied in future work.

(2) The application of the framework to the Shagou reservoir in the Shuhe River basin showed that the flood control risk caused by the uncertainty of flood volume and peak is 0.29, which indicates that the design value obtained by the bivariate joint return is much greater than the value from univariate frequency analysis. Multivariable flood events can be described more reasonably and may provide a new theoretical basis for flood control operations.

(3) The flood control risk and the benefit of floodwater utilization increased with the rising flood-limited water level, and different rate increases occurred between the benefit and risk. The marginal benefit may be in floodwater utilization. The flood operation function, such as different maximum control outflows, also has a considerable impact on the flood control risk and may play an important role in floodwater utilization. The transmission effect of flood control risk is not quantitatively evaluated, which will be improved in future research.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

HD: conceptualization, methodology, writing original, and resources. ZW: review and editing, investigation, and resources. JY: review and provided advice for analyzing the data and figures. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the Natural Science Foundation of Jiangsu Province of China (No. BK20211023).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Brodie, I. M. (2013). Rational Monte Carlo method for flood frequency analysis in urban catchments. J. Hydrol. 486, 306–314. doi:10.1016/j.jhydrol.2013.01.039

CrossRef Full Text | Google Scholar

Brunner, M. I., and Sikorska-Senoner, A. E. (2019). Dependence of flood peaks and volumes in modeled discharge time series: Effect of different uncertainty sources. J. Hydrol. 572, 620–629. doi:10.1016/j.jhydrol.2019.03.024

CrossRef Full Text | Google Scholar

Chang, J., Guo, A., Du, H., and Wang, Y. (2017). Floodwater utilization for cascade reservoirs based on dynamic control of seasonal flood control limit levels. Environ. Earth Sci. 76, 260. doi:10.1007/s12665-017-6522-z

CrossRef Full Text | Google Scholar

Chen, J., Shi, H., Sivakumar, B., and Peart, M. R. (2016). Population, water, food, energy and dams. Renew. Sustain. Energy Rev. 56, 18–28. doi:10.1016/j.rser.2015.11.043

CrossRef Full Text | Google Scholar

Chen, J., Zhong, P.-A., An, R., Zhu, F., and Xu, B. (2019). Risk analysis for real-time flood control operation of a multi-reservoir system using a dynamic Bayesian network. Environ. Model. Softw. 111, 409–420. doi:10.1016/j.envsoft.2018.10.007

CrossRef Full Text | Google Scholar

Clare, M. C. A., Piggott, M. D., and Cotter, C. J. (2022). Assessing erosion and flood risk in the coastal zone through the application of multilevel Monte Carlo methods. Coast. Eng. 174, 104118. doi:10.1016/j.coastaleng.2022.104118

CrossRef Full Text | Google Scholar

Cloke, H. L., and Pappenberger, F. (2009). Ensemble flood forecasting: A review. J. Hydrol. 375, 613–626. doi:10.1016/j.jhydrol.2009.06.005

CrossRef Full Text | Google Scholar

Daneshkhah, A., Remesan, R., Chatrabgoun, O., and Holman, I. P. (2016). Probabilistic modeling of flood characterizations with parametric and minimum information pair-copula model. J. Hydrol. 540, 469–487. doi:10.1016/j.jhydrol.2016.06.044

CrossRef Full Text | Google Scholar

De Michele, C., Salvadori, G., Canossi, M., Petaccia, A., and Rosso, R. (2005). Bivariate statistical approach to check adequacy of dam spillway. J. Hydrol. Eng. 10, 50–57. doi:10.1061/(asce)1084-0699(2005)10:1(50)

CrossRef Full Text | Google Scholar

Delenne, C., Cappelaere, B., and Guinot, V. (2012). Uncertainty analysis of river flooding and dam failure risks using local sensitivity computations. Reliab. Eng. Syst. Saf. 107, 171–183. doi:10.1016/j.ress.2012.04.007

CrossRef Full Text | Google Scholar

Diao, Y., and Wang, B. (2010). Risk analysis of flood control operation mode with forecast information based on a combination of risk sources. Sci. China-technological Sci. 53, 1949–1956. doi:10.1007/s11431-010-3124-3

CrossRef Full Text | Google Scholar

Ding, W., Zhang, C., Cai, X., Li, Y., and Zhou, H. (2017). Multiobjective hedging rules for flood water conservation. Water Resour. Res. 53, 1963–1981. doi:10.1002/2016WR019452

CrossRef Full Text | Google Scholar

Ding, W., Zhang, C., Peng, Y., Zeng, R., Zhou, H., and Cai, X. (2015). An analytical framework for flood water conservation considering forecast uncertainty and acceptable risk. Water Resour. Res. 51, 4702–4726. doi:10.1002/2015WR017127

CrossRef Full Text | Google Scholar

Dong, W. (2009). Rethinking risk analysis: The risks of risk analysis in water issues as the case. Hum. Ecol. Risk Assess. Int. J. 15, 1079–1083. doi:10.1080/10807030903304690

CrossRef Full Text | Google Scholar

Du, H., Wang, Y., Liu, K., and Cheng, L. (2019). Exceedance probability of precipitation for the Shuhe to futuan water transfer project in China. Environ. Earth Sci. 78, 240. doi:10.1007/s12665-019-8207-2

CrossRef Full Text | Google Scholar

Dung, N. V., Merz, B., Bárdossy, A., and Apel, H. (2015). Handling uncertainty in bivariate quantile estimation – an application to flood hazard analysis in the Mekong Delta. J. Hydrol. 527, 704–717. doi:10.1016/j.jhydrol.2015.05.033

CrossRef Full Text | Google Scholar

Fan, Y. R., Huang, W. W., Huang, G. H., Li, Y. P., Huang, K., and Li, Z. (2016). Hydrologic risk analysis in the Yangtze River basin through coupling Gaussian mixtures into copulas. Adv. Water Resour. 88, 170–185. doi:10.1016/j.advwatres.2015.12.017

CrossRef Full Text | Google Scholar

Fang, H.-B., Fang, K.-T., and Kotz, S. (2002). The meta-elliptical distributions with given marginals. J. Multivar. Anal. 82, 1–16. doi:10.1006/jmva.2001.2017

CrossRef Full Text | Google Scholar

Gao, S., Liu, P., Pan, Z., Ming, B., Guo, S., Cheng, L., et al. (2018). Incorporating reservoir impacts into flood frequency distribution functions. J. Hydrol. 568, 234–246. doi:10.1016/j.jhydrol.2018.10.061

CrossRef Full Text | Google Scholar

Giles, M. B. (2008). Multilevel Monte Carlo path simulation. Oper. Res. 56, 607–617. doi:10.1287/opre.1070.0496

CrossRef Full Text | Google Scholar

Gräler, B., van den Berg, M. J., Vandenberghe, S., Petroselli, A., Grimaldi, S., De Baets, B., et al. (2013). Multivariate return periods in hydrology: A critical and practical review focusing on synthetic design hydrograph estimation. Hydrol. Earth Syst. Sci. 17, 1281–1296. doi:10.5194/hess-17-1281-2013

CrossRef Full Text | Google Scholar

Gringorten, I. I. (1963). A plotting rule for extreme probability paper. J. Geophys. Res. 68, 813–814. doi:10.1029/jz068i003p00813

CrossRef Full Text | Google Scholar

Guan, X., Xia, C., Xu, H., Liang, Q., Ma, C., and Xu, S. (2022). Flood risk analysis integrating of Bayesian-based time-varying model and expected annual damage considering non-stationarity and uncertainty in the coastal city. J. Hydrol. 617, 129038. doi:10.1016/j.jhydrol.2022.129038

CrossRef Full Text | Google Scholar

Guo, A., Chang, J., Wang, Y., Huang, Q., and Li, Y. (2020). Uncertainty quantification and propagation in bivariate design flood estimation using a Bayesian information-theoretic approach. J. Hydrol. 584, 124677. doi:10.1016/j.jhydrol.2020.124677

CrossRef Full Text | Google Scholar

Guo, S., Muhammad, R., Liu, Z., Xiong, F., and Yin, J. (2018). Design flood estimation methods for cascade reservoirs based on copulas. Water 10, 560. doi:10.3390/w10050560

CrossRef Full Text | Google Scholar

Hofert, M. (2008). Sampling archimedean copulas. Comput. Stat. Data Anal. 52, 5163–5174. doi:10.1016/j.csda.2008.05.019

CrossRef Full Text | Google Scholar

Hosking, J. (1990). L-Moments: Analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. Ser. B 52, 105–124. doi:10.1111/j.2517-6161.1990.tb01775.x

CrossRef Full Text | Google Scholar

Huang, Y., Liang, Z., Hu, Y., Li, B., and Wang, J. (2020). Theoretical derivation for the exceedance probability of corresponding flood volume of the equivalent frequency regional composition method in hydrology. Hydrol. Res. 51, 1274–1292. doi:10.2166/nh.2020.027

CrossRef Full Text | Google Scholar

Kriauciuniene, J., Jakimavicius, D., Sarauskiene, D., and Kaliatka, T. (2013). Estimation of uncertainty sources in the projections of Lithuanian river runoff. Stoch. Environ. Res. Risk Assess. 27, 769–784. doi:10.1007/s00477-012-0608-7

CrossRef Full Text | Google Scholar

Li, J., Zhong, P., Wang, Y., Yang, M., Fu, J., Liu, W., et al. (2022). Risk analysis for the multi-reservoir flood control operation considering model structure and hydrological uncertainties. J. Hydrol. 612, 128263. doi:10.1016/j.jhydrol.2022.128263

CrossRef Full Text | Google Scholar

Li, X., Guo, S., Liu, P., and Chen, G. (2010). Dynamic control of flood limited water level for reservoir operation by considering inflow uncertainty. J. Hydrol. 391, 124–132. doi:10.1016/j.jhydrol.2010.07.011

CrossRef Full Text | Google Scholar

Liu, K., Wang, Z., Cheng, L., Zhang, L., Du, H., and Tan, L. (2019). Optimal operation of interbasin water transfer multireservoir systems: An empirical analysis from China. Environ. Earth Sci. 78, 238. doi:10.1007/s12665-019-8242-z

CrossRef Full Text | Google Scholar

Liu, P., Li, L., Guo, S., Xiong, L., Zhang, W., Zhang, J., et al. (2015). Optimal design of seasonal flood limited water levels and its application for the Three Gorges Reservoir. J. Hydrol. 527, 1045–1053. doi:10.1016/j.jhydrol.2015.05.055

CrossRef Full Text | Google Scholar

Liu, Z., Xu, X., Cheng, J., Wen, T., and Niu, J. (2018). Hydrological risk analysis of dam overtopping using bivariate statistical approach: A case study from geheyan reservoir, China. Stoch. Environ. Res. Risk Assess. 32, 2515–2525. doi:10.1007/s00477-018-1550-0

CrossRef Full Text | Google Scholar

Malekmohammadi, B., Kerachian, R., and Zahraie, B. (2009). Developing monthly operating rules for a cascade system of reservoirs: Application of Bayesian Networks. Environ. Model. Softw. 24, 1420–1432. doi:10.1016/j.envsoft.2009.06.008

CrossRef Full Text | Google Scholar

Melching, C. S. (1992). An improved first-order reliability approach for assessing uncertainties in hydrologic modeling. J. Hydrol. 132, 157–177. doi:10.1016/0022-1694(92)90177-W

CrossRef Full Text | Google Scholar

Meng, X., Chang, J., Wang, X., and Wang, Y. (2018). Multi-objective hydropower station operation using an improved cuckoo search algorithm. Energy 168, 425–439. doi:10.1016/j.energy.2018.11.096

CrossRef Full Text | Google Scholar

Michailidi, E. M., and Bacchi, B. (2017). Dealing with uncertainty in the probability of overtopping of a flood mitigation dam. Hydrol. Earth Syst. Sci. 21, 2497–2507. doi:10.5194/hess-21-2497-2017

CrossRef Full Text | Google Scholar

Moridi, A., and Yazdi, J. (2017). Optimal allocation of flood control capacity for multi-reservoir systems using multi-objective optimization approach. Water Resour. Manag. 31, 4521–4538. doi:10.1007/s11269-017-1763-x

CrossRef Full Text | Google Scholar

Nakamura, S., and Oki, T. (2018). Paradigm shifts on flood risk management in Japan: Detecting triggers of design flood revisions in the modern era. Water Resour. Res. 54, 5504–5515. doi:10.1029/2017WR022509

CrossRef Full Text | Google Scholar

Nelson, R. B. (2006). An introduction to copulas. New York, NY: Springer.

Google Scholar

Ocio, D., Le Vine, N., Westerberg, I., Pappenberger, F., and Buytaert, W. (2017). The role of rating curve uncertainty in real-time flood forecasting. Water Resour. Res. 53, 4197–4213. doi:10.1002/2016WR020225

CrossRef Full Text | Google Scholar

Ozga-Zielinski, B., Ciupak, M., Adamowski, J., Khalil, B., and Malard, J. (2016). Snow-melt flood frequency analysis by means of copula based 2D probability distributions for the Narew River in Poland. J. Hydrol. Reg. Stud. 6, 26–51. doi:10.1016/j.ejrh.2016.02.001

CrossRef Full Text | Google Scholar

Parkes, B., and Demeritt, D. (2016). Defining the hundred year flood: A bayesian approach for using historic data to reduce uncertainty in flood frequency estimates. J. Hydrol. 540, 1189–1208. doi:10.1016/j.jhydrol.2016.07.025

CrossRef Full Text | Google Scholar

Peng, Y., Chen, K., Yan, H., and Yu, X. (2017). Improving flood-risk analysis for confluence flooding control downstream using copula Monte Carlo method. J. Hydrol. Eng. 22, 04017018. doi:10.1061/(ASCE)HE.1943-5584.0001526

CrossRef Full Text | Google Scholar

Plackett, R. L. (1965). A class of bivariate distributions. J. Am. Stat. Assoc. 60, 516–522. doi:10.1080/01621459.1965.10480807

CrossRef Full Text | Google Scholar

Salvadori, G., De Michele, C., and Durante, F. (2011). On the return period and design in a multivariate framework. Hydrol. Earth Syst. Sci. 15, 3293–3305. doi:10.5194/hess-15-3293-2011

CrossRef Full Text | Google Scholar

Sancetta, A., and Satchell, S. (2004). The bernstein copula and its applications to modeling and approximations of multivariate distributions. Econom. Theory 20, 535–562. doi:10.1017/s026646660420305x

CrossRef Full Text | Google Scholar

Serinaldi, F. (2013). An uncertain journey around the tails of multivariate hydrological distributions. Water Resour. Res. 49, 6527–6547. doi:10.1002/wrcr.20531

CrossRef Full Text | Google Scholar

Shaked, M., and Joe, H. (1998). Multivariate models and dependence concepts. J. Am. Stat. Assoc. 93, 1237. doi:10.2307/2669872

CrossRef Full Text | Google Scholar

Shiau, J. T. (2003). Return period of bivariate distributed extreme hydrological events. Stoch. Environ. Res. Risk Assess. 17, 42–57. doi:10.1007/s00477-003-0125-9

CrossRef Full Text | Google Scholar

Simonovic, S. P., and Arunkumar, R. (2016). Comparison of static and dynamic resilience for a multipurpose reservoir operation. Water Resour. Res. 52, 8630–8649. doi:10.1002/2016WR019551

CrossRef Full Text | Google Scholar

Sklar, A. (1959). Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Stat. Univ. Paris 8, 229–231. doi:10.1007/978-3-642-33590-7

CrossRef Full Text | Google Scholar

Sraj, M., Bezak, N., and Brilly, M. (2015). Bivariate flood frequency analysis using the copula function: A case study of the litija station on the sava river. Hydrol. Process. 29, 225–238. doi:10.1002/hyp.10145

CrossRef Full Text | Google Scholar

Strupczewski, W. G., Singh, V. P., and Feluch, W. (2001). Non-stationary approach to at-site flood frequency modelling I. Maximum likelihood estimation. J. Hydrol. 248, 123–142. doi:10.1016/S0022-1694(01)00397-3

CrossRef Full Text | Google Scholar

Sun, Y., Zhu, F., Chen, J., and Li, J. (2018). Risk analysis for reservoir real-time optimal operation using the scenario tree-based stochastic optimization method. Water 10, 606. doi:10.3390/w10050606

CrossRef Full Text | Google Scholar

Tung, Y., and Wong, C. (2014). Assessment of design rainfall uncertainty for hydrologic engineering applications in Hong Kong. Stoch. Environ. Res. Risk Assess. 28, 583–592. doi:10.1007/s00477-013-0774-2

CrossRef Full Text | Google Scholar

Wallington, K., and Cai, X. (2020). Feedback between reservoir operation and floodplain development: Implications for reservoir benefits and beneficiaries. Water Resour. Res. 56. doi:10.1029/2019WR026610

CrossRef Full Text | Google Scholar

Wang, J., Liang, Z., Hu, Y., and Wang, D. (2015). Modified weighted function method with the incorporation of historical floods into systematic sample for parameter estimation of Pearson type three distribution. J. Hydrol. 527, 958–966. doi:10.1016/j.jhydrol.2015.05.023

CrossRef Full Text | Google Scholar

Wang, K., Wang, Z., Liu, K., Du, H., Mo, Y., Wang, M., et al. (2022). Assessing the floodwater utilization potential in a reservoir-controlled watershed: A novel method considering engineering regulations and an empirical case from China. Ecol. Inf. 68, 101581. doi:10.1016/j.ecoinf.2022.101581

CrossRef Full Text | Google Scholar

Wang, Z., Wang, K., Liu, K., Cheng, L., Wang, L., and Ye, A. (2019). Interactions between lake-level fluctuations and waterlogging disasters around a large-scale shallow lake: An empirical analysis from China. Water 11, 318. doi:10.3390/w11020318

CrossRef Full Text | Google Scholar

Wang, Z., Zhang, L., Cheng, L., Liu, K., Ye, A., and Cai, X. (2020). Optimizing operating rules for a reservoir system in northern China considering ecological flow requirements and water use priorities. J. Water Resour. Plan. Manag. 146. doi:10.1061/(ASCE)WR.1943-5452.0001236

CrossRef Full Text | Google Scholar

Wu, S.-J., Yang, J.-C., and Tung, Y.-K. (2011). Risk analysis for flood-control structure under consideration of uncertainties in design flood. Nat. Hazards 58, 117–140. doi:10.1007/s11069-010-9653-z

CrossRef Full Text | Google Scholar

Wu, Z., Shen, Y., Wang, H., and Wu, M. (2020). Urban flood disaster risk evaluation based on ontology and Bayesian Network. J. Hydrol. 583, 124596. doi:10.1016/j.jhydrol.2020.124596

CrossRef Full Text | Google Scholar

Xie, A., Liu, P., Guo, S., Zhang, X., Jiang, H., and Yang, G. (2018). Optimal design of seasonal flood limited water levels by jointing operation of the reservoir and floodplains. Water Resour. Manag. 32, 179–193. doi:10.1007/s11269-017-1802-7

CrossRef Full Text | Google Scholar

Xiong, F., Guo, S., Liu, P., Xu, C.-Y., Zhong, Y., Yin, J., et al. (2019). A general framework of design flood estimation for cascade reservoirs in operation period. J. Hydrol. 577, 124003. doi:10.1016/j.jhydrol.2019.124003

CrossRef Full Text | Google Scholar

Xiong, F., Guo, S., Yin, J., Tian, J., and Rizwan, M. (2020). Comparative study of flood regional composition methods for design flood estimation in cascade reservoir system. J. Hydrol. 590, 125530. doi:10.1016/j.jhydrol.2020.125530

CrossRef Full Text | Google Scholar

Xiong, W., and Qi, H. (2010). “A extended TOPSIS method for the stochastic multi-criteria decision making problem through interval estimation,” in 2010 2nd International Workshop on Intelligent Systems and Applications, China, 22-23 May 2010.

CrossRef Full Text | Google Scholar

Xu, P., Wang, D., Singh, V. P., Wang, Y., Wu, J., Wang, L., et al. (2017). A two-phase copula entropy-based multiobjective optimization approach to hydrometeorological gauge network design. J. Hydrol. 555, 228–241. doi:10.1016/j.jhydrol.2017.09.046

CrossRef Full Text | Google Scholar

Yan, B., Guo, S., and Chen, L. (2014). Estimation of reservoir flood control operation risks with considering inflow forecasting errors. Stoch. Environ. Res. Risk Assess. 28, 359–368. doi:10.1007/s00477-013-0756-4

CrossRef Full Text | Google Scholar

Ye, A., Wang, Z., Zhang, L., Wang, L., and Wang, K. (2019). Assessment approach to the floodwater utilization potential of a basin and an empirical analysis from China. Environ. Earth Sci. 78, 52. doi:10.1007/s12665-019-8050-5

CrossRef Full Text | Google Scholar

Yin, J., Guo, S., He, S., Guo, J., Hong, X., and Liu, Z. (2018a). A copula-based analysis of projected climate changes to bivariate flood quantiles. J. Hydrol. 566, 23–42. doi:10.1016/j.jhydrol.2018.08.053

CrossRef Full Text | Google Scholar

Yin, J., Guo, S., Liu, Z., Yang, G., Zhong, Y., and Liu, D. (2018b). Uncertainty analysis of bivariate design flood estimation and its impacts on reservoir routing. Water Resour. Manag. 32, 1795–1809. doi:10.1007/s11269-018-1904-x

CrossRef Full Text | Google Scholar

Zhang, L., and Singh, V. P. (2006). Bivariate flood frequency analysis using the copula method. J. Hydrol. Eng. 11, 150–164. doi:10.1061/(asce)1084-0699(2006)11:2(150)

CrossRef Full Text | Google Scholar

Zhang, L., and Singh, V. P. (2007a). Bivariate rainfall frequency distributions using Archimedean copulas. J. Hydrol. 332, 93–109. doi:10.1016/j.jhydrol.2006.06.033

CrossRef Full Text | Google Scholar

Zhang, L., and Singh, V. P. (2007b). Gumbel–hougaard copula for trivariate rainfall frequency analysis. J. Hydrol. Eng. 12, 409–419. doi:10.1061/(asce)1084-0699(2007)12:4(409)

CrossRef Full Text | Google Scholar

Zhang, L., and Singh, V. P. (2007c). Trivariate flood frequency analysis using the gumbel–hougaard copula. J. Hydrol. Eng. 12, 431–439. doi:10.1061/(asce)1084-0699(2007)12:4(431)

CrossRef Full Text | Google Scholar

Zhao, T., Zhao, J., Lei, X., Wang, X., and Wu, B. (2017). Improved dynamic programming for reservoir flood control operation. Water Resour. Manag. 31, 2047–2063. doi:10.1007/s11269-017-1599-4

CrossRef Full Text | Google Scholar