Evidence of poro-elastic inflation at the onset of the 2021 Vulcano Island (Italy) unrest

Thermal and pore-pressure variations induced by the circulation of hydrothermal-magmatic fluids in porous and permeable media contribute to ground deformation in volcanic areas. Here, we use solutions for the calculation of the displacements induced by pore-pressure and temperature changes for simplified geometry sources embedded in an elastic half-space with homogeneous mechanical and porous properties. The analytical solution for a spherical source is reviewed, and a semi-analytical approach for the calculation of the displacement for a cylindrical source is presented. Both models were used for the inversion of the daily deformation data recorded on Vulcano Island (Italy) during the 2021 unrest. Starting from September 2021, Vulcano Island experienced an increase in gas emission, seismic activity, and edifice inflation. The deformation pattern evolution from September until mid-October 2021 is indicative of a spatially stationary source. The modeling of the persistent and continuous edifice inflation suggests a deformation source located below the La Fossa crater at a depth of approximately 800 m from the ground surface undergoing a volume change of approximately 10⁵ m³, linked to the rise in fluids from a deeper magmatic source. Corroborated by other sources of geophysical and geochemical evidence, the modeling results support that thermo-poro-elastic processes are sufficient to explain the observed displacement without necessarily invoking the migration of magma to shallow levels. Our findings demonstrate that thermo-poro-elastic solutions may help interpret ground deformation and gain insights into the evolution of the hydrothermal systems, providing useful implications for hazard assessment during volcanic crises.

1 Introduction

In recent years, an increasing number of observations have shown that hydrothermal-magmatic fluid circulation plays an active role in inducing stress variations and, consequently, in modulating ground deformation in volcanic areas (Hurwitz et al., 2007; Hutnak et al., 2009; Rinaldi et al., 2010; Troiano et al., 2011; Fournier and Chardot, 2012; Currenti et al., 2017; Miller et al., 2017). The ground surface deformation events, including inflation and deflation episodes that can differ drastically in duration and amplitude depending on the volcanic activity, are usually associated with magmatic processes where the transfer of new magma to shallow depth is involved (Dzurisin, 2007; Battaglia et al., 2008; Napoli et al., 2008; Currenti et al., 2011; Napoli et al., 2011). Concurrently, magma movement and degassing may drive the convection of hydrothermal fluids in the surrounding rocks. Indeed, poro-elastic and thermal processes, induced by hot fluid flow in a permeable medium, can be responsible for surface deformation (Bonafede, 1990; Chiodini et al., 2003; Hurwitz et al., 2007; Rinaldi et al., 2010; Belardinelli et al., 2019). These processes involve temperature and pore-pressure changes that necessarily induce thermal, stress, and strain variations. The inflation (or deflation) of a hydrothermal system is closely linked to the disequilibrium between the quantity of fluids entering the system and the quantity of fluids released at the surface, as well as their release velocity (Todesco, 2021). Injection of high-temperature fluids, originating from deeper magmatic sources, or tectonic activity enhances the circulation of hot fluids within shallow portions of hydrothermal systems. These processes, often accompanied by thermal expansion of the saturated host rock, can rapidly accelerate local overpressurization and fracturing that are reflected on the ground surface as observable deformation. Unrest, characterized by pressure-induced fracturing and associated deformation, has been studied at many volcanoes worldwide (Newhall and Dzurisin, 1988; Gambino and Guglielmino, 2008; Cannata et al., 2012; Harris et al., 2012; Phillipson et al., 2013; Acocella et al., 2015; Kobayashi et al., 2018; Narita et al., 2020). Many efforts have been made to estimate surface displacement induced by the migration of hot hydrothermal-magmatic fluids (McTigue, 1986; Bonafede, 1990; Bonafede, 1991; Battaglia et al., 2007; Mantiloni et al., 2020; Todesco, 2021).

The modeling of ground deformation associated with thermal and pore-pressure changes can be based on the linear theory of thermo-poro-elasticity (McTigue, 1986; Wang, 2000; Shapiro, 2015). Several approaches have been used for devising solutions for the thermo-poro-elastic problem (Wang, 2000; Davies, 2003).

Semi-analytical and analytical models proposed by Belardinelli et al. (2019) (sphere and spherical shell) and Mantiloni et al. (2020) (thin disk) are suitable to model displacement, strain, and stress fields induced by pore-pressure and temperature changes in a homogeneous 3D full-space and 3D half-space, respectively. Their models were applied to represent both the seismicity distribution and the heterogeneities of focal mechanisms observed at Campi Flegrei during the 1982–84 (Belardinelli et al., 2019; Mantiloni et al., 2020) and 2011–13 (Belardinelli et al., 2019) unrest episodes. Nespoli et al. (2021) proposed a numerical approach for modeling the displacement and stress fields produced by thermo-poro-elastic inclusions of cylindrical shape immersed in a half-space to overcome the limit of the thin thickness of the disk in the analytical formulation of Mantiloni et al. (2020). The numerical approach allowed Nespoli et al. (2021) to extend the results to an arbitrary geometry, non-uniform pressure and temperature within the inclusion, and the vertical heterogeneities of the elastic parameters of the medium enclosing the source. Recently, Nespoli et al. (2022) modeled thermo-poro-elastic sources with an arbitrary geometry in a layered medium. Todesco (2021) assumed a cylindrical hydrothermal reservoir to prove that the measured subsidence and the post-1985 uplift at Campi Flegrei are consistent with a poro-elastic rock response to pore-pressure variations associated with changes in the fluid content entering or leaving the shallow hydrothermal system.

The lack of straightforward analytical solutions for easily computing thermo-poro-elastic displacements has hampered their use in inverting the observed deformation linked to these processes. Numerical solutions are, in general, too computationally heavy to be used in the inversion scheme. On the other hand, simple analytical solutions can be efficiently and easily applied to obtain a first approximation of the deformation source for a rapid response during unrest periods. Indeed, the computation of the deformation due to prescribed temperature and pore-pressure distributions can be simplified and reduced to the determination of the Newtonian potential for a mass distribution whose density coincides with the given temperature and/or pore-pressure field (Goodier, 1937; Fung, 1965). The analogy between gravitational and displacement potential permits the generation of equations mathematically similar to those describing the gravitational field due to an assigned density distribution, by replacing the displacement field u with the gravity acceleration g (Goodier, 1937; Sternberg and McDowell, 1957; Fung, 1965; Wang, 2000). Exact closed analytical solutions for gravity acceleration have been widely devised for simplified geometries of homogeneous density distributions (Blakely, 1996), whereas semi-analytical approaches have been used when analytical solutions cannot be straightforwardly derived (Na et al., 2015; Hemmings et al., 2016).

By benefiting from the simplification of the displacement potential formulation, here we aim to revise and derive solutions for easily computing thermo-poro-elastic displacements for simple spherical and cylindrical sources in this paper. The semi-analytical formulations have been developed by exploiting the analogy between the gravitational and displacement problems. First, we verified the derived solutions by comparing with finite-element (FE) results. Then, we applied the model to explore whether the ground deformation observed at the onset of the 2021 Vulcano Island (Italy; Figure 1) crisis could be explained as a response of the porous medium to the rise in fluids from a deeper magmatic source located below the La Fossa crater. Unlike the major unrests of this volcanic complex in the past, significant ground deformation was recorded from September until mid-October 2021 (INGV Report, 2022). A rapid areal expansion of approximately 22 ppm (part per million), in addition to an uplift of approximately 1.3 cm in the northern sector of the cone, was indeed observed (Guglielmino et al., 2022). To determine the nature, size, and depth of the deformation source, the daily horizontal and vertical deformation data measured by the continuously running GPS monitoring network at Vulcano Island (Figure 1) were inverted by combining the derived straightforward thermo-poro-elastic model with a genetic algorithm (GA).

FIGURE 1

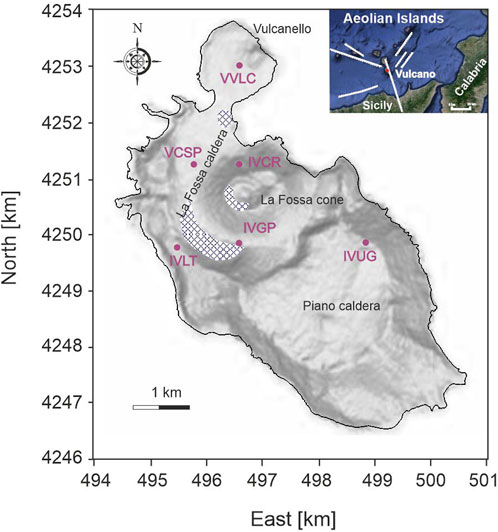
FIGURE 1. Map of Vulcano Island (latitude and longitude are given in the UTM33S system) showing locations of the GPS monitoring stations. The GNSS permanent network consists of six stations equipped with Leica GRX1200/GX1220 receivers and LEIAT504 antennas. The dashed areas indicate the locations of gas emission increase (after Inguaggiato et al., 2022). The white lines in the figure in the upper right represent the main faults.

2 Thermo-poro-elastic deformation

The mathematical model is designed based on the governing equations of the thermo-poro-elasticity theory, which describes the elastic response of a porous medium to the propagation of hot and pressurized fluids through pores. Assuming that the rock is in the quasi-static equilibrium, the displacement can be found by solving the equations of stress equilibrium coupled with thermo-poro-elastic extension of the Hooke’s law, giving the following set of equations (Fung, 1965; Wang, 2000; Jaeger et al., 2007):

$\nabla \cdot \mathbf{\sigma }=0,(1)$

$\mathbf{\sigma }=\lambda tr\left(\mathbf{\epsilon }\right)\mathbf{I}+2\mu \mathbf{\epsilon }+{\alpha }_T{K}_d\Delta T\mathbf{I}+\beta \Delta P\mathbf{I},(2)$

$\mathbf{\epsilon }=\frac{1}{2}\left(\nabla \mathbf{u}+{\left(\nabla \mathit{u}\right)}^T\right),(3)$

where σ and ε are the stress and strain tensors, respectively, I is the identity matrix, and u is the deformation vector. Equation 2 is the thermo-poro-elastic extension of the Hooke’s law σ $=\lambda$ tr(ε)I $+2\mu$ ε, where $\lambda$ and $\mu$ represent the Lamé’s first parameter and the modulus of rigidity, respectively, obtained by adding the $\Delta P$ pore-pressure change through the Biot–Willis coefficient $\beta$ and the $\Delta T$ temperature variation through the volumetric thermal expansion coefficient ${\alpha }_T$. The relationship between the coefficient $\beta$ and the drained $K_d$ and solid $K_s$ bulk moduli is given as $\beta =1-\frac{K_d}{K_s}$. The quantity, expressed as

${\epsilon }_0=\frac{\beta }{K_d}\Delta P+{\alpha }_T\Delta T,(4)$

is the stress-free strain, that is, the strain associated with changes in pore-pressure and/or in temperature within a thermo-poro-elastic source (Belardinelli et al., 2019; Nespoli et al., 2021).

Pore-pressure and/or temperature variations induce volume changes $\Delta V$, whose relationship with the stress-free strain ${\epsilon }_0$ is given by ${\epsilon }_0=\frac{\Delta V}{V_0}$ (Rinaldi et al., 2010), where $V_0$ is the initial volume of the source. The relationship suggests that ${\epsilon }_0$ also represents the relative change (dilatation or compression) in volume of the thermo-poro-elastic deformation source. It is worth noting that $\Delta V$ represents a stress-free volume change, that is, the volume change that the source undergoes if not immersed in the elastic medium. The actual volume changes that the thermo-pore-elastic source undergoes if immersed in the elastic medium is given by $\Delta \overline{V}=\frac{1}{3}\frac{1+\nu }{1-\nu }\Delta V$ (Belardinelli et al., 2019; Belardinelli et al., 2022).

Closed analytical solutions to Eqs 1–3 can be derived only under simplified assumptions for material properties, pore-pressure and temperature change distributions, and domain and source geometries.

A solution for the stress equilibrium equations of thermo-poro-elastic deformation sources can be expressed in terms of a displacement potential $\varphi$ that satisfies a Poisson’s equation in the form ${\nabla }^2\varphi$ = const. (Fung, 1965; Wang, 2000), stating the analogy between pressure/temperature change in thermo-poro-elastic problems and charge density and mass anomaly in electrical and gravitational potential problems in an infinite space, respectively (Wang, 2000). Therefore, for a thermo-poro-elastic deformation source located in unbounded, isotropic and homogeneous medium in isothermal and drained conditions, from Eqs (1–3), it follows that (Goodier, 1937; Fung, 1965)

${\nabla }^2\varphi =-\frac{1}{\lambda +2\mu }\left(\beta \Delta P+{\alpha }_T{K}_d\Delta T\right),(5)$

and the thermo-poro-elastic displacement u at an observation point $Q\left(x_Q,y_Q,z_Q\right)$ is calculated as

$u_x=\frac{\partial \varphi }{\partial x_Q},u_y=\frac{\partial \varphi }{\partial y_Q},u_z=\frac{\partial \varphi }{\partial z_Q},(6)$

where the displacement potential $\varphi$ is given by (Goodier, 1937; Fung, 1965):

$\varphi \left(x_Q,y_Q,z_Q\right)=-\frac{1}{\lambda +2\mu }\frac{\beta }{4\pi }\underset{D}{\iiint }\frac{\Delta P\left(x_c,y_c,z_c\right)}{\overline{R}}\mathrm{d}{x}_C\mathrm{d}{y}_C\mathrm{d}{z}_C-\frac{1}{\lambda +2\mu }\frac{{\alpha }_T{K}_d}{4\pi }\underset{D}{\iiint }\frac{\Delta T\left(x_c,y_c,z_c\right)}{\overline{R}}\mathrm{d}{x}_C\mathrm{d}{y}_C\mathrm{d}{z}_C.(7)$

In (7), $C$ = $\left(x_C,y_C,z_C\right)$ is the center of the source subjected to pore-pressure and/or temperature changes, $D$ is an infinite domain, and $\overline{R}=\sqrt{{\left(x_C-x_Q\right)}^2+{\left(y_C-y_Q\right)}^2+{\left(z_C-z_Q\right)}^2}$. The displacement vanishes as $\overline{R}$ reaches infinity. The displacement at the surface $z_Q=0$ of a half-space is calculated by considering the direct proportionality with the solution at $z_Q=0$ in an infinite space (Wang, 2000).

In the following section, we illustrate the derivation of the mathematical formulations to compute the displacement induced by temperature and pore-pressure changes for a half-space domain with the homogeneous distribution of mechanical and porous rock properties. Furthermore, pore-pressure and temperature change distributions are assumed to be homogeneous within a simplified source geometry. Spherical- and cylindrical-shaped sources are investigated.

2.1 Spherical source

We report the solution for the displacement field in a half-space domain due to a stress-free strain ${\epsilon }_0$ within a spherical geometry source (Rinaldi et al., 2010). We assume that the observation points $Q\left(x_Q,y_Q,z_Q\right)$ are placed on the surface of the half-space domain. Since the model has an axial symmetry, a 2D axi-symmetric domain is used in cylindrical coordinates $Q^{\prime }\left(\rho ,\vartheta ,z_Q\right)$, where $\rho =\sqrt{{\left(x_C-x_Q\right)}^2{+\left(y_C-y_Q\right)}^2}$ and $\vartheta =\arctan \left(\left(y_C-y_Q\right)/\left(x_C-x_Q\right)\right)$. The dependence on $\vartheta$ disappears because of the axial-symmetry condition. The axis of symmetry is vertical and passes through the center $\left(0,z_C\right)$ of the source. The displacement, in the radial $U_r$ and vertical $U_z$ components, respectively, generated by a spherical source at the observation point $Q^{\prime }\left(\rho ,z_Q\right)$ is given as follows (Mindlin, 1936; Mindlin and Cheng, 1950; Davies, 2003; Rinaldi et al., 2011):

$U_r\left(Q^{\prime }\right)=\frac{\left(1+\nu \right)\Delta V_s}{3\pi {\overline{R}}^{\prime 3}}\rho ,(8)$

$U_z\left(Q^{\prime }\right)=\frac{\left(1+\nu \right)\Delta V_s}{3\pi {\overline{R}}^{\prime 3}}\left(z_Q-z_C\right).(9)$

Here, $\Delta V_S={\epsilon }_0{V}_{0_S}$ is the stress-free volume change, where $V_{0_S}$ represents the initial volume of the sphere, $\nu$ is the Poisson’s ratio, and ${\overline{R}}^{\prime }=\sqrt{{\rho }^2+{\left(z_Q-z_C\right)}^2}$ is the Euclidean distance between the observation point $Q^{\prime }\left(\rho ,z_Q\right)$ and the center $\left(0,z_C\right)$ of the deformation source.

The horizontal deformation components, $U_x$ and $U_y$, respectively, at the observation point $Q$ in Cartesian coordinates can be easily derived as follows:

$U_x\left(Q\right)=\frac{\left(1+\nu \right)\Delta V_s}{3\pi {\overline{R}}^3}\left(x_Q-x_C\right),(10)$

$U_y\left(Q\right)=\frac{\left(1+\nu \right)\Delta V_s}{3\pi {\overline{R}}^3}\left(y_Q-y_C\right).(11)$

It is worth noting that formulations (8) and (9) are similar to the Mogi solution, which provides ground deformation generated by a spherical cavity under the action of an overpressure $\Delta P_M$ on its wall, that reads as (Mogi, 1958)

$U_r\left(Q^{\prime }\right)=\frac{a^3\left(1-\nu \right)\Delta P_M}{\mu {\overline{R}}^{\prime 3}}\rho =\frac{\left(1-\nu \right)\Delta {\overline{V}}_M}{\pi {\overline{R}}^{\prime 3}}\rho ,(12)$

$U_z\left(Q^{\prime }\right)=\frac{a^3\left(1-\nu \right)\Delta P_M}{\mu {\overline{R}}^{\prime 3}}\left(z_Q-z_C\right)=\frac{\left(1-\nu \right)\Delta {\overline{V}}_M}{\pi {\overline{R}}^{\prime 3}}\left(z_Q-z_C\right),(13)$

where $\Delta {\overline{V}}_M=\frac{\pi a^3\Delta P_M}{\mu }$ is the actual volume change and $a$ is the radius of the Mogi source. Because of this similarity, it is not possible to distinguish between the magmatic and thermo-poro-elastic processes using deformation data alone (Lu et al., 2002), since they engender the same deformation pattern. In the Mogi model, the actual volume change $\Delta {\overline{V}}_M$ represents the actual radial expansion of the source wall, whereas the volume change $\Delta V_S=3\frac{1-\nu }{1+\nu }\Delta {\overline{V}}_S$, which appears in the thermo-poro-elastic equation (Eqs 8, 9), represents the stress-free volume change if the source could expand freely under the action of the stress-free strain ${\epsilon }_0$. The Mogi solution is identical to the solution for a thermo-poro-elastic spherical source embedded within an elastic medium if an overpressure $\Delta P_S=\frac{1+\nu }{1-\nu }\frac{\mu \Delta V_S}{3\pi a^3}$ acts from within (Belardinelli et al., 2019).

2.2 Cylindrical source

Ground deformation induced by thermo-poro-elastic strain changes within a cylindrical source has been described by Wang (2000). The mathematical formulation exploits the analogy between thermo-poro-elastic deformation and gravity change problems. For the gravity changes, closed analytical solutions were derived but only at the observation point along the axis of symmetry of the cylindrical source (Telford et al., 1981). Benefiting from these solutions, recently Todesco (2021) estimated the expected poro-elastic vertical deformation at Campi Flegrei induced by a cylindrical-shaped hydrothermal system. However, this closed-form analytical solution only allows the computation of the vertical deformation at a point along the axis of symmetry. Semi-analytical solutions can be derived using spherical harmonic series of Legendre polynomials (Na et al., 2015). Examinations of both gravity (Na et al., 2015) and, more recently, thermo-poro-elastic deformation (Mantiloni et al., 2020) have shown that the solutions are accurate under the assumption that the height $h$ of the cylinder is much smaller than its radius $R$ ($h/R\ll 1$). The analytical solutions for thin disk-shaped sources (Mantiloni et al., 2020) can be easily generalized to model thick cylindrical sources by stacking two or more disks (Nespoli et al., 2021; Belardinelli et al., 2022).

We provide an alternative way to compute the displacement induced by pore-pressure and temperature changes for a cylindrical source by extending the formulation proposed by Hemmings et al. (2016) for the gravity changes. Starting from this formulation, we have derived the semi-analytical solution to compute the analogous radial and vertical displacements. In the cylindrical coordinate system, each elementary source (${\rho }_i,z_i$), with which the source is composed of, represents a portion of an elementary source ring centered in ($0,z_i$) and radius ${\rho }_i$ (Supplementary Figure S1). The distance between the observation point $Q^{\prime }$ and the elementary source at (${\rho }_i$, $z_i$) is, in cylindrical coordinates, a function of $\vartheta$, that is, $s\left(\vartheta \right)=\sqrt{{\rho }_i^2-2{\rho }_i\rho \mathit{cos}\left(\vartheta \right)+{\rho }^2+{\left(z_Q-z_i\right)}^2}$. Under this configuration, from Eq. 7, we derived the displacement potential $\varphi =\frac{1+\nu }{3\pi }{\epsilon }_{0_i}{\rho }_i\mathrm{d}{\rho }_i\mathrm{d}{z}_i{\displaystyle \underset{0}{\overset{2\pi }{\int }}}\frac{1}{s\left(\vartheta \right)}\mathrm{d}\vartheta$ for a single ring and obtained the displacement field at $Q^{\prime }$ by computing the gradient of the potential (Eq. 6):

$U_{i_r}\left(Q^{\prime }\right)=\frac{1+\nu }{3\pi }{\epsilon }_{0_i}{\rho }_i\mathrm{d}{\rho }_i\mathrm{d}{z}_i{\displaystyle \underset{0}{\overset{2\pi }{\int }}}\frac{\rho -{\rho }_i\mathit{cos}\left(\vartheta \right)}{s{\left(\vartheta \right)}^3}\mathrm{d}\vartheta ,(14)$

$U_{i_z}\left(Q^{\prime }\right)=\frac{1+\nu }{3\pi }{{\epsilon }_{0_i}\rho }_i\mathrm{d}{\rho }_i\mathrm{d}{z}_i\left(z_Q-z_i\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}}\frac{1}{s{\left(\vartheta \right)}^3}\mathrm{d}\vartheta ,(15)$

where $V_i={\rho }_i\mathrm{d}{\rho }_i\mathrm{d}{z}_i\mathrm{d}\vartheta$ is the volume of each elementary source (${\rho }_i$, $z_i$) on the ring and $G_r\left({\rho }_i,z_i\right)=\frac{1+\nu }{3\pi }{\rho }_i\mathrm{d}{\rho }_i\mathrm{d}{z}_i\frac{\rho -{\rho }_i\mathit{cos}\left(\vartheta \right)}{s{\left(\vartheta \right)}^3}$ and $G_z\left({\rho }_i,z_i\right)=\frac{1+\nu }{3\pi }{\rho }_i\mathrm{d}{\rho }_i\mathrm{d}{z}_i\frac{z_Q-z_i}{s{\left(\vartheta \right)}^3}$ are the Green’s functions. Equations 14, 15 represent, respectively, the radial and vertical components of the displacement field due to a single ring. The integrals in the equations are solved numerically using a recursive adaptive Simpson quadrature scheme.

Finally, the displacement, recorded at the observation point $Q^{\prime }$, is obtained by summing up the contributions of each elementary ring:

$U_r\left(Q^{\prime }\right)=\frac{1+\nu }{3\pi }{\epsilon }_0{\displaystyle \sum _{\left({\rho }_i,z_i\right)}}{\rho }_i\mathrm{d}{\rho }_i\mathrm{d}{z}_i{\displaystyle \underset{0}{\overset{2\pi }{\int }}}\frac{\rho -{\rho }_i\mathit{cos}\left(\vartheta \right)}{s{\left(\vartheta \right)}^3}\mathrm{d}\vartheta ,(16)$

$U_z\left(Q^{\prime }\right)=\frac{1+\nu }{3\pi }{\epsilon }_0{\displaystyle \sum _{\left({\rho }_i,z_i\right)}}{\rho }_i\mathrm{d}{\rho }_i\mathrm{d}{z}_i\left(z_Q-z_i\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}}\frac{1}{s{\left(\vartheta \right)}^3}\mathrm{d}\vartheta .(17)$

Equations 16, 17 represent the semi-analytical formulations to compute the ground displacements generated by a cylindrical source consisting of many elementary rings as a function of the position of the observation point $Q^{\prime }\left(\rho ,z_Q\right).$

This approach only allows us to compute the surface displacements (i.e., $z_Q=0$). In order to compute displacement, strain, and stresses in the interior points of the half-space domain, it is no longer possible to use the scalar potential because the displacement field is not irrotational (Mantiloni et al., 2020).

In order to verify the results and check the accuracy of the numerical integration, solutions from Formulas 16, 17 were compared with the numerical thermo-poro-elastic results (Supplementary Material) calculated using COMSOL Multiphysics software (COMSOL, 2012), which solves Eqs 1–3 with a finite-element (FE) discretization (Currenti and Napoli, 2017; Stissi et al., 2021).

The accuracy of the semi-analytical solution depends on the discretization of the source in elementary rings with finite thickness. The smaller the element, the better the solution. For shallow and/or large cylindrical sources, a more accurate solution is obtained by considering the cylindrical source as the superposition of smaller sources (Supplementary Figure S3). The surface displacement is calculated, according to Eqs 16, 17, as the sum of the displacements induced by the single smaller sources. The comparison shows a good agreement between the proposed semi-analytical and numerical solutions (Supplementary Figures S2, S3).

In the following section, we applied the derived solutions to invert the ground deformations observed at the onset of the 2021 unrest episode in Vulcano Island.

3 Thermo-poro-elastic deformations at Vulcano Island during the 2021 unrest

During the last century, Vulcano Island has been characterized by significant solfataric fumarolic activity, concentrated along the main structural features of the volcanic complex (Selva et al., 2020). This solfataric fumarolic activity represents the main evidence of the presence of an extensive hydrothermal system, inferred by different geophysical and geochemical investigations beneath the La Fossa Caldera at a depth between 500 and 1,500 m below sea level (b.s.l.) (Chiodini et al., 1992; Berrino, 2000; Alparone et al., 2010; Napoli and Currenti, 2016; Ruch et al., 2016). After its last eruption in 1888–1890 (Keller, 1980), a number of unrest phases (e.g., in 1978–1980, 1988–1991, 1996, 2004–2007, and 2009–2010) have been characterized by the occurrence of generalized increases in the crater fumaroles’ temperature and the expansion of exhalative areas (Carapezza et al., 1981; Chiodini et al., 1992; Diliberto, 2017). These anomalies were also accompanied by the rise in CO₂ fluxes in soils and SO₂ fluxes in the plume. In the last 30 years, the unrest phases were accompanied by a significant increase in the volcano seismicity associated with variations in the hydrothermal system (Milluzzo et al., 2010; Cannata et al., 2012), but neither volcano-tectonic events nor significant ground deformation has been concurrently observed (Selva et al., 2020).

The last unrest phase, which began in September 2021, has been characterized by anomalous soil degassing producing dangerous levels of CO₂ in different areas of the island, reaching a maximum value of 34,000 g m⁻² day⁻¹, which is 20 times higher than the average background values recorded in the last decades. At the same time, SO₂ in the plume emitted in the summit area reached 2.7 kg s^-1, that is, one order of magnitude over the mean value of the last 13 years (Aiuppa et al., 2022; Inguaggiato et al., 2022). These geochemical anomalies were accompanied by a rapid increase in seismicity, characterized by long period (LP) and very long period (VLP) seismic events, up to 78 events per day in September, located to the northeast of the La Fossa Cone at an average depth of 750 m b.s.l., and by significant ground deformation (INGV Report, 2022; Currenti et al., 2023; Federico et al., 2023). This is the first unrest episode in which sharp and fast deformation, although with small magnitude, has been detected at Vulcano Island since the setup of the GPS monitoring network.

3.1 Deformation data

Figure 2 shows the daily horizontal (${\mathbf{U}}_x$ and $\left.{\mathbf{U}}_y\right)$ and vertical $\left({\mathbf{U}}_z\right)$ deformation data measured by the GPS monitoring network at Vulcano Island from January 2019 to December 2021. Raw daily GPS data were processed using GIPSY software (Bertiger et al., 2020) in a precise point positioning mode applied to the ionospheric-free carrier phase and using JPL’s final orbit and clock products. Solutions were first aligned to IGS14 by applying a daily seven-parameter Helmert transformation. Finally, to remove the, albeit minor, regional long-term tectonic movements, each time series of local positions was corrected from residual trends estimated up to August 2021 as a linear trend. To reduce the noise, a moving centered median filter was applied with a fixed window length of 35 days. No significant variations were observed before September 2021 after which the crisis started with sudden increases in gas emission (Aiuppa et al., 2022) and seismicity (INGV Report, 2022; Federico et al., 2023). Concurrent ground deformations of a few centimeters were recorded at almost all the stations from the beginning of September until mid-October, when the deformation ceased. The average deformation rate at the closest station to the summit (IVCR) was approximately 4.06 x 10⁻² cm/day. Data disclosed a clear radial pattern centered in the La Fossa Cone area (Figure 3A). The ground deformation observed between 2 September and 13 October indicated a continuous expansion of the volcano edifice. During the entire period, a continuous amplification of the deformation was recorded at all the stations with a persistent pattern (Figure 3A). Indeed, the ratio between ground deformation components at different stations was fairly constant (Figure 3B), suggesting that the deformation source, which was observed from the onset of the Vulcano Island crisis, is almost spatially stationary.

FIGURE 2

FIGURE 2. Daily raw deformation component data (black lines) and smooth data (colored lines) for the different stations in Vulcano from January 2019 to December 2021. Gray bars highlight the deformation data between 2 September 2021 and 13 October 2021, when most of the volcano edifice expansion occurred.

FIGURE 3

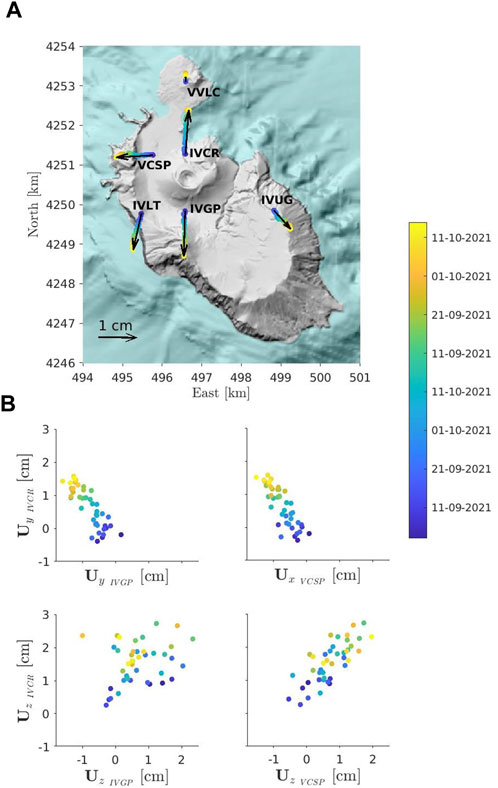
FIGURE 3. (A) Observed displacement path lines at each station. The colored dots indicate the deformation pattern over time, from 2 September 2021 to 13 October 2021. (B) Relationships between deformations in different stations from 2 September 2021 to 13 October 2021. The figure shows the relationships between the north components in the stations IVCR and IVGP (top left panel) and between the north component in the station IVCR and the east component in the station VCSP (top right panel). The relationships between the vertical displacements for the stations IVCR and IVGP (bottom left panel) and IVCR and VCSP (bottom right panel) are also shown.

3.2 Inversion modeling

The horizontal and vertical displacements observed at Vulcano Island have been inverted to constrain the source and gain insights into the deformation process. We explore both the spherical and cylindrical sources in order to find the best-fitting solution.

The inverse method combines the derived forward models with GA (Tiampo et al., 2000; Currenti et al., 2007; Carbone et al., 2008), in order to find the model parameters that minimize the misfit between the observed and computed deformations. Following an evolutionary scheme, GA iteratively explores the model parameter space and tries to find the global optimal solution. The misfit is quantified using an objective function defined as the root mean square error (RMSE) between the observed data ${\mathbf{U}}_{\mathbf{obs}}$ = (${{\mathbf{U}}_{\mathbf{obs}}}_{\mathbf{x}}$, ${{\mathbf{U}}_{\mathbf{obs}}}_{\mathbf{y}}$, ${{\mathbf{U}}_{\mathbf{obs}}}_{\mathbf{z}}$) and the deformation computed by the forward model ${\mathbf{U}}_{\mathbf{calc}}=({{\mathbf{U}}_{\mathbf{calc}}}_{\mathbf{x}},{{\mathbf{U}}_{\mathbf{calc}}}_{\mathbf{y}},{{\mathbf{U}}_{\mathbf{calc}}}_{\mathbf{z}}$):

$\text{RMSE}=\sqrt{\frac{1}{n}\left({\displaystyle \sum _{i=1}^{n_1}}{\left({U_{obs}}_{x_i}-{U_{calc}}_{x_i}\right)}^2+{\displaystyle \sum _{i=1}^{n_2}}{\left({U_{obs}}_{y_i}-{U_{calc}}_{y_i}\right)}^2+{\displaystyle \sum _{i=1}^{n_3}}{\left({U_{obs}}_{z_i}-{U_{calc}}_{z_i}\right)}^2\right)}.(18)$

Here, $n=n_1+n_2+n_3$, where $n_1$, $n_2$, and $n_3$ represent the number of observation points for each deformation component.

For the spherical source, the model parameter vector is represented by $p=\left\{x_C,y_C,z_C,\Delta V_S\right\}$, where $\left(x_C,y_C,z_C\right.$) are the coordinates of the center of the source and $\Delta V_S$ is the stress-free volume change, while for the cylindrical source, it is represented by $p=$ {$\left.x_C,y_C,d,R,h,{\epsilon }_0\right\}$, where $\left(x_C{,y}_C\right)$ are the coordinates of the center of the source, $d$ is the depth of the top of the cylinder, $R$ is the radius, $h$ is the height, and ${\epsilon }_0$ is the stress-free strain (Tables 1, 2).

TABLE 1

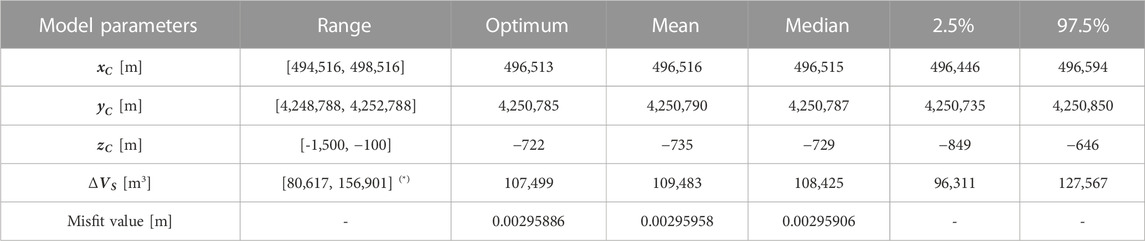
TABLE 1. Parameters that define the spherical source: $x_C$, $y_C$, and $z_C$ are the coordinates of the center of the source, and $\Delta V_S$ is the volume change. For each parameter, we report the search range, the optimum, the mean, and the median solutions obtained by the inversion algorithm. The misfit value and the 2.5 and 97.5 percentiles are reported. (*) The range of $\Delta V_S$ was obtained by using the least squares method (Eq. 19).

TABLE 2

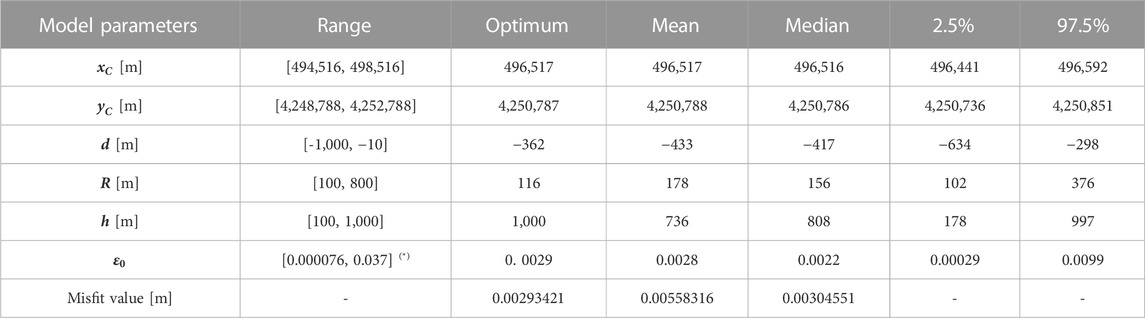
TABLE 2. Parameters that define the cylindrical source: $x_C$ and $y_C$ are the coordinates of the center of the source, $d$ is the depth of the top, $R$ is the radius, $h$ is the height, and ${\epsilon }_0$ is the stress-free strain. For the cylindrical source, $z_C=d-h/2$. For each parameter, we report the search range, the optimum, the mean, and the median solutions obtained by the inversion algorithm. The misfit value and the 2.5 and 97.5 percentiles are reported. (*) The range of ${\epsilon }_0$ was obtained by using the least squares method (Eq. 19).

For each set $p$ of parameters, the forward model computes an initial population of solutions ${\mathbf{U}}_{\mathbf{calc}}\left(p\right)$ whose fit with the observed data is evaluated by means of the objective function (Currenti et al., 2007) to evaluate the “best” sets of parameters in the entire population, i.e., the model that minimizes the objective function. The best sets of parameters are modified by applying evolutionary rules for the generation of a new set of parameters that on average are better than the previous parameters. The procedure is iterated, and the initial population evolves over several generations (Currenti et al., 2005), until the algorithm converges to the global optimal solution.

It is worth noting that the deformation solutions (Eqs 8, 9 and Eqs 16, 17) are linearly proportional to $\Delta V_S$ for the spherical source and ${\epsilon }_0$ for the cylindrical source. For this reason, the parameters $\Delta V_S$ and ${\epsilon }_0$ are omitted in the set of the inversion parameters and are computed at each step by the least squares method:

$\Delta V_S\text{\hspace{0.17em}or\hspace{0.17em}}{\epsilon }_0={\left({\mathbf{U}}_{\mathbf{calc}}\times {\mathbf{U}}_{\mathbf{calc}}^{\mathit{T}}\right)}^{-1}\times {\mathbf{U}}_{\mathbf{calc}}\times {\mathbf{U}}_{\mathbf{obs}}^{\mathit{T}}.(19)$

In such a case, the dimension of the search domain for optimization is reduced to $p=\left\{x_C,y_C,z_C\right\}$ and $p=$ {$\left.x_C,y_C,d,R,h\right\}$ for the spherical and cylindrical geometries, respectively.

An extensive search was performed on the model parameter space, whose ranges are reported in Tables 1, 2. Since the deformation pattern clearly points to a deformation source located below the La Fossa Cone, the search range for the source position is limited within a 4-km-wide box centered in the summit area. GA is initialized with a random population consisting of 100 individuals, and it iterates till it converges. A single GA inversion takes on average 3.5 s for the sphere and 12 s for the cylinder. The GA inversion is performed 5,000 times to obtain an estimate of the model uncertainty. The models obtained after the convergences are used to appraise the results by computing the 1D and 2D marginal distributions. The 1D marginal distributions, given by the histograms of the model parameters in the solution set, provide the confidence intervals, whereas the 2D marginal distributions, calculated for selected pairs of parameters, offer further information about their trade-offs (Sambridge, 1999).

4 Numerical results

4.1 Deformation models

The computed displacements for the optimal spherical solution (Figure 4), whose parameters are reported in Table 1, generally fit with the observed data with an RMSE of approximately 3 mm. The solution indicates a deformation source centered in the La Fossa Cone, as already suggested from the radial pattern of the data (Figure 4A), at an average depth of 720 m below the ground surface. The 1D marginal distributions (Figure 5) indicate that the model parameters are well constrained. The mean, the median, and the optimal solutions are well within the 95% confidence intervals which are very narrow for all the parameters (Table 1). The 2D marginal distributions of the estimated source parameters from the inversions show that they concurrently converge toward the optimal solution.

FIGURE 4

FIGURE 4. Comparison between observed and optimum computed deformation for the spherical source. (A) ${\mathbf{U}}_x$ and ${\mathbf{U}}_y$ components of the radial deformation in each station; the red circle indicates the position of the source. (B) Radial deformation as a function of the radial distance of the stations from the deformation source. (C) Vertical deformation as a function of the radial distance of the stations from the source.

FIGURE 5

FIGURE 5. 1D (diagonal) and 2D (off-diagonal) marginal distributions of the solutions set provided by the inversion algorithm for the spherical source. For each parameter ($x_C,y_C,z_C,\Delta V_S$), we report the optimum (in orange), the mean (in blue), and the median (in magenta) values (Table 1) of the ensemble solutions. In each contour plot, the black dot (located by the dashed gray lines) indicates the optimal solution.

For the cylindrical source, the computed displacements of the optimal solution (Figure 6; Table 2) are very similar to those obtained for the spherical source (Figure 4) with a comparable RMSE (3 mm) (Tables 1, 2). The source position is almost the same, and the 95% confidence intervals of the two solutions show considerable overlap. The top of the source lies at 360 m depth providing a cylinder center depth of approximately 860 m, which is almost the same center depth estimated for the spherical source (720 m). Nonetheless, the cylinder center depth is slightly outside the confidence interval of the sphere depth, which ranges between 646 and 849 m. The radius $R$ and height $h$ parameters are not well constrained (Figure 7A) and have larger confidence intervals. The examination of the 2D marginal distributions shows that the radius and height parameters are not fully independent (Figure 7A). The smaller the radius, the taller the cylinder. The marginal distributions show that these parameters have a wide range of variability, and, starting from the optimal solution, there are several pairs of parameters ($R$, $h$) values and associated stress-free strain ${\epsilon }_0$ values, for which the computed deformation fits the observations as well (Supplementary Figures S5, S6). This implies that diverse cylindrical sources with different radii, heights, and strain variations can be equally responsible for the observed ground deformations.

FIGURE 6

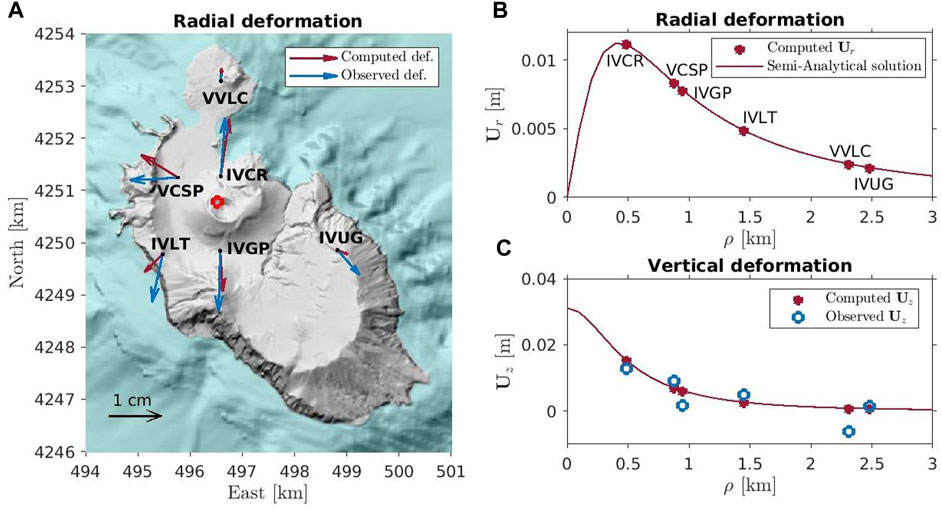
FIGURE 6. Comparison between observed and optimum computed deformations for the cylindrical source. (A) ${\mathbf{U}}_x$ and ${\mathbf{U}}_y$ components of the radial deformation in each station; the red circle indicates the position of the source. (B) Radial deformation as a function of the radial distance of the stations from the deformation source. (C) Vertical deformation as a function of the radial distance of the stations from the source.

FIGURE 7

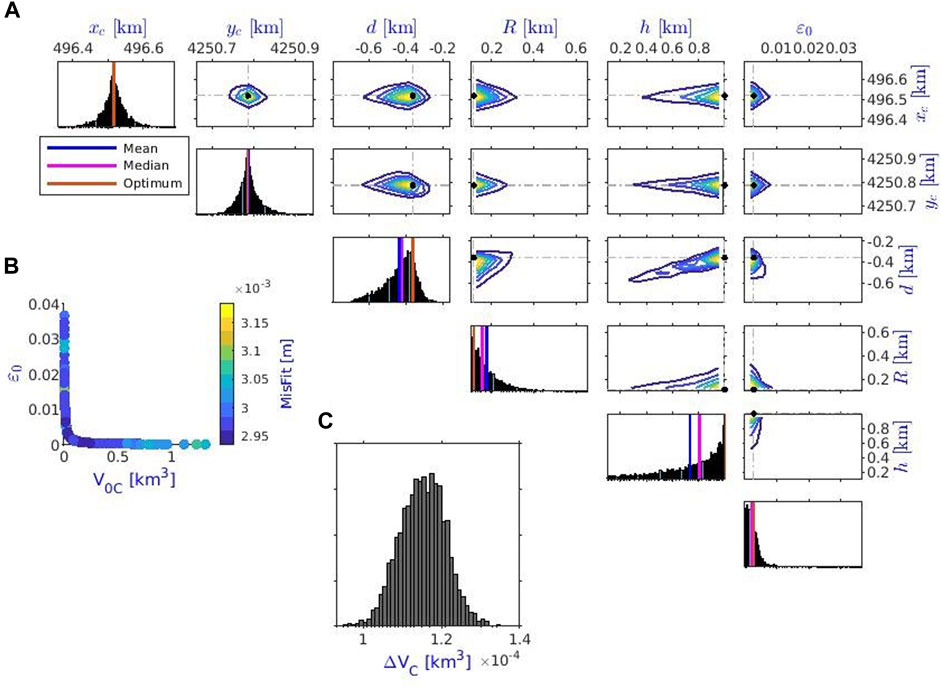
FIGURE 7. (A) 1D (diagonal) and 2D (off-diagonal) marginal distributions of the GA solutions set for the cylindrical source. For each parameter ($x_C,y_C$, $d$, $R$, $h$, ${\epsilon }_0$), we report the optimum (in orange), the mean (in blue), and the median (in magenta) values (Table 2) of the ensemble solutions. In each contour plot, the black dot (located by the dashed gray lines) indicates the optimal solution. (B) Relationship between $V_{0_C}$ and ${\epsilon }_0$ for the cylindrical source. The misfit is indicated for each pair ($V_{0_C}$, ${\epsilon }_0$) of the GA solutions set. (C) Volume change distribution for the cylindrical source.

Under the action of thermo-poro-elastic effects, both the optimal spherical and cylindrical sources undergo a comparable volume change. For the spherical source, an optimal value of $\Delta V_S=$ 1.07 x 10⁵ m³ is obtained. For the cylindrical source, the volume change is also well constrained (Figure 7C). Its distribution assumes values between 0.9 x 10⁵ m³ and 1.4 x 10⁵ m³ centered around a value of $\Delta V_C={\epsilon }_0{V}_{0_C}=$ 1.15 x 10⁵ m³ (Figure 7C), which is very similar to that of the spherical source.

Despite the reasonable and similar fits of the spherical and cylindrical source models, discrepancies between the observed and computed deformations are obtained, for both geometries, at VCSP, IVUG, and IVLT stations. At VCSP and IVLT stations, although the amplitudes of the computed deformations are comparable to those observed, the computed radial deformation vector appears to be rotated by approximately 40° clockwise with respect to the observations. Moreover, at IVUG, the model predicts a strong attenuation. We further investigated whether these discrepancies could be explained by the volcano topography, with an edifice that extends from −1,180 m b.s.l. to 497 m a.s.l. We performed finite-element modeling for the spherical source using COMSOL (Supplementary Figure S7). The COMSOL numerical results are similar to the analytical solutions. The only slight difference is observed at the IVCR station, closest to the La Fossa cone, where the maximum radial deformation is observed. In fact, at this station, the COMSOL deformation solution appears rotated clockwise with respect to both the semi-analytical solution and the observed data. Overall, the RMSE is approximately 3 mm, similar to that achieved for the analytical solution. Therefore, the surface topography alone is not sufficient to justify the rotation at VCSP and IVLT and the larger displacement at IVUG.

4.2 Global sensitivity analysis

A sensitivity analysis is performed to evaluate the impact of the parameters on the solutions of the spherical and cylindrical sources. We applied the Morris method (Morris, 1991), a widely used one-at-a-time (OAT) global sensitivity analysis (GSA) (Feng et al., 2019). In particular, the Morris method represents an excellent tool for identifying the influential parameters of a model with a large number of inputs and quantifying the response of the model to the change in the input parameters (Conca et al., 2016; Liu et al., 2020).

Starting from a sample of the input parameters $\left(x_1^{*},\dots ,x_{i-1}^{*},x_i^{*},x_{i+1}^{*},\dots ,x_n^{*}\right)$, a trajectory is built within the input space by modifying one parameter at a time $\left(x_1^{*},\dots ,{x_{i-1}^{*},x}_i^{*}\pm \Delta ,x_{i+1}^{*},\dots ,x_n^{*}\right)$ and evaluating, for each variation, the elementary effect $E{E}_i^j$ ($i$th parameter and $j$th trajectory) given by the ratio between the variation of the output solution $y$ and the variation $\Delta$ of the input:

$E{E}_i^j=\frac{y\left(x_1^{*},\dots ,{x_{i-1}^{*},x}_i^{*}+\Delta ,x_{i+1}^{*},\dots ,x_n^{*}\right)-y\left(x_1^{*},\dots ,x_i^{*},\dots ,x_n^{*}\right)}{\Delta }\text{\hspace{0.17em}or\hspace{0.17em}}E{E}_i^j=\frac{y\left(x_1^{*},\dots ,x_i^{*},\dots ,x_n^{*}\right)-y\left(x_1^{*},\dots ,{x_{i-1}^{*},x}_i^{*}-\Delta ,x_{i+1}^{*},\dots ,x_n^{*}\right)}{\Delta }.(20)$

Having iterated this procedure for a $r$ number of trajectories for each parameter $i$, the absolute value of the mean ${\mu }_i^{*}$ and the standard deviation ${\sigma }_i$ of the variations is computed, respectively, as follows:

${\mu }_i^{*}=\frac{1}{r}{\displaystyle \sum _{j=1}^r}\left|E{E}_i^j\right|,(21)$

${\sigma }_i=\sqrt{\frac{1}{r-1}{\displaystyle \sum _{j=1}^r}{\left(E{E}_i^j-{\mu }_i\right)}^2},(22)$

where ${\mu }_i=\frac{1}{r}{\displaystyle \sum _{j=1}^r}E{E}_i^j.$

These quantities provide a measure of the sensitivity of the model. High values of ${\mu }_i^{*}$ indicate that the $i$th parameter has a great influence on the output solution.

The results of the Morris method applied to our models are shown in a (${\mu }^{*}$, $\sigma$) plot (Figure 8). For the cylindrical source model, the results are in agreement with the marginal distributions of the GA solutions set (Figure 7A). The points of the plot in the lower left ($R$ and $h$) have smaller mean ${\mu }^{*}$ values, indicating that a variation in these parameters causes negligible effects on the output (Conca et al., 2016). Indeed, these parameters show a wide range of variability in the marginal distributions (Figure 7A). On the other hand, the points at the top right of the plot ($x_C,y_C$, and $d$) show larger values of the ${\mu }^{*}$, which denotes that a variation in these parameters strongly influences the output of the model (Conca et al., 2016). In fact, these parameters are well constrained as shown in the 1D marginal distributions (Figure 7A).

FIGURE 8

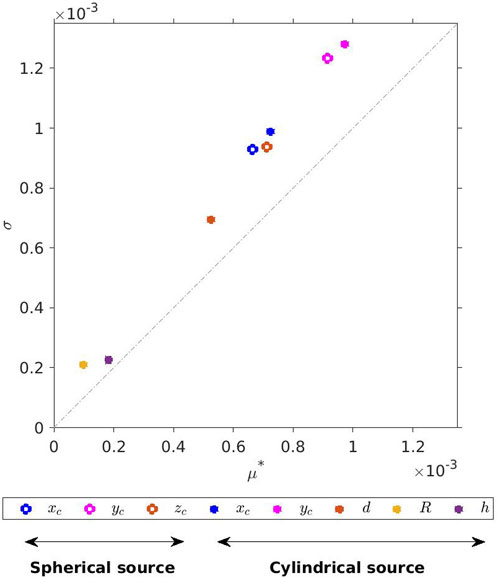
FIGURE 8. Sensitivity analysis carried out with the Morris method for the parameters of the spherical source (open dots) and cylindrical source (full dots). Higher mean values come with slightly higher uncertainty.

For the spherical source model, the mean values ${\mu }^{*}$ of the parameters do not differ significantly from each other. All the parameters are well constrained and equally concur with the solution as already seen from the inspection of the marginal distributions.

4.3 Estimates of overpressure

The thermo-poro-elastic deformation is the result of the volumetric strain variations linked to changes in pore-pressure and temperature (Eq. 4). Thermal effects can be much greater than those due to pressure (e.g., Nespoli et al., 2021; Belardinelli et al., 2022) but are usually much slower than the pore-pressure buildup (Coco et al., 2016; Currenti and Napoli, 2017). However, thermal effects may be faster when advection processes develop. In the 2021 Vulcano Island crisis, although the thermo-elastic effect could have also contributed to the deformation (temperature increase up to 50°C; INGV Report, 2022), we focused on the estimation of pore-pressure increase. Assuming that the observed deformation is driven only by the pore-pressure variation at the source, we can estimate the pressure change from the relationship between $\Delta P$ and ${\epsilon }_0$ (Eq. 4). This relationship suggests that the pressure variation also depends on the elastic properties of the rock, which are closely related to lithology, rock type, degree of fracturing, water content, depth, confining pressure, temperature, compaction, and hydrothermal alteration (Heap et al., 2014; Juncu et al., 2019; Todesco, 2021). In the literature, no data are available on the elastic properties of Vulcano rocks. For this reason, we refer to the values reported in similar volcanic environments, according to which $K_s$ generally does not exceed 30 GPa (Rinaldi et al., 2010; Todesco et al., 2010; Currenti and Napoli, 2017; Juncu et al., 2019), while $K_d$ and $\beta$ vary from ∼10⁻¹ to ∼10 GPa and from 0.5 to 1, respectively. In order to satisfy this last condition, we have chosen $K_d$ in the range between 0.1 and 15 GPa.

For the spherical source, the inversion enabled to constrain the source volume change $\Delta V_S=$ 1.07 x 10⁵ m³, from which we can derive the stress-free strain ${\epsilon }_0=\Delta V_S/V_{0_S}$ using reasonable values of the source radius. Using the end-member values of the elastic parameters and a radius ranging from 500 to 700 m, which corresponds to a volume $V_{0_S}$ between 5.2 x 10⁸ and 1.4 x 10⁹ m³, the pore-pressure change varies approximately from 0.01 MPa to 6 MPa.

For the cylindrical source, the stress-free strain ${\epsilon }_0$ is not well constrained. Solutions with larger ${\epsilon }_0$ and lower source volumes (Figure 7B) fit the observations as well (Supplementary Figure S8). However, larger ${\epsilon }_0$ values correspond to unrealistic pore-pressure changes. In addition, the optimal solution (Table 2) could require large overpressure (0.3–80 MPa for lower and higher $K_d$ values). A compromise is found by selecting those solutions whose source volume $V_{0_C}$ ranges between 5 x 10⁸ and 9.5 x 10⁸ m³. This solution leads to an increasing attenuation of the deformation at the IVCR station as the radius increases, causing similar radial displacements at the IVCR and VCSP stations. As an example, Figure 9 shows the displacements induced from a cylindrical source, with a radius of 400 m and a volume of 5 x 10⁸ m³, which undergoes a volume variation $\Delta V_C$ of 1.25 x 10⁵ m³ and a pressure change from 0.02 to 7 MPa for lower and higher $K_d$ values, respectively.

FIGURE 9

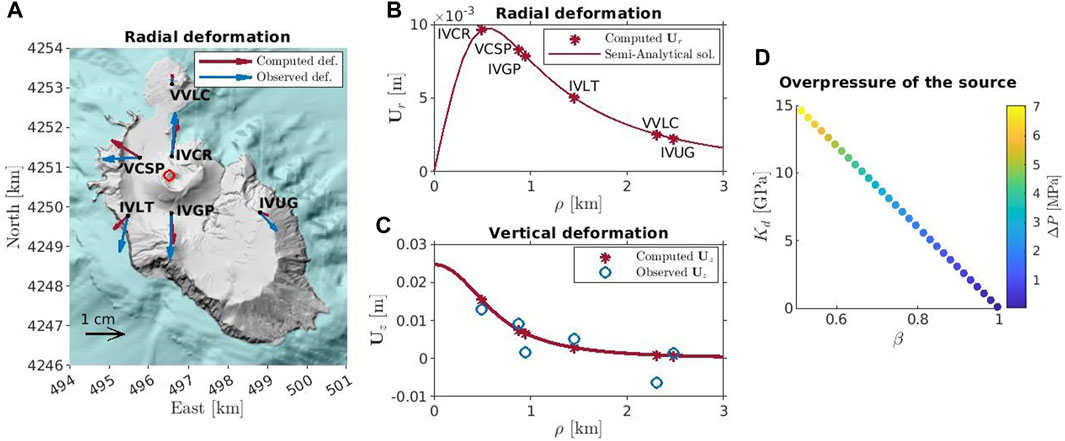
FIGURE 9. Comparison between observed and computed deformation for the cylindrical source. (A) ${\mathbf{U}}_x$ and ${\mathbf{U}}_y$ components of the radial deformation in each station; the red circle indicates the position of the source. (B) Radial deformation as a function of the radial distance of the stations from the deformation source. (C) Vertical deformation as a function of the radial distance of the stations from the source. (D) Pressure variations at the source as a function of the values of the elastic parameters. The computed deformations were calculated using the following parameters: $x_C$ = 496,517 m, $y_C$ = 4,250,787 m, $d$ = −362 m, $R$ = 400 m, $h$ = 1,000 m, and ${\epsilon }_0$ = 2.5 x 10⁻⁴.

5 Discussion and conclusion

The 2021 Vulcano crisis, as opposed to other past unrests in the last 30 years (Chiodini et al., 1992; Capasso et al., 1999; Selva et al., 2020), was marked by the occurrence of significant and persistent ground deformations at the La Fossa Cone in concomitance with the increases in both gas emissions from the soil and fumaroles temperatures in different areas of the island. On the basis of past activity (De Astis et al., 2013; Barbano et al., 2017; Selva et al., 2020), this scenario alerted the scientific community resulting in the definition of a hazard alert level corresponding to the occurrence of a phreatic event. The pore-pressure buildup at shallow depth can result in the triggering of phreatic explosions that represent one of the greater hazards occurring in active volcanic systems hosting a pervasive hydrothermal system, such as Vulcano Island (Kobayashi et al., 2018; Narita et al., 2020).

In the case of Vulcano, the island represents only the summit area of a larger volcanic edifice rising up from the seafloor. Indeed, the local population lives close to the extensive hydrothermal area that poses a significant threat. Therefore, it was essential to carefully examine the origin of the observed deformation that was indicative of a local over-pressurization of the system.

The continuous and stable radial expansion of the volcano edifice continuing until mid-October 2021, affecting the stations closer to the summit crater and rapidly decaying moving away, suggests a shallow source. The shape of the horizontal and vertical displacements implies the action of an isotropic strain source that could be linked to a spherical overpressured magmatic body (Mogi solution) or to thermo-poro-elastic strain changes. Although neither the data nor the results of modeling allow distinguishing between them, it is reasonable to hypothesize that deformation is generated by thermo-poro-elastic effects rather than by a shallow magmatic accumulation or intrusion. Moreover, considering the radial deformation pattern, we can exclude the occurrence of a dyke intrusion that should have fractured and displaced the rocks along its pathway toward the ground surface and engendered a typical “butterfly” pattern (Currenti et al., 2008). Additionally, the lack of significant volcano-tectonic (VT) seismic events and seismic swarms at shallow depths (Federico et al., 2023), which usually accompany magmatic intrusions, is a further indicator of no shallow magma migration. Indeed, the majority of the seismic events recorded during the unrest were dominated by a low-frequency content. These events, characterized by a great variety of waveforms, were composed of two main frequency bands from 0.1 to 0.2 Hz (VLP) and from 3 to 5 Hz (LP). The events were located to the northeast of La Fossa Cone at a depth between 500 and 1,500 m b.s.l. in correspondence with the hydrothermal system. Their location did not undergo variation in time, and they were interpreted as the effect of the fluid pressurization within a series of resonating fractures extending from the hydrothermal system to the surface (Currenti et al., 2023; Federico et al., 2023). Finally, no evidence of pre-existing shallow magmatic chambers that could have been replenished with fresh magma has been found from seismic tomographies (Chiarabba et al., 2004), recent magneto-telluric investigations (Isaia, personal communication), and geochemical data analysis (Aiuppa et al., 2022). Therefore, we rule out a possible involvement of shallow magma migration in driving the observed displacement and hypothesize that it was generated by the thermo-poro-elastic response of the rocks to the increase in hot fluid flow at shallow depth originating from deeper magma degassing. Using the derived thermo-poro-elastic displacement solutions, we verify whether this hypothesis agrees with the amplitude and extent of the recorded deformation.

Owing to the low number of observation points and, hence, constraints for the inversion modeling, we preferred to explore simple shaped geometry models with few parameters. The simple geometries provide a straightforward mathematical description of the displacement induced by pore-pressure and temperature changes that could be easily combined in inversion procedures at a low computational cost. Analytical and semi-analytical solutions have the advantage of providing a first estimate of the deformation source parameters. We have revised and derived solutions for the spherical and cylindrical isotropic sources to interpret the Vulcano displacement data. When the number of constraints is limited, surface displacement modeling can lead to a non-unique description of the deformation source and different combinations of parameters may fit the data as well. While the spherical source is described by only four parameters, linked to its position and volume change, which have all been well constrained, the cylindrical source is described by six parameters. Despite the low RMSE (approximately 3 mm), the increase in parameters and the lack of additional information do not allow us to better constrain them. Nonetheless, the inversion algorithm has well constrained the position and the volume variation of both deformation sources. Discrepancies between the computed and the observed displacements were found for both models mostly at the VCSP, IVUG, and IVLT stations. The COMSOL solution, which is based on a numerical FE model, showed that the topography effect cannot account for these discrepancies that could be ascribed to small-scale structures, medium heterogeneity, and non-symmetrical horizontal shape of the source (Yunjun et al., 2021). The crude simplification of the investigated models (i.e., simple geometries, constant strain changes within the source, and homogeneous medium parameters) is challenging in thermo-poro-elastic processes where the spatial distributions of pore-pressure and temperature changes are generally more complex than those described by simple spherical or cylindrical homogeneous distributions. Usually, pore-pressure and temperature changes are very sensitive to rock permeability, which strongly governs the fluid circulation in hydrothermal systems (Stissi et al., 2021). The presence of narrow permeable pathways (e.g., fractures and weak zones) may locally perturb the fluid circulation and, hence, may induce local pore-pressure or temperature changes. Discretizing the deformation source into smaller sub-sources, each with different pore-pressure and/or temperature values (Barbot, 2018; Nespoli et al., 2021), may allow the introduction of pore-pressure distributions and/or temperature changes that may better fit the data at the cost of increasing the model complexity.

The spherical solution could be representative of a confined region where local porosity and/or permeability of the porous medium could hinder fluid propagation and, hence, increase the local pore pressure. On the other hand, the long cylindrical source (1 km height) could describe the pressurization of the narrow long fluid pathway from depth toward the ground surface. Unfortunately, due to the similar data fit of spherical and cylindrical geometries, it is not possible to favor one solution over another. Moreover, we observe a challenge in constraining the size of the cylindrical source with implications in the estimates of strain changes and, hence, in pore-pressure variations. The larger the size, the smaller the strain variation and the pressure. Pressure estimates are also hampered by the lack of accurate information about material property values, which is then reflected in high ambiguity in pore-pressure estimates. Nevertheless, modeling results for both spherical and cylindrical geometries clearly point to a stress-free volume change in the order of ∼10⁵ m³. Assuming reasonable values for the source volume and material properties, pore-pressure buildup may range between 0.01 and 7 MPa. The source is located at a depth of approximately 800 m from the ground surface that falls within the depth range (0–1.5 km b.s.l.) of the hydrothermal system hypothesized by previous studies (Chiodini et al., 1992; Berrino, 2000; Alparone et al., 2010; Napoli and Currenti, 2016; Ruch et al., 2016). The constant deformation ratio among the stations also reveals that the overpressure source is spatially stationary throughout the considered period. In addition, the high spatial resolution DInSAR data (Guglielmino et al., 2022) confirms that the extent of the deformed area, approximately circular with a maximum displacement positioned in the northern sector of the cone, did not change throughout the unrest. Therefore, we can exclude the migration of the pressure source toward shallower zones of the volcanic edifice. This is supported by the lack of local and shallow ground inflation patterns in the InSAR data gathered during the unrest time span (Guglielmino et al., 2022).

The potential involvement of the hydrothermal system in the past unrest phases of Vulcano Island has been already documented (Cannata et al., 2012; Selva et al., 2020). The fast deformation rate and the concurrent increase in gas emission, characterizing the onset of the 2021 unrest, are indicative of a disequilibrium between the fluid input from the degassing of a deeper magmatic system (Aiuppa et al., 2022) and the fluid release at the surface, engendering inflation. In particular, we hypothesize that a growing fluid input sustained both source inflation and gas discharge from September to mid-October 2021. Therefore, in this period, hot fluids rose from the deeper reservoir, injected into a shallower depth, and generated a local overpressure, which produced the symmetric inflation pattern, centered in the La Fossa crater. Although the deformation stopped increasing in mid-October, gas emission still continued at a level above the background. This is an indication of a change in the response of the porous medium. Indeed, the interaction between rocks and fluid could have modified the porous medium properties by enhancing the permeability and, hence, favoring fluid release and hampering further pressure increases. Moreover, we cannot exclude a possible plastic response of the rocks.

To sum up, our deformation modeling results ruled out the action of very shallow overpressurized zones that could have triggered a phreatic eruption. We demonstrate that the development of thermo-poro-elastic models may help interpret ground displacement that provides hints on the evolution of the hydrothermal activity during volcanic crises and aids in volcano hazard assessment.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

GC and SCS conceived and conceptualized the study. RN focused on data interpretation and result discussion. SCS developed the code and performed the computations. FC analyzed the GPS time series. GC managed and administered the funding acquisition for conducting the research. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the projects Pianeta Dinamico—WUnderVul (code CUP D53J1900010001) funded by MUR (Fondo Finalizzato al rilancio degli investimenti delle amministrazioni centrali dello Stato e allo sviluppo del Paese, legge 145/2018).

Acknowledgments

The authors are grateful to the Editors NV and Valerio Acocella and the reviewers who helped improve the manuscript. The authors thank the technical team for maintenance of the Aeolian GPS permanent network at INGV-OE.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1179095/full#supplementary-material

References

Acocella, V., Di Lorenzo, R., Newhall, C., and Scandone, R. (2015). An overview of recent (1988 to 2014) caldera unrest: knowledge and perspectives. Rev. Geophys. 53 (3), 896–955. doi:10.1002/2015RG000492

CrossRef Full Text | Google Scholar

Aiuppa, A., Bitetto, M., Calabrese, S., Delle Donne, D., Lages, J., La Monica, F. P., et al. (2022). Mafic magma feeds degassing unrest at Vulcano Island, Italy. Commun. EARTH Environ. 3 (1), 255. doi:10.1038/s43247-022-00589-1

CrossRef Full Text | Google Scholar

Alparone, S., Cannata, A., Gambino, S., Gresta, S., Milluzzo, V., and Montalto, P. (2010). Time-space variation of volcano-seismic events at La Fossa (vulcano, aeolian islands, Italy): new insights into seismic sources in a hydrothermal system. Bull. Volcanol. 72, 803–816. doi:10.1007/s00445-010-0367-6

CrossRef Full Text | Google Scholar

Barbano, S., Castelli, V., and Pirrotta, C. (2017). Materiali per un catalogo di eruzioni di Vulcano e di terremoti delle isole Eolie e della Sicilia nordorientale (secc. XV-XIX). Quad. Geofis. 142. ISSN 1590-2595.

Google Scholar

Barbot, S. (2018). Deformation of a half-space from anelastic strain confined in a tetrahedral volume. Bull. Seism. Soc. Am. 108 (5A), 2687–2712. doi:10.1785/0120180058

CrossRef Full Text | Google Scholar

Battaglia, S., Gherardi, F., Gianelli, G., Leoni, L., and Origlia, F. (2007). Clay mineral reactions in an active geothermal area (Mt. Amiata, southern Tuscany, Italy). Clay Miner. 42 (3), 353–372. doi:10.1180/claymin.2007.042.3.08

CrossRef Full Text | Google Scholar

Battaglia, M., Gottsmann, J., Carbone, D., and Fernández, J. (2008). 4D volcano gravimetry. Geophysics 73, WA3–WA18. doi:10.1190/1.2977792

CrossRef Full Text | Google Scholar

Belardinelli, M. E., Bonafede, M., and Nespoli, M. (2019). Stress heterogeneities and failure mechanisms induced by temperature and pore-pressure increase in volcanic regions. Earth Planet. Sci. Lett. 525, 115765. doi:10.1016/j.epsl.2019.115765

CrossRef Full Text | Google Scholar

Belardinelli, M. E., Nespoli, M., and Bonafede, M. (2022). Stress changes caused by exsolution of magmatic fluids within an axisymmetric inclusion. Geophys. J. Int. 230 (2), 870–892. doi:10.1093/gji/ggac093

CrossRef Full Text | Google Scholar

Berrino, G. (2000). Combined gravimetry in the observation of volcanic processes in Southern Italy. J. Geodyn. 30 (3), 371–388. doi:10.1016/S0264-3707(99)00072-1

CrossRef Full Text | Google Scholar

Bertiger, W., Bar-Sever, Y. E., Dorsey, A., Haines, B., Harvey, N., Hemberger, D., et al. (2020). GipsyX/RTGx, a new tool set for space geodetic operations and research. Adv. Space Res. 66 (3), 469–489. doi:10.1016/j.asr.2020.04.015

CrossRef Full Text | Google Scholar

Blakely, R. J. (1996). Potential theory in gravity and magnetic Applications. Cambridge: Cambridge University Press, 437.

Google Scholar

Bonafede, M. (1990). Axi-symmetric deformation of a thermo-poro-elastic half-space: inflation of a magma chamber. Geophys. J. Int. 103 (2), 289–299. doi:10.1111/j.1365-246X.1990.tb01772.x

CrossRef Full Text | Google Scholar

Bonafede, M. (1991). Hot fluid migration: an efficient source of ground deformation: application to the 1982–1985 crisis at Campi Flegrei-Italy. J. Volcanol. Geotherm. Res. 48 (1-2), 187–198. doi:10.1016/0377-0273(91)90042-X

CrossRef Full Text | Google Scholar

Cannata, A., Diliberto, I. S., Alparone, S., Gambino, S., Gresta, S., Liotta, M., et al. (2012). Multiparametric approach in investigating volcano-hydrothermal systems: the case study of vulcano (aeolian islands, Italy). Pure Appl. Geophys. 169, 167–182. doi:10.1007/s00024-011-0297-z

CrossRef Full Text | Google Scholar

Capasso, G., Favara, R., Francofonte, S., and Inguaggiato, S. (1999). Chemical and isotopic variations in fumarolic discharge and thermal waters at vulcano island (aeolian islands, Italy) during 1996: evidence of resumed volcanic activity. J. Volcanol. Geotherm. Res. 88 (3), 167–175. doi:10.1016/S0377-0273(98)00111-5

CrossRef Full Text | Google Scholar

Carapezza, M., Nuccio, P. M., and Valenza, M. (1981). Genesis and evolution of the fumaroles of vulcano (aeolian islands, Italy): A geochemical model. Bull. Volcanol. 44, 547–563. doi:10.1007/BF02600585

CrossRef Full Text | Google Scholar

Carbone, D., Currenti, G., and Del Negro, C. (2008). Multiobjective genetic algorithm inversion of ground deformation and gravity changes spanning the 1981 eruption of Etna volcano. J. Geophys. Res. 113, B07406. doi:10.1029/2006JB004917

CrossRef Full Text | Google Scholar

Chiarabba, C., Pino, N. A., Ventura, G., and Vilardo, G. (2004). Structural features of the shallow plumbing system of Vulcano Island Italy. Bul.l Volcanol. 66, 477–484. doi:10.1007/s00445-003-0331-9

CrossRef Full Text | Google Scholar

Chiodini, G., Cioni, R., Falsaperla, S., Montalto, A., Guidi, M., and Marini, L. (1992). Geochemical and seismological investigations at vulcano (aeolian islands) during 1978–1989. J. Geophys. Res. 97 (B7), 11025–11032. doi:10.1029/92JB00518

CrossRef Full Text | Google Scholar

Chiodini, G., Todesco, M., Caliro, S., Del Gaudio, C., Macedonio, G., and Russo, M. (2003). Magma degassing as a trigger of bradyseismic events: the case of phlegrean fields (Italy). Geophys. Res. Lett. 30 (8). doi:10.1029/2002GL016790

CrossRef Full Text | Google Scholar

Coco, A., Gottsmann, J., Whitaker, F., Rust, A., Currenti, G., Jasim, A., et al. (2016). Numerical models for ground deformation and gravity changes during volcanic unrest: simulating the hydrothermal system dynamics of a restless caldera. Solid Earth 7 (2), 557–577. doi:10.5194/se-7-557-2016

CrossRef Full Text | Google Scholar

COMSOL (2012). Comsol Multiphysics 4,3. Stockholm: Comsol Ab.

Google Scholar

Conca, P., Currenti, G., Carapezza, G., Del Negro, C., Costanza, J., and Nicosia, G. (2016). “Multi-objective modeling of ground deformation and gravity changes of volcanic eruptions,” in Machine learning, optimization, and big data. MOD 2015. Lecture notes in computer science. Editors P. Pardalos, M. Pavone, G. Farinella, and V. Cutello (Cham: Springer), Vol 9432. doi:10.1007/978-3-319-27926-8_32

CrossRef Full Text | Google Scholar

Currenti, G. M., and Napoli, R. (2017). Learning about hydrothermal volcanic activity by modeling induced geophysical changes. Front. Earth Sci. 5 (41). doi:10.3389/feart.2017.00041

CrossRef Full Text | Google Scholar

Currenti, G., Del Negro, C., and Nunnari, G. (2005). Inverse modelling of volcanomagnetic fields using a genetic algorithm technique. Geophys. J. Int. 163 (1), 403–418. doi:10.1111/j.1365-246X.2005.02730.x

CrossRef Full Text | Google Scholar

Currenti, G., Del Negro, C., Fortuna, L., and Gangi, G. (2007). Integrated inversion of ground deformation and magnetic data at Etna volcano using a genetic algorithm technique. Ann. Geophys. 50 (1), 21–30. doi:10.4401/ag-3082

CrossRef Full Text | Google Scholar

Currenti, G., Del Negro, C., Ganci, G., and Williams, C. (2008). Static stress changes induced by the magmatic intrusions during the 2002-2003 Etna eruption. J. Geophys. Res. 113, B10206. doi:10.1029/2007JB005301

CrossRef Full Text | Google Scholar

Currenti, G., Napoli, R., Di Stefano, A., Greco, F., and Del Negro, C. (2011). 3D integrated geophysical modeling for the 2008 magma intrusion at etna: constraints on rheology and dike overpressure. Phys. Earth Planet. Inter. 168, 44–52. doi:10.1016/j.pepi.2011.01.002

CrossRef Full Text | Google Scholar

Currenti, G., Napoli, R., Coco, A., and Privitera, E. (2017). Effects of hydrothermal unrest on stress and deformation: insights from numerical modeling and application to vulcano island (Italy). Bull. Volcanol. 79, 28. doi:10.1007/s00445-017-1110-3

CrossRef Full Text | Google Scholar

Currenti, G., Allegra, M., Cannavò, F., Jousset, P., Prestifilippo, M., Napoli, R., et al. (2023). Distributed dynamic strain sensing of very long period and long period events on telecom fiber-optic cables at Vulcano, Italy. Sci. Rep. 13, 4641. doi:10.1038/s41598-023-31779-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Davies, J. H. (2003). Elastic field in a semi-infinite solid due to thermal expansion or a coherently misfitting inclusion. J. Appl. Mech. 70 (5), 655–660. doi:10.1115/1.1602481

CrossRef Full Text | Google Scholar

De Astis, G., Lucchi, F., Dellino, P., La Volpe, L., Tranne, C. A., Frezzotti, M. L., et al. (2013). Chapter 11 Geology, volcanic history and petrology of Vulcano (central Aeolian archipelago). Geol. Soc. Lond. Mem. 37, 281–349. doi:10.1144/M37.11

CrossRef Full Text | Google Scholar

Diliberto, I. S. (2017). Long-term monitoring on a closed-conduit volcano: A 25 year long time-series of temperatures recorded at La Fossa cone (vulcano island, Italy), ranging from 250 °C to 520 °C. J. Volcanol. Geotherm. Res. 346, 151–160. doi:10.1016/j.jvolgeores.2017.03.005

CrossRef Full Text | Google Scholar

Dzurisin, D. (2007). Volcano deformation – geodetic monitoring techniques. Chichester: Springer-Praxis Publishing Ltd.

Google Scholar

Federico, C., Cocina, O., Gambino, S., Paonita, A., Branca, S., Coltelli, M., et al. (2023). Inferences on the 2021 ongoing volcanic unrest at vulcano island (Italy) through a comprehensive multidisciplinary surveillance network. Remote Sens. 15, 1405. doi:10.3390/rs15051405

CrossRef Full Text | Google Scholar

Feng, K., Lu, Z., and Yang, C. (2019). Enhanced Morris method for global sensitivity analysis: good proxy of sobol’ index. Struct. Multidiscip. Optim. 59, 373–387. doi:10.1007/s00158-018-2071-7

CrossRef Full Text | Google Scholar

Fournier, N., and Chardot, L. (2012). Understanding volcano-Hydrothermal unrest from geodetic observations: insights from numerical modeling and application to white island volcano, New Zealand. JGR 117, B11208. doi:10.1029/2012JB009469

CrossRef Full Text | Google Scholar

Fung, Y. (1965). Foundations of solid mechanics. Englewood Cliffs, NJ: Prentice-Hall.

Google Scholar

Gambino, S., and Guglielmino, F. (2008). Ground deformation induced by geothermal processes: A model for La Fossa crater (vulcano island, Italy). J. Geophys. Res. 113, B07402. doi:10.1029/2007JB005016

CrossRef Full Text | Google Scholar

Goodier, J. N. (1937). “XCVII. On the integration of the thermo-elastic equations,” in The London, Edinburgh, and Dublin philosophical magazine and journal of science, series 7, 1017–1032. doi:10.1080/14786443708561872

CrossRef Full Text | Google Scholar

Guglielmino, F., Bonforte, A., and Puglisi, G. (2022). “The 2021 unrest phase of Vulcano volcano (Aeolian islands) detected by SAR, GNSS and GB-RAR,” in EGU General Assembly 2022, Vienna, Austria, 23–27 May 2022. EGU22-12183. doi:10.5194/egusphere-egu22-12183

CrossRef Full Text | Google Scholar

Harris, A., Alparone, S., Bonforte, A., Dehn, J., Gambino, S., Lodato, L., et al. (2012). Vent temperature trends at the vulcano Fossa fumarole field: the role of permeability. Bull. Volcanol. 74, 1293–1311. doi:10.1007/s00445-012-0593-1

CrossRef Full Text | Google Scholar

Heap, M. J., Baud, P., Meredith, P. G., Vinciguerra, S., and Reuschlé, T. (2014). The permeability and elastic moduli of tuff from Campi Flegrei, Italy: implications for ground deformation modelling. Solid Earth 5 (1), 25–44. doi:10.5194/se-5-25-2014

CrossRef Full Text | Google Scholar

Hemmings, B., Gottsmann, J., Whitaker, F., and Coco, A. (2016). Investigating hydrological contributions to volcano monitoring signals: A time-lapse gravity example. Geophys. J. Int. 207 (1), 259–273. doi:10.1093/gji/ggw266

CrossRef Full Text | Google Scholar

Hurwitz, S., Christiansen, L. B., and Hsieh, P. A. (2007). Hydrothermal fluid flow and deformation in large calderas: inferences from numerical simulations. J. Geophys. Res. 112, B02206. doi:10.1029/2006JB004689

CrossRef Full Text | Google Scholar

Hutnak, M., Hurwitz, S., Ingebritsen, S. E., and Hsieh, P. A. (2009). Numerical models of caldera deformation: effects of multiphase and multicomponent hydrothermal fluid flow. J. Geophys. Res. 114, B04411. doi:10.1029/2008JB006151

CrossRef Full Text | Google Scholar

Inguaggiato, S., Vita, F., Diliberto, I., Mazot, A., Calderone, L., Mastrolia, A., et al. (2022). The extensive parameters as a tool to monitoring the volcanic activity: the case study of vulcano island (Italy). Remote Sens. 14 (5), 1283. doi:10.3390/rs14051283

CrossRef Full Text | Google Scholar

INGV Report (2022). Tutti i bollettini precedenti al 2018 è possibile trovarli sul vecchio portale di sezione. Available at: https://www.ct.ingv.it/index.php/monitoraggio-e-sorveglianza/prodotti-del-monitoraggio/bollettini-settimanali-multidisciplinari.

Google Scholar

Jaeger, J., Cook, N., and Zimmerman, R. (2007). Fundamentals of rock mechanics 4th Edn. Oxford: Blackwell Publishing.

Google Scholar

Juncu, D., Árnadóttir, Th., Geirsson, H., and Gunnarsson, G. (2019). The effect of fluid compressibility and elastic rock properties on deformation of geothermal reservoirs. Geophys. J. Int. 217 (1), 122–134. doi:10.1093/gji/ggz011

CrossRef Full Text | Google Scholar

Keller, J. (1980). The island of Vulcano. Rend. Soc. Ital. Mineral. Petrol. 36, 369–414.

Google Scholar

Kobayashi, T., Morishita, Y., and Munekane, H. (2018). First detection of precursory ground inflation of a small phreatic eruption by InSAR. Earth Planet. Sci. Lett. 491, 244–254. doi:10.1016/j.epsl.2018.03.041

CrossRef Full Text | Google Scholar

Liu, D., Li, L., Rostami-Hodjegan, A., Bois, F. Y., and Jamei, M. (2020). Considerations and caveats when applying global sensitivity analysis methods to physiologically based pharmacokinetic models. AAPS J. 22, 93. doi:10.1208/s12248-020-00480-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, Z., Masterlark, T., Power, J., Dzurisin, D., and Wicks, C. (2002). Subsidence at kiska volcano, western aleutians, detected by satellite radar interferometry. Geophys. Res. Lett. 29 (18), 2-1–2-4. doi:10.1029/2002GL014948

CrossRef Full Text | Google Scholar

Mantiloni, L., Nespoli, M., Belardinelli, M. E., and Bonafede, M. (2020). Deformation and stress in hydrothermal regions: the case of a disk-shaped inclusion in a half-space. J. Volcanol. Geotherm. Res. 403, 107011. doi:10.1016/j.jvolgeores.2020.107011

CrossRef Full Text | Google Scholar

McTigue, D. F. (1986). Thermoelastic response of fluid-saturated porous rock. J. Geophys. Res. Solid Earth 91 (B9), 9533–9542. doi:10.1029/JB091iB09p09533

CrossRef Full Text | Google Scholar

Miller, C. A., Le Mével, H., Currenti, G., Williams-Jones, G., and Tikoff, B. (2017). Microgravity changes at the laguna del maule volcanic field: magma-induced stress changes facilitate mass addition. J. Geophys. Res. 122 (4), 3179–3196. doi:10.1002/2017JB014048

CrossRef Full Text | Google Scholar

Milluzzo, V., Cannata, A., Alparone, S., Gambino, S., Hellweg, M., Montalto, P., et al. (2010). Tornillos at vulcano: clues to the dynamics of the hydrothermal system. J. Volcanol. Geotherm. Res. 198 (3–4), 377–393. doi:10.1016/j.jvolgeores.2010.09.022

CrossRef Full Text | Google Scholar

Mindlin, R. D., and Cheng, D. H. (1950). Nuclei of strain in the semi-infinite solid. J. Appl. Phys. 21 (9), 926–930. doi:10.1063/1.1699785

CrossRef Full Text | Google Scholar

Mindlin, R. D. (1936). Force at a point in the interior of a semi-infinite solid. Physics 7 (5), 195–202. doi:10.1063/1.1745385

CrossRef Full Text | Google Scholar

Mogi, K. (1958). Relation between eruptions of various volcanoes and the deformations of the ground surfaces around them. Bull. Earthq. Res. Inst. 36, 99–134.

Google Scholar

Morris, M. D. (1991). Factorial sampling plans for preliminary computational experiments. Technometrics 33 (2), 161–174. doi:10.1080/00401706.1991.10484804

CrossRef Full Text | Google Scholar

Na, S. H., Rim, H., Shin, Y. H., Lim, M., and Park, Y. S. (2015). Calculation of gravity due to a vertical cylinder using a spherical harmonic series and numerical integration. Explor. Geophys. 46 (4), 381–386. doi:10.1071/EG14123

CrossRef Full Text | Google Scholar

Napoli, R., and Currenti, G. (2016). Reconstructing the Vulcano Island evolution from 3D modeling of magnetic signatures. J. Volcanol. Geother. Res. 320, 40–49. doi:10.1016/j.jvolgeores.2016.04.011

CrossRef Full Text | Google Scholar

Napoli, R., Currenti, G., Del Negro, C., Greco, F., and Scandura, D. (2008). Volcanomagnetic evidence of the magmatic intrusion on 13th May 2008 Etnaeruption. Geophys. Res. Lett. 35, L22301. doi:10.1029/2008GL035350

CrossRef Full Text | Google Scholar

Napoli, R., Currenti, G., Del Negro, C., Di Stefano, A., Greco, F., and Boschi, E. (2011). Magnetic features of the magmatic intrusion that occurred in the 2007 eruption at Stromboli Island (Italy). Bull. Volcanol. 73, 1311–1322. doi:10.1007/s00445-011-0473-0

CrossRef Full Text | Google Scholar

Narita, S., Ozawa, T., Aoki, Y., Shimada, M., Furuya, M., Takada, Y., et al. (2020). Precursory ground deformation of the 2018 phreatic eruption on Iwo-Yama volcano, revealed by four-dimensional joint analysis of airborne and spaceborne InSAR. Earth, Planets Space 72, 145. doi:10.1186/s40623-020-01280-5

CrossRef Full Text | Google Scholar

Nespoli, M., Belardinelli, M. E., and Bonafede, M. (2021). Stress and deformation induced in layered media by cylindrical thermo-poro-elastic sources: an application to Campi Flegrei (Italy). J. Volc. Geotherm. Res. 415, 107269. doi:10.1016/j.jvolgeores.2021.107269

CrossRef Full Text | Google Scholar

Nespoli, M., Belardinelli, M. E., Cal, M., Tramelli, A., and Bonafede, M. (2022). Deformation induced by distributions of single forces in a layered half-space: EFGRN/EFCMP. Comput. Geosci. 164, 105136. doi:10.1016/j.cageo.2022.105136

CrossRef Full Text | Google Scholar

Newhall, C. G., and Dzurisin, D. (1988). Historical unrest at large calderas of the world. Bullettin 1855. doi:10.3133/b1855

CrossRef Full Text | Google Scholar

Phillipson, G., Sobradelo, R., and Gottsmann, J. (2013). Global volcanic unrest in the 21st century: an analysis of the first decade. J. Volcanol. Geotherm. Res. 264, 183–196. doi:10.1016/j.jvolgeores.2013.08.004

CrossRef Full Text | Google Scholar

Rinaldi, A. P., Todesco, M., and Bonafede, M. (2010). Hydrothermal instability and ground displacement at the Campi Flegrei caldera. Phys. Earth Planet. Interiors 178 (3-4), 155–161. doi:10.1016/j.pepi.2009.09.005

CrossRef Full Text | Google Scholar

Rinaldi, A. P., Todesco, M., Vandemeulebrouck, J., Revil, A., and Bonafede, M. (2011). Electrical conductivity, ground displacement, gravity changes, and gas flow at solfatara crater (Campi Flegrei caldera, Italy): results from numerical modeling. J. Volcanol. Geother. Res. 207 (3-4), 93–105. doi:10.1016/j.jvolgeores.2011.07.008

CrossRef Full Text | Google Scholar

Ruch, J., Vezzoli, L., De Rosa, R., Di Lorenzo, R., and Acocella, V. (2016). Magmatic control along a strike-slip volcanic arc: the central aeolian arc (Italy). Tectonics 35 (2), 407–424. doi:10.1002/2015TC004060

CrossRef Full Text | Google Scholar

Sambridge, M. (1999). Geophysical inversion with a neighbourhood algorithm: II. Appraising the ensemble. Geophys. J. Int. 138 (3), 727–746. doi:10.1046/j.1365-246x.1999.00900.x

CrossRef Full Text | Google Scholar

Selva, J., Bonadonna, C., Branca, S., De Astis, G., Gambino, S., Paonita, A., et al. (2020). Multiple hazards and paths to eruptions: A review of the volcanic system of vulcano (aeolian islands, Italy). Earth Sci. Rev. 207, 103186. doi:10.1016/j.earscirev.2020.103186

CrossRef Full Text | Google Scholar

Shapiro, S. A. (2015). Fluid-induced seismicity. Cambridge University Press. doi:10.1017/CBO9781139051132

CrossRef Full Text | Google Scholar

Sternberg, E., and McDowell, E. L. (1957). On the steady-state thermoelastic problem for the half-space. Qu. Appl. Math. 14, 381.

CrossRef Full Text | Google Scholar

Stissi, S. C., Napoli, R., Currenti, G., Afanasyev, A., and Montegrossi, G. (2021). Influence of permeability on the hydrothermal system at vulcano island (Italy): inferences from numerical simulations. Earth, Planets Space 73, 179. doi:10.1186/s40623-021-01515-z

CrossRef Full Text | Google Scholar

Telford, W. M., Geldart, L. P., Sheriff, R. E., and Keys, D. A. (1981). Applied geophysics. Cambridge, New York, U.S.A.

Google Scholar

Tiampo, K. F., Rundle, J. B., Fernandez, J., and Langbein, J. O. (2000). Spherical and ellipsoidal volcanic sources at Long Valley caldera, California, using a genetic algorithm inversion technique. J. Volcan. Geotherm. Res. 102 (3-4), 189–206. doi:10.1016/S0377-0273(00)00185-2

CrossRef Full Text | Google Scholar

Todesco, M., Rinaldi, A. P., and Bonafede, M. (2010). Modeling of unrest signals in heterogeneous hydrothermal systems. J. Geophys. Res. 115, B09213. doi:10.1029/2010JB007474

CrossRef Full Text | Google Scholar

Todesco, M. (2021). Caldera’s breathing: poroelastic ground deformation at Campi Flegrei (Italy). Front. Earth Sci. 9, 70266. doi:10.3389/feart.2021.702665

CrossRef Full Text | Google Scholar

Troiano, A., Di Giuseppe, M., Petrillo, Z., Troise, C., and De Natale, G. (2011). Ground deformation at calderas driven by fluid injection: modelling unrest episodes at Campi Flegrei (Italy): ground deformation driven by fluid injection. Geophys. J. Int. 187 (2), 833–847. doi:10.1111/j.1365-246X.2011.05149.x

CrossRef Full Text | Google Scholar

Wang, H. F. (2000). Theory of linear poroelasticity with Applications to Geomechanics and hydrogeology. Princeton University Press.

Google Scholar

Yunjun, Z., Amelung, F., and Aoki, Y. (2021). Imaging the hydrothermal system of kirishima volcanic complex with L-band InSAR time series. Geophys. Res. Lett. 48 (11), e2021GL092879. doi:10.1029/2021GL092879

CrossRef Full Text | Google Scholar