Strain-based forward modeling and inversion of seismic moment tensors using distributed acoustic sensing (DAS) observations

This study used a waveform inversion of distributed acoustic sensing (DAS) data, acquired in two horizontal monitoring wells, to estimate the moment tensor (MT) of two induced microearthquakes. An analytical forward model was developed to simulate far-field tangential strain generated by an MT source in a homogeneous and anisotropic medium, averaged over the gauge length along a fiber of arbitrary orientation. To prepare the data for inversion, secondary scattered waves were removed from the field observations, using f-k filtering and time-windowing. The modeled and observed primary arrivals were aligned using a cut-and-paste approach. The MT parameters were inverted via a least-squares approach, and their uncertainties were determined through bootstrap analysis. Using simulated data with additive noise derived from the field data and the same fiber configuration as the monitoring wells, the inversion method adequately resolved the MT. Despite the assumption of Gaussian noise, which underlies the least-squares inversion approach, the method was robust in the presence of heavy-tailed noise observed in field data. When the inversion was applied to field data, independent inversion results using P-waves, S-waves, and both waves together yielded results that were consistent between the two events and for different wave types. The agreement of the inversion results for two events resulting from the same stress field illustrated the reliability of the method. The uncertainties of the MT parameters were small enough to make the inversion method useful for geophysical interpretation. The variance reduction obtained from the data predicted for the most probable MT was satisfying, even though the polarity of the P-waves was not always correctly reproduced.

1 Introduction

Anthropogenic earthquakes are a worldwide phenomenon associated with oil and gas production, geothermal projects, carbon capture and storage, and other industrial processes (Ellsworth, 2013; Atkinson et al., 2016). In Canada, induced earthquakes have been associated with a small fraction of hydraulic fracturing operations, including those in the Duvernay and Montney plays. In the Montney of northern British Columbia, significant numbers and magnitudes (M_w) of events have been observed, including an M_w > 4 earthquake sequence in 2018. The occurrence of these events has caused many challenges to regulators, operators, and residents in the area. Nonetheless, the physical processes that lead to the activation of existing faults due to hydraulic fracturing remain poorly understood in this area. This lack of knowledge makes it difficult to implement a meaningful regulatory framework.

Distributed acoustic sensing (DAS) systems consist of optical fiber connected to an interrogator unit, which emits a laser pulse into the fiber and records Rayleigh-backscattered light on a photonic sensor (Parker et al., 2014). Changes in phase due to the fiber undergoing deformation under seismic strain make this strain measurable. Thus, DAS gives access to a different observable quantity to characterize the seismic wavefield compared to displacement or particle velocity provided by more traditional methods. It also offers an almost continuous sampling in space and time, measuring strain over kilometers with a resolution of a few meters and with a large frequency band, from $\sim 1$ Hz to $\sim 10$ kHz (Daley et al., 2013). In addition, the sensor only consists in a commercial optic fiber, making it cost-effective and easy to deploy without modifying existing boreholes and taking advantage of previous installations. All these advantages have led to a large variety of applications, including CO₂ storage surveys (Daley et al., 2013), ambient noise interferometry (Dou et al., 2017), regional seismometry (Lindsey et al., 2017), microseismics (Karrenbach et al., 2017), and induced seismicity (Lellouch et al., 2021). In the last context, DAS deployed near the injection well provides closer proximity to the source than surface geophones. The main limitation of DAS is that instead of providing a three-component measurement, as seismometers, it only measures strain coaxial to the optic fiber, which is one component.

The seismic source can be described as a dislocation propagating at a finite speed over an extended surface (e.g., Burridge and Knopoff, 1964). However, in the far field, the source can be approximated by a point whose energy is released by six force-couples following an unknown function of time. This source parametrization is known as the centroid moment tensor (CMT) and can be simplified into the moment tensor (MT) if the position and depth of the point source are assumed to be known. The inversion of the MT is a linear problem that can be solved using a linear least-squares approach in either the time or in frequency domains (Jost and Herrmann, 1989). Once the position of the source and the MT are separately inverted, they can be used as initial solutions that are perturbated together in an iterative procedure to solve the non-linear problem of the CMT inversion (Dziewonski et al., 1981). This method has been automated and is routinely used to create the Global CMT catalog (Ekström et al., 2012). The non-linear problem of CMT inversion can also be solved using Bayesian inference (Wéber, 2006; Stähler and Sigloch, 2014), which is an efficient way to obtain the uncertainty of the inverted parameters and the covariance of the data. This method has led to the development of the ISOLA software (Vackář et al., 2017), based on waveform inversion, and BEAT (Vasyura-Bathke et al., 2020), which can take advantage of seismic and geodetic data.

Although the measurement of a single component of strain (rate) rather than 3C particle velocity or displacement introduces some complications, progress has been made toward full MT inversion of DAS data. With field data from a single linear fiber, a microseismic source cannot be localized with a unique position; nevertheless, a classification based on amplitude analysis and polarity can be applied to obtain information on the nodal planes (Cole et al., 2018). Using simulated data produced by an analytical model, the resolvability of the MT for compressional waves (P-waves), shear waves (S-waves), and a variable number of non-coplanar wells has been studied (Vera Rodriguez and Wuestefeld, 2020). In simulated data produced by ray tracing, the characteristics of S-waves measured by a single fiber provide additional constraints on the position of the source, whereas the polarity reversals in P- and S-waves help constrain the fault plans (Baird et al., 2020). In data produced by a one-component sensor in a laboratory experiment, machine learning and waveform fitting MT solutions showed discrepancies mainly localized in the azimuthal direction (Vera Rodriguez and Myklebust, 2022), which cannot be resolved with only one fiber. Most of these studies focused on the information that could be extracted from a single fiber. This is probably the most widely applicable case in an industrial context, since operational constraints do not necessarily allow for multiple fibers; however, a full inversion of the MT is not achievable in this configuration.

This paper illustrated the full MT inversion of field data acquired by two DAS fibers deployed in the Montney Formation. Our method was applied to two induced seismic events that occurred within 1 h and 100 m away from each other. For the calculation of the Green functions used in the inversion, while avoiding the inaccuracies linked to the conversion of strain data into displacement data, and those associated with the spatial differentiation of simulated displacement to obtain strain, we designed an analytical forward model to predict the far-field terms of the strain generated in a homogeneous isotropic medium by an MT along a fiber of arbitrary geometry (Section 2.1). The field data were filtered to remove reflections and time-windowed to remove secondary arrivals (Section 2.3). Only the first arrivals of the P- and S-waves were kept, as they best compared with the arrivals predicted by the forward model, with very simplified assumptions. The difference in arrival times between field data and simulated data was measured using cross-correlation, and the latter was time-shifted to the arrival time of the field data. This procedure was applied to produce the Green functions for the six independent components of the MT, for the two centroid solutions for the two events of interest. With the assumption of no volume change, the least-squares solution provided the linear combination of Green functions that best approximated the field data. The uncertainties of the inverted parameters were determined through bootstrap analysis (Section 2.4). This method was first validated using synthetic data produced with the forward model. It is possible to resolve the MT, even if the data are polluted with the non-Gaussian noise observed in field data. The MT error increased with the decreasing signal-to-noise ratio (SNR) but remained reasonable for the SNR of the events of interest.

The inversion method was then applied to the field data. Small differences were observed between the inversion of P-waves and the inversion of S-waves, with the inversion of both P- and S-waves almost identical to the last. The three types of inversion, however, remained in relatively good agreement. The important similarity between the MT inverted for the two events of interest justified our confidence in the method. The uncertainties were small enough to encourage future geological interpretation.

2 Materials and methods

2.1 Forward modeling of strain

The far-field terms (i.e., terms with an amplitude that decays as 1/r) of the displacement generated along the direction i in an isotropic homogeneous medium of density ρ, P-wave velocity α, an S-wave velocity β, at a distance r from a seismic point source characterized by moment tensor M, is given at any time t by $u_j^P$ for P-waves and $u_j^S$ for S-waves (Aki and Richards, 2009):

$\begin{array}{cc}\hfill u_i^P& =\frac{1}{4\pi \rho {\alpha }^3}\frac{m{\gamma }_i}{r}{s}_t\left(t-r/\alpha \right),\hfill \\ \hfill \text{and\hspace{0.17em}}{u}_j^S& =-\frac{1}{4\pi \rho {\beta }^3}\frac{m{\gamma }_i-{\gamma }_i^{\prime }}{r}{s}_t\left(t-r/\beta \right),\hfill \end{array}(1)$

where s_t is the far-field source time function, γ_i is the ith component of the unit vector pointing from the source to the point where strain is measured, m = γ_pM_pqγ_q, and ${\gamma }_i^{\prime }={\gamma }_p{M}_{pi}$. Note that Einstein summation over p and q is applied.

Equation 1 is used to derive the far-field terms of the strain generated by a seismic source in a homogeneous medium (Eaid, 2022). The contribution of P-waves to the strain exerted over direction i by direction j is

${ϵ}_{ij}^P=-\frac{1}{4\pi \rho }\frac{m{\gamma }_i{\gamma }_j}{{\alpha }^{4}r}{\dot{s}}_t\left(t-r/\alpha \right).(2)$

Similarly, the contribution ${ϵ}_{ij}^S$ for S-waves is

${ϵ}_{ij}^S=\frac{1}{4\pi \rho }\frac{m{\gamma }_i{\gamma }_j-{\mathrm{\Gamma }}_{ij}}{{\beta }^{4}r}{\dot{s}}_t\left(t-r/\beta \right),(3)$

where ${\mathrm{\Gamma }}_{ij}=({\gamma }_i{\gamma }_j^{\prime }+{\gamma }_i^{\prime }{\gamma }_j)/2$. Once the components ϵ_ij of the strain tensor are obtained by summing the contributions of P- and S-waves, the tangential strain ϵ_tt(s) measured by DAS along a fiber at an arclength s can be derived as follows. Assuming a constant strain over the gauge length G_L (Eaid, 2022) gives

$\begin{array}{ll}\hfill {ϵ}_{tt}\left(s\right)& =\frac{1}{G_L}\left({ϵ}_{xx}{\int }_{-G_L/2}^{G_L/2}{T}_x{\left(u\right)}^2\mathrm{d}u+2{ϵ}_{xy}{\int }_{-G_L/2}^{G_L/2}{T}_x\right.\times \left(u\right)T_y\left(u\right)\mathrm{d}u\hfill \\ \hfill & +2{ϵ}_{xz}{\int }_{-G_L/2}^{G_L/2}{T}_x\left(u\right)T_z\left(u\right)\mathrm{d}u+{ϵ}_{yy}{\int }_{-G_L/2}^{G_L/2}{T}_y{\left(u\right)}^2\mathrm{d}u\hfill \\ \hfill & +2{ϵ}_{yz}{\int }_{-G_L/2}^{G_L/2}{T}_y\left(u\right)T_z\left(u\right)\mathrm{d}u\left.+{ϵ}_{zz}{\int }_{-G_L/2}^{G_L/2}{T}_z{\left(u\right)}^2\mathrm{d}u\right),\hfill \end{array}(4)$

where T_x, T_y, and T_z are the three components of the unit vector $\widehat{\mathbf{T}}$ tangential to the fiber. A fiber whose position is known with finite precision can be approximated by multiple linear segments. If the lengths of these segments are larger than half the gauge length, it is convenient to break the integrals in Equation (4) into two halves: one between −G_L/2 and 0 and one between 0 and G_L/2. Over these two halves, $\widehat{\mathbf{T}}$ can be considered constant, and for the strain ${ϵ}_{tt}^i$ measured at the ith point along the fiber, Equation 4 simplifies to

$\begin{array}{ll}\hfill {ϵ}_{tt}^i& =\frac{1}{2}\left[\left(T_{i-1,x}^2+T_{i,x}^2\right){ϵ}_{xx}+\left(T_{i-1,y}^2+T_{i,y}^2\right){ϵ}_{yy}\right.\left.+\left(T_{i-1,z}^2+T_{i,z}^2\right){ϵ}_{zz}\right]\hfill \\ \hfill & +\left(T_{i-1,x}{T}_{i-1,y}+T_{i,x}{T}_{i,y}\right){ϵ}_{xy}+\left(T_{i-1,x}{T}_{i-1,z}+T_{i,x}{T}_{i,z}\right){ϵ}_{xz}\hfill \\ \hfill & +\left(T_{i-1,y}{T}_{i-1,z}\right.\left.+T_{i,y}{T}_{i,z}\right){ϵ}_{yz},\hfill \end{array}(5)$

where T_i,x, T_i,y, and T_i,z are the three components of the unit vector pointing from the ith to the (i + 1)th point of the fiber.

To calculate the strain at the ith point of the fiber, Equations 2, 3 are applied to obtain the six components of the strain field. By means of the vector pointing from the ith to the (i + 1)th point of the fiber and of the vector pointing from the (i − 1)th to the ith point of the fiber, the six components of the strain field can be projected to create the tangential strain at the ith point of the fiber, according to Equation 5.

2.2 Data provenance

The DAS data considered in this study were acquired on three fibers with a 4 m gauge length and a 2000 Hz sampling frequency located in two horizontal wells (referred to as H and J) and one vertical well (referred to as M) within the Montney Formation, British Columbia, Canada. The three wells are shown in Figure 1, in addition to the location of the two events of interest, Event 1 and Event 2. These microseismic events occurred at 1 h intervals within a radius of $\sim 100$ m after stimulation in an adjacent well (not shown). The sources are located based on the DAS data, ray tracing, and grid search (Ma et al., 2023). A downhole three-component geophone array in well H, operating concurrently with the DAS acquisition system was utilized to estimate magnitudes based on the Brune model (Brune, 1970). The estimated moment magnitudes were −0.8 (Event 1) and −0.5 (Event 2). Data from the three wells were used to locate the source with an uncertainty of ±20 m, but only data from the two horizontal wells H and J were used in MT inversion. It would have been impossible to approximate the data from a vertical well with a forward model assuming a homogeneous medium.

FIGURE 1

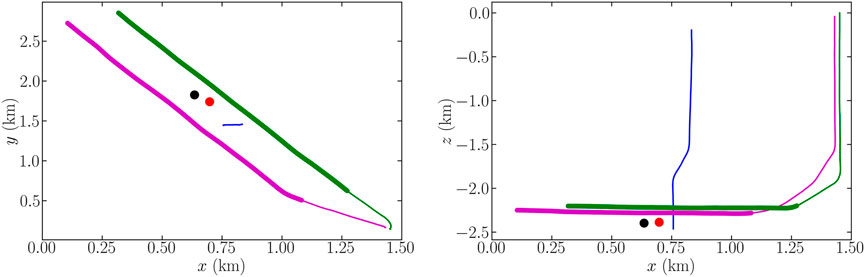
FIGURE 1. Geometry of wells H (blue), J (green), and M (cyan) and the position of the source of Events 1 (red) and 2 (black). The channels of wells H and J used in the inversion are emphasized (thick lines).

2.3 Data processing

The simple forward model presented in Section 2.1 can only predict strain propagating in isotropic homogeneous media. However, the Montney Formation shows numerous reflections from lithographic boundaries and fractures (Ma et al., 2022). Therefore, we applied data processing to select the direct arrivals of the P- and S-waves, enabling the quantitative comparison between observed and predicted data, which is crucial for the inversion.

After conversion from phase to strain, we removed constant bias, spikes, and system noise. Then, data were bandpass-filtered between 10 and 150 Hz. Figure 2A shows the strain measured for Event 1 along well H after this pre-processing. The successive arrivals of the P- and S-waves are clearly visible but are followed by secondary arrivals due to reflections from the horizontal layers of the Montney Formation (Karrenbach et al., 2017). In addition, where the primary and secondary arrivals cross fault planes, they generate reflected waves that propagate in a direction opposite to that of the direct waves, which makes them noticeable in a time–distance diagram (Ma et al., 2022; Staněk et al., 2022). To the right of the apex, the first arrivals propagated rightward and leftward to the left of the apex. Hence, it was straightforward to remove reflected waves by using filtering in the wavenumber–frequency domain to filter out waves propagating leftward on the right of the apex and rightward on the left of the apex. In this process, the position of the apex was defined manually. Noise with wavelengths <24 m was also filtered out. Figure 2B shows the data after filtering in the wavenumber–frequency domain. Secondary arrivals were removed by time-windowing, zero-padding the data above and below hyperbolas parallel to the direct arrivals. Finally, channels with a poor SNR, particularly around and at a large distance from the apex, were muted. Figure 2C shows the final data used for inversion.

FIGURE 2

FIGURE 2. Strain measured during Event 1 along well H: pre-processed data (A), data after filtering in the wavenumber–frequency domain (B), and data after time-windowing and muting of channels with poor SNR (C).

To illustrate the ability of the forward model to predict useful data, we simulated the strain generated along wells H, in a medium with a density ρ = 2,650 kg m⁻³, P-wave velocity α = 5.1 km s⁻¹, and S-wave velocity β = 3.5 km s⁻¹ by a source at the location predicted for Event 1. The environmental parameters were based on observations in the Montney Formation at the depth of the wells. The source is characterized by a double-couple moment tensor

$\mathbf{M}=\frac{1}{\sqrt{2}}\left(\begin{array}{ccc}\hfill -M_0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill M_0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),(6)$

with M₀ = 7.08 × 10⁷ Nm to mimic the moment magnitude of M_w = −0.8 for Event 1. To match the observed data, we used the first derivative of a Gaussian as a far-field source time function

${\dot{s}}_t\left(t-r/c\right)=\left(t-r/c\right){\mathrm{e}}^{-{\pi }^2{f}^2{\left(t-r/c\right)}^2},(7)$

where c = α or β, depending on the consideration of P- or S-waves, and f is the dominant frequency of the signal. We used this source time function for the remainder of the present study. The frequency f was chosen for each event, well, and type of wave by generating simulated data for various frequencies between 75 and 115 Hz. In the frequency–wavenumber domain, the simulated data were then summed along the wavenumber axis to create an aggregated spectrum. The coefficient of determination for this aggregated spectrum and the coefficient of determination created from observed data were finally computed (Figure 3). The frequency with the highest coefficient of determination for each event, well, and type of wave was kept as the frequency for producing simulated data thereafter (Table 1). The chosen frequencies were higher for P-waves than for S-waves, which may reflect higher inelastic attenuation on S-waves than on P-waves. For this first example, f = 100 Hz.

FIGURE 3

FIGURE 3. Coefficients of determination of the regression between the aggregated spectra of the observed and simulated data for various frequencies. Blue: P-waves; red: S-waves.

TABLE 1

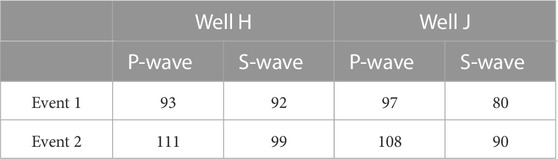
TABLE 1. Frequencies used to calculate the simulated data for two seismic events, two wells, and P- and S-waves.

Figure 4A shows the strain simulated along well H with the forward model using the previous environmental parameters. The first obvious difference compared to the observed data (Figure 2) is the polarity of the signals. The double-couple source in equation 6 likely differs from the actual moment tensor, but only inversion can provide a better approximation. Another difference is that the strain amplitudes were up to 3.70 × 10⁻¹⁰ for the predicted data, but only 1.51 × 10⁻¹⁰ for the observed data. This result indicated that the magnitude estimated from geophone data was likely too high. Despite these differences in polarity and amplitudes, the predicted data correctly represented the direct arrivals of the P- and S-waves as two successive parabolas and their general appearance in the time–distance diagram. However, small differences remained in the arrival times, which are likely due to errors in the source position, inhomogeneity, and/or anisotropy in the medium.

FIGURE 4

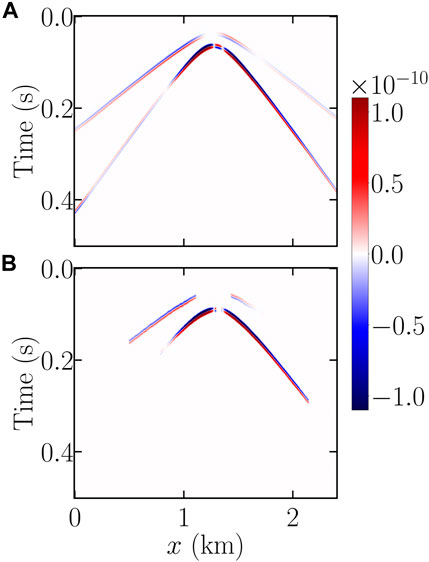
FIGURE 4. Strain along well H simulated for Event 1 using the forward model: output of the simulation (A) and after time-shift to match the observed arrivals (B). The color scale is saturated to help visualize the P-waves.

These arrival-time differences can cause erroneous inversion results. To overcome this issue, we shifted the predicted traces (Figure 4A) based on the maximum cross-correlation between the absolute values of the predicted and the processed observed data, where only primary arrivals of the P- and S-waves were conserved (Figure 2A). The lags used in this procedure are shown in Figure 5 for the two events and two wells. This approach was similar to the well-known cut-and-paste method used in waveform inversion (Zhu and Helmberger, 1996). Its advantage is that it makes inversion insensitive to inaccuracies in arrival times when applying a forward model with homogeneous velocities to the multi-layered Montney Formation. Previously muted channels were also muted in the predicted data.

FIGURE 5

FIGURE 5. Lags between the arrivals of simulated and observed P-waves (blue) and S-waves (red).

2.4 Inversion method

Herein, we present the results for the inversion of the strain data measured along wells H and J for moment tensors of the two events. The forward model (Section 2.1) generated the six independent Green functions for the inversion. The Green functions were calculated in the same way as the predicted data in Section 2.3 with identical environmental parameters and source time function. However, the six independent components of the moment tensor were chosen instead of the moment tensor shown in Equation 6. In addition, the centroids were the two event locations. Run on one core of an AMD Ryzen 7 5800X 8-Core 4.4 GHz processor, the calculation of the six Green functions along one well required 0.37 s to complete. The Green functions were time-shifted according to Section 2.3. Our hypothesis was that the simplified forward model presented in Section 2.1 could correctly predict the polarity and amplitude of the primary arrivals of the P- and S-waves, although it was unable to reproduce their arrival times or the complex secondary arrivals. This approach also supposed that the paths between the seismic sources and the fibers were short enough for ignoring the effects of inelastic attenuation and wave dispersion.

Once the Green functions are computed, the moment tensor can be inverted, taking the least-squares solution of the linear matrix equation Am = d, where d is a vector of observation data of length N, A is a 6 × N matrix that contains the Green functions, and m is a vector of length 6 containing the moment tensor parameters.

To quantify parameter uncertainties, we applied the bootstrap method (Efron and Tibshirani, 1986; Tichelaar and Ruff, 1989). For this purpose, 225 of the 300 channels available after data processing were selected randomly, and the least-squares solution was computed. This process was repeated 10,000 times through a sampling scheme with replacement where each of the 300 channels had the same probability of being sampled. Taking statistical inferences from the 10,000 samples provided uncertainty estimates. Run on one core of an AMD Ryzen 7 5800X 8-Core 4.4 GHz processor, the bootstrap analysis required 150 s to complete.

We present the results in terms of the moment tensor parametrization proposed by Tape and Tape (2012). In this Lune representation, the moment tensor of unit magnitude is characterized by the five parameters of strike angle, slip angle, dip angle, latitude u that gives the amount of volume change, and longitude v that describes the mechanism on a scale from double-couple to positive or negative compensated linear vector dipole (CLVD). A pure isotropic explosion yields u = 0, and an absence of volume change corresponds to u = 3π/8 ≃ 1.178. The longitude v is equal to 0 for a pure double-couple, equal to −1/3 for a pure negative CLVD, and equal to +1/3 for a pure positive CLVD.

3 Results

3.1 Results for the simulated data

First, we present inversion results for noisy simulated data generated using the forward model and a known moment tensor. The noise was taken from DAS observations in the two wells during a period of relative quiescence. The observed distribution of the absolute value of the seismic noise along well H is shown in Figure 6A. It is clearly heavy-tailed, as the best fit obtained with a Gaussian distribution underestimates the probability of the largest events. A heavier-tailed distribution is the Student’s t-distribution

$f\left(x\right)=\frac{\mathrm{\Gamma }\left(\left(\nu +1\right)/2\right)}{\sqrt{\pi \nu }\mathrm{\Gamma }\left(\nu /2\right)}{\left(1+{\left(x/b\right)}^2/\nu \right)}^{-\left(\nu +1\right)/2},(8)$

where Γ is the gamma function, ν is the number of degrees of freedom, and b is the scale parameter. We obtained a better agreement between the noise and the Student’s t distribution with parameters ν = 6.54 and b = 5.1 × 10⁻¹¹ than for a Gaussian distribution. For a sample of the length used for the inversion (0.5 s long, sampled at 2000 Hz, and for 300 channels, resulting in 3 × 10⁵ data), the Kolmogorov–Smirnov test with a threshold p-value of 0.05 failed to reject the Student’s t-distribution (p = 0.833). The p-value started dropping below 0.05 for samples $>6\times 10^6$ data points. For a sample of 3.6 × 10⁷ data points (1 of data), the observed distribution appeared less heavy-tailed than the best t-Student’s fit (Figure 6B). Nonetheless, the Student’s t-distribution was a closer match than a Gaussian distribution.

FIGURE 6

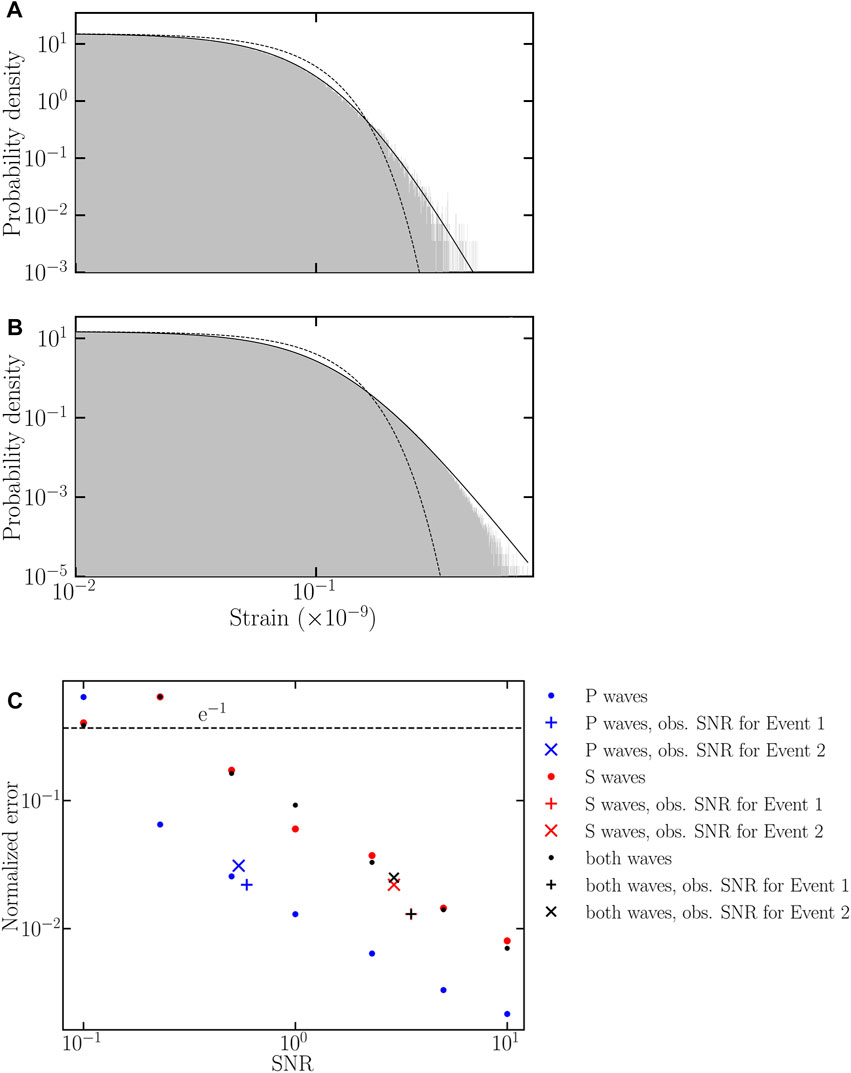
FIGURE 6. (A) Distribution of the absolute value of the seismic noise along well H for 3 × 10⁵ data points (gray histogram) where no events were present. The best fits with a Student t-distribution (black) and a Gaussian distribution (black dash line) are shown. (B) Distribution of the seismic noise for 3.6 ×10⁷ data points and best fits. (C) Normalized errors versus SNR when inverted from P-waves (blue), S-waves (red), or both P- and S-waves (black). Results with identical SNR along the two wells are shown as dots and results with the observed SNR (different along each well) are given by pluses for Event 1 and crosses for Event 2. The black dashed line is the e⁻¹ threshold of the acceptable error.

The noise distribution was not the same along the two wells, nor was it stable over time. The latter explains why Event 1, despite causing strain one order of magnitude lower than that for Event 2, still showed a similar SNR. The best fits with a Student’s t for the last 0.5 s of noise before each event occurred showed the same one order of magnitude difference in the b parameter. For Event 1, we obtained {ν = 6.89, b = 3.49 × 10⁻¹², p = 0.051} along well H, and {ν = 10.83, b = 4.46 × 10⁻¹², p = 0.550} along well J. For Event 2, we obtained {ν = 6.45, b = 5.23 × 10⁻¹¹, p = 0.542} along well H, and {ν = 9.88, b = 6.70 × 10⁻¹¹, p = 0.881} along well J. ν looked stable over time but the scale parameter b was 15 times larger before Event 2 that before Event 1, which explains the similar SNR between both events, despite the observed strain being ten times larger in Event 2 than in Event 1. This lack of stability over time can account for the difficulty in fitting a long noise sample with a Student’s t.

The moment tensor used for generating the simulated data can be expressed in the Lune representation as u = 3π/8, v = −0.2, with a strike of 105°, a slip of 40°, a dip of 12°, and an amplitude of M₀ = 7.08 × 10⁸ Nm. The simulated data were contaminated with noise for various SNRs ranging from 0.1 to 10 (two orders of magnitude). The SNR was defined as the ratio of the maximum amplitude of the signal over the maximum amplitude of the noise. The noise was normalized to obtain the same SNR in the data acquired along the two wells, even if the seismic source was located at different distances from the wells.

Another case was considered with the SNR measured for the observed data. For Event 1, the SNR was 0.59 for the P-waves and 3.52 for the S-waves along well H, and 0.83 for the P-waves and 5.24 for the S-waves along well J. For Event 2, the SNR was 0.55 for the P-waves and 5.3 for the S-waves along well H, and 0.70 for the P-waves and 2.92 for the S-waves along well J. In a manner similar to that of Eaton and Forouhideh (2011), the inversion method was applied to the noisy simulated data, and the normalized error was computed as follows:

$E=\frac{1}{9}{\left[\sum _{i=1}^3\sum _{j=1}^3\left({\widehat{M}}_{ij}-M_{ij}\right)\right]}^{1/2},(9)$

where M_ij are the elements of the moment tensor used for generating simulated data and ${\widehat{M}}_{ij}$ are the elements of the inverted moment tensor. Both moment tensors were normalized to unity to compute the normalized error. Consequently, the normalized error did not account for the error in the inversion of the magnitude.

Figure 6C shows the normalized errors versus SNR, when inverting using different types of waves. When the SNR was the same along both wells, and at a given SNR, inversion of the P-waves gave the smallest normalized errors. Inversion of only the S-waves and inversion of both P- and S-waves gave similar errors. The normalized errors decreased with increasing SNR, following a logarithmic trend.

The threshold of acceptable errors of e⁻¹$(\sim 0.3679)$ was exceeded for SNR $\le 0.23$ for the inversion of the S-waves and the inversion of both P- and S-waves. Similarly, for an SNR of $\le 0.1$ for the inversion of P-waves. When the SNR values based on observed data were used, the lower SNR for P-waves resulted in the inversions of the different types of waves not having significantly different normalized errors. For Event 1, the normalized errors were 0.022 for P-waves, 0.013 for S-waves, and 0.013 for the joint inversion of the P- and S-waves. For Event 2, the normalized errors were 0.031 for P-waves, 0.022 for S-waves, and 0.025 for the joint inversion of the P- and S-waves. In Figure 6C, these normalized errors appear consistent with the others when plotted with the SNR of the well with the lower SNR.

These results showed that in a case with no theoretical error, our method produced reliable results, even for non-Gaussian noise. This is important since the least-squares method makes assumes Gaussian-distributed noise in the data. With the SNR measured from the observed data, the inversion of the P- and S-waves appeared to be as reliable as the inversion of S-waves alone and the largest error appeared in the inversion of the P-waves.

3.2 Results for the observed data from wells J and H

This section presents the inversion results for the field observations made on two wells (J and H). We carried out three types of inversions and compared the results for these cases: S-waves only, P-waves only, and the joint inversion of P- and S-waves. The uncertainty estimates for the inverted source parameters, obtained by bootstrapping are shown in Figure 7. Table 2 gives the most probable values of the inverted parameters and the bounds of the 95% uncertainty interval.

FIGURE 7

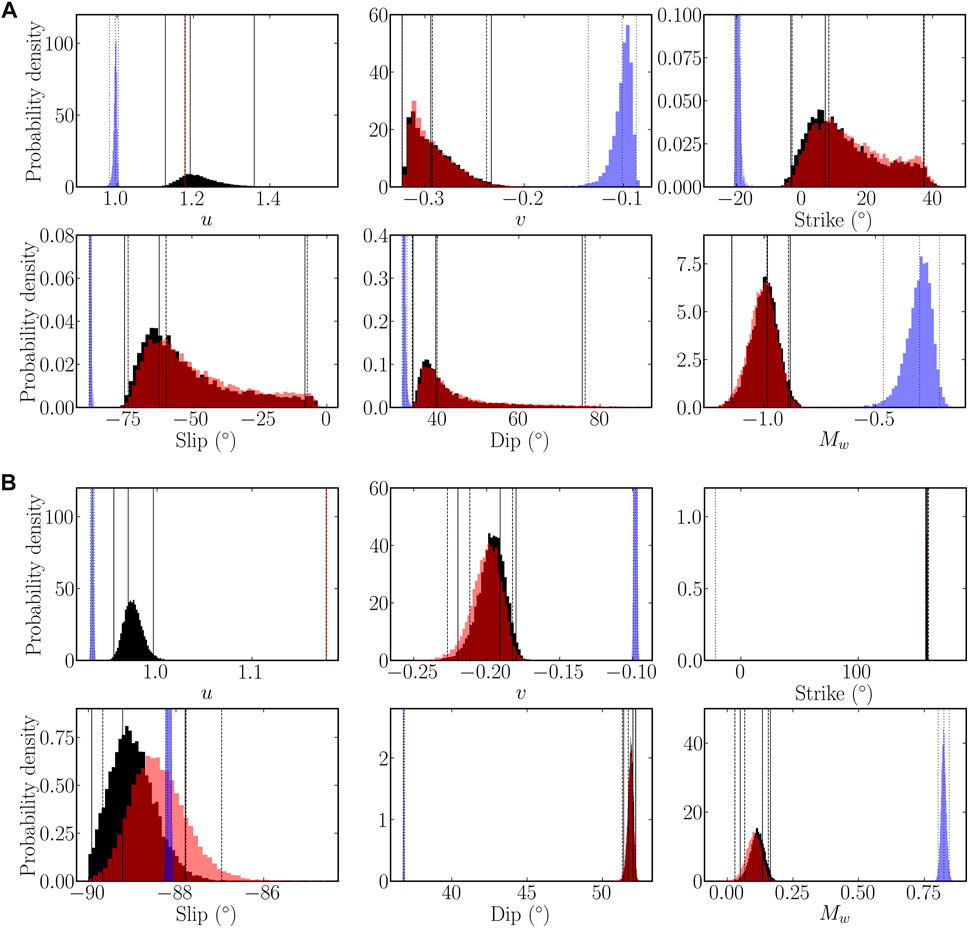
FIGURE 7. Histograms of the distributions of the source parameters for Event 1 (A) and Event 2 (B) sampled by bootstrapping and inverted using S-waves (red), P-waves (blue), and both P- and S-waves (black). From left to right, the vertical lines show the lower bound of the 95% uncertainty, the most probable value, and the upper bound of the 95% uncertainty for source parameters inverted using S-waves (dotted line), P-waves (dash line), and both P- and S-waves (solid line).

TABLE 2

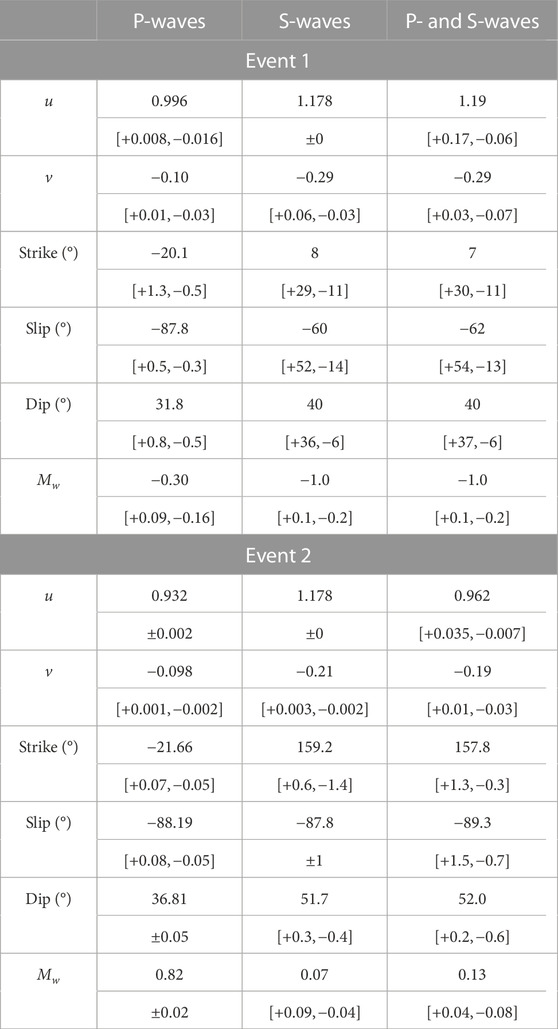
TABLE 2. Most probable values with the bounds of the 95% uncertainty of the source parameters inverted using S-waves, P-waves, and both P- and S-waves.

The three types of inversion exhibited unimodal distributions for both events. The inversion of the u parameter using S-waves naturally gave the theoretical value for no volume change: u = 3π/8 ≃ 1.178. The inversion of this parameter using P-waves points toward a small positive isotropic component. The inversion using P- and S-waves was consistent with an absence of a volume change for Event 1 and suggested a small positive isotropic component for Event 2. The inverted explosive component was not necessarily linked to fluid injection. It can, in fact, account for the complexity of the source; for example, if the rupture propagates along a curved fault plane.

For the five other parameters, the inversion results obtained from S-waves alone were nearly identical to those for both P- and S-waves together. Both of these types of inversion point toward a large negative CLVD component for Event 1 (v = −0.29) and a slightly smaller one for Event 2 (v = −0.21 from S-waves and v = −0.19 from P- and S-waves). By contrast, the inversion of the P-waves appears more biased toward a smaller CLVD component, with v ≃ 0.1 for both events. The inversion of P-waves also exhibited smaller uncertainties for the v parameter. A CLVD component is not unexpected for an induced earthquake resulting from fluid injection (Baig and Urbancic, 2010).

For the three angle parameters, the inversion of the P-waves always yielded the smallest uncertainties. This probably occurred due to the polarity reversal visible in the P-wave data, but not in the S-wave data, which helped to resolve the nodal planes. The three inversion types gave close values for Event 1, even if the uncertainties did not overlap. The uncertainties obtained by the inversion of the S-waves or P- and S-waves were large, several tens of degrees, while the uncertainties for the inversion of P-waves were below 2°. For Event 2, a difference of 180° was observed between the strikes inverted using P-waves and S-waves or P- and S-waves, corresponding to a classical ambiguity of the employed parametrization. The inversion of the dip also gave two disjoint values, with a difference of 18°, whereas the uncertainties of the slip values given by the three inversion types overlapped. All the uncertainties were below 2°.

For both events, the inversion of P-waves yielded the largest magnitude. For Event 1, the magnitude estimate from geophone data (M_w = −0.8) was within the uncertainties of the magnitude derived from the S-waves or P- and S-waves (M_w = −1.0). For Event 2, the magnitude estimate from geophone data (M_w = −0.5) was well below the value inverted from S-waves (M_w = −0.07), P- and S-waves (M_w = −0.13), and P-waves (M_w = 0.82). The different values obtained from the different waves can reflect differences in the transmission coefficients between the layers of the Montney Formation. This effect is expected to be more noticeable for Event 2 than for Event 1, since its sources are buried deeper.

Figure 8 presents the results in terms of lower-hemisphere projections of the moment tensor, often referred to as beachballs, and using the north-west-up coordinate system. To visualize the uncertainty of the moment-tensor parameters, we use fuzzy beachballs, where the gray-scale represents the uncertainty (the probability density of the ensemble of solutions from bootstrapping in the lower-hemisphere projection). Magnitudes are ignored in Figure 8.

FIGURE 8

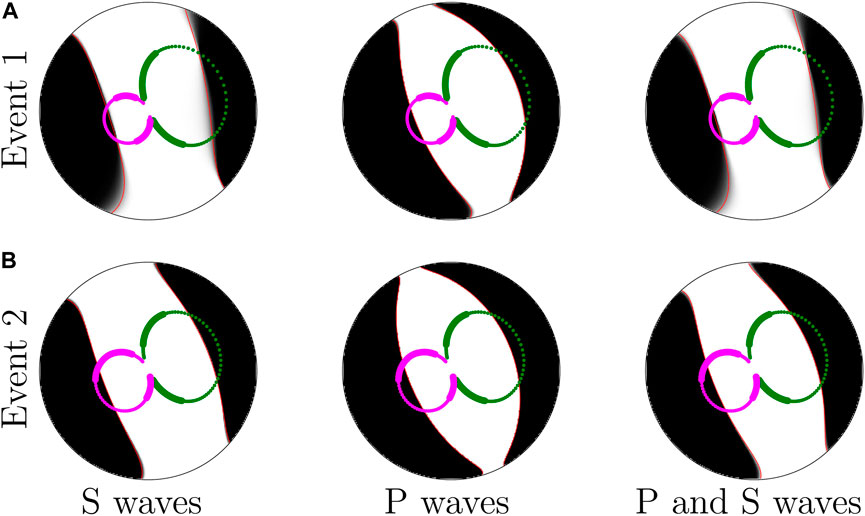
FIGURE 8. Fuzzy beachballs showing the moment tensors and their uncertainties inverted for Event 1 (A) and Event 2 (B) using, from left to right: S-waves; P-waves; both P- and S-waves. The red lines show the most probable moment tensor for each case. The scatter plot shows the projection on the beachballs of the 300 channels of well H (magenta) and well J (green) used in the inversion. Channels that are not muted in the P-wave data are magnified.

The inverted mechanisms were generally consistent between the two events and the three types of inversion. For both events, the moment tensors inversions of S-waves and of both P- and S-waves gave very similar results. Event 2 showed a difference in the greater closeness between the black areas of the fuzzy beachball for the moment tensor inverted from P- and S-waves, which illustrated its greater similarity to a double-couple. With v = 0, the two black areas indeed intersected at the two poles of the beachball. The similarity between the moment tensors inverted using S-waves and both P- and S-waves was mainly due to the significantly larger amplitude of S-waves compared to P-waves in the data. Their agreement should not necessarily lead to the conclusion that their results are more reliable than the one obtained using P-waves only.

The most probable moment tensor inverted based on S-waves, P-waves, and both P- and S-waves was used to generate simulated data using a linear combination of the Green functions. The agreement of these simulated data with field data made it possible to evaluate the accuracy of our inversion method. A first qualitative assessment can be carried out by comparing the time–distance diagrams of simulated and field data (Figure 9). For both events, the polarity of the S-wave arrival was correctly reproduced in simulated data, with a negative strain followed by a positive strain. The polarity of the P-wave arrival was also correctly reproduced along well J. Along well H, the P-wave on the right of the apex showed a polarity reversed with respect to the left of the apex. In the simulated data, only the channels closest to the apex showed the correct positive polarity while a polarity reversal appeared further on the right. In the simulated data based on the inversion of the P-waves, a significant number of channels showed correct polarity; however, in simulated data based on the inversion of both P-and S-waves, only a few channels showed positive polarity. The amplitude of the strain measured for Event 1 along well H was correctly reproduced in simulated data; however, the simulated strain was almost twice as weak as the observed strain in all the other cases, which suggested that the magnitude of both events was undervalued.

FIGURE 9

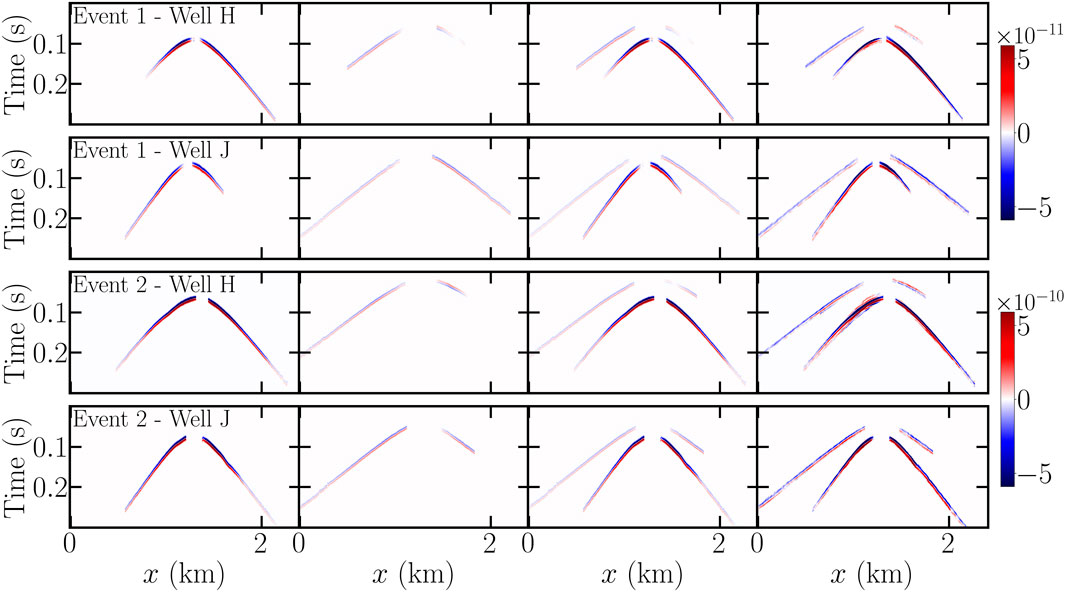
FIGURE 9. Simulated data for Event 1 (rows 1 and 2) and Event 2 (rows 3 and 4) at wells H (rows 1 and 3) and J (rows 2 and 4) based on the most probable moment tensors inverted using S-waves (column 1), P-waves (column 2), and both P- and S-waves (column 3). Field data are given for comparison (column 4). The color scale is saturated to help visualize the P-waves.

For a quantitative evaluation of the data fit of the inversions, we used variance reduction

$VR=1-\frac{{\left(x_i-d_i\right)}^2}{d_i^2},(10)$

where i is the channel, x_i is the simulated strain, and d_i is the observed strain. The variance reduction takes the value 1 when the simulated and observed strains are identical. Along with this variance reduction, Figure 10 gives the variance reduction obtained when the observed and simulated data were normalized to their maximums, which removed the effect of the amplitude of the strain for focusing on its polarity and the shape of the signal. Note that for noisy data, a variance reduction of unity implies over-fitting of the data.

FIGURE 10

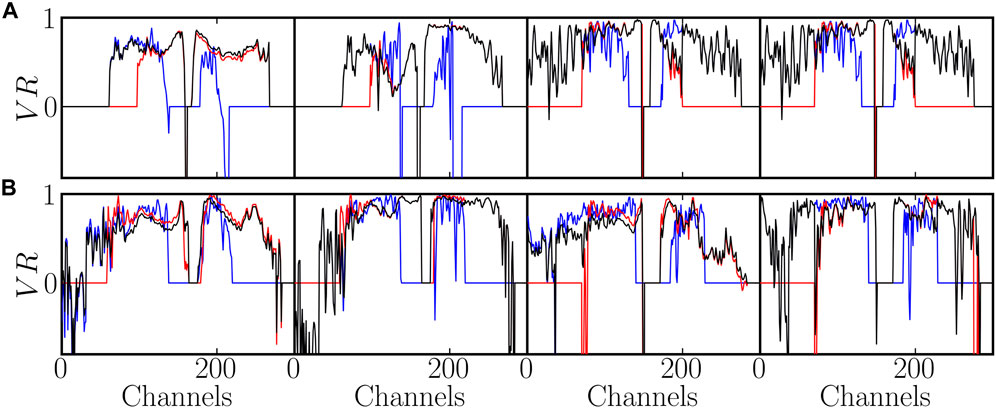
FIGURE 10. Variance reduction for Event 1 (A) and Event 2 (B) with the simulated data (columns 1 and 3) and normalized simulated data (columns 2 and 4) at well H (columns 1 and 2) and well J (columns 3 and 4), based on the most probable moment tensors inverted using S-waves (red), P-waves (blue), and both P- and S-waves (black). The value VR =0 is arbitrarily assigned to channels with no data.

In both events, the best variance reductions occurred relatively close to the apex and decreased far from the apex. This could be due to the inelastic attenuation not being considered in the forward model, especially since the decreased variance reduction was moderated when looking at normalized signals. The paths between the seismic sources were indeed shorter close to the apex. Another possible explanation is the limited azimuthal coverage of the DAS. The difficulty in reproducing the polarity of the P-waves along well H was responsible for a clear drop in the variance reduction, which did not appear when the two types of waves were taken together, due to the larger amplitude of S-waves. For Event 2, the variance reduction for S-waves dropped below 0.5 along well J for channels 218 to 299 (x ≳ 1.7 km, Figure 10A, right), which was linked to a sudden drop in the measured strain in the observed data (Figure 2). This was probably a path effect, perhaps due to a region of the ground with higher inelastic attenuation. In any case, the polarity of the strain or the shape of the signal were unaffected, and the variance reduction calculated for data normalized to their maximum was, therefore, quite good $(>0.5)$.

The difference between field data and the simulated data based on the most probable moment tensors and the signification of the variance reduction could be better understood using direct comparisons of signals (Figure 11). Despite the relatively good variance reductions (VR > 0.5) obtained on channel 191 of well H for both events, the two problems already described are made very clear: the polarity of the P-waves was not correctly reproduced when inverting from both P- and S-waves and the amplitude of the simulated data was smaller than the amplitude of the field data. Unexpectedly, for Event 1, the difference in amplitude was slightly smaller when inverted from both P- and S-waves, which probably explains the better variance reduction than when inverting from S-waves alone, despite the incorrect polarity predicted for the P-waves.

FIGURE 11

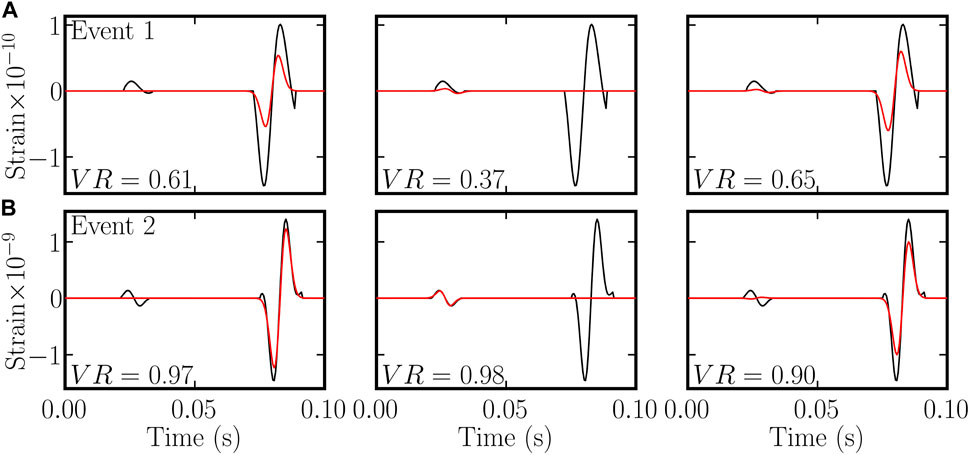
FIGURE 11. Field (black) and simulated (red) data from channel 191 of well H for Event 1 (A) and Event 2 (B). Simulated data are based on the most probable moment tensors inverted using S-waves (left), P-waves (center), and both P- and S-waves (right).

4 Discussion

The inversion of geophysical data relies on fast and accurate forward modeling, used for generating the predicted data that are compared to observed data. In this study, we choose a forward model able to simulate strain, which avoids the sources of uncertainty linked to the conversion of the observed strain data into displacement data. We did not retain the possibility of employing a state-of-the-art forward model written for predicting displacement before applying spatial differentiation to approximate the strain, which may introduce artifacts in the simulated data. Therefore, the strain was obtained by analytically calculating the far-field components of the strain in a homogeneous and anisotropic medium before projecting those components on the fiber of interest and averaging the tangential strain on the gauge length of the DAS sensor.

The field data acquired in the Montney Formation showed secondary arrivals and numerous reflections from lithographic boundaries and fractures and must be prepared for inversion. The reflections were removed using f-k filtering, and only the primary arrivals were kept using time-windowing. The channels with too low an SNR were muted. The simulated data were shifted to the arrival times of the observed primary arrivals, using cross-correlation of both signals at each channel, in an approach similar to the cut-and-paste method. The method was made insensitive to the inaccuracies in the prediction of the arrival times. However, our inversion method expected that the polarity and amplitude of the first arrivals of the P- and S-waves were correctly predicted by the forward model. Thus, we supposed that the amplitude was mainly affected by geometrical attenuation. Indeed, our method does not account for inelastic attenuation or the effects of heterogeneities, such as layers with different velocities and transmission coefficients in the Montney Formation. For the two events of interest, the short distances between the sources and the fibers (180 m for Event 1 and 210 m for Event 2) made these assumptions reasonable.

The linear problem of MT inversion (six dimensions) was solved with the least-squares method, using the processed data and the Green functions calculated by the forward model and time-shifted to the arrival times of the field data. However, the least-squares inversion relied on the assumption of Gaussian noise, and the observed noise was better approximated by a heavy-tailed Student’s t distribution. The uncertainties in the inverted parameters were provided by bootstrap analysis. We checked the robustness of our inversion method under heavy-tailed noise by applying it to data predicted by the forward model and polluted with different levels of real noise. Measured by normalized errors, the performances of the inversion method for this case without theoretical error appeared satisfying with the SNR found in real data.

The inversion method was applied to field data from two seismic events that occurred within 1 h with sources located approximately 100 m from each other. Magnitude aside, the inversion results were consistent between the two events for a given type of wave, which was expected since they both resulted from the same stress field. For a given event, the inversion results were consistent between the three types of inversion: using P-waves alone, S-waves alone, and both P- and S-waves together. The uncertainties in the inverted parameters were small enough to make possible future geological interpretations. The accuracy of the inversion method was evaluated by comparing the observed data to the data predicted for the most probable MT. The polarity of the S-waves was correctly reproduced for both fibers and both events; however, a polarity change in the P-waves along well H did not appear in predicted data for the joint inversion of the P- and S-waves. Thus, our assumption of no path effect on the polarity may be incorrect for P-waves. The evaluation can be refined using variance reduction. This shows the possible effect of inelastic attenuation on the amplitude of the measured strain. Comparisons of the observed and predicted signals for a single location highlighted a possible underestimation of the magnitudes for both events.

This paper provides encouraging results supporting a new method for inverting MT from DAS data. However, this method should be validated by comparison to a state-of-the-art inversion method, for example, in a dataset where both DAS data and abundant seismometer data are available. Then, the inversion method must be systematized and applied to a large number of events to improve our understanding of the local geology and fault activation under hydraulic fracturing in the Montney Formation. The forward model must be improved to reduce the theoretical errors that arise from simplifying assumptions. While keeping the hypothesis of a homogeneous and isotropic medium, the terms of the intermediate and near field could easily be considered, which is expected to improve the resolvability of the MT in events where the source is close enough to the wells (e.g.,Vera Rodriguez and Wuestefeld, 2020). The resolvability of the moment tensor using strain-simulated and field data was studied by Luo et al. (2021). It would be crucial to work with a forward model able to consider more complex environments, such as layered or anisotropic mediums. Finally, the inversion procedure itself should be improved to invert for source location, source time function, or more complex parametrizations of the source, which would force the use of non-linear methods.

Data availability statement

The data analyzed in this study is subjected to the following licenses/restrictions: the data are proprietary. Requests to access these datasets should be directed to jean.lecoulant@ucalgary.ca.

Author contributions

JL contributed to developing the inversion method, performing the DAS data analysis, and drafting the paper. YM contributed to processing the raw data, as well as localizing and selecting the seismic events of interest. JD contributed to the elaboration of the moment tensor inversion and critical revision of the paper. DE contributed to the results interpretation and critical revision of the paper. All authors contributed to the article and approved the submitted version.

Funding

JL thanks the Natural Sciences and Engineering Research Council of Canada (NSERC) for the financial support (Grant No. ALLRP⧵548576-2019) through the Alliance program.

Acknowledgments

The authors are grateful to ConocoPhillips Canada for permission to publish the DAS examples. The authors thank Mahdi Hamidbeygi and Pejman Shahsavari for useful discussions about the observed noise distribution.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aki, K., and Richards, P. G. (2009). “Quantitative seismology (mill valley, calif: Univ. Science books,” in corr, 2. print edn.

Google Scholar

Atkinson, G. M., Eaton, D. W., Ghofrani, H., Walker, D., Cheadle, B., Schultz, R., et al. (2016). Hydraulic fracturing and seismicity in the western Canada sedimentary basin. Seismol. Res. Lett.87, 631–647. doi:10.1785/0220150263

CrossRef Full Text | Google Scholar

Baig, A., and Urbancic, T. (2010). Microseismic moment tensors: A path to understanding frac growth. Lead. Edge29, 320–324. doi:10.1190/1.3353729

CrossRef Full Text | Google Scholar

Baird, A. F., Stork, A. L., Horne, S. A., Naldrett, G., Kendall, J.-M., Wookey, J., et al. (2020). Characteristics of microseismic data recorded by distributed acoustic sensing systems in anisotropic media. GEOPHYSICS85, KS139–KS147. doi:10.1190/geo2019-0776.1

CrossRef Full Text | Google Scholar

Brune, J. N. (1970). Tectonic stress and the spectra of seismic shear waves from earthquakes. J. Geophys. Res.75, 4997–5009. doi:10.1029/JB075i026p04997

CrossRef Full Text | Google Scholar

Burridge, R., and Knopoff, L. (1964). Body force equivalents for seismic dislocations. Bull. Seismol. Soc. Am.54, 1875–1888. doi:10.1785/BSSA05406A1875

CrossRef Full Text | Google Scholar

Cole, S., Karrenbach, M., Kahn, D., Rich, J., Silver, K., and Langton, D. (2018). “Source parameter estimation from DAS microseismic data,” in SEG technical program expanded abstracts 2018 (Anaheim, California: Society of Exploration Geophysicists), 4928–4932. doi:10.1190/segam2018-2995716.1

CrossRef Full Text | Google Scholar

Daley, T. M., Freifeld, B. M., Ajo-Franklin, J., Dou, S., Pevzner, R., Shulakova, V., et al. (2013). Field testing of fiber-optic distributed acoustic sensing (DAS) for subsurface seismic monitoring. Lead. Edge32, 699–706. doi:10.1190/tle32060699.1

CrossRef Full Text | Google Scholar

Dou, S., Lindsey, N., Wagner, A. M., Daley, T. M., Freifeld, B., Robertson, M., et al. (2017). Distributed acoustic sensing for seismic monitoring of the near surface: A traffic-noise interferometry case study. Sci. Rep.7, 11620. doi:10.1038/s41598-017-11986-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Dziewonski, A. M., Chou, T.-A., and Woodhouse, J. H. (1981). Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. Solid Earth86, 2825–2852. doi:10.1029/JB086iB04p02825

CrossRef Full Text | Google Scholar

Eaid, M. (2022). Distributed acoustic sensing: Modelling, full waveform inversion, and its use in seismic monitoring. Calgary, AB: Ph.D. thesis, University of Calgary. doi:10.11575/PRISM/39485

CrossRef Full Text | Google Scholar

Eaton, D. W., and Forouhideh, F. (2011). Solid angles and the impact of receiver-array geometry on microseismic moment-tensor inversion. GEOPHYSICS76, WC77–WC85. doi:10.1190/geo2011-0077.1

CrossRef Full Text | Google Scholar

Efron, B., and Tibshirani, R. (1986). Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat. Sci.1, 54–75. Publisher: Institute of Mathematical Statistics.

CrossRef Full Text | Google Scholar

Ekström, G., Nettles, M., and Dziewoński, A. (2012). The global CMT project 2004–2010: Centroid-moment tensors for 13,017 earthquakes. Phys. Earth Planet. Interiors200-201, 1–9. doi:10.1016/j.pepi.2012.04.002

CrossRef Full Text | Google Scholar

Ellsworth, W. L. (2013). Injection-induced earthquakes. Science341, 1225942. doi:10.1126/science.1225942

PubMed Abstract | CrossRef Full Text | Google Scholar

Jost, M. L., and Herrmann, R. B. (1989). A student’s guide to and review of moment tensors. Seismol. Res. Lett.60, 37–57. doi:10.1785/gssrl.60.2.37

CrossRef Full Text | Google Scholar

Karrenbach, M., Kahn, D., Cole, S., Ridge, A., Boone, K., Rich, J., et al. (2017). Hydraulic-fracturing-induced strain and microseismic using in situ distributed fiber-optic sensing. Lead. Edge36, 837–844. doi:10.1190/tle36100837.1

CrossRef Full Text | Google Scholar

Lellouch, A., Schultz, R., Lindsey, N., Biondi, B., and Ellsworth, W. (2021). Low-magnitude seismicity with a downhole distributed acoustic sensing array—examples from the FORGE geothermal experiment. J. Geophys. Res. Solid Earth126. doi:10.1029/2020JB020462

CrossRef Full Text | Google Scholar

Lindsey, N. J., Martin, E. R., Dreger, D. S., Freifeld, B., Cole, S., James, S. R., et al. (2017). Fiber-optic network observations of earthquake wavefields. Geophys. Res. Lett.44. doi:10.1002/2017GL075722

CrossRef Full Text | Google Scholar

Luo, B., Jin, G., and Stanek, F. (2021). Near-field strain in distributed acoustic sensing-based microseismic observation. GEOPHYSICS86, P49–P60. doi:10.1190/geo2021-0031.1

CrossRef Full Text | Google Scholar

Ma, Y., Eaton, D., Igonin, N., and Wang, C. (2023). Machine learning-assisted processing workflow for multi-fiber DAS microseismic data. Front. Earth Sci.11, 1096212. doi:10.3389/feart.2023.1096212

CrossRef Full Text | Google Scholar

Ma, Y., Eaton, D. W., and Wang, C. (2022). “Fracture imaging using DAS-recorded microseismic reflections,” in Second international meeting for applied geoscience and energy (Houston, Texas: Society of Exploration Geophysicists and American Association of Petroleum Geologists), 587–591. doi:10.1190/image2022-3745381.1

CrossRef Full Text | Google Scholar

Parker, T., Shatalin, S., and Farhadiroushan, M. (2014). Distributed Acoustic Sensing – a new tool for seismic applications. First Break32. doi:10.3997/1365-2397.2013034

CrossRef Full Text | Google Scholar

Stähler, S. C., and Sigloch, K. (2014). Fully probabilistic seismic source inversion – Part 1: Efficient parameterisation. Solid earth.5, 1055–1069. doi:10.5194/se-5-1055-2014

CrossRef Full Text | Google Scholar

Staněk, F., Jin, G., and Simmons, J. (2022). Fracture imaging using DAS-recorded microseismic events. Front. Earth Sci.10, 907749. doi:10.3389/feart.2022.907749

CrossRef Full Text | Google Scholar

Tape, W., and Tape, C. (2012). A geometric setting for moment tensors: A geometric setting for moment tensors. Geophys. J. Int.190, 476–498. doi:10.1111/j.1365-246X.2012.05491.x

CrossRef Full Text | Google Scholar

Tichelaar, B. W., and Ruff, L. J. (1989). How good are our best models? Jackknifing, bootstrapping, and earthquake depth. Eos, Trans. Am. Geophys. Union70, 593. doi:10.1029/89EO00156

CrossRef Full Text | Google Scholar

Vackář, J., Burjánek, J., Gallovič, F., Zahradník, J., and Clinton, J. (2017). Bayesian ISOLA: New tool for automated centroid moment tensor inversion. Geophys. J. Int.210, 693–705. doi:10.1093/gji/ggx158

CrossRef Full Text | Google Scholar

Vasyura-Bathke, H., Dettmer, J., Steinberg, A., Heimann, S., Isken, M. P., Zielke, O., et al. (2020). The bayesian earthquake analysis tool. Seismol. Res. Lett.91, 1003–1018. doi:10.1785/0220190075

CrossRef Full Text | Google Scholar

Vera Rodriguez, I., and Myklebust, E. B. (2022). Deep compressed seismic learning for fast location and moment tensor inferences with natural and induced seismicity. Sci. Rep.12, 15230. doi:10.1038/s41598-022-19421-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Vera Rodriguez, I., and Wuestefeld, A. (2020). Strain microseismics: Radiation patterns, synthetics, and moment tensor resolvability with distributed acoustic sensing in isotropic media. GEOPHYSICS85, KS101–KS114. doi:10.1190/geo2019-0373.1

CrossRef Full Text | Google Scholar

Wéber, Z. (2006). Probabilistic local waveform inversion for moment tensor and hypocentral location. Geophys. J. Int.165, 607–621. doi:10.1111/j.1365-246X.2006.02934.x

CrossRef Full Text | Google Scholar

Zhu, L., and Helmberger, D. V. (1996). Advancement in source estimation techniques using broadband regional seismograms. Bull. Seismol. Soc. Am.86, 1634–1641. doi:10.1785/BSSA0860051634

CrossRef Full Text | Google Scholar