Electromagnetic imaging and deep learning for transition to renewable energies: a technology review

Castillo-Reyes, Octavio; Hu, Xiangping; Wang, Bochen; Wang, Yanyi; Guo, Zhenwei

doi:10.3389/feart.2023.1159910

REVIEW article

Front. Earth Sci., 17 August 2023

Sec. Geoscience and Society

Volume 11 - 2023 | https://doi.org/10.3389/feart.2023.1159910

Electromagnetic imaging and deep learning for transition to renewable energies: a technology review

Octavio Castillo-Reyes^1,2*

Xiangping Hu³

Bochen Wang^4,5,6

Yanyi Wang^4,5,6

Zhenwei Guo^4,5,6*

¹Barcelona Supercomputing Center, Barcelona, Spain
²Department of Computer Architecture, Universitat Politècnica de Catalunya, Barcelona, Spain
³Department of Energy and Process Engineering, Faculty of Engineering, Norwegian University of Science and Technology, Trondheim, Sør-Trøndelag, Norway
⁴School of Geosciences and Info Physics, Central South University, Changsha, Hunan Province, China
⁵Hunan Key Laboratory of Nonferrous Resources and Geological Hazard Exploration, Central South University, Changsha, Anhui Province, China
⁶Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring, Central South University, Changsha, Hunan Province, China

Electromagnetic imaging is a technique that has been employed and perfected to investigate the Earth subsurface over the past three decades. Besides the traditional geophysical surveys (e.g., hydrocarbon exploration, geological mapping), several new applications have appeared (e.g., characterization of geothermal energy reservoirs, capture and storage of carbon dioxide, water prospecting, and monitoring of hazardous-waste deposits). The development of new numerical schemes, algorithms, and easy access to supercomputers have supported innovation throughout the geo-electromagnetic community. In particular, deep learning solutions have taken electromagnetic imaging technology to a different level. These emerging deep learning tools have significantly contributed to data processing for enhanced electromagnetic imaging of the Earth. Herein, we review innovative electromagnetic imaging technologies and deep learning solutions and their role in better understanding useful resources for the energy transition path. To better understand this landscape, we describe the physics behind electromagnetic imaging, current trends in its numerical modeling, development of computational tools (traditional approaches and emerging deep learning schemes), and discuss some key applications for the energy transition. We focus on the need to explore all the alternatives of technologies and expertise transfer to propel the energy landscape forward. We hope this review may be useful for the entire geo-electromagnetic community and inspire and drive the further development of innovative electromagnetic imaging technologies to power a safer future based on energy sources.

1 Introduction

The energy transition concerns the shift from fossil-based fuels (e.g., oil, natural gas, andcoal) to renewable energy sources (e.g., wind, solar, hydrogen, bio-energy, carbon capture and storage, and geothermal) to reduce CO₂ emissions. This type of transition is not new: coal in the middle of the 19th century, oil in the middle of the 20th, and nuclear power for civil purposes in the 1970s, all brought about significant changes in the energy mixes, although back then, the different sources did not supplant one another, but were more complimentary (Steg et al., 2015).

Innovation and competitiveness in the energy transition entail the capacity to produce and use affordable, reliable, and accessible green energies through clean technologies to compete in energy technology markets and benefit the economy and people. In 2015, the United Nations General Assembly (UNGA) adopted the 2030 Agenda for Sustainable Development and its Sustainable Development Goals (SDGs (SDG, 2019)), which include a dedicated and stand-alone goal on energy, SDG 7: ”Ensure access to affordable, reliable, sustainable and modern energy for all. Energy lies at the heart of both the 2030 SDGs and the Paris Agreement on Climate Change (PACC (United-Nations, 2015)), which aims to ensure access to affordable, reliable, sustainable and modern energy.

With the European Green Deal (EGD (Fetting, 2020)), the European Union (EU) aims to become the first climate-neutral continent by 2050. This vision was enshrined into legislation with the European Climate Law, which transformed the EU’s climate-neutrality pledge into a binding obligation and increased the EU’s 2030 emissions reductions target from 40% to at least 55% compared to 1990s levels. To deliver on this climate target, the EU must pursue one main goal: make its energy sector climate neutral. But change will not happen overnight. Should the previous climate target be successfully achieved, the following challenges need to be addressed by 2050:

1) Reduce energy mix and import dependency: In 2022, the EU imported 57.5% of the energy it consumed as its production and satisfied only 42.5% of its needs. Russia is the EU’s leading natural gas, oil, and coal supplier (Eurostat, 2022).

2) Decarbonization of the energy sector: the production and use of energy across economic sectors account for more than 75% of the EU’s greenhouse gas (GHG) emissions. Today, almost three-quarters of the EU energy system relies on fossil fuels. Oil dominates the EU energy mix (with a share of 35%), followed by natural gas (24%) and coal (14%) (Eurostat, 2022).

3) Improve performance and reliability of geo-resources: ensure a reliable pre-drilling assessment of geo-energy to increase the production rates with reduced operational and maintenance costs that allow widespread and cost-effective exploitation of them.

4) Accelerate the deployment of renewable sources: despite renewables growing in share, they still play a limited role of 14% and account for no more than 5% of the renewables market (Eurostat, 2022). It is critical to extend renewable energy uses to complex and untested geological conditions and reduce its environmental impact.

5) Increase citizen engagement: generating actionable knowledge to draw a complete understanding of renewable energy’s environmental and social impacts.

Geophysical imaging technologies can be applied to face the mentioned issues. Through in silico methods (mathematics, physics, geophysics, computer science, artificial intelligence), these technologies address two key questions related to geo-resources for the energy transition and a high-tech society:

1) Where to find the geo-resources that we need today and in the future?

2) How to access those geo-resources most sustainably?

Electromagnetic (EM) methods are among the most important tools for exploring the subsurface (Andreis and MacGregor, 2008). EM imaging technologies have been used for hydrocarbon exploration for several decades, but lately, worldwide recognition of the importance of the method has significantly increased (Wang et al., 2021). Its widespread applications range from regional-scale geo-energy studies (Kana et al., 2015; Castillo-Reyes et al., 2021) and mineral exploration to mapping thin shallow layers (Guo Z. et al., 2020) or characterization of unexploited groundwater reservoirs (Weymer et al., 2018). Because maturity of numerical methods, deep learning (DL) schemes, and exponential growth in the performance of computers, the development of increasingly sophisticated EM imaging software solutions, which, when combined with high-quality data, have become a right-hand man to geophysicists and have produce impressive results. With a growing world population and incremental use of sophisticated technologies, the demand for geo-energy and raw materials to sustain the current energy needs is steadily (Perez and Perez, 2022). For example, the minerals required to develop battery components are scarce but fundamental for an electrified mobility model. At the same time, the conventional dependence on fossil fuels and the high-access cost to many resources are currently major challenges (Khan et al., 2021). EM imaging technologies are one viable approach to provide mapping solutions to address these problems on a global scale (since the technology is software-based, it is not geographically restricted). In light of this, we believe EM imaging solutions (both traditional and DL-based) will be a crucial technology in the future and likely one of the most important investigative methods for exploring and managing geo-energy resources with reduced costs and risks (Newman, 2014; Castillo-Reyes et al., 2021).

Numerical methods, DL schemes, and computational strategies are in a symbiotic relationship for EM imaging. These methods and approaches have developed so rapidly that even among scientists and professionals, only a few have a complete overview of the state of EM imaging technologies and their applicability for the transition to renewable energies. This knowledge gap gives disjointed development to the detriment of the three areas, which is something we hope to help mend with this work. This review aims to provide the reader with an overview of EM data for enhanced imaging of the Earth and identify the opportunity to transfer expertise from coal energies to renewable sources. Many numerical and computational strategies, including traditional methods, and DL schemes for processing EM data, are reviewed and summarized. Our review shows great potential to use numerical and computational strategies to move from traditional to zero-carbon energy systems.

The rest of the paper is organized as follows. In Section 2, we introduce EM data for subsurface imaging, followed by an overall view of its applications. In Section 3, we assess the knowledge transfer potential from coal energies to renewable sources. In Section 4, we discuss the key applications, potentials, and limitations of EM imaging for the energy transition. In Section 5, we review DL technologies as a solution to the challenges faced by traditional EM imaging technologies. Finally, in Section 6, we provide summary remarks and conclusions.

2 Electromagnetic data for enhanced imaging of the Earth

Imaging of the Earth’s subsurface is of great societal value since this process is fundamental to earthquake prediction and seismic hazard estimation, mine detection, prospecting of energy (hydrocarbons, geothermal) and water reservoirs, seismic monitoring, and management of CO₂ sequestration, among others (Etgen et al., 2009). Several diverse methods, such as seismic, EM, well-logging, magnetic, and gravity, generate high-quality Earth’s subsurface maps. Each of these techniques obtains a corresponding data type that must be analyzed and interpreted by experts in the field to determine the expected profitability of the region of interest. Complex computational tools carry out this assessment.

Over the last three decades, EM methods have become fundamental research tools in geophysics exploration (Um and Alumbaugh, 2007; Constable, 2010; Castillo-Reyes et al., 2018). By using EM methods, Maxwell’s diffusive equations in the time-domain or frequency-domain are solved to obtain a prediction of the EM signature. The behavior of the response depends on the excitation source type (natural or artificial) and the distribution of geological properties. From this input-response dependence, it is possible to build accurate 3D resistivity maps of the Earth’s subsurface. These EM data are useful for enhanced Earth imaging and de-risk any applications that exploit the associated geo-resources.

Since EM methods can display resistivity/conductivity variations concerning their surrounding materials, EM imaging has greatly complemented seismic methods (sensitive to subsurface structure). As a result, EM imaging technologies have been applied in different areas of geophysics such as off-shore hydrocarbon (Newman and Alumbaugh, 1997; Eidesmo et al., 2002; Avdeev, 2005; Constable, 2006; Srnka et al., 2006; Orange et al., 2009; Constable, 2010; Wirianto et al., 2010; Castillo-Reyes et al., 2018; Castillo-Reyes et al., 2019; Castillo-Reyes et al., 2022b), mineral and resource mining (Sheard et al., 2005; Yang and Oldenburg, 2012), crustal conductivity studies (Hördt et al., 1992; Hördt et al., 2000), CO₂ storage characterization (Chen et al., 2007; Girard et al., 2011; Vilamajó et al., 2013; Zhdanov et al., 2013; Vilamajó et al., 2016; Park et al., 2017; Tveit et al., 2020), geothermal reservoir imaging (Kana et al., 2015; Coppo et al., 2016; Darnet et al., 2018; Omisore et al., 2020; Castillo-Reyes et al., 2021), and water prospecting (Palacky et al., 1981; McNeill, 1990; Nabighian and Macnae, 1991; Palacky, 1993; Nobes, 1996; Chang et al., 2019). Regardless of the application context, the authors stand out on the potential of EM methods for exploration, appraisal, and soil characterization. The literature also highlights that EM imaging is one of the most cost-effective geophysical data and its transversality for soil characterization and energy reservoir monitoring. Figure 1 shows the summary of the most relevant applications for EM imaging. In additionFurthermore, Table 1 shows an overview of the literature reviewed. Furthermore, Table 2 provides a summary of applications discussed in the paper, listing the input features (data used as input for the EM imaging process) and the output features (information obtained as a result of the imaging process).

FIGURE 1

FIGURE 1. Application mapping of EM imaging technologies.

TABLE 1

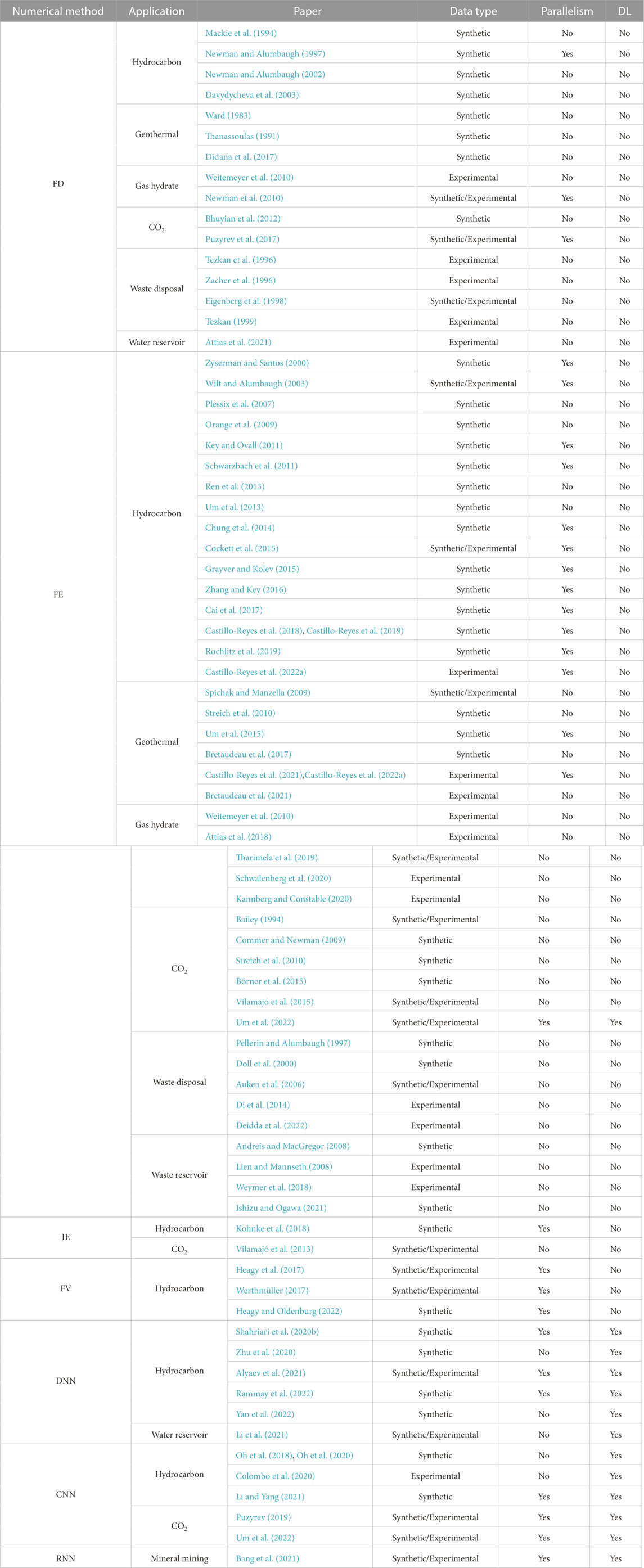
TABLE 1. Summary of articles selected in the literature review organized by numerical method, application context, and year of publication.

TABLE 2

TABLE 2. Main applications of electromagnetic imaging in renewable energy transition.

Although over the last years, a significant effort has been made in the EM imaging community to build 3D resistivity maps of the Earth’s subsurface, additional work is still needed to improve the accuracy and efficiency of computational tools. Also, the development of workflows that combine different geophysical data (e.g., seismic and EM data) and computational techniques (e.g., artificial intelligence and DL) is required to improve geophysical exploration tasks. In the following sections, we focus on completing our revision in these relevant aspects and applications.

3 Expertise transfer from coal energies to renewable sources

Climate change and current geopolitical developments call for a revamp of our strategies regarding primary resources and energy in a carbon-neutral future (United-Nations, 2015; SDG, 2019; Fetting, 2020). The subsurface of the Earth holds substantial reservoirs of green energy (e.g., geothermal), freshwater, and storage space to sequester carbon dioxide. The characterization of such reservoirs can provide untapped resources of local nature that can assist the environmental and economic sustainability of the next generations. Furthermore, the ores required to develop battery components are scarce but fundamental to achieving a zero-carbon electrified mobility model (Xu et al., 2020).

EM surveys, aerial and ground-based, are among the most widely used methods for subsurface exploration. The EM imaging technology has been developed and perfected for hydrocarbon exploration, as it can detect conductivity contrasts caused by changes in lithology or fluids. Several works and experiments demonstrated the potential of EM imaging for detecting hydrocarbon-rich zones (Eidesmo et al., 2002; Edwards, 2005; Sheard et al., 2005; Srnka et al., 2006; Newman and Commer, 2009; Gray et al., 2012; Chung et al., 2014; Cai et al., 2017; Castillo-Reyes et al., 2018). Furthermore, the literature reviews by Andreis and MacGregor (2008), Constable (2010), Newman (2014), and Wang et al. (2021) detailed the journey of EM methods and its applicability in the hydrocarbon industry. However, the same technological basis can be deployed to detect fluids or minerals or monitor their migration. Combined with the exponential growth in the performance of computers in the last decade, our capacity to transform EM data into subsurface models can now be massively deployed. As data acquisition is inexpensive and has a small footprint on the terrain, exploring vast territory regions can become routine in the current decade.

Regarding applications, integrated approaches, including EM data, have been used on different scales and with diverse objectives. Still, there is a shortage of studies targeting carbon-neutral energy options. Significant developments can be made with an enormous impact on primary resources for the clean energy transition. The design of more affordable, secure, and sustainable energy systems will demand expertise transfer and data sharing. Therefore, by tapping into EM imaging expertise transfer from the hydrocarbon sector to carbon-neutral systems, the energy industry can pave a more intelligent, efficient, and resilient route for exploring non-conventional energy resources. In this sense, we identify three expertise topics with high transfer potential: physical behavior, numerical methods, and computational strategies. Below we discuss the most relevant aspects of each one. In addition, Figure 2 depicts a summary of the technological ecosystem for EM imaging.

FIGURE 2

FIGURE 2. Overview of the EM imaging ecosystem.

3.1 Physical behavior

For the diversity of remote sensing techniques deployed in the past century, EM methods seem to be less important than seismic techniques in the hydrocarbon sector. However, the activity in EM imaging for exploration has been present, and in the 1970s and 1980s, improved equipment and increasing data-processing power led to extensive development. The achievements of EM imaging and its physical behavior have recently been reviewed in comprehensive papers (Avdeev, 2005; Chopra et al., 2007; Um and Alumbaugh, 2007; Constable, 2010; Chave et al., 2017a,b; Eide and Carter, 2020).

Three elements describe the EM properties of a medium: the electric permittivity or dielectric constant (ϵ_r), magnetic permeability (μ), and electric conductivity (σ) or its reciprocal called electric resistivity (1/σ). EM techniques investigate the Earth’s subsurface using EM signals generated by artificial or natural sources in both land and marine environments. Analyzing differences between the conductivity/resistivity of the various subsurface strata enables us to map geological bodies. Because of the ability to map significant variations between electric material properties, EM methods are very useful for detecting hydrocarbon locations since they exhibit different resistivities from the surrounding rocks (Li and Key, 2007). However, EM measurements and their analysis can also be applied to other environmental and engineering applications such as mining, carbon capture/storage, and water reservoir prospecting (Evans, 2007; Weymer et al., 2018). As a result, these engineering sectors can benefit from all the knowledge and experience developed by the hydrocarbon industry.

3.2 Numerical strategies

Rigorous interpretation of EM data in complex geological setups requires accurate and efficient numerical strategies. The industrial needs, mainly those related to the oil sector, encouraged tremendous advances in numerical schemes for EM imaging. Börner (2010) presented a review of numerical method developments for the discrete solution of the EM problem in geophysics, which is governed by Maxwell’s equations (Zhdanov, 2009).

The numerical techniques for solving these fundamental equations are based on four strategies: integral equations (IE, (Raiche, 1974; Wannamaker et al., 1984; Wannamaker, 1991; Xiong and Tripp, 1997)), finite differences (FD (Mackie et al., 1994; Newman and Alumbaugh, 2002; Davydycheva et al., 2003)), finite volumes (FV (Hermeline, 2009; Jahandari and Farquharson, 2014)), and finite elements (FE (Jin et al., 1999; Key and Ovall, 2011; Um et al., 2013; Castillo-Reyes et al., 2019)). Each numerical scheme could have advantages or disadvantages depending on the input EM problem. The use of, IE, discretizations results in a dense linear system of equations (LSE) that can be solved efficiently for simplified layered models (e.g., models with flat and few resistivity layers). However, if the model complexity increases (e.g., models with several resistivity layers), the computational cost (e.g., runtime and memory needs) can be prohibitive for modest computational architectures (Avdeeva et al., 2015). The FD method is one of the most used in EM imaging. The popularity of FD schemes is due to their easy computational implementation. Nevertheless, its main disadvantage is the inability to work with unstructured meshes. Thus, to approximate complex subsurface bodies, a stair-case grid approach is required. Like the FD strategy, the FV method is simple in terms of numerical formulation and computational implementation. Furthermore, the FV scheme can be applied to unstructured meshes, allowing us to represent geometrically complex models. However, when grids with similar features are compared, the numerical accuracy of FV solutions is generally inferior to FD or FE computations (Bondeson et al., 2012; Jahandari et al., 2017). The FE scheme employs fully unstructured meshes, avoiding the above-mentioned geometrical representation issue. Furthermore, the numerical accuracy of FE computations can be improved by employing tailored mesh refinement techniques (both in h − and p − spaces) (Plessix et al., 2007; Key and Ovall, 2011; Schwarzbach et al., 2011; Ren et al., 2013; Grayver and Kolev, 2015; Zhang and Key, 2016; Castillo-Reyes et al., 2019). Recently, Castillo-Reyes et al. (2022) and Castillo-Reyes et al. (2022a) evaluated the benefits and computational cost of goal-oriented mesh refinement for diverse geophysical exploration setups (hydrocarbons, geothermal energy, and mining). The analysis of these numerical experiments confirms that adaptive meshing is beneficial for building high-quality 3D resistivity images.

The study and improvement of these numerical methods in terms of quality discretization (both in time and space), numerical stability, convergence, meshing, and computational cost, have resulted in many diverse EM imaging technologies for the hydrocarbon sector. All this knowledge base is valuable for appraising new and eco-friendly energy sources.

3.3 Computational strategies

The last two decades have been a period of the rapid growth of heterogeneous computing systems. These architectures offer tremendous potential for performance and efficiency in numerous and diverse large-scale applications for science and engineering. In particular, High-performance Computing (HPC) systems play a fundamental role in solving actual and the next-generation of real-life geoscience problems that usually are challenging and computationally demanding (Osseyran and Giles, 2015). Advances in software and hardware for HPC architectures have decisively contributed to the maturity of EM imaging technologies. Below we discuss the most relevant advancements in terms of computational strategies for EM imaging of the subsurface.

Developing and improving fast and efficient algorithms and numerical strategies is a constantly evolving task. These computational and numerical schemes in EM imaging were initially programmed using commercial software (e.g., MATLAB) and executed in single-core architectures. This approach effectively addresses the topic of validation (proof of concept). As a result, many proprietary codes for geophysical applications have been developed (Li and Oldenburg, 1996; Li and Oldenburg, 1998; Li and Key, 2007). These modeling tools are adapted and adequate for a particular application. However, the proprietary features of these codes make it hard for other researchers to assess whether their underlying formulation and algorithmics suit whichever computational architecture those tools are deployed on. The latter issue motivated the development of EM imaging technologies based on an open-source paradigm, which allows for a complete exploration of its underlying formulation and algorithmics. Furthermore, this feature facilitates its efficient deployment on diverse computing platforms. The most relevant EM imaging projects under open source initiatives are that developed by Cockett et al. (2015), Heagy et al. (2017), Rücker et al. (2017), Werthmüller (2017), Castillo-Reyes et al. (2018), Befus (2018), and Rochlitz et al. (2019).

In realistic configurations, the LSE resulting from the numerical discretization of Maxwell’s equations is large, sparse, and highly ill-conditioned. Consequently, solving the large-scale LSE is the most critical and expensive phase of the overall EM imaging work. Several numerical methods have been developed to solve these linear systems of equations, which can be classified into two groups: direct and iterative methods. Both groups have pros and cons, and the choice of a given method is generally problem-dependent. The main advantage of iterative methods is their low-storage requirement, which resolves the memory issue of direct methods. However, since linear systems are usually ill-conditioned, iterative approaches are susceptible to numerical instability, which results in poor convergence rates. Several ad hoc preconditioning techniques have been proposed to face this poor convergence performance (Axelsson, 1996; Um et al., 2013; Grayver and Kolev, 2015).

On the other hand, direct solvers are a robust solution to the LSE with highly ill-conditioned matrices. Despite its numerical stability benefits, direct solvers can be memory-consuming and prohibitive (especially for large-scale simulations). Although expensive, the use of direct solvers has gained momentum due to numerical advancements and the maturity of HPC technologies. Pioneer works in the context of HPC for EM imaging are presented by Alumbaugh et al. (1996), Newman and Alumbaugh (1997), Oristaglio and Spies (1999), Zyserman and Santos (2000), Key and Ovall (2011), Grayver et al. (2013), Grayver and Kolev (2015), Heagy et al. (2017), Castillo-Reyes et al. (2018), Castillo-Reyes et al. (2019), and Rochlitz et al. (2019).

Regardless of the chosen numerical scheme and target application, the state-of-art remarks that parallel computing technologies are fundamental for enhanced EM imaging of the Earth’s subsurface. The positive impact of HPC approaches on EM imaging has been recently reviewed by Newman (2014) and Osseyran and Giles (2015). Here, we identify two valuable HPC contributions to the geo-electromagnetic community. First, given the high computational cost of the solver computations, heterogeneous HPC technologies (general purpose processors and graphics processing units) can provide electrical resistivity maps in a feasible run-time. Second, HPC algorithms can help us work on the Frontier of geo-computing knowledge. In particular, it allows us to design and simulate increasingly realistic models in terms of scale and physical parameters.

4 Role of EM imaging for energy transition

The energy landscape forward requires, among other things, rethinking its value chain: exploration, exploitation, and monitoring. This reinvention process is crucial to designing energy transition routes and understanding their impacts. Several technological solutions are available to characterize and monitor new energy resources. In this section, we identify current trends in the field of EM imaging for critical applications in the energy transition. We also discuss some of the key associated potentials and limitations.

4.1 CO₂ sequestration and storage

Geological sequestration of CO₂ provides a temporary solution for reducing GHG emissions to the atmosphere (Vilamajó et al., 2013). This technique involves the capture of CO₂ emissions produced from industrial and power generation sources, followed by transport to underground geological storage sites and long-term isolation from the atmospheric system. We need to characterize and monitor sites suitable for CO₂ sequestration and storage for safety and operational reasons. EM imaging technologies are commonly used to characterize such storage sites by electrical resistivities distinctly different from those of the surrounding sediments.

Among the wide options of EM techniques, active-source methods may be particularly suitable to identify and characterize suitable sites for CO₂ storage. In this regard, we identify three advantages of active-source EM methods. First, it can resolve both electrically resistive and conductive geological structures. Second, in comparison with passive-source schemes, active-source methods offer better noise control and thus facilitate campaigns in regions with high cultural noise levels. Third, its penetration deep range is accessible by drilling, a useful feature to address the topic of validation through a direct comparison between synthetic and experimental data. With recent numerical and technological developments, the logistical challenges and the high computing cost for EM data processing have gradually been mitigated, and EM imaging for CO₂ sequestration and storage gained traction. One of the first EM imaging attempts for CO₂ storage dates to the 1990s, when Bailey (1994) and Fisher et al. (1994) analyzed the potential of EM data to characterize carbon storage sites in South America. Later, several numerical and computational techniques for EM imaging of CO₂ applications were developed. Commer and Newman (2009) presented joint EM experiments (active-source and passive-source) to significantly improve the delineation of a CO₂ plume, thus avoiding false assumptions about plume geometries. Streich et al. (2010) investigated the feasibility of EM techniques for exploring and monitoring different reservoir types (gas shales, geothermal reservoirs, and CO₂ storage sites). Numerical experiments of CO₂ reservoir models with varying configurations of resistivity provided valuable insights about the potential and limitations of EM methods to detect and monitor reservoirs. Bhuyian et al. (2012) conducted active-source EM experiments to map anomalies in CO₂ sequestration sites with shallow traps. Analysis of numerical results warns of CO₂ migration for the proposed models. A study about physico-chemical interaction and the spectral electrical properties of CO₂ sites was presented by Börner et al. (2015). This study also provides an empirical relationship for the impact of CO₂ storage on pore water conductivity. Impressive EM studies in real scenarios have been proposed by Ogaya et al. (2013), Vilamajó et al. (2013), and Ogaya et al. (2016). Here, the authors investigated the geoelectrical baseline model of the Hontomín site (Spain) for CO₂ geological storage in a deep saline aquifer.

Recently, Righetti et al. (2020) recognized CO₂ sequestration and storage technologies as a key component to stabilizing atmospheric GHG concentrations to reach the European Commission’s 55% emissions reduction target by 2030. However, the progress of EM imaging technologies for CO₂ applications has been slow, partially because CO₂ storage will facilitate the continued use of carbon energy sources fuels. Then, new EM technologies (modeling and inversion) will need to be developed and validated to characterize and monitor existing and new CO₂ infrastructures. In this regard, experimental data is fundamental to verify the robustness of the EM imaging technologies.

4.2 Geothermal reservoirs

Geothermal energy is one of the most promising alternatives for switching from conventional to renewable energy sources. It is making its way worldwide as an energy alternative to other fossil fuels, offering as advantages its renewable and innate nature of the land. Geothermal energy has zero emissions, and its continuous production is 24 h a day, 365 days a year. Also, its manageable nature makes it relevant in improving the grid stability of the renewables mix. However, geothermal energy is still immature, and several geothermal anomalies still need to be explored. By exploring these geothermal fields, we will understand the potential of its environmentally friendly energy source and its application to key social and industrial sectors. Later issues encourage researchers to develop technologies around geothermal energy. Most of these efforts aimed to develop models to appraise geothermal systems in an integrated way with greater accuracy, thereby maximizing the success rate and reducing the cost of drilling associated with geothermal projects. In addition, such accurate models would lessen any potential environmental impact.

EM imaging has proven to be a fundamental tool for scrutinizing the subsurface. In geothermal energy environments, EM techniques provide electrical resistivity distribution maps of great value. One of the first EM imaging attempts for geothermal applications dates to the 1980s/1990s, when Ward (1983) and Thanassoulas (1991) investigated synthetic EM responses for typical-form geothermal sites. Later, diverse and several impressive studies demonstrated the value of EM data sets for the detection, characterization, and monitoring of 2D/3D geothermal reservoirs (Spichak and Manzella, 2009; Streich et al., 2010; Peacock et al., 2013; Munoz, 2014; Bretaudeau et al., 2017; Didana et al., 2017; Darnet et al., 2019; 2020; Bretaudeau et al., 2021). All the aforementioned studies showed that EM surveys provide complementary and valuable information for the assessment of geothermal resources. Furthermore, it has been observed that high-quality EM data play a critical role in reducing the cost, risks, and uncertainty associated with the appraisal of geothermal sites.

Despite previous advancements, geothermal reservoir development with EM imaging technologies is still in its infancy. The study of EM measurements in the presence of metallic infrastructures (telephone networks, pipelines, railways, industrial facilities, and wells, among others) is of particular interest because the target areas are usually urbanized. Although numerically challenging, several studies have been performed in this regard, revealing a direct relationship between the presence of metallic artifacts and signal-to-noise ratio in EM responses (Um et al., 2015; Vilamajó et al., 2015; Wilt et al., 2020; Castillo-Reyes et al., 2021; Heagy and Oldenburg, 2022). The aforementioned authors remark on the importance of studying this behavior to avoid the misinterpretation of EM maps. Furthermore, careful survey design (synthetic data), dedicated data acquisition (experimental data), and robust numerical and computational techniques are required to build high-quality EM maps in geothermal regions (low, medium, and high enthalpy).

4.3 Gas hydrate

Several articles have reviewed fossil energy exploration using EM imaging technologies (Unsworth, 2005; Constable, 2006; Key and Ovall, 2011). In particular, the controlled-source electromagnetic (CSEM) technique has been widely used to explore hydrocarbon reservoirs since 2002 (Eidesmo et al., 2002; Ellingsrud et al., 2002). However, under increasing pressure to reduce its carbon footprint, the energy sector must develop and optimize its technology portfolios to enhance long-term value.

Clean energy plays a key role in the world’s low-carbon development, since it provides power for economic growth and social progress with less GHG emissions than carbon-based energy sources (Lin and Li, 2022). Gas hydrate is a clean, efficient, and promising environmentally friendly energy source (Makogon, 2010). Gas hydrate consists of natural gas molecules (the chief constituent of natural gas: methane) enclosed within a solid lattice of water molecules. Gas hydrate sources are of interest primarily for three reasons:

1) Potential as a clean energy source: Recently, have been recognized that there are huge amounts of natural gas, mainly methane, tied up in gas hydrate globally. Thus, gas hydrates are a potential energy resource (Boswell et al., 2020).

2) Role in climate change: methane is a potent GHG, so its escape to the atmosphere from natural gas hydrate could result in global warming (Boswell et al., 2020).

3) Production risks: Gas hydrate is a hazard in conventional hydrocarbon exploration. Hydrates may affect climate because when warmed or depressurized, they decompose and dissociate into water and methane gas, one of the GHG that warms the planet (Hunter et al., 2013), and even lead to geological disasters (Mienert et al., 2005; Pei et al., 2022).

On top of that, the exploration of gas hydrate reservoirs has become a hot spot nowadays, and EM imaging technologies could be applied to face the mentioned issues significantly. Gas hydrate is electrically resistive (ranging from hundreds to thousands of Ω m) compared to the surrounding water-saturated sediments (ranging from few to tens of Ω m) (Max, 2003). This electrical resistivity contrast provides the physical basis for exploring gas hydrates using EM techniques and obtaining information about gas hydrate distribution.

The CSEM technique has been widely recognized as one of the most effective methods for gas hydrate exploration (Schwalenberg et al., 2005; Zach and Brauti, 2009). One of the first attempts to introduce CSEM into gas hydrate exploration dates to the 1990s (Edwards, 1997). From that date, several CSEM experiments have been carried out to accurately infer the existence of gas hydrate resources and improve its drilling success rate (Weitemeyer et al., 2006; Evans, 2007; Newman et al., 2010; Weitemeyer et al., 2010; Key, 2016; Attias et al., 2018; Tharimela et al., 2019; Kannberg and Constable, 2020; Schwalenberg et al., 2020). EM imaging technologies can also estimate the hydrate saturation and concentration, providing valuable information for assessing this energy resource.

Another tool to investigate gas hydrate resources is the bottom simulating reflector (BSR), which is an essential presence mark of gas hydrate in seismic profiles (Singh et al., 1993; Majumdar et al., 2016). BSR usually indicates the bottom interface of the gas hydrate stability zone (BHSZ). Its seismic imaging corresponds to the wave impedance interface between the hydrate layer and the underlying free gas layer (Hillman et al., 2017). Therefore, it is common to use BSR as an indicator of gas hydrate stable zones (McConnell and Kendall, 2002; Mosher, 2011; Boswell et al., 2012; Monteleone et al., 2022). However, identifying BSR patterns from massive seismic data is remarkably challenging. The recognition of BSR signatures is usually obtained from visual interpretations of seismic images, such as biased judgments (Souza et al., 2019). Besides, recognizing weak, discontinuous, and absent BSR is another challenge (Chenin and Bedle, 2020). DL is a helpful tool for solving the above image identification problems, and its application to recognize BSR has been increasing rapidly. Geng and Wang (2020) proposes SeismicPatchNet, an efficient and resource-saving convolutional neural network for BSR identification. Chenin and Bedle (2020) developed an unsupervised machine-learning solution that combines multiple seismic attributes to improve BSR characterization. From these studies, the authors concluded that EM imaging and DL solutions could reveal helpful information about the gas hydrate reservoir and its content.

4.4 Environmental applications

EM imaging can also be applied to environmental applications. Examples which is most likely to lead to significant improvements are in the field of buried waste deposits and water reservoir characterization. Locating, delineating, and characterizing such areas requires accurate 3D subsurface models.

Waste disposal is one of the current and future environmental problems. It causes air and water pollution, enhances GHG emissions, produces hazardous gases and leachates, promotes massive land use, and exposure to dangerous chemicals (El-Fadel et al., 1997). Despite this, waste deposits in landfills remain the most economical and attractive disposal path for solid waste. In Europe, 2 151 million tonnes of waste were generated in 2020 (Eurostat, 2020). 31.3% of this waste quantity was landfilled in 2020 (Eurostat, 2020). These waste disposals constitute a severe problem for the region. Unfortunately, these settings remain poorly understood and explored by geophysical strategies. EM imaging technologies are an effective and faster option for obtaining detailed information about the extent and electric distribution of such waste deposits. Pioneer works about waste disposal characterization through EM techniques were presented by Tezkan et al. (1996), Zacher et al. (1996), and Pellerin and Alumbaugh (1997).

Furthermore, Tezkan (1999), Eigenberg et al. (1998), and Auken et al. (2006) revised the potential of EM imaging for hazardous-waste characterization studies. Recently, case studies about the electrical conductivity of such waste disposals were reported (Doll et al., 2000; Zhang et al., 2011; Di et al., 2014; Deidda et al., 2022). All these experiments were carefully designed to investigate waste disposals in industrialized regions and have confirmed the potential of EM techniques for the exploration and characterization of waste sites.

EM imaging technologies have also been applied for groundwater applications. Specifically, EM imaging has been used to reveal and understand the distribution of freshwater reservoirs because the electrical resistivity in these water resources is mainly controlled by the porosity and salinity of the pore water (Evans, 2007). Impressive case studies demonstrate the use of EM measurements for detecting and characterizing freshwater deposits (Andreis and MacGregor, 2008; Lien and Mannseth, 2008; Weymer et al., 2018; Attias et al., 2021; Ishizu and Ogawa, 2021). The aforementioned scientific works showed that EM imaging is a promising technique for imaging freshwater resistivity reservoirs in semi-arid and coastal areas. Finally, excellent literature reviews about EM techniques for near surface applications in freshwater and environmental applications were given by Pellerin (2002), Reynolds (2011), and Cassiani et al. (2020).

5 Deep learning in EM imaging

EM subsurface imaging aims to produce large-scale high-resolution soil maps that can provide essential information for geo-resources (e.g., energy, water). The rigorous generation of EM subsurface images requires solving the direct problem and the inverse problem (Chen, 2018). In the direct problem, also referred to as forward modeling, synthetic EM fields of the subsurface are computed. Then in the inverse problem, forward modeling EM responses are iteratively approximated to the real EM data. EM forward modeling is a non-linear mapping, and EM inversion is a non-linear approximation, which belongs to mathematical regression problems.

DL is very suitable for solving regression problems, and it has shown the potential in EM imaging (Puzyrev, 2019; Moghadas, 2020; Oh et al., 2020; Li et al., 2020; Shahriari et al., 2020a,b). As the first successful case of applying DL for EM inversion, Puzyrev (2019) pointed out that DL methods may open a new era for computational geosciences. In this section, we first elaborate on the application scenarios of DL in EM imaging, and then we identify the different types of coupled physics-DL, DL architectures and procedures in EM imaging. The suitability and accuracy of DL models are also presented. Finally, we discuss the potential and challenges of DL solutions in EM imaging in the future.

5.1 Application scenarios

DL has a wide application range for EM imaging, including onshore (Puzyrev, 2019; Li et al., 2021; Liu et al., 2021), offshore (Oh et al., 2018; 2020; Oh and Byun, 2021), induction (Moghadas, 2020; Zhu et al., 2020; Li et al., 2022), airborne (Li et al., 2020; Noh et al., 2020; Bang et al., 2021; Wu X. et al., 2022), and borehole (Shahriari et al., 2020a; Shahriari et al., 2020b; Shahriari et al., 2021; Shahriari et al., 2022). DL inversion methods can be flexibly applied to different EM data types mainly due to its complete standardization framework, which covers three stages: data generation, model training, and model prediction.

DL inversion methods have been demonstrated to effectively solve the computational difficulties caused by the complexity and multiplicity of available parameters and maximize the integration of multiple data while ensuring consistency. Recently, Wu S. et al. (2022) discussed several factors that affect DL inversion results, such as dimension, noise level, sample richness, and prior information. Notice that these factors are present in all DL inversion methods.

In comparison with traditional inversion methods (e.g., deterministic and probabilistic physics-based solutions), DL-based inversion routines require less computational effort (Puzyrev, 2019). Furthermore, DL inversion methods support near real-time reconstruction of subsurface resistivity distribution while ensuring numerical accuracy (Bai et al., 2020; Puzyrev and Swidinsky, 2021). Real-time DL inversion techniques also have the potential to perform statistical or probabilistic inversion processes (Alyaev et al., 2021). Real-time DL probabilistic inversion greatly improves the practicability of data-driven forward modeling in practical applications (Rammay et al., 2022). In addition, DL inversion methods also have great application potential in geophysical monitoring (Puzyrev, 2019). Real-time monitoring is an essential and challenging task for geophysical methods, especially for reservoir characterization studies (Colombo et al., 2020). Recently, Li and Yang (2021) successfully applied DL technologies to the real-time monitoring of fracturing fluid flow and solved the EM imaging problem with remarkable accuracy and computational efficiency.

5.2 Coupled physics-deep learning

DL in EM imaging is mainly based on data-driven strategies, avoiding the direct solution to the physical process of EM responses, thus significantly reducing the complexity of the non-linear solution. However, entirely data drive is heavily dependent on the EM data itself. In other words, the training process is absolutely divorced from physics, which may lead to DL results that do not satisfy Maxwell’s theory. Therefore, when the data set is incomplete, a common situation in EM imaging, the best solution is to couple DL with the physical process. This approach can fully use DL advantages and provide numerical approximations that meet EM physics. Recently, Guo et al. (2022) classified and summarized the coupled physics-DL strategies in EM imaging. Three types of physics-embedded models for EM imaging have been identified:

1) Learning after physics processing: This aims to add physical information before the model training process. Almost all the work mentioned in Subsection 5.1 belongs to this type.

2) Learning with physics loss: This type embeds the forward operator into the network parameter optimization. Then, the regularization of non-physical solutions is performed as composite loss functions. Physics-informed neural network (PINN) (Raissi et al., 2019; Gong and Tang, 2022) is one the most representative coupled physics-DL solutions. Recently, Liu et al. (2022) embeds the forward operator into the network architecture. However, the loss of the partial differential equation is calculated by a traditional EM forward modeling scheme instead of the automatic differentiation of the neural network proposed by PINN. Thus, reducing its applicability to complex geological models with experimental data.

3) Learning with physics models: This aims to surrogate models by directly solving the EM responses (Shahriari et al., 2020a). This type is the most complex since it resolves the entire EM physical phenomena (Guo et al., 2022).

After examining these coupled physics-DL strategies in EM imaging, one can see that substantial potential exists for EM imaging (Bording et al., 2021; Yan et al., 2022). However, additional effort is still needed to design, implement, and validate DL schemes for EM imaging. Such progress must address increasing performance and accuracy of different DL-based solutions (e.g., deep neuronal networks (DNN), recurrent neural networks (RNN), convolutional neural network (CNN), physics-informed generative adversarial network (GAN)) (Chen et al., 2020). In this regard, Colombo et al. (2021a), Colombo et al. (2021b) has proposed a hybrid workflow for embedding physics into an inversion routine with a DNN kernel. In this regard, Figure 3 shows an overview of modern DL-based work flow for EM imaging.

FIGURE 3

FIGURE 3. Overview of DL-based work flow for EM imaging.

5.3 DL architectures and procedures

The DL architectures used in EM imaging are summarized in Table 3. These architectures have been employed to extract spatial and temporal features from EM data, learn representations, and enhance the imaging performance (Chen et al., 2020). In particular, CNN have demonstrated effectiveness in capturing spatial features, while RNN are suitable for processing sequential EM data and capturing temporal dependencies. GAN have been utilized for generating synthetic EM data to augment training datasets or for data reconstruction. Autoencoders, as unsupervised learning approaches, have shown potential in denoising EM data and reducing dimensionality.

TABLE 3

TABLE 3. DL architectures in EM imaging.

On the other hand, Table 4 provides an overview of the DL procedures employed in EM imaging. These procedures encompass several stages of the workflow, including data preprocessing, model training, model evaluation, comparison with baselines, and considerations of computational resources (Hestness et al., 2019; Hestness et al., 2020; Hestness et al., 2021a) Data preprocessing techniques are applied to enhance the quality of EM data through noise reduction, normalization, and augmentation. Model training involves the optimization of DL models using specific algorithms and hyperparameter tuning. Model evaluation metrics, such as mean squared error (MSE), accuracy, or F1 score, are utilized to assess the performance of DL models. Comparison with baselines involves comparing the performance of DL models with traditional methods or existing state-of-the-art techniques in EM imaging. Computational resources, including hardware (e.g., GPUs, HPC systems) and software libraries, play a crucial role in facilitating the training process of DL models in EM imaging.

TABLE 4

TABLE 4. DL procedures in EM Imaging.

5.4 Suitability and accuracy of DL models

DL techniques have demonstrated their efficacy in a wide range of fields, including EM imaging. When considering the suitability of data for DL in EM imaging, several technical aspects come into play (Hestness et al., 2019; Hestness et al., 2022). Firstly, the availability of large and diverse datasets is crucial for training accurate DL models (Alzubaidi et al., 2021). These datasets should encompass a broad spectrum of EM signals, representing different frequencies, polarizations, and propagation characteristics. Additionally, including corresponding ground truth information, such as geological formations or subsurface features, enhances the learning process and enables more precise imaging.

Fortunately, the geo-electromagnetic community has made significant strides in generating extensive datasets over the past three decades. Traditional geophysical surveys have contributed to these datasets, covering applications like hydrocarbon exploration and geological mapping Yu and Ma, 2021. Furthermore, emerging areas such as geothermal energy reservoir characterization, CO₂ capture and storage, water prospecting, and monitoring of hazardous-waste deposits have enriched the available data. These datasets, accumulated from diverse sources and applications, offer valuable resources for training DL models in EM imaging. In this context, Table 5 depicts the input and output features for DL-based EM imaging solutions.

TABLE 5

TABLE 5. Input and output features for DL solutions.

In parallel with the availability of comprehensive datasets, advancements in numerical schemes, algorithms, and access to HPC systems have revolutionized the development of innovative EM imaging technologies (Shams et al., 2017). Sophisticated numerical techniques, such as FD and FE methods, have been refined to accurately model the complex interactions between EM waves and subsurface structures. Additionally, novel algorithms have been devised to optimize the performance of DL models in processing EM data. The proliferation of HPC systems has provided the computational power necessary for handling large datasets and training complex DL architectures.

The combination of these technical advancements and the availability of diverse data has created a conducive environment for deploying DL models in EM imaging. DL models have shown remarkable accuracy in numerous published papers, with significant improvements over traditional approaches (Guo et al., 2019; Guo et al., 2019; Guo R. et al., 2020; Guo et al., 2020; Guo et al., 2021a; Guo et al., 2021b; Guo et al., 2021; Guo et al., 2021; Guo et al., 2022). However, assessing the accuracy of DL models in EM imaging requires careful consideration of various factors. The complexity of the imaging problem, the quality and diversity of the training data, the architectural choices, hyperparameter tuning, regularization techniques, and the selection of appropriate evaluation metrics all influence the performance of DL models.

To provide a comprehensive evaluation of DL models in EM imaging, future studies should emphasize rigorous benchmarking. This entails comparing DL models against existing methods using standardized datasets and well-defined evaluation metrics. Additionally, conducting thorough sensitivity analyses and uncertainty quantification studies can shed light on the robustness and reliability of DL models in different EM imaging scenarios. These technical aspects contribute to a deeper understanding of the capabilities and limitations of DL models in EM imaging, facilitating further advancements in this field.

5.5 Potential and challenges

Although images obtained from a single geophysical data type can help to improve subsurface models, ambiguity often must be addressed. An alternative strategy for reducing model ambiguities is performing a joint inversion of two or more geophysical data types to produce a single model that unifies the relevant information of the individual data sets. Therefore, the joint inversion can be considered a multi-physics inversion method aiming to establish the relationship between different physical parameters with higher resolution than that obtained from a single geophysical data type.

Multi-physics inversion schemes have become popular for building subsurface models that agree with data acquired with different geophysical methods. Combining data sets with complementary sensitivity and resolution properties in a joint routine can mitigate problems related to the inverse modeling task, such as limited resolution and non-uniqueness. Subsurface models obtained from joint inversion techniques are inherently consistent with multiple data types and can thus reduce ambiguities. These advantages are essential for EM imaging, whose resolution is much lower than seismic imaging.

From a computer science perspective, the multi-physics inversion process is understood as complex algorithms trying to find accurate solutions to highly challenging parameter-dependent problems. Thus, inverse modeling in realistic applications requires high computational effort and intensive human interaction (Um et al., 2022). In this context, the use of DL technologies to solve coupling relationships between different geophysical data types is undoubtedly a highlight. DL methods can learn both prior parameter relationships and structural similarity of the multi-physics data sets. Therefore, the accuracy of EM imaging may be greatly improved (Chen et al., 2022; Guo et al., 2022), and the uncertainty of imaging could be reduced (Um et al., 2022). These aspects are crucial for DL decision-making inversion and need further study (Oh and Byun, 2021).

On top of that, DL for EM imaging is currently an active research topic. For example, learning methods such as deep reinforcement learning have been recently explored by Wang et al. (2022). Despite its popularity, using DL to build EM subsurface maps is an open topic and requires additional effort. Such progress could address in three aspects. First, the initial problem of establishing a complete EM data set has yet to be solved (Puzyrev, 2019). Second, the generalization of DL solutions is widely questioned due to data dependency. Although coupled physics-DL can reduce the severe dependence on data to a certain extent, the research on the portability of the trained DL models (e.g., transfer learning mentioned in Puzyrev (2019); Puzyrev and Swidinsky (2021)) needs to be further developed. Finally, the third aspect should focus on DL technology development for multi-physics inversion, thus extending its uses to complex and untested renewable energies in particular and geo-resources in general.

6 Discussion and conclusions

In this paper, we have reviewed the literature in EM imaging and DL to find the path for a sustainable transition from oil fuels to renewable energies (United-Nations, 2015; SDG, 2019). The analysis framework is formed by advances in numerical methods, computational strategies (traditional and DL-based solutions), and its relevant applications for the energy transition route. As modern society is directed toward a future where geo-resources are a dominant figure in the energy sector, the utilization of EM imaging technologies is becoming a key factor for achieving the next step. It became evident that incorporating such subsurface exploration technologies in energy transition strategies is necessary to have enough potential to completely submerge in zero-carbon energy systems.

After examining the points raised in this review, one can see that a substantial agenda exists for EM imaging and DL-based solutions for the transition to renewable energies. Such progress must address in increasing detail the geological complexity of geo-resources and increasing target depths, fostering an unprecedented EM imaging technological development for renewable fuels at local and regional levels. The development, improvement, and application of new EM imaging techniques coupled with innovative simulation strategies will reduce the average cost for exploration while increasing the drilling success rate. These EM imaging tools can also be used to improve measurement precision and apply faster analysis of acquired EM data to achieve a feasible model of the target regions. In addition, such accurate models would lessen any potential environmental impact. This article highlights areas of progress, challenges, and opportunities to transfer expertise from coal energies to renewable sources. Continued complexities in zero-carbon energy pathways and the timeless nature of transitions research underscore a genuine and ongoing need for innovative EM imaging solutions.

Although over the last few years, a big effort has been made in the EM imaging community to investigate the subsurface, an additional effort is still needed to:

1) Obtain more detailed and better-resolved reconstructions of the subsurface conductivity/resistivity in a wide range of geological settings, enabling performance and reliability improvement of shallow and deep energy geo-resources.

2) Reduce and quantify model ambiguities to ensure a reliable pre-drilling assessment of geo-resources, thus reducing costs, environmental impact, and risks.

3) Accelerate EM data processing and reduce its cost, enabling renewable energy development in new regions and supporting the assessment of new concepts for local energy supply.

4) Increase the maturity of HPC-enabled and DL-based EM imaging solutions to face massive data sets with accuracy and computational efficiency. Furthermore, studying emerging technologies and their potential (e.g., quantum computing (Piattini et al., 2020)) for EM imaging is critical for the near future.

5) Generate actionable knowledge that increases social engagement about energy efficient, environmentally sound, and economically viable electricity generation and heating/cooling from renewable resources.

The main limitation encountered in this analysis was data dependence. Several included model studies dealt with idealized complete global/regional-scale EM experiments using ad hoc EM routines. In line with this, EM imaging development should be conducted in such a way that it leads to analyzing the whole EM behavior of any realistic and relevant setup for the renewable energy sector. In this regard, further research should be conducted to identify how numerical methods, HPC technologies, and DL solutions mark the development of EM imaging tools used for geo-resources exploration and which features these have and need. Furthermore, open access to codes and their input data must be promoted. Doing so could enhance the exploitation of EM imaging tools and allow for a more active engagement with a broader audience that can actively contribute and enrich the energy transition discussion by using imaging outcomes while also validating the robustness of EM imaging technologies in real-world scenarios.

In summary, this review sheds light on the current status, challenges, and prospects of EM imaging technologies for building a carbon-neutral future in the energy sector. However, to bridge the gap between the zero-carbon energy rhetoric system and reality, the urgent need to restructure global development systems and protect geo-resources requires swift and collaborative actions by researchers, policymakers, investors, and consumers around the world, aiming at reducing GHG emissions and promoting renewable energies development. Furthermore, the global scientific and technological innovations that foster the green economy must be financially and strategically rewarded to build a safer future based on zero-carbon energy sources.

Author contributions

OC-R conceived and supervised the overall study, wrote the manuscript, critically revised the manuscript. XH contributed to the application scenarios section and critically revised the manuscript. BW contributed to the DL theory. ZG critically revised the manuscript. YW contributed to the gas hydrate theory. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the European Union’s Horizon 2020 research and innovation programme under grant agreements No. 955606 (DEEP-SEA) and No. 777778 (MATHROCKS). Furthermore, the research leading of this study has received funding from the Ministerio de Educación y Ciencia (Spain) under Project TED2021-131882B-C42.

Conflict of interest

Author OC was employed by Barcelona Supercomputing Center.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alumbaugh, D. L., Newman, G. A., Prevost, L., and Shadid, J. N. (1996). Three-dimensional wideband electromagnetic modeling on massively parallel computers. Radio Sci. 31, 1–23. doi:10.1029/95rs02815

REVIEW article

Electromagnetic imaging and deep learning for transition to renewable energies: a technology review

1 Introduction

2 Electromagnetic data for enhanced imaging of the Earth

3 Expertise transfer from coal energies to renewable sources

3.1 Physical behavior

3.2 Numerical strategies

3.3 Computational strategies

4 Role of EM imaging for energy transition

4.1 CO2 sequestration and storage

4.2 Geothermal reservoirs

4.3 Gas hydrate

4.4 Environmental applications

5 Deep learning in EM imaging

5.1 Application scenarios

5.2 Coupled physics-deep learning

5.3 DL architectures and procedures

5.4 Suitability and accuracy of DL models

5.5 Potential and challenges

6 Discussion and conclusions

Author contributions

Funding

Conflict of interest

Publisher’s note

References

4.1 CO₂ sequestration and storage