- 1School of Management, Xi’an University of Architecture and Technology, Xi’an, China
- 2College of Economics and Management, Shenyang University of Chemical Technology, China
- 3Lazaridis School of Business and Economics, Wilfrid Laurier University, Waterloo, ON, Canada
Risk assessment is critical to ensure the safe operation of oil and gas pipeline systems. The core content of such risk assessment is to determine the failure probability of the pipelines quantitatively and accurately. Hence, this study combines the MATLAB neural network toolbox and adopts an Radial Basis Functions (RBF) neural network with a strong non-linear mapping relationship to build a corrosion failure probability prediction model for buried oil and gas gathering and transmission pipelines. Based on the hazard identification of pipeline corrosion failure, the model summarizes the causes of corrosion failure and determines the input and output vectors of the neural network based on the fault tree. According to the selected learning samples, through the design and training of network parameters, the RBF neural network that can predict the system failure probability is finally obtained. Taking the failure probability of 30 groups of high-pressure gathering and transmission pipelines of gas storage as an example, the capability of inputting the probability of the bottom event and outputting the probability of the top event is demonstrated through training data. Our results show that the calculated failure probability based on the fault tree analysis model is consistent with the predicted failure probability based on the RBF neural network model. Hence, the RBF neural network model is shown to be reliable in predicting the corrosion failure probability of buried pipelines.
1 Introduction
Oil and gas pipelines bring a convenient and efficient energy supply to economic development. Due to the vulnerability of pipeline materials and the particularity of transmission medium, long-term oil, and gas pipelines face the risk of corrosion failure (Amaechi et al., 2022; Li et al., 2022; Wu et al., 2022). In the corrosion failure risk assessment of oil and gas pipelines, the failure probability assessment of pipelines is the core content of a quantitative risk assessment of corrosion failure. The assessment of failure probability can provide a basis for making monitoring and maintenance plans for corroded pipelines, which is more practical. Therefore, it is necessary to study the evaluation method of corrosion failure probability of oil and gas pipelines.
Many scholars have studied the calculation method of corrosion failure probability of oil and gas pipelines. According to the principle of Bayesian network analysis, Hu et al. (2009) calculated the probability of pipeline corrosion failure by analyzing the probability and statistical relationship between the sub-node and the root node and using conditional independence. Luo and Jiang (2015) proposed an evaluation method for calculating the reliability of oil and gas pipelines based on the probabilistic artificial neural network of the Bayesian classification decision. Yu et al. (2016) combined the grey theory and Markov chain theory to predict the corrosion life of oil and gas pipelines through the constructed model. In order to predict the occurrence of pipeline corrosion failure and reasonably control pipeline corrosion, Liu et al. (2019) established the failure probability analysis model of the minimum cut-set basic event parallel system based on the failure fault tree. Based on the JC method and orthogonal transformation, Zhang et al. (2019) proposed a multi-mode failure probability calculation method for corroded pipelines considering relevant random variables using a multidimensional normal distribution function. To improve the prediction accuracy of pipeline corrosion rate, Li et al. (2021) built an unbiased grey model based on the traditional grey model. They introduced the Markov model to modify the prediction results.
According to the existing research, the mathematical models for estimating the corrosion failure probability of oil and gas pipelines mainly include the Markov model, common cause failure model, Bayesian network model, and artificial neural network model (Li et al., 2017; Taleb-Berrouane et al., 2021). However, these estimation methods have limitations. For example, the main problem of the Markov model is that it is based on exponential distribution and assumes that the failure probability of the bottom event remains unchanged. The distribution of conditional failure probability in the common cause failure model cannot be obtained. Still, it is assumed that it obeys a certain distribution, and the result deviates significantly from reality. The Bayesian network model can effectively combine prior knowledge and subjective probability. However, it requires a lot of data, and its analysis and calculation are more complex. In the case of complex problems, this contradiction will be more prominent. In addition, the traditional fault tree analysis method combines the importance method and the fuzzy evaluation method. Although it can calculate the more comprehensive failure probability, it cannot make a large number of probability predictions. At the same time, the comprehensive application of multiple models makes the fault tree software unable to play its expected role in the calculation, which also leads to a considerable amount of calculation. Thus, the neural network has irreplaceable advantages in predicting the failure probability of oil and gas pipelines.
So far, the application of neural network models in oil and gas transportation safety evaluation has not been comprehensive. Although a neural network model can evaluate pipeline corrosion rates and risks, there is no mature research on pipeline failure probability prediction (Xiao et al., 2022; Yu et al., 2022). However, the RBF neural network can better capture the multidimensional non-linear correlation between the relevant parameters and the pipeline failure probability. Hence, this paper attempts to apply the RBF neural network model to predict the corrosion failure probability of oil and gas pipelines. An RBF neural network is adopted for prediction. Through network training and learning of the known samples, the optimal parameters are derived, based on which the corrosion failure probability of other samples is predicted.
The rest of the paper is organized as follows. The necessity of the RBF neural network is analyzed, and its MATLAB implementation is explained based on the introduction of the RBF neural network model in Section 2. After identifying the hazards of corrosion failure of oil and gas pipelines, the input and output vectors of the RBF neural network are designed, and appropriate network parameters are selected through training and learning samples in Section 3. In Section 4, based on the comparative analysis of fault tree analysis results and RBF neural network prediction results, the feasibility of using RBF neural network to predict the corrosion failure probability of buried oil and gas pipelines is verified. Finally, a summary of the results and further understanding are considered.
2 Neural network model and its implementation in MATLAB
2.1 Selection of neural network model
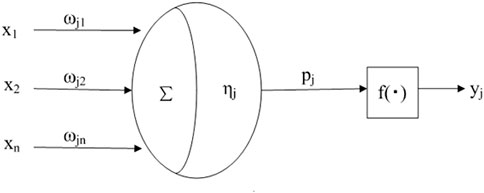
The artificial neural network is a theoretical mathematical model modeled on brain activity. It is a non-linear adaptive system composed of a large number of processing units (i.e., neurons) connected in a certain way. A typical feature of a neural network is that it can predict multivariable models without any correlation transformation or assumption of relevant input variables. It is based on actual observation data or other theoretical data used for training verification. The implicit non-linear relationship between input and output variables is extracted and approximated by a training neural network model (Xu et al., 2021; Zhang et al., 2021; Zhang et al., 2022). The elements of the neural network include neurons, weights, etc. The relationship between the elements is shown in Figure 1.
According to the relationship between the elements of the neural network, the neural model can be expressed as follows:
where
At present, the BP network and RBF network are used in the prediction of pipeline failure probability. BP network model is a feedforward neural network that propagates the error back. It uses the stored mapping relationship to output the data to be predicted without function. That is to say that the output value can be obtained without function operation. Before reaching the set error square sum, the weight value and threshold value can be adjusted by continuous backpropagation. Although the BP network is simple for calculation, it is easy to fall into a local minimum value, and its error cannot be reduced no matter how many iterations. Compared with many disadvantages of the BP network, the RBF (radial basis function) neural network shows its advantages. Its network topology can be changed according to specific problems. The network has adaptive and self-organizing capabilities and can also perform data fusion in a wide range in computing speed, thus reducing the network computing time (Peng et al., 2020). Therefore, this study intends to use RBF neural network to predict the corrosion failure probability of buried oil and gas pipelines.
2.2 RBF neural network
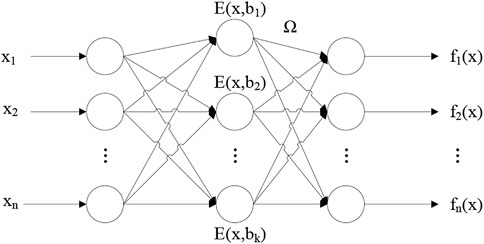
The RBF neural network is a supervised learning network. It has a simple structure, fast training speed, and can approximate non-linear functions with arbitrary accuracy. The most basic RBF neural network includes three layers: input layer, hidden layer, and output layer. After the samples are input into the network through the input layer, they reach the hidden layer. The hidden layer maps the input to a new space through an activation function, and then the system will linearly weigh the output of the hidden layer neurons to obtain the output value of the network (Wang et al., 2021; Yang and Fang, 2022). The topology of the RBF neural network is shown in Figure 2.
In Figure 2,
2.3 Implementation of MATLAB
Since MATLAB provided a neural network toolbox, it has become the first choice for engineers to analyze and design neural networks (Zhu et al., 2021). The neural network toolbox is one of many toolboxes developed in the MATLAB environment. It is based on the artificial neural network theory. It uses Matlab programming language to form many activation functions of neural networks, such as S-type, linear, competitive layer, saturated linear, and other activation functions, so that the designer’s calculation of the selected network output can be transformed into the call of activation functions. In addition, we can use MATLAB language to compile various subprograms for network weight training according to different typical procedures for modifying network weights and the training process of the network.
3 Corrosion failure probability prediction model for buried oil and gas pipelines
3.1 Hazard identification of corrosion failure of buried oil and gas pipelines
Based on fault tree analysis, this study analyzes the corrosion hazards of buried oil and gas pipelines. First, the top event of the fault tree should be defined. The top event is the starting point and main body of the fault tree analysis. The top event should be determined according to the characteristics of the analysis object. According to the risk degree of possible accidents in the fault tree, the hazardous event that has the most significant impact on the system should be taken as the top event of the fault tree. Then, the specific analysis should be carried out according to the principle of preparing a fault tree for one accident (Zhou et al., 2021; Chen et al., 2022; Irfan et al., 2022).
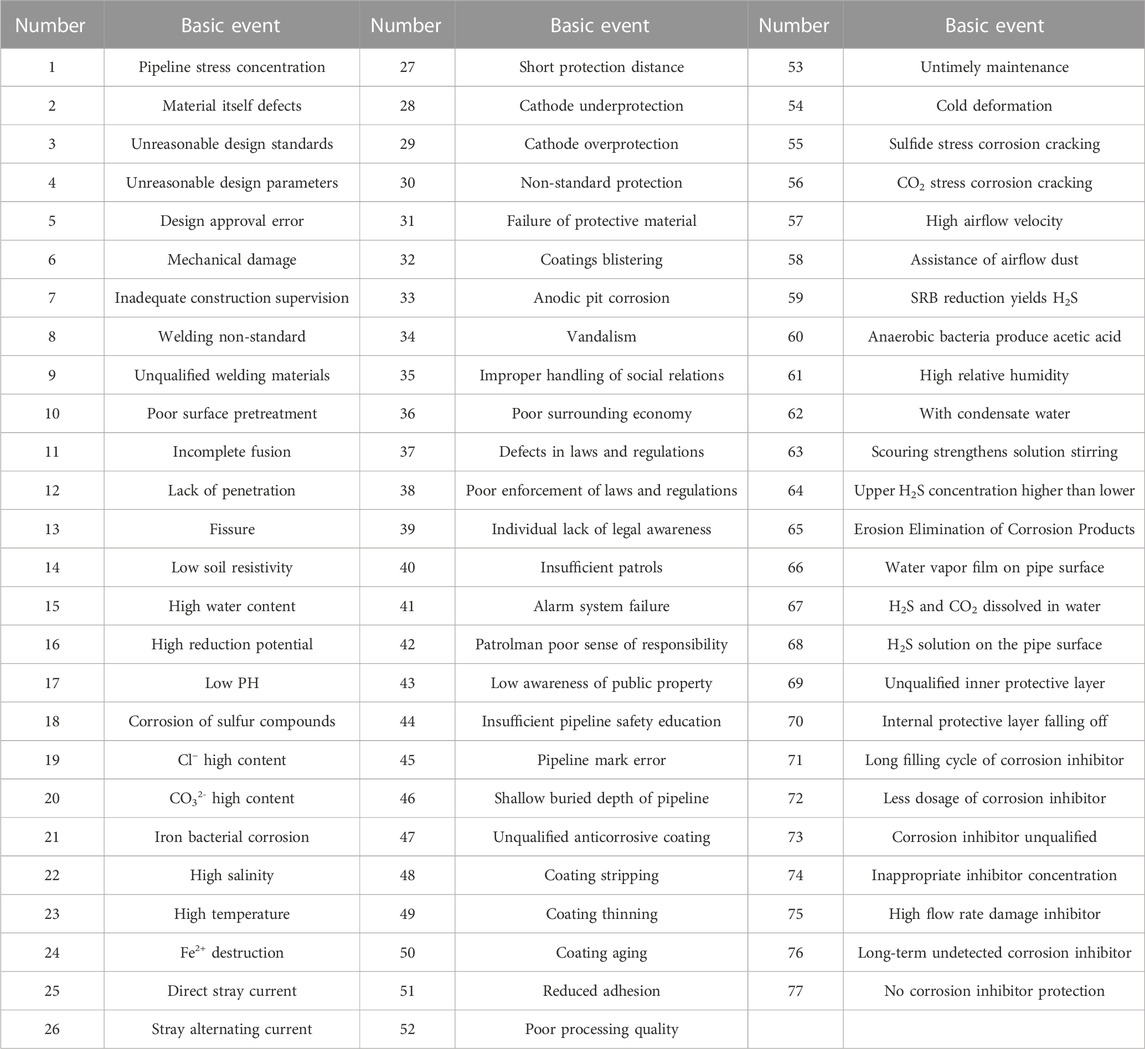
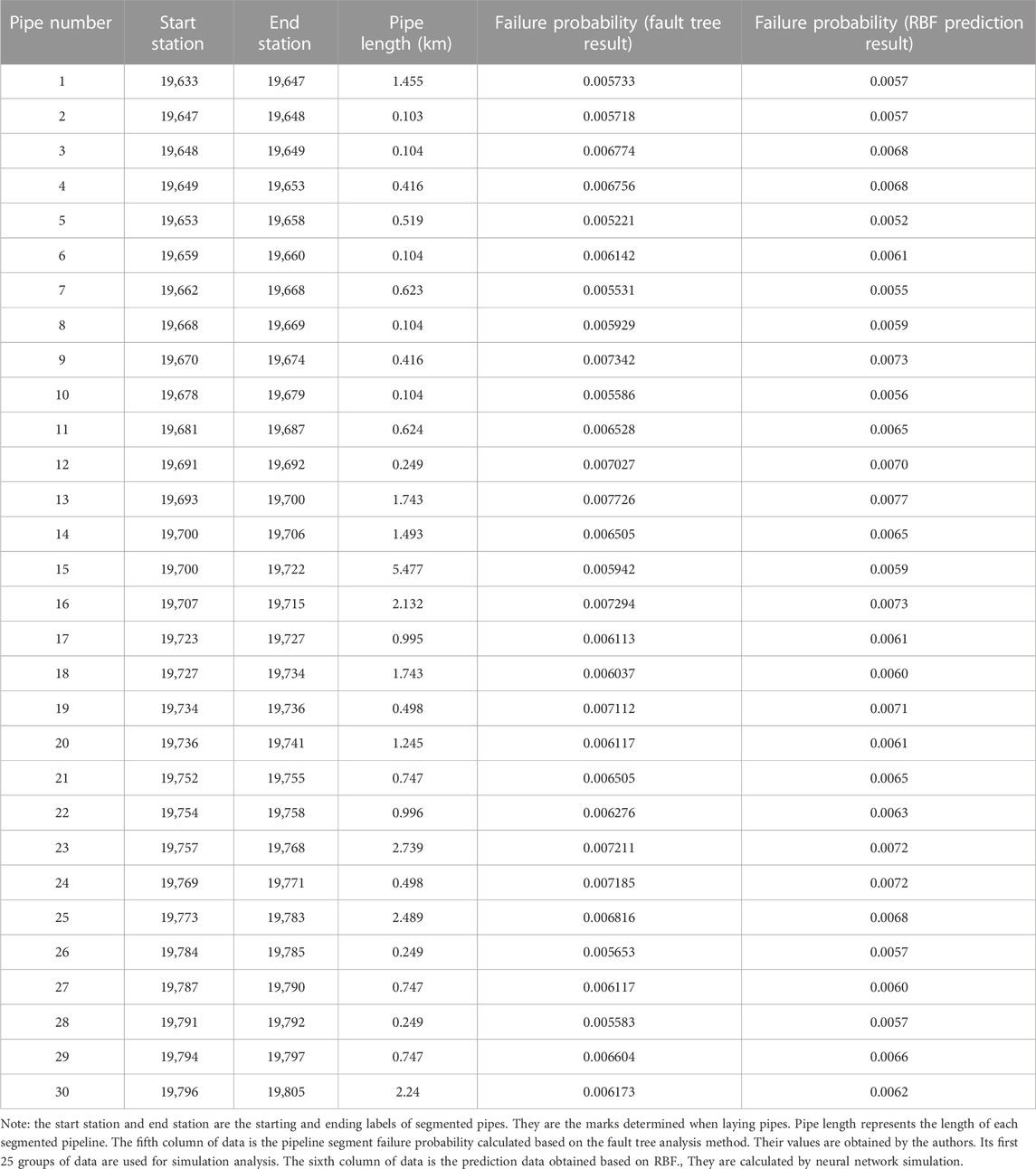
According to the above fault tree analysis principles, this study regards buried pipeline corrosion leakage as a top event. The direct cause of pipeline leakage is buried corrosion and internal corrosion, and any of these two causes will lead to pipeline failure. These two causes are taken as the second top events and analyzed similarly until the basic events representing various fault events are found (Ding et al., 2019; Huang et al., 2020). The specific list of basic events is shown in Table 1.
3.2 Establishment of RBF neural network prediction model
The corrosion failure probability of buried oil and gas pipelines is a non-linear function related to the basic event factors of the fault tree. The neural network model for predicting the failure probability of buried oil and gas pipelines established in this study is essentially a non-linear relationship mapping model between 77 input variables of failure influencing factors and one output variable of failure probability. The specific process is as follows.
3.2.1 Design input and output vectors
In this study, 77 basic events determined by fault tree analysis are taken as neuron parameter vectors of the neural network input layer. According to the analysis, when hiring experts to evaluate the basic events of the fault tree, the experts give a linguistic description of their probability of occurrence based on the attributes of the basic events. There are five natural language variables: little, fairly little, medium, fairly big, and big. Since the input variable must be a specific value between (0, 1) when conducting RBF neural network prediction training, this study will try to convert the language variable into a numerical variable (Landquist et al., 2016; Guo et al., 2019; Zhang et al., 2020), as shown in Table 2.
Through the corresponding transformation between language variables and numerical variables, it can be determined that the input layer neuron is a 77-dimension numerical vector, and the output layer neuron is a 1-dimension numerical vector.
3.2.2 Select learning samples
The training verification samples proposed in this study are from the high-pressure buried gathering and transmission pipeline network of the Suqiao Gas Storage Complex in North China Oilfield. At present, there is no general method for selecting the number of training samples. Theoretically, fewer training samples may make a neural network insufficient, leading to inadequate extrapolation ability of neural network prediction. Too many training samples will make the input variables of the neural network redundant, increasing the burden of neural network training. At the same time, the neural network will be overfitted due to excessive information surplus (Lin et al., 2018; Jiang et al., 2022; Xu et al., 2022). Based on this, this study extracts the first 25 pipeline segments from the 30 pipeline segments included in the gathering and transportation network as learning samples to train the network.
3.2.3 Design and training parameters
RBF neural network is a model widely used in system prediction and has mature technology. According to the design principle of the RBF neural network, the value of spread has a great impact on the network performance, which will be discussed in detail later.
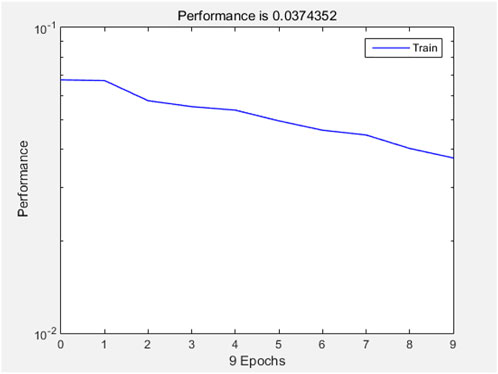
Based on MATLAB programming operation, RBF neural network training curve is shown in Figure 3 (see the Supplementary Material for Matlab code). It can be observed that the global error of the network can reach below 0.05 after nine times of training. Therefore, the established RBF neural network can converge quickly.
3.3 Parameter selection of RBF neural network
The RBF neural network model mainly includes two parameters: the radial basis function and the value of the spread. In the study, the relative error
where
In Eq. 4, the performance of the neural network model is inversely proportional to the value of the relative error
The general creation functions of RBF networks include newrb and newrbe. Combined with the calculation of the evaluation index, the influence of the value of spread on the performance of the RBF network mainly includes the following two cases.
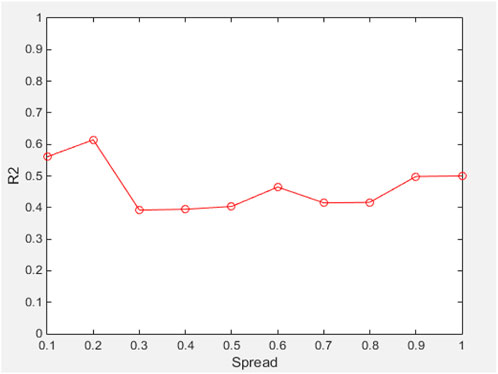
3.3.1 Newrb radial basis function network creation function and spread value
When newrb is selected as the RBF network creation function, the network is trained according to the spread value, and the corresponding deermination coefficient
3.3.2 Newrbe strict radial basis function and spread value
When newrbe is selected as the RBF network creation function, the network is trained according to the spread value, and the corresponding determination coefficient
It can be seen from Figures 4, 5 that different spread values have different effects on RBF neural network performance. For the newrb function, when the spread is 0.2, the network performance is the best, and the corresponding test set determination coefficient is 0.6145. For the newrbe function, when the spread value is 0.5, the network performance is the best, and the corresponding test set determination coefficient is 0.6864. Generally, the value of the spread is proportional to the smoothness of the function. According to the principle of network parameter selection, newrbe is selected as the radial basis function in this study, and the spread value is 0.5.
4 Comparative analysis of prediction results
The corrosion failure probability of buried gathering pipelines is calculated based on the trained RBF neural network, and the specific results are shown in Table 3.
According to the data in Table 3, the comparison results are shown in Figure 6.
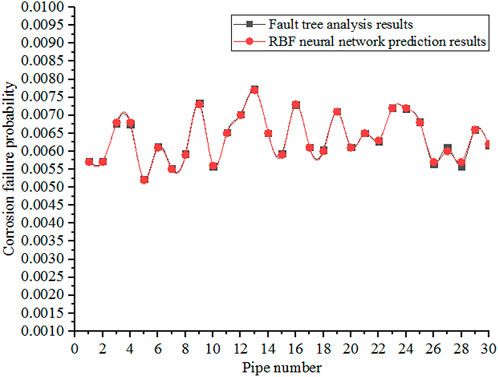
FIGURE 6. Comparison diagram of corrosion failure probability results of buried gathering and transmission pipeline.
It can be seen that the failure probability calculated based on the fault tree analysis model is consistent with the failure probability predicted based on the RBF neural network model. It is feasible to use the RBF neural network to predict the corrosion failure probability of buried oil and gas pipelines. Therefore, managers can directly calculate the failure probability prediction data from the network by combining the actual original data and using the trained RBF neural network model. Because the neural network has a strong non-linear mapping relationship, the RBF neural network model improves the accuracy of pipeline corrosion failure probability prediction when the input and output relationships are completely unknown. At the same time, the RBF neural network model avoids the huge amount of calculation. It can save a lot of time and improve calculation efficiency, providing an evaluation method for the safety and reliability of the oil and gas transportation system.
5 Conclusion
In this study, an RBF neural network is introduced to predict the corrosion failure probability of buried oil and gas pipelines. A prediction model based on Matlab neural network toolbox is established. The prediction model is applied to calculate the corrosion failure probability of the high-pressure gathering and transmission pipeline network of the gas storage. Our results are consistent with the failure probability results obtained based on the fault tree model. Hence, the effectiveness of the RBF neural network prediction model is verified.
In this study, when using neural networks to solve practical problems, it is found that the radial basis function and the spread value of the RBF neural network prediction model will significantly affect the prediction accuracy. Through repeated trial and analysis, when the radial basis function is newrbe and the spread value is 0.5, the network performance of the RBF prediction model is optimal.
The accuracy of the prediction results of the RBF neural network model constructed in this paper is related to various factors. The selection of model layers, number of neurons, transfer function and training error values, and even the choice of training samples will significantly affect the accuracy of the prediction results. Therefore, for future research, it is necessary to conduct a more in-depth study on the selection of model-related parameters.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
GD research is supported by 2020 Liaoning Provincial Education Department Research Project (Project # WJ2020002; Project Title: Theoretical Expansion, Empirical Test and Applied Research on Local Market Effect).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1148407/full#supplementary-material
References
Amaechi, C. V., Hosie, G., and Reda, A. (2022). Review on subsea pipeline integrity management: An operator’s perspective. Energies 16 (1), 98–12. doi:10.3390/en16010098
Chen, L. N., Qi, G. F., Han, Q., Peng, X. W., and Ji, J. (2022). Study on failure probability calculation method of water injection pipeline based on T-S fuzzy fault tree and Bayesian network. Saf. Health & Environ. 22 (9), 38–45. doi:10.3969/j.issn.1672-7932.2022.09.008
Ding, R., Yao, B. H., and Fang, X. B. (2019). Analysis of corrosion factors and discussion of protection countermeasures of long-distance buried oil and gas pipeline. Appl. Chem. Ind. 48 (12), 2972–2977. doi:10.16581/j.cnki.issn1671-3206.2019.12.016
Gao, X., Ma, Y. X., Tang, X. B., and Lu, X. R. (2019). Study on self-learning and automatic design of smart station’s fiber optic circuit based on MATLAB neural network algorithm. Power Syst. Prot. Control 47 (22), 159–167. doi:10.19783/j.cnki.pspc.181543
Guo, J. M., Qi, J. P., and Li, X. Y. (2019). Fault tree reliability analysis of EMU braking system based on fuzzy theory. Meas. Control Technol. 38 (4), 73–77. doi:10.19708/j.ckjs.2019.04.016
Hu, M., Gao, J., and Tan, L. W. (2009). Application of Bayes net analysis in calculation of corrosion failure probability. Process Equip. Pip. 46 (5), 52–56. doi:10.3969/j.issn.1009-3281.2009.05.015
Huang, K., Yang, L., and Li, A. R. (2020). Influencing factors of interference between corrosion defects in the inner and outer wall of oil & gas transportation pipelines. Surf. Technol. 49 (3), 199–223. doi:10.16490/j.cnki.issn.1001-3660.2020.03.025
Irfan, M., Elavarasan, R. M., Ahmad, M., Mohsin, M., Dagar, V., and Hao, Y. (2022). Prioritizing and overcoming biomass energy barriers: Application of AHP and G-TOPSIS approaches. Technol. Forecast. Soc. Change 177, 121524. doi:10.1016/j.techfore.2022.121524
Jiang, F., Zhang, W. Y., and Peng, Z. J. (2022). Multivariate adaptive step fruit fly optimization algorithm optimized generalized regression neural network for short-term power load forecasting. Front. Environ. Sci. 10, 1–13. doi:10.3389/fenvs.2022.873939
Landquist, H., Rosén, L., Lindhe, A., and Hassellöv, I. M. (2016). VRAKA—A probabilistic risk assessment method for potentially polluting shipwrecks. Front. Environ. Sci. 4, 1–14. doi:10.3389/fenvs.2016.00049
Li, H. R., Zheng, D. K., Cheng, Y. P., He, T. L., and Tang, S. F. (2021). Application of optimized grey Markov model in corrosion prediction of oil and gas gathering and transportation pipeline. Corros. Prot. 42 (5), 42–46+58. doi:10.11973/fsyfh-202105009
Li, X. H., Chen, G. M., and Zhu, H. W. (2017). Research on risk-based early-warning method for corrosion failure of subsea oil and gas pipelines. China Saf. Sci. J. 27 (7), 163–168. doi:10.16265/j.cnki.issn1003-3033.2017.07.029
Li, X. H., Wang, J. W., Abbassi, R., and Chen, G. M. (2022). A risk assessment framework considering uncertainty for corrosion-induced natural gas pipeline accidents. J. Loss Prev. Process Industries 75, 104718–104811. doi:10.1016/j.jlp.2021.104718
Lin, N. T., Zhang, D., Zhang, K., Wang, S. J., Fu, C., Zhang, J. B., et al. (2018). Predicting distribution of hydrocarbon reservoirs with seismic data based on learning of the small-sample convolution neural network. Chin. J. Geophys. 61 (10), 4110–4125. doi:10.6038/cjg2018J0775
Liu, Y. L., Peng, X. Y., Yao, D. C., Tang, F., and Xu, P. F. (2019). A new algorithm for fault tree of pipeline corrosion based on failure correlation. Oil Gas Storage Transp. 38 (1), 31–39. doi:10.6047/j.issn.1000-8241.2019.01.005
Luo, Z. S., and Jiang, L. Y. (2015). Reliability assessment of oil and gas pipelines based on probabilistic neural network. Fire Sci. Technol. 34 (11), 1517–1520. doi:10.3969/j.issn.1009-0029.2015.11.033
Peng, B. B., Yan, X. G., and Du, J. (2020). Surface quality prediction based on BP and RBF neural networks. Surf. Technol. 49 (10), 324–328. doi:10.16490/j.cnki.issn.1001-3660.2020.10.03
Taleb-Berrouane, M., Khan, F., and Hawboldt, K. (2021). Corrosion risk assessment using adaptive bow-tie (ABT) analysis. Reliab. Eng. Syst. Saf. 214, 107731–107812. doi:10.1016/j.ress.2021.107731
Wang, Y. F., An, K., and Meng, J. (2021). Nonlinear model predictive control of hysteresis based on RBF neural network. Electron. Meas. Technol. 44 (23), 42–47. doi:10.19651/j.cnki.emt.2107830
Wu, M., Xie, F., Chen, X., Wang, D., and Sun, D. X. (2022). Research progress and thinking on corrosion failure of buried oil and gas pipelines. Oil Gas Storage Transp. 41 (6), 712–722. doi:10.6047/j.issn.1000-8241.2022.06.013
Xiao, R. G., Wang, D., and Wang, Q. X. (2022). Prediction of corrosion rate of submarine oil and gas pipelines based on ASO-BP neural network. Chem. Industry Eng. 39 (6), 109–116. doi:10.13353/j.issn.1004.9533.20216004
Xu, H. L., Shang, Z. G., Dong, S. B., and Su, Q. Y. (2022). Review on few-shot learning for DNN applications. J. Nanjing Univ. Aeronautics Astronautics 54, 80–86. doi:10.16356/j.1005-2615.2022.S.013
Xu, L. W., Yu, X., and Gulliver, A. (2021). Intelligent outage probability prediction for mobile IOT networks based on an IGWO-Elman neural network. IEEE Trans. Veh. Technol. 70 (2), 1365–1375. doi:10.1109/TVT.2021.3051966
Yang, J. Q., Lin, N. T., Zhang, K., Tian, G. P., and Cui, Y. (2022). Hyperparametric selection and evaluation of deep neural network models: A case study of feature extraction of multi-wave seismic response in an oil-gas reservoir. Geophys. Prospect. Petroleum 61 (2), 236–244. doi:10.3969/j.issn.1000-1441.2022.02.005
Yang, X. H., and Fang, H. X. (2022). RBF neural network-based sliding mode control for modular multilevel converter with uncertainty mathematical model. Energies 15 (5), 1634–1718. doi:10.3390/en15051634
Yu, F. Y., Gao, W. X., He, R. R., Yan, H., and Liu, M. X. (2022). Research on failure risk prediction system of girth weld in long-distance pipeline based on BP neural network. Oil-Gas Field Surf. Eng. 41 (4), 71–77. doi:10.3969/j.issn.1006-6896.2022.04.014
Yu, S. R., Han, J. Y., and Li, S. X. (2016). Predictive grey Markov chain model for pitting corrosion in piplines. J. Mech. Strength 38 (4), 850–856.
Zhang, C., Guo, Y., and Li, M. (2021). Review of development and application of artificial neural network models. Comput. Eng. Appl. 57 (11), 57–69. doi:10.3778/j.issn.1002-8331.2102-0256
Zhang, J., Alharthi, M., Abbas, Q., Li, W. Q., Mohsin, M., Jamal, K., et al. (2020). Reassessing the environmental kuznets curve in relation to energy efficiency and economic growth. Sustainability 12 (20), 8346–8421. doi:10.3390/su12208346
Zhang, P., Su, L. B., Qin, G. J., Kong, X. H., and Peng, Y. (2019). Failure probability of corroded pipeline considering the correlation of random variables. Eng. Fail. Anal. 99 (9), 34–45. doi:10.1016/j.engfailanal.2019.02.002
Zhang, S. K., Bai, L., Li, Y. W., Li, W. L., and Xie, M. L. (2022). Comparing convolutional neural network and machine learning models in landslide susceptibility mapping: A case study in wenchuan county. Front. Environ. Sci. 10, 1–12. doi:10.3389/fenvs.2022.886841
Zhou, C. C., Chang, Q., Zhou, C. C., Zhao, H. D., and Shi, Z. K. (2021). Fault tree analysis of an aircraft flap system based on a non-probability model. J. Tsinghua Univ. 61 (6), 636–642. doi:10.16511/j.cnki.qhdxxb.2020.22.44
Keywords: buried oil and gas pipeline, RBF neural network, fault tree analysis, failure probability, risk assesment
Citation: Zhao L, Luo Z, Deng G and Shi V (2023) Prediction of corrosion failure probability of buried oil and gas pipeline based on an RBF neural network. Front. Earth Sci. 11:1148407. doi: 10.3389/feart.2023.1148407
Received: 24 January 2023; Accepted: 16 March 2023;
Published: 30 March 2023.
Edited by:
Jon Jincai Zhang, Sinopec Tech Houston Center (STHC), United StatesReviewed by:
Ahmed Reda, Curtin University, AustraliaMohammad Yazdi, Macquarie University, Australia
Copyright © 2023 Zhao, Luo, Deng and Shi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lexin Zhao, emhhb2xleGluQHhhdWF0LmVkdS5jbg==
 Lexin Zhao
Lexin Zhao Zhengshan Luo
Zhengshan Luo Guangya Deng2
Guangya Deng2 Victor Shi
Victor Shi