Influence of geomechanics parameters on stress sensitivity in fractured reservoir

The complex fractures aggravate stress sensitivity and heterogeneity of the reservoir and seriously restrict effective development. Therefore, it is of great significance to study and quantitatively evaluate the stress sensitivity of the fractured reservoir. Taking the typical block of the Longmaxi shale reservoir in southern Sichuan as the engineering background, one uses the finite element method to develop a numerical model of a two-dimensional fracture closure variation subjected to the non-hydrostatic stress field. It explores the influence of different fracture occurrences and rock mechanical parameters on stress sensitivity. The theoretical model verifies the numerical simulation results to reveal the stress sensitivity mechanism of the fractured reservoir. The results show that the influence of the dip angle of fracture on the stress sensitivity depends on the anisotropy of applied in-situ stresses. The stronger stress sensitivity occurs in low-dip angles where the lateral pressure coefficient is less than 1. One defines the lateral pressure coefficient. On the contrary, the stronger stress sensitivity occurs in high-dip angles where the lateral pressure coefficient is more significant than 1. It is because the normal stress differences under different stress fields apply to the fracture. Under a given stress condition, the stress sensitivity of fracture negatively correlates with aspect ratio, elastic modulus, and Poisson’s ratio. Pressure maintenance may be more critical in a reservoir with a low aspect ratio and rich in soft minerals. The theoretical predicting model of fracture permeability under different conditions is established based on the linear elastic theory. The relative error between theoretically predicted results and numerical simulation ones is less than 10%, which verifies the accuracy of numerical simulation results. The fundamental reason for stress sensitivity in the fractured reservoir is the fracture geometry and mineral deformation change. The research results are of great significance for establishing the productivity equation considering the stress sensitivity, accurately evaluating the variation of reservoir seepage capacity, and formulating reasonable drainage and production system.

1 Introduction

With the decrease of pore pressure in the process of reservoir exploitation, the effective stress on the reservoir significantly increases, resulting in the geometry deformation of pores and fractures in the rock and the change of reservoir permeability (Gutierrez et al., 2000; Liu et al., 2009; Chen et al., 2015; Gutierrez et al., 2015; Pan et al., 2015; Tao et al., 2018; Zhou et al., 2019). It is often referred to as the stress sensitivity of reservoir rocks. Fatt and Davis (1952) first proposed the stress sensitivity of rock, and found that the decreased rate of rock permeability with the increase of effective stress was 11%–41%. Since then, experts have conducted extensive research on the stress sensitivity of rocks through experimental and theoretical methods (Tan et al., 2021). Stress sensitivity varies with rock type (Zhu et al., 2018). The permeability of tight sandstone and shale usually suffers from more significant loss as the effective stress increases (Warplnski and Teufel, 1992; Suri et al., 1997; Han and Dusseault, 2003; İşcan et al., 2006; Worthington, 2008; Turcio et al., 2013; Li et al., 2014; Meng et al., 2015; Luo et al., 2018; Li et al., 2019; Wang et al., 2019; Li, 2022). It is because of the poor relative physical properties, complex pore structure, and rich natural fractures. Natural fracture is an essential part of a low permeability reservoir, which will aggravate the stress sensitivity and heterogeneity of the reservoir (Wu et al., 2022; Li et al., 2023; Sun, 2023). The intensity of stress sensitivity affects the depletion rate of reservoirs, and seriously restricts the seepage and practical development of the reservoir. When formulating the development plan for oil and gas reservoirs, it is necessary to consider the stress sensitivity of fractures to accurately evaluate the percolation capacity of reservoirs, develop a reasonable production system and predict the productivity of oil and gas wells. Therefore, it is essential to study and quantitatively evaluate the stress sensitivity of fractured reservoirs.

Currently, the methods to analyze the stress sensitivity of fractured reservoirs include indoor experiments, theoretical research, and micro-scale analysis (Zhang et al., 2014; Zhang et al., 2015a; Zhang et al., 2015b; Duan et al., 2017; Foroozesh et al., 2021; Wu et al., 2022). Evaluation methods by indoor experiment mainly include the changes in confining pressure and pore pressure. The former approach is often adopted, but the latter is difficult to control the pressure variation and is rarely used (Kang et al., 2020). The naturally fractured rock has a stronger stress sensitivity than that of the intact rock (Warplnski and Teufel, 1992; Suri et al., 1997; Han and Dusseault, 2003; İşcan et al., 2006; Worthington, 2008; Li et al., 2011; Turcio et al., 2013; Li et al., 2014; Meng et al., 2015; Luo et al., 2018; Wang et al., 2019) conducted a visual experiment to measure the variation of fracture width subjected to increasing effective stress. Zhao et al. (2013) studied the stress sensitivity of the fractured rock samples to different filled extents of fractures. The experiment results show that the decreasing stress sensitivity depends on increasing filling extents. Dong et al. (2010) studied the stress sensitivity related to the physical properties of ultra-low permeability gas reservoirs. They showed that the stress sensitivity of shale is more than two times of sandstone. The experimental results of Kassis and Sondergeld (2010) show that the stress sensitivity of fracture is influenced by the loading path of effective stress, fracture development status, and proppant properties.

In terms of theoretical research, Greenwood and Williamson (1996) first proposed the G&W model using the classical Hertz elastic contact theory to describe the mechanical process of contact surfaces between rough and smooth cracks (Greenwood and Williamson, 1966). Walsh and Grosenbaugh (1979) further studied the variation of the fracture deformation based on the abovementioned model. They found that a specific functional relationship occurs between the fracture closure and the standard deviation of the height concerning the micro-convex surface. Brown and Scholz (1986) proposed the B & S model that the fracture closure problem addresses a contact problem between the rough and smooth surfaces of fracture. The pressure-related permeability models include exponential (Reyes and Osisanya, 2002), power (Xiao et al., 2015), logarithmic (Xiao et al., 2016), and binomial (Halsey et al., 1986).

Many further studies discuss the influence of pore throat and fracture structure, mineral components, and rock characteristics on stress-sensitive behavior (Cai, 2020; Tan et al., 2021; Zhu et al., 2022). Kang et al. (2020) pointed out that the stress sensitivity of low permeability reservoir is affected by burial depth, pore throat structure, mineral type, and fracture development scale. Sheng et al. proposed that the content of plastic minerals, the width, and the number of fractures in low and ultra-low permeability reservoirs are critical factors in determining stress sensitivity. The stress sensitivity is more robust than the medium and high permeability reservoirs because of the threshold pressure gradient (Sheng et al., 2016). A study conducted by Chalmers et al. (2012) shows that the geological control factors of permeability on the change in effective stress are the properties of the pore structure, mineral type, and anisotropy and that the sensitivity of permeability increases as the increasing aspect ratio and decreased elastic modulus of the rock. Wang et al. (2022) pointed out that fracture permeability is not only related to fracture compressibility but also influenced by the fracture direction, reservoir shape, and elastic properties of the reservoir and surrounding rock.

In terms of the finite element model, Walsh (1981) found a linear relationship between the cube root concerning permeability and the natural logarithm of confining pressure through numerical simulation. Warpinski and Teufel (1993) found that the fracture will shrink and close with increasing effective stress on the rock sample. Kang et al. (2014) studied the influencing factors of changing fracture width by using a finite element method and established a prediction model for fracture width. Wang et al. (2016) used a finite element model to obtain the closure variations of fractures with different occurrences under different conditions, which provided a theoretical basis for oil exploitation in fracture-vuggy reservoirs.

Therefore, previous studies on the stress sensitivity of fractured reservoirs have primarily used experimental analysis and theoretical models. In contrast, few comprehensive studies have considered the effects of the parameters of the fracture system and rock mechanics parameters on the stress sensitivity of reservoirs. Most of them are limited to the study on the stress sensitivity of fractures under a uniaxial stress state, which cannot reflect the deformation characteristics of fractures under complex in-situ stress conditions. Based on the in-situ stress parameters of the typical block of the Longmaxi shale reservoir in the southern Sichuan area, this paper provides a theoretical model to study the influence of different fracture occurrences and rock mechanical parameters on the closure variation of fractures under the action of in-situ stress. One evaluates their stress sensitivity, comprehensively analyzes the main control factors of stress sensitivity and reveals the stress sensitivity mechanism of fractured reservoirs. The results of the numerical model verify this theoretical model. The research results of this paper are of great significance for establishing a productivity equation considering the influence of stress sensitivity, accurately evaluating the change of reservoir seepage capacity, and formulating proper production scheduling and production system.

2 Model set-up and numerical procedure

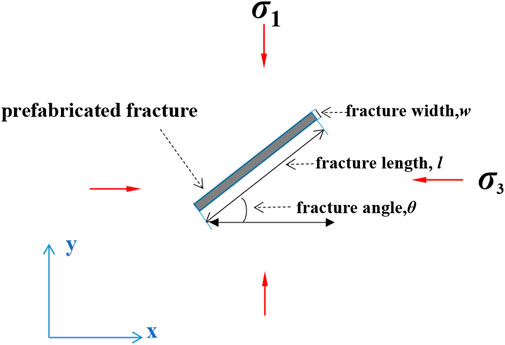
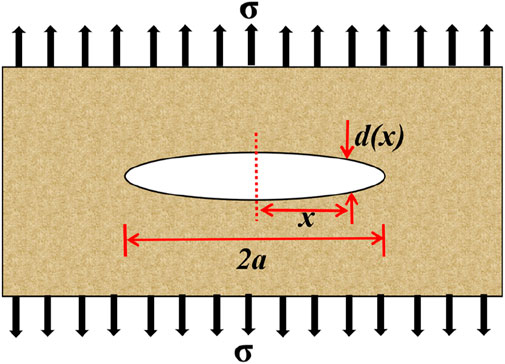
Finite element simulation is a primary means to simulate fracture initiation and propagation. Based on the finite element method theory, the finite element inlays the analysis and solution process to make the simulation steps simple and convenient. The ideal fractured reservoir with a flaky fracture structure represents the complex fracture system. One uses ABAQUS to simulate the morphological characteristics of ideal fractures subjected to anisotropic in-situ stresses. The plane strain assumption holds within the discussion concerning the variation of the fracture closure in this work. Namely, the CPE4P element is used during the model development. Thus, the normal and shear strains are null along the width direction. A rectangle fracture shape is prefabricated by cutting a groove in the middle of the numerical model. Figure 1 shows the numerical model and boundary conditions. The fracture occurs in the in-situ stress field under the combined action of the ${\sigma }_1$ (Y direction) and ${\sigma }_3$ (X direction) of the overlying strata. The stresses ${\sigma }_1$ and ${\sigma }_3$ are prescribed as the ${\sigma }_1>{\sigma }_3$ and depend on the in-situ stresses (${\sigma }_v,{\sigma }_H$, and ${\sigma }_h$) in faulting stress regimes (see Figure 2). The stress ratio ${\sigma }_3/{\sigma }_1$ is called the coefficient of lateral pressure. The model analysis makes the following assumptions. 1) The crack closure is simulated by loading stress on the upper, lower, left, and right sides of the prefabricated crack surface, which is equivalent to considering the simultaneous action of horizontal and vertical stresses; 2) The contact deformation of the crack surface behaves as elastic deformation. One explores the variation of the rock mechanical parameters (Elastic modulus $E$, Poisson’s ratio $\mathrm{\nu }$), fracture angle $\theta$, and fracture aspect ratio $\epsilon \left(w/l\right)$ impact on the stress sensitivity of fractured reservoirs.

FIGURE 1

FIGURE 1. Diagram of the numerical analysis Model.

FIGURE 2

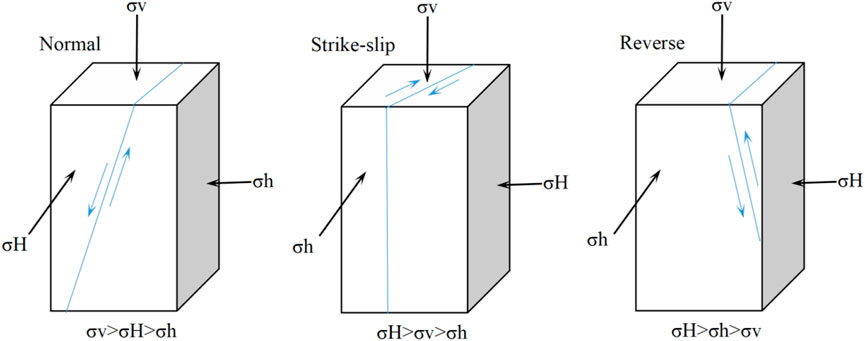
FIGURE 2. The distribution of principal in-situ stress (σ_v, σ_H, and σ_h) based on different stress magnitude and directions and the resulting fault types (normal fault, strike-slip fault, and reverse fault regimes).

2.1 Model design and material parameters

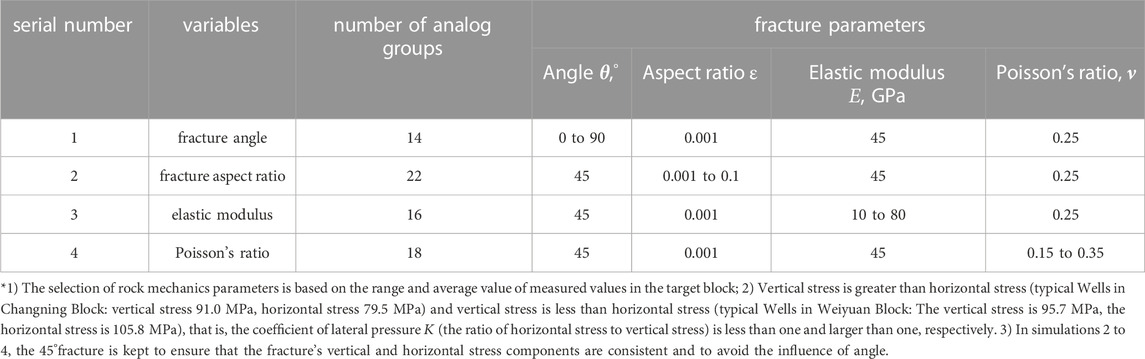
The model variables include the characteristic parameters of fracture (fracture angle $\theta$, fracture aspect ratio $\epsilon$) and rock mechanics parameters (Elastic modulus $E$, Poisson’s ratio $\mathrm{\nu }$). Considering the complex geological processes, the angle between the fracture and the vertical stress is usually random, so the model finds the fracture with different angles of 0°–90°. The aspect ratio characterizes the pore fracture morphology. According to the fracture size, one assigns the aspect ratio variable to be 0.001 to 0.1 in the model.

The rock mechanics parameters include elastic and strength characteristic parameters. Elastic properties to describe the elastic deformation of a material under loading, including Poisson’s ratio and Young’s modulus, determine the brittleness of rock. Rock strength characteristics, including compressive strength, shear strength, tensile strength, and internal friction angle, describe the plastic deformation of rock (Iferobia and Ahmad, 2020). Since the contact deformation of the fracture surface behaves as elastic deformation in the model, the elastic parameters are set as variables, but the strength parameters are fixed.

The characteristics of the underground fluid and the magnitude of in-situ stress will affect the reservoir characteristics in a complex geological environment. The ground stress acting on the depth of the reservoir includes vertical and horizontal (minimum and maximum) in-situ stress. Vertical stress (${\sigma }_v$) results from the overlying weight of the strata and the fluid contained in the pore space, which causes the underlying strata to expand and expand horizontally and laterally due to Poisson’s ratio effect. The horizontal stresses $\left({\sigma }_h,{\sigma }_H\right)$ are formed by surrounding rock and lateral movement caused by caprock stress (Djurhuus and Aadnøy, 2003). Iferobia and Ahmad (2020) classified different faults (normal, strike-slip, and reverse). Figure 2 shows the fault types and their corresponding stresses. For the two-dimensional plane strain model, the cracks are mainly affected by the external forces of the vertical and horizontal stresses. Therefore, two cases are considered. The vertical stress is greater than the horizontal one, and the vertical stress is less than the horizontal one, namely, the normal fault and reverse fault (or strike-slip fault). The principal stress of the model is set according to the measured value of the target block. According to the triaxial rock mechanics analysis and test of 12 wells (95 samples) in the Longmaxi Formation in southern Sichuan, the distribution range of elastic modulus (Young’s modulus) is 11.02–78.33 GPa, with an average value of 45.35 GPa. Poisson’s ratio ranges from 0.154 to 0.335, with an average of 0.251; The average uniaxial compressive strength is 176.85 MPa, the average tensile strength is 12.38, and the average values of internal friction angle and cohesion are 45.59°and 2 MPa respectively. The strike-slip fault is easy to form in Weiyuan Block, and the vertical stress of typical wells ranges from 83.4 to 102.6 MPa, with an average of 95.7 MPa. The maximum horizontal principal stress is 96.2–120.2 MPa, with an average of 105.8 MPa. Normal faults are easy to form in Changning Block. The vertical stress of typical wells ranges from 82.5 to 96.2 MPa, with an average of 91.0 MPa; The maximum horizontal principal stress is 65.4–88.2 MPa, with an average of 79.5 MPa.

2.2 Evaluation criteria

Evaluating the element damage uses the maximum tensile strength criterion and the damage threshold of the Mohr-Coulomb criterion. The expression with tensile failure criterion is as follows

$\left\{\begin{array}{c}{\sigma }_v-{\frac{1+\sin \phi }{1-\sin \phi }\sigma }_H\ge {\sigma }_c,\hspace{0.17em}{\sigma }_v>{\sigma }_c-{\lambda \sigma }_t\\ {\sigma }_H\le {-\sigma }_t,\hspace{0.17em}{\sigma }_v\le {-\sigma }_c-{\lambda \sigma }_t\end{array}\right.(1)$

where, ${\sigma }_v$, ${\sigma }_H$ is the principal in-situ stress, MPa; $\phi$ is the friction angle, (°); $\lambda$ is the residual strength coefficient; ${\sigma }_t$ is the tensile strength, MPa; ${\sigma }_c$ is the uniaxial compressive strength under ultimate stress, MPa.

The whole process of fracture closure is predicted and dynamically demonstrated. The vertical and horizontal output stress values are converted into the constant change of fracture effective stress $P$, and the fracture flow space of each closure step is output to calculate the fracture permeability under different closure degrees.

2.3 Simulation design and data processing

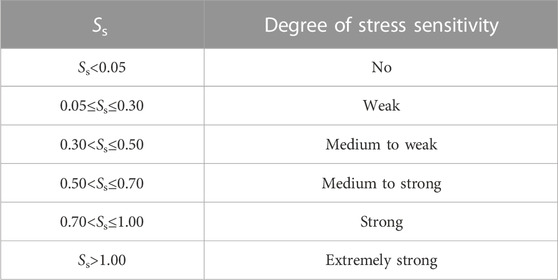
Jiang and Yang (2018) evaluated the stress sensitivity of the fracture by deducting the fracture pore size in the model and converting it into fracture permeability according to the classical cubic law. The evaluation method concerning the stress sensitivity of fractured reservoirs is different from that of matrix reservoirs. The data processing and evaluation standard of stress sensitivity in industry standards (SY/T5358-2010) is also controversial (Kang et al., 2020). Therefore, the stress sensitivity coefficient is used to evaluate the stress sensitivity of the fractured reservoir. The stress sensitivity coefficient S_s is expressed in Eq. 2, and the evaluation indexes are shown in Table 1 (Jones, 1975; Jones and Owens, 1980).

$S_s=\frac{1-{\left(\frac{K_i}{K_o}\right)}^{1/3}}{\lg \frac{{\sigma }_i}{{\sigma }_{\mathit{o}}}}(2)$

TABLE 1

TABLE 1. Evaluation index of stress sensitivity coefficient.

The above symbols include stress sensitivity coefficient $S_s$, dimensionless; initial stress value ${\sigma }_o$, MPa; Initial permeability value $K_o$, 10⁻³ μm²; Effective stress value of each experimental point ${\sigma }_i$, MPa; Corresponding permeability value of each practical point $K_i$, 10⁻³μm².

3 Characteristics of fracture deformation and influencing factors

Although many experiments have proved the high dependence of fracture permeability on effective stress, it is difficult to be characterized by a formula due to the difference in rock type and pore structure, and theoretical studies on numerical models are still insufficient (Chen et al., 2015). In this section, the fracture permeability model is derived based on the simulation variables, and the theoretical model is used to fit the numerical simulation results. One also discusses the influencing factors and characteristics of stress sensitivity.

3.1 Fracture angle

Under the same underground stress condition, the closure variation of fractures with different occurrences, such as low-angle and high-angle fractures, are significantly different. The closure variation usually depends on the in-situ stress, fracture dip angle, and the angle between the fracture strike and the maximum horizontal principal stress (Fan et al., 2020; Liu et al., 2021).

The following conditions are assumed to establish the predicting model of fracture deformation with different angles under non-hydrostatic stress. 1) The matrix is an isotropic linear continue. 2) A linear correlation occurs between stress and displacement of fractures. 3) The influence of shear stress is not considered.

According to the force analysis diagram (Figure 1), when the fracture angle is $\alpha$, the normal force (${\sigma }_n$) on the fracture surface is written as (Feng et al., 2021):

${\sigma }_n={\sigma }_v{\cos }^2\alpha +{\sigma }_H{\sin }^2\alpha (3)$

According to the effective principle stress (Ma et al., 2020), the normal displacement of the fracture is given by

$u_n=b_{\mathrm{o}}\frac{{\sigma }_n}{E_f}=\frac{b_{\mathrm{o}}\left({\sigma }_v{\cos }^2\alpha +{\sigma }_H{\sin }^2\alpha -{\alpha }_{f}p\right)}{E_f}(4)$

The fracture width after stress deformation reads

$b_f=b_{\mathrm{o}}-u_n=b_{\mathrm{o}}-\frac{b_{\mathrm{o}}\left({\sigma }_v{\cos }^2\alpha +{\sigma }_H{\sin }^2\alpha -{\alpha }_{f}p\right)}{E_f}(5)$

Based on the classical cubic law, the permeability retention rate is derived after stress-sensitive damage of fractures

$\frac{k_f}{k_{\mathrm{o}}}=\frac{{\left(b_{\mathrm{o}}-\frac{b_{\mathrm{o}}\left({\sigma }_v{\cos }^2\alpha +{\sigma }_H{\sin }^2\alpha -{\alpha }_{f}p\right)}{E_f}\right)}^2}{{b_{\mathrm{o}}}^2}\times 100\%(6)$

In the above, the parameters include fracture permeability after deformation $k_f$, mD; Initial fracture permeability $k_{\mathrm{o}}$, mD; The normal displacement of the fracture $u_n$, mm; Initial fracture width of the fracture $b_{\mathrm{o}}$, mm; Fracture width after deformation $b_f$, mm; The normal force on the joint surface ${\sigma }_n$, MPa; the vertical and horizontal stress ${\sigma }_v$, ${\sigma }_H$, MPa; The elastic modulus of fracture $E_f$, MPa; the fracture effective stress coefficient ${\alpha }_f$, default as 1; the angle of fracture $\alpha$, °; The pore fluid pressure $p$, MPa.

Based on the simulation experiment scheme (see Table 2), one predicts the permeability decreasing tendency of fractures at different angles with changes in effective stress and compares it with the simulation results.

TABLE 2

TABLE 2. List of performed numerical experiments.

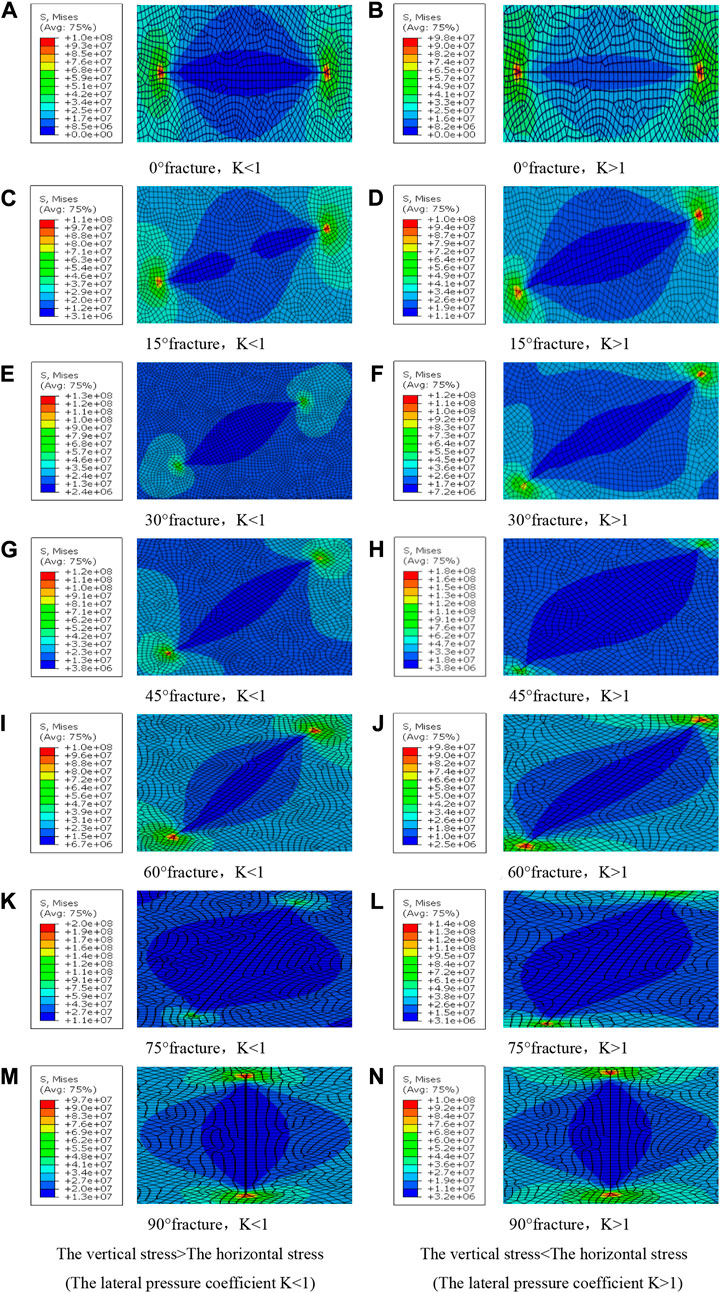
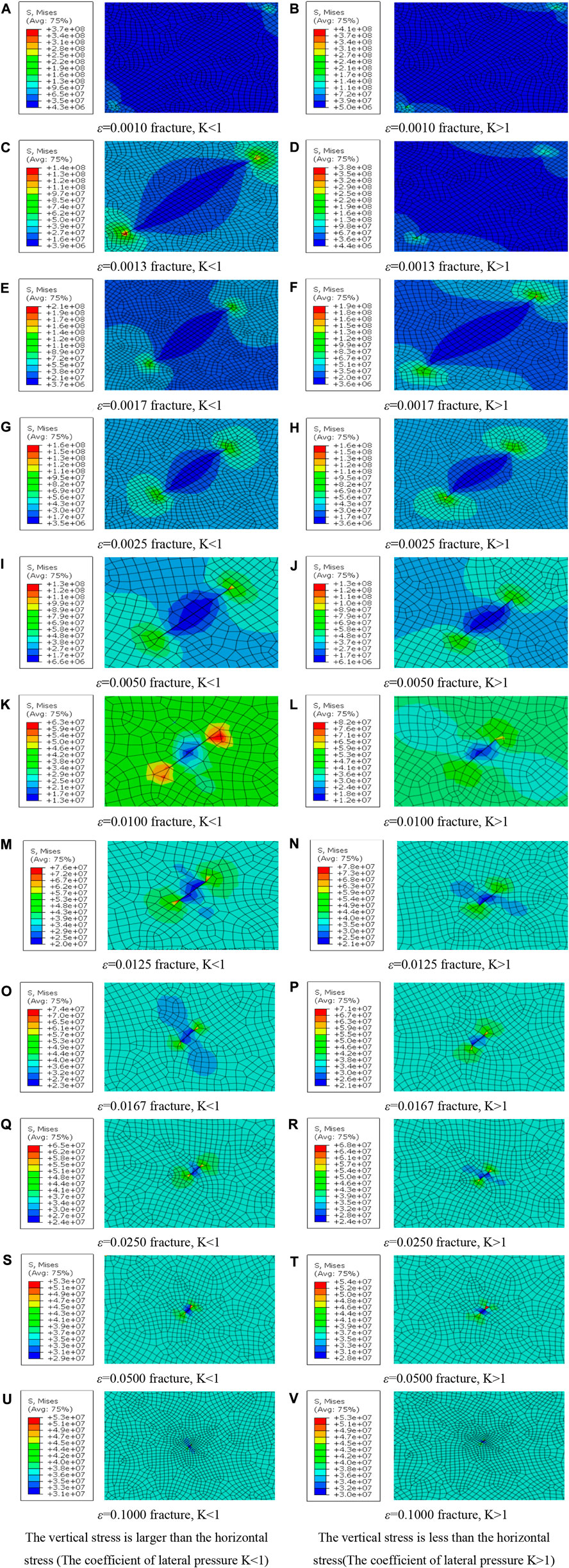
Under two in-situ stress condition, the use of ABAQUS finite element simulation obtains the stress nephogram of fractures at all angles. Figure 3 shows the stress and expansion state of fractures at different angles. When the non-equal stress is applied to the fracture, the pressure contour line is elliptic distribution, and the pressure emanates outward from the fracture. The pressure value gradually increases outward from the low-stress value near the fracture. In other words, the stress effect transfers pressure in an ellipse to the interior around the fracture.

FIGURE 3

FIGURE 3. Stress nephogram of fractures with different angles under stress in two directions.

Meanwhile, stress concentration appears at both ends of the fracture, decreasing outward and diverging. With the increasing stress in both directions, the formation pressure in the fracture continuously decreases, and the fracture gradually is compressed and deforms to reduce the width. Finally, the fracture is completely closed.

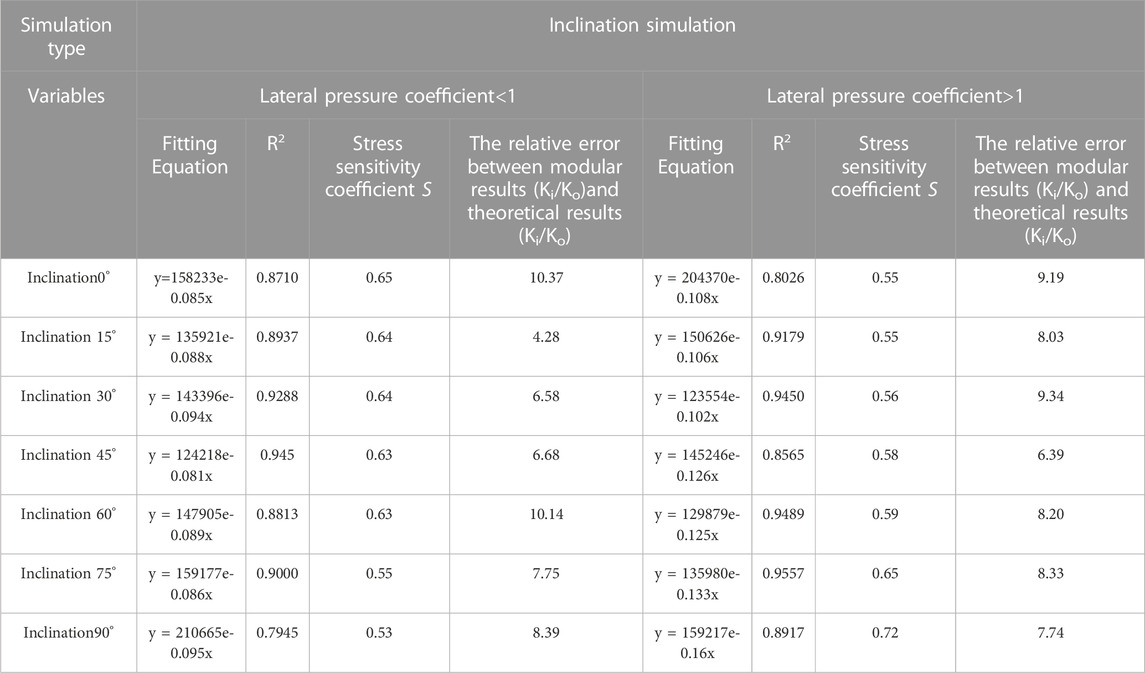
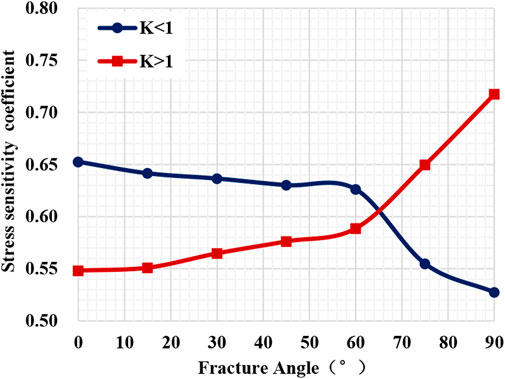
The fracture permeability ratio at different angles changes with effective stress (see Figure 4). The overall closure variation shows that the seepage capacity of the fracture decreases with increasing effective stress. The fracture width continuously decreases due to deformation closure when the fracture is subjected to the action of in-situ stress. As the effective stress begins to decline, the fracture deformation is relatively large, but the permeability rapidly decreases. Therefore, stress sensitivity is vital. When the stress decreases to a specific value, the fracture deformation tends to be stable, and the permeability slowly decreases. The correlation curve shows an exponential downward tendency. The fitting formula is shown in Table 3. R² reaches 0.7945–0.9450, with an average of 0.8943, consistent with previous research results (Dong et al., 2010; Metwally and Sondergeld, 2011; Chalmers et al., 2012; Ghanizadeh et al., 2014; Bhandari et al., 2015; Chen et al., 2019). When the coefficient of lateral pressure is less than 1, the fracture with a lower dip angle is easier to close (Figure 4A). The stress sensitivity coefficient $S_s$ is 0.53–0.65, which belongs to medium to severe damage, and decreases with the increasing dip angle (Figure 5). In other words, the fracture with a greater dip dangle has weaker stress sensitivity damage. When the lateral pressure coefficient is larger than one, the fracture with a higher dip angle is easier to close (Figure 4B). The stress sensitivity coefficient $S_s$ is 0.55–0.72, which belongs to medium to severe damage, and increases with the increasing dip angle (Figure 5). The fracture with a greater dip dangle has more serious stress sensitivity damage.

FIGURE 4

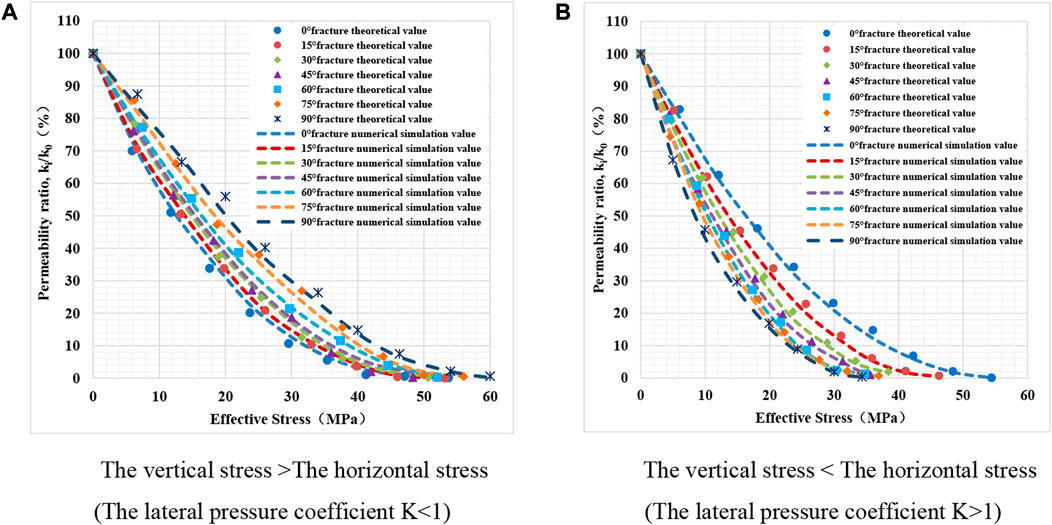
FIGURE 4. Variation curve of permeability ratio of fractures at different angles with effective stress.

TABLE 3

TABLE 3. The related parameters of numerical simulation and the theoretical calculation result.

FIGURE 5

FIGURE 5. Curve of stress sensitivity coefficient changing with fracture angle.

Figure 4 shows the fitting curve based on the numerical simulation and the theoretically predicted results. The average relative errors of numerical simulation and theoretically predicted ones are 7.74% and 8.17%, respectively (see Table 3), indicating a high degree of agreement. Under the same stress condition, the normal effective stress of fracture surfaces is different. Thus, the fracture permeability presents different response characteristics and stress sensitivity coefficients during loading. When vertical stress is larger than horizontal stress, the permeability change of the fracture is lower for a larger angle, since the vertical stress component applied to the fracture with a large angle is smaller than that of a slight dip angle. On the contrary, when the vertical stress is less than the horizontal stress, the vertical stress component applied to the fracture with a large angle is greater than that of a slight angle. The results of numerical simulation and theoretical prediction are in good agreement, which verifies the accuracy and practicability of the predicting model for fracture deformation based on different angles, and can be further used to deduce the natural fracture network deformation and productivity prediction.

3.2 Aspect ratio

The compressibility of reservoir pore space also depends on the geometric shape. Generally, the flow path can be described as a circular pipe, an ellipsoidal pore, or a plane fracture (Bernabe et al., 1982; Sisavath et al., 2000; Izadi et al., 2011; Schwartz et al., 2019; Li et al., 2022). The aspect ratio $\mathrm{\epsilon }$ ($\mathrm{\epsilon }=w/l$) is the main parameter to distinguish the type and size of the pore spaces, which $w$ is the minor axis length and $l$ is the major axis length. In this study, the aspect ratio variable of 0.001–0.1 based on the crack size is considered in the model.

The general expression of the pore compression coefficient of elliptic pores is usually described as Eq. 7 under plane strain condition (Schwartz et al., 2019). The pore is considered a fracture when the aspect ratio is small. The aspect ratio is the ratio of the width and length of the fracture. According to Eq. 7, rock compressibility is mainly affected by aspect ratio, young’s modulus, and Poisson’s ratio, which respectively reflect the influence of fracture occurrence and rock mechanical properties on the stress sensitivity of a fractured reservoir.

$C_p=\frac{2\left(1-\nu \right)}{E}\left(\epsilon +\frac{1}{\epsilon }\right)(7)$

where $C_p$ is the coefficient of pore compression, other definitions include Poisson’s ratio $\nu$, elastic modulus $E$, and fracture aspect ratio $\epsilon$. As $\epsilon$ is much smaller than unity, Eq. 7 can be simplified as

$C_p=\frac{2\left(1-\nu \right)}{E\epsilon }(8)$

Strain in the pore space is defined as:

${\epsilon }_p=\sigma C_p(9)$

where ${\epsilon }_p$ is the pore strain, and $\sigma$ is the applied stress. We invoke the constraint that the aspect ratio $\epsilon$ can be assumed constant under hydrostatic pressure. According to the two-dimensional pore strain formula rederived by B. Schwartz et al. (2019), and considering the seepage characteristics of parallel plate fractures in the model, the permeability retention rate after stress-sensitive fracture damage can be characterized as follows

$\frac{K_i}{K_o}={\left(1-△\sigma C_p\right)}^{\frac{3}{2}}(10)$

In the case that the aspect ratio does not hold constant, by changing the area change of the elliptic model, the following formula is derived

$\frac{K_i}{K_o}={\left(1-△\sigma C_p\right)}^3(11)$

Based on the simulation experiment scheme, the permeability decreasing tendency of fractures is predicted according to Eq. 11 and compared with the simulation results for different aspect ratios under different effective stress.

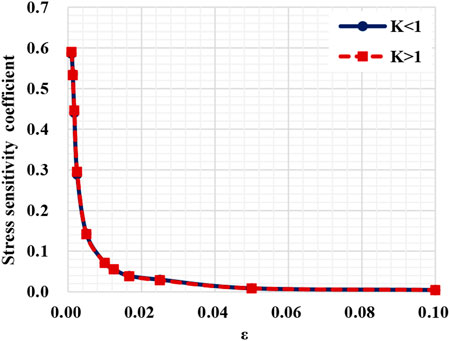
Figure 6 shows the stress nephogram of fractures with different aspect ratios under non-hydrostatic stress conditions. Figure 7 presents the variation of fracture permeability ratio against effective stress (since the lateral pressure coefficient does not affect the variation tendency of fracture aspect ratio with effective stress, one selects any stress condition is herein only fitted). The fracture permeability decreases with the increasing effective stress, and the coefficient of lateral pressure does not affect the variation tendency of the fracture aspect ratio with the effective stress. The permeability decreases with decreasing aspect ratio (see Figure 7). When the aspect ratio is $\epsilon$ ≤0.0025, the fracture permeability ratio decreases exponentially with the increasing effective stress. The fracture permeability ratio decreases linearly when the aspect ratio is $\epsilon$ > 0.0025. Under the non-hydrostatic stress conditions, the variation tendency of the stress sensitivity coefficient coincides (see Figure 8). $S_s$ ranges from 0.004 to 0.586, and shows an exponential downward trend with the increasing aspect ratio. When the aspect ratio $\epsilon$ ≤0.0025, $S_s$ ranges from 0.302 to 0.586 with an average value of 0.463, corresponding to medium-weak and medium-strong damage. When the aspect ratio $\epsilon$ >0.0025, $S_s$ ranges from 0.004 to 0.143, with an average value of 0.049, indicating no damage. In other words, the stress-sensitive damage degree of fractures with an aspect ratio $\epsilon$ ≤0.0025 is significantly higher than that of fractures with an aspect ratio $\epsilon$ >0.0025, which is consistent with previous studies. Namely, the rock is richer in fractures, and the stress sensitivity of the reservoir is stronger (Schwartz et al., 2019).

FIGURE 6

FIGURE 6. (Continued).

FIGURE 7

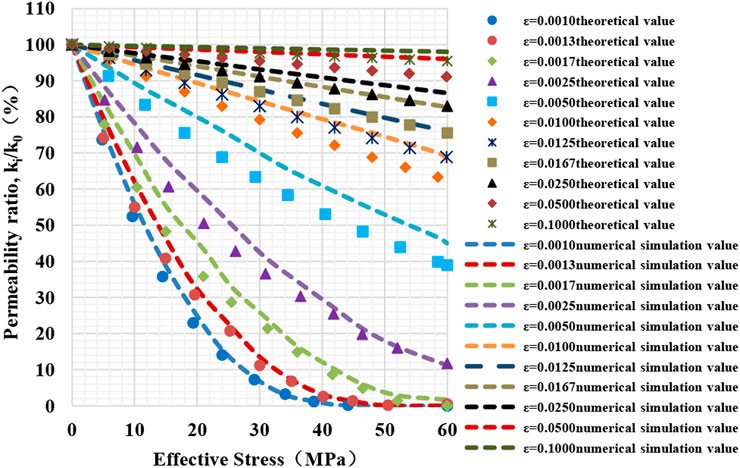
FIGURE 7. Variation curve of permeability ratio of fractures with different aspect ratios with effective stress.

FIGURE 8

FIGURE 8. Variation of stress sensitivity coefficient with the fracture aspect ratio.

Figure 7 shows the fitting curve based on the numerical simulation and theoretically predicted results. When the aspect ratio is less than 0.0025, the numerical and theoretical values exponentially decrease with the increasing effective stress. Still, the aspect ratio is more significant than 0.0025, and the numerical and theoretical values decrease linearly. When the aspect ratio is less than 0.01, the relative error between the numerical simulation value and the theoretically predicted value is more significant, ranging from 6.13% to 13.45%, with an average of 9.45%. On the contrary, when the aspect ratio is less than 0.01, the relative error value of the two decreased significantly, ranging from 1.46% to 4.92%, with an average of 3.24%. In other words, the theoretical prediction has higher fitting accuracy and minor relative error in the case of modeling with a larger aspect ratio.

The influence of fracture aspect ratio on stress sensitivity is usually more important than the mechanical properties of the rock. It suggests pressure maintenance may be more critical in a fractured reservoir with a low aspect ratio.

3.3 Elastic modulus

Griffith (1920) was the first to derive the formula of fracture propagation in elliptic holes by the theory of elastic energy conversion. As shown in Figure 9, the variation $d\left(x\right)$ of the ellipse’s short axis width is described as under effective stress

$d\left(\chi \right)=\frac{4\sigma }{E^{\prime }}\sqrt{{\alpha }^2-{\chi }^2}(12)$

where $\sigma$ is the effective stress, $E^{\prime }$ is the elastic energy, $\alpha$ is the radius of the long axis of the ellipse hole, and the value of the horizontal coordinate $x$ of the ellipse hole is $\left[-\alpha ,\alpha \right]$ under the plane strain condition $E^{\prime }=\frac{E}{1-{\nu }^2}$.

FIGURE 9

FIGURE 9. Schematic of the growth conditions derivation of Griffith crack.

When the ratio of the short axis to the long axis (the aspect ratio) of the elliptical pore gradually decreases, it can be approximated as a fracture. Therefore, the model is usually assumed to be an elliptical hole, and its stress deformation is derived. Based on the above theory, Du et al. (2022) obtain the permeability expression with one fracture can be ed from the Poiseuille equation and Darcy’s law

$K=\frac{\varphi b^2}{3}(13)$

where $b$ is the radius of the short axis of the elliptical hole. The expressions of initial permeability and permeability are under different effective stress states

$K_{\mathrm{o}}=\frac{\varphi {b_{\mathrm{o}}}^2}{3};K_i=\frac{\varphi {b_i}^2}{3}(14)$

where $b_{\mathrm{o}}$ is the initial short axis radius of the elliptical hole, and $b_i$ is the short axis radius after stress deformation. The formula of permeability retention rate after stress-sensitive fracture damage is further derived:

$\frac{K_{\mathrm{i}}}{K_{\mathrm{o}}}={\left[1-\frac{1}{\epsilon }\frac{2\left(1-{\nu }^2\right)\left({\sigma }_e+{\sigma }_{e\mathrm{o}}\right)}{E}\right]}^2(15)$

where ${\sigma }_e$ is the effective stress, and ${\sigma }_{eo}$ is the initial effective stress.

Based on the simulation experiment scheme, the permeability decreasing tendency of fractures is predicted according to Eq. 15 and compared with the simulation results with different elastic modulus under different effective stress.

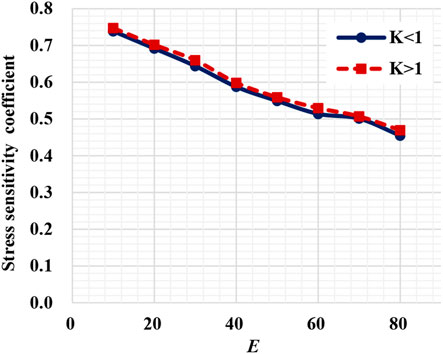
The stress nephograms of fractures with different elastic modulus under non-hydrostatic stress conditions are obtained by numerical simulation. Figure 10 shows the variation of the fracture permeability ratio with stress (since the lateral pressure coefficient does not affect the variation tendency of fracture elastic modulus with effective stress, one selects any stress condition is herein only fitted). The fracture permeability decreases with increasing effective stress, and the permeability ratio shows an exponential downward tendency. The coefficient of lateral pressure does not influence the variation of the fracture aspect ratio against the effective stress. The changing tendency of the stress sensitivity coefficient coincides under the non-hydrostatic stress conditions (see Figure 11). Figure 10 shows a more obvious permeability decrease for a smaller elastic modulus. With the elastic modulus increase, a linear downward tendency with S_s of 0.45–0.74 shows medium, weak, severe fracture damage. The smaller elastic modulus of the fracture has stronger stress sensitivity.

FIGURE 10

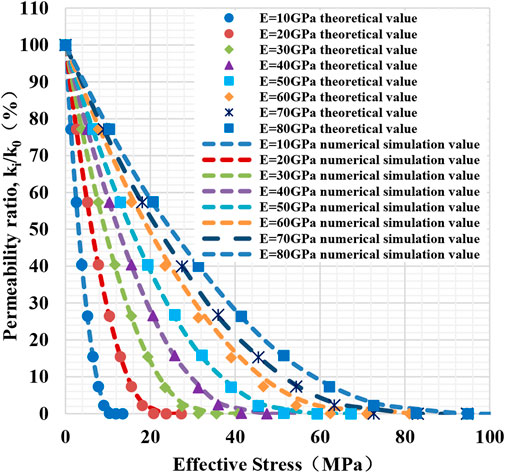
FIGURE 10. Curve of permeability ratio of fractures with different elastic modulus changing with effective stress.

FIGURE 11

FIGURE 11. Variation of stress sensitivity coefficient against the elastic modulus.

Figure 10 shows the fitting curve based on the numerical simulation and theoretically predicted results. With the increase of elastic modulus, the decreasing tendency of permeability becomes slow, and the stress sensitivity uniformly decreases. That is to say, the fracture with a larger Young’s modulus is harder to compress. The relative error between the numerical simulation value and the theoretically predicted one is 4.22%–9.63%, with an average of 5.46%, which is in good agreement.

The stress sensitivity of rock is essentially caused by the change in pore structure and mineral deformation, which reflects the change in pore-throat connectivity and electrical conductivity. The elastic modulus is the internal factor that affects stress sensitivity. Harder mineral components are harder to compress than softer ones (Xu et al., 2018a; Xu et al., 2018b). The quartz and calcite minerals with high elastic modulus are difficult to deform under loading, so the increase in the content of these brittle minerals reduces the stress sensitivity of the rock (Li et al., 2014). On the contrary, plastic minerals such as gypsum and clay have better toughness and lower elastic modulus. Research indicates that clay minerals play a significant role in rock deformation, and the stress sensitivity is 25 times that of quartz. Therefore, the higher content of clay minerals possesses stronger stress sensitivity (Xu et al., 2018a,; Xu et al., 2018b). Meanwhile, the type of clay minerals will also affect stress sensitivity. For example, kaolinite reduces stress sensitivity, but the illite or mixed layer enhances the stress sensitivity (Xiao et al., 2016).

3.4 Poisson’s ratio

According to Eq. 15, the decreasing tendency of fracture permeability is predicted with different Poisson’s ratios and effective stress and is further compared with the simulation results.

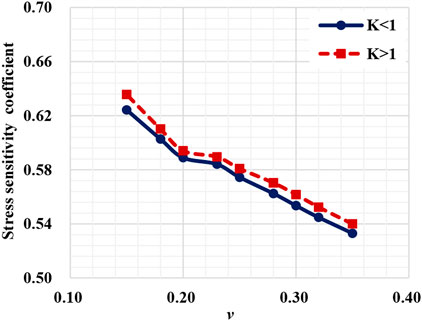
Stress nephograms of fractures against different Poisson’s ratios under non-hydrostatic conditions are obtained by numerical simulation. Figure 12 shows the variation of the fracture permeability ratio against the effective stress. The fracture permeability decreases with the effective stress increase, and the permeability ratio shows an exponential downward tendency. The coefficient of lateral pressure does not affect the changing preference of the fracture aspect ratio with the effective stress, indicating that the permeability decrease is more evident for smaller Poisson’s ratio $\mathrm{\nu }$. Still, the change range is small (see Figure 12). Figure 13 shows the variation tendency of stress sensitivity coefficients is the same under non-hydrostatic stress conditions. With the increase of Poisson’s ratio $\mathrm{\nu }$, there is an approximate linear downward tendency with $S_s$ 0.53 to 0.64, which is medium to severe damage. The smaller Poisson’s ratio of the fracture presents stronger stress sensitivity.

FIGURE 12

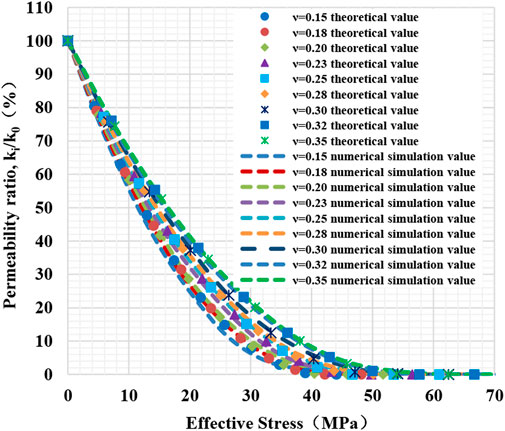
FIGURE 12. Variation curve of permeability ratio of fractures with different Poisson’s ratios as a function of effective stress.

FIGURE 13

FIGURE 13. Variation of stress sensitivity coefficient against Poisson’s ratio.

Figure 12 shows the fitting curve based on the theoretical model’s numerical simulation and calculation results. Noting that the coefficient of lateral pressure does not influence the changing tendency of fracture elastic modulus with effective stress, herein, the model is only fitted under any stress condition. With the increase of Poisson’s ratio, the decreasing tendency of permeability progressively slows down, and the stress sensitivity uniformly decreases. The fracture is more challenging to be compressed where the rock has a larger Poisson’s ratio, while the decreased range is generally reduced. It is not significant the influence of Poisson’s ratio on the stress sensitivity of fracture. The relative error between the numerical simulation value and the theoretical calculation value ranges from 3.48% to 11.98% and averages 8.53%, which is in good agreement.

In terms of mechanical properties, Poisson’s ratio varies with rock properties. For example, the elastic modulus of calcite and quartz are similar. Still, Poisson’s ratio is much higher than quartz, which has higher compressive resistance and can play a better-supporting role on the fracture surface. The stress sensitivity is weaker when the reservoir has a higher calcite content. Clay minerals are typical minerals with low elastic modulus and high Poisson’s ratio. Still, compared to elastic modulus, Poisson’s ratio has much less influence on rock stress sensitivity, so clay minerals still have strong plasticity.

The internal factor of rock is the most critical factor affecting the stress sensitivity of fracture. The internal factors are mineral composition, grain structure, pore structure, water saturation, mechanical morphology, geometric structure, and filling degree. External factors mainly comprise the effective stress, reservoir temperature, loading mode, threshold pressure, and working fluid invasion. Specifically, under external stress, the stress sensitivity increases with the decreasing hardness of minerals. For example, the experimental studies from Zhang Rui et al. show that the pore compressibility of shale is 1–2 orders of magnitude higher than that of sandstone. That is, the porosity of shale decreases more significantly than sandstone under the given stress. It is because shale reservoirs develop microfractures, and the nanopores have a low aspect ratio. In addition, shale is rich in clay and organic matter, so the elastic modulus is usually lower than that of sandstone. The low aspect ratio of pore and young’s modulus leads to high pore compressibility, which is why shale permeability is more sensitive to effective stress (Zhang et al., 2015a; Zhang et al., 2015b). For example, dolomite has the highest elastic modulus among common carbonate minerals, followed by calcite and clay. When dolomite and calcite contain a certain amount of clay, the reservoir is more sensitive to stress. Therefore, the stress sensitivity of fracture in micritic limestone and micritic dolomite is more robust than that of natural and bioclastic limestone (Feng et al., 2019).

During the development of a fractured reservoir, it is necessary to carry out detailed research on the distribution characteristics of reservoir lithology, pore structure parameters, mechanical properties, natural fractures, and fractured fractures, and obtain a full understanding of the variation, including fracture closure, fracture deformation and seepage characteristics of fracture, and influencing factors under in-situ stress state. Meanwhile, it is also required to consider both internal and external influencing factors and combine them with the characterization and development demand of the reservoir. Thus, formulating reasonable development modes and exploitation speed ensures efficient and stable production of oil and gas reservoirs and maximizes economic benefits.

4 Conclusion

1. Taking the typical block of the Longmaxi shale reservoir in southern Sichuan as the engineering background, one uses the linear elastic theory to establish theoretical models to simulate the variation of fracture closure under the two-directional stress loading. There is an exponential relationship between permeability and effective stress with different applied angles to fractures, and the influence of applied angle on stress sensitivity is related to the local stress field. When the coefficient of lateral pressure is less than one, and the applied angle is smaller, the stress sensitivity is more robust, and the coefficient of stress sensitivity $S_s$ ranges from 0.53 to 0.65. When the coefficient of the lateral pressure is greater than one, and the applied angle is larger, the stress sensitivity is greater, and the coefficient of stress sensitivity $S_s$ is 0.55–0.72. The abovementioned difference depends on the difference between normal stresses with different angles applied to fractures under different stress field conditions. Under the normal faulting stress regime, the fractured reservoirs with horizontal and low-angle fractures are suggested to exploit while timely maintaining formation pressure. On the contrary, attention should be paid to high-angle fractures under the reverse or strike-slip faulting regimes.

2. Under the same stress state, the stress sensitivity of fracture correlates with aspect ratio, elastic modulus, and Poisson’s ratio. Geometry determines the compressibility of pore space. The aspect ratio of fracture much more influence the stress sensitivity than the mechanical properties of rock. Meanwhile, elastic modulus and Poisson’s ratio act as the internal factors to affect stress sensitivity, and the affecting intensity depends on the type and content of mineral components. Pressure maintenance is more critical for fractured reservoirs with low aspect ratios and rich in soft minerals.

3. Based on the linear elastic deformation theory and the stress analysis applied to the fracture surface, one develops a theoretical model of fracture permeability under different conditions. The results show that the values of relative error between the numerical simulation and the theoretical model are less than 10%, which has a good consistency and verifies the accuracy of the simulation results. Meanwhile, the theoretical model considers the fracture occurrence and elastic parameters and has broader applicability than the standard empirical formulas. Thus, the theoretical model can be further applied to describe the deformation of real fracture networks and productivity prediction.

4. Both internal and external factors determine the strong stress sensitivity of a fractured reservoir, and the internal factor is the most important one. The change in fracture geometry and mineral deformation essentially causes stress sensitivity. In developing a fractured reservoir, it is necessary to conduct detailed research on the lithologic characteristics, pore structure, mechanical properties, and fracture distribution characteristics—A complete understanding of the variation of deformation and seepage characteristics of fracture and the corresponding influencing factors. Based on the reservoir features and development demands, formulating a reasonable development method and production speed ensures the efficient and stable production of the reservoir and maximizes the economic benefits.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

YF: Research idea, conceptualization and technical implementation, data interpretation, drafted and revised the work. HoT: Suggestions and supervisions for the work. HaT: Suggestions and technical supports for the work. YL: Suggestions and data interpretation for the work. XS: Data interpretation, drafted and revised the work. JL: Data interpretation, drafted and revised the work. ZW: Polishgrammar, suggestions, and technical supports for the work. CD: Polishgrammar, suggestions, and technical supports for the work.

Funding

This research is supported by the Innovation Consortium Project of China National Petroleum Corporation and Southwest Petroleum University (Grant No. 2020CX020102).

Conflict of interest

Authors XS and JL are employed by PetroChina Southwest Oil and Gas Field Company. This study received funding from the Innovation Consortium Project of China National Petroleum Corporation and Southwest Petroleum University (Grant No. 2020CX020102). The funder had the following involvement with the study design, data collection, and analysis.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bernabe, Y., Brace, W. F., and Evans, B. (1982). Permeability, porosity and pore geometry of hot-pressed calcite. Mech. Mater 1 (3), 173–183. doi:10.1016/0167-6636(82)90010-2

CrossRef Full Text | Google Scholar

Bhandari, A. R., Flemings, P. B., Polito, P. J., Cronin, M. B., and Bryant, S. L. (2015). Anisotropy and stress dependence of permeability in the barnett shale. Transp. Porous Med. 108 (2), 393–411. doi:10.1007/s11242-015-0482-0

CrossRef Full Text | Google Scholar

Brown, S. R., and Scholz, C. H. (1986). Closure of rock joints. J. Geophys. Res. 91 (91), 4939–4948. doi:10.1029/jb091ib05p04939

CrossRef Full Text | Google Scholar

Cai, M. F. (2020). Key theories and technologies for surrounding rock stability and ground control in deep mining. J. Min. Strata Control Eng. 2 (3), 033037. doi:10.13532/j.jmsce.cn10-1638/td.20200506.001

CrossRef Full Text | Google Scholar

Chalmers, G. R. L., Ross, D. J. K., and Bustin, R. M. (2012). Geological controls on matrix permeability of devonian gas shales in the horn river and liard basins, northeastern British columbia, Canada. Int. J. Coal Geol. 103, 120–131. doi:10.1016/j.coal.2012.05.006

CrossRef Full Text | Google Scholar

Chen, D., Pan, Z., and Ye, Z. (2015). Dependence of gas shale fracture permeability on effective stress and reservoir pressure: Model match and insights. Fuel 139, 383–392. doi:10.1016/j.fuel.2014.09.018

CrossRef Full Text | Google Scholar

Chen, Y., Jiang, C., Yin, G., Zhang, D., Xing, H., and Wei, A. (2019). Permeability evolution under true triaxial stress conditions of Longmaxi shale in the Sichuan Basin, Southwest China. Powder Technol. 354, 601–614. doi:10.1016/j.powtec.2019.06.044

CrossRef Full Text | Google Scholar

Djurhuus, J., and Aadnøy, B. S. (2003). In situ stress state from inversion of fracturing data from oil wells and borehole image logs. J. Petrol Sci. Eng. 38 (3), 121–130. doi:10.1016/S0920-4105(03)00026-3

CrossRef Full Text | Google Scholar

Dong, J., Hsu, J., Wu, W., Shimamoto, T., Hung, J., Yeh, E., et al. (2010). Stress-dependence of the permeability and porosity of sandstone and shale from TCDP Hole-A. Int. J. Rock Mech. Min. 47 (7), 1141–1157. doi:10.1016/j.ijrmms.2010.06.019

CrossRef Full Text | Google Scholar

Du, S. H., Shen, W. H., and Zhao, Y. B. (2022). Quantitative evaluation of stress sensitivity in shale reservoirs: Ideas and applications. Chin. J. Theor. Appl. Mech. 54 (8), 2235–2247. doi:10.6052/0459-1879-22-262

CrossRef Full Text | Google Scholar

Duan, X. G., An, W. G., Hu, Z. M., Gao, S. S., Ye, L. Y., and Chang, J. (2017). Experimental study on fracture stress sensitivity of Silurian Longmaxi shale formation, Sichuan Basin. Nat. Gas. Geosci. 28 (9), 1416–1424. doi:10.11764/j.issn.1672-1926.2017.07.013

CrossRef Full Text | Google Scholar

Fan, C. H., Li, H., Qin, Q. R., He, S., and Zhong, C. (2020). Geological conditions and exploration potential of shale gas reservoir in Wufeng and Longmaxi Formation of southeastern Sichuan Basin, China. J. Petroleum Sci. Eng. 191, 107138. doi:10.1016/j.petrol.2020.107138

CrossRef Full Text | Google Scholar

Fatt, I., and Davis, D. (1952). Reduction in permeability with overburden pressure. J. Petrol. Technol. 4 (12), 16. doi:10.2118/952329-g

CrossRef Full Text | Google Scholar

Feng, J. W., Sun, Z. X., Wang, Y. D., and She, J. F. (2019). Study on stress sensitivity of ordovician fractures in hetianhe gas field, tarim basin. Geol. J. China Univ. 25 (02), 276–286. doi:10.16108/j.issn1006-7493.2018059

CrossRef Full Text | Google Scholar

Feng, Y. L., Liu, Y. T., Ding, Z. P., Chen, J., and Mao, X. L. (2021). Deformation characteristics of fractures in different directions under anisotropic stress boundary conditions. Sci. Technol. Eng. 21 (2), 694–702.

Google Scholar

Foroozesh, J., Mohamed Abdalla, A. I., Zivar, D., and Douraghinejad, J. (2021). Stress-dependent fluid dynamics of shale gas reservoirs: A pore network modeling approach. J. Nat. Gas. Sci. Eng. 95, 104243. doi:10.1016/j.jngse.2021.104243

CrossRef Full Text | Google Scholar

Ghanizadeh, A., Gasparik, M., Amann-Hildenbrand, A., Gensterblum, Y., and Krooss, B. M. (2014). Experimental study of fluid transport processes in the matrix system of the European organic-rich shales: I. Scandinavian alum shale. Mar. Petrol Geol. 51, 79–99. doi:10.1016/j.marpetgeo.2013.10.013

CrossRef Full Text | Google Scholar

Greenwood, J., and Williamson, J. (1966). Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 295 (1442), 300–319.

Google Scholar

Griffith, A. A. (1920). The phenomenon of rupture and flow in solids. Philosophical Trans. R. Soc. A 221, 163–198.

Google Scholar

Gutierrez, M., Katsuki, D., and Tutuncu, A. (2015). Determination of the continuous stress-dependent permeability, compressibility and poroelasticity of shale. Mar. Petrol Geol. 68, 614–628. doi:10.1016/j.marpetgeo.2014.12.002

CrossRef Full Text | Google Scholar

Gutierrez, M., øino, L. E., and Nygard, R. (2000). Stress-dependent permeability of a de-mineralised fracture in shale. Mar. Petrol Geol. 17 (8), 895–907. doi:10.1016/S0264-8172(00)00027-1

CrossRef Full Text | Google Scholar

Halsey, T. C., Meakin, P., and Procaccia, I. (1986). Scaling structure of the surface layer of diffusion-limited aggregates. Phys. Rev. Lett. 56 (8), 854–857. doi:10.1103/PhysRevLett.56.854

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, G., and Dusseault, M. B. (2003). Description of fluid flow around a wellbore with stress-dependent porosity and permeability. J. Petrol Sci. Eng. 40 (1), 1–16. doi:10.1016/S0920-4105(03)00047-0

CrossRef Full Text | Google Scholar

Iferobia, C. C., and Ahmad, M. (2020). A review on the experimental techniques and applications in the geomechanical evaluation of shale gas reservoirs. J. Nat. Gas. Sci. Eng. 74, 103090. doi:10.1016/j.jngse.2019.103090

CrossRef Full Text | Google Scholar

İşcan, A. G., Kök, M. V., and Bagcı, A. S. (2006). Estimation of permeability and rock mechanical properties of limestone reservoir rocks under stress conditions by strain gauge. J. Petrol Sci. Eng. 53 (1), 13–24. doi:10.1016/j.petrol.2006.01.008

CrossRef Full Text | Google Scholar

Izadi, G., Wang, S., Elsworth, D., Liu, J., Wu, Y., and Pone, D. (2011). Permeability evolution of fluid-infiltrated coal containing discrete fractures. Int. J. Coal Geol. 85 (2), 202–211. doi:10.1016/j.coal.2010.10.006

CrossRef Full Text | Google Scholar

Jiang, J., and Yang, J. (2018). Coupled fluid flow and geomechanics modeling of stress-sensitive production behavior in fractured shale gas reservoirs. Int. J. Rock Mech. Min. 101, 1–12. doi:10.1016/j.ijrmms.2017.11.003

CrossRef Full Text | Google Scholar

Jones, F. O. (1975). A laboratory study of the effects of confining pressure on fracture flow and storage capacity in carbonate rocks. J. Petroleum Technol. 27 (01), 21–27. doi:10.2118/4569-PA

CrossRef Full Text | Google Scholar

Jones, F. O., and Owens, W. W. (1980). A laboratory study of low-permeability gas sands. J. Petroleum Technol. 32 (09), 1631–1640. doi:10.2118/7551-PA

CrossRef Full Text | Google Scholar

Kang, Y. L., Li, C. J., You, L. J., Li, J. X., Zhang, Z., and Wang, T. (2020). Stress sensitivity of deep tight gas-reservoir sandstone in Tarim Basin. Nat. Gas. Geosci. 31 (4), 532–541. doi:10.11764/j.issn.1672-1926.2020.01.002

CrossRef Full Text | Google Scholar

Kang, Y., Xu, C., You, L., Yu, H., and Zhang, B. (2014). Comprehensive evaluation of formation damage induced by working fluid loss in fractured tight gas reservoir. J. Nat. Gas. Sci. Eng. 18, 353–359. doi:10.1016/j.jngse.2014.03.016

CrossRef Full Text | Google Scholar

Kassis, S., and Sondergeld, C. H. (2010). “Fracture permeability of gas shale: Effects of roughness, fracture offset, proppant, and effective stress,” in International oil and gas conference and exhibition in China (Beijing. SPE-131376-MS.

CrossRef Full Text | Google Scholar

Li, D. Q., Kang, Y. L., and You, L. J. (2014). Experimental study on permeability stress sensitivity of carbonate rocks. Nat. Gas. Geosci. 25 (03), 409–413. doi:10.11764/j.issn.1672-1926.2014.03.0409

CrossRef Full Text | Google Scholar

Li, D. Q., Kang, Y. L., and Zhang, H. (2011). New evaluation method of permeability stress sensitivity based on visual fracture aperture measurement. Nat. Gas. Geosci. 22 (3), 494–500.

Google Scholar

Li, H. (2022). Research progress on evaluation methods and factors influencing shale brittleness: A review. Energy Rep. 8, 4344–4358. doi:10.1016/j.egyr.2022.03.120

CrossRef Full Text | Google Scholar

Li, H., Tang, H. M., Qin, Q. R., Zhou, J. L., Qin, Z. J., Fan, C. H., et al. (2019). Characteristics, formation periods and genetic mechanisms of tectonic fractures in the tight gas sandstones reservoir: A case study of xujiahe Formation in YB area, sichuan basin, China. J. Petroleum Sci. Eng. 178, 723–735. doi:10.1016/j.petrol.2019.04.007

CrossRef Full Text | Google Scholar

Li, H., Zhou, J. L., Mou, X. Y., Guo, H. X., Wang, X. X., An, H. Y., et al. (2022). Pore structure and fractal characteristics of the marine shale of the Longmaxi Formation in the changning area, southern sichuan basin, China. Front. Earth Sci. 10, 1018274. doi:10.3389/feart.2022.1018274

CrossRef Full Text | Google Scholar

Li, J., Li, H., Yang, C., Ren, X. H., and Li, Y. D. (2023). Geological characteristics of deep shale gas and their effects on shale fracability in the Wufeng–Longmaxi Formations of the southern Sichuan Basin, China. Lithosphere 2023 (1), 4936993. doi:10.2113/1970/4936993

CrossRef Full Text | Google Scholar

Liu, H., Rutqvist, J., and Berryman, J. G. (2009). On the relationship between stress and elastic strain for porous and fractured rock. Int. J. Rock Mech. Min. 46 (2), 289–296. doi:10.1016/j.ijrmms.2008.04.005

CrossRef Full Text | Google Scholar

Liu, Q., Cheng, Q., Sun, Z. G., and Hu, Q. T. (2021). Stress sensitivity of coal seam with different fractures: Case study of Fuxin Basin. Nat. Gas. Geosci. 32 (3), 437–446. doi:10.11764/j.issn.1672-1926.2020.11.016

CrossRef Full Text | Google Scholar

Luo, W., Tang, C., Feng, Y., and Zhu, M. (2018). Mechanism of fluid flow along a dynamic conductivity fracture with pressure-dependent permeability under constant wellbore pressure. J. Petrol Sci. Eng. 166, 465–475. doi:10.1016/j.petrol.2018.03.059

CrossRef Full Text | Google Scholar

Ma, J., Querci, L., Hattendorf, B., Saar, M. O., and Kong, X. Z. (2020). The effect of mineral dissolution on the effective stress law for permeability in a tight sandstone. Geophys Res. Lett. 47 (15). doi:10.1029/2020GL088346

CrossRef Full Text | Google Scholar

Meng, Y., Li, Z., and Lai, F. (2015). Experimental study on porosity and permeability of anthracite coal under different stresses. J. Petrol Sci. Eng. 133, 810–817. doi:10.1016/j.petrol.2015.04.012

CrossRef Full Text | Google Scholar

Metwally, Y. M., and Sondergeld, C. H. (2011). Measuring low permeabilities of gas-sands and shales using a pressure transmission technique. Int. J. Rock Mech. Min. 48 (7), 1135–1144. doi:10.1016/j.ijrmms.2011.08.004

CrossRef Full Text | Google Scholar

Pan, Z., Ma, Y., Connell, L. D., Down, D. I., and Camilleri, M. (2015). Measuring anisotropic permeability using a cubic shale sample in a triaxial cell. J. Nat. Gas. Sci. Eng. 26, 336–344. doi:10.1016/j.jngse.2015.05.036

CrossRef Full Text | Google Scholar

Reyes, L., and Osisanya, S. O. (2002). Empirical correlation of effective stress dependent shale rock properties. J. Can. Petroleum Technol. 41 (12). doi:10.2118/02-12-02

CrossRef Full Text | Google Scholar

Schwartz, B., Huffman, K., Thornton, D., and Elsworth, D. (2019). The effects of mineral distribution, pore geometry, and pore density on permeability evolution in gas shales. Fuel 257, 116005. doi:10.1016/j.fuel.2019.116005

CrossRef Full Text | Google Scholar

Sheng, Y. S., Hu, Q. X., Gao, H., Shi, Y. M., Dang, Y. C., Shao, F., et al. (2016). Evaluation on stress sensibility of low reservoir in situ conditions. Acta Sci. Nat. Univ. Pekin. 52 (06), 1025–1033. doi:10.13209/j.0479-8023.2016.050

CrossRef Full Text | Google Scholar

Sisavath, S., Jing, X. D., and Zimmerman, R. W. (2000). Effect of stress on the hydraulic conductivity of rock pores. Phys. Chem. Earth, Part A Solid Earth Geodesy 25 (2), 163–168. doi:10.1016/S1464-1895(00)00026-0

CrossRef Full Text | Google Scholar

Sun, Z. M. (2023). Superimposed hydrocarbon accumulation through multi-source and multi-stage evolution in the cambrian xixiangchi group of eastern sichuan basin: A case study of the pingqiao gas-bearing anticline. Energy Geosci. 4 (1), 131–142. doi:10.1016/j.engeos.2022.09.001

CrossRef Full Text | Google Scholar

Suri, P., Azeemuddin, M., Zaman, M., Kukreti, A. R., and Roegiers, J. C. (1997). Stress-dependent permeability measurement using the oscillating pulse technique. J. Petrol Sci. Eng. 17 (3), 247–264. doi:10.1016/S0920-4105(96)00073-3

CrossRef Full Text | Google Scholar

Tan, Q., Kang, Y., You, L., Xu, C., Zhang, X., and Xie, Z. (2021). Stress-sensitivity mechanisms and its controlling factors of saline-lacustrine fractured tight carbonate reservoir. J. Nat. Gas. Sci. Eng. 88, 103864. doi:10.1016/j.jngse.2021.103864

CrossRef Full Text | Google Scholar

Tao, S., Chen, S., Tang, D., Zhao, X., Xu, H., and Li, S. (2018). Material composition, pore structure and adsorption capacity of low-rank coals around the first coalification jump: A case of eastern junggar basin, China. Fuel 211, 804–815. doi:10.1016/j.fuel.2017.09.087

CrossRef Full Text | Google Scholar

Turcio, M., Reyes, J. M., Camacho, R., Lira-Galeana, C., Vargas, R. O., and Manero, O. (2013). Calculation of effective permeability for the BMP model in fractal porous media. J. Petrol Sci. Eng. 103, 51–60. doi:10.1016/j.petrol.2013.02.010

CrossRef Full Text | Google Scholar

Walsh, J. B. (1981). Effect of pore pressure and confining pressure on fracture permeability. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 18 (5), 429–435. doi:10.1016/0148-9062(81)90006-1

CrossRef Full Text | Google Scholar

Walsh, J. B., and Grosenbaugh, M. A. (1979). A new model for analyzing the effect of fractures on compressibility. J. Geophys. Res. Solid Earth 84 (B7), 3532–3536. doi:10.1029/jb084ib07p03532

CrossRef Full Text | Google Scholar

Wang, C., Zhang, Q. Y., Liu, Z. C., Zhang, Y., and Li, X. J. (2016). Prediction model for fracture width changes in vug-fracture oil reservoirs and its application. J. China Univ. Petroleum(Edition Nat. Sci. 40 (1), 86–91. doi:10.3969/j.issn.1673-5005.2016.01.012

CrossRef Full Text | Google Scholar

Wang, M. Y., Li, L. X., Peng, X., Hu, Y., Wang, X., Luo, Y., et al. (2022). Influence of stress redistribution and fracture orientation on fracture permeability under consideration of surrounding rock in underground gas storage. ENERGY Rep. 8, 6563–6575. doi:10.1016/j.egyr.2022.04.076

CrossRef Full Text | Google Scholar

Wang, X. Q., Zhu, Y. M., and Fu, C. Q. (2019). Experimental investigation of the stress-dependent permeability in the Longmaxi Formation shale. J. Petrol Sci. Eng. 175, 932–947. doi:10.1016/j.petrol.2019.01.037

CrossRef Full Text | Google Scholar

Warpinski, N. R., and Teufel, L. W. (1993). Laboratory measurements of the effective-stress law for carbonate rocks under deformation. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 30 (7), 1169–1172. doi:10.1016/0148-9062(93)90088-U

CrossRef Full Text | Google Scholar

Warplnski, N. R., and Teufel, L. W. (1992). Determination of the effective stress law for permeability and deformation in low-permeability rocks. SPE Form. Eval. 7 (02), 123–131. doi:10.2118/20572-PA

CrossRef Full Text | Google Scholar

Worthington, P. F. (2008). A diagnostic approach to quantifying the stress sensitivity of permeability. J. Petrol Sci. Eng. 61 (2), 49–57. doi:10.1016/j.petrol.2008.03.003

CrossRef Full Text | Google Scholar

Wu, J. F., Fan, H. C., Zhang, J., Hu, H. R., Yuan, S. S., and Li, J. J. (2022). An experimental study on stress sensitivity of hydraulic fractures in shale: A case study on Longmaxi Formation shale in the southern sichuan basin. Nat. Gas. Ind. 42 (2), 71–81. doi:10.3787/j.issn.1000-0976.2022.02.008

CrossRef Full Text | Google Scholar

Xiao, W., Jiang, L., Li, M., Zhao, J., Zheng, L., Li, X., et al. (2015). Effect of clay minerals on the effective pressure law in clay-rich sandstones. J. Nat. Gas. Sci. Eng. 27, 1242–1251. doi:10.1016/j.jngse.2015.09.067

CrossRef Full Text | Google Scholar

Xiao, W., Li, T., Li, M., Zhao, J., Zheng, L., and Li, L. (2016). Evaluation of the stress sensitivity in tight reservoirs. Petrol Explor Dev+ 43 (1), 115–123. doi:10.1016/S1876-3804(16)30013-1

CrossRef Full Text | Google Scholar

Xu, C. Y., Lin, C., Kang, Y. L., and You, L. J. (2018a). An experimental study on porosity and permeability stress-sensitive behavior of sandstone under hydrostatic compression: Characteristics, mechanisms and controlling factors. Rock Mech. Rock Eng. 51 (8), 2321–2338. doi:10.1007/s00603-018-1481-6

CrossRef Full Text | Google Scholar

Xu, C. Y., You, Z. J., Kang, Y. L., and You, L. J. (2018b). Stochastic modelling of particulate suspension transport for formation damage prediction in fractured tight reservoir. Fuel 221, 476–490. doi:10.1016/j.fuel.2018.02.056

CrossRef Full Text | Google Scholar

Zhang, R., Ning, Z. F., Yang, F., Zhao, H. W., Du, L. H., and Liao, X. W. (2014). Experimental study on microscopic pore structure controls on shale permeability under compaction process. Nat. Gas. Geosci. 25 (8), 1284–1289. doi:10.11764/j.issn.1672-1926.2014.08.1284

CrossRef Full Text | Google Scholar

Zhang, R., Ning, Z. F., Yang, F., and Zhao, H. W. (2015a). Shale stress sensitivity experiment and mechanism. Acta Pet. Sin. 36 (2), 224–231. doi:10.7623/syxb201502012

CrossRef Full Text | Google Scholar

Zhang, R., Ning, Z., Yang, F., Wang, X., Zhao, H. W., and Wang, Q. (2015b). Impacts of nanopore structure and elastic properties on stress-dependent permeability of gas shales. J. Nat. Gas. Sci. Eng. 26, 1663–1672. doi:10.1016/j.jngse.2015.02.001

CrossRef Full Text | Google Scholar

Zhao, L., Chen, Y., Ning, Z., Wang, X., Zhao, H. W., Wang, Q., et al. (2013). Stress sensitive experiments for abnormal overpressure carbonate reservoirs: A case from the Kenkiyak low-permeability fractured-porous oilfield in the littoral Caspian Basin[J]. Pet. Explor. Dev. 40 (2), 194–200.

CrossRef Full Text | Google Scholar

Zhou, J., Zhang, L., Li, X., and Pan, Z. (2019). Experimental and modeling study of the stress-dependent permeability of a single fracture in shale under high effective stress. Fuel 257, 116078. doi:10.1016/j.fuel.2019.116078

CrossRef Full Text | Google Scholar

Zhu, Q. Y., Dai, J., Yun, F. F., Zhai, H. H., Zhang, M., and Feng, L. R. (2022). Dynamic response and fracture characteristics of granite under microwave irradiation. J. Min. Strata Control. Eng. 4 (1), 019921. doi:10.13532/j.jmsce.cn10-1638/td.20210926.001

CrossRef Full Text | Google Scholar

Zhu, S. Y., Du, Z. M., Li, C. L., Salmachi, A., Peng, X. L., Wang, C. W., et al. (2018). A semi-analytical model for pressure-dependent permeability of tight sandstone reservoirs. Transp. Porous Med. 122 (2), 235–252. doi:10.1007/s11242-018-1001-x

CrossRef Full Text | Google Scholar