
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
METHODS article
Front. Earth Sci. , 22 March 2023
Sec. Geohazards and Georisks
Volume 11 - 2023 | https://doi.org/10.3389/feart.2023.1127889
This article is part of the Research Topic Geo-information for Geohazard and Georisk View all 11 articles
Given the inconsistency between the information value and the weight value in the weighted information value model, a weight model based on the Apriori algorithm is established in this paper to analyze the correlation between the second-level intervals of disaster factors and the susceptibility of geological disasters. The objective weight of the second-level intervals of each index factor is calculated through the mining of association rules by the Apriori algorithm. The subjective uncertainty of the existing second-level factor weighting method is eliminated. Taking the geological disaster data of Xiangtan urban area as an example, 10 evaluation indexes were selected to establish the entropy weight method-information value (EWM-IV) model and the entropy weight method-Apriori algorithm-information value (EWM-Apriori-IV) model to evaluate the geological disaster susceptibility, and the disaster area ratio and the receiver operating characteristic curve (ROC) verification method were used to test and analyze the evaluation results. The results showed that compared with the EWM-IV model, the EWM-Apriori-IV model is used to evaluate the disaster area ratio of high-prone area increased by 58.3%, and the disaster area ratio of low-prone area decreased by 43.1%, the area under the curve (AUC) increased by 7.4%, and the evaluation accuracy was relatively improved compared with the former. This paper proves the rationality and practicability of the weighting method of the geological hazard susceptibility evaluation index based on the Apriori algorithm.
Geological hazard susceptibility evaluation is an important link and basis for disaster prevention and reduction (Chen et al., 2005; Ma et al., 2021). Currently, the commonly used susceptibility evaluation models include analytic hierarchy process model (Chung and Fabbri, 1999; Wang et al., 2009; Xu et al., 2009), weighted information value model (Wang et al., 2014; Jiao et al., 2019; Alsabhan et al., 2022), logistic regression model (Budimir et al., 2015; Tang and Ma, 2015), artificial neural network model (Nourani et al., 2014), support vector machine model (Kavzoglu et al., 2014), etc., among which the weighted information value model is widely used in the research field of geological disaster susceptibility evaluation due to its clear physical significance and simple algorithm. Shen H et al. (Shen et al., 2021) established a weighted information value model based on the weight value and information quantity value of each index obtained by the analytic hierarchy process (AHP) and information value model to conduct a comprehensive assessment of landslide susceptibility. Liang L et al. (Liang et al., 2019) used the certainty factor model to determine the first-level weight of each index factor, and then multiplied the information value to establish a weighted information value model to evaluate the susceptibility of geological disasters. Yang P et al. (Yang et al., 2020) multiplied the weight of each first-level index factor determined by the random forest model and the information value of each second-level index factor determined by the information value model respectively, and established the weighted information value model for the evaluation of landslide susceptibility. All of the above studies are based on the establishment of weighted information value model for susceptibility evaluation by obtaining the weight of first-level factors and combining with the second-level interval information value of each factor. However, the problem of inconsistency between the weight value of first-level factors and the information value of second-level factors may occur, thus affecting the accuracy of geological disaster susceptibility evaluation. Aiming at this problem, some scholars (Xie, 2011; Wang et al., 2012) determined the second-level interval weights of indicators based on the trapezoidal fuzzy number with subjective experience for susceptibility evaluation, but the evaluation results were worse than the mathematical statistics model with objective weighting. In view of this, this paper introduces the weighting method of geological disaster susceptibility evaluation index based on Apriori algorithm, and obtains the second-level factor weight value by analyzing objective data. Apriori algorithm was proposed by R.Aglawal et al. based on previous research results of AIS algorithm (Agrawal and Srikant, 1994; Yu, 2004). This algorithm is applicable to transaction database association rule mining and can reflect the interdependence and correlation between one thing and other things through association rules. Wu T et al. (Wu and Niu, 2011) used the Apriori algorithm to dig for the correlation between disaster scale and various single and multiple factors. Li J et al. (Li and Niu, 2013) obtained the relationship between land use type and landslide stability through the Apriori algorithm. Jie Q et al. (Jie et al., 2015) used the Apriori algorithm to excavate the deformation laws of several landslides. The above scholars use Apriori algorithm to dig out the internal connection between geological disasters and first-level disaster factors, and prove the feasibility of Apriori algorithm in the field of geological disasters. Therefore, according to the principle that the Apriori algorithm can mine the commonness of historical disaster data, it is integrated into the weighted information value model and weighted to the second-level interval information value of each evaluation factor to solve the problem that the factor weight value is inconsistent with the caliber of the information value.
Based on this, this paper takes Xiangtan urban area in Hunan Province as the research area, introduces the Apriori algorithm to mine and analyze the association rules between historical disaster data and geological disaster susceptibility, establishes the evaluation index system of geological disaster susceptibility in Xiangtan urban area, determines the objective weights of the second-level intervals of each index factor, and combines with the objective weight of first-level index factor of entropy weight method. The EWM-IV model and the EWM-Apriori-IV model were established respectively to evaluate the susceptibility of geological disasters. The feasibility and accuracy of the weight model based on the Apriori algorithm were demonstrated through accuracy verification and comparative analysis.
Xiangtan urban area, Hunan Province, with a total area of 657.4 km2, is located in the middle part of the Hengshan Mountain range and belongs to the alluvial plain and red soil terrace on both sides of the Xiangjiang River. The terrain is high and convex in the east and west, and low and concave in the middle. The overall terrain is relatively flat, with an elevation between −82 m and 289 m. The outlying strata in Xiangtan urban area are relatively complete and are characterized by the wide distribution of red beds and pre-Devonian shallow metamorphic clastic rocks and a complex and diverse sedimentary environment. From old to new, Lengjiaxi Group, Banxi Group, Sinian System, Cambrian system, Ordovician system, Devonian system, Carboniferous system, Permian system, Triassic system, Jurassic system, Cretaceous system, Paleogene system and Quaternary system (including alluvium and residual slope layer) are exposed successively. The regional structure can be divided into three types: the Heling-Nanzhushan fault folds belt in the northwest, the Xiangtan fault depression basin in the middle, and the Baimalong-Shuangmazhen fault folds belt in the east. The river system in the territory is mainly composed of the Xiangjiang River and its main tributaries Lianshui River and JinJiang River. Affected by the subtropical humid monsoon climate, it enjoys abundant sunshine, and high temperature and rain in summer. The annual rainfall is between 1,250 and 1,500 mm, mainly in spring and summer, with 68% of the annual rainfall. There are 121 geological disaster spots in Xiangtan urban area (Figure 1), mainly landslide, collapse, and ground collapse disasters. The threatened population is about 2,500, and the potential economic loss is nearly 10,000 yuan. The main data sources of this paper are shown in Table 1.
The Apriori algorithm is the most classic algorithm for mining frequent item sets, which can extract association rules from large data sets (Zhang, 2016; Hidayanto et al., 2017). Algorithm steps (Han and Kamber, 2001; Yu, 2004; Li et al., 2020) are shown in Figure 2 below.
Apriori algorithm adopts iterative method to find frequent item sets. In the mining process of association rules, the frequent item sets of k-1 items will be connected all the time to generate k item sets. Then, the minimum support threshold is set by calculating the support degree of k item sets, namely, the probability of X and Y appearing simultaneously in the data set, and the frequent item sets of k items are obtained by pruning the k item sets that do not meet the threshold. The frequent item sets of k items are searched and iterated layer by layer until there are no new k item sets.
The Apriori algorithm is applied to mine the correlation between the susceptibility of geological disasters and the second-level interval of the disaster factor. The second-level interval of the disaster factor is a data type in the form of Boolean (binary type). According to the requirement of the Apriori algorithm that the data type must be a Boolean value, the objective weight of the second-level interval of each disaster factor reflecting the correlation of geological disaster susceptibility can be obtained. The specific implementation process is as follows:
(1) Storing data sets.
The data set contains historical geological disaster data and all geological data in the study area. Boolean data after data processing, each set in the data set contains a disaster point and the second-level interval to which all corresponding disaster factors belong. Each set represents the occurrence of a disaster point and the emergence of second-level intervals of all disaster factors. The data set is scanned and the Apriori algorithm is run, searching for each transaction until the search result is obtained.
(2) Generate the candidate item set.
Scan the transaction set and defines all the second-level intervals in the transaction set and the occurrence of geological hazards as the members of the candidate set. Each member of the candidate item set is an independent item set.
(3) Calculate the weight of the index factor second-level interval.
Eq. 1 was used to calculate the support degree of each member in the candidate set. Support degree of association rule X→Y refers to the probability of the combination of second-level intervals in the geographic data set of the study area and the occurrence of geological disasters at the same time. If the occurrence occurs once, the support degree accumulates once. The support result is the weight of the second-level intervals of each indicator factor.
(4) Determine the weight of the index factor’s second-level interval.
In the process of mining association rules, by setting the minimum support threshold, the association rules that do not meet the minimum support threshold are pruned to improve the efficiency of the algorithm. If the minimum threshold of the above support is met, it can be determined as the second-level weight of the index factor.
As an objective weight method with a good evaluation effect, the entropy weight method (EWM) has been widely used in research and practice of geological disaster susceptibility evaluation (Liang et al., 2010; Jiang et al., 2019). The specific calculation method is as follows (Devkota et al., 2013):
Where
The entropy value of the
Where
Finally, the objective weight
Where
The information value (IV) model is a mathematical statistics method commonly used to analyze data. Through statistical analysis of historical data, the information value of each impact factor is calculated to determine the importance of each impact factor (Fan et al., 2012; Chen et al., 2021). The calculation method is as follows:
Where
Combined with the weight model, the weighted information value (WIV) model is constructed. The calculation formula is as follows:
Where
According to the characteristics of historical geological disaster data in the study area and previous research results (Lan et al., 2002; Shahri et al., 2019), 10 geological disaster susceptibility factors including altitude, slope angle, slope aspect, landform, lithology, vegetation coverage, average annual rainfall, distance to faults, distance to roads and land use pattern were initially selected to evaluate the geological disaster susceptibility in the study area (Meng et al., 2010; Chen et al., 2013; Zhao et al., 2021). With 30 m×30 m grid units as evaluation units, the research area was divided into 907,823 units. In order to facilitate data processing by the Apriori algorithm, each factor needs to be classified to convert into Boolean data. The natural breakpoint method was used to classify each factor in ArcGIS software, and the data characteristics of each factor in the study area were analyzed by adhering to the principle of “similar within the interval, different outside the interval”. The partitioning results of each evaluation factor were shown in Figure 4.
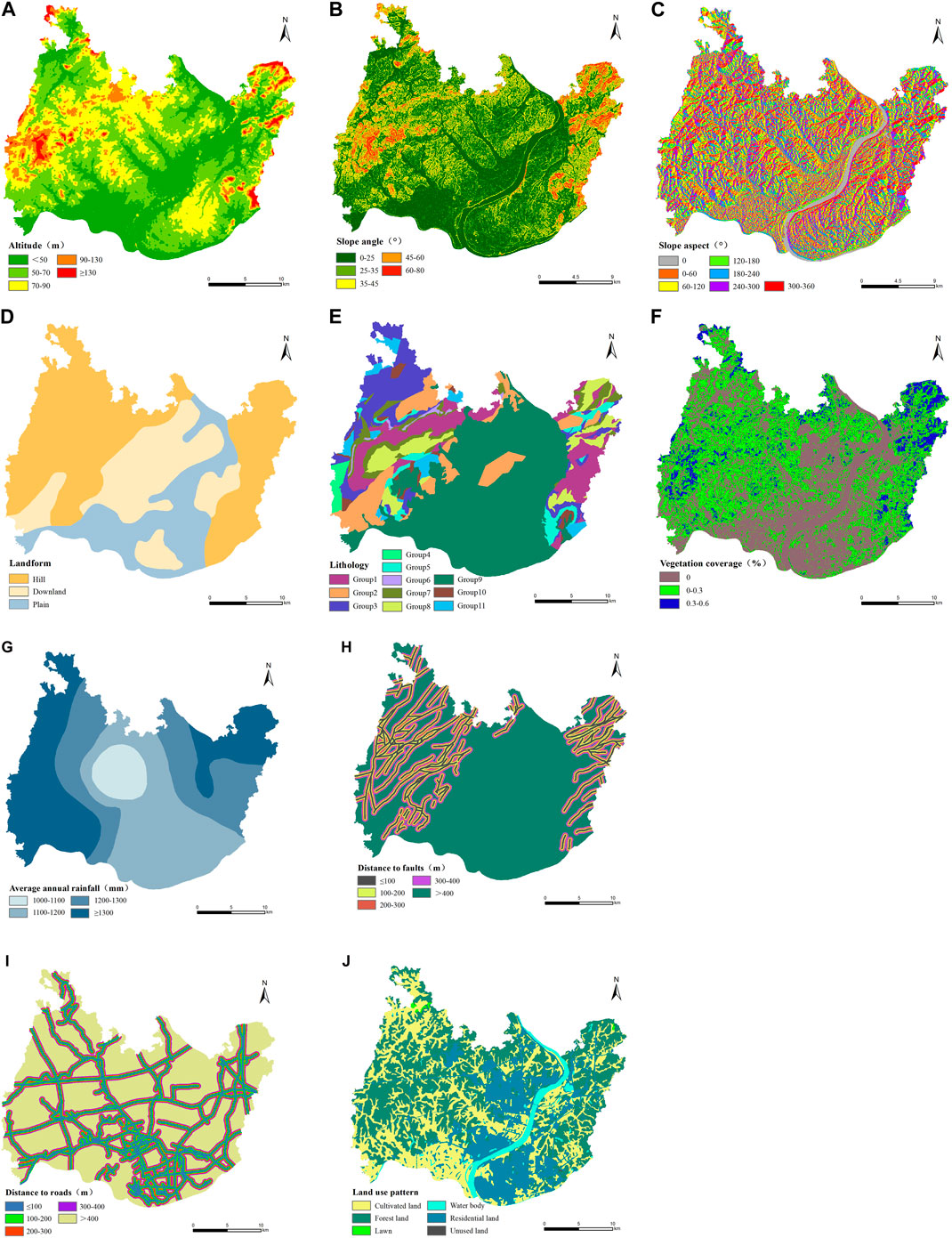
FIGURE 4. Zoning map of geological hazard susceptibility assessment factors in Xiangtan urban area (A) Altitude; (B) Slope angle; (C) Slope aspect; (D) Landform; (E) Lithology; (F) Vegetation coverage; (G) Average annual rainfall; (H) Distance to faults; (I) Distance to roads; (J) Land use pattern.
According to the historical landslide disaster point and the second-level interval Boolean data of each index factor in the study area (Table 3), the Apriori algorithm is applied for data mining to analyze the association rules that have guiding significance for the construction of geological disaster susceptibility evaluation index system in the study area, as shown in Table 2.
According to Table 2, the confidence level of the association rule “G4, D1, J2, E9, A5, B5, F2″ is the highest, indicating that the index factors contained in the disaster causing condition obtained when mining this association rule should be the favorable candidate factors for the evaluation index system of geological disaster susceptibility in the study area. Meanwhile, four association rules in the table cover all index factors with high confidence, indicating that 10 index factors initially selected, including altitude, slope angle, slope aspect, landform, lithology, vegetation coverage, average annual rainfall, distance to faults, distance to roads, and land use pattern, should be selected as index factors for the evaluation of geological disaster susceptibility in the study area.
Through the analysis and processing of geographical data and historical geological disaster data of the study area, the internal commonness of historical disaster points is explored. According to the above 10 susceptibility evaluation indexes such as altitude, slope angle, slope aspect, lithology, and average annual rainfall, the Apriori algorithm is used to calculate the correlation between the second-level interval of each index factor and the occurrence of geological disasters. To determine the contribution rate (weight) of different second-level intervals of each indicator factor to the geological disasters in the study area (Zhang and Jiang, 2004), that is, to explore the statistical relationship between the point value data of each indicator factor located in different second-level intervals and the distribution of geological disasters in the study area.
The different second-level intervals of each susceptibility evaluation index factor were numbered, that is, the altitude was “1″, and the five second-level factor intervals were “1.1, 1.2, 1.3, 1.4, and 1.5″respectively. The slope angle is classified as “2″, and its 5 second-level factor intervals are respectively “2.1, 2.2, 2.3, 2.4, 2.5″, and so on. Data of all second-level factor intervals of each historical geological disaster point are numbered. According to the implementation process of the Apriori algorithm in Section 2.2.1, the statistical data set of the disaster point is input into the software for program implementation by Python language, and the objective weight value of the second-level interval of each index factor is finally obtained, as shown in Table 3.
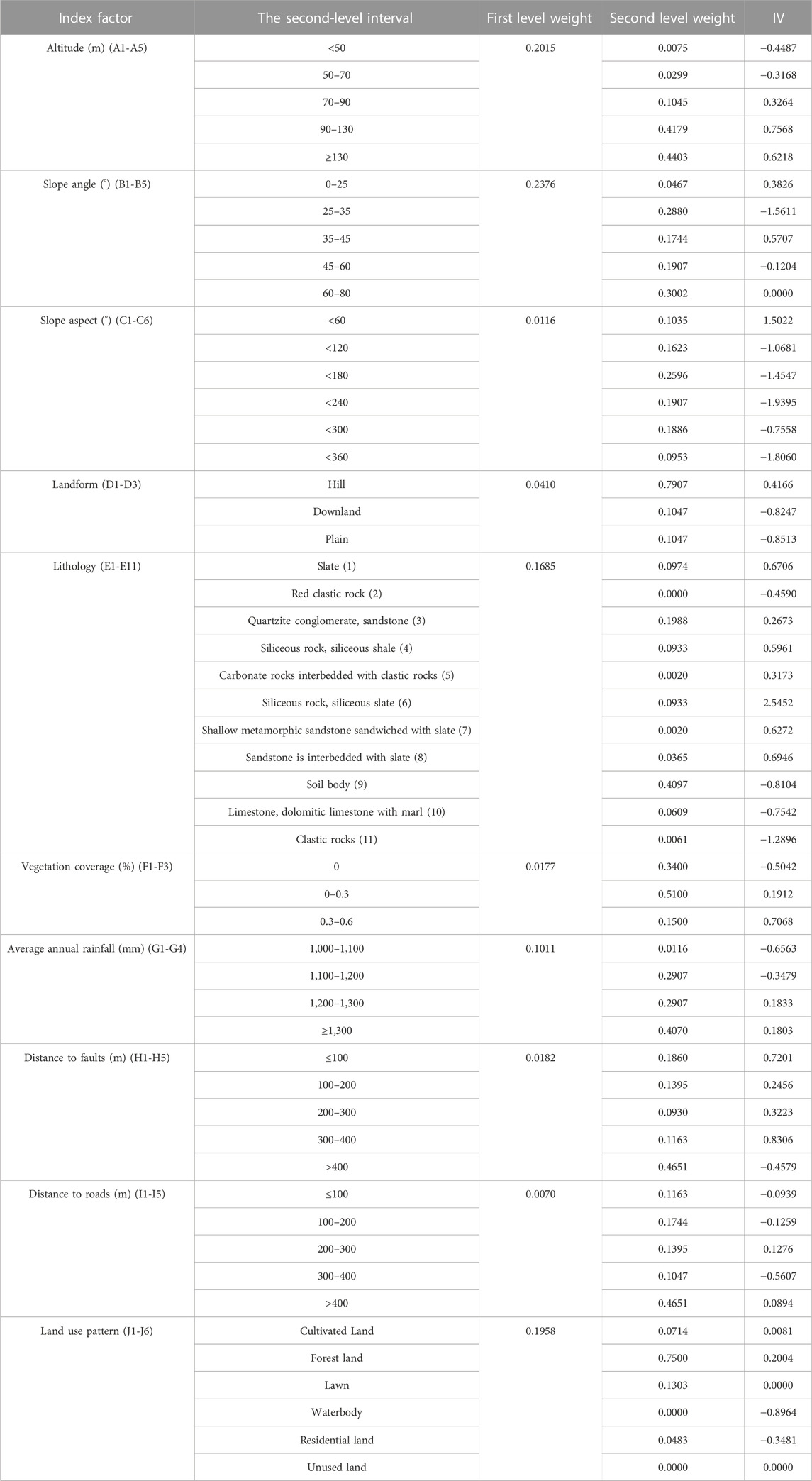
TABLE 3. Calculation results of grading weight and information value (IV) of each evaluation factor.
The entropy weight method was used to calculate the first-level objective weight of each evaluation index, and the information value of the second-level factor interval of each evaluation index was obtained by the information value model. The calculation results are shown in Table 3. According to the superposition analysis function of ArcGIS software, combined with the weight results of the above evaluation indicators and the information value calculation results, the EWM-IV model and the EWM-Apriori-IV model was established according to Eq. 7 respectively to evaluate the susceptibility of geological disasters in the study area. The natural breakpoint method was used to partition the evaluation results of the two models, and the results of geological disaster susceptibility evaluation of Xiangtan urban area were respectively obtained, as shown in Figure 5.
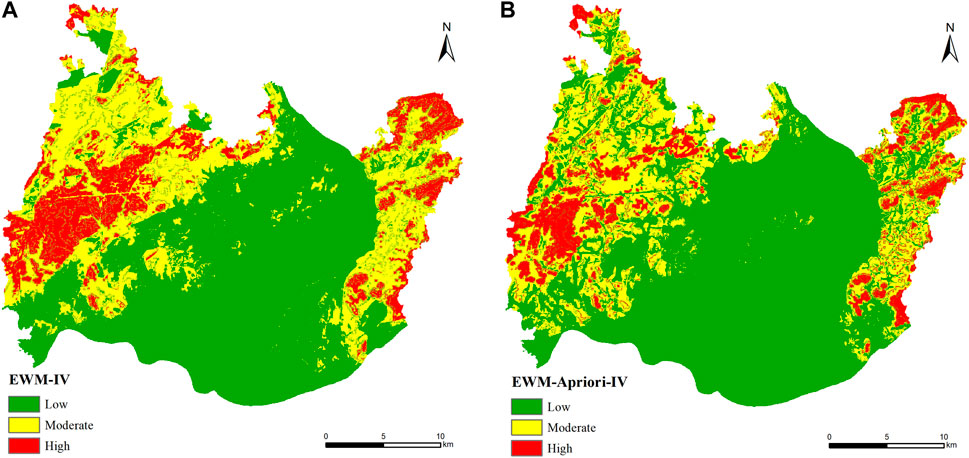
FIGURE 5. Zoning map of geological hazard susceptibility assessment in Xiangtan urban area (A) EWM-IV model; (B) EWM-Apriori-IV model.
At present, there are disaster area ratio verification methods and ROC curve verification methods to verify the evaluation results of geological disaster susceptibility (Kamp et al., 2008; Bai et al., 2010; Fan et al., 2014). The disaster area ratio verification method compares and verifies the ratio between the number of historical disaster points and the area in each prone area. The larger the disaster area ratio in the high-prone area and the smaller the disaster area ratio in the low-prone area, the more accurate and effective the evaluation results will be (Chen et al., 2019). ROC curve refers to the receiver operating characteristic curve, and the area under the curve (AUC) is used to judge the accuracy of model evaluation results. The higher the AUC value, the better the prediction ability of the model (Pradhan, 2013; Wang et al., 2013).Tables 4, 5 indicates the disaster area ratio statistics of the EWM-IV model and the EWM-Apriori-IV model.
By comparing the statistical results of the disaster area ratio evaluated by the two models, the disaster area ratio of the high-prone areas evaluated by the EWM-Apriori-IV model is 1.141, which is higher than 0.721 of the EWM-IV model, and a relative increase of 58.3%. The disaster area ratio of the low-prone areas evaluated by the EWM-Apriori-IV model is 0.033, lower than the EWM-IV model’s 0.058, which is a relative decrease of 43.1%. The results show that the use of the EWM-Apriori-IV model to evaluate the susceptibility of geological disasters in the study area greatly improves the disaster area ratio of the high-prone area and reduces the disaster area ratio of the low-prone area, and the evaluation effect is more accurate and effective.
The ROC curve test was conducted according to the evaluation results of geological disaster susceptibility generated by the two evaluation models. The sensitivity was taken as the vertical coordinate and the specificity was taken as the horizontal coordinate, and the evaluation results were imported into SPSS software for analysis. The results were presented in Figure 6.
The area under the ROC curve (AUC) generated by the two models is both 0.7%-0.9, indicating that the success rate and prediction degree of the results obtained by the two evaluation models used in this paper are between 70% and 90% when evaluating the susceptibility of geological disasters in the study area, with high accuracy. It can be seen from Figure 6 that the AUC values of the EWM-IV model and the EWM-Apriori-IV model are respectively 0.753 and 0.809, that is, the predictive ability of the model is 75.3% and 80.9%, and the latter is 7.4% higher than the former, showing better predictive ability.
Accuracy of geological hazard susceptibility evaluation is affected by the weighting method of evaluation index. As a commonly used susceptibility evaluation model, the weighted information value model is established in most studies by combining the first-level index factor weighting method with the second-level interval information value of each factor, while the second-level interval weight of the index factor is rarely analyzed. Therefore, the inconsistent caliber of information value and weight value will be generated by using this model for evaluation, which will affect the evaluation accuracy. In this paper, the Apriori algorithm is introduced to improve the weighted information value model. By analyzing the correlation between the second-level interval of each disaster causing factor and the occurrence of geological disasters, the objective weight of the second-level interval of each evaluation index is determined, and the susceptibility evaluation of geological disasters is completed by combining the second-level interval information value of each index factor. Thus, the problem that the information value is inconsistent with the weight value in the weighted information value model is solved.
According to the evaluation results, the regionalization effect of EWM-Apriori-IV model is better than that of EWM-IV model. Compared with EWM-IV model, the disaster area ratio of high and low prone areas evaluated by EWM-Apriori-IV model increased by 58.3% and decreased by 43.1%, respectively, and the AUC value of the area under ROC curve increased by 7.4%. Therefore, it is proved that the accuracy and rationality of introducing Apriori algorithm to obtain the second-level interval weight of the index factor and combining with the information value model to predict susceptibility. In addition, this paper only analyzes the feasibility of improving the weighted information value model based on Apriori algorithm. For more susceptibility evaluation methods, it is worth further discussion and discussion to combine them with the weighting method of geological hazard susceptibility evaluation index based on Apriori algorithm to carry out index second-level factor weighting and susceptibility evaluation.
Taking the Xiangtan urban area of Hunan Province as the research area, this paper selected 10 evaluation indexes, introduced the Apriori algorithm as the weight model of the second-level interval of the evaluation index, constructed two evaluation models to evaluate the susceptibility of geological disasters in the research area, and carried out precision verification and comparative analysis on the evaluation results. The results are as follows.
(1) The Apriori algorithm is introduced to analyze the correlation between the second-level intervals of disaster-causing factors and the susceptibility to geological disasters. A weighted model based on the Apriori algorithm is established to achieve the objective weighting of the second-level intervals of disaster-causing factors in the susceptibility evaluation of geological disasters and to solve the problem of the inconsistency between the information value and the weight value in the weighted information value model.
(2) The EWM-IV model and the EWM-Apriori-IV model are established respectively to evaluate the susceptibility of geological disasters in the study area. The results show that: When the weight model based on the Apriori algorithm is used to assign a weight, the accuracy of susceptibility evaluation is significantly increased by 7.4%, and the disaster area ratio of the high-prone area is increased by 58.3%, while the disaster area ratio of the low-prone area is reduced by 43.1%, indicating that the EWM-Apriori-IV model is more accurate and rational in evaluation.
(3) According to the susceptibility evaluation results of the EWM-Apriori-IV model, the study was divided into high, medium, and low susceptibility areas. The high-prone area covers 68.4 km2, accounting for 10.4% of the Xiangtan urban area, and contains 78 geological disaster points, accounting for 64.4% of the total geological disaster points. The middle-prone area is 158.4 km2, accounting for 24.1% of the Xiangtan urban area, including 29 geological disaster points, accounting for 24.0% of the total geological disaster points. The low-prone area covers 430.6 km2, accounting for 65.5% of the Xiangtan urban area, and contains 14 geological disaster points, accounting for 11.6% of the total geological disaster points.
The original contributions presented in the study are included in the article/Supplementary Material further inquiries can be directed to the corresponding author.
BC: Conceptualization, methodology, paper writing and revision; NW: Data collation and analysis, paper writing; TQ: Resource provision; LZ, YiL, XL, and YoL: All participated in the revision, reading and approval of manuscripts, as well as the supervision and management of the process.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1127889/full#supplementary-material
Agrawal, R., and Srikant, R. (September, 1994). Fast Algorithms for mining association rules, Proceedings of the 20th international conference on very large data bases. IEEE. San Francisco, CA, USA,
Alsabhan, A. H., Singh, K., Sharma, A., Alam, S., Pandey, D. D., Rahman, S. A. S., et al. (2022). Landslide susceptibility assessment in the Himalayan range based along Kasauli – parwanoo road corridor using weight of evidence, information value, and frequency ratio. J. King Saud. Univ–Sci. 34 (2), 101759. doi:10.1016/j.jksus.2021.101759
Bai, S., Wang, J., Lü, G., Zhou, P., Hou, S., and Xu, S. (2010). GIS-based logistic regression for landslide susceptibility mapping of the Zhongxian segment in the Three Gorges area, China. Geomorghlogy 115 (1), 23–31. doi:10.1016/j.geomorph.2009.09.025
Budimir, M. E. A., Atkinson, P. M., and Lewis, H. G. (2015). A systematic review of landslide probability mapping using logistic regression. Landslides 12 (3), 419–436. doi:10.1007/s10346-014-0550-5
Chen, P., Qiao, J., Peng, Z., Xie, K., and Yu, H. (2013). Screening of debris flow risk factors and risk evaluation based on rank correlation. Rock Soil Mech. 34 (5), 1409–1415. doi:10.16285/j.rsm.2013.05.015
Chen, G., Tang, M., Zhou, H., Qu, F., Li, Y., and Xin, Y. (2019). Dynamic risk assessment method of geological hazard of linear engineering in mountainous area and its application. J. Disaster Prev. Mitig. Eng. 39 (3), 524–532. doi:10.13409/j.cnki.jdpme.2019.03.020
Chen, J., Yang, Z., and Liu, H. (2005). Landslide susceptibility zoning and its probabilistic forecast. Chin. J. Rock Mech. Eng. 13, 2392–2396. doi:10.3321/j.issn:1000-6915.2005.13.032
Chen, L., Guo, H., Gong, P., Yang, Y., Zuo, Z., and Gu, M. (2021). Landslide susceptibility assessment using weights-of-evidence model and cluster analysis along the highways in the Hubei section of the Three Gorges Reservoir Area. Comput. Geosciences 156, 104899. doi:10.1016/j.cageo.2021.104899
Chung, C., and Fabbri, A. G. (1999). Probabilistic prediction models for landslide hazard mapping. Photogrammetric Eng. Remote Sens. 65 (12), 1389–1399.
Devkota, K. C., Regmi, A. D., Pourghasemi, H. R., Yoshida, K., Pradhan, B., Ryu, I. C., et al. (2013). Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling–Narayanghat road section in Nepal Himalaya. Nat. Hazards 65 (1), 135–165. doi:10.1007/s11069-012-0347-6
Fan, L., Hu, R., Zeng, F., Wang, S., and Zhang, X. (2012). Application of weighted information value model to landslide susceptibility assessment—a case study of enshi city, hubei province. J. Eng. Geol. 20 (4), 508–513. doi:10.3969/j.issn.1004-9665.2012.04.005
Fan, Q., Ju, N., Xiang, X., and Huang, J. (2014). Landslides hazards assessment with weights of evidence—A case study in guizhou, China. J. Eng. Geol. 22 (3), 474–481. doi:10.13544/j.cnki.jeg.2014.03.017
Han, J., and Kamber, M. (2001). Data mining concepts and techniques. Beijing, China: Higher Education Press.
Hidayanto, B. C., Muhammad, R. F., Kusumawardani, R. P., and Syafaat, A. (2017). Network intrusion detection systems analysis using frequent item set mining algorithm FP-max and Apriori. Procedia Comput. Sci. 124, 751–758. doi:10.1016/j.procs.2017.12.214
Jiang, Y., Wu, G., Zhao, Z., and He, L. (2019). Channel selection method for mountain railway based on terr-ain and geomorphological parameters. J. Eng. Geol. 27 (4), 903–913. doi:10.13544/j.cnki.jeg.xq2019010
Jiao, Y., Zhao, D., Ding, Y., Liu, Y., Xu, Q., Qiu, Y., et al. (2019). Performance evaluation for four GIS-based models purposed to predict and map landslide susceptibility: A case study at a world heritage site in southwest China. CATENA 183, 104221. doi:10.1016/j.catena.2019.104221
Jie, Q., Shi, B., Luo, W., Fei, B., and Sun, Y. (2015). Analysis of DFOS-based association rules on multi-fields data monitoring of slope. J. Eng. Geol. 23 (6), 1146–1152. doi:10.13544/j.cnki.jeg.2015.06.015
Kamp, U., Growley, B. J., Khattak, G. A., and Owen, L. A. (2008). GIS-based landslide susceptibility mapping for the 2005 Kashmir earthquake region. Geomorphology 101 (4), 631–642. doi:10.1016/j.geomorph.2008.03.003
Kavzoglu, T., Sahin, E. K., and Colkesen, I. (2014). Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 11 (3), 425–439. doi:10.1007/s10346-013-0391-7
Lan, H., Wu, F., Zhou, C., and Wang, S. (2002). Sensitivity analysis of landslide factors in xiaojiang basin of yunnan province based on GIS. Chin. J. Rock Mech. Eng. 21 (10), 1500–1506. doi:10.3321/j.issn:1000-6915.2002.10.014
Li, B., Li, Y., and Cai, M. (2020). Research on key factors of water environment for cyanobacteria growth in Taihu Lake based on data mining. J. Hohai Univ. Nat. Sci. 48 (6), 506–513. doi:10.3876/j.issn.1000-1980.2020.06.004
Li, J., and Niu, R. (2013). Association rule mining and using between stability and land use of landslides—Taking area from zigui to badong in three gorges reservoir area as an example. Comput. Eng. Appl. 49 (6), 234–239. doi:10.3778/j.issn.1002-8331.1107-0608
Liang, G., Xu, W., and Tan, X. (2010). Application of extension theory based on entropy weight to rock quality evaluation. Rock Soil Mech. 31 (2), 535–540. doi:10.16285/j.rsm.2010.02.024
Liang, L., Liu, Y., Tang, Z., Zou, Q., and Li, J. (2019). Geologic hazards susceptibility assessment based on weighted information value—a case study in luding county, sichuan province. Bull. Soil Water Conservation 39 (6), 176–182+321. doi:10.13961/j.cnki.stbctb.2019.06.026
Ma, Z., and Mei, G. (2021). Deep learning for geological hazards analysis: Data, models, applications, and opportunities. Earth Sci. Rev. 223, 103858. doi:10.1016/j.earscirev.2021.103858
Meng, F., Li, G., Li, M., Ma, J., and Wang, Q. (2010). Application of stepwise discriminant analysis to screening evaluation factors of debris flow. Rock Soil Mech. 31 (9), 2925–2929. doi:10.16285/j.rsm.2010.09.003
Nourani, V., Pradhan, B., Ghaffari, H., and Sharifi, S. S. (2014). Landslide susceptibility mapping at Zonouz Plain,Iran using genetic programming and comparison with frequency ratio,logistic regression,and artificial neural network models. Nat. Hazards 71 (1), 523–547. doi:10.1007/s11069-013-0932-3
Pradhan, B. (2013). A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. &Geosciences 51, 350–365. doi:10.1016/j.cageo.2012.08.023
Shahri, A. A., Spross, J., Johansson, F., and Larsson, S. (2019). Landslide susceptibility hazard map in southwest Sweden using artificial neural network. CATENA 183, 104225. doi:10.1016/j.catena.2019.104225
Shen, H., Dong, Y., Yang, M., Shi, C., and Yang, X. (2021). Assessment on landslide susceptibility in Gansu Province based on AHP and information quantity method. Res. Soil Water Conservation 28 (6), 412–419. doi:10.13869/j.cnki.rswc.2021.06.034
Tang, C., and Ma, G. (2015). Study on the zoning method of small regional geological disaster susceptibility based on geomorphic unit. Sci. Geogr. Sin. 35 (1), 91–98. doi:10.13249/j.cnki.sgs.2015.01.011
Wang, J., Guo, J., Wang, W., and Fang, L. (2012). Application and comparison of weighted linear combination model and logistic regression model in landslide susceptibility mapping. J. Central South Univ. Sci. Technol. 43 (5), 1932–1939.
Wang, J., Yin, K., and Xiao, L. (2014). Landslide susceptibility assessment based on GIS and weighted information value: A case study of wanzhou district, three gorges reservoir. Chin. J. Rock Mech. Eng. 33 (4), 797–808. doi:10.13722/j.cnki.jrme.2014.04.012
Wang, L. J., Sawada, K., and Moriguchi, S. (2013). Landslide susceptibility analysis with logistic regression model based on FCM sampling strategy. Comput. Sci. 57, 81–92. doi:10.1016/j.cageo.2013.04.006
Wang, W. D., Xie, C. M., and Du, X. G. (2009). Landslides susceptibility mapping in Guizhou province based on fuzzy theory. Min. Sci. Technol. 19 (3), 399–404. doi:10.1016/S1674-5264(09)60075-2
Wu, T., and Niu, R. (2011). Association rule mining of geological hazard factors in Badong area of Three Gorges Reservoir Area. Comput. Eng. Appl. 47 (11), 240–244. doi:10.3778/j.issn.1002-8331.2011.11.068
Xie, C. (2011). Landslides hazard susceptibility evaluation based on weighting model. J. Central South Univ. Sci. Technol. 42 (6), 1772–1779.
Xu, C., Dai, F., Yao, X., Chen, J., Tu, X., Sun, Y., et al. (2009). GIS-based landslide susceptibility assessment using analytical hierarchy process in Wenchuan earthquake region. Chin. J. Rock Mech. Eng. 28 (2), 3978–3985. doi:10.3321/j.issn:1000-6915.2009.z2.100
Yang, P., Wang, N., Guo, Y., and Ma, X. (2020). Assessment of landslide susceptibility in Lintong District using weighted information value model. J. Yangtze River Sci. Res. Inst. 37 (9), 50–56. doi:10.11988/ckyyb.20190726
Yu, W. (2004). Implementation of data mining based on Apriori algorithm using VB. Comput. Eng. 2, 196–197. doi:10.3969/j.issn.1000-3428.2004.02.075
Zhang, L., and Jiang, S. (2004). A data-driven weighting model for regional landslide sensitivity evaluation and its application. Hydrogeology Eng. Geol. 6, 33–36. doi:10.16030/j.cnki.issn.1000-3665.2004.06.007
Keywords: apriori algorithm, susceptibility evaluation, weighted information value model, rule of association, second-level factor weight
Citation: Chen B, Wei N, Qu T, Zhang L, Li Y, Long X and Lin Y (2023) Research on weighting method of geological hazard susceptibility evaluation index based on apriori Algorithm. Front. Earth Sci. 11:1127889. doi: 10.3389/feart.2023.1127889
Received: 20 December 2022; Accepted: 13 March 2023;
Published: 22 March 2023.
Edited by:
Wei Zhao, Institute of Mountain Hazards and Environment (CAS), ChinaReviewed by:
Yi Wang, China University of Geosciences Wuhan, ChinaCopyright © 2023 Chen, Wei, Qu, Zhang, Li, Long and Lin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tianqiang Qu, MjE0OTg1OTM3NUBxcS5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.