- 1College of Water Resources Science and Engineering, Yangzhou University, Yangzhou, Jiangsu, China
- 2Intelligent Water Conservancy Research Institute, Nanjing Jurise Engineering Technology Co., Ltd., Nanjing, Jiangsu, China
- 3Civil Engineering Department, College of Engineering, Thamar University, Dhama, Yemen
In recent years, as AI technology has advanced, online monitoring of dams has garnered increasing interest. In addition, surrogate model technology is a crucial component of online monitoring. As a result, developing a high-quality surrogate model has become one of the pillars of dam online monitoring. This work proposes a local radial basis function based on sensitivity modification to address the deficiencies of the current radial basis function. In addition, a benchmark function is utilized to validate the method’s viability. Comparisons with BP neural network and RBF demonstrate the usefulness of the proposed strategy. The analysis demonstrates that the proposed strategy for constructing a surrogate model of the dam’s structural behavior is possible and accurate. This paper aims to establish a high-quality surrogate model to provide technical support for dam online monitoring.
1 Introduction
As an important part of national infrastructure (Sevieri et al., 2019), the safety of dams has been paid more and more attention to. Thanks to the development of digital twin (Cunbo et al., 2017; Fei et al., 2017; Uhlemann et al., 2017) and parallel intelligence (FeiYue, 2004; Xi et al., 2017) technology, dam online monitoring (Han et al., 2022) has increasingly become a trend and hotspot in dam safety monitoring. It is required to obtain the structural behavior of dam operation in real-time to assess, diagnose, and evaluate the dam safety condition online and identify the abnormal dam operation behavior in time. On the other hand, the traditional deterministic method based on physical models relies on simulation techniques such as finite element (Salazar et al., 2015) and finite difference models (Jinping, 2010). Even though this method can produce accurate results, it often takes a lot longer to do the calculations and cannot be used to track how a dam is behaving in real-time. Therefore, the surrogate model comes into being and is widely used in the fields of parameter optimization (Savic and Walters, 1997), model calibration (Duan et al., 1992; Beven and Freer, 2001), multi-objective optimization (Castelletti et al., 2010), global sensitivity analysis (Hornberger and Spear, 1981), reliability analysis (Skaggs and Barry, 1997), and so on.
In current research on dam engineering, surrogate model technology mainly focuses on the field of parameter identification. By establishing the approximate mapping relationship between parameter space and response space, the repeated time-consuming simulation model calculation is replaced to form an online model base, which can significantly improve identity efficiency and realize online parameter identification. Lin et al. (2022) established a multi-output surrogate model based on the Gaussian process to identify the viscoelastic parameters of the dam system. An inverse analysis method based on a novel hybrid fireworks algorithm (FWA) and the radial basis function (RBF) model is proposed by Dou et al. (2019) to diagnose the health condition of concrete dams. This method identifies the elastic modulus of materials to determine whether a dam will fail. Das and Soulaimani. (2021) established a surrogate model in the form of polynomial regression and used GA, FDTD, and PSO to identify the relevant parameters of the dam. Li et al. (2023) presented a surrogate-assisted stochastic optimization inversion (SASOI) algorithm to identify the static and dynamic parameters based on LHS. Shahzadi and Soulaïmani. (2021) constructed a surrogate model by combining polynomial chaos expansion and deep learning networks to assess the effect of constitutive soil parameters on the behavior of a rockfill dam based on sobol sampling. Zhang et al. (2023) taken the multi-layer perceptron algorithm as a surrogate model to determine deformation monitoring indexes based on LHS. By solving the RBDO problem of the gravity dam design, Rad et al. (2022) constructed a new surrogate model by combine a hybrid Support Vector Regression (SVR) based generalized normal distribution optimization (GNDO) with the Monte Carlo Simulation (MCS). Online analysis of structural behavior is the basis of online parameter identification, anomaly detection, and sensitivity analysis. An issue with online structural analysis will have repercussions for any calculations or analyses that follow. So, it is important to create a surrogate model that’s both precise and reliable. Once there is a problem in online structural analysis, it will repercuss the following analysis and calculation. So, it is important to establish surrogate model that’s both precise and reliable.
The surrogate model, also called a meta-model (Forrester and Keane, 2009), is a simplified model with a small computation scale, but the calculation outcomes are quite similar to those of a high precision model. Popular surrogate models include the polynomial response surface model (RSM) (BUCHER and BOURGUND, 1990; Schultz et al., 2004; Schultz et al., 2006), Kriging model (Jones et al., 1998; Baú and Mayer, 2006), neural network model (Theocaris and Panagiotopoulos, 1995; Papadrakakis et al., 1996; Furukawa and Yagawa, 1998; Karimi et al., 2010), support vector machine model (SVM) (Rocco and Moreno, 2002; Zhao, 2008; Zhang et al., 2009; Li et al., 2016), radial basis function interpolation model (RBF) (Mugunthan et al., 2005; Mugunthan and Shoemaker, 2006; Li et al., 2018; Jing et al., 2019), and so on. Radial basis function interpolation, as a function of the distance between data points, has the characteristics of dimensionality independent and meshless. As an exact interpolation model, it has been extensively acknowledged in the study of surrogate models due to its high interpolation accuracy, straightforward methodology, well-defined principles, small number of parameters, and easy-to-understand implementation (Bui-Thanh et al., 2008). Therefore, the surrogate model based on radial basis function interpolation is studied in this paper.
The stability and accuracy of radial basis function interpolation are heavily dependent on shape parameters, which are mainly affected by the basis function and node distribution. Consequently, numerous scholars have conducted extensive research on the selection of shape parameters. The Multiquadric function (MQ) was suggested by Hardy. (1971) in 1971 as the basis function for the radial basis function interpolation shape parameters reference formula. Rippa. (1999) determined the shape parameters of the radial basis function interpolation with Multiquadric (MQ), Inverse multiquadric (IMQ), and Gaussian as the basis function by minimizing a cost function. To identify shape parameters, Fasshauer and Zhang. (2007) proposed an RBF pseudo-spectral technique based on leave-one-out cross-validation. This method is applicable for the iterated approximate moving least squares approximation of function value data and for the solution of partial differential equations.
In most cases, shape parameters obtained through trial error or some other ad hoc means (Fasshauer and Zhang, 2007). The shape parameters determined by these approaches are called global shape parameters. However, the interpolation precision of the radial basis function is highly dependent on grid densities and shape parameters. Therefore, selecting a single shape parameter in the state space may result in a loss of precision. In recent years, several scholars have developed a novel method for selecting shape parameters based on the preceding theory. In other words, the original shape parameters are substituted by a variable, also known as the local shape parameters. Bayona et al. (2011) calculated the shape parameters using the local radial basis function algorithm in order to reduce the inaccuracy in approximation. Davydov and Oanh. (2011) addressed adaptive meshless discretization of the Dirichlet problem for the Poisson equation using numerical differentiation stencils derived using the radial basis function. Gao et al. (2020) computed adaptively the shape parameters of the local radial basis function using the local point densities of the points, and then implemented adaptive interpolation of the radial basis function. Acar. (2014) optimized the shape parameters and weight factor on the basis of an ensemble of standard RBFs. The outcome shown that the proposed strategy enhanced the accuracy of prediction.
Currently, the dam surrogate model research is mainly based on ANN, RSM, and other methods. And radial basis function is primarily applied to RBF neural network in the form of the basis function. Few literatures directly use radial basis function interpolation to establish a dam surrogate model. The radial basis function is an interpolation function based on distance, and different parameters have different sensitivity coefficients to the response space. Magnus and Vasnev. (2015) applied the relative sensitivity to forecast combinations, and introduced the sensitivity-based weights. And by compared with the multivariate and random walk benchmarks, different forecasting models are combined using equal, fit-based and sensitivity-based weights. Li et al. (2013) analyzed the sensitivity of the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method in water quality assessment mainly includes sensitivity to the parameter weights and sensitivity to the index input data. In the distance calculation process, modifying the distance by parameter sensitivity is equivalent to assigning weight coefficients to the parameters in the calculation process, which dramatically reduces the influence of parameters insensitive to response space in distance calculation and enhances the effect of parameters more sensitive to static behavior. The process adaptively adjusts the weight of parameters to the response space to improve the model’s accuracy.
Therefore, based on local shape parameters and sensitivity analysis, a local radial basis function based on sensitivity modification is proposed in this paper. The method is applied to modeling the dam structural behavior surrogate model, and the static and dynamic behaviors of the dam are established, respectively. The feasibility and advantages of the proposed method are verified by comparing with the radial basis function and BP neural network. The remainder of this paper is organized as follows. Section 2 describes the process of establishing a local radial basis function surrogate model in detail. In Section 3, the feasibility of the proposed method is verified by the benchmark function. The surrogate model of dam structural behavior is established in Section 4, and the effect of the surrogate model is analyzed. In Section 5, the applicability of the local radial basis function surrogate model is analyzed by comparing it with the radial basis function and BP neural network. Section 6 draws some conclusions.
2 Establishment of local radial basis function surrogate model
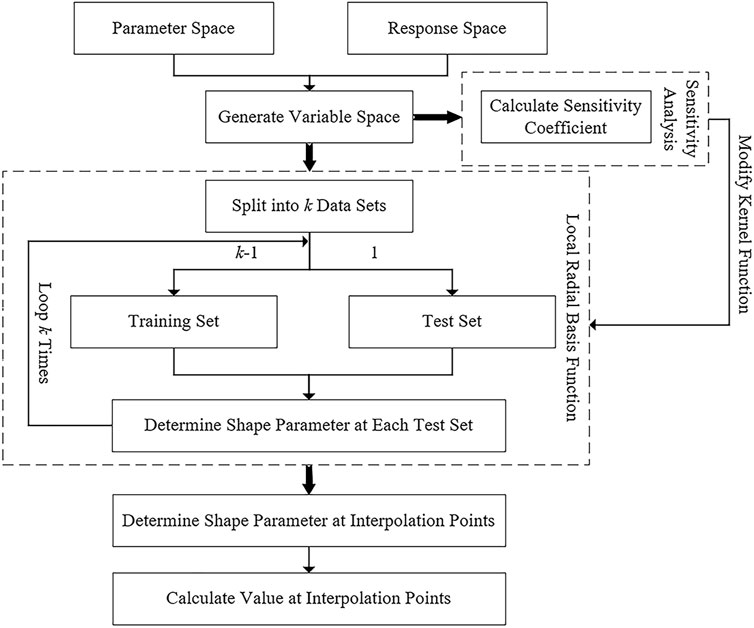
In this study, the sensitivity coefficients of parameter space to response space are determined first, followed by the determination of local shape parameters using leave-one-out cross-validation (LOOCV) and genetic algorithm (GA). Sensitivity coefficients are used to adjust the kernel function during calculating local shape parameters in order to realize the local radial basis function based on sensitivity modification. Figure 1 depicts the specific process.
2.1 Radial basis function interpolation model
The radial basis function (RBF) interpolation model is a non-linear scatter interpolation model that fits the high-dimensional function with a one-dimension expression. As an accurate interpolation model, it not only has high interpolation accuracy but also has a simple principle and requires few parameters to be specified. As a result, it has received widespread recognition in surrogate model research (Jin et al., 2001; Xuefeng et al., 2005; Zhao and Xue, 2010).
Suppose n samples are randomly taken as the training set, denoted as
Where
Where, c is the radial basis function’s shape parameter, whose value determines the specific shape of the kernel function.
Eq. 1 of the n sampling points can be utilized to create the equations system indicated in Eq. 3, which gives the weight coefficient
The above expression can be represented by the matrix
Micchelli theorem states that
After obtaining the weight matrix
2.2 Kernel function modification based on sensitivity coefficient
In this paper, global sensitivity analysis based on variance (Saltelli, 2002) is used to modify r (Euclidean distance) in kernel function (Eq. 2). First-order and total-order sensitivity coefficients are calculated as follows.
(1) Generate a
(2) Define a matrix Ci formed by all columns of B except the ith column, which is taken from A.
(3) Compute the model output for all input parameters in the sample matrices A, B, and Ci, obtaining three vectors of model outputs of dimension N × 1.
(4) The first-order sensitivity coefficient is calculated as follows.
Where
(5) The total-order sensitivity coefficient is calculated as follows.
The kernel function is modified by the total-order sensitivity coefficient as follows. Assuming that there are two groups of parameters
2.3 Establishment of local radial basis function
Generally speaking, mean square error (MSE) is a common method to test the quality of the surrogate model. However, because the radial basis function adopts the complete interpolation method, the model strictly passes through each sample point, and the MSE is 0, which is not conducive to the evaluation of model quality. Therefore, in order to evaluate the quality of the model, cross-validation (Jiang and Wang, 2017) is usually used to calculate the MSE of the model. Cross-validation divides the sample set into k mutually exclusive subsets of the same size. Then, k-1 subsets are randomly selected as the training set, and the remaining 1 subset is used to verify the prediction performance of the model. When k is equal to the sample size n, this cross-validation is called Leave-one-out cross-validation (LOOCV). In order to accurately find the most appropriate shape parameter c under the current test set, a genetic algorithm (GA) is used for optimization calculation, and its objective function is:
Where,
After the most appropriate shape parameter is obtained under the current test set, the new test set is selected according to LOOCV until the whole sample set is traversed. After n loops, the local shape parameters of the whole model can be obtained.
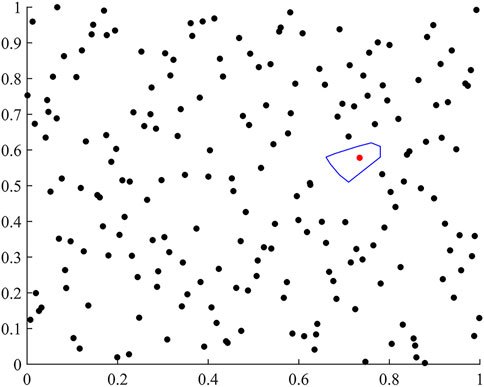
When the local radial basis function is used for prediction, the nearest neighbor method (kNN) is first used to find the sample point that is closest to the prediction parameter, and then the corresponding shape parameter and weight coefficient matrix of this sample point is used to predict the results. Figure 2 selects a two-dimensional parameter space to explain. The blue area represents the set of all neighboring points of the red dot. When the predicted parameter is within the range of the blue area, the shape parameter corresponding to the red dot should be used for prediction.
3 Method feasibility verification
In order to verify the feasibility of the proposed local radial basis function based on sensitivity modification, a benchmark function is constructed in this paper, and the local radial basis function, radial basis function, and BP neural network (Basheer and Hajmeer, 2000) are respectively used for benchmark testing.
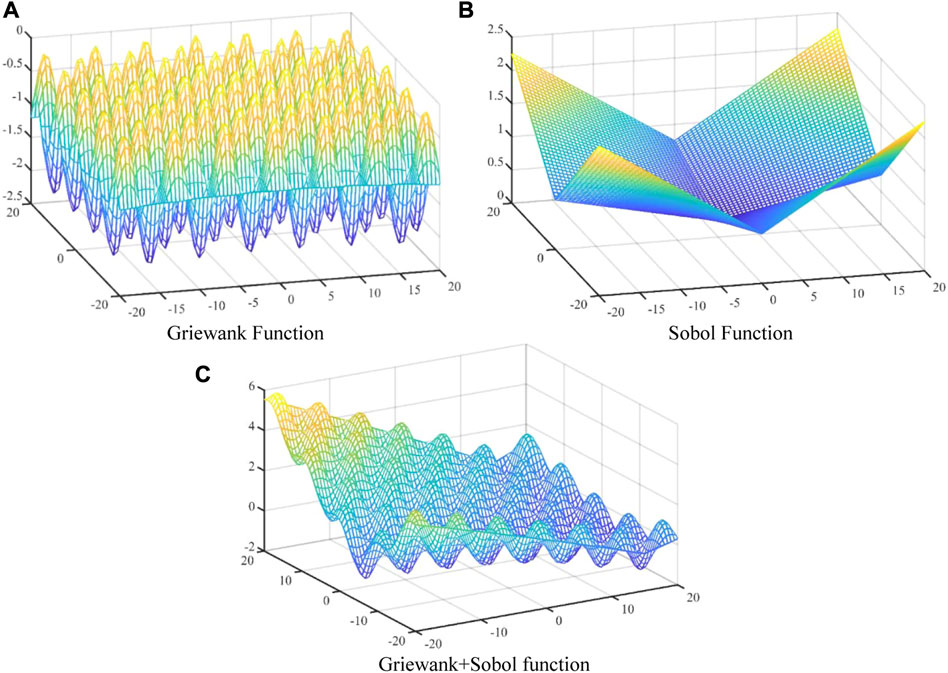
Griewanke Function (Eq. 14) is used to test the applicability of this method to complex function models. The Sobol function (Tarantola et al., 2006) (Eq. 15) is used to change the sensitivity of the input parameters. In this paper, two functions are superimposed (Griewanke+Sobol), and the specific is shown in Eq. 13. The graphs of these three functions are shown in Figure 3.
Where,
It can be seen that the newly constructed benchmark function retains the complexity of the original Griewank function and solves the problem that the parameter sensitivity of the original function is the same. It makes the newly constructed test function more complex and closer to the actual engineering situation. This section firstly calculates the sensitivity coefficient of each parameter, and then modifies the kernel function based on sensitivity coefficients. The modified radial basis function is used to determine the shape parameter on each test set. Finally, a local radial basis surrogate model is established on the sample space.
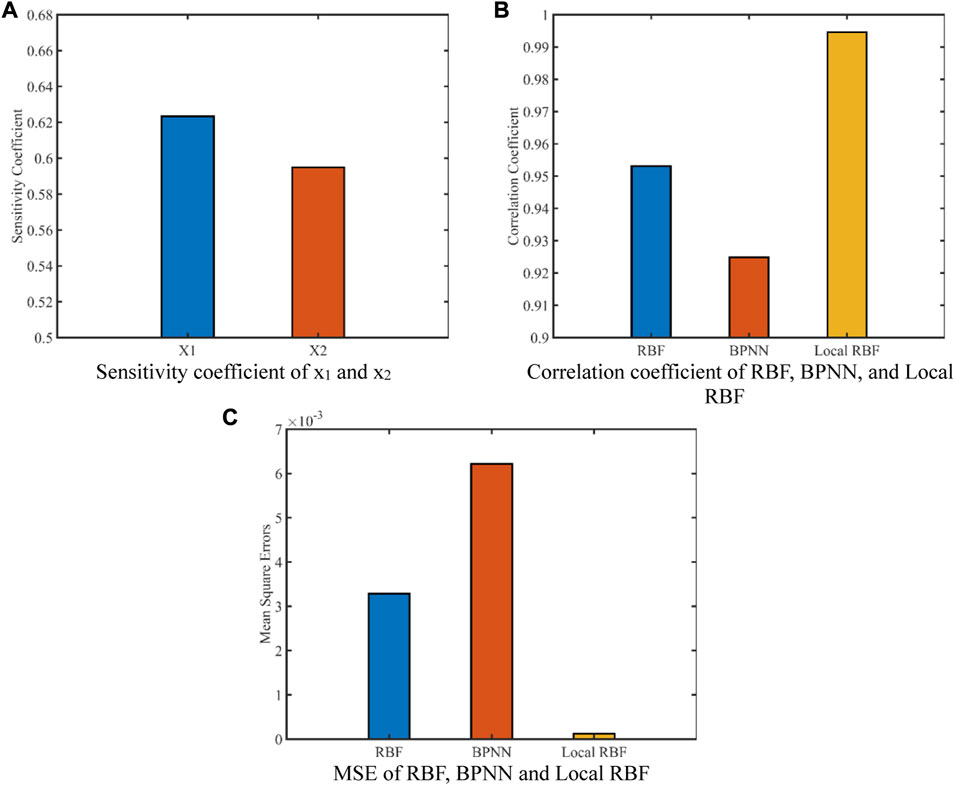
Figure 4 shows the sensitivity coefficient of each parameter to benchmark function, the correlation coefficient of three different models, and their MSE. The sensitivity coefficient of x1 and x2 to the benchmark function is 0.6233 and 0.5949, respectively. In terms of the correlation coefficient, local RBF model has the highest correlation, BP neural network model has the worst correlation, and RBF model has the medium correlation on the validation set. Among them, the correlation degree of local RBF model is 4.36% higher than that of RBF model and 7.54% higher than that of BP neural network model. In terms of MSE, local RBF model has the smallest MSE, BP neural network has the largest MSE, and RBF model has the medium MSE.
For the newly constructed benchmark function, local RBF model proposed in this paper has the best effect, followed by RBF model, and BP neural network model has the worst effect. It can be seen that the method proposed in this paper is reasonable and feasible.
4 Establishment and analysis of dam structural behavior surrogate model
This paper takes the gravity dam and arch dam as examples, and the static and dynamic behavior surrogate models of dams are established and analyzed. Static behavior includes deformation, stress, and temperature, while dynamic behavior mainly analyzes the tensile damage under earthquake. In the static behavior, deformation mainly includes U, V, and W, that is, the deformation along the x, y, and z directions. The stress mainly includes
4.1 Static behavior surrogate model of dam
This section takes a gravity dam as an example to study the static behavior surrogate model of the dam. The dam is located on the Brahmaputra River in Tibet, China. The controlled catchment area of dam toe is 157,407 km2, the annual average flow is 1,010 m3/s, the total reservoir capacity is 57.89 million m3, the normal water level of the reservoir is 3,477.00 m, and the corresponding reservoir capacity is about 55.28 million m3. The dam is an RCC gravity dam with a maximum dam height of 118.0 m and a total crest length of 389 m. It is divided into 17 sections, among which 6#∼9# is the overflow dam section and the rest is the water retaining dam section.
According to the steps of establishing a surrogate model, the set of sample parameters, namely, the Design of Experiment (DoE), is designed first. The probability distribution and value range of parameters are shown in Table 1. The parameters are sampled in the Sobol sequence (Saltelli and Sobol, 1995) to generate parameter space. As it is commonly recognized that in the absence of any priori knowledge on the problem under consideration, uniform sampling of the design space throughout the whole space is favourable. Sobol sequence has the property of uniform distribution in space. Unlike random numbers, quasi-random points are deterministic sequences that know about the position of previously sampled points and are constructed to avoid the presence of clusters as much as possible. It should be noted that all parameters in Table 1 are used to establish the deformation and stress behavior surrogate model, while only four parameters are needed to establish the temperature behavior surrogate model: time, upstream and downstream water level, and thermal conductivity. Then the response space is generated by numerical analysis of the model based on parameter space. The specific numerical model is shown in Figure 5. Finally, the mapping model is established according to the method proposed in this paper.
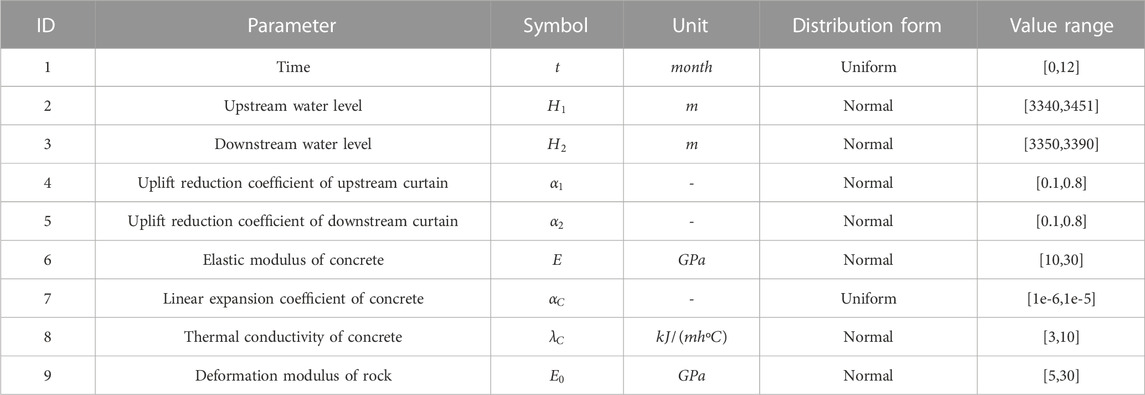
TABLE 1. The probability distribution and value range of the parameters of static behavior surrogate model.
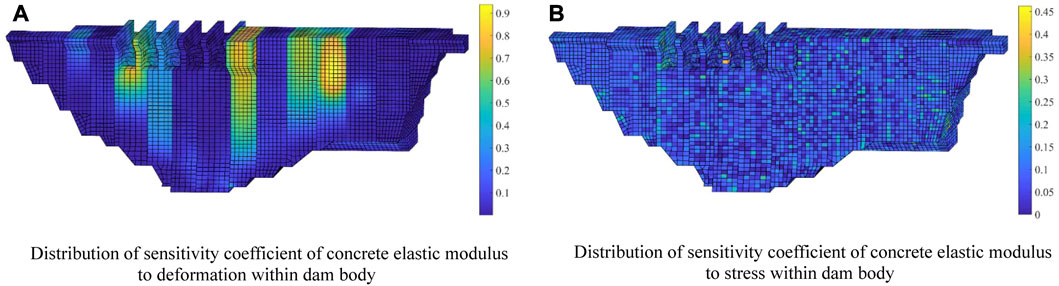
According to the proposed local RBF based on sensitivity modification, the sensitivity coefficient of parameter space to response space should be analyzed first. The sensitivity coefficient of concrete elastic modulus to U in deformation and
The kernel function is modified based on the sensitivity coefficient calculated above, and the deformation, stress, and temperature surrogate models are established based on local RBF.
4.1.1 Establishment and analysis of dam deformation behavior surrogate model
This paper divides the sample data into three parts: training set, test set, and validation set. The training set and test set are used to determine the local shape parameters and the training model, and the validation set is used to test the overall effect of the surrogate model. In terms of testing the effect of the surrogate model, in addition to the MSE mentioned above, this paper also uses the correlation coefficient between the response value of the validation set and the fitting value calculated by the surrogate model to test the effect of the surrogate model. Correlation coefficient can effectively reflect the correlation between variables and its direction, so it is widely used in the effect evaluation of surrogate model. Goel et al. (2007) used correlation coefficient, RMS error and maximum error to evaluate the model effect of the ensemble of surrogates. Jin and Jung. (2016) taken correlation coefficient and RMSE as the stopping criteria to conduct adaptive sampling on surrogate model. In this paper, the correlation coefficient is used to characterize the trend relationship between the response value and the fitting value, and MSE is used to characterize the error between the response value and the fitting value. Therefore, the correlation coefficient and MSE between the response value of the validation set and the fitting value obtained through deformation behavior surrogate model are shown in Figures 7A–F, and the cumulative probability distribution is shown in Figures 7G, H.
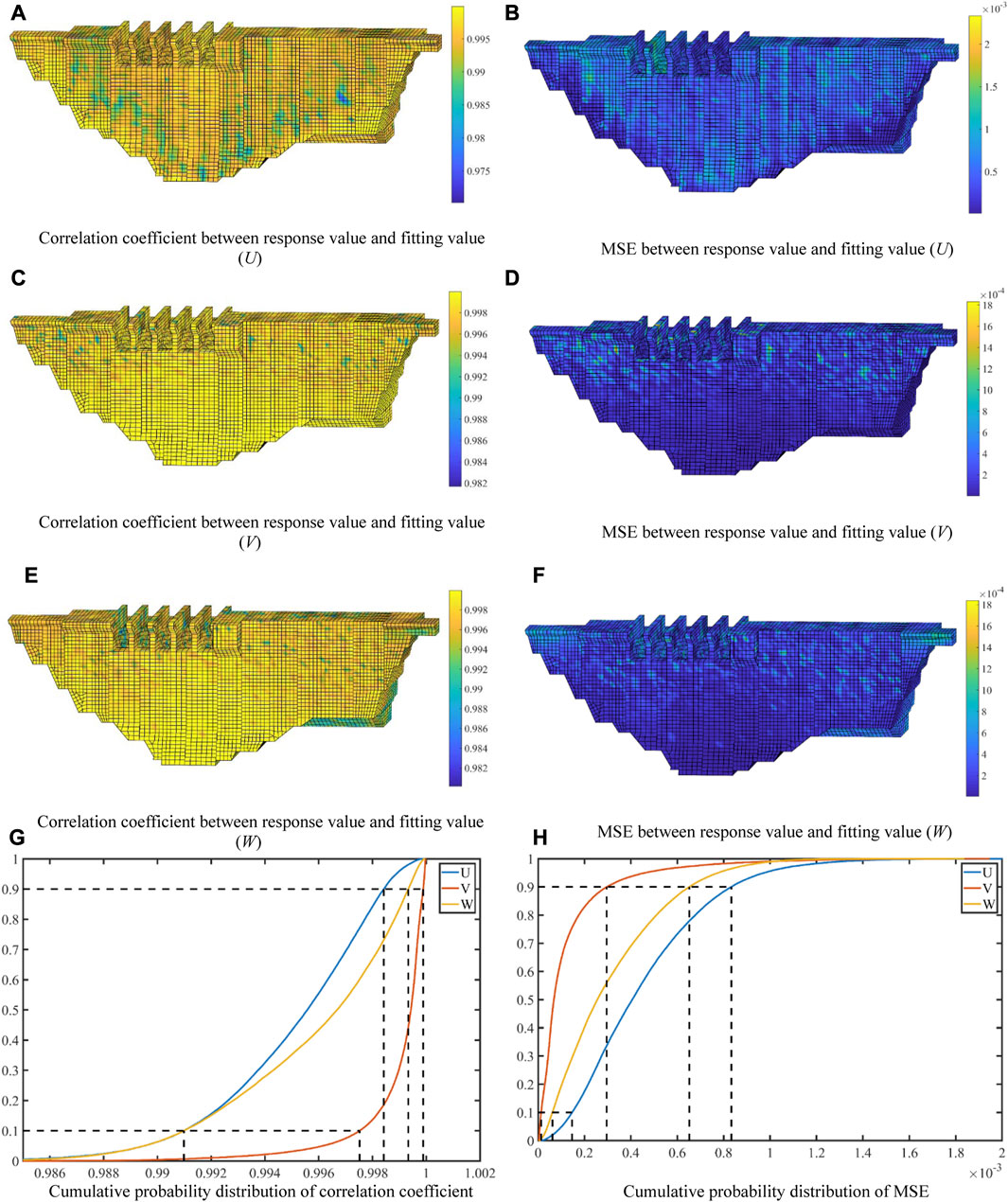
FIGURE 7. (A–F) correlation coefficient and MSE distribution of deformation behavior surrogate model within the dam body; (G,H) cumulative probability distribution of correlation coefficient and MSE of deformation behavior surrogate model.
According to Figure 7, the performance of deformation behavior surrogate model is analyzed. For U, a 90% probability of its correlation coefficient is greater than 0.9910, and a 10% probability reaches 0.9982. In different dam sections, although the correlation degree fluctuates to a certain extent, the correlation degree is relatively high. Only some nodes on the right part of the dam have a low correlation degree of about 0.9750. MSE has a 90% probability below 0.0008. As can be seen from the figure, the distribution rule of MSE is opposite to the correlation coefficient. That is, at a certain node, the larger the correlation coefficient, the smaller MSE. For V, its correlation coefficient is the highest among the three models of deformation behavior, with a 90% probability above 0.9967 and a 10% probability reaching 1. Similarly, its MSE has a 90% probability below 0.0003. It can be seen from the correlation coefficient distribution that its correlation degree is significantly higher than that of U and W. In cumulative probability distribution, U and W show a slow growth trend. While at 0.9980, V shows a sudden growth trend with a very large growth range, and the correlation coefficient increases from 0.9980 to close to 1. For W, its correlation coefficient is higher than that of U. The same with U is that there is a 90% probability makes the correlation coefficient greater than 0.9910, while there is a 10% probability of reaching 0.9986. It can be seen from the correlation coefficient distribution within the dam body that the correlation degree of W is significantly higher than that of U. Although the correlation degree also fluctuates to a certain extent, the overall correlation degree is relatively high.
As can be seen from the above analysis, through the verification of the correlation coefficient and MSE, it can be found that the local RBF based on sensitivity modification is suitable for deformation behavior surrogate model and has a good effect. And it can ensure that the surrogate model has more than 92% confidence to achieve 99% accuracy of the original model. In deformation behavior surrogate model, the effect of V is significantly better than that of U and W. There is a phenomenon that the correlation coefficient and MSE of U and W fluctuate to a certain extent, and this phenomenon has been obviously improved in V. In addition, it can be found from the figure that the distribution rule of correlation coefficient and MSE within dam body is basically completely opposite, except for different values, the distribution shape is basically the same.
4.1.2 Establishment and analysis of dam stress behavior surrogate model
Stress behavior includes six aspects:
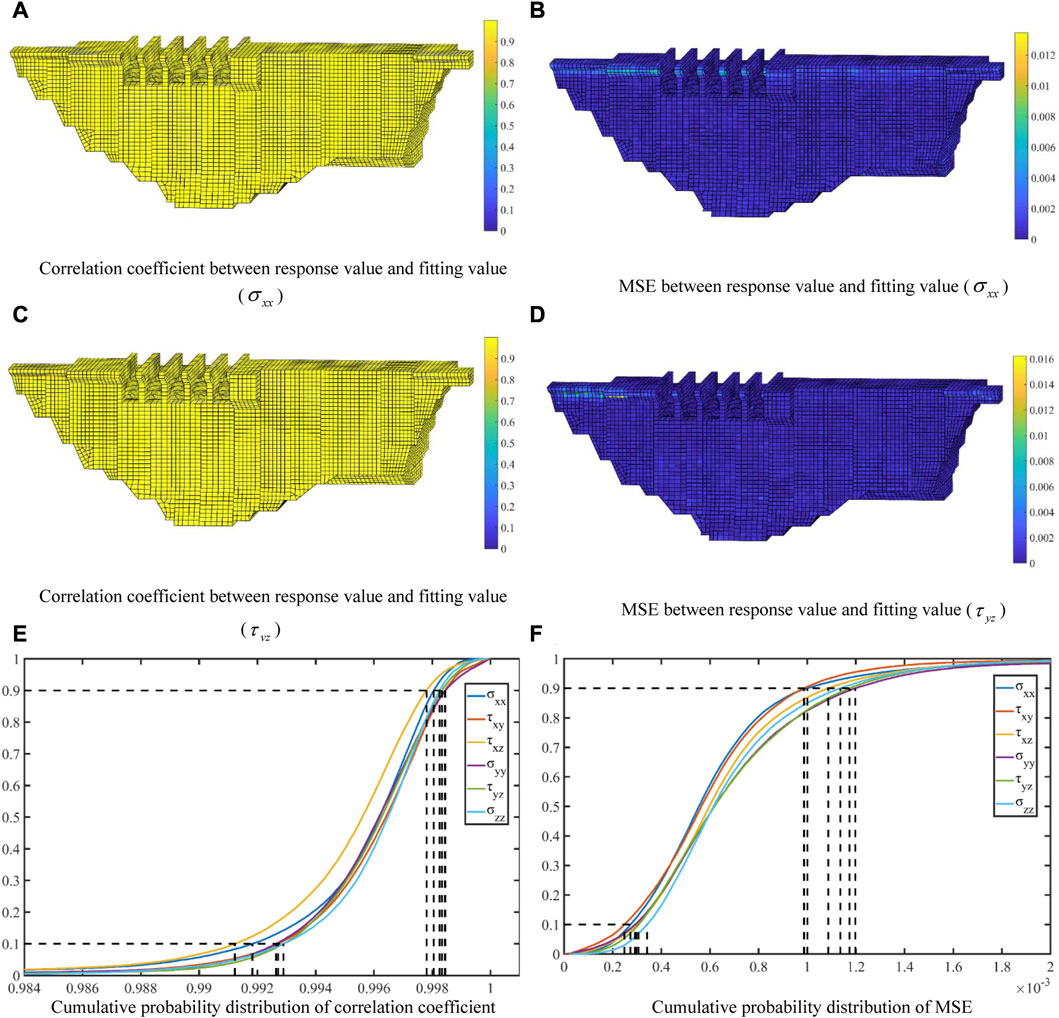
FIGURE 8. (A–D) correlation coefficient and MSE distribution of stress behavior surrogate model within the dam body; (E,F) cumulative probability distribution of correlation coefficient and MSE of stress behavior surrogate model.
According to Figure 8, the effects of
From the above analysis, it can be seen that the model effect of other elements is very good except that the model effect of the individual elements is poor. Therefore, local RBF based on sensitivity modification is also suitable for stress behavior. And the confidence of at least 90% enables the surrogate model to achieve 99% accuracy of the original model. In stress behavior surrogate model, although there are some differences among the model effects of each stress behavior, the differences are not significant on the whole. It can be seen that local RBF surrogate model has good stability in application.
4.1.3 Establishment and analysis of dam temperature behavior surrogate model
The distribution of the correlation coefficient and MSE of temperature behavior surrogate model within the dam body is shown in Figures 9A, B, and the cumulative probability distribution of the correlation coefficient and MSE of temperature behavior surrogate model are shown in Figures 9C, D. As can be seen from the figure, a 90% probability correlation coefficient is above 0.977, and a 10% probability basically reaches 1. In addition, the cumulative probability suddenly increases around 0.995, indicating that the model has a high correlation coefficient at most nodes. Similarly, MSE has a 90% probability of less than 0.0075, but there is also a shape drop phenomenon, which makes the MSE of most nodes small. It can be found from the distribution of the correlation coefficient within the dam body that most nodes are highly correlated. The correlation between the top and bottom of the dam decreases to some extent, but the decreasing degree of the top is smaller than that of the bottom. The distribution rule of MSE within the dam body is contrary to that of the correlation coefficient. By comparing the above deformation and stress behavior surrogate models, it can be found that the correlation degree of temperature behavior is lower, and MSE is higher than that of the two behavior surrogate models. The result shows that the effect of temperature behavior surrogate model is slightly weaker than that of deformation and stress behavior surrogate models.
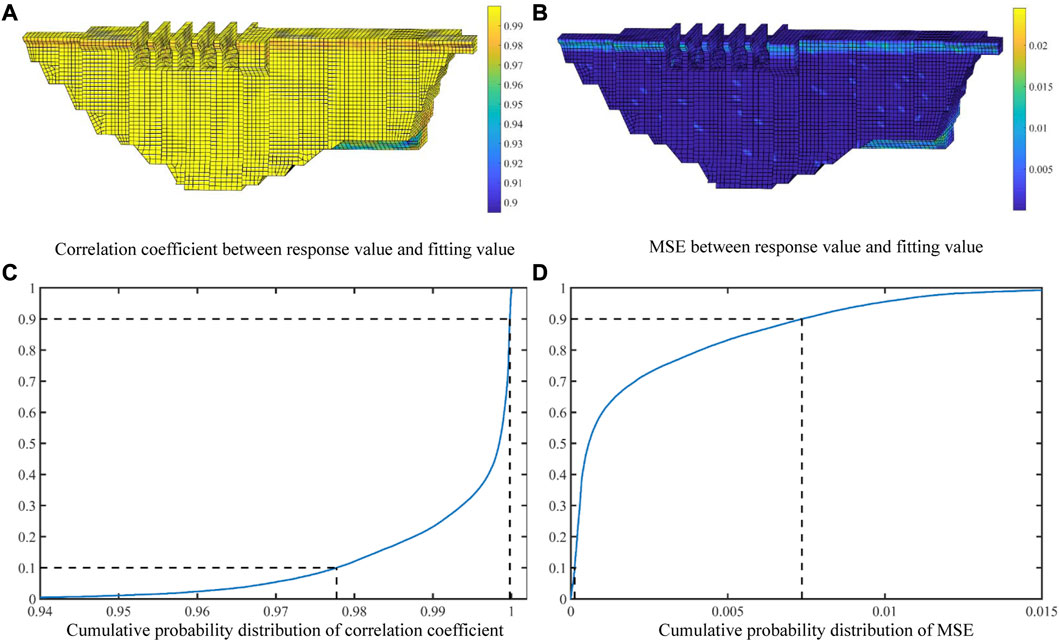
FIGURE 9. (A,B) correlation coefficient and MSE distribution of temperature behavior surrogate model within the dam body; (C,D) cumulative probability distribution of correlation coefficient and MSE of temperature behavior surrogate model.
From the above analysis, it can be seen that although temperature behavior surrogate model has a good effect, deformation and stress behavior surrogate models have a better effect. For temperature behavior surrogate model, the confidence of at least 75% enables the surrogate model to achieve 99% accuracy of the original model. And there is the confidence of 90% enables the surrogate model to achieve 97.7% accuracy of the original model. Although the surrogate model has a poor effect at some nodes, it basically achieves 90% accuracy, indicating that local RBF based on sensitivity modification is suitable for temperature behavior. Compared with deformation and stress behaviors, temperature behavior has only 4 parameters, while deformation and stress behaviors have 9 parameters. Therefore, whether local RBF has a certain correlation with the size of parameter space remains to be studied.
4.2 Dynamic behavior surrogate model of dam
This section takes an arch dam as an example to study the dynamic behavior surrogate model of a dam. Located in the downstream of Jinsha River in China, the hydropower station is the second stage of a cascade of power stations along downstream of the Jinsha River. The power station consists of barrage, flood discharge, and energy dissipation facilities, water diversion and power generation systems, and other main buildings. The barrage is an RCC double-curvature arch dam with a crest height of 834 m, a maximum dam height of 289 m, a normal water level of 825 m, a dead water level of 765 m, and a total storage capacity of 20.627 billion m3.
As with the construction of the static surrogate model, the parameter space should be determined first. The probability distribution and value range of parameters are shown in Table 2. The parameter space is also generated by the Sobol sequence, and then the response space is generated by analyzing the tensile damage of the arch dam under seismic load based on the parameter space. The numerical model is shown in Figure 10. Finally, the surrogate model based on parameter space and response space is established. Due to the particularity of the damage, some elements may not be damaged, or some elements may reach the damage limit, have been broken, and no further damage will occur. Therefore, in order to better establish the surrogate model, before using the local RBF based on sensitivity modification to establish the surrogate model, the damage degree should be first classified, and the three cases of complete damage, damage occurrence, and no damage should be distinguished. In this paper, SVM (Chen et al., 2018) is used to classify the damage, and then local RBF is used to train the damaged elements.

TABLE 2. The probability distribution and value range of the parameters of dynamic behavior surrogate model.
According to the local RBF proposed in this paper, the sensitivity coefficient of parameter space to tension damage within the dam body is firstly analyzed. The distribution of the sensitivity coefficient of gravity acceleration to tensile damage within the arch dam is shown in Figure 11. It can be seen from the figure that the distribution of gravity acceleration to tensile damage within the dam body is very uneven. The sensitivity coefficient of the connection between dam body and foundation is significant, and the sensitivity coefficient of other parts is low. In the main part of the arch dam, the sensitivity degree of gravity acceleration to damage is not high, which is basically concentrated between 0 and 0.1.
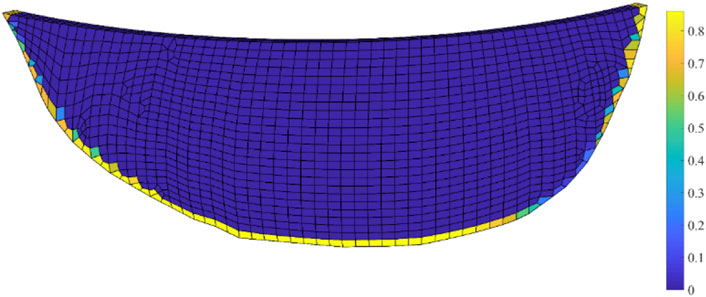
FIGURE 11. Distribution of sensitivity coefficient of Gravitational acceleration to tensile damage within dam body.
In the connection between the dam body and the foundation, the sensitivity coefficient of the dam bottom is slightly higher than that of the two sides of the dam body, about 0.8–0.9. Although the sensitivity coefficient on both sides of the dam has decreased, the overall value is still above 0.7. Because the damage to the dam body is mainly concentrated in the connection between the dam body and the foundation, although there is damage in the main body of the dam, the degree of damage is not significant, which conforms to the rule of sensitivity distribution. Therefore, in general, the sensitivity degree of gravity acceleration to tensile damage of arch dam is greatly affected by the damage degree.
The kernel function is modified based on the sensitivity coefficient calculated above, and the tensile damage surrogate model is established based on local RBF.
The distribution of correlation coefficient and MSE of tensile damage surrogate model within the dam body is shown in Figures 12A, B, and the cumulative probability distribution of the correlation coefficient and MSE of tensile damage surrogate model are shown in Figures 12C, D. Due to the particularity of the damage, the damage degree of the main part of the dam body is small or no damage, so the correlation and MSE are greatly affected by the classification results. As can be seen from the figure, in the main part of the dam body, the correlation coefficient is basically kept above 0.98 and MSE is below 0.005. While the correlation coefficient between dam body and foundation is obviously lower than that of the dam body. Among them, the correlation coefficient of the right side of the dam is between 0.965 and 0.985, which is slightly higher than that of the left side of the dam. The correlation coefficient of the bottom of the dam is the lowest, which is 0.91. As mentioned above, the distribution of MSE is opposite to that of the correlation coefficient, so it will not be analyzed in detail here. In terms of the correlation coefficient, more than 90% probability of the surrogate model is better than 0.988, and about 30% probability is exactly equal to the original value. In terms of MSE, more than 90% probability of the surrogate model is less than 0.0022. Similar to the correlation coefficient, it has a high probability exactly equal to the original value.
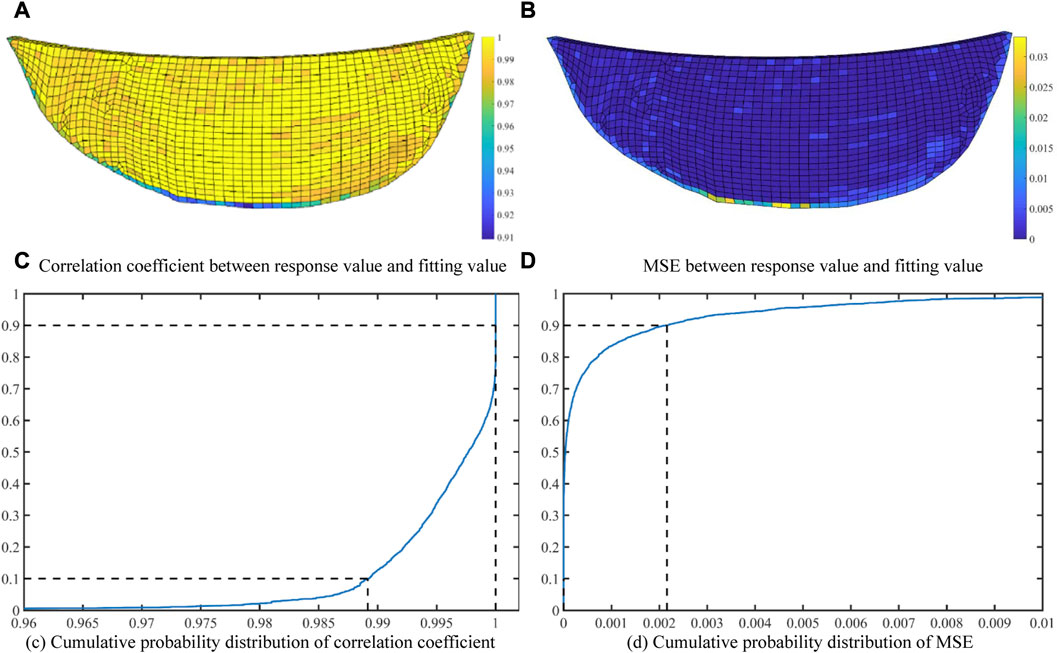
FIGURE 12. (A,B) correlation coefficient and MSE distribution of tensile damage surrogate model within the dam body; (C,D) cumulative probability distribution of correlation coefficient and MSE of tensile damage surrogate model.
From the above analysis, it can be seen that the effect of the surrogate model is significantly affected by the classification results at elements with no or complete damage. In this case, the correlation coefficient is strictly equal to 1 and the MSE is strictly 0. While among other elements, model effects are influenced by classification and local RBF. Although the model effect of the dam bottom is not ideal, the model accuracy of most elements is 98%. Therefore, the feasibility of local RBF in dynamic behavior surrogate model can be proved.
5 Discussion
The static and dynamic behavior surrogate models of dams are developed using local RBF, and the effect of the surrogate models are tested using the correlation coefficient and MSE. The results suggest that the method proposed in this study is appropriate for establishing a dam structural behavior surrogate model, and the surrogate model’s accuracy meets the criteria of various applications. This section compares the proposed method to RBF and BP neural networks to demonstrate the method’s viability and advantages.
5.1 Comparison and research of dam static behavior surrogate model
The correlation coefficient and MSE are used in this section, as in the section above, to confirm the influence of the surrogate model. The cumulative probability distribution of three different surrogate model types is displayed to help explain and analyze the findings.
5.1.1 Comparison and research of deformation behavior surrogate model
The cumulative probability distribution comparison of correlation coefficient and MSE on the validation set of the deformation behavior surrogate model established by local RBF, RBF, and BP neural network is shown in Supplementary Figure S1. As can be seen from the figure, the model effect of local RBF is always better than the other two methods, regardless of the deformation direction. For U, the correlation coefficient of local RBF on the validation set is significantly higher than that of BP neural network and RBF, and the correlation coefficient is lower than 0.985 only at a finite number of nodes. While for neural network and RBF, 25% and 40% of nodes have correlation coefficients lower than 0.985. Similarly, the MSE of local RBF is significantly lower than that of neural network and RBF, which is less than 0.0015. For V and W, the correlation degree of local RBF is still the highest, but the correlation degree of neural network and RBF is relatively close. In this case, for MSE, RBF is significantly lower than the neural network. This is because the correlation coefficient measures the linear trend between two groups of data, while MSE measures the difference between two groups of data. In some cases, the correlation degree may be high while the MSE is also significant. Therefore, it is reasonable that the correlation coefficients of the neural network and RBF are similar, but the MSE of RBF is more significant than that of the neural network.
On the whole, the effect of the surrogate model established by local RBF is significantly better than that of BP neural network and RBF, and the effect of BP neural network is better than that of RBF. The above analysis shows that the local shape parameters improve the accuracy of the model to a certain extent than the single global shape parameters. Similarly, by modifying the kernel function based on sensitivity coefficients, the weights of input parameters can be updated adaptively, and the accuracy of the surrogate model can be improved to a certain extent. Compared with RBF, the effect of local RBF based on sensitivity modification is significantly enhanced. Therefore, local RBF based on sensitivity modification proposed in this research is practicable and has high accuracy in the establishment of deformation behavior surrogate model.
5.1.2 Comparison and research of stress behavior surrogate model
Similar to deformation behavior, Supplementary Figure S2 depicts the cumulative probability distribution comparison of correlation coefficient and MSE on the validation set of stress behavior surrogate model established by local RBF, RBF, and BP neural network. As observed in the figure, local RBF performs noticeably better than neural network and RBF for stress behavior surrogate models
Overall, the dam stress behavior surrogate model established by local RBF has the best effect, followed by BP neural network, and RBF has the worst effect. Although the probability that a neural network or RBF is superior to local RBF is very small, the accuracy of the surrogate model at this time is very high, and the surrogate model established by these three methods can meet the application requirements. Similar to deformation behavior, by replacing the global shape parameters with local shape parameters and modifying the kernel function according to sensitivity coefficients, the model effect of local RBF is improved to a certain extent, which is better than RBF. Therefore, it can be considered that local RBF based on sensitivity modification proposed in this paper is very suitable for the establishment of a stress behavior surrogate model.
5.1.3 Comparison and research of temperature behavior surrogate model
Supplementary Figure S3 depicts the cumulative probability distribution comparison of correlation coefficient and MSE on the validation set of temperature behavior surrogate model established by local RBF, RBF, and BP neural network. As observed in the figure, the effect of local RBF is better than the other two models, both in terms of correlation coefficient and MSE. In the cumulative probability distribution comparison of the correlation coefficient, local RBF starts to grow from 0.94, while the correlation coefficient between the neural network and RBF is less than 0.94 at some nodes. Although the cumulative probability of local RBF and RBF is similar in the range of 0.99–0.993, the correlation coefficient of RBF is significantly lower than that of local RBF with the increase of cumulative probability. Although neural network and RBF have their advantages and disadvantages in different areas, the effects of these two models are generally similar. In the cumulative probability distribution comparison of MSE, local RBF is obviously better than neural network and RBF.
While BP neural network and RBF surrogate models have their advantages and disadvantages, the local RBF surrogate model generally has the best effect on dam temperature behavior surrogate models. Similar to deformation and stress behavior, local RBF replaces global shape parameters with local shape parameters and modifies the kernel function with sensitivity coefficients, making the model effect better than RBF. Therefore, the proposed local RBF based on sensitivity modification can replace BP neural network and RBF to establish the temperature behavior surrogate model.
5.2 Comparison and research of dam dynamic behavior surrogate model
Similar to the above, the cumulative probability distribution comparison of the correlation coefficient and MSE of dynamic behavior surrogate model established by local RBF, RBF, and BP neural network is shown in Supply Figure 4. As can be seen from the figure, different from static behavior surrogate model, dynamic surrogate model is also affected by SVM classification results. Therefore, the effects of undamaged and completely damaged elements are not considered. So, the correlation coefficient and MSE of local RBF are significantly better than those of neural network and RBF in damaged elements. In the cumulative probability distribution comparison of the correlation coefficient, local RBF shows an increasing trend at 0.987, while in neural network and RBF, about 30% of elements have correlation coefficients less than 0.987. The neural network and RBF effect are similar to that of the temperature behavior surrogate model. Although there are some advantages and disadvantages in different areas, the overall effect is relatively identical. By substituting local shape parameters for global shape parameters and altering the kernel function based on sensitivity coefficients, RBF is enhanced similarly to static behavior. As a result, it can be said that local RBF based on sensitivity modification has better applicability than BP neural network and RBF.
In conclusion, the proposed local RBF based on sensitivity modification is significantly better than BP neural network and RBF for both the static and dynamic behavior of the dam. For deformation and stress behavior, BP neural network surrogate model is better than RBF surrogate model. While BP neural network and RBF surrogate model have their own advantages and disadvantages in temperature and dynamic behavior.
6 Conclusion
On the basis of dam online monitoring technology, this study explains the notion of the surrogate model and explores the limitations of RBF in light of the surrogate model technology’s current state of development. Then, in an effort to address the drawbacks of RBF, a novel local RBF based on sensitivity modification is developed using local shape parameters and sensitivity analysis, and the method’s feasibility is confirmed using a benchmark function. Finally, the dam structural behavior surrogate model is developed in order to assess the model’s influence. In addition, the differences between these three methods are determined by comparing them to BP neural networks and RBF surrogate models. The subsequent conclusions are reached.
(1) The proposed local RBF surrogate model based on sensitivity modification is entirely feasible. In establishing the dam structural behavior surrogate model, the accuracy of this model is better than BP neural network and RBF surrogate model, which has good applicability.
(2) In this research, the correlation coefficient and MSE are utilized to validate the model’s effectiveness. MSE is used to represent the inaccuracy between the response value and the fitting value, whereas the correlation coefficient is used to characterize the trend relationship between the response value and the fitting value. The example analysis demonstrates that these two indices can indicate the established surrogate model’s effect from different levels.
(3) The deformation surrogate model based on the suggested method has the best effect on the static behavior surrogate model of the dam, followed by the stress surrogate model, and the temperature surrogate model has the worst effect. Despite having the weakest performance, the temperature behavior surrogate model still has a good correlation coefficient and a low MSE. Additionally, this model’s results are still superior than those of RBF and BP neural networks. As for dynamic behavior surrogate model of the dam, this research primarily examines the tensile damage surrogate model. Due to the unique nature of the damage, this paper uses SVM to classify the damage and then train the model. The outcome shows that while the surrogate model’s effect is not optimal for all elements, it generally has a high correlation coefficient and a low MSE.
(4) In constructing static and dynamic behavior surrogate models of the dam, local RBF based on sensitivity modification has greater universality than BP neural network and RBF surrogate model. In terms of deformation and stress behavior, the BP neural network surrogate model is superior to the RBF model. In terms of temperature and dynamic behavior, these two surrogate models each have their own benefits and drawbacks.
(5) The local RBF based on sensitivity modification proposed in this paper is limited by the characteristics of RBF and is only suitable for the training of a single target model. Therefore, the computational cost will significantly increase once the response variable type increases. So how to train a muti-objective model using RBF to ensure accuracy and efficiency will be the focus of future research.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
JL: methodology, conceptualization, writing—original draft, and validation. ZL: review, editing, and validation. EK: editing.
Funding
This work was supported by the Major Scientific and Technological Project of Shandong Gangshiyuan Construction Engineering Group Co., Ltd. [Grant No. 2020RS-1058], the Natural Science Foundation of Jiangsu Province [Grant No. BK20171288] and the National Natural Science Foundation of China [Grant No. 51779215].
Conflict of interest
LZ was employed by the Intelligent Water Conservancy Research Institute, Nanjing Jurise Engineering Technology Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1125691/full#supplementary-material
References
Acar, E. (2014). Simultaneous optimization of shape parameters and weight factors in ensemble of radial basis functions. Struct. Multidiscip. Optim. 49, 969–978. doi:10.1007/s00158-013-1028-0
Basheer, I. A., and Hajmeer, M. (2000). Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 43, 3–31. doi:10.1016/S0167-7012(00)00201-3
Baú, D. A., and Mayer, A. S. (2006). Stochastic management of pump-and-treat strategies using surrogate functions. Adv. Water Resour. 29, 1901–1917. doi:10.1016/j.advwatres.2006.01.008
Bayona, V., Moscoso, M., and Kindelan, M. (2011). Optimal constant shape parameter for multiquadric based RBF-FD method. J. Comput. Phys. 230, 7384–7399. doi:10.1016/j.jcp.2011.06.005
Beven, K., and Freer, J. (2001). Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 249, 11–29. doi:10.1016/S0022-1694(01)00421-8
Bucher, C., and Bourgund, U. (1990). A fast and efficient response surface approach for structural reliability problems. Struct. Saf. 7, 57–66. doi:10.1016/0167-4730(90)90012-E
Bui-Thanh, T., Willcox, K., and Ghattas, O. (2008). Model reduction for large-scale systems with high-dimensional parametric input space. SIAM J. Sci. Comput. 30, 3270–3288. doi:10.1137/070694855
Castelletti, A., Pianosi, F., Soncini-Sessa, R., and Antenucci, J. P. (2010). A multiobjective response surface approach for improved water quality planning in lakes and reservoirs. Water Resour. Res. 46. doi:10.1029/2009WR008389
Chen, W., Pourghasemi, H. R., and Naghibi, S. A. (2018). A comparative study of landslide susceptibility maps produced using support vector machine with different kernel functions and entropy data mining models in China. Bull. Eng. Geol. Environ. 77, 647–664. doi:10.1007/s10064-017-1010-y
Cunbo, Z., Jianhua, L., Hui, X., and Xiaoyu, D. (2017). Connotation, architecture and trends of product digital twin. Comput. Integr. Manuf. Syst. 23, 753–768.
Das, R., and Soulaimani, A. (2021). Non-deterministic methods and surrogates in the design of rockfill dams. Appl. Sci. 11, 3699. doi:10.3390/app11083699
Davydov, O., and Oanh, D. T. (2011). Adaptive meshless centres and RBF stencils for Poisson equation. J. Comput. Phys. 230, 287–304. doi:10.1016/j.jcp.2010.09.005
Dou, S.-q., Li, J.-j., and Kang, F. (2019). Health diagnosis of concrete dams using hybrid FWA with RBF-based surrogate model. Water Sci. Eng. 12, 188–195. doi:10.1016/j.wse.2019.09.002
Duan, Q. Y., Sorooshian, S., and Gupta, V. (1992). Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 28, 1015–1031. doi:10.1029/91WR02985
Fasshauer, G. E., and Zhang, J. G. (2007). On choosing “optimal” shape parameters for RBF approximation. Numer. Algorithms 45, 345–368. doi:10.1007/s11075-007-9072-8
Fei, T., Meng, Z., Jiangfeng, C., and Qinglin, Q. (2017). Digital twin workshop: A new paradigm for future workshop. Comput. Integr. Manuf. Syst. 23, 1–9.
FeiYue, W. (2004). Parallel system methods for management and control of complex systems. Control Decis. 19, 485–489. doi:10.13195/j.cd.2004.05.6.wangfy.002
Forrester, A. I. J., and Keane, A. J. (2009). Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 45, 50–79. doi:10.1016/j.paerosci.2008.11.001
Furukawa, T., and Yagawa, G. (1998). Implicit constitutive modelling for viscoplasticity using neural networks. Int. J. Numer. Methods Eng. 43, 195–219. doi:10.1002/(SICI)1097-0207(19980930)43:2<195:AID-NME418>3.0.CO;2-6
Gao, K., Mei, G., Cuomo, S., Piccialli, F., and Xu, N. (2020). Arbf: Adaptive radial basis function interpolation algorithm for irregularly scattered point sets. Soft Comput. 24, 17693–17704. doi:10.1007/s00500-020-05211-0
Goel, T., Haftka, R. T., Shyy, W., and Queipo, N. V. (2007). Ensemble of surrogates. Struct. Multidiscip. Optim. 33, 199–216. doi:10.1007/s00158-006-0051-9
Han, Z., Li, Y., Zhao, Z., and Zhang, B. (2022). An Online safety monitoring system of hydropower station based on expert system. Energy Rep. 8, 1552–1567. doi:10.1016/j.egyr.2022.02.040
Hardy, R. L. (1971). Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 76, 1905–1915. doi:10.1029/JB076i008p01905
Hornberger, G. M., and Spear, R. C. (1981). An approach to the preliminary-analysis of environmental systems. J. Environ. Manage. 12, 7–18.
Jiang, G., and Wang, W. (2017). Error estimation based on variance analysis of k-fold cross-validation. Pattern Recognit. 69, 94–106. doi:10.1016/j.patcog.2017.03.025
Jin, R., Chen, W., and Simpson, T. W. (2001). Comparative studies of metamodelling techniques under multiple modelling criteria. Struct. Multidiscip. Optim. 23, 1–13. doi:10.1007/s00158-001-0160-4
Jin, S.-S., and Jung, H.-J. (2016). Self-adaptive sampling for sequential surrogate modeling of time-consuming finite element analysis. Smart Struct. Syst. 17, 611–629. doi:10.12989/sss.2016.17.4.611
Jing, Z., Chen, J., and Li, X. (2019). RBF-GA: An adaptive radial basis function metamodeling with genetic algorithm for structural reliability analysis. Reliab. Eng. Syst. Saf. 189, 42–57. doi:10.1016/j.ress.2019.03.005
Jinping, H. (2010). Theory and application of dam safety monitoring. Beijing, China: China Water Power Press.
Jones, D. R., Schonlau, M., and Welch, W. J. (1998). Efficient global optimization of expensive black-box functions. J. Glob. Optim. 13, 455–492. doi:10.1023/A:1008306431147
Karimi, I., Khaji, N., Ahmadi, M. T., and Mirzayee, M. (2010). System identification of concrete gravity dams using artificial neural networks based on a hybrid finite element–boundary element approach. Eng. Struct. 32, 3583–3591. doi:10.1016/j.engstruct.2010.08.002
Li, P., Qian, H., Wu, J., and Chen, J. (2013). Sensitivity analysis of TOPSIS method in water quality assessment: I. Sensitivity to the parameter weights. Environ. Monit. Assess. 185, 2453–2461. doi:10.1007/s10661-012-2723-9
Li, X., Gong, C., Gu, L., Gao, W., Jing, Z., and Su, H. (2018). A sequential surrogate method for reliability analysis based on radial basis function. Struct. Saf. 73, 42–53. doi:10.1016/j.strusafe.2018.02.005
Li, X., Li, X., and Su, Y. (2016). A hybrid approach combining uniform design and support vector machine to probabilistic tunnel stability assessment. Struct. Saf. 61, 22–42. doi:10.1016/j.strusafe.2016.03.001
Li, Y., Hariri-Ardebili, M. A., Deng, T., Wei, Q., and Cao, M. (2023). A surrogate-assisted stochastic optimization inversion algorithm: Parameter identification of dams. Adv. Eng. Inf. 55, 101853. doi:10.1016/j.aei.2022.101853
Lin, C., Li, T., Chen, S., Yuan, L., van Gelder, P. H. A. J. M., and Yorke-Smith, N. (2022). Long-term viscoelastic deformation monitoring of a concrete dam: A multi-output surrogate model approach for parameter identification. Eng. Struct. 266, 114553. doi:10.1016/j.engstruct.2022.114553
Magnus, J. R., and Vasnev, A. L. (2015). Interpretation and use of sensitivity in econometrics, illustrated with forecast combinations. Int. J. Forecast. 31, 769–781. doi:10.1016/j.ijforecast.2013.08.001
Mugunthan, P., and Shoemaker, C. A. (2006). Assessing the impacts of parameter uncertainty for computationally expensive groundwater models. Water Resour. Res. 42. doi:10.1029/2005WR004640
Mugunthan, P., Shoemaker, C. A., and Regis, R. G. (2005). Comparison of function approximation, heuristic, and derivative-based methods for automatic calibration of computationally expensive groundwater bioremediation models. Water Resour. Res. 41. doi:10.1029/2005WR004134
Papadrakakis, M., Papadopoulos, V., and Lagaros, N. D. (1996). Structural reliability analyis of elastic-plastic structures using neural networks and Monte Carlo simulation. Comput. Methods Appl. Mech. Eng. 136, 145–163. doi:10.1016/0045-7825(96)01011-0
Rad, M. J. G., Ohadi, S., Jafari-Asl, J., Vatani, A., Ahmadabadi, S. A., and Correia, J. A. F. O. (2022). GNDO-SVR: An efficient surrogate modeling approach for reliability-based design optimization of concrete dams. Structures 35, 722–733. doi:10.1016/j.istruc.2021.11.048
Rippa, S. (1999). An algorithm for selecting a good value for the parameter c in radial basis function interpolation. Adv. Comput. Math. 11, 193–210. doi:10.1023/A:1018975909870
Rocco, C. M., and Moreno, J. A. (2002). Fast Monte Carlo reliability evaluation using support vector machine. Reliab. Eng. Syst. Saf. 76, 237–243. doi:10.1016/S0951-8320(02)00015-7
Salazar, F., Morán, R., Toledo, M. Á., and Oñate, E. (2015). Data-based models for the prediction of dam behaviour: A review and some methodological considerations. Archives Comput. Methods Eng. 24, 1–21. doi:10.1007/s11831-015-9157-9
Saltelli, A. (2002). Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 145, 280–297. doi:10.1016/S0010-4655(02)00280-1
Saltelli, A., and Sobol, I. M. (1995). About the use of rank transformation in sensitivity analysis of model output. Reliab. Eng. Syst. Saf. 50, 225–239. doi:10.1016/0951-8320(95)00099-2
Savic, D. A., and Walters, G. A. (1997). Genetic algorithms for least-cost design of water distribution networks. J. Water Resour. Plann. Manage 123, 67–77. doi:10.1061/(asce)0733-9496(1997)123:2(67)
Schultz, M., Small, M., Farrow, R., and Fischbeck, P. (2004). State water pollution control policy insights from a reduced-form model. J. Water Resour. Plan. Manag. 130, 150–159. doi:10.1061/(asce)0733-9496(2004)130:2(150)
Schultz, M. T., Small, M. J., Fischbeck, P. S., and Farrow, R. S. (2006). Evaluating response surface designs for uncertainty analysis and prescriptive applications of a large-scale water quality model. Environ. Model. Assess. 11, 345–359. doi:10.1007/s10666-006-9043-9
Sevieri, G., Andreini, M., De Falco, A., and Matthies, H. G. (2019). Concrete gravity dams model parameters updating using static measurements. Eng. Struct. 196, 109231–231. doi:10.1016/j.engstruct.2019.05.072
Shahzadi, G., and Soulaïmani, A. (2021). Deep neural network and polynomial chaos expansion-based surrogate models for sensitivity and uncertainty propagation: An application to a rockfill dam. Water 13, 1830. doi:10.3390/w13131830
Skaggs, T. H., and Barry, D. A. (1997). The first-order reliability method of predicting cumulative mass flux in heterogeneous porous formations. Water Resour. Res. 33, 1485–1494. doi:10.1029/97WR00660
Tarantola, S., Gatelli, D., and Mara, T. A. (2006). Random balance designs for the estimation of first order global sensitivity indices. Reliab. Eng. Syst. Saf. 91, 717–727. doi:10.1016/j.ress.2005.06.003
Theocaris, P. S., and Panagiotopoulos, P. D. (1995). Generalised hardening plasticity approximated via anisotropic elasticity: A neural network approach. Comput. Methods Appl. Mech. Eng. 125, 123–139. doi:10.1016/0045-7825(94)00769-J
Uhlemann, T. H. J., Lehmann, C., and Steinhilper, R. (2017). The digital twin: Realizing the cyber-physical production system for industry 4.0. Procedia CIRP 61, 335–340. doi:10.1016/j.procir.2016.11.152
Xi, L., Xiao, W., Weishan, Z., and Jianji, W. (2017). Parallel data: From big data to data intelligence. Pattern Recognit. Artif. Intell. 30, 673–381.
Xuefeng, M., Weixing, Y., Xiongqing, Y., Kelong, L., and Fei, X. (2005). A survey of surrogate models used in MDO. Chin. J. Comput. Mech. 5, 608–612.
Zhang, K., Gu, C., Zhu, Y., Li, Y., and Shu, X. (2023). A mathematical-mechanical hybrid driven approach for determining the deformation monitoring indexes of concrete dam. Eng. Struct. 277, 115353. doi:10.1016/j.engstruct.2022.115353
Zhang, X., Srinivasan, R., and Van Liew, M. (2009). Approximating SWAT model using artificial neural network and support vector machine. JAWRA J. Am. Water Resour. Assoc. 45, 460–474. doi:10.1111/j.1752-1688.2009.00302.x
Zhao, D., and Xue, D. (2010). A comparative study of metamodeling methods considering sample quality merits. Struct. Multidiscip. Optim. 42, 923–938. doi:10.1007/s00158-010-0529-3
Keywords: dam online monitoring, surrogate model, radial basis function, sensitivity analysis, BP neural network
Citation: Liang J, Li Z and Khailah EY (2023) Research on the modified surrogate model based on local RBF for concrete dam static and dynamic response analysis. Front. Earth Sci. 11:1125691. doi: 10.3389/feart.2023.1125691
Received: 16 December 2022; Accepted: 31 March 2023;
Published: 11 April 2023.
Edited by:
Lei Wang, Institute of Tibetan Plateau Research (CAS), ChinaReviewed by:
Fei Kang, Dalian University of Technology, ChinaSalim Heddam, University of Skikda, Algeria
Copyright © 2023 Liang, Li and Khailah. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhanchao Li, MDA2NTIwQHl6dS5lZHUuY24=
 Jiaming Liang1
Jiaming Liang1 Zhanchao Li
Zhanchao Li