Study on stability and bearing characteristics of macroscopic pressure arch of surrounding rock in western deep buried stope of China

In view of the obvious loose and weak occurrence characteristics of the deeply buried thick weakly cemented stratum in the western mining area of China, the bearing characteristics and stability mechanism of the macrography surrounding rock pressure arch (SRPA) are studied. Firstly, considering the engineering characteristics of deep mining, a SRPA model with trapezoidal load was constructed based on the three-hinged arch theory, the shape characteristic, rise-span ratio and arch thickness equations were derived, the arch thickness under different stress paths is analyzed to characterize the bearing performance of pressure arch. Secondly, the internal force distribution law and destabilization damage type were studied by establishing a two-dimensional bearing SRPA model through arch without articulation theory. The instability type and location can be accurately judged and verified by simulation of similar materials. The results show that, the rational arch axis of SRPA is a cubic parabola with opening downward, its rise-span ratio is between 0.3 and 0.5. Increasing the rise-span ratio and lateral pressure coefficient can promote the stable bearing capacity of arch. Axial force distribution on the SRPA section is basically consistent with the arch axis, and the arch has the best bearing characteristics. The positive bending moment occurs in the ranges of [0°, 30°] and [81°, 90°] on both sides of the symmetry axis, where is prone to tensile failure. The maximum shear force is concentrated on the arch waist and skewback, and these sections are prone to shear failure. The instability modes of SRPA can be divided into “skewback—vault (arch waist)” and “vault (arch waist)—skewback”. The research results have theoretical guiding significance for mining roof management.

1 Introduction

A series of mining damage and environmental problems caused by coal mining are related to strata movements; therefore, revealing the bearing characteristics of mining overburden is the key to understand the movement law of overburden in stope (Ning et al., 2017; Genis et al., 2018; Li et al., 2020; Zhang et al., 2021). The mining area in western China is a typical Cretaceous and Jurassic coal-rich area, and the stratum in this area has the particularity of diagenetic environment, diagenetic age, and sedimentary process. Rocks often exhibit low strength, weak cementation, large porosity, easy weathering, sensitivity to disturbance, etc., thus, many scholars collectively refer to this layer type as weakly cemented stratum (Zhao and Liu 2021). The stratum has poor self-stabilization ability due to mining disturbances, and accidents such as partial roof caving, coal wall spalling, and step sinking often occur in the mining process. At present, the shallow resources with buried depth of 100–300 m in typical western mining areas are gradually being exhausted, and coal mining gradually enters depths of 400–700 m. With the continuous increase in mining depth and intensity, large areas of coal wall spalling, large shrinkage of the hydraulic support column, and even support crushing appear frequently during the mining process (Mark, 2019; Bednarek and Majcherczyk 2020; Zhang et al., 2020). It was found out that the mining area with rich groundwater, such as in Shaanxi, Mongolia, etc., can show a deep mechanical state when the mining depth is 400–500 m (Xie et al., 2015; Zhang et al., 2019). Existing analyses of the bearing characteristics and stability of the overlying strata spatial structure in the mining field focus mainly on the cracked overlying strata in the beam or plate structure. The previous research results have proven that weakly cemented rocks have obvious loose and weak characteristics (Sun et al., 2019), and their bearing performance under the influence of disturbance is characterized by the pressure arch structure.

Surrounding rock pressure arches (SRPAs) exist widely in underground cavern engineering, such as mining fields and tunnels (Dancygier et al., 2016; Wang et al., 2019a; Oge 2020). As a classical problem of geomechanics, SRPAs have always been a research hotspot, including the stress distribution in pressure arch (Pardo and Saez 2014; Shabanimashcool and Li 2015), and application of the pressure arch in geotechnical engineering (Chen and Martin 2002; Yang et al., 2021). Since Platt’s collapse arch theory and the “pressure arch hypothesis” of mining overlying strata were proposed, the arch shape of the fracture boundary line of the mining rock and the arch effect of stress self-adjustment have been widely considered (Das 2000; Poulsen 2010; Kong et al., 2018). The earliest theory using the arching effect of surrounding rock to explain the ground pressure during longwall mining is the stress arch hypothesis (Kratzsch 1983). In this hypothesis, the stress arch is regarded as the bearing structure during overlying strata movement. Based on the research of the macroscopic SRPA, the theory of internal and external stress fields of the overlying strata spatial structure in the mining field, the near-field “cracked arch” and the far-field “stress arch” structure model were proposed. The “double arch” model of the mining field overlying strata is the mechanical expression of the self-bearing characteristics of the rock body and the arch effect of compressive stress (Wen et al., 2015). Zou (1989) analyzed a series of mechanical phenomena caused by mining activities from the point of view of the stress field and deduced that there was a “large structure” in the form of a macroscopic pressure arch in the overlying strata in the longwall working face. Du et al., 2011 discussed the stress transfer in surrounding rock during the advancing process of the working face combining numerical simulation and similar physical model methods, indicating that high stress concentration areas are formed in the far-field high level rock layer and surrounding rocks on both sides, which is called mining SRPA. There is no unified standard for the morphological characteristics of SRPA in rock movement. On the one hand, a theoretical model of the stress arch is established based on the three-hinged arch model in structural mechanics, the stress on the vertical boundary being a uniform load, and the stress on the horizontal boundary being a uniform load or trapezoidal load (Xia et al., 2018; Wang et al., 2019b; Kong et al., 2021). On the other hand, the derivation of morphological characteristic equations and instability discrimination were carried out based on Platt’s pressure arch theory and the Terzaghi soil arch effect assuming the arch to be a semicircular, semielliptical and parabolic model (Pardo et al., 2014; Zhao et al., 2021); however, which is the most reasonable arch axis has not been considered according to engineering practice. Regarding the bearing characteristics and stability analysis of SRPA, previous studies were conducted mainly from the distribution characteristics and deflection direction of the principal stress in surrounding rock through numerous numerical simulations (Yavuz 2004; El Kamash et al., 2021). There is no index to characterize the load-bearing performance of the SRPA and the factors affecting the characteristics of the arch effect area. Meanwhile, the instability area of the SRPA is not accurately judged according to the stability criterion.

In this paper, the bearing characteristics and stabilization mechanism of the macroscopic SRPA are investigated with respect to the occurrence characteristics of the deeply buried giant-thickness and weakly cemented stratum in the western mining area. First, based on the three-hinged arch theory a mechanical model of the macroscopic pressure arch was established. The boundary conditions were trapezoidal loads in both the vertical and horizontal directions, consistent with actual engineering practice. Then, the axis equation and rise-span relationship of SRPA were deduced. Second, the range of the arch area under different stress paths was determined according to the morphology of the arch axis, combining with the inner and outer boundary positions of the pressure arch. The arch thickness and its bearing characteristics were studied. Finally, based on the arch without articulation theory, combining with the calculated arch axis equation, a two-dimensional mechanical model of SRPA was established to study the distribution of internal forces and failure types when the model was loaded.

2 Theoretical model

The SRPA is the mechanical root cause of the elevated abutment pressure of the coal rock body around the working face and dramatic mine pressure behaviors. The SRPA a redistribution of stress state caused by the self-adjustment of overlying strata to resist the uneven deformation of the medium caused by mining, that is, the principal stress changes, the direction is deflected, and the load transfer path deviates from the arch structure tangential compression area (Jaouhar et al., 2018). At the same time, the load is transferred to the stable rock mass at the skewback position, giving full play to its self-bearing capacity manifestation. The characteristics of SRPA conform to the arch without articulation in structural mechanics, which is a typical cubic statically indeterminate structure. In the calculation of the internal force distribution law of the statically indeterminate arch, the equation of the arch axis and the variation law of the arch section must be determined. Due to the complicated analysis process of statically indeterminate problems, studies have shown that if the influence of axial deformation is neglected when calculating statically indeterminate arch structures, the reasonable axis of statically indeterminate arches is the same as the corresponding three-hinged arch (Jiang et al., 2008). In this paper, the reasonable arch axis of the three-hinged arch is used as the reasonable arch axis of the SRPA. The axis equation of the SRPA is calculated, and then the arch without articulation is taken as the research object to calculate the internal force distribution law of the SRPA.

2.1 Assumptions and boundary conditions

Before theoretical analysis, the model is simplified as follows.

• The SRPA dynamically evolves with the mining influence, and the pressure arch in the far-field under the condition of full mining (the working face length is equal to the advancing length) was selected for analysis, as shown in Figure 3.

• The physical and mechanical properties of the giant-thick weakly cemented laminated rock mass are relatively similar. The tensile strength of weakly cemented rock is less than 2 MPa, the compressive strength is less than 20 MPa, the elastic modulus is less than 2 GPa, and the cohesion is less than 10 MPa. So we assumed that the surrounding rock is a homogeneous and continuous medium (Li et al., 2016).

• The SRPA is a shell structure with a certain thickness, and the centroid line of the arch structure is the research object when analyzing the characteristics of the pressure arch shape.

• The SRPA contains an unstable and broken rock mass, and the supporting reaction force to the arch is not considered in the model construction process.

• The SRPA formed under certain buried depth conditions, For the convenience of calculation, the boundary conditions are set as follows: The vault bears a centrally symmetrical vertical trapezoidal load, and both sides of the arch bear a horizontal linear trapezoidal load.

2.2 Morphological characteristics

The three-hinged arch rational arch axis equation of structural mechanics is used as the morphological characteristic equation of the SRPA. For SRPA, to maintain balance and stability, the bending moment M and the shear force Q on the section where the arch axis located must be zero. To study the morphological characteristics of SRPA (rational arch axis and rise-span ratio), a mechanical model is established, as shown in Figure 1. Among them; Figure 1A shows the actual load distribution state of SRPA in deep mining area. The vault bears a centrally symmetrical filling load, and both sides of the arch bear a horizontal linear trapezoidal load. For convenience of calculation, the vertical stress of overlying is equivalent to trapezoidal load, as shown in Figure 2B.

FIGURE 1

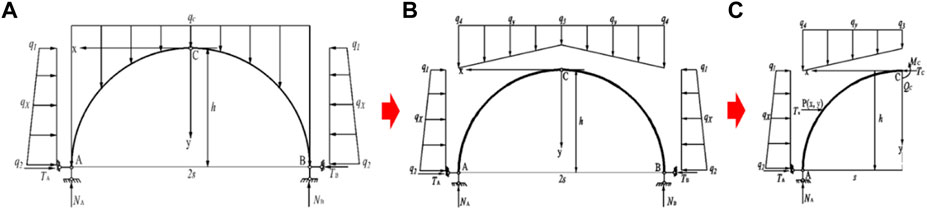
FIGURE 1. Diagram of SRPA (Surrounding rock pressure arch): (A) Stress analysis of filling load; (B) Stress analysis of trapezoidal load state; (C) Left half-span isolator.

As displayed in Figure 1A, the force analysis shows that the horizontal thrusts T_A and T_B and the vertical reaction forces N_A and N_B act on the front and rear arch feet A and B, respectively, and the horizontal trapezoidal load $q_x=\left(q_2-q_1\right)y/h+q_1$ while, the vertical trapezoidal load $q_y=\left(q_4-q_3\right)x/s+q_3$ are act on any Section P (x, y). For trapezoidal load $q_1=\lambda \gamma \left(H-h\right)$, $q_2=\lambda \gamma H$, $q_3=\gamma \left(H-h\right)$ and $q_4=\gamma H$, in these formulae h is arch rise, s is half of the arch span, λ is the lateral pressure coefficient, γ is the density of the rock mass; and H is the mining depth.

$\mathrm{H}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{u}\mathrm{s}\mathrm{t}:T_x={\int }_0^y{q}_x\mathrm{d}y=\frac{\left(q_2-q_1\right)y^2}{2h}+q_{1}y,(1)$

$\mathrm{V}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}:T_y={\int }_0^x{q}_y\mathrm{d}x=\frac{\left(q_4-q_3\right)x^2}{2s}+q_{3}x.(2)$

Taking any point P (x, y) on the left span axis of the SRPA, as shown in Figure 1B, a force analysis is performed and according to the moment balance equation, obtained as follows:

$T_{c}y=\frac{x\left(q_4+2q_3\right)}{3\left(q_4+q_3\right)}\cdot T_y+\frac{y\left(q_2+2q_1\right)}{3\left(q_2+q_1\right)}\cdot T_x,(3)$

where T_c is the horizontal force at point C of the vault, $\frac{y\left(q_2+2q_1\right)}{3\left(q_2+q_1\right)}$ and $\frac{x\left(q_4+2q_3\right)}{3\left(q_4+q_3\right)}$ are the concentrated load action points of the horizontal trapezoidal stress and the vertical trapezoidal stress, respectively.

Substituting Eqs. 1–2 into Eq. 3, the following equation is obtained as follows

$T_c=\frac{\left[\left(3H-2h\right)\gamma \right]\left(\lambda s{y}^3+h{x}^3\right)+\left[2\left(3H-2h\right)\left(H-h\right)\gamma \right]\left(\lambda y^2+s{x}^2\right)}{6\left(2H-h\right)sy}.(4)$

According to the force balance condition in the X-axis direction

$T_c=T_x+fs{q}_y,(5)$

where f is the coal-rock friction factor, which is related to the hardness of the coal and rock mass. Generally, the harder the rock is, the larger the value (Cai 2013).

Substituting Eqs. 1–2 into Eq. 5, the following equation can be obtained

$T_c=\frac{1}{2}\lambda \gamma y^2+\lambda \gamma \left(H-h\right)y+\gamma sfH+\gamma hf\left(x-s\right).(6)$

By combining Eqs. 4, 6, the axis equation of the SRPA can be obtained as follows

$\frac{\left(3H-2h\right)\gamma h}{6\left(2H-h\right)s}{x}^3+\frac{\left(3H-2h\right)\left(H-h\right)\gamma }{3\left(2H-h\right)}{x}^2=\frac{\gamma \lambda \left(3H-h\right)}{6\left(2H-h\right)}{y}^3+\frac{\left(3H-h\right)\left(H-h\right)\lambda \gamma }{3\left(2H-h\right)}{y}^2+\gamma sf\left(H-h\right)y+\gamma hfxyx\in \left[0,s\right],y\in \left[0,\mathrm{h}\right].(7)$

The axis equation of SRPA can be written as

$a\cdot y^3+b\cdot y^2+c\cdot y+d=0,(8)$

where

$\left\{\begin{array}{l}a=\frac{\gamma \lambda \left(3H-h\right)}{6\left(2H-h\right)}\\ b=\frac{\left(3H-h\right)\left(H-h\right)\lambda \gamma }{3\left(2H-h\right)}\\ c=\gamma sf\left(H-h\right)+\gamma hfx\\ d=-\left[\frac{\left(3H-2h\right)\gamma h}{6\left(2H-h\right)s}{x}^3+\frac{\left(3H-2h\right)\left(H-h\right)\gamma }{3\left(2H-h\right)}{x}^2\right].\end{array}\right.(9)$

Eq. 8 is a cubic equation of one variable. In the range of $x\in \left[0,s\right],y\in \left[0,h\right]$, it has a unique real number root

$y=m+n-\frac{b}{3a},(10)$

where

$\left\{\begin{array}{l}m=\sqrt[3]{u+v}\\ n=\frac{b^2-3ac}{9am}\end{array}\right..(11)$

In Eq. 11, u and v are calculated by the following equations

$\left\{\begin{array}{l}u=\frac{9abc-27a^{2}d-2b^3}{54a^3}\\ v=\frac{\sqrt{3\left(4a{c}^3-b^2{c}^2-18abcd+27a^2{d}^2+4b^{3}d\right)}}{18a^2}\end{array}\right..(12)$

Substituting x=s and y=h into Eq. 7, then the relationship between the arch rise (h) and span (2 s) of the SRPA can be derived, expressed by

$\frac{{\left(3H-2h\right)}^2{s}^2}{\left(2H-h\right)}-6Hhfs-\left(3H-h\right)\lambda h^2=0.(13)$

2.3 Internal force distribution

The reasonable axis of the SRPA is a unary cubic function curve, and the rational axis equation of the arch is established based on the bending moment of any section of the three-hinged arch structure being zero. When the arch without an articulation structure is used for internal force analysis, the bending moment, shear force and axial force still need to be generated due to the influence of the additional internal force of the statically indeterminate structure. Therefore, based on determining the reasonable axis of the SRPA, the internal force distribution law of the SRPA is analyzed through the force method equation of the cubic statically indeterminate problem of the arch without articulation in structural mechanics. A coordinate system is established, as shown in Figure 2A, with the origin at the center of the arch without an articulation structure. Due to the symmetry of the arch structure, establishing half of the structure for analysis (see Figure 2B) and cutting along the middle of the arch with three unknown forces X₁, X_2, and X₃ in the cross section, which are the bending moment, axial force and shear force respectively. Due to the symmetry of the structure and load, the antisymmetric internal shear force on the central section is 0, that is X₃=0. X₁, and X₂ can be solved according to the force method equations.

$\left\{\begin{array}{l}{\delta }_{11}{X}_1+{∆}_{1p}=0\\ {\delta }_{22}{X}_2+{∆}_{2p}=0,\end{array}\right.(14)$

where δ₁₁ and δ₂₂ are the displacements generated under the action of unit force $\overline{X_1}=1,\overline{X_2}=1$ and Δ_1p and Δ_2p represent the displacements of point C along the X₁ and X₂ directions under the action of external force.

FIGURE 2

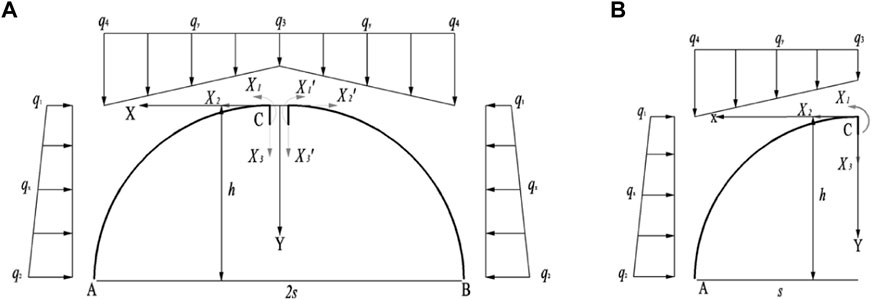
FIGURE 2. Calculating model of internal force of SRPA (Surrounding rock pressure arch): (A) Stress analysis, (B) Left half-span isolator.

According to the displacement calculation equation of the statically determinate structure, the rotation angle and displacement δ₁₁ and δ₂₂ of point C under the action of unit force $\overline{X_1}=1,\overline{X_2}=1$ can be calculated as follows

$\left\{\begin{array}{l}{\delta }_{11}=\frac{1}{EI}{\int }_0^s\sqrt{1+y^{\prime }}\mathrm{d}x\\ {\delta }_{22}=\frac{1}{EI}{\int }_0^s{\mathrm{y}}^2\sqrt{1+y^{\prime }}\mathrm{d}x.\end{array}\right.(15)$

The bending moment of any section under an external load can be written as

$M_c=\frac{x\left(q_4+2q_3\right)}{3\left(q_4+q_3\right)}\cdot T_y+\frac{y\left(q_2+2q_1\right)}{3\left(q_2+q_1\right)}\cdot T_x.(16)$

Accordingly, the displacements Δ_1p and Δ_2p of point C under an external load can be calculated as follows

$\left\{\begin{array}{l}{\Delta }_{1p}=\frac{{\int }_0^s{M}_c\sqrt{1+y^{\prime }}\mathrm{d}x}{EI}\\ {\Delta }_{2p}=\frac{{\int }_0^s{M}_c{\mathrm{y}}^2\sqrt{1+y^{\prime }}\mathrm{d}x}{EI}\end{array}\right..(17)$

Substituting Eqs. 15, 17 into Eq. 14, can be obtained as follows

$\left\{\begin{array}{l}{X}_1=\frac{{\int }_0^{\mathrm{s}}{M}_c\sqrt{1+y^{\prime }}\mathrm{d}x}{{\int }_0^{\mathrm{s}}\sqrt{1+y^{\prime }}\mathrm{d}x}\\ X_2=\frac{{\int }_0^{\mathrm{s}}{M}_c{\mathrm{y}}^2\sqrt{1+y^{\prime }}\mathrm{d}x}{{\int }_0^{\mathrm{s}}{\mathrm{y}}^2\sqrt{1+y^{\prime }}\mathrm{d}x}\end{array}\right..(18)$

Substituting Eqs. 1, 2, 16, into Eq. 18, the following equation can be obtained

$\left\{\begin{array}{l}{X}_1=\frac{{\int }_0^{\mathrm{s}}\left[\frac{x\left(q_4+2q_3\right)}{3\left(q_4+q_3\right)}\cdot \left[\frac{\left(q_4-q_3\right)x^2}{2s}+q_{3}x\right]+\frac{y\left(q_2+2q_1\right)}{3\left(q_2+q_1\right)}\cdot \left[\frac{\left(q_2-q_1\right)y^2}{2h}+q_{1}y\right]\right]\sqrt{1+y^{\prime }}\mathrm{d}x}{{\int }_0^{\mathrm{s}}\sqrt{1+y^{\prime }}\mathrm{d}x}\\ X_2=\frac{{\int }_0^{\mathrm{s}}\left[\frac{x\left(q_4+2q_3\right)}{3\left(q_4+q_3\right)}\cdot \left[\frac{\left(q_4-q_3\right)x^2}{2s}+q_{3}x\right]+\frac{y\left(q_2+2q_1\right)}{3\left(q_2+q_1\right)}\cdot \left[\frac{\left(q_2-q_1\right)y^2}{2h}+q_{1}y\right]\right]{\mathrm{y}}^2\sqrt{1+y^{\prime }}\mathrm{d}x}{{\int }_0^{\mathrm{s}}{\mathrm{y}}^2\sqrt{1+y^{\prime }}\mathrm{d}x}\end{array}\right..(19)$

After calculating the redundant unknown forces X₁ and X₂ of the statically indeterminate structure, the internal force formula of any section of the arch without articulation can be obtained according to the equilibrium conditions of the isolated body, as shown below

$\left\{\begin{array}{l}M\left(x\right)=M_{\mathrm{c}}+X_1+X_2\cdot y\\ Q\left(x\right)=X_2\cdot \sin \theta -T_x\cdot \sin \theta -T_y\cdot \cos \theta \\ N\left(x\right)=X_2\cdot \cos \theta +T_y\cdot \sin \theta -T_x\cdot \cos \theta \end{array}\right.,(20)$

where M(x), Q(x) and N(x) are the bending moment, shear force and axial force of any section of arch without articulation respectively; and $\sin \theta =y^{\prime }/\sqrt{1+{\left(y^{\prime }\right)}^2}$, $\cos \theta =1/\sqrt{1+{\left(y^{\prime }\right)}^2}$.

Substituting Eqs. 1, 2, 16, 19 into Eq. 20, the internal force distribution of any section of SRPA can be written as

$\left\{\begin{array}{l}M\left(x\right)=\left\{\frac{x\left(q_4+2q_3\right)}{3\left(q_4+q_3\right)}\cdot \left[\frac{\left(q_4-q_3\right)x^2}{2s}+q_{3}x\right]+\frac{y\left(q_2+2q_1\right)}{3\left(q_2+q_1\right)}\cdot \left[\frac{\left(q_2-q_1\right)y^2}{2h}+q_{1}y\right]\right\}+\\ \frac{{\int }_0^{\mathrm{s}}\left\{\frac{x\left(q_4+2q_3\right)}{3\left(q_4+q_3\right)}\cdot \left[\frac{\left(q_4-q_3\right)x^2}{2s}+q_{3}x\right]+\frac{y\left(q_2+2q_1\right)}{3\left(q_2+q_1\right)}\cdot \left[\frac{\left(q_2-q_1\right)y^2}{2h}+q_{1}y\right]\right\}\sqrt{1+y^{\prime }}\mathrm{d}x}{{\int }_0^{\mathrm{s}}\sqrt{1+y^{\prime }}\mathrm{d}x}+\\ \left\{\frac{x\left(q_4+2q_3\right)}{3\left(q_4+q_3\right)}\cdot \left[\frac{\left(q_4-q_3\right)x^2}{2s}+q_{3}x\right]+\frac{y\left(q_2+2q_1\right)}{3\left(q_2+q_1\right)}\cdot \left[\frac{\left(q_2-q_1\right)y^2}{2h}+q_{1}y\right]\right\}\cdot \mathrm{y}\\ N\left(x\right)=\frac{{\int }_0^{\mathrm{s}}\left\{\frac{x\left(q_4+2q_3\right)}{3\left(q_4+q_3\right)}\cdot \left[\frac{\left(q_4-q_3\right)x^2}{2s}+q_{3}x\right]+\frac{y\left(q_2+2q_1\right)}{3\left(q_2+q_1\right)}\cdot \left[\frac{\left(q_2-q_1\right)y^2}{2h}+q_{1}y\right]\right\}{\mathrm{y}}^2\sqrt{1+y^{\prime }}\mathrm{d}x}{{\int }_0^{\mathrm{s}}{\mathrm{y}}^2\sqrt{1+y^{\prime }}\mathrm{d}x}\cdot \frac{1}{\sqrt{1+{\left(y^{\prime }\right)}^2}}\\ +\left[\frac{\left(q_4-q_3\right)x^2}{2s}+q_{3}x\right]\cdot \frac{y^{\prime }}{\sqrt{1+{\left(y^{\prime }\right)}^2}}-\left[\frac{\left(q_2-q_1\right)y^2}{2h}+q_{1}y\right]\cdot \frac{1}{\sqrt{1+{\left(y^{\prime }\right)}^2}}\\ Q\left(x\right)=\frac{{\int }_0^{\mathrm{s}}\left\{\frac{x\left(q_4+2q_3\right)}{3\left(q_4+q_3\right)}\cdot \left[\frac{\left(q_4-q_3\right)x^2}{2s}+q_{3}x\right]+\frac{y\left(q_2+2q_1\right)}{3\left(q_2+q_1\right)}\cdot \left[\frac{\left(q_2-q_1\right)y^2}{2h}+q_{1}y\right]\right\}{\mathrm{y}}^2\sqrt{1+y^{\prime }}\mathrm{d}x}{{\int }_0^{\mathrm{s}}{\mathrm{y}}^2\sqrt{1+y^{\prime }}\mathrm{d}x}\cdot \frac{y^{\prime }}{\sqrt{1+{\left(y^{\prime }\right)}^2}}\\ -\left[\frac{\left(q_2-q_1\right)y^2}{2h}+q_{1}y\right]\cdot \frac{y^{\prime }}{\sqrt{1+{\left(y^{\prime }\right)}^2}}-\left[\frac{\left(q_4-q_3\right)x^2}{2s}+q_{3}x\right]\cdot \frac{1}{\sqrt{1+{\left(y^{\prime }\right)}^2}}\end{array}\right..(21)$

3 Model application and discussion

3.1 Research background

The Hongqinghe Coal Mine is located in the Dongsheng Coalfield, which is a typical mine with weakly cemented strata, and the main mining coal seam is 3^–1, with an average burial depth of 650 m, an average thickness of 6 m and an average dip angle of 2°. The working face adopts the comprehensive mechanized coal mining method of single inclined longwall mining with full height at one time, and the roof is managed by the full caving method. The length of the working face is approximately 300 m, the strike length is approximately 3,300 m, and the average propulsion speed is 12 m/d. The measured uniaxial compressive strength of rock is 11.56–37.89 MPa, the tensile strength is 0.74–2.4 MPa, the cohesion is 0.66–6.77 MPa, the internal friction angle is 10.56–30.65, and the friction coefficient of the coal and rock is approximately 0.22–0.34. The lateral pressure coefficient is between 0.8 and 1.5 (Sun et al., 2019). The immediate roof is a composite roof composed of mudstone, carbonaceous mudstone and coarse sandstone with an average thickness of 12 m, and the main roof is fine sandstone with an average thickness of 20 m. Above the main roof are mainly Jurassic and cretaceous weakly cemented strata. The occurrence characteristics and fracture morphology of overlying strata rocks are shown in Figure 3.

FIGURE 3

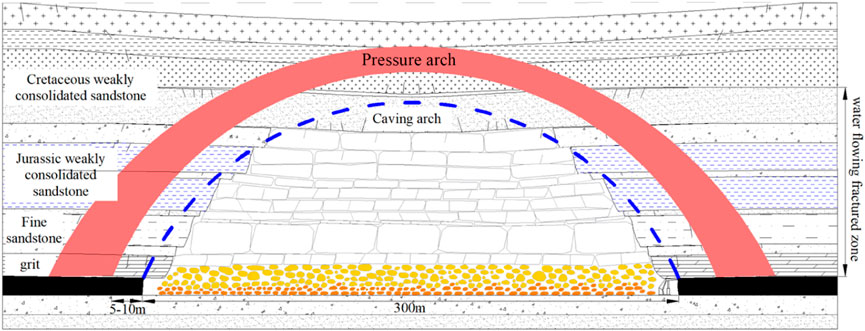
FIGURE 3. Occurrence characteristics and fracture morphology of overlying strata in Hongqinghe Coal Mine.

3.2 Reasonable axis analysis

The rational arch axis equation is an important characterization of the morphological characteristics of SRPA. According to the calculation results of Eq. 9, the rational arch axis equation of SRPA is a unary cubic function. In the range of $x\in \left[0,s\right],y\in \left[0,\mathrm{h}\right]$, selecting λ=1.2, f=0.3 and γ=27 kN/m³, the morphological characteristics of the rational axis of the pressure arch in the far field surrounding rock in the full mining stage of the Hongqinghe Coal Mine are described in combination with Eq. 10.

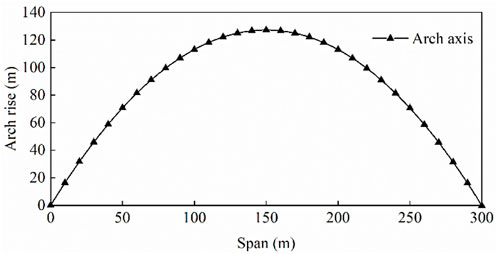
As shown in Figure 4, the morphological characteristics are a cubic parabola with a downward opening, which is different from the axis equations of semicircle, semi-ellipse and quadratic parabola obtained by uniformly distributed load studies (Xia et al., 2018, Wang et al., 2019), thus, the change of boundary conditions affects the shape of arch axis. The height of SRPA at the stage of full mining is 127 m. According to the prediction model of the water-conducting fracture zone (He et al., 2020), the height of the water-conducting fracture zone at the stage of full mining of the Hongqinghe Coal Mine is 105.5–114 m. Combined with Figure 3, the limit equilibrium zone range is 5–10 m. The calculated development height of the water-conducting fracture zone is 117–122 m, similar to the prediction model.

FIGURE 4

FIGURE 4. Morphological characteristic curve of SRPA (Surrounding rock pressure arch).

3.3 Rise-span relationship analysis

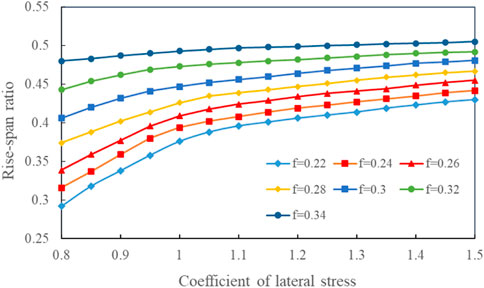
The rise-span relationship of the SRPA can be used to characterize the degree of the arch structure frankness and steepness, and it is an important index to reflect the force characteristics and distribution in arch. According to Eq. 13, the rise-span relationship of SRPA is related to mining depth H, friction factor f of the coal-rock mass, and lateral pressure coefficient λ. According to the measured data of the Hongqinghe Coal Mine, different parameters in Table 1 are selected and substituted into Eq. 13 to calculate, and the variation of SRPA rise-span ratio with lateral pressure coefficient λ and friction factor f of coal and rock mass is obtained.

TABLE 1

TABLE 1. Parameter assignment of SRPA (Surrounding rock pressure arch).

As shown in Figure 5, according to the field-measured data, the rise-span ratio is between 0.3 and 0.5, and the long axis of the SRPA is the span, which is a flat arch structure along the advancing direction of the working face. The rise-span ratio increases non-linearly with lateral pressure coefficient increasing. When λ < 1, the growth rate is larger, and when λ > 1, the growth rate is slower. Lithology change has a significant influence on the mechanical characteristics of SRPA. With the enhancement of lithology, the larger the rise-span ratio of SRPA is, the less the influence of the lateral pressure coefficient is. Under the same lateral pressure coefficient, the harder the overlying strata are, the smaller the flattening rate. The analysis results are consistent with the numerical results in the literature obtained by Zhao (Zhao 2018).

FIGURE 5

FIGURE 5. Variation law of rise-pan ratio of SRPA (Surrounding rock pressure arch).

3.4 Internal force analysis

The internal force distribution of SRPA is related to the morphological characteristics of the arch and external load. Since it is difficult to find the analytical solution for the calculation result of Eq. 21, Mathematica software is used to find the numerical solution. According to the actual data of the Hongqinghe Coal Mine, λ=1.2, f =0.3 and γ =27 kN/m³ are selected, and the internal force distribution in the unhinged arch is calculated.

The illustration is displayed in Figure 6: under the trapezoidal load, the internal force distribution law of any section of the SRPA is as follows:

• The internal force at any section of SRPA has shear force, bending moment and axial force, and the axial force is always greater than the bending moment, and shear force. According to the provisions of “structural mechanics”, the axial forces in the figure are pressures, so the SRPA is maintained mainly by axial compression of any section to maintain the stability and bearing characteristics of the pressure arch.

• The axial compression of any section of SRPA is axially symmetric, and the distribution characteristics are basically consistent with the arch axis equation. In this case, the SRPA can achieve the best bearing performance. The pressure value increases from 77 kN at the vault position to 114 kN at the skewback position, by 48%.

• The bending moment of any section of SRPA is also axially symmetric, and three regions can be defined. The bending moment of any section of SRPA is greater than zero in the range of [0°, 30°] and [81°, 90°] on both sides of the axis of SRPA symmetry. According to the provisions of the bending moment direction in Figure 2 (counterclockwise is positive), the bending moment of any section of this region is taken for analysis. The bending moment of any section of the arch is tensile stress inside and compressive stress outside, and the SRPA is vulnerable to tensile failure in this region. Within the range of [30°, 81°] of the SRPA symmetry axis, the bending moment of the section is less than zero, indicating that the inner side of the arch is subjected to compressive stress, while the outer side is tensile stress.

• The shear force at any section of SRPA still presents an axisymmetric distribution, which can be divided into two parts. The value of shear stress is greater than zero in the range of [0°, 62°] on both sides of the SRPA symmetry axis, and the shear direction is directed to the center of the SRPA. Within the range of [62°, 90°], the sectional shear is less than zero, indicating that the shear direction deviates from the center of the SRPA.

FIGURE 6

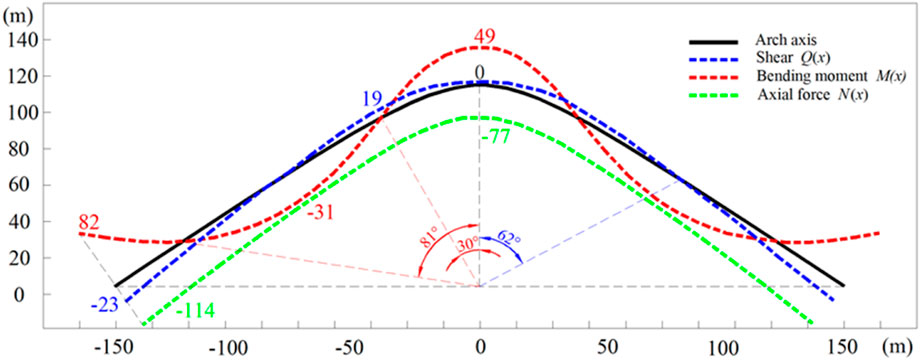
FIGURE 6. Distribution rule of internal force of SRPA (Unit of bending moment: kNm; Unit of shear and axial force: kN).

4 Analysis of mechanical properties

4.1 Bearing characteristics

The reasonable axis equation and rise-span relationship are calculated by the SRPA model, and the calculation process of pressure arch is simplified into a compressive stress line, but in fact, the pressure arch is a shell structure with a certain thickness. Meanwhile, to form a stable bearing structure, SRPA should satisfy the arch structure of the rise-span relationship and arch thickness. Here, the thickness of the pressure arch is used to characterize its bearing characteristics. The thickness indicates the degree and range of the disturbed surrounding rock, which means that a small arch thickness can bear the small load of the arch itself and surrounding rock, and a large thickness can bear a larger surrounding rock load. Additionally, the thickness of the arch is determined mainly by the position of the inner and outer boundary lines of the pressure arch.

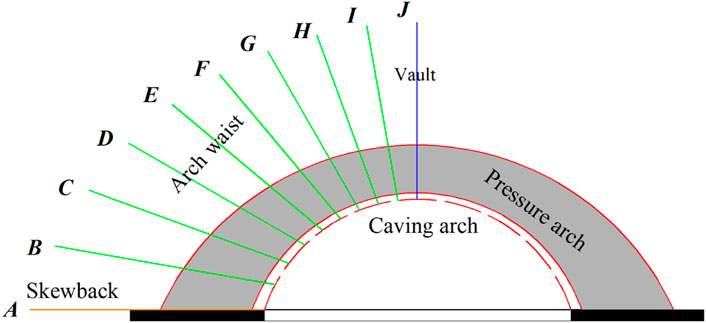
Currently, the determination of the inner and outer boundaries of the pressure arch is focused mainly on tunnel excavation, which is determined by the stress field characteristics. Three main criteria judge the outer boundary of the pressure arch: tangential stress, principal stress deflection, and the maximum principal stress judging criterion. Two main criteria determine the inner boundary of the pressure arch: The tangential stress judging criterion and the extreme value of the principal stress inside the arch (Chen et al., 2011; Rezaei et al., 2015, He and Zhang 2015). However, the mining field surrounding rock is different from small section excavation projects such as tunnels and caverns. As the coal seam continues to be mined, it is damaged rock range and the structural characteristics of the pressure arch develop dynamically upward, resulting in different stress distribution characteristics of the rock in different areas. It is unreasonable if the boundary location of different paths is determined by using the criterion of determining the boundary inside and outside the arch of the same SRPA. Therefore, it is necessary to determine the optimal arch range according to the judging criterion of the inner and outer boundaries of different stress paths. The stress examination path of the SRPA is defined as the vertical path from the center of the vault upward (such as “J” path in Figure 7), the arc path of arch waist backward to the arch body (such as “B-I” path in Figure 7) and the horizontal path of the skewback away from the arch body (such as “A” path in Figure 7). To facilitate the analysis, this study considers mainly the variability of stress distribution characteristics of the vault path and skewback path, the arch waist and skewback path are approximately the same, and the stress increasing is expressed as the abutment pressure magnitude of each stratified overlying stratum.

FIGURE 7

FIGURE 7. Schematic diagram of the stress examination path.

The outer boundary of the vault path can be discerned according to the definition of the SRPA. After coal mining, the surrounding rock formed a circular flow line of the maximum principal stress, and the direction of the maximum principal stress was deflected above the vault of the pressure arch. Assuming that the maximum compressive stress inside the arch is vertical, the maximum compressive stress from the arch upward turned from vertical to horizontal, and the maximum principal stress deflection point is taken as the base point of the outer boundary of the pressure arch, i.e., the main stress deflection judging criterion. Description of the degree of deflection of the maximum principal stress vector at various points in the surrounding rock after mining relative to its original direction can be expressed as the relative magnitude of the maximum principal stress compared to the vertical stress or horizontal stress. For example, for a stratum where the vertical stress is the maximum principal stress, an index of relative deflection δ is introduced to indicate the degree of deviation of the maximum principal stress vector from the vertical direction, as shown in Figure 8 (point A), which is defined as follows.

$\delta =\frac{\left({\sigma }_{\max }-{\sigma }_z\right)}{{\sigma }_{\max }},(22)$

where σ_max is the maximum principal stress, and σ_z is the vertical stress.

FIGURE 8

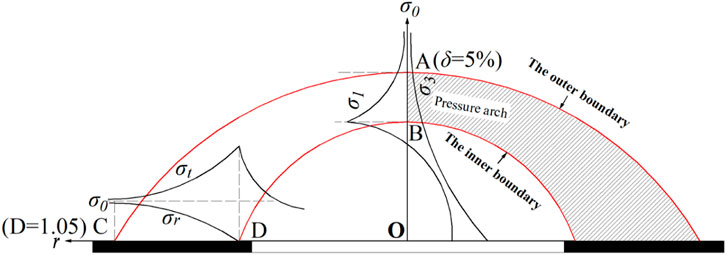
FIGURE 8. Location of inner and outer boundaries of different stress paths in the SRPA (Surrounding rock pressure arch).

To facilitate the calculation, the direction of the maximum principal stress vector gradually reverts to the vertical direction when δ $<$ 5%; however, the physical significance expressed by the relative deflection index is not considered when δ$>$ 5%.

The outer boundary of the skewback path can be analyzed according to the stress characteristics of the skewback position. The skewback position stress state is the range of unstable loads transmitted above the arch or the degree of stress concentration in the skewback part, i.e., the elastic zone range of over-abutment pressure at the working surface. The tangential stress increase factor D is introduced to reflect the degree of stress concentration at the skewback location and the arch effect pressure transfer range, such as the location shown at point C in Figure 8. For the convenience of calculation, D=1.05 is defined as the outer boundary of the skewback path.

$D=\frac{{\sigma }_{zz}}{{\sigma }_{zz-ini}},(23)$

where σ_zz is the tangential stress of the skewback path and σ_zz-ini is the tangential stress of the skewback path in the original rock stress state.

For the vault and skewback path, inner boundary determination can be based on the maximum main stress extreme value determination criteria of the SRPA. After mining, the tangential stress gradually increases, and then gradually returns to the original stress. The point at maximum tangential stress is taken as the inner boundary of the pressure arch. The specific applicable criterion is shown in Table 2, and the locations of the inner and outer boundary lines are shown in Figure 8 (point B, D).

TABLE 2

TABLE 2. Criterions for the application of different stress examination paths.

The relative deflection index of the SRPA vault path is difficult to find by theoretical calculation, but it can be found by numerical simulation of the deflection characteristics of the principal stress (Kong et al., 2018), which is not discussed here. To study the influencing factors and variation laws of the SRPA thickness, the theoretical formula for calculating the arch thickness is proposed through the limit equilibrium conditions at the skewback.

${\sigma }_{tA}={\sigma }_{rA}{\tan }^2\left({45}^{\circ }+\frac{\phi }{2}\right)+2C\tan \left({45}^{\circ }+\frac{\phi }{2}\right),(24)$

where σ_tA and σ_rA are the tangential stress and radial stress at skewback A, respectively; C is the cohesion; and φ is the internal friction angle.

${\sigma }_{tf}=\frac{T_c}{t\sin \phi }=\frac{\lambda rHh+rsfH-1/2\lambda r{h}^2}{t\sin \phi },(25)$

${\sigma }_{rf}=\frac{rhs}{2\sin \phi },(26)$

where σ_tf and σ_rf are the tangential and radial stress extremes at the base of the SRPA, respectively, and t is the thickness of the SRPA.

Substitute Eqs. 24, 25 into Eq. 26 to simplify, we can obtain the thickness of SRPA

$t=\frac{\lambda rHh+rsfH-\frac{1}{2}\lambda r{h}^2}{rhs{\tan }^2\left({45}^{\circ }+\frac{\phi }{2}\right)+2\mathrm{C}\mathrm{t}\mathrm{a}\mathrm{n}\left({45}^{\circ }+\frac{\phi }{2}\right)\sin \phi }.(27)$

Eq. 27 shows that the arch thickness is affected mainly by the lateral pressure coefficient λ, the friction factor f of coal-rock body, the internal friction angle φ of overlying strata, the cohesion C and the burial depth H. According to the actual measurement data of the Hongqinghe Coal Mine, the values assigned to different parameters are listed in Table 3.

TABLE 3

TABLE 3. Assignment of overlying strata parameters.

According to the analysis of all curve changes in Figure 9, when the rise-span ratio is in the range of 0.2–0.4, the thickness of the SRPA grows slowly with the increase of the rise-span ratio under the same parameter. When in the range of 0.4–0.6, the arch thickness increases rapidly with increasing rise-span ratio increasing, indicating that larger rise-span ratio can achieve the stable bearing characteristics. As shown in Figure 9A, when the rise-span ratio of SRPA is kept constant, the arch thickness increases as the lateral pressure coefficient rising. The larger the growth rate of the lateral pressure coefficient is, the more obvious the bearing characteristics of the arch, indicating that the increase in the lateral pressure coefficient has significant beneficial effects on the arch stability. As shown in Figure 9B, when the rise-span ratio of SRPA remains constant, the arch thickness increases basically linearly with lithological enhancement. For every 0.1 increase in friction factor, the arch thickness increases by 10.0% on average, illustrating that harder rocks increase the bearing performance of the arch, which can ensure the overhanging overlying strata load is effectively transferred to unmined rock formation in far field. As shown in Figures 9C, D, with the increase in cohesion and internal friction angle of the overlying strata, the tensile and shear strength gradually increase, but the SRPA thickness gradually decreases at the same time. The smaller the cohesion and internal friction angle are, the greater range of the surrounding rock for stress adjustment, and the larger arch thickness is needed to maintain a stable bearing. In Figure 9D, when the rise-span ratio is less than 3.5, the arch thickness is shown to be largely unaffected by the cohesion. According to the results of Section 3.2, the rise-span ratio of the weakly cemented stratum lies between 0.3 and 0.5 at the fully mining stage. According to the analysis of the actual measurement data of the Hongqinghe Coal Mine, the arch thickness of the weakly cemented stratum in the fully mining stage is within 28–47 m.

FIGURE 9

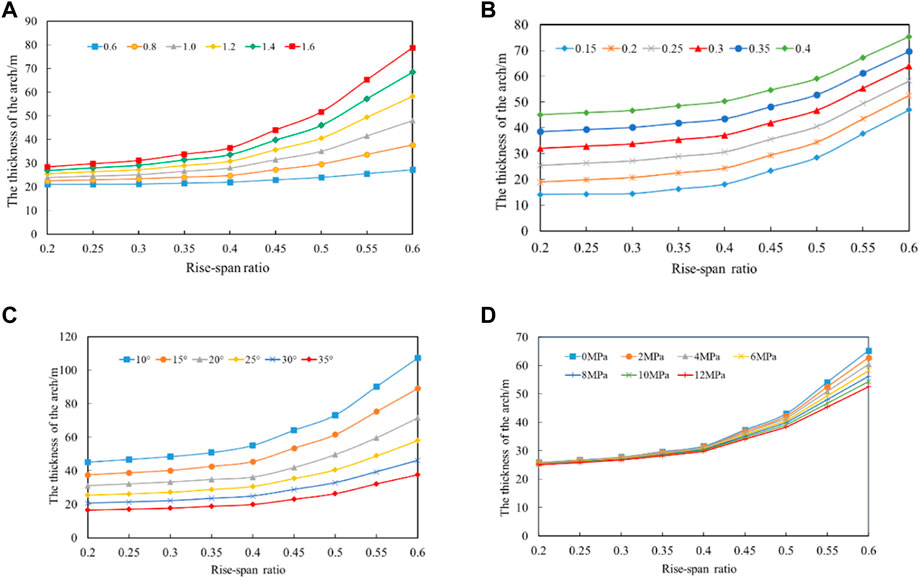
FIGURE 9. The variation law of the arch thickness of the SRPA (Surrounding rock pressure arch) with the rise-span ratio: (A) Lateral pressure coefficient, (B) Friction factor, (C) Angle of internal friction, (D) Cohesion.

4.2 Stabilization mechanism

4.2.1 Instability criterion of SRPA

As the working face advances, the overlying stratum fractures continue to evolve and penetrate, and the roof strata periodically produce separation, fracture and collapse. With the self-organization of surrounding rock, the peak area of the advance abutment pressure at the working face moves deeper into the coal wall, and the high stress area of the overlying strata moves deeper into the roof. The SRPA shows a dynamic evolution of equilibrium—expansion—limit—moving. The evolution and stability of the SRPA is non-linear and dynamic. The stress equilibrium state of the pressure arch determines its stability characteristics. In other words, when the maximum stress value at each place exceeds its rock limit bearing capacity, the pressure arch is destabilized at that position, leading to the high stress continuing to transfer to the deeper part and forming a new pressure arch. The SRPA stability is expressed in the form of the relationship between the degree of stress concentration caused by mining disturbances and the strength of the layered rock mass. Due to the large variability of the bearing capacity of the layered rock mass, the different space distributions of the strength envelope and the different degrees of stress concentration in each part of the vault, arch waist and skewback caused by mining disturbance, different strength criteria should be used to judge the stability of each part. Therefore, the dynamic evolution instability modes of the SRPA under insufficient mining conditions are classified into four types: Compression failure instability, tensile failure instability, shear failure instability, and compound failure instability.

$\left\{\begin{array}{l}\mathrm{C}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{f}\mathrm{a}\mathrm{i}\mathrm{l}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}:{\sigma }_i\ge {\sigma }_c\\ \mathrm{T}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{a}\mathrm{i}\mathrm{l}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}:{\sigma }_i\ge {\sigma }_t\\ \mathrm{S}\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{i}\mathrm{l}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}:{\sigma }_i\ge \tau \\ \mathrm{C}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{f}\mathrm{a}\mathrm{i}\mathrm{l}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}:{\sigma }_i\ge \mathrm{Min}\left({\sigma }_c,{\sigma }_t,\tau \right)\end{array}\right.,(28)$

where σ_i is the equivalent stress suffered by each part of the vault, arch waist and skewback, MPa, it can be obtained by theoretical calculation, numerical and similar simulations. σ_c, σ_t, and τ are compressive strength, tensile strength and shear strength of the layered rock mass, respectively, MPa. Where σ_c, σ_t, and τ are obtained by rock mechanics experiments.

4.2.2 Types of instability in the SRPA

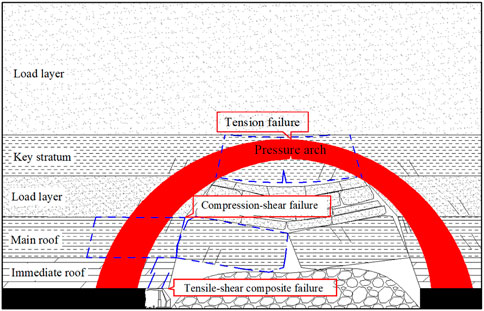
According to the bearing characteristics and destabilization criterion of SRPA, its instability is first caused by the concentrated stress in a key position exceeding the ultimate bearing capacity of the surrounding rock, which causes the instability of other parts of the pressure arch under the chain reaction and finally the dynamic instability of the whole pressure arch. Through the distribution law of the internal force of the cross-section shown in Figure 6, and the exploration of the stability of surrounding rock shown in Figure 10, the rock mass in the key part of the SRPA producing mainly the following forms of damage destabilization.

• Tension failure of vault. As shown in Figure 6, the vault location is subject mainly to the joint action of the section bending moment and the section axial force, and the vault is presented as compressive stress under the action of the section axial force. Under the action of the section bending moment, the section bending moment here is greater than 0, and the maximum value of the bending moment of the vault reaches 49 kNm. According to the provisions of the direction of the bending moment in Figure 2 (counterclockwise is positive), the vault position in the section of the bending moment under the action of the performance of the arch inner side of the tension outside the pressure easily undergoes tensile failure. From the analysis of the stability of the surrounding rock, the vault of the SRPA is located in the complete rock layer at the top of the fractured rock mass. The articulated rock block structure formed at its lower part will produce inclined upward support reverse stress on the vault in the process of maintaining stability, which can be decomposed into tensile stress σ_z along the vertical direction Z and compressive stress σ_x along the horizontal direction X. When σ_z ≥ σ_c, tensile failure occurs at the vault; when σ_x ≥ σ_t, compression failure occurs at the vault. The tensile strength of the rock is much smaller than the compressive strength. Usually, the compressive stress σ_x has not yet reached the compressive strength σ_c, and the tensile stress σ_z has exceeded the tensile strength σ_t of the rock, leading to tensile damage to vault of SRPA. For example, the initial breaking of main roof and key stratum.

• Compression-shear failure of the arch waist. As shown in Figure 6, the location of the arch waist of the pressure arch is affected by the joint influence of the section axial force and shear force. The section shear force in this region is greater than 0, the maximum value is 19 kN, where shear failure is very likely to occur at the maximum location. From the analysis of the stability of the surrounding rock, the arch waist is located in the complete rock layer on both sides of the fractured rock mass. Under the action of overlying strata clamping, the inclined upward compressive stress of the articulated rock block structure acts on the arch waist. Meanwhile, the arch waist is also subjected to vertical compressive stress exerted by the mass of the overlying strata. When the shear stress on the shear surface at this location σ_i ≥ τ, shear failure occurs at the location of the arch waist of the SRPA. For example, the periodic breaking of main roof and key stratum.

• Tensile-shear composite failure of skewback. As shown in Figure 6, the skewback of the SRPA will be affected by the joint effect of the section shear force, section bending moment and section axial force, and the internal forces here all reach the maximum value in axis region of arch. The section bending moment at skewback is positive, and the maximum value of 82 kNm, as in the above analysis, showing that this position is very vulnerable to tensile failure. Meanwhile, the section shear force is negative, and the maximum value is −23 kN, where shear failure is easily induced. From the analysis of the stability of surrounding rock, the skewback is located in the peak area of the abutment pressure around the working face. The coal-rock body at the skewback is subjected to the stress k₀γh in the vertical direction, while the coal-rock interlayer thrust T makes the rock layer misalign, leading to the skewback part of the larger mining disturbance stress σ_i, generally having σ_i ≥ max (σ_c, σ_t, and τ), so tensile and compression-shear compound failure destabilization occurs at the skewback. At the same time, the instability of the skewback is regional and sequential. For example, the periodic breakage of the immediate roof along the coal wall is manifested as compression shear failure of the skewback, and rib spalling at the working face is manifested as tensile failure of the skewback.

FIGURE 10

FIGURE 10. Types of instability in the SRPA (Surrounding rock pressure arch).

In summary, the types of failure instability of the SRPA are as follows: Tension failure at the vault, compression-shear failure at arch waist, and tension-shear composite failure at the skewback. The above types of instability occur independently, not simultaneously but in sequence. According to the instability process of key parts of pressure arch, the instability modes of SRPA can be divided into two categories:

1) “Skewback—vault (arch waist)” instability mode. That is, working face mining results in the gradual shift of skewback to the depth of coal wall, and the instability of the skewback leads to the instability of the vault (arch waist). Verified by similar material simulation experiments, as shown in Figure 11. When the working face advance to 75 m, the state is the stable state after the initial fracture of key stratum I. At this time, the vault of pressure arch develops to the position of key stratum II, as shown in Figure 11A. When the working face continues to advance to 100 m, the key stratum I is periodically broken. The excavation of the working face leads to the compression-shear failure of the direct roof at the skewback, which leads to the tension and shear fracture of the key stratum I at the arch waist, leading to the instability of the pressure arch. At this time, the pressure arch develops toward the depth of the coal wall, but not upward, as shown in Figure 11B. When the working face continues to advance to 150 m, the key stratum II will be broken for the first time. Similarly, the excavation of the working face will lead to the direct roof breaking at the skewback, which will lead to the tensile failure and instability of the key stratum II at the vault. At this time, the pressure arch will not only develop toward the depth of the coal wall, but also develop upward, as shown in Figure 11C.

FIGURE 11

FIGURE 11. “Skewback—vault (arch waist)” instability mode: (A) State of key stratum I after initial fracture, (B) State of “skewback—arch waist” instability, (C) State of “skewback—vault” instability.

2) “Vault (arch waist)—skewback” instability mode. That is, working face mining results in primary and periodic fracture of main roof or key stratum, the mining fissure and high stress zone of surrounding rock gradually transfer to the deep coal and rock mass, and a new pressure arch structure is formed in the depth. The instability of the vault (arch waist) causes the composite instability of the skewback. Verified by similar material simulation experiments, as shown in Figure 12. When the working face advances to 70 m, this state is the critical instability state of key stratum I. At this time, vault of the pressure arch develops to the position of key stratum I, as shown in Figure 12A. During the 30 min interval between the stoping of the working face, the key stratum I is initial fracture at this stage. The vault of the pressure arch is subject to tensile failure and instability, resulting in the skewback position transferring to the depth of the coal wall and the vault growing up to the position of key stratum II, as shown in Figure 12B. When the working face continues to advance to the 100 m position, at this time, the key stratum I is periodically broken, and the tension shear fracture occurs at the arch waist of the pressure arch, causing the skewback to transfer to the depth of the coal wall, as shown in Figure 12C.

FIGURE 12

FIGURE 12. “Vault (arch waist)—skewback” instability mode: (A) Critical instability state of key stratum I, (B) State of “vault - skewback” instability, (C) State of “arch waist—skewback” instability.

5 Conclusion and discussions

This paper aims mainly at the structural characteristics of deep buried giant-thick weakly cemented strata in the western mining area of China. The bearing characteristics and stability mechanism of macroscopic SRPA are studied, and the conclusions are as follows.

(1) The macroscopic SRPA rational arch axis is calculated to be a cubic parabola with the opening downward, and the rise-span ratio is between 0.3 and 0.5. The pressure arch is a flat arch structure along the advancing direction of the working face, and the rise-span ratio increases non-linearly with lateral pressure coefficient and lithology increasing.

(2) According to the morphology of the arch axis, considering the internal and external boundary position of the pressure arch and the arch thickness, the range of the arch area under different stress paths is determined. The SRPA thickness at the full extraction stage is 28–47 m. Increasing the rise-span ratio and lateral pressure coefficient of the pressure arch is conducive to promote the stable bearing of the arch itself; the smaller the cohesion and internal friction angle are, the thicker the arch is needed to be maintain a stable bearing capacity.

(3) Based on arch without articulation theory and the calculated arch axis equation, a two-dimensional mechanical model of SRPA is established. The axial force distribution of the section of the SRPA is basically consistent with the arch axis, which can have the best bearing capacity. Within the range of [0°, 30°] and [81°, 90°] on both sides of the symmetry axis, tensile failure easily occurs at the vault (49 kN·m) and skewback (82 kN·m). The maximum shear force is 19 kN at the arch waist and −23 kN at the skewback, and the pressure arch is prone to shear failure. According to the instability process of pressure arch key parts, the instability modes of SRPA can be divided into “skewback—vault (arch waist)” and “vault (arch waist)—skewback”.

The study of the bearing characteristics and stability mechanism of macroscopic SRPA is used mainly to characterize the strong ground pressure behavior and surface subsidence in the mining process of the working face. In the future, we will focus on actively regulating the dynamic evolution of arches. By adopting the technology of overlying strata separation grouting, the grouting position can be accurately determined to control the surface subsidence and maintain the stability of the arch. Considering that the long-term existence of arches will cause potential safety hazards, the strong ground pressure behavior is controlled by roof hydraulic fracturing arch breaking technology.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YY: Conceptualization, Investigation, Data curation, Formal analysis, Writing—Original Draft, Funding acquisition. YZ: Supervision, Resources, Writing—Review and Editing, Project administration. JM: Formal analysis, Investigation. PH: Writing—Review and Editing.

Funding

This work has been supported by the National Natural Science Foundation of China (Grant Nos. 52225402 and U1910206) and the Program of Shanxi Natural Foundation of China (20210302123336).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bednarek, L., and Majcherczyk, T. (2020). An analysis of rock mass characteristics which influence the choice of support. Geomechanics and Engineering 21 (4), 371–377. doi:10.12989/gae.2020.21.4.371

CrossRef Full Text | Google Scholar

Cai, M. F. (2013). Rock mechanics and engineering. 2nd Edition. Beijing, China: Science press.

Google Scholar

Chen, C., and Martin, G. R. (2002). Soil structure interaction for landslide stabilizing piles. Comput. Geotech 29 (5), 363–386. doi:10.1016/S0266-352X(01)00035-0

CrossRef Full Text | Google Scholar

Chen, C. N., Huang, W. Y., and Tseng, C. T. (2011). Stress redistribution and ground arch development during tunneling. Tunnelling and Underground Space Technology 26 (1), 228–235. doi:10.1016/j.tust.2010.06.012

CrossRef Full Text | Google Scholar

Dancygier, A. N., Karinski, Y. S., and Chacha, A. (2016). A model to assess the response of an arched roof of a lined tunnel. Tunnelling and Underground Space Technology 56, 211–225. doi:10.1016/j.tust.2016.03.009

CrossRef Full Text | Google Scholar

Das, S. K. (2000). Observations and classification of roof strata behaviour over longwall coal mining panels in India. International Journal of Rock Mechanics and Mining Sciences 37 (4), 585–597. doi:10.1016/S1365-1609(99)00123-9

CrossRef Full Text | Google Scholar

Du, X. L., Song, H. W., and Chen, J. (2011). Numerical simulation of the evolution of the pressure arch during coal mining. J. China U. Min. Techno 40 (6), 863–867.

Google Scholar

El Kamash, W., El Naggar, H., and Nagaratnam, S. (2021). Numerical analysis of lateral Earth pressure coefficient in inclined mine stopes. Geomech. Geophys. Geo-Energy Geo-Resour 7 (3), 61–24. doi:10.1007/s40948-021-00255-4

CrossRef Full Text | Google Scholar

Genis, M., Akcin, H., Aydan, O., and Bacak, G. (2018). Investigation of possible causes of sinkhole incident at the Zonguldak Coal Basin, Turkey. Geomechanics and Engineering 16 (2), 177–185. doi:10.12989/gae.2018.16.2.177

CrossRef Full Text | Google Scholar

He, X., Zhao, Y. X., Zhang, C., and Han, P. H. (2020). A model to estimate the height of the water-conducting fracture zone for longwall panels in Western China. Mine Water Environ 39 (4), 823–838. doi:10.1007/s10230-020-00726-2

CrossRef Full Text | Google Scholar

Jaouhar, E. M., Li, L., and Aubertin, M. (2018). An analytical solution for estimating the stresses in vertical backfilled stopes based on a circular arc distribution. Geomechanics and Engineering 15 (3), 889–898. doi:10.12989/gae.2018.15.3.889

CrossRef Full Text | Google Scholar

Jiang, Y., Xu, S., and Hu, Y. (2008). Structural Mechanics. Beijing, China: Science Press.

Google Scholar

Kong, D. Z., Li, Q., Wu, G. Y., and Song, G. F. (2021). Characteristics and control technology of face-end roof leaks subjected to repeated mining in close-distance coal seams. Bulletin of Engineering Geology and the Environment 80 (11), 8363–8383. doi:10.1007/s10064-021-02438-5

CrossRef Full Text | Google Scholar

Kong, X. X., Liu, Q. S., Zhang, Q. B., Wu, Y. X., and Zhao, J. (2018). A method to estimate the pressure arch formation above underground excavation in rock mass. Tunnelling and Underground Space Technology 71, 382–390. doi:10.1016/j.tust.2017.09.004

CrossRef Full Text | Google Scholar

Kratzsch, H. (1983). Mining Subsidence Engineering. New York, NY, USA: Springer-Verlag Berlin Heidelberg.

Google Scholar

Li, A., Ma, Q., Lian, Y. Q., Ma, L., Mu, Q., and Chen, J. B. (2020). Numerical simulation and experimental study on floor failure mechanism of typical working face in thick coal seam in Chenghe mining area of Weibei, China. Environmental Earth Sciences 79 (5), 118–122. doi:10.1007/s12665-020-8839-2

CrossRef Full Text | Google Scholar

Li, H. M., Li, H. G., Song, G. J., and Wang, K. L. (2016). Physical and mechanical properties of the coal-bearing strata rock in Shen dong coal field. Journal of China Coal Society 41 (11), 2661–2671. doi:10.13225/j.cnki.jccs.2016.1218

CrossRef Full Text | Google Scholar

Mark, C., Agioutantis, Z., and Agioutantis, Z, (2019). Analysis of coal pillar stability (ACPS): A new generation of pillar design software. International Journal of Mining Science and Technology 29 (1), 87–91. doi:10.1016/j.ijmst.2018.11.007

CrossRef Full Text | Google Scholar

Ning, J. G., Wang, J., Tan, Y. L., Zhang, L. S., and Bu, T. T. (2017). In situ investigations into mining-induced overburden failures in close multiple-seam longwall mining: A case study. Geomechanics and Engineering 12 (4), 657–673. doi:10.12989/gae.2017.12.4.657

CrossRef Full Text | Google Scholar

Oge, I. F. (2020). Field evaluation of flexible support system with radial gap (FSRG) under a squeezing rock condition in a coal mine development. Geomech. Geophys. Geo-Energy Geo-Resour 6 (3), 52–20. doi:10.1007/s40948-020-00175-9

CrossRef Full Text | Google Scholar

Pardo, G. S., and Saez, E. (2014). Experimental and numerical study of arching soil effect in coarse sand. Computers and Geotechnics 57, 75–84. doi:10.1016/j.compgeo.2014.01.005

CrossRef Full Text | Google Scholar

Poulsen, B. A. (2010). Coal pillar load calculation by pressure arch theory and near field extraction ratio. International Journal of Rock Mechanics and Mining Sciences 47 (7), 1158–1165. doi:10.1016/j.ijrmms.2010.06.011

CrossRef Full Text | Google Scholar

Rezaei, M., Hossaini, M. F., and Majdi, A. (2015). Determination of longwall mining-induced stress using the strain energy method. Rock Mechanics and Rock Engineering 48 (6), 2421–2433. doi:10.1007/s00603-014-0704-8

CrossRef Full Text | Google Scholar

Shabanimashcool, M., and Li, C. C. (2015). Analytical approaches for studying the stability of laminated roof strata. International Journal of Rock Mechanics and Mining Sciences 79, 99–108. doi:10.1016/j.ijrmms.2015.06.007

CrossRef Full Text | Google Scholar

Sun, L. H., Ji, H. G., and Yang, B. S. (2019). Physical and mechanical characteristic of rocks with weakly cemented strata in Western representative mining area. Journal of China Coal Society 44 (3), 866–874. doi:10.13225/j.cnki.jccs.2018.6039

CrossRef Full Text | Google Scholar

Wang, F., Xu, J. L., and Xie, J. L. (2019b). Effects of arch structure in unconsolidated layers on fracture and failure of overlying strata. International Journal of Rock Mechanics and Mining Sciences 114, 141–152. doi:10.1016/j.ijrmms.2018.12.016

CrossRef Full Text | Google Scholar

Wang, S. R., Wu, X. G., Zhao, Y. H., Hagan, P., and Cao, C. (2019a). Evolution characteristics of composite pressure-arch in thin bedrock of overlying strata during shallow coal mining. International Journal of Applied Mechanics 11 (3), 1950030. doi:10.1142/S1758825119500303

CrossRef Full Text | Google Scholar

Wen, Z. J., Rinne, M., Song, Z., Han, Z. Z., and Wen, J. H. (2015). Research on modelling of spatial dynamic structural mechanics and spatio-temporal evolution of coal mine stopes. Teh. Vjesn 22 (3), 607–613. doi:10.17559/TV-20150427175109

CrossRef Full Text | Google Scholar

Xia, B. W., Zhang, X., Yu, B., and Jia, J. L. (2018). Weakening effects of hydraulic fracture in hard roof under the influence of stress arch. International Journal of Mining Science and Technology 28 (6), 951–958. doi:10.1016/j.ijmst.2017.12.024

CrossRef Full Text | Google Scholar

Xie, H. P., Gao, F., Ju, Y., Gao, M. Z., Zhang, R., and Gao, Y. N., (2015). Quantitative definition and investigation of deep mining. Journal of China Coal Society 40 (1), 1–10.

Google Scholar

Yang, W. B., Jiang, Y. J., Gu, X. X., Wang, Z. X., Shang, Y. C., and Zeng, W. H. (2021). Deformation mechanism and mechanical behavior of tunnel within contact zone: A case study. Bulletin of Engineering Geology and the Environment 80 (7), 5657–5673. doi:10.1007/s10064-021-02255-w

CrossRef Full Text | Google Scholar

Yavuz, H. (2004). An estimation method for cover pressure re-establishment distance and pressure distribution in the goaf of longwall coal mines. International Journal of Rock Mechanics and Mining Sciences 41 (2), 193–205. doi:10.1016/S1365-1609(03)00082-0

CrossRef Full Text | Google Scholar

Zhang, G. J., Guo, G. L., Lv, Y. N., and Gong, Y. Q. (2020). Study on the strata movement rule of the ultrathick and weak cementation overburden in deep mining by similar material simulation: A case study in China. Mathematical Problems in Engineering 2020, 1–21. doi:10.1155/2020/7356740

CrossRef Full Text | Google Scholar

Zhang, J. M., Li, Q. S., Zhang, Y. Z., Cao, G., and Wang, X. Z. (2019). Definition of deep coal mining and response analysis. Journal of China Coal Society 44 (5), 1314–1325. doi:10.13225/j.cnki.jccs.2019.6018

CrossRef Full Text | Google Scholar

Zhang, J., Zhang, Y. S., Du, W. Z., Wang, H. W., and Serati, M. (2021). An analytical approach to estimate the mechanical state of roof strata in underground longwall mining. Geomechanics and Engineering 27 (1), 55–62. doi:10.12989/gae.2021.27.1.055

CrossRef Full Text | Google Scholar

Zhao, Y. H. (2018). Research On Evolution Characteristics And Instability Mechanism Of Composite Pressure Arch Of Overlying Strata During Shallow Coal Mining. Jiaozuo, China: Ph.D. Dissertation, Henan Polytechnic University.

Zhao, Y. H., Yu, J., Zhou, C. H., Zhao, K., and Xiao, H. G. (2021). Characterization of pressure arching effect of arch shell surrounding rock considering deviation of principal stress axis. Chinese Journal of Geotechnical Engineering 43 (10), 1842–1850.

Google Scholar

Zhao, Y. X., and Liu, B. (2021). Deformation field and acoustic emission characteristics of weakly cemented rock under Brazilian splitting test. Natural Resources Research 30 (2), 1925–1939. doi:10.1007/s11053-020-09809-x

CrossRef Full Text | Google Scholar

Zou, X. Z. (1989). New explanation on the hypothesis of pressure arch. Ground Press. Roof Control 1989 (01), 67–68+93.

Google Scholar