Study on the correlation between river network patterns and topography in the Haihe River basin

In recent decades, the river network patterns (RNPs) in China’s Haihe River basin have changed dramatically, and the topology of the river network has become increasingly complex. It is important to quantitatively study the correlation between river network patterns and topography (CRNPT) and the changes in the correlation. In this paper, the Haihe River basin was spatially gridded (4 km × 4 km), and different geomorphological areas were extracted for a multiarea study. We selected topographic and river network indicators and proposed new indicators to characterize regional topographic ‘stressfulness’ and then used redundancy analysis for correlation studies. The results showed that the variance of RNP explained by topography was 53.39%. The combined contribution of the topographic wetness index (TWI) and topographic wetness stress index (TSI) ranged from 35.66% to 78.29% in multiple areas, and the TSI showed stronger explanatory power. The regional effect of the CRNPT was significant, with mountains and transition areas having higher effects than plain areas. Compared to the natural river network, the CRNPT of the current river network was significantly lower. Among the RNP indicators, the artificial channel proportion ($P_{ac}$) had the highest proportion of variance, and the CRNPT was strongly influenced by artificial channels. Artificial channels changed the consistency of topography with the RNP and reduced the topographic interpretation of the RNP, which may weaken the stability and hydrological connectivity of the river network. The variation in interpretation was related to the distribution of artificial channels, which showed a logarithmic function relationship between them.

1 Introduction

Rivers are multiscale systems that interact with climate, tectonics, erosion, sediment transfer patterns, and human activity (Carbonneau et al., 2012; Scorpio et al., 2018; Sarker et al., 2019; Walley et al., 2020), and their network branching models have a complicated topology (Barabási and Albert, 1999; Albert and Barabási, 2002). The river network is a fundamental feature of the basin and is a channel for horizontal effects (Heasley et al., 2019), influencing hydrological processes throughout the basin and regulating the biological population diversity and the spatial distribution of channel and riparian physical attributes (Benda et al., 2004). The river network is not a random topology (Perron et al., 2012), and its spatial pattern is determined by the physical properties of the catchment (Zanardo et al., 2013). It is critical to study the structural, geometric, and topological properties of the river network as well as to quantify the physical factors that shape differential river network patterns (RNPs) to better understand the dynamics of the river network in changing environments (Biswal and Marani, 2010; Shelef and Hilley, 2014; Abed Elmdoust et al., 2016).

In the landscape pattern of a catchment, the evolution of the topography and changes in the river network are strongly linked (Willett et al., 2014). Topography determines the path and residence time of water flow (Curie et al., 2007), which greatly influences the spatial pattern of the river network. Therefore, exploring the intrinsic links between river networks and topography is important for predicting the topological development of river networks and their stability, as well as for watershed planning. Chang. (1979) divided rivers into straight, meandering, and braided patterns and found that the channel pattern is straight when the channel slope is equal to the valley slope. However, when multiple channel slopes exist on a uniform valley slope, the river is sinuous. Alabyan and Chalov. (1998) analysed the stream power defined by river slope and discharge and noted that it is one of the most important factors in river development. The greater the stream power is, the stronger the branching tendency. Niemann et al. (2001) confirmed the importance of elevation in river network changes using river network growth models. Changes in elevation cause significant changes in the physical properties of the river network. In areas with gentle topography, the boundaries and water flow are less constrained, resulting in rivers that meander and twist (Piégay et al., 2005). Chen et al. (2019) subdivided China’s Yangtze and Yellow River basins into 60 subbasins. The study found that slope had a significant positive relationship with the river network density, bifurcation ratio, and side branch ratio. Based on a study of 100 small watersheds in the United States, Sangireddy et al. (2016) found a strong positive correlation between river network density and topographic relief in wet environments and a weaker correlation in arid and semiarid environments. Zhao et al. (2016) discovered that tectonic uplift controls gully (channel) density, which is correlated with overall slope and vegetation cover, and that longitudinal slope and elevation integrals of the river network were correlated with gully density on China’s Loess Plateau. Li et al. (2022) used correlation analysis, partial correlation analysis and multiple linear regression to analyse the quantitative relationships between topographic and river network parameters in the 18 subbasins of the Haihe River basin. The results showed significant correlations but strong spatial heterogeneity. The influence of topography on the formation and development of the river network varies from region to region and has obvious regional effects (Finnegan et al., 2005; Piégay et al., 2005; Tong et al., 2020).

These studies are mostly qualitative or small-scale, with no clear quantification of the correlation between river network patterns and topography (CRNPT). Furthermore, hydrological and geomorphological studies on river networks have long been based on networks with specific assumptions, such as that water always flows in the direction of the steepest downslope and that there is no ring structure in the network (Ni J R, 1998; Chen et al., 2019; Sarker et al., 2019). Most of these river networks are created using DEMs and are similar to natural dendritic river networks in terms of morphological features and topology (Vörösmarty et al., 2000; Cohen et al., 2018). They follow Horton’s law (Horton, 1945) and the law of optimal channel networks (Rodríguez Iturbe et al., 1992; Abed Elmdoust et al., 2016) with the lowest total energy. However, there are significant differences between generated river networks and the actual “natural + artificial” river networks, particularly in basins with extensive floodplains, where the actual river network is a complex network structure subjected to multiple influences rather than a natural dendritic structure. Thus, the quantitative relationship between large watershed topography and actual network structure is still difficult to describe clearly.

The Haihe River basin is one of China’s seven major river basins, and it has a significant role in politics, economy, and agriculture and a highly complicated river network. In recent years, China proposed and included in the 14th Five-Year Plan the “National Water Network Major Project,” with the goal of speeding the building of the main skeleton and artery of the national river network. Watershed management based on river networks necessitates a greater scientific understanding of river morphology and function at multiple scales, as well as enhanced interdisciplinary studies of watershed topography, geomorphology, and hydrology (Heasley et al., 2019). This interdisciplinary approach is critical for understanding the complex relationships between factors in river systems (Dollar et al., 2007). In this paper, we gridded the Haihe River basin and extracted several topographic and geomorphic areas. Then, we used redundancy analysis to investigate the relationship between the actual “natural + artificial” river network and topography and to answer three important questions based on a thorough understanding of the RNP: 1) To what extent does topography explain the spatial distribution of the actual river network patterns? Do different areas of the basin behave in the same way? 2) Which topographic features have the most influence on river network patterns, and how can we understand the coupling effect between them? 3) Is the relationship between RNP and topography stable, and does the addition of artificial channels affect their consistency (i.e., how does the CRNPT change)? The findings of this paper can provide a basis for the study of the consistency of river networks and topography in large watersheds around the world.

2 Materials and methods

2.1 Study flow

The aim of this paper was to quantify the correlation between RNP and topography and to compare the difference in the CRNPT between the current river network and the natural river network. Figure 1 shows the flow chart of the research in this paper. This paper used the Haihe River basin in China as the study area, and its main flow is as follows: 1) divide the spatial grid as a spatial sample; 2) determine the analysis area for comparative study; 3) select and calculate characteristic indicators, including topographical indicators and river network indicators; 4) conduct collinearity analysis on the characteristic indicators and remove those that are collinear; 5) use topographical indicators as explanatory variables and river network indicators as response variables for redundancy analysis; and 6) analyse the CRNPT of the current river network and the natural river network and discuss the differences in the results of the current river network and their reasons combined with the findings of previous studies.

FIGURE 1

FIGURE 1. Study flow chart.

2.2 Study area

The Haihe River basin, with a basin area of 320,600 km², is in the eastern part of China’s Bohai Sea region. It has a dense population and many large and medium-sized cities, with the Taihang Mountains and Yanshan Mountains in the upper reaches and the North China Plain, an important grain-producing region, in the lower reaches. The Haihe River basin is fan-shaped, with distinct mountain and plain boundaries and a trend of contraction from upstream to downstream. The upstream mountain area is rugged, while the downstream plain is gentle, and the topography and geomorphology are distributed spatially in a remarkable way. The Haihe River basin belongs to the temperate East Asian monsoon climate zone, with an average annual temperature of 0–14.5°C and an average annual relative humidity of 50%–70%. The average annual precipitation in the basin is 535 mm, which is representative of a semi-humid and semiarid zone. The average annual temperature and average annual precipitation basically decrease from southeast to northwest, but there are two extreme centres of annual precipitation in front of the windward slopes in the western and northeastern mountains. The density of the river network is 0.51, the natural length is 85,638.02 km, and the artificial length is 75,267.49 km, which indicates the complexity of the river network structure. Artificial channels are primarily constructed to serve flood control, irrigation, and water supply functions and have become an important component of the river network in the basin, causing drastic changes in the topology and spatial characteristics of the original natural river network, which has a dense mesh structure. The river network is very well connected, particularly in the vast downstream plain areas. Figure 2 provides a schematic diagram of the Haihe River basin’s river network.

FIGURE 2

FIGURE 2. Schematic diagram of the river network in the Haihe River basin.

2.3 Topography and river data

The development of topographic data and remote sensing image data has aided in the quantification of structural and morphological characteristics of river networks (Benstead and Leigh, 2012), forming the foundation for the CRNPT study. The river network data in this paper were obtained from the National Catalogue Service for Geographic Information (https://www.webmap.cn/main.do?method=index). These data were formed by actual surveying and mapping and describe the actual river network in the Haihe River basin. The DEM and slope data were from the Geospatial Data Cloud (https://www.gscloud.cn/), and the climate and vegetation data were from the Resource and Environment Science and Data Center (https://www.resdc.cn/Default.aspx).

2.4 Methods

2.4.1 Topography and river network indicators

Many metrics, such as the Horton ratio (Horton, 1945), river network density (Horton, 1932; Abrahams, 1984), branching angle (Devauchelle et al., 2012), width function (Leopold, 1971), or ranking the degree of river branching by hierarchical methods such as Horton, Strahler, and others (Horton, 1945; Strahler, 1952; Tokunaga, 1984), can be used to characterize river network geometry and topology. However, in the Haihe River basin, where there are many artificial channels, the river network has very different characteristics than the natural network. Because the natural dendritic structure is not satisfied, the flow sequence in the reaches cannot be determined, and calculating the Horton ratio, branching angle, and other indicators characterizing the natural network is difficult. Finally, indicators such as network density ($D_r$), fractal dimension ($D_n$), junctions ($N_j$), and artificial channel proportion ($P_{ac}$) were chosen to characterize the river network. The analysis of RNP not only focuses on the network structure but also includes the network composition, which can more comprehensively reflect the characteristics of the river network and be integrated with basin management practice.

River network density is expressed as the ratio of total river length to total watershed area. River network density is a characteristic of the spatial distribution of rivers and can reflect the density of regional water flow channels. It is calculated by the following formula (Horton, 1932):

${\mathit{D}}_{\mathit{r}}=\frac{{\mathit{L}}_{\mathit{i}}}{\mathit{A}}(1)$

where $D_r$ is the network density (km/km²); $L_i$ is the length of the river within grid i (km); and $A$ is the area of the grid (km²).

Box dimension is the most basic and widely used characterization indicator of fractal dimension, and it can be used to study the scalar properties of complex structures describing river morphology and processes (Mandelbrot, 1982). Additionally, the box dimension of a river system can reflect the developmental stage of river erosion as follows (Hong, 1996): 1) a river is in the early (young) stage if the box dimension is less than 1.6; 2) a river is in the middle (mature) stage if the box dimension value is between 1.6 and 1.89; and 3) a river is in the late (old) stage if the box dimension value is between 1.89 and 2.0.

${\mathit{D}}_{\mathit{n}}=-\underset{\mathit{r}\to \mathbf{0}}{\mathit{lim}}\frac{\mathit{lg}{\mathit{N}}_{\left(\mathit{r}\right)}}{\mathit{l}\mathit{g}\mathit{r}}(2)$

where $D_n$ is the box dimension; $N_{\left(r\right)}$ is the number of boxes with rivers; and $r$ is the box side length (m). The box size should reflect the planform of the river, and its side length is determined by the degree of curvature of the river in the study area, taking multiple values from small to large (Mandelbrot, 1982). The calculation workload (total number of boxes) should also be taken into account. Finally, we used r values of 400 m, 500 m, 800 m, 1,000 and 2000 m based on the density and curvature of the rivers in the Haihe River basin.

Junctions are the number of intersections of the regional river network that can be obtained through spatial analysis and statistical calculation. Junctions characterize the degree of physical connectivity of regional rivers. The artificial channel proportion is the ratio of the length of the artificial channel to the total length of the river, and it indicates the composition structure of the network. The proportion of artificial channels can characterize the extent to which the river network has been modified and rebuilt by humans. The higher the human activity in the watershed is, the higher the artificial channel proportion. The calculation formula is as follows:

${\mathit{P}}_{\mathit{a}\mathit{c}}=\frac{{\mathit{L}}_{\mathit{r},\mathit{i}}}{{\mathit{L}}_{\mathit{i}}}(3)$

where $P_{ac}$ is the artificial channel proportion; $L_i$ is the total length of the river in grid i (km); and $L_{r,i}$ is the length of the artificial channel in grid i (km).

Not all topographic and geomorphological indicators were correlated with the RNP, so we chose some representative indicators based on the characteristics of the Haihe River basin, including elevation, slope, relief, topographic wetness index (TWI), elevation stress index (ESI), slope stress index (SSI), relief stress index (RSI), topographic wetness stress index (TSI), and farmland area (Farmland). Furthermore, the precipitation and moisture index (IM) were chosen to analyse the impact of climatic factors on the RNP. The climatic factor was not the focus of this paper, and it was included to assist in validating the results of the topography analysis (i.e., whether the results of climate and topography were consistent). Therefore, only two climatic indicators were selected. These indicators were chosen because they had a significant impact on the topology of the river network or the hydrological processes in the basin, as evidenced by many studies (Seibert and McGlynn, 2006; Zanardo et al., 2013; Kleidon, 2016; Zhao et al., 2016; Chen et al., 2019; Tong et al., 2020). Among them, elevation (m), slope (°), relief (m), Farmland (km²), and precipitation (mm) were in standard units, and the TWI, ESI, SSI, RSI, TSI, and IM were dimensionless indicators. In this paper, the topographic indicators were extracted and calculated using ArcGIS 10.3.

The topographic wetness index is a function of the regional catchment area and slope. It can characterize the effect of regional topography on runoff flow and storage and reflect spatially produced flow characteristics. The higher the value of the TWI is, the larger the flow-producing area and storage capacity are. It is calculated as follows (Beven and Kirkby, 1979):

$\mathit{T}\mathit{W}\mathit{I}=\mathbf{ln}\left({\mathit{\alpha }}_{\mathit{s}}/\mathbf{tan}\mathit{\beta }\right)(4)$

where ${\alpha }_s$ is the upstream confluence area per unit contour length (km²) and $\mathit{\beta }$ is the slope (rad).

The elevation stress index is an index proposed based on existing research. Riparian features and topographic constraints influence the range of channel stability (Piégay et al., 2005), and Tong et al. (2020) demonstrated that topography influences the spatial variations in channel width and slope, and nearby topographic constraints on river boundaries and water flow can determine the degree of channel curvature, which is well reflected by free-flowing meandering and braided channels on floodplains. The topography of the hillsides on both sides of the river therefore had a large limiting effect on the morphology and structure of the river, which could be reflected by the difference between the hillside elevation and the riverbed elevation. To reflect the limiting effect of topography, we defined the stress (or limiting) index by calculating the ratio of the terrain index without river pixels to the geomorphology index with river pixels based on the raster pixels. The higher the stress index is, the greater the limiting effects of the slope on the morphology and structure of the river are. The SSI, RSI, and TSI are all calculated in the same way:

$\mathit{S}\mathit{I}=\frac{{\mathit{T}}_{\mathit{n}}}{{\mathit{T}}_{\mathit{h}}}(5)$

where $SI$ is the stress index; $T_n$ is the topographic index value without river pixels; and $T_h$ is the topographic index value of the river pixels.

Explanatory factors may have serious collinearity issues, thus increasing parameter variance estimation and causing large errors in the analysis results (Greene, 2003). To assess the degree of collinearity, the variance inflation factor (VIF) was used (O Brien, 2007). When VIF>10, it is widely assumed that there is a serious collinearity problem (Hair et al., 1992; Kennedy, 2008), and the indicators were selected again following this standard (Table 1). Figure 3 shows the spatial distribution of the final selected network and topographic indicators.

TABLE 1

TABLE 1. VIF values of explanatory variables.

FIGURE 3

FIGURE 3. Spatial distribution of network and topographic indicators in the Haihe River basin.

2.4.2 Spatial grids and areas

The Haihe River basin is a large area with a dense network of rivers. According to the topographic characteristics and RNP of the basin, and considering the calculation efficiency, it can be divided into 19,826 square grids with a spatial resolution of 4 km × 4 km. To investigate the local CRNPT as well as the differences, the Haihe River basin was divided into mountain, transition, and plain areas based on topographic distribution, and the windward and leeward sides of the Taihang Mountains and Yanshan Mountains were extracted as different spatial areas (Figure 4). Table 2 displays the statistical data for each spatial area.

FIGURE 4

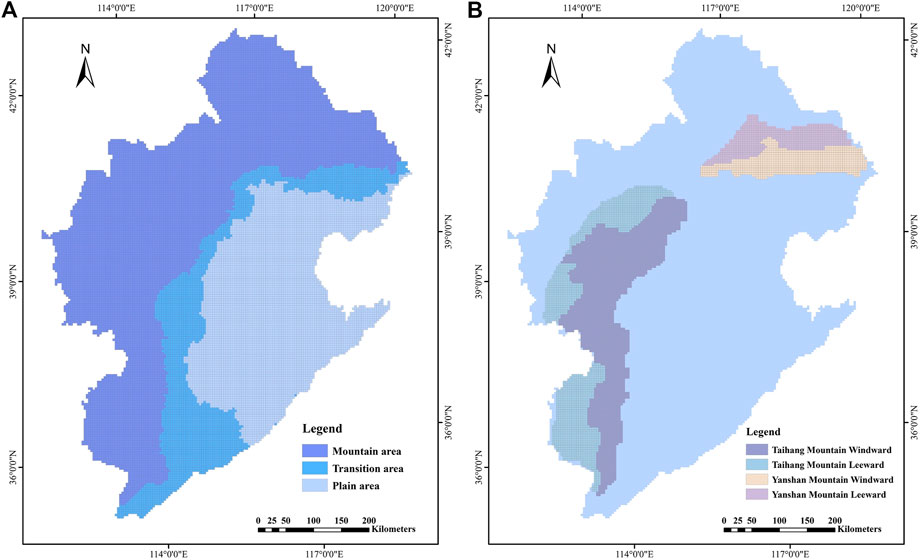
FIGURE 4. Spatial analysis areas of the Haihe River basin. The basin is divided into 7 analysis areas in addition to itself. (A) shows the mountain area, transition area and plain area. (B) shows the windward and leeward sides of the Taihang Mountains and the windward and leeward sides of the Yanshan Mountains.

TABLE 2

TABLE 2. The statistical data of each spatial area.

2.4.3 Redundancy analysis

Multivariate statistical analysis is a powerful tool for investigating the interactions between hydrological elements and natural and human factors (Wang et al., 2017; Rakotondrabe et al., 2018). Redundancy analysis (RDA) (Rao, 1964) is a widely used form of asymmetric canonical analysis (Legendre et al., 2011). Redundancy analysis (RDA) examines the causes of variation in the response variable by explicitly modelling it as a function of the explanatory variables (Israels, 1984). Its goal is to determine the rate at which a given set of explanatory variables explains the variation (or dispersion) in the response variable. The greatest advantage of RDA is that this statistical method can independently maintain the contribution of each explanatory variable for each dependent variable without performing a simple analysis for the explanatory variable vector and by converting some of the variables into virtual complex variables. RDA has already been successfully implemented and is commonly used in geomorphic studies (Zhao et al., 2015), ecological studies (Wagner, 2004), hydrobiological studies (Obolewski and Strzelczak, 2009), and many others. The main steps of RDA are as follows (Makarenkov and Legendre, 1999; Mazouz et al., 2013):

I) For each response variable Y, a multiple regression on all explanatory variables X is performed.

$\widehat{\mathit{Y}}=\mathit{X}\mathit{B}=\mathit{X}{\left[{\mathit{X}}^{\prime }\mathit{X}\right]}^{-\mathbf{1}}{\mathit{X}}^{\prime }\mathit{Y}(6)$

II) Calculate the covariance matrix S of the fitted value matrix $\widehat{Y}$.

$\mathit{S}=\left[\mathbf{1}/\left(\mathit{n}-\mathbf{1}\right)\right]{\widehat{\mathit{Y}}}^{\prime }\widehat{\mathit{Y}}=\left[\mathbf{1}/\left(\mathit{n}-\mathbf{1}\right)\right]\mathit{Y}\prime \mathit{X}{\left[{\mathit{X}}^{\prime }\mathit{X}\right]}^{-\mathbf{1}}\mathit{X}\prime \mathit{X}{\left[{\mathit{X}}^{\prime }\mathit{X}\right]}^{-\mathbf{1}}\mathit{X}\prime \mathit{Y}(7)$

III) Eigenvalue and eigenvector decomposition is performed on the covariance matrix S.

$\left(\mathit{S}-{\mathit{\lambda }}_{\mathit{k}}\mathit{I}\right){\mathit{u}}_{\mathit{k}}=\mathbf{0}(8)$

where ${\lambda }_k$ is the regular eigenvalue and $u_k$ is the corresponding regular feature vector.

IV) The ranking of the samples (rows of Y) in the dependent variable space is obtained directly from the central matrix Y. The principal components are calculated using the standard equations.

${\mathit{O}\mathit{r}\mathit{d}}_{{\left(\mathbf{Y}\mathbf{s}\mathbf{p}\mathbf{a}\mathbf{c}\mathbf{e}\right)}_{\mathit{k}}}=\mathit{Y}{\mathit{u}}_{\mathit{k}}(9)$

Similarly, the ranking of the samples in the space of explanatory variables is obtained from the central matrix X.

${\mathit{O}\mathit{r}\mathit{d}}_{{\left(\mathbf{X}\mathbf{s}\mathbf{p}\mathbf{a}\mathbf{c}\mathbf{e}\right)}_{\mathit{k}}}=\widehat{\mathit{Y}}{\mathit{u}}_{\mathit{k}}\mathit{X}\mathit{B}{\mathit{u}}_{\mathit{k}}(10)$

V) The contributions of the explanatory variables to the various canonical axes are estimated by calculating the linear correlations between the variables X and the ranking axes using Eq. 9 in Y-space and Eq. 10 in X-space.

In this paper, river network indicators were used as response variables, and topographic features were used as explanatory variables for redundancy analysis. Furthermore, the precipitation and moisture index were used as explanatory variables to compare the correlation between the RNP and climatic factors.

3 Results and discussion

3.1 Spatial distribution of river network and topography

Figure 3 shows the spatial distribution of the RNP, topography, and climate indicators, while Figure 5 depicts the box plots for each indicator in various spatial areas. For the mountain-transition-plain areas, the mean values of $D_r$ were 0.42, 0.47, and 0.73, those of $D_n$ were 1.19, 1.22, and 1.35, those of $N_j$ were 0.49, 0.91, and those of 2.84 and $P_{ac}$ are 0.00, 0.45, and 0.72, respectively. The network indicator values increased gradually from the mountains to the plains. Under the influence of human activity, the river network in the plain area had a high density and many artificial channels. The topology of the river network in the plain area was complex, with a high degree of river development and physical connectivity. The greatest differences in spatial distribution were found for $P_{ac}$, (Q1, Q3) are (0, 0), (0, 0.973), and (0.545, 1.0); $D_r$ are (0.26, 0.59), (0.28, 0.64), and (0.46, 0.98); $D_n$ are (1.05, 1.33), (1.08, 1.35), and (1.20, 1.50); and $N_j$ are (0.0, 1.0), (0.0, 2.0), and (1.0, 5.0). The (Q1, Q3) interval was small in the mountain area, as were the spatial differences in the river network. The spatial differences in river network topology were greater in the plains than in the mountains, and the regional river network varied more dramatically. Comparing the windward and leeward sides of Taihang and Yanshan, the mean values of $D_r$ were 0.41, 0.46, 0.40, and 0.40, those of $D_n$ were 1.18, 1.22, 1.17, and 1.17, those of $N_j$ were 0.49, 0.90, 0.44, and 0.49, and those of $P_{ac}$ were 0.0, 0.02, 0.0, and 0.0; additionally, the mean variances of the indicators were 0.028, 0.037, 0.026, and 0.029, respectively. The spatial differences in the river network leeward of Taihang were significant, while the differences in the other three areas were minor.

FIGURE 5

FIGURE 5. Box plots of network indicators, topographic indicators, and climate indicators in various areas.

Along the mountain-transition-plain gradient, the mean elevation values were 1,016.10, 91.57, and 17.63, respectively. The ESI values were 1.11, 1.07, and 1.01; the SSI values were 1.41, 1.10, and 0.93; and the RSI values were 1.44, 1.19, and 0.97. The upstream mountain area was steep, and the topography had a greater restrictive effect on the river. The topography in the plain area was gentle, with the lowest restrictive effect. The topographic characteristics of the transition area were between those of the two areas. The TWIs were 7.39, 9.60, and 10.60, respectively, with the plain area having the largest runoff production area and storage capacity. The TSI values were 0.73, 0.88, and 0.99, with lower values indicating a greater restriction effect and the plain area having the lowest restriction effect. The precipitation was 528.34, 551.39, and 552.38, and the IM was −13.13, −15.11, and −18.91. The plain area received 22.04 mm more annual precipitation than the mountain area, and the three areas of IM were (−18.79, −7.36), (−20.48, −9.84), and (−26.43, −16.16), with little variation in the distribution of climatic factors. The TWIs were (6.79, 8.05), (8.77, 10.50), and (10.39, 10.81), respectively, and the stress indices had similar distribution characteristics. The distribution intervals of the topographic indices were large and spatially varied in the mountain area, while they were small in the plain area. The mean elevations of Taihang windward and leeward were 1,010.03 and 1,123.16; those of the TWI were 6.90 and 8.06; those of the ESI were 1.19 and 1.05; those of the SSI were 1.46 and 1.28; those of the RSI were 1.51 and 1.30; those of the TSI were 0.68 and 0.79; and those of Farmland were 2.42 and 7.83, respectively. The windward area had a low capability for runoff storage, and the topography had a significant constraining effect on the channel. The windward side had high rainfall and a wet climate, while the leeward side had low rainfall and a dry climate. The mean elevations of Yanshan windward and leeward were 411.86 and 546.27; those of the TWI were 7.10 and 7.10; those of the ESI were 1.38 and 1.26; those of the SSI were 1.52 and 1.57; those of the RSI were 1.58 and 1.63; those of the TSI were 0.67 and 0.66; and those of Farmland were 2.42 and 3.18. Thus, the topography was slightly different. The windward side had high rainfall and a wet climate, and the leeward side had low rainfall and an arid climate.

3.2 Correlation analysis

The river network indicators had a negative correlation with the elevation, ESI, SSI, and RSI, a positive correlation with the TWI, TSI, and farmland, and an unstable correlation with the precipitation and IM (Figure 6). The correlation coefficients of $D_r,D_n,and{N}_j$ with elevation, TWI, ESI, SSI, RSI, TSI, and Farmland were between 0.1 and 0.39, indicating weak correlations. The coefficients of $P_{ac}$ with the TWI and TSI were greater than 0.7, indicating strong correlations. $P_{ac}$ had a moderate correlation with elevation and farmland and a weak correlation with the ESI, SSI, RSI, and IM. The mean coefficient between $P_{ac}$ and environmental factors (including topography and climate) was 0.42, which was significantly higher than $D_r$ (0.25), $D_n$ (0.20), and $N_j$ (0.21). The intensity of human activity was influenced by topography, with more artificial channels in plain areas with gentle topography and fewer in mountainous areas. The distribution of artificial channels reflected the spatial nature of the topography. The TWI and TSI had correlation coefficients of 0.49 and 0.45 with network indicators, which were greater than those of elevation (−0.39), ESI (−0.22), SSI (−0.17), RSI (−0.18), and Farmland (0.38), indicating that regional runoff flow and storage capacity had a greater influence on the RNP.

FIGURE 6

FIGURE 6. Heatmap of Pearson’s correlation coefficient (* means significance test p < 0.05)

Correlations were weaker in the local area than in the whole basin. The $D_r$, $D_n$, $N_j$, and $P_{ac}$ correlation coefficients with environmental factors in mountain areas were 0.23, 0.17, 0.18, and 0.24, respectively. $D_r$, $D_n$, and $N_j$ were not correlated with environmental factors in the transition area, and the correlation coefficient between $P_{ac}$ and environmental factors was 0.31. The correlation between the river network and environmental factors was relatively weak in the plains. In the mountain area, topography played a greater role in influencing the RNP, and the correlation was higher than it was downstream. The correlation coefficients between network and environmental factors in Taihang were 0.17, 0.12, 0.13, and 0.19 for the windward side and 0.31, 0.24, 0.25, and 0.31 for the leeward side, with the leeward being higher than the windward. Climate had a greater influence on the leeward side of the Taihang than on the windward side. There were small differences in the correlation coefficients between network and environmental factors on both sides of Yanshan. The windward and leeward areas did not show consistency, with Taihang, showing greater differences in river network and topography, while the differences in Yanshan were not obvious (Figures 3, 5).

3.3 Redundancy analysis

Table 3 shows the results of the redundancy analysis, where the p values (>F) for the first two significant axes, RDA1 and RDA2, were both 0.001, indicating a significant correlation between the river network reflected by the two ranking axes and the topography. The variance explained by the topography on the network indicators was 53.39%. The elevation, TWI, and TSI contributed 21.46%, 25.45%, and 30.07%, respectively. The coefficients of the network ranking axis determine the contribution, and the explanatory variables in the redundancy analysis are based on the variance of the response variables. $P_{ac}$ had the highest variance (0.169), and the coefficient’s absolute value in the first ranking axis RDA1 (variance explained 52.68%) was 4.75 (Table 4), so the TSI, which had the highest correlation with $P_{ac}$ (0.73), was the indicator with the largest contribution. Artificial channels changed the natural network pattern, and $P_{ac}$ became the most interpretative network indicator, which also overshadowed the interpretation of other indicators. There was a negative correlation between elevation and the river network. The RNP in the plain area was severely affected by artificial channels because human activities were primarily concentrated in the gentle terrain area (Figure 2). The TWI and TSI were most strongly correlated with the RNP; the TWI reflected the regional stream power, and the TSI represented the corresponding physical restrictiveness. This is an important factor in determining the RNP (Chang, 1979; Alabyan and Chalov, 1998). The efficiency of kinetic power dissipation in the channel is reduced in areas with large catchment areas and small slopes, and the more energetic flow during a flood may remove its channel in locations where the restriction effect is weak, promoting the lateral development of the river network and the increasing density of the network. The human renovation of the river network for flood protection is also based on this phenomenon. The ESI, SSI, and RSI are indicators that characterize only topography compared to the TSI, which contains the definition of stream power. The SSI describes the limiting effect of slope but cannot define the water flow, and differences in values did not cause a strong response in the RNP (weak correlation). As a result, the impact of the ESI, SSI, and RSI on the river network was minor. People have been excavating diversion irrigation channels in areas with a high concentration of Farmland and are constantly changing the river network structure, which causes Farmland to be correlated with RNP. Table 5

TABLE 3

TABLE 3. Results of redundancy analysis of RNP and topography.

TABLE 4

TABLE 4. Variance and ranking axis coefficients of river network indicators.

TABLE 5

TABLE 5. Results of redundancy analysis of RNP and climatic factors.

The variance in the river network explained by topography was 28.25% in the mountain area, 30.13% in the transition area, and 9.59% in the plain area. The contribution rates of the TWI, TSI, and Farmland in mountain areas were 31.82%, 32.96%, and 18.05%, respectively. $P_{ac}$ had the largest coefficient in the ranking axis, so the TSI had the largest contribution rate. The river network and TSI distribution in the mountain area are depicted in Figure 7A. The artificial channels were spatially consistent with the distribution of high TSI values, and the alignment of artificial channels was always along the narrow area of high TSI values. In the transition area, $D_r$, $D_n$, and $N_j$ were not correlated with topography, and the variance explanation of the RNP mainly relied on $P_{ac}$. The correlation coefficient between the TSI and $P_{ac}$ was 0.64, and the contribution of the TSI was 69.20%, making the explanation rate of the transition area greater than that of the mountain and plain areas. Figure 7B shows the river network and TSI distribution in the transition area. The stream power constraint was large upstream of the transition area, and the river network was dominated by natural channels. As the constraint decreased downstream, the artificial channels increased, and the composition structure of the river network changed, which was consistent with the distribution of the TSI. In the plain area, the numerical interval of topography varied very little compared to the river network (Figure 5). The correlation coefficients between network indicators and topography were low, indicating that the consistency between the regional actual network and topography in the region was poor.

FIGURE 7

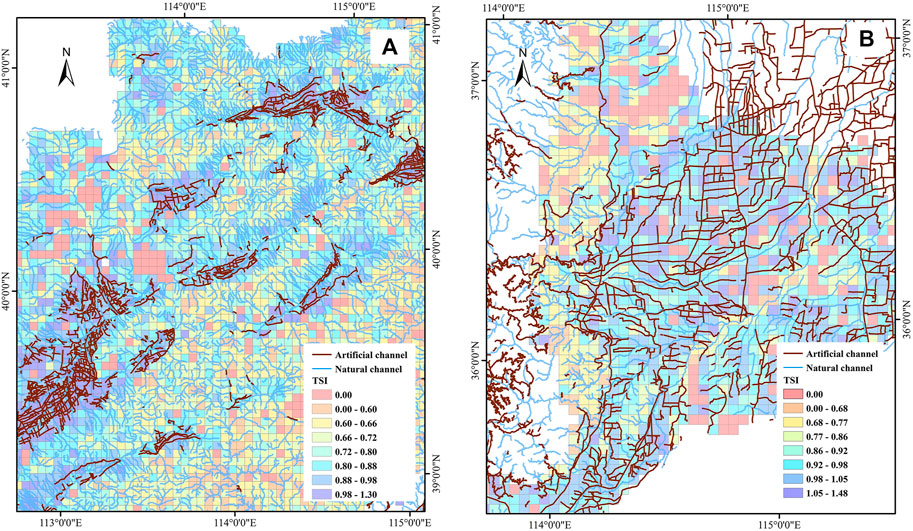
FIGURE 7. Local river network and TSI distribution, (A) is the mountain area, (B) is the transition area; a TSI value of 0 means no river in the grid.

The variances in the river network explained by topography were 21.18% and 33.48% for the windward and leeward sides of Taihang, respectively. The CRNPT was greater leeward than windward. The variances in the river network explained by topography were 16.79% and 13.21% for the windward and leeward sides of Yanshan, respectively. The CRNPT was greater windward than leeward, but the difference between the two was small. The river network and topography on the windward and leeward sides did not follow a consistent pattern, and the differences in correlation were dependent on the respective regional characteristics. Taihang is located inland, trends northeast to southwest and is influenced by the southeastern monsoon and geomorphological evolution, with significant topographic and climatic differences between the windward and leeward sides. The numerical interval of the river network and topographic indicators on the leeward side is large, and the influence of topography increases the spatial variation in the river network. On the windward side, the internal differentiation is reduced, resulting in a larger difference between the CRNPT on the windward and leeward sides. Yanshan has a smaller spatial extent and elevation than Taihang, as well as a different geographic location and mountain range orientation. The Yanshan is oriented east‒west and is close to the Bohai Sea, with similar overall topography and climate, so the CRNPT differences were minor.

The network variance explained by climatic factors in all areas did not exceed 15%, and the value was 10.62% for the whole basin, with the correlation coefficients for climatic and river network indicators being low. Existing research in other regions found that climate has a large influence on river network geometry and topology (Abrahams, 1984; Zanardo et al., 2013; Seybold et al., 2017; Ranjbar et al., 2018; Chen et al., 2019) and that there was a correlation between them, but no significant effect was found in the Haihe basin. The inconsistency is mainly due to the following factors. First, the choice of response variables and statistical analysis results were dependent on the variables analysed, and the correlation between different indicators varied significantly. This view is demonstrated in the study of Zanardo et al. (2013), where the indicators characterizing the network branching may be more strongly correlated with climate. Second, it may be related to the analysis area, where the climatic differences within the Haihe River basin are small, resulting in a weak correlation between the RNP and climatic factors. The difference in precipitation was only 22.04 mm, and the difference in IM was 5.77 on the mountain-plain gradient with a significant distribution of the RNP, whereas studies by Seybold et al. (2017), Ranjbar et al. (2018), and others were based on the entire U.S. or larger areas, with significant differences in climate. Finally, the distribution of artificial channels diminished the consistency between climate and river networks.

The above results show that there is a significant regional effect of topography on the interpretation of the RNP. On the one hand, there were differences in linear correlations between indicators in different areas; on the other hand, there were differences in the interpretation of each river network indicator. When multiple indicators characterized the RNP, those with large variance and more correlation with topography had a stronger role in determining the explanatory rate, as is the case with $P_{ac}$ in multiple areas. The variance of $P_{ac}$ was 0.169 (80% of the total variance), and the correlation coefficient was 0.49 with topography in the whole basin. The variation in the indicators decreased in the local area, and the correlations between river network indicators and topography were all weaker than those in the whole basin. The $P_{ac}$ variance and proportion in the mountain, transition, and plain areas were 0.056 (0.58), 0.167 (0.73), and 0.103 (0.66), respectively. Therefore, the explanatory rate was greater in the whole basin than in local areas. The $P_{ac}$ variance and its windward and leeward proportions in Taihang were 0.045 (0.39) and 0.086 (0.58), respectively, and the correlation coefficients were 0.21 and 0.32, respectively. The $P_{ac}$ variance and proportion of windward and leeward Yanshan were 0.02 (0.19) and 0.018 (0.15), respectively, and the correlation coefficients were 0.15 and 0.15, respectively. As a result, the explanation rate of the leeward side of Taihang was significantly higher than that of the windward side, and the difference between the windward and leeward sides of Yanshan was very small.

Although there was a regional effect within the basin and a low explanation rate in the local areas, the combined contributions of the TWI and TSI in each area were 55.52%, 64.78%, 78.29%, 35.66%, 59.68%, 62.12%, 52.12%, and 51.48%, respectively. In fact, the power dissipation of water flow, as described by the TWI, is also an important component of channel erosion forces (Thorne et al., 1997), and it has been demonstrated that a dense branching network is continuously and significantly influenced by erosion forces (Perron et al., 2012). Both the TSI and the riverbanks are important factors that interfere with channel flow movement, which can limit or facilitate the cutting of side slopes and encroachment on nearby channels, affecting the lateral stability of the channels. The TWI is also an important geomorphological indicator for characterizing hydrological properties, as it reflects the spatial distribution of soil moisture, surface saturation, and the runoff generation process (Beven and Kirkby, 1979). Hydrological similarity exists between two points of equal TWI, indicating an inherent relationship between the RNP and hydrology. Slope, as an intrinsic factor of the TWI and TSI, has a strong influence on the RNP and hydrological processes, and the river network develops more rapidly in areas with low slope and good hydrological conditions. The TWI and TSI are the most strongly correlated indicators with the river network and are consistent with the river network pattern in different areas.

3.4 Correlation between river network patterns and topography influence factor analysis

The RNP in the Haihe River basin has complex spatial characteristics, and the regional effect of the CRNPT was significant. However, the correlation between the topography and actual RNP was not very strong in multiple areas, which was inconsistent with some previous studies. Several studies have revealed the potential relationship between the RNP and topography, involving river networks of different characteristics in Asia, Africa, and the Americas. As mentioned in the introduction, significant relationships between numerous topographic factors (slope, relief, tectonic movement, etc.) and river network indicators (river network density, branching ratio, confluence angle, etc.) have been demonstrated by statistical, geomorphological, and remote sensing methods (Perron et al., 2012; Molin and Corti, 2015; Sangireddy et al., 2016; Chen et al., 2019; Beeson and McCoy, 2022; Li et al., 2022). Furthermore, results from small-scale studies in the laboratory have shown a correlation between water flow channels and topography (Darboux et al., 2002). The inconsistency in the conclusions may be due to differences in the scale of the study (grid size) and especially the type of river network data (actual river network was used in this study, natural river network was used in previous studies). There are numerous artificial channels in the Haihe River basin, whose combined length is close to that of natural rivers (0.88:1). The variance proportion of $P_{ac}$ in the whole basin, mountain area, transition area, plain area, and Taihang leeward area was greater than 50%, which was the most interpretative indicator of the river network. The correlation between the topography and actual RNP was strongly influenced by the distribution of artificial channels, but we did not have a clear understanding of their extent. Therefore, this paper continues to explore the response of the CRNPT to changes in the river network and clarifies the impact of artificial channels on the quantitative natural correlation between the RNP and topography. First, to compare the effect of artificial channels on the spatial distribution of the river network, Moran’s I was used to assess the spatial distribution of the RNP (Fortin, 1999; Haining and Haining, 2003; Wagner and Fortin, 2005). Moran’s I is a spatial autocorrelation measure that generally ranges from −1 (discrete) to 1 (clustering), with values close to 0 indicating spatially random data (Qi and Wu, 1996; Fortin, 1999). To investigate the impact of artificial channels, the indicator $P_{ac}$ was removed, and only three indicators, $D_r$, $D_n$, and $N_j$, were used to characterize the RNP.

Table 6 compares the Moran’s I of the natural and actual networks in each area, with the mean values of the indices as follows: whole basin (0.3, 0.5), mountain area (0.19, 0.33), transition area (0.32, 0.32), plain area (0.28, 0.55), Taihang windward (0.15, 0.21), Taihang leeward (0.28, 0.35), Yanshan windward (0.06, 0.07), and Yanshan leeward (0.14, 0.16); these results indicate a positive spatial autocorrelation of the RNP. Due to the needs of flood control, irrigation, etc., numerous artificial channels are concentrated in areas with gentle topography, which increases the autocorrelation of the RNP in each area, and the spatial distribution is more aggregated, reducing the spatial heterogeneity of the RNP. There are fewer artificial channels in areas with rugged topography and little change in spatial distribution. The correlation results showed that artificial channel construction changed the original intrinsic relationship between the natural river network and the topography. The natural river network is positively and weakly correlated with the elevation (0.29), ESI (0.34), SSI (0.17), and RSI (0.22) and negatively and weakly correlated with the TWI (−0.28) (Figure 8). After combining the artificial channels, the actual river network is negatively and weakly correlated with the elevation (−0.31), ESI (−0.19), SSI (−0.14), and RSI (−0.15) and positively and weakly correlated with the TWI (0.42). The trend is consistent across all areas, and the artificial channels cause a positive or negative shift in the weak correlation between the RNP and the topography, but the difference in correlation degree is not significant. This shift in correlation is progressively promoted with the construction of artificial channels. The RNP is constantly changing, and its correlation with topography is also changing towards the same trend.

TABLE 6

TABLE 6. Moran’s I of the actual and natural river networks.

FIGURE 8

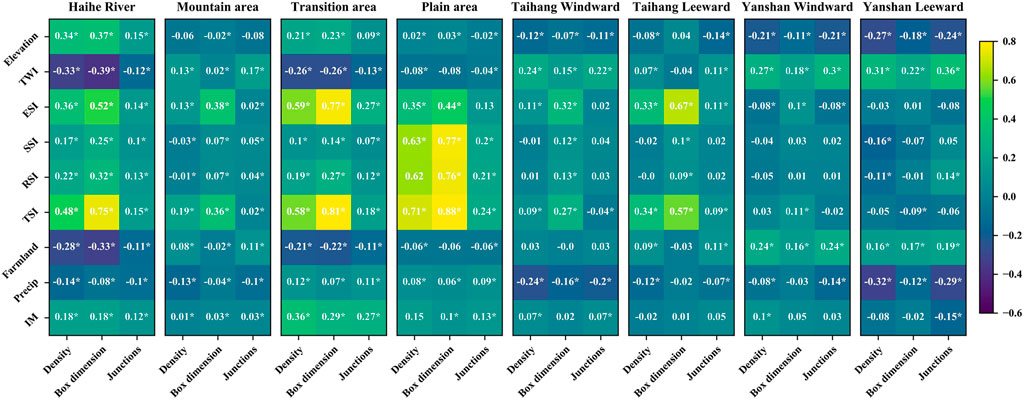
FIGURE 8. Correlation of the natural river network with topographic and climatic factors (* means significance test p < 0.05)

The artificial channels altered the correlation between the natural river network and the topography, and Figure 9 depicts the comparative results of the redundancy analysis. The explained rates of natural and actual river network in the whole basin were 73.69% and 17.96%, 32.05% and 15.94% in mountain area, 76.51% and 1.14% in transition area, 82.27% and 14.32% in plain area, 23.65% and 11.19% in Taihang windward, 52.71% and 13.91% in Taihang leeward, 19.44% and 16.13% in Yanshan windward, and 13.05% and 13.96% in Yanshan Leeward. The construction of artificial channels significantly reduces the correlation between the original natural network and topography, and the length of the artificial channels increases the variations in the explanation rate. Additionally, the relationship between the two showed a logarithmic function (R²=0.87). Therefore, the spatial stability of the CRNPT was poor and influenced by the disturbance effect of human activities, and the construction of artificial channels will cause the CRNPT to change continuously. The consistency between the natural river network and topography is reduced or even reversed, making its topography significantly less capable of explaining it. The natural network is generally dense in the upstream higher terrain areas and sparse in the downstream plain area (Chen et al., 2019). The Haihe River basin has completely changed the natural RNP due to the concentrated construction of quantities of artificial channels in local areas, raising the plain area $D_r$ higher than the mountain area and effectively increasing the spatial autocorrelation, but changing the original natural CRNPT, and the correlation continues to decrease. This is an unavoidable trend in the basins’ downstream area to ensure flood control, irrigation, and water supply.

FIGURE 9

FIGURE 9. Comparison of variance explained by the RNP; the river network indicators are $D_r$, $D_n$, and $N_j$

The variation in the CRNPT reflected changes in consistency. Topography was the determining factor of hydrological processes, and the river network pattern matched the hydraulic gradient to ensure the healthy operation of the network. The consistency of the river network with the topography in its natural state is conducive to ecosystem health and biodiversity, while changes in consistency can affect the stability of the river network ecosystem. The river network has evolved from a natural topographic feature to a natural-artificial dual feature under human influence (Sun et al., 2021), which can increase the network connectivity by providing routes around natural barriers and other water conveyance channels (Cote et al., 2009). However, the addition of a large number of artificial channels has severely fragmented the flow of the river network, leaving the lower river network without sufficient flow to maintain a healthy ecosystem (and the disappearance of large floods), ultimately severely disrupting the hydrological connectivity and habitat health of the network (Xingyuan et al., 2023). Moreover, multiple modifications and reconstructions within the river network may cumulatively impair ecologically relevant flow characteristics (Merenlender et al., 2008; Deitch et al., 2009). The serious problems facing the river network in the lower reaches of the Hai River basin also validate this conclusion. The lower reaches of the Hai River basin have serious ecological problems, with the river network often in a state of disconnection and little water flowing out of the estuary, resulting in the severe shrinkage of many estuaries (Hu et al., 2001). The water quality of the lower river network is poor, and sediments contain high levels of pollutants (Liu et al., 2014). Moreover, the Haihe River basin faces threats such as habitat degradation and biodiversity reduction (Chen et al., 2012). The changing river network and the reduced consistency are continuously driving these problems. This inconsistency will be a long-term state, as human activity in the basin greatly limits the dynamics of the river network derived from natural factors such as topography and climate.

The renovation and reconstruction of large river networks is always based on single purposes and lacks systematic planning and assessment, leading to an evolutionary imbalance in the structure and function of the river network. We revealed the disruption of the correlation between the RNP and topography by artificial channels and its consequences. Basin management should pay attention to changes in the physical characteristics of the river network and runoff processes caused by the instability between the RNP and topography and the impact of spatially concentrated construction of artificial channels on the RNP. As a large catchment of 320,000 km², we explored the relationship between the RNP and topography based on a gridding approach. In China, similar changes in river networks are very common in large watersheds (Yangtze River, Taihu Lake, etc.) (Deng et al., 2018; Song et al., 2019). The human influence on river networks in watersheds is so great that large-scale analysis can reveal the intrinsic relationships at the watershed level as well as the changes in such relationships, and this approach can be better generalized for use in other watersheds.

4 Conclusion

This paper examined the potential relationship between the current river network and topography, taking the Haihe River basin as an example, and revealed the change law of the CRNPT of the basin, as well as the influence of artificial channels. This research can serve as a foundation for watershed river network planning and management. The main conclusions are as follows.

The mountainous terrain is rugged, and the river network is sparse, with natural rivers dominating. The plain area has gentle topography and a dense river network, and it has 72% of the artificial channels. The variance explanation of topography on the RNP was 53.39%. With variance explanations of 28.25%, 30.13%, and 9.59% for mountain, transition, and plain areas, respectively, the regional effect of the CRNPT was significant, indicating that the more complex the topography is, the more the RNP is affected. The RNP and topography in the windward and leeward directions did not follow a consistent pattern.

The elevation, TWI, and TSI had the highest correlation with the RNP, and their contributions to variance explanation were 21.46%, 25.45%, and 30.07%, respectively, which had the greatest influence on the RNP. The combined contribution of the TWI and TSI in each area ranged from 35.66% to 78.29%. The TWI characterized the spatial water flow power dissipation and soil hydrology, and the TSI characterized the limiting effect of regional topography on hydrology and runoff processes, which demonstrated a stable correlation with the evolution of the RNP.

Artificial channels played the most important role in the CRNPT. The concentrated construction of artificial channels reduced the correlation between topography and RNP, with the difference in the explanation of natural and actual networks ranging from 0.91% to 75.37% in multiple areas, and the variation was related to the distribution of artificial channels, which showed a logarithmic function relationship (R²=0.87). Human influence has reduced or even reversed the consistency of the natural river network with the topography, resulting in a lower CRNPT for the current network. The changes in the RNP are profound, and the connectivity of the network and ecosystems will respond to this change. The “degree” of RNP evolution can be researched in the future to determine the extent to which artificial channel construction can serve human demands while reducing expenditure and ensuring the health of the river network.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

LF contributed to the study conception and design. Analysis was performed by ZX and LF. The first draft of the manuscript was written by ZX and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Funding

This work was supported by the National Natural Science Foundation of China [grant numbers Grant no. 52179020].

Acknowledgments

Also, many thanks to the Editors and three Reviewers for their very helpful comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

RNPs, River network patterns; CRNPT, Correlation between river network patterns and topography; $D_r$, Network density; $D_n$, Fractal dimension; $N_j$, Junctions; $P_{ac}$, Artificial channel proportion; TWI, Topographic wetness index; ESI, Elevation stress index; SSI, Slope stress index; RSI, Relief stress index; TSI, Topographic wetness stress index; Farmland, Farmland area; IM, Moisture index; Taihang, Taihang Mountains; Yanshan, Yanshan Mountains.

References

Abed Elmdoust, A., Miri, M. A., and Singh, A. (2016). Reorganization of river networks under changing spatiotemporal precipitation patterns: An optimal channel network approach. Water Resour. Res. 52, 8845–8860. doi:10.1002/2015wr018391

CrossRef Full Text | Google Scholar

Abrahams, A. D. (1984). channel networks: A geomorphological perspective. Water Resour. Res. 20, 161–188. doi:10.1029/wr020i002p00161

CrossRef Full Text | Google Scholar

Alabyan, A. M., and Chalov, R. S. (1998). Types of river channel patterns and their natural controls. Earth Surf. Process. Landforms J. Br. Geomorphol. Group 23, 467–474. doi:10.1002/(sici)1096-9837(199805)23:5<467::aid-esp861>3.0.co;2-t

CrossRef Full Text | Google Scholar

Albert, R., and Barabási, A. (2002). Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97. doi:10.1103/revmodphys.74.47

CrossRef Full Text | Google Scholar

Barabási, A., and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512. doi:10.1126/science.286.5439.509

PubMed Abstract | CrossRef Full Text | Google Scholar

Beeson, H. W., and McCoy, S. W. (2022). Disequilibrium river networks dissecting the Western slope of the Sierra Nevada, California, USA, record significant late Cenozoic tilting and associated surface uplift. Bulletin 134, 2809–2853. doi:10.1130/b35463.1

CrossRef Full Text | Google Scholar

Benda, L., Poff, N. L., Miller, D., Dunne, T., Reeves, G., Pess, G., et al. (2004). The network dynamics hypothesis: How channel networks structure riverine habitats. BioScience 54, 413–427. doi:10.1641/0006-3568(2004)054[0413:TNDHHC]2.0.CO;2

CrossRef Full Text | Google Scholar

Benstead, J. P., and Leigh, D. S. (2012). An expanded role for river networks. Nat. Geosci. 5, 678–679. doi:10.1038/ngeo1593

CrossRef Full Text | Google Scholar

Beven, K. J., and Kirkby, M. J. (1979). A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d'appel variable de l'hydrologie du bassin versant. Hydrological Sci. J. 24, 43–69. doi:10.1080/02626667909491834

CrossRef Full Text | Google Scholar

Biswal, B., and Marani, M. (2010). Geomorphological origin of recession curves. Geophys. Res. Lett. 37, n/a. doi:10.1029/2010gl045415

CrossRef Full Text | Google Scholar

Carbonneau, P., Fonstad, M. A., Marcus, W. A., and Dugdale, S. J. (2012). Making riverscapes real. Geomorphology 137, 74–86. doi:10.1016/j.geomorph.2010.09.030

CrossRef Full Text | Google Scholar

Chang, H. H. (1979). Minimum stream power and river channel patterns. J. Hydrol. 41, 303–327. doi:10.1016/0022-1694(79)90068-4

CrossRef Full Text | Google Scholar

Chen, Q., Liu, J., Ho, K. C., and Yang, Z. (2012). Development of a relative risk model for evaluating ecological risk of water environment in the Haihe River Basin estuary area. Sci. Total Environ. 420, 79–89. doi:10.1016/j.scitotenv.2011.09.044

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Wang, Y., and Ni, J. (2019). Structural characteristics of river networks and their relations to basin factors in the Yangtze and Yellow River basins. Sci. China Technol. Sci. 62, 1885–1895. doi:10.1007/s11431-019-9531-0

CrossRef Full Text | Google Scholar

Cohen, S., Wan, T., Islam, M. T., and Syvitski, J. (2018). Global river slope: A new geospatial dataset and global-scale analysis. J. Hydrol. 563, 1057–1067. doi:10.1016/j.jhydrol.2018.06.066

CrossRef Full Text | Google Scholar

Cote, D., Kehler, D. G., Bourne, C., and Wiersma, Y. F. (2009). A new measure of longitudinal connectivity for stream networks. Landsc. Ecol. 24, 101–113. doi:10.1007/s10980-008-9283-y

CrossRef Full Text | Google Scholar

Curie, F., Gaillard, S., Ducharne, A., and Bendjoudi, H. (2007). Geomorphological methods to characterise wetlands at the scale of the Seine watershed. Sci. Total Environ. 375, 59–68. doi:10.1016/j.scitotenv.2006.12.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Darboux, F., Davy, P., Gascuel-Odoux, C., and Huang, C. (2002). Evolution of soil surface roughness and flowpath connectivity in overland flow experiments. Catena 46, 125–139. doi:10.1016/s0341-8162(01)00162-x

CrossRef Full Text | Google Scholar

Deitch, M. J., Kondolf, G. M., and Merenlender, A. M. (2009). Hydrologic impacts of small-scale instream diversions for frost and heat protection in the California wine country. River Res. Appl. 25, 118–134. doi:10.1002/rra.1100

CrossRef Full Text | Google Scholar

Deng, X., Xu, Y., and Han, L. (2018). Impacts of human activities on the structural and functional connectivity of a river network in the Taihu Plain. Land Degrad. Dev. 29, 2575–2588. doi:10.1002/ldr.3008

CrossRef Full Text | Google Scholar

Devauchelle, O., Petroff, A. P., Seybold, H. F., and Rothman, D. H. (2012). Ramification of stream networks. Proc. Natl. Acad. Sci. 109, 20832–20836. doi:10.1073/pnas.1215218109

CrossRef Full Text | Google Scholar

Dollar, E., James, C. S., Rogers, K. H., and Thoms, M. C. (2007). A framework for interdisciplinary understanding of rivers as ecosystems. Geomorphology 89, 147–162. doi:10.1016/j.geomorph.2006.07.022

CrossRef Full Text | Google Scholar

Finnegan, N. J., Roe, G., Montgomery, D. R., and Hallet, B. (2005). Controls on the channel width of rivers: Implications for modeling fluvial incision of bedrock. Geology 33, 229–232. doi:10.1130/g21171.1

CrossRef Full Text | Google Scholar

Fortin, M. (1999). Effects of sampling unit resolution on the estimation of spatial autocorrelation. Ecoscience 6, 636–641. doi:10.1080/11956860.1999.11682547

CrossRef Full Text | Google Scholar

Greene, W. H. (2003). Econometric analysis. Chennai: Pearson Education India.

Google Scholar

Haining, R. P., and Haining, R. (2003). Spatial data analysis: Theory and practice. Cambridge: Cambridge University Press.

Google Scholar

Hair, J. F., Anderson, R. E., Tatham, R. L., and Black, W. C. (1992). Multivariate data analysis. 3rd edn. New York: Macmillan.

Google Scholar

Heasley, E. L., Clifford, N. J., and Millington, J. D. (2019). Integrating network topology metrics into studies of catchment-level effects on river characteristics. Hydrol. Earth Syst. Sc. 23, 2305–2319. doi:10.5194/hess-23-2305-2019

CrossRef Full Text | Google Scholar

Hong, H. L. Z. (1996). The fractal dimension of river networks and its interpretation. Sci. Geogr. Sin. 16, 124–128.

Google Scholar

Horton, R. E. (1932). Drainage-basin characteristics. Eos, Trans. Am. Geophys. union 13, 350–361. doi:10.1029/tr013i001p00350

CrossRef Full Text | Google Scholar

Horton, R. E. (1945). Erosional development of streams and their drainage basins; hydrophysical approach to quantitative morphology. Geol. Soc. Am. Bull. 56, 275–370. doi:10.1130/0016-7606(1945)56[275:edosat]2.0.co;2

CrossRef Full Text | Google Scholar

Hu, S., Wang, Z., and Lee, J. H. (2001). Flood control and shrinkage in the Haihe River mouth. Sci. China Ser. B Chem. 44, 240–248. doi:10.1007/bf02884832

CrossRef Full Text | Google Scholar

Israels, A. Z. (1984). Redundancy analysis for qualitative variables. Psychometrika 49, 331–346. doi:10.1007/bf02306024

CrossRef Full Text | Google Scholar

Kennedy, P. (2008). A guide to econometrics. Oxford: Blackwell Publishing.

Google Scholar

Kleidon, A. (2016). Thermodynamic foundations of the Earth system. Cambridge: Cambridge University Press.

Google Scholar

Legendre, P., Oksanen, J., and ter Braak, C. J. (2011). Testing the significance of canonical axes in redundancy analysis. Methods Ecol. Evol. 2, 269–277. doi:10.1111/j.2041-210x.2010.00078.x

CrossRef Full Text | Google Scholar

Leopold, L. B. (1971). Trees and streams: The efficiency of branching patterns. J. Theor. Biol. 31, 339–354. doi:10.1016/0022-5193(71)90192-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, F., Wang, H., and Liu, H. (2022). Research on the quantitative relationship between topographic features and river network structures. Phys. Geogr. 2022, 1–19. doi:10.1080/02723646.2022.2163541

CrossRef Full Text | Google Scholar

Liu, J. L., Zhang, J., Liu, F., and Zhang, L. L. (2014). Polycyclic aromatic hydrocarbons in surface sediment of typical estuaries and the spatial distribution in Haihe river basin. Ecotoxicology 23, 486–494. doi:10.1007/s10646-014-1233-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Makarenkov, V., and Legendre, P. (1999). Une méthode d'analyse canonique non linéaire et son application à des données biologiques. Math. Soc. Sci. 37, 135–147. doi:10.4000/msh.2796

CrossRef Full Text | Google Scholar

Mandelbrot, B. B. (1982). The fractal geometry of nature. New York: W. H. Freeman.

Google Scholar

Mazouz, R., Assani, A. A., and Rodríguez, M. A. (2013). Application of redundancy analysis to hydroclimatology: A case study of spring heavy floods in southern québec (Canada). J. Hydrol. 496, 187–194. doi:10.1016/j.jhydrol.2013.05.035

CrossRef Full Text | Google Scholar

Merenlender, A., Deitch, M. J., and Feirer, S. (2008). Decision support tool seeks to aid stream-flow recovery and enhance water security. Calif. Agr. 62, 148–155. doi:10.3733/ca.v062n04p148

CrossRef Full Text | Google Scholar

Molin, P., and Corti, G. (2015). Topography, river network and recent fault activity at the margins of the Central Main Ethiopian Rift (East Africa). Tectonophysics 664, 67–82. doi:10.1016/j.tecto.2015.08.045

CrossRef Full Text | Google Scholar

Ni, J. R. (1998). Fluvial dynamic geomorphology. Beijing: Peking University Press.

Google Scholar

Niemann, J. D., Bras, R. L., Veneziano, D., and Rinaldo, A. (2001). Impacts of surface elevation on the growth and scaling properties of simulated river networks. Geomorphology 40, 37–55. doi:10.1016/s0169-555x(01)00036-8

CrossRef Full Text | Google Scholar

O Brien, R. M. (2007). A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 41, 673–690. doi:10.1007/s11135-006-9018-6

CrossRef Full Text | Google Scholar

Obolewski, K., and Strzelczak, A. (2009). Epiphytic fauna inhabiting Stratiotes aloides in a new lake of the Słowiński National Park (Smołdzińskie lake, Poland). Ecohydrol. Hydrobiology 9, 257–267. doi:10.2478/v10104-010-0003-2

CrossRef Full Text | Google Scholar

Perron, J. T., Richardson, P. W., Ferrier, K. L., and Lapôtre, M. (2012). The root of branching river networks. Nature 492, 100–103. doi:10.1038/nature11672

PubMed Abstract | CrossRef Full Text | Google Scholar

Piégay, H., Darby, S. E., Mosselman, E., and Surian, N. (2005). A review of techniques available for delimiting the erodible river corridor: A sustainable approach to managing bank erosion. River Res. Appl. 21, 773–789. doi:10.1002/rra.881

CrossRef Full Text | Google Scholar

Qi, Y., and Wu, J. (1996). Effects of changing spatial resolution on the results of landscape pattern analysis using spatial autocorrelation indices. Landsc. Ecol. 11, 39–49. doi:10.1007/bf02087112

CrossRef Full Text | Google Scholar

Rakotondrabe, F., Ngoupayou, J. R. N., Mfonka, Z., Rasolomanana, E. H., Abolo, A. J. N., and Ako, A. A. (2018). Water quality assessment in the bétaré-oya gold mining area (east-Cameroon): Multivariate statistical analysis approach. Sci. Total Environ. 610, 831–844. doi:10.1016/j.scitotenv.2017.08.080

PubMed Abstract | CrossRef Full Text | Google Scholar

Ranjbar, S., Hooshyar, M., Singh, A., and Wang, D. (2018). Quantifying climatic controls on river network branching structure across scales. Water Resour. Res. 54, 7347–7360. doi:10.1029/2018WR022853

CrossRef Full Text | Google Scholar

Rao, C. R. (1964). The use and interpretation of principal component analysis in applied research. Sankhyā Indian J. Statistics, Ser. A 26, 329–358.

Google Scholar

Rodríguez Iturbe, I., Rinaldo, A., Rigon, R., Bras, R. L., Marani, A., and Ijjász Vásquez, E. (1992). Energy dissipation, runoff production, and the three-dimensional structure of river basins. Water Resour. Res. 28, 1095–1103. doi:10.1029/91wr03034

CrossRef Full Text | Google Scholar

Sangireddy, H., Carothers, R. A., Stark, C. P., and Passalacqua, P. (2016). Controls of climate, topography, vegetation, and lithology on drainage density extracted from high resolution topography data. J. Hydrol. 537, 271–282. doi:10.1016/j.jhydrol.2016.02.051

CrossRef Full Text | Google Scholar

Sarker, S., Veremyev, A., Boginski, V., and Singh, A. (2019). Critical nodes in river networks. Sci. Rep. UK 9, 11178–11211. doi:10.1038/s41598-019-47292-4

CrossRef Full Text | Google Scholar

Scorpio, V., Zen, S., Bertoldi, W., Surian, N., Mastronunzio, M., Dai Prá, E., et al. (2018). Channelization of a large alpine river: What is left of its original morphodynamics? Earth Surf. Proc. Land. 43, 1044–1062. doi:10.1002/esp.4303

CrossRef Full Text | Google Scholar

Seibert, J., and McGlynn, B. (2006). “Landscape element contributions to storm runoff,” in Encyclopedia of hydrological sciences. Hoboken: Wiley.

CrossRef Full Text | Google Scholar

Seybold, H., Rothman, D. H., and Kirchner, J. W. (2017). Climate's watermark in the geometry of stream networks. Geophys. Res. Lett. 44, 2272–2280. doi:10.1002/2016gl072089

CrossRef Full Text | Google Scholar

Shelef, E., and Hilley, G. E. (2014). Symmetry, randomness, and process in the structure of branched channel networks. Geophys. Res. Lett. 41, 3485–3493. doi:10.1002/2014GL059816

CrossRef Full Text | Google Scholar

Song, S., Zeng, L., Wang, Y., Li, G., and Deng, X. (2019). The response of river network structure to urbanization: A multifractal perspective. J. Clean. Prod. 221, 377–388. doi:10.1016/j.jclepro.2019.02.238

CrossRef Full Text | Google Scholar

Strahler, A. N. (1952). Hypsometric (area-altitude) analysis of erosional topography. Geol. Soc. Am. Bull. 63, 1117–1142. doi:10.1130/0016-7606(1952)63[1117:haaoet]2.0.co;2

CrossRef Full Text | Google Scholar

Sun, C., Chen, L., Zhu, H., Xie, H., Qi, S., and Shen, Z. (2021). New framework for natural-artificial transport paths and hydrological connectivity analysis in an agriculture-intensive catchment. Water Res. 196, 117015. doi:10.1016/j.watres.2021.117015

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorne, C. R., Hey, R. D., and Newson, M. D. (1997). “Applied fluvial geomorphology for river engineering and management,” in Applied fluvial geomorphology for river engineering and management. Hoboken: Wiley.

Google Scholar

Tokunaga, E. (1984). Ordering of divide segments and law of divide segment numbers. Trans. Jpn. Geomorphol. Union 5, 71–77.

Google Scholar

Tong, B., Li, Z., Wang, J., Yao, C., and He, M. (2020). Development of topography-based river width estimation model for medium-sized mountainous watersheds. J. Hydrol. Eng. 25, 04020018. doi:10.1061/(asce)he.1943-5584.0001888

CrossRef Full Text | Google Scholar

Vörösmarty, C. J., Fekete, B. M., Meybeck, M., and Lammers, R. B. (2000). Global system of rivers: Its role in organizing continental land mass and defining land-to-ocean linkages. Glob. Biogeochem. Cy. 14, 599–621. doi:10.1029/1999gb900092

CrossRef Full Text | Google Scholar

Wagner, H. H. (2004). Direct multi-scale ordination with canonical correspondence analysis. Ecology 85, 342–351. doi:10.1890/02-0738

CrossRef Full Text | Google Scholar

Wagner, H. H., and Fortin, M. (2005). Spatial analysis of landscapes: Concepts and statistics. Ecology 86, 1975–1987. doi:10.1890/04-0914

CrossRef Full Text | Google Scholar

Walley, Y., Henshaw, A. J., and Brasington, J. (2020). Topological structures of river networks and their regional-scale controls: A multivariate classification approach. Earth Surf. Proc. Land. 45, 2869–2883. doi:10.1002/esp.4936

CrossRef Full Text | Google Scholar

Wang, J., Liu, G., Liu, H., and Lam, P. K. (2017). Multivariate statistical evaluation of dissolved trace elements and a water quality assessment in the middle reaches of Huaihe River, Anhui, China. Sci. Total Environ. 583, 421–431. doi:10.1016/j.scitotenv.2017.01.088

PubMed Abstract | CrossRef Full Text | Google Scholar

Willett, S. D., McCoy, S. W., Perron, J. T., Goren, L., and Chen, C. Y. (2014). Dynamic reorganization of River Basins. Science 343, 1248765. doi:10.1126/science.1248765

PubMed Abstract | CrossRef Full Text | Google Scholar

Xingyuan, Z., Fawen, L., and Yong, Z. (2023). Impact of changes in river network structure on hydrological connectivity of watersheds. Ecol. Indic. 146, 109848. doi:10.1016/j.ecolind.2022.109848

CrossRef Full Text | Google Scholar

Zanardo, S., Zaliapin, I., and Foufoula Georgiou, E. (2013). Are American rivers Tokunaga self-similar? New results on fluvial network topology and its climatic dependence. J. Geophys. Res. Earth Surf. 118, 166–183. doi:10.1029/2012jf002392

CrossRef Full Text | Google Scholar

Zhao, J., Lin, L., Yang, K., Liu, Q., and Qian, G. (2015). Influences of land use on water quality in a reticular river network area: A case study in shanghai, China. Landsc. Urban Plan. 137, 20–29. doi:10.1016/j.landurbplan.2014.12.010

CrossRef Full Text | Google Scholar

Zhao, J., Vanmaercke, M., Chen, L., and Govers, G. (2016). Vegetation cover and topography rather than human disturbance control gully density and sediment production on the Chinese Loess Plateau. Geomorphology 274, 92–105. doi:10.1016/j.geomorph.2016.09.022

CrossRef Full Text | Google Scholar