Reliability analysis of an inter-story isolated structure under a main-aftershock sequence based on the Laplace asymptotic method

After a strong mainshock, subsequent ground motion is the result of a sequence of multiple aftershocks, and the damage to a structure under these conditions is more severe than from a single earthquake. Most seismic studies are based on a single earthquake event. To explore the influence of a main-aftershock sequence on an isolated inter-story structure, we constructed a three-dimensional finite-element model of such a structure and subjected it to repeated main-aftershock sequences. The Laplace asymptotic method of second-order second-moment was used to calculate the reliability of the structure under the action of a single mainshock and after a main-aftershock sequence at different seismic levels. The effects of the number of aftershocks, the location of the isolation layer, and the stiffness of the isolation bearing in the structure were analyzed. The results showed that aftershocks increased the failure probability of each sub-structural part of the inter-story isolated structure. The failure probability of the lower structure had the greatest influence, which was about 3.89 times that for the mainshock alone. The probability of failure from multiple vs single aftershocks was similar, but the magnitude of the aftershock plays a major role in failure. The number of aftershocks reduced the overall reliability of an inter-story isolation structure. In the case of different isolation layer positions, the placement of the isolation layer at the top of the seventh story under an extremely rare earthquake level resulted in a reduction of 6.01%. With isolation bearings of different stiffness, the largest decrease was 7.88% when the stiffness was 50%.

1 Introduction

Based on historical earthquake reports, nearly 90% of strong mainshocks are accompanied by multiple strong aftershocks. Within 1 year after the 1999 Chi-Chi earthquake in Taiwan, 87 aftershocks of magnitude 5.0 or above occurred. In fact, a strong aftershock of magnitude 6.8 occurred half an hour after the Chi-Chi earthquake mainshock and was the main cause of casualties and building destruction (Shin and Teng, 2001). Under aftershock conditions, structures suffer from the effects of cumulative damage. When a structure is initially damaged by a strong mainshock, the aftershocks will exacerbate the damage, especially when the natural vibration period of the damaged structure is close to the predominant period of the aftershock. Analysis of many post-earthquake cases showed that the risk of structural failure from cumulative aftershock damage should not be ignored (Augenti and Parisi, 2010; Jing et al., 2011; Yu et al., 2013; Kossobokov and Nekrasova, 2019; Huang et al., 2020a). However, the seismic codes of most countries in the world mainly consider the effect of a single earthquake, without taking into account the potential damage from aftershocks.

In recent years, a large number of studies have been carried out to analyze the seismic performance of structures subjected to main-aftershock sequences (Aloisio et al., 2022; Aloisio et al., 2022; Torti et al., 2022; Tauheed and Alam, 2023). Wu and Ou (1993) proposed a method for determining the damage to reinforced concrete (RC) structures from the action of a main-aftershock and established a multi-layer RC structural model to conduct elastic–plastic time-history analyses. They found that aftershocks significantly increased the damage to the structure and concluded that it was critical to consider the effects of aftershocks in the design of collapse-resistant structures. Amadio et al. (2003) analyzed the dynamic response of a non-linear, single degree-of-freedom (DOF) steel frame system under the action of a main-aftershock sequence based on behavior factors and damage parameters. The equivalent single-DOF system underestimated the damage as the aftershock increased the degree of damage to the structure. Zhai et al. (2016) presented an inelastic single-DOF system with an input energy spectrum under the action of a main-aftershock. They quantitated the impact of the aftershocks on input energy, proposed a simplified expression of input energy, and verified the necessity of considering aftershocks in an energy-based seismic design. Qu and Pan (2022) investigated a vulnerability model considering the correlation between the maximum interlayer displacement and the residual displacement under the action of main-aftershocks. The building model has a higher probability of overrun after considering the correlation of the two indices. Afsar Dizaj et al. (2021) studied the vulnerability of aging concrete frames under the action of main-aftershocks by quantifying the damage state of corrosion variables. The PGA ratio of aftershocks to mainshocks played a key role in the assessment of the seismic vulnerability of aging in highly corroded RC frames.

The inter-story isolated structure is a kind of shock absorption technology used in the development of base isolated structures (De Luca and Guidi, 2019). Several studies on the principles and methods of analysis of inter-story isolated structures have been conducted by researchers all over the world. Zhou et al. (2009) proposed a method for the optimal design of isolation layers by establishing a simplified two-particle model and a multi-particle dynamic time-history analysis model, which verified the effectiveness of the inter-story isolated system in reducing earthquake damage. The damping effect was significantly detected when lowering the isolation layer position. Faiella et al. (2022) used the inter-story isolated system to retrofit a masonry structure and succeeded in significantly reducing the seismic response. Keivan et al. (2022) demonstrated the rate-independent linear damping of a 14-story inter-story isolation structure using a numerical model and real-time hybrid simulation of shaking table. They proved that rate-independent linear damping provided better control by limiting the displacement of the isolation layer without amplifying the acceleration. Wu et al. (2021) carried out shaking table test research with an inter-story isolated structure model on a foundation of soft soil. The floor acceleration and displacement responses of the isolation layer and the isolated structure under far-field, long-period, and ordinary ground motions were compared and analyzed, and the dynamic response law and damping effect of the pile–soil-–layer isolated structure was determined.

Structural reliability refers to the ability of a structure to perform a predetermined function in a specified time period or under specified conditions, which could be used to investigate the probability that the structure will not fail under specified conditions. Sun et al. (2013) reported the stationary random seismic response and dynamic reliability of isolated structures under different period ratios, yield-to-weight ratios, and damping ratios. The appropriate selection of the period ratio, yield/weight ratio, and damping ratio of the isolated structure led to an increase in the overall reliability of the structure. Dang et al. (2018) studied the reliability of isolated structures using statistical methods and probability. Although horizontal seismic action was reduced by 60–70%, the fortification targets of “no damage under moderate earthquake” and “no collapse under great earthquake” were not satisfied. Higher performance requirements for isolated buildings are necessary. Huang et al. (2019) employed a seismic damage model to determine reliability in terms of the resistance to progressive vertical collapse of a base-isolated frame shear wall structure. The quadratic fourth-moment method based on maximum entropy principles was used to calculate the probability of structural collapse, which provided a reliable basis for structural design and post-earthquake reinforcement. Jiang et al. (2018) discussed slope reliability analysis based on spatial variability modeling of undrained soil.

However, in most of the studies on inter-story isolated structures, inclusion of the effects of a main-aftershock sequence was rare. Herein, the inter-story isolation structure was taken as the research object, and a three-dimensional finite-element model was established. Under the main-aftershock sequence, the number of aftershocks, the position of the isolation layer, and the stiffness of the isolation bearing in the inter-story isolated structure were analyzed and evaluated by reliability probability.

2 Methods and materials

2.1 Engineering situations

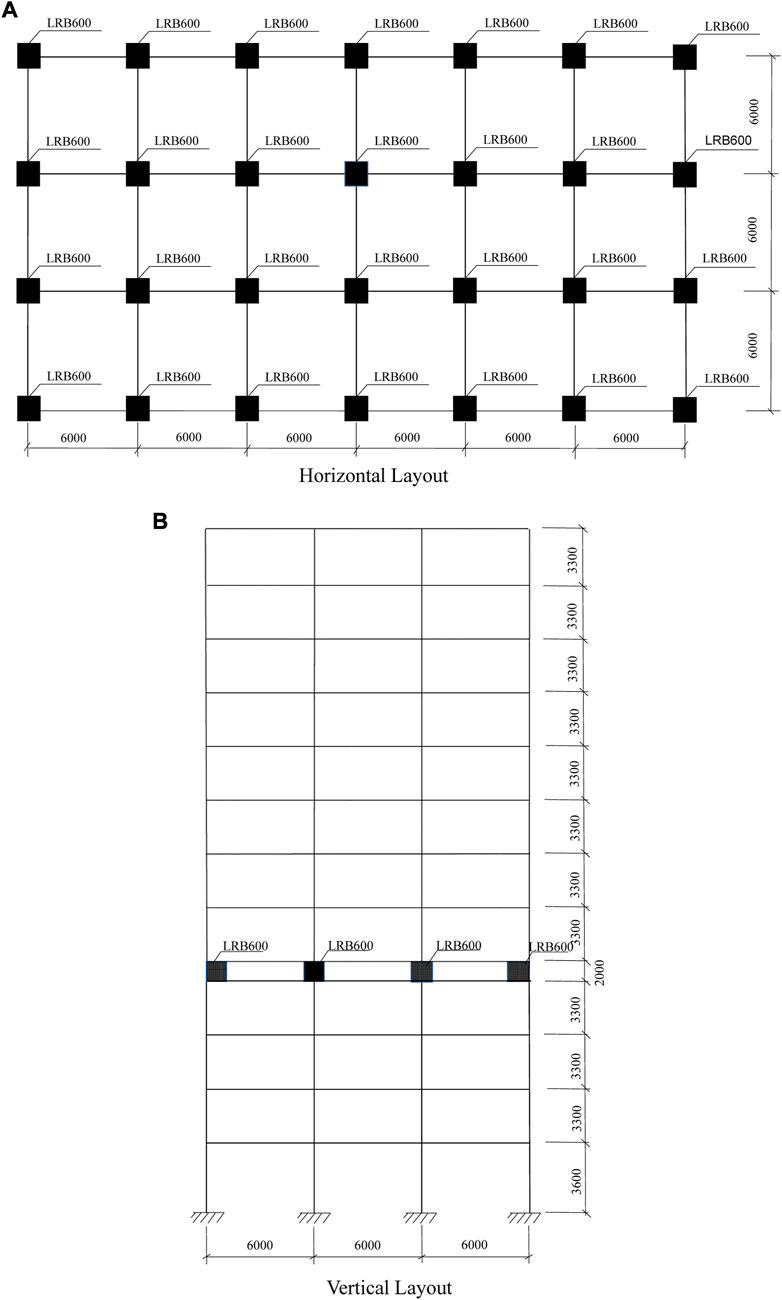
A 12-story reinforced concrete frame model was used for analysis. According to Chinese standards for seismic isolation design of buildings (GB/T 51408-2021, Standard, 2021), the site classification was 2, the designed earthquake grouping was the second group, the site characteristic period was 0.4 s, and the designed basic acceleration was 0.2 g. The plane size of the structure was 30 m × 18 m, the first story was 3.6 m, the labeled story was 3.3 m, and the isolation layer was set on the top of the fourth story. The section size of the frame column of the first through fourth stories was 800 mm × 800 mm, the section size of the frame column of the fifth through seventh stories was 600 mm × 600 mm, and the section size of the beam was 300 mm × 600 mm. RC grade C30, with an elastic modulus; E₀, of 3 × 10⁴ N/mm²; compressive strength, f_c of 14.3 N/mm²; tensile strength, f_t = 1.43 N/mm²; and HRB400 steel, with an elastic modulus, E₀, of 2 × 10⁵ N/mm², and yield strength, f_y = 360 N/mm². The isolation layer was set at the top of the third story, and the first-order vibration period of the story isolation structure was 2.74 s. The plane and vertical layout of the structure is shown in Figure 1. A rubber LRB600 isolation bearing was used with a thickness of 110 mm, vertical stiffness of 1581 kN/mm, pre-yield stiffness of 11.507 kN/mm, post-yield stiffness of 0.886 kN/mm, and a yield force of 90 kN.

FIGURE 1

FIGURE 1. Structural diagram.

2.2 Model establishment

In this study, the Abaqus finite element platform was used for finite element modeling. A beam element was used for the beam and column, a layered shell element was used for the floor, and the isolation bearing was simulated using connectors. Common node coupling was used between the components. The PQ-fiber (Qu and Ye, 2011) beam elements were used to reproduce the non-linearity of the structure. The constitutive models of steel and concrete were simulated by the Usteel02 Clough model for testing bearing capacity degradation (Clough, 1966; Liu et al., 1998; Qu and Ye, 2011) and the Uconcrete02 (McKenna, 1997; Qu and Ye, 2011) model for measuring tensile strength. The isolation bearing used a double-line model, as shown in Figure 2.

FIGURE 2

FIGURE 2. Structural non-linear constitutive relationships.

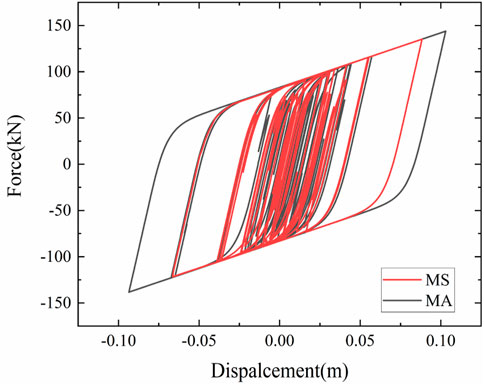
Figure 3 shows the hysteretic curve of the least favorable bearing under a rare earthquake event. The curve is full, indicating that the established isolated model has good seismic performance and energy dissipation capacity. The energy dissipated under the action of the main-aftershock was larger than that during the mainshock (Figure 3).

FIGURE 3

FIGURE 3. Hysteretic curve of structure.

2.3 Earthquake-induced ground motions

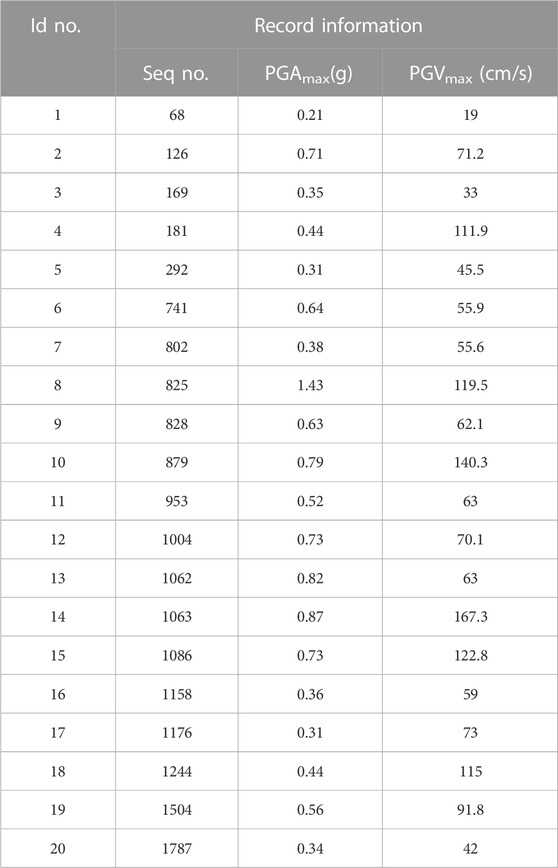
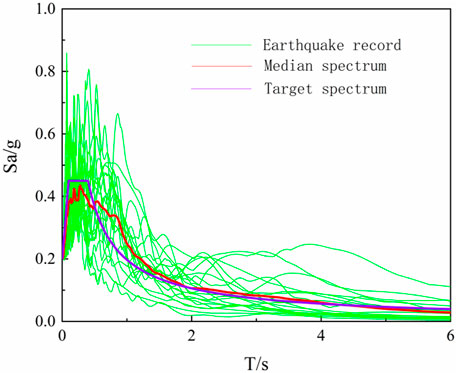
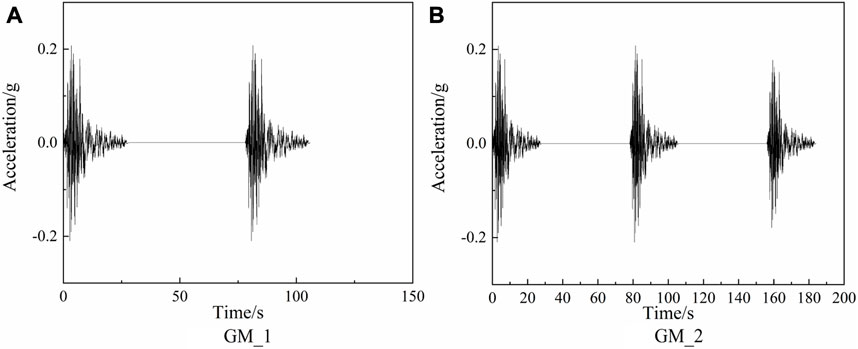
FEMA P58-1 (Fema, 2012) pointed out that when performing non-linear dynamic time-history analysis, if the response spectrum of the selected ground motion was well-fitted to the target response spectrum, the use of eleven or more ground motions per intensity level was sufficient to model the uncertainty effects of ground motions when there are few natural main-aftershock records. Thus, twenty ground motions were randomly selected from the ground motions recommended by Atc-63, and the repeated structure method was used to establish the main-aftershock sequence. The selected ground motions are listed in Table 1. The main-aftershock sequence of one aftershock GM_1 (1.00; 1.00) and two aftershocks GM_2 (1.00; 1.00; 0.8526) were created. GM_0, GM_1, and GM_2 were the single mainshock, the main-aftershock sequence of one aftershock, and the main-aftershock sequence of two aftershocks, respectively. The amplitude modulation coefficient 0.8526 was taken from the Gutenberg–Richter law (Gutenberg, 2013) and the Joyner–Boore empirical formula (Joyner and Boore, 1982), as shown in Figure 5. The selected ground motion included all types of far-field, near-field with pulses, and near-field without pulses. The acceleration response spectrum of the main-aftershock sequence is represented in Figure 4. In order to quit the structural response completely after the mainshock and restore the structure to the equilibrium position, a time interval of 40 s was set between the mainshock record and the aftershock record (Figure 5). The ground motion amplitudes were adjusted to 400 cm/s⁻² and 600 cm/s⁻², respectively, which were input into the finite-element model to obtain the response value of the inter-story isolated structure under the main-aftershock sequence.

TABLE 1

TABLE 1. Ground motion information.

FIGURE 4

FIGURE 4. Acceleration response spectrum of main-aftershock sequence.

FIGURE 5

FIGURE 5. xample of acceleration time history of main-aftershock sequence.

3 Structural reliability analysis method

The common calculation methods of reliability included the first-order second-moment method, the second-order second-moment method, the second-order fourth-moment method, the response surface method, and the Monte Carlo method. In this study, the reliability of the inter-story isolated structure during a main-aftershock was analyzed by using the Laplace asymptotic method of second-order moment in the MATLAB program.

3.1 Basic principles of the Laplace asymptotic method

Suppose that $Y={\left(Y1,Y2,...Yn\right)}^T$ is an independent standard normal random variable, the performance function is $Z=gY\left(Y\right)$. The failure probability of the structure (Zhang and Jin, 2015; Zhang et al., 2022) is as follows:

$p\mathrm{f}={\int }_{gY\left(Y\right)\le 0}\mathrm{\phi }\mathrm{n}\left(y\right)dy={\int }_{gY\left(Y\right)\le 0}\frac{1}{{\left(2\mathrm{\pi }\right)}^{n/2}}\exp \left(-\frac{y^{T}y}{2}\right)dy.(1)$

When the Laplace asymptotic integral method is used to calculate the failure probability of multiple integral Eq. 1, the following Laplace integral with large parameter $\mathrm{\lambda }\left(\mathrm{\lambda }\to +\infty \right)$ should be used (Zheng et al., 2021):

$I\left(\mathrm{\lambda }\right)={\int }_{g\left(x\right)\le 0}p\left(x\right)\exp \left[{\mathrm{\lambda }}^{2}h\left(x\right)\right]dx.(2)$

The properties of Eq. 2 are determined by the properties in the field of the maximum position of the integrand. If the functions $g\left(x\right)$ and $h\left(x\right)$ are second-order and continuously differentiable, $p\left(x\right)$ is continuous, and $h\left(x\right)$ only takes the maximum value at a point $x*$ on the boundary of the integral domain $\left\{\left.x\right|g\left(x\right)=0\right\}$, then the integral value of Eq. 2 can be asymptotically expressed (Su et al., 2018) as

$I\left(\mathrm{\lambda }\right)\approx \frac{2{\mathrm{\pi }}^{\left(n-1\right)/2}}{{\mathrm{\lambda }}^{n+1}}\frac{p\left(x*\right)\exp \left[{\mathrm{\lambda }}^{2}h\left(x\right)\right]}{\sqrt{\left|J\right|}},(3)$

among them

$J={\left[▽\mathrm{h}\left(x*\right)\right]}^{T}B\left(x*\right)▽\mathrm{h}\left(x*\right),(4)$

where matrix $B\left(x*\right)$ is the adjoint matrix of matrix $C\left(x*\right)$:

$C\left(x*\right)={▽}^2\mathrm{h}\left(x*\right)-\frac{‖▽\mathrm{h}\left(x*\right)‖}{‖▽\mathrm{g}\left(x*\right)‖}{▽}^2\mathrm{g}\left(x*\right).(5)$

To make use of Eq. 3, a large number $\mathrm{\lambda }\left(\mathrm{\lambda }\to +\infty \right)$ may be chosen such that

$Y=\mathrm{\lambda }V.(6)$

The Jacobi determinant of the transformation is $\det JYV={\mathrm{\lambda }}^n$. Substituting Eq. 6 into Eq. 1, we obtain

$p\mathrm{f}={\int }_{gY\left(\mathrm{\lambda }v\right)\le 0}\frac{{\mathrm{\lambda }}^{\mathrm{n}}}{{\left(2\mathrm{\pi }\right)}^{n/2}}\exp \left(-\frac{{\mathrm{\lambda }}^2{v}^{T}v}{2}\right)dv.(7)$

Equation 7 is also the Laplace type integral shown in Eq. 2, and $p\left(V\right)=\frac{{\mathrm{\lambda }}^n}{{\left(2\mathrm{\pi }\right)}^{n/2}}$, $h\left(V\right)=-\frac{1}{2}{V}^{T}V$. The $h\left(V\right)$ function takes the maximum value at the coordinate origin $v=0$ in the $V$ space, while for the general structural reliability analysis problem, the $v=0$ point is in the reliability domain, which indicates that $h\left(V\right)$ has a maximum value at a point $v*=\frac{y*}{\mathrm{\lambda }}$ on the failure surfaces. Therefore, the integral value of the failure probability, pf, is mainly determined by the point $v*$ at which the failure surface $gY\left(\mathrm{\lambda }V\right)=0$ maximizes $h\left(V\right)$ and the geometric properties of the failure surface near $v*$. From the geometric meaning of the reliability index, $\mathrm{\beta }$, this key point, $v*$, is the checking point of the structure in $V$ space. If the performance function is quadratically derivable, according to Eq. 3, the asymptotic integral value of Eq. 7 is

$p\mathrm{f}Q=\frac{1}{\sqrt{2\mathrm{\pi }}\mathrm{\lambda }\sqrt{J1}}\exp \left(-\frac{{\mathrm{\lambda }}^{2}v{*}^{T}v*}{2}\right),(8)$

among them

$J1={\left[▽\mathrm{h}\left(v*\right)\right]}^{T}B1\left(v*\right)▽\mathrm{h}\left(v*\right)=v{*}^{T}B1\left(v*\right)v*=\frac{1}{{\mathrm{\lambda }}^2}y{*}^{T}B1\left(v*\right)y*.(9)$

$B1\left(v*\right)$ is the adjoint matrix of $C1\left(v*\right)$:

$C1\left(v*\right)={▽}^2\mathrm{h}\left(v*\right)-\frac{‖▽\mathrm{h}\left(v*\right)‖}{‖gY\left(\mathrm{\lambda }v*\right)‖}{▽}^2\mathrm{g}Y\left(\mathrm{\lambda }v*\right).(10)$

Substituting Eq. 9 into Eq. 8 and noting the geometric meaning of $\mathrm{\beta }$, ${\mathrm{\beta }}^2=y{*}^{T}y*$, Eq. 8 can be written in $Y$ space:

$p\mathrm{f}Q=\frac{1}{\sqrt{2\mathrm{\pi }}\sqrt{\left|J\right|}}\exp \left(-\frac{y{*}^{T}y*}{2}\right)=\frac{\mathrm{\phi }\left(\mathrm{\beta }\right)}{\sqrt{\left|J\right|}},(11)$

among them

$J=y{*}^{T}B\left(y*\right)y*,(12)$

where $B\left(y*\right)=B1\left(v*\right)$ is the adjoint matrix of the matrix $C\left(y*\right)=C1\left(v*\right)$:

$C\left(y*\right)=-I-\frac{\frac{1}{\mathrm{\lambda }}‖y*‖}{\mathrm{\lambda }‖▽\text{gY}\left(\mathrm{y}*\right)‖}{\mathrm{\lambda }}^2{▽}^2\mathrm{g}Y\left(y*\right)=-I-\frac{\mathrm{\beta }}{‖▽\text{gY}\left(y*\right)‖}{▽}^2\mathrm{g}Y\left(y*\right).(13)$

Since $\mathrm{\beta }$ is generally a larger positive value, $\mathrm{\phi }\left(\mathrm{\beta }\right)=\mathrm{\beta }\mathrm{\Phi }\left(-\mathrm{\beta }\right)$, Eq. 11 can also be expressed as

$p\mathrm{f}Q\approx \mathrm{\Phi }\left(-\mathrm{\beta }\right)\frac{\mathrm{\beta }}{\sqrt{\left|J\right|}.}(14)$

3.2 Limit state equation of an inter-story isolated structure

Generally, for RC structures, it is noted that the structural resistance obeys a lognormal distribution. The upper structure of the isolation layer and the lower structure of the isolation layer of the inter-story isolated structure were connected in series with the isolation layer (Wu et al., 2017). The failure mode is any substructure failure that leads to failure of the whole inter-story isolated structure. The performance function of the story isolation structure (Dang et al., 2018; Liu et al., 2019) is

$\mathrm{Z}\mathrm{j}=\mathrm{R}\mathrm{j}-\mathrm{S}\mathrm{j}.(15)$

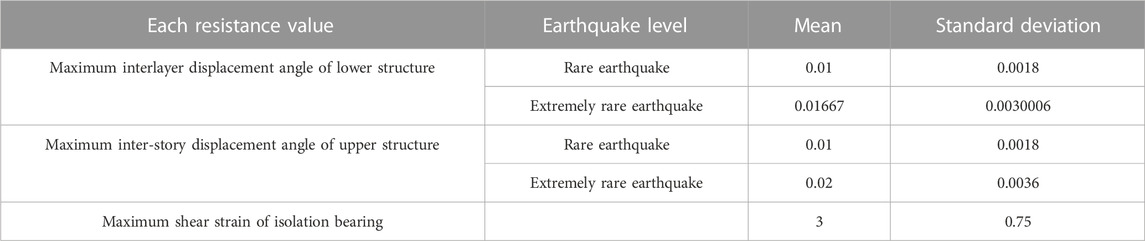
In the formula, R_j represents the limit of each response value of the structure under different seismic levels, and S_j represents each response value of the structure under different seismic levels. The mean value of the resistance of the upper structure and lower structure of the isolated structure is within the Chinese standards for seismic isolation design of buildings (GB/T 51408-2021, 2021), and the coefficient of variation is 0.18 (Liu et al., 2017; Liu et al., 2019). The maximum shear strain of the isolation bearing did not exceed 3, and the coefficient of variation was 0.25 (Liu et al., 2017; Liu et al., 2019). The probability eigenvalue of each resistance in the isolated structure is given in Table 2.

TABLE 2

TABLE 2. Probabilistic characteristic parameters of structural limiting values.

4 The influence of the number of aftershocks on the seismic isolation interlayer

4.1 Response probability distribution and parameters associated with the isolated structure

Since there are so few studies on the probability distribution type of the response of the isolated structure during an earthquake, we assumed that the upper and lower structures of the isolation layer were similar to those of the non-isolated structure. The upper structure and the lower structure were similar to the structures above and below the isolation layer, in that the interlayer displacement angle could better reflect the degree of damage to the structure. The maximum interlayer displacement angle was selected as the structural parameter, and the interlayer displacement angle of the isolated structure was assumed to obey the extreme value type I distribution. The maximum shear strain of the isolation bearing was selected as the isolation layer parameter, and it was assumed that the parameters of the isolation layer also obeyed the extreme value I distribution.

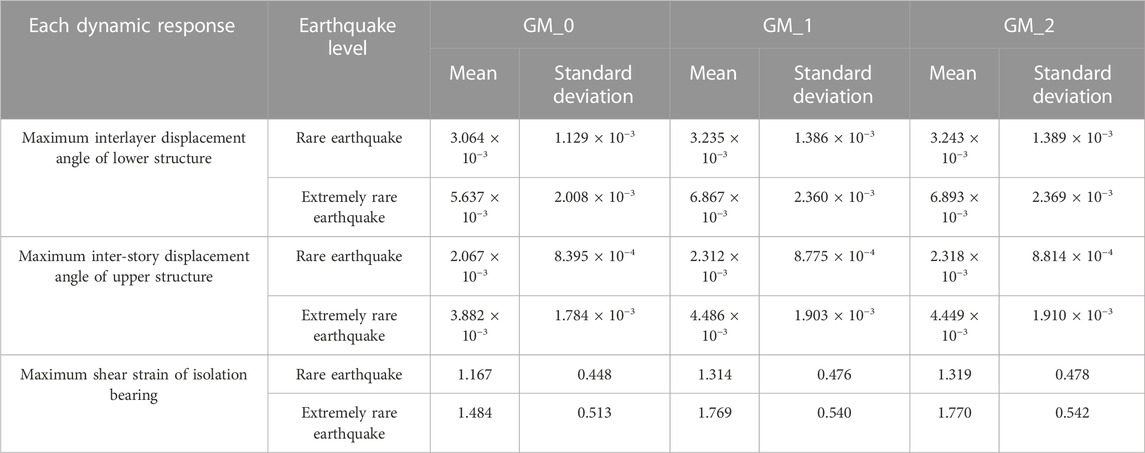
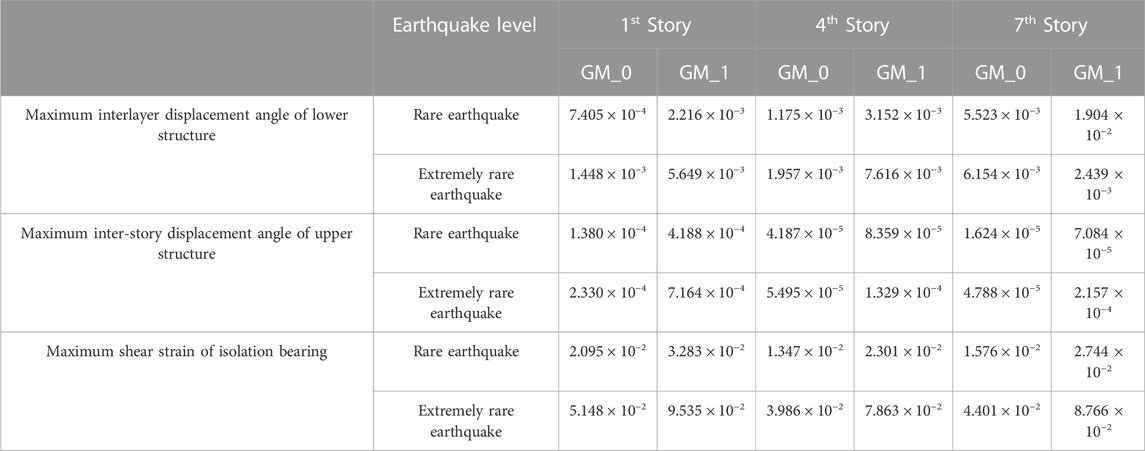
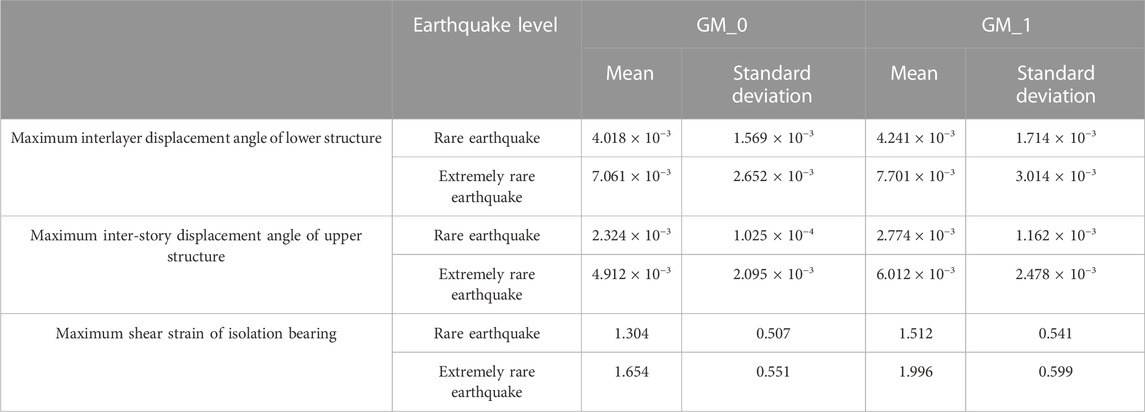
To test the hypothesis, the structural response obtained by time history analysis of the finite-element model was analyzed to determine the probability distribution characteristics of the isolated structure. The Lilliefors test in MatLab was employed to test the hypothesis for each response parameter. Consequently, each response parameter output, h = 0, indicated that under the confidence level of α = 0.05, the response parameters were unable to reject the null hypothesis. Each response parameter obeyed the extreme value type I distribution. The maximum likelihood estimation of the data samples was performed using the MLE function in MatLab to determine the mean and standard deviation of each response parameter under the extreme value type I distribution (Table 3).

TABLE 3

TABLE 3. Probabilistic characteristic parameters of structural response values.

4.2 Reliability of the inter-story isolated structure

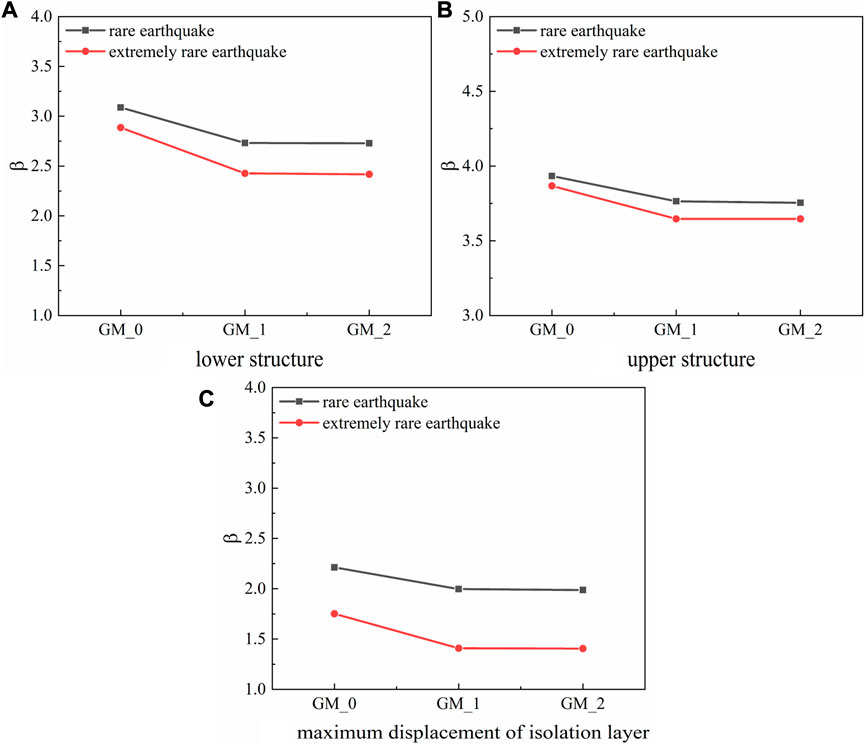
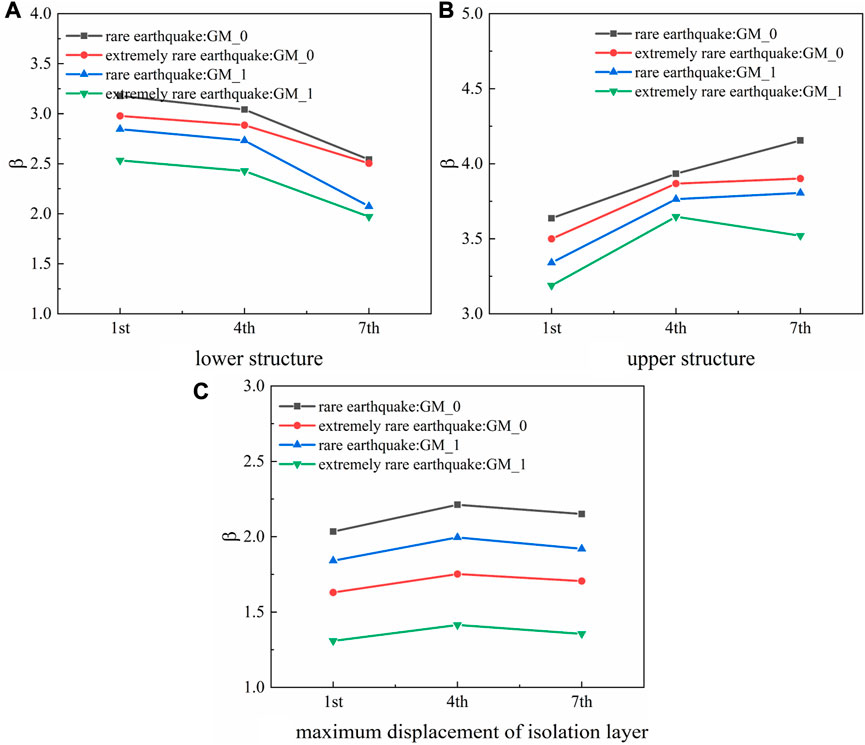
S_j and R_j are listed in Tables 1 and 2 respectively. The failure probability, P_f , of each substructure under the action of a mainshock and a main-aftershock sequence at different seismic levels was obtained by the Laplace asymptotic method. The results are shown in Table 3. Table 4 shows that the failure probability of each substructure response at different seismic levels under the action of the main-aftershock sequence was higher than that under the action of a single mainshock. It can be seen from Table 4 that the failure probability under multiple aftershocks was close to that under a single aftershock, indicating that the largest aftershock has the major role. Under an extremely rare earthquake level, the failure probability of the lower structure of the isolation layer was significantly affected by the main aftershock sequence, which was 3.89 times that of under the action of the mainshock alone. At a rare earthquake level, the displacement of the isolation layer was minimally affected by aftershocks but was increased 1.7-fold under the action of single mainshock. To intuitively show the influence of aftershocks on the structure, a comparison of the reliability index of each substructure under the action of a single mainshock and a main-aftershock sequence at different seismic levels is shown in Figure 6. It can also be seen in Figure 6 that the reliability index under the action of a main-aftershock was smaller than with a main shock alone, indicating that aftershocks can make the structure unreliable. The reliability index for multiple aftershocks was almost the same as that of a single aftershock, which again shows that the structure was affected most by the strongest aftershock.

TABLE 4

TABLE 4. Failure probability of each substructure of inter-story isolated structure.

FIGURE 6

FIGURE 6. Comparison of failure probability of each substructure.

The failure probability for maximum displacement of the isolation layer in each substructure of the inter-story isolated structure was the largest, and the reliability index was the smallest, indicating that the failure mode of the inter-story isolated structure could be attributed mainly to the deformation of the isolation bearing (Table 4 and Figure 5). An informed design of the isolation layer is crucial to the reliability of the inter-story isolated structure.

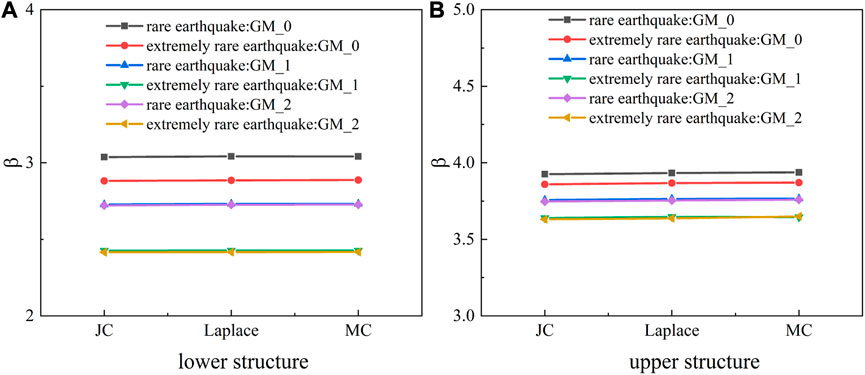
To verify the accuracy of the approximate calculation by the Laplace asymptotic method, the JC method and Monte Carlo method were compared in this paper (Figure 7). The results of the JC method and the Laplace asymptotic method were close to those of the Monte Carlo method, confirming the accuracy of the results obtained by the approximate calculation method. However, compared with the two methods, the results of the Laplace asymptotic method were more accurate. The second-order second-moment method could not utilize the local properties of the performance function near the design check point. The quadratic second-order moment method did take into account non-linear properties such as the concave direction and curvature of the limit state surface near the check point by calculating the second derivative of the performance function, thereby improving the accuracy of the reliability index.

FIGURE 7

FIGURE 7. Comparison of failure probability of different methods.

The inter-story isolated structure could be regarded as a series structure system. Assuming that there is no correlation between the failure modes of the inter-story isolated structure, the overall reliability probability of the story isolation structure is expressed as

$\mathrm{P}\mathrm{s}=\left(1-\mathrm{P}\mathrm{f}\mathrm{b}\right)\times \left(1-\mathrm{P}\mathrm{f}\mathrm{s}\right)\times \left(1-\mathrm{P}\mathrm{f}\mathrm{p}\right).(16)$

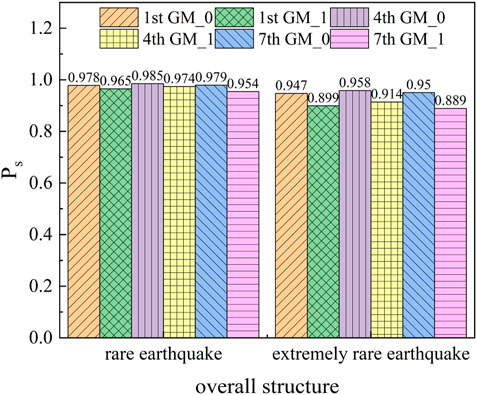
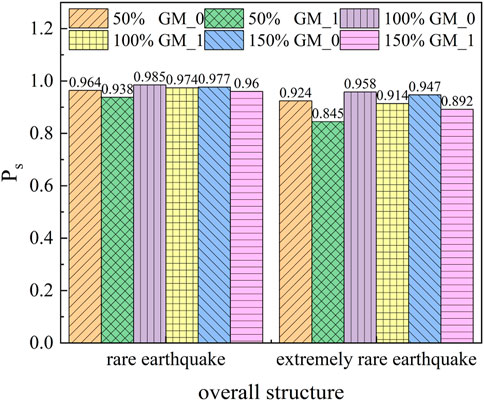
In the formula, P_s is the reliability probability of the whole structure, P_fb is the failure probability of the upper structure, P_fs is the failure probability of the isolation layer, and P_fp is the failure probability of the lower structure. The failure probability of the maximum displacement of the isolation layer was utilized in the failure probability of the isolation layer. The reliability probability of the whole structure was calculated by using the Laplace asymptotic method, and the results are shown in Figure 8.

FIGURE 8

FIGURE 8. Comparison of reliability probability of the overall structure.

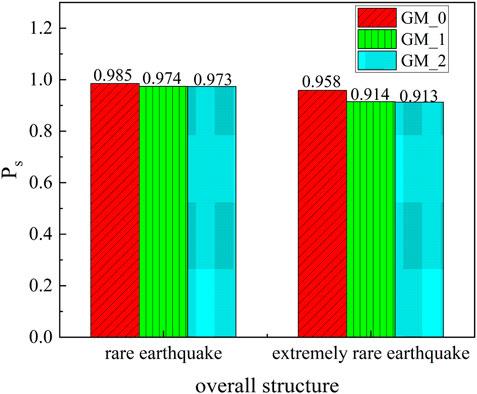
As shown in Figure 8, at the level of a rare earthquake, the reliability probability of the overall structure under the action of the mainshock was 0.985, the reliability probability under a single aftershock was 0.974, and the reliability probability under multiple aftershocks was 0.973. The effect of aftershocks reduced the reliability probability of the overall structure by 1.1%. At an extremely rare earthquake level, the reliability probability of the overall structure under the mainshock was 0.958, the reliability probability under a single aftershock was 0.914, and the reliability probability under multiple aftershocks was 0.913. The effect of aftershocks reduced the reliability probability of the overall structure by 4.4%. In summary, the reliability probability under multiple aftershocks was similar to that under a single aftershock, again confirming the importance of the largest aftershock in reliability. The influence of aftershocks should not be ignored in the design of a story isolation structure.

5 Influence of isolation layer position on the reliability of an inter-story isolated structure under main-aftershock conditions

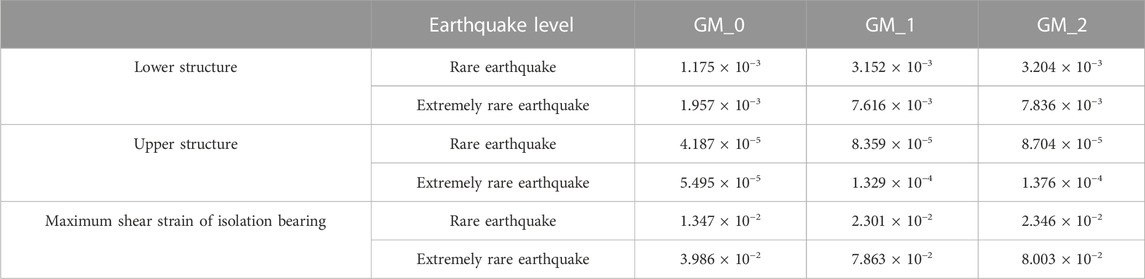
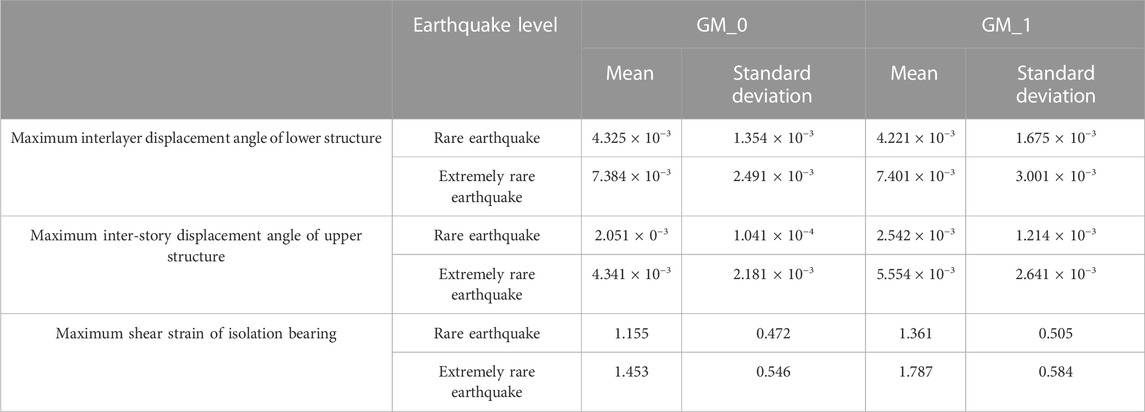
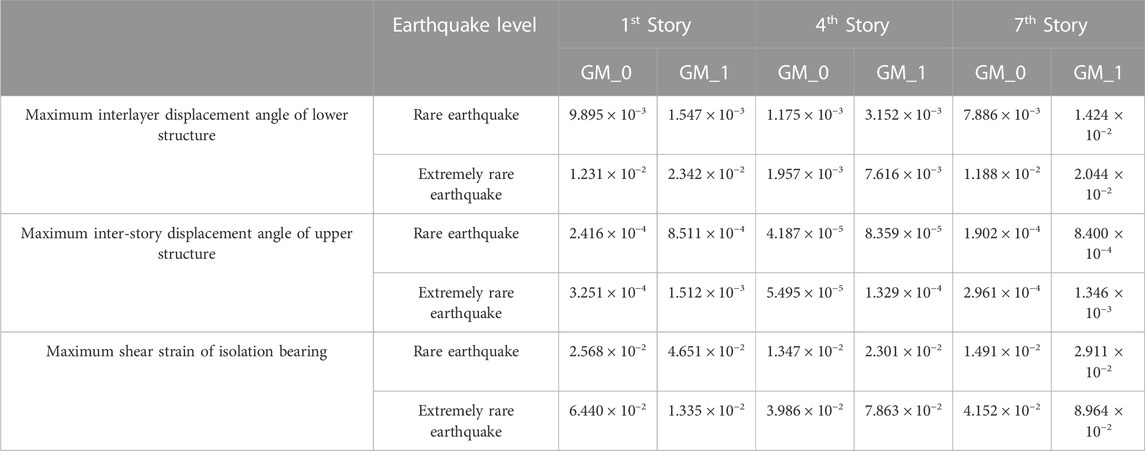
In order to explore the influence of different locations of the isolation layer on reliability under a main-aftershock, the reliability of inter-story isolated structures with isolation layers at the top of the first, fourth, and seventh stories were compared under mainshock and main-aftershock sequences. The mean and standard deviation of isolation layers at the top of the first, fourth, and seventh stories are shown in Tables 5 and 6.

TABLE 5

TABLE 5. Probabilistic characteristic parameters of structural response values of the isolation layer set in the first story.

TABLE 6

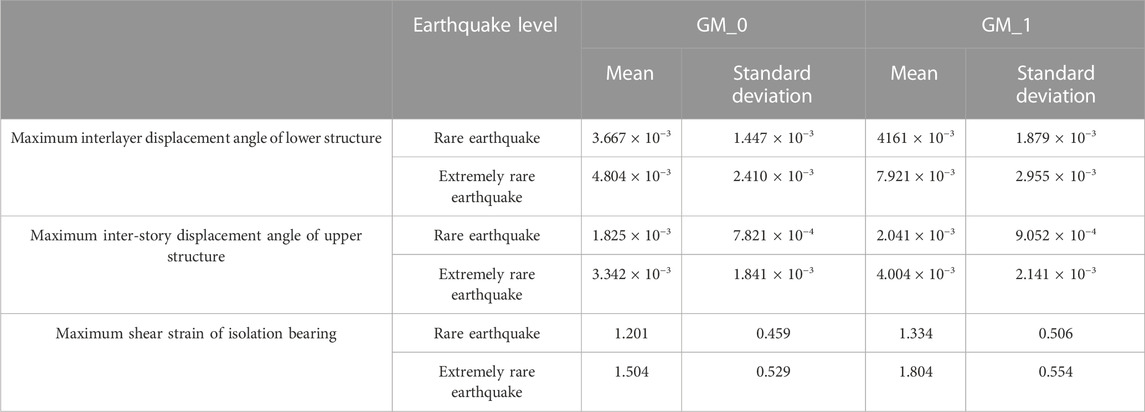
TABLE 6. Probabilistic characteristic parameters of structural response values of the isolation layer set in the seventh story.

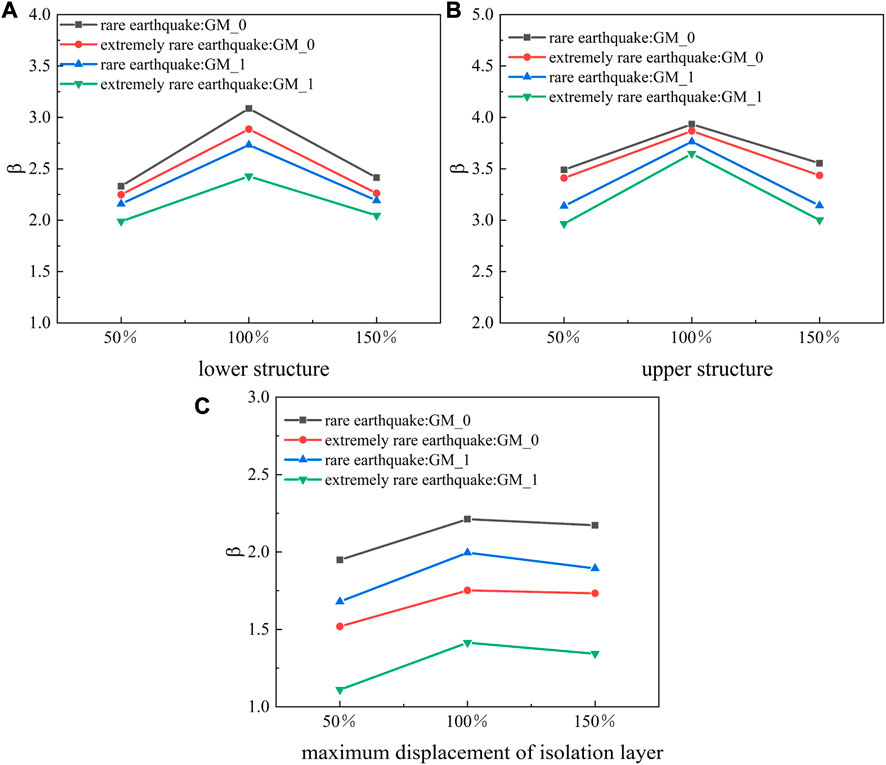
The Laplace asymptotic method was used to calculate the failure probability P_f of each substructure of the inter-story isolated structure with the isolation layer at different positions (Table 7). For the lower structure, the failure probability increased with the increase of the setting position of the isolation layer under different seismic levels. For the upper structure, the failure probability decreased with the increase of the isolation layer position, except for the rare earthquake level main-aftershock. Under the action of the main-aftershock of the rare earthquake level, the failure probability was lowest when the isolation layer was at the top of the fourth story. When the isolation layer was at the top of the fourth layer, the failure probability of the isolation layer was the lowest, followed by the seventh layer. In order to show the influence of aftershocks more intuitively, the reliability index of each substructure is illustrated in Figure 9. It can be seen from Figure 8 that no matter where the isolation layer was located, the aftershocks significantly reduced the reliability index of the structure, making it unreliable.

TABLE 7

TABLE 7. Failure probability of isolation layers set at different stories.

FIGURE 9

FIGURE 9. Comparison of failure probability with different isolation layer positions.

The overall reliability probability of different isolation layer locations was calculated using Eq. 16 and listed in Figure 10. Under the rare earthquake level, the overall reliability probability under the mainshock was the highest at 0.985 when the isolation layer was set at the fourth story, and the overall reliability probability under the main-aftershock was 0.974. At the extremely rare earthquake level, the reliability probability under the mainshock was the highest when the isolation layer was set at the top of the fourth story (0.958), and the reliability probability under the aftershock was 0.914. Under the rare earthquake level, aftershocks reduced the overall reliability probability of the isolation layer at the top of the first story by 1.36%, of the isolation layer at the top of the fourth story by 1.15%, and of the isolation layer at the top of the seventh story by 2.48%. Under the extremely rare earthquake level, aftershocks reduced the overall reliability probability of the isolation layer at the top of the first story by 4.8%, of the isolation layer at the top of the fourth story by 4.4%, and of the isolation layer at the top of the seventh story by 6.01%. Thus, precise isolation layer setting can reduce the impact of aftershocks.

FIGURE 10

FIGURE 10. Comparison of overall reliability probability with different isolation layer positions.

6 Influence of stiffness of isolation bearing on reliability of inter-story isolated structures under main-aftershock sequences

In order to study the influence of the stiffness of the isolation bearing on the reliability of the inter-story isolated structure under main-aftershock conditions, the structural reliability was determined with the isolation structure set at the top of the fourth story for 50% (0.443 kN/mm), 100% (0.886 kN/mm) and 150% (1.329 kN/mm) of the designed post-yield stiffness. The mean and standard deviation for 50% and 150% stiffness are listed in Tables 8 and 9, respectively. The mean and standard deviation for 100% stiffness are shown in Table 3.

TABLE 8

TABLE 8. Probabilistic characteristic parameters of structural response values at 50% stiffness.

TABLE 9

TABLE 9. Probabilistic characteristic parameters of structural response values at 150% stiffness.

The failure probability of each substructure of the inter-story isolated structure under different bearing stiffness levels was calculated by the Laplace asymptotic method (Table 10). Regardless of the seismic conditions, the failure probability of the lower structure, the upper structure, and the isolation layer of the story isolation structure were lowest when the stiffness was 100% of the design stiffness. In order to show the influence of aftershocks more intuitively, the reliability index of each substructure is illustrated in Figure 11. As shown in Figure 10, regardless of the stiffness, the aftershocks significantly reduced the reliability index of the structure and made the structure unreliable.

TABLE 10

TABLE 10. Failure probability at different bearing stiffness levels.

FIGURE 11

FIGURE 11. Comparison of failure probability with different bearing stiffness.

The overall reliability probability of different stiffness was calculated by Eq. 16 in Figure 11. As shown in Figure 12, under different seismic levels, the reliability probability was the highest for 100% stiffness, whether under mainshock only or with main-aftershocks. At the rare earthquake level, the aftershocks reduced the overall reliability probability at 50% stiffness by 2.65%, at100% stiffness by 1.15%, and at 150% stiffness by 1.68%. At the extremely rare earthquake level, aftershocks reduced the overall reliability probability at 50% stiffness by 7.88%, 100% stiffness by 4.4%, and 150% stiffness by 5.41%. Thus, the standard 100% stiffness of the isolation bearing will reduce the impact of aftershocks.

FIGURE 12

FIGURE 12. omparison of overall reliability probability with different bearing stiffness.

7 Discussion

In this study, finite element software was utilized to establish an inter-story isolated structure model, and an elastic–plastic time history analysis was carried out at different seismic levels. The reliability probability of the structure under the action of a single mainshock and main-aftershock sequence was analyzed using the Laplace asymptotic method. The failure probability of each substructure of the inter-story isolated structure under the action of main-aftershock sequence was studied. However, the research was mainly about the numerical analysis of a framed inter-story isolation structure. Different structures or parameter settings might lead to errors in the results. Subsequently, the randomness of the structure was tested (Castaldo et al., 2015; Johari et al., 2021). The parameters of the random variables formed a sample space (Xu and Feng, 2018; Shi and Du, 2019; Amjadi and Johari, 2022) of randomly selected structural parameters and the shaking table test (Mei et al., 2018; Huang et al., 2020b) was used to verify the results of this study.

The overall reliability probability of the inter-story isolated structure under the action of a main-aftershock demonstrated that aftershocks have a strong influence on reliability probability. The construction of the main-aftershock sequence only used the repetition method for artificial synthesis. The main-aftershock sequence construction could also use natural ground motion (Goda and Taylor, 2012; Li et al., 2014), random artificial synthesis (Hatzigeorgiou and Beskos, 2009; Goda and Taylor, 2012), or attenuated artificial synthesis (Zhou et al., 2018; Chang et al., 2020). The influence of the main-aftershock sequence as constructed by other methods on structural reliability needs further study.

The JC method in the linear second-order moment method, the Laplace asymptotic method in the quadratic second-order moment method, and the Monte Carlo method were used to calculate reliability. However, there are many other calculation methods for reliability such as the response surface method (Olsson et al., 2003) and the probability density evolution method (Gu et al., 2018; Pang et al., 2018; Ye et al., 2021; Chang et al., 2022). Different methods with specific influences on the failure probability of the structure could be tested in subsequent research.

The selection of statistical parameter indices could have a certain impact on the results of reliability analysis. In this study the response value of the elastic–plastic time history of the structure was analyzed, and the damage model (Liu et al., 2015; Du et al., 2016; Huang et al., 2020c; Hua and Ye, 2022) considered the maximum deformation and cumulative hysteretic energy of the structure at the same time. Damage could be used as a parametric index for reliability analysis in subsequent studies.

8 Conclusions

In this study, the three-dimensional finite element model of an inter-story isolated structure was established and an elastic–plastic time history analysis was carried out. The seismic response parameters of the structure were obtained, and the probability distribution types and probability characteristic parameters were evaluated. The reliability of the inter-story isolated structure under a single mainshock and main-aftershock sequences was obtained using the Laplace asymptotic method, and the influence of aftershock number, isolation layer location, and stiffness of isolation bearing on the structure was determined. From the results of the aforementioned calculations and analysis, the following conclusions can be drawn:

(1) Aftershocks increase the failure probability of each substructure under different seismic levels. The failure probability of the lower structure was the most affected by the main-aftershock sequence, which was 3.89 times that of the mainshock alone. The failure probability of the maximum displacement of the isolation layer in each substructure of the inter-story isolated structure was the largest, which indicates that the failure mode of the inter-story isolated structure was mainly the deformation overrun of the isolation bearing. The reliability probability of multiple aftershocks was similar to that of a single aftershock, indicating that the largest aftershock plays a major role in reliability.

(2) The Laplace asymptotic method is highly accurate. The quadratic second-order moment method considers the concave direction, curvature, and other non-linear properties of a limit state surface near the checking point by calculating the second derivative of the performance function, which improved the accuracy of reliability compared with the linear second-order moment method.

(3) At the rare earthquake level, aftershocks reduced the overall reliability probability of the isolation layer at the top of the first story by 1.36%, the fourth story by 1.15%, and the seventh story by 2.48%. Under an extremely rare earthquake event, aftershocks reduced the overall reliability probability of the isolation layer at the top of the first story by 4.8%, the fourth story by 4.4%, and the seventh story by 6.01%. Choosing the optimal isolation layer setting can reduce the impact of aftershocks.

(4) At the rare earthquake level, aftershocks reduced the overall reliability probability of 50% stiffness by 2.65%, 100% stiffness by 1.15%, and 150% stiffness by 1.68%. Under an extremely rare earthquake event, aftershocks reduced the overall reliability probability at 50% stiffness by 7.88%, at 100% stiffness by 4.4%, and at 150% stiffness by 5.41%. Choosing the optimal stiffness of the isolation bearing can reduce the influence of aftershocks. For the proper application of an inter-story isolation structure, a reasoned isolation layer design is critically important for structural reliability.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

FY, DL, CL, and SY contributed to conception and design of the study. FY wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The writers gratefully acknowledge the financial support of the Humanities and Social Science Research Project of Hebei Education Department (SZ2021012).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Afsar Dizaj, E., Salami, M. R., and Kashani, M. M. (2021). Seismic vulnerability assessment of ageing reinforced concrete structures under real mainshock-aftershock ground motions. Struct. Infrastructure Engineering1 17, 1674. doi:10.1080/15732479.2021.1919148

CrossRef Full Text | Google Scholar

Aloisio, A., Contento, A., Alaggio, R., Briseghella, B., and Fragiacomo, M. (2022). Probabilistic assessment of a light-timber frame shear wall with variable pinching under repeated earthquakes. J. Struct. Eng. 148, 4022178. doi:10.1061/(asce)st.1943-541x.0003464

CrossRef Full Text | Google Scholar

Aloisio, A., Pelliciari, M., Bergami, A. V., Rocco, A., Bruno, B., Massimo, F., et al. (2022). Effect of pinching on structural resilience: Performance of reinforced concrete and timber structures under repeated cycles. Struct. Infrastructure Eng. 17, 1. doi:10.1080/15732479.2022.2053551

CrossRef Full Text | Google Scholar

Amadio, C., Fragiacomo, M., and Rajgelj, S. (2003). The effects of repeated earthquake ground motions on the non-linear response of SDOF systems. Earthq. Eng. Struct. Dyn. 32, 291–308. doi:10.1002/eqe.225

CrossRef Full Text | Google Scholar

Amjadi, A. H., and Johari, A. (2022). Stochastic nonlinear ground response analysis considering existing boreholes locations by the geostatistical method. Bull. Earthq. Eng. 20, 2285–2327. doi:10.1007/s10518-022-01322-1

CrossRef Full Text | Google Scholar

Augenti, N., and Parisi, F. (2010). Learning from construction failures due to the 2009 L’Aquila, Italy, earthquake. J. Perform. Constr. Facil. 24, 536–555. doi:10.1061/(asce)cf.1943-5509.0000122

CrossRef Full Text | Google Scholar

Castaldo, P., Palazzo, B., and Della Vecchia, P. (2015). Seismic reliability of base-isolated structures with friction pendulum bearings. Eng. Struct. 95, 80–93. doi:10.1016/j.engstruct.2015.03.053

CrossRef Full Text | Google Scholar

Chang, Z., Catani, F., Huang, F., Liu, G., Meena, S. R., Huang, J., et al. (2022). Landslide susceptibility prediction using slope unit-based machine learning models considering the heterogeneity of conditioning factors. J. Rock Mech. Geotechnical Eng. doi:10.1016/j.jrmge.2022.07.009

CrossRef Full Text | Google Scholar

Chang, Z., Du, Z., Zhang, F., Huang, F., Chen, J., Li, W., et al. (2020). Landslide susceptibility prediction based on remote sensing images and GIS: Comparisons of supervised and unsupervised machine learning models. Remote Sens. 12, 502. doi:10.3390/rs12030502

CrossRef Full Text | Google Scholar

Clough, R. W. (1966). Effect of stiffness degradation on earthquake ductility requirements. Proc. Jpn. Earthq. Eng. symposium 2, 35. doi:10.1002/eqe.4290020104

CrossRef Full Text | Google Scholar

Dang, Y., Zhang, Z., and Tao, L. (2018). Study on aseismic relibaility of isolated structures based on probability statistics method. Eng. Mech. 35, 146–154. doi:10.6052/j.issn.1000-4750.2017.07.0591

CrossRef Full Text | Google Scholar

De Luca, A., and Guidi, L. G. (2019). State of art in the worldwide evolution of base isolation design. SOIL Dyn. Earthq. Eng. 125, 105722. doi:10.1016/j.soildyn.2019.105722

CrossRef Full Text | Google Scholar

Du, D., Wang, S., and Liu, W. (2016). Reliability-based damage performance of base-isolated structures. J. Vib. Shock 35, 222–227.

Google Scholar

Faiella, D., Calderoni, B., and Mele, E. (2022). Seismic retrofit of existing masonry buildings through inter-story isolation system: A case study and general design criteria. J. Earthq. Eng. 26, 2051–2087. doi:10.1080/13632469.2020.1752854

CrossRef Full Text | Google Scholar

Fema, P. (2012). Seismic performance assessment of buildings Volume 1-Methodology. California: Applied Technology Council.

Google Scholar

Goda, K., and Taylor, C. A. (2012). Effects of aftershocks on peak ductility demand due to strong ground motion records from shallow crustal earthquakes. Earthq. Eng. Struct. Dyn. 41, 2311–2330. doi:10.1002/eqe.2188

CrossRef Full Text | Google Scholar

Gu, Z., Wang, S., and Du, D. (2018). Random seismic responses and reliability of isolated structures based on probability density evolution method. J. Vib. Shock 37, 97–103.

Google Scholar

Gutenberg, B. (2013). Seismicity of the earth and associated phenomena. ENGLAND: Read Books Ltd.

Google Scholar

Hatzigeorgiou, G. D., and Beskos, D. E. (2009). Inelastic displacement ratios for SDOF structures subjected to repeated earthquakes. Eng. Struct. 31, 2744–2755. doi:10.1016/j.engstruct.2009.07.002

CrossRef Full Text | Google Scholar

Hua, W., and Ye, X. (2022). Study on two-parameter criterion of reticulated shell structures under earthquake action based on Park-Ang damage model. Eng. Mech. 39, 48–57. doi:10.6052/j.issn.1000-4750.2021.05.0375

CrossRef Full Text | Google Scholar

Huang, F., Cao, Z., Guo, J., and Jiang, S. H. (2020a). Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. CATENA 191, 104580. doi:10.1016/j.catena.2020.104580

CrossRef Full Text | Google Scholar

Huang, F., Cao, Z., Jiang, S., Zhou, C., Huang, J., and Guo, Z. (2020b). Landslide susceptibility prediction based on a semi-supervised multiple-layer perceptron model. Landslides 17, 2919–2930. doi:10.1007/s10346-020-01473-9

CrossRef Full Text | Google Scholar

Huang, F., Zhang, J., Zhou, C., Wang, Y., Huang, J., and Zhu, L. (2020c). A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 17, 217–229. doi:10.1007/s10346-019-01274-9

CrossRef Full Text | Google Scholar

Huang, X., Wang, N., and Du, Y. (2019). Reliability analysis of the vertical progressive collapse of base-isolated frame-wall structures under earthquakes. Eng. Mech. 36, 89–94. doi:10.6052/j.issn.1000-4750.2018.07.0389

CrossRef Full Text | Google Scholar

Jiang, S., Huang, J., Huang, F., Yang, J., Yao, C., and Zhou, C. B. (2018). Modelling of spatial variability of soil undrained shear strength by conditional random fields for slope reliability analysis. Appl. Math. Model. 63, 374–389. doi:10.1016/j.apm.2018.06.030

CrossRef Full Text | Google Scholar

Jing, L., Liang, H., Li, Y., and Liu, C. (2011). Characteristics and factors that influenced damage to dams in the Ms 8.0 Wenchuan earthquake. Earthq. Eng. Eng. Vib. 10, 349–358. doi:10.1007/s11803-011-0071-3

CrossRef Full Text | Google Scholar

Johari, A., Amjadi, A. H., and Heidari, A. (2021). Stochastic nonlinear ground response analysis: A case study site in Shiraz, Iran. Sci. Iran. 28, 2070–2086.

Google Scholar

Joyner, W. B., and Boore, D. M. (1982). Prediction of earthquake response spectra: US geological survey open-file report. Reston, Virginia: U.S. Geological Survey.

Google Scholar

Keivan, A., Zhang, R., Keivan, D., Phillips, B. M., Ikenaga, M., and Ikago, K. (2022). Rate-independent linear damping for the improved seismic performance of inter-story isolated structures. J. Earthq. Eng. 26, 793–816. doi:10.1080/13632469.2019.1693444

CrossRef Full Text | Google Scholar

Kossobokov, V. G., and Nekrasova, A. K. (2019). Aftershock sequences of the recent major earthquakes in New Zealand. PURE Appl. Geophys. 176, 1–23. doi:10.1007/s00024-018-2071-y

CrossRef Full Text | Google Scholar

Li, Y., Song, R., and Van De Lindt, J. W. (2014). Collapse fragility of steel structures subjected to earthquake mainshock-aftershock sequences. J. Struct. Eng. 140, 4014095. doi:10.1061/(asce)st.1943-541x.0001019

CrossRef Full Text | Google Scholar

Liu, B., Bai, S., and Xu, Y. (1998). Expermental study of low-cyclic behavior of concrete columns. Earthq. Eng. Eng. Dyn. 89, 82. doi:10.13197/j.eeev.1998.04.012

CrossRef Full Text | Google Scholar

Liu, X., Zhang, Y., and Liu, Y. (2017). Random response and dynamic reliability of story isolation structure. J. Guangzhou Univ. Sci. Ed. 16, 50–55.

Google Scholar

Liu, Y., Liu, W., and He, W. (2015). Damage performance evaluation of eccentric isolated struture system considering impact under long-period ground motions. J. Vibartion Eng. 28, 910–917. doi:10.16385/j.cnki.issn.1004-4523.2015.06.008

CrossRef Full Text | Google Scholar

Liu, Y., Liu, X., and Tan, P. (2019). Dynamic reliability for inter-story hybrid isolation structure. J. Vib. Eng. 32, 324–330. doi:10.16385/j.cnki.issn.1004-4523.2019.02.016

CrossRef Full Text | Google Scholar

McKenna, F. T. (1997). Object-oriented finite element programming: Frameworks for analysis, algorithms and parallel computing. Berkeley: University of California.

Google Scholar

Mei, Z., Hou, W., and Guo, Z. (2018). Shaking table tests and dynamic reliability analysis for aseismic structures with viscous dampers. J. Vib. Shock 37, 136–142. doi:10.13465/j.cnki.jvs.2018.03.022

CrossRef Full Text | Google Scholar

Olsson, A., Sandberg, G., and Dahlblom, O. (2003). On Latin hypercube sampling for structural reliability analysis. Struct. Saf. 25, 47–68. doi:10.1016/s0167-4730(02)00039-5

CrossRef Full Text | Google Scholar

Pang, R., Xu, B., Zou, D., and Kong, X. (2018). Stochastic seismic performance assessment of high CFRDs based on generalized probability density evolution method. Comput. GEOTECHNICS 97, 233–245. doi:10.1016/j.compgeo.2018.01.016

CrossRef Full Text | Google Scholar

Qu, J., and Pan, C. (2022). Incremental dynamic analysis considering main aftershock of structures based on the correlation of maximum and residual inter-story drift ratios. Appl. Sci. 12, 2042. doi:10.3390/app12042042

CrossRef Full Text | Google Scholar

Qu, Z., and Ye, L. (2011). Strength deterioration model based on effective hysteretic energy dissipation for RC members under cyclic loading. Eng. Mech. 28, 45–51.

Google Scholar

Shi, C., and Du, Y. (2019). Robustness analysis on progressive collapse of isolation structure based on double randomness of structure and seismic wave. J. Hunan Univ. Sci. 46, 11–20. doi:10.16339/j.cnki.hdxbzkb.2019.09.002

CrossRef Full Text | Google Scholar

Shin, T., and Teng, T. (2001). An overview of the 1999 chi-chi, taiwan, earthquake. Bull. Of Seismol. Soc. Of Am. 91, 895–913. doi:10.16339/j.cnki.hdxbzkb.2019.09.002

CrossRef Full Text | Google Scholar

Standard (2021). Standard for seismic isolation design of building: GB/T 51408-2021. Beijing: Beijing Jihua Presss.

Google Scholar

Su, Y., Li, S., and Su, Y. (2018). Second-order second-moment evaluation method for failure probability of rock-soil structure. J. Hunan Univ. Sci. 45, 120–126. doi:10.16339/j.cnki.hdxbzkb.2018.11.015

CrossRef Full Text | Google Scholar

Sun, Z., Liu, W., and Wang, S. (2013). Parametric optimization of a base-isolated structure based on system reliability. J. Vib. Shock 32, 6–10.

Google Scholar

Tauheed, A., and Alam, M. (2023). “Seismic response of RC frame with stiffness irregularity under sequential loading of main shock and repeated aftershocks,” in International Conference on Advances in Structural Mechanics and Applications. Springer, Germany, 06-08 October (Berlin: ASMA), 17–38.

CrossRef Full Text | Google Scholar

Torti, M., Sacconi, S., Venanzi, I., and Ubertini, F. (2022). Monitoring-informed life-cycle cost analysis of deteriorating RC bridges under repeated earthquake loading. J. Struct. Eng. 148, 4022145. doi:10.1061/(asce)st.1943-541x.0003449

CrossRef Full Text | Google Scholar

Wu, B., and Ou, J. (1993). Response and damage analysis of reinforced concrete structures under main shock and aftershocks. J. Build. Eng. 53, 45. doi:10.15959/j.cnki.0254-0053.1993.04.008

CrossRef Full Text | Google Scholar

Wu, D., Li, J., Tan, P., Yan, X., Wei-gang, H., et al. (2017). Seismic vulnerability analysis of series isolated structural systems. Eng. Mech. 34, 227–232. doi:10.6052/j.issn.1000-4750.2016.04.S047

CrossRef Full Text | Google Scholar

Wu, Y., Zheng, Z., and Yan, G. (2021). Shaking table test of pile-soil inter-story isolated structure under far-field long-period ground motion. J. Build. Eng. 42, 11–22. doi:10.14006/j.jzjgxb.2020.0474

CrossRef Full Text | Google Scholar

Xu, J., and Feng, D. (2018). Seismic response analysis of nonlinear structures with uncertain parameters under stochastic ground motions. SOIL Dyn. Earthq. Eng. 111, 149–159. doi:10.1016/j.soildyn.2018.04.023

CrossRef Full Text | Google Scholar

Ye, D., Liu, Y., and Qin, X. (2021). Random response analysis of base-isolated structures based on probability density evolution. China Earthq. Eng. J. 43, 1487–1494. doi:10.3969/j.issn.1000-0844.2021.06.1487

CrossRef Full Text | Google Scholar

Yu, H., Tao, K., and Cai, C. (2013). Focal mechanism solutions of the tohoku—oki earthquake sequence and their geodynamical implications. Chin. J. Geophys. 56, 2655–2669. doi:10.6038/cjg20130815

CrossRef Full Text | Google Scholar

Zhai, C., Ji, D., Wen, W., Lei, W., Xie, L., and Gong, M. (2016). The inelastic input energy spectra for main shock–aftershock sequences. Earthq. SPECTRA 32, 2149–2166. doi:10.1193/121315eqs182m

CrossRef Full Text | Google Scholar

Zhang, D., Shu, S., and Gong, W. (2022). Reliability analysis of slope based on neural network and Laplace asymptotic method. J. Civ. Eng. Manag. 39, 131–136. doi:10.13579/j.cnki.2095-0985.2022.20210982

CrossRef Full Text | Google Scholar

Zhang, M., and Jin, F. (2015). Structural reliability calculation. Beijing: Science Press.

Google Scholar

Zheng, W., Lu, J., and Li, S. (2021). Improved second-order second-moment method applying to reliability analysis for slope project. J. Civ. Eng. Manag. 38, 205–210. doi:10.13579/j.cnki.2095-0985.2021.02.029

CrossRef Full Text | Google Scholar

Zhou, F., Zhang, Y., and Tan, P. (2009). Theoretical study on story isolation system. China Civ. Eng. J. 42, 1–8. doi:10.15951/j.tmgcxb.2009.08.008

CrossRef Full Text | Google Scholar

Zhou, Z., Yu, X., and Lv, D. (2018). Fragility analysis and safety evaluation of reinforced concrete frame structures subjected to mainshock-aftershock earthquake sequences. Eng. Mech.35, 134–145. doi:10.6052/j.issn.1000-4750.2017.07.0588

CrossRef Full Text | Google Scholar