Fracturing criterion of rock hydrofracturing considering pore pressure effect

Traditional hydraulic fracturing theory believes that as the initial pore pressure increases, the breakdown pressure of the rock will decrease. Previous experimental studies have shown that the breakdown pressure of rock hydraulic fracturing may increase with the increase of initial pore pressure (gradient), which cannot be explained by traditional theory. The current understanding of the effect of pore pressure and its gradient during hydraulic fracturing is still unclear. In this study, the pore pressure effect of rock hydraulic fracturing is analyzed based on a large number of macroscopic and microscopic phenomena of rock hydraulic fracturing in the previous study. Then, a new fracture criterion of rock fracturing is built considering the pressure-gradient effect. This new fracture criterion can reflect the main influence factors, including the rock particle size, porosity, pumping flow, inner diameter of open hole section, length of main fracture, height of main fracture (or length of open hole section), fluid viscosity, pore pressure, minimum initial in situ stress and rock tensile strength. The new fracture criterion is examined by the rock fracturing experiment which considering the pressure-gradient effect. The results show that the proposed fracture criterion considering the pore pressure effect can well predict the breakdown pressure of rock, and the prediction trend is consistent with the experimental results. The average error is less than 1% when adopting the present fracture criterion. The parameter sensitivity of the fracture criterion is analyzed. Results show that the fracture pressure increases with the rock porosity and this trend becomes more apparent with a larger initial pore pressure. It shows that the fracture pressure increases with the pumped flow rate. Besides, it shows that the fracture pressure decreases when increasing the particle size of the rock, but the decreasing trend gradually slows down. The research results can provide a theoretical basis for the mechanism of rock hydraulic fracturing and the structural modification effect of fluids in rock engineering.

1 Introduction

Hydrofracturing refers to injecting high-pressure fluid (water, gas, etc.) into the formation through drilling, which induces the wellbore broken and fractures propagation under the action of hydro-mechanical coupling. Finally, artificial fractures are formed in the formation (Fjaer et al., 2008; King, 2012). Hydraulic fracturing is the most widely used and mature hydrofracturing technology. At present, it has been successfully applied to the development of shale oil and gas, tight oil and gas, coalbed methane and dry hot rock (Clarkson et al., 2016; Hou et al., 2018; Li et al., 2018; Zhang et al., 2018). Recently, hydraulic fracturing technology has been widely used in the coal industry. It is utilized for control of hard roofs, weakening of hard top coal, improvement of coal seam permeability, prevention of coal and gas outbursts, and rock bursts, which have achieved remarkable results (Huang et al., 2016; Huang et al., 2017; Wu and Kang, 2017; Lv et al., 2020).

The hydraulic fracturing mechanism for coal and rock mass refers to the essential reason of borehole fracturing under the coupling effect of fluid pressure and solid stress field. It is to explain how coal and rock mass is cracked during hydraulic fracturing. It includes analysis of fracture mode and establishment of fracture criterion, prediction of breakdown pressure and determination of fracture direction. Fracture modes include tensile fracture and shear fracture, corresponding to tensile fracture criterion and shear fracture criterion.

Breakdown pressure refers to the pressure at which the high-pressure water injected into the wellbore (borehole) causes the wellbore (borehole) to rupture during the hydraulic fracturing. It is also known as the initiation pressure. The size of the breakdown pressure is mainly determined by the in-situ stress, the tensile strength of the stratum and the initial pore pressure. Breakdown pressure is a key technical parameter of fracturing design and construction process, which directly affects the effect of fracturing construction operations. The failure of hydraulic fracturing construction operations due to inaccurate prediction of breakdown pressure often occurs during engineering construction (Cuisiat and Haimson, 1992; Enever et al., 1992; Guo et al., 1993). Therefore, it is significant to study the fracture mechanism of coal and rock mass and give the corresponding breakdown pressure prediction formula for coal and rock mass hydraulic fracturing construction.

The early classical hydraulic fracturing theory believes that under the borehole water pressure and stress field, the borehole wall would undergo tensile fracture, resulting in a single hydraulic fracture. At the same time, the effective stress principle is introduced to consider the initial pore pressure of the stratum. The fracture process of rock hydraulic fracturing is analyzed, and many theoretical calculation formulas of the breakdown pressure are derived (Ito and Hayashi, 1991; Hossain et al., 2000; Huang et al., 2012; Zhang et al., 2011; Detournay and Carbonell, 1997; Jeffrey, 1989; Hubbert and Willis, 1957). Among them, the most widely used model is the classic H-W formula proposed by Hubbret M.K. and Willis D G in 1957 (Hubbert and Willis, 1957).

$P_b=3{\sigma }_h-{\sigma }_H+T-P_0(1)$

Where ${\sigma }_h$ is the minimum horizontal principal stress, MPa; ${\sigma }_H$ is the maximum horizontal principal stress, MPa; $T$ is the rock tensile strength, MPa; $P_0$ is the rock pore pressure, MPa. This formula uses elastic theory to analyze the stress distribution around the borehole before fracturing. It is derived based on the maximum tensile stress strength criterion. Besides, it is aimed at the fracturing process of impermeable rock masses without considering the seepage effect of rock pore fluids. Therefore, the calculation results are larger than the actual value.

In 1967, under the assumptions of isotropy, homogeneity and small deformation, Bezalel Haimson and Charles Fairhurst (Haimson and Fairhurst, 1967; Haimson and Fairhurst, 1969) introduced Darcy’s law and Biot’s effective stress principle based on the H-W formula. Then, they proposed the H-F formula for calculating the breakdown pressure of permeable rock.

$P_b=\frac{3{\sigma }_h-{\sigma }_H+T-2\eta P_i}{2\left(1-\eta \right)}(2)$

When the rock is not structurally deformed, there are:

$\eta =\frac{\varphi \left(1-2\upsilon \right)}{2\left(1-\upsilon \right)}(3)$

In the formula, $\eta$ is the parameter of rock permeability, ranging from 0 to ∼.5. $\varphi$ is the porosity of the stratum, and $\upsilon$ is the Poisson’s ratio of the rock. This formula takes into account the influence of filtration of fracturing fluid on the breakdown pressure. For rocks with high permeability, the calculated breakdown pressure is higher than the actual value.

Anderson et al., 1973 proposed the calculation formula of the breakdown pressure under uniform horizontal in-situ stress, which considered the stress concentration of the borehole wall and the influence of pore pressure on the stress and strain of the rock.

$P_b=\frac{2\upsilon }{1-\upsilon }\left(P_v-\beta P_p\right)+\alpha P_p(4)$

Where $P_v$ is the overburden pressure, $P_p$ is the stratum pore pressure, and $\beta$ is the Biot coefficient. This formula is modified on the basis of the H-W formula, but does not consider the influence of tectonic stress on the breakdown pressure.

Huang 1981 revised the H-W formula, and proposed the following formula for calculating breakdown pressure, which comprehensively considered the influence of borehole wall stress concentration, pore pressure, tectonic stress and tensile strength on breakdown pressure.

$P_b=\left(\frac{2\upsilon }{1-\upsilon }+3c_1-c_2\right)\left(P_v-P_p\right)+P_p+{\sigma }_t(5)$

Where $c_1$ and $c_2$ are the two geological structural stress coefficients in the horizontal principal stress direction. ${\sigma }_t$ is the rock tensile strength. The Terzaghi effective stress principle used in H-W is still used to calculate the effective stress in this formula, but the considerations are more comprehensive.

Li and Kong 2000 re-derived the effective stress principle of porous media, and deduced the breakdown pressure formula that can be applied to any permeable rock.

$P_b=\frac{3{\sigma }_h-{\sigma }_H+{\sigma }_t-\phi \frac{1-2\upsilon }{1-\upsilon }{P}_p}{1+{\phi }_c-\phi \frac{1-2\upsilon }{1-\upsilon }}(6)$

Where $\phi$ is the rock porosity, ${\phi }_c$ is the rock contact porosity, and $\upsilon$ is the Poisson’s ratio. This formula effectively unifies the H-W formula and the H-F formula. The basic principle is the same as the H-W formula, and a modified effective stress principle is introduced at the same time.

Compared with the research on tensile failure mechanism in traditional hydraulic fracturing theory, the shear failure mechanism in hydraulic fracturing is rarely involved. In recent years, with the large-scale development of unconventional natural gas resources such as shale gas and coalbed methane, it has been discovered that not a single hydraulic fracture but a complex fracture network system is produced during hydraulic fracturing (Yao et al., 2016). The traditional single fracture theory based on tension fracture can no longer explain the fracture process of unconventional natural gas reservoir hydraulic fracture. Therefore, based on tension fracture and shear fracture, it has become a theoretical problem that studying the fracture mechanism of the fracture network system, which needs to be solved urgently. This problem has gradually become one of the current research hotspots in the field of hydraulic fracturing.

Some studies are conducted on whether the borehole wall undergo shear failure during fracturing. The results show that when the three-dimensional principal stresses are all compressive stresses, shear failure may also occur at the borehole wall (Lockner and Byerlee, 1977). The shear failure condition of the borehole wall is analyzed by the Mohr-Coulomb failure criterion, and the identification method of hole wall failure mode is given (Yang et al., 1993). However, the analysis process is still using the elastic theory. The possibility of shear fracture of borehole wall under compressive principal stress is analyzed. But the effect of fluid pressure in the borehole is ignored during the hydraulic fracturing, and the permeability of the rock is not considered. The source of shear stress that causes shear fracture of borehole wall during the hydraulic fracturing is also not analyzed.

Traditional hydraulic fracturing theory does not consider the permeability of the rock (Hubbert and Willis, 1957; Haimson and Fairhurst, 1967), and uses the tensile fracture criterion to describe its fracture and propagation behavior (Olovyanny, 2005). Pressurized water penetrates into the rock along the fractures, forms pore pressure, and generates pore pressure gradient (Lenoach, 1995; Tang et al., 2002). The influence on pore pressure is mainly based on the effective stress principle of saturated soil mechanics. But the understanding of the influence of pore pressure and its gradient during hydraulic fracturing is still unclear (Takatoshi, 2008). The practice of hydraulic fracturing of gas-bearing coal seams and the previous theoretical experimental research show that the breakdown pressure of hydraulic fracturing may increase with the increase of pore pressure (gradient) (Huang et al., 2018). This is unexplainable by traditional theory. Therefore, it is necessary to deeply understand the effect mechanism of the pore pressure gradient on hydraulic fracturing from the root.

In this study, aiming at the effect of pore pressure and its gradient during hydraulic fracturing, the mesoscopic structure of the rock is taken as the entry point of this study. The mesoscopic effect of fluid pressure on matrix particles during rock hydraulic fracturing is analyzed by constructing a mesoscopic structure model of rock. A rock mesoscopic fracture model considering the effect of pore pressure and its gradient is established. The effect mechanism of pore pressure and its gradient on rock hydraulic fracturing is revealed. The research results can provide a theoretical basis for the mechanism of rock hydraulic fracturing and the structural modification effect of fluids in rock engineering.

2 Pore pressure gradient effect of rock hydraulic fracturing

When the rock hydraulic fracturing experiment is performed, the rose-red dye used in the poster is add to the fracturing fluid. Then stir it evenly, so that the sample is opened to observe the shape of the hydraulic fracture after the experiment (Figure 1). It is found that there is an osmotic water pressure zone at the front of the hydraulic fracture tip. It indicates that the particle bonding plane is permeable before it is fractured in the hydraulic fracturing process. The pressure water is osmotically filtered along the particle bonding plane, forming pore pressure and producing pore pressure gradient. When the borehole walls fracture, the hydraulic fracture tip and the front of the seepage zone expand forward simultaneously. Besides, the front of seepage pressure zone is ahead of the hydraulic fracture tip.

FIGURE 1

FIGURE 1. Rock hydraulic fracturing. (A) Hydraulic fracturing in borehole under true triaxial stress and permeability water pressure zone morphology at hydraulic fracture tip; (B) Microcrack zone at hydraulic fracture tip.

Through the above analysis, it is clear that the following factors must be considered when analyzing the fracture of the matrix particle bonding during hydraulic fracturing: 1) The rock is a permeable pore medium composed of mineral particles and has a certain initial pore pressure; 2) hydraulic fracturing leads to an increase in pore pressure in front of the fracture tip, which in turn generates a pore pressure gradient; 3) seepage caused dynamic water pressure (drop).

3 Construction of rock fracture model considering pore pressure effect

3.1 Typical rock mesoscopic structure

Traditional hydraulic fracturing theory uses the effective stress principle of saturated soil mechanics to deal with the pore pressure when analysing the fracture process of rock. It is believed that the pore pressure and the particle framework share the external load, and the rock is assumed to be an impermeable medium. Therefore, the greater the initial pore pressure, the lower the breakdown pressure of the rock. The theory of hydraulic fracturing has been continuously updated in recent years, especially with the development of numerical calculations. There are many hydraulic fracturing theoretical models considering rock permeability and fluid-solid coupling, but the effect of pore pressure is still analyzed based on the effective stress principle.

When dealing with the problem of rock fracture induced by fluid pressure, pore pressure will affect the seepage process of fluid. Therefore, whether the effective stress principle of saturated soil mechanics is still applicable? This requires deep thinking.

To bypass the principle of effective stress and analyze the mechanism of pore pressure and its gradient on rock hydraulic fracturing, it is necessary to start from the mesoscopic structure of the rock. The effect of pore pressure on the mesoscopic framework of the rock during the hydraulic fracturing can be analyzed by constructing a rock mesoscopic structure model.

Hydraulic fracturing technology is mainly used in sedimentary rock series such as oil and gas reservoirs and coal strata, the typical lithology is sandstone. The mesoscopic structure of the sandstone sample is scanned, and the mesoscopic structure including the matrix structure and pore structure is observed. On this basis, the mesoscopic conceptual model can be abstracted to perform the mesoscopic mechanical analysis and establish the mesoscopic fracture model of rock hydraulic fracturing.

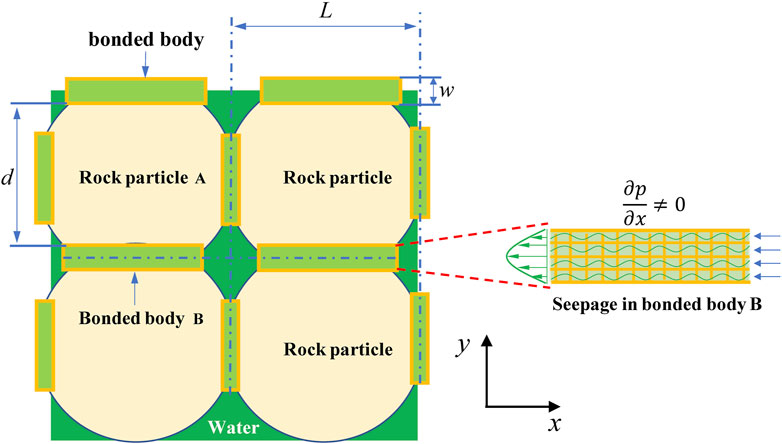
It can be seen from the scan results of the rock mesoscopic structure that the rock is formed by the bonding of mineral particles with pores between the particles. The pores contain fluid and have a certain pore pressure. The particles squeeze each other to form matrix stress under the action of external force. The matrix stress interacts with the pore pressure to form the stable mesoscopic structure of the sandstone. Based on the above analysis, a two-dimensional mesoscopic bond particle model of the rock is constructed, including particles, pores, and bonding plane between particles (Figure 2).

FIGURE 2

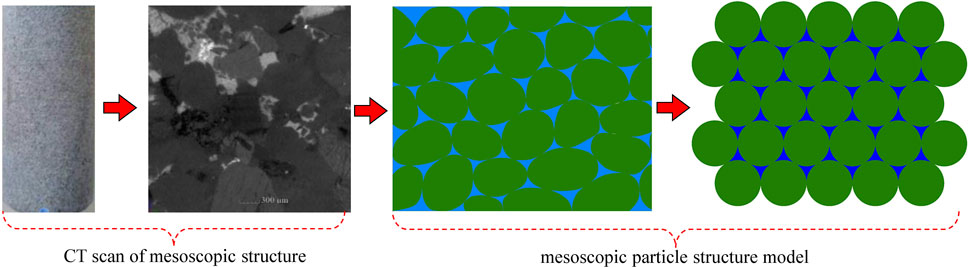
FIGURE 2. Mesoscopic structure of sandstone (Zhao, 2019).

The actual shape of the rock matrix particles is irregular spherical, and the size is different. Their shape and size distribution have certain randomness. This paper focuses on the failure process of the bonding plane between mineral particles under the action of matrix stress and pore pressure. Therefore, the influence of particle shape and size is ignored, and it is simplified into circular equal-diameter particles.

3.2 Basic assumptions

(1) Because real rocks are composed of rock matrix and pores, it is assumed that rocks are composed of basic units that include: i) Rock particles A, and ii) inter-rock binders B.

(2) Assuming that rock particles A are dense non-permeable elastomers.

(3) Assuming that the binder B is a permeable porous medium.

(4) Rock fracture occurs only between the rock particles A and the binder B, including tension and shear.

(5) Seepage exists within the binder under the action of pore pressure gradient, and the flow obeys Darcy’s law.

3.3 Relationship between tensile failure and pore pressure gradient

In the process of water injection and pressurization, the water pressure inside the main fracture is significantly higher than the pore pressure inside the rock. So, there is seepage from the fracture into the rock. The nature of seepage is pressure-driven flow. The direction of seepage flow is the same as the direction of fluid pressure gradient. The fracture in y-direction is used as an example for illustration. The pressure gradient direction is approximately along the x-direction, as shown in Figure 3. The following discussion is based on the case of zero water pressure gradient and the case with water pressure gradient respectively.

(1) At zero water pressure gradient, the bond stress is

${\sigma }_b^{\prime }=p_w^{\prime }-p_w^{\prime }{\phi }_b-p_0{\phi }_0(7)$

Where, $p_w^{\prime }$ is the water pressure in fracture, ${\phi }_b$ is the binder porosity, ${\phi }_0$ is the blind pore porosity, $p_0$ is the pore pressure in the blind pore.

(2) When there is a water pressure gradient (Figure 4), the bond stress is

${\sigma }_b=p_w-\left(p_w-\frac{\partial p}{\partial x}L\right){\phi }_b-p_0{\phi }_0(8)$

Where, $p_w$ is the water pressure in fracture, $\frac{\partial p}{\partial x}L$ indicates the pressure difference between the left and right sides of the particle. When the water pressure in fracture is the same $p_w^{\prime }=p_w$, take $\Delta {\sigma }_b={\sigma }_b-{\sigma }_b^{\prime }$, then

$\Delta {\sigma }_b={\sigma }_b-{\sigma }_b^{\prime }=\frac{\partial p}{\partial x}L{\phi }_b(9)$

Where $\Delta {\sigma }_b$ indicates the bond bear the additional compressive stress due to the existence of the water pressure gradient effect. That is, if the rock particles and the bond undergo tensile failure in the x direction, the additional stress increment which need to be overcome. At this point, the tensile failure condition is

$p_b\ge \left({\sigma }_3+{\sigma }_t\right)+\frac{\partial p}{\partial x}L{\phi }_b(10)$

Where, ${\sigma }_3$ is the minimum in situ stress, ${\sigma }_t$ is the rock tensile strength. A similar idea is used to analyze the effect of water pressure gradient at the crack tip on the rock rupture, as shown in Figure 5. According to the basic theory of seepage and seepage phenomenon, the water pressure gradient at the crack tip approximately shows a semicircular distribution around the tip. The unit body composed of rock particles and binder is selected. Under the action of the water pressure gradient, the additional stress to be borne by the binder along the direction of the water pressure gradient is $\Delta {\sigma }_b$, as shown in Figure 5. Then, the additional stress increment that needs to be overcome for the binder to break at the crack tip is $\Delta {\sigma }_{bx}$. The following relationship exists with $\Delta {\sigma }_b$ and $\Delta {\sigma }_{bx}$

$\Delta {\sigma }_{bx}=\Delta {\sigma }_b\mathit{cos}\beta (11)$

FIGURE 3

FIGURE 3. Size of the basic particle unit.

FIGURE 4

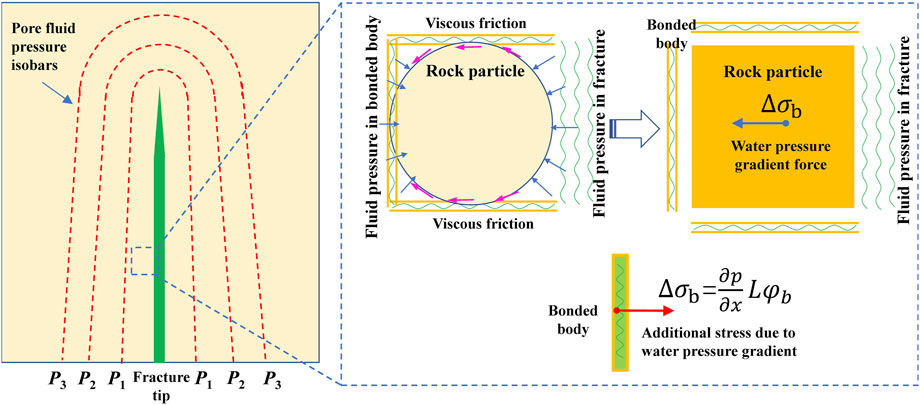
FIGURE 4. Stress diagram of rock unit on the left wall of the crack: additional stress due to water pressure gradient.

FIGURE 5

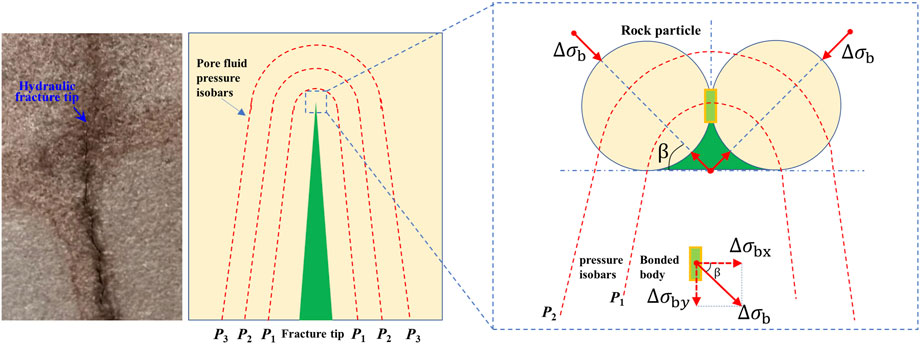
FIGURE 5. Schematic diagram of the stress on the rock unit at the crack tip: the additional stress increment required on the crack tip binder due to the water pressure gradient effect.

Based on the approximate semicircular distribution of the water pressure gradient at the tip of the seam, it is known that $\beta =45^{\circ }$. Therefore, the tensile failure condition of crack tip at this time is

$p_b\ge \left({\sigma }_3+{\sigma }_t\right)+\frac{\sqrt{2}}{2}\frac{\partial p}{\partial x}L{\phi }_b(12)$

3.4 Relationship between shear failure and pore pressure gradient

Considering the general situation, the schematic diagram of the water pressure on the rock particles is shown in Figure 6. Shear failure occurs when the shear force in x-directional is greater than the shear strength between the particle and the binder. Therefore, the shear failure condition in x-direction is

$\frac{{\partial }^{2}p}{\partial x\partial y}{L}^2\ge {\tau }_x(13)$

FIGURE 6

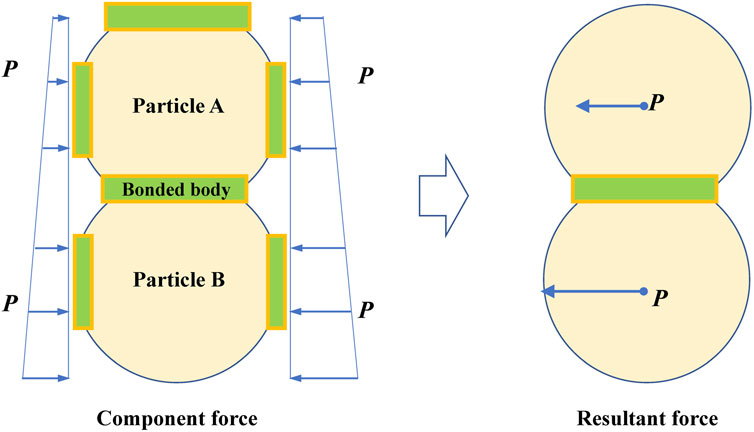
FIGURE 6. Schematic diagram of pore water pressure distribution and resultant force when x-direction shear failure is considered.

For hydraulic fracturing in round borehole, $\frac{{\partial }^{2}p}{\partial x\partial y}$ usually tends to 0. So, shear failure generally does not occur. The failure form is mainly tensile failure. Based on the above analysis, this study mainly considers the rock fracture criterion under the tensile failure condition.

4 Fracturing criterion of rock hydraulic fracturing considering pore pressure effect

4.1 Relationship between rock porosity φ and particle size d and binder size w

The rock is composed of rock matrix particles and pores, which is confirmed by experimental electron microscopy scans. The rock matrix structure is formed by rock particles under the action of in situ stress through bonding. Objectively speaking, rock particles have various shapes, including ellipsoidal, spherical, tetrahedral, hexahedral, and irregular particles. In order to describe rock porosity quantitatively more conveniently, spherical particles are temporarily equated to square particles here, and it is assumed that the rock is composed of square particles and a cemented body. The porosity of rock is mainly related to the size and stacking form of rock particles. Therefore, under the above assumptions, the characteristic length of the rock particles and the width of the binder are the keys to describe the rock porosity. Based on the above assumptions, the definition of rock porosity is given as

$\phi ={\phi }_b\left(1-\frac{d^3}{{\left(d+w\right)}^3}\right)={\phi }_b\left(1-\frac{1}{{\left(1+w/d\right)}^3}\right)(14)$

Where d is the rock particle length (size after equivalence for spherical particles), w is the equivalent width of the binder, usually .5≤ ${\phi }_b$ ≤1. In the above porosity definition process, although the assumption of square particle structure is used, the particle characteristic size is based on the approximation of the real rock particle size, and the real porosity is only related to the particle equivalent size. Therefore, the above porosity formula is feasible. For rocks with different porosity characteristics, it is only necessary to adjust the particle size d, binder size w and binder porosity ${\phi }_b$ in the formula to obtain rock materials with the same porosity as the real rock. Denote a=w/d, then

$\phi ={\phi }_b\left(1-\frac{1}{{\left(1+a\right)}^3}\right)(15)$

Rectifying the formula gives

$a={\left(\frac{1}{1-\phi /{\phi }_b}\right)}^{\frac{1}{3}}-1(16)$

4.2 Relationship of pump injection flow rate and pore pressure gradient

The basic particle unit is composed of particle A, its lower side binder Bx, right side binder By, and rear side binder Bz. According to Darcy’s law, the flow rate within the binder is.

$Q_{Bx}=-\frac{\nabla p}{12\mu }L\cdot h^3=-\frac{\partial p}{\partial x}\frac{1}{12\mu }L\cdot {\phi }_b{w}^3(17)$

Where h denotes the seepage channel width, which is equal to the binder width w, $\mu$ is the fluid viscosity, L is the characteristic length of the rock unit, then the flow rate along the x-direction within the particle unit is

$Q_{cx}=Q_{Bx}+Q_{Bz}=-\frac{\partial p}{\partial x}\frac{1}{12\mu }\left(L+d\right)\cdot {\phi }_b{w}^3(18)$

Neglecting the flow direction (negative sign), then the relationship between the pore pressure gradient and the flow rate in the x-direction is

$\frac{\partial p}{\partial x}=\frac{12\mu }{\left(L+d\right)\cdot {\phi }_b{w}^3}{Q}_{cx}(19)$

The relationship between the flow rate Q_cx in the particle cell along the x-direction and the pumping flow rate Q_i is

$Q_{cx}=\frac{L^2}{\left(2\pi R+2L_f\right)L_z}{Q}_i(20)$

Where R is the radius of the injection hole, L_f is the length of the main fracture, and L_z is the length of the naked hole section (or refers to the main fracture height). The final pressure gradient is

$\frac{\partial p}{\partial x}=\frac{6\mu }{\left(L+d\right)\cdot {\phi }_b{w}^3}\frac{L^2}{\left(\pi R+L_f\right)L_z}{Q}_i(21)$

Then the differential pressure is

$\begin{array}{l}\frac{\partial p}{\partial x}L=\frac{12\mu }{\left(L+d\right)\cdot {\phi }_b{w}^3}L{Q}_{cx}=\frac{12\mu }{\left(L+d\right)\cdot {\phi }_b{w}^3}L\frac{L^2}{2\pi R{L}_z}{Q}_i\\ =\frac{12\mu }{\left(2d+ad\right)\cdot {\phi }_b{a}^3{d}^3}\frac{{\left(1+a\right)}^3{d}^3}{\left(2\pi R+2L_f\right)L_z}{Q}_i=\frac{6\mu }{\left(\pi R+L_f\right)L_{z}d}\frac{{\left(1+a\right)}^3}{{\phi }_b\left(2+a\right)a^3}{Q}_i\end{array}(22)$

That is

$\frac{\partial p}{\partial x}L=\frac{6\mu }{\left(\pi R+L_f\right)L_{z}d}\frac{{\left(1+a\right)}^3}{{\phi }_b\left(2+a\right)a^3}{Q}_i(23)$

Considering the porosity factor, then

$\frac{\partial p}{\partial x}L{\phi }_b=\frac{6\mu }{\left(\pi R+L_f\right)L_{z}d}\frac{{\left(1+a\right)}^3}{\left(2+a\right)a^3}{Q}_i(24)$

4.3 Tensile failure criterion of rock hydraulic fracturing considering pore pressure effect

The tensile failure criterion of rock hydraulic fracturing considering pore pressure effect has been given in the previous section, which takes the following form:

$p_b\ge \left({\sigma }_3+{\sigma }_t\right)+\frac{\sqrt{2}}{2}\frac{\partial p}{\partial x}L{\phi }_b(25)$

Then considering the influence of pore pressure pφ^2/3 and combined with the definition of pore pressure gradient effect given in Eq. 24, the following tensile failure criterion of rock hydraulic fracturing is obtained.

$p_b\ge \left({\sigma }_3+p{\phi }^{2/3}+{\sigma }_t\right)+\frac{3\sqrt{2}\mu }{\left(\pi R+L_f\right)L_{z}d}\frac{{\left(1+a\right)}^3}{\left(2+a\right)a^3}{Q}_i(26)$

Consider the effect of instanton deformation on rock particle size d in fluid-solid coupling:

$d=\frac{d_0}{e^{\xi p}}(27)$

Where d₀ is the rock particle diameter at zero pore pressure, $\xi$ is a small amount and determined by experiment.

According to the compressive experiments of rock materials, it is known that the strain per unit length of rock materials before compressive damage is negligible relative to the unit length 1. Analogously, it is known that the compression of the finite pore pressure on the rock particle size is also very limited. Therefore, (27) can be approximated as $d\approx d_0$. Eq. 26 is still applicable to the problem of rock breakdown pressure prediction under the action of fluid-solid coupling.

The above tensile failure criterion takes into account the effects of rock particle size d, porosity φ, pumping flow Q_i, inner diameter of naked hole section R, main fracture length L_f, main fracture height (or length of naked hole section) L_z, fluid viscosity μ, pore pressure, initial minimum in situ stress σ₃, and tensile strength σ_t.

Note: The effect of porosity φ is reflected in parameter a, as detailed in the previous equation; σ₃ denotes the initial minimum in situ stress.

4.4 Shear failure of rock hydraulic fracturing considering pore pressure effect

Shear failure condition in x-direction

$\frac{{\partial }^{2}p}{\partial x\partial y}{L}^2\ge {\tau }_x(28)$

Pore pressure gradient in x-direction

$\frac{\partial p}{\partial x}=\frac{6\mu }{\left(L+d\right)\cdot {\phi }_b{w}^3}\frac{L^2}{\left(\pi R+L_f\right)L_z}{Q}_i(29)$

The physical quantities to the right of the equal sign are all independent of the parameter y, so

$\frac{{\partial }^{2}p}{\partial x\partial y}=\frac{6\mu }{\left(L+d\right)\cdot {\phi }_b{w}^3}\frac{L^4}{\left(\pi R+L_f\right)L_z}\frac{\partial Q_i}{\partial y}=0(30)$

Therefore, there is no shear failure.

5 Experimental verification of fracture criterion

To examine the new fracturing criterion proposed in this paper, we choose the recent experimental data based on hydraulic fracturing to validate the present model.

The experiment was carried out using standard cylindrical coarse sandstone samples, as shown in Figure 7, with a diameter of 50 mm and a height of 100 mm. Drill a cylindrical water injection hole on the end face of the cylindrical rock sample, where the hole length is 65 mm and its diameter is 6 mm. An open hole section with a length of 30 mm is reserved at the bottom of the borehole as the fracture zone. The experiment was carried out on the pseudo triaxial fluid-solid coupling hydraulic fracturing experimental system. For detailed physical experiment parameter settings and experimental steps, please refer to the previous research of our research group (Huang et al., 2018; Zhao, 2019).

FIGURE 7

FIGURE 7. The size of sample (Zhao, 2019).

The mechanical property parameters of rock samples are obtained by averaging the values obtained through multiple tests in indoor experiments. See Table 1 for detailed mechanical property parameters of rock samples.

TABLE 1

TABLE 1. Structural and mechanical characteristic parameters of sample materials (Huang et al., 2018; Zhao, 2019).

During triaxial pressurization experiments, the axial pressure is 12 MPa, and the confining pressure is 8 MPa. Then the experiments were carried out under six different pore pressure conditions, including 0 MPa, 1.5 MPa, 3 MPa, 4.5 MPa, 6 MPa, and 7.5 MPa, respectively (Table 2). The rock fracture pressure obtained from the experiment is summarized in Table 3. From experimental results shown in Table 3, it is found that the fracture pressure of rock samples increases gradually with pore pressure, and there is an approximate linear relationship between the fracture pressure and pore pressure P_b=.4586P_f +12.762 where the linear correlation coefficient reaches R²=.9973.

TABLE 2

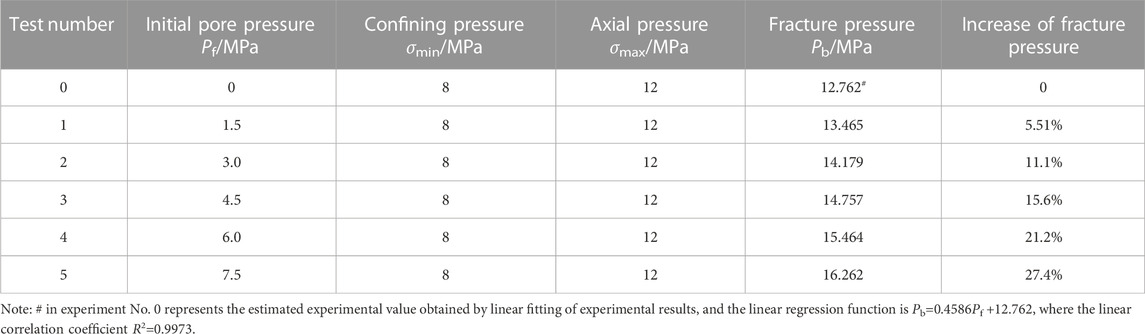
TABLE 2. Pressure environment and corresponding fracture pressure of rock samples in the experiment.

TABLE 3

TABLE 3. Comparison of fracture pressure when the pore pressure is zero.

First, under the condition of zero pore pressure, we compare the fracture pressure obtained from the experiment with that given by the traditional H-W and H-F criterion models. As shown in Table 3, the experimental results are between the traditional H-W and H-F criteria, and are the closest to the L-K model results, which indicates that the experimental results given by us are qualitatively reasonable. This is because when the pore pressure is equal to zero (P_f=0), the traditional H-W criterion usually overestimates the rock fracture pressure, while the H-F criterion usually underestimates the rock fracture pressure, which can also be judged from the two definitions (refer to the previous Formulas shown in introduction). For zero pore pressure, compared with several existing fracture criteria, it is found that the predicted value of fracture pressure given by our fracture criteria is more consistent with the experimental test results, and the relative error of predicted fracture pressure is only −.47%, which is significantly less than the relative error of traditional fracture criteria as shown in Table 4.

TABLE 4

TABLE 4. Basic parameters of rock fracturing.

In addition, by comparing with the experimental data, it is found that the relative error of the predicted fracture pressure in this paper is −.35% when the pore pressure is 1.5 MPa. When the pore pressure is 3.0 MPa, the relative error of the predicted fracture pressure is −.32%. When the pore pressure increases to 4.5 MPa, the relative error of the predicted fracture pressure in this paper is .64%. Under the condition that the pore pressure is 6.0 MPa, the relative error of the predicted fracture pressure in this paper is .67%. When the pore pressure further increases to 7.5 MPa, the relative error of the predicted fracture pressure in this paper is only .13%. The overall prediction error is within 1%. It is worth noting that the contact porosity of .58 (twice the porosity) is selected in the calculation process of L-K criterion in this paper. In fact, according to Li’s rock fracture theory [25], the contact porosity is between the porosity and 1, and the selection of contact porosity will affect the final prediction results. How to accurately measure the contact porosity is also noteworthy, which is crucial for the L-K criterion model.

To compare the predicted accuracy of different models, we draw the fracture pressure lines in the same Figure, as shown in Figure 8. It is seen that fracture pressure predicted by the traditional H-W criterion, H-F criterion and L-K criterion is quite different from the experimental results, especially the predicted trend is contrary to the experimental results. The present experimental results indicate that the fracture pressure of rock increases with the pore pressure, which is also verified by the previous theoretical analysis. However, the prediction results of the traditional fracture criteria show that the fracture pressure of rock decreases with the increase of pore pressure. It is obvious that the traditional fracture criterion is insufficient in accurately predicting the rock fracture pressure under the influence of variable pore pressure. By contrast, the new fracture criterion (HLZX criterion) proposed in this paper can well predict the rock fracture pressure, the prediction trend is consistent with the experimental results, and the predicted values are also very consistent with the experimental results.

FIGURE 8

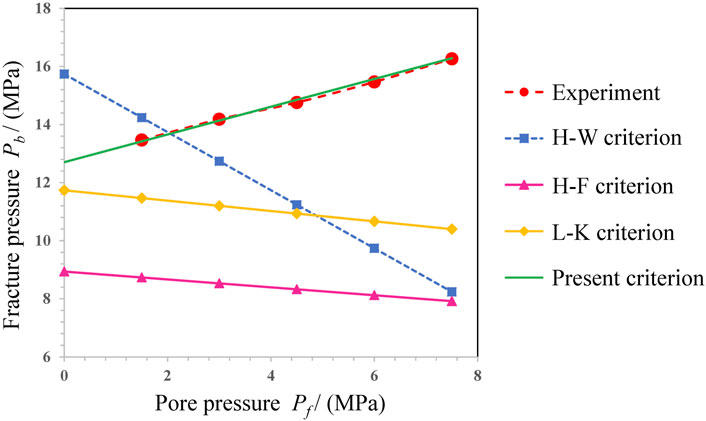
FIGURE 8. Comparison of rock fracture pressures predicted by different fracture criteria under variable pore water pressure.

6 Sensitive parameter analysis

In the calculation process, the parameters set include: minimum geo-stress, rock tensile strength, length of water-injected hole (open hole), inner diameter of water-injected hole, length of main fracture, porosity of bonded body, and fluid viscosity. See Table 4 for specific parameters. In the following part, we discuss the effects of rock porosity, pumping capacity and particle size on rock fracture pressure.

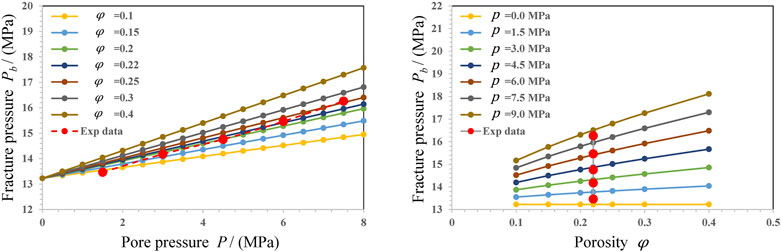
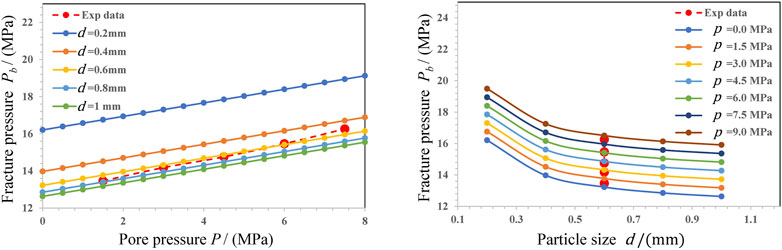
6.1 Influence of rock porosity on fracture pressure

In this part, we discuss the influence of rock porosity on fracture pressure. Results are shown in Figure 9. It is shows that the fracturing pressure of the rock increases with the rock porosity during the hydraulic fracturing process. When the porosity of the rock is larger, its permeability is better. The larger the permeability range of the same water injection pressure in the rock, the smaller the pore pressure gradient formed. Therefore, when the initial pore pressure is constant, the greater the rock porosity, the greater the fracture pressure of rock hydraulic fracturing. The essential reason is that, with the increase of rock porosity, the additional compressive stress $\Delta {\sigma }_b$ increases, which is borne by the bounded body, causing the increase of fracturing pressure. It is also found that the increasing trend of the fracturing pressure is more significant if giving a larger initial pore pressure.

FIGURE 9

FIGURE 9. Influence regularity of the rock porosity φ on the fracture pressure P_b.

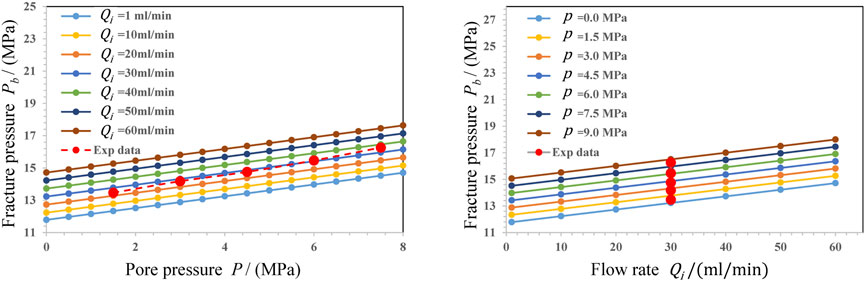
6.2 Influence of pump injection rate on fracture pressure

In this part, we discuss the influence of pump injection rate on the fracture pressure. Results are shown in Figure 10. With the increase of pump flow rate, the fracturing pressure of rock hydraulic fracturing increases correspondingly. It can be seen from Eqs. 3, 8 that the larger the pump injection flow is, the greater the pore pressure gradient on both sides of the particle is the greater the additional pressure stress that the particle binder needs to bear due to the effect of water pressure gradient, therefore, the greater the fracturing pressure of rock hydraulic fracturing is.

FIGURE 10

FIGURE 10. Influence regularity of the pumped flow rate Q_i on the fracture pressure P_b.

6.3 Influence of rock particle size on fracture pressure

In this part, we analyze the influence regularity of the particle size on the rock fracturing pressure. Results are shown in Figure 11. With the increase of the rock particle size, the fracturing pressure of rock hydraulic fracturing decreases, and the decreasing trend gradually slows down. From the formula of rock fracture criterion (3.9), it is found that there is a negative correlation between the fracture pressure P_b and particle size d. Therefore, as the particle size decreases, the fracture pressure increases.

FIGURE 11

FIGURE 11. Influence regularity of the particle size d on the fracture pressure P_b.

7 Conclusion

(1) This study analyzes the pressure-gradient effect of the pore fluid during the rock fracturing process. Based on the observation of the morphology of microcrack zone near the fracture tip, the key factors are identified and clarified when analyzing the fracture of the bonding surface of the skeleton particles in the process of hydraulic fracturing. It shows that the rock is a porous medium composed of mineral particles and has a certain initial pore pressure. It is the fracturing that leading to the change of pore pressure in the front area of the fracture tip, thus producing pore pressure gradient. Besides, there is a hydrodynamic pressure (drop) caused by the seepage.

(2) Based on the mesoscopic structure of rock, this paper analyzes the rock fracturing process when considering the pressure-gradient effect of the pore fluid. Then, a new fracture criterion of rock fracturing is built considering the pressure-gradient effect. This new fracture criterion can reflect the main influence factors, including the rock particle size, porosity, pumping flow, inner diameter of open hole section, length of main fracture, height of main fracture (or length of open hole section), fluid viscosity, pore pressure, minimum initial geo-stress and rock tensile strength.

(3) The new fracture criterion is examined by the rock fracturing experiments which consider the pressure-gradient effect. Results show that the fracture pressure predicted by the traditional criterion is quite different from the experimental results, especially the predicted trend. The traditional theory gives an inversed trend line, which is inconsistent with the experiments. In contrast, the present fracture criterion provides a satisfied prediction, including the variation trend and magnitude of the fracture pressure, which agrees well with the experiments. The average error is less than 1% when adopting the present fracture criterion.

(4) The parameter sensitivity of the fracture criterion is analyzed. Results show that the fracture pressure increases with the rock porosity and this trend becomes more apparent with a larger initial pore pressure. It shows that the fracture pressure increases with the pumped flow rate. Besides, it shows that the fracture pressure decreases when increasing the particle size of the rock, but the decreasing trend gradually slows down.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BH presented the idea and write the original manuscript, HL built the new fracture model, XZ performed the experiment, YX analysis the datas, all authors reviewed the manuscript.

Funding

Financial support for this work, provided by the National Key Research and Development Program of China (No. 2021YFC2902102), the National Natural Science Foundation of China (No. 52004269), is gratefully acknowledged.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anderson, R. A., Ingram, D. S., and Zanier, A. M. (1973). Determining fracture pressure gradients from well logs. J. Pet. Technol. 25 (11), 1259–1268. doi:10.2118/4135-pa

CrossRef Full Text | Google Scholar

Clarkson, C. R., Ghaderi, S. M., Kanfar, M. S., Iwuoha, C., Pedersen, P., Nightingale, M., et al. (2016). Estimation of fracture height growth in layered tight/shale gas reservoirs using flowback gas rates and compositions–Part II: Field application in a liquid-rich tight reservoir. J. Nat. Gas. Sci. Eng. 36, 1031–1049. doi:10.1016/j.jngse.2016.11.014

CrossRef Full Text | Google Scholar

Cuisiat, F. D., and Haimson, B. C. (1992). Scale effects in rock mass stress measurements. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 29 (2), 99–117. doi:10.1016/0148-9062(92)92121-r

CrossRef Full Text | Google Scholar

Detournay, E., and Carbonell, R. (1997). Fracture-mechanics analysis of the breakdown process in minifracture or leakoff test. SPE. Prod. Fac. 12 (03), 195–199. doi:10.2118/28076-pa

CrossRef Full Text | Google Scholar

Enever, J. R., Cornet, F., and Roegiers, J. C. (1992). ISRM commission on interpretation of hydraulic fracture records. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 29, 69–72.

Google Scholar

Fjaer, E., Holt, R. M., Horsrud, P., Raaen, A. M., and Risnes, R. (2008). Mechanics of hydraulic fracturing” in developments in petroleum science. Amsterdam: Elsevier, 369–390.

Google Scholar

Guo, F., Morgenstern, N. R., and Scott, J. D. (1993). Interpretation of hydraulic fracturing breakdown pressure. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 30 (6), 617–626. doi:10.1016/0148-9062(93)91221-4

CrossRef Full Text | Google Scholar

Haimson, B., and Fairhurst, C. (1969). Hydraulic fracturing in porous-permeable materials. J. Pet. Technol. 21 (07), 811–817. doi:10.2118/2354-pa

CrossRef Full Text | Google Scholar

Haimson, B., and Fairhurst, C. (1967). Initiation and extension of hydraulic fractures in rocks. Spe. J. 7 (03), 310–318. doi:10.2118/1710-pa

CrossRef Full Text | Google Scholar

Hossain, M. M., Rahman, M. K., and Rahman, S. S. (2000). Hydraulic fracture initiation and propagation: Roles of wellbore trajectory, perforation and stress regimes. J. Pet. Sci. Eng. 27 (3-4), 129–149. doi:10.1016/s0920-4105(00)00056-5

CrossRef Full Text | Google Scholar

Hou, B., Zhang, R. X., Zeng, Y. J., Fu, W. N., Muhadasi, Y., and Chen, M. (2018). Analysis of hydraulic fracture initiation and propagation in deep shale formation with high horizontal stress difference. J. Pet. Sci. Eng. 170, 231–243. doi:10.1016/j.petrol.2018.06.060

CrossRef Full Text | Google Scholar

Huang, B. X., Chen, S. L., and Cheng, Q. Y. (2016). Basic problems of hydraulic fracturing for mining and control zone gas in coal seams. J. China Coal Soc. 41 (01), 128–137.

Google Scholar

Huang, B. X., Zhao, X. L., Chen, S. L., and Liu, J. W. (2017). Theory and technology of controlling hard roof with hydraulic fracturing in underground mining. Chin. J. Rock Mech. Eng. 36 (12), 2954–2970.

Google Scholar

Huang, B. X., Zhao, X. L., Xue, W. C., and Sun, T. Y. (2018). Experimental investigation on the impact of initial pore pressure on breakdown pressure of borehole radial fracture for unsaturated mortar hydraulic fracturing under true triaxial stress. J. Porous. Media 21 (11), 1041–1057. doi:10.1615/jpormedia.2018021402

CrossRef Full Text | Google Scholar

Huang, J. S., Griffiths, D. V., and Wong, S. W. (2012). Initiation pressure, location and orientation of hydraulic fracture. Int. J. Rock Mech. Min. 49, 59–67. doi:10.1016/j.ijrmms.2011.11.014

CrossRef Full Text | Google Scholar

Huang, Z. R. (1981). Crack initiation and expansion of hydraulic fracturing. Petroleum Explor. Dev. 7 (5), 44–74.

Google Scholar

Hubbert, M. K., and Willis, D. G. (1957). Mechanics of hydraulic fracturing. Trans 210 (01), 153–168. doi:10.2118/686-g

CrossRef Full Text | Google Scholar

Ito, T., and Hayashi, K. (1991). Physical background to the breakdown pressure in hydraulic fracturing tectonic stress measurements. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 28 (4), 285–293. doi:10.1016/0148-9062(91)90595-d

CrossRef Full Text | Google Scholar

Jeffrey, R. G. (1989). “The combined effect of fluid lags and fracture toughness on hydraulic fracture propagation,” in Low Permeability Reservoirs Symposium, March 68, 1989, Denver, Colorado, USA. SPE-18957-MS.

Google Scholar

King, G. E. (2012). “Hydraulic fracturing 101: What every representative, environmentalist, regulator, reporter, investor, university researcher, neighbor and engineer should know about estimating frac risk and improving frac performance in unconventional gas and oil wells,” in SPE Hydraulic Fracturing Technology Conference, February 68, 2012, The Woodlands, Texas, USA. SPE-152596-MS. doi:10.2118/152596-MS

CrossRef Full Text | Google Scholar

Lenoach, B. (1995). The crack tip solution for hydraulic fracturing in a permeable solid. J. Mech. Phys. Solids. 43 (7), 1025–1043. doi:10.1016/0022-5096(95)00026-f

CrossRef Full Text | Google Scholar

Li, C. L., and Kong, X. Y. (2000). A theoretical study on rock breakdown pressure calculation equations of fracturing process. Oil Drill. Prod. Technol. 22 (2), 54–56.

Google Scholar

Li, Y. W., Yang, S., Zhao, W. C., Li, W., and Zhang, J. (2018). Experimental of hydraulic fracture propagation using fixed-point multistage fracturing in a vertical well in tight sandstone reservoir. J. Pet. Sci. Eng. 171, 704–713. doi:10.1016/j.petrol.2018.07.080

CrossRef Full Text | Google Scholar

Lockner, D., and Byerlee, J. D. (1977). Hydrofracture in Weber Sandstone at high confining pressure and differential stress. J. Geophys. Res. 82 (14), 2018–2026. doi:10.1029/jb082i014p02018

CrossRef Full Text | Google Scholar

Lv, S. F., Wang, S. W., Liu, H. T., Li, R., and Dong, Q. X. (2020). Analysis of the influence of natural fracture system on hydraulic fracture propagation morphology in coal reservoir. J. China Coal Soc. 45 (07), 2590–2601.

Google Scholar

Olovyanny, A. G. (2005). Mathematical modeling of hydraulic fracturing in coal seams. J. Min. Sci. 41 (1), 61–67. doi:10.1007/s10913-005-0064-6

CrossRef Full Text | Google Scholar

Takatoshi, I. (2008). Effect of pore pressure gradient on fracture initiation in fluid saturated porous media: Rock. Eng. Fract. Mech. 75, 1753–1762. doi:10.1016/j.engfracmech.2007.03.028

CrossRef Full Text | Google Scholar

Tang, C. A., Tham, L. G., Lee, P. K. K., Yang, T., and Li, L. (2002). Coupled analysis of flow, stress and damage (FSD) in rock failure. Int. J. Rock Mech. Min. 39 (4), 477–489. doi:10.1016/s1365-1609(02)00023-0

CrossRef Full Text | Google Scholar

Wu, Y. Z., and Kang, H. P. (2017). Pressure relief mechanism and experiment of directional hydraulic fracturing in reused coal pillar roadway. J. China Coal Soc. 42 (05), 1130–1137.

Google Scholar

Yang, Y. K., Xiao, C. F., Wu, G., and Qiu, X. D. (1993). Hydrofracturing breakdown modes under different in-situ stress states. J. Chongqing Univ. 16 (03), 30–35.

Google Scholar

Yao, J., Sun, Z. U., Zhang, K., Zeng, Q. D., and Yan, X. (2016). Scientific engineering problems and development trends in unconventional oil and gas reservoirs. Petroleum Sci. Bull. 1 (01), 128–142.

Google Scholar

Zhang, X., Jeffrey, R. G., Bunger, A. P., and Thiercelin, M. (2011). Initiation and growth of a hydraulic fracture from a circular wellbore. Int. J. Rock Mech. Min. 48 (6), 984–995. doi:10.1016/j.ijrmms.2011.06.005

CrossRef Full Text | Google Scholar

Zhang, Z. X., Wang, H. T., Deng, B. Z., Li, M. H., and Zhang, D. M. (2018). Field investigation of hydraulic fracturing in coal seams and its enhancement for methane extraction in the Southeast Sichuan Basin, China. Energies 11 (12), 3451. doi:10.3390/en11123451

CrossRef Full Text | Google Scholar

Zhao, X. L. (2019). The Mechanism of pore pressure gradient effect and the fracturing effect induced by disturbing stress during hydrofracturing. [PhD thesis]. Xuzhou: China University of Mining and Technology.

Google Scholar